Effects of Reduced Frequency on the Aerodynamic Characteristics of a Pitching Airfoil at Moderate Reynolds Numbers
Abstract
1. Introduction
2. Methodology
Numerical Methods and Validation
3. Results
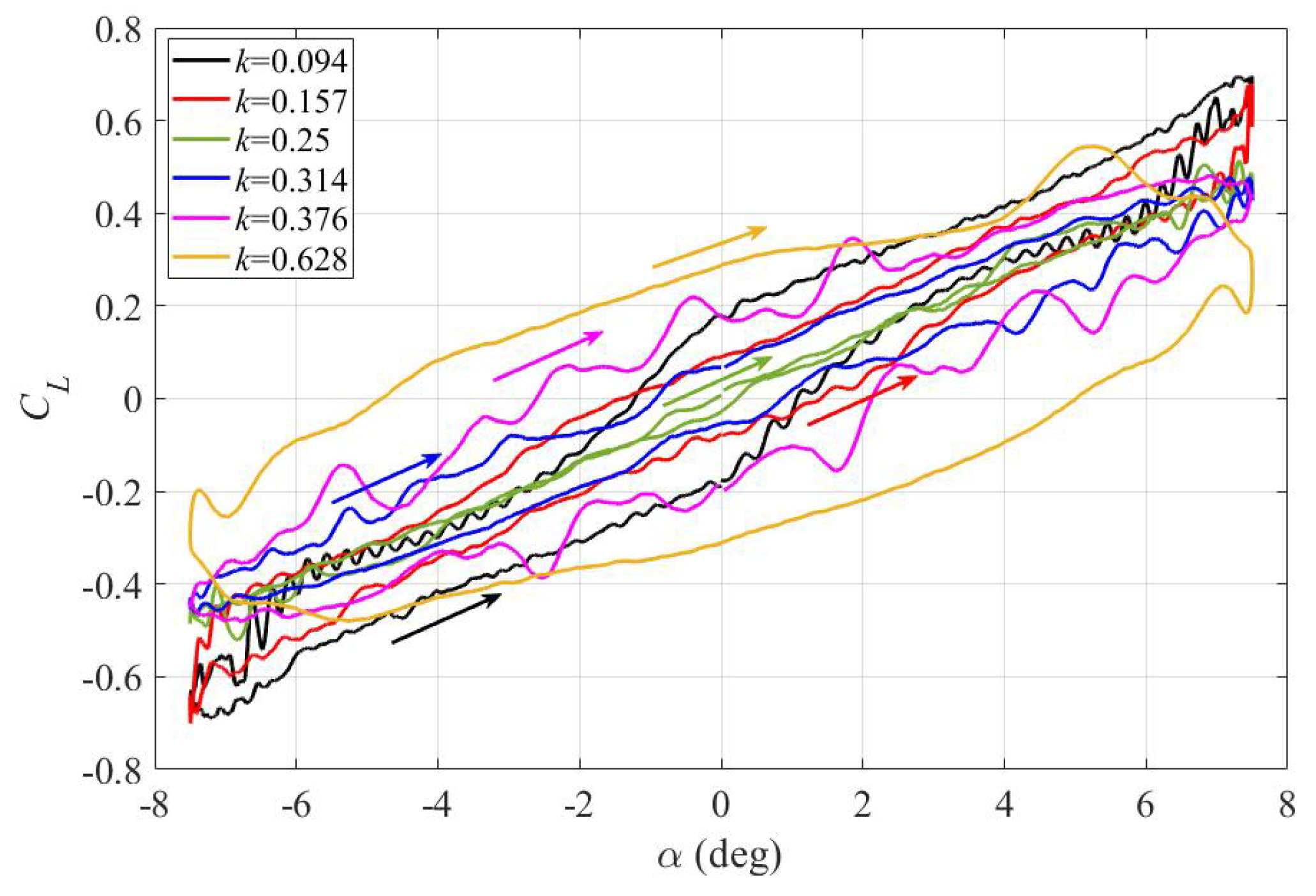
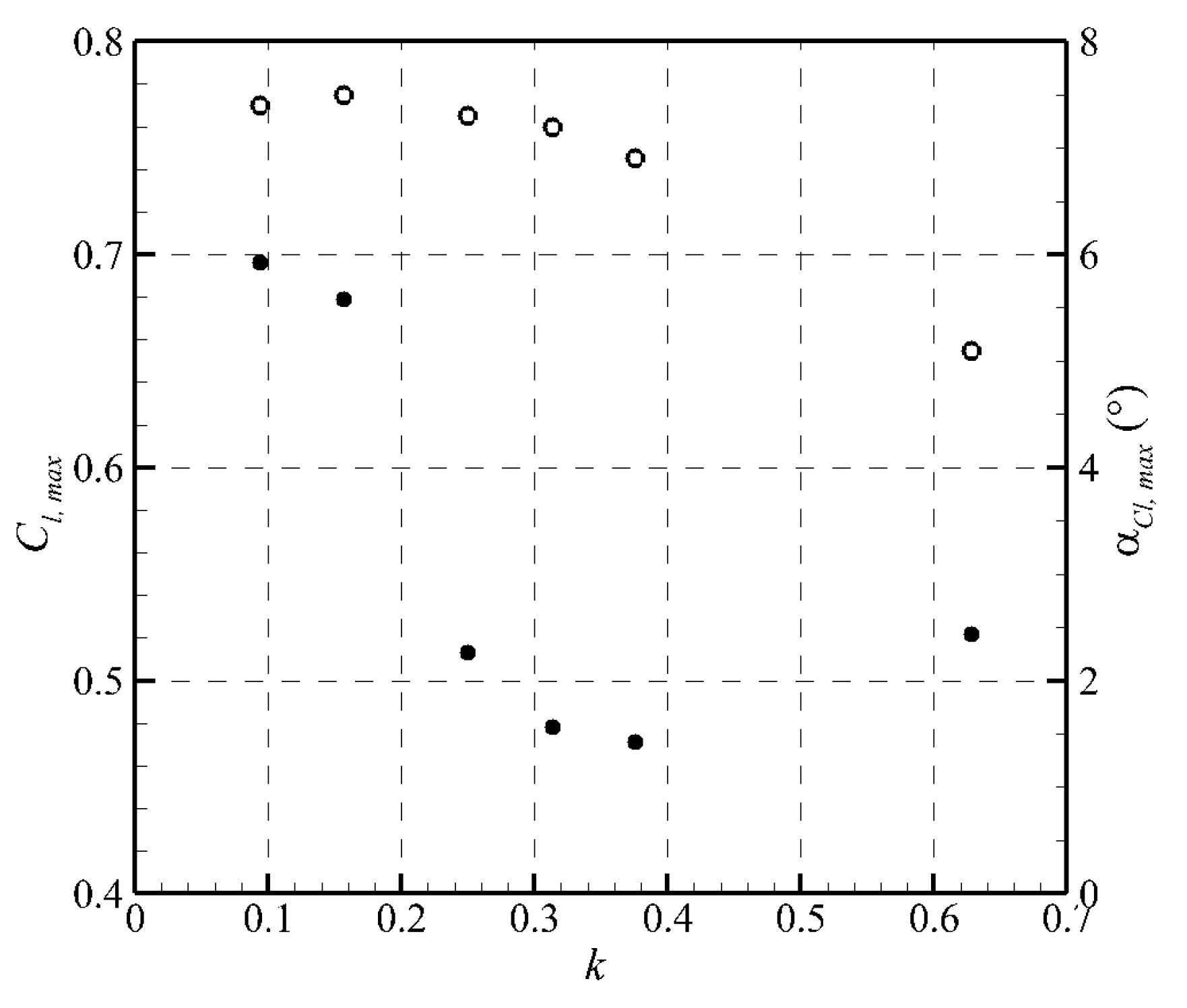
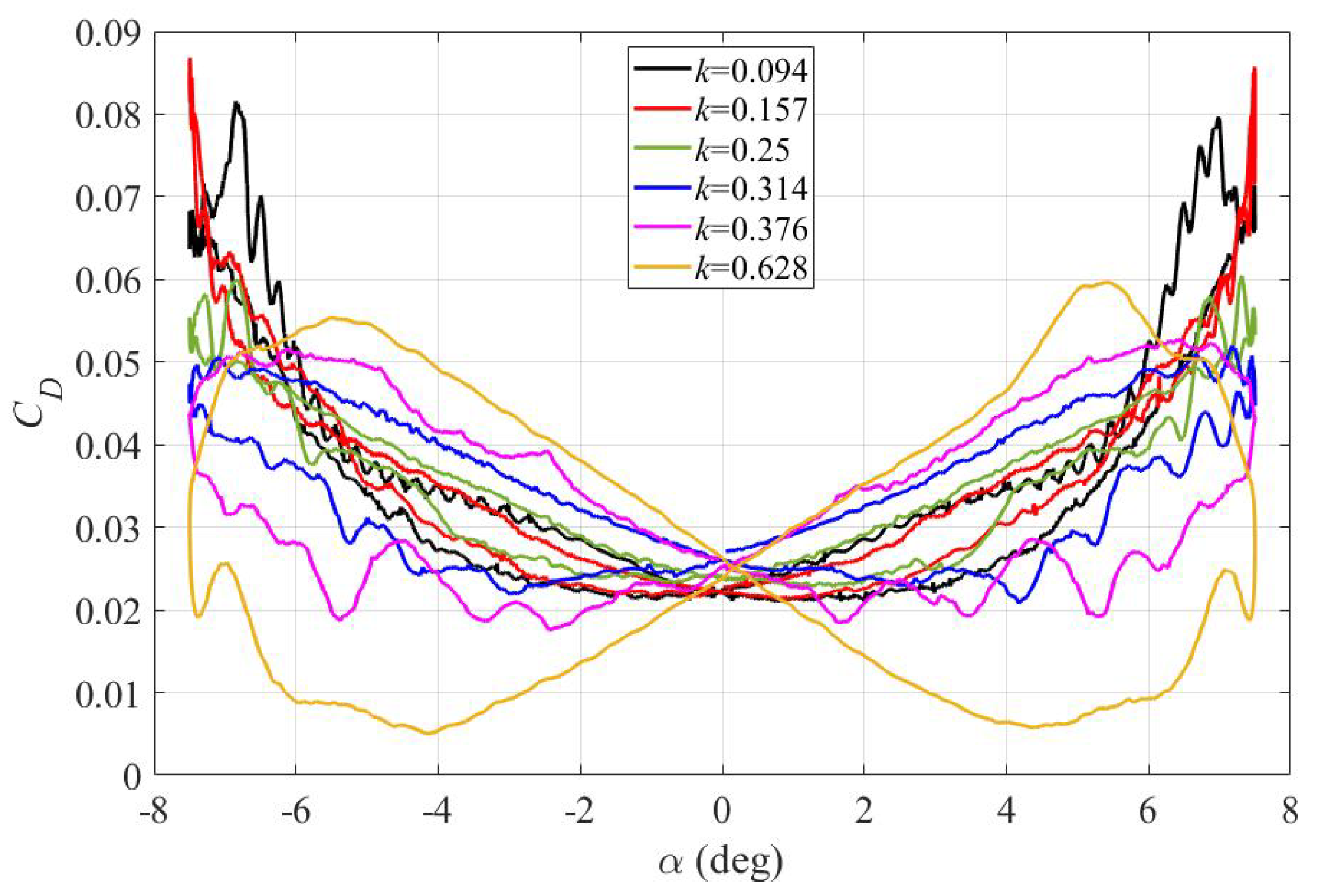
3.1. Aerodynamic Loads
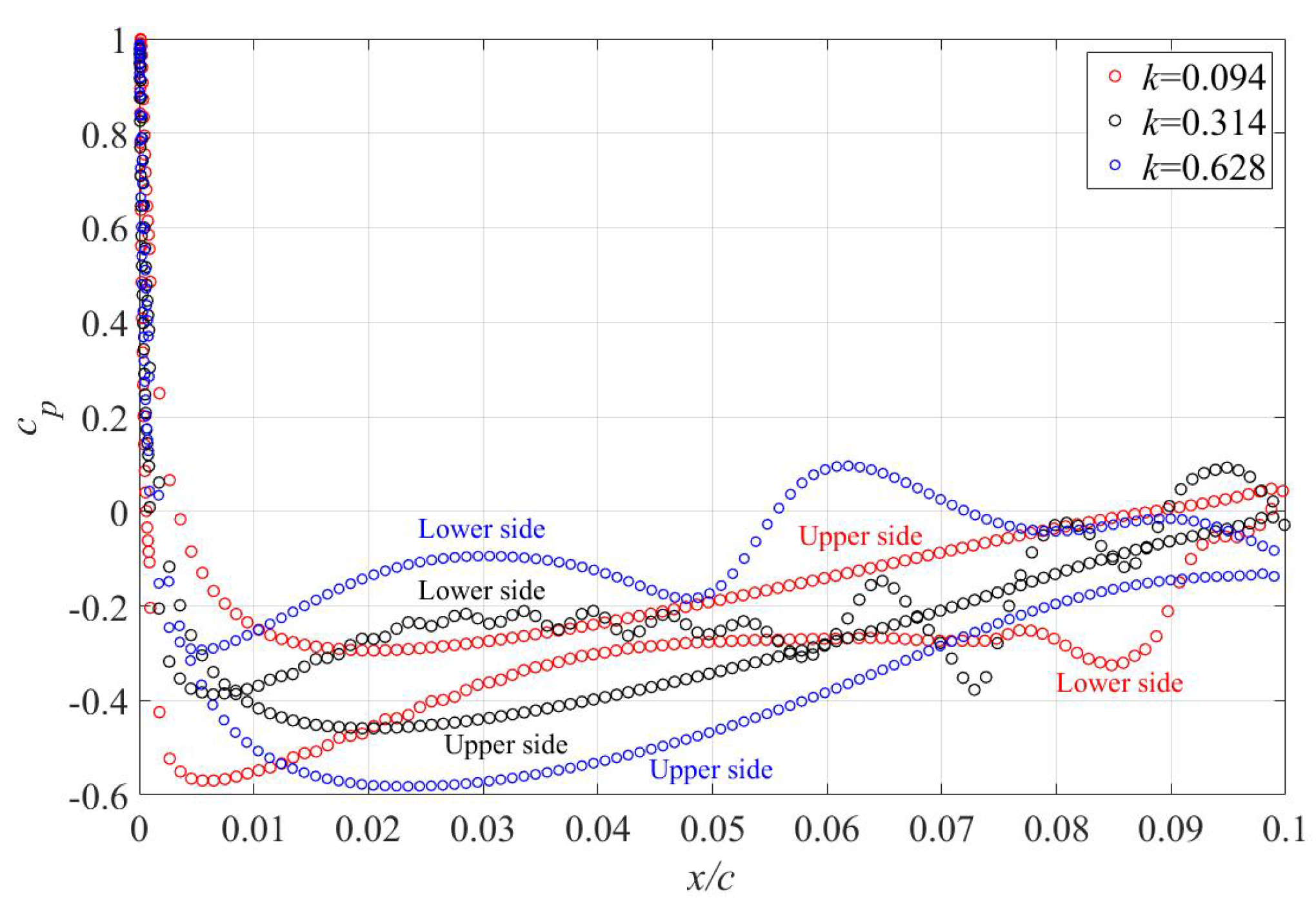
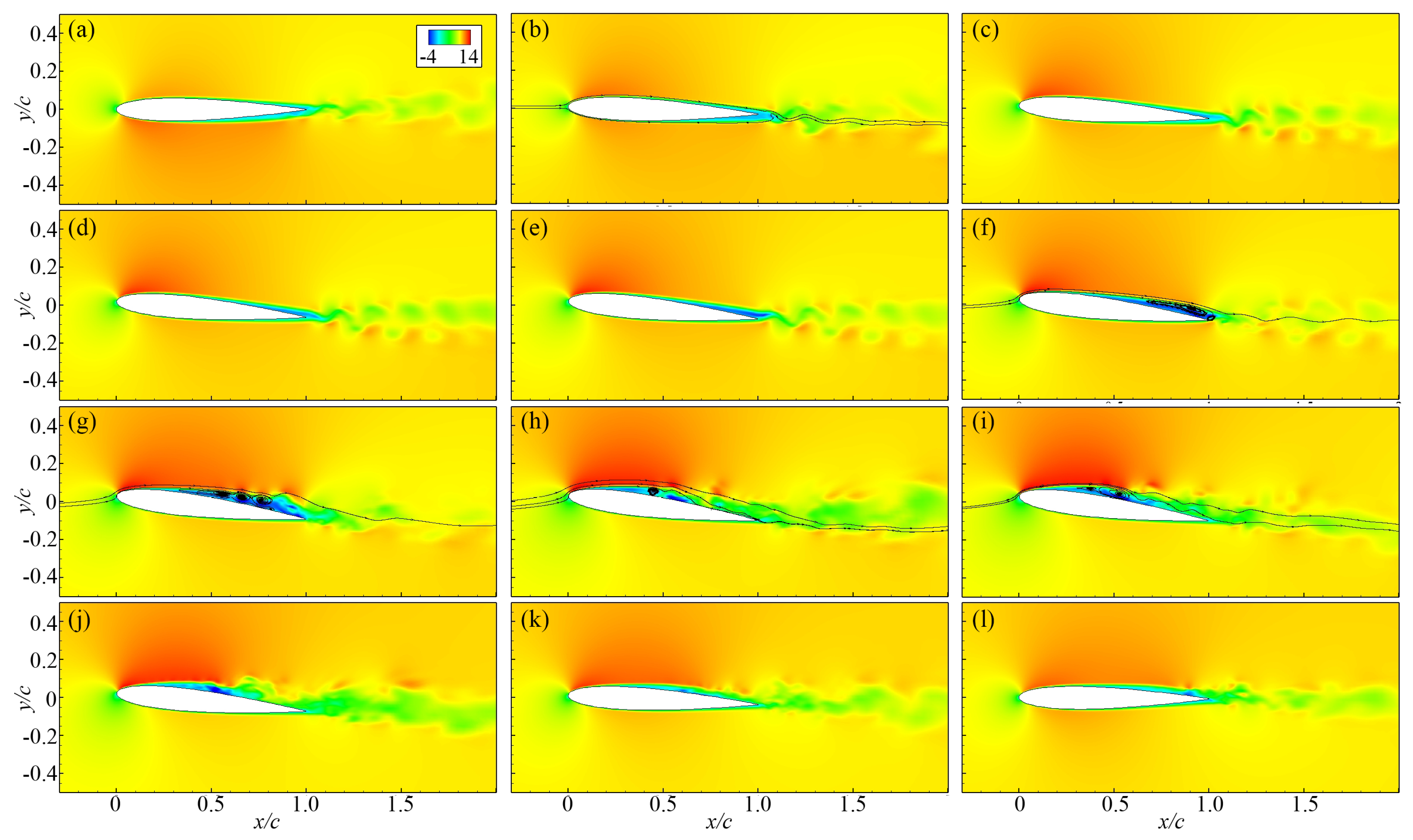
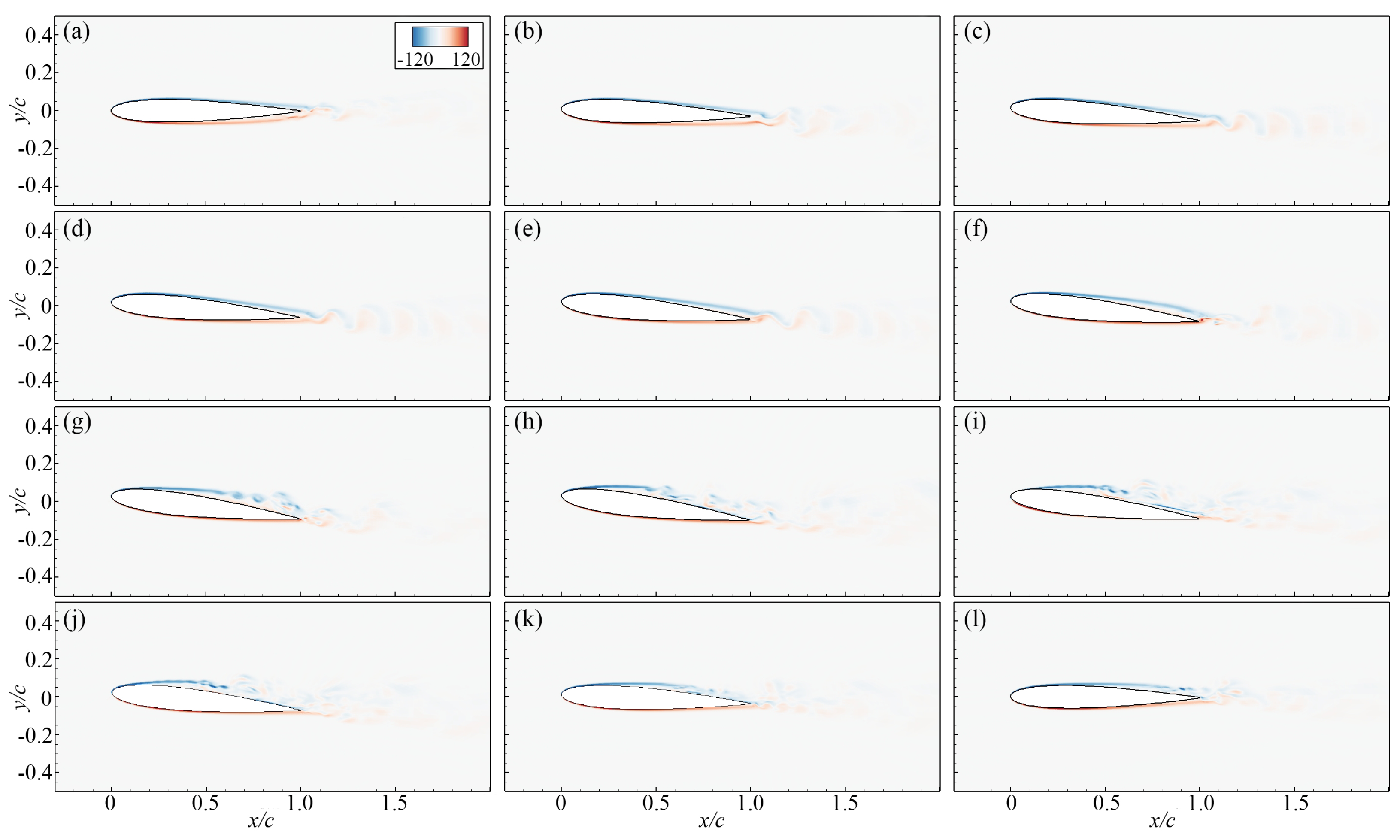
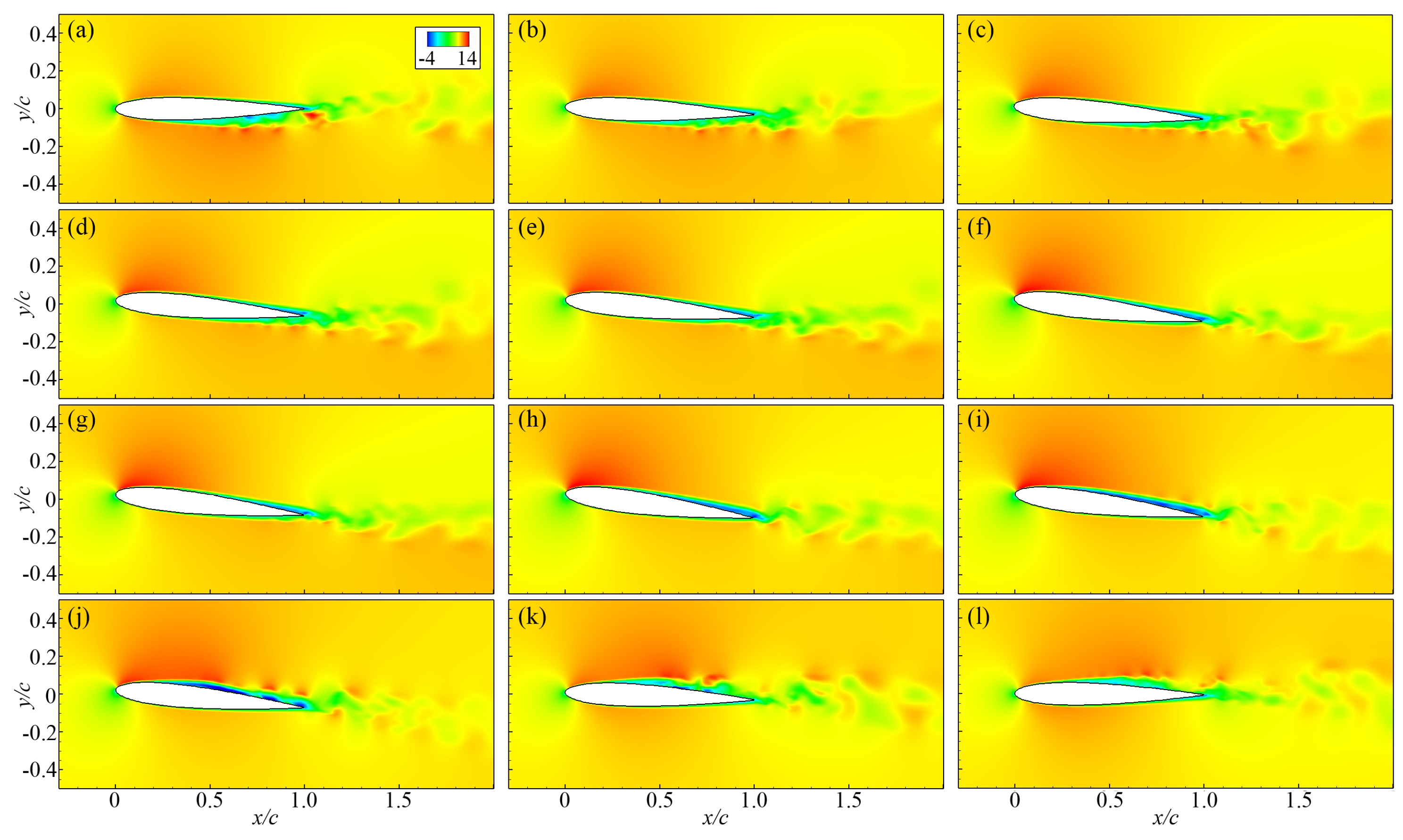
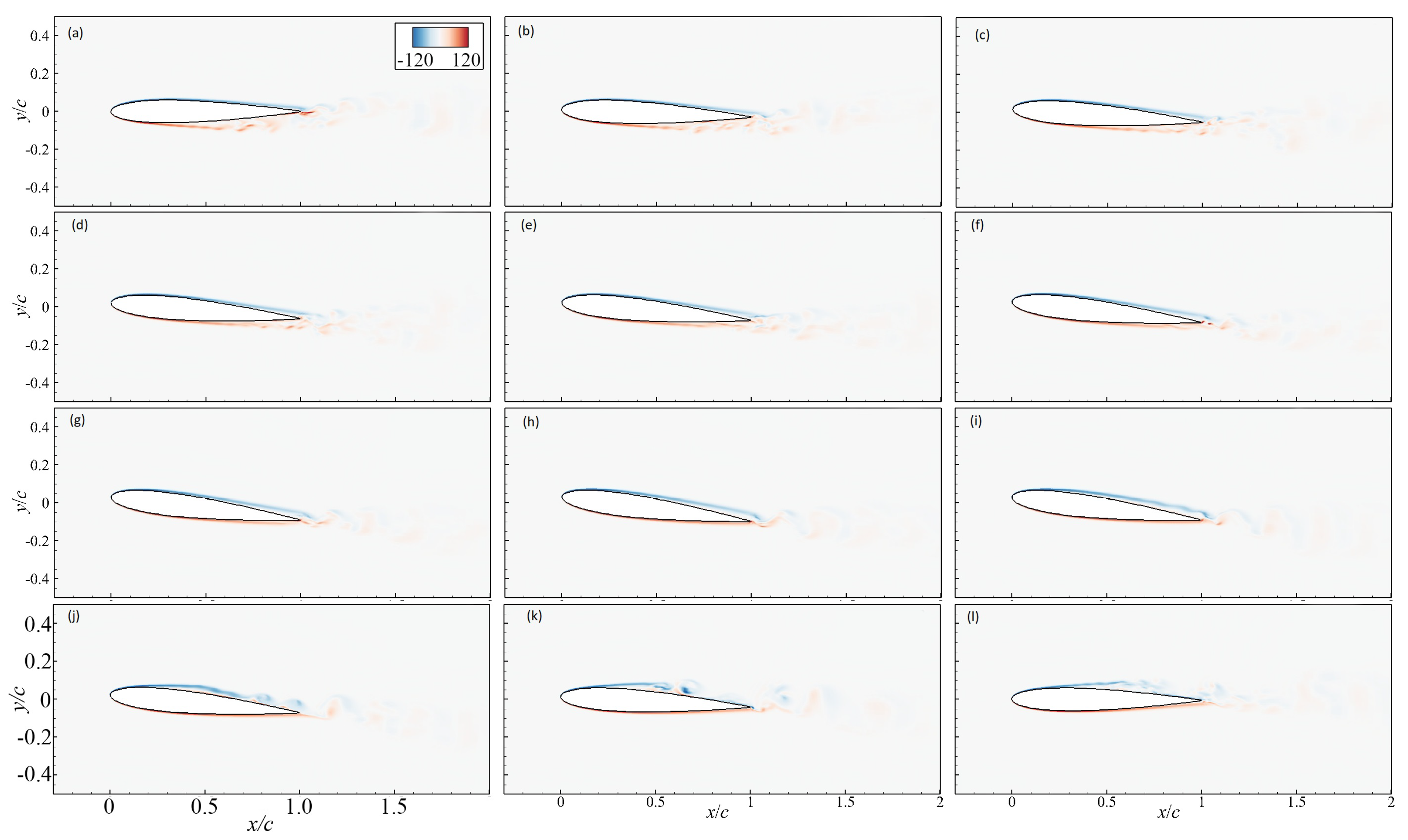
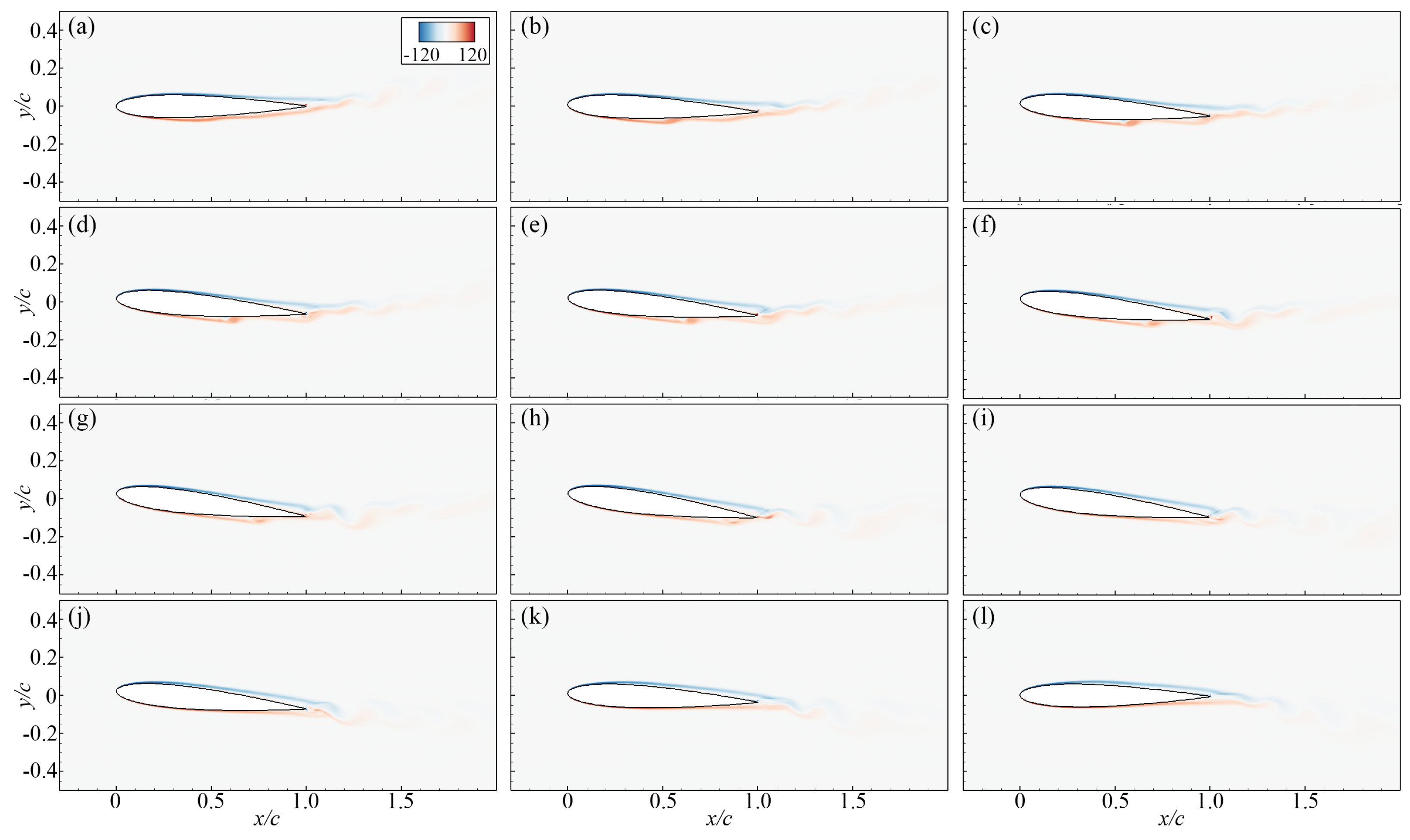
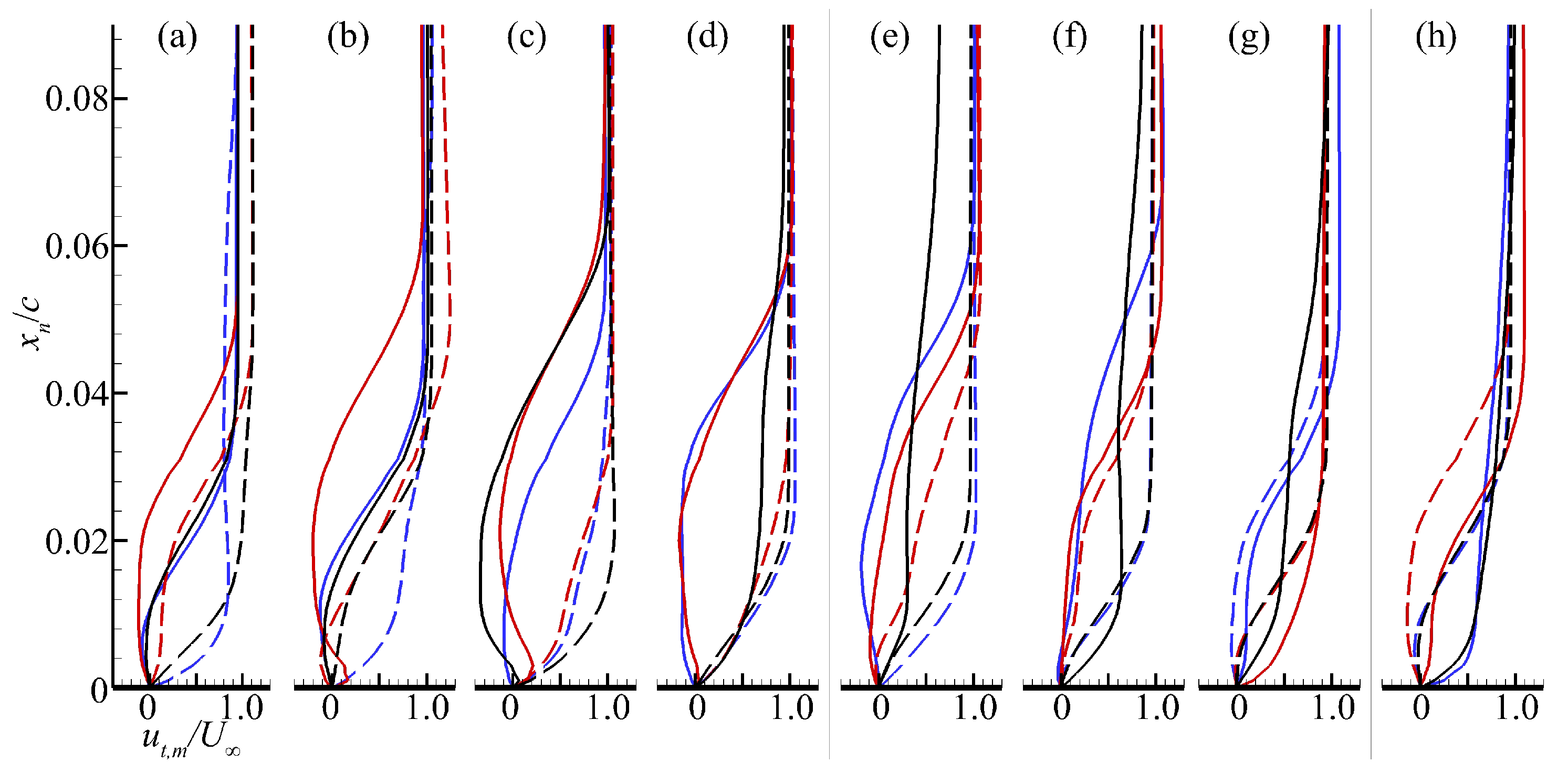
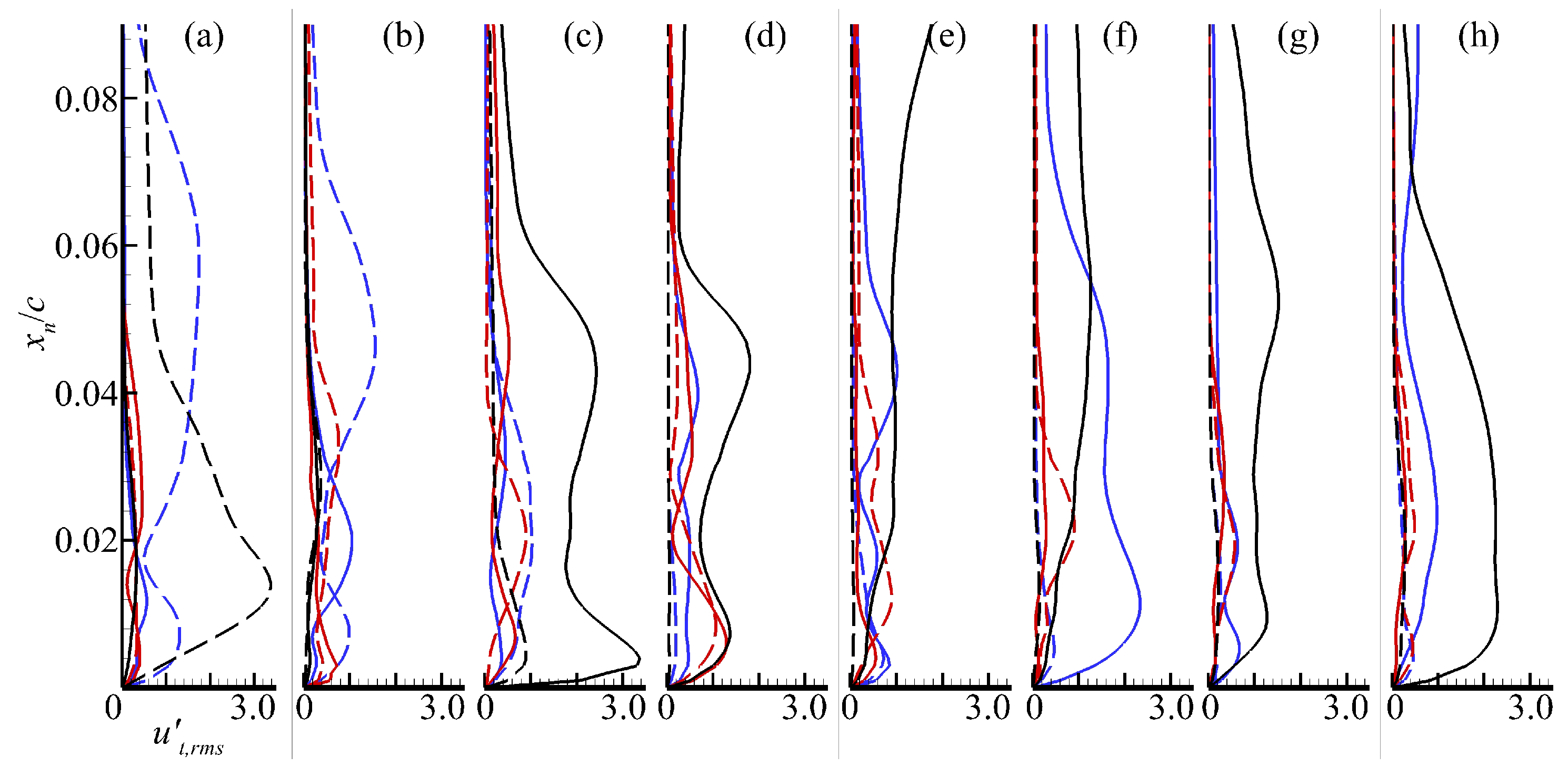
3.2. Flow Pattern near the Pitching Wing
4. Conclusions and Future Work
- As the reduced frequency increases from 0.094 to 0.628, the maximum lift coefficient shows a decreasing trend, and the pitching angle at which it is achieved becomes smaller. In one pitching cycle, the circling direction turns from counter-clockwise to clockwise as the reduced frequency exceeds 0.25; consequently, signs of the zero-angle lift coefficient change correspondingly.
- Besides the phase-lag effect, the pitching motion induces combinations of flow profiles on the upper and lower sides that are not present on a static airfoil at the corresponding Reynolds number, and it is more obvious as the reduced frequency increases. This phenomenon has been rarely reported in previous research. This suggests that the pitching motion not only delays the onset of certain flow patterns, but also induces new observations that are not present on the static airfoil.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, H.; Lee, D.-J. Rotor interactional effects on aerodynamic and noise characteristics of a small multirotor unmanned aerial vehicle. Phys. Fluids 2020, 32, 047107. [Google Scholar] [CrossRef]
- Zhao, B.; Li, B.; Cui, W.; Huang, C.; Zhou, T. Approximate entropy identification of flow unsteadiness and surge precursor in both subsonic centrifugal and axial compressors. Phys. Fluids 2025, 37, 027144. [Google Scholar] [CrossRef]
- McCroskey, W.J.; Carr, L.W.; McAlister, K.W. Dynamic stall experiments on oscillating airfoils. AIAA J. 1976, 14, 57–63. [Google Scholar] [CrossRef]
- Intaratep, N.; Alexander, W.N.; Devenport, W.J.; Grace, S.M.; Dropkin, A. Experimental study of quadcopter acoustics and performance at static thrust conditions. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016. [Google Scholar]
- Knoller, R. Die Gesetze des Luftwiderstandes; Flug- und Motortechnik: Wien, Austria, 1909; Volume 3. [Google Scholar]
- Betz, A. Ein beitrag zur erklaerung des segelfluges. Z. Flugtech. Motorluftsch. 1912, 3, 269–270. [Google Scholar]
- Garrick, I. Propulsion of a Flapping and Oscillating Airfoil; Tech. Rep. NACA-TR-567; NACA: Washington, DC, USA, 1937. [Google Scholar]
- McAlister, K.; Pucci, S.; McCroskey, W.; Carr, L. An Experimental Study of Dynamic Stall on Advanced Airfoil Section; Volume 2: Pressure and Force Data; Tech. Rep. TM-84345-VOL-2; NASA: Washington, DC, USA, 1982. [Google Scholar]
- Sheng, W.; Galbraith, R.; Coton, F. Prediction of dynamic stall onset for oscillatory low-speed airfoils. J. Fluids Eng. 2008, 130, 101204. [Google Scholar] [CrossRef]
- Rival, D.; Tropea, C. Characteristics of pitching and plunging airfoils under dynamic-stall conditions. J. Aircr. 2010, 47, 80–86. [Google Scholar] [CrossRef]
- Carr, L.W.; McAlister, K.W.; McCroskey, W.J. Analysis of the Development of Dynamic Stall Based on Oscillating Airfoil Experiments; Tech. Rep. TN-D-8382; NASA: Washington, DC, USA, 1977. [Google Scholar]
- Carr, L.W. Progress in analysis and prediction of dynamic stall. J. Aircr. 1988, 25, 6–17. [Google Scholar] [CrossRef]
- Wernert, P.; Geissler, W.; Raffel, M.; Kompenhans, J. Experimental and numerical investigations of dynamic stall on a pitching airfoil. AIAA J. 1996, 34, 982–989. [Google Scholar] [CrossRef]
- Sarkar, S.; Venkatraman, K. Influence of pitching angle of incidence on the dynamic stall behavior of a symmetric airfoil. Eur. J. Mech. B Fluids 2008, 27, 219–238. [Google Scholar] [CrossRef]
- Guillaud, N.; Balarac, G.; Goncalvès, E. Large eddy simulations on a pitching airfoil: Analysis of the reduced frequency influence. Comput. Fluids 2018, 161, 1–13. [Google Scholar] [CrossRef]
- Negi, P.S.; Vinuesa, R.; Hanifi, A.; Schlatter, P.; Henningson, D.S. Unsteady aerodynamic effects in small-amplitude pitch oscillations of an airfoil. Int. J. Heat Fluid Flow 2018, 71, 378–391. [Google Scholar] [CrossRef]
- Kim, D.-H.; Chang, J.-W. Unsteady boundary layer for a pitching airfoil at low Reynolds numbers. J. Mech. Sci. Technol. 2010, 24, 429–440. [Google Scholar] [CrossRef]
- Kim, D.-H.; Chang, J.-W. Low-Reynolds-number effect on the aerodynamic characteristics of a pitching NACA0012 airfoil. Aerosp. Sci. Technol. 2014, 32, 162–168. [Google Scholar] [CrossRef]
- Kim, D.-H.; Chang, J.-W.; Sohn, M.H. Unsteady aerodynamic characteristics depending on reduced frequency for a pitching NACA0012 airfoil at Rec=2.3×104. Int. J. Aeronaut. Space Sci. 2017, 18, 8–16. [Google Scholar] [CrossRef]
- Carmichael, B. Low Reynolds Number Airfoil Survey; Tech. Rep. CR-165803-VOL-1; NASA: Washington, DC, USA, 1981; Volume 1. [Google Scholar]
- Zhou, T.; Sun, Y.; Fattah, R.; Zhang, X.; Huang, X. An experimental study of trailing edge noise from a pitching airfoil. J. Acoust. Soc. Am. 2019, 145, 2009–2021. [Google Scholar] [CrossRef]
- Zhou, T.; Zhang, X.; Zhong, S. An experimental study of trailing edge noise from a heaving airfoil. J. Acoust. Soc. Am. 2020, 147, 4020–4031. [Google Scholar] [CrossRef]
- Zhou, T.; Zhong, S.; Fang, Y. Trailing-edge boundary layer characteristics of a pitching airfoil at a low Reynolds number. Phys. Fluids 2021, 33, 033605. [Google Scholar] [CrossRef]
- Camacho, E.A.; Neves, F.; Silva, A.R.; Barata, J.M. Plunging airfoil: Reynolds number and angle of attack effects. Aerospace 2021, 8, 216. [Google Scholar] [CrossRef]
- Zhao, M.; Zhao, Y.; Liu, Z.; Du, J. Proper orthogonal decomposition analysis of flow characteristics of an airfoil with leading edge protuberances. AIAA J. 2019, 57, 2710–2721. [Google Scholar] [CrossRef]
- Zhao, M.; Zhao, Y.; Liu, Z. Dynamic mode decomposition analysis of flow characteristics of an airfoil with leading edge protuberances. Aerosp. Sci. Technol. 2020, 98, 105684. [Google Scholar] [CrossRef]
- Piomelli, U.; Balaras, E. Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 2002, 34, 349–374. [Google Scholar] [CrossRef]
- Cao, H.; Zhang, M.; Cai, C.; Zhang, Z. Flow topology and noise modeling of trailing edge serrations. Appl. Acoust. 2020, 168, 107423. [Google Scholar] [CrossRef]
- Zhao, M.; Xu, L.; Tang, Z.; Zhang, X.; Zhao, B.; Liu, Z.; Wei, Z. Onset of dynamic stall of tubercled wings. Phys. Fluids 2021, 33, 081909. [Google Scholar] [CrossRef]
- Miklosovic, D.; Murray, M.; Howle, L. Experimental evaluation of sinusoidal leading edges. J. Aircr. 2007, 44, 1404–1408. [Google Scholar] [CrossRef]
- Pröbsting, S.; Serpieri, J.; Scarano, F. Experimental investigation of aerofoil tonal noise generation. J. Fluid Mech. 2014, 747, 656–687. [Google Scholar] [CrossRef]
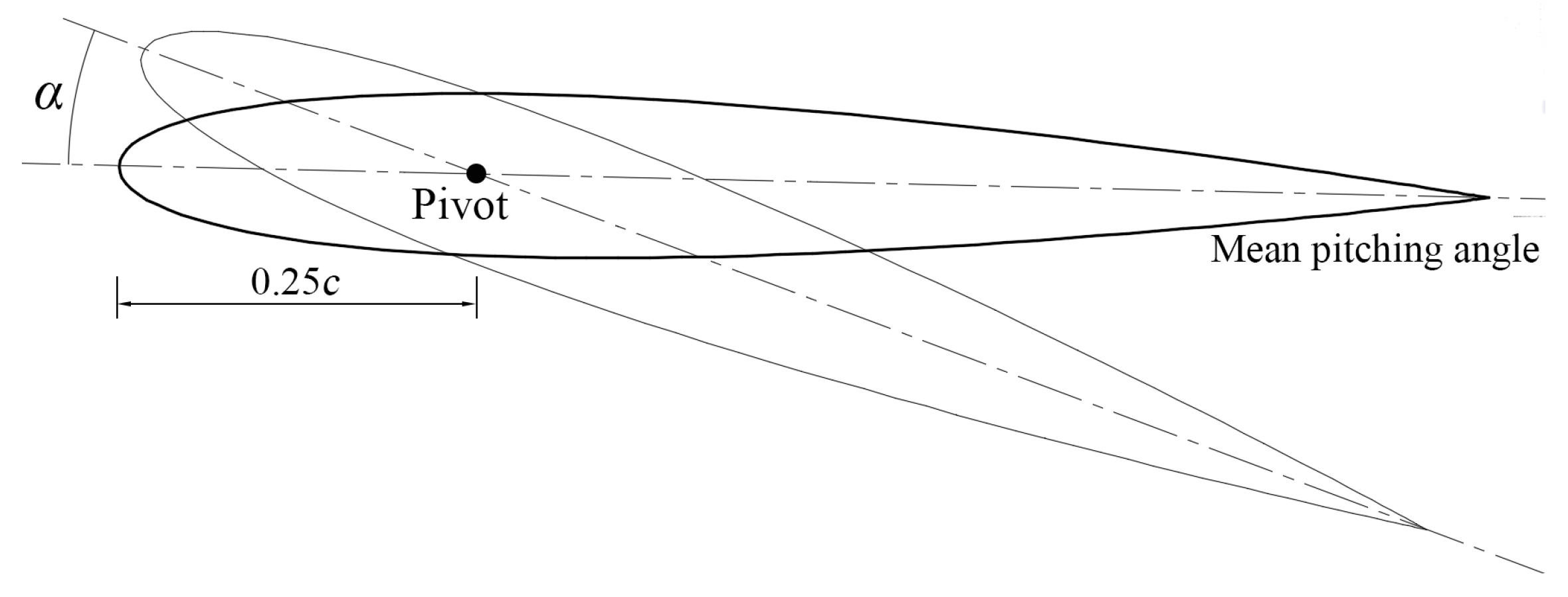




| Case Index | S1 | S2 | S3 | S4 | P1 | P2 | P3 | P4 | P5 | P6 |
|---|---|---|---|---|---|---|---|---|---|---|
| Re | ||||||||||
| (Hz) | - | 3 | 5 | 8 | 10 | 12 | 20 | |||
| k | - | 0.094 | 0.157 | 0.25 | 0.314 | 0.376 | 0.628 | |||
| (°) | - | 7.5 | ||||||||
| (°) | - | 0 | ||||||||
| AoA (°) | 0 | 2 | 5 | 7.5 | - | |||||
| Mesh Index | Number of Cells | Number of Cells on Foil | Lift Coefficient |
|---|---|---|---|
| Mesh #1 | 2,681,100 | 6400 | 0.477 |
| Mesh #2 | 6,288,540 | 13,000 | 0.479 |
| Mesh #3 | 9,739,380 | 18,000 | 0.479 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, T.; Cao, H.; Zhao, B. Effects of Reduced Frequency on the Aerodynamic Characteristics of a Pitching Airfoil at Moderate Reynolds Numbers. Aerospace 2025, 12, 457. https://doi.org/10.3390/aerospace12060457
Zhou T, Cao H, Zhao B. Effects of Reduced Frequency on the Aerodynamic Characteristics of a Pitching Airfoil at Moderate Reynolds Numbers. Aerospace. 2025; 12(6):457. https://doi.org/10.3390/aerospace12060457
Chicago/Turabian StyleZhou, Teng, Huijing Cao, and Ben Zhao. 2025. "Effects of Reduced Frequency on the Aerodynamic Characteristics of a Pitching Airfoil at Moderate Reynolds Numbers" Aerospace 12, no. 6: 457. https://doi.org/10.3390/aerospace12060457
APA StyleZhou, T., Cao, H., & Zhao, B. (2025). Effects of Reduced Frequency on the Aerodynamic Characteristics of a Pitching Airfoil at Moderate Reynolds Numbers. Aerospace, 12(6), 457. https://doi.org/10.3390/aerospace12060457






