Simulations and Analyses of the Influence of a Vacuum Back-Pressure Environment on Laser Ablation Thrusters
Abstract
1. Introduction
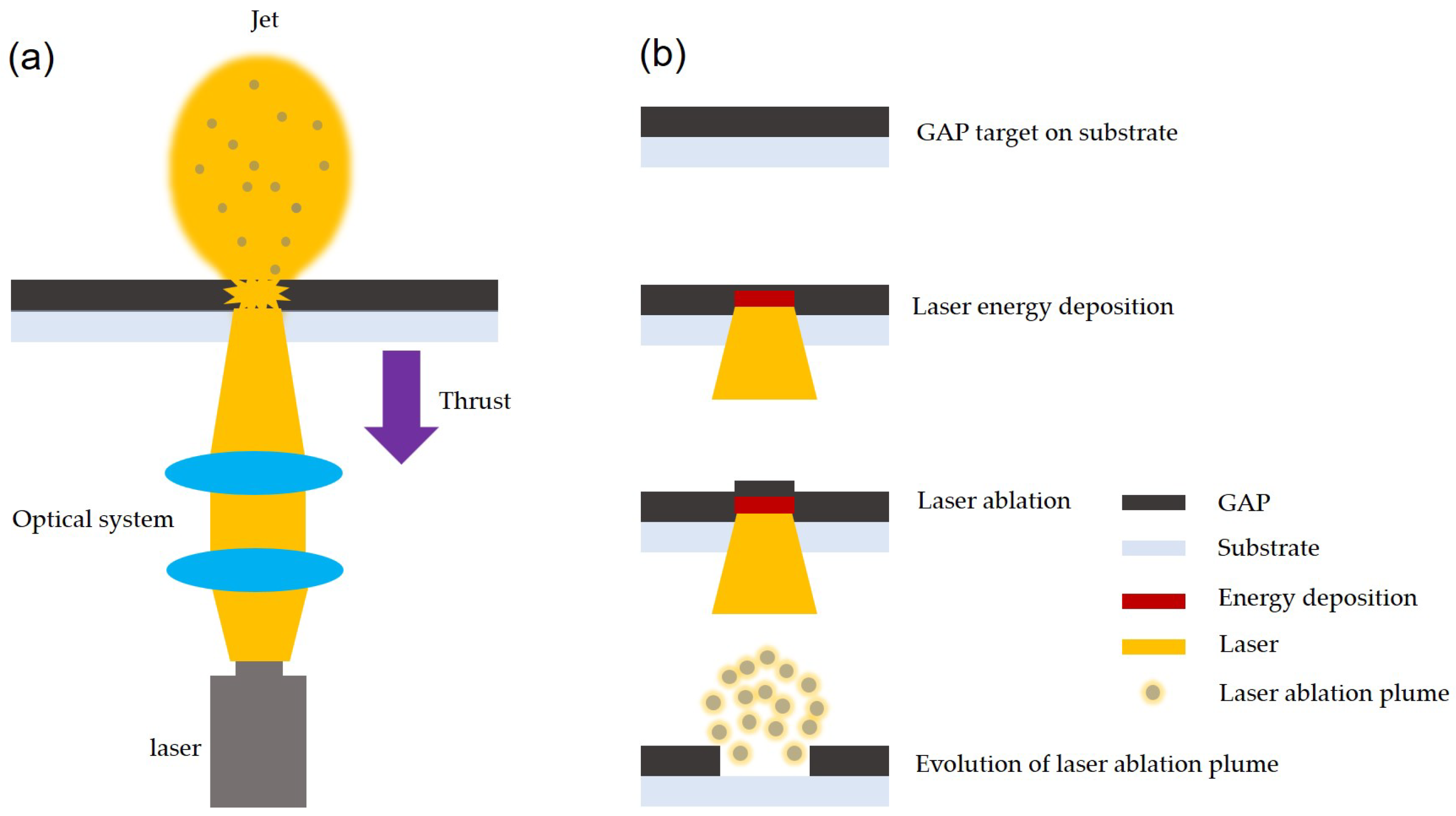
2. Model Analysis of the Ignition Process of a Laser Thruster
2.1. Model of Laser Thruster Ignition
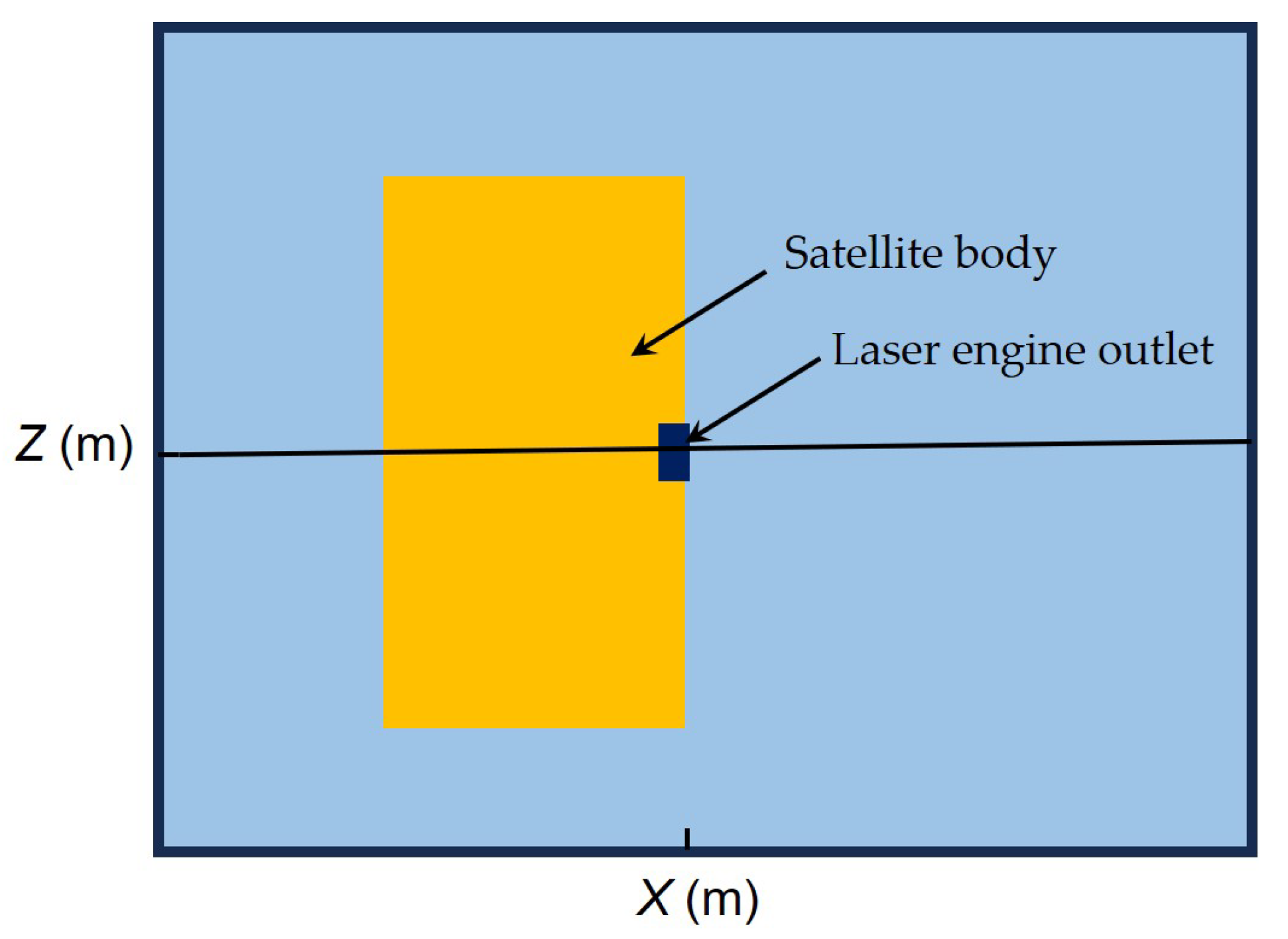
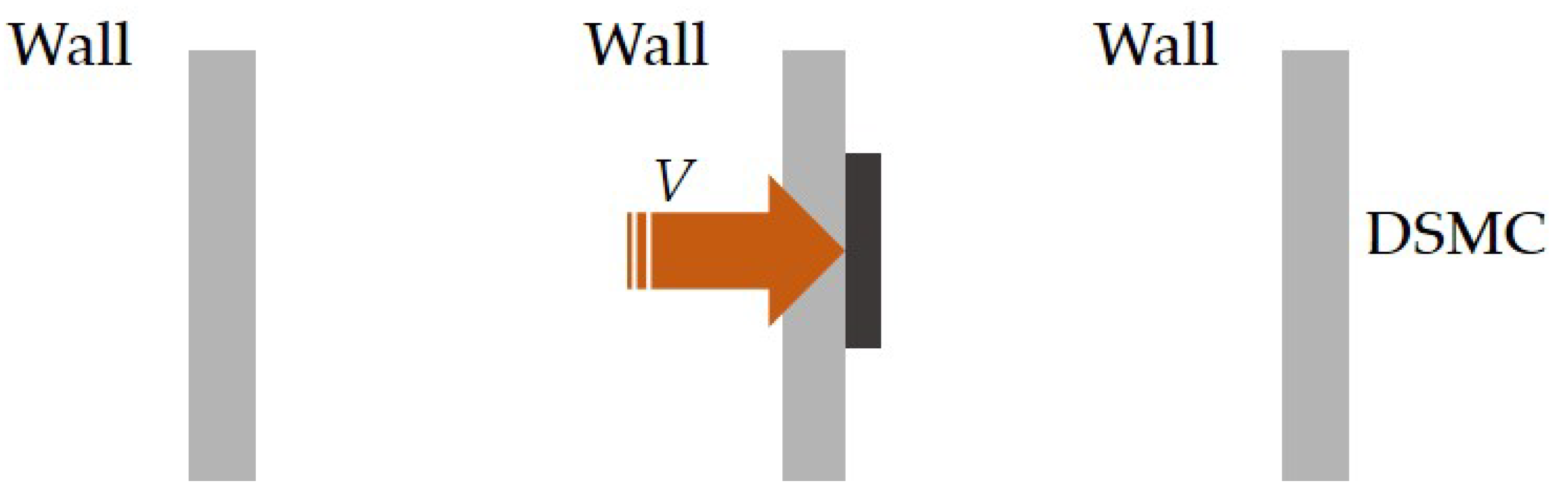
2.2. Simulation Analysis Method
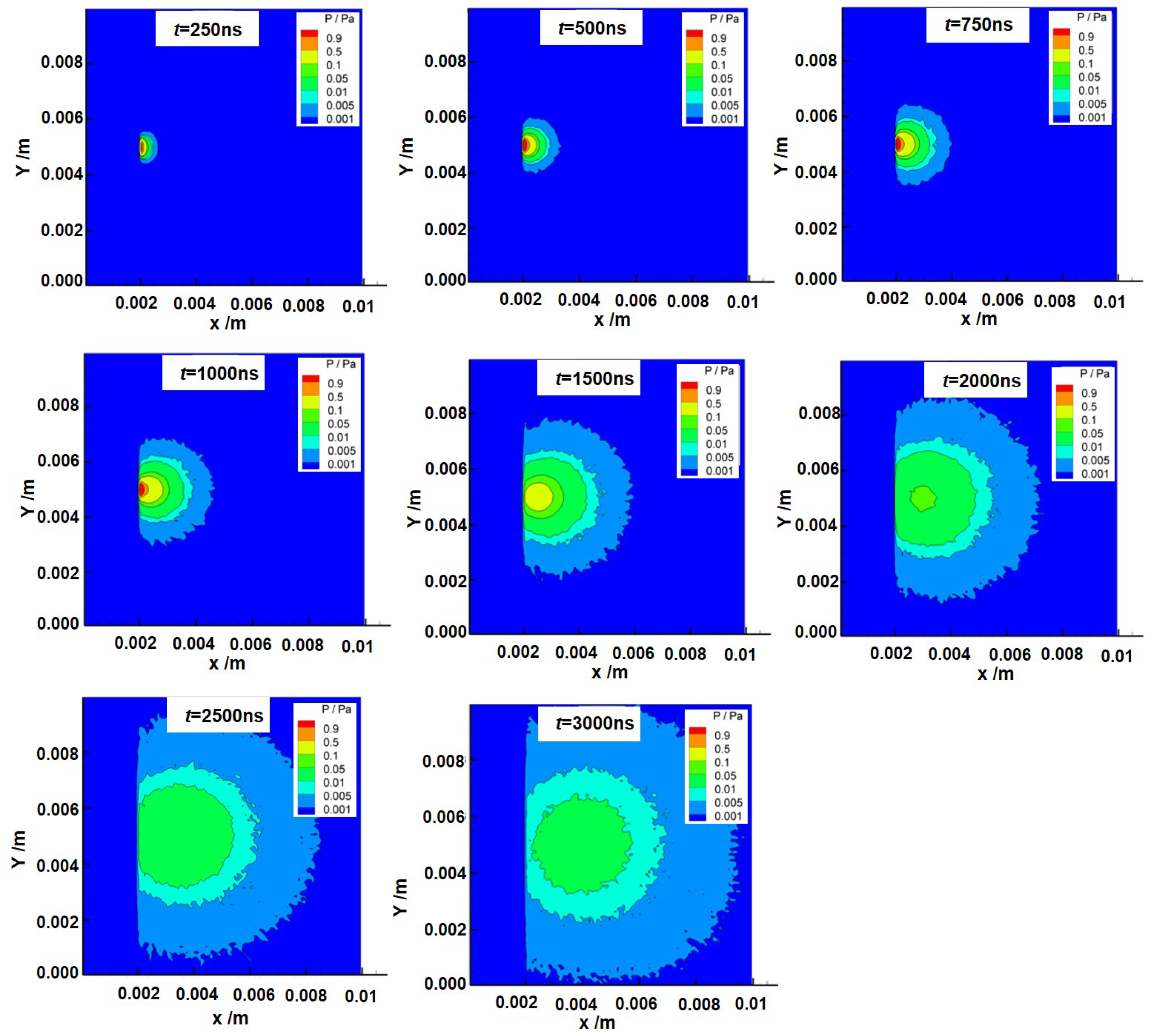
3. Simulation Test Results and Discussion
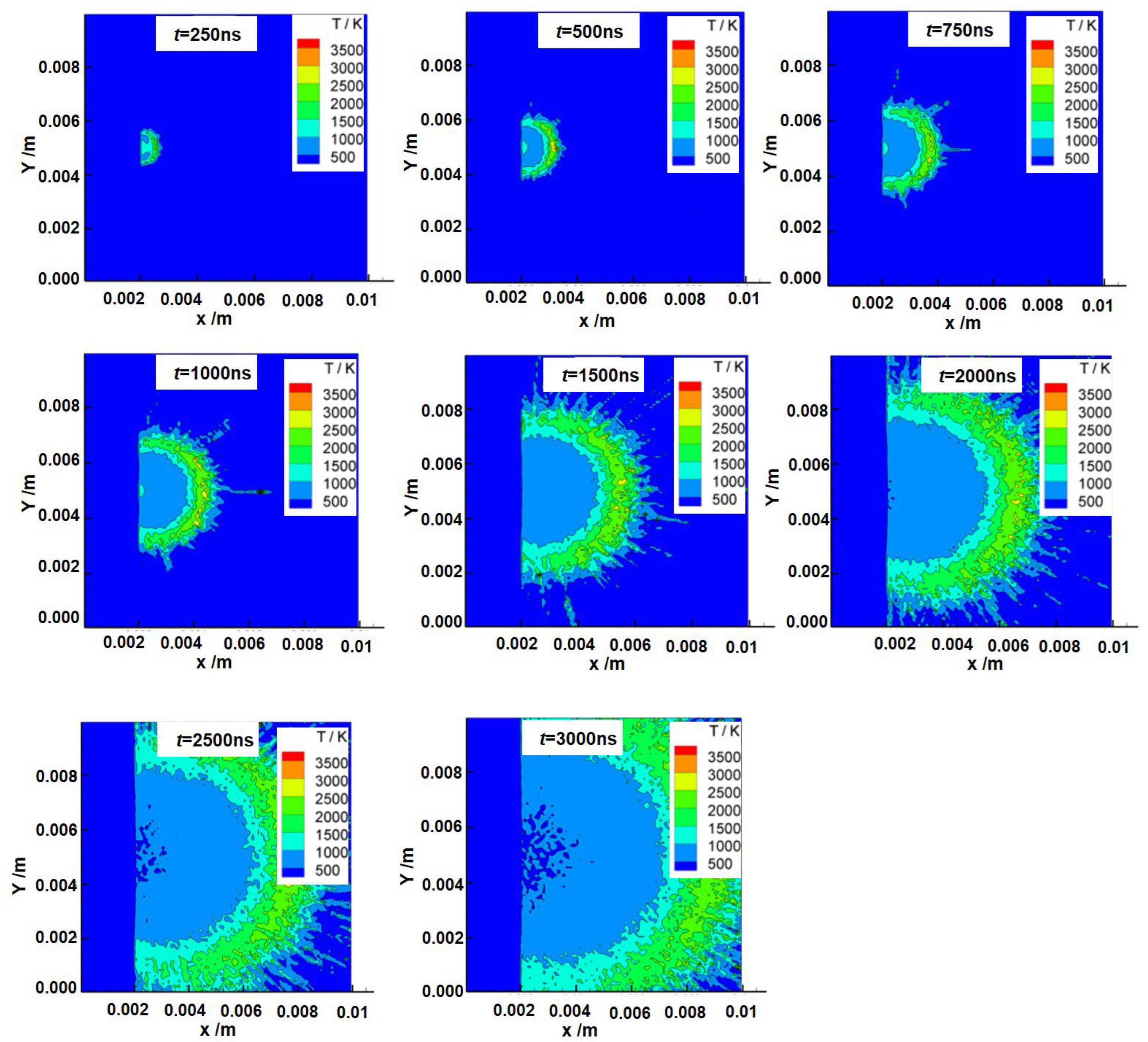
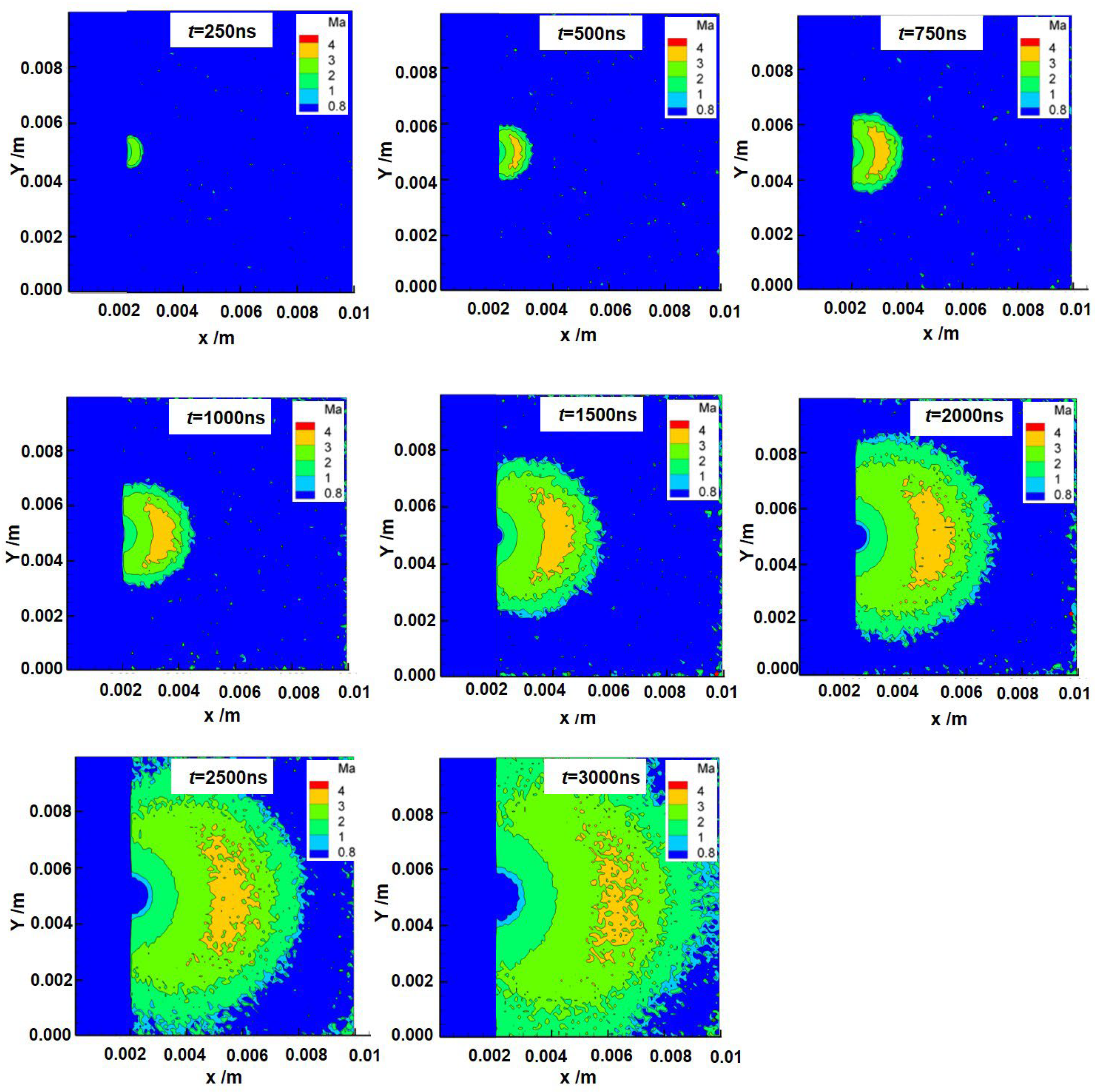
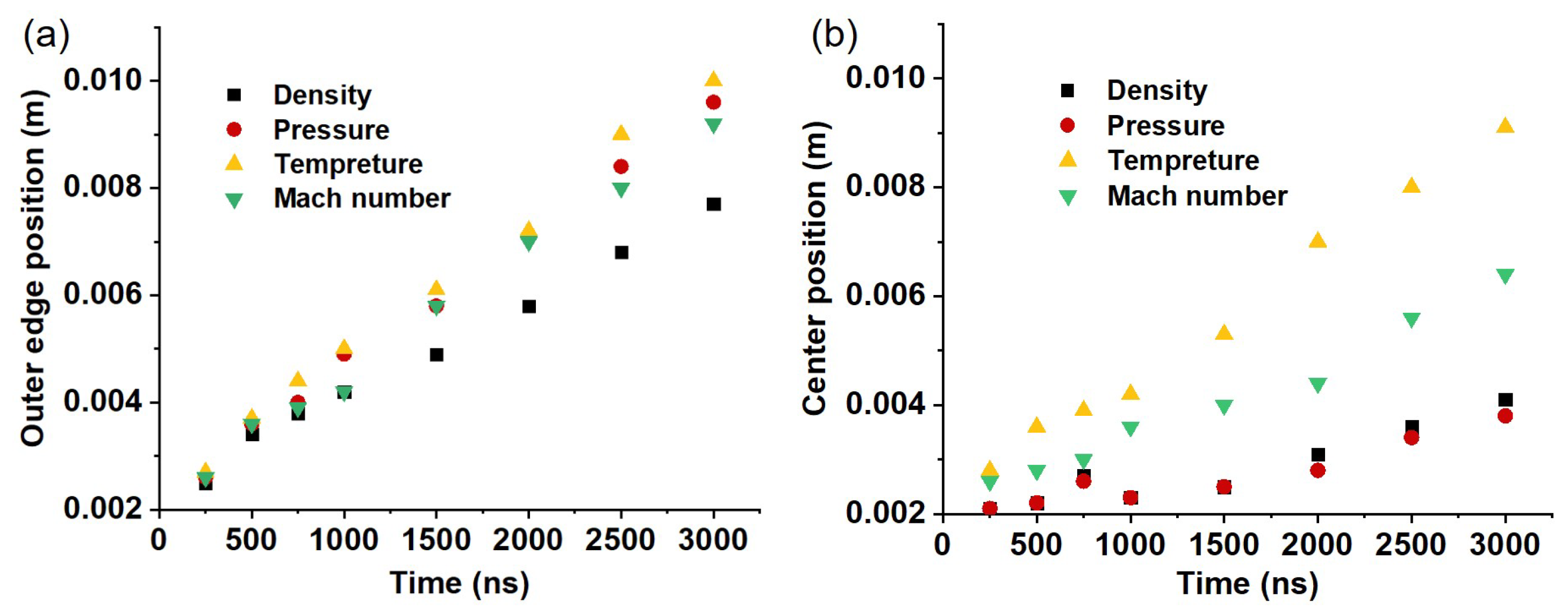
3.1. Test Results
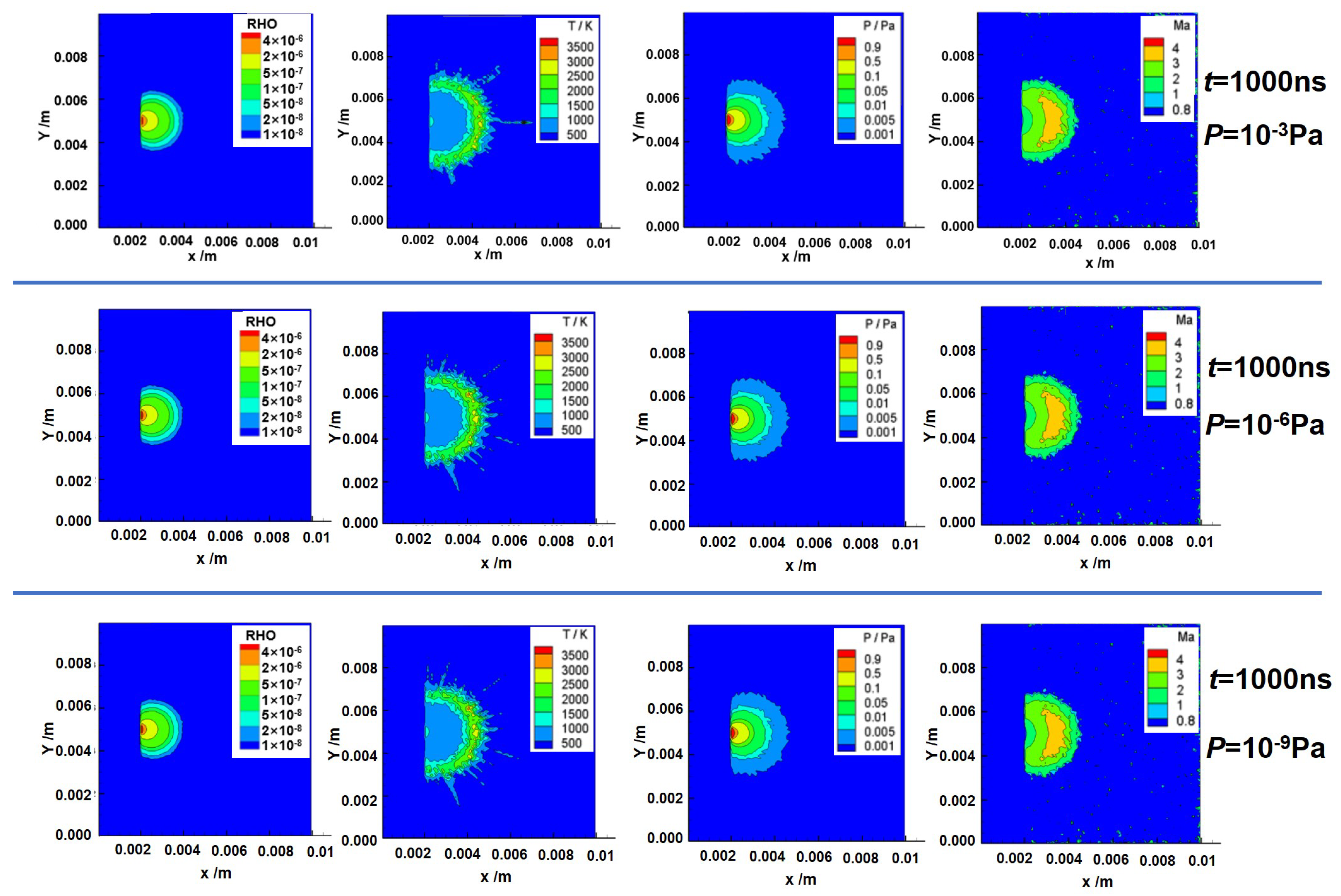
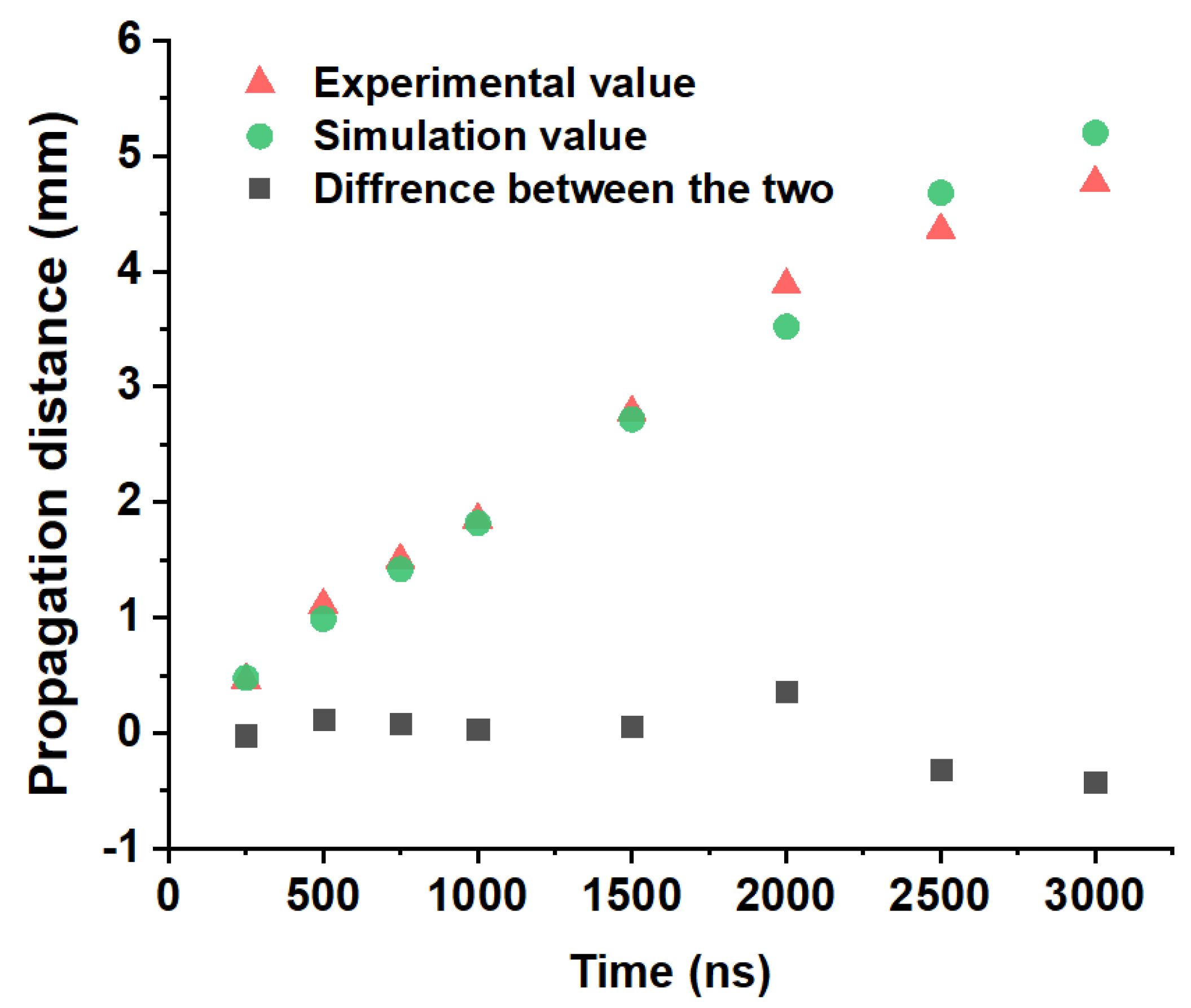
3.2. Test Verification and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Abbas, A.; Iqbal, S.T.; Jamil, Y. Ablative laser propulsion, the propellants and measuring parameters: A brief review. J. Laser Appl. 2024, 36, 021201. [Google Scholar] [CrossRef]
- Yu, H.C.; Li, H.Y.; Wang, Y.; Cui, L.G.; Liu, S.Q.; Yang, J. Brief review on pulse laser propulsion. Opt. Laser. Technol. 2018, 100, 57–74. [Google Scholar] [CrossRef]
- Chen, J.; Li, G.X.; Zhang, T.; Wang, M.; Yu, Y.S. Experimental investigation of the catalytic decomposition and combustion characteristics of a non-toxic ammonium dinitramide (ADN)-based monopropellant thruster. Acta Astronaut. 2016, 129, 367–373. [Google Scholar] [CrossRef]
- Rahman, A.; Chin, J.; Kabir, F.; Hung, Y.M. Characterisation and thrust measurements from electrolytic decomposition of Ammonium Dinitramide (ADN) based liquid monopropellant FLP-103 in MEMS thrusters. Chin. J. Chem. Eng. 2018, 26, 1992–2002. [Google Scholar] [CrossRef]
- Sandu, C.; Silivestru, V.; Cican, G.; Șerbescu, H.; Tipa, T.; Totu, A.; Radu, A. On a new type of combined solar–thermal/cold gas propulsion system used for LEO satellite’s attitude control. Appl. Sci. 2020, 10, 7197. [Google Scholar] [CrossRef]
- Martínez, J.M.; Lafleur, T. On the selection of propellants for cold/warm gas propulsion systems. Acta Astronaut. 2023, 212, 54–69. [Google Scholar] [CrossRef]
- Jiao, L.; Cai, J.; Ma, H.H.; Li, G.X.; Li, L.; Shen, Z.W.; Tang, Z.P. Research on applications of rectangular beam in micro laser propulsion. Appl. Surf. Sci. 2014, 301, 481–487. [Google Scholar] [CrossRef]
- Mori, K. Laser-propelled launch of a spherical capsule guided by a donut-mode beam. J. Spacecr. Rocket. 2017, 54, 1180–1183. [Google Scholar] [CrossRef]
- Wang, S.B.; Du, B.D.; Du, B.S.; Zheng, Y.Z.; Hong, Y.J.; Ye, J.F.; Xing, B.Y.; Li, C.L.; Zhang, Y.H. Impacts of laser pulse width and target thickness on laser micro-propulsion performance. Plasma Sci. Technol. 2022, 24, 105504. [Google Scholar] [CrossRef]
- Du, B.S.; Zheng, Y.Z.; Mao, C.T.; Cui, H.C.; Han, J.H.; Jiang, L.Y.; Ye, J.F.; Hong, Y.J. Transmissive Mode Laser Micro-Ablation Performance of Ammonium Dinitramide-Based Liquid Propellant for Laser Micro-Thruster. Micromachines 2023, 14, 1219. [Google Scholar] [CrossRef]
- Lemmer, K. Propulsion for CubeSats. Acta Astronaut. 2017, 134, 231–243. [Google Scholar] [CrossRef]
- Xu, R.P.; Tang, Z.P. Numerical simulation for laser propulsion of air breathing mode considering multi-pulses. High Power Laser Part. Beams 2007, 19, 369–372. [Google Scholar]
- Blockley, R.; Shyy, W. Laser Propulsion, Encyclopedia of Aerospace Engineering; John Wiley & Sons Ltd.: Chichester, UK, 2010. [Google Scholar] [CrossRef]
- Bondar, Y.A.; Schweigert, V.A.; Ivanov, M.S. Modeling of the hall-effect thruster plume by combined PIC-MCC/DSMC method. AIP Conf. Proc. 2003, 663, 549–556. [Google Scholar]
- Nishii, K.; Levin, D.A. Three dimensional kinetic simulations of carbon back sputtering in vacuum chambers from ion thruster plumes. J. Propul. Power 2024, 40, 123–137. [Google Scholar] [CrossRef]
- Fang, H.K.; Oyama, K.I.; Cheng, C.Z. Plasma measurements in the space plasma operation chamber (SPOC). Chin. J. Phys. 2015, 53, 123–137. [Google Scholar]
- Aslanov, V.S.; Ledkov, A.S. The ion beam interceptor concept for a space station collision avoidance with space debris. Acta Astronaut. 2024, 223, 49–57. [Google Scholar] [CrossRef]
- Tan, R.; Hang, G.R.; Wang, P.Y. Optimization of magnetic field design for Hall thrusters based on a genetic algorithm. Plasma Sci. Technol. 2024, 26, 075503. [Google Scholar] [CrossRef]
- Yamashita, Y.; Tsukizaki, R.; Nishiyama, K. Effect of ion beam extraction on neutral density distribution inside a gridded microwave discharge ion thruster. Vacuum 2022, 200, 100962. [Google Scholar] [CrossRef]
- He, B.J.; Zhang, J.H.; Cai, G.B. Research on vacuum plume and its effects. Chin. J. Aeronaut. 2013, 26, 27–36. [Google Scholar] [CrossRef]
- Tani, H.; Ohmaru, T. Hybrid continuum/rarefied flow simulations of plume interaction with full-sized spacecraft. J. Spacecr. Rocket. 2022, 59, 660–673. [Google Scholar] [CrossRef]
- Copplestone, S.; Ortwein, P.; Munz, C.D.; Binder, T.; Mirza, A.; Nizenkov, P.; Pfeiffer, M.; Fasoulas, S. Coupled PIC-DSMC Simulations of a Laser-Driven Plasma Expansion. In High Performance Computing in Science and Engineering ’15; Nagel, W., Kröner, D., Resch, M., Eds.; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Richard, J.T.; Trevor, M.M. Computational investigations of performance improvements for microlaser ablation plasma thrusters using nozzles. IEEE Trans. Plasma Sci. 2011, 39, 2932–2933. [Google Scholar]
- Boyd, I.D.; Keidar, M. Simulation of the plume generated by a micro laser-ablation plasma thruster. In Proceedings of the High-Power Laser Ablation IV, Taos, NM, USA, 13 September 2002. [Google Scholar]
- Tang, Z.P.; Xu, R.P. Numerical study on thermal mechanical impact failure mechanism for annular focusing laser thrusters. AIP Conf. Proc. 2010, 111, 1230. [Google Scholar]
- Chen, H.; Shi, L.; Ma, L.H.; Chen, Y.G. Numerical simulation of air-breathing nanosecond laser propulsion considering subsonic inflow and multi-pulse. Optik 2014, 125, 3444–3448. [Google Scholar] [CrossRef]
- Mao, C.T.; Jing, L.Y.; Du, B.S.; Zheng, Y.Z.; Cui, H.C.; Wang, D.K.; Ye, J.F.; Han, J.H.; Hong, Y.J. Theoretical investigation of laser ablation propulsion using micro-scale fluid in atmosphere. Aerospace 2024, 11, 622. [Google Scholar] [CrossRef]


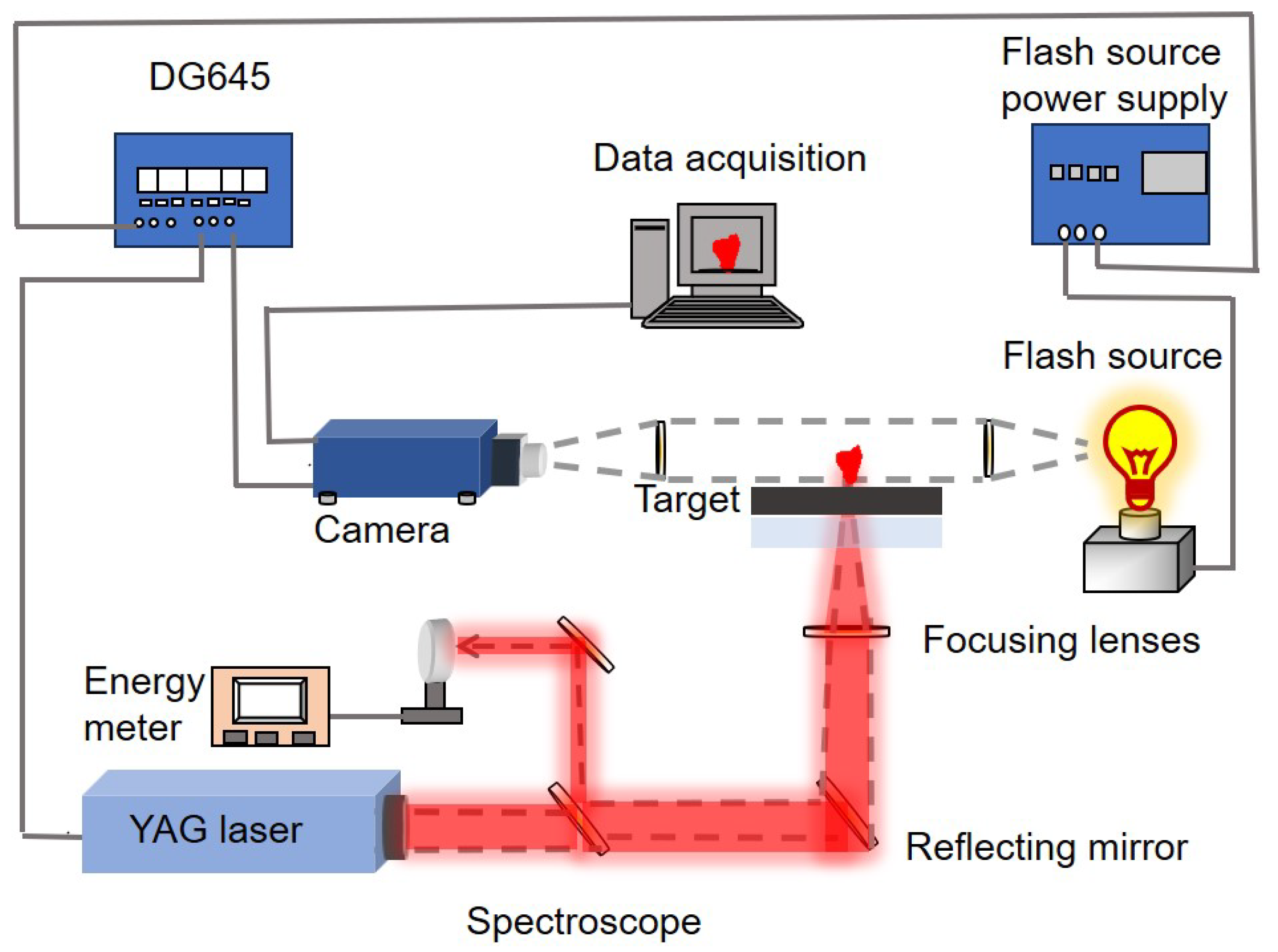

| Boundary Condition Parameters | Value |
|---|---|
| Target material | C-doped GAP |
| Thickness of target material | 100 µm |
| Quality loss | 10 µg/s |
| Laser power density | 105 W/cm2 |
| Laser spot | 0.3 mm × 0.3 mm |
| Laser pulse width | 1 ms |
| Laser energy | 40 mJ |
| Laser energy deposition efficiency | ~80% |
| Pressure at the outlet | 10−3 Pa; 10−6 Pa; 10−9 Pa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, M.; Du, B.; Cui, H.; Han, J. Simulations and Analyses of the Influence of a Vacuum Back-Pressure Environment on Laser Ablation Thrusters. Aerospace 2025, 12, 445. https://doi.org/10.3390/aerospace12050445
Wen M, Du B, Cui H, Han J. Simulations and Analyses of the Influence of a Vacuum Back-Pressure Environment on Laser Ablation Thrusters. Aerospace. 2025; 12(5):445. https://doi.org/10.3390/aerospace12050445
Chicago/Turabian StyleWen, Ming, Baosheng Du, Haichao Cui, and Jianhui Han. 2025. "Simulations and Analyses of the Influence of a Vacuum Back-Pressure Environment on Laser Ablation Thrusters" Aerospace 12, no. 5: 445. https://doi.org/10.3390/aerospace12050445
APA StyleWen, M., Du, B., Cui, H., & Han, J. (2025). Simulations and Analyses of the Influence of a Vacuum Back-Pressure Environment on Laser Ablation Thrusters. Aerospace, 12(5), 445. https://doi.org/10.3390/aerospace12050445






