Imitation-Reinforcement Learning Penetration Strategy for Hypersonic Vehicle in Gliding Phase
Abstract
1. Introduction
- A novel imitation-reinforcement learning method is developed, which unifies the optimization objectives of imitation learning and reinforcement learning through the truncated horizon. By adjusting the truncated horizon length, this method progressively increases the difficulty of learning tasks, providing a new way to enhance the efficiency of reinforcement learning in solving complex problems.
- A result-oriented composite reward function based on the Zero-Effort Miss (ZEM) is designed, which incorporates both terminal rewards and process rewards. The constituent term ZEM of the reward function establishes a direct link between the current penetration situation and the final penetration outcome, enabling a more accurate evaluation of the effectiveness of the penetration actions. This effectively reduces the difficulty of learning the penetration strategy for hypersonic vehicles.
- An intelligent penetration strategy for hypersonic vehicles during the gliding phase, utilizing the THIL-SAC algorithm, is proposed. By employing reward shaping and truncated experience sampling, this approach integrates imitation learning with reinforcement learning, thereby effectively enhancing the convergence rate of penetration strategy learning based on reinforcement learning. Furthermore, this method avoids any need for model simplifications or assumptions, thereby delivering improved penetration performance and greater adaptability.
2. Materials and Methods
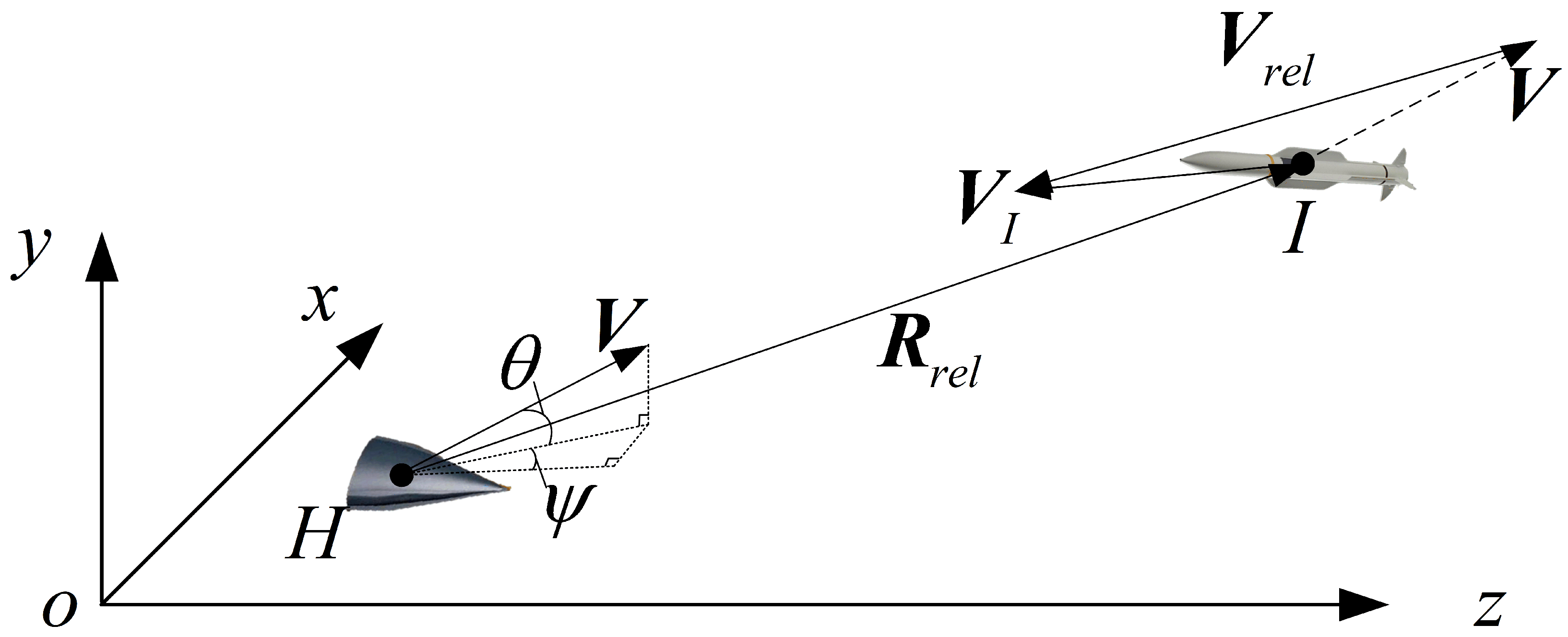
2.1. Penetration Model of Hypersonic Vehicle in Gliding Phase
2.1.1. Mathematical Model of Hypersonic Vehicle
2.1.2. Mathematical Model of Interceptor
2.2. Design of MDP Model for Hypersonic Vehicle Penetration in Gliding Phase
2.2.1. State Space
2.2.2. Action Space
2.2.3. Reward Function
- Terminal reward termThe objective of the hypersonic vehicle penetration is to maximize the line-of-sight normal displacement (ZEM) between itself and the interceptor at the time of miss. Therefore, the reward function should include a reward term, , at the time of miss.where is a positive constant. is the ZEM at the time of miss.
- Process reward termSince the interceptor uses a near-optimal inverse trajectory for interception, the miss distance is initially at its maximum. As the distance between the hypersonic vehicle and the interceptor decreases, the miss distance will typically decrease as well [23,24]. However, if the rate of decrease in the miss distance slows down or even increases, it indicates that the hypersonic vehicle may eventually succeed in penetrating. Therefore, a process reward term, , is introduced to account for the rate of change in the miss distance.where is a positive constant. is the ZEM at the time of t.If only is used as the process reward term, the reward obtained from the agent–environment interactions would almost always be negative, which is detrimental to the diversity of training samples. Therefore, to address this issue, a “dense penalty + sparse reward” reward function format is considered, and an additional reward term, , is introduced.where is a positive constant.In summary, the reward function for the hypersonic vehicle penetration during the gliding phase is as follows:
3. Design of Penetration Strategy Based on Imitation-Reinforcement Learning
3.1. Truncated Horizon Imitation-Reinforcement Learning Model
3.2. THIL-SAC-Based Penetration Strategy
3.2.1. SAC Algorithm
- Policy evaluationThe purpose of policy evaluation is to the evaluation accuracy of the Critic network. To fully utilize the available data, increase sampling efficiency, and improve learning stability, the SAC algorithm constructs four identical networks, : two main Q-networks () and two target Q-networks (), where and are the network parameters.The main Q-networks update their parameters by minimizing the soft Bellman error, with the loss function given bywhere D is the replay buffer. is the updating target, which can be calculated by the following formula.where is the policy, and is the action given in the state by .To ensure the accuracy of and minimize the loss function, it is common to update the parameter by using gradient descent as follows:where indicates the learning rate of and satisfies a small value, and denotes the gradient of .The parameters are then soft-updated according to the parameters with the following update equation:where is the soft update coefficient.
- Policy improvementThe purpose of policy improvement is to enhance the policy of the agent by updating the policy network , where represents the policy network parameters. is updated by the Kullback–Leibler (KL) divergence between the current policy and the target policy, and the loss function is as follows:In the equation, the temperature coefficient is dynamically adjusted based on the state to enhance the randomness of policy exploration. This update rule is as follows:The update formula for the policy network iswhere indicates the learning rate.
3.2.2. Expert Experience Imitation Based on Reward Shaping and Sampling
3.2.3. Optimization of the Training Process Based on TH
- Truncated horizon learning frameworkBased on the unified imitation-reinforcement learning framework with the truncated horizon established in Section 3.1, the truncated length k can be introduced into the soft value functions and , which can be rewritten as follows:Therefore, using the truncated value functions and for penetration strategy learning is equivalent to learning within the truncated horizon length k.Considering that in the actual training process, the truncated value functions are calculated from data sampled from the experience replay buffer, the time step range t of the sampled data determines the learning scope. Therefore, compared to the traditional SAC algorithm, the THIL-SAC algorithm’s experience replay buffer stores data considering the time step t. The truncated experience replay buffer is constructed based on the original experience replay buffer to enable training within the truncated length k. The truncated experience replay buffer is defined aswhere i is the number of training episodes.At this point, the loss functions for the main Q-network and the target Q-network are as follows:where
- Adaptive adjustment of truncated length kThe truncated length k determines the learning range and difficulty during penetration strategy training. To achieve low-difficulty, rapid learning based on expert experience in the initial training phase, and to enable exploration of the optimal penetration strategy using reinforcement learning in the later stages, in this paper, the truncated length k is adjusted as follows:where N is the epoch of a single training episode, i is the number of training episodes, and and are positive constants.In the THIL-SAC based penetration strategy network training process, the truncated length within episode at the start of training is to satisfy imitation learning of the penetration strategy. As training progresses, the truncated length k is gradually increased in each episode until it reaches the length of a single training episode, N. This gradual increase transitions the learning process from imitation learning to reinforcement learning, enabling the exploration and optimization of the optimal penetration strategy.
3.3. Theoretical Analysis of TH and Expert Imitation in Reducing Learning Difficulty
3.4. Training Process of THIL-SAC-Based Penetration Strategy
| Algorithm 1 Penetration algorithm based on THIL-SAC. |
|
4. Simulation Experiments and Analysis
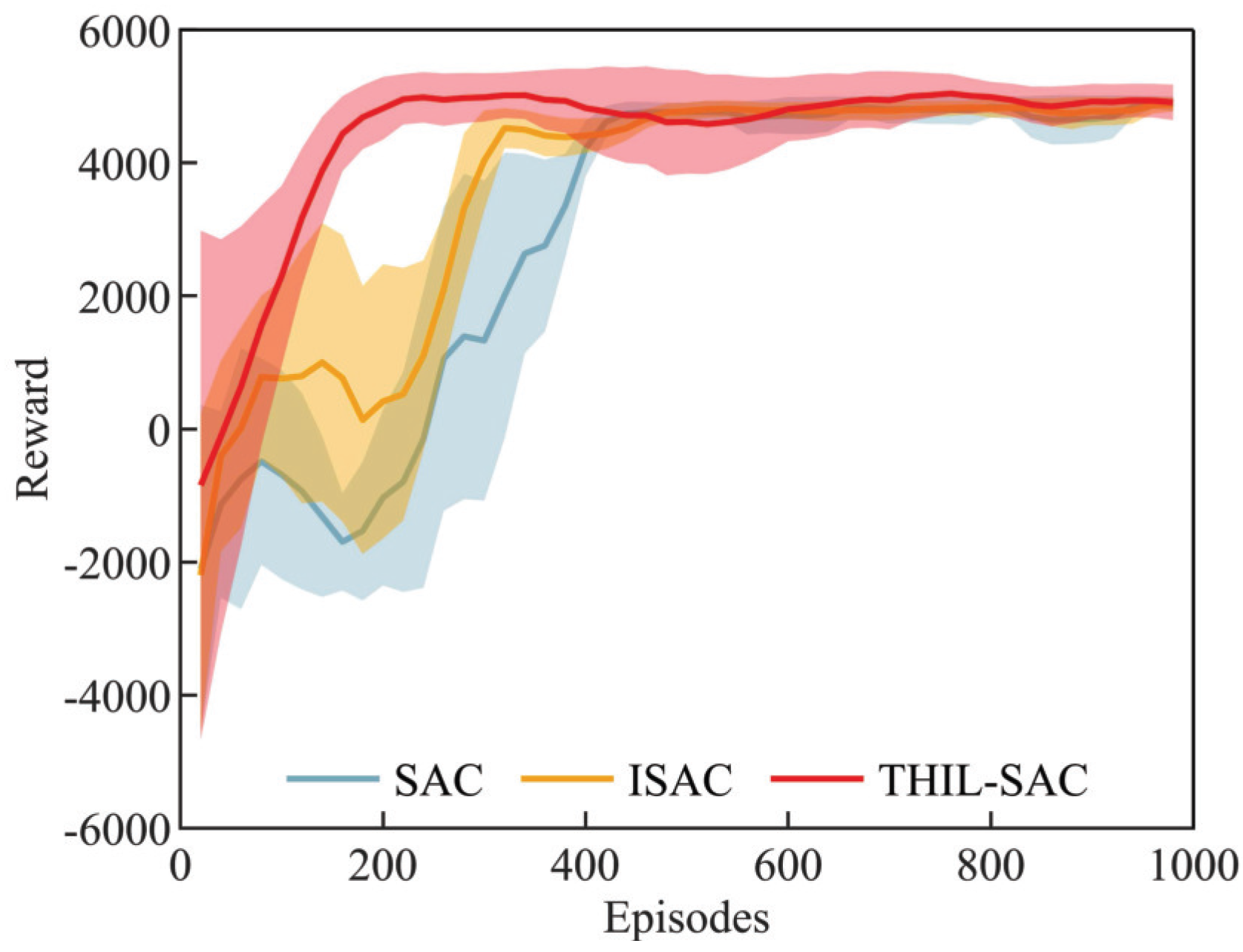
- The Learning Efficiency of the Penetration Strategy: The SAC algorithm and the proposed algorithm were used to learn penetration strategies under identical conditions, and the learning speeds were compared.
- The Effectiveness of the Penetration Strategy: The trained penetration strategies were applied to a realistic penetration scenario, where the performance of the expert strategy, the SAC-based penetration strategy, and the proposed method were evaluated and compared to demonstrate their effectiveness.
4.1. Simulation Condition
4.2. Simulation Results and Analysis
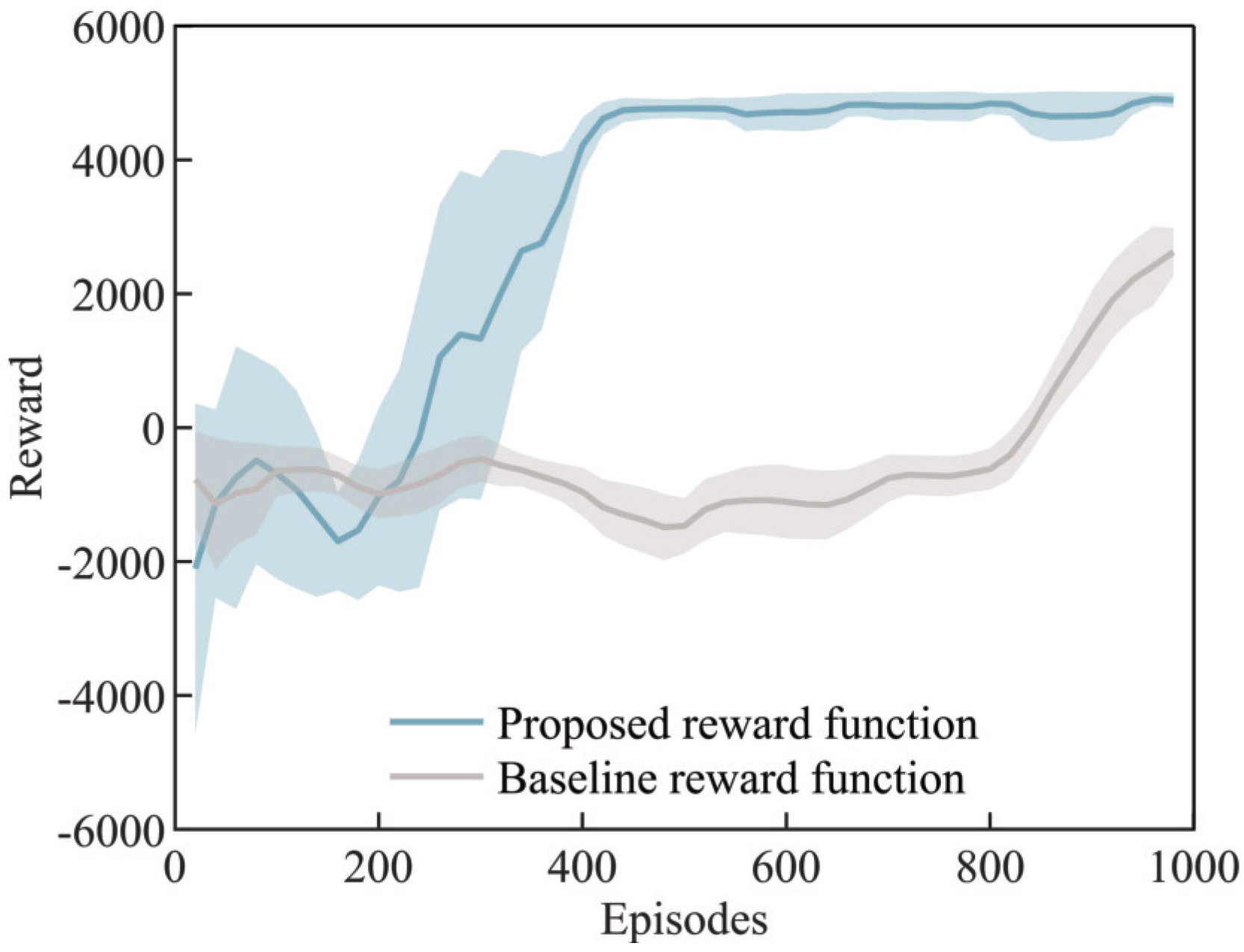
4.2.1. Different Reward Functions Comparison
4.2.2. Results of Penetration Strategy Training
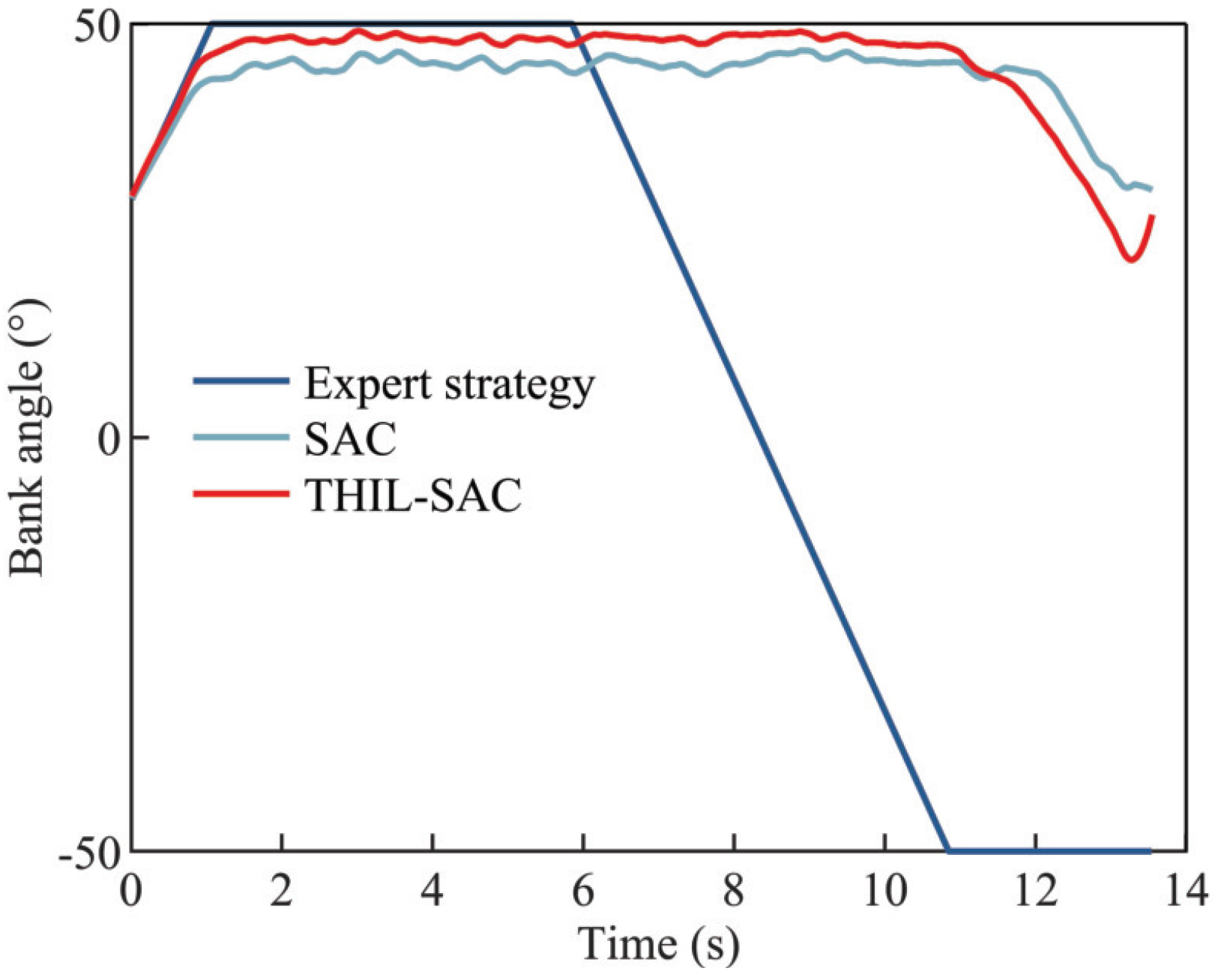
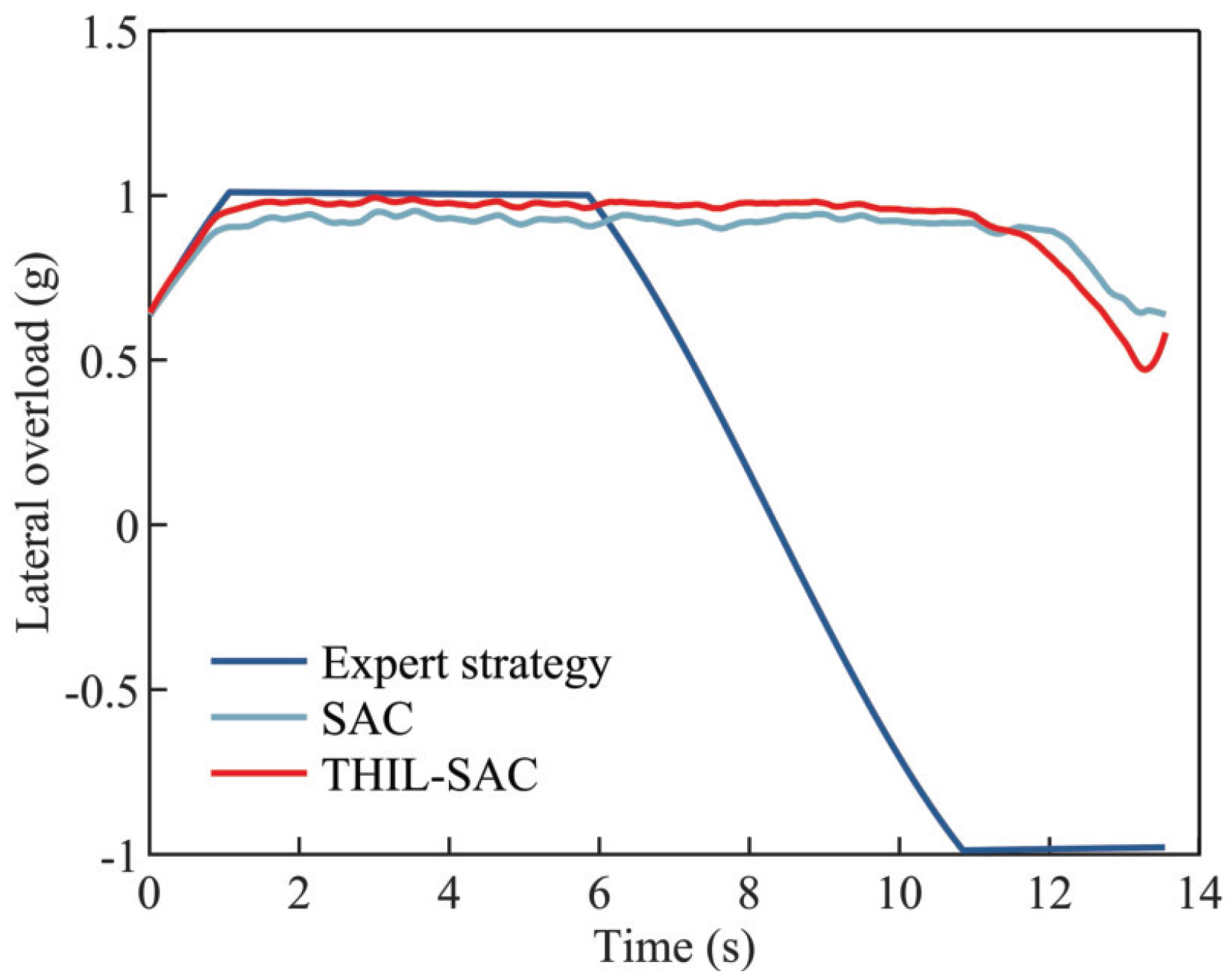
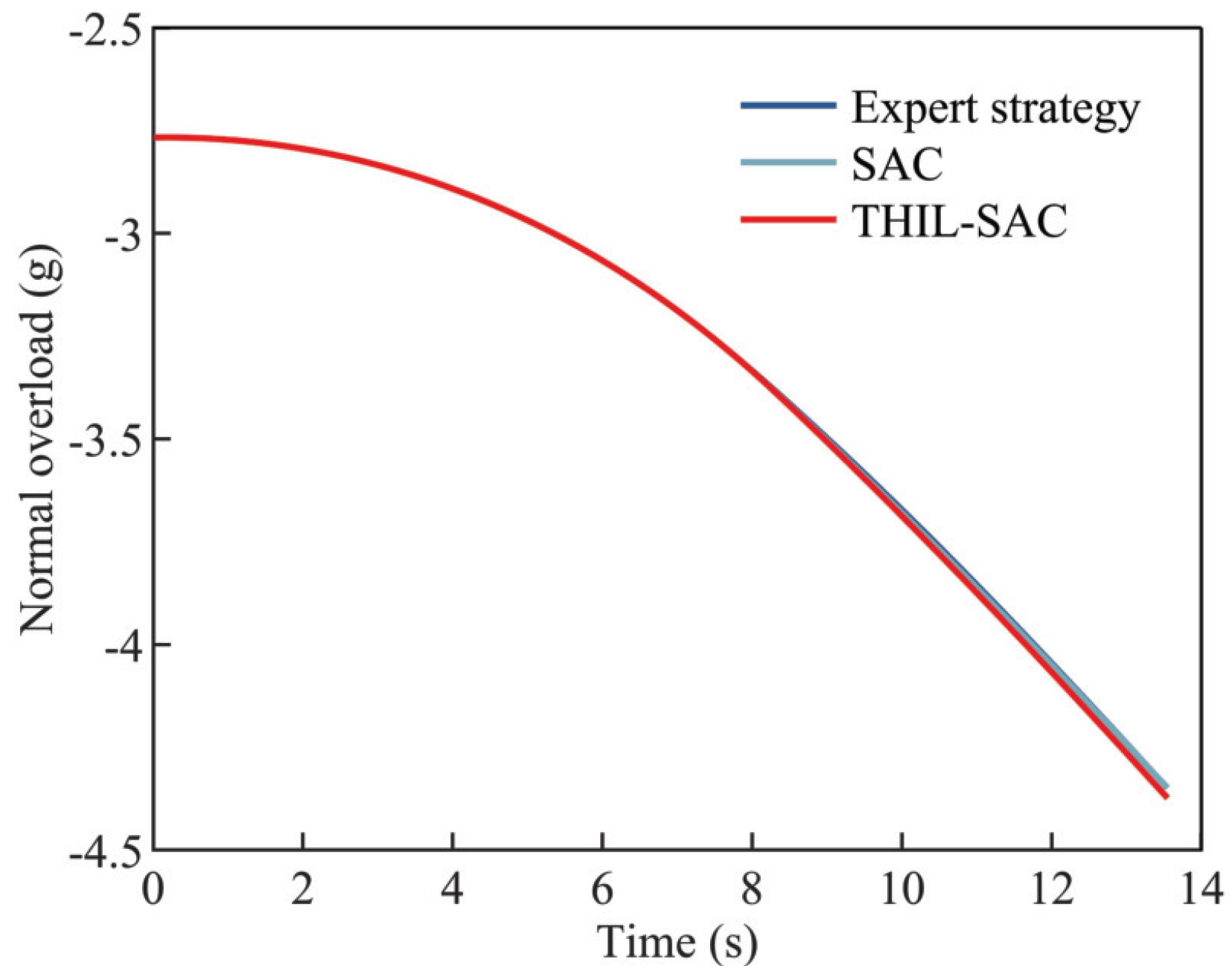
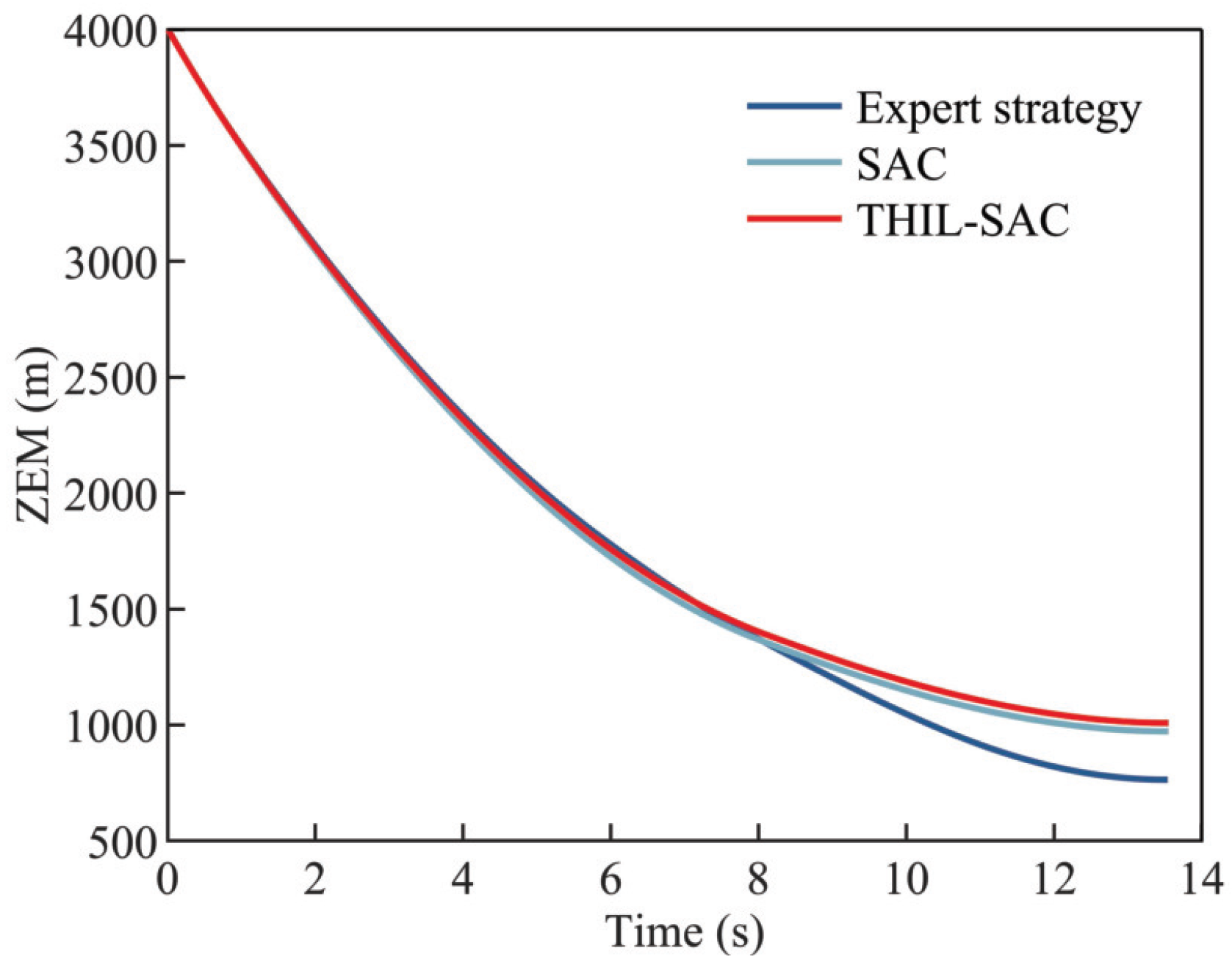
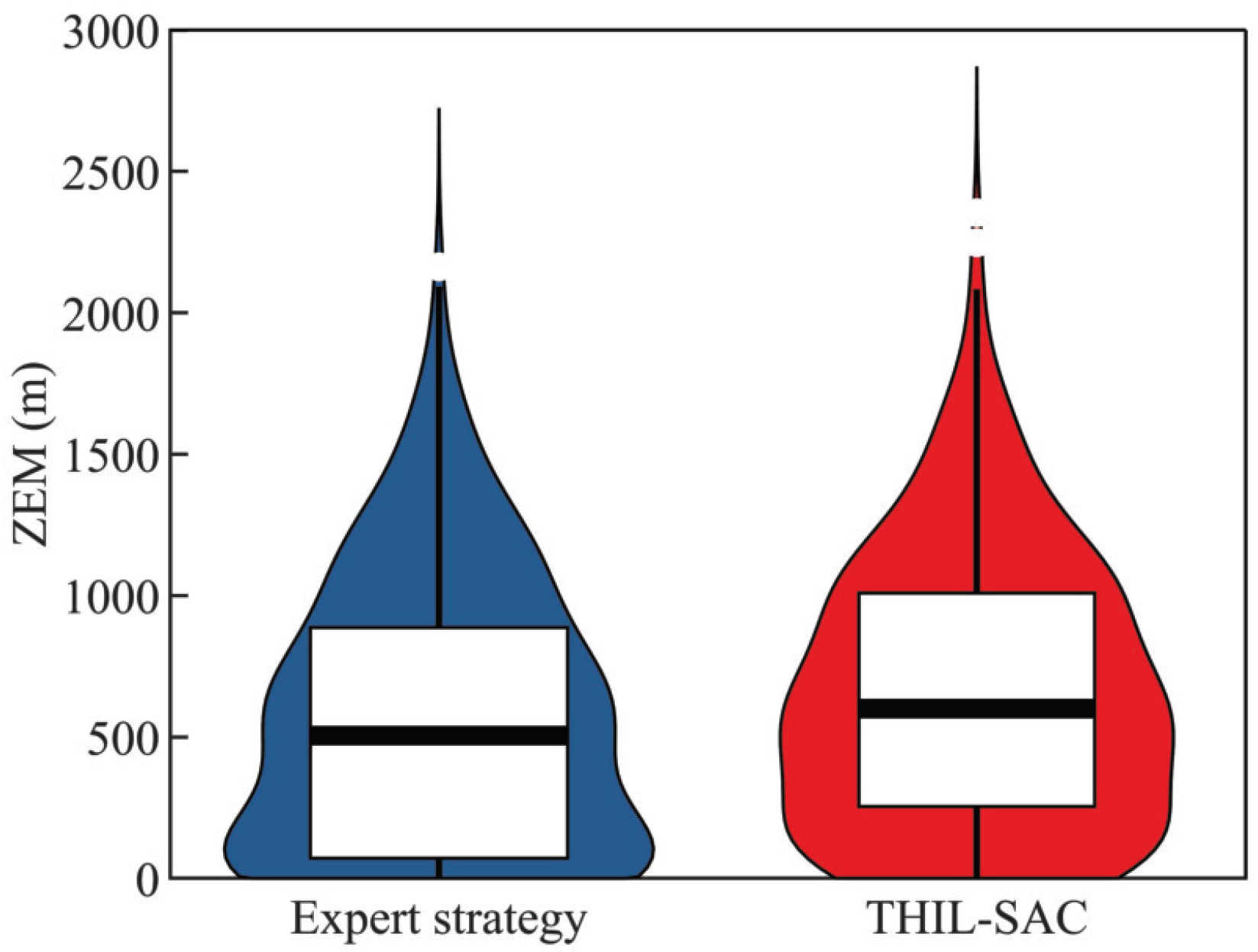
4.2.3. Testing Results of the Penetration Strategy in Typical Scenarios
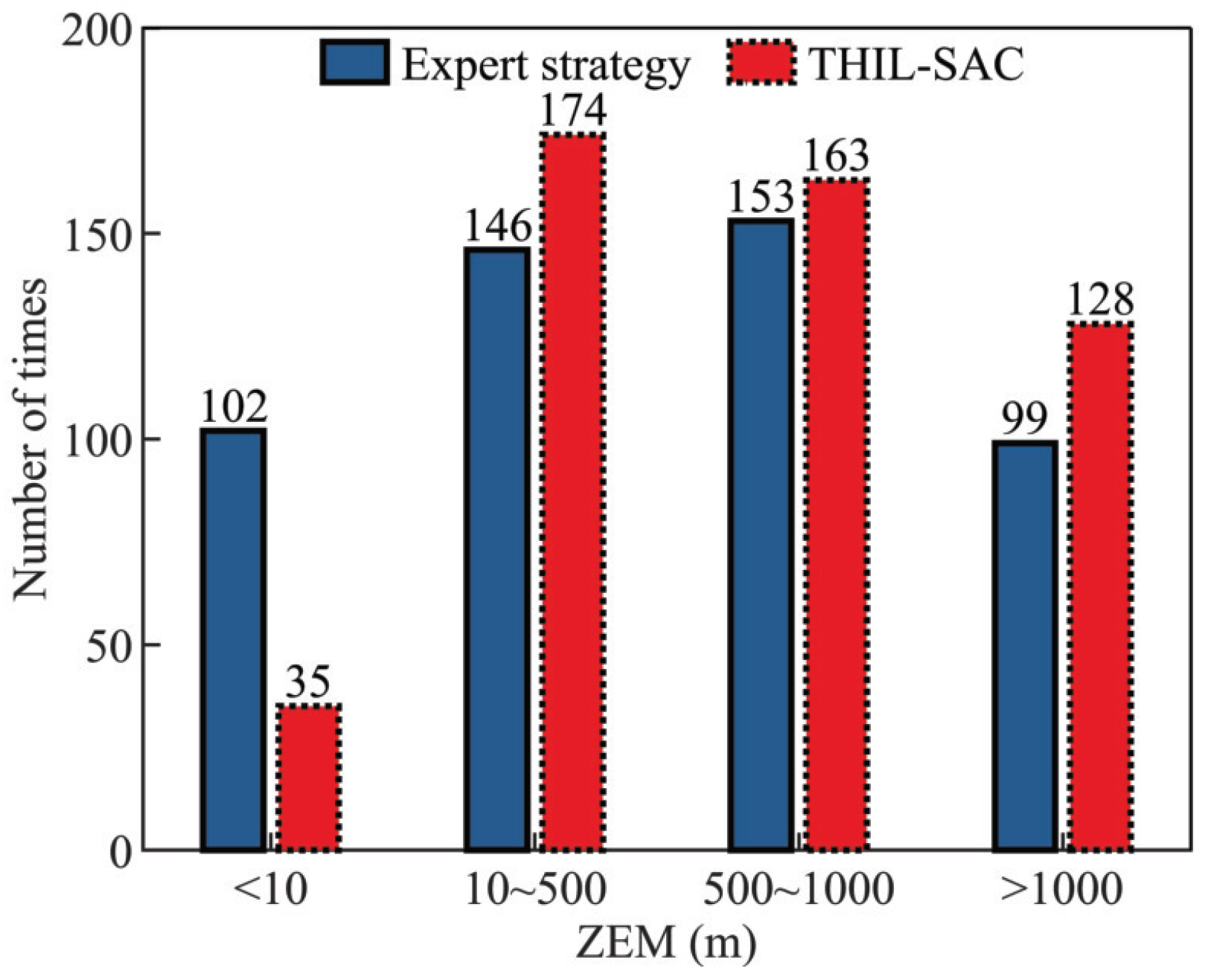
4.2.4. Analysis of the Generalization of the Penetration Strategy Network
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| 1 | 5 | 10 | 20 | |
|---|---|---|---|---|
| 1 | 280 | 410 | 771 | 1000+ |
| 5 | 200 | 450 | 1000+ | 1000+ |
| 10 | 350 | 485 | 1000+ | 1000+ |
| 20 | 400 | 495 | 1000+ | 1000+ |
References
- Lv, C.; Lan, Z.; Ma, T.; Chang, J.; Yu, D. Hypersonic vehicle terminal velocity improvement considering ramjet safety boundary constraint. Aerosp. Sci. Technol. 2024, 144, 108804. [Google Scholar] [CrossRef]
- Zhengxin, T.; Shifeng, Z. A Novel Strategy for Hypersonic Vehicle With Complex Distributed No-Fly Zone Constraints. Int. J. Aerosp. Eng. 2024, 2024, 9004308. [Google Scholar] [CrossRef]
- Fan, L.; Jiajun, X.; Xuhui, L.; Hongkui, B.; Xiansi, T. Hypersonic vehicle trajectory prediction algorithm based on hough transform. Chin. J. Electron. 2021, 30, 918–930. [Google Scholar] [CrossRef]
- Nichols, R.K.; Carter, C.M.; Drew II, J.V.; Farcot, M.; Hood, C.J.P.; Jackson, M.J.; Johnson, P.D.; Joseph, S.; Kahn, S.; Lonstein, W.D.; et al. Progress in Hypersonics Missiles and Space Defense [Slofer]. In Cyber-Human Systems, Space Technologies, and Threats; New Prairie Press: Manhattan, KS, USA, 2023. [Google Scholar]
- Rim, J.W.; Koh, I.S. Survivability simulation of airborne platform with expendable active decoy countering RF missile. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 196–207. [Google Scholar] [CrossRef]
- Kedarisetty, S.; Shima, T. Sinusoidal Guidance. J. Guid. Control Dyn. 2024, 47, 417–432. [Google Scholar] [CrossRef]
- Zarchan, P. Proportional navigation and weaving targets. J. Guid. Control Dyn. 1995, 18, 969–974. [Google Scholar] [CrossRef]
- Lee, H.I.; Shin, H.S.; Tsourdos, A. Weaving guidance for missile observability enhancement. IFAC-PapersOnLine 2017, 50, 15197–15202. [Google Scholar] [CrossRef]
- Rusnak, I.; Peled-Eitan, L. Guidance law against spiraling target. J. Guid. Control Dyn. 2016, 39, 1694–1696. [Google Scholar] [CrossRef]
- Ma, L. The moedling and simulation of antiship missile terminal maneuver penetration ability. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; IEEE: New York, NY, USA, 2017; pp. 2622–2626. [Google Scholar]
- Shinar, J.; Steinberg, D. Analysis of optimal evasive maneuvers based on a linearized two-dimensional kinematic model. J. Aircr. 1977, 14, 795–802. [Google Scholar] [CrossRef]
- Ben-Asher, J.; Cliff, E.M.; Kelley, H.J. Optimal evasion with a path-angle constraint and against two pursuers. J. Guid. Control Dyn. 1988, 11, 300–304. [Google Scholar] [CrossRef]
- Shinar, J.; Tabak, R. New results in optimal missile avoidance analysis. J. Guid. Control Dyn. 1994, 17, 897–902. [Google Scholar] [CrossRef]
- Shaferman, V. Near optimal evasion from acceleration estimating pursuers. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Grapevine, TX, USA; 2017; p. 1014. [Google Scholar]
- Shaferman, V. Near-optimal evasion from pursuers employing modern linear guidance laws. J. Guid. Control Dyn. 2021, 44, 1823–1835. [Google Scholar] [CrossRef]
- Shinar, J. Solution techniques for realistic pursuit-evasion games. In Control and Dynamic Systems; Elsevier: Amsterdam, The Netherlands, 1981; Volume 17, pp. 63–124. [Google Scholar]
- Gutman, S. On optimal guidance for homing missiles. J. Guid. Control 1979, 2, 296–300. [Google Scholar] [CrossRef]
- Segal, A.; Miloh, T. Novel three-dimensional differential game and capture criteria for a bank-to-turn missile. J. Guid. Control Dyn. 1994, 17, 1068–1074. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, H.; Yan, T.; Wang, X.; Sun, W.; Fu, W.; Yan, J. Penetration Strategy for High-Speed Unmanned Aerial Vehicles: A Memory-Based Deep Reinforcement Learning Approach. Drones 2024, 8, 275. [Google Scholar] [CrossRef]
- Li, K.; Wang, Y.; Zhuang, X.; Yin, H.; Liu, X.; Li, H. A penetration method for uav based on distributed reinforcement learning and demonstrations. Drones 2023, 7, 232. [Google Scholar] [CrossRef]
- Li, Y.; Han, W.; Wang, Y. Deep reinforcement learning with application to air confrontation intelligent decision-making of manned/unmanned aerial vehicle cooperative system. IEEE Access 2020, 8, 67887–67898. [Google Scholar] [CrossRef]
- Zhuang, X.; Li, D.; Wang, Y.; Liu, X.; Li, H. Optimization of high-speed fixed-wing UAV penetration strategy based on deep reinforcement learning. Aerosp. Sci. Technol. 2024, 148, 109089. [Google Scholar] [CrossRef]
- Yan, T.; Liu, C.; Gao, M.; Jiang, Z.; Li, T. A Deep Reinforcement Learning-Based Intelligent Maneuvering Strategy for the High-Speed UAV Pursuit-Evasion Game. Drones 2024, 8, 309. [Google Scholar] [CrossRef]
- Guo, Y.; Jiang, Z.; Huang, H.; Fan, H.; Weng, W. Intelligent maneuver strategy for a hypersonic pursuit-evasion game based on deep reinforcement learning. Aerospace 2023, 10, 783. [Google Scholar] [CrossRef]
- Zeming, H.; Zhang, R.; Huifeng, L. Parameterized evasion strategy for hypersonic glide vehicles against two missiles based on reinforcement learning. Chin. J. Aeronaut. 2024, 38, 103173. [Google Scholar]
- Zhao, S.; Zhu, J.; Bao, W.; Li, X.; Sun, H. A Multi-Constraint Guidance and Maneuvering Penetration Strategy via Meta Deep Reinforcement Learning. Drones 2023, 7, 626. [Google Scholar] [CrossRef]
- Fu, X.; Zhu, J.; Wei, Z.; Wang, H.; Li, S. A UAV Pursuit-Evasion Strategy Based on DDPG and Imitation Learning. Int. J. Aerosp. Eng. 2022, 2022, 3139610. [Google Scholar] [CrossRef]
- He, L.; Aouf, N.; Whidborne, J.F.; Song, B. Deep reinforcement learning based local planner for UAV obstacle avoidance using demonstration data. arXiv 2020, arXiv:2008.02521. [Google Scholar]
- Jiang, S.; Ge, Y.; Yang, X.; Yang, W.; Cui, H. UAV Control Method Combining Reptile Meta-Reinforcement Learning and Generative Adversarial Imitation Learning. Future Internet 2024, 16, 105. [Google Scholar] [CrossRef]
- WANG, X.; GU, K. A Penetration Strategy Combining Deep Reinforcement Learning and Imitation Learning. J. Astronaut. 2023, 44, 914. [Google Scholar]
- Wu, T.; Wang, H.; Liu, Y.; Li, T.; Yu, Y. Learning-based interfered fluid avoidance guidance for hypersonic reentry vehicles with multiple constraints. ISA Trans. 2023, 139, 291–307. [Google Scholar] [CrossRef]
- Guo, H. Penetration Game Strategy for Hypersonic Vehicles. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2018. [Google Scholar]
- Ross, S.; Gordon, G.; Bagnell, D. A reduction of imitation learning and structured prediction to no-regret online learning. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 11–13 April 2011; JMLR Workshop and Conference Proceedings. pp. 627–635. [Google Scholar]
- Ng, A.Y.; Harada, D.; Russell, S. Policy invariance under reward transformations: Theory and application to reward shaping. In Icml; Morgan Kaufmann: San Francisco, CA, USA, 1999; Volume 99, pp. 278–287. [Google Scholar]
- Sun, W.; Bagnell, J.A.; Boots, B. Truncated horizon policy search: Combining reinforcement learning & imitation learning. arXiv 2018, arXiv:1805.11240. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; PMLR: Cambridge, MA, USA, 2018; pp. 1861–1870. [Google Scholar]
- Jiang, N.; Agarwal, A. Open problem: The dependence of sample complexity lower bounds on planning horizon. In Proceedings of the Conference on Learning Theory, Stockholm, Sweden, 6–9 July 2018; PMLR: Cambridge, MA, USA, 2018; pp. 3395–3398. [Google Scholar]
- Wang, R.; Du, S.S.; Yang, L.F.; Kakade, S.M. Is long horizon reinforcement learning more difficult than short horizon reinforcement learning? arXiv 2020, arXiv:2005.00527. [Google Scholar]
- Kakade, S.M. On the Sample Complexity of Reinforcement Learning; University of London, University College London: London, UK, 2003. [Google Scholar]
- Zipser, D. Subgrouping reduces complexity and speeds up learning in recurrent networks. Adv. Neural Inf. Process. Syst. 1989, 2, 638–641. [Google Scholar] [CrossRef]
- Schulman, J.; Moritz, P.; Levine, S.; Jordan, M.; Abbeel, P. High-dimensional continuous control using generalized advantage estimation. arXiv 2015, arXiv:1506.02438. [Google Scholar]
- Nair, A.; McGrew, B.; Andrychowicz, M.; Zaremba, W.; Abbeel, P. Overcoming exploration in reinforcement learning with demonstrations. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; IEEE: New York, NY, USA, 2018; pp. 6292–6299. [Google Scholar]
- Fujimoto, S.; Meger, D.; Precup, D. Off-policy deep reinforcement learning without exploration. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019; PMLR: Cambridge, MA, USA, 2019; pp. 2052–2062. [Google Scholar]
- Wang, C.; Ross, K. Boosting soft actor-critic: Emphasizing recent experience without forgetting the past. arXiv 2019, arXiv:1906.04009. [Google Scholar]




| Parameters | Hypersonic Vehicle | Interceptor |
|---|---|---|
| Longitude (°) | 148.95 | 149.30 |
| Latitude (°) | 23.72 | 23.99 |
| Altitude (m) | 26997.33 | 29967.40 |
| X-direction speed (m/s) | −2165.21 | 1404.25 |
| Y-direction speed (m/s) | 42.11 | −153.45 |
| Z-direction speed (m/s) | −366.06 | −48.79 |
| Parameters | Value |
|---|---|
| Policy network learning rate | 0.0003 |
| Q-network learning rate | 0.0003 |
| Replay buffer size | 1e5 |
| Batch size | 256 |
| Discount factor | 0.99 |
| Temperature coefficient | 0.12 |
| Soft update coefficient | 0.01 |
| Parameters of reward function | |
| Parameters of truncated length |
| Strategy | ZEM at the Miss Time |
|---|---|
| Expert strategy | 763.76 m |
| SAC-based strategy | 972.34 m |
| THIL-SAC-based strategy | 1008.76 m |
| Parameters | Standard Deviation |
|---|---|
| Initial position deviation along the X-axis | 2500 m |
| Initial position deviation along the Y-axis | 2500 m |
| Initial position deviation along the Z-axis | 2500 m |
| Initial velocity deviation along the X-axis | 25 m/s |
| Initial velocity deviation along the Y-axis | 25 m/s |
| Initial velocity deviation along the Z-axis | 25 m/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Guan, Y.; Pu, J.; Wei, C. Imitation-Reinforcement Learning Penetration Strategy for Hypersonic Vehicle in Gliding Phase. Aerospace 2025, 12, 438. https://doi.org/10.3390/aerospace12050438
Xu L, Guan Y, Pu J, Wei C. Imitation-Reinforcement Learning Penetration Strategy for Hypersonic Vehicle in Gliding Phase. Aerospace. 2025; 12(5):438. https://doi.org/10.3390/aerospace12050438
Chicago/Turabian StyleXu, Lei, Yingzi Guan, Jialun Pu, and Changzhu Wei. 2025. "Imitation-Reinforcement Learning Penetration Strategy for Hypersonic Vehicle in Gliding Phase" Aerospace 12, no. 5: 438. https://doi.org/10.3390/aerospace12050438
APA StyleXu, L., Guan, Y., Pu, J., & Wei, C. (2025). Imitation-Reinforcement Learning Penetration Strategy for Hypersonic Vehicle in Gliding Phase. Aerospace, 12(5), 438. https://doi.org/10.3390/aerospace12050438






