Model for Evaluation of Aircraft Boarding Under Disturbances

Abstract

Aircraft boarding is one of the most essential handling processes carried out at an airport. Its importance derives from the fact that it is part of the critical path; that is, the time of its completion determines the aircraft’s departure time. It is desirable to examine how the efficiency of the boarding process changes depending on the disruptions that may occur. It is particularly important to check how they affect existing and partially applied boarding strategies that are assumed to improve the process. This article aimed to develop a microscale model of the boarding process implemented as a hierarchical, timed, colored Petri net (HTCPN). This model makes it possible to consider various disturbances in the boarding process, two of which were the subject of simulation experiments that were realized. As a result, it was found that due to disruption, not only did the effectiveness of boarding strategies change, but also their ordering relative to the total completion time of the process. This led to the conclusion that using models similar to those presented in this article is necessary, where input parameters can be determined dynamically. This means that it can be recommended to observe the currently ongoing boarding and, if any disruption is detected, perform a fast simulation to answer the question about the most advantageous boarding strategy in this situation.

1. Introduction

1.1. Aircraft Handling at the Airport

Air traffic occurs in separate airspace areas and a designated portion of space at the airport. The airport handles aircraft (taking off and landing) and passengers (departing, arriving, transferring, and in transit). The main task of the airport is to hold both of these streams safely, efficiently, and at a low cost in the shortest possible time.

An effective way to solve emerging airport capacity problems is to streamline organizational and operational processes. Reducing aircraft turnaround times at the airport reduces costs, tightens rotations, i.e., makes better use of the fleet, and enables more takeoffs and landings.

Ground handling begins with the locking of the aircraft’s wheels and the placement of a passenger ramp or the propping up of a passenger platform. Next, baggage and passenger handling and transport to the terminal are performed. Next, the aircraft is equipped with electricity, water, compressed air, and air conditioning; the waste is collected; and then the aircraft is cleaned and refueled. Next, the passenger-boarding process takes place, and the luggage is loaded. Once these activities are completed, the aircraft doors are closed, and the aircraft’s wheel locks are removed. The last ground handling activity is pushing the aircraft onto the taxiway.

This paper deals with analyzing ground handling in terms of the boarding process. It begins when the aircraft is ready to receive passengers, with the announcement of boarding by airport personnel. The process takes a relatively long time, and the boarding time is mainly affected by the allocation of seats to passengers, the boarding order, and the number of hand luggage taken by passengers. Efforts are made to minimize the duration of this process. Boarding is one of the most critical parts of the ground handling of aircraft and passengers, as it lies on the critical path of the turnaround process. Lengthening or shortening means reducing or extending the total time an aircraft stays at an airport. According to [1], it is estimated that for a large airline with more than 5000 flights per day, a reduction of one minute in the boarding time results in savings of USD 50 million per year.

The high economic importance of the boarding process has resulted in a high level of research activity and a large number of scientific papers devoted to the issue. Many boarding strategies have also been developed that determine the order in which passengers board an aircraft, depending on their assigned seats. Most methods involve dividing passengers into small groups and then sequentially seating each group. There are also more complicated strategies, such as precisely determining the boarding order for each passenger individually.

Operational disruptions greatly impact the boarding process and, more specifically, the total seating time in the aircraft. By operational disruptions, we mean random disruptions and passenger insubordination. This is because even the most complex boarding strategy may not produce the expected results if something unexpected happens or passengers do not follow its rules. A preliminary analysis indicated that the resilience of boarding methods changes the assessment of their usefulness in a nominal situation without disruptions.

1.2. Literature Review

An analysis of bibliographic sources was carried out to check the current state of knowledge and research in the field, consistent with the subject of this article, including studies on the following:

• Boarding methods and suggested ways to improve the process;
• Factors affecting the boarding process and the parameters analyzed;
• Interactions that cause the process to be prolonged;
• Modeling methods, with a special emphasis on Petri nets.

The effectiveness of boarding methods shows differences depending on the aircraft type used and the passengers’ characteristics. Bachmat and Elkin [2] analyzed a back-to-front boarding strategy and showed that it could be 20% more effective than a random strategy. Meanwhile, Milne et al. [3] proposed a method to optimize the process by considering the number of hand luggage carried by passengers. The optimal distribution assigns passengers with a small number of pieces of luggage to the rows of the plane closest to the entrance. Harrison et al. [4] proposed a new algorithm for passenger segmentation in the boarding process based on the value of time lost by a passenger. A similar approach was presented by Schultz and Reitmann [5], which estimates boarding times using machine learning.

Steffen and Hotchkiss [6] presented the results of an analysis of the effectiveness of five boarding methods. The study was conducted to board 72 passengers of different ages on a Boeing 757 aircraft with twelve rows, six seats, and one aisle. It was shown that the optimized methods gave better results than the traditional methods. The best results were obtained using Steffen’s method. Li et al. [7] used a genetic algorithm to analyze the different boarding methods. The results showed that the window-to-aisle method was the best, and the back-to-front method gave worse results than random. The authors recommended a hybrid boarding process, combining the window-to-aisle and alternating half-row methods. This technique remains a three-zone process but allows families to board at the beginning, simultaneously with the passengers seated at the windows.

Nyquist and McFadden [8] discussed finding an effective boarding method while maintaining service quality and passenger satisfaction. It was found that the best method is outside-in or some modification. The research also indicated that a more effective hand luggage management policy should be developed. Fabrin et al. [9] also addressed customer satisfaction and airplane efficiency, showing that outside-in boarding performed best in total and individual boarding times. Moreira et al. [10] analyzed different boarding strategies for the Airbus A320. The results indicated that the most effective methods are the outside-in and reverse pyramid, with results that are better than those of the random strategy by up to 15%. The back-to-front strategy was indicated as the least effective. In [11], selected strategies were analyzed, and it was found that the frequently used block strategies are ineffective and extend the boarding time compared with the random strategy. As a result, passengers who ignore the strategy assumptions improve the process efficiency. Half-block, by-row, and half-row strategies are not recommended there.

Zeineddine [12] described a method of dynamically optimized boarding that allows for shorter boarding times, minimizes disruptions on board, and, at the same time, enables passengers to board in groups. Passengers are assigned to a queue based on the seat number they are to occupy, related groups, and anticipated disruptions. It is recommended that passengers gather in small groups before boarding begins, according to their place in the queue. Steffen [13] presented an interesting boarding strategy concept without assigning seats to individual passengers. The model is based on the principles of statistical mechanics, and each seat in the plane is expressed by energy that reflects passengers’ preferences.

Several factors that affect boarding times have been identified and can be used to develop boarding methods. These include passenger movement speed and the number of carry-on luggage items. Erland et al. [14] analyzed the impact of carry-on luggage on the boarding order. It was shown that the “slowest first” policy can be improved when passengers are divided into more than two groups based on the number of carry-on luggage items they have. Hutter et al. [15] presented the results of an empirical study to determine the extent to which factors such as the number of passengers, aircraft capacity, and the amount of carry-on luggage affect boarding times. Ren et al. [16] analyzed the time of stowing carry-on luggage. Qiang et al. [17] developed a new boarding strategy based on the number of hand luggage passengers carry. The authors argued that their proposed method is superior to others. Tang et al. [18] described a new passenger-boarding model considering individual passenger characteristics. Passengers are divided into groups based on their speed.

The interactions between passengers inside the aircraft are of fundamental importance for the boarding time. In [19], the interactions among passengers were analyzed. A model minimizing these disruptions was created and applied to the Airbus A320 aircraft. In [20], empirical measurements and analysis of the time taken to occupy passenger cabin seats and the interactions occurring in this process were carried out. In [21], the effectiveness of different boarding strategies in the context of disruptions occurring in the corridors and the rows was checked. The analysis was performed for the Airbus A320 aircraft. A model was developed using a genetic algorithm that minimizes the expected number of interferences between passengers.

Recently, attempts have been made to consider fragmentary disruptions in the boarding process. In [22], the sensitivity of the most popular boarding strategies to the number of priority passengers was investigated to some extent. Zeineddine [23] analyzed the possibility of counteracting non-compliance with boarding rules. The work showed that the performance degradation caused by passengers’ non-compliance with boarding rules can be significantly reduced by intercepting non-compliant passengers and grouping them for boarding at the end of the process. In [24], passenger boarding was assumed to be a stochastic process. The stochastic model used includes individual passenger behavior and, in part, operational constraints and deviations.

Practically all the publications mentioned above assumed that passengers would comply with the boarding procedure, show up at the time and place specified by the boarding strategy, and cooperate with the handling agent. However, observation of the actual process indicates that some passengers do not comply with the boarding order arrangements. In addition, there may also be random disturbances that alter the boarding process. In our work, we extend previous research, address this problem, and present a model and simulation experiments to evaluate the effectiveness of individual boarding methods under the conditions of the disturbances mentioned above.

1.3. Concept of This Paper

The literature review indicates that the boarding time obtained with different strategies is variable, with sensitivity to many factors. Thus, it is difficult to determine which boarding strategy is best. Moreover, the strategies that many studies indicate as most favorable require complex preparation by handling agents and passengers. In such cases, sensitivity to disruption is even greater. The extensive literature quantifying the effectiveness of boarding strategies by the duration of the boarding process and ranking strategies in terms of preference for particular aircraft types tends to ignore the adverse effects of disruptions.

This research’s primary goal was to analyze the boarding process and existing strategies in the context of possible disruptions. Its result was to expand the knowledge of their impact on determining the preferred strategy. However, due to the size of the issue, we divided the presentation of the course of this research and the results into two parts. The first, presented in this article, is about the methods used and the model created. So, the idea of this article was to present the model and show that it can be used to study the impact of disturbances in the future. Hence, there was a greater emphasis on modeling a nominal situation (which allows validation) and presenting only two disturbances (to show that the model is well suited for the task). The second part of the presentation of the research results focuses on analyzing the impact of various types of disturbances (discussed in Section 3.1) on the efficiency of the boarding process, particularly the boarding strategies used. It will be the subject of another planned publication.

The problem analysis indicated that we are dealing with a dynamic system that is continuous in time and has discrete states. In such a situation, discrete simulation methods and a queuing model are adequate. The simulation study of the boarding process using its model makes it possible to select the best strategy under disturbances occurring in actual conditions. Of the various possible approaches to the boarding process modeling technique, hierarchical, timed, colored Petri nets (HTCPNs) were chosen. They are used to model, describe, and formally analyze discrete concurrent systems. The HTCPN method enables discrete event simulation while facilitating the creation of microscale models, including real process concurrency (which is very important in boarding issues) or the possibility of the dynamic modification of model parameters, facilitating the use of built models in real time. For HTCPNs, the convenience of modeling concurrent events is key. Concurrency is the nature of the process we are dealing with. For example, at the same time, some passengers take their seats on board, others board the aircraft, and other passengers are still being handled at the departure gate. They have also been successfully used to solve air traffic problems [25,26,27,28].

The HTCPN formalism allows mapping the process of assigning seats to passengers, the process of passengers moving to their seats, determining situational conflicts between passengers, the priority of boarding, the priority of taking a seat, whether a passenger after taking his seat must get up to allow another passenger to take his seat, the process of passengers stowing their luggage, and the impact of luggage placement on creating a queue in the aisle. The boarding process model was designed in the CPN Tools simulation environment.

This article is structured as follows. Section 1 presents the research problem, reviews the literature, and proposes a new approach to the topic. Section 2 presents the boarding process, including existing strategies for implementing the process aimed at shortening it. Section 3 discusses disruptions in the boarding process, some of which are included in the presented results. Section 4 presents the boarding process model we developed and implemented as a hierarchical, timed, colored Petri net. In particular, the modeling technique, the general assumptions, the structure of the model, and its validation are discussed. Section 5 presents the results obtained from simulation experiments using the model. Section 6 presents a summary and conclusions.

2. Passenger-Boarding Process

2.1. Boarding Process Stages

Boarding is the process that conditions the boarding of passengers to travel to their destination. Well-executed boarding procedures ensure that only passengers with the correct ticket board the aircraft and that the plane departs on time. Boarding procedures are established to ensure that passengers occupy an assigned or available seat. Handling agents prepare and display signs indicating the departure information, such as the flight number, destination, and scheduled or revised departure time in the event of a disruption. Passengers can be boarded via one, two, or more gates, and the number of gates used affects the efficiency of the handling process.

Boarding begins with consultation and coordination with the flight crew so that all the necessary boarding activities have been completed, and the boarding process can be started. Passengers who have purchased special services and use loyalty program privileges are invited to board first. Airlines usually respect the principle of priority boarding for those traveling with small children, pregnant women, and people with disabilities. Passengers who have purchased priority boarding services and those traveling in a higher service class are also invited to board first.

The general boarding process then begins. Suppose a boarding strategy is used on a particular flight. In that case, the ground agent is responsible for adequately arranging passengers and placing them correctly in front of the gates, depending on the method adopted. Before boarding, each passenger must present a boarding pass, and the ground agent scans the document to confirm the passenger’s appearance on the flight. In addition, the agent may also note the dimensions of the passengers’ carry-on luggage and whether they are within the permitted limit. The agent may also ask them to show their ID or passport.

When the passengers arrive at the plane, they find the assigned seat, the description of which is on the boarding pass (the row number and location). If, however, the seats are not assigned, the passengers occupy any seat. Before the passengers finally take their seats, they must place their hand luggage in the overhead compartments or under their seats, depending on the aircraft’s design and availability. If passengers put their luggage in the overhead compartment, other passengers have to wait, since it is impossible to pass each other in the aisle due to the narrow aisle. The possibility of overtaking is excluded. This also means that the passengers’ orderliness does not change from the time of boarding.

After the final notification of the completion of the boarding process, passengers arriving at the gate after this announcement are considered late, withdrawn from the flight, and unable to travel. A few minutes before departure, there is another consultation with the crew with the information that all eligible passengers have been admitted and that the gate is prepared to close the door. The captain decides when to close the door.

A general diagram of the boarding process is shown in Figure 1.

2.2. Boarding Strategies

Due to the widespread interest in the boarding process, the analysis of accompanying phenomena, and the search for solutions resulting in the improvement of the process and the optimization of time, many boarding strategies have been developed, often re-examined and modified as needed.

In previous years, the “open seating” method was used, where the passenger chose any seat during boarding. The advantage of this approach was that there was no need to organize groups, passengers could approach at any time (in terms of the process time), and travelers could board together. Moreover, if passengers chose consecutive appropriate seats, disruptions could be minor. Nowadays, it is more common to assign a seat to a passenger to occupy for the duration of the flight. This is primarily due to the desire to eliminate the time required for the passenger to decide, potential conflicts between passengers trying to occupy the same seat, and to take advantage of the opportunity to introduce fees for choosing a preferred seat.

The boarding of passengers can be carried out randomly, in groups, or according to a specific sequence of travelers, and the different types of strategies differ primarily in the number of groups into which passengers are divided and the order in which those with specific seats are boarded. The following sections discuss how selected existing boarding strategies work and provide assumptions for their use.

2.2.1. Random

In this method, passengers form a single group. They queue up at the gate and board in whatever order they arrive. This method of seating gives you, on the one hand, no need to follow the rules, the opportunity to board in the group of people you are traveling with, the chance to wait in line if you want to board first, and a more extended time spent at the airport if you wish to board last. The process can run relatively smoothly if passengers spontaneously divide into such two groups. Disruptions and uncomfortable situations, on the other hand, can occur if all passengers want to get on board at once and take their seats as quickly as possible.

2.2.2. Back to Front

This type of strategy involves passengers boarding according to the row of seats in which they are to take their seats: those in the back rows board first, and those seated at the front of the plane continue in turn. Usually, passengers are divided into zones, depending on the rows in the plane. Zones can be any number, ranging from two to the total number of rows in the plane, but usually, in this method, passengers are divided into three zones. This strategy is easy to implement but vulnerable to inefficiency, as congestion is relatively common when moving between rows onboard.

2.2.3. Front to Back

The front-to-back strategy reverses the back-to-front method: seats are taken first for those seated in the first rows of the plane. However, this method is far less frequently used than the back-to-front method. It can be useful and effective when boarding is carried out only through the rear entrance of the aircraft.

2.2.4. Half-Block

This method divides passengers into zones, just like the back-to-front strategy, with the difference that there are more zones, and the boarding order is within one-half of the plane. First, the seats are occupied by the zone at the back on one side of the aircraft, and then, sequentially, all the zones on that side of the plane move to the front. The process is then repeated for the other side of the seats. The boarding sequence used in the half-block method is shown schematically in Figure 2.

2.2.5. By Row and by Half-Row

The by-row method divides passengers into as many groups as rows on the plane. Passengers board in whole rows. This method comes in back-to-front and front-to-back variants. The by-half-row method is a modification of the by-row method, which divides passengers according to the row in which they are assigned a seat and by the part of the plane (right and left of the aisle). Passengers are boarded three at a time and take their seats individually until all passengers on one side of the plane are seated. Then, boarding begins in the same order as the other side. This method also comes in back-to-front and front-to-back variants.

2.2.6. Outside in

This method is also sometimes referred to as window–middle–aisle. This strategy prioritizes boarding for passengers whose seats are by the window. Then, after these passengers are seated, the passengers in the middle enter, and finally, those sitting at the aisle are boarded. This method can achieve high process efficiency and the expected short time. Potentially, this method reduces passenger interference due to stowing of baggage and eliminates the interference of passengers who often have to get up and leave the row to let another person in. This method is relatively easy to implement, but the temporary separation of passengers traveling in a group can be problematic.

2.2.7. Reverse Pyramid

This method consists of boarding passengers in sequence from the seats at the end of the plane and simultaneously from the outside to the beginning of the aircraft and the seats near the aisle. Thus, this strategy combines two methods: back to front and outside in. The boarding sequence used in the reverse pyramid method is shown schematically in Figure 3.

2.2.8. Rotating Zone

In this method, the rows of the aircraft are divided into zones (each zone includes a certain number of rows). Boarding begins with the last seating zone at the back and continues with the first zone at the front. Boarding continues with the farthest still unoccupied zone at the back and, in turn, with the first unoccupied zone at the front. The advantage of this method is that passengers who board at the back and the front do not interfere with each other while locating luggage and taking their seats.

2.2.9. Steffen Method

This method involves taking seats according to the specific seat assigned. The even seats (depending on the number of rows in the plane, as the procedure starts from the last row) at the windows on one side of the aircraft from the end of the plane are taken first, followed by the even seats at the windows on the other side. Next, the odd-numbered seats are taken in the same manner. Then, the even seats in the middle of the aircraft—on one side and, successively, on the other side—and the odd seats are taken. Lastly, the aisle seats are taken, maintaining the division between the sides of the plane and the even and odd seats. The boarding sequence used in the Steffen method is shown schematically in Figure 4.

3. Disturbances in the Boarding Process

The boarding process does not always go as planned. Many reasons can cause this. Identifying and analyzing possible disturbances in the process is a component of quantitative boarding research. Disruptions can be of various types and occur at different stages, both in the departure hall—concerning the service process and boarding strategies—and also difficulties at the aircraft level. Regardless of the term used (disturbances or disruptions), the analysis covers the phenomena described in Section 3.1, mainly related to passenger activity or the reliability of the equipment used in the process. The phenomena described in Section 3.2, called interferences, are unavoidable, although their frequency and severity depend on those mentioned earlier and how the entire process is managed.

A passenger survey was conducted to investigate boarding awareness, experiences with the process, and a broader view of the issue, and the analysis results indicate specific patterns of behavior. Some of the data obtained were also used as input parameters for a model of boarding with interference.

One particular phenomenon during boarding is taking seats by passengers with reduced mobility or disabilities. Based on observations, passengers with reduced mobility or disabilities are almost always boarded at the beginning or end of the process, i.e., as preboarding, so they do not affect the boarding of other passengers and, in this context, do not constitute a disturbance.

3.1. Disturbances in the Departure Hall

The first stage of boarding begins at the gate with the appropriate announcement. From the passenger’s perspective, the goal is to get to one’s seat as smoothly as possible without unnecessarily waiting. Some passengers want to board as soon as possible to take their seats and wait for departure. Meanwhile, others prefer to wait until the last minute in the departure hall to spend the shortest possible time in a cramped space waiting for departure.

Passengers often travel in groups: tour groups, a family of several people, and friends. Usually, these people want to board together. Typically, these people are assigned seats on the plane next to each other, but even if not, they prefer to see that a person from the group is on board and then take their seat rather than parting at the gate.

Passengers also sometimes include those requiring special assistance, appropriately handled according to extended special procedures, and passengers boarding with priority. The number of priority passengers and the timing of their approach to the gate can affect the efficiency of the process. Families with little children often receive extra care during the boarding process. In addition, there are also sometimes standby passengers who receive boarding passes only at the gate, provided there is a vacant seat for them. There is a certain randomness about the described groups of passengers; they appear on flights, but only for a specific flight can it be assessed whether a group occurs and how many people it has.

In addition to the various groups of passengers who modify the boarding order, random situations also affect the process. These include passengers late at the gate, whether for their own reasons or because of delayed flights preceding them. For transfer passengers, a decision is often made to wait for the aircraft to arrive. Another case may be a passenger underestimating the time for service at security or passport control.

It can also happen that a passenger does not show up at the gate, for example, spending too much time at commercial facilities. If such a passenger has checked-in baggage, there is usually a maximum wait because when such a passenger is withdrawn from the flight, the procedure for searching for and withdrawing checked baggage is triggered, which can take a relatively long time.

Other disruptions may also occur on a case-by-case basis. The size and dimensions of carry-on luggage are often checked at the gate. If the limits are not met, an excess baggage charge is applied, which usually takes a few minutes. Passengers with more belongings tend to move more slowly and hold up the line, thus causing other passengers to pass them.

Sometimes, in the case of a high load factor, passengers are encouraged to check their hand luggage and put it on hold during boarding. Then, passengers leave their suitcases right before boarding the plane at the end of the path in the jetway. This sometimes causes a build-up of passengers and queue stops.

Another problem may be the event that a passenger loses their boarding pass while already at the airport and asks at the gate to print a new one, or does not fulfill other formal requirements, and in such a case, the service takes additional time. Sometimes, there is overbooking on flights, meaning more tickets are sold than the physical number of seats on the plane. In such a situation, the agent’s task is to select people ready to change their travel plans. This may cause a delay at the start of the boarding process. Technical problems may also occur, such as the readers’ failure to scan boarding passes or problems with the check-in system.

In addition to all the more or less apparent disruptions described, which occur with varying probability, passenger insubordination can be classified as another disruption affecting the boarding process. Insubordination means the lack of willingness of passengers to cooperate with the handling agent during the boarding process. The reasons for insubordination can be various, such as a lack of awareness or a psychological basis. The behavior of people who travel for the first time and people who travel very often may be different.

Let us take into account the possibility of using a boarding strategy. Additional disruptions may include a passenger’s lack of awareness of the method used or the assigned zone, joining a different group than the one assigned, and, later, passengers overtaking each other on the way to the plane via the jetty. In the context of passenger cooperation, the other side is also essential, i.e., the involvement of employees in the process, their motivation, openness, and support.

Another essential issue is the time available for boarding. If there is enough time before the scheduled departure, the staff may not see the need to enforce the boarding strategy rules strictly. In reality, they can only announce the rules and not enforce them. This can have adverse effects in the long term. Passengers know that the boarding strategy is being used, but nobody enforces the rules, so there is nothing to worry about. Once such a habit is formed, there is much uncertainty about the possibility of achieving the boarding strategy goals. This can be very important in cases where there is little time for boarding, for example, when it starts late. These issues can contribute to the unreliability of the boarding process.

3.2. Interference Inside the Aircraft

When a passenger is at the boarding stage, there may be further difficulties before taking a seat. The first main factor blocking passengers is the need to place their hand luggage. If passengers place their luggage under the seat, they clear the passage faster, but if they want to store their luggage in the overhead bin, often without a free space directly above their seat, they are forced to look for it in another place on the plane. This causes difficulties and prevents the passage of other passengers. In this case, the dimensions and number of pieces of hand luggage are essential. How the luggage is placed in the bin is also important. Suppose the arrangement of items does not maximize the available luggage space. In that case, there is less free space in the bin, and sometimes reorganization is required by removing some items from the bin and putting them back differently.

Another factor is waiting in the corridor. The first passenger who boards has an unobstructed path to their seat. For each subsequent passenger, the factor determining the path is the assigned seat and the seats of passengers who board before a given person. This means there is no interaction if passenger A has a seat at the back of the plane and passenger B, who boards after him, in any row before passenger A’s. However, if passenger B has a seat assigned in the same row as passenger A or at a further distance from the entrance than passenger A, there is a disruption and the need to wait. For all subsequent passengers, the principle is similar, except that the disruption of passengers A and B may also affect the need to wait for all other passengers. Therefore, disruptions can be cumulative.

A common occurrence on board an aircraft is the need to let a passenger in a row pass. This happens, for example, when a passenger assigned a seat in the aisle or the middle takes a seat in the row first, and only then does the person with a window seat reach the row. This creates a blockade until the passengers get up and take their seats in the correct order.

Another situation occasionally occurs when a passenger takes a seat other than the one assigned. For example, a group travels but has seats in different parts of the plane because they checked in late. However, they are in the same group and want to fly together, so they sit next to each other on the plane, hoping to switch seats with the people to whom they were assigned. In such a situation, there may be extra wandering around the plane.

Another disruption, which happens relatively rarely but impacts the boarding process time, is a passenger who cancels the flight while already on board. In this situation, the passenger’s checked baggage (if any) is searched in the hold and withdrawn. On board, however, a thorough check is carried out to see if all the remaining hand luggage has an owner, with precise identification of each item in the overhead bin, and this process takes a relatively long time, depending on the aircraft’s size.

3.3. Implementation of Boarding Strategy

Assuming a specific boarding strategy, we determine the order in which individual passengers board. Let us assume that using the back-to-front strategy, we divide passengers into three groups. Passengers with priority boarding board first and are not assigned to any group. The first group consists of passengers occupying the first rows of the plane. The second group consists of people assigned seats in the middle rows, and the third group consists of passengers occupying seats at the back of the aircraft. We assume that when the announcement is made that boarding has started, passengers with priority boarding will approach the gate first, followed by all passengers from the third group. However, several questions arise. Are passengers aware that the boarding strategy is being applied to their flight? Are passengers from the third group at the gate? If they are at the gate, do they know they are in the third group? Are they aware that their group is boarding? Do they realize in good time that they should approach the gate? For each subsequent group, the questions asked are the same.

If passengers are disciplined, oriented, and cooperative, the boarding process will proceed smoothly, according to theoretical assumptions. However, passengers often do not realize when they should approach the gate, ignore or do not hear or do not understand announcements, do not read boarding passes, are reluctant to approach the gate, etc. This can affect the effectiveness of the boarding strategy used and is one of the aspects generating uncertainty about the reliability of the process. It should also be noted that passengers reporting to the gate not in their group but at any time of their choosing are often not withdrawn by the staff in order to not cause even more confusion.

It was observed that depending on ”he t’pe of flight, the behavior of passengers is different. Passengers on regular flights, often business flights, on which passengers are much more disciplined and willing to cooperate, will have a different approach to the boarding process than on charter flights, when the purpose of the passengers’ trip is vacation. Boarding looks different on short-haul flights, where the number of passengers to be boarded is 180 or less, and on long-haul flights, where 250–400 people board. These comments do not apply to all passengers; they are general but characterize individual situations well.

The issue of passenger insubordination and its impact on boarding efficiency will be the subject of the next stage of our research.

4. Petri Net Boarding Process Model

This section describes the passenger-boarding process model developed using Petri nets based on the CPN Tools software (Version 4.0.1). It reflects situations on the passengers’ path from approaching the gate until they take their assigned seats on the plane. The program includes assigning seats to passengers and then models moving to their seats. Situational conflicts between passengers are identified, such as priority boarding, passing passengers at the gate, the priority of taking a seat, the need to temporarily leave one’s seat to allow another passenger to take a seat, the process of stowing baggage by passengers, and the impact of baggage placement on the formation of a queue in the aisle.

4.1. Petri Nets

Petri nets are used as a tool for modeling, describing, and formally analyzing concurrent systems in many fields of science. They are characterized by an intuitive graphical modeling language supported by advanced methods of formal analysis of their properties. The theory of Petri nets was created in 1962, and as a result of its development, thanks to the flexibility of this theory, many different types of nets were created, and the scope of their applications was expanded [29].

Initially, so-called low-level Petri nets were created due to the expression of the state (marking) of the network only by the number of tokens collected in a given place. Then, the ability to distinguish tokens from each other was introduced, which is the basis of high-level nets, and their representative is colored Petri nets. The graphical notation of colored Petri nets is the same as for low-level ones, but it was combined with the properties of programming languages, thanks to which colored net tokens have their value.

The basis for building a Petri net is a bipartite graph, and the net can have a hierarchical structure. A Petri net model is not only a graphical representation of a given system, but it is also possible to simulate the operation of the network (supported by appropriate tools), thanks to which the model becomes a virtual prototype of the represented system.

A Petri net is defined as follows [30]:

$$\mathrm{N}=<\mathrm{P},\mathrm{T},\mathrm{F},\mathrm{W},\mathrm{H},\mathrm{C},{\mathrm{M}}_0>$$

(1)

where

• $\mathrm{P}$—the set of places;
• $\mathrm{T}$—the set of transitions;
• $\mathrm{F}\subseteq (\mathrm{P}\times \mathrm{T})\cup (\mathrm{T}\times \mathrm{P})—\mathrm{t}\mathrm{h}\mathrm{e}$ set of arcs;
• $\mathrm{W}:\mathrm{F}\to \mathrm{N}—\mathrm{t}\mathrm{h}\mathrm{e}$ arc weighting function (N—natural number);
• $\mathrm{H}\subseteq (\mathrm{T}\times \mathrm{P})$—a set of inhibiting arcs (the definition of the weighting function is omitted here because $\mathrm{W}:\mathrm{H}\to \left\{1\right\}$);
• $\mathrm{C}:\mathrm{P}\to \mathrm{N}—\mathrm{t}\mathrm{h}\mathrm{e}$ space capacity function;
• ${\mathrm{M}}_0:\mathrm{P}\to \mathrm{N}—\mathrm{t}\mathrm{h}\mathrm{e}$ initial marking function;

Places, transitions, and arcs are used to model the static structure of processes, while markers allow for the modeling of their dynamics. Modeling processes in Petri nets is performed as follows:

• Places—represent the passive elements of processes;
• Transitions—represent the active elements of processes;
• Arcs—represent cause-and-effect relationships;
• Tokens—represent states and data.

The state of a process is modeled by the distribution of tokens in the network.

The state ${\mathrm{S}}_{\mathrm{i}}$ of the Petri net $\mathrm{N}$ is described by the marking ${\mathrm{M}}_{\mathrm{i}}$ written as ${\mathrm{S}}_{\mathrm{i}}=\left({\mathrm{M}}_{\mathrm{i}}\right)$, so the state ${\mathrm{S}}_0$ is marked by the initial marking ${\mathrm{M}}_0$. The state change happens by transitioning from one state to another and results from firing one active transition [30]. The appearance of tokens at all inputs of a given transition activates this transition, and only active transitions can be fired. Firing involves taking tokens from all input locations and adding them to all output locations of a given transition.

The transition ${\mathrm{t}}_{\mathrm{i}}$ is active in marking $\mathrm{M}$ only if [30]

• Each input place contains a sufficient number of tokens;
• None of the input places with an inhibiting arc contain tokens.

So, for transition ${\mathrm{t}}_{\mathrm{i}}$ to fire, Equations (2) and (3) must be satisfied.

$$(\forall \mathrm{p})\left(\mathrm{M}\right(\mathrm{p})\ge \mathrm{W}(\mathrm{p},{\mathrm{t}}_{\mathrm{i}}\left)\right)$$

(2)

$$(\forall \mathrm{p})\left(\right(\mathrm{I}\left({\mathrm{t}}_{\mathrm{i}},\mathrm{p}\right)=1)\Rightarrow \mathrm{M}(\mathrm{p})=0))$$

(3)

Firing the ${\mathrm{t}}_{\mathrm{i}}$ transition consists of two steps:

• Removing W(p,t_i) tokens from each input place;
• Adding W(t_i,p) tokens to each output place.

This process is described in Equation (4).

$$\forall \left(\mathrm{p}\right){\mathrm{M}}^{\prime }\left(\mathrm{p}\right)=\mathrm{M}\left(\mathrm{p}\right)-\mathrm{W}\left(\mathrm{p},{\mathrm{t}}_{\mathrm{i}}\right)+\mathrm{W}\left({\mathrm{t}}_{\mathrm{i}},\mathrm{p}\right)$$

(4)

4.2. General Assumptions of the Model

Constructing a simulation model of the passenger-boarding process began with determining the boarding method. The order of boarding of individual passengers was determined by the selected method. Selected boarding strategies were modeled: back to front, outside in, random, rotating zone, by row, reverse pyramid, and the Steffen method. The time in the model was represented by real numbers. The basic method of handling departing passengers was adopted, and the process was analyzed in the case of the service taking place at one gate. The analyzed case was boarding from the passenger bridge because only then can the effectiveness of boarding methods be objectively assessed. An assumption was made regarding the passenger service time at the gate, with two scanners available. It was assumed that passengers were at the gate, and the first passenger arrived at the boarding start time. This assumption was based entirely on observations of the actual situation. Passengers should be in the departure hall near the gates at the scheduled boarding time. And this is the case in reality. The vast majority of passengers (if not all) obey this recommendation. A queue of people is ready to enter, practically always before boarding begins. Therefore, we did not analyze the case of a delayed process start due to the absence of passengers. Approaching the gate is continuous, and the time difference between subsequent passengers is due only to the short time needed to move to the boarding pass reader.

To conduct a model study of the passenger service system at an airport, appropriately verified input data should be accepted. An essential input datum necessary for the analysis of the functioning of the process is the identification of the flow of reports. Let us analyze the flow of passengers reporting to service at the gate. We can see that these passengers have different characteristics of reports, which result from various factors, but mainly from the passengers’ behavior.

The diagram in Figure 5 shows the model’s components with references to the corresponding parts in the simulation program.

The Boeing 737–800 aircraft was used for the analysis. The Boeing 737 is the world’s most popular narrow-body, medium-range passenger aircraft. In the analyzed case, the single-aisle configuration of the Boeing 737–800 contains 31 rows and 186 seats arranged in threes on both sides of the aircraft. The model developed in this paper allows for easy updating of the configuration for a different single-aisle aircraft, with a different number of rows, seats per row, baggage compartments, etc. The Boeing 737 was selected for modeling to enable the comparison of results with other studies that also consider this type of aircraft.

We assume that boarding takes place through one gate with two boarding pass readers and then one entrance to the plane at the front of the aircraft. The tokens representing passengers are assigned attributes regarding the seat at the initial stage. Depending on the chosen method, passengers enter the plane randomly or in a set order, which is determined by defining the times when the tokens appear at the entrance to the program.

We assume that there are precisely as many places in the corridor as rows in the plane, plus one place designated as “0” at the entrance to the aircraft. By design, there should only be one passenger in one place in the corridor and at the entrance to the plane. This means that if one passenger is at the entrance to the aircraft, no one else can be there, and a moving passenger occupies the places in the corridor. An exception to this rule is when a passenger leaves a seat to let another passenger take a seat in the row. To simplify the model and avoid taking into account the process of moving the entire queue back, we assume that in such a situation, two or three passengers can be in one place in the corridor (in reality, the exiting passenger can often also go forward or wait in the sector opposite).

The base model assumes different values for the load factor of the aircraft, assuming that the entire aircraft is filled with economy-class passengers. This allows us to best examine the strategy’s effectiveness when all 186 seats (the aircraft’s maximum operational capacity) are available for sale. This is a typical approach in this type of research because, in such a case, all people are subject to the applied boarding method, and the time required to complete it is the longest, which allows us to observe the differences best. At the same time, it makes it easier to compare results. The model developed allows for easy implementation of other travel classes by defining separate groups of passengers with higher priority. Also, it is easy to adopt different ways of assuring the comfort of business class passengers, such as excluding the use of the middle seat (practiced, for instance, by LOT Polish Airlines). However, this research did not consider them because it compares boarding methods, and passengers from other classes are not subject to them.

The primary purpose of the program is to measure the boarding time. This time is counted from the moment the first token appears in the first place of the model until the last passenger takes their designated seat. Passengers are assumed to enter directly, one after another, without delays at the entrance. The time of service at the gate and the time of passengers passing through the jet bridge are represented by random numbers from the assumed intervals. At the same time, the appropriate times of passenger passage from the plane entrance to the first row, the time of passage between subsequent rows, and the time of taking a seat in the row were assumed. For example, the procedure for generating the time of passengers passing through the jet bridge is as follows.

Data on the average speed of human movement and the distance that must be covered in the case study were used to estimate the time needed for passengers to walk from the departure gate to the aircraft’s entrance. It was assumed, based on [31], that the walking speed of a passenger is a random number between 0.60 [m/s] (for passengers over 65 years of age) and 1.34 [m/s] (for passengers younger than 30). The distance passengers need to walk from the gate to the aircraft’s entrance was measured at Warsaw Chopin Airport (ICAO code: EPWA; IATA code: WAW). Based on the distance and speed of the passengers, the time required to walk from the departure gate to the entrance to the aircraft was determined. Assuming that the number of passengers in each age group (from 20 to 90 years) is the same, the random variable describing this time for each passenger is generated using the bridge() function. The empirical cumulative distribution function used in the bridge() function is presented in Figure 6.

An additional attribute assigned to a passenger that impacts the boarding process is the number of pieces of hand luggage. It was assumed that a passenger could have one or two pieces of luggage. The number of bags is randomly assigned, with a priori assumed probability. In reality, passengers most often have one piece of luggage. The case when passengers have more is omitted. A matrix of luggage racks is developed, which is used to check and update their occupancy. The number of overhead bins in the plane is 32, of which 28 have space for four pieces of luggage and 4 for three pieces.

The first passenger approaches one of the two service points at the gate, where the boarding pass is scanned, and documents are checked, which takes a random amount of time from the accepted time interval. Simultaneously, another passenger approaches the second position at the gate (the second boarding pass reader). The time spent by a particular passenger at the gate is generated using the gate() function, which uses measurements taken at WAW, and an empirical cumulative distribution function created on that basis, presented in Figure 7.

After the passengers have been served, they go to the jet bridge and move toward the plane entrance, which takes a random amount of time. Passengers can overtake each other during the gate service and transition to the plane. This was assumed based on the observations. Please note that overtaking is allowed only at the gate and jet bridge, not inside the aircraft. Then, the first passenger takes place at the plane entrance, designated as place “0” in the corridor. The time of the passenger’s entry into the aircraft is based on the observations and measurements at WAW.

On board, the passenger first moves along the corridor to his row. Moving through the corridor is determined by taking successive places in the corridor (at the same time, the token indicating the occupancy of the place in the corridor appears and disappears, depending on the passenger’s presence in a given place). After the passenger reaches his row, the passenger’s seat is checked on which side of the plane he has a seat, and then the status of the occupancy of the seats in the sector is checked. When taking subsequent seats, the occupancy status is automatically updated. In the meantime, it is assessed whether the passenger’s seat is by the window, in the middle, or by the corridor. The time of passenger passage between subsequent rows and the time of blocking the aisle, depending on the actual occupancy in the sector, is based on the values provided by [32].

Additionally, if the passenger has luggage, it is loaded into the overhead luggage bin or under the seat, depending on the current occupancy status of the overhead luggage bins. If the overhead compartment runs out of space, the passenger locates the luggage under the seat. Then, the passenger takes his seat.

Table 1. General assumptions.

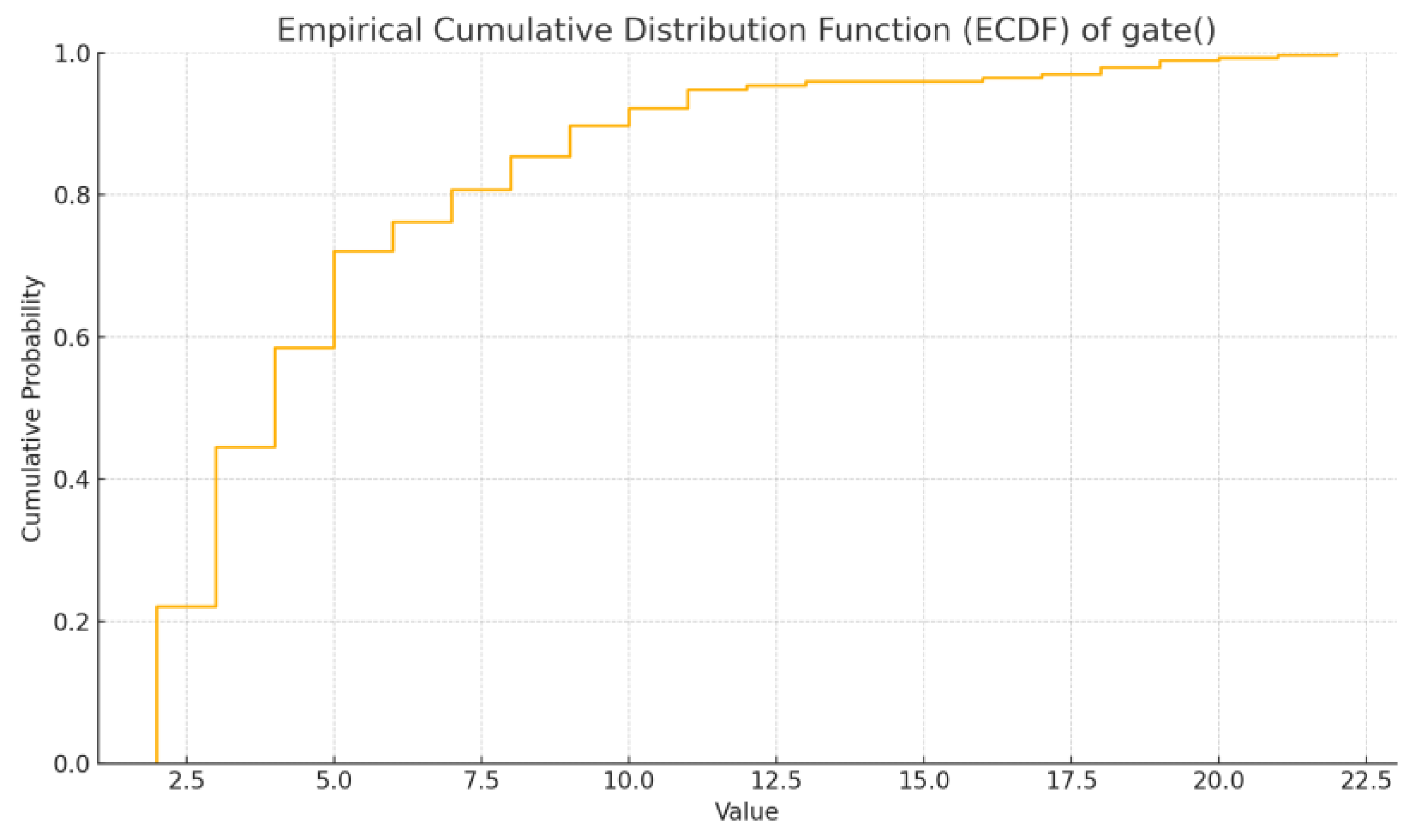
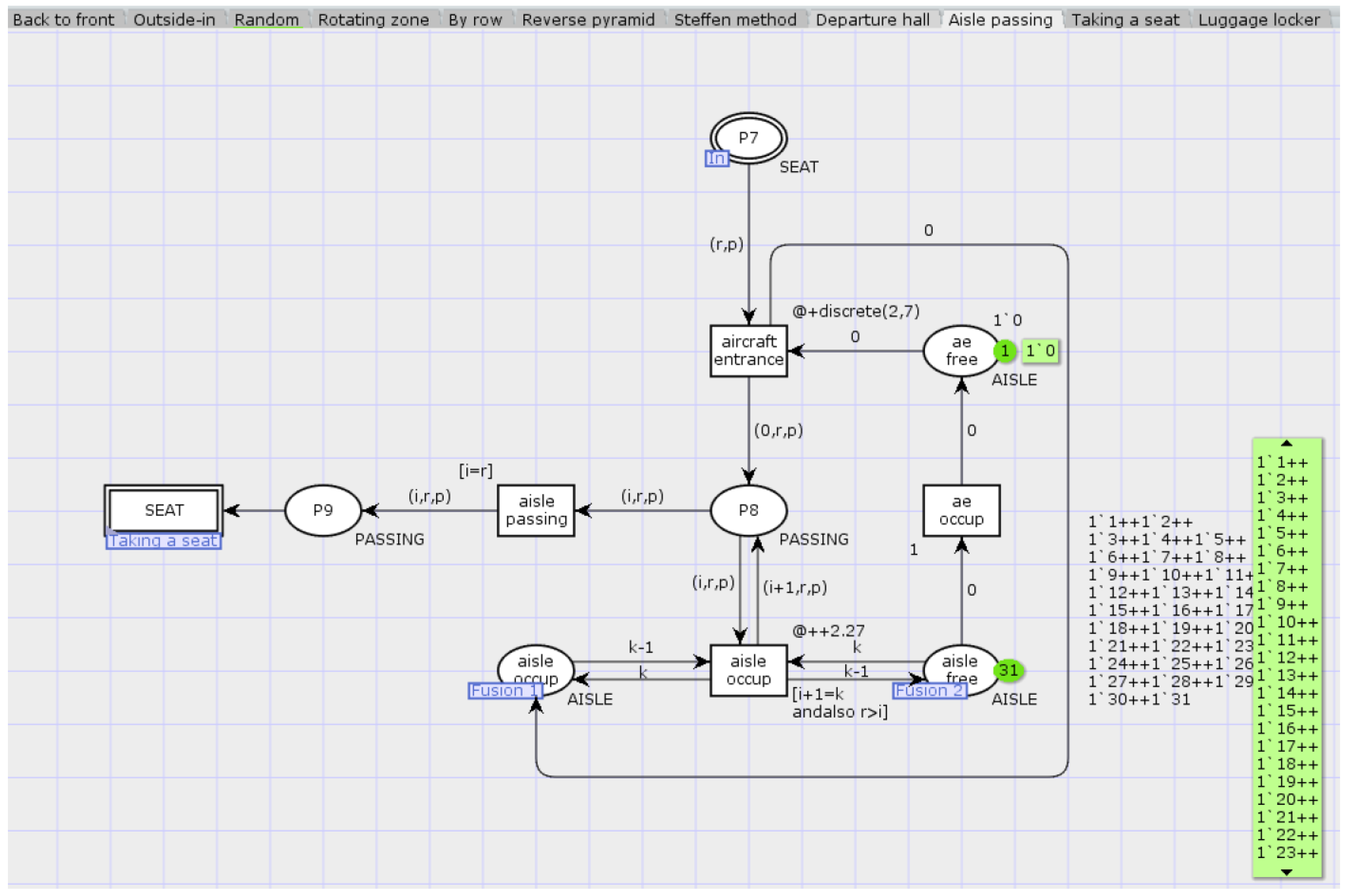
Parameter	Value
Aircraft type	Boeing 737–800
Number of seats in the aircraft	186
Number of corridors in the aircraft	1
Number of places in the corridor in the aircraft	31 + “0”
Number of rows in the aircraft	31
Number of seats in one row	6
Boarding type	Passenger bridge
Number of open entrances to the aircraft	1
Seat factor	Different values
Number of gates for flight service	1
Number of readers for scanning boarding passes at the gate	2
Service time at the gate	2–22 [s] 1
Time of the passenger’s passage through the jet bridge	42.54–95.00 [s] 2
Time of the passenger’s entry into the aircraft	2–7 [s] 3
Time of the passenger’s passage between subsequent rows	2.27 [s]
Time to occupy a place in a row (the time of blocking the corridor), in the following cases:
Seats by the corridor and in the middle are occupied;	4.2 [s]
A seat in the middle is occupied;	3.6 [s]
A seat by the corridor is occupied;	3.0 [s]
The seats are free.	0 [s]
Number of pieces of passenger’s hand luggage	1 or 2
Time to put luggage in the overhead bin	6–30 [s] 4
Time to put luggage under the seat	0 [s]
Number of luggage overhead bins	32

¹ Cumulative distribution function presented in Figure 7; ² cumulative distribution function presented in Figure 6; ³ discrete random variable, uniformly distributed; ⁴ discrete random variable, uniformly distributed.

presents a summary of the adopted model assumptions. To properly parameterize the model, the assumptions were based on data available in the literature and specific data obtained from a selected airport regarding the passenger-handling process during a single flight. The model parameters in Table 1 represent average values or ranges of possible values. The model allows easy modification of the parameters and treating them as (i) constant values, beneficial for comparing results, or (ii) random variables generated for each simulation run or passenger.

4.3. Color and Function Declarations

Table 2. Description of the declaration of a set of colors.

Declaration	Description
colset AISLE = INT;	A set defining places in the corridor
colset ROW = INT;	The row in which the passenger is assigned a seat
colset POSITION = with A|B|C|D|E|F;	Position in the row of the seat assigned to the passenger
colset SEAT = product ROW*POSITION timed;	Passenger seat description
colset PASSING = product AISLE*ROW*POSITION timed;	Current place in the corridor
colset SECTOR = product ROW*BOOL*BOOL*BOOL;	Occupancy status in a given row on one side of the plane
colset LUGGAGE = INT;	The number of pieces of luggage that a passenger has
colset PAXATTRIBUTES = product ROW*POSITION*LUGGAGE timed;	Designation of the passenger’s row, seat, and luggage
colset LOCKER = with L1|L2|L3|L4|L5| L6|L7|L8|L9|L10|L11|L12|L13|L14|L15|L16;	A set of available storage spaces
colset SCANNER = unit timed;	A set representing the scanner occupancy in the gate
colset LIST = list SEAT timed;	A set representing an ordered list of passengers
colset LISTA = list SEAT timed;	A set representing a group of passengers
colset LISTB = list LISTA timed;	A set representing an ordered list of passenger groups

describes the defined color declarations.

Table 3. Function descriptions.

Function	Description
fun gate;	Function for determining the time of gate service
fun bridge;	Function for determining the time of passage in the jetway
fun numberofluggage;	Function for determining how many pieces of baggage a passenger has
fun left(right);	Functions for determining on which side of the plane a passenger will take a seat
fun occupation;	Function for updating the status of sector occupancy
fun statusofsector;	Function for checking the status of sector occupancy
fun luggage;	Function for determining the time of placing baggage
fun locker;	Function for updating the status of luggage overhead bin occupancy

contains a description of the functions defined in the program.

4.4. Model Structure

In this study, the developed model of the boarding process uses the possibility of creating a hierarchical structure offered by the CPN Tools package, which makes it convenient to use the formalism of hierarchical, timed, colored Petri nets to model, simulate, and analyze discrete systems. So-called pages represent individual functional elements. Below, the pages representing the essential elements of the model structure will be discussed.

4.4.1. Departure Hall Page

The adopted model assumes that service occurs at one gate with two scanners. This is the most typical way when using a jet bridge and for a narrow-body aircraft. The service time at the gate is a random integer in the range of 2–22 [s] implemented in the gate() function and generated by passing through the transitions “gate scanner1” or “gate scanner2”, respectively. One passenger can be served at one scanner at a time. Then, through the transition “jet bridge passing”, the passenger passes through the jet bridge to the plane entrance. The passage time is assumed as a random real value in the range of 42.54–95.00 [s], implemented in the bridge() function. When two scanners are used (as in the model developed), the passenger who first approaches the scanner can take longer to be served than the passenger who approaches the second scanner later. Therefore, they change their order. In the jet bridge, if passengers move at different speeds, they may overtake each other. Random service times at the gate and passage through the jet bridge cause passengers to overtake each other and disrupt the established original order, which happens in reality. Figure 8 presents the model of passenger service at the gate, together with passage through the jet bridge.

4.4.2. Aisle Passing Page

The next page implements entering the plane and moving the passenger along the corridor. First, the transition “aircraft entrance” checks whether the place at the aircraft entrance “0” is free. If it is free, the token appears there, and the next passenger cannot enter the plane. Entering the plane takes a random time in the range of 2–7 [s]. A uniform discrete distribution describes this random variable. The transition “ae occup” implements the releasing of a place at the aircraft entrance, and a token in the place (ae free) represents a free place at the aircraft entrance. Then, the transition “aisle occup” implements moving along the corridor. The row the passenger must reach is checked, and the occupancy of the places in the corridor is checked. The current status of the corridor occupancy is represented in the places (aisle free) and (aisle occup). The place (aisle free) stores the free places in the corridor, and the place (aisle occup) stores the tokens of the places in the corridor that are currently occupied. The process continues until the passenger reaches the place in the corridor, at the row where he is assigned a seat, and takes it. Only after taking a seat is the corridor token released at the given row. Passing between the successive rows takes 2.27 [s]. Each time the next place in the corridor is occupied, the passenger must wait to continue the passage along the corridor because only one person can be in one place in the corridor at a time. Figure 9 shows the implementation of the aisle passing page in the program.

4.4.3. Taking a Seat Page

When the passenger reaches the row in which he is to sit, he is assigned an attribute regarding having baggage (transition “luggage assign”) using the function “fun numberofluggage”. Then, the side of the plane on which the passenger is to sit is checked, and the transition is realized using the transition conditions “left side” (or “right side”) defined by the functions “fun left” and “fun right”, respectively.

The passenger’s transition is realized successively, depending on whether he has luggage. If the passenger has luggage, through the transition “L pass with bag” (or “R pass with bag”), he is directed to the next page, “Luggage locker”, where the process of placing luggage is realized. After passing this process, the token returns, and through the transition “L bag placed” (or “R bag placed”) is directed to the transition checking the current occupancy of seats in the sector “L check sector status” (or “R check sector status”). In the case where the passenger does not have luggage, directly through the transition “L pass no bag” (or “R pass no bag”), he is directed to the transition checking the sector status.

Places (L sector status) and (R sector status), respectively, store tokens showing the presence of passengers in the seats in the row. If all seats in the row on one side of the aircraft are free, the sector status is specified by “(row number, false, false, false)”. In such a situation, the passenger who arrives can immediately take his seat, and the “fun status of sector” function implemented in the “L check sector status” transition (or “R check sector status”) for such a case does not add time, because the corridor is immediately vacated. Passing through the “L sector occup update” transition (or “R sector occup update”) during the implementation of the “fun occupation” function changes the occupancy status of the sector. Depending on the assigned seat, the appropriate value of the Boolean variable representing the given seat changes to “true”.

Then, when the next passenger arrives at the row and has a seat assigned on the selected side of the plane, the sector’s occupancy is rechecked. Suppose at least one value is in the “true” position. In that case, the conditions of the “fun statusofsector” function, defined for each seat, are checked one after another—near the corridor, in the middle, by the window. If a passenger sitting near the corridor enters, they can take their seat immediately. However, when the entering passenger is to take a seat in the middle, the current occupancy of the seat near the corridor is checked. If the seat is occupied, the passenger sitting near the corridor must stand up to allow the passenger sitting in the middle to take their seat. We assume the passenger waiting and then taking their seat lasts 3 [s], so this time is added. We proceed similarly in other cases when letting a passenger pass in the row is necessary.

After taking a seat, by going through the transition “L aisle occup” (or “ R aisle oc-cup”) to the place (L seats occup)/(R seats occup), where the tokens representing passengers in occupied seats are stored, the aisle occupancy token at the passenger’s row is released. Figure 10 shows the “Taking a seat” page implementation in the program.

4.4.4. Luggage Locker Page

If passengers have luggage, locking the luggage is carried out before they take their seats. Because there are fewer places in the overhead luggage bins than seats in the plane, passengers place their luggage partly in the overhead bins and partly under the seat. A process was modeled to show the available places in the overhead bins and update occupancy after passengers have stored their luggage. It is carried out in the “locker update” transitions via the “fun locker” function. Places (locker free) and (locker occup) store markers showing how many places in the overhead bins are currently free and how many are occupied.

It is assumed that if there are free places, passengers first put their luggage in the overhead bins, and after each baggage placement, the occupancy of the overhead bins changes. If no more places exist in the overhead bins, the passenger puts their luggage under the seat. In the case of putting their luggage in the overhead bin, an additional time is added, calculated using the “fun luggage” function, through the “put bag in locker” transition, which specifies that the time of putting one piece of luggage is a random integer in the range of 6–30 [s]. This parameter was determined based on the values presented in [32]. The random value is defined using the luggage() function. The random variable describing the baggage placement time was assumed to be characterized by a uniform discrete distribution. It reflects the dependence on the quantity of luggage carried aboard and the amount of luggage in the overhead bin when the passenger reaches the row of their seat.

If there is no space in the appropriate overhead bin, the passenger will have to put their luggage under the seat, and in this situation, no additional time is added. We do not consider that passengers walk in the aisle to search for the overhead bin space available in other aircraft parts. These situations are not very frequent, and, commonly, the crew searches for the available space in the overhead bins in the different parts of the aircraft. Other papers addressing the boarding process took a similar approach, where inserting luggage took a certain amount of time, fixed or random. Usually, the details were not considered.

If the passenger has two pieces of luggage, the condition is first checked to see whether any space is available in the overhead bin. If space is available, the passenger puts the first piece of luggage in the overhead bins, and the time for stowing the luggage is added. Then, checking the availability in the overhead bin is carried out analogously for the second piece of luggage. After placing the luggage, the program returns to the “Taking a seat” page through the “End” transition. Figure 11 shows the implementation of the “Luggage locker” page in the program.

4.4.5. Boarding Strategy Representation

The passengers’ boarding order is defined in the pages representing the appropriate boarding strategies. A token with attributes regarding the row number and the seat position in the row represents each passenger. The selection of the boarding strategy, and thus, the defined order of boarding, is performed by unlocking the appropriate strategy. Then, after starting the program, the tokens appear in a specific order in the queue at the gate. Due to the size of this article, the representation method is presented only for the back-to-front strategy. The remaining strategies are mapped analogously.

The model created for the back-to-front strategy assumed a division into three zones. The existence of three zones is only illustrative, although very typical. Zone 1 includes rows 1–10, zone 2 includes rows 11–20, and zone 3 includes rows 21 to 31. Passengers with seats in zone 3 board first, then zone 2, and lastly, zone 1. Figure 12 shows how this strategy is represented in the simulation program. We can see three sets of tokens corresponding to passengers in three zones. The developed model allows the number of zones in the block strategies to be modified and also allows for different ways of allocating passengers to various zones. This is the case with the other boarding methods used.

4.4.6. Passenger Behavior Modeling

Passenger behavior modeling can be considered on several levels.

The first is the activities passengers perform during the boarding procedure. These activities depend, in part, on the characteristics of the passengers and the seats occupied. For example, a passenger with hand luggage behaves differently from a passenger without luggage. The associated behaviors (which vary from passenger to passenger but follow the procedure) are modeled by including them in the model structure. For example, in Figure 10, the “L pass with bag” and “L pass no bag” transitions are used.

The second level is behavioral differences, which result in different times for completing particular activities. Here, one can point out, for example, differences in the way of moving on the jet bridge that result in differences in passage times. This behavior is modeled by functions that generate random execution times of activities according to a given probability distribution. An example is the luggage() function shown in Figure 11, used in the “put bag in locker” transition.

The third level is behavior concerning the ground-handling agent’s recommendations to execute the adopted boarding strategy correctly. This behavior, in particular, disobedience to the applied strategy and approaching the gate at a different time than scheduled, is modeled by changes in the timestamps assigned to the tags corresponding to each passenger. For example, in Figure 12, showing how the back-to-front method is implemented, all timestamps (marked with @ and a real number) are 0.0, corresponding to the correct situation. If one wanted to model that one of the passengers approaches the gate out of sequence, it would be necessary to modify the corresponding timestamp accordingly.

4.5. Model Validation

To verify the correctness of the adopted model parameters, a comparative analysis of the obtained simulation results was performed with data obtained by other researchers. The variable used for validation was the total boarding time of a group of passengers. According to [33], the average boarding time of 162 passengers to a Boeing 737–800 aircraft is 22 min and 15 s. According to [34], the standard boarding time obtained when boarding a Boeing 737–800 is 22 min, with a wholly filled aircraft with a capacity of 170 seats. It is important to emphasize that the validation aim was not to achieve exact numerical agreement with previous studies but to demonstrate qualitative consistency. Various model parameters may not be incorporated identically across papers, often due to incomplete or ambiguous methodological descriptions. Therefore, a direct comparison with specific numerical values reported in previous studies is of limited relevance. Instead, we focused on showing that, under roughly similar conditions, our results align with those previously reported in a general sense. The consistency in the relative effectiveness of the boarding strategies is more relevant, that is, their ranking from best to worst, which should be maintained in the baseline scenario.

Model calibration was carried out in two stages. The first one concerned refining the number of pieces of luggage held by a passenger and the number of seats available in the luggage bins. Especially about the former, it is challenging to establish any general characteristics, as it depends on the distance, destination, and many other parameters that are difficult to capture. The second calibration stage concerned the passenger’s transition time from the gate to the aircraft entrance and the speed of movement inside the aircraft. The first of these values was determined after a precise determination of the distance to walk and a deeper analysis of the speed of human movement. We determined the second with an accuracy of two decimal places, which allowed for the precise calibration of the model.

To validate the model, simulations were performed for the random strategy for the number of passengers, 162 and 170, respectively, as in the referenced studies, and 186 for the full capacity of the aircraft. Average values were used to compare the results. For example, the gate service time values in Table 1 were randomly generated (according to the empirical probability distribution) for each passenger separately. Thus, 186 different values of this time were used (for a fully booked aircraft). Therefore, in a single simulation run, these values were averaged. The same applied to the other random parameters. With such a random mechanism, we obtained (as a result of the modeling) a single value of the boarding time. In subsequent runs, these values were similar, but of course, they varied slightly. To minimize the effect of these differences, 1000 simulation runs were performed, and the obtained boarding times were averaged.

Table 4. Simulation results for the random strategy: model validation.

Strategy	Number of Passengers	Average Boarding Time [m:s]	Minimum Boarding Time [m:s]	Maximum Boarding Time [m:s]
Random	162	22:04	19:06	25:44
	170	22:26	19:32	25:48
	186	23:25	19:56	27:06

presents the details of the simulations performed along with the obtained results. The average time obtained by performing 1000 simulations for boarding 162 passengers was 22 min 4 s, and for 170 passengers, 22 min 26 s, which, with the reference results, proves the correctness of the model. The average boarding time for 186 passengers was 23 min and 25 s.

Section 5.1 further validates the model and presents our model’s results for the no-disturbance situation for the other boarding strategies. An in-depth analysis of the performance of various methods was conducted, followed by a comparison of their rankings with those from existing studies. The analysis was made by comparing the results obtained not only with [33] or [34], as mentioned before, but also, among others, with [1,7,10]. They were consistent (in a qualitative sense) with studies published earlier. This means their rankings from best to worst were the same. It is important to notice that the methods are often examined selectively in different studies, and the list of methods analyzed varies. It can be seen that the number of zones and the allocation of seats in each zone were important in terms of the boarding times obtained. Consequently, how the zones are structured can also influence the order of the preferred strategies. However, we managed to obtain analogous results by quite precisely reproducing the conditions used in other studies, which is one of the elements of positive validation of the model.

Section 5.1 also contains the tests performed to verify the statistical significance of the results. These tests support the conclusion that the differences observed in boarding times were statistically significant with extremely high probabilities.

Sensitivity analysis is an essential part of simulation modeling. In this paper, the impacts of different numbers of boarding pass scanners at the gate and the number of passengers (the seat factor) on the boarding time were analyzed. The results are presented in Section 5.2 and Section 5.4.

5. Simulation Experiments with the Model

First, several variants were modeled in the correct course of the process to examine the strategies’ behavior and compare their effectiveness in the process without disruptions, but with different levels of the aircraft seat factor and other parameters tested. During the analysis, attention was paid to the average process duration obtained based on a simulation sample repeated 1000 times. We decided that the average boarding time would allow a clear comparison of the studied strategies. All random variables were generated in each run according to their probability distributions. Similarly, the minimum and maximum values were selected from all 1000 simulation runs.

Then, a series of simulations were performed for the given disruptions. Different types of disruptions were defined and simulated. Then, it was verified how the boarding time with the applied methods would change during disruption compared with the nominal boarding time. This analysis allowed for selecting the best boarding strategy in the analyzed cases.

5.1. Correct Process Flow: No Disruptions and Seat Factor of 100%

First, the boarding strategies were analyzed for the correct course and assuming maximum cabin occupancy (186 passengers).

Table 5. Simulation results for different methods at a seat factor of 100%.

Strategy	Average Boarding Time [m:s]	Minimum Boarding Time [m:s]	Maximum Boarding Time [m:s]
Back to front	26:05	23:10	31:23
Outside in	23:04	20:06	26:52
Random	23:25	19:56	27:06
Rotating zone	24:10	21:19	29:11
By row	27:00	23:11	32:28
Reverse pyramid	23:36	20:39	28:04
Steffen method	22:58	20:05	26:53

summarizes the simulation results obtained for the individual boarding methods, and Figure 13 shows the graphical representation of the results.

In the correct course of the boarding process (without disruptions), the best results were obtained with the Steffen method strategy, followed by the outside-in and random strategies. The worst results, i.e., the longest boarding time, were obtained using the by-row method. The back-to-front method showed results that were slightly better than those of the worst strategy.

To check the statistical significance of the results obtained through simulation, statistical tests were performed for all pairs of boarding strategies presented in Table 5. The results for the random, back-to-front, and outside-in strategies are presented.

Table 6. Boarding times for three strategies used for statistical tests (excerpt).

Simulation Run	Random [s]	Back to Front [s]	Outside In [s]
1	1196.2	1389.7	1205.5
2	1235.5	1394.1	1214.7
3	1240.3	1395.7	1225.5
4	1246.4	1397.9	1230.5
5	1246.9	1398.3	1235.7
6	1252.5	1399.2	1238.4
7	1262.4	1401.9	1239.9
…	…	…	…
Mean	1404.6	1565.1	1383.6
Variance	3900.7	5198.9	3696.1
Standard deviation	62.5	72.1	60.8

shows the first few rows of the original simulation source data. As already stated, each column corresponding to a boarding strategy contains 1000 rows (for 1000 simulation runs). In addition, the last lines show the mean, variance, and standard deviation values calculated for the sample.

The histograms showing the distributions of boarding times for all three strategies are shown in Figure 14, and the box plot visualizing the distributions is shown in Figure 15.

Welch’s t-test was used for the data shown in Table 6. Welch’s t-test is a parametric test to determine whether the means of two independent samples differ significantly, particularly when their variances are unequal. Two hypotheses were adopted for each pair of boarding strategies, A and B:

H₀: 

Mean of boarding time for strategy A = mean of boarding time for strategy B;

H₁: 

Mean of boarding time for strategy A < mean of boarding time for strategy B.

The test uses the t-statistic for two independent samples, which is calculated using the following formula:

$$t={\displaystyle \frac{\overline{X_1}-\overline{X_2}}{\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}}$$

(5)

where

• $\overline{X_1}$ and $\overline{X_2}$ are the samples’ means;
• $s_1^2$ and $s_2^2$ are the samples’ variances;
• $n_1$ and $n_2$ are the samples’ sizes.

The test also uses p-values to infer statistical significance. The p-value is computed by comparing the calculated t-statistic with the theoretical t-distribution. Essentially, it represents the probability of observing a difference as extreme as (or more extreme than) the one measured, assuming that the actual means are equal.

The commonly used boundary (significance level) is α = 0.05. This means if p < 0.05, the difference in the means is considered statistically significant, i.e., there is strong evidence to reject the H₀ hypothesis of equal means. Conversely, if p ≥ 0.05, then the data do not provide strong enough evidence to conclude that there is a difference between the means.

In our model, for the random versus back-to-front strategies, the t-statistic was −53.2, and the p-value was less than 0.001. For the random versus outside-in strategies, the t-statistic was 7.6, and the p-value was less than 5·10⁻¹⁴. For the back-to-front versus outside-in strategies, the t-statistic was 60.9, and the p-value was less than 0.001.

The t-test for the random vs. back-to-front strategies showed a very large negative t-statistic with an effective p-value of 0, suggesting that the back-to-front strategy boarding time was significantly longer than that of the random strategy.

The t-test for the random vs. outside-in strategies yielded a positive t-statistic with a very small p-value, indicating a significant difference, where the random strategy boarding time was significantly longer than the outside-in strategy time.

The t-test for the back-to-front vs. outside-in strategies showed a very high t-statistic with an effective p-value of 0, again confirming that back-to-front strategy boarding time was significantly longer than that of the outside-in strategy.

The Mann–Whitney U test was also applied to confirm the significant differences between the methods. The output showed the following:

–

For the random vs. back-to-front methods, U-statistic = 43,328.5, and p-value = 5.95·10⁻²⁷⁴;

–

For the random vs. outside-in methods, U-statistic = 594,663.0, and p-value = 2.29·10⁻¹³;

–

For the back-to-front vs. outside-in methods, U-statistic = 975,488.0, and p-value = 8.2·10⁻²⁹⁷.

These non-parametric tests and the medians support the conclusion that the differences observed in the boarding times were statistically significant, with extremely low p-values across the comparisons.

5.2. Correct Process Flow: Variable Seat Factor

Planes are often not 100% full. Air carriers strive to maximize the revenue from each flight and the appropriate profitability. This is achieved by balancing the seat factor and the value (revenue) from the sold seat [35]. Demand analyses and specialist revenue management systems are used for this purpose. The main challenges faced by analysts are managing the availability of seats in such a way that by limiting the availability of cheap tickets while waiting for high-priced demand, they do not lose passengers and, as a result, cause the plane to fly with empty seats, or, conversely, fill the plane too early with low-priced demand, which means that there are no more seats for passengers who would be able to pay more.

In this section, we analyze whether there were differences between the results obtained for the different boarding strategies in the case of a 100%-filled aircraft and a seat factor at a lower level. We randomly removed tokens representing selected seats in the model to obtain the appropriate lower seat factor.

Table 7. Simulation results for different seat factor values.

Strategy	Average Boarding Duration [m:s]
	SF 100% (186 pax)	SF 85% (158 pax)	SF 70% (130 pax)	SF 55% (102 pax)
Back to front	26:05	23:51	20:54	18:05
Outside in	23:04	21:16	19:06	17:09
Random	23:25	21:29	19:18	17:21
Rotating zone	24:10	21:57	19:40	17:29
By row	27:00	24:32	21:29	18:27
Reverse pyramid	23:36	21:32	19:15	17:12
Steffen method	22:58	21:06	18:56	17:02

presents the results obtained during the simulation for the individual boarding strategies and the corresponding seat factor level. As can be seen, for all boarding strategies, the processing time decreased with the decrease in the number of passengers. Regarding the strategy performance, the by-row strategy showed the longest boarding time for all the tested seat factor (SF) levels, followed by the back-to-front strategy, the two worst methods. For example, it can be seen that the time obtained by the back-to-front strategy at an SF of 85% was longer than the process time obtained at an SF of 100% for most of the other methods. The best method for all SF levels remained the Steffen method and the outside-in method. At an SF equal to 70%, the result of the reverse pyramid strategy changed, which showed a shorter time than the random strategy, and this could also be observed at an SF of 55%. Figure 16 shows the boarding times obtained by the different strategies for different seat factor values in graphical form.

The results show that the load factor issue was significant in the effectiveness of the boarding strategy. Methods susceptible to the adverse effects of interactions inside the aircraft tended to improve efficiency quickly with a lower load factor. Therefore, there is a very interesting decision-making problem here regarding the choice of boarding method depending on the load factor. We plan to continue research in this area.

5.3. Boarding with Disruptions: Groups of Passengers

Passengers often travel in groups (e.g., families, friends, or business partners). This can shorten the boarding time of such a group if these people board together and help each other when looking for a row or seat, or when placing their baggage in the overhead bins. However, suppose people from a given group have seats assigned in different plane sectors (not next to each other) when using a boarding strategy. In that case, these passengers often disrupt the method because they board together and do not follow the strategy rule. This fact was noticed thanks to the survey we conducted among passengers to understand their attitudes and concerns regarding the boarding methods used by airlines.

This section uses a back-to-front strategy to examine passenger groups’ impact on the boarding process. According to our survey data, most passengers travel in small groups of 2 to 4 people (69%), 27.5% travel alone, and a small percentage travel in larger groups (3.5%). Based on these data, the group distribution was assumed at a load factor of 100%.

The following was assumed:

• One hundred and twenty-eight passengers traveled in small groups, including the following:

  ○

  Twenty-one groups of two (forty-two passengers);

  ○

  Fourteen groups of three (forty-two passengers);

  ○

  Eleven groups of four (forty-four passengers).

• Fifty-one passengers traveled individually.
• Seven people traveled in a larger group (as one group).

The back-to-front strategy in the model was modified accordingly. In each zone, places were created to represent individual passenger groups. Group passengers boarded together, groups appeared randomly, and individual passengers appeared between groups. This process was carried out for each zone.

Table 8. Results of simulation with disturbance: passenger groups.

Strategy	Average Boarding Duration [m:s]
	SF 100%—Base Model (186 pax)	SF 100%—Passenger Groups (186 pax)	Difference [s]	%
Back to front	26:05	25:54	−11	−1%

presents the simulation results for this type of disturbance.

As can be seen, the boarding time when there were groups of passengers on board, divided as in the analyzed case, was slightly shorter than the nominal boarding time obtained using this method.

5.4. Boarding with Disruptions: Boarding Pass Reader Damaged

An example of a random technical disruption could be boarding pass scanner failure. This section examines the impact of the unavailability of one of two scanners on the boarding time. It also examines whether the effects of such an event vary for different boarding strategies.

Table 9. Results of simulation with disturbances: boarding card reader failure.

Strategy	Average Boarding Duration [m:s]
	SF 100%—Base Model (186 pax)	SF 100%—Boarding Card Reader Failure (186 pax)	Difference [s]	%
Back to front	26:05	28:00	+01:55	+7%
Outside in	23:04	22:56	−00:08	−1%
Random	23:25	23:24	−00:01	−0%
Rotating zone	24:10	25:57	+01:47	+7%
By row	27:00	30:15	+03:15	+12%
Reverse pyramid	23:36	23:51	+00:15	+1%
Steffen method	22:58	22:41	−00:17	−1%

and Figure 17 present the simulation results.

As can be seen, the behaviors of the individual methods were different in the event of a disruption in the form of a scanner failure. When using some methods, i.e., the back-to-front, rotating zone, and by-row methods, boarding was extended by 7% to 12% compared with the average time obtained when handling with two scanners. For the remaining methods, the time obtained considering this disruption compared with the nominal time did not differ significantly (by about 1%). The effectiveness of using one versus two boarding pass scanners depended on where the bottlenecks occurred within the boarding process, which, in turn, varied based on the boarding strategy. The presence of a larger number of passengers on the jet bridge (occurring when boarding using two scanners) can lead to deviations from the intended boarding sequence. This significantly impacts structured boarding strategies, where maintaining order is essential for efficiency.

For instance, the boarding order is critical for the Steffen method to minimize passenger interference. Using a single scanner helps maintain the intended boarding sequence, reducing the likelihood of aisle interference. That is why, despite the disturbance, we observed a slightly shorter boarding time for the Steffen method. Meanwhile, we observed an extension in time for the by-row strategy because too few passengers were on board. They proceeded to the plane’s rear, typically without interference in the aisle, as the seats in the forward rows remained unoccupied. With only one scanner in operation, passenger spacing increased, ultimately prolonging the overall boarding process.

6. Discussion

This article aimed to develop a model that reflects the operation during the last phase of passenger service: the boarding process. The model was created as a hierarchical, timed, colored Petri net and was used with the help of simulation techniques. This allowed for the reflection of the process at the airport and then for checking its effectiveness. The main element of the analysis of the passenger service system in the developed scope was to check the stream of passenger reports arriving at the gate, the process of moving the passengers from the gate to the plane, the process of taking up a designated seat, including the location of hand luggage, and the analysis of disruptions that may occur in these processes.

Ensuring smooth boarding is one of the essential goals of airlines, as the boarding process is on the critical path of the aircraft turnaround time, and it is vital to perform it as fast as possible. A good solution that shortens the boarding time and reduces traffic congestion on board is to choose an appropriate boarding method. This paper assessed the effectiveness of selected boarding methods in conditions of disruptions. The obtained results indicate that depending on various input parameters and disruptions in the process, the effectiveness of the methods varies. Another possibility of increasing the time available for boarding is shortening the deboarding time. Research on this issue is scarce because of limited management possibilities. However, we believe that this issue is worth studying in the future.

It has been shown that the average time for the random strategy and the maximum aircraft load factor is 23 min 25 s in the correct course of the boarding process. In other variants, using other boarding methods and successively introduced disruptions, this time changes. However, no clearly visible rule states that one of the boarding strategies is obviously better for a given type of disruption.

Our research does not indicate that the HTCPN technique has any limitations regarding the results obtained. It allows for discrete event simulation while facilitating (i) the creation of microscale models, (ii) the inclusion of real process concurrency (which is very important in boarding issues), or (iii) the possibility of the dynamic modification of model parameters, which facilitates the use of built models in real time.

This leads to the observation that using models similar to those presented in this article is necessary, where the input parameters must be determined dynamically. This means that for each boarding process, the probabilities of occurrence of individual types of disruptions should be estimated, and the boarding strategies should be adjusted accordingly. Alternatively, it can be recommended to observe the currently ongoing boarding and, if any disruption is detected, perform a simulation to answer the question about the most advantageous boarding strategy in this situation.

7. Conclusions

This article presented a methodology and model for the analysis of disruptions’ impact on the effectiveness of aircraft boarding. In the results obtained from our study, we observed the following:

• Boarding is a critical part of the aircraft turnaround process, so performing it efficiently and quickly is essential. Boarding strategies help achieve this goal.
• Hierarchical, timed, colored Petri nets are an adequate methodology to model the aircraft boarding process, including boarding methods. The CPN Tools package allows one to easily create a model and run simulations.
• In the correct boarding process flow, the best results for a Boeing 737–800 with 186 economy class passengers were obtained using the Steffen method, and the worst with the by-row method, followed by the back-to-front method.
• The aircraft load factor is significant in the context of a boarding strategy’s effectiveness and the impact of disruptions. Methods susceptible to the adverse effects of interactions inside the aircraft tend to improve efficiency with a lower load factor.
• Passengers often travel in groups and want to board the plane together. A disruption consisting of boarding the entire group together at the cost of not following the rules of the boarding method may affect the boarding time.
• Technical issues, such as a boarding pass scanner failure, affect individual boarding methods differently.