ELVO-Based Autonomous Satellite Collision Avoidance with Multiple Debris
Abstract
1. Introduction
- Severely constrained computational resources conflict sharply with high real-time responsiveness requirements for collision avoidance algorithms.
- Precious propellant and energy reserves necessitate minimizing frequent maneuvers, as they significantly shorten operational lifespans. Optimal orbital maneuvers must balance collision avoidance, propellant conservation, energy consumption, and mission continuity. (The term “balance” refers to the need to find an optimal trade-off between multiple objectives during orbital maneuvers. In general, these objectives may conflict with each other, meaning that prioritizing one goal could negatively impact others).
- Cascading collision risks emerge in constellation satellite clusters or densely populated orbital regions. A single collision avoidance maneuver may trigger domino-like collision chains, creating a situation that is exceptionally difficult to resolve. Indeed, mitigating global collision risks should be a priority and requires a systematic approach.
2. Problem Formulation
- Control saturation;
- Fuel efficiency;
- Mission continuity.
2.1. Coordinate System
- Introduce a reference orbit, whose orbital elements are consistent with those of the satellite at time before any maneuver is performed. The semi-major axis, eccentricity, inclination, right ascension of the ascending node, argument of periapsis, and true anomaly of the reference orbit are denoted by
- The origin of the LVLH coordinate system is located at the center of mass of the reference satellite. The x-axis points from the center of the Earth to the satellite’s center of mass (local vertical), the z-axis points in the direction of the orbital angular momentum vector (perpendicular to the orbital plane), and the y-axis completes the right-handed coordinate system by pointing in the direction of the satellite’s velocity vector (local horizontal).
2.2. Dynamics Models
3. Elvo-Based Space Debris Avoidance
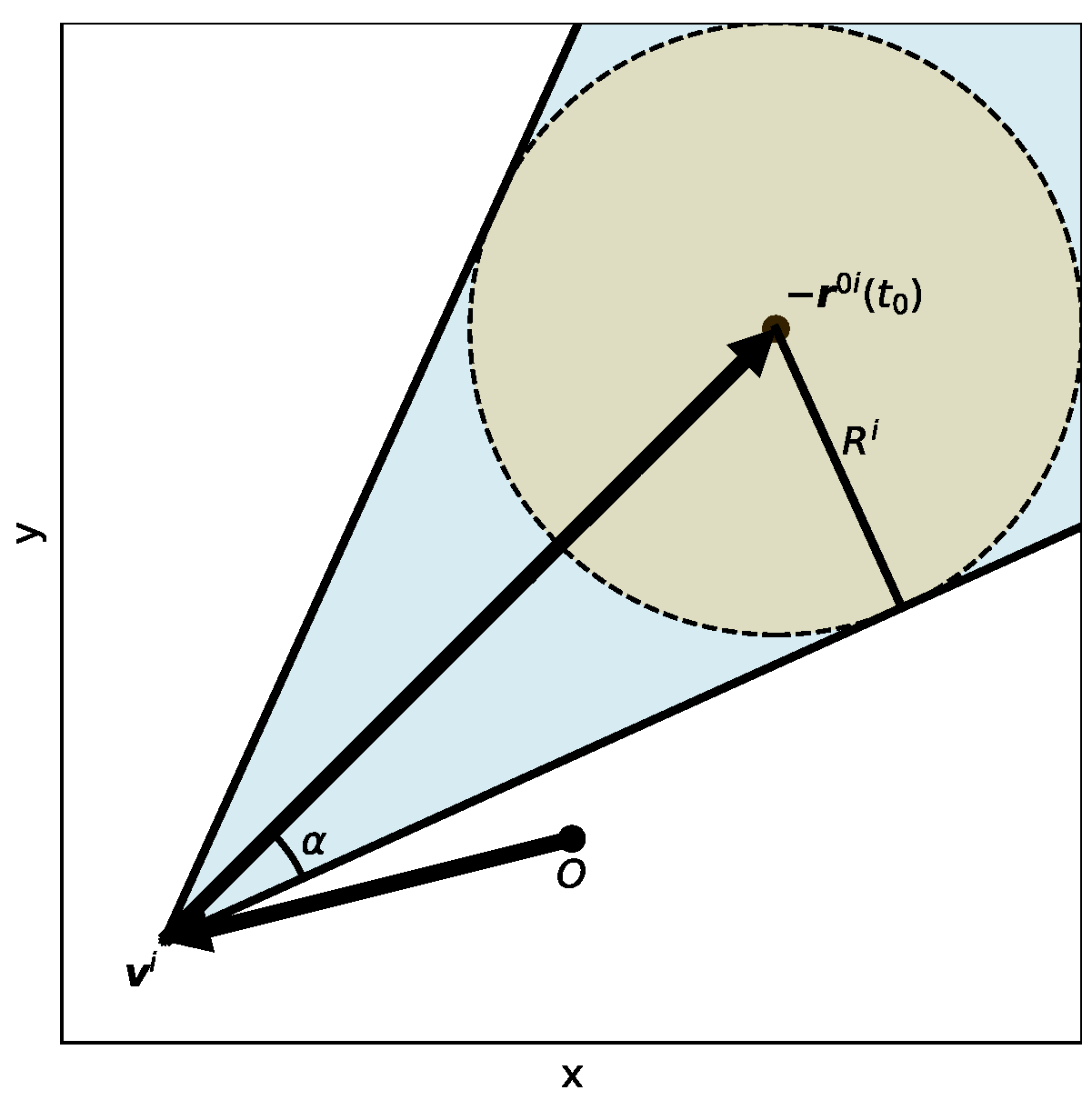
3.1. Velocity Obstacle
3.2. Equivalent Linear Velocity Obstacle
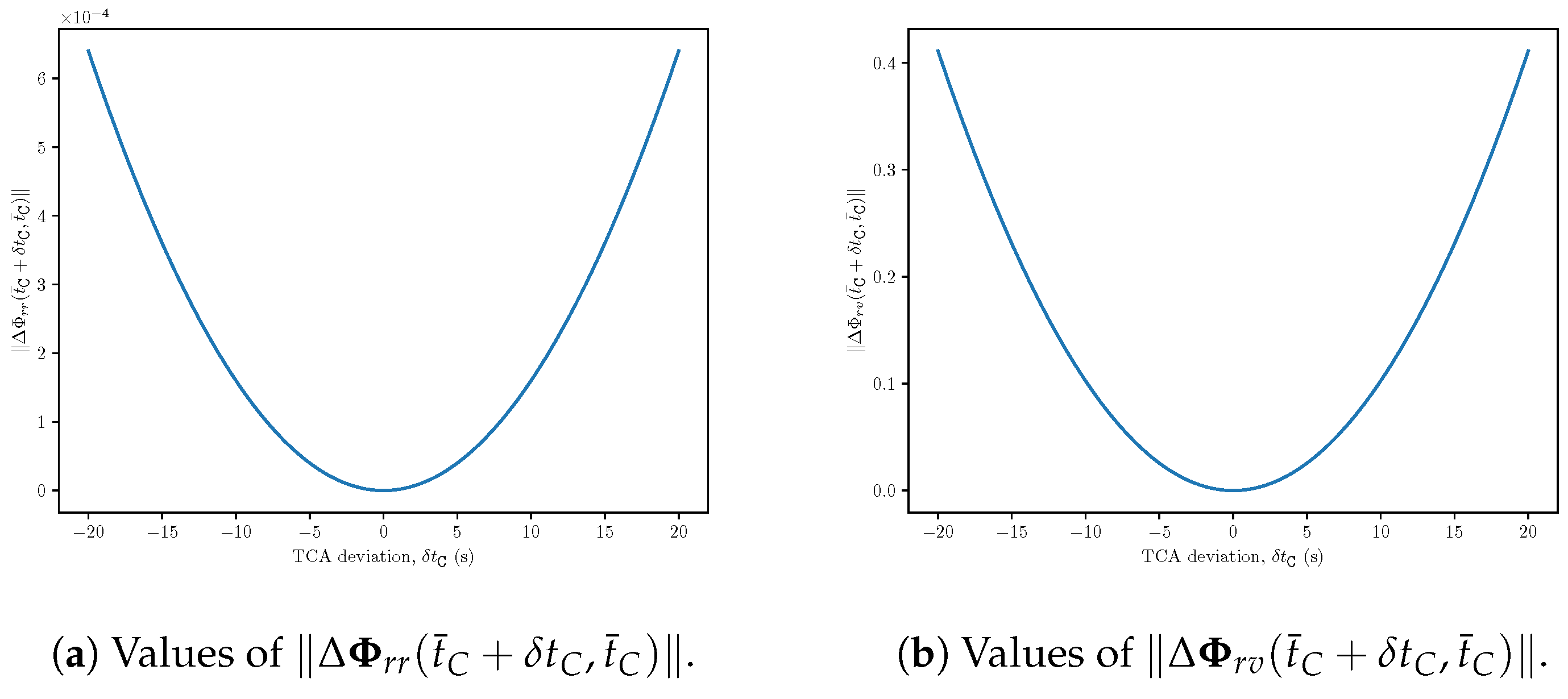
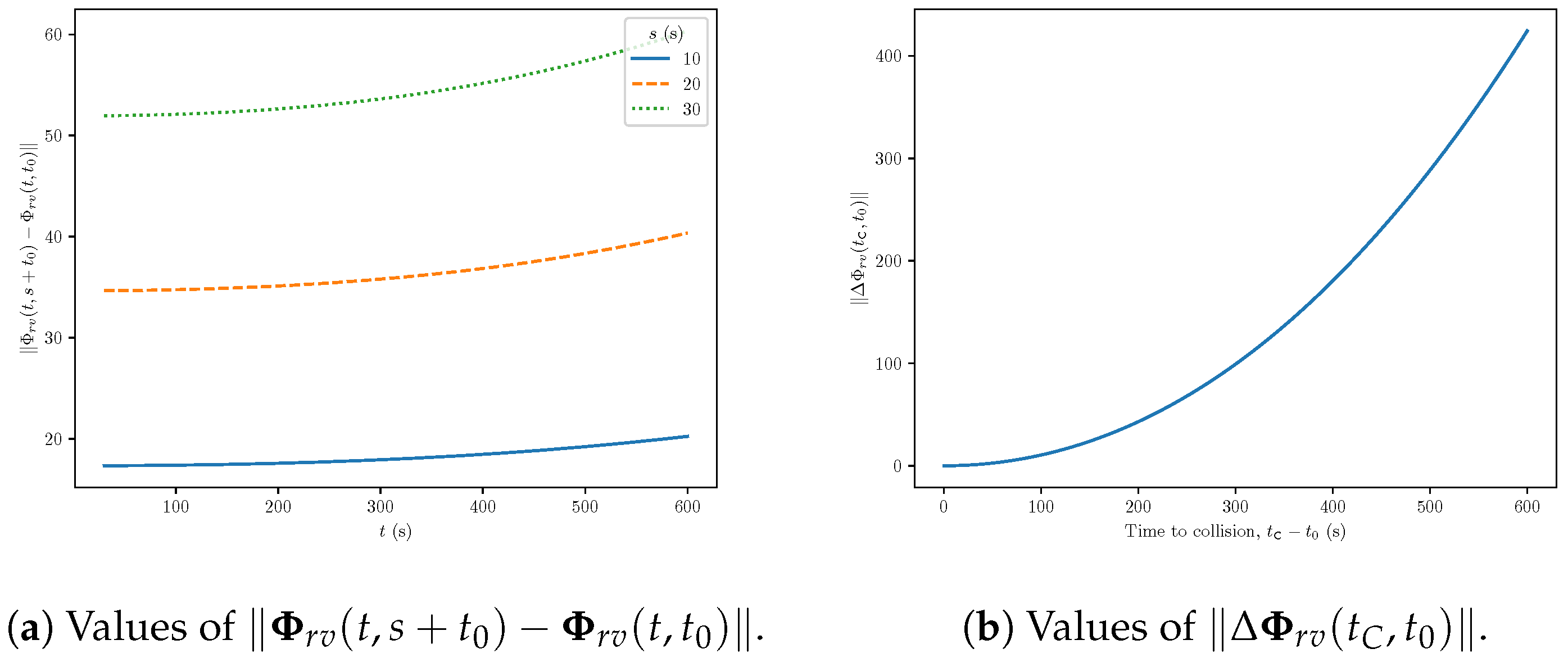
3.3. Compensated Safe Distance
- I.
- Estimation of
- II.
- Estimation of
- III.
- Estimation of
- IV.
- Computation of
3.4. Elvo-Based Avoidance Algorithm
| Algorithm 1 Closest Approach ELVO |
|
| Algorithm 2 Adaptive ELVO-Bases Avoidance |
|
- The ELVO algorithm inherently achieves higher targeting precision during high-velocity relative motion between satellites and debris. But due to satellites’ limited lateral acceleration capability, its in-field autonomous avoidance may prove insufficient to prevent high-speed collisions in such scenarios. This necessitates a critical trade-off analysis.
- When the underlying satellite and debris trajectories exhibit excessive nonlinearity, the safety distance compensation term calculation becomes computationally complex and tends to produce conservative values. This may reduce operational efficiency.
4. Elvo-Based Algorithm into Avoidance Framework
- After the pieces of space debris enter the field of view of the satellite’s sensing system, does the satellite have the capability to successfully avoid them autonomously?
- Early avoidance is more fuel-efficient, but it risks unnecessary fuel expenditure due to false alarms. Waiting for the debris to approach to obtain high-precision information by satellite-borne sensors requires more fuel consumption for short-term maneuvers. How to balance the two?
5. Simulation and Analysis
5.1. Simulation Set-Up
5.2. Simulation Results
6. Conclusions
- Develop an RL framework where the ELVO method serves as the reward function, enabling autonomous policy optimization under dynamic orbital constraints.
- Design hybrid imitation learning algorithms that leverage ELVO-generated trajectories as expert demonstrations to improve sample efficiency and safety guarantees.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EFC | Expected Fuel Consumption |
| ELVO | Equivalent Linear Velocity Obstacle |
| LEO | Low Earth Orbit |
| LVLH | Local Vertical Local Horizontal |
| TCA | Time of Closest Approach |
| VO | Velocity Obstacle |
References
- Bigdeli, M.; Srivastava, R.; Scaraggi, M. Mechanics of space debris removal: A review. Aerospace 2025, 12, 277. [Google Scholar] [CrossRef]
- Mehrholz, D.; Leushacke, L.; Flury, W.; Jehn, R.; Klinkrad, H.; Landgraf, M. Detecting, tracking and imaging space debris. ESA Bull. 2002, 109, 128–134. [Google Scholar]
- Schildknecht, T. Optical surveys for space debris. Astron. Astrophys. Rev. 2007, 14, 41–111. [Google Scholar] [CrossRef]
- Kessler, D.; Johnson, N. The Kessler syndrome: Implications to future space operations. In Proceedings of the 33rd Annual AAS Guidance and Control Conference, Breckinridge, CO, USA, 5–10 February 2010. [Google Scholar]
- Muntoni, G.; Montisci, G.; Pisanu, T.; Andronico, P.; Valente, G. Crowded space: A review on radar measurements for space debris monitoring and tracking. Appl. Sci. 2021, 11, 1364. [Google Scholar] [CrossRef]
- Garcia, L.P.; Furano, G.; Ghiglione, M.; Zancan, V.; Imbembo, E.; Ilioudis, C.; Clemente, C.; Trucco, P. Advancements in on-board processing of synthetic aperture radar (SAR) data: Enhancing efficiency and real-time capabilities. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 16625–16645. [Google Scholar] [CrossRef]
- Burroni, T.; Husain, S.; Servidia, P.; Thangavel, K.; Sabatini, R. Constellation of formations for autonomous resident space objects detection using star trackers. In Proceedings of the 74th International Astronautical Congress (IAC), Milan, Italy, 14–18 October 2024. [Google Scholar]
- Srinithi, B.; Sruthi, N.S.R.; Senthil Kumar, T.; Somasundaram, K.; Ramasamy, M. Enhancing milk yield forecasting in dairy farming using an interpretable machine learning framework. In Proceedings of the 2025 4th International Conference on Sentiment Analysis and Deep Learning (ICSADL), Janakpur, Nepal, 18–20 February 2025; pp. 1549–1557. [Google Scholar]
- Kim, E.H.; Kim, H.D.; Kim, H.J. A study on the collision avoidance maneuver optimization with multiple space debris. J. Astron. Space Sci. 2012, 29, 11–21. [Google Scholar] [CrossRef]
- Wang, C.; Chen, D.; Liao, W.; Liang, Z. Autonomous obstacle avoidance strategies in the mission of large space debris removal using potential function. Adv. Space Res. 2023, 72, 2860–2873. [Google Scholar] [CrossRef]
- Mu, C.; Liu, S.; Lu, M.; Liu, Z.; Cui, L.; Wang, K. Autonomous spacecraft collision avoidance with a variable number of space debris based on safe reinforcement learning. Aerosp. Sci. Technol. 2024, 149, 109–131. [Google Scholar] [CrossRef]
- Chen, X.; Wang, T.; Qiu, J.; Feng, J. Mission planning on autonomous avoidance for spacecraft confronting orbital debris. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 4115–4126. [Google Scholar] [CrossRef]
- Yang, H.; Xie, Z.; Zhao, X.; Jin, M. Ground micro-gravity emulation system for space robot capturing the target satellite. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics (ROBIO), Zhuhai, China, 6–9 December 2015; pp. 2585–2590. [Google Scholar]
- Artigas, J.; De Stefano, M.; Rackl, W.; Lampariello, R.; Brunner, B.; Bertleff, W.; Burger, R.; Porges, O.; Giordano, A.; Borst, C.; et al. The OOS-SIM: An on-ground simulation facility for on-orbit servicing robotic operations. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2854–2860. [Google Scholar]
- Olivares-Mendez, M.; Makhdoomi, M.R.; Yalçın, B.C.; Bokal, Z.; Muralidharan, V.; Ortiz Del Castillo, M.; Gaudilliere, V.; Pauly, L.; Borgue, O.; Alandihallaj, M.; et al. Zero-G Lab: A multi-purpose facility for emulating space operations. J. Space Saf. Eng. 2023, 10, 509–521. [Google Scholar] [CrossRef]
- Schlotterer, M.; Edlerman, E.; Fumenti, F.; Gurfil, P.; Theil, S.; Zhang, H. On-ground testing of autonomous guidance for multiple satellites in a cluster. In Proceedings of the 8th International Workshop on Satellite Constellations and Formation Flying, Delft, The Netherlands, 8–10 June 2015; p. 386043. [Google Scholar]
- Fiorini, P.; Shiller, Z. Motion planning in dynamic environments using velocity obstacles. Int. J. Robot. Res. 1998, 17, 760–772. [Google Scholar] [CrossRef]
- Vesentini, F.; Muradore, R.; Fiorini, P. A survey on Velocity Obstacle paradigm. Robot. Auton. Syst. 2024, 174, 104645. [Google Scholar] [CrossRef]
- Van Den Berg, J.; Lin, M.; Manocha, D. Reciprocal velocity obstacles for real-time multi-agent navigation. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 1928–1935. [Google Scholar]
- Van Den Berg, J.; Guy, S.J.; Lin, M.; Manocha, D. Reciprocal n-body collision avoidance. In Proceedings of the Robotics Research: The 14th International Symposium ISRR; Springer: Berlin/Heidelberg, Germany, 2011; pp. 3–19. [Google Scholar]
- An, R.; Guo, S.; Zheng, L.; Hirata, H.; Gu, S. Uncertain moving obstacles avoiding method in 3D arbitrary path planning for a spherical underwater robot. Robot. Auton. Syst. 2022, 151, 104011. [Google Scholar] [CrossRef]
- Li, A.; Guo, S.; Li, C.; Yin, H.; Liu, M.; Shi, L. A moving obstacle avoidance strategy-based collaborative formation for the bionic multi-underwater spherical robot control system. Ocean. Eng. 2025, 329, 121120. [Google Scholar] [CrossRef]
- Shiller, Z.; Large, F.; Sekhavat, S. Motion planning in dynamic environments: Obstacles moving along arbitrary trajectories. In Proceedings of the 2001 IEEE International Conference on Robotics and Automation, Seoul, Republic of Korea, 21–26 May 2001; Volume 4, pp. 3716–3721. [Google Scholar]
- Jenie, Y.I.; van Kampen, E.J.; de Visser, C.C.; Ellerbroek, J.; Hoekstra, J.M. Three-dimensional velocity obstacle method for uncoordinated avoidance maneuvers of unmanned aerial vehicles. J. Guid. Control. Dyn. 2016, 39, 2312–2323. [Google Scholar] [CrossRef]
- Lin, Z.; Castano, L.; Mortimer, E.; Xu, H. Fast 3D collision avoidance algorithm for fixed wing UAS. J. Intell. Robot. Syst. 2020, 97, 577–604. [Google Scholar] [CrossRef]
- Sullivan, J.; Grimberg, S.; D’Amico, S. Comprehensive survey and assessment of spacecraft relative motion dynamics models. J. Guid. Control. Dyn. 2017, 40, 1837–1859. [Google Scholar] [CrossRef]
- De Maesschalck, R.; Jouan-Rimbaud, D.; Massart, D.L. The mahalanobis distance. Chemom. Intell. Lab. Syst. 2000, 50, 1–18. [Google Scholar] [CrossRef]
- Leleux, D.; Spencer, R.; Zimmerman, P.; Propst, C.; Frisbee, J.; Wortham, M.; Heilman, W. Probability-based space shuttle collision avoidance. In Proceedings of the SpaceOps 2002 Conference, Houston, TX, USA, 9–12 October 2002; p. 50. [Google Scholar]
- Broucke, R.A. Solution of the elliptic rendezvous problem with the time as independent variable. J. Guid. Control. Dyn. 2003, 26, 615–621. [Google Scholar] [CrossRef]
- Gonzalo, J.L.; Colombo, C.; Di Lizia, P. Analytical framework for space debris collision avoidance maneuver design. J. Guid. Control. Dyn. 2021, 44, 469–487. [Google Scholar] [CrossRef]
- Li, J.S.; Yang, Z.; Luo, Y.Z. A review of space-object collision probability computation methods. Astrodynamics 2022, 6, 95–120. [Google Scholar] [CrossRef]
- Patera, R.P. General method for calculating satellite collision probability. J. Guid. Control. Dyn. 2001, 24, 716–722. [Google Scholar] [CrossRef]


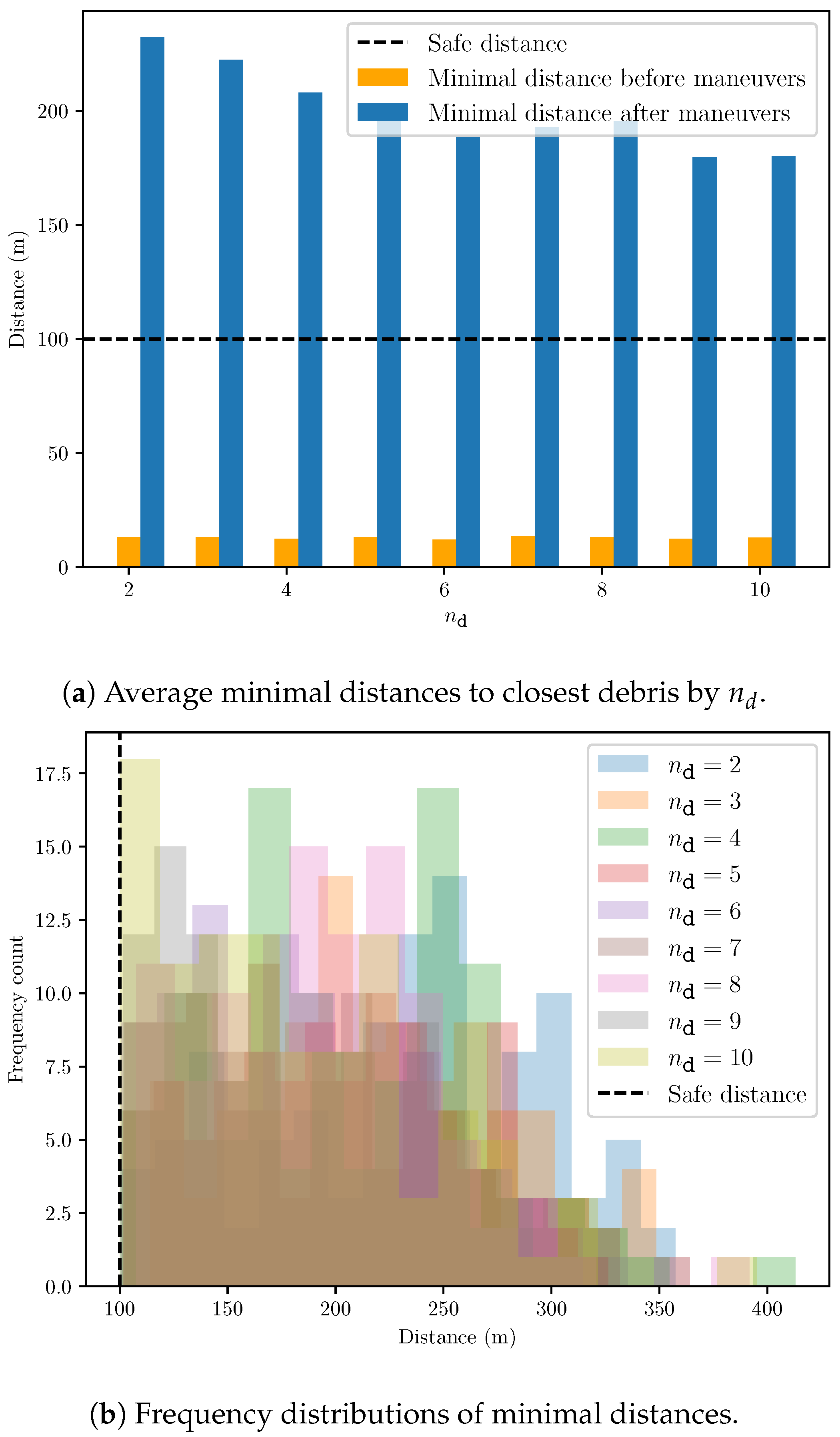
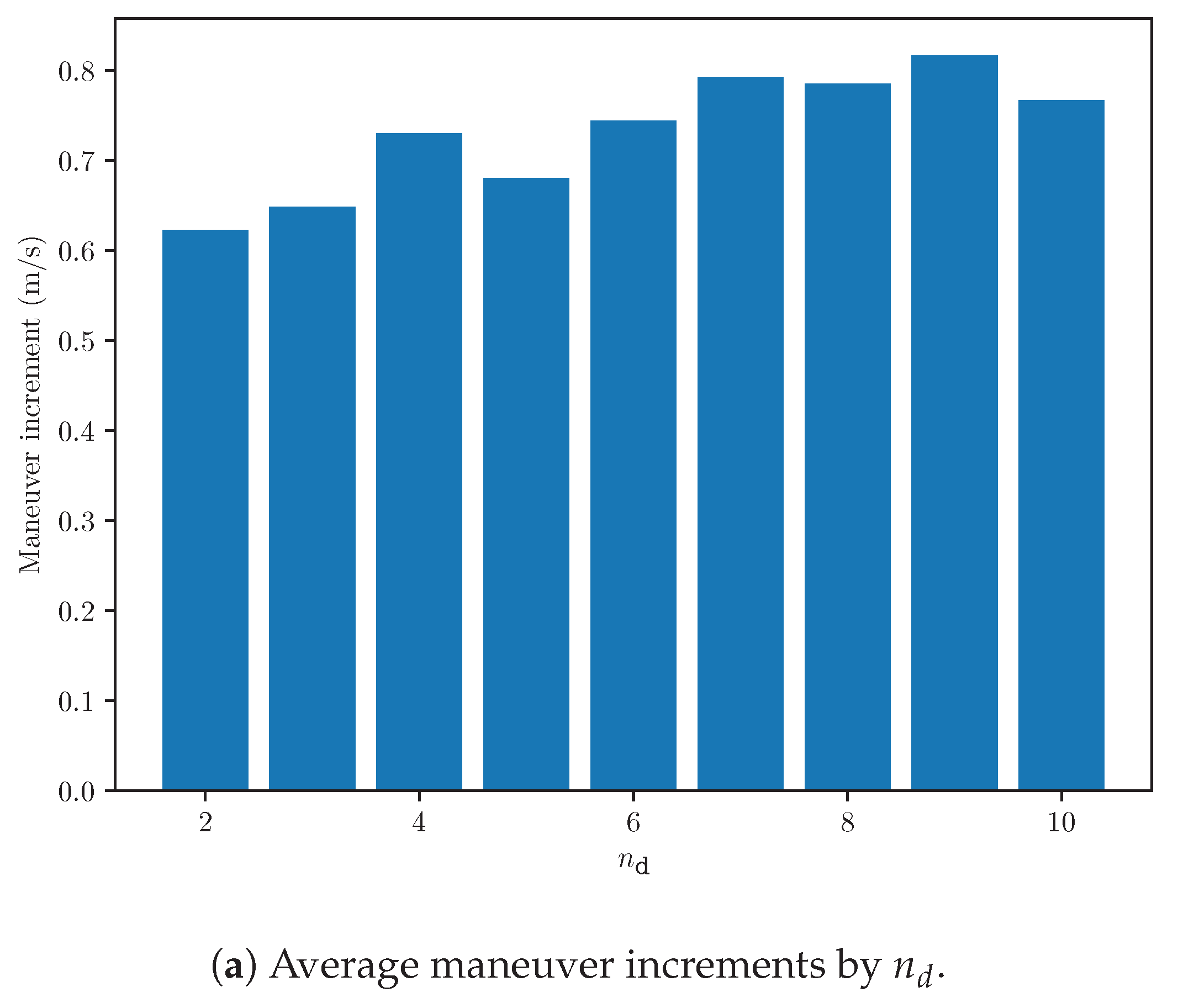

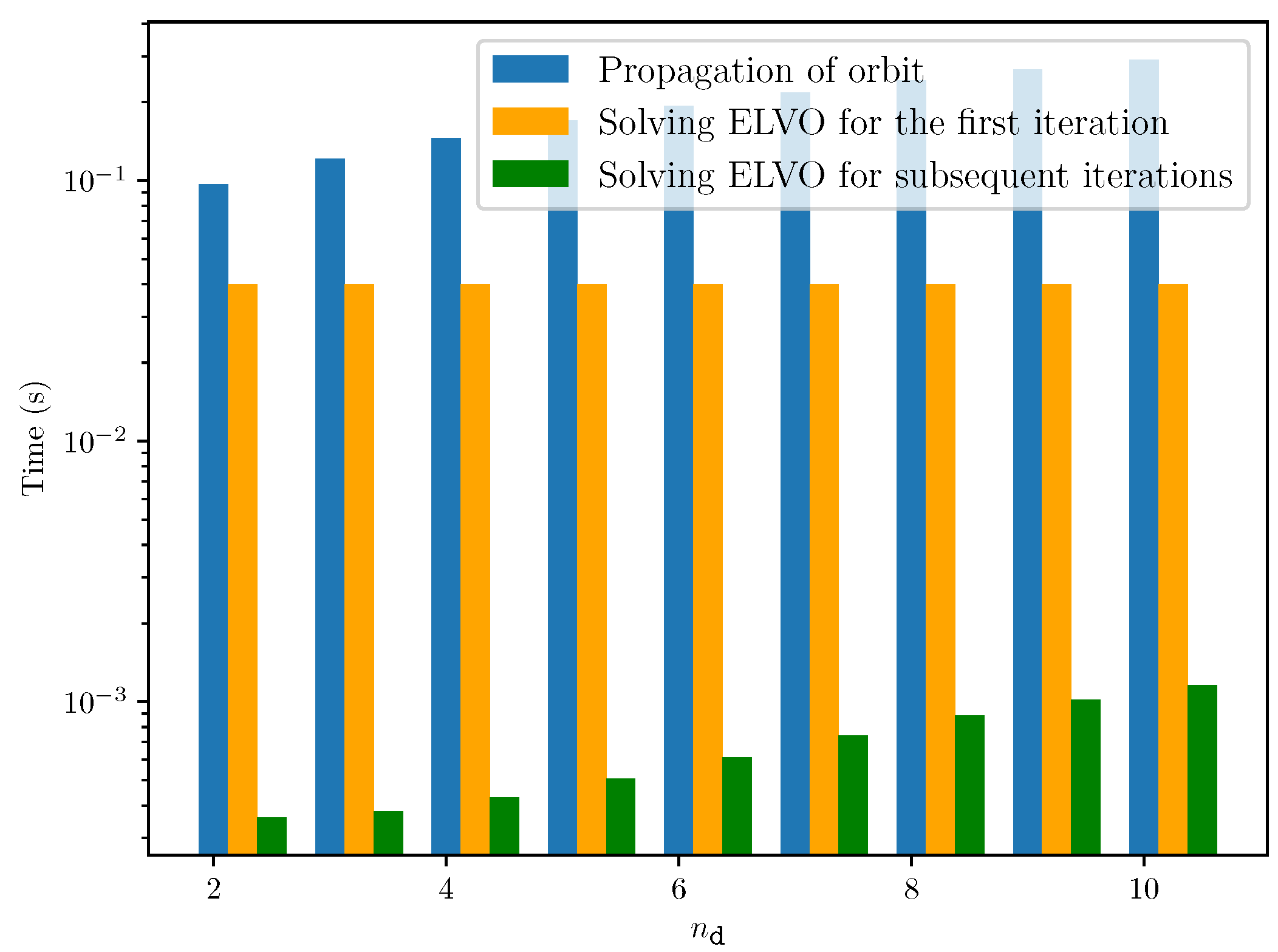
| Criteria | ELVO | Safe RL [11] | Potential Field [10] |
|---|---|---|---|
| ine Relative Velocity | Hundreds of meters per second | Arbitrary | Meters per second |
| Time to Collision | Minutes | Hours | Minutes |
| Theoretical Guarantees | Yes | No | Partial |
| Symbol | Description | Value |
|---|---|---|
| Semi-Major Axis | 7155.459 km | |
| Eccentricity | 1.174 × | |
| Inclination | 1.292 rad | |
| RAAN | 0.301 rad | |
| Argument of Periapsis | 1.468 rad | |
| True Anomaly | 0.234 rad |
| Symbol | Description | Value |
|---|---|---|
| Maximal acceleration | 0.03 m/ | |
| max standard deviation of on-board position observation | 10 m | |
| max standard deviation of on-board velocity observation | 1 m/s | |
| T | Programming horizon | 20 s |
| Symbol | Description | Value |
|---|---|---|
| Number of debris pieces | 2∼10 | |
| safe distance | 100 m | |
| TCA | 400∼600 s | |
| TCA distance in x | 0∼500 m | |
| TCA distance in y | 0∼500 m | |
| TCA distance in z | 0∼500 m | |
| TCA velocity in x | 0∼50 m/s | |
| TCA velocity in y | 0∼100 m/s | |
| TCA velocity in z | 0∼100 m/s |
| Symbol | Description | Value |
|---|---|---|
| - | safe distance given by ground-based prediction | 8 km |
| TCA | 3600 s | |
| TCA distance in x | 0 m | |
| TCA distance in y | 0 m | |
| TCA distance in z | 0 m | |
| TCA velocity in x | 0 km/s | |
| TCA velocity in y | −7.440 km/s | |
| TCA velocity in z | −7.440 km/s |
| Symbol | Description | Value |
|---|---|---|
| Initial Semi-Major Axis | 7168.867 km | |
| Initial Eccentricity | 2.990 × | |
| Initial Inclination | 0.874 rad | |
| Initial RAAN | 2.115 rad | |
| Initial Argument of Periapsis | 0.833 rad | |
| Initial True Anomaly | −0.235 rad |
| Symbol | Description | Value |
|---|---|---|
| Maneuver increment | 0.82 m/s | |
| Target Semi-Major Axis | 7157.034 km | |
| Target Eccentricity | 1.39 × | |
| Target Inclination | 1.292 rad | |
| Target RAAN | 0.301 rad | |
| Target Argument of Periapsis | 1.504 rad | |
| Target True Anomaly | 0.197 rad |
| Elements | Avoidance Orbit (Impulse) | Reference Orbit (No Maneuver) | Actual Orbit (ELVO-Based) |
|---|---|---|---|
| a (km) | 7164.859 | 7163.280 | 7165.757 |
| e | 2.733 × | 2.524 × | 2.850 × |
| i (rad) | 1.292 | 1.292 | 1.292 |
| (rad) | 0.301 | 0.301 | 0.301 |
| (rad) | 1.399 | 1.373 | 1.414 |
| (rad) | 0.931 | 0.956 | 0.914 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Li, H.; Li, C. ELVO-Based Autonomous Satellite Collision Avoidance with Multiple Debris. Aerospace 2025, 12, 402. https://doi.org/10.3390/aerospace12050402
Li Z, Li H, Li C. ELVO-Based Autonomous Satellite Collision Avoidance with Multiple Debris. Aerospace. 2025; 12(5):402. https://doi.org/10.3390/aerospace12050402
Chicago/Turabian StyleLi, Ziyao, Hongchao Li, and Chanying Li. 2025. "ELVO-Based Autonomous Satellite Collision Avoidance with Multiple Debris" Aerospace 12, no. 5: 402. https://doi.org/10.3390/aerospace12050402
APA StyleLi, Z., Li, H., & Li, C. (2025). ELVO-Based Autonomous Satellite Collision Avoidance with Multiple Debris. Aerospace, 12(5), 402. https://doi.org/10.3390/aerospace12050402






