A Strategy for Predicting Transonic Compressor Performance at Low Reynolds Number
Abstract
1. Introduction
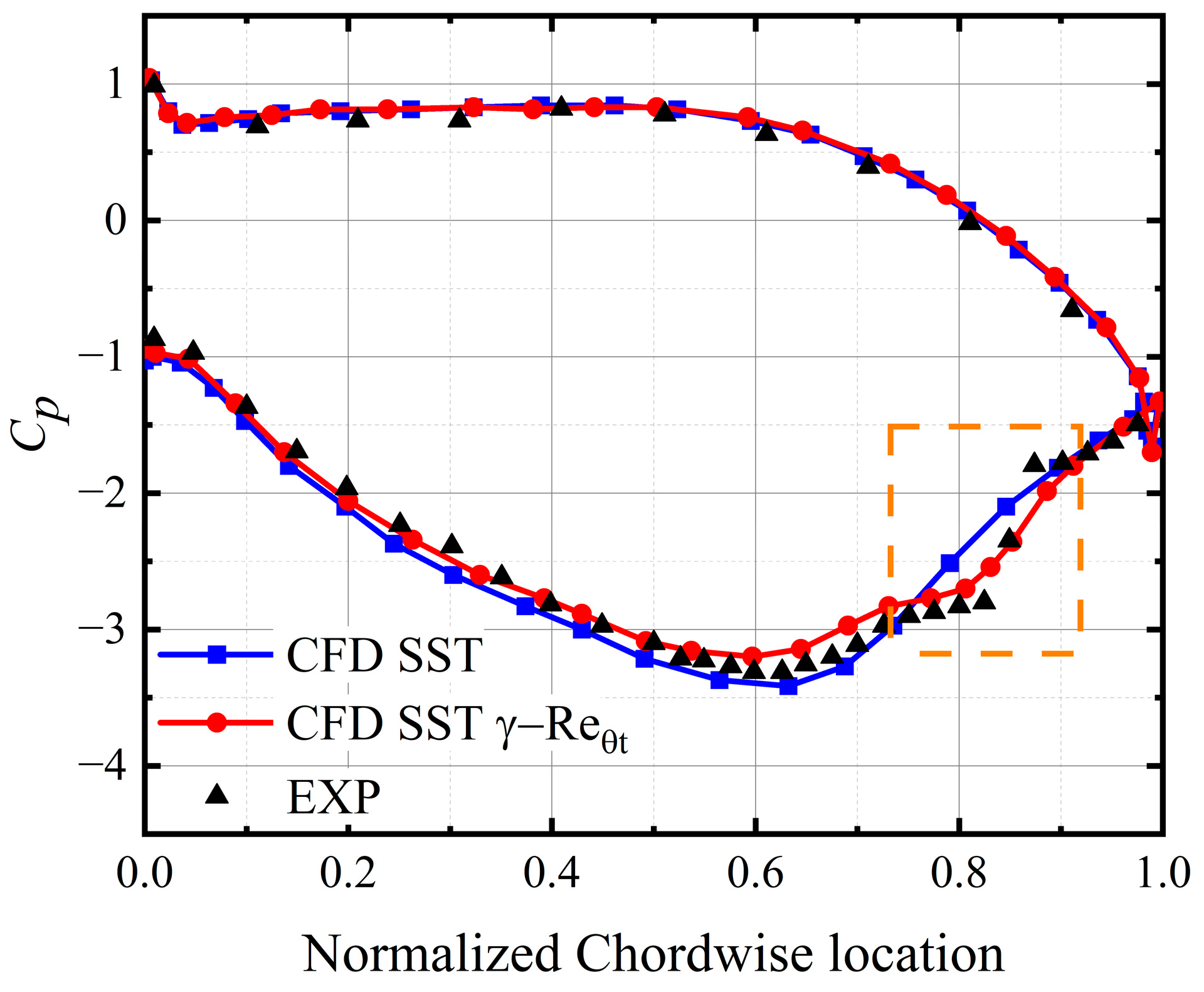
2. Numerical Methods and Validations
3. Flow Characteristics of the Transonic Compressor at a Low Re
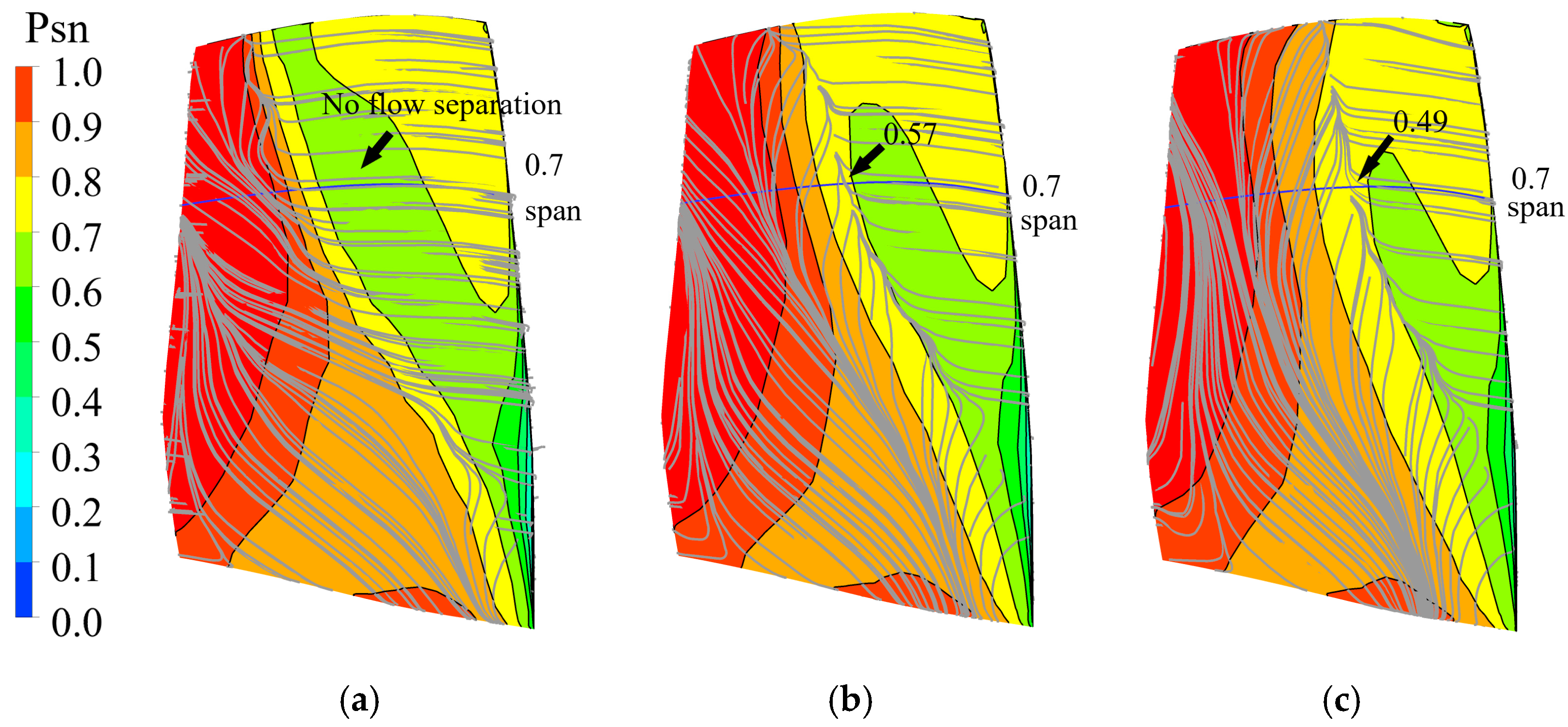
3.1. Subsonic Flow Regions
3.2. Transonic Flow Regions
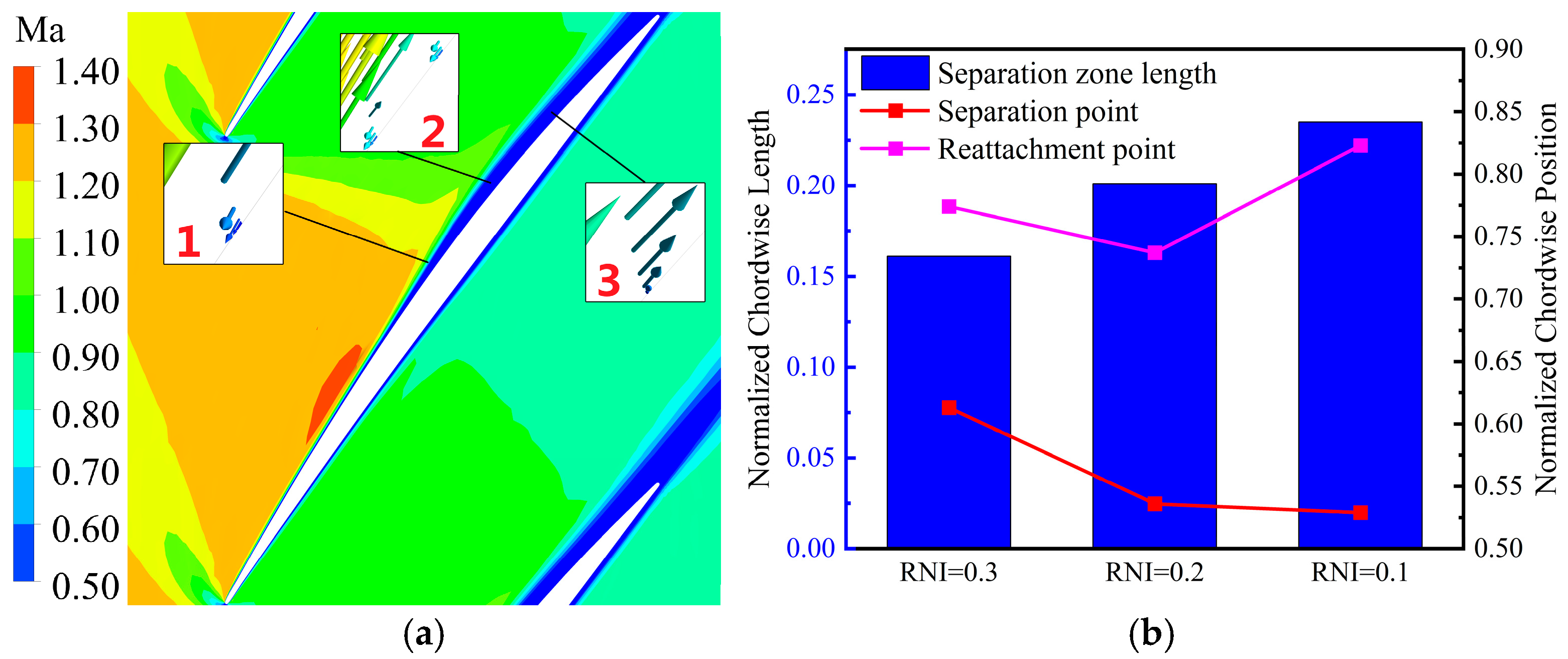
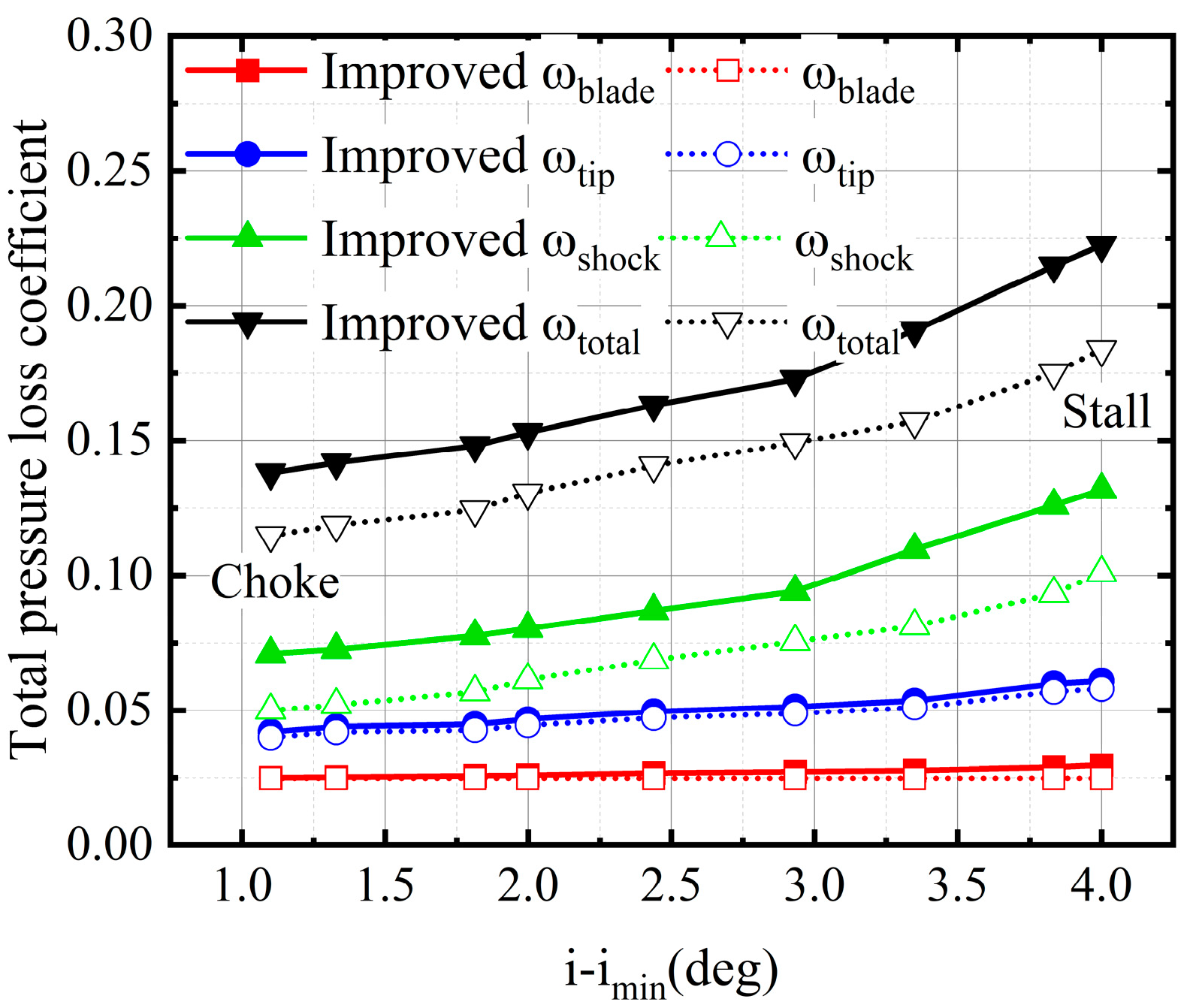
3.3. Challenges for Performance Prediction Due to Low Re Effects
4. A Multiline Calculation Strategy Based on the Equivalent Aerodynamic Profile
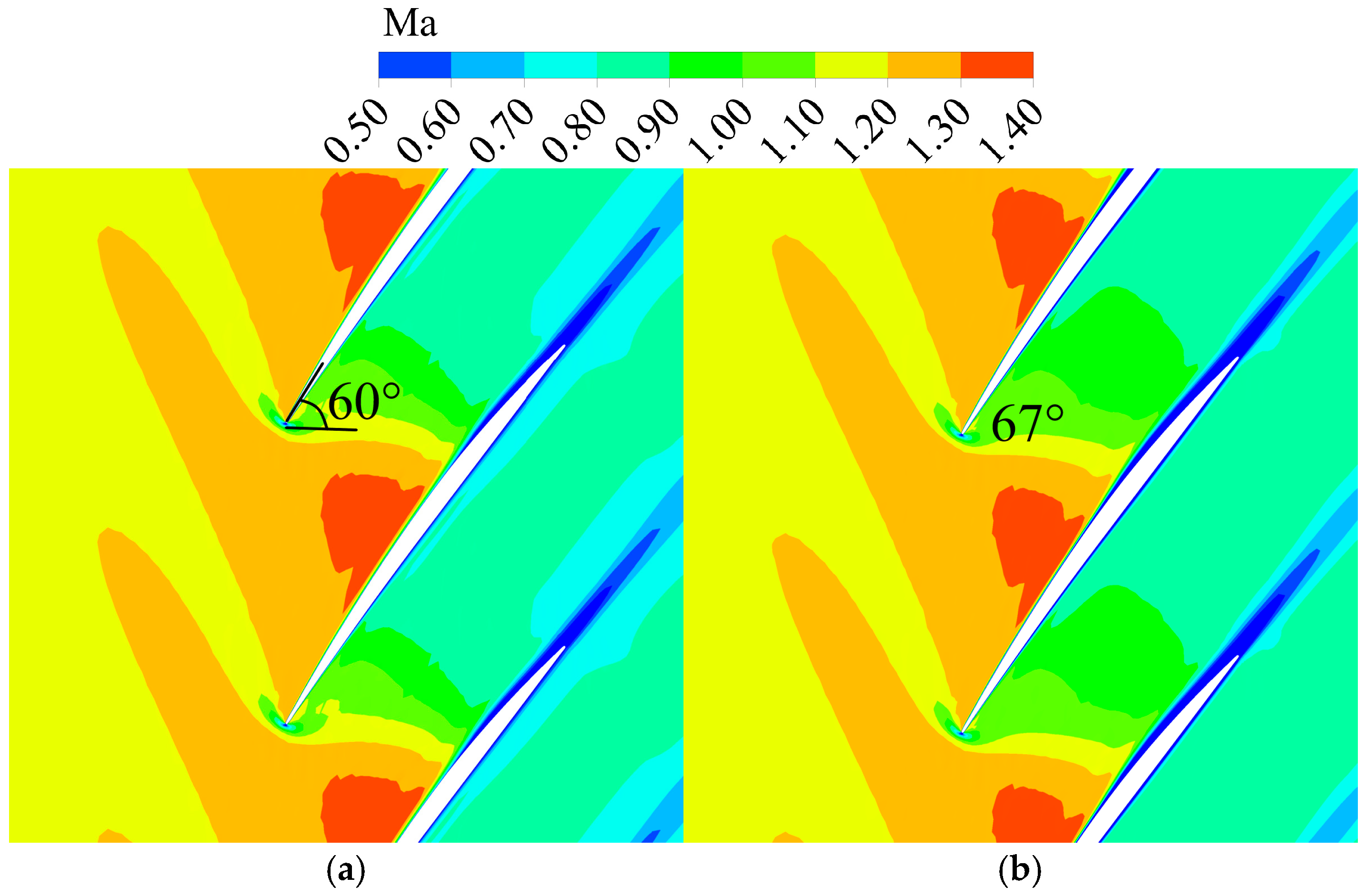
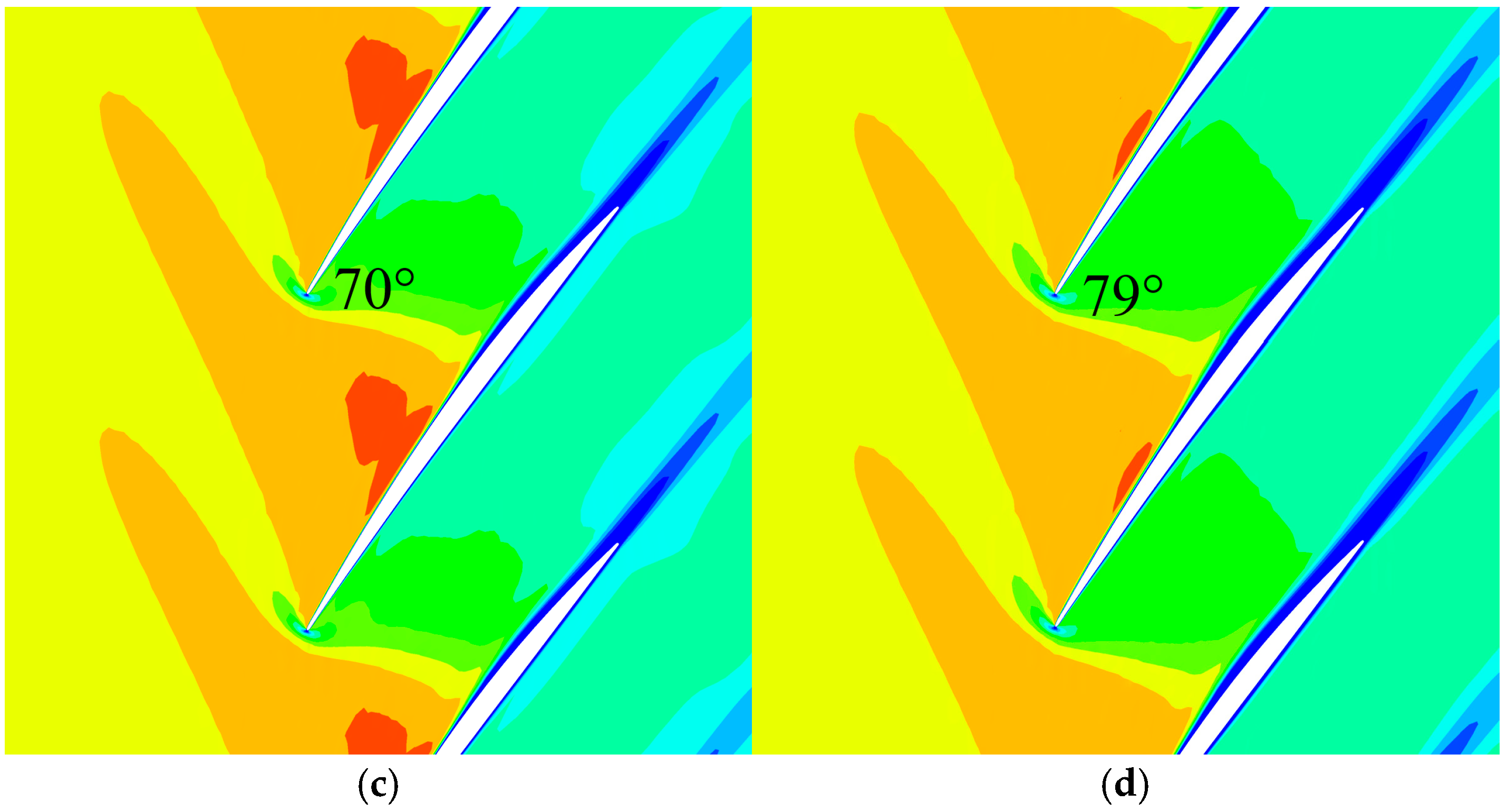
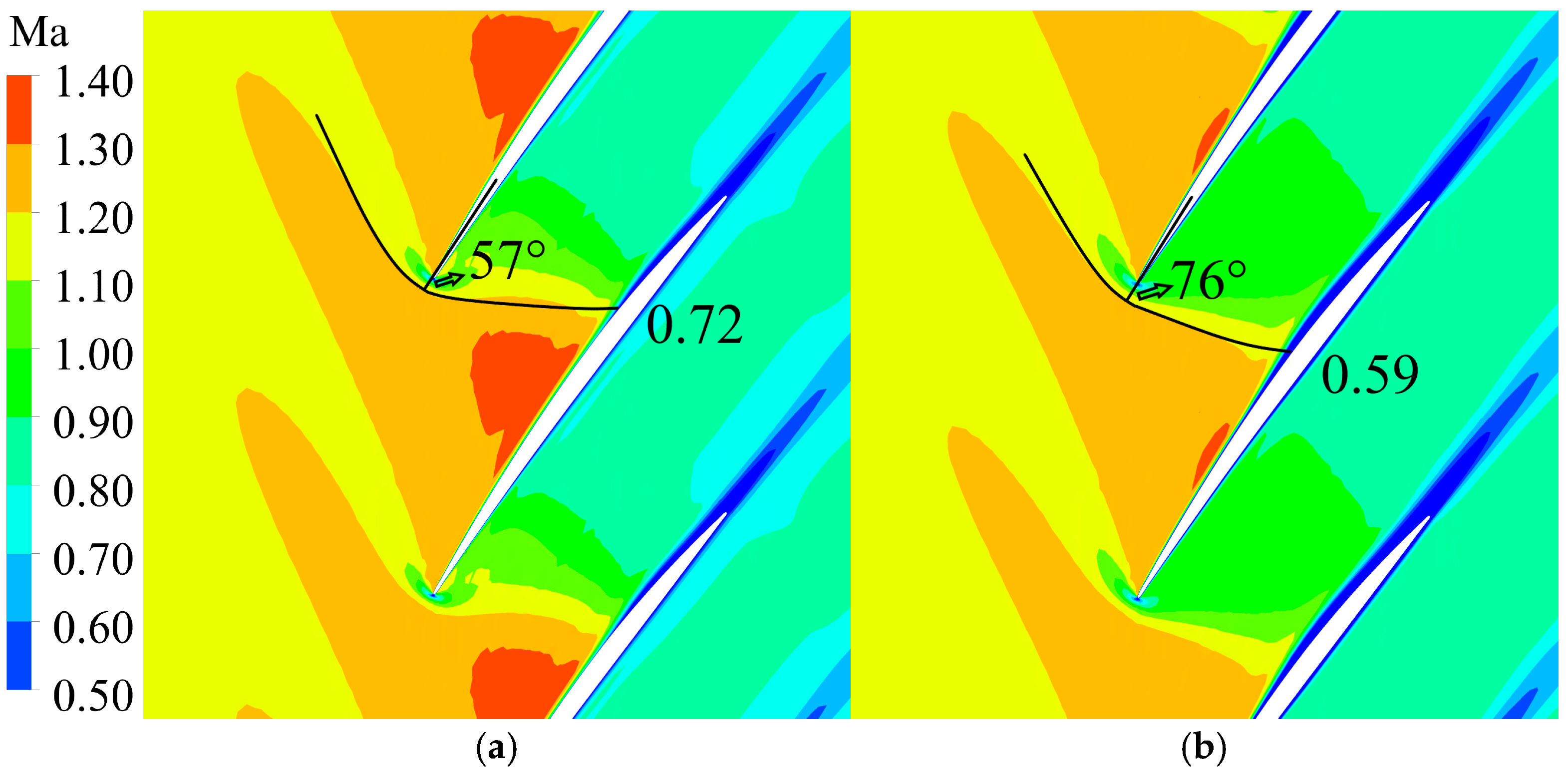
4.1. Structural Prediction of Detached Shock at Low Reynolds Number
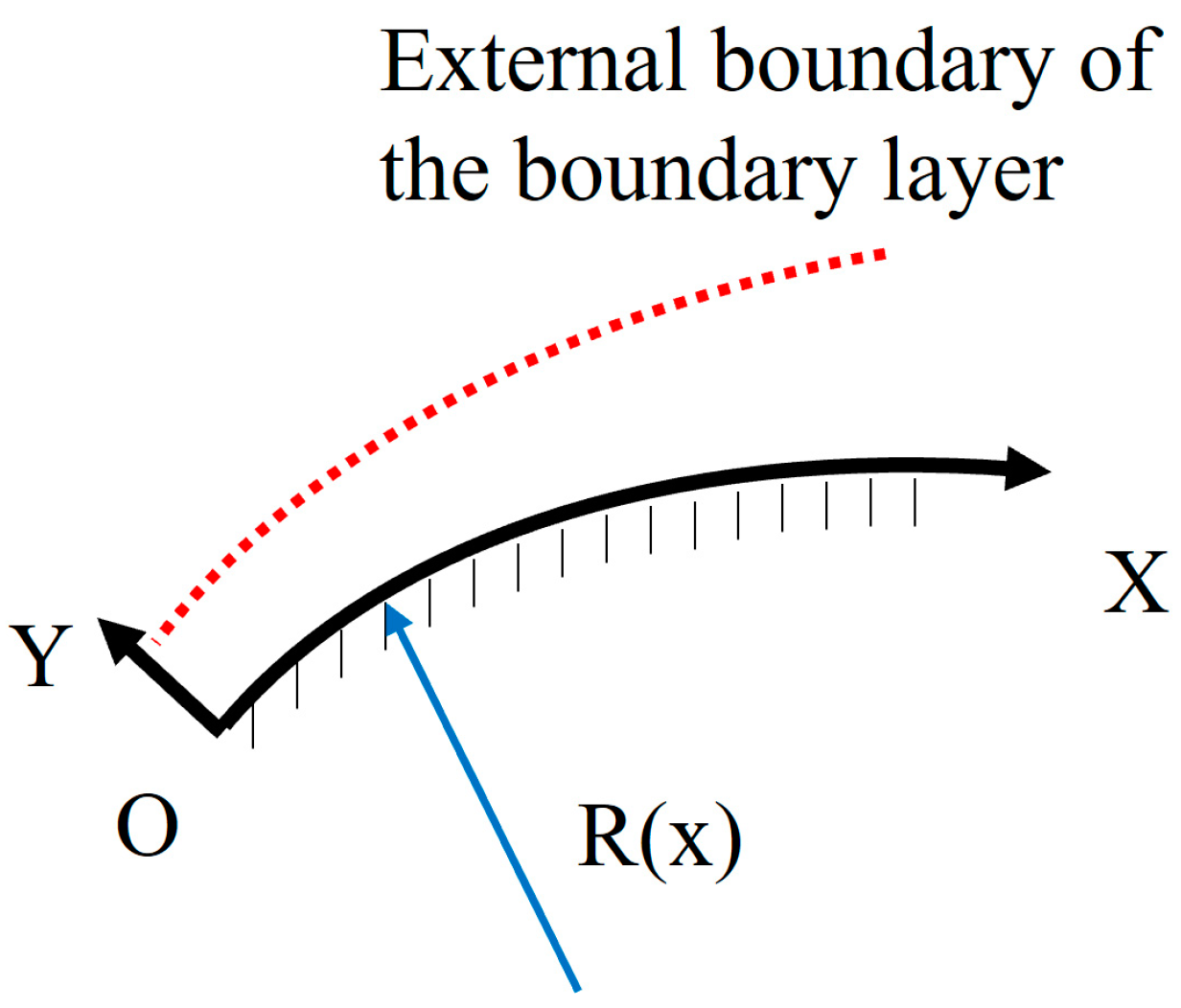
4.2. Equivalent Aerodynamic Profile Prediction Based on Boundary-Layer Theory
4.3. Partitioned Multiline Calculation Targeted at Equivalent Aerodynamic Profile
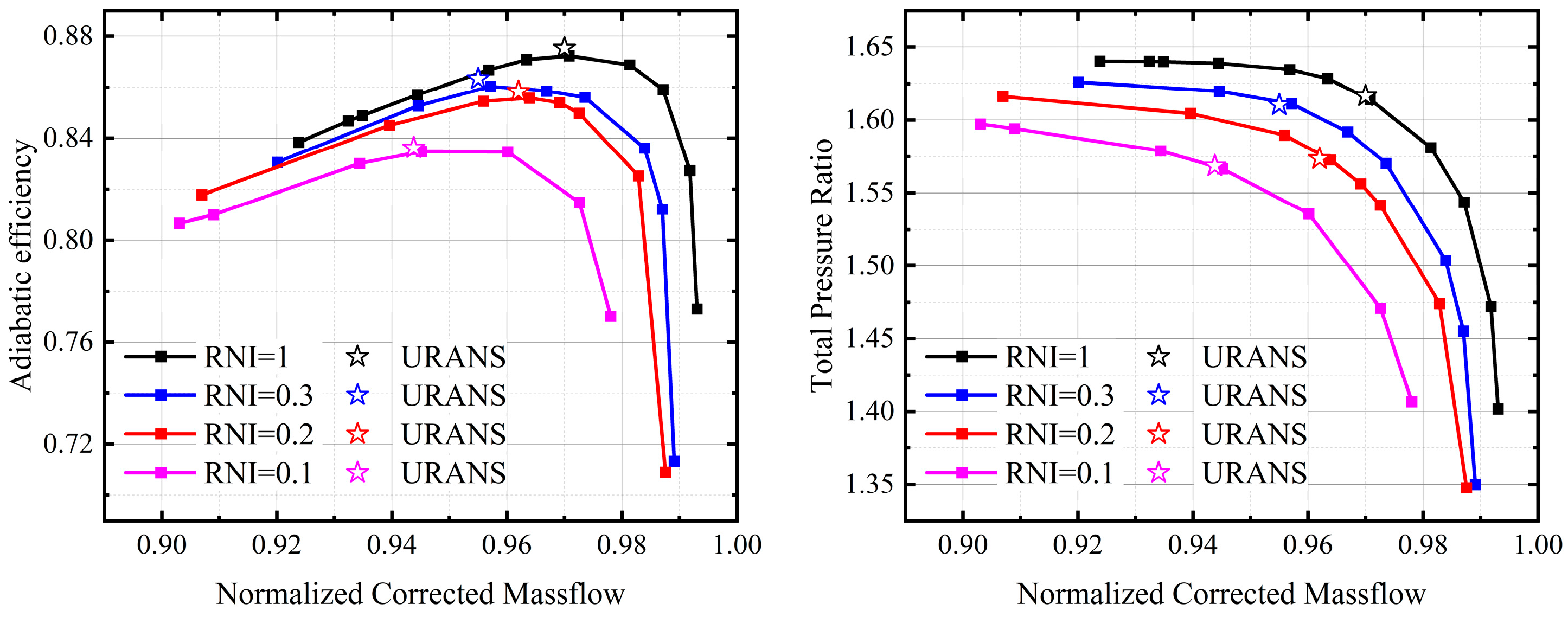
5. Results and Discussion
6. Conclusions
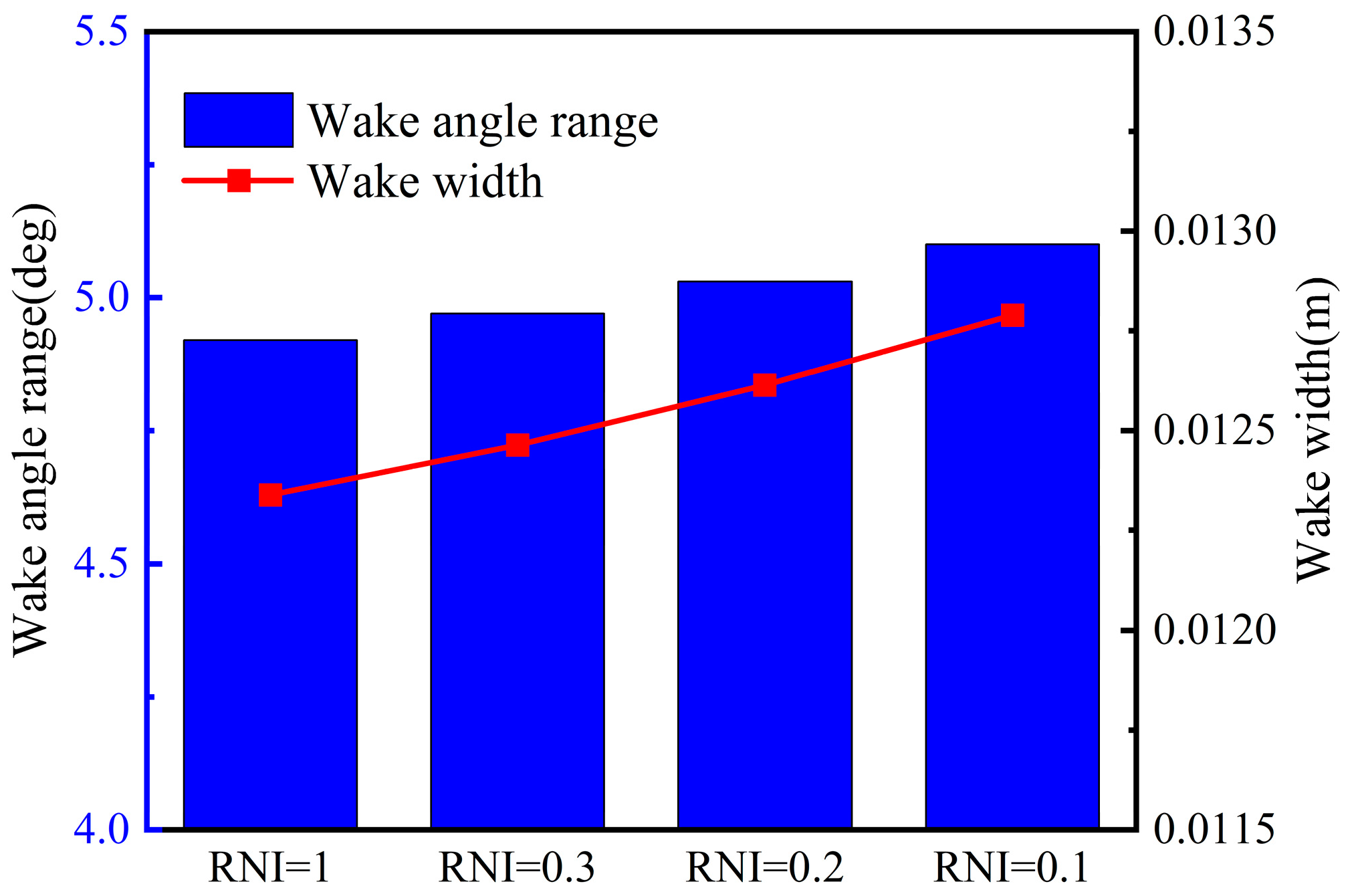
- The microscopic influence of a low Re on the compressor flow field is mainly reflected in the viscous effect on the boundary layer of the blade surface. In the subsonic region, the development of the boundary layer is accelerated, and the width of the wake increases at a low Re. In the transonic region, the boundary layer interacts strongly with the shock wave at a low Re, and the flow separation enhances the change in the boundary layer. Both of them cause the increase in the boundary-layer thickness, changing the equivalent aerodynamic profile.
- Based on the boundary-layer theory, a prediction model is proposed for the growth of the boundary layer on the blade in the transonic region. Starting from the development law of the boundary layer at the leading edge of the blade, the maximum prediction error of the boundary-layer thickness at the leading edge is 3.2%. In addition, a detached shock prediction model applicable at a low Re is developed on the basis of the Moeckel method, which is able to accurately predict the shock parameters. The boundary layer calculation method is proposed for the SWBLI, with an equivalent aerodynamic profile calculation error of no more than 7.8% at different Re.
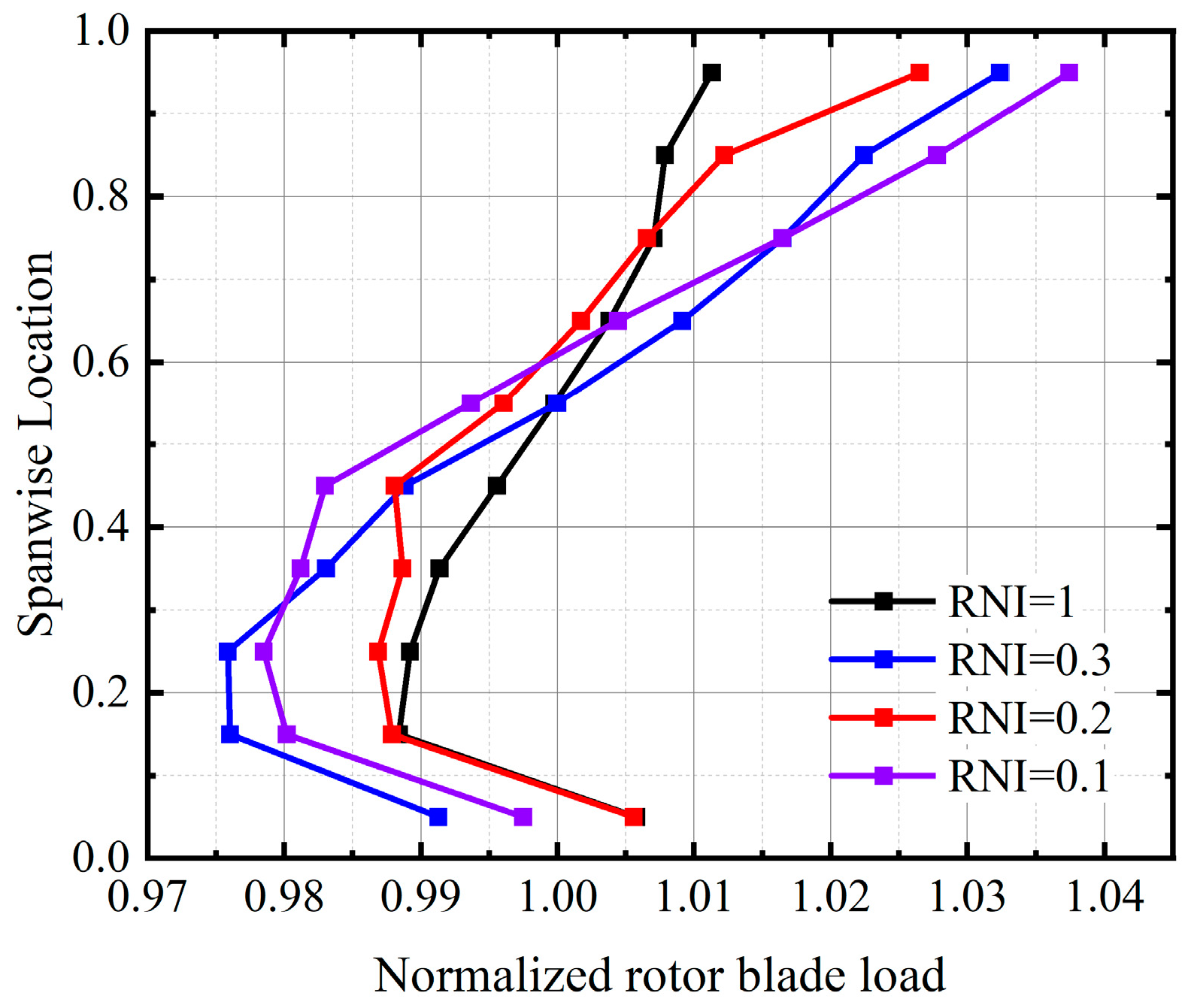
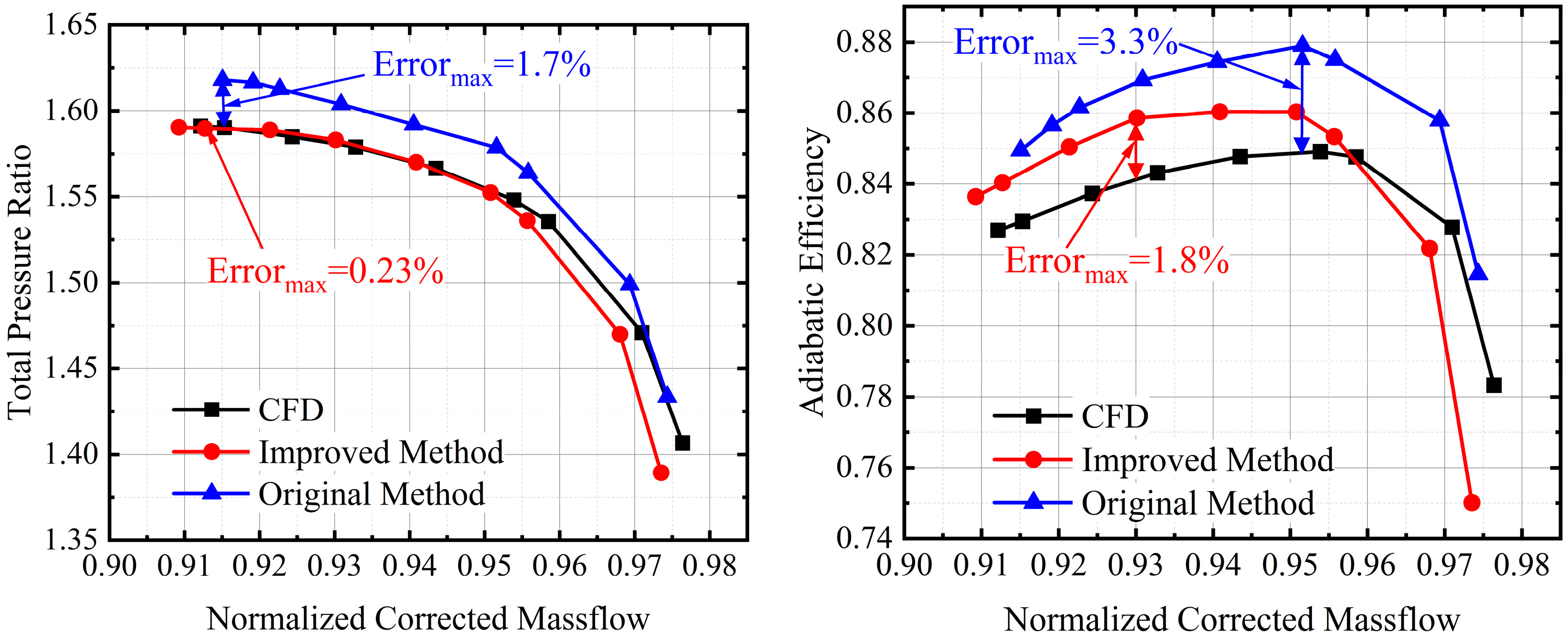
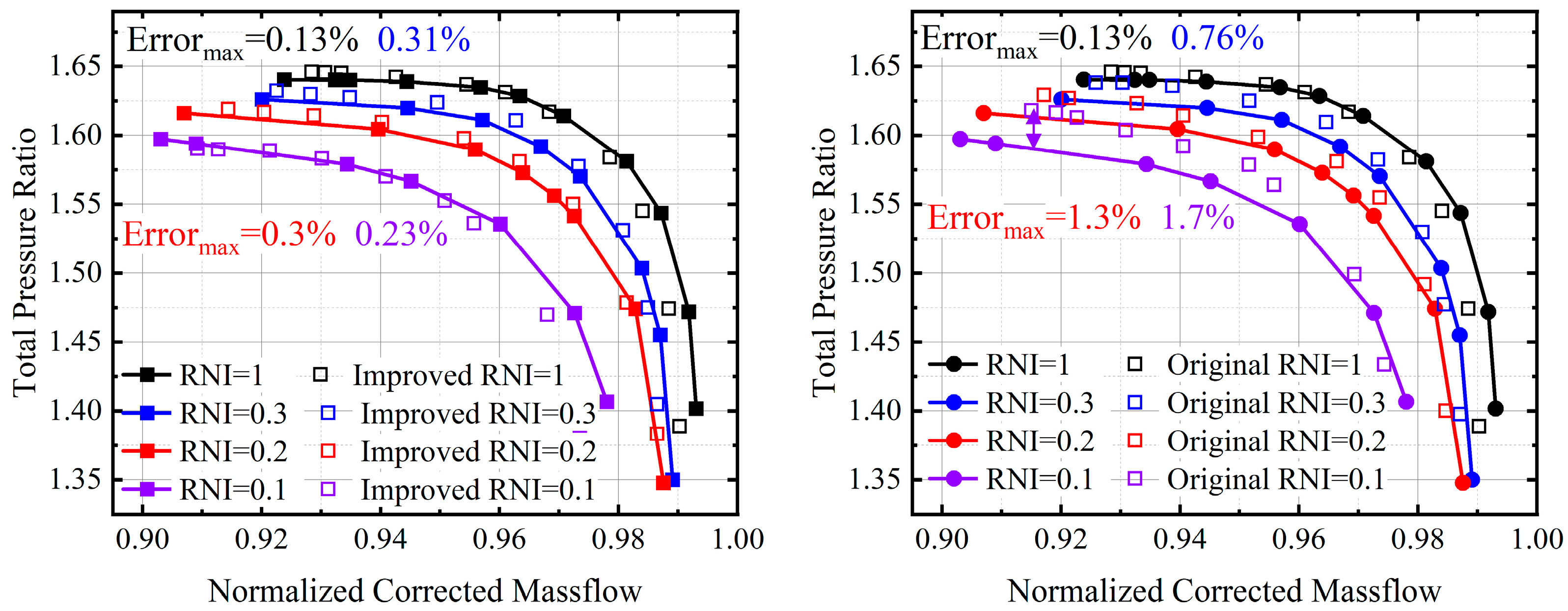
- A partitioned multiline calculation strategy based on the equivalent profile is proposed. This strategy modifies the effect of the equivalent profile on the loss models and stall criteria, and it accurately calculate the performance at different spans with a maximum error of less than 2%, which marks an improvement of 2.6% in accuracy compared to the original method. The calculation strategy that takes into account the equivalent profile and radial load redistribution opens up the computational dimension in the radial direction, and it improves the accuracy of the overall performance of the compressor at a low Re, with a pressure ratio error of only 0.23% and an efficiency error of 1.8% at an RNI = 0.1. Considering the assumptions made in the calculation process, the method may not be applicable for an Ma > 2. In the lower Re range, new flow phenomena may occur, rendering the method inapplicable.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Static pressure coefficient | |
| Reynolds Number Index | |
| PE | Peak efficiency |
| Wake form factor | |
| Angle of attack (deg) | |
| Density (kg/m3) | |
| Pressure (Pa) | |
| Total pressure (Pa) | |
| Total temperature (K) | |
| Dynamic viscosity (Pa·s) | |
| Shock angle (deg) | |
| Blade solidity | |
| Dimensionless radial velocity coefficient (m/s) | |
| Deflection angle (deg) | |
| Angle between the sonic line and normal to main flow direction (deg) | |
| Boundary-layer displacement thickness | |
| Tangent of the angle between the direction of friction stress and the direction of flow outside the boundary layer | |
| Total pressure loss coefficient | |
| Blade maximum thickness (m) | |
| Blade chord length (m) | |
| Camber angle (deg) | |
| Stagger angle (deg) | |
| Momentum thickness of the wake |
References
- Slameršak, A.; Kallis, G.; O’Neill, D.W. Energy requirements and carbon emissions for a low-carbon energy transition. Nat. Commun. 2022, 13, 6932. [Google Scholar] [CrossRef] [PubMed]
- Perlaviciute, G.; Steg, L.; Sovacool, B.K. A perspective on the human dimensions of a transition to net-zero energy systems. Energy Clim. Change 2021, 2, 100042. [Google Scholar] [CrossRef]
- Wassell, A.B. Reynolds Number Effects in Axial Compressor. J. Eng. Gas Turbines Power 1968, 4, 149–156. [Google Scholar] [CrossRef]
- Casey, M.V. The effects of Reynolds number on the efficiency of centrifugal compressor stages. J. Eng. Gas Turbines Power 1985, 107, 541–548. [Google Scholar] [CrossRef]
- Casey, M.V.; Robinson, C.J. A unified correction method for Reynolds number, size, and roughness effects on the performance of compressors. Proc. Inst. Mech. Eng. Part A J. Power Energy 2011, 225, 864–876. [Google Scholar] [CrossRef]
- Casey, M.V.; Krahenbuhl, D.; Zwyssig, C. The design of ultra-high-speed miniature centrifugal compressors. In Proceedings of the 10th European Conference on Turbomachinery Fluid Dynamics and Thermodynamics ETC, Lappeenranta, Finland, 15–19 April 2013; Volume 10, pp. 1–13. [Google Scholar]
- Pelz, P.F.; Stonjek, S.S. The influence of Reynolds number and roughness on the efficiency of axial and centrifugal fans—A physically based scaling method. J. Eng. Gas Turbines Power 2013, 135, 1–8. [Google Scholar] [CrossRef]
- Horlock, J.H.; Denton, J.D. A review of some early design practice using computational fluid dynamics and a current perspective. J. Turbomach. Trans. ASME 2005, 127, 5–13. [Google Scholar] [CrossRef]
- Johnsen, I.A.; Bullock, R.O. Aerodynamic Design of Axial-Flow Compressors; Chapter 10; NASA: Washington, DC, USA, 1965; p. 297. Available online: https://ntrs.nasa.gov/citations/19650013744 (accessed on 14 April 2025).
- Howell, A.R.; Bonham, R.P. Overall and stage characteristics of axial-flow compressors. Proc. Inst. Mech. Eng. 1950, 163, 235–248. [Google Scholar] [CrossRef]
- Howell, A.R.; Calvert, W.J. A new stage stacking technique for axial-flow compressor performance prediction. J. Eng. Gas Turbines Power Trans. ASME 1978, 100, 698–703. [Google Scholar] [CrossRef]
- Smith, S.L. One-Dimensional Mean Line Code Technique to Calculate Stage-by-Stage Compressor Characteristics. Master’s Thesis, University of Tennessee, Knoxville, TN, USA, 1999. [Google Scholar]
- Miller, A.S. Compressor Conceptual Design Optimization. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2015. [Google Scholar]
- White, N.M.; Tourlidakis, A.; Elder, R.L. Axial compressor performance modelling with a quasi-one-dimensional approach. Proc. Inst. Mech. Eng. Part A J. Power Energy 2002, 216, 181–193. [Google Scholar] [CrossRef]
- Dahlquist, A.N. Investigation of Losses Prediction Methods in 1D for Axial Gas Turbine. Master’s Thesis, Lund University, Scania, Sweden, 1990. [Google Scholar]
- Back, S.C.; Hobson, G.V.; Song, S.J.; Millsaps, K.T. Effects of Reynolds Number and Surface Roughness Magnitude and Location on Compressor Cascade Performance. J. Turbomach. Trans. ASME 2012, 134, 051013. [Google Scholar] [CrossRef]
- Liu, Q.; Ager, W.; Hall, C.; Wheeler, A.P. Low Reynolds Number Effects on the Separation and Wake of a Compressor Blade. J. Turbomach. Trans. ASME 2022, 144, 101008. [Google Scholar] [CrossRef]
- Xu, H.F.; Zhao, S.F.; Wang, M.Y.; Sheng, X.Y.; Han, G.; Lu, X.G. Investigation of unsteady flow mechanisms and modal behavior in a compressor cascade. Aerosp. Sci. Technol. 2023, 142, 108596. [Google Scholar] [CrossRef]
- Pan, T.; Li, T.; Yan, Z.; Li, Q. Investigation of turbulence-induced disturbances and their evolution to stall onset in a compressor cascade using large eddy simulation. Chin. J. Aeronaut. 2025. [Google Scholar] [CrossRef]
- Wang, M.; Yang, C.; Li, Z.; Zhao, S.; Zhang, Y.; Lu, X. Effects of surface roughness on the aerodynamic performance of a high subsonic compressor airfoil at low Reynolds number. Chin. J. Aeronaut. 2021, 34, 71–81. [Google Scholar] [CrossRef]
- Li, Z.L.; Wu, Y.F.; Li, L.; Lu, X.G.; Han, G. Numerical Investigation of Low Reynolds Number Effects on Energy Loss Inside Centrifugal Compressor with Different Inlet Conditions. Aerosp. Sci. Technol. 2024, 146, 108923. [Google Scholar] [CrossRef]
- Cheng, H.; Lu, X.; Zhao, S.; Huang, S.; Zhu, J. Effect of tip clearance variation in the transonic axial compressor of a miniature gas turbine at different Reynolds numbers. Aerosp. Sci. Technol. 2022, 128, 107793. [Google Scholar] [CrossRef]
- Cheng, H.; Li, Z.; Zhou, C.; Lu, X.; Zhao, S.; Han, G. Effect of blade surface cooling on a micro transonic axial compressor performance at low Reynolds number. Appl. Therm. Eng. 2023, 226, 120353. [Google Scholar] [CrossRef]
- Diehl, M.; Schreiber, C.; Schiffmann, J. The Role of Reynolds Number Effect and Tip Leakage in Compressor Geometry Scaling at Low Turbulent Reynolds Numbers. ASME. J. Turbomach. 2020, 142, 031003. [Google Scholar] [CrossRef]
- Irps, T.; Kanjirakkad, V. Wake–Separation Bubble Interaction Over an Experimentally Simulated Axial Compressor Blade Under Low Reynolds Number Flow. ASME. J. Turbomach. 2025, 147, 081018. [Google Scholar] [CrossRef]
- Strazisar, A.J.; Wood, J.R.; Hathaway, M.D.; Suder, K.L. Laser Anemometer Measurements in a Transonic Axial-Flow Fan Rotor; NASA-TP-2879; NASA: Cleveland, OH, USA, 1990. Available online: https://ntrs.nasa.gov/citations/19900001929 (accessed on 14 April 2025).
- Ferrar, A.M. Measurement and Uncertainty Analysis of Transonic Fan Response to Total Pressure Inlet Distortion. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2015. [Google Scholar]
- Spotts, N. Unsteady Reynolds-Averaged Navier-Stokes Simulations of Inlet Flow Distortion in the Fan System of a Gas-Turbine Aero-Engine. Master’s Thesis, Colorado State University, Fort Collins, CO, USA, 2015. [Google Scholar]
- Murawski, C.G.; Sondergaard, R.; Rivir, R.B.; Vafai, K.; Simon, T.W.; Volino, R.J. Experimental Study of the Unsteady Aerodynamics in a Linear Cascade with Low Reynolds Number Low Pressure Turbine Blades. In Proceedings of the ASME 1997 International Gas Turbine and Aeroengine Congress and Exhibition, Orlando, FL, USA, 2–5 June 1997. [Google Scholar]
- Zhang, P.; Lu, J.; Wang, Z.; Song, L.; Feng, Z. Adjoint-Based Optimization Method with Linearized SST Turbulence Model and a Frozen Gamma-Theta Transition Model Approach for Turbomachinery Design. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015; Volume 2B, pp. 1–15. [Google Scholar]
- Karimipanah, M.T.; Olsson, E. Calculation of three-dimensional boundary layer on rotor blades using integral methods. In Proceedings of the ASME 1992 International Gas Turbine and Aeroengine Congress and Exposition, Cologne, Germany, 1–4 June 1992; Volume 1, pp. 1–14. [Google Scholar] [CrossRef]
- Maskell, E.C. Flow Separation in Three Dimensions; Ministry of Supply, Royal Aircraft Establishment, RAE: Farnborough, UK, 1955. [Google Scholar]
- Li, Z.; Zhu, X.; Yan, Z.; Pan, T. Effects of Re on blade load temporal-spatial distribution and correlation with flow stability of transonic compressor under inlet distortion. Aerosp. Sci. Technol. 2024, 147, 109007. [Google Scholar] [CrossRef]
- Koch, C.C.; Smith, L.H. Loss sources and magnitudes in axial-flow compressors. J. Eng. Gas Turbines Power Trans. ASME 1976, 98, 411–424. [Google Scholar] [CrossRef]
- Moeckel, W.E. Approximate Method for Prediction Form and Location of Detached Shock Waves Ahead of Plane or Axially Symmetric Bodies; NACA TN-1921; NASA: Cleveland, OH, USA, 1949. Available online: https://ntrs.nasa.gov/api/citations/19930082597 (accessed on 14 April 2025).
- Qiu, M.; Zhou, Z.G.; Liu, L.L. Prediction of detached shockwaves from leading edge of supersonic cascade. J. Aerosp. Power 2014, 29, 363–373. [Google Scholar]
- Prandtl, L. On boundary layer layers in three dimensional flow. 1946, Reps. And Trans. No.64, British M. A. P.
- Gruschwitz, E. Turbulente Reibungsschichten mit Sekundärströmung. Ing. Arch. 1935, 6, 355–365. [Google Scholar] [CrossRef]
- Lieblein, S.; Roudebush, W.H. Theoretical Loss Relations for Low-Speed Two-Dimensional-Cascade Flow; NACA TN3662; NASA: Cleveland, OH, USA, 1956. Available online: https://ntrs.nasa.gov/citations/19930084888 (accessed on 14 April 2025).
- Bloch, G.S. Flow Losses in Supersonic Compressor Cascades. Ph.D. Thesis, Mechanical Engineering Dept, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 1996. [Google Scholar]
- Hearsey, R.M. Program HT0300 NASA 1994 version. 1994, Doc. No. D6-81569TN, Volumes 1 and 2, the Boeing Company.
- Boyer, K.M. An Improved Streamline Curvature Approach for Off-Design Analysis of Transonic Compression System. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2001. [Google Scholar]
- Aungier, R.H.; Farokhi, S. Axial-Flow Compressors: A Strategy for Aerodynamic Design and Analysis; ASME Press: New York, NY, USA, 2003. [Google Scholar]
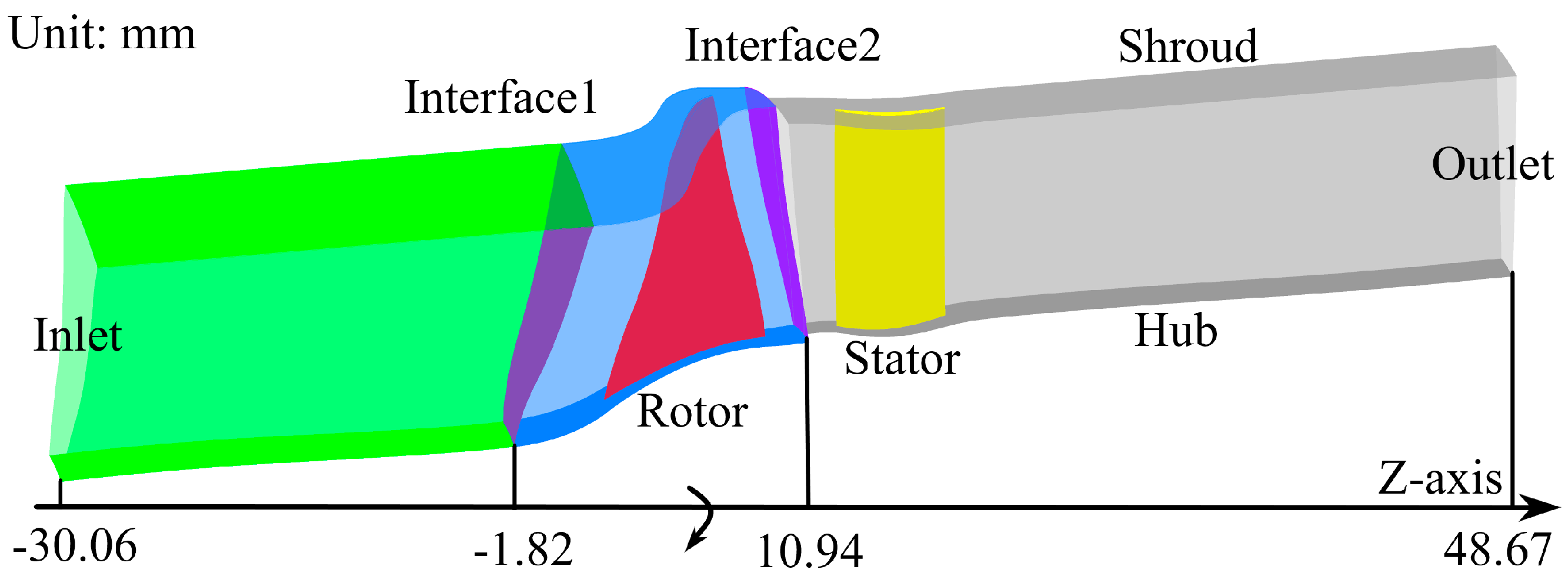
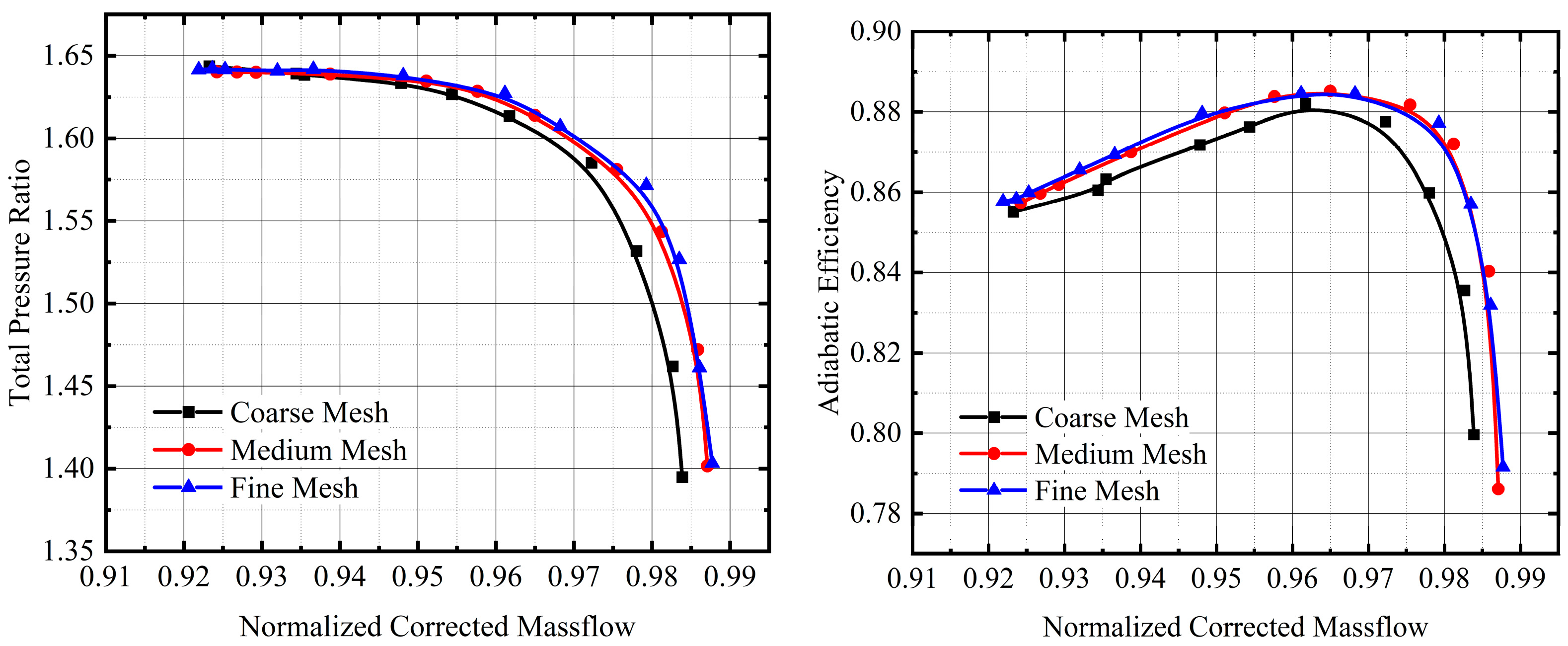

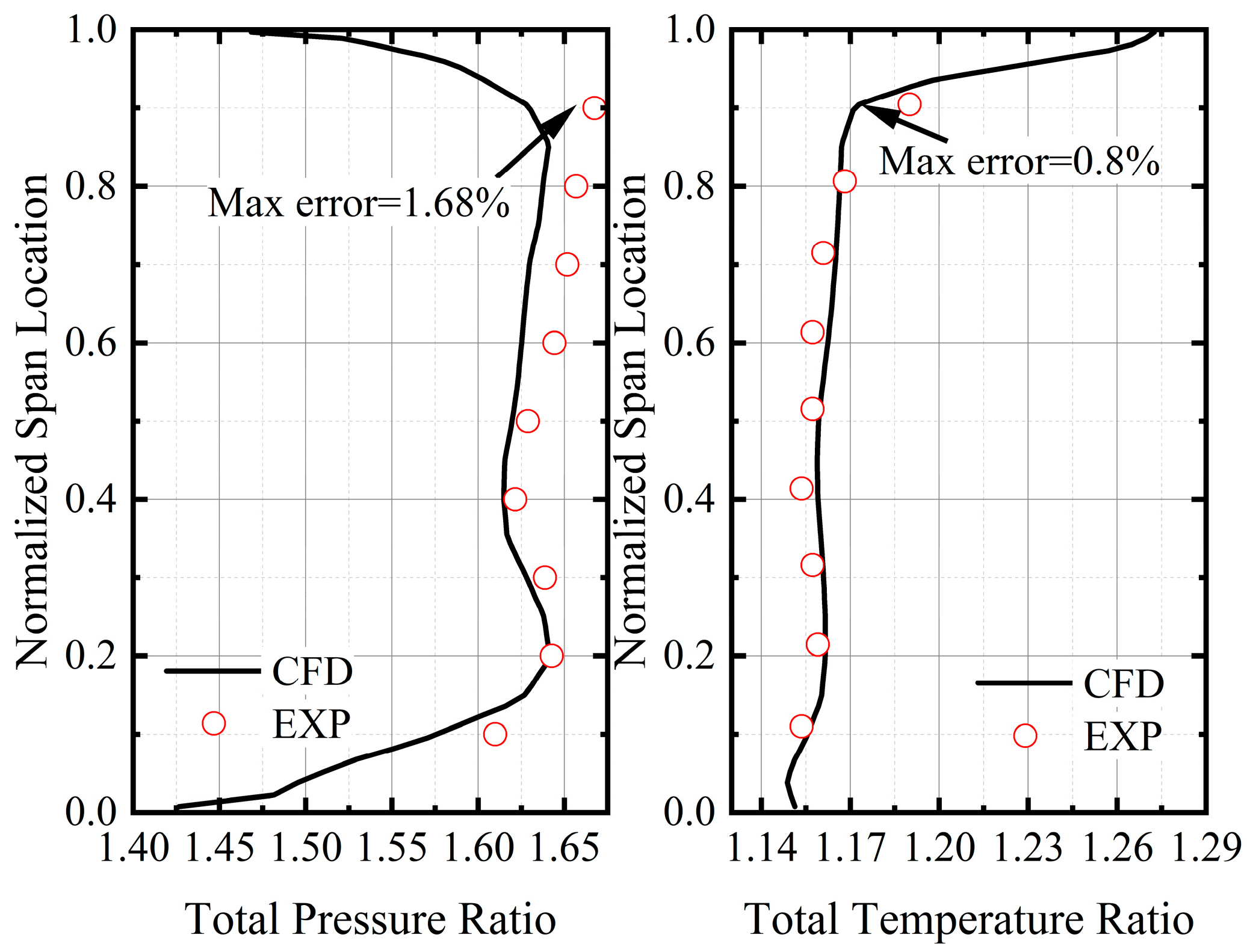
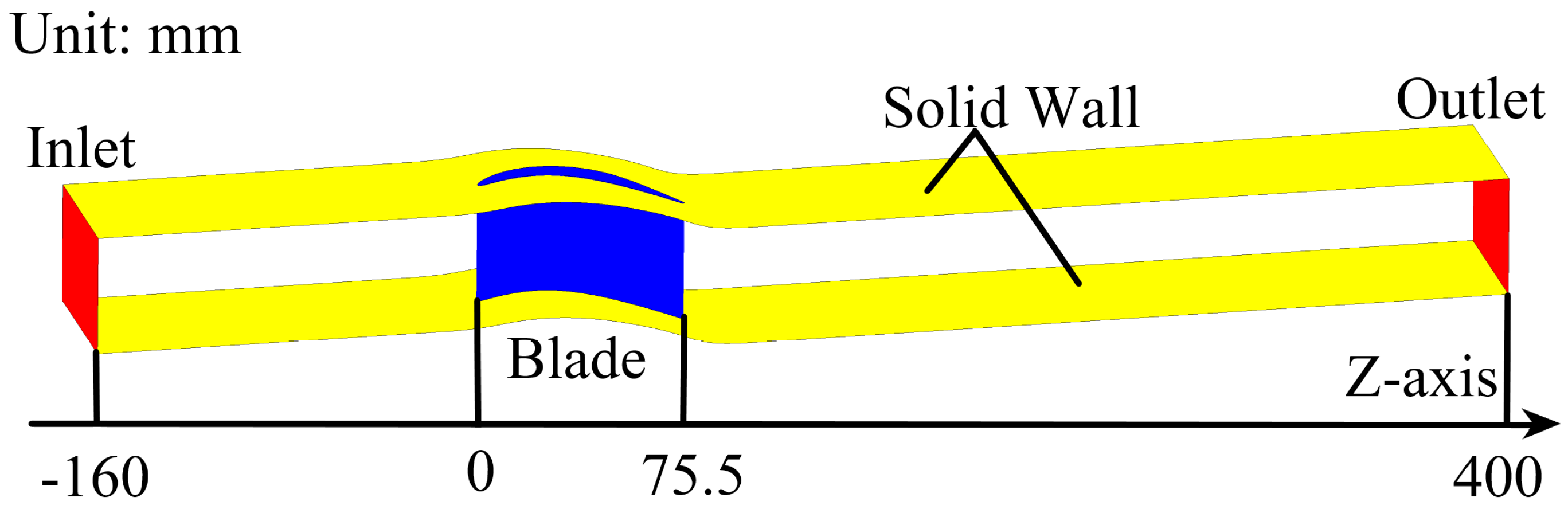







| Parameters | Rotor | Stator |
|---|---|---|
| Blade number | 22 | 34 |
| Rotational speed (rpm) | 16,042.8 | / |
| Mass flow rate (kg/s) | 33.25 | / |
| Total pressure ratio | 1.63 | / |
| Tip clearance (mm) | 1.006 | / |
| Blade tip aerodynamic chord (cm) | 9.522 | 5.768 |
| Rotor aspect ratio | 1.56 | / |
| Inlet/Exit hub/tip radius ratio | 0.375/0.478 | 0.5/0.53 |
| Tip relative Mach number | 1.38 | / |
| Mesh Number | In Block | Rotor | Stator | Total |
|---|---|---|---|---|
| Coarse | 1.8 × 104 | 1.6 × 105 | 1.1 × 105 | 3.1 × 105 |
| Medium | 4.2 × 104 | 4 × 105 | 3 × 105 | 7.4 × 105 |
| Fine | 5.4 × 104 | 5.3 × 105 | 4 × 105 | 9.8 × 105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, D.; Pan, T.; Zhu, X.; Li, Z. A Strategy for Predicting Transonic Compressor Performance at Low Reynolds Number. Aerospace 2025, 12, 349. https://doi.org/10.3390/aerospace12040349
Shi D, Pan T, Zhu X, Li Z. A Strategy for Predicting Transonic Compressor Performance at Low Reynolds Number. Aerospace. 2025; 12(4):349. https://doi.org/10.3390/aerospace12040349
Chicago/Turabian StyleShi, Dalin, Tianyu Pan, Xingyu Zhu, and Zhiping Li. 2025. "A Strategy for Predicting Transonic Compressor Performance at Low Reynolds Number" Aerospace 12, no. 4: 349. https://doi.org/10.3390/aerospace12040349
APA StyleShi, D., Pan, T., Zhu, X., & Li, Z. (2025). A Strategy for Predicting Transonic Compressor Performance at Low Reynolds Number. Aerospace, 12(4), 349. https://doi.org/10.3390/aerospace12040349





