Abstract
This study proposes an advanced space radiation shielding design method that integrates multi-objective optimization with reliability evaluation to mitigate the impact of harsh space radiation environments on electronic systems. A genetic algorithm is employed to optimize multi-layer shielding configurations with respect to radiation dose reduction, mass efficiency, and structural thickness. To ensure practical applicability, a reliability evaluation framework incorporating uncertainty factors is developed, where shielding designs are considered acceptable when the risk confidence level (CL) remains below 5%. A case study simulating long-duration deep space missions demonstrates that the optimized five-layer shielding configuration reduces the radiation-induced failure rate by approximately 57%, enhancing the long-term reliability of core electronic components to 0.94 over a five-year mission. These findings validate the effectiveness of the proposed approach in supporting the development of reliable, lightweight radiation shielding for future space missions.
1. Introduction
Space radiation primarily consists of galactic cosmic rays (GCRs) and solar particle events (SPEs), both of which pose significant threats to spacecraft electronics during long-duration missions (see Appendix A). These high-energy particles continuously bombard spacecraft, generating secondary radiation that degrades electronic components, compromises system integrity, and increases the risk of mission failure. Effective radiation shielding is, therefore, a critical requirement for ensuring the reliability and operational longevity of electronic systems in space.
Materials with a high charge-to-mass ratio (Z/A)—where Z denotes the atomic number and A the mass number—are often considered for passive shielding against high-energy particles, particularly heavy ions (HZE particles) [1]. Lower Z/A materials, such as hydrogen-rich compounds, are more effective in suppressing nuclear fragmentation, whereas higher Z/A materials tend to increase its likelihood despite good energy attenuation. Each nucleus’s linear energy transfer (LET) changes as it slows down and loses energy within the shielding material. Although high-Z materials can effectively reduce LET in certain scenarios, particles with higher LET tend to deposit more energy in lower-energy portions of the particle spectrum. Therefore, shielding material selection must be optimized based on specific radiation environments and application needs [2]. The attenuation performance of a shielding material depends on its atomic number (Z), physical thickness, and the type and energy of the incident radiation. In practical applications, designing an appropriate material thickness is crucial for effective radiation shielding [3]. An effective shielding system should be adaptable, cost-efficient, non-toxic, and durable, and minimize secondary radiation production [4]. It is necessary to optimize the materials’ attenuation characteristics and depth transmission properties, selecting appropriate thicknesses and layered structures.
Traditional shielding designs, often based on homogeneous single-layer or simple composite materials, are limited in adapting to the space radiation environment’s multidimensional and dynamic characteristics. These designs typically rely on empirical expertise for material selection and thickness estimation, which may result in suboptimal performance [5]. Such approaches also neglect the need to address multiple conflicting objectives simultaneously, including radiation attenuation, mass minimization, and structural feasibility.
To address these challenges, multi-objective optimization algorithms have been increasingly adopted for the design of shielding systems [6]. In particular, multi-layer and hybrid materials have shown promise in outperforming conventional materials in terms of both shielding efficiency and mass reduction [7]. For instance, hydrogen-rich composites, such as boron nitride–polyethylene blends, have demonstrated superior neutron attenuation characteristics due to their high hydrogen content and low atomic number of elements [8]. In addition, radiation-resistant aluminum alloys featuring thermodynamically stable T-phase structures have been developed specifically for deep space missions, offering both mechanical robustness and enhanced radiation survivability [9]. Recent studies have highlighted the growing potential of polymeric composites, nanocomposites, and multi-layered materials as lightweight and effective alternatives to traditional radiation shielding, particularly in space applications [10].
However, designing efficient multi-layer shielding systems that account for complex material interactions and mission constraints remains a considerable challenge. Additives and a base material are combined to form composite shields [11]. Uneven shielding capabilities might result from the components’ challenges in achieving homogeneous mixing. Because of the uneven material mixing, pure regions or pinholes may emerge inside the composite, enabling radiation to flow through [12]. Gadolinium oxide (Gd2O3)-based composite films have recently been developed and shown to effectively attenuate space radiation within aircraft environments, offering a promising lightweight shielding alternative [13]. The shielding design significantly influences the total ionizing dose (TID) level received by sensitive electronics. The shielding system must meet radiation protection and reliability requirements for electronic equipment [14]. Optimizing multi-layer shielding materials can mitigate this issue [15].
The radiation dose to electronic devices is affected by spacecraft design parameters (e.g., wall thickness and shell position) and mission parameters (e.g., orbit, duration, and altitude) [16]. These variables must be carefully accounted for during design to achieve optimal shielding with minimal weight [17]. Composite structures hold considerable potential for improving efficiency and reducing mass. According to studies, multi-layered shielding reduces electron penetration by around 60% for a given amount of material, making it more effective than single-material shielding [18]. The International Space Station (ISS) currently employs a combination of aluminum and polyethene layers for enhanced shielding [19]. Previous studies have shown that, for the same areal density, composite or multi-layer shielding configurations can provide improved radiation attenuation compared to single-layer aluminum shielding, particularly in mitigating secondary particle production [20,21,22].
In this context, the present study proposes a novel radiation shielding optimization framework that integrates multi-objective design principles with uncertainty-based reliability evaluation [23,24].The proposed shielding design and reliability evaluation framework is intended for critical applications in deep space missions, where electronic components are exposed to prolonged high-radiation environments. By incorporating uncertainties in radiation transport, material behavior, and mission parameters, the proposed approach aims to identify shielding configurations that meet reliability targets under specified confidence levels. The method integrates radiation simulation, reliability modeling [25], and algorithmic optimization to design lightweight and reliable shielding for deep space missions.
In this paper, Section 2 outlines the multi-objective and multi-parameter mathematical challenges in radiation shielding design. Section 3 presents the key components of the genetic algorithm (GA) and its application in optimizing shielding solutions. The reliability-based shielding design methodology is detailed in Section 4, accompanied by an in-depth analysis of dose-equivalent results from the multi-layer study. Finally, Section 5 summarizes the findings and insights from the preceding discussions.
2. Radiation Shielding Design
2.1. Radiation Environment
GCRs primarily consist of protons (~85%), alpha particles (~14%), and heavy nuclei (~1%). When interacting with matter, these cosmic rays generate secondary particles such as neutrons, ions, and gamma rays [26]. Both neutron and ion production cross-sections and the generation processes of secondary particles are highly influenced by the energy of the incoming GCRs and the nature of the target material.
All analyses in this study were conducted assuming a GCR environment at 1 AU in free space. The GCR spectrum was derived from the Badhwar–O’Neill 2014 model, corresponding to the 2010 solar minimum conditions with a solar modulation parameter of 475 MV. The spectrum was obtained using the SPENVIS online tool and has been widely adopted in previous transport code validation studies [27]. The resulting spectrum, illustrated in Figure 1, spans an energy range from 1 keV/n to 100 GeV/n and includes ions with atomic numbers from 1 to 28. Figure 1 presents the annual GCR energy spectra for four representative ions with atomic numbers Z = 1, Z = 2, Z = 8, and Z = 26, which collectively characterize the radiation environment encountered during deep space missions. The spectral distribution exhibits a pronounced inverse power-law trend, indicating that lower-energy particles dominate in flux, whereas high-energy particles, though less frequent, pose significant shielding challenges due to their strong penetration capability and LET. Helium and oxygen ions follow similar spectral trends but at reduced magnitudes, while iron ions—though rare—contribute disproportionately to the total dose equivalent due to their high LET. This highlights the critical need for shielding materials capable of attenuating a wide energy range, particularly HZE particles that pose serious risks to electronic systems in deep space missions.
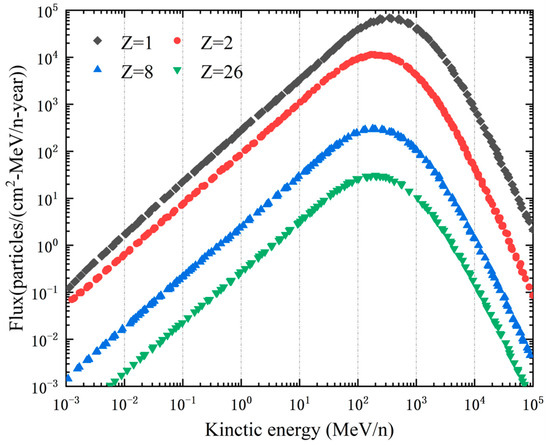
Figure 1.
Annual GCR energy spectra for ions with Z = 1, 2, 8, 26.
2.2. Geometry and Materials
In this study, we conducted simulations of various shielding materials (in Table 1) utilizing the slab mode, wherein the total shielding thickness ranged from 0 to 100 g/cm2. Analysis shows that materials containing hydrogen, boron, and nitrogen offer strong radiation shielding, while polymer- and resin-based fiber materials effectively attenuate radiation particle energy. This study focused on 10 types of shielding materials.

Table 1.
Material information sheet.
This study selected a finite flat plate that receives spatial radiation on only one side as the shielding shape. The shielding effect is related to the thickness of the shielding medium. As shown in Figure 2, a complex multi-layer shielding structure is created.
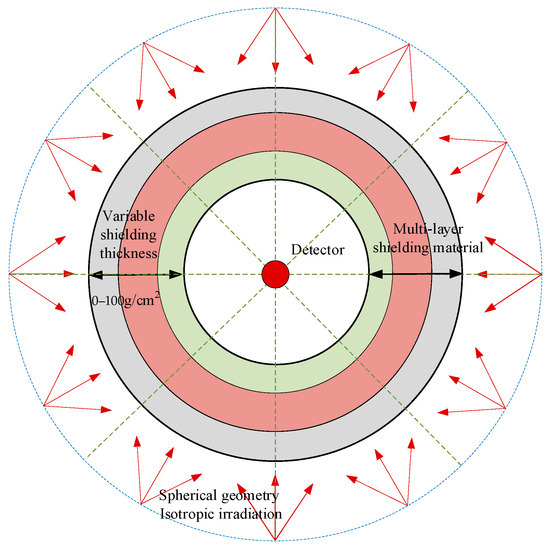
Figure 2.
Schematic of complex multi-layered shielding materials.
2.3. Boundary Conditions
SPEs are composed primarily of protons that are accelerated during solar eruptions, such as solar flares and coronal mass ejections (CMEs). In this study, we distinguish between two types of SPEs: impulsive SPEs, which are short-duration, high-intensity proton events typically associated with solar flares, and pulsed SPEs, which refer to sequences of multiple, temporally separated bursts occurring over a limited period. These terms do not refer to the steady-state solar wind, which is excluded from the current radiation environment analysis.
The composition of impulsive SPEs [28] is detailed in Table 2. While protons constitute more than 90% of the total particle abundance, they contribute only approximately 8% to the overall dose equivalent. In contrast, although iron nuclei represent just 0.03% of the GCR flux—three orders of magnitude lower than protons—they contribute nearly 20% of the total dose equivalent due to their high LET characteristics. Therefore, when studying the shielding performance characteristics of spacecraft materials, it is necessary to consider the radiation damage of heavy ions. Specific spacecraft radiation shielding designs incorporate designated areas intended as storm shelters, allowing human occupants to seek refuge during SPEs.

Table 2.
The element abundances of the photosphere, GCRs, impulsive SPEs, and coronal mass ejections.
2.4. Multi-Objective Optimization Model
An optimal radiation shielding design should balance multiple objectives, including minimizing weight, volume, and radiation dose outside the shield [29]. Nevertheless, it should be emphasized that these goals are intrinsically conflicting and cannot be optimized all at once. Considering the total radiation dose after shielding, the total shielding thickness, and the total mass of the shielding material, a three-parameter optimization model was developed. The optimization objective is dose-equivalent. The model minimizes these three parameters to achieve optimization under the constraint that the total radiation dose, total thickness, and total mass do not exceed their maximum permissible limits. A multi-objective optimization model was proposed, incorporating parameters such as shielding design, decision variables, and constraints.
where is the TID after shielding, which is the absorbed radiation dose of the first layer closest to the protected material (0.1 mm silicon material), and is the maximum allowable TID. is the total thickness of the shielding scheme. is the upper limit of the total thickness (mm). is the equivalent areal density of the shielding material. is the upper limit of the material surface density.
In this study, the shielding structure is modeled as a finite flat plate. If the area of each layer of the shielding layer can be considered identical, then the total mass of the shielding scheme is directly proportional to its area density. The equivalent areal density could be used to measure the mass of the shielding material. represents each shielding scheme, n represents the number of layers of the shielding scheme, and represents layer of the shielding scheme. is the density of the material.
3. Optimization and Analysis of Results
3.1. Shielding Design with Genetic Algorithm
The radiation shielding design uses a genetic algorithm to solve multi-objective optimization problems. Within this framework, chromosomes (or genes) represent candidate shielding solutions for multi-objective optimization. Through successive iterations of evolution, these representations aim to approach better solutions. MCNP version 6.2 was the software used for the computational simulations in this study. Figure 3 shows a schematic of the shielding design process using the genetic algorithm, demonstrating an automated optimization workflow.
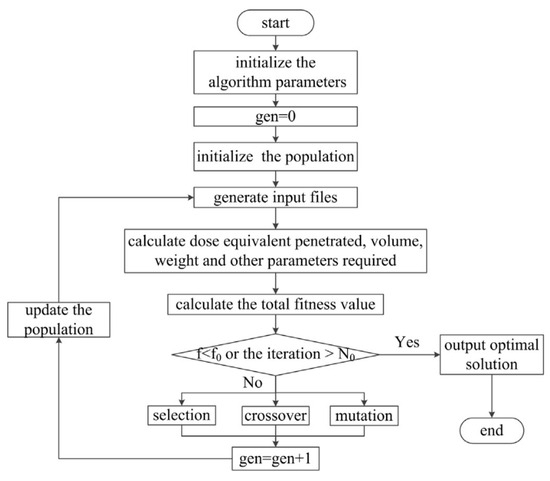
Figure 3.
General scheme of radiation shielding design with genetic algorithm.
GA was chosen for this study due to its well-established robustness in solving complex, multi-objective, and constraint-heavy design problems. Compared to Particle Swarm Optimization (PSO) and Simulated Annealing (SA), GA offers higher global search capability and better resilience to local minima, particularly in high-dimensional, discrete search spaces such as material type, stacking sequence, and layer thickness. In addition, GA maintains diversity through population-based search, reducing premature convergence risks [6,17].
3.2. Fitness Function for Multi-Layer Material Shielding Design
When optimizing the design using a genetic algorithm, the radiation shielding should be evaluated based on fitness to achieve the optimal shielding solution. is the benchmark for assessing the quality of radiation shielding solutions. The smaller its value, the closer the solution is to the optimal shielding configuration. However, the three variables representing differ in their physical quantities and units. Therefore, we utilized the GA Fortran package to define a fitness function for evaluating the solutions.
The GCR particle distribution data obtained from numerical analysis serve as the environmental input, and parameterized boundary conditions are defined as follows.
To ensure mission safety and maintain hardware operability, specific dose and mass constraints are imposed on the shielding design. The maximum allowable total radiation dose (107 rad) defines the upper bound for radiation exposure, while the corresponding shielding material’s maximum areal density is limited to 100 g/cm2. The permissible maximum surface density is also defined based on the equivalent mass of a given aluminum thickness. Any shielding solution that exceeds these boundary limits is considered non-compliant and is categorized as ineffective against high-energy particles.
If the materials of several consecutive shielding layers are identical, they are considered a single shielding layer, with the total thickness equal to the sum of these layers. The radiation dose measured in the silicon film layer behind the shield and the shielding material’s total thickness and surface density are used to define the fitness function . This function assigns a value to each shielding solution, and the genetic algorithm selects the optimal shielding solution based on .
A lower quality factor indicates a more effective shielding design. Since the genetic algorithm in this study optimizes for the maximum rather than the minimum, the final fitness value should be .
3.3. Evolutionary Optimization Strategy
Following multiple generations of evolution facilitated by genetic algorithms, the simulation culminates in attaining the Pareto optimal shielding solution.
is the objective function of optimization. Among them, , , and are defined as follows:
where , , and are the weights of the TID after shielding, the total thickness, and the equivalent areal density. , , and are the corresponding weight factors. Since the radiation dose level after shielding is the main optimization target in this study, different weighting factors are applied, and the value of can be used to evaluate the values of different shielding solutions.
The genetic algorithm generates individuals representing the initial structural data, forming an initial population. Each individual corresponds to a multi-layer material radiation shielding solution X, and the information for each individual includes the number of material layers, the type of shielding material for each layer, the thickness, and the stacking order of different shielding materials.
A decimal encoding scheme is used, with the number of bits for each chromosome defined as 8 n, where n is the number of shielding material layers. In this study, each shielding solution consists of 10 material layers, i.e., n = 10. Figure 4 shows the chromosome encoding corresponding to a particular shielding solution.
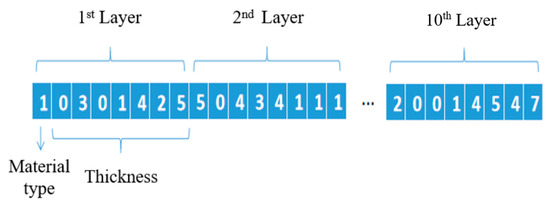
Figure 4.
Schematic diagram of chromosome coding.
The encoding consists of 80 bits, with each 8-bit segment representing the properties of one shielding material layer. For example, the first 8 bits represent the properties of the first shielding material layer. The leftmost bit of the 8-bit segment indicates the type of shielding material, which is denoted by a number from 1 to 10, ordered according to the atomic number. The remaining 7 bits represent the thickness of the shielding layer. The surface density of each shielding layer can be calculated using the material’s thickness and density.
Figure 5 illustrates the evolution of shielding solutions throughout the genetic algorithm optimization process, specifically showing radiation dose and areal density distributions at the initial, 20th, 40th, and 50th iterations. After each generation, candidate solutions are visualized to facilitate intuitive comparison and performance assessment. As the algorithm progresses, the design space contracts toward the Pareto front, with marked improvements in shielding performance observed during early iterations. By the 50th generation, the solutions demonstrate clear convergence, indicating the algorithm’s stability and efficiency in balancing dose reduction and material usage under multi-objective constraints.
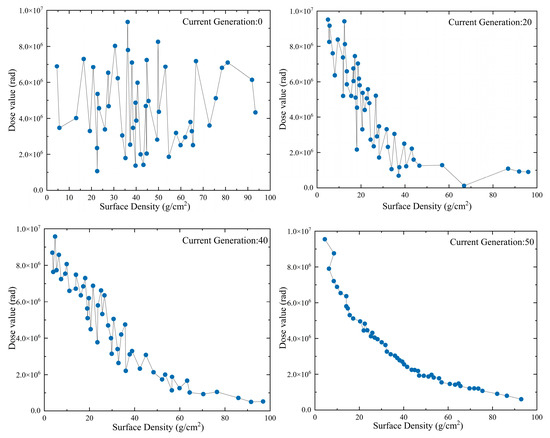
Figure 5.
Iterative convergence behavior of multi-layer shielding solutions optimized.
3.4. Design of Multi-Layer Materials
Based on the optimization criteria of the objective function, a genetic algorithm is constructed for iterative optimization, with range constraints applied to each variable to identify the optimal shielding material configuration. Specifically, the domain of each variable is normalized within the range of 0 to 1, corresponding to a physical thickness of 0 to 100 g/cm2. The population size is dynamically set between 50 and 300 based on the number of variables, typically at a scale of approximately 10 times the number of variables. In addition, the cumulative probability distribution parameter q is adjusted between 0.1 and 0.4, depending on the population size, with higher values of q imposing greater selection pressure. The genetic algorithm is configured with a population size of 100, a crossover probability of 0.85, and a mutation rate of 0.05. The algorithm runs for 50 generations, using a decimal encoding scheme with 8 bits per gene to represent the shielding material type and thickness. These parameter settings were chosen based on established practices in multi-objective optimization and were validated through preliminary sensitivity analyses to ensure convergence efficiency and population diversity. After multiple empirical iterations, the number of generations is fixed at 150 to ensure convergence within a reasonable computation time.
Appropriate domain constraints and boundary control mechanisms are implemented throughout the optimization process to improve solution efficiency and avoid physically unrealistic configurations. These constraints help guide the search toward feasible regions of the solution space, reduce unnecessary exploration of extreme thickness values, and accelerate convergence toward optimal shielding performance.
In this calculation example, the maximum allowable TID is 107 rad, the maximum total thickness of the shielding scheme is 10 mm, and the maximum allowable areal density is defined as the equivalent areal density of Al with a thickness of 100 g/cm2. With the TID after shielding as the main optimization objective, the weighting factors, , , and , are set to 0.7, 0.2, and 0.1, respectively.
This study employs the NSGA-II algorithm for optimization analysis of the multi-layer radiation shielding. It aims to identify the optimal solution and propose various material combinations, considering the type and performance of shielding materials. Assumptions regarding radiation transport schemes, geometry, GCR radiation input boundary conditions, and damage assessment models are consistent to ensure consistency in the calculation results. Experimental data related to this study can be found in Table 3.

Table 3.
Complex multi-layer material designs 1 to 5.
The shielding performance and parameters of various materials were determined using an optimization search within the genetic algorithm. Five multi-layer shielding material combinations were designed, with the shielding effectiveness shown in Figure 6. Among them, the fifth group, characterized by the composition Al + C21H25CIO5 + LiH + PBO + BN + Al, represents the optimal design in the sandwich structures, providing the best shielding performance. All five shielding combinations outperform single-layer aluminum. Group 1 has a shielding effect similar to aluminum, while the shielding effectiveness of Group 5 is improved by 68.2%. The superior performance of Group 5 is attributed to the combined use of hydrogen-rich and high-Z materials. Hydrogen-rich layers such as LiH and CH4 are highly effective at attenuating protons and secondary neutrons due to their low atomic mass and high scattering cross-sections. Meanwhile, the inclusion of high-Z materials (e.g., BN and Al) helps absorb secondary gamma radiation and enhances mechanical robustness. By strategically alternating between these material types, the shielding design leverages synergistic attenuation across multiple particle types and energies, resulting in significantly enhanced dose reduction efficiency. Notably, in this optimized structure, the inclusion of LiH significantly attenuates GCR and secondary radiation when interacting with Al. However, adding a PBO layer may produce secondary particles, reducing shielding effectiveness.
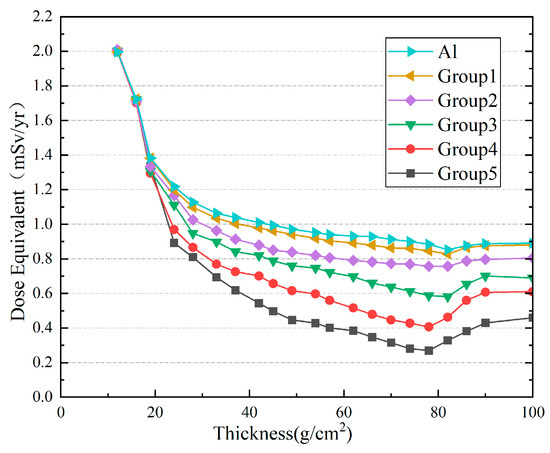
Figure 6.
Sandwich structure against solar minimum GCR.
In the radiation shielding optimization design process, hydrogen-rich materials outperform single Al layers in reducing radiation dose. The shielding effectiveness of hydrogen-rich materials is up to 36.7% higher than that of single-layer aluminum. This experimental result is influenced by factors such as the thickness of structural layers and the content of hydrogen-rich materials. These materials are highly effective in reducing neutron dose and may offer limited attenuation of gamma rays, although high-Z materials are typically more suitable for gamma-ray shielding. Experiments were conducted to evaluate the shielding efficiency of various multi-layer structures, with a focus on the effects of layer sequence and material positioning. Notably, Groups 4 and 5 demonstrated significant reductions in secondary neutron flux, highlighting the importance of structural configuration. In Group 3, a multi-layer structure of hydrogen-rich materials and aluminum reduced the secondary neutron flux by 50% compared to a single aluminum layer without hydrogen-rich materials. In Group 5, introducing multiple hydrogen-rich layers reduced the secondary neutron flux by 60% compared to the single-aluminum-layer shielding structure.
Analysis of Groups 4 and 5 reveals that these two designs exhibit the best shielding performance at a thickness of 82 g/cm2, with radiation dose equivalents reduced to 0.46 and 0.42 mSv/year, respectively, significantly outperforming the other combinations. Groups 2 and 4 show higher dose equivalents at the same thickness, at 1.20 and 0.65 mSv/year, respectively, demonstrating lower shielding effectiveness. These results indicate that Groups 4 and 5 provide more effective shielding configurations, particularly in reducing total radiation dose, including contributions from primary ions (SPE and GCR) and secondary neutrons. Under identical test conditions, the proposed multi-layer structure demonstrates superior shielding performance compared to the configurations reported in previous studies [6,16]. A detailed comparison between the shielding effectiveness of the optimized multi-layer structure designed in this study and Gohel’s results [30] shows a maximum improvement of 17.2%, quantifying the percentage increase. This suggests that an effective multi-layer structure may achieve superior performance under specific conditions, providing insights for shielding material design. These results strongly support the multi-layer shielding design and highlight the advantages of combining hydrogen-rich materials with aluminum layers.
Upon analysis of Groups 4 and 5, it was revealed that at a thickness of 82 g/cm2, the dose equivalent plummeted to 0.46 and 0.42 mSv/year, respectively, representing the most effective shielding designs among all combinations. Conversely, other combination designs exhibited lower efficacy. It is noteworthy that all trials were conducted under consistent conditions. However, in the case of the optimal combination, it was observed that the dose equivalent increased beyond 82 g/cm2, suggesting that neutrons and photons remain highly penetrating at greater depths.
However, for deep space missions, radiation dose alone is not sufficient to guarantee long-term electronic system performance. It is essential to quantify how shielding performance affects system reliability over the mission duration. To this end, the next section introduces a reliability evaluation framework that incorporates radiation transport outputs into probabilistic degradation and failure modeling of electronic devices.
4. Reliability Shield Design
4.1. Reliability Risk Modeling Analysis
The preceding section focused on optimizing shielding configurations to minimize radiation dose, thickness, and areal density. However, these parameters alone do not fully capture the long-term reliability of electronic systems in space. To bridge this gap, we propose a reliability-driven assessment framework that incorporates mission-specific uncertainties. Subsequent sections integrate shielding outcomes into a probabilistic degradation model to quantify system reliability under both nominal and uncertain scenarios.
For a shielding system composed of N distinct layers, the radiation attenuation can be modeled as follows:
The final flux reaching the electronic device is
where E denotes the kinetic energy (e.g., MeV/n) of the incident radiation particle, which affects both the attenuation coefficient and flux spectrum. is the linear attenuation coefficient of the Nth shielding layer. is the thickness of the Nth shielding layer. is incident radiation particle flux. is the particle flux after all the shielding layers.
Equations (5) and (6) model flux attenuation through multi-layer shielding using an exponential form similar to the Beer–Lambert law, under standard assumptions of mono-directional flux and uniform planar geometry.
Considering the production of secondary radiation, the total energy deposition in the electronic device is
where is obtained via Monte Carlo simulations. is the particle flux after the Nth layer of shielding material. Equation (7) calculates energy deposition in electronic components using post-shield flux outputs. The energy deposition term is calibrated through Monte Carlo simulations (MCNP6.2), ensuring its consistency with realistic transport physics.
A linear energy transfer is calculated for further analysis, which will affect the storage of electronic devices.
Equation (8) defines LET, which characterizes energy deposition per unit path length and links the shielding effect to electronic degradation potential.
The non-ionizing energy loss (NIEL) and TID are calculated by particle transport code.
where is the total ionization dose. is displacement damage dose. is the task duration. Equations (9) and (10) outline the integration of TID and NIEL, which are both fundamental inputs to the subsequent exponential degradation and reliability models.
Therefore, the reliability exponential degradation model of electronic equipment considering radiation dose is proposed.
where is the intrinsic failure rate of the electronic device. are empirical coefficients obtained from experimental data. The coefficients and were adopted from experimental and modeling results reported in [31,32], which describe the degradation behavior of COTS and space-qualified electronics under cumulative ionizing and displacement damage. D_TNID and D_TID are non-ionizing energy loss and total ionizing dose, respectively.
For a mission time T, the remaining lifetime of an electronic device is
Based on the existing knowledge framework, this study explores the research implications of radiation shielding reliability assessment, incorporating uncertainty-related response distributions to evaluate the reliability of radiation shielding.
The primary sources of uncertainty include variations in the space radiation environment, the degradation behavior of shielding materials, and the probabilistic modeling of system reliability. The uncertainties associated with the radiation environment and shielding degradation are discussed below.
where follows a normal distribution, and .
In order to further explore the failure probability of electronic devices, according to the analysis of Xapsos et al., the failure probability (FP) is defined as follows [33]:
Let denote the cumulative distribution function (CDF) of the environmental radiation dose in space and represent the probability density function (PDF) for device failure as a function of total dose. Failure probability is defined as the probability that a randomly selected device from a production lot—represented by the distribution —experiences total dose failure in a space environment characterized by , where is the TID.
Equation (15) assumes that radiation-induced degradation is a cumulative and irreversible process driven by both TID and NIEL. A Weibull distribution is used to represent variability in component failure thresholds. Device degradation is considered monotonic over time, without recovery, reflecting the continuous exposure environment of long-duration space missions.
Secondary particles—such as neutrons and gamma photons generated by nuclear interactions within high-Z shielding materials—are included in the cumulative dose estimates through radiation transport simulations. These particles contribute significantly to deep-layer damage and are an essential factor in the reliability evaluation of multi-year missions.
Therefore, a reliability evaluation model considering radiation shielding is established. The reliability distribution .
We investigate how these uncertainties affect a basic geometric spacecraft design, aiming to understand the implications of electronic uncertainty on mission design [34]. The material’s internal risk range is expressed as a function of shielding thickness while accounting for the uncertainty in risk model factors, thus linking physical parameter uncertainty to radiation shielding evaluation.
The random variable is generated by the Monte Carlo method, and the reliability failure probability is calculated by the following formula:
Using the Monte Carlo method, the reliability is analyzed statistically, the mean and variance of reliability are calculated, and the confidence interval is obtained.
where is the quantile under the standard normal distribution.
Based on the previous derivation, the reliability of radiation shielding can be assessed. Given specific target parameters (such as shielding thickness, number of material layers, and types), a corresponding risk sequence exists in the multi-objective multi-material radiation shielding design optimization process. When the CL of risks in this sequence falls below 5%, the shielding is considered acceptable, meeting the CL.
4.2. Sensitivity Analysis
Sensitivity analysis helps identify the impact of changes in material properties or environmental conditions on the overall system reliability and understand the contribution of each design parameter to the shielding effectiveness and mission reliability.
Through optimization algorithms for radiation shielding design, it is found that the key parameters affecting reliability are material properties, shielding thickness, number of layers, and changes in radiation intensity (such as radiation type and dose).
A system’s sensitivity can be quantitatively evaluated by decomposing the output variance into the main and interaction effects of input parameters, as illustrated in Figure 7. The figure highlights the relative importance of each parameter to the overall system response, providing a basis for shielding optimization.
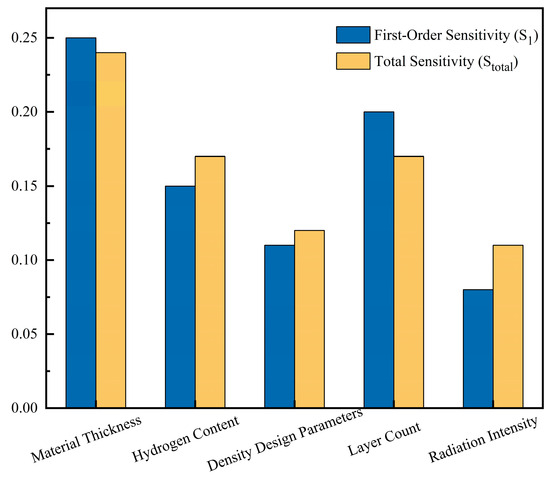
Figure 7.
Parameter sensitivity analysis.
Furthermore, based on the above derivation, the reliability of radiation shielding for deep space missions can be further evaluated. The variable x, representing a vector of shielding design parameters (e.g., material type, layer sequence, and thickness), must be determined to satisfy the predefined reliability threshold. If a mission utilizing this shielding configuration is carried out, we can reasonably expect that the failure risk of electronic devices will not exceed 5% at a given CL. This provides a quantitative reliability assessment framework for multi-objective, multi-material radiation shielding in the context of deep space missions.
4.3. Case Analysis
A ten-year Mars mission using a hybrid core electronic configuration was considered to demonstrate the radiation shielding reliability method. The mission was based on NASA Langley Research Center’s conditions, requiring an optimal spacecraft volume of 98 m3. This setup allows for evaluating multi-layer radiation shielding materials using the developed reliability assessment method. The shielding material is designed as Group 5. The space radiation environment is set in Section 2.1.
Figure 8 shows the absorption dose over 15 years for Al and Group 5 shielding materials. The characteristics of single-layer aluminum materials and the proposed radiation shielding materials were studied, focusing on the comparative shielding effects across different design configurations. The results highlight the impact of uncertainties on design reliability. In the absence of uncertainty factors, the shielding effect of Group 5 proposed in this study is 57% higher than that of a single aluminum material. When uncertainty factors are considered, the shielding effect at the 95% CL improves by approximately 13% compared to Group 5.
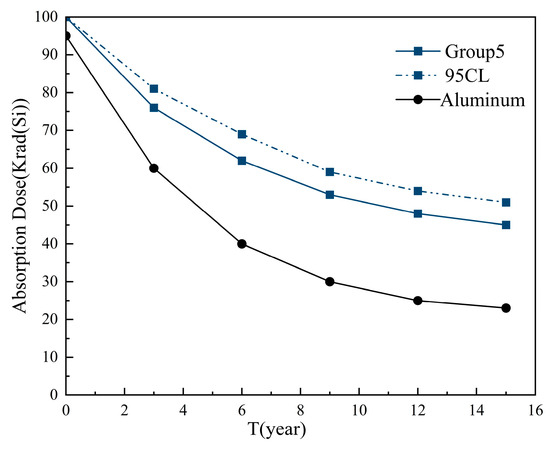
Figure 8.
Absorption dose over 15 years for Al and Group 5 shielding materials.
The radiation parameters of electronic devices are calculated and analyzed according to typical values, that is, LET = 5 keV/μm and NIEL = 0.2. According to the optimal radiation shield of Group 5 designed before, we obtain the attenuation coefficients of different shielding materials under the condition of optimal thickness, where the attenuation factors of each shielding material to particle flux are as follows (in Table 4).

Table 4.
Attenuation coefficients of different shielding materials.
The particle flux entering the electronic devices is then
Using Monte Carlo simulations, the energy deposition per layer and the total energy deposition are assumed to be MeV/cm2 and MeV/cm2. Radiation doses are calculated based on different dose models: rad; dpa.
Substituting the known values by Equation (17), the failure rate is
The values of factors that bring uncertainty to the model are calculated as . Based on an exponential decay model, the reliability is then
Figure 9 shows the reliability variation trend of electronic devices based on multi-layer radiation shielding. A 10% error was introduced to the radiation flux data to account for uncertainty in predicting flux fluctuations. These fluctuations must be considered when designing shielding for electronic devices, especially during solar cycle peaks when radiation flux increases, necessitating shield optimization. The shielding efficiency of multi-layer materials declines over time due to material decay and fatigue, with a 1–2% error applied to reflect this uncertainty. This margin indicates yearly fluctuations in shielding effectiveness, particularly towards the mission’s end when decay reaches 5–6%.
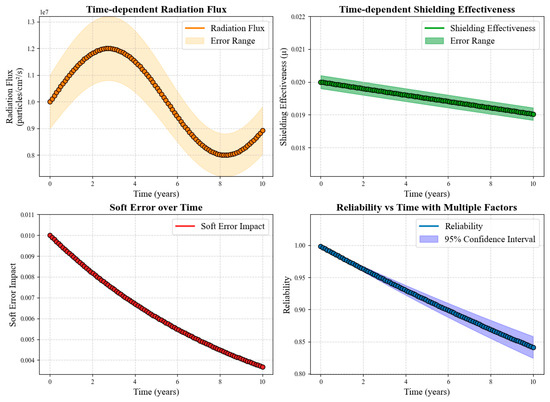
Figure 9.
Time-dependent reliability of electronic components over a 10-year mission under Group 5 shielding configuration.
The reliability curve shows the probability that the system will operate continuously during the mission. At the beginning of the mission, the reliability was close to 1, indicating no failures, but it dropped to about 0.94 after five years, indicating some risk of failure during long-duration deep space missions. The 95% confidence interval gradually expands with the task time, indicating that the reliability uncertainty gradually increases with the change in task conditions. In the middle of the mission (about five years), the lower reliability limit is about 0.90, while the upper limit is closer to 0.94. The reliability values in Figure 9 are derived from the exponential degradation model (Equation (23)), using cumulative TID and NIEL calculated via Monte Carlo simulations. The decline over time reflects accumulated radiation damage and gradual loss of shielding efficiency. The widening 95% confidence interval indicates increasing uncertainty in space radiation and material performance, especially beyond five years.
Using the radiation shielding reliability model, Figure 10 demonstrates three different shielding strategies for electronic device reliability while considering uncertainty (95% confidence interval).
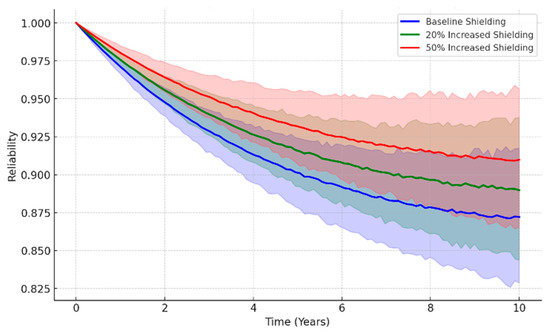
Figure 10.
Reliability analysis with different shielding strategies and 95% CL.
Figure 10 presents the time-dependent reliability of electronic devices under varying shielding configurations, highlighting the influence of shielding mass on system survivability over long-duration missions. The baseline configuration exhibits a rapid reliability decline, falling below 30% by year 7. In contrast, increasing shielding by 20% or 50% significantly enhances long-term performance, with the 50% enhancement maintaining reliability above 60%. While the differences are marginal in short missions (T < 3 years), the performance divergence becomes increasingly pronounced beyond five years, emphasizing the critical role of shielding in extended deep space operations. The figure also illustrates the widening confidence intervals over time, reflecting the accumulation of environmental and modeling uncertainties, which further underscores the need for robust shielding strategies in high-risk mission profiles.
For short-duration missions, baseline shielding is sufficient; however, a 20% increase in shielding further enhances reliability and mitigates uncertainty. The reliability model’s confidence interval offers valuable insights into the probability of success in future missions. This is especially critical for deep space exploration and the long-term operation of space stations, as it ensures the continued reliability of equipment over extended periods. The combination of mass optimization and material selection aims to balance shielding effectiveness with spacecraft weight.
The reliability-based design approach will play a central role in mission analysis and design, further unveiling the relationship between the dose distribution of electronic devices and the LET. By appropriately implementing this reliability-based design approach, it is possible to control and assess the uncertainties in radiation shielding effectively, ultimately achieving reliable radiation shielding design.
5. Conclusions
Space radiation shielding design constitutes a complex, multi-parameter, and multi-objective optimization problem that is critical for ensuring the long-term reliability of electronic systems in deep space missions. This study presents a comprehensive shielding design framework that integrates genetic algorithm-based multi-objective optimization with uncertainty-aware reliability evaluation. The proposed method simultaneously minimizes radiation dose, structural mass, and shielding thickness while accounting for environmental and parametric uncertainties.
The optimization algorithm demonstrated robust convergence behavior, with near-Pareto-optimal solutions emerging by the 50th iteration. The final shielding configuration—based on a five-layer composite structure combining high-Z and hydrogen-rich materials—achieved a significant reduction in both total dose and secondary particle generation. Compared to a baseline aluminum shield, the optimized design reduced the radiation-induced failure rate of electronic components by approximately 57% and enhanced system reliability to 0.94 over a five-year mission duration.
Time-dependent reliability analysis further revealed that shielding differences are negligible in short missions (T < 3 years) but become critical for longer durations. For example, at T = 7 years, the baseline configuration led to reliability dropping below 30%, while a 50% increase in shielding preserved reliability above 60%. This trend is consistent with cumulative radiation damage models and highlights the necessity of mass-efficient, high-performance shielding in deep space mission architectures.
The reliability framework incorporates Monte Carlo simulations and probabilistic modeling to evaluate the impact of shielding uncertainties on system performance. Risk-based metrics, such as CL thresholds, were employed to quantify acceptable design margins. The design was deemed acceptable when the system failure probability remained below 5% at a 95% confidence level, aligning with aerospace reliability engineering standards.
The presented approach provides practical tools for rapid trade space exploration in early-stage design, supporting spacecraft that lack legacy shielding baselines. In particular, the framework offers decision support for component-level protection of control units, memory, and avionics subsystems in harsh radiation environments.
Overall, this work contributes a scalable, data-driven, and theoretically supported methodology for designing lightweight, high-reliability radiation shielding systems under uncertainty. Future efforts will focus on validating the predicted shielding performance through real-world radiation simulation experiments and environmental testing, thereby bridging the gap between model-based design and in-orbit deployment.
Author Contributions
S.G.: data curation, writing—original draft preparation, writing—review and editing; G.F.: methodology, project administration, supervision; B.W.: investigation, funding acquisition, resources, conceptualization; X.W.: validation, visualization; Z.C.: software, formal analysis. All authors have read and agreed to the published version of the manuscript.
Funding
The authors received no financial support for this research or writing and publishing this article.
Data Availability Statement
The data supporting the findings of this study are not publicly available but can be obtained from the corresponding author upon reasonable request.
Conflicts of Interest
Author Zhiqiang Chen is employed by the company China Electronics Information Industry Group Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A
To ensure clarity and consistency throughout the manuscript, Table A1 summarizes the key technical terms used in the study. The table includes abbreviations, full terms, definitions, and corresponding physical units. These terms are essential for understanding the radiation transport models, dose metrics, and optimization framework employed in the analysis.

Table A1.
Radiation and optimization terminology table.
Table A1.
Radiation and optimization terminology table.
| Term | Full Name | Term | Full Name |
|---|---|---|---|
| GCRs | galactic cosmic rays | CL | confidence level |
| SPEs | solar particle events | Z | atomic number |
| HZE | high-charge and high-energy particles | TID | total ionizing dose |
| LET | linear energy transfer | GA | genetic algorithm |
| CMEs | coronal mass ejections | PSO | Particle Swarm Optimization |
| NIEL | non-ionizing energy loss | SA | Simulated Annealing |
| CDF | cumulative distribution function | probability density function |
References
- Wilson, J.W.; Slaba, T.C.; Badavi, F.F.; Reddell, B.D.; Bahadori, A.A. 3dhzetrn: Shielded Icru Spherical Phantom. Life Sci. Space Res. 2015, 4, 46–61. [Google Scholar] [CrossRef] [PubMed]
- Toto, E.; Lambertini, L.; Laurenzi, S.; Santonicola, M.G. Recent Advances and Challenges in Polymer-Based Materials for Space Radiation Shielding. Polymers 2024, 16, 382. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimi, M.; Luo, B.; Wang, Q.; Attarilar, S. Enhanced Multifaceted Properties of Nanoscale Metallic Multilayer Composites. Materials 2024, 17, 4004. [Google Scholar] [CrossRef]
- Norbury, J.W.; Schimmerling, W.; Slaba, T.C.; Azzam, E.I.; Badavi, F.F.; Baiocco, G.; Benton, E.; Bindi, V.; Blakely, E.A.; Blattnig, S.R. Galactic Cosmic Ray Simulation at the Nasa Space Radiation Laboratory. Life Sci. Space Res. 2016, 8, 38–51. [Google Scholar] [CrossRef]
- Cai, Y.; Hu, H.; Pan, Z.; Hu, G.; Zhang, T. A Method to Optimize the Shield Compact and Lightweight Combining the Structure with Components Together by Genetic Algorithm and Mcnp Code. Appl. Radiat. Isot. 2018, 139, 169–174. [Google Scholar] [CrossRef]
- Cordella, F.; Cappelli, M.; Ciotti, M.; Claps, G.; De Leo, V.; Mazzotta, C.; Pacella, D.; Tamburrino, A.; Panza, F. Genetic algorithm for multilayer shield optimization with a custom parallel computing architecture. Eur. Phys. J. Plus 2024, 139, 150. [Google Scholar] [CrossRef]
- Cha, J.-H.; Noh, J.-S.; Sathish Kumar, S.K.; Jin, D.; Lee, D.-Y.; Kim, C.-G. Origami multi-layer space shield for cylindrical space structure. Chin. J. Aeronaut. 2024, 37, 294–312. [Google Scholar] [CrossRef]
- Vira, A.D.; Mone, E.M.; Ryan, E.A.; Connolly, P.T.; Smith, K.; Roecker, K.E.; Orlando, T.M.; Jiang, Z.; First, P.N. Designing a boron nitride polyethylene composite for shielding neutrons. APL Mater. 2023, 11, 101104. [Google Scholar] [CrossRef]
- Willenshofer, P.D.; Tunes, M.A.; Vo, H.T.; Stemper, L.; Renk, O.; Greaves, G.; Uggowitzer, P.J.; Pogatscher, S. Radiation-resistant aluminum alloy for space missions in the extreme environment of the solar system. arXiv 2022, arXiv:2210.03397. [Google Scholar]
- Shahzad, K.; Kausar, A.; Manzoor, S.; Rakha, S.A.; Uzair, A.; Sajid, M.; Arif, A.; Khan, A.F.; Diallo, A.; Ahmad, I. Views on radiation shielding efficiency of polymeric composites/nanocomposites and multi-layered materials: Current state and advancements. Radiation 2022, 3, 1–20. [Google Scholar] [CrossRef]
- Osman, A.M.; Abdel-Monem, A.M.; Abdo, A.E.-S. Studying the Shielding Properties of Lead Glass Composites Using Neutrons and Gamma Rays. Ann. Nucl. Energy 2015, 78, 146–151. [Google Scholar] [CrossRef]
- Yoonkwan, K.; Park, S.; Seo, Y. Enhanced X-Ray Shielding Ability of Polymer–Nonleaded Metal Composites by Multilayer Structuring. Ind. Eng. Chem. Res. 2015, 54, 5968–5973. [Google Scholar]
- Kim, S.C.; Kim, S.H. Fabrication of a Gd2O3-Based Film to Shield from Space Radiation inside Aircraft and Its Effectiveness. Aerospace 2023, 10, 968. [Google Scholar] [CrossRef]
- Shukai, G.; Wan, B.; Zhong, J.; Fu, G.; Wang, X. A Reliability Assessment Methodology of System-in-Package Based Virtual Qualification. Microelectron. Reliab. 2023, 150, 115212. [Google Scholar]
- Seongeun, P.; Kim, H.; Kim, Y.; Kim, E.; Seo, Y. Multilayer-Structured Non-Leaded Metal/Polymer Composites for Enhanced X-Ray Shielding. MRS Adv. 2018, 3, 1789–1797. [Google Scholar]
- Daneshvar, H.; Milan, K.G.; Sadr, A.; Sedighy, S.H.; Malekie, S.; Mosayebi, A. Multilayer radiation shield for satellite electronic components protection. Sci. Rep. 2021, 11, 20657. [Google Scholar] [CrossRef]
- Chowdhury, R.P.; Stegeman, L.A.; Lund, M.L.; Fry, D.; Madzunkov, S.; Bahadori, A.A. Hybrid methods of radiation shielding against deep-space radiation. Life Sci. Space Res. 2023, 38, 67–78. [Google Scholar] [CrossRef]
- Fan, W.C.; Drumm, C.R.; Roeske, S.B.; Scrivner, G.J. Shielding Considerations for Satellite Microelectronics. IEEE Trans. Nucl. Sci. 1996, 43, 2790–2796. [Google Scholar] [CrossRef]
- Shavers, M.R.; Zapp, N.; Barber, R.E.; Wilson, J.W.; Qualls, G.; Toupes, L.; Ramsey, S.; Vinci, V.; Smith, G.; Cucinotta, F.A. Implementation of ALARA radiation protection on the ISS through polyethylene shielding augmentation of the Service Module Crew Quarters. Adv. Space Res. 2004, 34, 1333–1337. [Google Scholar] [CrossRef]
- Micheli, D.; Apollo, C.; Pastore, R.; Barbera, D.; Morles, R.B.; Marchetti, M.; Moglie, F. Optimization of multilayer shields made of composite nanostructured materials. IEEE Trans. Electromagn. Compatibility 2011, 54, 60–69. [Google Scholar] [CrossRef]
- Dommeti, V.S.; Cheruku, D.R. Multi-layer composites shielding for electromagnetic radiation protection. Int. J. Adv. Intell. Paradig. 2020, 17, 139–158. [Google Scholar] [CrossRef]
- Iyer, K.A.; Mehoke, D.S.; Batra, R.C. Interplanetary dust particle shielding capability of spacecraft multi-layer insulation. In Proceedings of the 2014 IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2014; IEEE: Piscataway, NJ, USA. [Google Scholar]
- Jooq, M.K.Q.; Moaiyeri, M.H.; AI-Shidaifat, A.; Song, H. Ultra-efficient and robust auto-nonvolatile schmitt trigger-based latch design using ferroelectric CNTFET technology. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 1829–1840. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, R.K.; Simonsen, L.C.; Nealy, J.E.; Troutman, P.A.; Wilson, J.W. Shield Optimization in Simple Geometry for the Gateway Concept. SAE Technical Paper. 2002. Available online: https://www.sae.org/publications/technical-papers/content/2002-01-2332/ (accessed on 27 February 2025).
- Autran, J.; Munteanu, D. Electronics Reliability Assessment of Future Power Fusion Machines: Neutron Interaction Analysis in Bulk Silicon. Microelectron. Reliab. 2021, 126, 114223. [Google Scholar] [CrossRef]
- Vozenin, M.-C.; Alaghband, Y.; Drayson, O.G.G.; Piaget, F.; Leavitt, R.; Allen, B.D.; Doan, N.-L.; Rostomyan, T.; Stabilini, A.; Reggiani, D.; et al. More May Not be Better: Enhanced Spacecraft Shielding May Exacerbate Cognitive Decrements by Increasing Pion Exposures during Deep Space Exploration. Radiat. Res. 2024, 201, 93–103. [Google Scholar] [CrossRef]
- O’Neill, P.M.; Golge, S.; Slaba, T.C. Badhwar-O’Neill 2014 Galactic Cosmic Ray Flux Model Description; NASA/TP–2015–218569; NASA: Washington, DC, USA, 2015.
- Nelson, G.A. Space radiation and human exposures, a primer. Radiat. Res. 2016, 185, 349–358. [Google Scholar] [CrossRef]
- Valentin, J. The 2007 Recommendations of the International Commission on Radiological Protection; Elsevier: Oxford, UK, 2007. [Google Scholar]
- Gohel, A.; Makwana, R. Multi-layered shielding materials for high energy space radiation. Radiat. Phys. Chem. 2022, 197, 110131. [Google Scholar] [CrossRef]
- Xapsos, M.A.; Summers, G.P.; Barth, J.L.; Stassinopoulos, E.G.; Burke, E.A. Probability model for worst case solar proton event fluences. IEEE Trans. Nucl. Sci. 1999, 46, 1481–1485. [Google Scholar] [CrossRef]
- Duzellier, S. Radiation effects on electronic devices in space. Aerosp. Sci. Technol. 2005, 9, 93–99. [Google Scholar] [CrossRef]
- Wang, J.-Z.; Huo, Z.-X.; Wang, F.-F. Tid Evaluation Based on Variabilities of Space Radiation and Device Failure Dose in Typical Navigation Satellite Orbits. Microelectron. Reliab. 2022, 137, 114747. [Google Scholar] [CrossRef]
- Dobynde, M.; Harikumaran, J.; Guo, J.; Wheeler, P.; Galea, M.; Buticchi, G. Cosmic Radiation Reliability Analysis for Aircraft Power Electronics. IEEE Trans. Transp. Electrif. 2023, 10, 344–352. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).