Theoretical and Numerical Study on a Scale Model Test of Planetary Cratering Impact
Abstract
:1. Introduction
2. Numerical Model and Scaling Model of the Scale Model Tests
2.1. Numerical Method and Geometry Model
2.2. Scaling Analysis Model
3. Design of Scale Model Tests
4. Numerical Verification and Comparative Analysis of Scale Model Tests
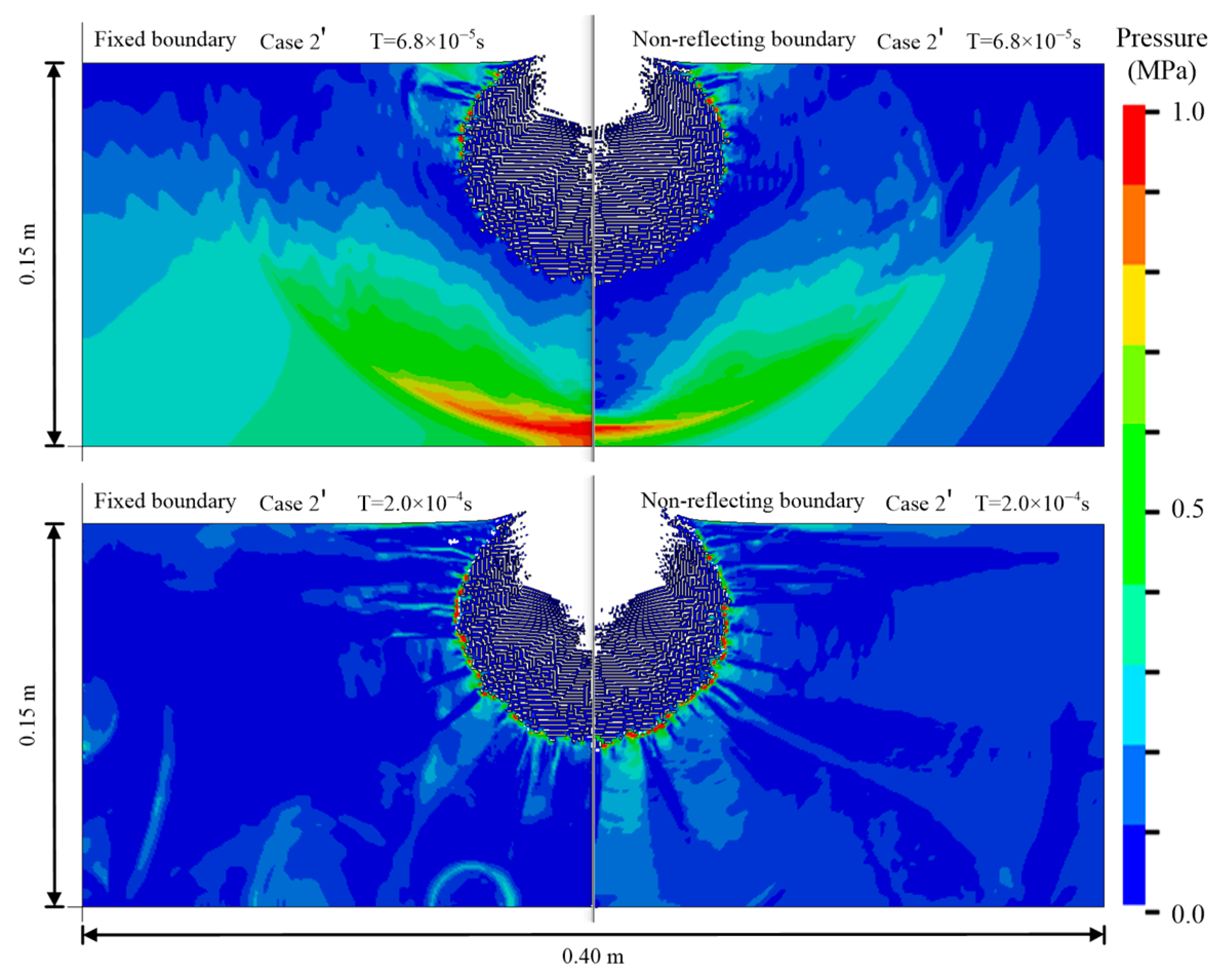
4.1. Boundary Effect on Numerical Simulation of Scale Model Tests
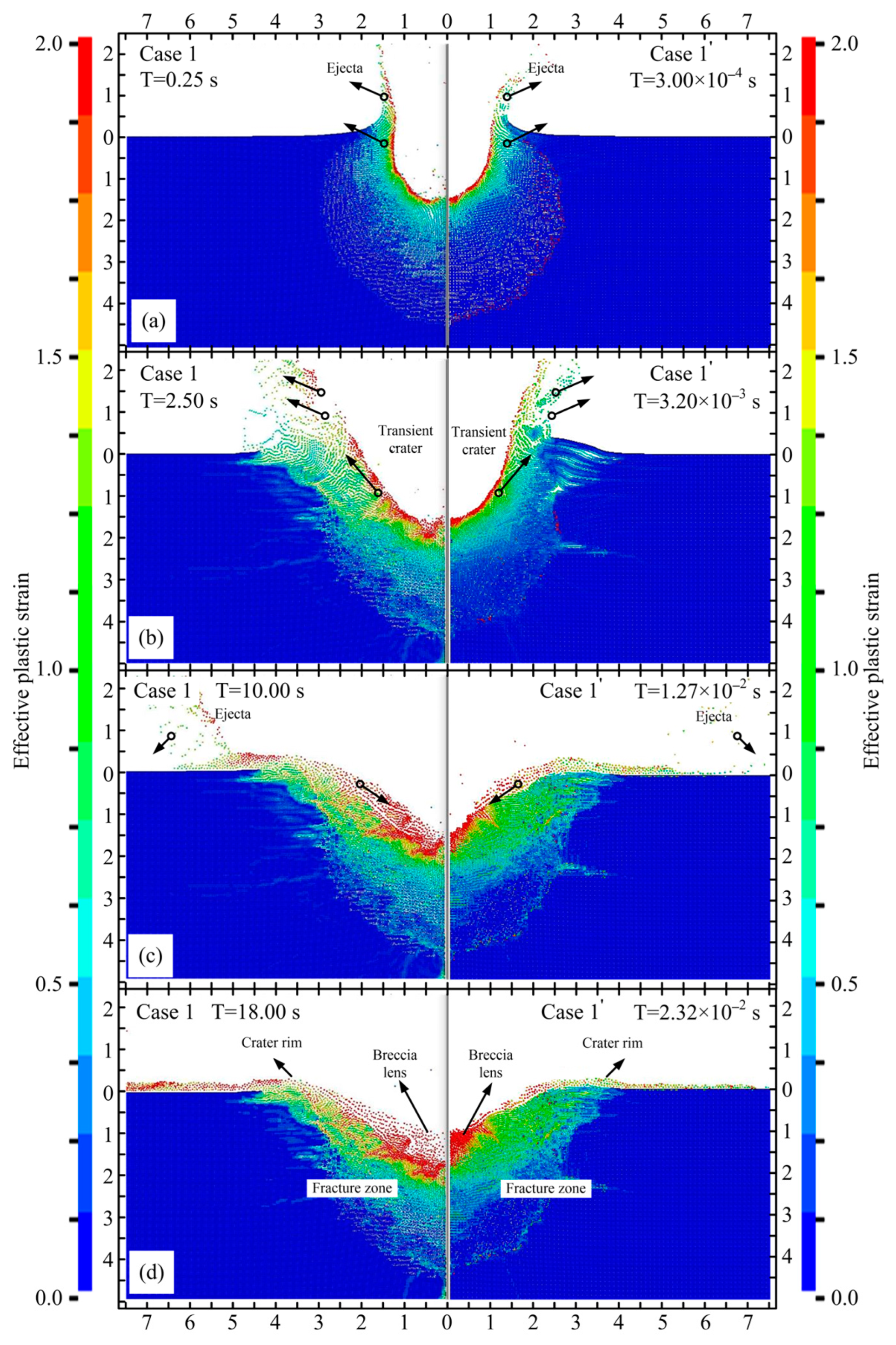
4.2. Numerical Simulation Verification of Scale Model Tests
5. Discussion
5.1. The Transition Threshold of Crater Morphology
5.2. The Diameter of Crater Morphology Transition in Prototype Tests and the Gravity Threshold of Crater Morphology Transition in Scale Model Tests
5.3. The Effect of Projectile Diameter and Gravity on the Depth–Diameter Ratio and Formation Time of Impact Craters
5.4. The Cratering Time Relationship Between Prototype Tests and Scale Model Tests
6. Conclusions
- (1)
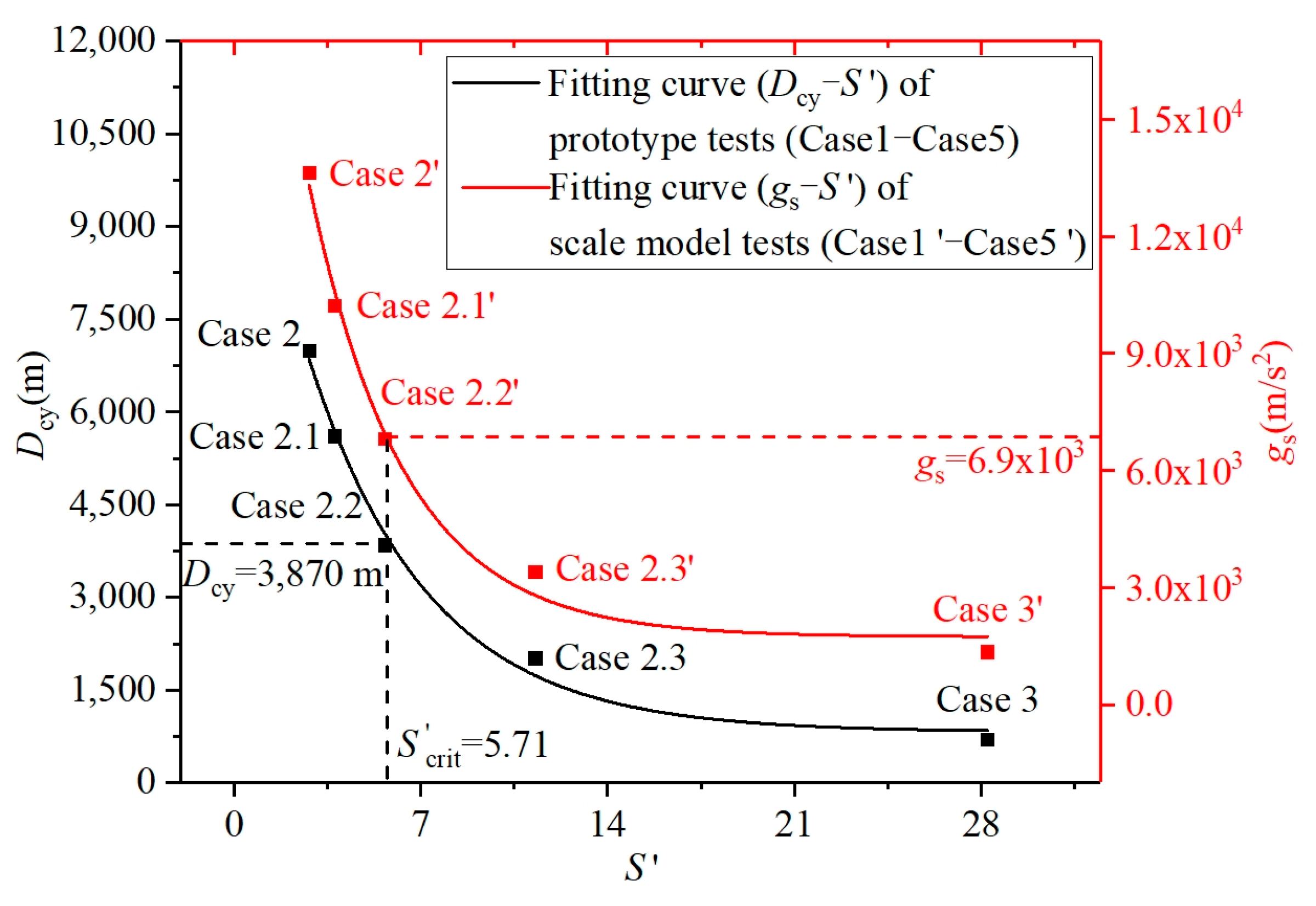
- The scaling analysis effectively replicates prototype tests, with the transition threshold (S′crit) and transition diameter (Dcy) of craters on Earth determined to be 5.71 and 3870 m, respectively. These values align closely with geological analyses, further validating our approach.
- (2)
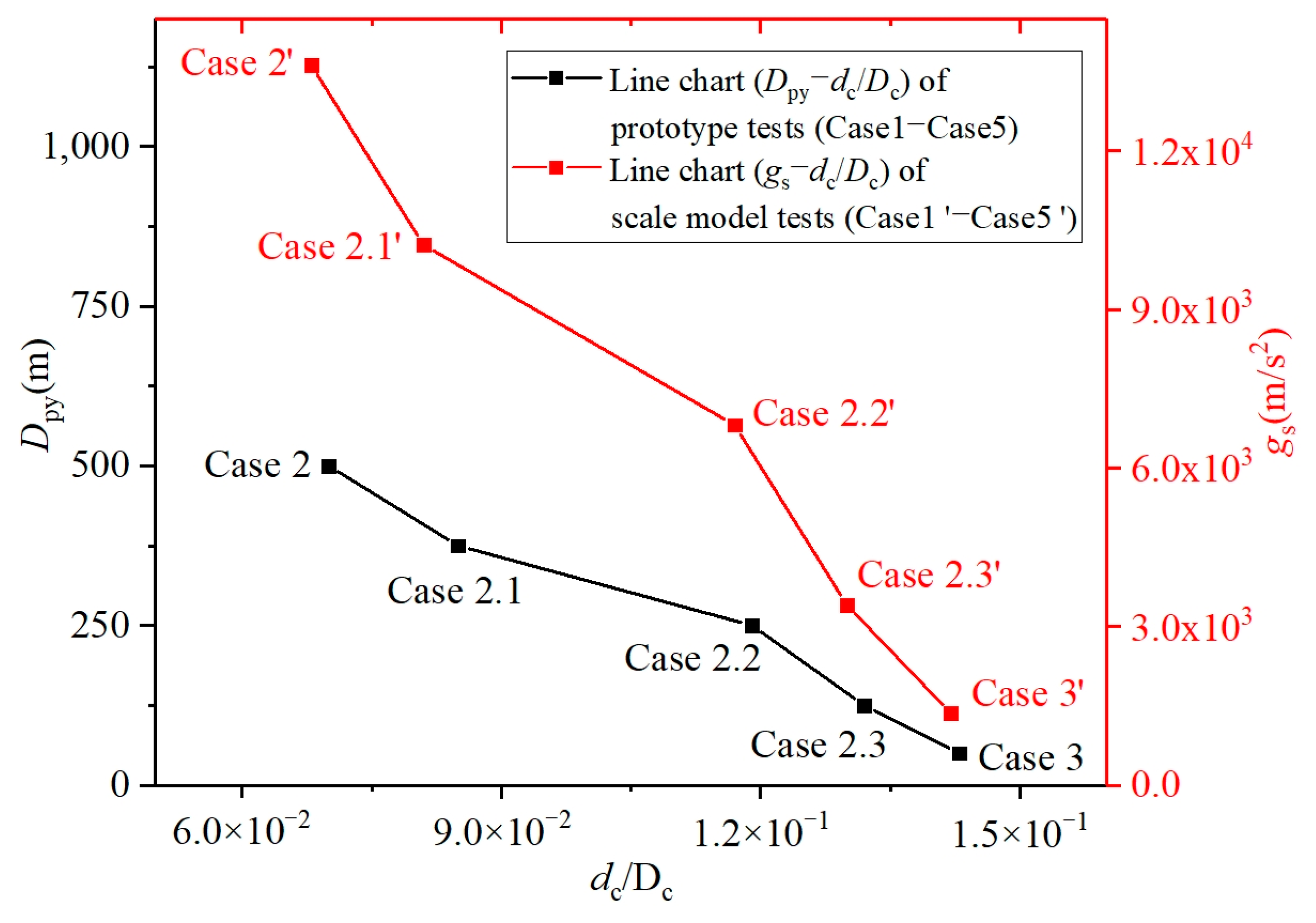
- Controlling for projectile diameter, we observed a negative correlation between the depth–diameter ratio (dc/Dc) of craters and projectile diameter, alongside a positive correlation with cratering time.
- (3)
- Similarly, controlling for gravity, we noted a negative correlation between the depth–diameter ratio (dc/Dc) of craters and gravity, coupled with a negative correlation with cratering time.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kenkmann, T.; Wulf, G. Impact cratering. In Planetary Geology; Springer Praxis Books: Berlin/Heidelberg, Germany, 2018; pp. 123–145. [Google Scholar]
- Turtle, E.P.; Pierazzo, E.; Collins, G.S.; Osinski, G.R.; Melosh, H.J.; Morgan, J.V.; Reimold, W.U.; Kenkmann, T.; Hörz, F.; Deutsch, A. Impact structures: What does crater diameter mean? In Large Meteorite Impacts III; Geological Society of America: Annapolis, MD, USA, 2005; Volume 384. [Google Scholar]
- Güldemeister, N.; Wünnemann, K.; Poelchau, M.H.; Osinski, G.R.; Kring, D.A. Scaling impact crater dimensions in cohesive rock by numerical modeling and laboratory experiments. In Large Meteorite Impacts and Planetary Evolution V; Geological Society of America: Annapolis, Maryland, USA, 2015; Volume 518. [Google Scholar]
- Suárez-Cortés, Á.D.; Flandes, A.; Durand-Manterola, H.J. Planetary impact craters study through low-speed laboratory experiments. Int. J. Impact Eng. 2021, 156, 103954. [Google Scholar] [CrossRef]
- Ormö, J.; Raducan, S.D.; Housen, K.R.; Wünnemann, K.; Collins, G.S.; Rossi, A.P.; Melero-Asensio, I. Effect of target layering in gravity-dominated cratering in nature, experiments, and numerical simulations. J. Geophys. Res. Planets 2024, 129, e2023JE008110. [Google Scholar] [CrossRef]
- Housen, K.R.; Holsapple, K.A. Scale effects in strength-dominated collisions of rocky asteroids. Icarus 1999, 142, 21–33. [Google Scholar] [CrossRef]
- Prieur, N.C.; Rolf, T.; Luther, R.; Wünnemann, K.; Xiao, Z.; Werner, S.C. The effect of target properties on transient crater scaling for simple craters. J. Geophys. Res. Planets 2017, 122, 1704–1726. [Google Scholar] [CrossRef]
- Housen, K.R.; Sweet, W.J.; Holsapple, K.A. Impacts into porous asteroids. Icarus 2018, 300, 72–96. [Google Scholar] [CrossRef]
- Silber, E.A.; Osinski, G.R.; Johnson, B.C.; Grieve, R.A.F. Effect of impact velocity and acoustic fluidization on the simple-to-complex transition of lunar craters. J. Geophys. Res. Planets 2017, 122, 800–821. [Google Scholar] [CrossRef]
- Schmidt, R.M.; Holsapple, K.A. Estimates of crater size for large-body impact: Gravity-scaling results. Spec. Pap. Geol. Soc. Am. 1982, 190, 93–102. [Google Scholar] [CrossRef]
- Croft, S.K. The scaling of complex craters. J. Geophys. Res. Solid Earth 1985, 90, C828–C842. [Google Scholar] [CrossRef]
- Tsujido, S.; Arakawa, M.; Suzuki, A.I.; Yasui, M. Ejecta velocity distribution of impact craters formed on quartz sand: Effect of projectile density on crater scaling law. Icarus 2015, 262, 79–92. [Google Scholar] [CrossRef]
- Housen, K.R.; Holsapple, K.A. Ejecta from impact craters. Icarus 2011, 211, 856–875. [Google Scholar] [CrossRef]
- Holsapple, K.A.; Schmidt, R.M. Point source solutions and coupling parameters in cratering mechanics. J. Geophys. Res. Solid Earth 2012, 92, 6350–6376. [Google Scholar] [CrossRef]
- Holsapple, K.A. The scaling of impact phenomena. Int. J. Impact Eng. 1987, 5, 343–355. [Google Scholar] [CrossRef]
- Holsapple, K.A. The Scaling of Impact Processes in Planetary Sciences. Annu. Rev. Earth Planet. Sci. 1993, 21, 333–373. [Google Scholar] [CrossRef]
- Takizawa, S.; Katsuragi, H. Scaling laws for the oblique impact cratering on an inclined granular surface. Icarus 2020, 335, 113409. [Google Scholar] [CrossRef]
- Liu, W.; Zang, Q.; Ma, X. A review of the models of near-Earth object impact cratering on Earth. Explos. Shock Waves 2021, 41, 16. [Google Scholar] [CrossRef]
- Lv, H.; He, Q.; Chen, X. Experimental and Numerical Advances in Planetary Cratering Impacts. Mech. Solids 2024, 59, 2322–2365. [Google Scholar] [CrossRef]
- Lv, H.; He, Q.; Chen, X.; Han, P. Numerical simulation of impact crater formation and distribution of high-pressure polymorphs. Acta Astronaut. 2023, 203, 169–186. [Google Scholar] [CrossRef]
- Collins, G.S.; Melosh, H.J.; Osinski, G.R. The impact-cratering process. Elements 2012, 8, 25–30. [Google Scholar] [CrossRef]
- He, Q.-G.; Chen, X.; Chen, J.-F. Finite element-smoothed particle hydrodynamics adaptive method in simulating debris cloud. Acta Astronaut. 2020, 175, 99–117. [Google Scholar] [CrossRef]
- Wünnemann, K.; Collins, G.; Osinski, G. Numerical modelling of impact melt production in porous rocks. Earth Planet. Sci. Lett. 2008, 269, 530–539. [Google Scholar] [CrossRef]
- Wünnemann, K.; Ivanov, B.A. Numerical modelling of the impact crater depth–diameter dependence in an acoustically fluidized target. Planet. Space Sci. 2003, 51, 831–845. [Google Scholar] [CrossRef]
- Krüger, T.; Hergarten, S.; Kenkmann, T. Deriving morphometric parameters and the simple-to-complex transition diameter from a high-resolution, global database of fresh lunar impact craters (D≥~ 3 km). J. Geophys. Res. Planets 2018, 123, 2667–2690. [Google Scholar] [CrossRef]
- Osinski, G.R.; Pierazzo, E. Impact Cratering: Processes and Products. In Impact Cratering; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 1–20. [Google Scholar]




| Group | Test Type | Case | Dp (m) | Up (km/s) | g (m/s2) | ρ (kg/m3) | Yt (MPa) | π2 | Ca | S′ |
|---|---|---|---|---|---|---|---|---|---|---|
| G1 | Prototype | 1 | 50.00 | 12.0 | 9.81 | 2600 | 18 | 1.70 × 10−6 | 2.08 × 104 | 28.23 |
| Scale model | 1′ | 0.01 | 2.0 | 1362.50 | 1800 | 0.346 | ||||
| G2 | Prototype | 2 | 125.00 | 12.0 | 9.81 | 2600 | 18 | 4.26 × 10−6 | 11.29 | |
| Scale model | 2′ | 0.01 | 2.0 | 3406.25 | 1800 | 0.346 | ||||
| G3 | Prototype | 3 | 250.00 | 12.0 | 9.81 | 2600 | 18 | 8.52 × 10−6 | 5.64 | |
| Scale model | 3′ | 0.01 | 2.0 | 6812.50 | 1800 | 0.346 | ||||
| G4 | Prototype | 4 | 375.00 | 12.0 | 9.81 | 2600 | 18 | 1.28 × 10−5 | 3.76 | |
| Scale model | 4′ | 0.01 | 2.0 | 10,218.75 | 1800 | 0.346 | ||||
| G5 | Prototype | 5 | 500.00 | 12.0 | 9.81 | 2600 | 18 | 1.70 × 10−5 | 2.83 | |
| Scale model | 5′ | 0.01 | 2.0 | 13,625.00 | 1800 | 0.346 |
| Group | Case | dc (m) | Dc (m) | t (s) | dc/Dc | The Average of dc/Dc in Each Group | The Relative Error of dc/Dc in Each Group (%) | as/ay | gt/Up |
|---|---|---|---|---|---|---|---|---|---|
| G1 | 1 | 101.26 | 706.21 | 18.00 | 14.3 × 10−2 | 14.25 × 10−2 | −0.70 | 2.00 × 10−4 | 1.47 × 10−2 |
| 1′ | 0.0201 | 0.142 | 2.32 × 10−2 | 14.2 × 10−2 | 1.58 × 10−2 | ||||
| G2 | 2 | 267.63 | 2019.88 | 38.20 | 13.2 × 10−2 | 13.10 × 10−2 | −1.52 | 8.00 × 10−5 | 3.12 × 10−2 |
| 2′ | 0.0178 | 0.137 | 1.87 × 10−2 | 13.0 × 10−2 | 3.18 × 10−2 | ||||
| G3 | 3 | 457.83 | 3847.12 | 52.00 | 11.9 × 10−2 | 11.80 × 10−2 | −1.68 | 4.00 × 10−5 | 4.25 × 10−2 |
| 3′ | 0.0129 | 0.110 | 1.43 × 10−2 | 11.7 × 10−2 | 4.87 × 10−2 | ||||
| G4 | 4 | 476.71 | 5608.37 | 64.40 | 8.5 × 10−2 | 8.30 × 10−2 | −4.71 | 2.67 × 10−5 | 5.26 × 10−2 |
| 4′ | 0.0087 | 0.107 | 1.25 × 10−2 | 8.1 × 10−2 | 6.39 × 10−2 | ||||
| G5 | 5 | 490.51 | 6987.32 | 75.00 | 7.0 × 10−2 | 6.90 × 10−2 | −2.86 | 2.00 × 10−5 | 6.13 × 10−2 |
| 5′ | 0.0069 | 0.101 | 1.05 × 10−2 | 6.8 × 10−2 | 7.15 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, H.; He, Q.; Chen, X. Theoretical and Numerical Study on a Scale Model Test of Planetary Cratering Impact. Aerospace 2025, 12, 333. https://doi.org/10.3390/aerospace12040333
Lv H, He Q, Chen X. Theoretical and Numerical Study on a Scale Model Test of Planetary Cratering Impact. Aerospace. 2025; 12(4):333. https://doi.org/10.3390/aerospace12040333
Chicago/Turabian StyleLv, He, Qiguang He, and Xiaowei Chen. 2025. "Theoretical and Numerical Study on a Scale Model Test of Planetary Cratering Impact" Aerospace 12, no. 4: 333. https://doi.org/10.3390/aerospace12040333
APA StyleLv, H., He, Q., & Chen, X. (2025). Theoretical and Numerical Study on a Scale Model Test of Planetary Cratering Impact. Aerospace, 12(4), 333. https://doi.org/10.3390/aerospace12040333