Numerical Analysis of the Effect of S-Shaped Duct Key Geometry Parameters on the Inlet Distortion of Distributed Ducted Fans
Abstract
1. Introduction
2. Numerical Method Based on BFM
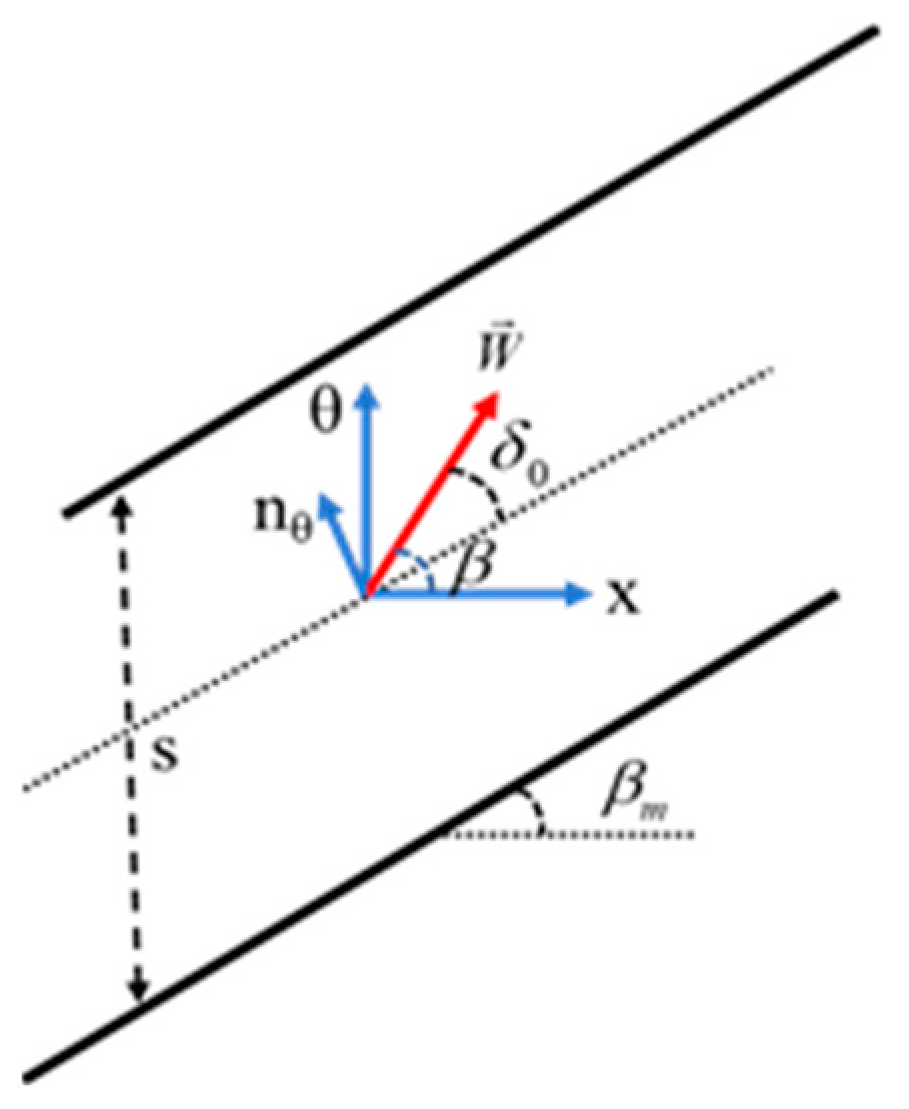
2.1. Development of BFM Model
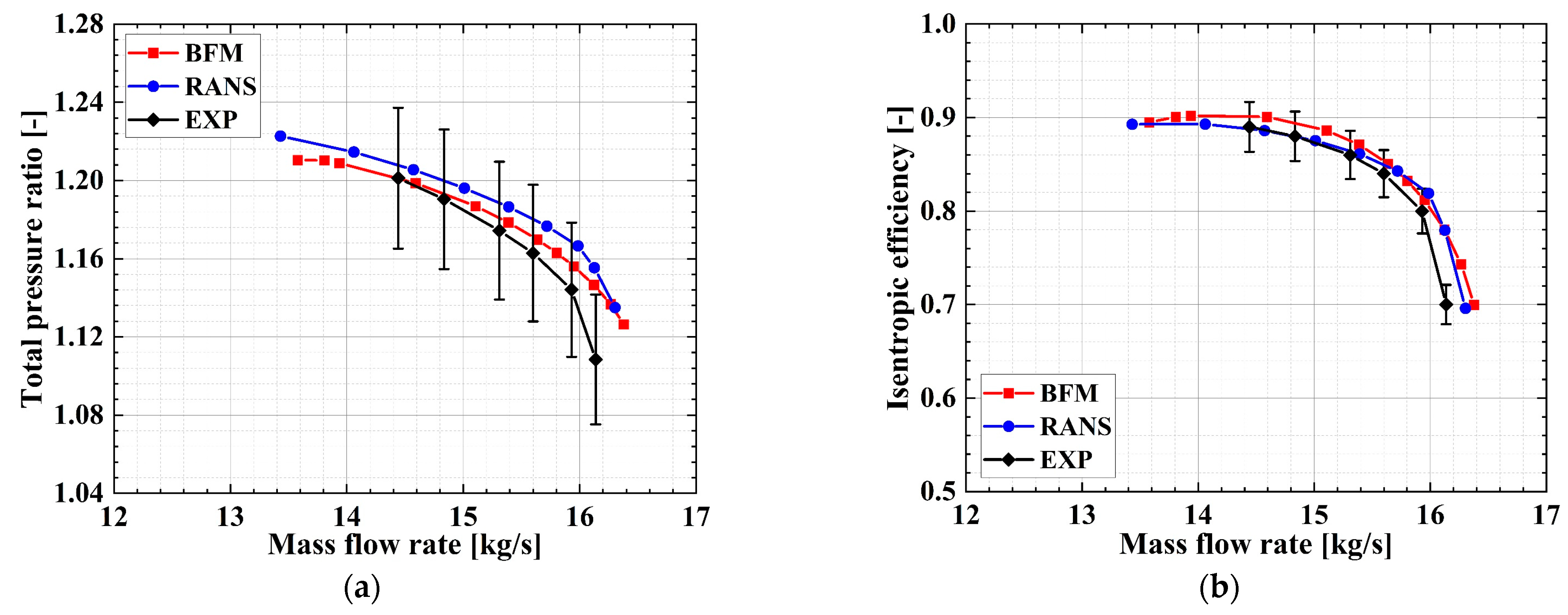
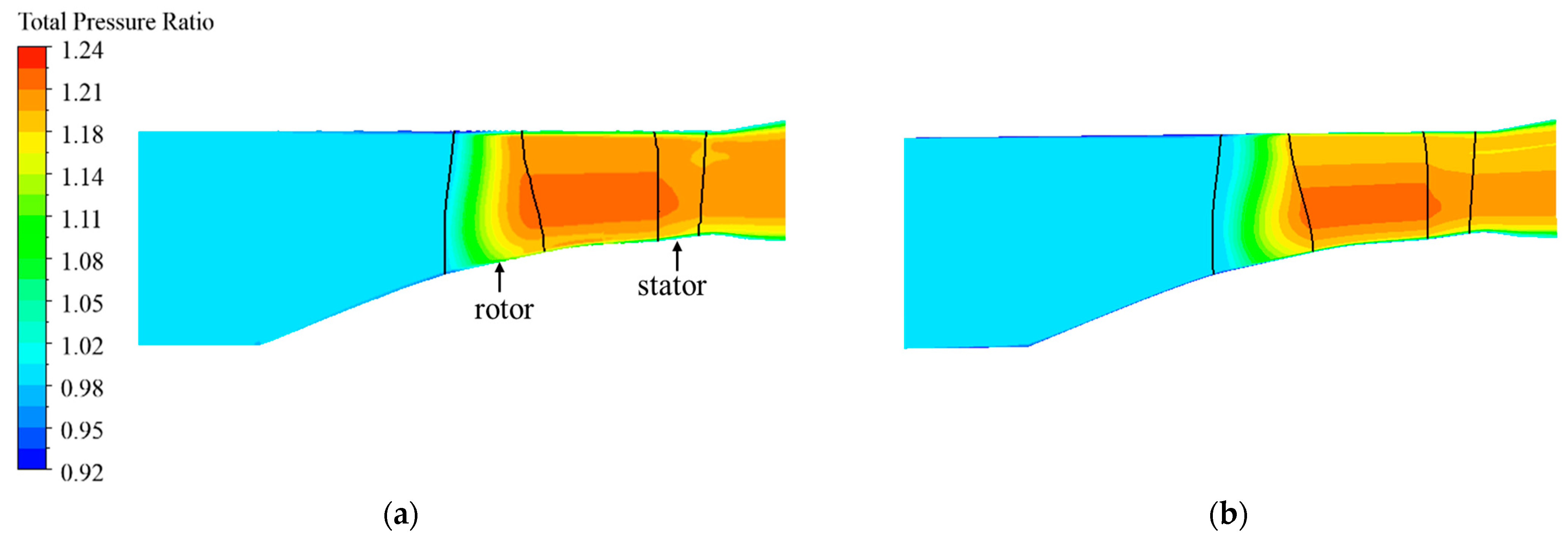
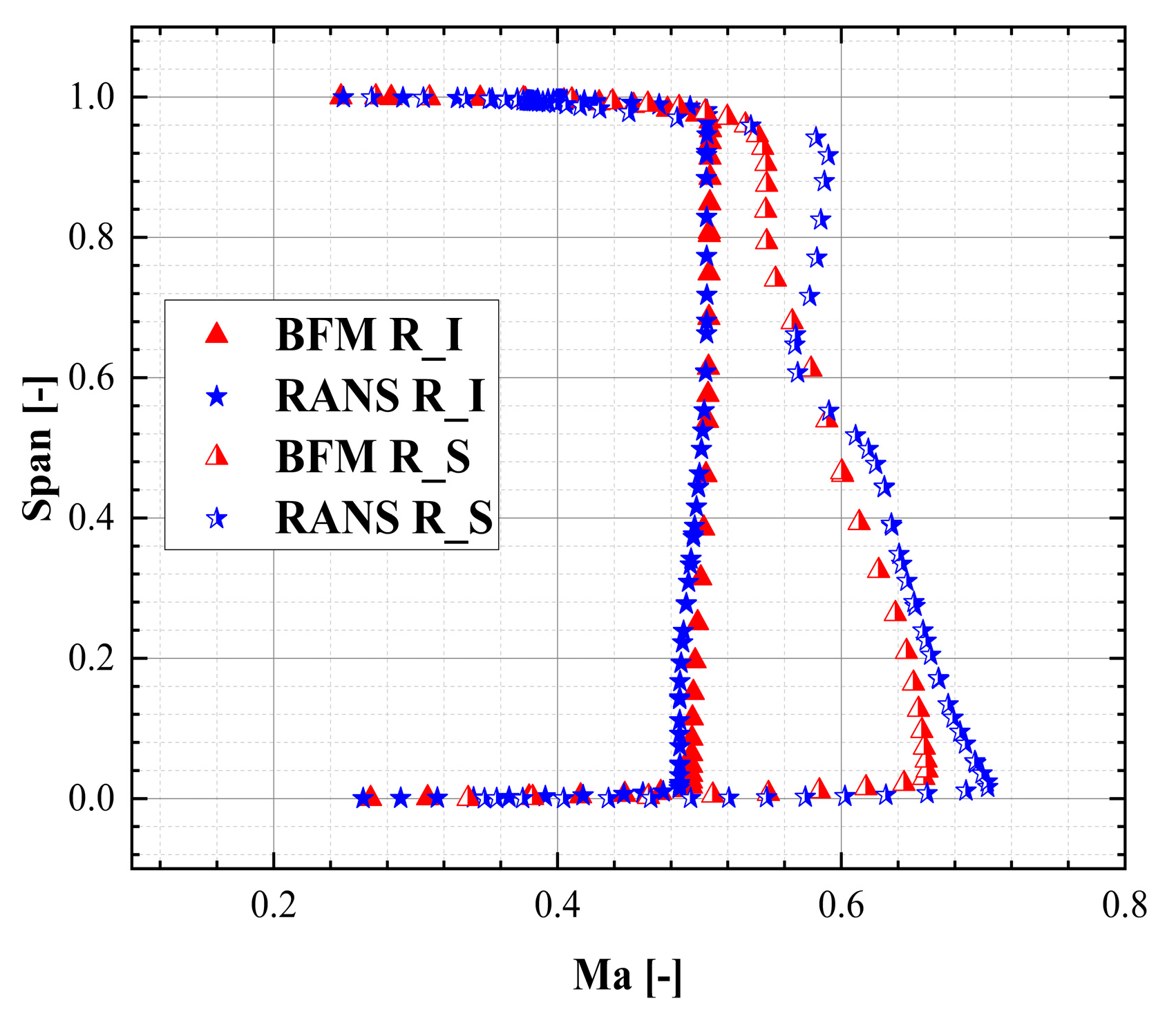
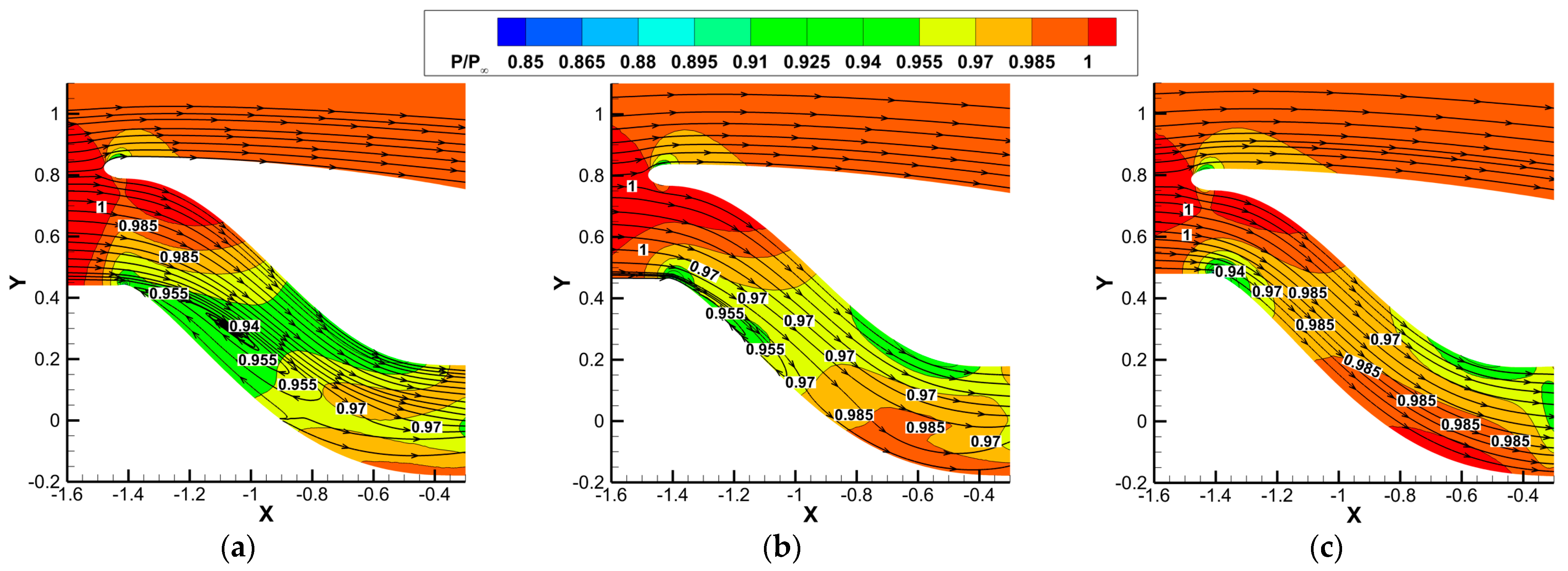
2.2. Validation of BFM Model
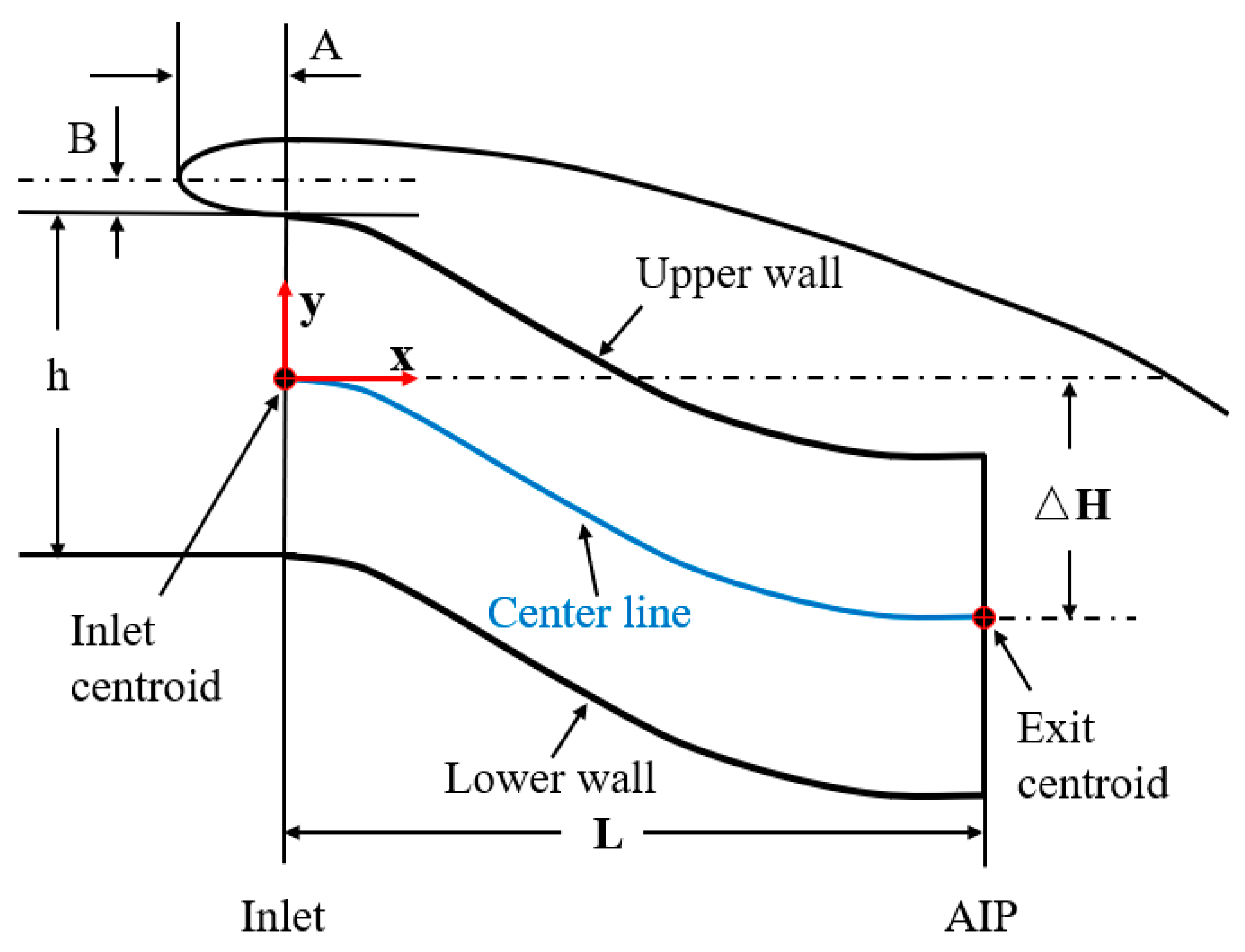
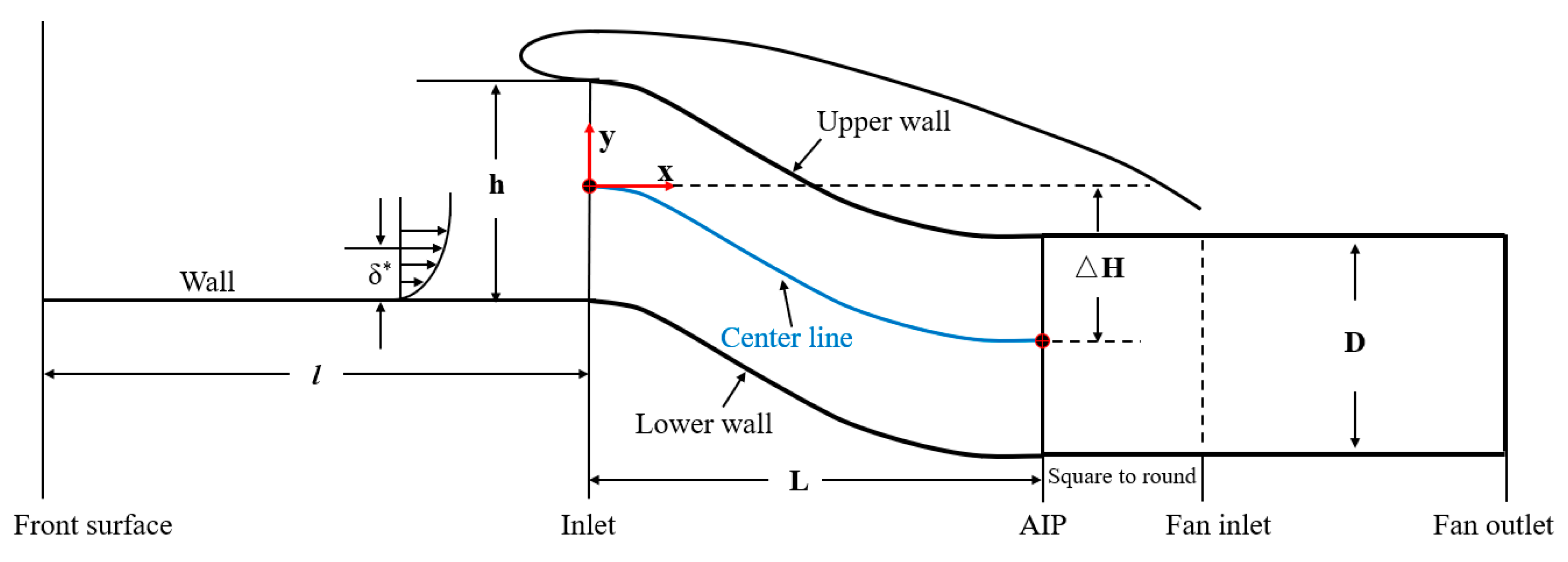
3. Design of an S-Shaped Duct
4. Computational Methods
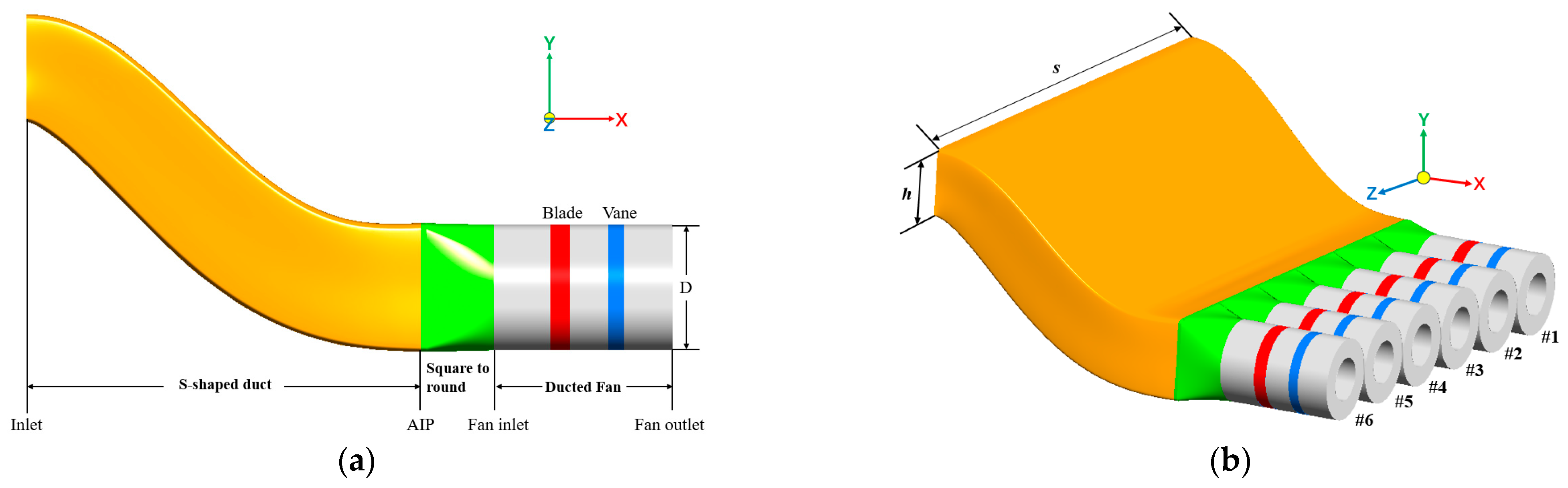
4.1. Distributed Ducted Fans with S-Shaped Duct
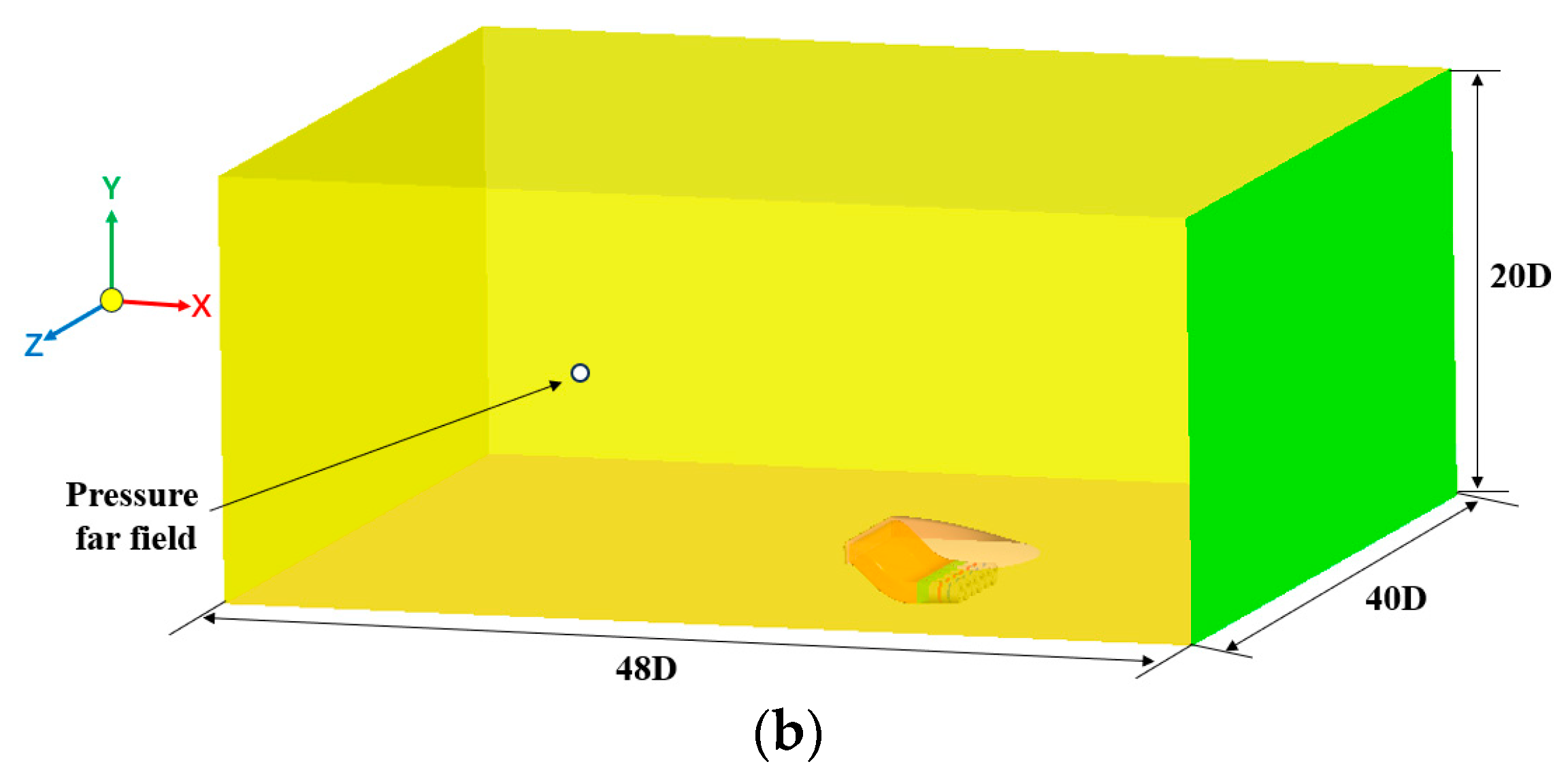
4.2. Numerical Method and Boundary Condition
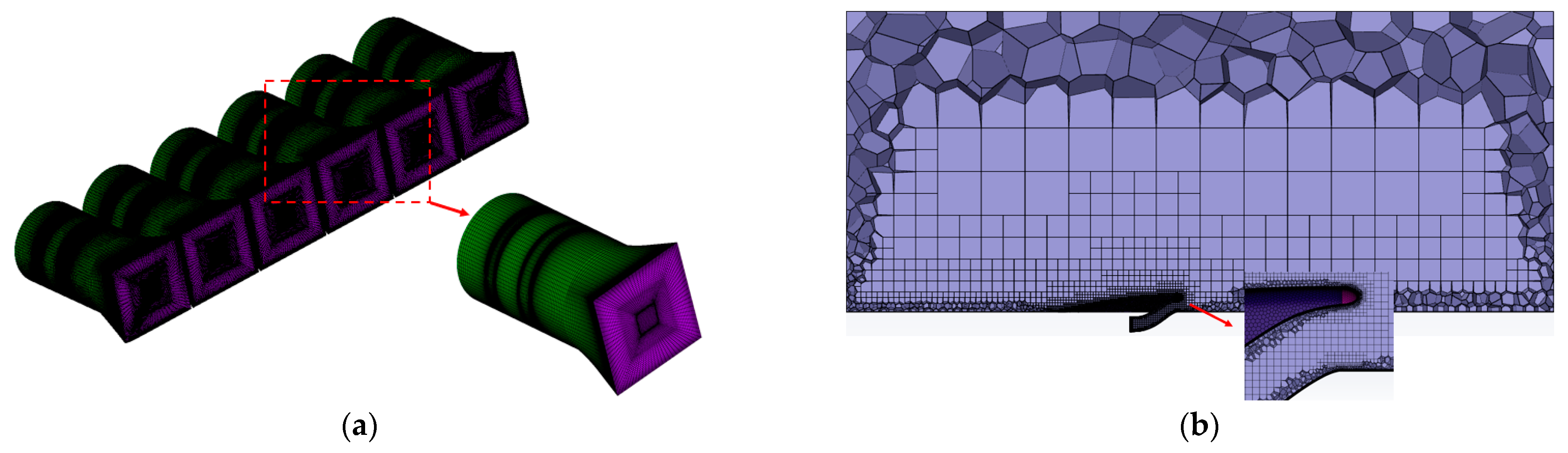
4.3. Computational Mesh
5. Results and Discussion
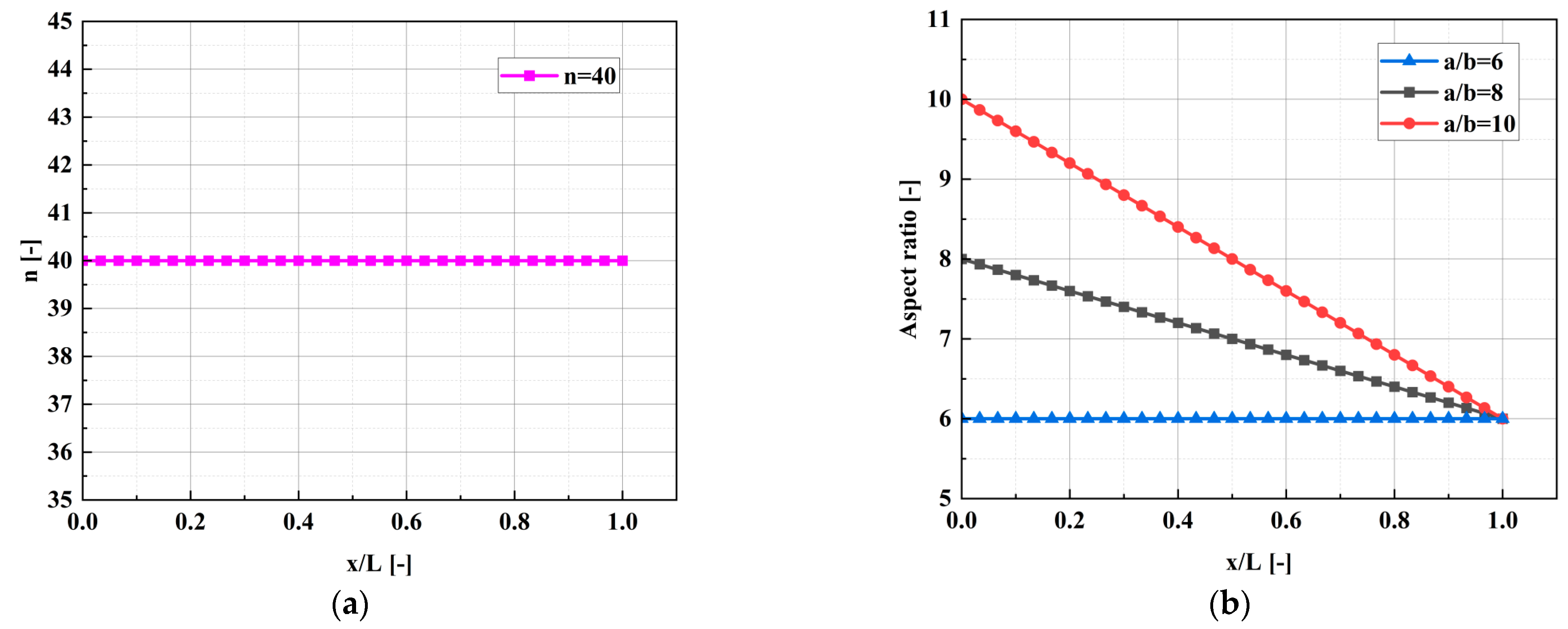
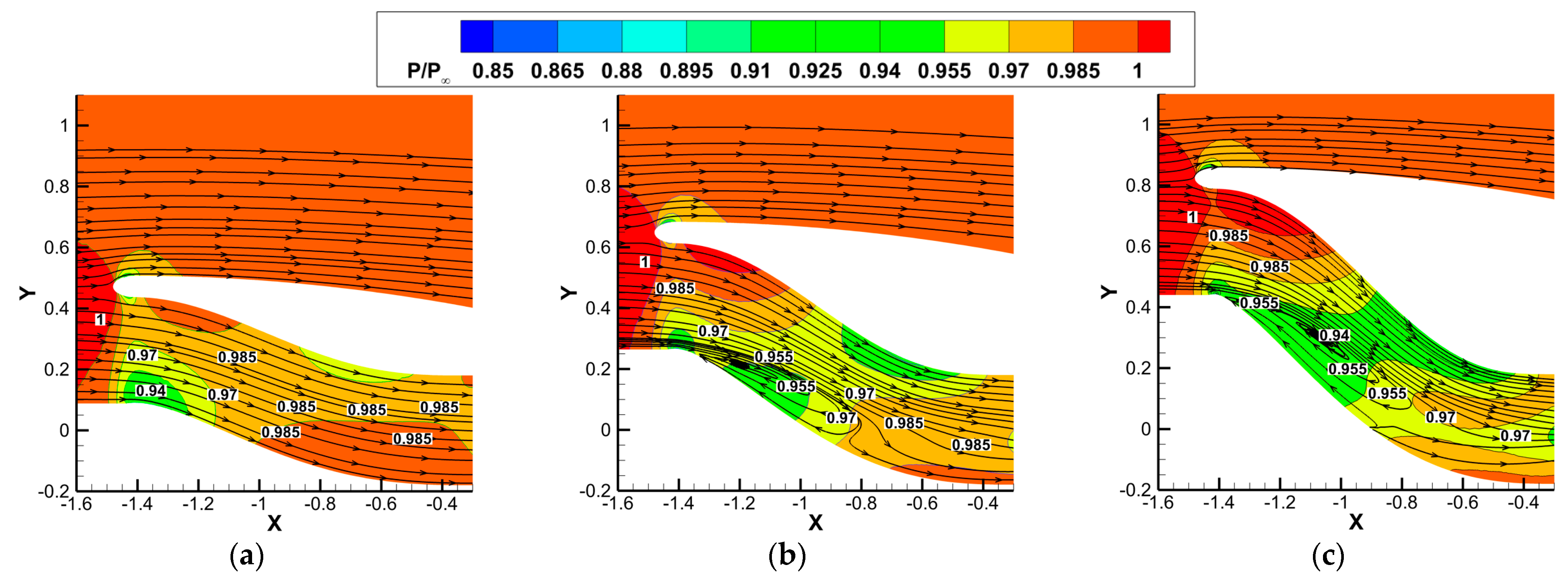
5.1. Key Geometry Parameters and Boundary Layer Thickness
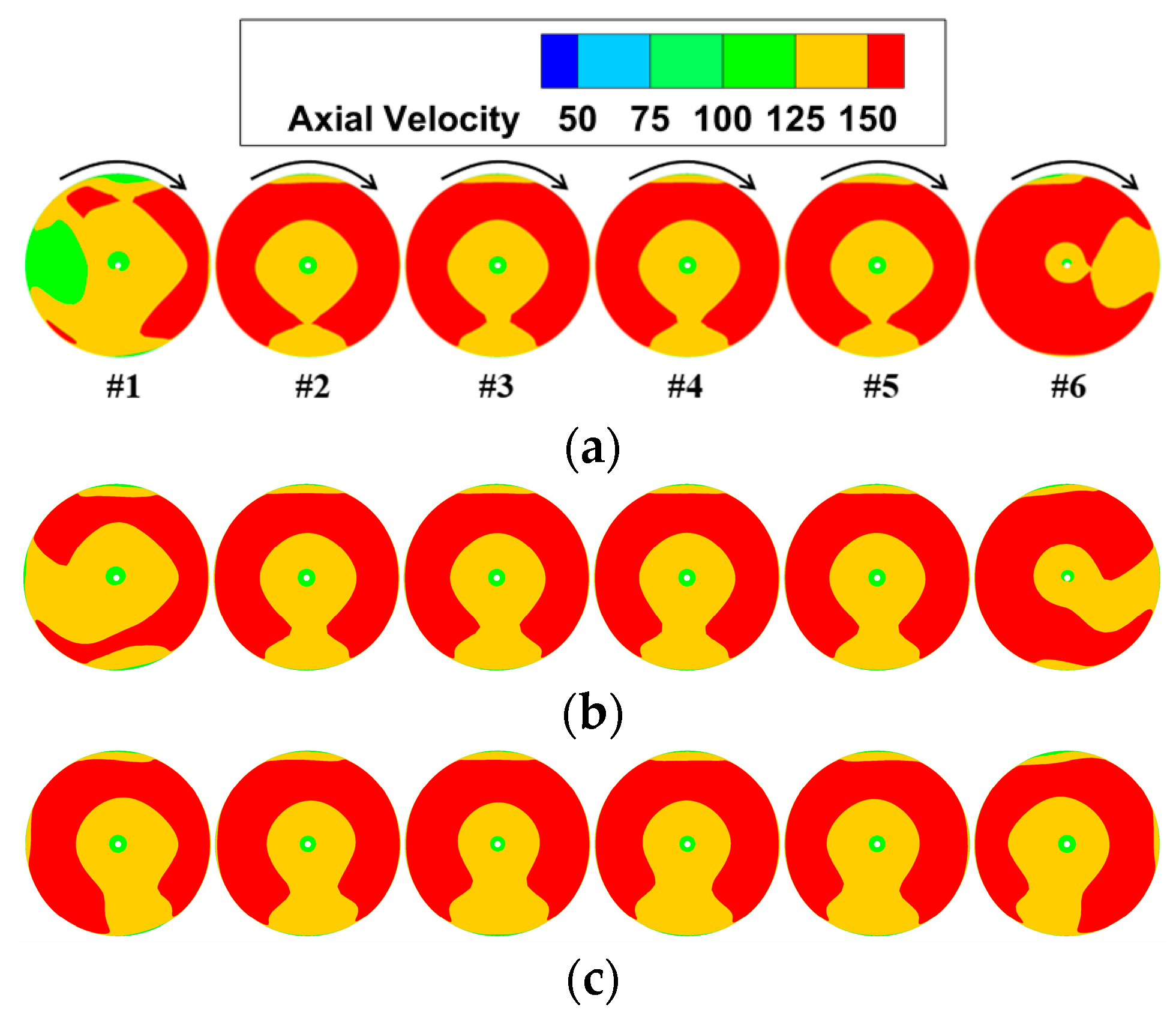
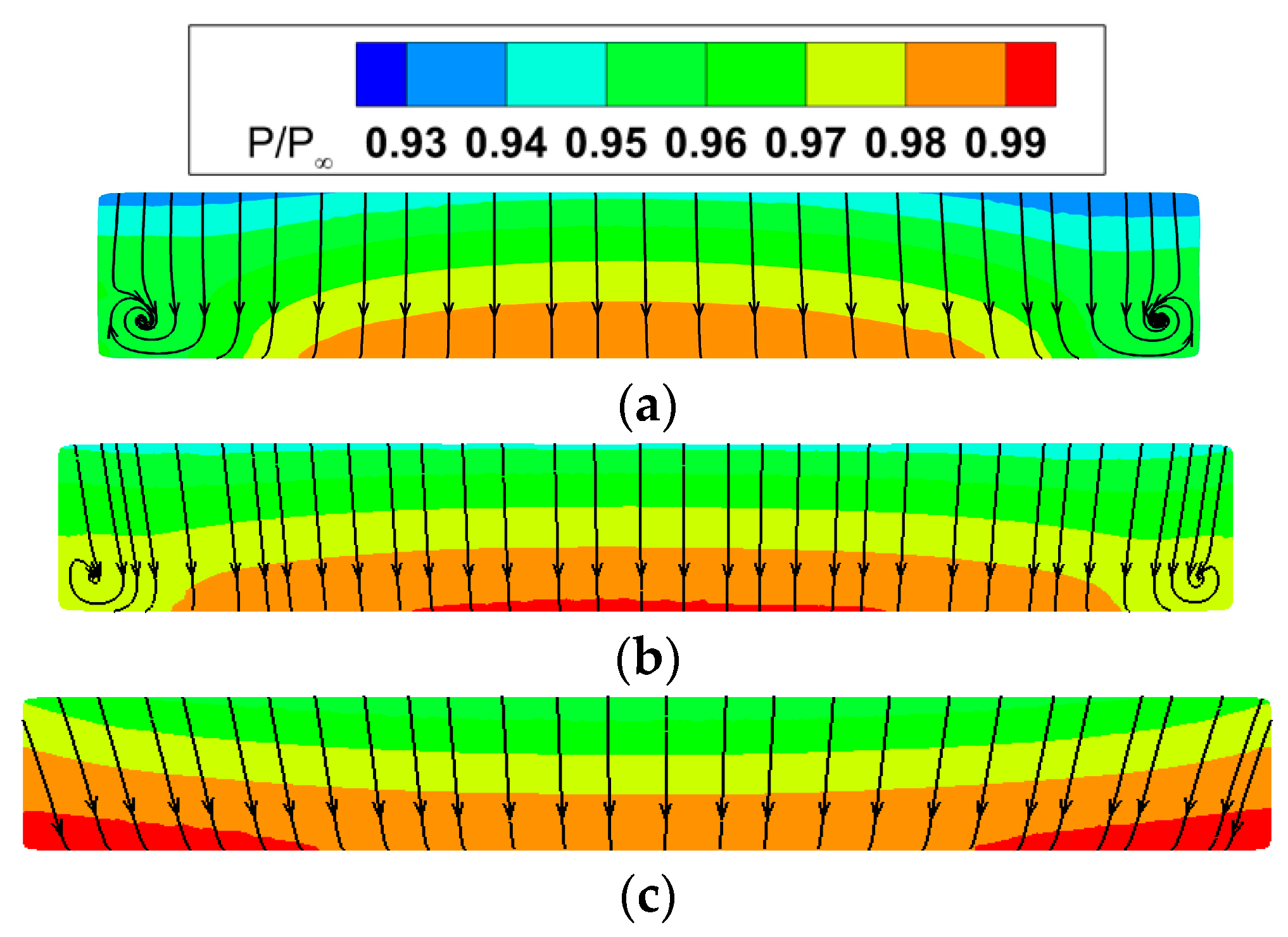
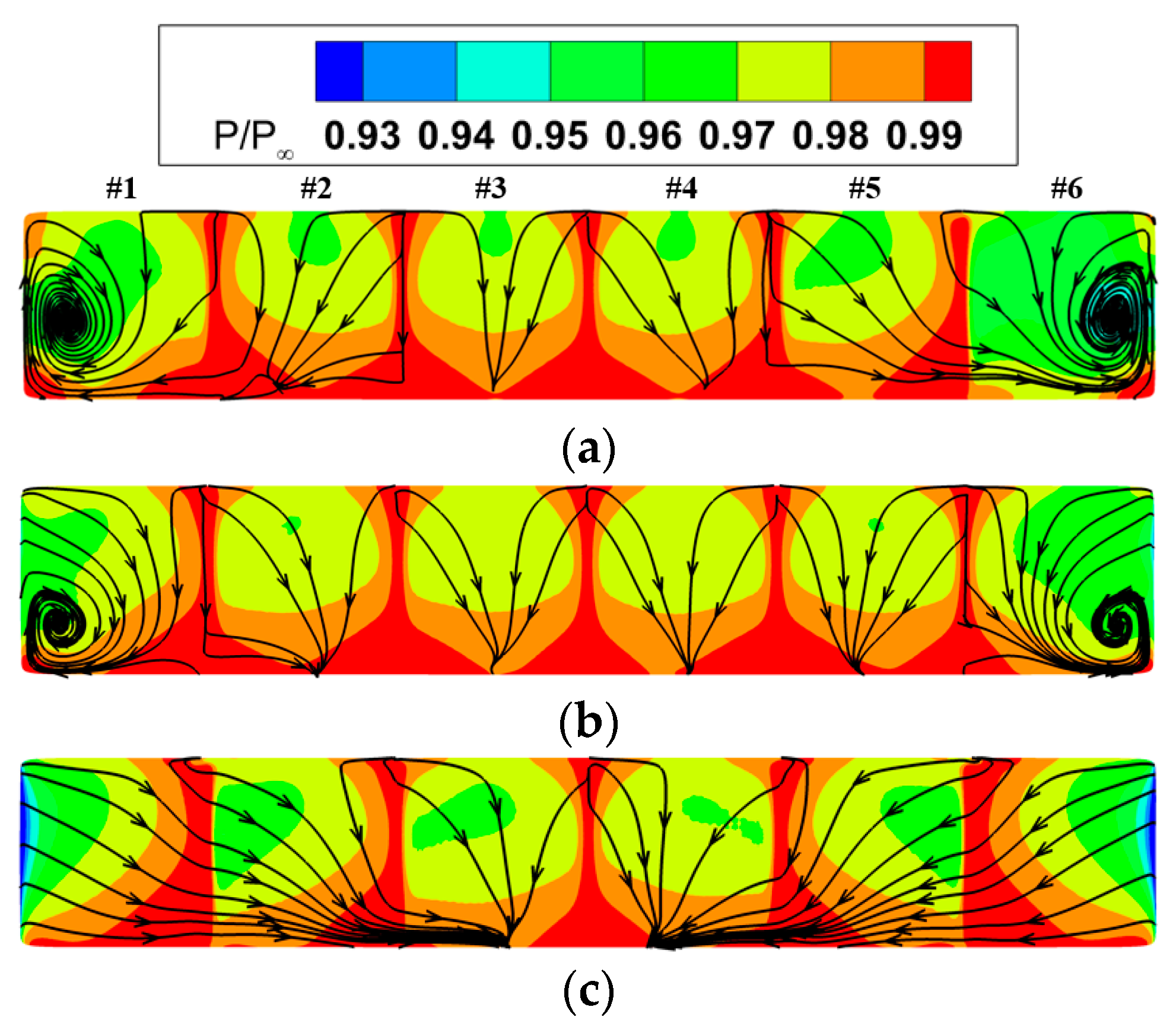
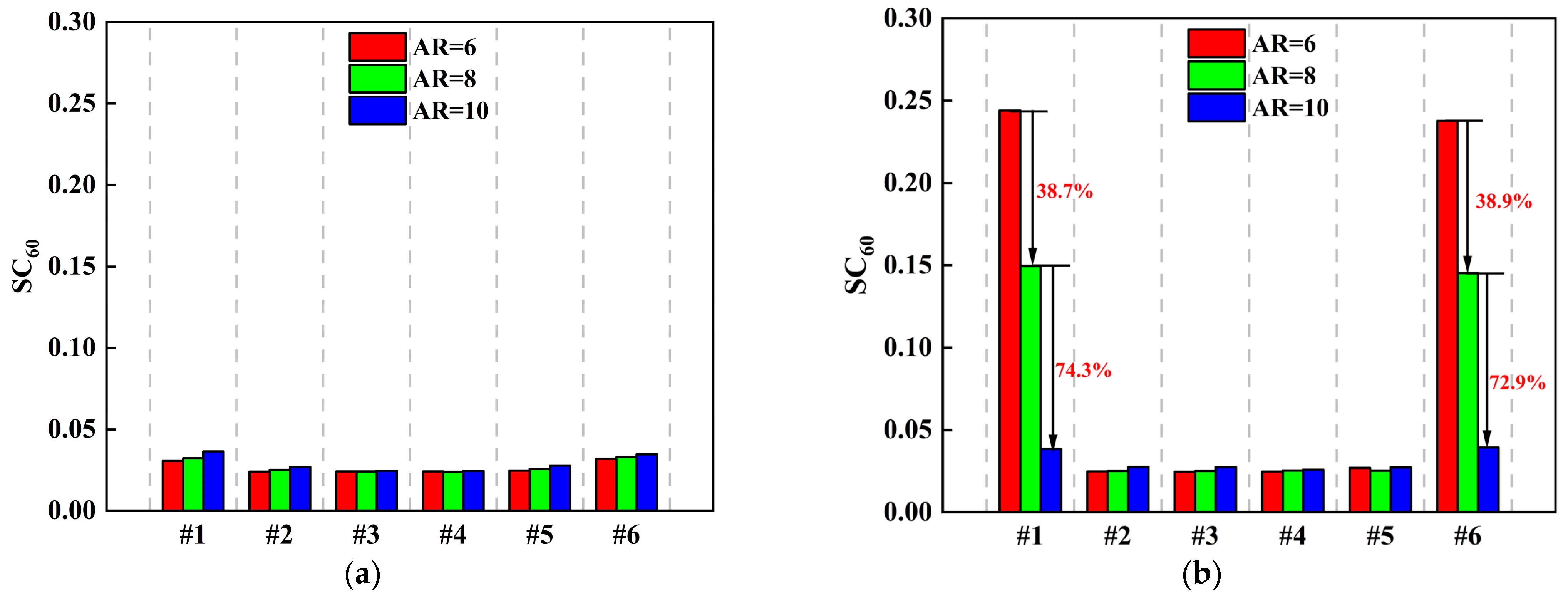
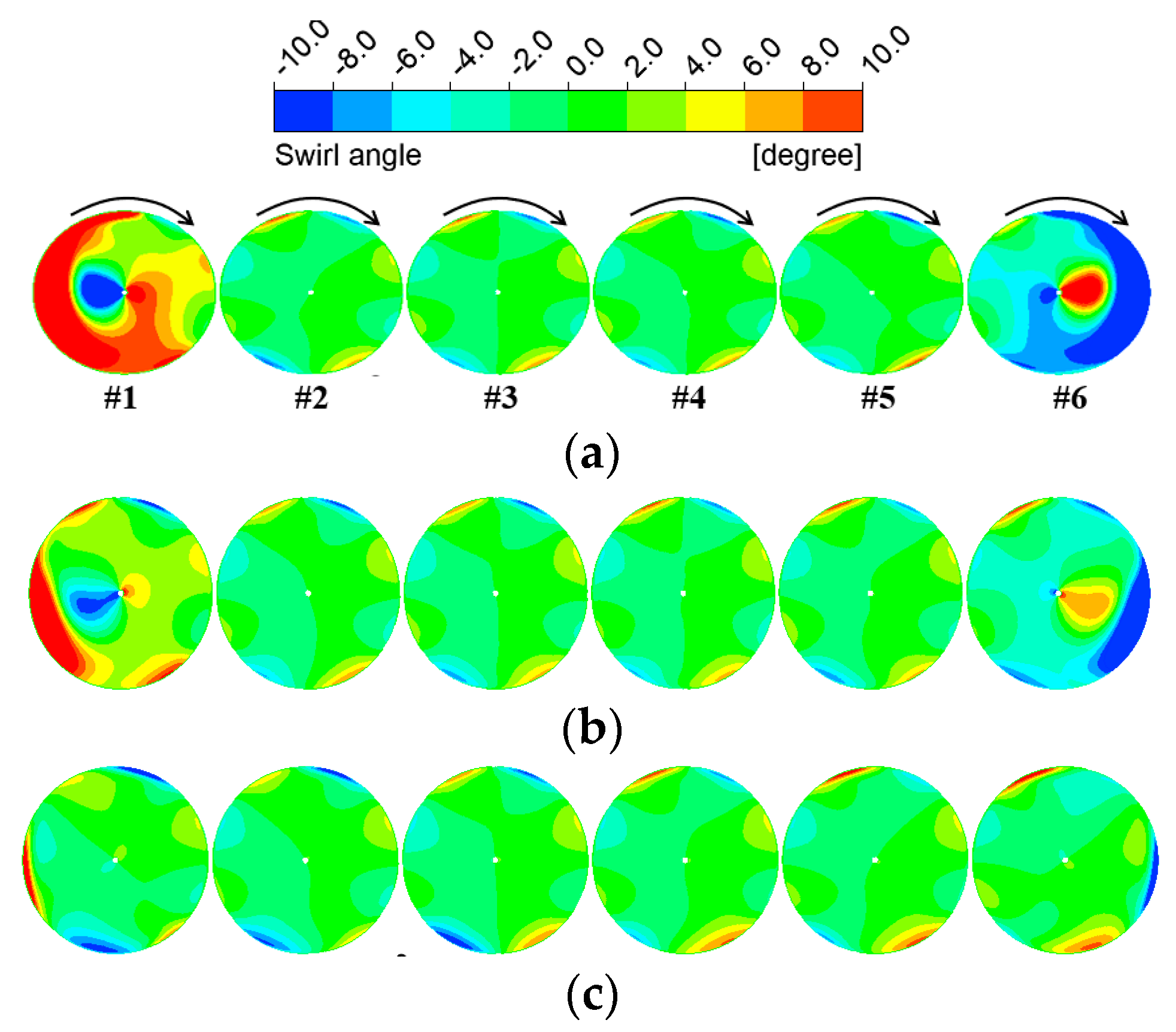
5.2. Effects of Inlet Aspect Ratio
5.3. Effects of Centerline Offset
6. Conclusions
- (1)
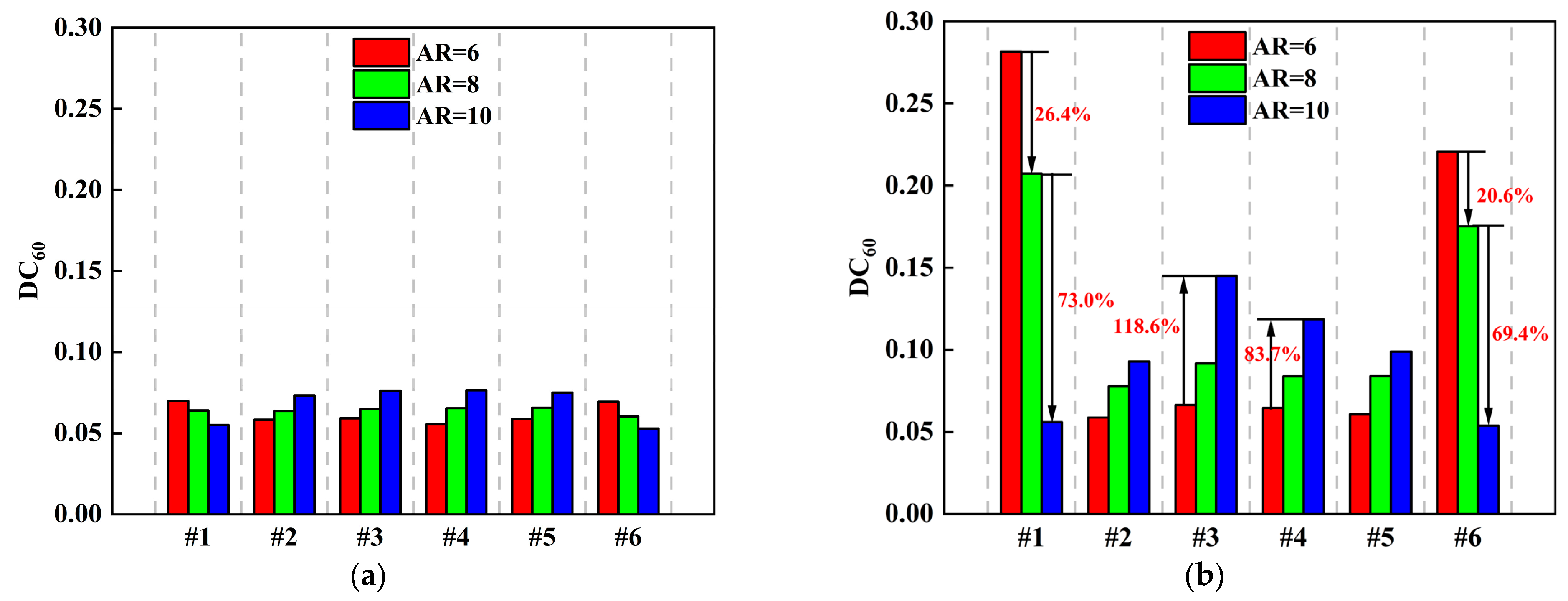
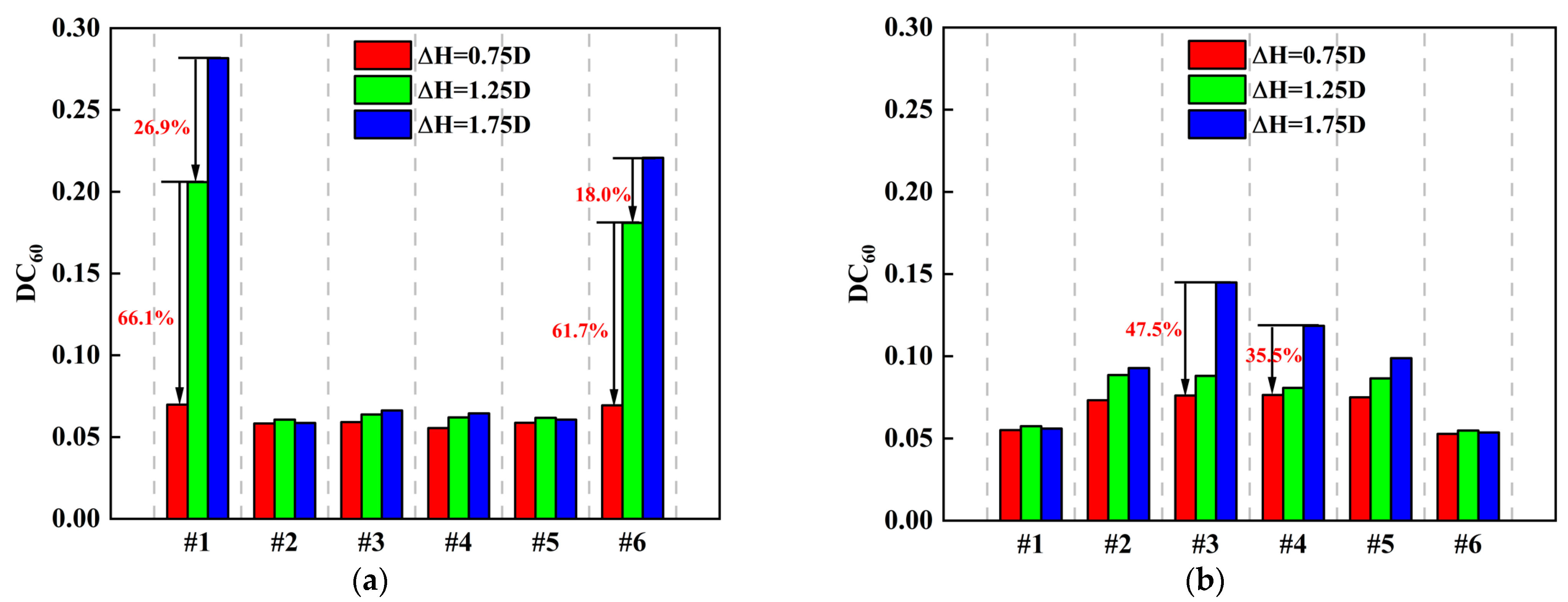
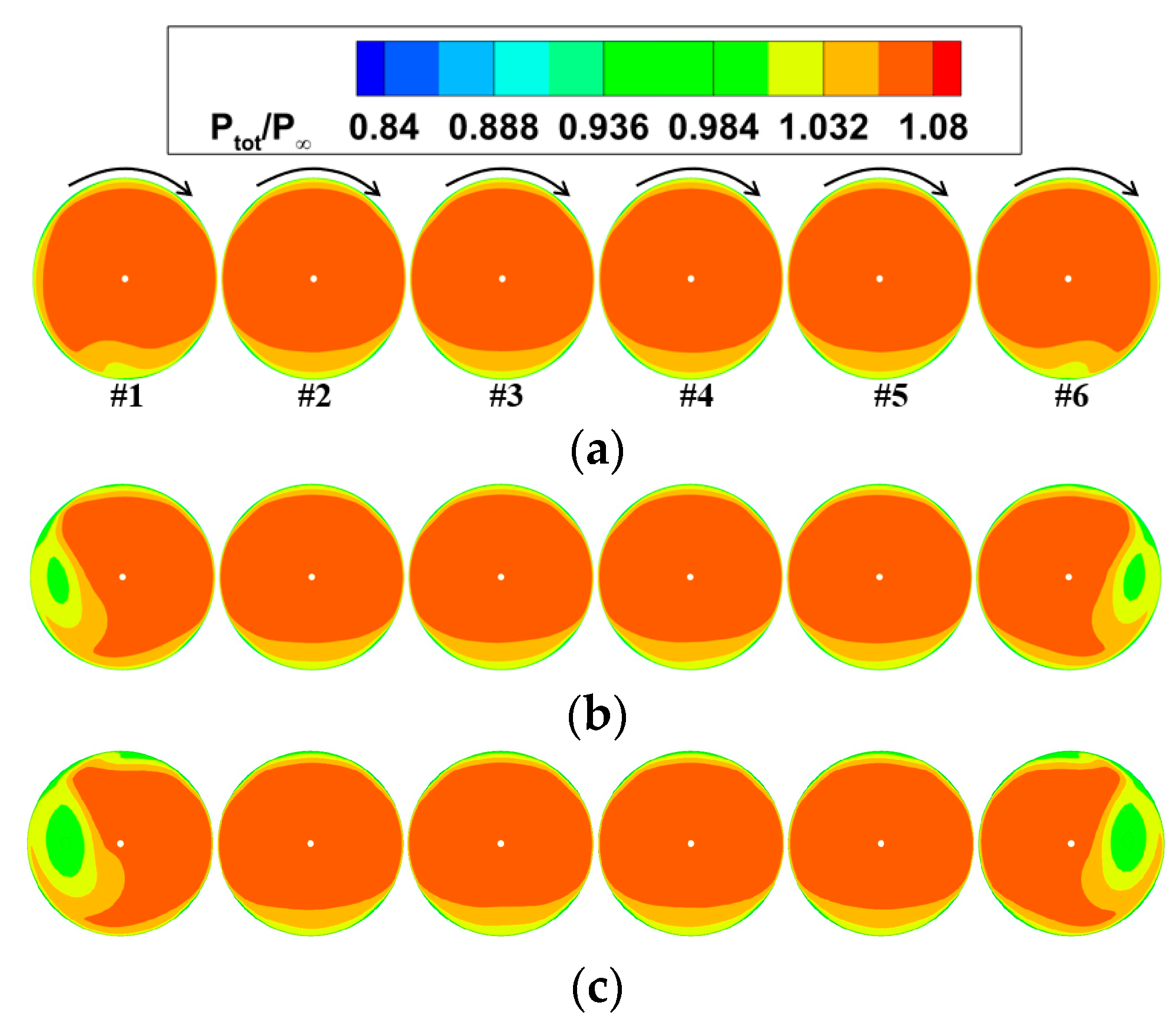
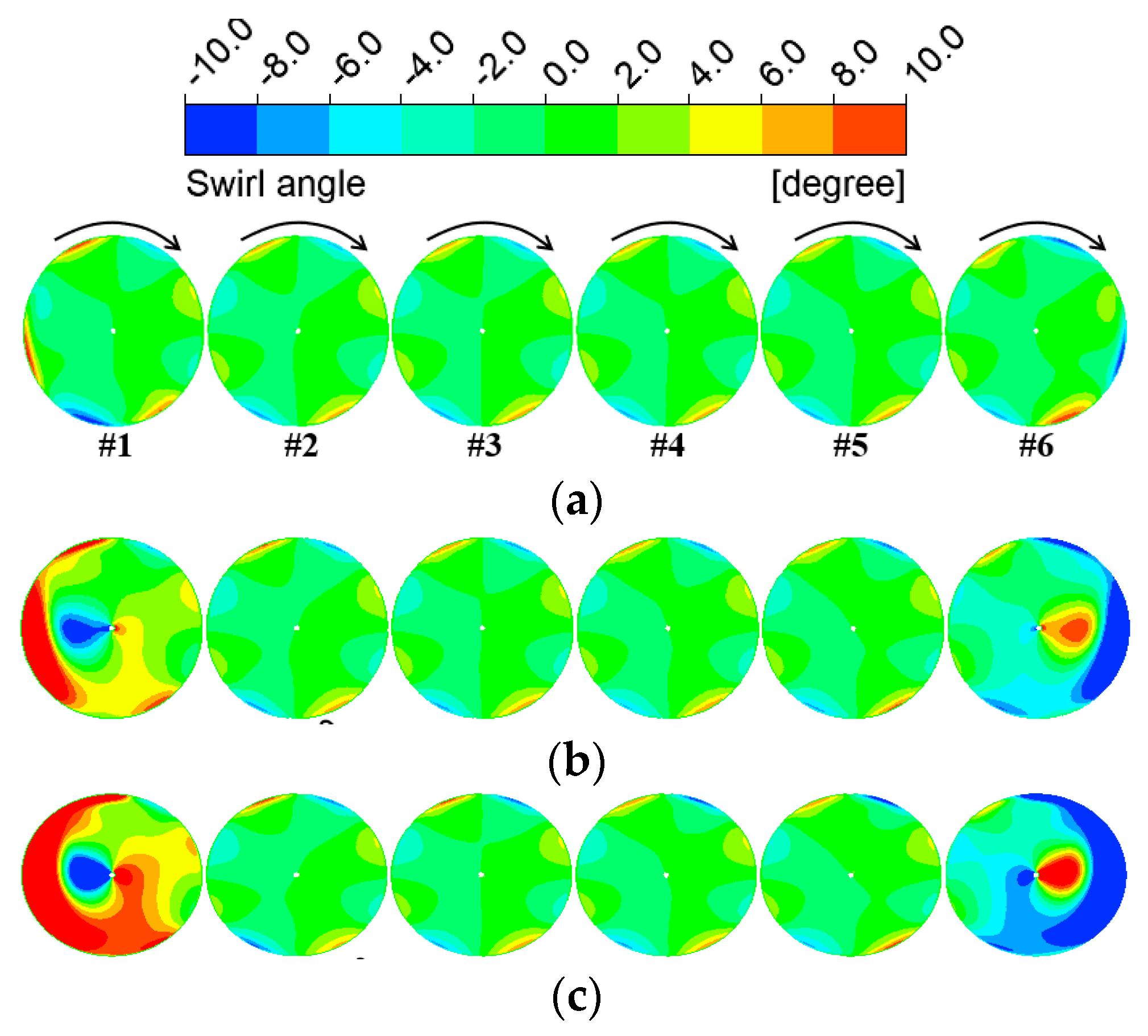
- As the inlet aspect ratio increases, edge fans experience a reduction in the total pressure distortion, whereas intermediate fans experience an increase. In an S-shaped duct with a large centerline offset, the total pressure distortion index DC60 for fans #1 and #6 is decreased by 80.1% and 75.7%, respectively, when the aspect ratio changes from 6 to 10. Conversely, the DC60 for fan #3 is increased by 118.6% under the same conditions.
- (2)
- In an S-shaped duct with a substantial centerline offset, changes in the aspect ratio significantly affect the swirl distortion of edge fans. When the aspect ratio increases from 6 to 10, the swirl distortion index SC60 is decreased by 84.2% and 83.4% for fans #1 and #6, respectively. Conversely, in an S-shaped duct with a small centerline offset, changes in the aspect ratio have a negligible impact on the swirl distortion of the ducted fans.
- (3)
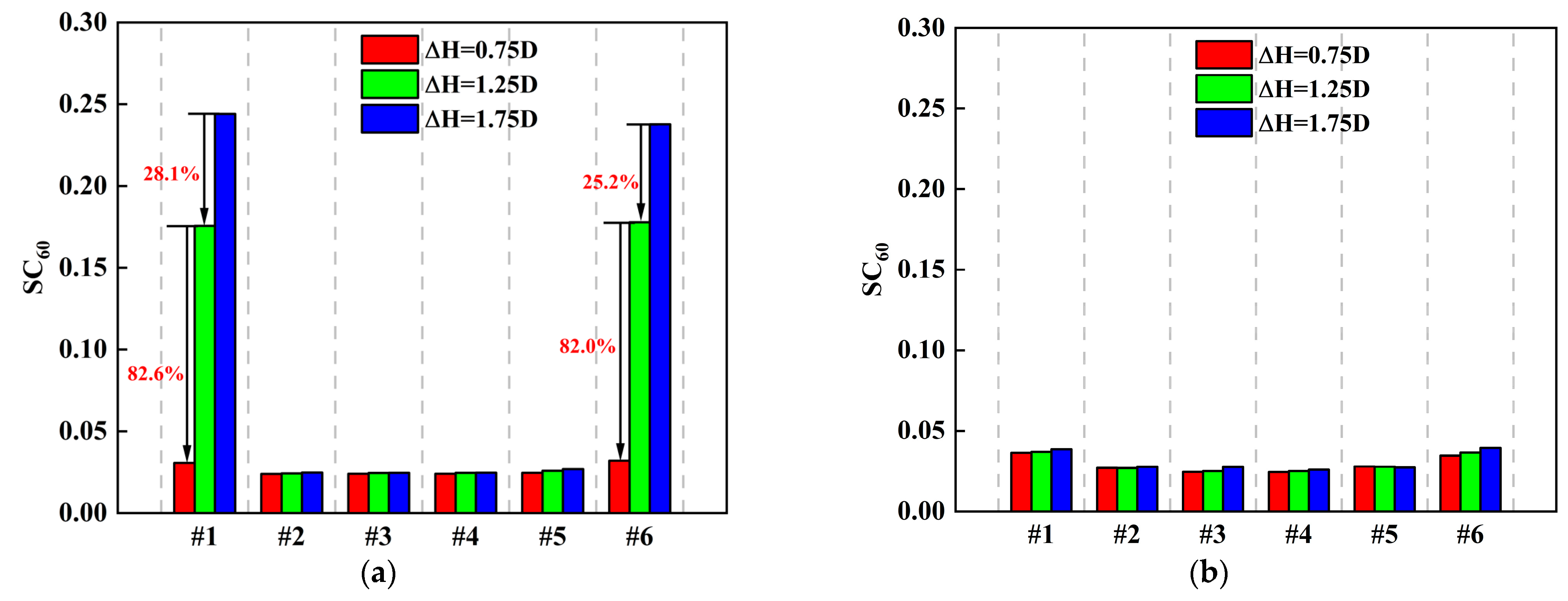
- When the aspect ratio is small, changes in the centerline offset have a more significant impact on the total pressure distortion of the edge fans. Reducing the centerline offset from 1.75D to 0.75D results in a 75.2% decrease in DC60 for fan #1 and a 68.6% decrease for fan #6. In contrast, for a large aspect ratio, the centerline offset has a more pronounced effect on the total pressure distortion of the intermediate fans. Decreasing the centerline offset from 1.75D to 0.75D leads to a 47.5% reduction in DC60 for fan #3 and a 35.5% reduction for fan #4.
- (4)
- In an S-shaped duct with a small aspect ratio, the centerline offset primarily affects the swirl distortion of edge fans. A reduction in centerline offset from 1.75D to 0.75D results in a significant decrease in the swirl distortion index SC60 for fan #1 and fan #6, with reductions of 87.5% and 86.5%, respectively. However, for an S-shaped duct with a large inlet aspect ratio, changes in the centerline offset have a minimal impact on the swirl distortion of the ducted fans.
- (5)
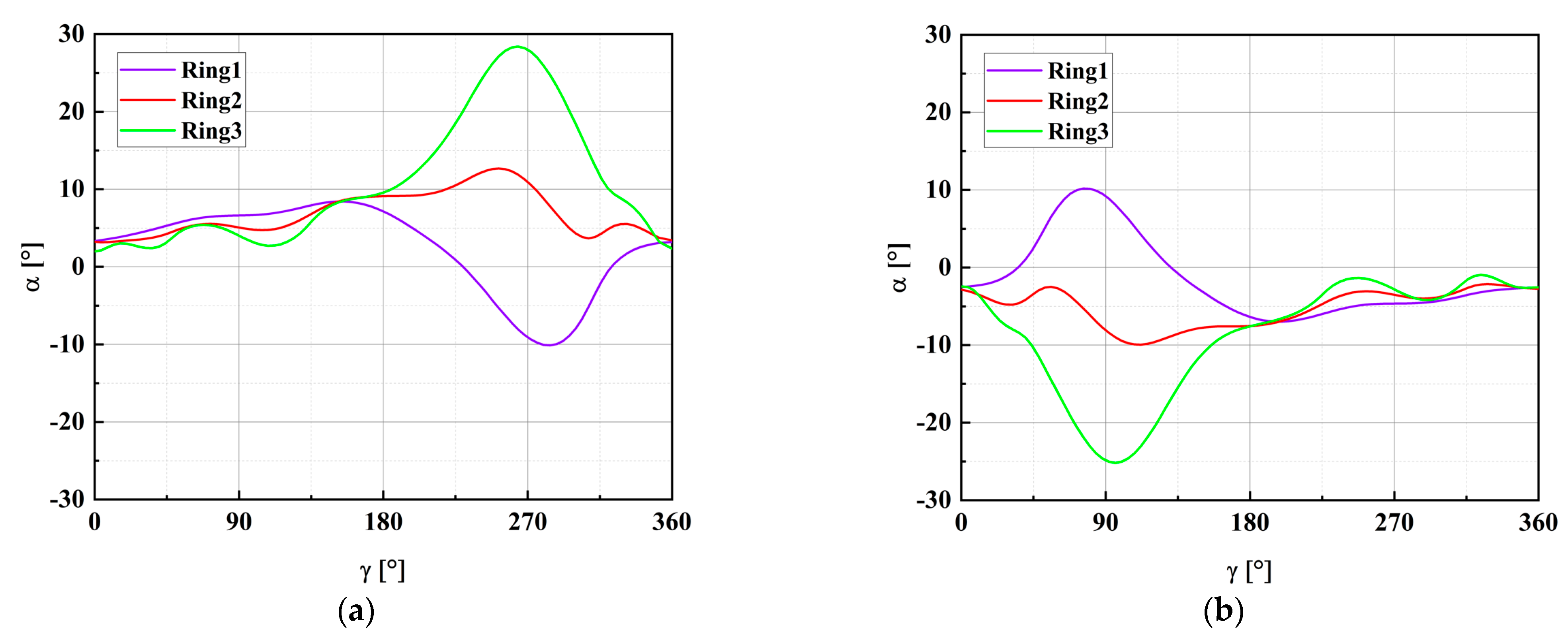
- The edge fans experience similar levels of swirl distortion, but their total pressure distortion varies slightly due to differences in the swirl angle directions at the fan inlet. Among all the configurations examined in this study, the most severe inlet distortion occurs when a large centerline offset is combined with a small aspect ratio. Therefore, it is crucial to consider both the centerline offset and aspect ratio when designing an S-shaped duct for distributed ducted fans.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| A | length of semi-major axis of elliptical lip (m) |
| a | length of semi-major axis of hyperellipse (m) |
| AR | inlet aspect ratio of S-shaped duct |
| B | length of semi-minor axis of elliptical lip (m) |
| b | blade blockage factor or length of semi-minor axis of hyperellipse (m) |
| c | chord (m) |
| Cf | local friction coefficient |
| D | fan diameter (m) |
| DC60 | total pressure distortion index |
| e | total energy per unit mass (J/kg) |
| f | body force per unit mass (N/kg) |
| fn | inviscid body force (N/kg) |
| fp | viscid body force (N/kg) |
| h | inlet height of S-shaped duct (m) |
| KMach | compressibility coefficient |
| L | axial length of S-shaped duct (m) |
| l | distance between front surface and inlet of S-shaped duct (m) |
| Min | Mach number of the incoming flow |
| Mrel | relative Mach number |
| N | number of blades |
| n | rotation speed (r/min) or hyperellipse index |
| nθ | unit normal vector in circumferential direction |
| P | static pressure (Pa) |
| Ptot | total pressure (Pa) |
| average total pressure (Pa) | |
| q | dynamic pressure (Pa) |
| Rex | Reynolds number |
| r | radius (m) |
| S | area (m2) |
| s | blade pitch (m) or inlet width of S-shaped duct (m) |
| SC60 | swirl distortion index |
| T | temperature (K) |
| t | time (s) |
| u | velocity in free-stream (m/s) |
| V | absolute velocity vector (m/s) |
| average velocity (m/s) | |
| W | relative velocity vector (m/s) |
| X, Y, Z | x-, y-, z-coordinate axis |
| x, y, z | x-, y-, z-coordinate (m) |
| ΔH | centerline offset (m) |
| Subscripts | |
| in | incoming flow |
| max | maximum |
| min | minimum |
| o | original |
| ref | reference |
| tot | total |
| x | axial direction |
| θ | circumferential direction |
| ∞ | free stream |
| Greek symbols | |
| α | swirl angle (°) |
| β | relative flow angle (°) |
| βm | blade metal angle (°) |
| γ | circumferential angle (°) |
| Γ | gamma function |
| δ | local deviation angle (°) |
| δ* | boundary layer thickness (m) |
| δ0 | reference local deviation angle (°) |
| θ | circumferential coordinate (°) |
| μ | dynamic viscosity (kg/m·s) |
| ρ | density (kg/m3) |
| τ | equivalent expansion angle (°) |
| Acronyms | |
| AIP | aerodynamic interface plane |
| BFM | body force model |
| BLI | boundary layer ingestion |
| BWB | blended wing body |
| CAEP | Committee on Aviation Environment Protection |
| DEP | distributed electric propulsion |
| EXP | experimental |
| HRR | height-to-radius ratio |
| NACA | National Advisory Committee for Aeronautics |
| NASA | National Aeronautics and Space Administration |
| RANS | Reynolds-averaged Navier–Stokes |
| RMS | root mean square |
| RPM | revolutions per minute |
| UDF | user-defined function |
References
- Lee, C.M. NASA project develops next generation low-emissions combustor technologies. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar] [CrossRef]
- Van Zante, D.E.; Suder, K.L. Environmentally responsible aviation: Propulsion research to enable fuel burn, noise and emissions reduction. In Proceedings of the 22nd International Symposium on Air Breathing Engines, Phoenix, AZ, USA, 25–30 October 2015; Available online: https://ntrs.nasa.gov/citations/20150023471 (accessed on 1 January 2025).
- Brouckaert, J.F.; Mirville, F.; Phuah, K.; Taferner, P. Clean Sky research and demonstration programmes for next-generation aircraft engines. Aeronaut. J. 2018, 122, 1163–1175. [Google Scholar] [CrossRef]
- Gelhausen, M.C.; Grimme, W.; Junior, A. Clean Sky 2 Technology Evaluator—Results of the first air transport system level assessments. Aerospace 2022, 9, 204. [Google Scholar] [CrossRef]
- Handa, S.; Srinivas, G. Recent developments of blended wing body aircraft: Experimental, numerical and theoretical approaches. Aerosp. Syst. 2022, 5, 171–183. [Google Scholar] [CrossRef]
- Wang, L.X.; Zhang, N.; Liu, H.L. Stability characteristics and airworthiness requirements of blended wing body aircraft with podded engines. Chin. J. Aeronaut. 2022, 35, 77–86. [Google Scholar] [CrossRef]
- Mahamuni, P.; Kulkarni, A.; Parikh, Y. Aerodynamic study of blended wing body. Int. J. Appl. Eng. Res. 2014, 9, 29247–29255. [Google Scholar]
- Ammar, S.; Legros, C.; Trépanier, J.Y. Conceptual design, performance and stability analysis of a 200 passengers blended wing body aircraft. Aerosp. Sci. Technol. 2017, 71, 325–336. [Google Scholar] [CrossRef]
- Karpuk, S.; Ma, Y.; Elham, A. Design Investigation of Potential Long-Range Hydrogen Combustion Blended Wing Body Aircraft with Future Technologies. Aerospace 2023, 10, 566. [Google Scholar] [CrossRef]
- Kim, H.D.; Felder, J.L.; Tong, M. Revolutionary aeropropulsion concept for sustainable aviation: Turboelectric distributed propulsion. In Proceedings of the 2013 International Society for Air Breathing Engines, Busan, Republic of Korea, 9–13 September 2013; Available online: https://ntrs.nasa.gov/citations/20140002510 (accessed on 1 January 2025).
- Hyun, D.K.; Felder, J.L.; Tong, M.T.; Haller, J.J.B.J. Turboelectric distributed propulsion benefits on the N3-X vehicle. Aircr. Eng. Aerosp. Technol. 2014, 86, 558–561. [Google Scholar] [CrossRef]
- Goldberg, C.; Nalianda, D.; Pilidis, P.; Singh, R. Economic viability assessment of NASA’s blended wing body N3-X aircraft. In Proceedings of the 53rd AIAA/SAE/ASEE Joint Propulsion Conference, Atlanta, GA, USA, 10–12 July 2017. [Google Scholar] [CrossRef][Green Version]
- Gohardani, A.S.; Doulgeris, G.; Singh, R. Challenges of future aircraft propulsion: A review of distributed propulsion technology and its potential application for the all electric commercial aircraft. Prog. Aerosp. Sci. 2011, 47, 369–391. [Google Scholar] [CrossRef]
- Seddon, J.; Goldsmith, E.L. Intake Aerodynamics, 2nd ed.; AIAA: Reston, VA, USA, 1999; pp. 169, 278–285. [Google Scholar]
- Perry, A.T.; Ansell, P.J.; Kerho, M.F. Aero-propulsive and propulsor cross-coupling effects on a distributed propulsion system. J. Aircr. 2018, 55, 2414–2426. [Google Scholar] [CrossRef]
- Zhou, F.; Wang, Y.G.; Wang, S.W.; Chen, Y.J.; Qiu, Y.S. Experimental and numerical study on coupling effect of ducted fan in distributed electric propulsion system. J. Propuls. Technol. 2024, 45, 154–164. [Google Scholar] [CrossRef]
- Li, Z.Y.; Yang, X.D.; Sun, K.; Xiong, J.H.; Shi, S. Aerodynamic configuration of distributed ducted fan with complex strong interference effect and performance influence. Acta Aeronaut. Astronaut. Sin. 2025, 46, 130805. Available online: https://link.cnki.net/urlid/11.1929.v.20241015.1437.002 (accessed on 1 January 2025).
- Zhang, X.; Zhang, W.; Li, W.L.; Zhang, X.B.; Lei, T. Experimental research on aero-propulsion coupling characteristics of a distributed electric propulsion aircraft. Chin. J. Aeronaut. 2023, 36, 201–212. [Google Scholar] [CrossRef]
- Gong, T.Y.; Yuan, W. Mechanism of internal/external flow coupling effects on the performance of distributed ducted fan. J. Aerosp. Power 2021, 36, 592–605. [Google Scholar] [CrossRef]
- Liu, H.R.; Zhao, X.Y.; Zhou, F.; Feng, Y.Y. Aero-propulsion analysis of distributed ducted-fan propulsion based on lifting-line driven body-force model. Chin. J. Aeronaut. 2025, 38, 103126. [Google Scholar] [CrossRef]
- Kerho, M.F. Aero-propulsive coupling of an embedded, distributed propulsion system. In Proceedings of the 33rd AIAA Applied Aerodynamics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar] [CrossRef]
- Zhang, T.; Barakos, G.N. High-fidelity numerical analysis and optimization of ducted propeller aerodynamics and acoustics. Aerosp. Sci. Technol. 2021, 113, 106708. [Google Scholar] [CrossRef]
- Kim, H.; Liou, M.S. Flow simulation and optimal shape design of N3-X hybrid wing body configuration using a body force method. Aerosp. Sci. Technol. 2017, 71, 661–674. [Google Scholar] [CrossRef]
- Hall, D.K. Analysis of Civil Aircraft Propulsors with Boundary Layer Ingestion; Massachusetts Institute of Technology: Cambridge, MA, USA, 2015; Available online: https://dspace.mit.edu/handle/1721.1/97353 (accessed on 1 January 2025).
- Lucas, J.R.; O’Brien, W.F.; Ferrar, A.M. Effect of BLI–type inlet distortion on turbofan engine performance. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Dusseldorf, Germany, 16–20 June 2014. [Google Scholar] [CrossRef]
- Rein, M.; Koch, S. Experimental study of boundary-layer ingestion into a diverterless S-duct intake. AIAA J. 2015, 53, 3487–3492. [Google Scholar] [CrossRef]
- Ferrar, A.; O’Brien, W. Flow in boundary layer ingesting serpentine inlets. In Proceedings of the 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, San Diego, CA, USA, 31 July–3 August 2011. [Google Scholar] [CrossRef]
- Berrier, B.L.; Morehouse, M.B. Evaluation of flush-mounted, s-duct inlets with large amounts of boundary layer ingestion. In Proceedings of the Symposium on Vehicle Propulsion Integration, Warsaw, Poland, 6–9 October 2003; Available online: https://ntrs.nasa.gov/citations/20030068030 (accessed on 1 January 2025).
- Couey, P.T.; McKeever, C.W.; Malak, M.F.; Balamurugan, S.; Raju Veeraraghava, H.; Dhinagaran, R. Computational study of geometric parameter influence on aggressive inter-turbine duct performance. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010. [Google Scholar] [CrossRef]
- Lee, J.; Cho, J. Effect of aspect ratio of elliptical inlet shape on performance of subsonic diffusing S-duct. J. Mech. Sci. Technol. 2018, 32, 1153–1160. [Google Scholar] [CrossRef]
- Asghar, A.; Stowe, R.A.; Allan, W.D.E.; Alexander, D. Entrance aspect ratio effect on S-Duct inlet performance at high-subsonic flow. J. Eng. Gas Turbines Power 2017, 139, 052602. [Google Scholar] [CrossRef]
- Li, Z.P.; Lu, Y.J.; Pan, T.Y.; Zhang, Y.F. Numerical investigation on the effect of height-to-radius ratio on flow separation features in S-shaped diffuser with boundary layer ingestion. Aerospace 2023, 10, 551. [Google Scholar] [CrossRef]
- Hall, D.K.; Greitzer, E.M.; Tan, C.S. Analysis of fan stage conceptual design attributes for boundary layer ingestion. J. Turbomach. 2017, 139, 071012. [Google Scholar] [CrossRef]
- Thollet, W. Body-Force Modeling of Fan-Airframe Interactions; ISAE-SUPAERO: Toulouse, France, 2017. [Google Scholar]
- Kong, Q.; Jia, W. A three-dimensional body force modeling of fans in windmilling condition and its application. Aerospace 2023, 10, 724. [Google Scholar] [CrossRef]
- Liu, L. Investigation of S-Shaped Inlet Distortion Control and Its Impact on the Flow Field of the Rear Transonic Fan-Stage; Harbin Institute of Technology: Harbin, China, 2015; Available online: https://d.wanfangdata.com.cn/thesis/D751741 (accessed on 1 January 2025). (In Chinese)
- Lee, C.; Boedicker, C. Subsonic diffuser design and performance for advanced fighter aircraft. In Proceedings of the AIAA/AHS/ASEE Aircraft Design Systems and Operation Meeting, Colorado Springs, CO, USA, 14–16 October 1985. [Google Scholar] [CrossRef]
- Ma, G. Design and Aerodynamic Performance Study of an S-Shaped Inlet of the UAV; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2007; Available online: https://d.wanfangdata.com.cn/thesis/D038129 (accessed on 1 January 2025). (In Chinese)
- Berrier, B.L.; Carter, M.B.; Allan, B.G. High Reynolds Number Investigation of a Flush-Mounted, S-Duct Inlet with Large Amounts of Boundary Layer Ingestion; NASA Langley Research Center: Hampton, VA, USA, 1 September 2005. Available online: https://ntrs.nasa.gov/citations/20050229940 (accessed on 1 January 2025).
- Wang, K.; Zhou, Z.; Guo, J.; Li, M. Propulsive/aerodynamic coupled characteristics of distributed-propulsion-wing during forward flight. Acta Aeronaut. Astronaut. Sin. 2024, 45, 137–155. Available online: https://d.wanfangdata.com.cn/periodical/hkxb202402010 (accessed on 1 January 2025).
- Wang, K.; Huang, H.; Tan, H.; Lin, Z.; Tang, X.; Cheng, T. Impact of shape factors on flow dynamics and performance in boundary layer ingesting inlet. Aerosp. Sci. Technol. 2025, 157, 109829. [Google Scholar] [CrossRef]
- Owens, L.R.; Allan, B.G.; Gorton, S.A. Boundary-layer-ingesting inlet flow control. J. Aircr. 2008, 45, 1431–1440. [Google Scholar] [CrossRef]
- Deng, W.; Wang, Z.; Zhou, L.; Zhao, H. Flow losses characteristics of BLI inlet. J. Aerosp. Power 2023, 38, 698–708. Available online: https://apps.wanfangdata.com.cn/perios/article:hkdlxb202303019 (accessed on 1 January 2025).
- Chen, J. Investigation of Active Flow Control in a Boundary Layer Ingesting Offset Inlet; Harbin Institute of Technology: Harbin, China, 2009; Available online: https://d.wanfangdata.com.cn/thesis/D258611 (accessed on 1 January 2025).
- Martensson, H. Harmonic Forcing from Distortion in a Boundary Layer Ingesting Fan. Aerospace 2021, 8, 58. [Google Scholar] [CrossRef]


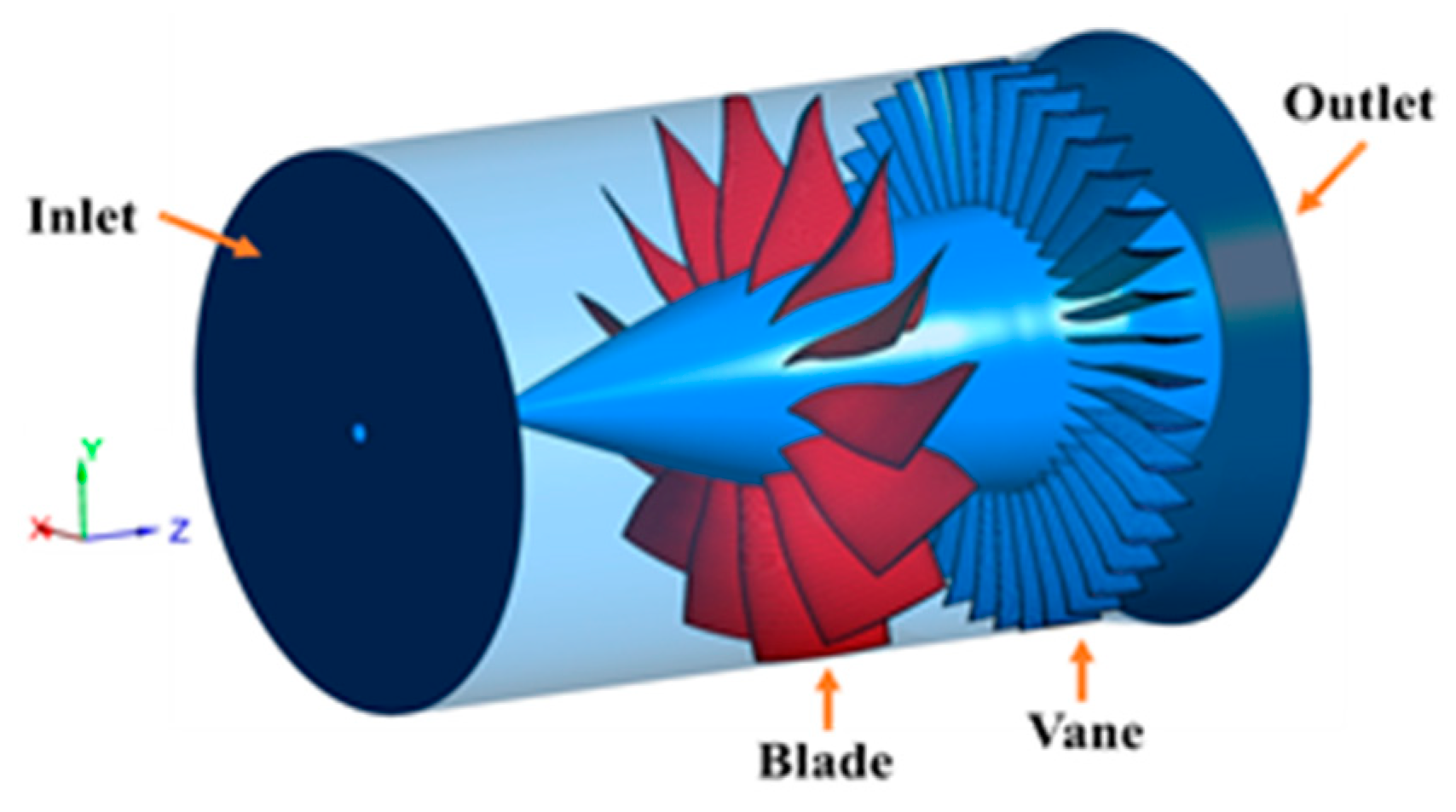







| Parameters | Value |
|---|---|
| Number of blades | 14 |
| Number of vanes | 40 |
| Rotation speed | 13,150 RPM |
| Inlet total temperature | 288.15 K |
| Inlet total pressure | 101,325 Pa |
| Total pressure ratio | 1.17 |
| Equivalent flow rate | 14.635 kg∙s−1 |
| Isentropic efficiency | 0.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, W.; Li, G.; Liu, T.; Kong, Q.; Ding, S. Numerical Analysis of the Effect of S-Shaped Duct Key Geometry Parameters on the Inlet Distortion of Distributed Ducted Fans. Aerospace 2025, 12, 316. https://doi.org/10.3390/aerospace12040316
Jia W, Li G, Liu T, Kong Q, Ding S. Numerical Analysis of the Effect of S-Shaped Duct Key Geometry Parameters on the Inlet Distortion of Distributed Ducted Fans. Aerospace. 2025; 12(4):316. https://doi.org/10.3390/aerospace12040316
Chicago/Turabian StyleJia, Wei, Guanghui Li, Tao Liu, Qingguo Kong, and Shuiting Ding. 2025. "Numerical Analysis of the Effect of S-Shaped Duct Key Geometry Parameters on the Inlet Distortion of Distributed Ducted Fans" Aerospace 12, no. 4: 316. https://doi.org/10.3390/aerospace12040316
APA StyleJia, W., Li, G., Liu, T., Kong, Q., & Ding, S. (2025). Numerical Analysis of the Effect of S-Shaped Duct Key Geometry Parameters on the Inlet Distortion of Distributed Ducted Fans. Aerospace, 12(4), 316. https://doi.org/10.3390/aerospace12040316







