Abstract
In the framework of lightweight aircraft preliminary design and optimisation, different computational approaches are formulated and assessed for the large-amplitude static aeroelastic response of very-flexible slender thin wings in subsonic incompressible flow at low speed. Starting from either a continuous or a discrete model, either numerical or semi-analytical solutions are derived and compared for several combinations of flow speed and angle of attack. Exploiting the Euler–Bernoulli beam idealisation for the wing structure and its local deformation, non-linear and quasi-linear models are presented where the elastic axis is inextensible and its global displacement is geometrically nonlinear; to this purpose, Hencky’s model is also adopted. Employing modified strip theory for the airload, reduced-order conceptual assessments and parametric evaluations are possible, and the results are shown for the Pazy wing which exhibit excellent agreement with nonlinear higher-fidelity simulations in the literature. Both closed-loop and open-loop solutions are then provided, with the latter being readily resumed from the former in the low-speed limit far away from static aeroelastic divergence. In conclusion, the novel approaches hereby explored demonstrate overall consistency while offering both theoretical insights and practical recommendations for their trust region, especially in terms of the impact and importance of the linear and nonlinear features as well as their effects.
1. Introduction
Recently, many works have been devoted to the optimal design of High-Altitude Long-Endurance (HALE) air vehicles and lightweight aircraft with very-flexible slender wings [,]. As lighter structural arrangements may favor catastrophic aeroelastic instabilities within the target operational envelope [], computationally efficient frameworks for a robust Multidisciplinary Design and Optimisation (MDO) [] become crucial at the preliminary design stage; novel approaches, methods, and tools are then highly sought in the form of reliable Reduced Order Models (ROMs) [,,], as effective multidisciplinary optimisation does require a large design space to be explored by intelligent algorithms and strategies while performing the different analyses involved in the definition of cost functions (to be minimised) and constraints (to be satisfied) []. To this respect, simplified aeroelastic models may conveniently be used on solid grounds and grant sound insights []; in particular, modified strip theory (MST) [] was already found well suited for fast aero-structural analyses and comprehensive parametric assessments [,] involving the fluid–structure interaction (FSI) [] from small perturbations of subsonic flow [], within a monolithic approach [].
In the aeronautical engineering practice [,], many aeroelastic solvers couple a beam- or plate-based finite element method (FEM) [] to model the aircraft structure and its deformation with a doublet lattice method (DLM) [,] or with a vortex lattice method (VLM) [,] to model the aircraft aerodynamics and its airload; however, such methods are inherently linear and hence also limited to small structural displacements and flow perturbations. Thus, as a very convenient alternative to adopting complex higher-order models and direct computational fluid dynamics (CFD) [], several recent studies focused on variable-fidelity investigations of very-flexible structures undergoing large displacements [,,,] and considerable efforts are still ongoing to assess all nonlinear effects (e.g., geometric, structural, aerodynamic) [,,] and then to correct legacy tools for at least the most relevant ones [,], within a staggered or monolithic approach []. The corrected lower-fidelity tools may then serve as ROMs within their (“extended”) trust region, especially for sensitivities estimation [,]; a metamodel-based strategy may instead be adopted to tune their output with a few full-order results outside such region [,], in order to minimise the overall complexity while retaining accuracy within a sound synthesis [].
As flight speed and angle of attack increase during flight (e.g., during aircraft takeoff), the torsional displacement of aircraft wings tends to remain rather moderate in real cases [,,] as a result of key integrity, controllability, and performance constraints in the aero-structural design (e.g., aeroelastic divergence and flutter, control surface effectiveness, aerodynamic efficiency) [,,]; nevertheless, the bending displacement of the inextensible wing may become rather large (although not extreme yet) and follows a nonlinear kinematics which preserves the total wing area (as crucial for calculating the correct airload and all the related derivatives []). Since the large amplitude of the static aeroelastic response may significantly affect both the aerodynamic performance and the aeroelastic stability boundary of the aircraft [], this work formulates and assesses different computational approaches for simulating the static aeroelastic behaviour of a thin very-flexible slender wing in a subsonic incompressible flow at low speed. Starting from either a continuous or a discrete model, all formulations result in a lower-order yet reliable computational framework for very fast and robust aeroelastic analyses where either numerical or semi-analytical solutions are derived; in such context, Hencky’s bar-chain discrete model (HBCM) [,,] is here monolithically coupled with MST and extended to static aeroelastic simulations for aeronautical applications. Non-linear and quasi-linear models are hence presented where Euler–Bernoulli’s beam idealisation is adopted for the wing structure and its local deformation (exploiting Hook’s law and de Saint-Venant’s theory [,]), while the elastic axis is inextensible [] and its global displacement is geometrically nonlinear; modified strip theory is employed for the steady airload [], allowing fast calculations and conceptual assessments. Both closed-loop and open-loop solutions are provided, with the latter being automatically resumed from the former in the low-speed limit far away from aeroelastic divergence.
While favoring fast sensitivities and uncertainties evaluations (which may further be accelerated by machine learning []), the derived aeroelastic computational framework also allows reducing the variables of the aircraft wing MDO problem rather significantly on solid physical and mathematical grounds. A parametric validation exercise is then successfully performed with reduced-order computations for several combinations of flow speed and angle of attack and the results (with and without gravity) are shown for the Pazy wing [], which exhibit excellent agreement with nonlinear higher-fidelity simulations in the literature coupling finite element models with steady vortex lattice models. In summary, the novel approaches hereby explored demonstrate overall consistency while offering valuable insights and practical recommendations for their own trust region (where the reduced-order models behave like the full-order ones), especially in terms of the impact and importance of the linear and nonlinear features as well as their effects. As fundamental side products, the quasi-linear semi-analytical model does not require any laborious pre/post-processing or complicated implementation [] and may be used to verify the higher-fidelity tools as full-order models on primal benchmark cases in the first place; a tuned semi-analytical model may finally combine the inexpensive robustness of a reduced-order model with the expensive accuracy of a full-order model both inside and outside the trust region, within a convenient hybrid approach [,].
2. Aeroelastic Problem Formulation
For a thin wing with slender structure, the Euler–Bernoulli beam model is suitably adopted to calculate both torsion (positive clockwise) and bending (positive upwards) displacements of its elastic axis (EA, where all applied loads are reacted) in the global reference frame [,]; with the flexural axis being axially unloaded and inextensible, the curvilinear coordinate runs from wing root to wing tip. In particular, the EA is drawn by the locus of the sectional shear centres [] and features Young’s and shear moduli of its elastic material as well as the second area moment of inertia and torsion factor of its cross-section. The spanwise axis is aligned with the undeformed EA (where ) and points towards the wing tip, whereas the chordwise axis is orthogonal to the EA and points towards the wing’s trailing edge, with for convenience; the vertical axis points upwards and the wing mass is distributed on the inertial axis , which is drawn by the locus of the sectional centres of gravity (CG, where loads due to the gravity acceleration are applied) []. Comprising both gravity and (follower) aerodynamic loads, the total torsion and bending sectional moments act on the EA and deform it according to the following coupled Ordinary Differential Equations (ODEs) [,]:
complemented by both natural and geometric boundary conditions for a clamped beam:
where the apostrophe ’ denotes a spatial derivation along the elastic axis, whereas denotes the local rate of the bending deformation and the corresponding bending angle in the global reference system [,,].
While the constitutive equations of the flexible beam are still linear in the absence of very large perturbations and excessive deformations, the kinematics of its inextensible flexural displacement in the global reference frame is nonlinear, namely as follows []:
which link the global coordinates with the curvilinear coordinate. In fact, linear theory may still calculate the correct local bending deformation but at an incorrect point in space for the global bending displacement []; therefore, semi-analytical solutions are still very useful and a similar rationale is behind the latest generalisations and numerical implementations of Hencky’s bar-chain (discrete) model too [,,], that will be coupled with MST and so extended to static aeroelastic simulations for aeronautical research and development later in this work.
The steady subsonic airflow is reasonably considered as attached and modelled as both inviscid and irrotational []; different potential-flow theories are then adopted to calculate the aerodynamic load for an incompressible fluid at low speed. According to thin aerofoil theory for incompressible flow [], both the lift and moment of each chordwise section act at its aerodynamic centre (AC, where the steady airload is applied), whereas the fluid–structure interaction [,] is enforced at its control point (CP, where the impermeability boundary condition is imposed) in all cases; in particular, the AC position and CP position fall at the first and last quarters of the wing section chord , respectively. Each wing section has its own camber and is characterised by its own zero-lift angle of attack , aerodynamic moment coefficient , and lift derivative ; with and as the reference air speed and density, the steady airloads are then directly proportional to the reference dynamic pressure and total angle of attack as well as the wing area , namely as follows [,]:
where is the angle of attack of the reference flow, whereas the wing aspect ratio is a key parameter in the calculation of three-dimensional downwash effects induced by the wing tips’ vortices. Adopting modified strip theory, the latter are substantially taken into account by the load-scaling function while the airflow around each wing section is formally treated as independent and two-dimensional (in the vertical plane); the steady aerodynamic lift and pitching moment at the elastic axis may then be generally written as follows []:
where the load-scaling function may suitably be approximated with Prandtl–Glauert’s expansion [] (see Appendix A) by best-fitting any reliable source of the lift distribution along the wing span (e.g., lifting-line theory, VLM, DLM, CFD) []. Since the aerodynamic influence and related downwash fade quite rapidly (with the inverse of the mutual distance []) and local wing deformations are small, the load-scaling function remains suitable for deformed shapes away from impractical wing displacements. For tuned strip theory (TST), the load-scaling function degenerates into a load-scaling factor (i.e., a uniform downwash distribution is assumed along the wing span) and standard strip theory (SST) is consistently obtained in the conservative bi-dimensional limit of a wing with infinite aspect ratio [,]. The aeroelastic feedback contribution of the wing torsion to the total angle of attack provides with a closed-loop response; when such term is negligible (e.g., at very low flow speed []), an open-loop response is obtained where torsion and bending displacements are fully independent.
Considering either a continuous or a discrete model of the flexible slender thin wing, different formulations of a nonlinear reduced-order computational framework for its static aeroelastic response in subsonic incompressible flow at low speed will hereafter be presented and solved by either numerical or semi-analytical means. In particular, the non-linear numerical approach is quite general but particularly effective for relatively simple wings without significant discontinuities in their aero-structural properties (i.e., less prone to suffering potential issues with the relative computational grid []), while the quasi-linear semi-analytical approach offers a straightforward physical and mathematical interpretation as well as theoretical validation of the numerical results for the case of an aeroelastic response with small-to-moderate displacements [].
3. Continuous Non-Linear and Quasi-Linear Models
In aeronautical applications, the wing deformation can be expressed as a continuous (monotonic) function along the span and the coupled governing equations for the static torsion and bending displacements can then be differentiated and rewritten with the following [,]:
where the “closely spaced rigid diaphragm” hypothesis is adopted [] and higher-order terms have been neglected [] since excessive displacements are out of scope (i.e., with ); any discontinuity in the applied load can be introduced via Dirac or Heaviside functions [,]. In the case of small to moderate displacement, superposition of effects applies [] and the torsion displacement becomes independent from the bending one, whereas the latter still depends on the former [,]; a quasi-linear model is then obtained by imposing the elastic axis as inextensible, namely as follows []:
with the nonlinear geometrical correction along the wing span. While the direction of the gravity acceleration stays vertical [], the steady aerodynamic load (typically far larger than the section weight) is of follower nature [] and remains normal to the elastic axis but with a progressively reduced angle of attack for the reference flow [,]; however, the present nonlinear models focus on practical applications where extreme deformations do not occur and such incremental nonlinear effects do remain rather limited, with the highest airload occurring where the wing is clamped and its deformation also remains rather limited []. Unfortunately, no exact analytical solution of the ODEs is available for arbitrary aero-structural properties along the wing span; yet, computational techniques, methods, and tools are quite common and mature nowadays and the first approach thus consists of solving the boundary value problem with a suitable numerical integration method (i.e., the ODEs do get discretised but the underlying physical model does remain continuous), using the linearised semi-analytical solution hereafter derived as best initial guess. In particular, the numerical simulations exploit an available finite difference code based on the four-stage Lobatto IIIa formula which is implemented as an implicit Runge–Kutta integration scheme where the collocation polynomial grants a C1-continuous solution that is fifth-order accurate within the entire integration interval (i.e., problem boundaries) []. With the numerical grid points dividing the latter into subintervals, the overall computational arrangement results in a global augmented system of algebraic equations where error control and mesh adaptation are driven by the residual through the tolerance criteria to be satisfied for acceptable accuracy and convergence (with a 10−6 absolute and a 10−3 relative tolerance imposed in this study) []. While the stability of the numerical scheme and its adaptive grid-refinement algorithm is demonstrated in the literature already, the fast and well-behaved convergence behaviour of the nonlinear aeroelastic simulations is enforced by the underlying physics before static aeroelastic divergence occurs: an increasing wing displacement lowers the applied load which then lowers the displacement in turn [], within a stable feedback loop that grants rigorous convergence in a few iterations from a suitable initial guess (especially when the linear analytical solution is adopted, as it demonstrates being reliable in the first place []). Besides, note that this work focuses on the strategic approaches rather than their implementation details, as several numerical routines and tools are nowadays available for scientific computing and standard engineering practice (e.g., Matlab https://www.mathworks.com/, Scilab https://www.scilab.org/, Python https://www.python.org/ and all the related libraries in the relative programming languages) [] and may then be adapted to the most convenient computational environment for the desired application (especially when significantly complex [,]).
3.1. Semi-Analytical Solution for a Uniform Beam-like Wing Structure
In the case of homogeneous aero-structural properties and special airload distributions along the wing span, very useful analytical solutions of the governing aeroelastic ODEs are possible [,] and hereafter obtained with incremental aero-structural contributions to (and hierarchical approximations of) the aeroelastic response of the flexible wing. Such an alternative semi-analytical approach allows a rigorous theoretical understanding and a fast estimation of core physical features and specific effects, also serving as optimal initial guess for more general models and advanced numerical solutions [].
In particular, the static aeroelastic equilibrium equations simplify as the following []:
complemented by both natural and geometric boundary conditions for a clamped beam:
where a lumped mass is also considered on the elastic axis at at the wing tip, for completeness [,] (see Appendix B); still, inertial coupling vanishes when inertial and elastic axes coincide (i.e., with and ). With no loss of generality for the fundamental purpose of this study, the uniform slender thin wing may be considered as rectangular and flat (i.e., with , , and directly from thin aerofoil theory []).
Accounting for the three-dimensional downwash effect from the vortices at the wing tips, standard strip theory is corrected for the effective sectional airload with either the scaling function of modified strip theory or the scaling factor of tuned strip theory [,], which are suitably expressed in the following related analytical forms:
where the two approximation coefficients and are found by fitting the spanwise normalised lift distribution obtained from any reliable aerodynamic source [], whereas the second formula represents an integral constraint which relates the MST scaling function and TST scaling factor; in this semi-analytical context, Weissinger’s line method (WLM) [] is successfully exploited as a very powerful reduced-order aerodynamic model based on lifting-line theory (LLT; see Appendix A) [].
3.1.1. Open-Loop Aero-Structural Response
Under gravity acceleration in the absence of aerodynamic loads (e.g., with or ), the wing’s torsion and bending uncoupled displacements due to the gravity loads from the distributed and concentrated inertia read as follows:
where the two contributions can separately be integrated and eventually superposed.
When aeroelastic feedback effects remain marginal at relatively low speed far from aeroelastic divergence (i.e., with for ) [], the wing’s torsion and bending uncoupled displacements due to steady TST aerodynamic loads in the absence of gravity are given by the following:
whereas the counterparts and due to steady MST aerodynamics are as follows:
which feature the same polynomial terms as the response calculated with TST aerodynamics yet tuned by the coefficients , , and , whereas the additional exponential terms ensure the natural boundary conditions are enforced at the unloaded wing tip but are rather small (since in standard cases) in fact.
The total static aero-structural response to gravity and steady aerodynamic loads for the wing’s torsion and bending may hence be obtained as follows:
according to TST and MST aerodynamics, respectively. Note that a “quasi-aeroelastic” simulation may be defined where the bending aero-structural response still accounts for the wing twist given by the torsional aero-structural response (see Appendix C); yet, this “intermediate” model is not recommended, because of the incoherent formulations of the sectional lift (without feedback) and pitching moment (with feedback). As explicitly evident from all previous analytical expressions, the magnitude of the open-loop response is inversely proportional to the wing stiffness whereas linear in the gravity acceleration, airflow dynamic pressure, wing chord, and aerodynamic coefficients, with the latter being suitably assumed as linear functions of the aerofoil camber [], airflow angle of attack, and downwash angle due to the vortices at the wing tips.
3.1.2. Closed-Loop Aeroelastic Response
As flight speed increases aeroelastic feedback effects also increase and the mathematical nature of the torsion equation changes until aeroelastic divergence occurs at the dynamic pressure [], before which the exact static aeroelastic response to gravity and steady TST aerodynamic loads for the wing’s torsion is given by the following:
from the singularity of which aeroelastic divergence conditions are explicitly obtained as follows:
where structural reaction and steady airload do not find a stable balance (i.e., the former generates a structural response inducing additional aerodynamic load in turn []); it is apparent that either softening the torsional stiffness or increasing the aerodynamic efficiency of the wing decreases its divergence dynamic pressure and speed when the elastic axis is beyond the aerodynamic axis. This result for the static stability boundary is confirmed by Galerkin’s energy-based approach [] when the change in strain energy from the static aeroelastic response balances the aerodynamic work that induces the structural deformation (within the simplest form of the principle of virtual work [,,]), where the divergence speed can be estimated via the generalised Rayleigh quotient as follows [,]:
with the exact “divergence mode shape” adopted for the wing twist; indeed, the latter becomes statically unstable as soon as the work performed by the aerodynamic load exceeds the induced change in strain energy. In fact, note that Galerkin’s approach allows using any approximate yet suitable “divergence mode shape” as long as it satisfies all the geometric boundary conditions (whereas satisfying all boundary conditions may not be a plus []); for instance, adopting the wing twist aero-structural response gives the following [,]:
in remarkable agreement with the exact solution. Before crossing the instability boundary for (i.e., when exists), the exact static aeroelastic response to gravity and steady TST aerodynamic loads for the wing’s bending is then found as follows:
where the aeroelastic increment inherits the divergence singularity from the torsional response (where no aeroelastic increment could separately be calculated, as the mathematical nature of the torsion equation changes without twist feedback and linear superposition cannot hold between analytical solutions of different equations []).
The limit behaviours of the exact aeroelastic response with TST aerodynamics hereafter demonstrates the overall consistency of the derived solutions, while offering key theoretical insights and reliability boundaries. In particular, in the absence of flow speed, the static structural response to gravity loads is then automatically recovered as follows:
whereas at low speed far from aeroelastic divergence conditions the static aero-structural response to gravity and steady TST aerodynamic loads is automatically resumed as follows:
and the term in the closed-loop solution appears to act as an aeroelastic amplification factor for the open-loop solution (automatically recovered with directly). In fact, by expanding the exact solutions with a Taylor series up to the same order as that of the respective differential equation originating them, the approximate general solution given by Galerkin’s method for the static aeroelastic response to gravity and steady TST aerodynamic loads [,] specialises as follows:
where the “aeroelastic amplification factor” [,] scales the relevant part of the aero-structural (open-loop) response to mimic the overall (closed-loop) aeroelastic feedback effect, based on the physical nature of the mathematical terms in the respective differential equation; considering additional Taylor terms, the quasi-aeroelastic increment appears (see Appendix C) and gets replaced by directly [,]. Due to cancellation of higher-order terms [], note that Galerkin’s approximation above is more accurate for a flat wing with coinciding inertial and elastic axes (e.g., the Pazy wing []); in general, a first enhancement of the analytical solution with TST aerodynamics may be enforced by adding the difference between the open-loop solutions based on steady MST and TST aerodynamics, exploiting linear superposition although slightly inconsistently.
An exact explicit expression for the closed-loop static aeroelastic response to gravity and aerodynamic loads is not available when MST aerodynamics is adopted; however, Galerkin’s energy-based method may still provide with a reliable and coherent analytical approximation away from aeroelastic divergence [,], namely as follows:
where the static divergence speed is estimated via the generalised Rayleigh quotient [] with the aero-structural twist response adopted as an approximate yet suitable “divergence mode shape” (inherently satisfying all boundary conditions []). The aeroelastic amplification factor is then obtained as follows [,]:
where an accurate aero-structural open-loop response is then key to obtain an accurate aeroelastic closed-loop response in the very first place (see Appendix C too), before any geometrically nonlinear effect is considered []. While most analytical formulae above pertain to the special case of a straight rectangular wing with constant structural properties, Galerkin’s semi-analytical method may still be exploited within the general framework of a modal approach (where just a few degrees of freedom may be required) for the case of a generic wing [,]. According to all analytical expressions above, the magnitude of the closed-loop response is still inversely proportional to the wing stiffness whereas linear in the gravity acceleration, airflow dynamic pressure, wing chord, and aerodynamic coefficients (which are suitably assumed as linear functions of the aerofoil camber [], airflow angle of attack, and downwash angle due to the vortices at the wing tips); yet, here the aeroelastic amplification factor acts as a multiplier which is a nonlinear function of both airflow dynamic pressure and aeroelastic divergence dynamic pressure, the latter being directly proportional to the torsional stiffness and inversely proportional to the chord, squared semispan, elastic axis position, and lift coefficient derivative of the wing.
4. Discrete Non-Linear Model
In general cases where the beam deformation is very large and cannot be expressed as a continuous (monotonic) function along the elastic axis due to an inflexion point or a discontinuity, multi-body formulations have recently been proposed [,] where the beam is physically divided in discrete rigid segments connected by springs with stiffness that mimic the structural flexibility with geometrically nonlinear kinematics; in the present case of linear springs [], de Saint-Venant’s theory and Euler–Bernoulli’s elastic model still hold for the local deformation of the elastic axis [,] and all uniform rigid elements may conveniently (yet not mandatorily) own the same small length , namely as follows []:
with being the bending rotation of the rigid-body segment , which owns constant structural properties and total external loads (applied at its midpoint [,]) given by the following:
where and represent the horizontal and vertical reactions of the internal loads insisting on the outboard edge of the rigid-body element, where the spring of the subsequent element is located []. In this respect, Hencky’s bar-chain model [] may be considered as the simplest implementation of a multi-body formulation which was already generalised for arbitrary geometrically nonlinear displacements [,,,] and is hereafter monolithically coupled with MST [] and extended to static aeroelastic simulations for aeronautical research and applications, eventually resulting in a nonlinear aeroelastic model with an algebraic semi-analytical solution where the wing is inherently inextensible; for small displacements of the flexible wing, the derived model can still be linearised and the superposition of effects applied as appropriate []. All aero-structural wing properties along the span can be totally arbitrary and any discontinuity (e.g., the weight of a lumped mass ; see Appendix B) may locally be introduced between two adjacent rigid-body elements, which are characterised by specific structural properties (which move and rotate with the latter) and external applied loads of either follower (e.g., aerodynamics) or non-follower (e.g., gravity) nature. In particular, the equilibrium equations for the torsion and bending rotation of each rigid body and the geometrically nonlinear kinematics of its mid-point may explicitly be written as follows:
where the “closely spaced rigid diaphragm” model still holds between all adjacent rigid segments [] and the torsion displacement is still independent from the bending one if a linearised formulation is considered [], whereas the bending displacement still does depend on the torsion one [,]. The continuous differential problem has then been converted into a system of nonlinear algebraic equations to be solved numerically and the linearised semi-analytical solution previously derived is used as best initial guess; in particular, the numerical nonlinear simulations exploit an available implementation of the interior-reflective Newton’s method [] with a trust-region algorithm [], where a quadratic Taylor’s expansion of the solution is adopted that involves gradient vector and Hessian matrix approximations []. Leveraging on Cholesky factorisation and LU decomposition [], each iteration involves the approximate solution of a large linear system using the method of preconditioned conjugate gradients [], where global (via the steepest descent direction or negative curvature direction) and local (via the Newton step, when it exists) convergence are achieved though error control and satisfaction of tolerance criteria on the residual (still with a 10−6 absolute and a 10−3 relative tolerance imposed) []. Again, the stability of the numerical scheme is already demonstrated in the literature, while the fast and well-behaved convergence behaviour of the nonlinear aeroelastic simulations is enforced by the underlying physics before static aeroelastic divergence occurs []; indeed, as numerical comparisons with nonlinear higher-fidelity results will also show hereafter for practical aeronautical research where excessive deformations are out of scope, incremental nonlinear effects do remain rather limited since mostly located towards the wing tip (where the applied load decays rapidly enough, with marginal contribution to the static aeroelastic response []). While this discrete nonlinear numerical approach based on Hencky’s bar-chain model is very general and apt for almost any application (e.g., aircraft with truss-braced wings [], wings with distributed propulsion [], frames buckling [,,], lateral–torsional buckling, and robotic automation []), also in the case of very large deflections, it tends to require relatively many degrees of freedom even for relatively simple configurations (which may not be an issue for static simulations, but may not be ideal or even practical for complex dynamic simulations), requiring both a physical and a mathematical convergence for the number of rigid beam elements and numerical solver iterations, respectively, as the governing system of ODEs is transformed into an algebraic system [].
5. Results and Discussion
The low-speed large-amplitude static aeroelastic response of the Pazy wing [,] is now computed and compared with high-fidelity results from test cases found in the literature at several speeds and angles of attack in incompressible subsonic flow [,,,]; an equivalent uniform wing is considered for the quasi-linear semi-analytical solutions and all aero-structural data are given in Table 1, with the elastic axis laying between 44% and 45% of the chord (depending on the specific test case). The wing is straight and rectangular, with an aspect ratio = 11; in all numerical case studies [,,,], it is considered as flat (even if the actual wing features a symmetric NACA0018 aerofoil). Despite the relatively large aspect ratio, the overall wing dimensions are small enough to fit a low-power subsonic wind tunnel; still, its rather soft structure (an aluminum 7075 spar and 3D-printed ribs [,]) allows for very large bending displacements even at relatively low airspeed.

Table 1.
Equivalent aero-structural properties of the Pazy wing for the semi-analytical solutions.
Figure 1 depicts the actual distributions of wing structural properties [], resulting in = 4.22 Hz and = 41.6 Hz as the frequencies of the first bending and torsion natural vibration modes calculated with finite element models [,]. Along with SST and TST, Figure 1 also depicts the airload scaling function for MST as obtained from best-fitting the steady lift distribution calculated by Wessinger’s line method (see Appendix A), which shows excellent agreement with the normalised lift distribution from the subsonic panel method implemented in the aeroelastic code ZAERO (https://www.zonatech.com/zaero.html) [,]; note that the approximation used for the tip-loss function in the UM/NAST code was instead obtained from matching the final aeroelastic results directly rather than the distribution of the steady airload [], which explains why it agrees with the MST airload scaling function towards the outboard wing only. In particular, the MST airload scaling function adopted for the numerical implementation of the derived nonlinear and quasi-linear models is written as a Glauert’s expansion (see Appendix A), where four odd sinusoidal terms were found sufficient to achieve a smooth convergence on thirty wing sections along the semispan. For the sake of clarity and completeness, it is worth stressing that the tip-loss function in the UM/NAST code aims at including three-dimensional (induced downwash) effects by tuning Peters’ two-dimensional aerodynamic model for a morphing aerofoil [], which can account for chord-wise wing deformations and be coupled with plate-based structural models [].
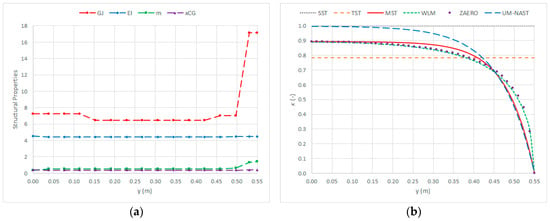
Figure 1.
Pazy wing characterisation: beam structural properties (a); MST scaling function (b).
Both open- and closed-loop responses of the Pazy wing as calculated by all models derived in this study (see the overview in Table 2) will hereafter be presented for several combinations of different physical perturbations: gravity acceleration, subsonic airspeed, angle of attack, three-dimensional downwash, and aeroelastic feedback; for the numerical results, an equivalent uniform wing structure will be adopted in the quasi-linear model.

Table 2.
Overview and characterisation of the derived and investigated aeroelastic approaches.
5.1. Open-Loop Aero-Structural Response
Figure 2 depicts the uniform structural properties of the equivalent wing resulting in the approximate frequencies reported in Table 1 for the first bending and torsion natural vibration modes as calculated semi-analytically [], showing very good agreement with the ones characterising the actual wing structural properties []; yet, no exact agreement may be expected unless enforced via tuning (which is intentionally disregarded, in order to quantify and highlight pros and cons of the derived semi-analytical solutions).
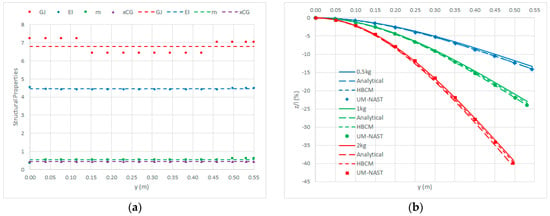
Figure 2.
Equivalent Pazy wing: average structural properties (a); structural weight response (b).
Considering all approaches formulated in this work, Figure 2 also depicts the static bending displacement of the open-loop wing response calculated when a lumped mass from 0.5 kg to 2 kg is placed on the flexural axis at the wing tip in still air: excellent agreement is again found with literature high-fidelity results obtained from nonlinear simulations employing a geometrically nonlinear beam formulation (recently replaced by a geometrically exact beam theory [,]), confirming that the uniform structural properties of the equivalent wing are representative of the actual ones also in terms of the resulting static structural behaviour. For the sake of direct cross-validation, both numerical and semi-analytical results feature linear load and nonlinear kinematics for all present models (which translates into considering their linear solutions until the beam length is reached); as per previous studies [], about 200 rigid segments were sufficient for convergence of the HBCM. Despite the bending displacement reaching 40% of the wing semispan (which shrinks more than 10%, since the elastic axis is inextensible), it appears from the remarkable and consistent agreement between the nonlinear literature results and the present quasi-linear results that the geometrically nonlinear effect on the gravity load is indeed significantly lower than on the kinematics of the elastic axis (see Appendix B).
Figure 3 depicts the static torsion and bending displacements of the open-loop response when gravity acceleration is neglected (e.g., when the Pazy wing was mounted vertically rather that horizontally in the wind tunnel []) but the steady airflow ranges from 30 m/s to 55 m/s with an angle of attack from 5 deg to 7 deg: for all approaches formulated in this work, remarkable agreement is still found with literature high-fidelity results (with bending displacement above 40% of the wing semispan) from linear static simulations in the aeroelastic code ZAERO [,], where the steady aerodynamic load of the undeformed wing is obtained from a panel method and then applied (via spline interpolation []) to a finite element structural model without inextensibility constraint; the aero-structural properties of the equivalent wing are then confirmed representative of their actual counterparts in terms of resulting static aero-structural (not yet aeroelastic) behaviour. From the remarkable and consistent agreement between the linear numerical results [,] and all nonlinear numerical results as well as quasi-linear semi-analytical results, it appears that the geometrically nonlinear effect on the steady airload of the undeformed wing is also significantly lower than on the kinematics of the elastic axis.
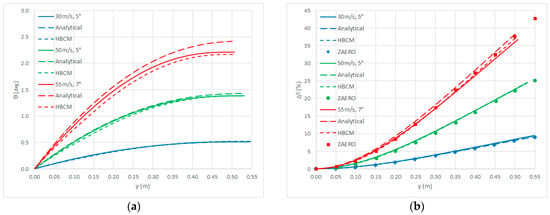
Figure 3.
Open-loop response without gravity: torsion (a); bending (b).
Considering SST and TST too, Figure 4 depicts the static torsion and bending displacements of the open-loop response when gravity acceleration is still neglected but the steady airflow ranges from 30 m/s to 50 m/s with a 5 deg angle of attack: extending the conclusions of previous studies [,,], considering linear three-dimensional downwash effects on the steady airload via MST appears even more crucial for obtaining any reliable static aero-structural behaviour of the wing in the presence of large flexural displacements.
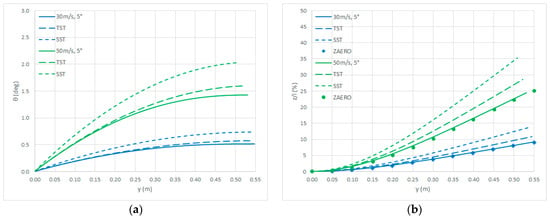
Figure 4.
Open-loop analytical response without gravity: torsion (a); bending (b).
5.2. Closed-Loop Aeroelastic Response
Even at low speed, aeroelastic effects may still become significant for a very-flexible wing with low divergence speed [,], with the magnitude of the aeroelastic amplification factor serving as a predictor of the flexibility influence [,,]; in particular, when the elastic axis is at 44.1% of the wing chord [], then the static divergence speed is calculated as 86.9 m/s, 98.2 m/s, and 105.1 m/s by employing SST, TST, and MST, respectively, whereas when the elastic axis is at 44.75% of the wing chord [], then the static divergence speed is calculated as 85.4 m/s, 96.6 m/s, and 103.4 m/s by employing SST, TST, and MST, respectively. Figure 5 depicts the static torsion and bending displacements of the closed-loop response when gravity acceleration is neglected but the steady airflow ranges from 30 m/s to 55 m/s with an angle of attack from 5 deg to 7 deg: for and among all the nonlinear and quasi-linear approaches formulated in this work, excellent agreement is again found with literature high-fidelity results (with bending displacement just below 50% of the wing semispan) from nonlinear static simulations coupling the aerodynamic panel method and structural finite element method implemented in the linear aeroelastic code ZAERO within the nonlinear framework of the modal rotation method (MRM, where geometrical nonlinearities affect both loads and kinematics) [,]; also, the aeroelastic amplification factor is confirmed as effective in quantifying steady aerodynamic feedback effects for the static aeroelastic behaviour of a flexible wing undergoing moderate torsional and large flexural displacements [,,], at low speed away enough from static divergence conditions [,]. From the remarkable and consistent agreement between all nonlinear numerical results and the quasi-linear semi-analytical results, it appears that the geometrically nonlinear effect on the steady airload of the flexible wing is also significantly lower than on the kinematics of the elastic axis, but in the case of very large bending displacements (still with limited impact, though).
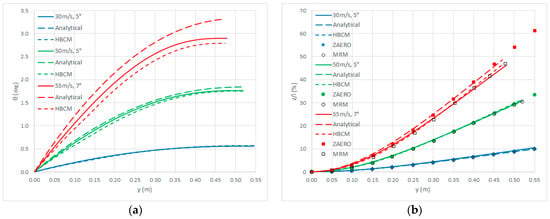
Figure 5.
Closed-loop response without gravity: torsion (a); bending (b).
Figure 6 depicts the static torsion and bending displacements of the closed-loop response when gravity acceleration is considered and the steady airflow ranges from 30 m/s to 50 m/s with a 7 deg angle of attack: the impact of wing weight decreasing with increasing airspeed, all nonlinear and quasi-linear results still agree remarkably well with literature high-fidelity results (with bending displacements just below 40% of the wing semispan) from nonlinear static simulations coupling an aerodynamic vortex lattice method with a structural finite element method implemented in the linear aeroelastic code NASTRAN (https://hexagon.com/products/product-groups/computer-aided-engineering-software/msc-nastran) within the nonlinear framework by DLR (where geometrical nonlinearities affect both loads and displacements) [], confirming all key linear and nonlinear aeroelastic effects are suitably addressed by the presented nonlinear and quasi-linear models for the static aeroelastic behaviour of a flexible wing undergoing moderate torsional and large flexural displacements at low speed away from static divergence conditions.
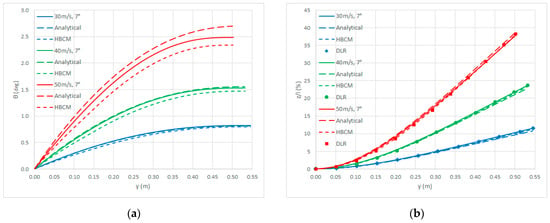
Figure 6.
Closed-loop response with gravity and different airspeed: torsion (a); bending (b).
Figure 7 depicts the static torsion and bending displacements of the closed-loop response when gravity acceleration is considered and the angle of attack ranges from 2 deg to 8 deg with 50 m/s steady airflow: an excellent agreement of all presented nonlinear and quasi-linear results is also consistently confirmed with the numerical results from nonlinear static simulations coupling an unsteady aerodynamic vortex lattice method and a structural finite element method implemented in the nonlinear aeroelastic code SHARPy (where geometrical nonlinearities affect both loads and displacements) []; in particular, note all the presented numerical solutions lay between DLR’s and SHARPy’s results, whereas the semi-analytical solution is close to the latter at a low angle of attack (due to the aerodynamic load from WLM being slightly lower than that from VLM) and to the former at a high angle of attack (due to larger impact of the geometric nonlinearities).
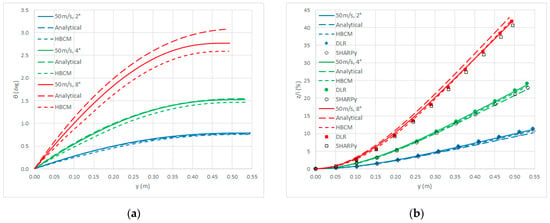
Figure 7.
Closed-loop response with gravity and different angle of attack: torsion (a); bending (b).
Figure 8 then depicts the geometric correction due to the nonlinear kinematics when gravity acceleration is considered and steady airflow ranges from 30 m/s to 55 m/s while the angle of attack ranges from 2 deg to 8 deg: with an overall trend mimicking the bending displacement, the impact of such nonlinear correction is negligible towards the wing root and grows towards the wing tip (where its magnitude exceeds 10% of the semispan).
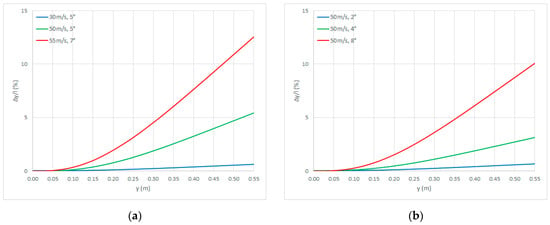
Figure 8.
Closed-loop response geometric correction: without gravity (a); with gravity (b).
Considering SST and TST too, Figure 9 depicts the static torsion and bending displacements of the closed-loop analytical response when gravity acceleration is neglected but the steady airflow ranges from 30 m/s to 50 m/s with a 5 deg angle of attack: extending the conclusions of previous studies [,,], the aeroelastic amplification factor [,,,] (where the divergence dynamic pressure is recalled inversely proportional to the effective lift coefficient derivative, which gets sensibly reduced by the induced downwash) makes even more apparent that considering linear three-dimensional downwash effects on the steady airload via MST appears even more crucial for obtaining any reliable static aeroelastic behaviour of the wing in the presence of large flexural displacements; yet, note Galerkin’s approach with the aeroelastic amplification factor may be slightly unconservative, as speculatively shown for the SST results (which may then be used for tuning purposes).
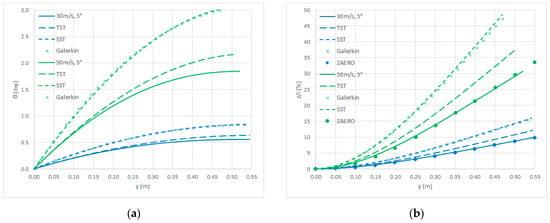
Figure 9.
Closed-loop analytical response without gravity: torsion (a); bending (b).
From the respective complementary perspectives, with both benefits and limitations within the methodological scope of this proof-of-concept work, the different approaches hereby presented feature diverse physical and mathematical characteristics and demonstrated as valid alternatives to the standard FEM-based modelling techniques which may typically be found in the literature. For the static aeroelastic response of the Pazy wing, (high) comparable accuracy and (low) computational costs are consistently found among all methods, which converged almost instantaneously to their solution on standard laptops; further investigations on their computational performance may then be explored in future works, considering more complex wing configurations which are out of scope here. In fact, the Pazy wing benchmark [] was intentionally selected in order to showcase both the conceptual differences and the validated robustness among all presented approaches, through a rather comprehensive parametric assessment in terms of gravity acceleration, subsonic flow speed, angle of attack, three-dimensional downwash, aeroelastic feedback, and their combinations at insignificant computational costs, highlighting the results’ accuracy from different physical and mathematical perspectives. In this respect, it is worth stressing the quasi-linear semi-analytical solutions demonstrated remarkable reliability even for rather large flexural displacement, while inherently offering costless trends and sensitivities as well as serving as solid mathematical references to estimate the order of magnitude of both physical assumptions and modelling or approximation errors (including those resulting from either physical or numerical discretisation) in the nonlinear simulations, the acceptability of which is driven by the application in engineering practice. Still, no exact agreement could be expected between numerical and semi-analytical solutions even for small flexural displacement, due to the (excellent yet not perfect) approximation of the Pazy wing’s aero-structural properties in the latter case.
6. Conclusions
In the context of preliminary multidisciplinary design for lightweight aircraft, nonlinear numerical and quasi-linear semi-analytical solutions were derived and presented for the static aeroelastic response of very-flexible wings undergoing moderate torsional and large flexural displacements at relatively low speed, far from static divergence conditions. All proposed approaches feature intuitive formulation and straightforward implementation, leveraging on first principles and available routines, respectively. Adopting modified strip theory for the steady airload, both conceptual assessments and effortless computational simulations were demonstrated as readily possible, even when the legacy Hencky’s bar-chain discrete model is extended to aeronautical applications. The open-loop solution is readily resumed from the closed-loop one in the low-speed limit, demonstrating overall consistency among all models as well as offering explicit validity boundaries and reliability insights, with a rigorous derivation of the aeroelastic amplification factor. All analytical formulae were obtained for the special case of a straight rectangular wing with constant structural properties, aiming at a straightforward physical and mathematical interpretation as well as theoretical validation of the numerical models in the presence of a small-to-moderate aeroelastic response; for the case of a generic wing undergoing moderate-to-large displacements, Galerkin’s semi-analytical method may still be exploited within the general framework of a modal approach with quasi-linear geometrical correction. The numerical assessments were successfully performed at marginal computation cost for the aero-structural and aeroelastic responses of the Pazy wing, with excellent and consistent agreement between the results of the presented nonlinear and quasi-linear models and the high-fidelity simulations in the literature from different codes. For practical aeronautical applications where very large deformations do not occur, it appears that nonlinear effects become progressively key on the kinematics of the flexible wing while remaining rather limited on its applied loads and that modified strip theory is still very effective in scaling the steady aerodynamic one and allowing for efficient static quasi-linear semi-analytical solutions. Once the key physical features and effects of the desired engineering application are identified, the most suitable approach may then be selected for a robust and accurate preliminary multidisciplinary optimisation of flexible wings in subsonic flow; in this respect, more complex wing configurations and their dynamics may then be considered and thoroughly investigated in future works.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Marco Berci was employed by the company Pilatus Aircraft Ltd. The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CFD | computational fluid dynamics |
| DLM | doublet lattice method |
| FEM | finite element method |
| HALE | High-Altitude Long-Endurance |
| HBCM | Hencky’s bar-chain model |
| LLT | lifting-line theory |
| MDO | Multidisciplinary Design and Optimisation |
| MRM | modal rotation method |
| MST | modified strip theory |
| POD | proper orthogonal decomposition |
| ROM | reduced-order model |
| SST | standard strip theory |
| TST | tuned strip theory |
| VLM | vortex lattice method |
| WLM | Weissinger’s line method |
Appendix A. Weissinger’s Line Method
Based on both Biot–Savart’s law [] and Helmholtz’s theorem [] for the potential (inviscid and irrotational) flow of an ideal fluid [], the lifting-line model is a powerful aerodynamic tool for calculating the airload distribution and integral forces on slender thin wings in the subsonic regime. Exploiting a flat wake and Kutta–Joukowski’s theorem [,] on each wing section, lifting-line theory [] places a sheet of horseshoe vortices along the wing span and accounts for the three-dimensional downwash induced by the tip vortices; as per thin aerofoil theory, bound vorticity and aerodynamic load are located at the first quarter chord (i.e., the aerodynamic centre), whereas impermeability boundary condition and fluid–structure interaction are imposed at the last quarter chord (i.e., the control point). Prandtl’s original formulation [] disregards the distance between the former and the latter, resulting in conservative airloads especially towards the wing tips (where the downwash rises and the airload decays rather rapidly, though); later formulations consider the rough mean distance between aerodynamic centre and control point, improving the results especially towards the wing root. Weissinger’s lifting-line method [,] cures all main caveats and considers the actual distance between aerodynamic centre and control point of each wing section, resulting in the correct (stronger) downwash towards the wing tips too and extending the full applicability to the generic swept wings. With the same fundamental clarity and convenience of Prandtl’s seminal formulation, the steady distributions of the bound circulation and the downwash angle along the span of a straight wing are obtained from the distribution of the lift coefficient for the isolated aerofoil as follows []:
respectively, where is a dummy integration variable running along the span and all integrals are Cauchy principal value []; in the case of the elliptical wing, note that the first one becomes an elliptic integral of the second kind and resumes Jones’s edge-velocity factor directly []. As a proof of overall consistency, also note that Helmbold’s formulation [] (leading to Diederich’s formula [,,]) is obtained when the mean effect of the radical in the first integral is roughly considered, whereas Prandtl’s equation is eventually resumed when such term is just omitted. Following Multhopp [,], the bound circulation is here expressed using Glauert’s expansion [] and so is the MST airload scaling function [], namely as follows:
which may then be substituted in the lifting-line equation for the latter to be solved on (at least) wing sections at different stations and so for the unknown generalised circulation coefficients to be found, with running along the span from unloaded tip to unloaded tip with ; odd and even sine terms give symmetric and antisymmetric circulation distributions [], respectively. In particular, further expressing the unknown generalised circulation coefficients with another sine series and taking advantage of Gauss’ quadrature (which is exact up to terms, due to trigonometric identities where Chebyshev polynomials of the second type are equivalent to the trigonometric functions and their roots coincide with Gauss nodes) [], a linear system of algebraic equations is then obtained and eventually solved for the steady airload on several wing sections (see Figure A1 for the case of the Pazy wing []). Finally, within a proper orthogonal decomposition (POD) [] perspective, airload scaling function and aerofoil normalised pressure difference distribution may be interpreted as the dominant orthogonal modes of the steady airload in the span-wise and chord-wise directions, respectively, with the airflow angle of attack driving their amplitude.
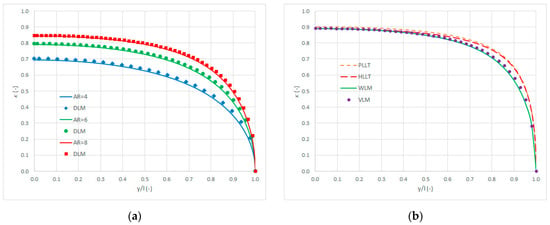
Figure A1.
MST scaling function: literature results comparison (a); Pazy wing assessment (b).
Appendix B. Structural Open-Loop Response to Tip Weight
Exploiting Leibniz’s integral rule [], the nonlinear ordinary differential problem for the large flexural displacement of a clamped elastic beam with uniform distributed mass and tip weight may be written as follows from its deformed shape and features [,,]:
Up to moderate displacements, the relative quasi-linear problem may be written as []:
Neglecting the distributed inertia and assuming uniform structural properties, explicit integrals exist and lead to mapping linear and nonlinear solutions as follows:
where the last nonlinear algebraic equation may then numerically be solved [] to describe the nonlinear kinematics of the elastic inextensible beam.
Appendix C. Quasi-Aeroelastic Model and Closed-Loop Response
A “quasi-aeroelastic” simulation may be defined where the bending aero-structural response still accounts for the wing twist given by the torsional aero-structural response , namely as follows:
according to steady TST and MST aerodynamics, respectively:
Still, MST features the same polynomial terms as the response calculated with TST yet tuned by the coefficients , , , , and , whereas additional exponential terms have fairly been neglected. Although this “intermediate” model would move the bending response closer to the aeroelastic one, it is not recommended because of the inconsistent formulations of the steady lift (with ) and pitching moment (with ).
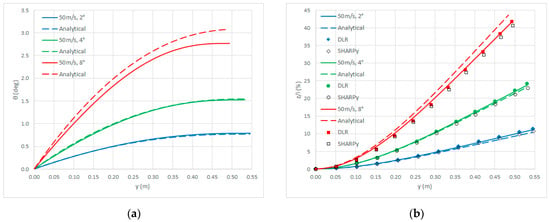
Figure A2.
Closed-loop response with gravity and different angle of attack: torsion (a); bending (b).
Indeed, the amplification factor still quantifies the magnitude of the aeroelastic feedback effects [,,] and does not apply to the quasi-aeroelastic increment unless it explicitly applies to the torsional aero-structural response in the first place; in such a case, there is no inconsistency between the formulations of the steady lift and pitching moment, as both of them do include an approximate aeroelastic feedback (with ) and eventually realise a refined closed-loop response as follows:
where the static divergence speed is estimated via the generalised Rayleigh quotient [,], still with the wing twist aero-structural response to steady aerodynamic loads adopted as an approximate yet suitable “divergence mode shape” satisfying all boundary conditions. An alternative analytical realisation of Galerkin’s energy-based method [,] is hence obtained where the amplification factor applies to the quasi-aeroelastic increment, obtaining similar results as long as starting from the same open-loop response (see Figure A2 for the case of the Pazy wing [,,,]).
References
- Tang, D.; Dowell, E.H. Experimental and Theoretical Study on Aeroelastic Response of High-Aspect-Ratio Wings. AIAA J. 2001, 39, 1430–1441. [Google Scholar] [CrossRef]
- Riso, C.; Cesnik, C. Geometrically Nonlinear Effects in Wing Aeroelastic Dynamics at Large Deflections. J. Fluids Struct. 2023, 120, 103897. [Google Scholar] [CrossRef]
- Livne, E. The Future of Aircraft Aeroelasticity. J. Aircr. 2003, 40, 1066–1092. [Google Scholar] [CrossRef]
- Martins, J.R.; Lambe, A.B. Multidisciplinary Design Optimization: A Survey of Architectures. AIAA J. 2013, 51, 2049–2075. [Google Scholar] [CrossRef]
- Quarteroni, A.; Rozza, G. Reduced Order Methods for Modeling and Computational Reduction; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Qu, Z.Q. Model Order Reduction Techniques with Applications in Finite Element Analysis; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Fossati, M. Evaluation of Aerodynamic Loads via Reduced-Order Methodology. AIAA J. 2015, 53, 2389–2405. [Google Scholar] [CrossRef]
- Vanderplaats, G.N. Numerical Optimization Techniques for Engineering Design: With Applications; McGraw Hill: New York, NY, USA, 1984. [Google Scholar]
- Berci, M.; Torrigiani, F. Multifidelity Sensitivity Study of Subsonic Wing Flutter for Hybrid Approaches in Aircraft Multidisciplinary Design and Optimisation. Aerospace 2020, 7, 161. [Google Scholar] [CrossRef]
- Berci, M. Semi-Analytical Static Aeroelastic Analysis and Response of Flexible Subsonic Wings. Appl. Math. Comput. 2015, 267, 148–169. [Google Scholar] [CrossRef]
- Berci, M.; Cavallaro, R. A Hybrid Reduced-Order Model for the Aeroelastic Analysis of Flexible Subsonic Wings—A Parametric Assessment. Aerospace 2018, 5, 76. [Google Scholar] [CrossRef]
- Vindigni, C.R.; Mantegna, G.; Orlando, C.; Alaimo, A.; Berci, M. A Refined Aeroelastic Beam Finite Element for the Stability Analysis of Flexible Subsonic Wings. Comput. Struct. 2025, 307, 107618. [Google Scholar] [CrossRef]
- Bungartz, H.J.; Schafer, M. Fluid-Structure Interaction: Modelling, Simulation, Optimization; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Anderson, J.D. Fundamentals of Aerodynamics; McGraw-Hill: New York, NY, USA, 2017. [Google Scholar]
- Heil, M.; Haze, A.; Boyle, J. Solvers for Large-Displacement Fluid–Structure Interaction Problems: Segregated Versus Monolithic Approaches. Comput. Mech. 2008, 43, 91–101. [Google Scholar] [CrossRef]
- Pike, E.C. Manual on Aeroelasticity; AGARD 578; AGARD: London, UK, 1971. [Google Scholar]
- Wright, J.R.; Cooper, J.E. Introduction to Aircraft Aeroelasticity and Loads; Wiley: Hoboken, NY, USA, 2014. [Google Scholar]
- Dhatt, G.; Lefrançois, E.; Touzot, G. Finite Element Method; Wiley: Hoboken, NY, USA, 2013. [Google Scholar]
- Rodden, W.P. Theoretical and Computational Aeroelasticity; Crest Publishing: Fort Worth, TX, USA, 2011. [Google Scholar]
- Demasi, L. Introduction to Unsteady Aerodynamics and Dynamic Aeroelasticity; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Katz, J.; Plotkin, A. Low-Speed Aerodynamics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Dimitriadis, G. Unsteady Aerodynamics: Potential and Vortex Methods; Wiley: Hoboken, NY, USA, 2023. [Google Scholar]
- Chung, T.J. Computational Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Avin, O.; Raveh, D.; Drachinsky, A.; Ben-Shmuel, Y.; Tur, M. Experimental Aeroelastic Benchmark of a Very Flexible Wing. AIAA J. 2022, 60, 1745–1768. [Google Scholar]
- Drachinsky, A.; Raveh, D. Nonlinear Aeroelastic Analysis of Highly Flexible Wings Using the Modal Rotation Method. AIAA J. 2022, 60, 3122–3134. [Google Scholar]
- Hilger, J.; Ritter, M. Nonlinear Aeroelastic Simulations and Stability Analysis of the Pazy Wing Aeroelastic Benchmark. Aerospace 2021, 8, 308. [Google Scholar] [CrossRef]
- Riso, C.; Cesnik, C. Impact of Low-Order Modeling on Aeroelastic Predictions for Very Flexible Wings. J. Aircr. 2023, 60, 662–687. [Google Scholar]
- Dowell, E.H. A Modern Course in Aeroelasticity; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Levy, R.; Spillers, W.R. Analysis of Geometrically Nonlinear Structures; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Dimitriadis, G. Introduction to Nonlinear Aeroelasticity; Wiley: Hoboken, NY, USA, 2017. [Google Scholar]
- Berci, M.; Gaskell, P.; Hewson, R.; Toropov, V. Multifidelity Metamodel Building as a Route to Aeroelastic Optimization of Flexible Wings. J. Mech. Eng. Sci. 2011, 225, 2115–2137. [Google Scholar]
- Berci, M.; Toropov, V.; Hewson, R.; Gaskell, P. Multidisciplinary Multifidelity Optimisation of a Flexible Wing Aerofoil with Reference to a Small UAV. Struct. Multidiscip. Optim. 2014, 50, 683–699. [Google Scholar]
- Sheldon, J.; Miller, S.; Pitt, J. Methodology for Comparing Coupling Algorithms for Fluid-Structure Interaction Problems. World J. Mech. 2014, 4, 54–70. [Google Scholar]
- Sucipto, T.; Berci, M.; Krier, J. Gust Response of a Flexible Typical Section via High- and (Tuned) Low-Fidelity Simulations. Comput. Struct. 2013, 122, 202–216. [Google Scholar]
- Berci, M.; Mascetti, S.; Incognito, A.; Gaskell, P.; Toropov, V. Dynamic Response of Typical Section Using Variable-Fidelity Fluid Dynamics and Gust-Modeling Approaches—With Correction Methods. J. Aerosp. Eng. 2014, 27, 1–20. [Google Scholar]
- Forrester, A.J.; Keane, A.J. Engineering Design via Surrogate Modelling: A Practical Guide; Wiley: Hoboken, NY, USA, 2008. [Google Scholar]
- Fung, Y.C. An Introduction to the Theory of Aeroelasticity; Dover: Mineola, NY, USA, 1993. [Google Scholar]
- Hodges, D.; Pierce, G. Introduction to Structural Dynamics and Aeroelasticity; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Weisshaar, T.A. Static and Dynamic Aeroelasticity; Wiley: Hoboken, NY, USA, 2010. [Google Scholar]
- Bisplinghoff, R.L.; Ashley, H.; Halfman, R.L. Aeroelasticity; Dover: Mineola, NY, USA, 1996. [Google Scholar]
- Bisplinghoff, R.L.; Ashley, H. Principles of Aeroelasticity; Dover: Mineola, NY, USA, 2013. [Google Scholar]
- Cavagna, L.; Ricci, S.; Travaglini, L. NeoCASS: An Integrated Tool for Structural Sizing, Aeroelastic Analysis and MDO at Conceptual Design Level. Prog. Aerosp. Sci. 2011, 47, 621–635. [Google Scholar]
- Sotoudeh, Z.; Hodges, D.; Chang, C.-S. Validation Studies for Aeroelastic Trim and Stability Analysis of Highly Flexible Aircraft. J. Aircr. 2010, 47, 1240–1247. [Google Scholar] [CrossRef]
- Murua, J.; Palacios, R.; Graham, J. Applications of the unsteady vortex-lattice method in aircraft aeroelasticity and flight dynamics. Prog. Aerosp. Sci. 2012, 55, 46–72. [Google Scholar] [CrossRef]
- Hencky, H. Über die Angenäherte Lösung von Stabilitätsproblemen im Raum Mittels der Elastischen Gelenkkette. Der Eisenbau 1920, 11, 437–452. [Google Scholar]
- Wang, C.; Zhang, H.; Challamel, N.; Pan, W. Hencky Bar-Chain/Net for Structural Analysis; World Scientific Publishing: Singapore, 2020. [Google Scholar]
- Le, V.; Nguyen, A.; Dang, N. Multibody-Dynamics Approach to Study the Deformation and Aerodynamics of an Insect Wing. AIAA J. 2023, 61, 2500–2516. [Google Scholar] [CrossRef]
- Young, W.C.; Budynas, R.G. Roark’s Formulas for Stress and Strain; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Megson, T.H.G. Aircraft Structures for Engineering Students; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Amabili, M. Nonlinear Vibrations and Stability of Shells and Plates; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Swischuk, R.; Mainini, L.; Peherstorfer, B.; Willcox, K. Projection-Based Model Reduction: Formulations for Physics-Based Machine Learning. Comput. Fluids 2019, 179, 704–717. [Google Scholar] [CrossRef]
- Farhat, C.; Lesoinne, M.; LeTallec, P. Load and Motion Transfer Algorithms for Fluid/Structure Interaction Problems with Non-Matching Discrete Interfaces: Momentum and Energy Conservation, Optimal Discretization and Application to Aeroelasticity. Comput. Methods Appl. Mech. Eng. 1998, 157, 95–114. [Google Scholar]
- Yang, B. Strain, Stress and Structural Dynamics; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Hampton, R.; Leamy, M.; Bryant, P.; Quraishi, N. Deformation and Flexibility Equations for Curved, End-Loaded, Planar Elastica. AIAA J. 2008, 46, 356–363. [Google Scholar]
- Parnes, R. On the Accuracy of Linear Beam Theory. AIAA J. 1979, 17, 219–220. [Google Scholar] [CrossRef]
- Peters, D.A. Two-Dimensional Incompressible Unsteady Airfoil Theory–A Review. J. Fluids Struct. 2008, 24, 295–312. [Google Scholar] [CrossRef]
- Glauert, H. The Elements of Aerofoil and Airscrew Theory; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Thwapiah, G.; Campanile, L.F. Nonlinear Aeroelastic Behavior of Compliant Aerofoils. Smart Mater. Struct. 2010, 19, 035020. [Google Scholar]
- Gal-Rom, Y.C.; Raveh, D. Simplified Aerostructural Static Model for Inflated Wings. AIAA J. 2011, 49, 1180–1190. [Google Scholar]
- Prandtl, L. Applications of Modern Hydrodynamics to Aeronautics; NACA-TR-116; NACA: Boston, MA, USA, 1921. [Google Scholar]
- Holmes, R.B. A Course on Optimization and Best Approximation; Springer: Berlin/Heidelberg, Germany, 1972. [Google Scholar]
- Berci, M. On the Incipient Indicial Lift of Thin Wings in Subsonic Flow: Acoustic Wave Theory with Unsteady Three-Dimensional Effects. Acoustics 2022, 4, 26–52. [Google Scholar] [CrossRef]
- Quarteroni, A.; Sacco, R.; Saleri, F. Numerical Mathematics; Springer-Verlag: Berlin, Germany, 2000. [Google Scholar]
- Antipov, Y. Nonlinear Bending Models of Beams and Plates. Proc. R. Soc.—A 2014, 470, 20140064. [Google Scholar] [PubMed]
- Belendez, T.; Neipp, C.; Belendez, A. Numerical and Experimental Analysis of a Cantilever Beam: A Laboratory Project to Introduce Geometric Nonlinearity in Mechanics of Materials. Int. J. Eng. Educ. 2003, 19, 885–892. [Google Scholar]
- Shvartsman, B.S. Large Deflections of a Cantilever Beam Subjected to a Follower Force. J. Sound Vib. 2007, 304, 969–973. [Google Scholar]
- Kierzenka, J.; Shampine, L.F. A BVP Solver that Controls Residual and Error. J. Numer. Anal. Appl. Math. 2008, 3, 27–41. [Google Scholar]
- Gürgöze, M. A Note on the Vibrations of Restrained Beams and Rods with Point Masses. J. Sound Vib. 1984, 96, 461–468. [Google Scholar]
- Belendez, T.; Neipp, C.; Belendez, A. Large and Small Deflections of a Cantilever Beam. Eur. J. Phys. 2002, 23, 371–379. [Google Scholar]
- Weissinger, J. The Lift Distribution of Swept-Back Wings; NACA TM 1120; NACA: Boston, MA, USA, 1947. [Google Scholar]
- Duncan, W.J. Galerkin’s Method in Mechanics and Differential Equations; ARC RM 1798; ARC: London, UK, 1937. [Google Scholar]
- Reddy, J.N. Energy Principles and Variational Methods in Applied Mechanics; Wiley: Hoboken, NY, USA, 2002. [Google Scholar]
- Flax, A.H. The Influence of Structural Deformation on Airplane Characteristics. J. Aeronaut. Sci. 1945, 12, 94–102. [Google Scholar]
- Pugsley, A.G. Influence of Wing Elasticity upon the Longitudinal Stability of an Aeroplane; ARC RM 1548; ARC: London, UK, 1933. [Google Scholar]
- Seifert, G. A Third Order Boundary Value Problem Arising in Aeroelastic Wing Theory. Q. Appl. Math. 1951, 9, 210–218. [Google Scholar]
- Ghiringhelli, G.; Masarati, P.; Mantegazza, P. Multibody Implementation of Finite Volume C0 Beams. AIAA J. 2000, 38, 131–138. [Google Scholar]
- Wang, Y.; Huston, R.L. A Lumped Parameter Method in the Nonlinear Analysis of Flexible Multibody Systems. Comput. Struct. 1994, 50, 421–432. [Google Scholar] [CrossRef]
- Duncan, W.J. A Critical Examination of the Representation of Massive and Elastic Bodies by Systems of Rigid Masses Elastically Connected. Q. J. Mech. Appl. Math. 1952, 5, 97–108. [Google Scholar]
- Leckie, F.A.; Lindberg, G.M. The Effect of Lumped Parameters on Beam Frequencies. Aeronaut. Q. 1963, 14, 224–240. [Google Scholar] [CrossRef]
- Rubinstein, D. Dynamics of a Flexible Beam and a System of Rigid Rods, with Fully Inverse (One-Sided) Boundary Conditions. Comput. Methods Appl. Mech. Eng. 1999, 175, 87–97. [Google Scholar]
- Giorgio, I.; Del Vescovo, D. Non-Linear Lumped-Parameter Modeling of Planar Multi-Link Manipulators with Highly Flexible Arms. Robotics 2018, 7, 60. [Google Scholar] [CrossRef]
- Turco, E. Discrete is it Enough? The Revival of Piola-Hencky Keynotes to Analyze Three-Dimensional Elastica. Contin. Mech. Thermodyn. 2018, 30, 1039–1057. [Google Scholar]
- Baroudi, D.; Giorgio, I.; Battista, A.; Turco, E.; Igumnov, L. Nonlinear Dynamics of Uniformly Loaded Elastica: Experimental and Numerical Evidence of Motion around Curled Stable Equilibrium Configurations. ZAMM J. Appl. Math. Mech. 2019, 99, e201800121. [Google Scholar]
- Turco, E.; Barchiesi, E.; Giorgio, I.; dell’Isola, F. A Lagrangian Hencky-Type Non-Linear Model Suitable for Metamaterials Design of Shearable and Extensible Slender Deformable Bodies Alternative to Timoshenko Theory. Int. J. Non-Linear Mech. 2020, 123, 103481. [Google Scholar]
- Coleman, T.F.; Li, Y. On the Convergence of Reflective Newton Methods for Large-Scale Nonlinear Minimization Subject to Bounds. Math. Program. 1994, 67, 189–224. [Google Scholar]
- Moré, J.J.; Sorensen, D.C. Computing a Trust Region Step. SIAM J. Sci. Stat. Comput. 1983, 3, 553–572. [Google Scholar] [CrossRef]
- Coleman, T.F.; Li, Y. An Interior, Trust Region Approach for Nonlinear Minimization Subject to Bounds. SIAM J. Optim. 1996, 6, 418–445. [Google Scholar] [CrossRef]
- Gilbert, J.R.; Peierls, T. Sparse Partial Pivoting in Time Proportional to Arithmetic Operations. SIAM J. Sci. Stat. Comput. 1988, 9, 862–874. [Google Scholar] [CrossRef]
- Coleman, T.F.; Verma, A. A Preconditioned Conjugate Gradient Approach to Linear Equality Constrained Minimization. Comput. Optim. Appl. 2001, 20, 61–72. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, J.; Ma, Q. Geometrically Nonlinear Static Analysis of High-Aspect-Ratio Truss-Braced Wing. Eng. Proc. 2024, 80, 18. [Google Scholar]
- Wu, X.; Zhou, Z.; Wang, Z. Effects of Propeller Distribution on the Aeroelastic Characteristics of Large-Deformation Wings. Aerospace 2024, 11, 971. [Google Scholar] [CrossRef]
- dell’Isola, F.; Giorgio, I.; Pawlikowski, M.; Rizzi, N. Large Deformations of Planar Extensible Beams and Pantographic Lattices: Heuristic Homogenization, Experimental and Numerical Examples of Equilibrium. Proc. R. Soc.—A 2016, 472, 20150790. [Google Scholar] [CrossRef]
- Pan, W.; Wang, C.; Zang, H. Hencky Bar-Chain Model for Buckling Analysis of Non-Symmetric Portal Frames. Eng. Struct. 2019, 182, 391–402. [Google Scholar] [CrossRef]
- Salinic, S. An Improved Variant of Hencky Bar-Chain Model for Buckling and Bending Vibration of Beams with End Masses and Springs. Mech. Syst. Signal Process. 2017, 90, 30–43. [Google Scholar] [CrossRef]
- Giorgio, I. A Discrete Formulation of Kirchhoff Rods in Large-Motion Dynamics. Math. Mech. Solids 2020, 25, 1081–1100. [Google Scholar] [CrossRef]
- Peters, D.; Hsieh, M.; Torrero, A. A State-Space Airloads Theory for Flexible Airfoils. J. Am. Helicopter Soc. 2007, 52, 329–342. [Google Scholar] [CrossRef]
- Berci, M.; Gaskell, P.; Hewson, R.; Toropov, V. A Semi-Analytical Model for the Combined Aeroelastic Behaviour and Gust Response of a Flexible Aerofoil. J. Fluids Struct. 2013, 38, 3–21. [Google Scholar] [CrossRef]
- Meirovitch, L. Analytical Methods in Vibrations; Macmillan: New York, NY, USA, 1967. [Google Scholar]
- Savu, D.C.; Higgins, A.J. Structural Stability of a Lightsail for Laser-Driven Interstellar Flight. Acta Astronaut. 2022, 201, 376–393. [Google Scholar]
- Harder, R.L.; Desmarais, R.N. Interpolation Using Surface Splines. J. Aircr. 1972, 9, 189–191. [Google Scholar]
- del Carre, A.; Munoz-Simon, A.; Goizueta, N.; Palacios, R. SHARPy: A Dynamic Aeroelastic Simulation Toolbox for Very Flexible Aircraft and Wind Turbines. J. Open Source Softw. 2019, 4, 1885. [Google Scholar]
- Biot, M.A.; Arnold, L. Low-Speed Flutter and its Physical Interpretation. J. Aeronaut. Sci. 1948, 15, 232–236. [Google Scholar]
- Karamcheti, K. Principles of Ideal-Fluid Aerodynamics; Wiley: Hoboken, NY, USA, 1967. [Google Scholar]
- Kutta, W.M. Auftriebskräfte in Strömenden Flüssigkeiten. Illus. Aeronaut. Mitteilungen 1902, 6, 133–135. [Google Scholar]
- Joukowski, N.E. Sur les Tourbillons Adjionts. Traraux Sect. Phys. Soc. Imp. Amis Sci. Nat. 1906, 13, 261–284. [Google Scholar]
- DeYoung, J. Theoretical Additional Span Loading Characteristics of Wings with Arbitrary Sweep, Aspect Ratio, and Taper Ratio; NACA TN 1491; NACA: Boston, MA, USA, 1947. [Google Scholar]
- Jones, R.T. Correction of the Lifting-Line Theory for the Effect of the Chord; NACA-TN-817; NACA: Boston, MA, USA, 1941. [Google Scholar]
- Helmbold, H.B. Der Unverwundene Ellipsenflügel als Tragende Fläche. Jahrb. Der Dtsch. Luftfahrtforsch. 1942, I, 111–113. [Google Scholar]
- Diederich, F.W. A Plan-Form Parameter for Correlating Certain Aerodynamic Characteristics of Swept Wings; NACA TN 2335; NACA: Boston, MA, USA, 1951. [Google Scholar]
- Diederich, F.W. Approximate Aerodynamic Influence Coefficients for Wings of Arbitrary Plan Form in Subsonic Flow; NACA TN 2092; NACA: Boston, MA, USA, 1950. [Google Scholar]
- Diederich, F.W.; Zlotnick, M. Calculated Spanwise Lift Distributions, Influence Functions and Influence Coefficients for Unswept Wings in Subsonic Flow; NACA 1228; NACA: Boston, MA, USA, 1955. [Google Scholar]
- Multhopp, H. Methods for Calculating the Lift Distribution of Wings (Subsonic Lifting-Surface Theory); ARC R&M 2884; ARC: London, UK, 1955. [Google Scholar]
- Simpson, R.W. An Extension of Multhopp’s Lifting Surface Theory; CoA Report 132; Cranfield University: Cranfield, UK, 1960. [Google Scholar]
- Hildebrand, F.B. A Least-Squares Procedure for the Solution of the Lifting-Line Integral Equation; NACA TN 925; NACA: Boston, MA, USA, 1944. [Google Scholar]
- Lee, K. Large Defections of Cantilever Beams of Non-Linear Elastic Material under a Combined Loading. Int. J. Non-Linear Mech. 2002, 37, 439–443. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).