Properties and Behavior of 3D-Printed ABS Fuel in a 10 N Hybrid Rocket: Experimental and Numerical Insights
Abstract
1. Introduction
2. Experimental Setup
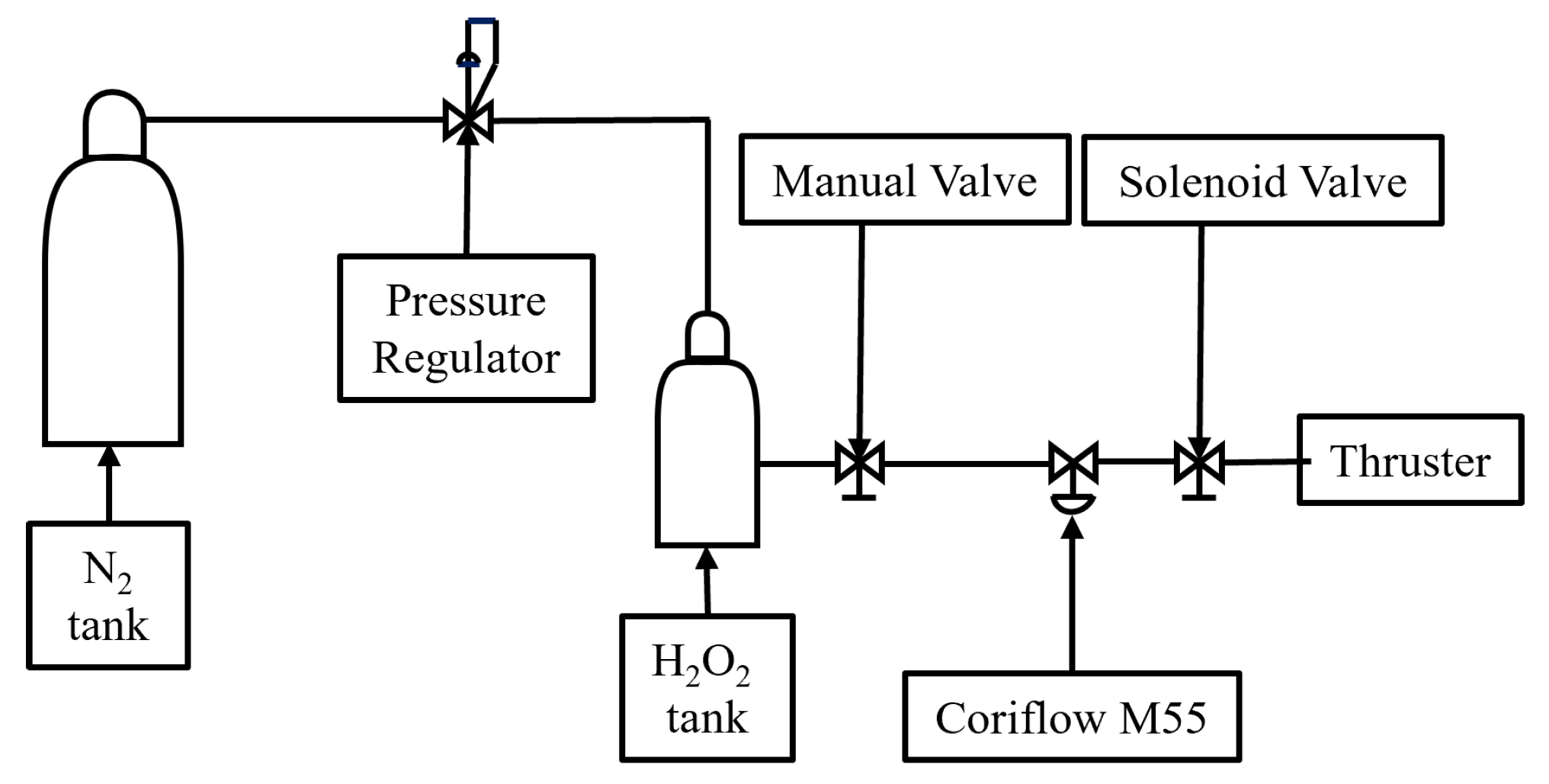
2.1. Laboratory Feed-Line
- Nitrogen tank pressurized at 200 bar.
- Pressure regulator downstream of the nitrogen tank to reduce the pressure to the value chosen depending on the test.
- Hydrogen peroxide tank with 2 L capacity.
- Manual safety valve which is opened just before starting the test.
- A Bronkhorst Cori-Flow M55 employed to measure the hydrogen peroxide flow rate.
- A Parker Miniature Calibrant Valve Series 9 solenoid valve with a reaction times of less than 5 ms, enabling both continuous and pulsed testing.
2.2. Experimental Breadboard and Propellants
3. Postprocessing and Data Reduction Techniques
3.1. Data Analysis Methods and Errors
- The burning duration, i.e., the time interval between the inflection point on the pressure rise branch at motor start-up and that on the pressure drop at the burnout.
- The diameter measurements for the grain port that exhibit dispersion.
- The scale sensitivity for the initial and final grain mass measurements.
- The signal oscillation during the oxidizer mass flow rate measurement.
- Thermocouple accuracy: ±5 K.
- Pressure transducer accuracy: ±0.7 × Pa.
- Load cell accuracy: ±0.05 N.
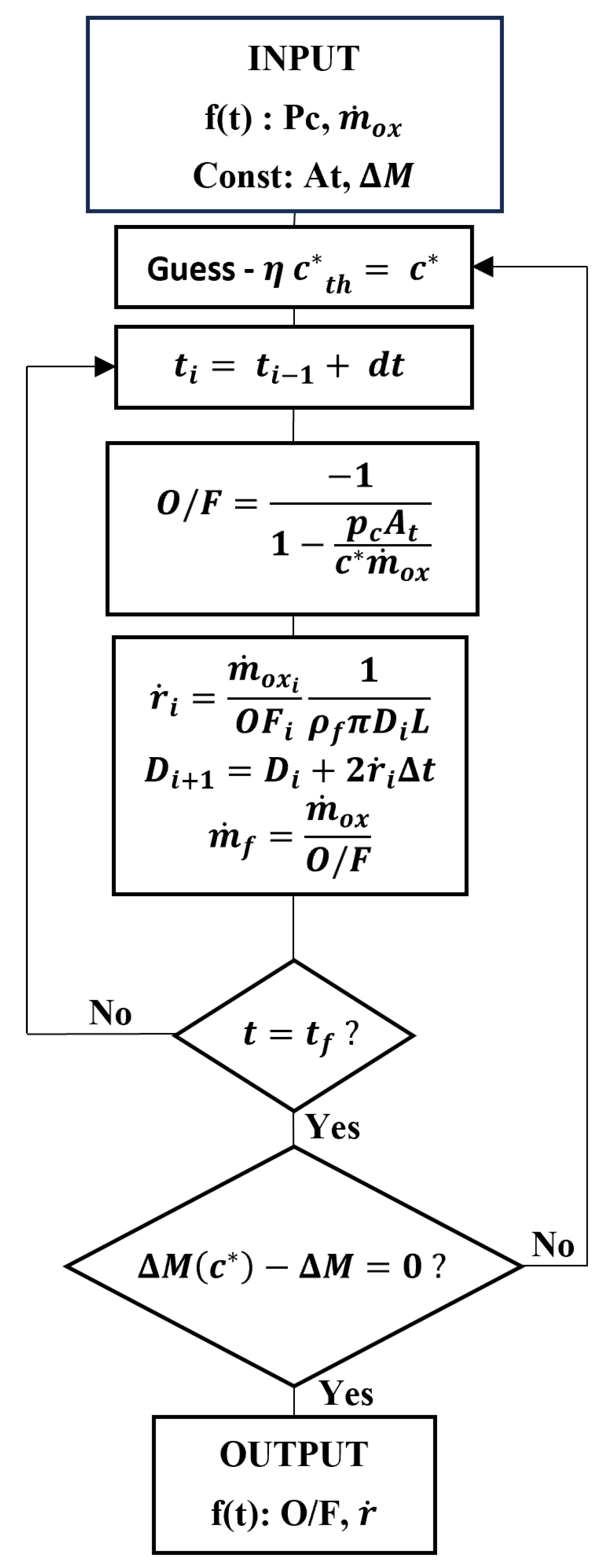
3.2. Ballistic Reconstruction Technique
3.3. Performance Calculation Procedure
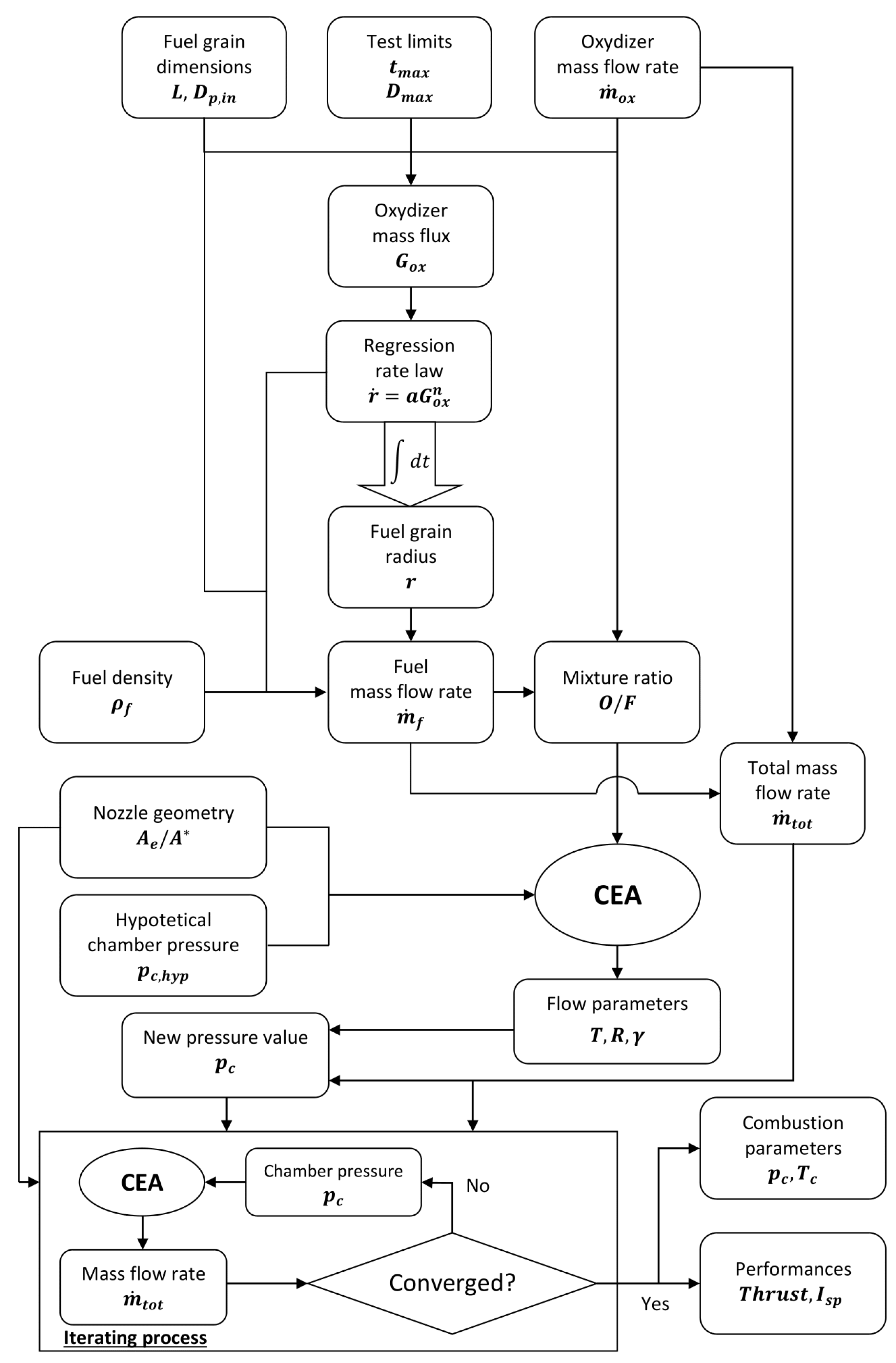
4. Computational Model
4.1. Numerical Model and Boundary Conditions
4.1.1. Numerical Model
- The selected turbulence model is the SST , due its superior ability to adequately capture the phenomena that occur in the near-wall region in comparison to other models. For the purposes of this study, such as for calculating the fuel grain regression rate and examining phenomena near the grain wall, it is the most suitable model [22].
- The combustion model is non-premixed between the oxidizer and the fuel injected from the grain surface. Considering the monomer C4H6 as a product of pyrolysis, it is assumed that the reactions are much faster than the rate at which the species diffuse into the engine. Thus, the model is formulated with a chemical equilibrium-based Probability Density Function (PDF) approach, with the entirety of the system being reduced to a single transport equation for the mean mixture fraction f = 1/(1 + ), where is the local oxidizer-to-fuel ratio of the equivalent non-burning field. Chemical–turbulence interaction is considered, closing the model with the variance equation of f [23].
- The thermodynamic and transport properties are derived from the solver chemical database. In particular, thermal conductivities and molecular dynamic viscosities are computed as a function of local temperature, with coefficients obtained from [20].
- Finally, it is necessary to describe the interface in the model between the gas phase and the fuel surface in order to describe the mechanism by which the fuel is consumed. Therefore, the following two equations are considered under the assumptions that no matter is removed from the condensed phase surface. In addition, convective and diffusive heat transfer in the energy balance equation are considered, while the radiative part is neglected:where is the gas density at the wall, v is the normal-to-wall velocity component due to injection of the pyrolysis products, is the solid fuel density, is the local regression rate, n is the normal-to-surface oriented from solid to gas, is the thermal conductivity of the gas, is the solid heat capacity per unit mass, is the heat of pyrolysis, is the fuel surface temperature, and is the initial temperature.
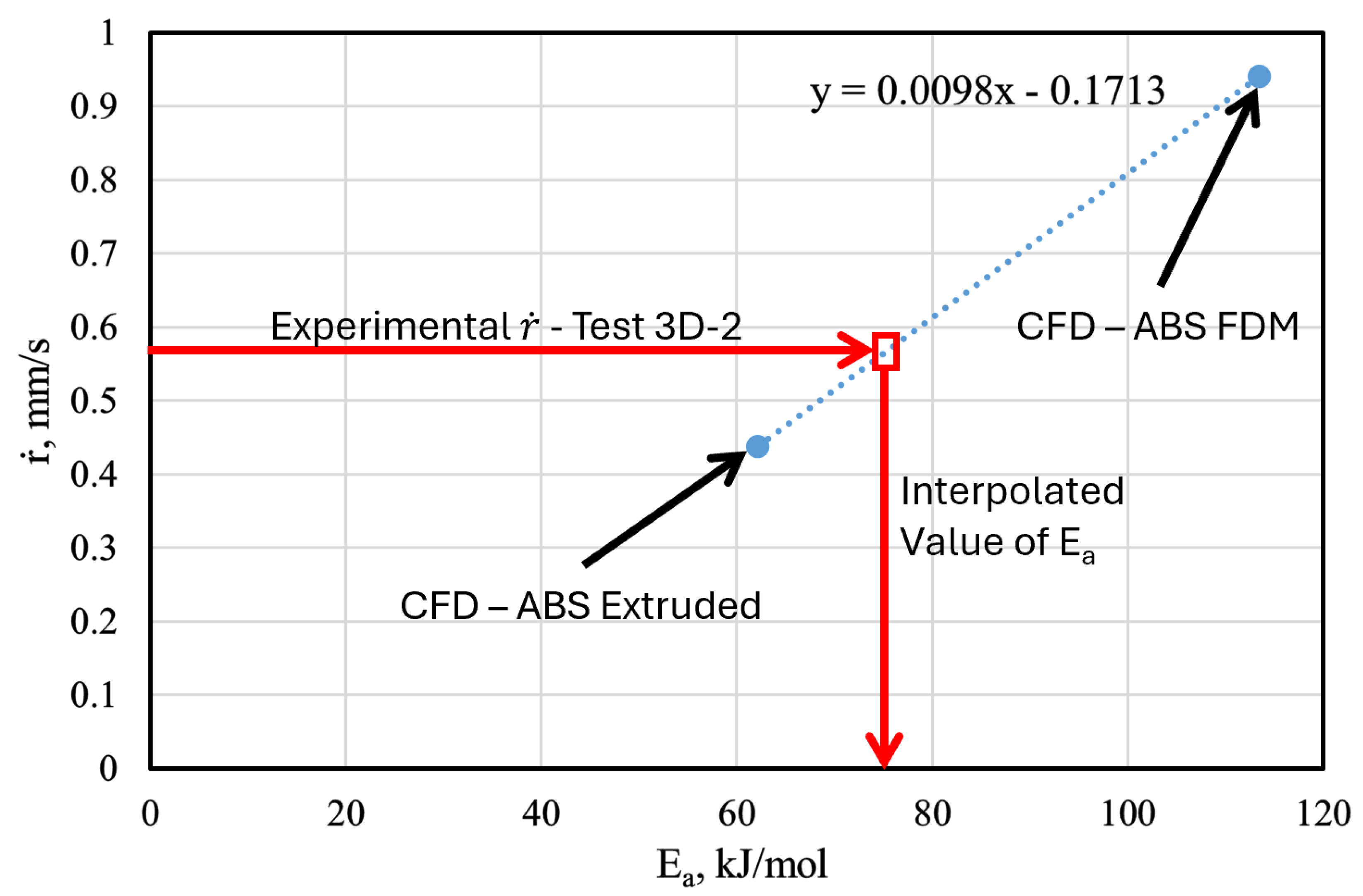
- Pyrolysis of the fuel is described by the semi-empirical Arrhenius-type equation, as in [24]:where A is the pre-exponential factor, is the activation energy, and R is the universal gas constant. The following paragraphs discuss the determination of the Arrhenius coefficients in detail.
- Transient simulations were conducted to address model limitations, including the neglect of non-uniform regression rates and inner grain diameters. In the stationary simulation, the regression rate was averaged and uniform along the grain length, and the same was true for the inner diameter. Consequently, a series of simulations was performed in which the local diameter of the port was updated at each instant based on the local regression rate calculated at the previous instant [25].
4.1.2. Boundary Conditions
4.2. Grid Sensitivity
4.3. Determination of the Arrhenius Coefficients
5. Results and Discussion
5.1. Test Matrix
5.2. On-Ground Performance
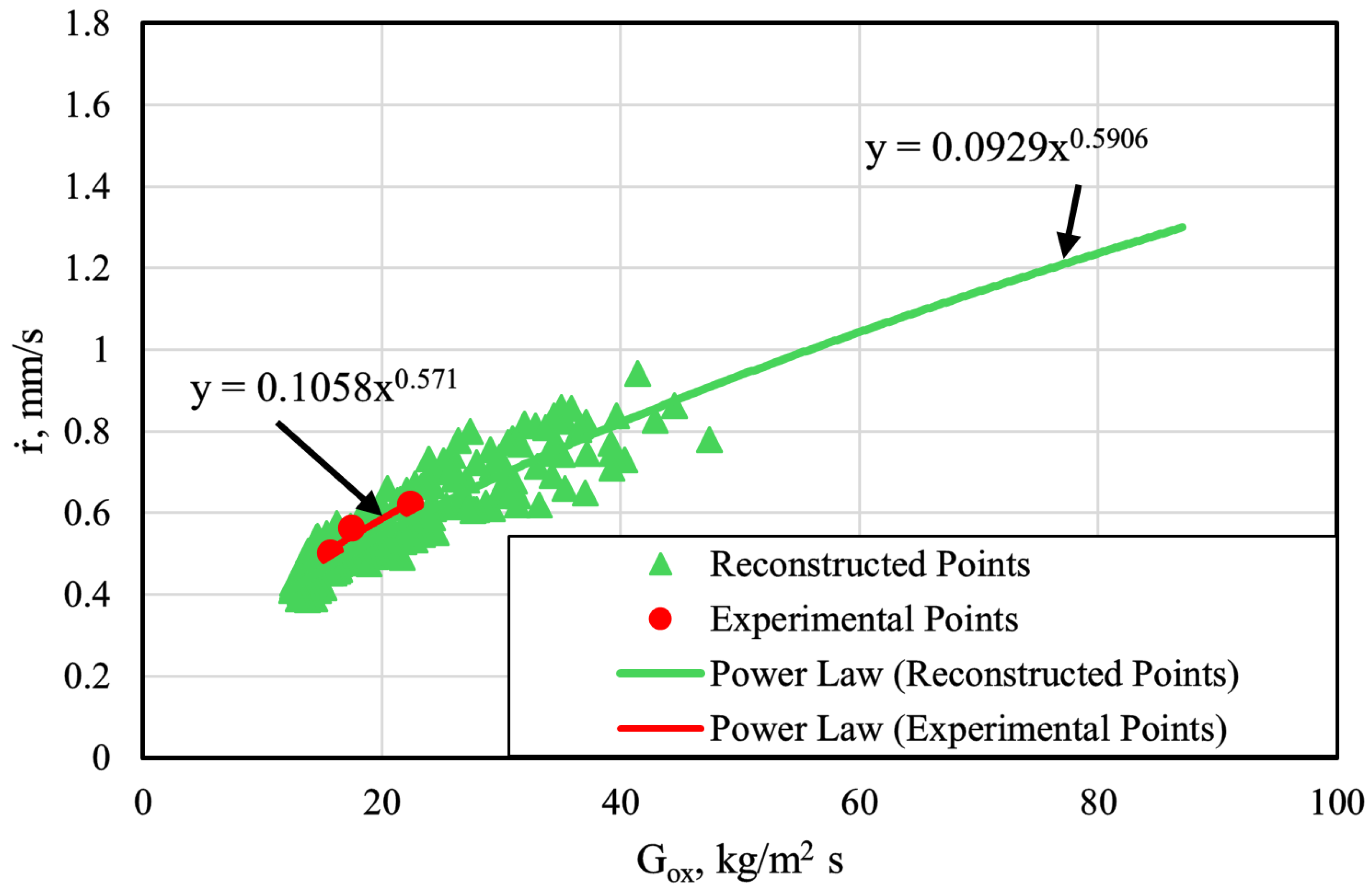
5.3. Reconstruction Technique Findings
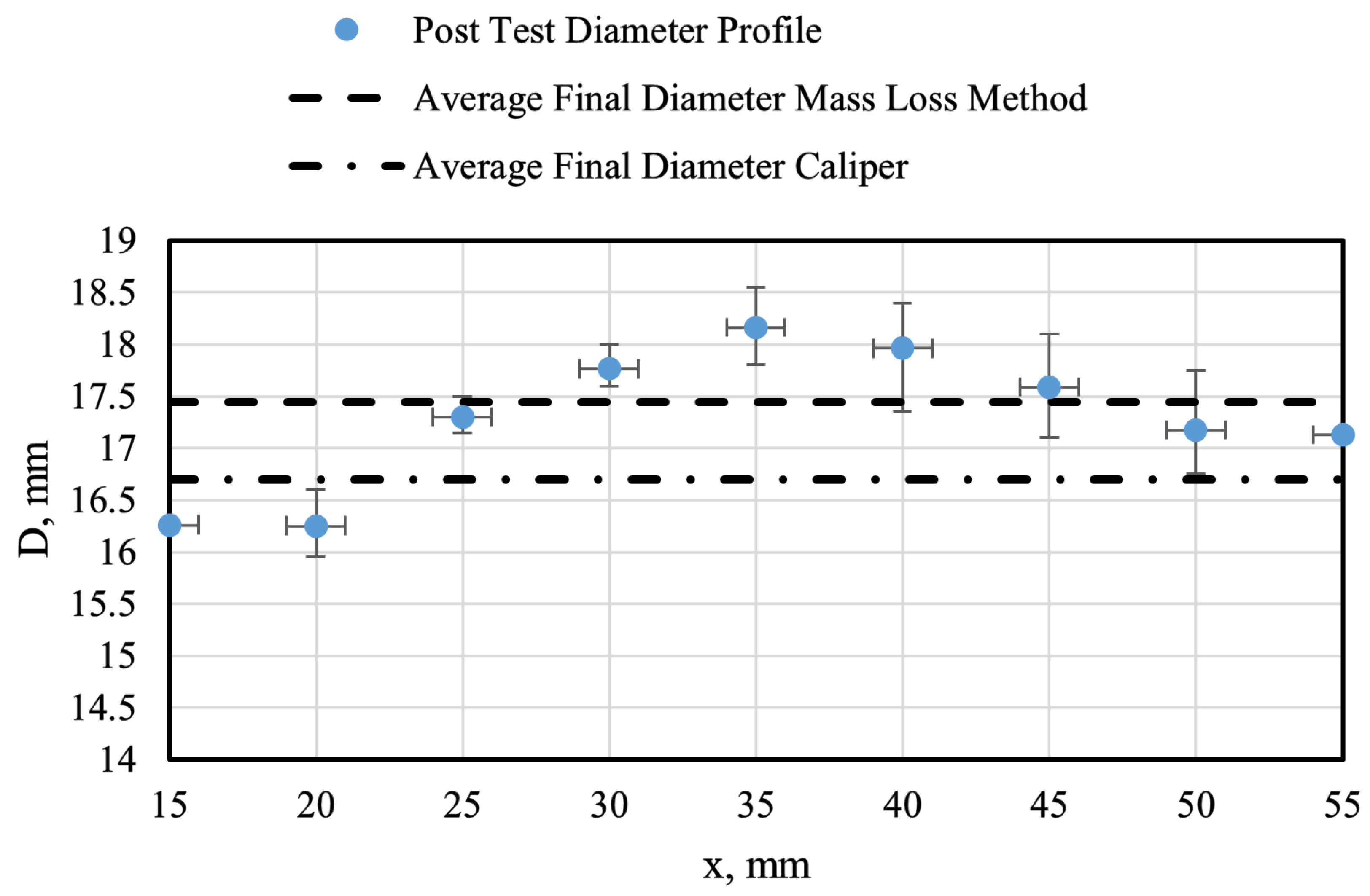
5.4. Local Distribution of the Fuel Consumption
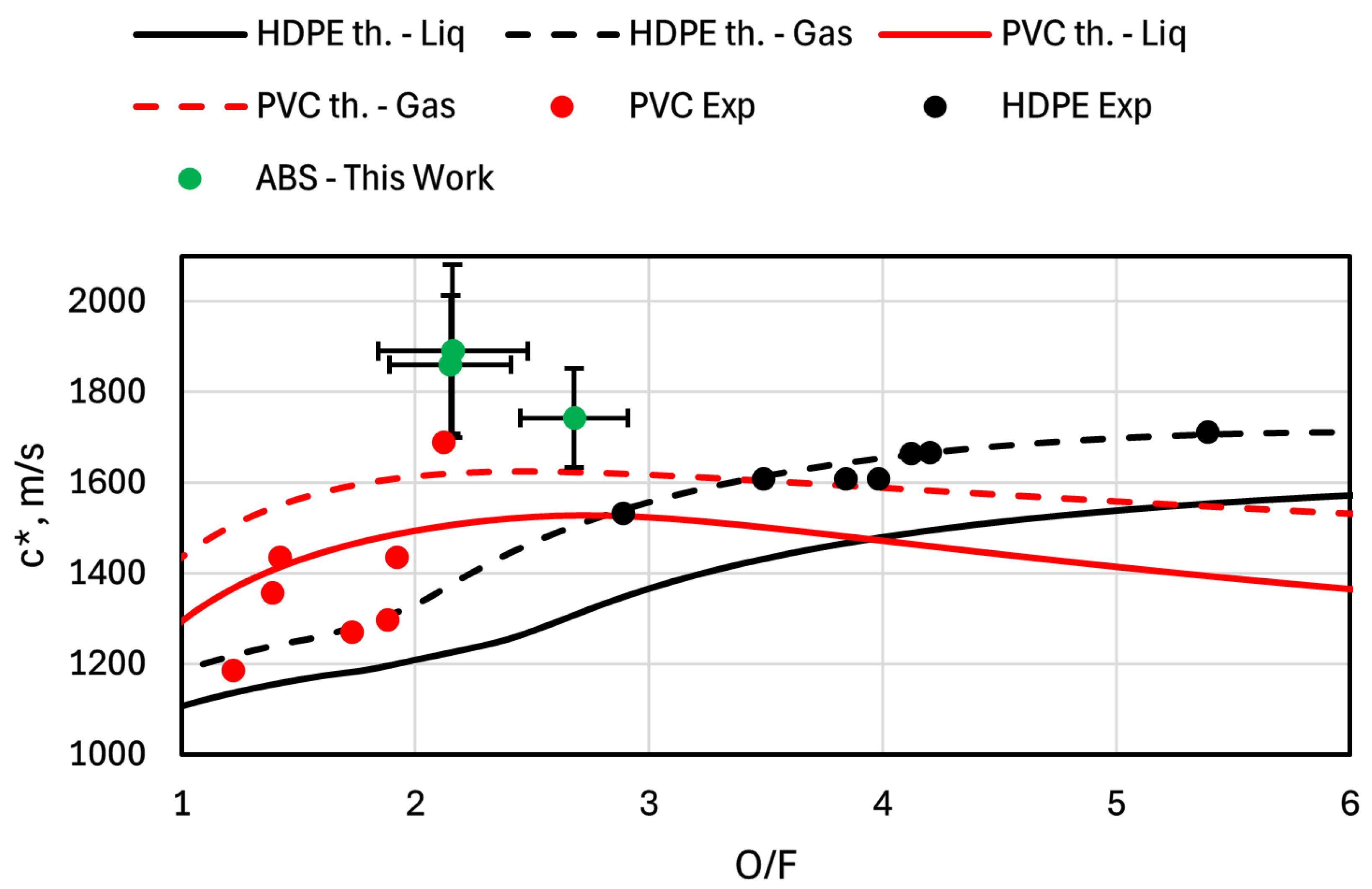
5.5. Fuel Characterization via CFD Simulations
5.5.1. Steady-State Simulation
5.5.2. Transient Simulation
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| ABS | Acrylonitrile butadiene styrene |
| A | Pre-exponential factor, mm/s |
| Throat area, mm2 | |
| Solid heat capacity, J/kg K | |
| Specific heat at constant pressure, J/kg K | |
| Characteristic velocity, m/s | |
| D | Diameter, mm |
| f | Numerical solution |
| Safety factor | |
| FDM | Fused deposition modeling |
| G | Mass flux, kg/m2 s |
| Grid convergence index | |
| HDPE | High-density polyethylene |
| Mass flow rate, g/s | |
| Mass consumption, g | |
| Oxidizer-to-fuel ratio | |
| p | Pressure, bar |
| PVC | Polyvinyl chloride |
| q | Thermal flux, W/m2 |
| R | Universal gas constant, J/mol K |
| r | Refinement Factor |
| Regression rate, mm/s | |
| t | Time, s |
| T | Temperature, K |
| v | Velocity normal to the wall, m/s |
| z | Order of accuracy |
| Greek Symbols | |
| Gas thermal conductivity, W/mK | |
| Efficiency | |
| Density, kg/m3 | |
| Superscripts | |
| ~ | Time-averaged value |
| - | Space-averaged value |
| n | n-th time step |
| Subscripts | |
| b | Burning |
| c | Chamber |
| Experimental | |
| f | Fuel |
| Final | |
| i | i-th node |
| Initial | |
| Numerical | |
| Oxidizer | |
| p | Port |
| Initial port | |
| Final port | |
| Reference | |
| Total | |
| w | Wall |
Appendix A. Governing Equations
| Constant | Value | Constant | Value |
|---|---|---|---|
| 0.850 | 1.00 | ||
| 0.500 | 0.856 | ||
| 0.075 | 0.0828 | ||
| 0.553 | 0.440 | ||
| 0.090 |
References
- Okninski, A.; Surmacz, P.; Bartkowiak, B.; Mayer, T.; Sobczak, K.; Pakosz, M.; Kaniewski, D.; Matyszewski, J.; Rarata, G.; Wolanski, P. Development of Green Storable Hybrid Rocket Propulsion Technology Using 98% Hydrogen Peroxide as Oxidizer. Aerospace 2021, 8, 234. [Google Scholar] [CrossRef]
- Cantwell, B.; Karabeyoglu, A.; Altman, D. Recent Advances in Hybrid Propulsion. Int. J. Energ. Mater. Chem. Propuls. 2010, 9, 305–326. [Google Scholar] [CrossRef]
- Pastrone, D. Approaches to Low Fuel Regression Rate in Hybrid Rocket Engines. Int. J. Aerosp. Eng. 2012, 2012, 649753. [Google Scholar] [CrossRef]
- Leccese, G. Propulsion Systems Trends in Italian Space Agency ALCOR Program; Technical Report; Italian Space Agency: Rome, Italy, 2024. [Google Scholar]
- Tummala, A.; Dutta, A. An Overview of Cube-Satellite Propulsion Technologies and Trends. Aerospace 2017, 4, 58. [Google Scholar] [CrossRef]
- Gotzig, U. Challenges and Economic Benefits of Green Propellants for Satellite Propulsion. In Proceedings of the 7th European Conference for Aeronautics and Space Sciences, Kraków, Poland, 29 June–3 July 2015. [Google Scholar] [CrossRef]
- Remissa, I.; Jabri, H.; Hairch, Y.; Toshtay, K.; Atamanov, M.; Azat, S.; Amrousse, R. Propulsion Systems, Propellants, Green Propulsion Subsystems and their Applications: A Review. Eurasian Chem.-Technol. J. 2023, 25, 3–19. [Google Scholar] [CrossRef]
- Cassese, S.; Gallo, G.; Mungiguerra, S.; Cecere, A.; Savino, R. Preliminary Design and Study of 5N HTP Monopropellant Thruster for Small Satellites. Acta Astronaut. 2023, 202, 94–103. [Google Scholar] [CrossRef]
- Cassese, S.; Mungiguerra, S.; Capone, V.; Guida, R.; Cecere, A.; Savino, R. Fuel Ignition in HTP Hybrid Rockets at Very Low Mass Fluxes: Challenges and Pulsed Preheating Techniques Using Palladium-Coated Catalysts. Aerospace 2024, 11, 884. [Google Scholar] [CrossRef]
- Mungiguerra, S.; Cassese, S.; Guida, R.; Savino, R. Experimental and Numerical Assessment of Regression Rate and Propulsive Performance of 10N-class Hybrid Rockets for Nanosatellite Maneuvering. In Proceedings of the 74th International Astronautical Congress (IAC), IAC-23-C4.4.7.x77592, Baku, Azerbaijan, 2–6 October 2023. [Google Scholar]
- Whitmore, S.; Wilson, J.; Ritter, M.; Williams, L. Estimating the Enthalpy of Gasification of Acrylonitrile-Butadiene-Styrene Hybrid Rocket Fuels. J. Propuls. Power 2015, 31, 1033–1040. [Google Scholar] [CrossRef]
- Yu, X.; Yu, H.; Gao, H.; Zhang, W.; DeLuca, L.; Shen, R. 3D printed different polymer fuel grains for hybrid rocket engine. FirePhysChem 2024, 4, 139–145. [Google Scholar] [CrossRef]
- Yu, X.; Yu, H.; Zhang, W.; DeLuca, L.; Shen, R. Effect of Penetrative Combustion on Regression Rate of 3D Printed Hybrid Rocket Fuel. Aerospace 2022, 9, 696. [Google Scholar] [CrossRef]
- McFarland, M.; Antunes, E. Small-Scale Static Fire Tests of 3D Printing Hybrid Rocket Fuel Grains Produced from Different Materials. Aerospace 2019, 6, 81. [Google Scholar] [CrossRef]
- Cassese, S.; Monteverde, F.; Gallo, G.; Mungiguerra, S.; Cecere, A.; Saraga, F.; Savino, R. Compositionally Complex Catalytic Oxide Beds Free of Noble Metals for H2O2 Fuelled Monopropellant Thrusters. J. Eur. Ceram. Soc. 2023, 43, 4854–4864. [Google Scholar] [CrossRef]
- Gallo, G.; Mungiguerra, S.; Savino, R. New Entrainment Model for Modelling the Regression Rate in Hybrid Rocket Engines. J. Propuls. Power 2021, 37, 893–909. [Google Scholar] [CrossRef]
- Saito, Y.; Kamps, L.; Komizu, K.; Soeda, K.; Bianchi, D.; Nasuti, F.; Nagata, H. The accuracy of reconstruction techniques for determining hybrid rocket fuel regression rate. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018. [Google Scholar] [CrossRef]
- Carmicino, C.; Sorge, A.R. Influence of a Conical Axial Injector on Hybrid Rocket Performance. J. Propuls. Power 2006, 22, 984–995. [Google Scholar] [CrossRef]
- Cassese, S.; Mungiguerra, S.; Guida, R.; Cecere, A.; Savino, R. Regression Rate and Performance Analysis via Ballistic Reconstruction of a small-scale H2O2-based Hybrid Rocket fuelled by Polyvinyl Chloride. Aerosp. Sci. Technol. 2024, 146, 108911. [Google Scholar] [CrossRef]
- Gordon, S.; Cleveland, A.; Mcbride, B.J. Computer Program for Calculation of Complex Chemical Equilibrium Compositions and Applications. Part 1: Analysis. In Proceedings of the NASA Reference Publication 1311, NASA, Cleveland, OH, USA, October 1994; Available online: https://akrmys.com/public/cea/doc/xRP-1311.pdf (accessed on 21 January 2025).
- Mungiguerra, S.; Di Martino, G.D.; Savino, R.; Zoli, L.; Silvestroni, L.; Sciti, D. Characterization of Novel Ceramic Composites for Rocket Nozzles in High-temperature Harsh Environments. Int. J. Heat Mass Transf. 2020, 163, 120492. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Sivathanu, Y.R.; Faeth, G.M. Generalized State Relationships for Scalar Properties in Nonpremixed Hydrocarbon/air Flames. Combust. Flame 1990, 82, 211–230. [Google Scholar] [CrossRef]
- Lengellè, G. Solid-Fuel Pyrolysis Phenomena and Regression Rate, Part 1: Mechanisms. In Fundamentals of Hybrid Rocket Combustion and Propulsion; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2007; pp. 127–166. [Google Scholar] [CrossRef]
- Bianchi, D.; Nasuti, F.; Carmicino, C. Hybrid Rockets with Axial Injector: Port Diameter Effect on Fuel Regression Rate. J. Propuls. Power 2016, 32, 984–996. [Google Scholar] [CrossRef]
- Roache, P.J. Verification of Codes and Calculations. AIAA J. 1998, 36, 696–702. [Google Scholar] [CrossRef]
- Roache, P. Perspective: A Method for Uniform Reporting of Grid Refinement Studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Wilson, J.; Whitmore, S. Pyrolysis of Acrylonitrile-Butadiene-Styrene (ABS) Under High Heat Flux Conditions. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Cleveland, OH, USA, 28–30 July 2014. [Google Scholar] [CrossRef][Green Version]
- Cassese, S.; Mungiguerra, S.; Savino, R. Design and Testing of a Hybrid Rocket for Small Spacecraft. In Proceedings of the AIAA SCITECH 2025 Forum, Orlando, FL, USA, 6–10 January 2025. [Google Scholar] [CrossRef]
- Marxman, G.; Gilbert, M. Turbulent Boundary Layer Combustion in the Hybrid Rocket. Symp. (Int.) Combust. 1963, 9, 371–383. [Google Scholar] [CrossRef]
- Glaser, C.; Gelain, R.; Bertoldi, A.E.M.; Levard, Q.; Hijlkema, J.; Lestrade, J.Y.; Hendrick, P.; Anthoine, J. Experimental regression rate profiles of stepped fuel grains in Hybrid Rocket Engines. Acta Astronaut. 2022, 204, 186–198. [Google Scholar] [CrossRef]
- Di Martino, G.D.; Carmicino, C.; Mungiguerra, S.; Savino, R. The Application of Computational Thermo-Fluid-Dynamics to the Simulation of Hybrid Rocket Internal Ballistics with Classical or Liquefying Fuels: A Review. Aerospace 2019, 6, 56. [Google Scholar] [CrossRef]
- Migliorino, M.T.; Bianchi, D.; Nasuti, F. Numerical Analysis of Paraffin-Wax/Oxygen Hybrid Rocket Engines. J. Propuls. Power 2020, 36, 806–819. [Google Scholar] [CrossRef]
- Di Martino, G.; Mungiguerra, S.; Carimcino, C.; Savino, R.; Cardillo, D.; Battista, F.; Invigorito, M.; Elia, G. Two-Hundred-Newton Laboratory-Scale Hybrid Rocket Testing for Paraffin Fuel-Performance Characterization. J. Propuls. Power 2018, 35, 224–235. [Google Scholar] [CrossRef]
- Di Martino, G.D.; Carmicino, C.; Savino, R. Transient Computational Thermofluid-Dynamic Simulation of Hybrid Rocket Internal Ballistics. J. Propuls. Power 2017, 33, 1395–1409. [Google Scholar] [CrossRef]
- Cebeci, T. Conservation Equations for Compressible Turbolent Flows. In Analysis of Turbulent Flows with Computer Programs, 3rd ed.; Butterworth-Heinemann, Elsevier Ltd.: Waltham, MA, USA, 2013; pp. 34–37. [Google Scholar]
- Jones, W.; Whitelaw, J. Calculation Methods for Reacting Turbulent Flows: A Review. Combust. Flame 1982, 48, 1–26. [Google Scholar] [CrossRef]


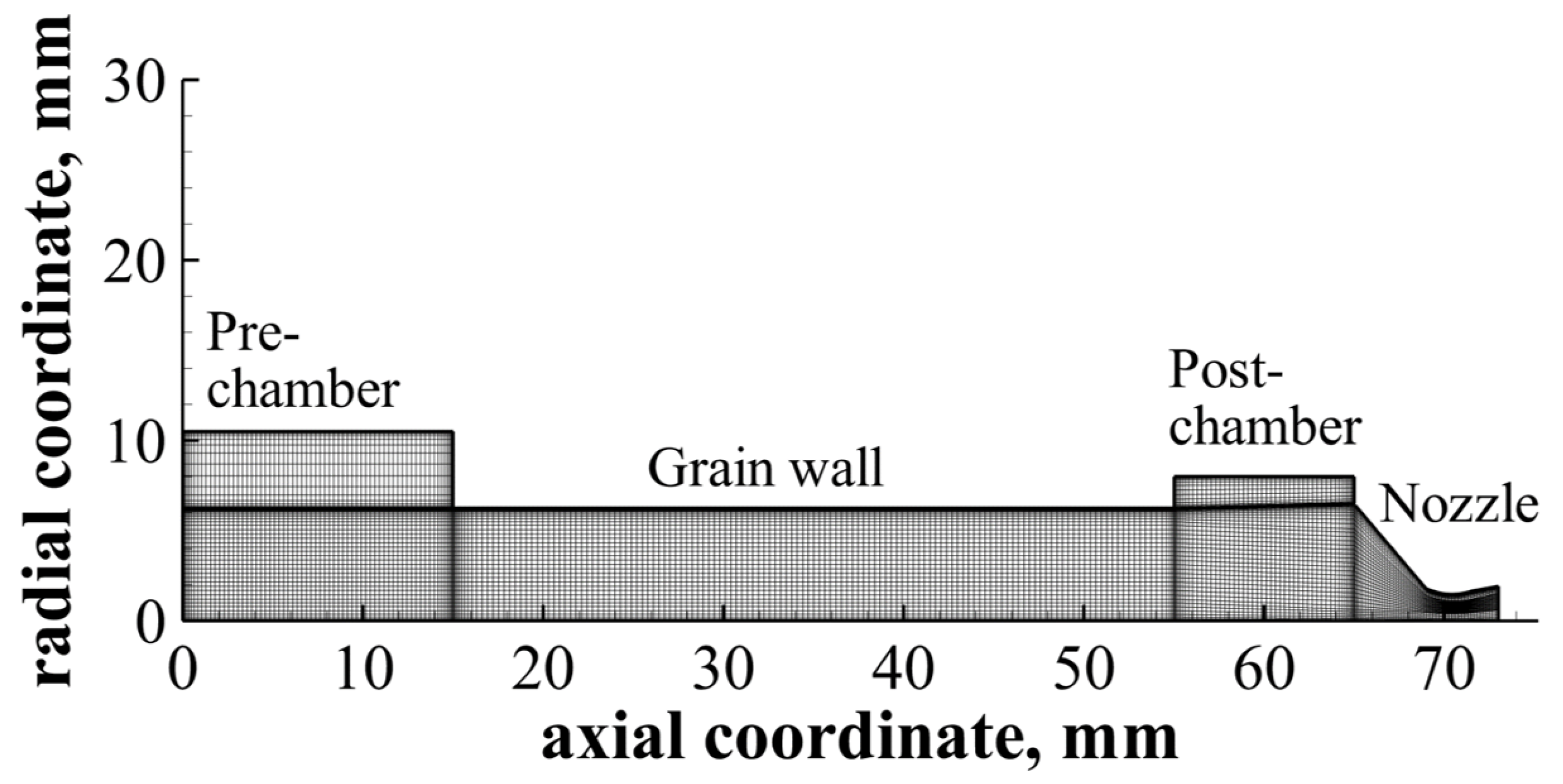






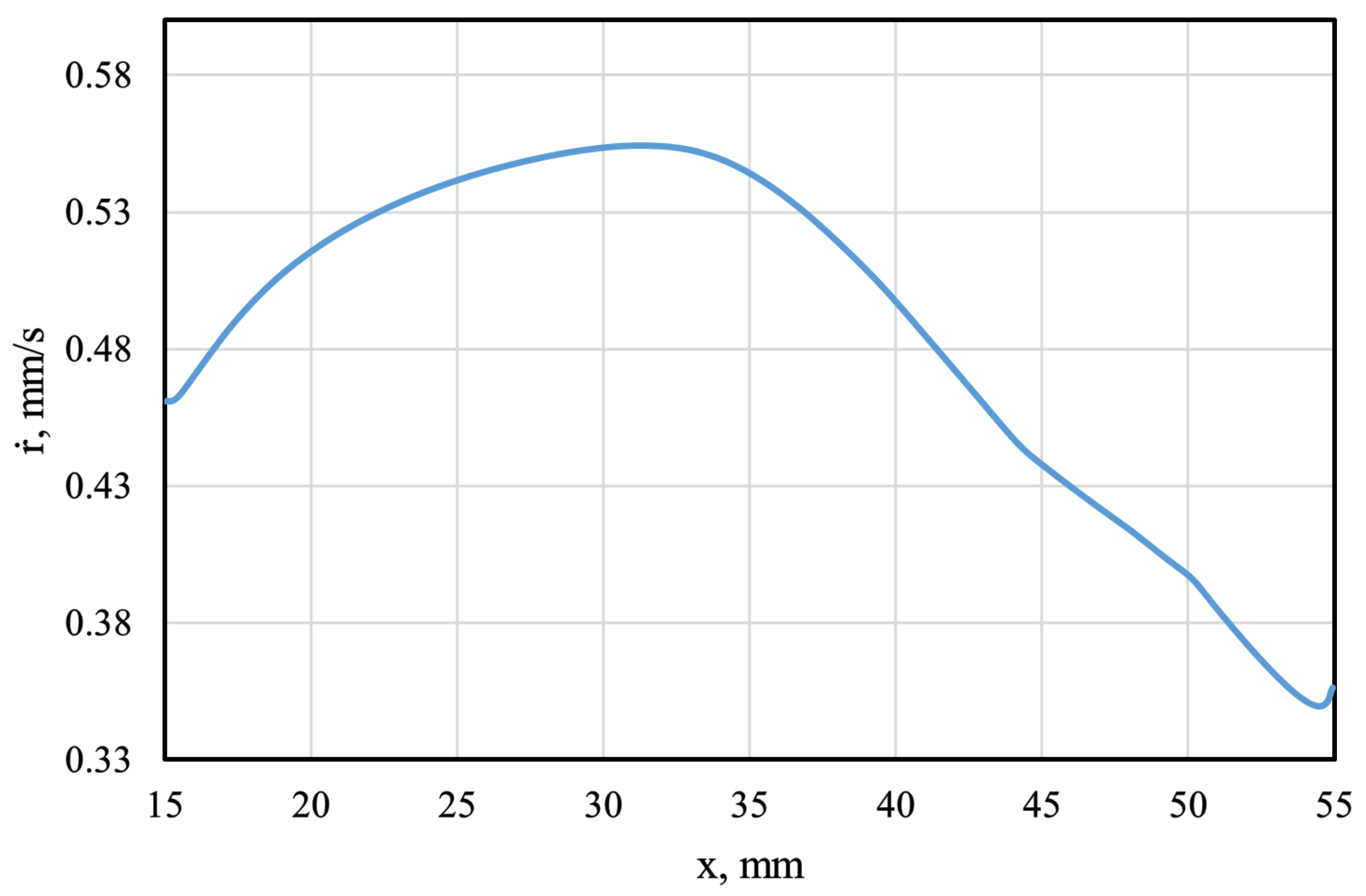
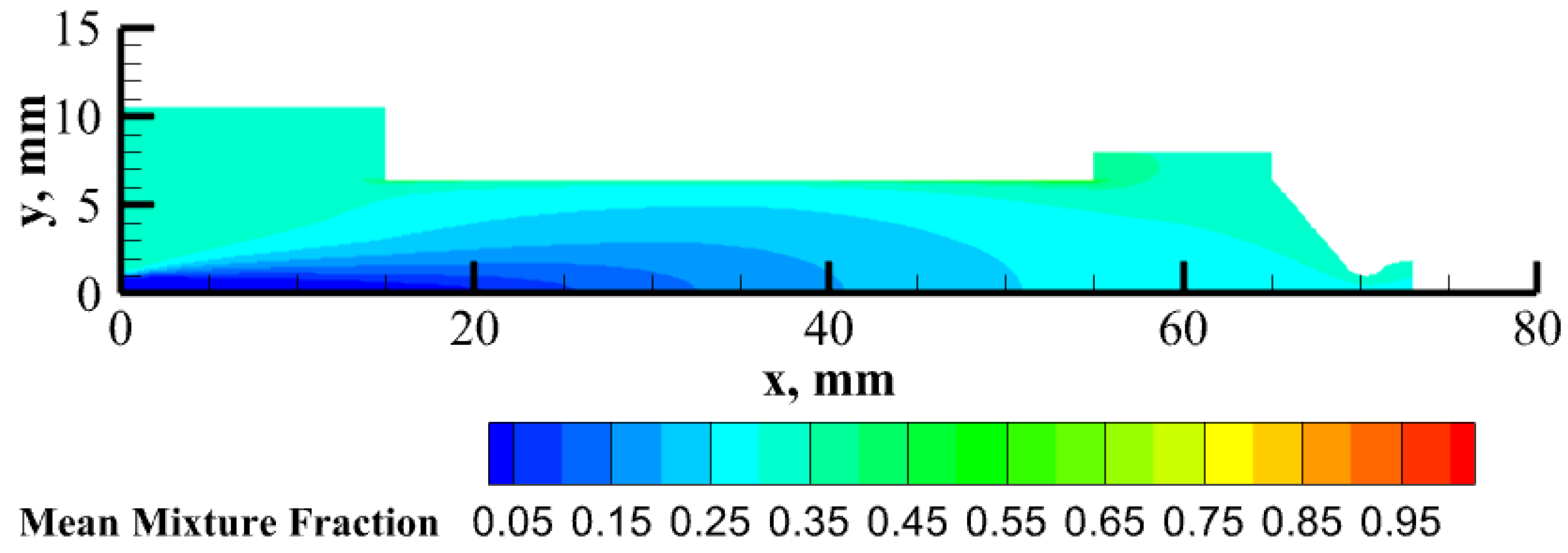

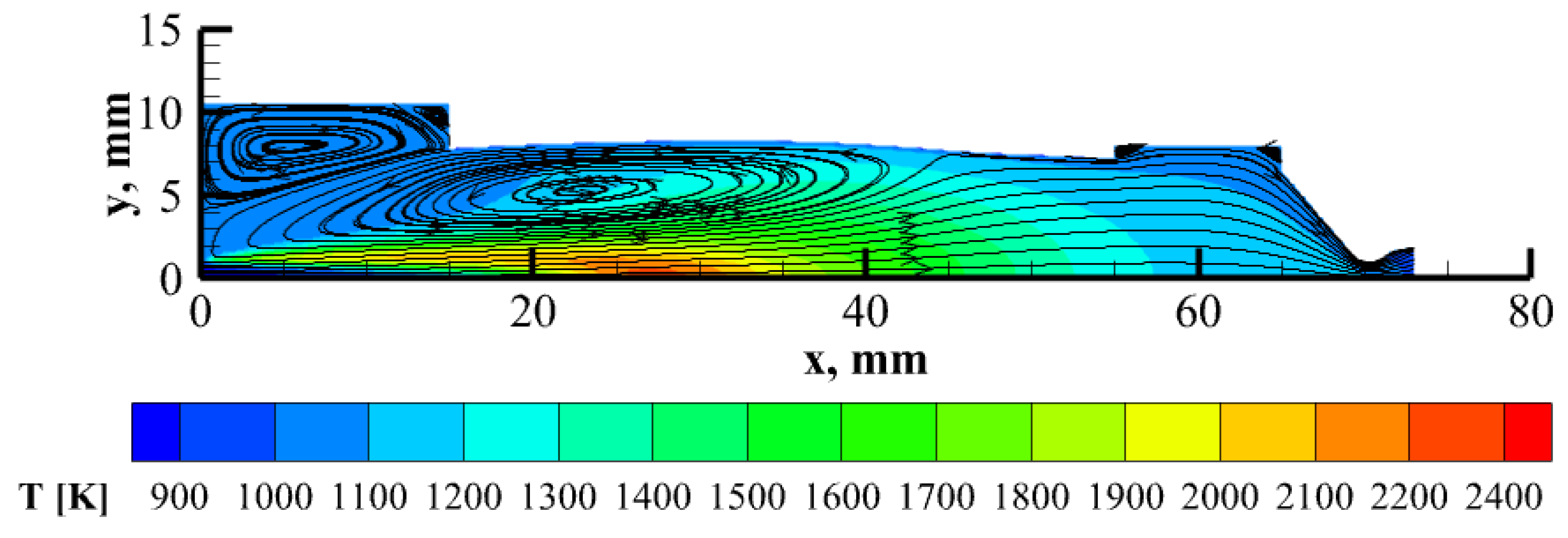

| Pre-Chamber Diameter | Pre-Chamber Length | Fuel Grain Length | Post-Chamber Diameter | Post-Chamber Length |
|---|---|---|---|---|
| 23 mm | 15 mm | 40 mm | 16 mm | 10 mm |
| Mesh Type | Coarse | Reference | Fine |
|---|---|---|---|
| , mm/s | 0.430 | 0.487 | 0.493 |
| , % | // | // | 0.179 |
| , % | 1.720 | // | // |
| Fuel Type | [kg/] | [J/kg K] | [MJ/kg] | A [mm/s] | [kJ/mol] |
|---|---|---|---|---|---|
| Extruded ABS | 1025 | 2714 | 0.2314 | 23.33 | 62.14 |
| FDM ABS | 971 | 2714 | 0.2426 | 5494.18 | 113.44 |
| Fuel Type | [kg/] | [J/kg K] | [MJ/kg] | A [mm/s] | [kJ/mol] |
|---|---|---|---|---|---|
| ABS 3D Printed | 1200 | 2714 | 0.2314 | 87.750 | 74.622 |
| Test 3D-1 | Test 3D-2 | Test 3D-3 | |
|---|---|---|---|
| Feeding pressure, bar | 19.6 | 24 | 29.4 |
| Expected oxidizer mass flow rate, g/s | 2 | 2.5 | 3.5 |
| Grain length, mm | 40 | 40 | 40 |
| Initial port diameter, mm | 9.335 | 9.54 | 9.56 |
| Nozzle throat diameter, mm | 2.1 | 2.1 | 2.1 |
| Area ratio | 3.812 | 3.812 | 3.812 |
| Injector diameter, mm | 2 | 2 | 2 |
| Test | 3D-1 | 3D-2 | 3D-3 |
|---|---|---|---|
| Duration, s | 7 | 7 | 7.2 |
| , g | 6.59 ± 0.01 | 8.19 ± 0.01 | 9.31 ± 0.01 |
| Ch. pressure, bar | 16 ± 0.07 | 19.5 ± 0.07 | 23.6 ± 0.07 |
| , m/s | 1889.73 ± 191.06 | 1859.65 ± 151.75 | 1742.55 ± 110.18 |
| Thrust, N | 5.36 ± 0.05 | 6.9 ± 0.05 | 8.7 ± 0.05 |
| 2.16 ± 0.32 | 2.15 ± 0.26 | 2.68 ± 0.23 | |
| , kg/m2 s | 15.74 ± 2.32 | 17.56 ± 2.10 | 22.48 ± 1.95 |
| , g/s | 0.94 ± 0.001 | 1.17 ± 0.001 | 1.29 ± 0.001 |
| , g/s | 2.03 ± 0.0006 | 2.51 ± 0.0007 | 3.46 ± 0.0007 |
| , g/s | 2.97 ± 0.3 | 3.68 ± 0.3 | 4.75 ± 0.3 |
| , mm/s | 0.50 ± 0.001 | 0.56 ± 0.001 | 0.62 ± 0.001 |
| , mm | 9.335 | 9.54 | 9.56 |
| , mm | 12.82 ± 0.01 | 13.49 ± 0.01 | 14.00 ± 0.01 |
| , mm | 16.30 ± 0.01 | 17.44 ± 0.01 | 18.44 ± 0.01 |
| Test | 3D-1 Code | Err % | 3D-2 Code | Err % | 3D-3 Code | Err % |
|---|---|---|---|---|---|---|
| 2.22 | 2.78 | 2.43 | 13.02 | 2.80 | 4.48 | |
| , kg/m2 s | 16.07 | 2.10 | 18.88 | 7.52 | 23.95 | 6.54 |
| , g/s | 0.91 | 3.19 | 1.03 | 11.97 | 1.23 | 4.65 |
| , g/s | 2.94 | 1.01 | 3.54 | 3.80 | 4.69 | 1.26 |
| , mm/s | 0.48 | 4.00 | 0.52 | 7.14 | 0.60 | 3.23 |
| , mm | 12.68 | 1.09 | 13.01 | 3.56 | 13.56 | 3.14 |
| , mm | 16.02 | 1.72 | 16.69 | 4.30 | 17.79 | 3.52 |
| Test | 3D-1 Code | Err % | 3D-2 Code | Err % | 3D-3 Code | Err % |
|---|---|---|---|---|---|---|
| 2.06 | 4.63 | 2.26 | 5.12 | 2.62 | 2.24 | |
| , kg/m2 s | 15.58 | 1.02 | 18.28 | 4.10 | 23.19 | 3.16 |
| , g/s | 0.98 | 4.26 | 1.11 | 5.13 | 1.32 | 2.33 |
| , g/s | 3.01 | 1.35 | 3.62 | 1.63 | 4.78 | 0.63 |
| , mm/s | 0.50 | 2.00 | 0.55 | 1.79 | 0.63 | 1.61 |
| , mm | 12.88 | 0.47 | 13.22 | 2.00 | 13.78 | 1.57 |
| , mm | 16.42 | 0.74 | 17.10 | 1.95 | 18.23 | 1.14 |
| Test | 3D-1 | 3D-2 | 3D-3 |
|---|---|---|---|
| Numerical Average Wall T, K | 863.14 | 874.62 | 900.30 |
| Experimental Average Regression Rate, mm/s | 0.50 | 0.56 | 0.62 |
| Numerical Average Regression Rate, mm/s | 0.49 | 0.52 | 0.60 |
| Regression Rate Relative Error, % | 2.6 | 6.9 | 2.9 |
| , mm/s | , mm/s | Relative Error, % |
|---|---|---|
| 0.56 | 0.525 | 6.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cassese, S.; Capone, V.M.; Guida, R.; Mungiguerra, S.; Savino, R. Properties and Behavior of 3D-Printed ABS Fuel in a 10 N Hybrid Rocket: Experimental and Numerical Insights. Aerospace 2025, 12, 291. https://doi.org/10.3390/aerospace12040291
Cassese S, Capone VM, Guida R, Mungiguerra S, Savino R. Properties and Behavior of 3D-Printed ABS Fuel in a 10 N Hybrid Rocket: Experimental and Numerical Insights. Aerospace. 2025; 12(4):291. https://doi.org/10.3390/aerospace12040291
Chicago/Turabian StyleCassese, Sergio, Veniero Marco Capone, Riccardo Guida, Stefano Mungiguerra, and Raffaele Savino. 2025. "Properties and Behavior of 3D-Printed ABS Fuel in a 10 N Hybrid Rocket: Experimental and Numerical Insights" Aerospace 12, no. 4: 291. https://doi.org/10.3390/aerospace12040291
APA StyleCassese, S., Capone, V. M., Guida, R., Mungiguerra, S., & Savino, R. (2025). Properties and Behavior of 3D-Printed ABS Fuel in a 10 N Hybrid Rocket: Experimental and Numerical Insights. Aerospace, 12(4), 291. https://doi.org/10.3390/aerospace12040291







