Dynamics Modeling and Analysis of a Vertical Landing Mechanism for Reusable Launch Vehicle
Abstract
1. Introduction
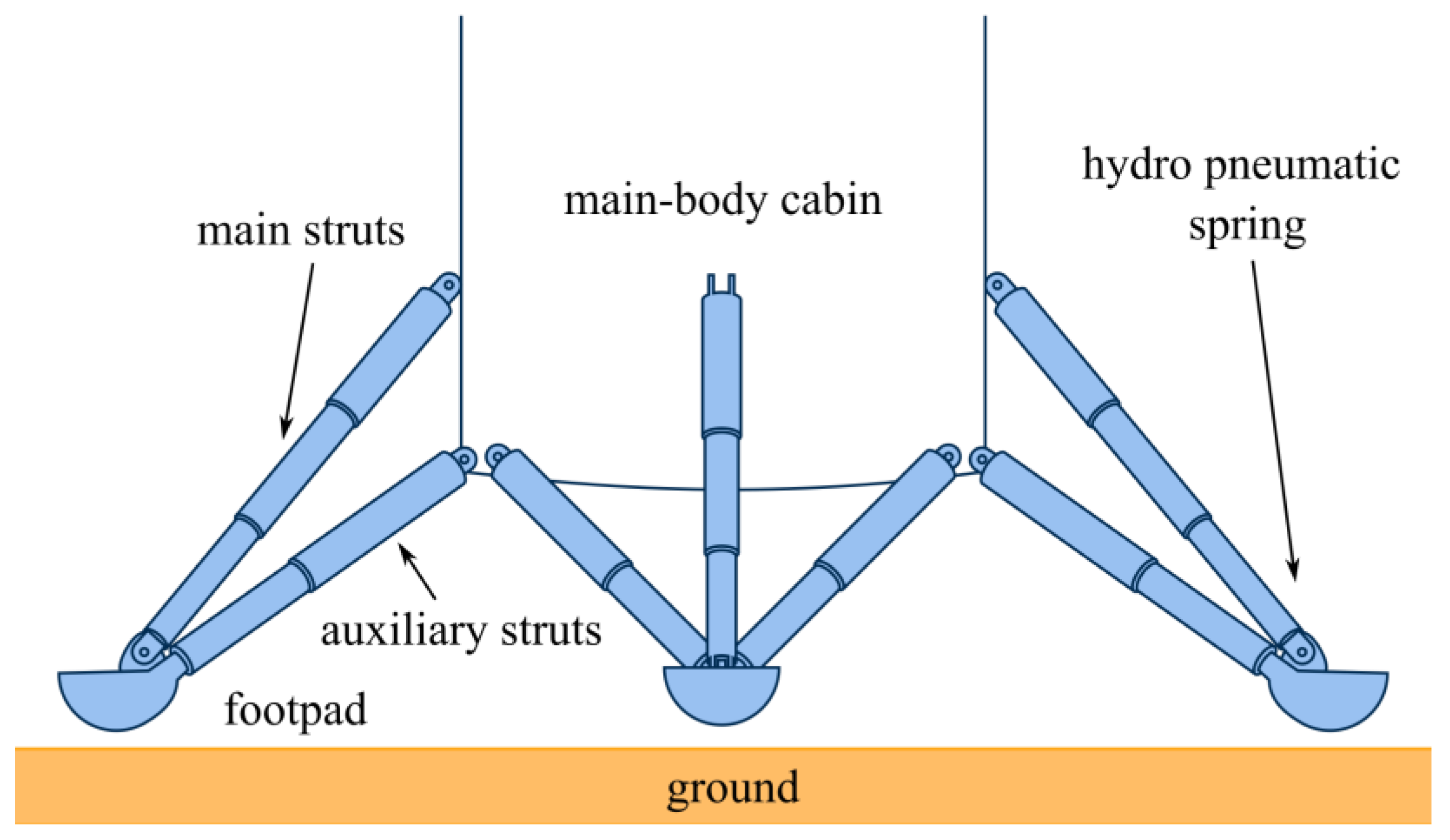
2. Landing Mechanisms
2.1. Overview of the System
2.2. Constraints and Action Forces
3. Dynamics Modeling of the Landing Mechanism
3.1. Kinematics of an Arbitrary Point and a Vector
3.2. Constraint Equations
3.3. Dynamic Equation
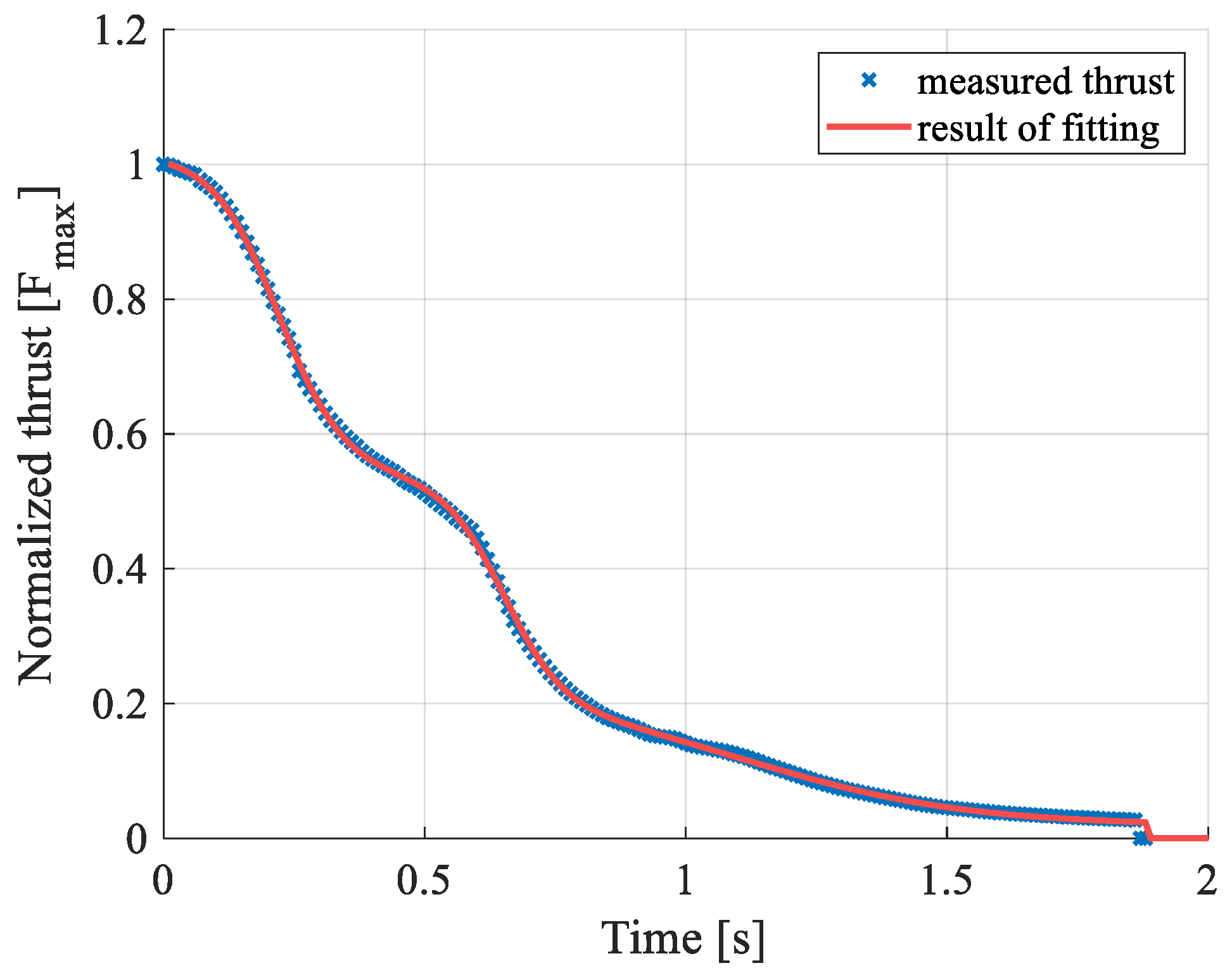
4. Numerical Simulations
4.1. Parameters
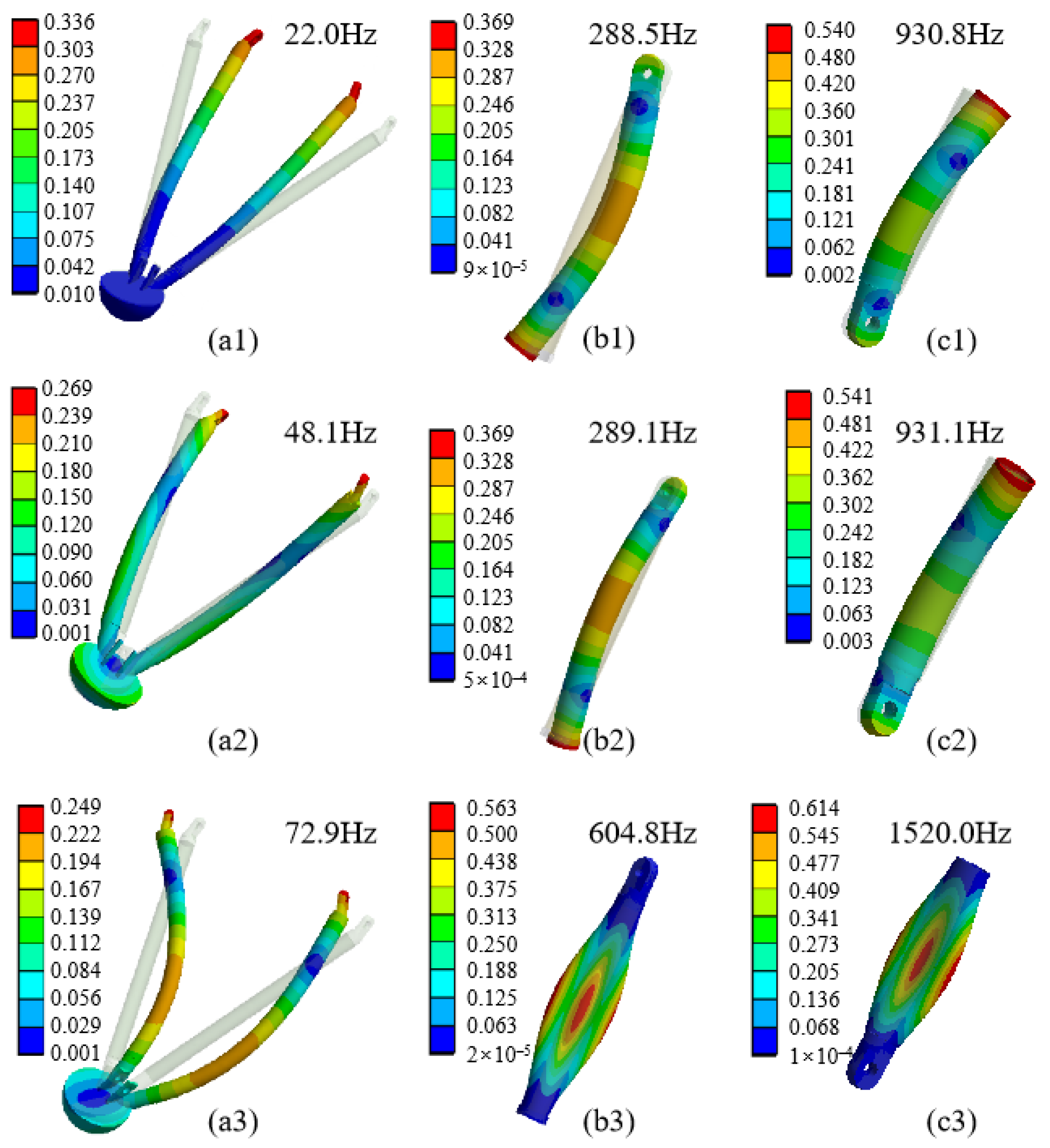
4.2. Modal Shapes of Flexible Bodies
4.3. Simulation Cases
- Cases 1 and 2 are simulations for comparison between rigid and flexible models;
- Case 3 is the simulation for a larger initial landing velocity compared with case 2;
- Case 4 provides results for load analysis of a single landing mechanism;
- Cases 5 and 6 are simulations for the landing stability and lateral motion analysis.
5. Discussion
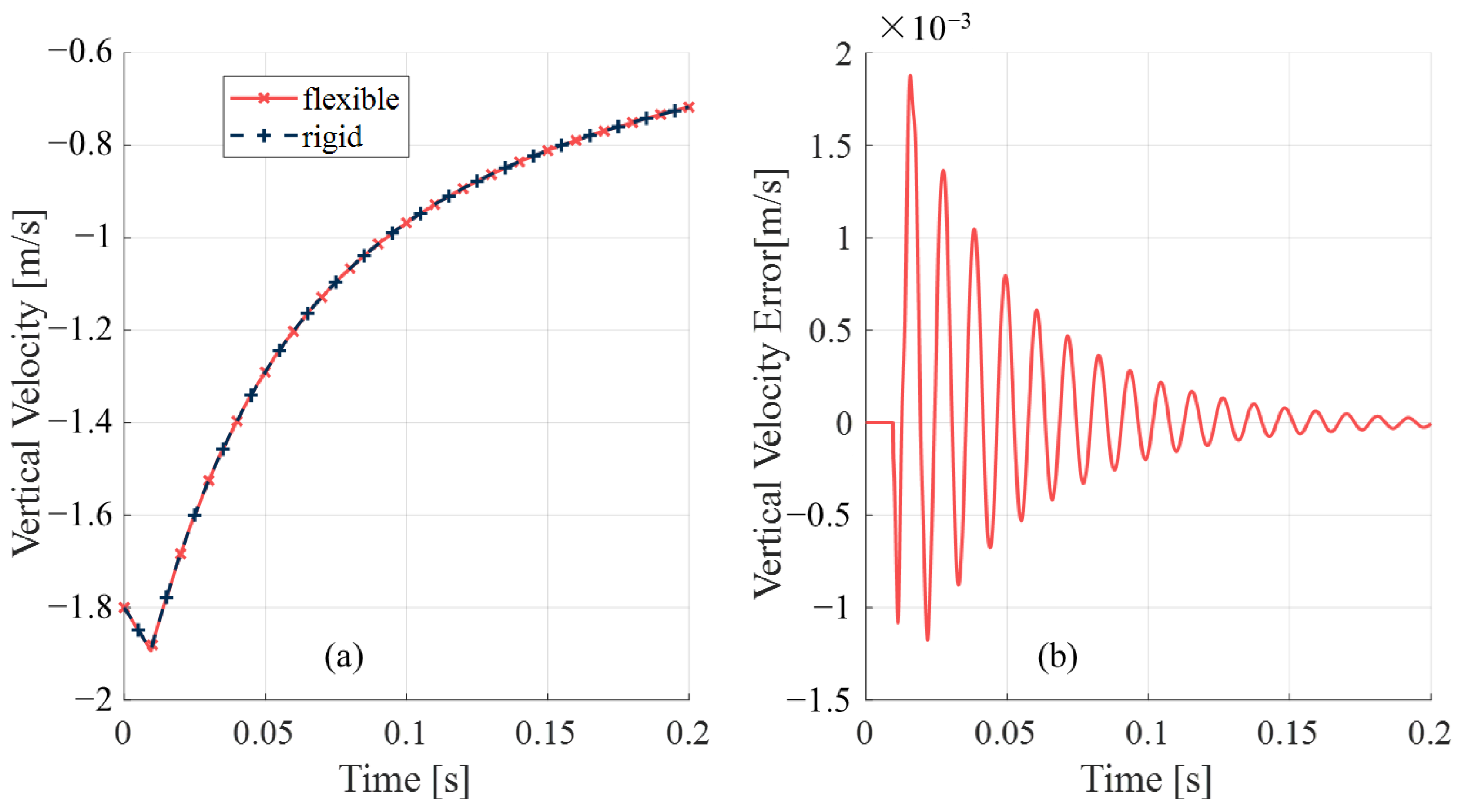
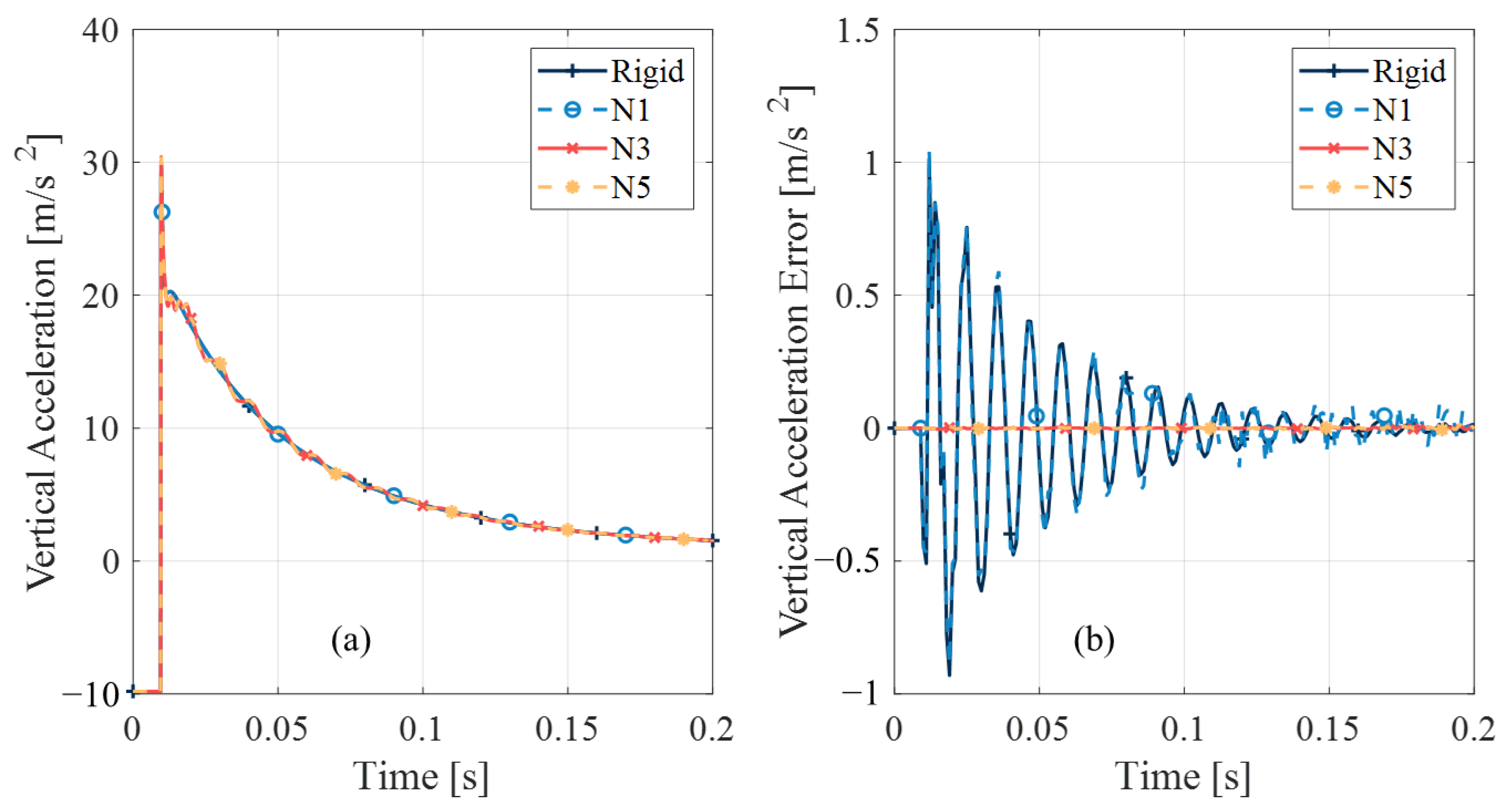
5.1. Comparison Between the Rigid Model and the Coupled One
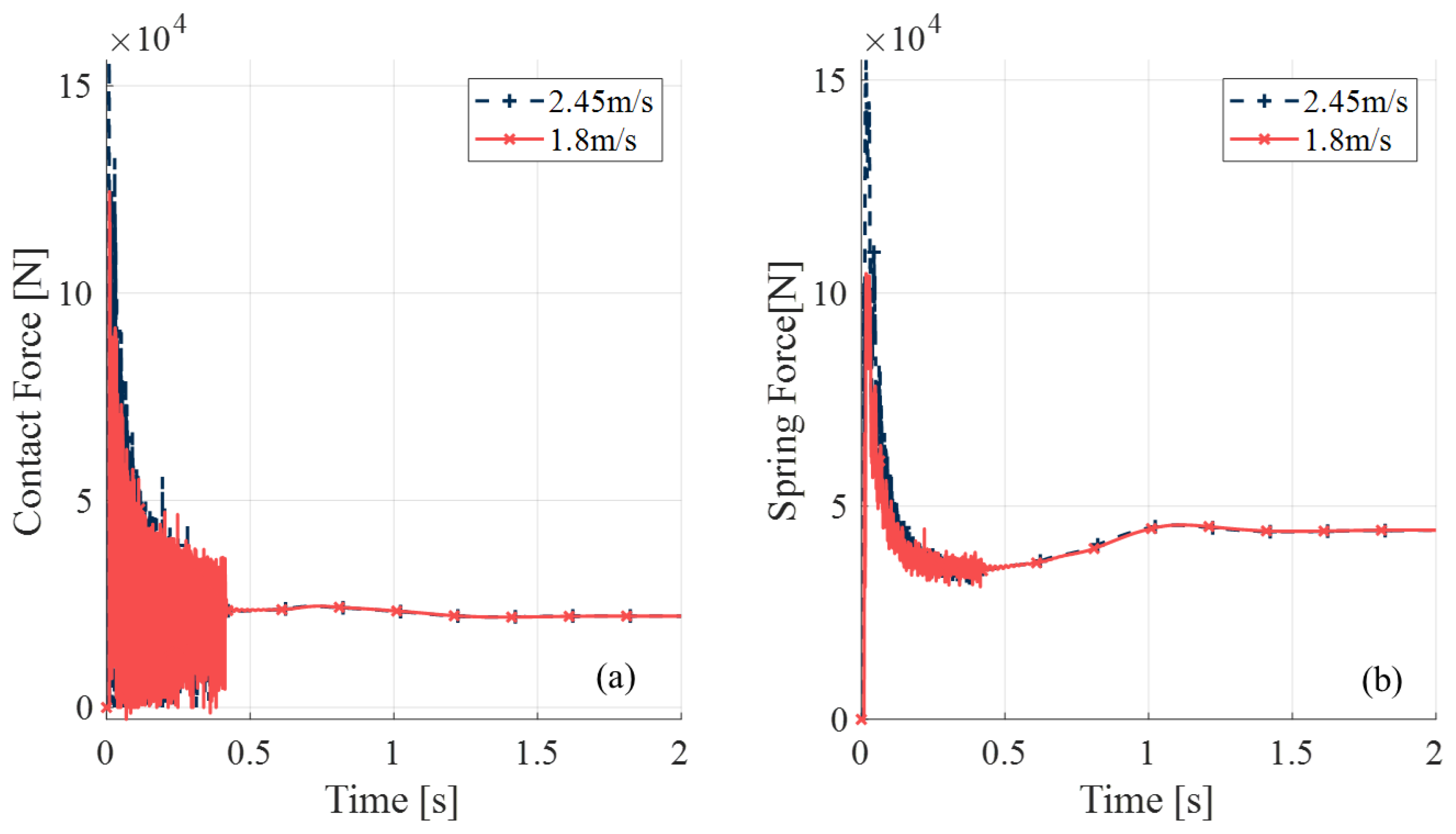
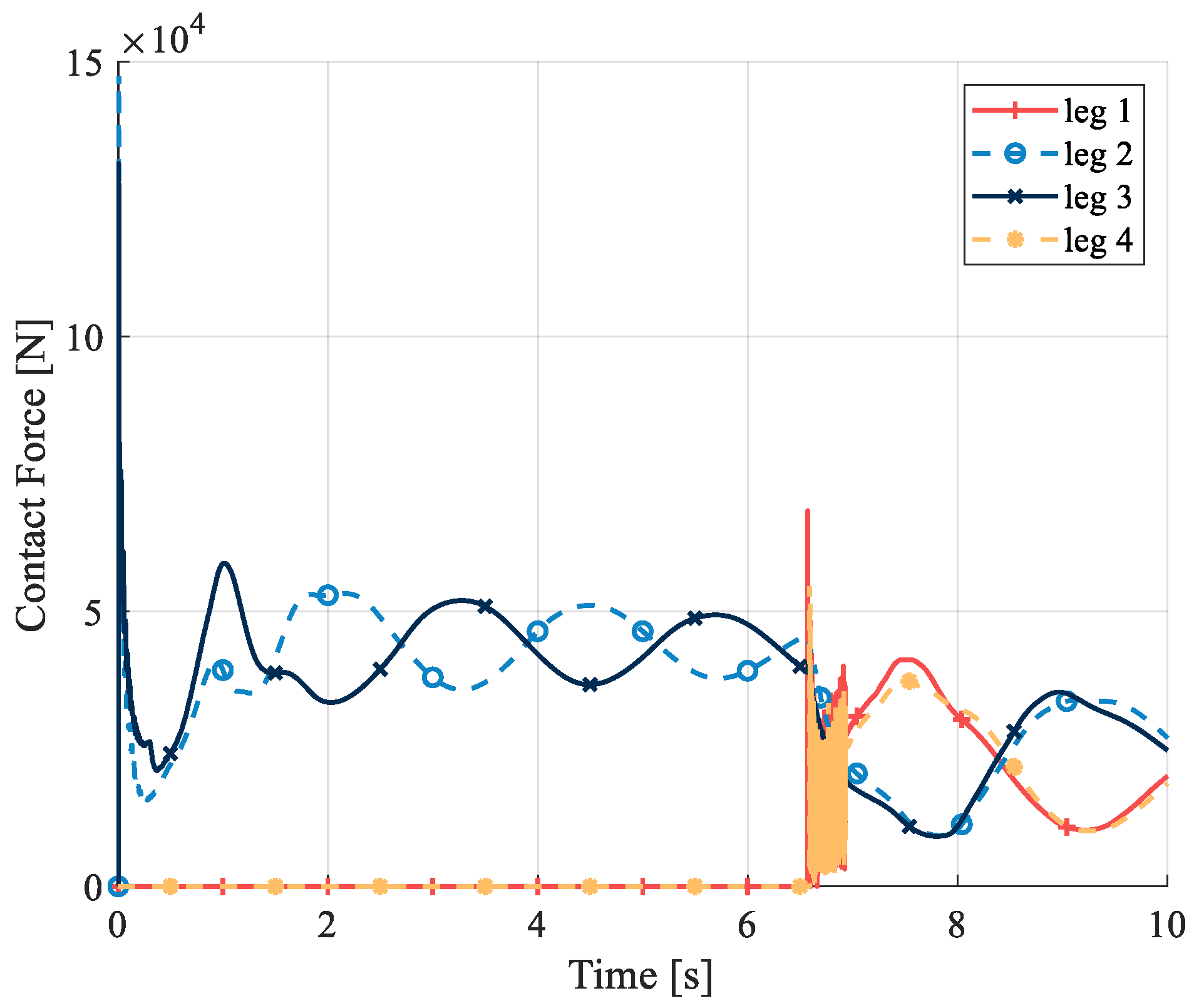
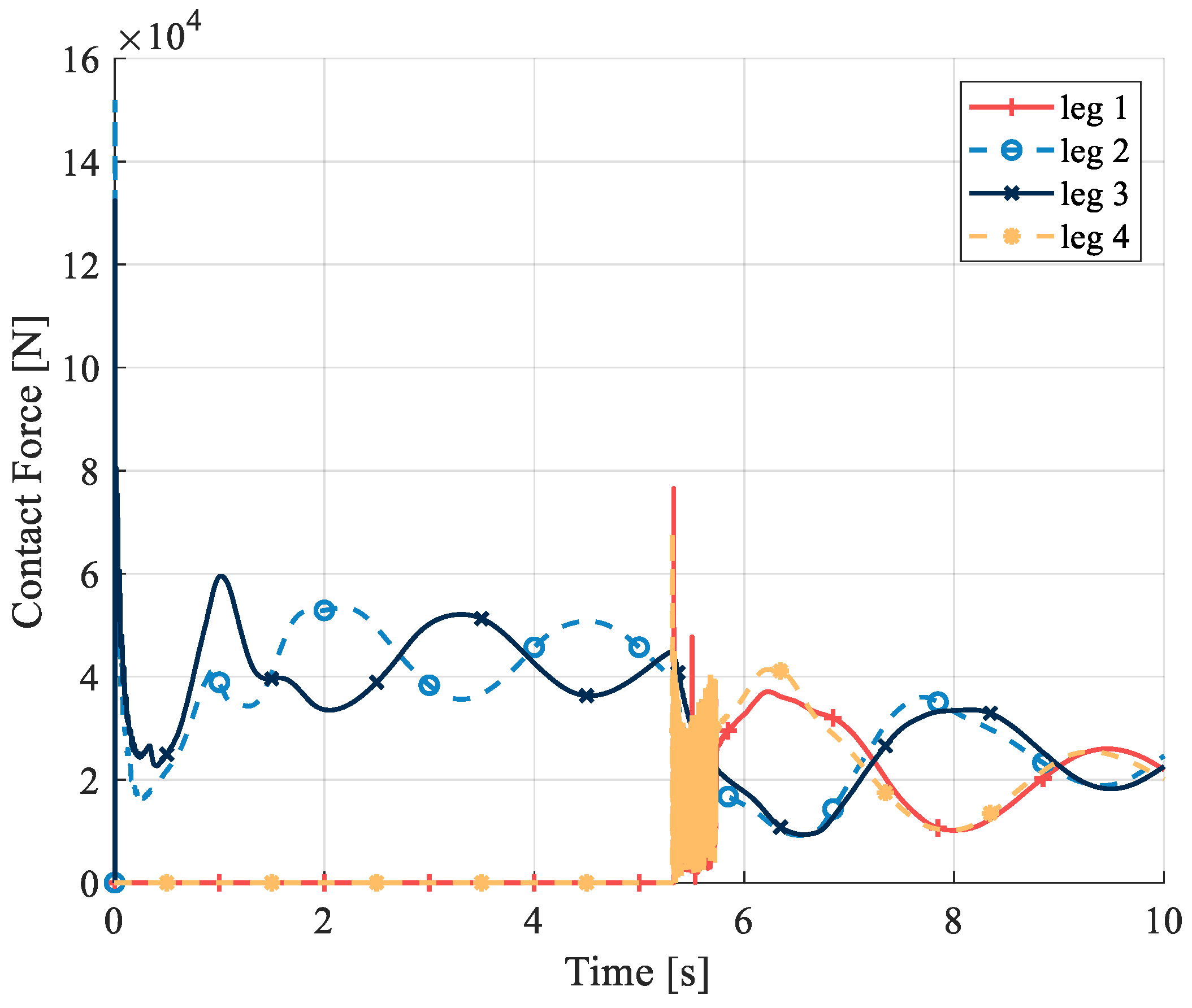
5.2. Comparison Between Different Initial Velocities
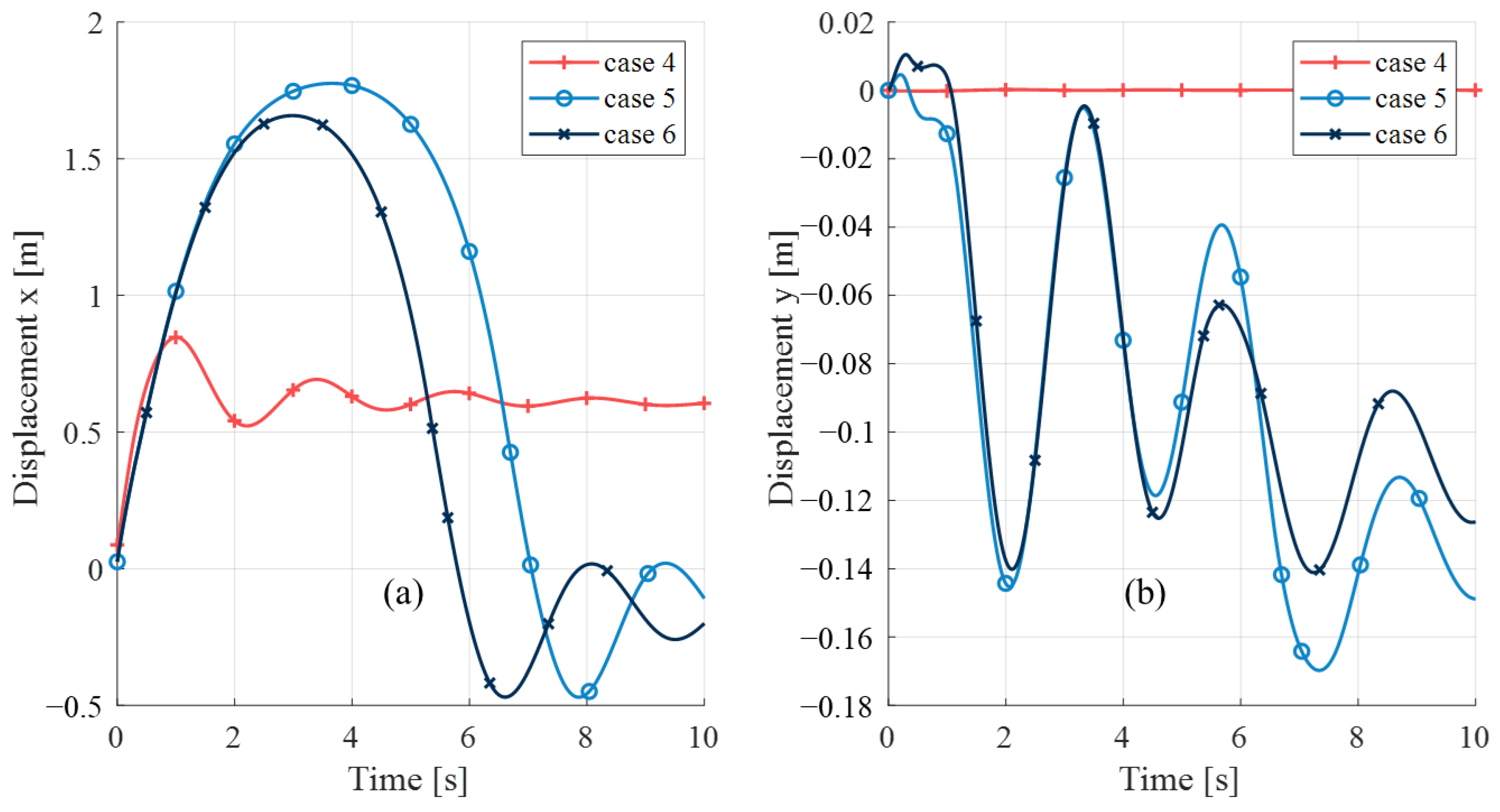
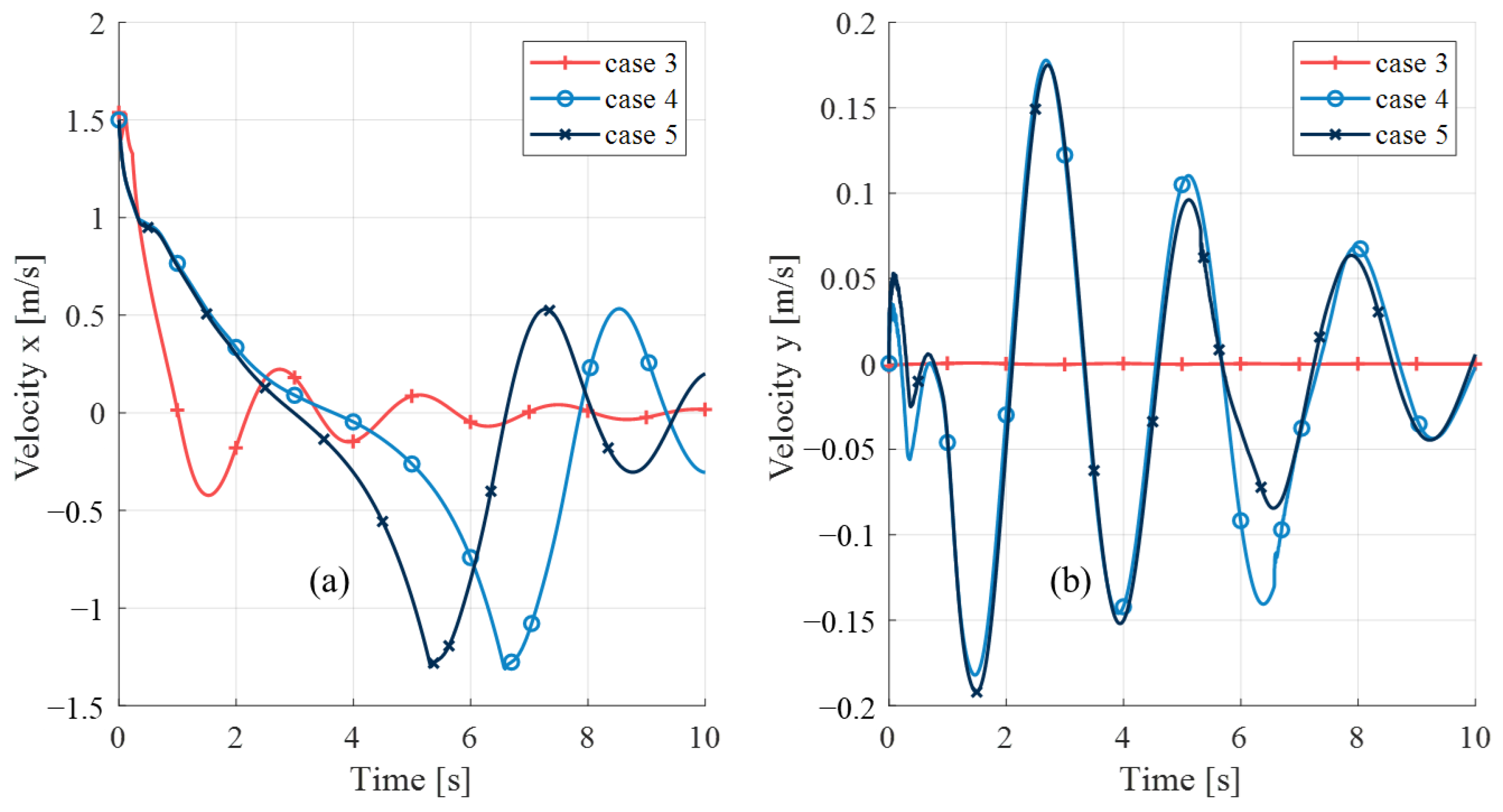
5.3. Analysis of Lateral Motion
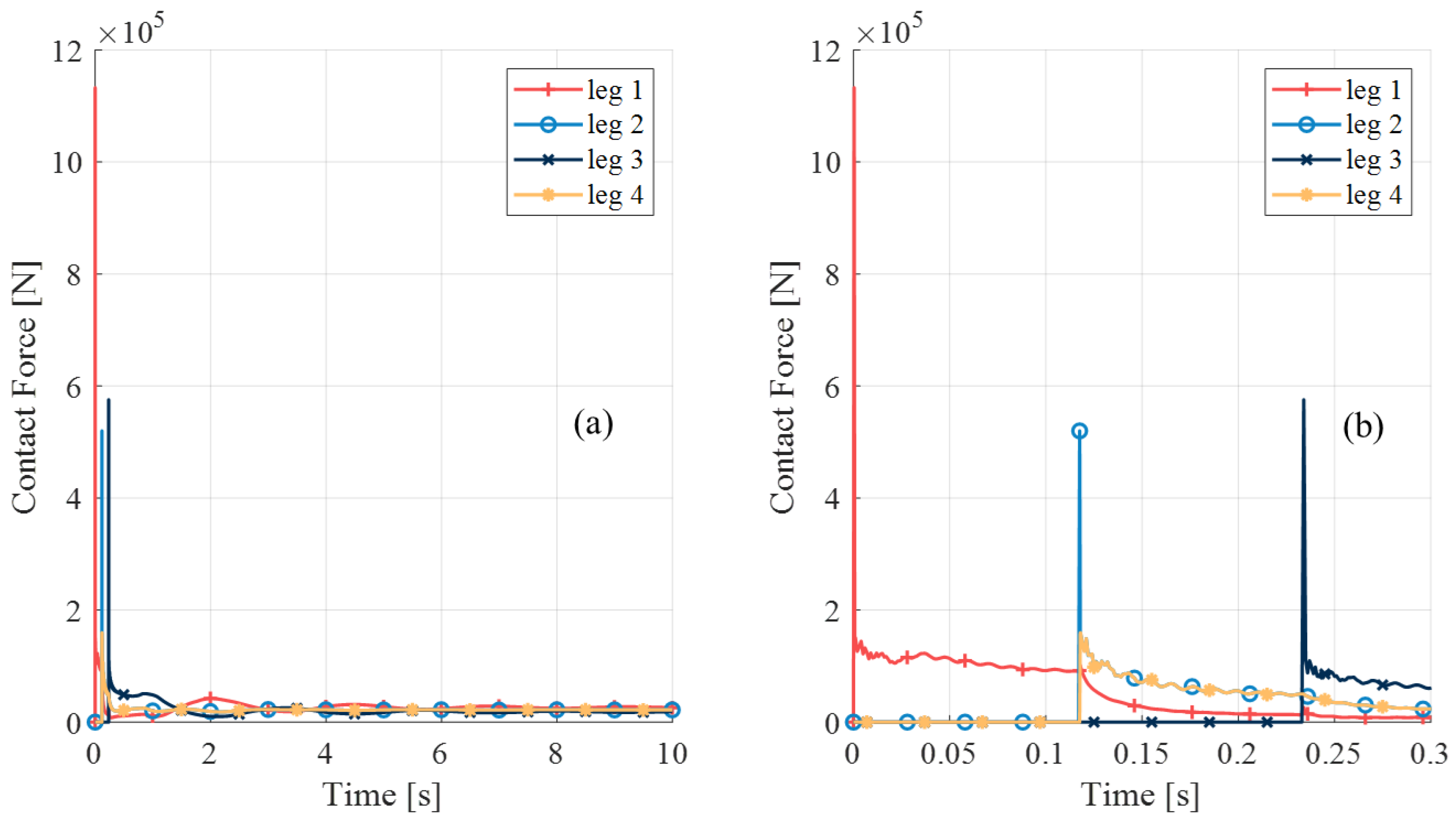
5.4. Maximum Load Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Yu, H.; Xie, J.; Yan, Z.; Tian, B.; Gao, H. The impact modeling and experimental verification of a launch vehicle with crushing-type landing gear. Actuators 2023, 12, 307. [Google Scholar] [CrossRef]
- Heckmann, A.; Otter, M.; Dietz, S.; Lopez, J.D. The DLR flexiblebodies library to model large motions of beams and of flexible bodies exported from finite element programs. In Proceedings of the 5th International Modelica Conference, Wien, Austria, 4–5 September 2006; pp. 85–95. [Google Scholar]
- Briese, L.; Acquatella, B.; Schnepper, K. Multidisciplinary Modeling and Simulation Framework for Launch Vehicle System Dynamics and Control. Acta Astronaut. 2020, 170, 652–664. [Google Scholar] [CrossRef]
- Thies, C. Investigation of the landing dynamics of a reusable launch vehicle and derivation of dimension loading for the landing leg. CEAS Space J. 2022, 14, 565–576. [Google Scholar] [CrossRef]
- Yue, S.; Lin, Q.; Zheng, G.; Du, Z. Modeling and experimental validation of vertical landing reusable launch vehicle under symmetric landing conditions. Chin. J. Aeronaut. 2022, 35, 156–172. [Google Scholar] [CrossRef]
- Yue, S.; Titurus, B.; Nie, H.; Zhang, M. Liquid spring damper for vertical landing reusable launch vehicle under impact conditions. Mech. Syst. Signal Process. 2019, 121, 579–599. [Google Scholar]
- Yue, S.; Nie, H.; Zhang, M.; Huang, M.; Zhu, H.; Xu, D. Dynamic analysis for vertical soft landing of reusable launch vehicle with landing strut flexibility. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 1377–1396. [Google Scholar] [CrossRef]
- Yue, S.; Titurus, B.; Li, Z.; Wu, C.; Du, Z. Analysis of liquid spring damper for vertical landing reusable launch vehicle with network-based methodology. Nonlinear Dyn. 2023, 111, 2135–2160. [Google Scholar]
- Witte, L.; Buchwald, R.; Schröder, S. Touch-down dynamics and terrain interaction of planetary landing systems. In Proceedings of the Global Lunar Conference, Beijing, China, 31 May 2010; pp. 1–10. [Google Scholar]
- Yu, H.; Tian, B.; Yan, Z.; Gao, H.; Zhang, H.; Wu, H.; Wang, Y.; Shi, Y.; Deng, Z. Watt linkage–based legged deployable landing mechanism for reusable launch vehicle: Principle, prototype design, and experimental validation. Engineering 2023, 20, 120–133. [Google Scholar]
- De Oliveira, A.; Lavagna, M. Development of a controlled dynamics simulator for reusable launcher descent and precise landing. Aerospace 2023, 10, 993. [Google Scholar] [CrossRef]
- Mo, R.; Li, W.; Su, S. UDE-based adaptive dynamic surface control for attitude-constrained reusable launch vehicle. Nonlinear Dyn. 2024, 112, 5365–5378. [Google Scholar]
- Xu, S.; Guan, Y.; Bai, Y.; Wei, C. Practical predefined-time barrier function-based adaptive sliding mode control for reusable launch vehicle. Acta Astronaut. 2023, 204, 376–388. [Google Scholar]
- Farì, S.; Seelbinder, D.; Theil, S. Advanced GNC-oriented modeling and simulation of vertical landing vehicles with fuel slosh dynamics. Acta Astronaut. 2023, 204, 294–306. [Google Scholar] [CrossRef]
- Wang, C.; Chen, J.; Jia, S.; Chen, H. Parameterized design and dynamic analysis of a reusable launch vehicle landing system with semi-active control. Symmetry 2020, 12, 1572. [Google Scholar] [CrossRef]
- Kobayakawa, T.; Kawato, H.; Mochizuki, K.; Sakamoto, N.; Habaguchi, Y. Abort recovery strategy for future vertical landing systems. Acta Astronaut. 2015, 116, 148–153. [Google Scholar] [CrossRef]
- Schneider, A.; Desmariaux, J.; Klevanski, J.; Schröder, S.; Witte, L. Deployment dynamics analysis of CALLISTO’s approach and landing system. CEAS Space J. 2023, 15, 343–356. [Google Scholar] [CrossRef]
- Li, W.; Zhang, X.; Dong, Y.; Lin, Y.; Li, H. Powered landing control of reusable rockets based on softmax double DDPG. Aerospace 2023, 10, 590. [Google Scholar] [CrossRef]
- Musso, G.; Figueiras, I.; Goubel, H.; Gonçalves, A.; Costa, A.; Ferreira, B.; Azeitona, L.; Barata, S.; Souza, A.; Afonso, F.; et al. A multidisciplinary optimization framework for ecodesign of reusable microsatellite launchers. Aerospace 2024, 11, 126. [Google Scholar] [CrossRef]
- Shabana, A.A. Dynamics of Multibody Systems; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Huang, G.; Zhu, W.; Yang, Z.; Feng, C.; Chen, X. Reanalysis-based fast solution algorithm for flexible multi-body system dynamic analysis with floating frame of reference formulation. Multibody Syst. Dyn. 2020, 49, 271–289. [Google Scholar] [CrossRef]
- Li, H.; Yu, Z.; Guo, S.; Cai, G. Investigation of joint clearances in a large-scale flexible solar array system. Multibody Syst. Dyn. 2018, 44, 277–292. [Google Scholar]
- Simeon, B. Computational Flexible Multibody Dynamics. A Differential-Algebraic Approach; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Haug, E. Computer-Aided Kinematics and Dynamics of Mechanical Systems. In Modern Methods, 4th ed.; Ed & Carol Haug Charitable Foundation: Silver City, NM, USA, 2024; Volume 2. [Google Scholar]
- Shock Absorption Tests. Advisory Circular from Federal Aviation Administration, U.S. Department of Transportation, No. 25.723-1; U.S. Department of Transportation: Washington, DC, USA, 2001. Available online: https://www.faa.gov/documentLibrary/media/Advisory_Circular/AC_25_723-1.pdf (accessed on 25 March 2025).
- No. HB 6645-1992; Test Methods and Requirements for Drop Shock of Aircraft Landing Gear Buffers. Chinese Industry Standard: Beijing, China, 1993. Available online: https://kns.cnki.net/kcms2/article/abstract?v=_GofKS1StuQnNqplTb-m5y50A1tPD2E6Ape1oprmx-CxBLFS2M6H8EBlkqY_-JuXzusEFtUNG-fETtFtdxpvZU9zai8I5Umbyg6UDp6FjOLVRJKIaeC1MWTw7n6pqewGVER-nGDIYkf4FbJ_fb1ZBPbbuBX68GBpMCyGjCosy2BfpKS1N_lQ1QITRlE3utMT&uniplatform=NZKPT&language=CHS (accessed on 25 March 2025). (In Chinese)





| Part | Mass (kg) | |||
|---|---|---|---|---|
| Main body cabin | 8325.38 kg | 1.628 × 105 kgm2 | 1.629 × 105 kgm2 | 9.37 × 103 kgm2 |
| Main strut | 43.64 kg | 7.47 kgm2 | 7.46 kgm2 | 0.16 kgm2 |
| Auxiliary strut | 191.70 kg | 65.8 kgm2 | 55.3 kgm2 | 1.18 kgm2 |
| Spring | 28.38 kg | 2.55 kgm2 | 2.54 kgm2 | 0.075 kgm2 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Wind velocity | 10 m/s | Contact stiffness | 1 × 108 N/m |
| Drag factor | 0.9 | Contact damping | 1 × 107 Ns/m |
| Windward area | 45.3 m2 | Contact radius | 0.2 m |
| Air density | 1.29 kg/m3 | Contact exponent | 2.0 |
| Static friction | 0.6 | Dynamical friction | 0.4 |
| Case | Vertical Velocity | Lateral Velocity | Initial Orientation | Angular Velocity | Thrust Aftereffect | Wind Load |
|---|---|---|---|---|---|---|
| 1 | 1.8 m/s | 0 m/s | [0, 0, 0]° | [0, 0, 0]°/s | no | no |
| 2 | 1.8 m/s | 0 m/s | [0, 0, 0]° | [0, 0, 0]° | no | no |
| 3 | 2.45 m/s | 0 m/s | [0, 0, 0]° | [0, 0, 0]° | no | no |
| 4 | 1.8 m/s | −1.5 m/s | [0, 4, 0]° | [0, 4, 0]°/s | no | yes |
| 5 | 1.8 m/s | −1.5 m/s | [45, 4, 0]° | [0, 4, 0]°/s | yes | yes |
| 6 | 1.8 m/s | −1.5 m/s | [45, 4, 0]° | [3, 4, 0]°/s | yes | yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Xu, W.; Zhao, Y.; Hong, A.; Han, M.; Ji, H.; Sun, C. Dynamics Modeling and Analysis of a Vertical Landing Mechanism for Reusable Launch Vehicle. Aerospace 2025, 12, 280. https://doi.org/10.3390/aerospace12040280
Li H, Xu W, Zhao Y, Hong A, Han M, Ji H, Sun C. Dynamics Modeling and Analysis of a Vertical Landing Mechanism for Reusable Launch Vehicle. Aerospace. 2025; 12(4):280. https://doi.org/10.3390/aerospace12040280
Chicago/Turabian StyleLi, Haiquan, Wenzhe Xu, Yun Zhao, Anzhu Hong, Mingjie Han, Haibo Ji, and Chaoyang Sun. 2025. "Dynamics Modeling and Analysis of a Vertical Landing Mechanism for Reusable Launch Vehicle" Aerospace 12, no. 4: 280. https://doi.org/10.3390/aerospace12040280
APA StyleLi, H., Xu, W., Zhao, Y., Hong, A., Han, M., Ji, H., & Sun, C. (2025). Dynamics Modeling and Analysis of a Vertical Landing Mechanism for Reusable Launch Vehicle. Aerospace, 12(4), 280. https://doi.org/10.3390/aerospace12040280







