Direct Numerical Simulation of Boundary Layer Transition Induced by Roughness Elements in Supersonic Flow
Abstract
1. Introduction
2. Numerical Methods
2.1. Navier–Stokes Equations
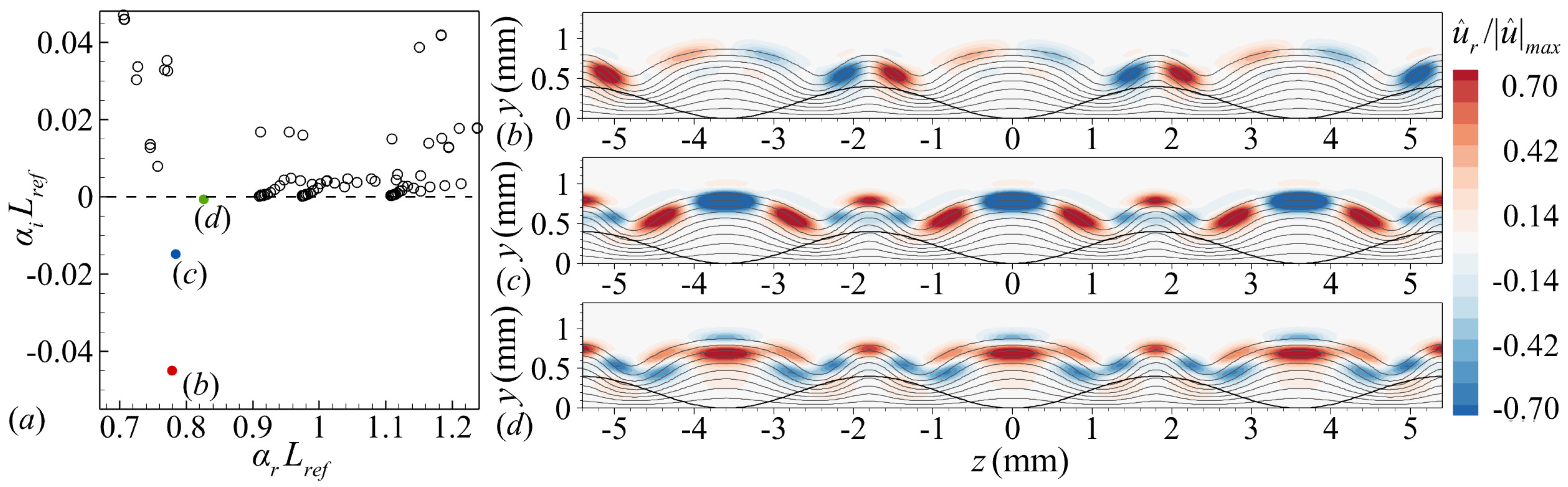
2.2. BiGlobal Stability Analysis
3. Computational Setup
3.1. Description of Problem
3.2. Grid Independence Study
4. Transition Analysis of Roughness Elements and Strips
4.1. General Flow Features
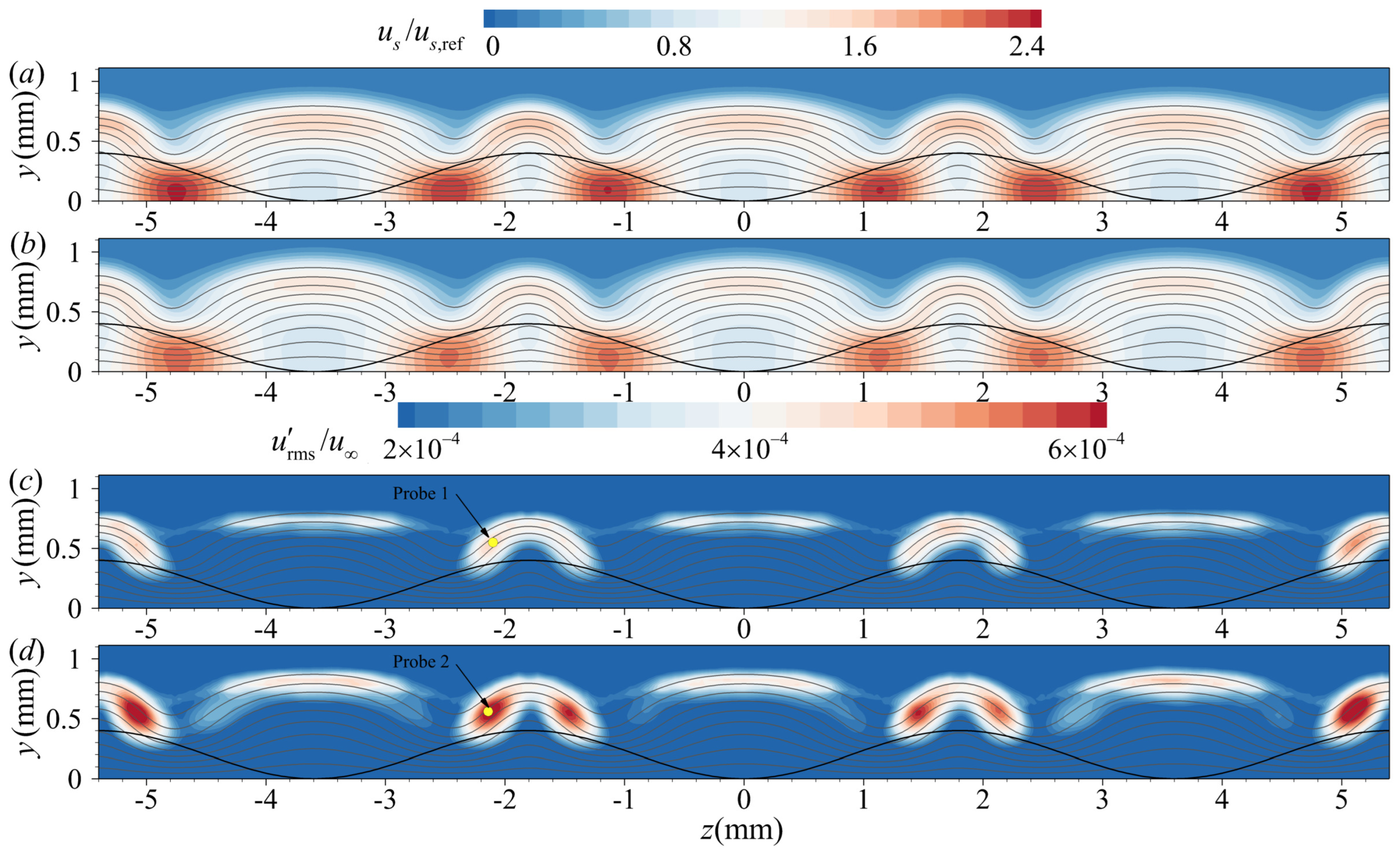
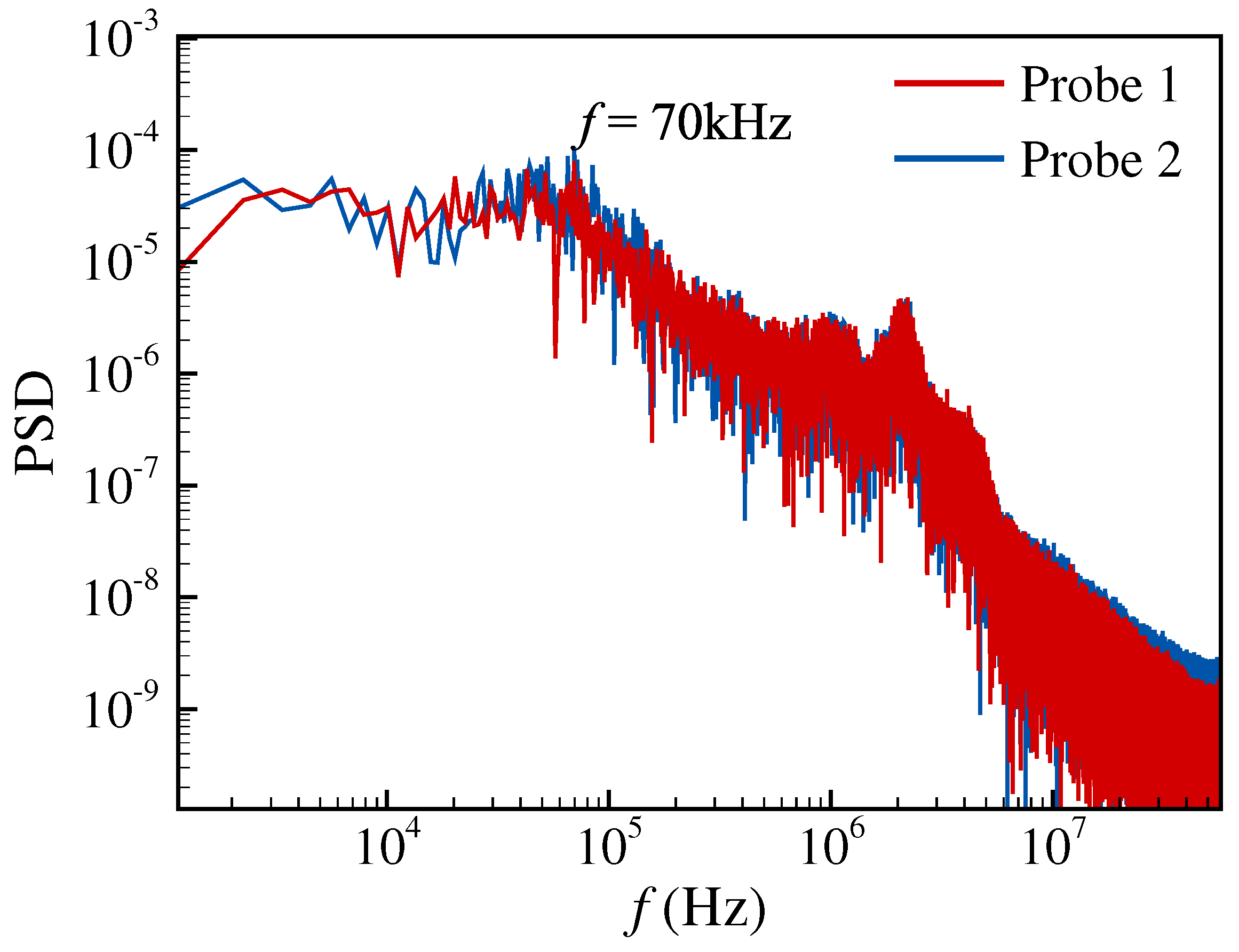
4.2. Instabilities in the Wake Region of the Roughness Element
4.3. Instabilities in the Wake Region of Roughness Strip
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Summary of Key π-Groups
| Dimensionless Parameter | Definition | Physical Significance | Role in the Investigated Problem |
|---|---|---|---|
| Mach number () | = | Characterizes compressibility effects, governing shock formation, energy conversion (kinetic to internal) and flow separation thresholds. | In supersonic flow ( = 3.5), compressibility dominates shock structures and shear layer stability, influencing vortex interactions. |
| Characteristic Reynolds number () | Quantifies inertial-to-viscous force ratio at roughness height, determining critical instability thresholds. | The critical = 770 triggers shear layer separation and vortex shedding, pivotal for transition onset. | |
| Relative roughness height () | Ratio of roughness height to boundary layer thickness, defining perturbation intensity and separation scales. | Moderate = 0.64 balances disturbance strength and boundary layer adaptability, directly governing shear layer and vortex generation. | |
| Spacing ratio () | Spanwise spacing-to-width ratio of roughness strips, modulating vortex interactions and energy transfer. | The S/W ratio magnitude affects vortex interactions and influences the variation in transition location. |
Appendix B. Description of Calculation Configuration and Information
References
- Bernardini, M.; Pirozzoli, S.; Orlandi, P.; Lele, S.K. Parameterization of Boundary-Layer Transition Induced by Isolated Roughness Elements. AIAA J. 2014, 52, 2261–22619. [Google Scholar] [CrossRef]
- Berry, S.A.; Horvath, T.J. Discrete-Roughness Transition for Hypersonic Flight Vehicles. J. Spacecr. Rocket. 2008, 45, 16–27. [Google Scholar] [CrossRef]
- Choudhari, M.; Norris, A.; Li, F.; Chang, C.-L.; Edwards, J. Wake Instabilities behind Discrete Roughness Elements in High Speed Boundary Layers. In Proceedings of the 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013; p. 81. [Google Scholar]
- Lu, Y.; Zeng, F.; Liu, H.; Liu, Z.; Yan, C. Direct numerical simulation of roughness-induced transition controlled by two-dimensional wall blowing. J. Fluid Mech. 2021, 28, 920. [Google Scholar] [CrossRef]
- Fu, S.; Wang, L. RANS modeling of high-speed aerodynamic flow transition with consideration of stability theory. Prog. Aerosp. Sci. 2013, 58, 36–59. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, Z.; Zhou, T.; Yan, C. Stability analysis of roughness-disturbed boundary layer controlled by wall-blowing. Phys. Fluids 2022, 34, 104–114. [Google Scholar] [CrossRef]
- Van den Eynde, J.P.; Sandham, N.D. Numerical Simulations of Transition due to Isolated Roughness Elements at Mach 6. AIAA J. 2016, 54, 53–65. [Google Scholar] [CrossRef]
- Kneer, S.; Guo, Z.; Kloker, M.J. Control of laminar breakdown in a supersonic boundary layer employing streaks. J. Fluid Mech. 2022, A53, 9–32. [Google Scholar] [CrossRef]
- De Tullio, N.; Paredes, P.; Sandham, N.D.; Theofilis, V. Laminar–turbulent transition induced by a discrete roughness element in a supersonic boundary layer. J. Fluid Mech. 2013, 735, 13–46. [Google Scholar] [CrossRef]
- Balakumar, P.; Kegerise, M. Roughness-Induced Transition in a Supersonic Boundary Layer. AIAA J. 2016, 54, 22–37. [Google Scholar] [CrossRef]
- Choudhari, M.; Li, F.; Chang, C.-L.; Edwards, J.; Kegerise, M.; King, R. LLaminar-Turbulent Transition behind Discrete Roughness Elements in a High-Speed Boundary Layer. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; p. 1575. [Google Scholar]
- Semper, M.T.; Bowersox, R.D.W. Tripping of a Hypersonic Low-Reynolds-Number Boundary Layer. AIAA J. 2017, 55, 8–17. [Google Scholar] [CrossRef]
- Bartkowicz, M.; Subbareddy, P.; Candler, G. Numerical Simulations of Roughness Induced Instability in the Purdue Mach 6 Wind Tunnel. In Proceedings of the 40th Fluid Dynamics Conference and Exhibit, Chicago, IL, USA, 28 June–1 July 2010; p. 4723. [Google Scholar]
- Casper, K.; Wheaton, B.; Johnson, H.; Schneider, S. Effect of Freestream Noise on Roughness-Induced Transition at Mach 6. In Proceedings of the 38th Fluid Dynamics Conference and Exhibit, Seattle, WA, USA, 23–26 June 2008; p. 4291. [Google Scholar]
- Wang, L.; Yang, R.; Zhou, Y.; Zhao, Y. Roughness effect of an acoustic metasurface on supersonic boundary layer transition. Appl. Phys. Lett. 2023, 123, 141701. [Google Scholar] [CrossRef]
- Kurz, H.B.E.; Kloker, M.J. Mechanisms of flow tripping by discrete roughness elements in a swept-wing boundary layer. J. Fluid Mech. 2016, 796, 58–94. [Google Scholar] [CrossRef]
- Bernardini, M.; Pirozzoli, S.; Orlandi, P. Compressibility effects on roughness-induced boundary layer transition. Int. J. Heat Fluid Flow 2012, 35, 45–51. [Google Scholar] [CrossRef]
- Subbareddy, P.K.; Bartkowicz, M.D.; Candler, G.V. Direct numerical simulation of high-speed transition due to an isolated roughness element. J. Fluid Mech. 2014, 748, 48–78. [Google Scholar] [CrossRef]
- De Tullio, N.; Sandham, N.D. Influence of boundary-layer disturbances on the instability of a roughness wake in a high-speed boundary layer. J. Fluid Mech. 2015, 763, 36–65. [Google Scholar] [CrossRef]
- Shrestha, P.; Candler, G.V. Direct numerical simulation of high-speed transition due to roughness elements. J. Fluid Mech. 2019, 868, 62–88. [Google Scholar] [CrossRef]
- Liu, Z.; Lu, Y.; Liang, J.; Huang, H. Roughness-Induced Transition in Supersonic Boundary Layers with Wall Heating and Cooling Effects. AIAA J. 2024, 62, 58–75. [Google Scholar] [CrossRef]
- Whitehead, A.H. Flow-Field and Drag Characteristics of Several Boundary-Layer Tripping Elements in Hypersonic Flow; NTRS: Chicago, IL, USA, 1969. [Google Scholar]
- Shrestha, P.; Candler, G.V. Direct Numerical Simulation of Trip Induced Transition. In Proceedings of the 46th AIAA Fluid Dynamics Conference, Washington, DC, USA, 13–17 June 2016; p. 4380. [Google Scholar]
- Shrestha, P.; Nichols, J.W.; Jovanovic, M.R.; Candler, G.V. Study of Trip-Induced Hypersonic Boundary Layer Transition. In Proceedings of the 47th AIAA Fluid Dynamics Conference, Denver, CO, USA, 5–9 June 2017; p. 4513. [Google Scholar]
- Schneider, S.P. Effects of Roughness on Hypersonic Boundary-Layer Transition. J. Spacecr. Rocket. 2008, 45, 193–208. [Google Scholar] [CrossRef]
- De Baets, G.; Szabó, A.; Nagy, P.T.; Paál, G.; Vanierschot, M. Vortex Characterization and Parametric Study of Miniature Vortex Generators and Their Near-Field Boundary Layer Effects. Appl. Sci. 2024, 14, 6966. [Google Scholar] [CrossRef]
- Huang, H.; Liu, Z.; Liu, M.; Tan, H. Direct numerical simulation of distributed roughness induced transition in a supersonic boundary layer. Phys. Fluids 2024, 36, 124115. [Google Scholar] [CrossRef]
- Liu, H.; Peng, K.; Zhao, Y.; Yu, Q.; Kong, Z.; Chen, J. Direct numerical simulation of supersonic boundary layer transition induced by gap-type roughness. Adv. Aerodyn. 2024, 6, 16. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, H.; Tan, H.; Liu, M. Control of Roughness-Induced Transition in Supersonic Flows by Local Wall Heating Strips. J. Fluid Mech. 2024, 999, A16. [Google Scholar] [CrossRef]
- Li, X.; Fu, D.; Ma, Y. Direct Numerical Simulation of Hypersonic Boundary Layer Transition over a Blunt Cone. AIAA J. 2008, 46, 899–913. [Google Scholar] [CrossRef]
- Jiang, G.; Shu, C. Efficient Implementation of Weighted ENO Schemes. J. Comput. Phys. 1996, 126, 2–28. [Google Scholar] [CrossRef]
- Martín, M.P.; Taylor, E.M.; Wu, M.; Weirs, V.G. A bandwidth-optimized WENO scheme for the effective direct numerical simulation of compressible turbulence. J. Comput. Phys. 2006, 220, 70–89. [Google Scholar] [CrossRef]
- Steger, J.L.; Warming, R.F. Flux vector splitting of the inviscid gasdynamic equations with application to finite-difference methods. J. Comput. Phys. 1981, 40, 63–93. [Google Scholar] [CrossRef]
- Zhang, W.; Samtaney, R. BiGlobal linear stability analysis on low-Re flow past an airfoil at high angle of attack. Phys. Fluids 2016, 28, 44–105. [Google Scholar] [CrossRef]
- Sun, Y.; Taira, K.; Cattafesta, L.N.; Ukeiley, L.S. Biglobal instabilities of compressible open-cavity flows. J. Fluid Mech. 2017, 826, 270–301. [Google Scholar] [CrossRef]
- Fernández-Gámiz, U.; Marika, V.C.; Réthoré, P.-E.; Sørensen, N.N.; Egusquiza, E. Testing of self-similarity and helical symmetry in vortex generator flow simulations. Wind. Energy 2016, 19, 43–52. [Google Scholar] [CrossRef]
- Fassbender, H.; Kressner, D. Structured Eigenvalue Problems. Gamm-Mitteilungen 2006, 29, 297–318. [Google Scholar] [CrossRef]
- Redford, J.A.; Sandham, N.D.; Roberts, G.T. Compressibility Effects on Boundary-Layer Transition Induced by an Isolated Roughness Element. AIAA J. 2010, 48, 18–30. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow, 3rd ed.; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Han, J.; He, L.; Xu, X.; Wu, Z. Experimental Investigation of a Roughness Element Wake on a Hypersonic Flat Plate. Aerospace 2022, 9, 574. [Google Scholar] [CrossRef]
- Nakagawa, K.; Takahiro, T.; Takahiro, I. DNS Study on Turbulent Transition Induced by an Interaction between Freestream Turbulence and Cylindrical Roughness in Swept Flat-Plate Boundary Layer. Aerospace 2023, 10, 128. [Google Scholar] [CrossRef]

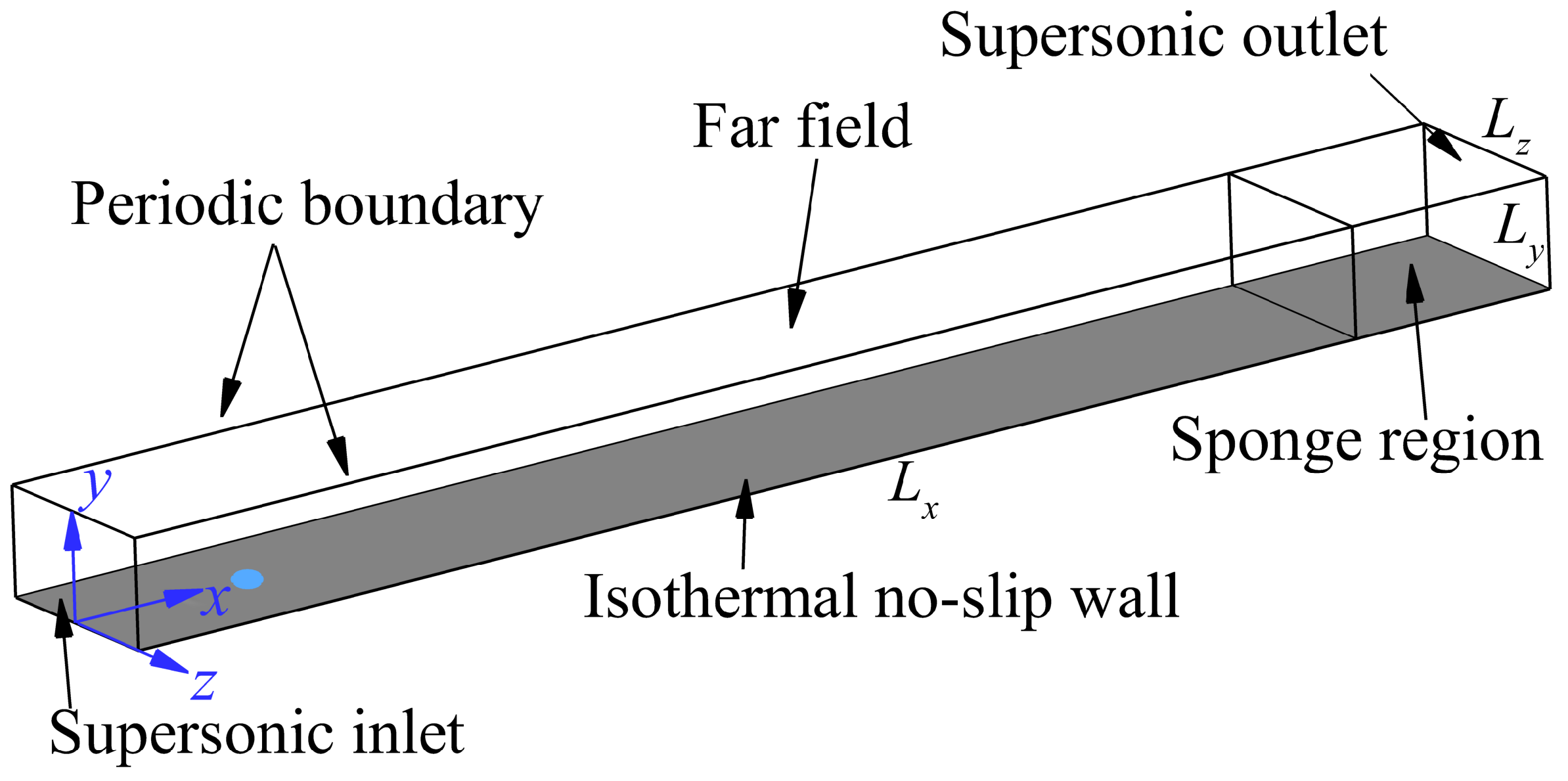
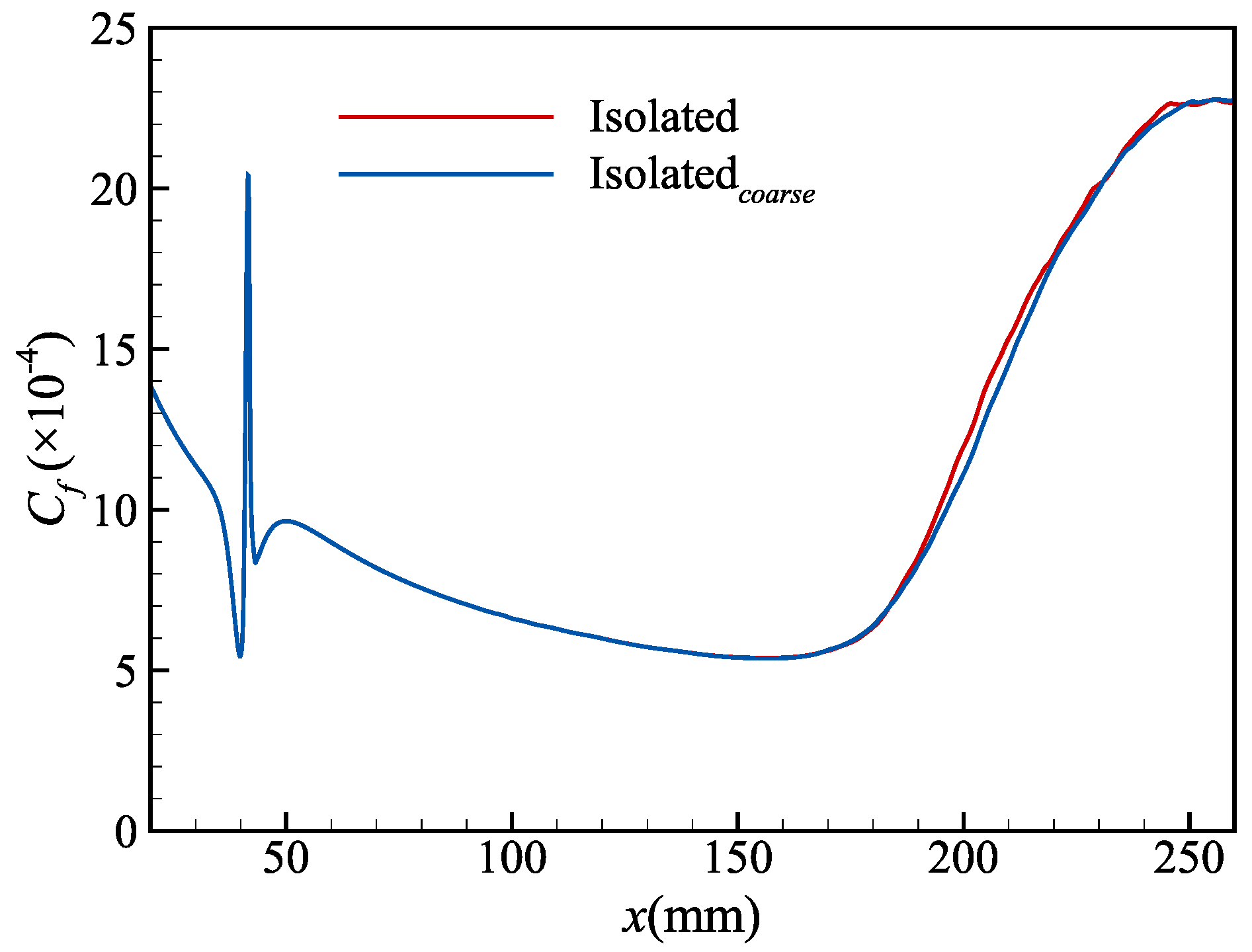
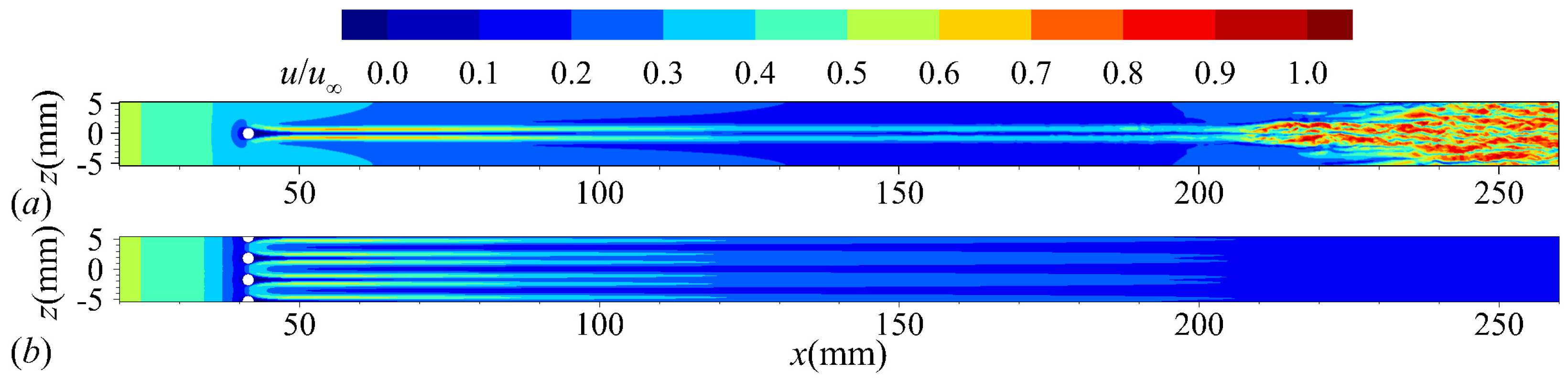
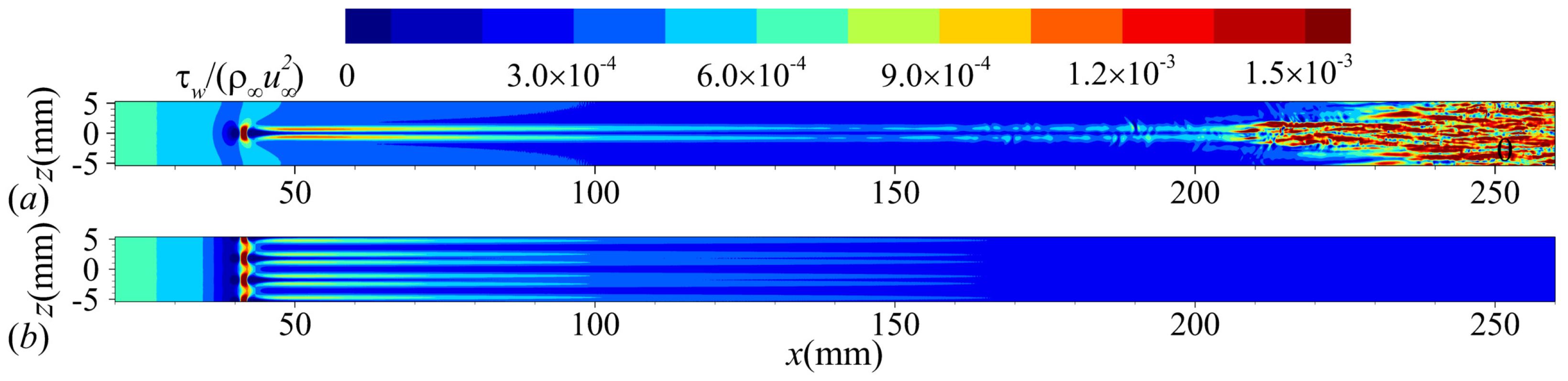
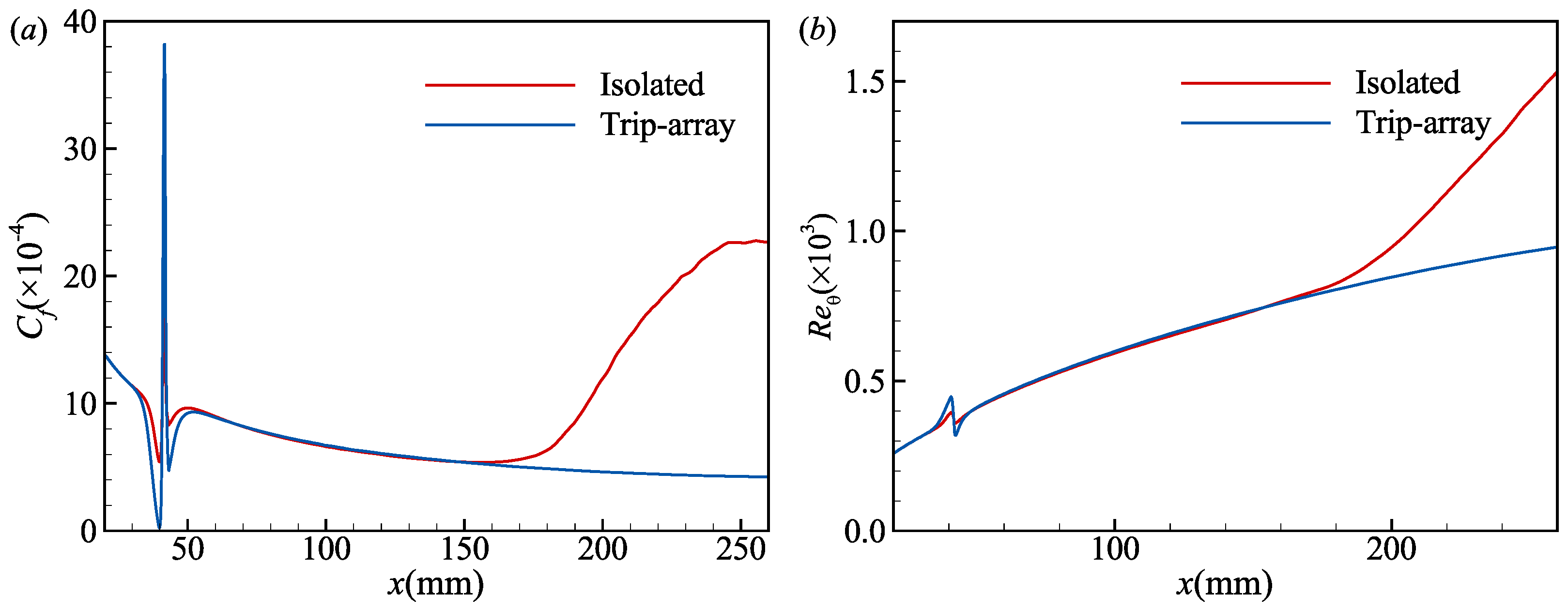
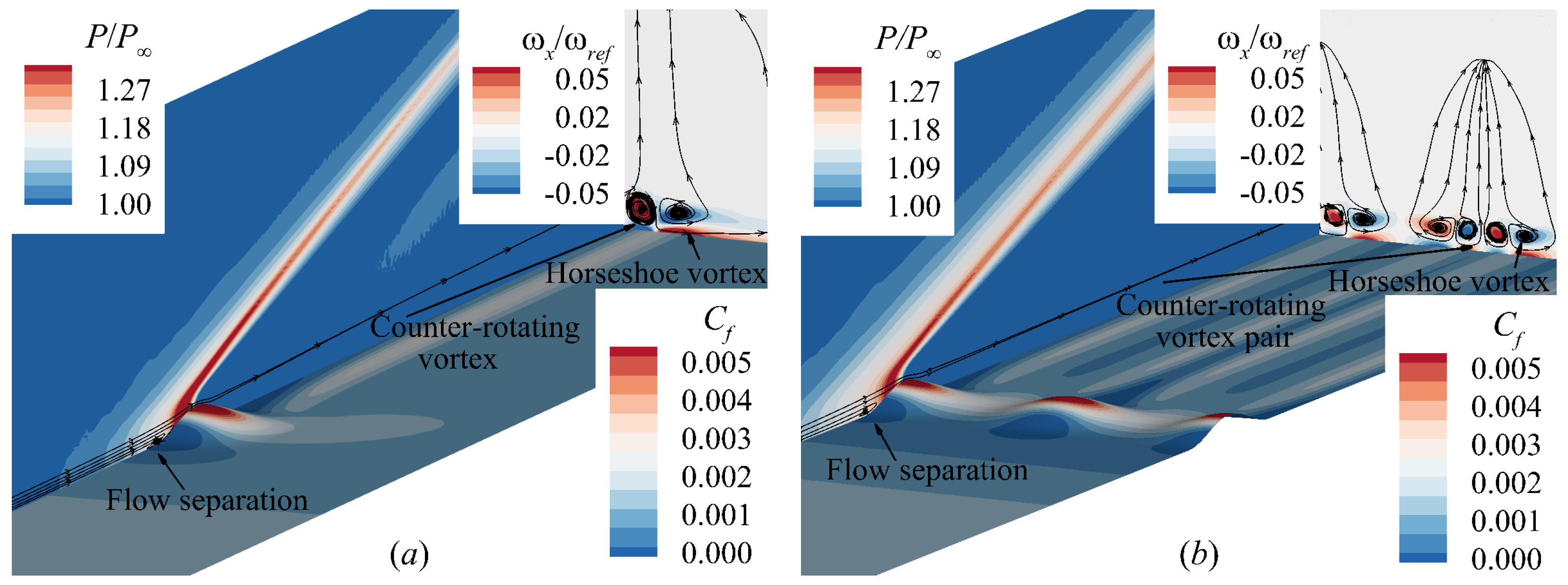


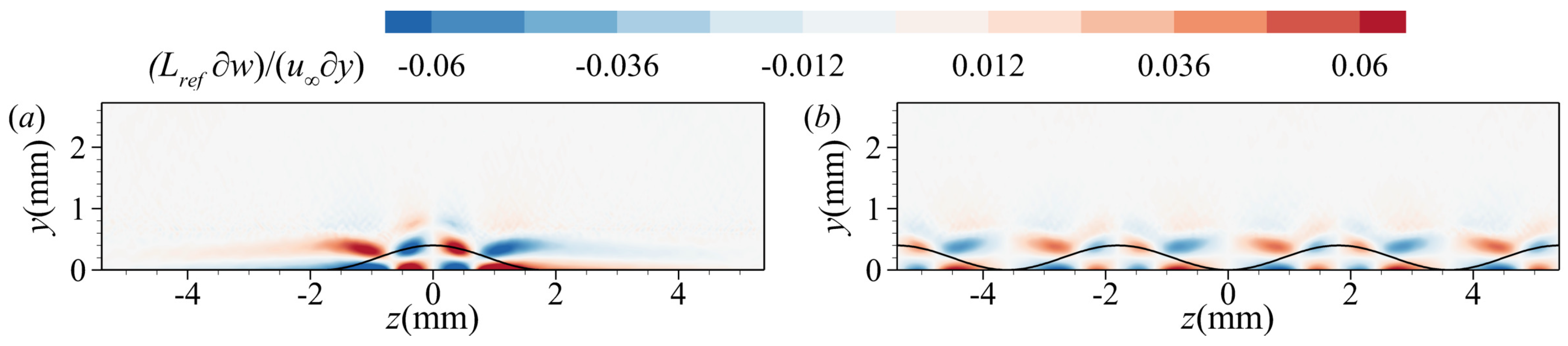

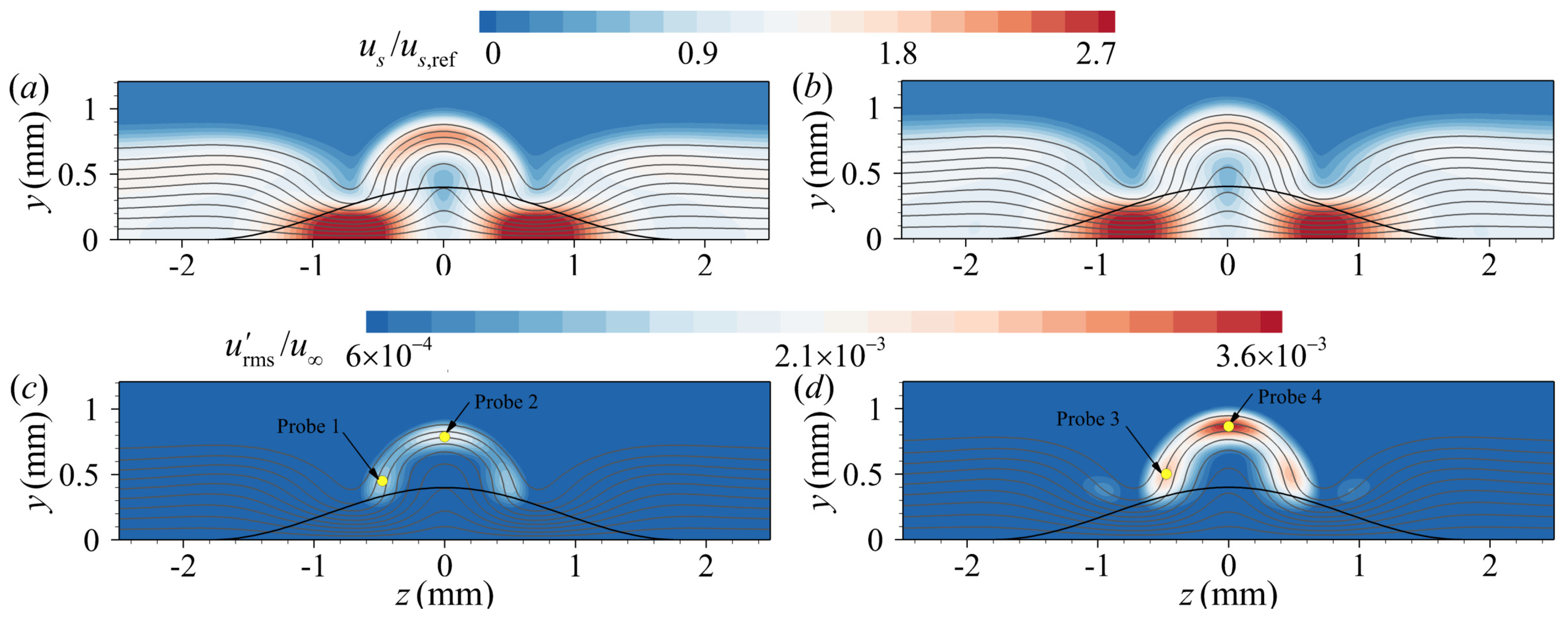


| , m−1 | , K | , K | , mm | ||
|---|---|---|---|---|---|
| 3.5 | 1.08 × 107 | 92.55 | 290 | 0.6242 | 770 |
| Case | ||
|---|---|---|
| Isolated | 3888 × 156 × 363 | 5.6 × 0.85 × 2.7 |
| Isolatedcoarse | 3120 × 135 × 289 | 7.0 × 0.95 × 3.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Liu, Z.; Huang, H.; Tan, H.; Zhao, D. Direct Numerical Simulation of Boundary Layer Transition Induced by Roughness Elements in Supersonic Flow. Aerospace 2025, 12, 242. https://doi.org/10.3390/aerospace12030242
Wang H, Liu Z, Huang H, Tan H, Zhao D. Direct Numerical Simulation of Boundary Layer Transition Induced by Roughness Elements in Supersonic Flow. Aerospace. 2025; 12(3):242. https://doi.org/10.3390/aerospace12030242
Chicago/Turabian StyleWang, Haiyang, Zaijie Liu, Hexia Huang, Huijun Tan, and Dan Zhao. 2025. "Direct Numerical Simulation of Boundary Layer Transition Induced by Roughness Elements in Supersonic Flow" Aerospace 12, no. 3: 242. https://doi.org/10.3390/aerospace12030242
APA StyleWang, H., Liu, Z., Huang, H., Tan, H., & Zhao, D. (2025). Direct Numerical Simulation of Boundary Layer Transition Induced by Roughness Elements in Supersonic Flow. Aerospace, 12(3), 242. https://doi.org/10.3390/aerospace12030242









