Abstract
This paper presents an attitude stabilization algorithm for a Low Earth Orbit (LEO) Earth-pointing spacecraft using magnetorquers as the only torque actuators and employing Model-Free Adaptive Control (MFAC) as the control algorithm. MFAC is a data-driven control algorithm that relies solely on input–output data from the plant. This paper validates the effectiveness of the proposed approach through numerical simulations in a specific case study. The simulations show that the proposed algorithm drives the spacecraft’s attitude to three-axis stabilization in the orbital frame from arbitrary initial tumbling conditions. The numerical study also shows that the proposed control algorithm outperforms a model-based Proportional–Derivative (PD) control in terms of pointing accuracy at the expense of higher energy consumption.
1. Introduction
Spacecraft often have an attitude stabilization system. They can be either passive (e.g., spin-stabilized or gravity gradient-stabilized systems [1]) or active. The most accurate active stabilization systems usually include momentum or reaction wheels. However, in some spacecraft flying in low Earth orbits, attitude stabilization is achieved using magnetorquers. These systems are composed of flat coils, which are activated by electric currents and securely positioned on the spacecraft, usually along three perpendicular axes. They function by utilizing the interaction between the magnetic dipole moment produced by these coils and the Earth’s magnetic field. Specifically, this interaction with the Earth’s field induces a torque that endeavors to orient the entire magnetic dipole moment in alignment with the direction of the field. Consequently, magnetorquers present the following strong points: (i) they offer simplicity, reliability, and affordability; (ii) they solely require renewable electrical power for their operation; (iii) they contribute to reducing overall system weight when compared to alternative torque actuators. However, magnetorquers come with significant drawbacks: (i) the control torque they produce is limited to the plane perpendicular to the Earth’s magnetic field; (ii) their maximum torque output is considerably lower compared to other types of torque actuators. As a result of these limitations, relying exclusively on magnetorquers for attitude control results in reduced pointing accuracy and slower convergence in comparison to alternative torque actuators [2]. Attitude stabilization through magnetorquers has been explored as a viable choice, particularly for cost-effective micro- and nanosatellites and satellites encountering failures in their primary torque actuators [3]. Paper [4] provides an extensive review of results on several methods for active attitude control using magnetic actuators.
This paper focuses on active three-axis attitude stabilization of an Earth-pointing spacecraft with magnetorquers as the only torque actuators and without onboard momentum storage. The literature in this specific area of research is vast, and several works propose PD-like stabilization laws. Since a spacecraft with magnetometers is intrinsically a time-varying plant due to the variation in the geomagnetic field along the orbit, selecting the PD gains is not a straightforward task. In [5], the scalar PD gains are selected to guarantee stability by considering the locus for the characteristic multipliers. Reference [6] presents a semi-analytic approach for selecting scalar gains that optimize the time response. Paper [7] proposes time-varying matrix gains that guarantee stability by solving linear–quadratic optimization problems. The same work also presents a method for designing constant matrix gains considering a time-invariant approximated model. However, the method does not guarantee stability, which must be checked separately. Work [8] also determines time-varying gains by a linear–quadratic approach and extends it to the rejection of generic disturbance torques. A similar approach in discrete time is employed in [9]. In [10,11], constant matrix gains are designed by solving a different linear–quadratic optimization problem by which stability is obtained. Paper [12] proposes an adaptation mechanism for the gains to guarantee stability and also convergence to the nominal attitude for almost all initial conditions. A different PD-like stabilization law is presented in [13], where the gains are determined through a heuristic optimization strategy without providing an analytical stability analysis. A reconfiguration method for a PD-like stabilization law in case of failure of a magnetometer is proposed in [14]. A Proportional–Integral–Derivative (PID)-like stabilization algorithm is employed in [15] to achieve more accurate pointing. However, similarly to before, the proposed method does not guarantee stability, which must be checked after having determined the gains. Reference [16] proposes a more complex law designed by a robust backstepping method which achieves global asymptotic stability. Work [17] presents a two-timescale control in which, first, the pitch axis is aligned to the orbit normal, and then the pitch rate is enforced to the desired value, thus achieving stability for the closed loop. Paper [18] presents an algorithm based on a sequence of Riccati equations for which stability is not guaranteed.
All the designs presented in the cited works present limitations in rejecting the effects of some disturbance torques. This is probably a consequence of the fact that those designs are model-based, and models for those disturbance torques are not included in the design process. To overcome the above limitation, data-driven control can be a valid alternative. Indeed, in data-driven control, there is no necessity for a mathematical spacecraft model in the design process. It relies completely on the measurements coming from the Input/Output (I/O) data of the plant that have to be controlled. Data-driven control methods are divided into two main categories: online and offline data-driven methods. In offline methods, controller parameters are estimated through a learning process before implementation on the controlled plant. Several offline data-driven methods have been developed including iterative feedback tuning [19], correlation-based tuning [20], virtual reference feedback tuning [21], and PID control [22]. On the other hand, in online data-driven methods, only initial values are assigned to the controller parameters, which are updated online without employing any identification process. Several online data-driven methods were developed such as Simultaneous Perturbation Stochastic Approximation (SPSA) [23], unfalsified control [24], dynamic neural network-based control [25], and model-free adaptive control [26,27,28].
Online data-driven control was employed for three-axis stabilization of an Earth-pointing spacecraft with magnetorquers in [29], in which dynamic neural networks were utilized. In this paper, the same type of attitude stabilization is performed by using a different online data-driven method known as Model-Free Adaptive Control (MFAC). The MFAC method is based on the dynamic linearization technique and a new concept called Pseudo Partitioned Jacobian Matrix (PPJM) [26]. The PPJM is employed to dynamically linearize the nonlinear plant in real time, based on I/O measurement data. By estimating the PPJM, the controller output can be calculated. The MFAC method stands out as a feasible solution for the attitude stabilization of spacecraft with magnetorquers due to the following reasons: (1) no mathematical model of the spacecraft with magnetorquer is required, leading to the design of an attitude controller which is solely based on the available I/O measurement data; (2) when contrasted with other data-driven controllers, MFAC requires the tuning of few parameters and low computational effort, making it a practical and efficient choice; (3) MFAC is known for its adaptive structure, allowing it to handle variations in the spacecraft’s dynamics and environmental conditions; in fact, spacecraft operations can involve different variations such as those due to changing payloads and orbital conditions, and MFAC can adapt control actions based on real-time measurements; (4) some control methods require knowledge of bounds on the plant initial conditions which are unnecessary for MFAC; such a feature is advantageous for spacecraft control, where obtaining those bounds could be unfeasible; (5) MFAC has demonstrated successful implementation in various practical fields such as combustion systems [30], combined spacecraft [31], unmanned surface vehicles [32], launch vehicles [33,34], air vehicle pitch channels [35], moving mass controlled flying robots [36], multiagent systems [37], autonomous cars [38], wastewater treatment processes [39], wind turbine rotors with controllable flaps [40], and satellites with large rotational components [41].
The effectiveness of the MFAC design is evaluated through numerical simulations. Specifically through Monte Carlo campaigns, it is shown that the designed attitude controller is able to achieve three-axis stabilization in the orbital frame from an arbitrary tumbling condition. Moreover, the numerical study also reveals that the proposed control algorithm outperforms a model-based PD control in terms of pointing accuracy at the expense of higher energy consumption.
Employing MFAC for three-axis stabilization of an Earth-pointing spacecraft using only magnetorquers represents a novel approach. In [31], the MFAC method is used for the attitude stabilization of a combined spacecraft that is fully actuated and is not affected by disturbance torques. The main differences compared to the attitude stabilization considered in [31] are as follows: (i) torque actuation is obtained by using magnetorquers in place of reaction flywheels; (ii) disturbance torques are considered in evaluating the performance of the proposed method; (iii) stabilization is performed with respect to the orbital frame instead of an inertial frame. As a result, in all above aspects, the present work presents advancements with respect to [31]. In [41], a modified version of MFAC called model-free prescribed performance adaptive control is employed for the attitude stabilization of a fully actuated satellite with large misaligned rotational components.
This paper is organized into the following sections: The next section describes the attitude of an Earth-pointing spacecraft with magnetorquers. Section 3 introduces the MFAC algorithm employed to stabilize the spacecraft’s attitude. Numerical simulations and evaluation of the obtained results are included in Section 4. Concluding remarks end the paper. The paper includes an appendix which concisely recalls the theoretical framework of MFAC.
2. Attitude of Earth-Pointing Spacecraft with Magnetorquers
2.1. Coordinate Frames
To describe the attitude motion of a rigid Earth-pointing spacecraft in a circular orbit, it is advantageous to introduce reference frames as follows:
- Geocentric Inertial Frame denoted by . This frame is commonly used for Earth orbits. It is centered at the Earth’s core. The axis corresponds to the vernal equinox direction, the axis points northward along the Earth’s axis of rotation, and the axis is chosen to create a right-handed coordinate system.
- Orbital frame denoted by . This frame is also known as the Local Vertical Local Horizontal (LVLH) frame. The origin of the frame is at the spacecraft’s center of mass. The axis aligns with the spacecraft’s velocity direction, the axis is aligned with the nadir direction, and the axis is oriented perpendicular to the orbital plane, forming a right-handed coordinate system.
- Spacecraft body frame denoted by . The origin of the body frame coincides with the spacecraft’s center of mass, and its axes align with principal axes of inertia of the spacecraft.
The desired Earth-pointing orientation corresponds to aligning with .
A summary of the notation used in this paper can be found in Table 1.

Table 1.
Notation.
2.2. Attitude Stabilization Using Magnetorquers
In this work, the primary focus is on the attitude of the spacecraft in relation to the orbital frame. The attitude of relative to is here represented by using quaternion denoted by that is indicated as follows:
with the condition . The angular velocity of relative to resolved in is denoted by .
The spacecraft employs three magnetic coils as torque actuators that are aligned with the axes of the spacecraft’s body frame . These coils generate a magnetic control torque through the following mechanism:
where represents the magnetic dipole moment generated by the three magnetorquers, represents the geomagnetic field at the position of the spacecraft, and both are resolved in .
The objective of this work is stabilizing the nominal Earth-pointing attitude corresponding to and . The available physical control input is given by the variable .
Let and denote the samples of and with sampling time . Since can be measured by using magnetometers, apply the preliminary control action
where denotes the samples of a new purely mathematical control input that will be designed later. The purpose of control in Equation (2) is enforcing that is perpendicular to to save energy, since Equation (1) shows that a term in along does not contribute to the control torque .
3. Attitude Stabilization Using Model-Free Adaptive Control
In this work, attitude stabilization is achieved by using an approach known as Model-Free Adaptive Control (MFAC). MFAC is a data-driven online control that relies on the real-time I/O data of the plant being controlled. In this study, the plant is the spacecraft with magnetorquers, and the variable appearing in Equation (2) is selected as input. Inspired by [31], the output is selected as follows:
in which matrices and are design parameters. and correspond to the nominal Earth-pointing attitude for the spacecraft. Consequently, the desired output is set as .
Let and denote the samples of and with sampling time . The attitude stabilization law employed in this research is known as Full-Form Dynamic Linearization (FFDL)–MFAC ([26] Section 5.4) and is described by the following equation:
In the previous equation, and . Non-negative integers and with are design parameters known as pseudo orders of the controlled plant ([26] Section 3.3.3). Magnitudes and are additional design parameters. Symbols denote 3 × 3 matrices which are obtained from an adaptation law as follows. Introduce the following matrix
which includes all matrices . (Matrix is an estimate of the so-called pseudo partitioned Jacobian matrix ([26] Section 3.3.3, see also Appendix A). Matrix is obtained from the following adaptation law:
In the above equation, is a column matrix of dimension defined as follows:
in which is also a column matrix of dimension given by
Magnitudes and are both design parameters.
The theoretical framework that leads to the FFDL-MFAC algorithm in Equations (4)–(8) is described in [26]. For convenience, a concise description of the framework is reported in Appendix A.
Figure 1 depicts a block diagram of the spacecraft with magnetorquers controlled by the FFDL-MFAC algorithm.
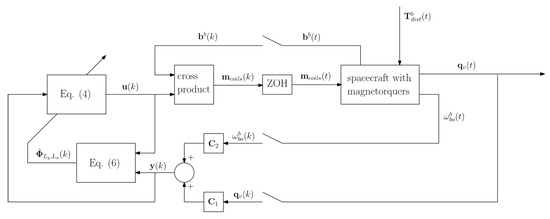
Figure 1.
Block diagram of the spacecraft with magnetorquers controlled by the FFDL-MFAC algorithm (ZOH = Zero-Order Hold, = disturbance torque).
4. Results
This section presents the results of numerical simulations conducted to evaluate the effectiveness of the MFAC method in stabilizing the Earth-pointing attitude of a spacecraft equipped with magnetorquers. Furthermore, the performances achieved with MFAC are compared to those of a model-based control of the PD type.
For the generation of I/O data in numerical simulations, employ the standard model of a rigid spacecraft given by the following attitude kinematics equation
along with the following attitude dynamics equation
where represents the inertia matrix of the spacecraft, , , and denote the gravity gradient torque, the control torque generated by magnetic coils (see Equation (1)), and the disturbance torque all resolved in .
The relation between and is obtained by considering the equation , in which, for the term , the following holds true: with , where n is the constant spacecraft orbital rate. Rotation matrix is obtained from through the following equation:
In the above equation, indicates the three-dimensional identity matrix, and symbol denotes the skew-symmetric matrix.
The model used for the gravity gradient torque resolved in is defined as follows ([1] Section 8.1):
where represents the body coordinates of the unit vector associated with the -axis, which are obtained as follows: .
The major disturbance torques affecting a spacecraft flying in low Earth orbit are considered, and to generate data in the numerical simulations, the following models described in [17] are adopted. The first of these is the residual magnetic torque, which is represented in body coordinates as follows:
in which is the residual magnetic dipole moment from onboard electrical components in body coordinates. The aerodynamic torque is modeled as follows:
where denotes the vector from the mass center to the pressure center resolved in , and represents the aerodynamic force exerted on the spacecraft, also in the frame. The model for is as follows:
in which represents the coefficient related to drag, denotes the area of the cross-section of the spacecraft, corresponds to the density of the atmosphere at the altitude of the orbit, and represents the body coordinates of the spacecraft’s velocity relative to the air, which is approximated using the spacecraft’s velocity. The model of the solar radiation pressure torque is as follows:
where is the vector from the spacecraft’s mass center to the spacecraft’s solar pressure center resolved in , and is the solar radiation pressure force in body coordinates, which is given by
In the above equation, is the constant related to the solar flux density, c is the speed of light, is a factor related to the reflectance, is the sunlit surface area which is assumed constant considering the worst-case scenario, and is the unit vector from the spacecraft to the Sun resolved in . Note that is obtained from , which denotes the same unit vector resolved in .
The numerical values of the parameters for the spacecraft model are obtained from [17] and are reported in Table 2.

Table 2.
Parameters for spacecraft model.
The performances of the MFAC method are compared with those of the following control of the Proportional–Derivative (PD) type
where and are positive scalar gains. The considered PD control law is widely employed in practice for stabilizing the attitude of a spacecraft using only magnetorquers. Thus, it represents a good benchmark for comparing magnetic attitude stabilization methods.
Gains and are selected by employing the approach presented in [5], which can be described as follows: Consider the model given by Equations (9)–(13) and neglect disturbance torques by setting . Use the so-called axial dipole model for the geomagnetic field [11,42] given by
where is the total strength of the axial dipole, is the orbit radius, is the orbit inclination, and is the satellite argument of latitude at time . The corresponding numerical values are reported in Table 2. The resulting spacecraft model is periodic with a period equal to . Thus, select and so that all characteristic exponents of the linearized closed loop have a modulus smaller than one to achieve asymptotic stability for the closed loop ([43] Section 1.2.3). The selected values for and are reported in Table 3.

Table 3.
PD gains.
The resulting characteristic exponents are indicated in Table 4.

Table 4.
Characteristic exponents.
To validate numerically the selection of the gains and , the closed loop obtained by combining Equations (9)–(13) with Equations (19) and (20) is numerically simulated. Specifically, a Monte Carlo campaign of 40 simulation runs is executed with . In each simulation, the initial quaternion is randomly selected with a uniform distribution over all its possible values. The angular velocity at time is randomly selected within the set 10 deg/sec with a uniform distribution. The initial value of the spacecraft argument of latitude is randomly selected with a uniform distribution over .
The three-axis alignment of the body frame to the orbital frame is evaluated through the principal angle of rotation (also known as the Euler angle of rotation) given by
The 40 time behaviors of and of obtained in the considered simplified scenario are represented in Figure 2 and Figure 3.
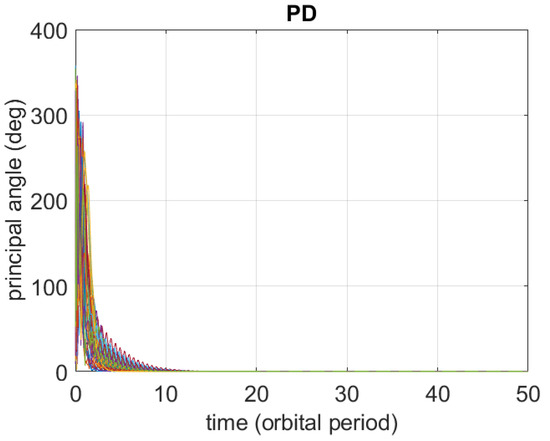
Figure 2.
Time histories of principal angle of rotation using PD control in the simplified scenario.
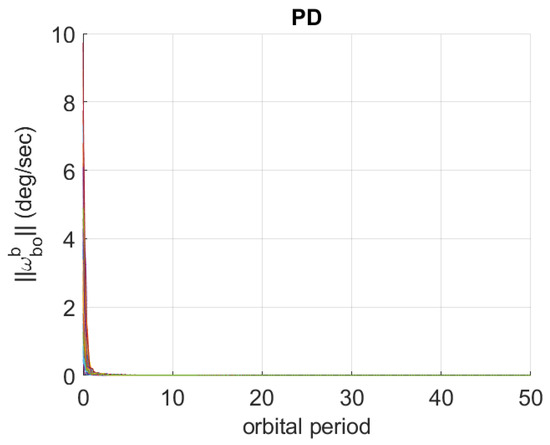
Figure 3.
Time histories of using PD control in the simplified scenario.
The time histories show that PD control is able to stabilize the nominal attitude even for large initial tumbling conditions.
Regarding the FFDL-MFAC algorithm described by Equations (2)–(8), to the best of the authors’ knowledge, a stability analysis is still an open problem ([26] Section 5.4.1.3). Thus, the numerical values of the MFAC parameters are selected by trial-and-error and are reported in Table 5.

Table 5.
MFAC parameters.
The MFAC algorithm is validated numerically first considering the same simplified scenario as for the validation of PD control. As a result, a new Monte Carlo campaign of 40 simulation runs with the same initial conditions as in the previous campaign is executed with MFAC replacing PD. The corresponding 40 time behaviors of the principal angle of rotation and of are represented in Figure 4 and Figure 5.
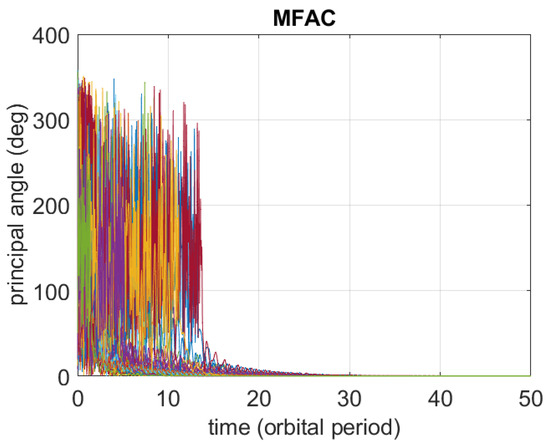
Figure 4.
Time histories of principal angle of rotation using MFAC in the simplified scenario.
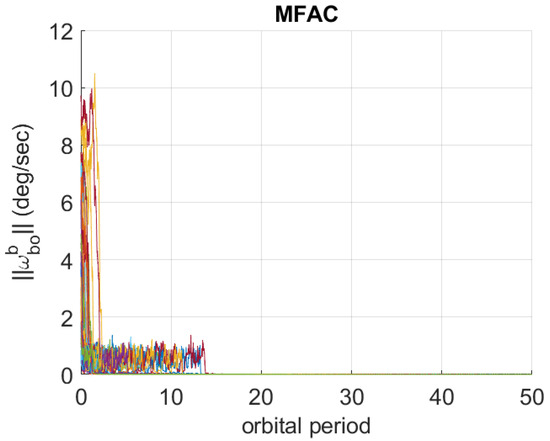
Figure 5.
Time histories of using MFAC in the simplified scenario.
The time histories show that MFAC is also able to stabilize the nominal attitude even for large initial tumbling conditions.
The effectiveness of the MFAC algorithm is evaluated more thoroughly by running more realistic numerical simulations. In those simulations, the disturbance torques in Equations (14), (15) and (17) are included. The geomagnetic field data are generated by using the International Geomagnetic Reference Field (IGRF) [42,44], which is more accurate than the axial dipole model in Equation (20). Navigation errors are introduced by adding Gaussian noise to and with standard deviations equal to and deg/s, respectively. The magnetometer’s measurement noise is modeled as a Gaussian noise with standard deviation equal to T. In each simulation, the initial quaternion , the initial angular velocity , and the initial value of the spacecraft argument of latitude are all randomly selected as in the previous Monte Carlo campaign. In addition, the Earth’s angle of rotation at denoted by (the Earth’s angle of rotation is the angle between the vernal equinox axis and the axis on the equatorial plane from the Earth’s center to the Earth’s prime meridian) is randomly selected with a uniform distribution over . Thus, a new Monte Carlo campaign with 40 simulation runs has been executed, and in such a scenario, the performances of the proposed MFAC method are compared with those of the following PD control:
where the values of and are kept as those indicated in Table 3, and denotes an estimate of the residual dipole moment , which is determined through a Kalman filter [11]. The term partially compensates for the residual magnetic torque in Equation (14), leading to an improvement in three-axis pointing accuracy.
Figure 6 displays a sample time behavior out of the 40 for the principal angle of rotation obtained using MFAC.
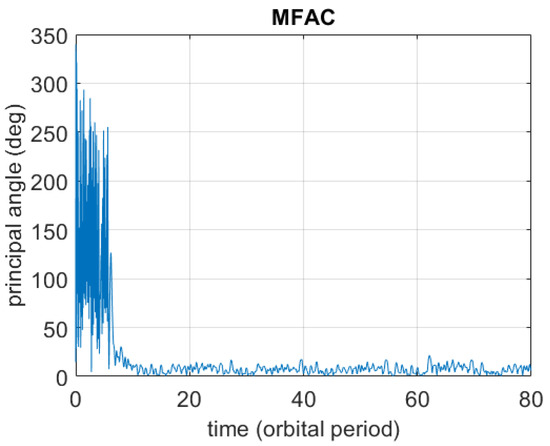
Figure 6.
Sample time history of the principal angle of rotation using MFAC in the realistic scenario.
The initial conditions employed to generate the plot are indicated in Table 6.

Table 6.
Initial conditions employed to generate the plots in Figure 6 through Figure 11.
Figure 7 displays the corresponding time behavior of the principal angle of rotation obtained by using PD control in Equation (22).
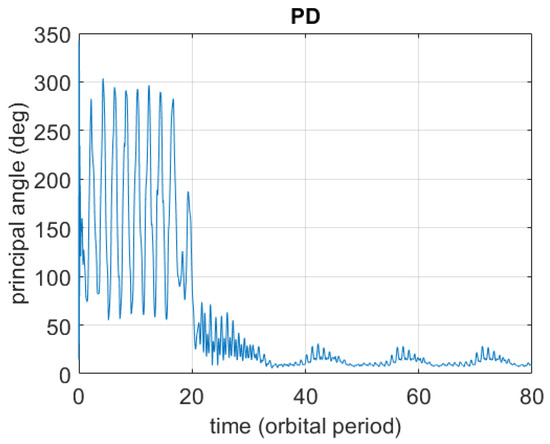
Figure 7.
Sample time history of the principal angle of rotation using PD control in the realistic scenario.
In these figures as well as in those that follow, the remaining 39 time behaviors are not showcased to obtain representations that can be read more easily. It occurs that in all 40 simulation runs, both MFAC and PD are able to effectively stabilize the nominal attitude.
To compare the performances of MFAC and PD control in terms of accuracy in three-axis alignment, the maximum value of the principal angle of rotation in the steady state is determined. Table 7 reports the mean values and standard deviations of those maximum values.

Table 7.
Statistics on maximum principal angle of rotation in steady state.
The statistics show that MFAC leads to significant reductions in both the mean values and the standard deviations of the principal angle in the steady state. Thus, in this numerical study, MFAC is able to achieve better three-axis pointing accuracy than PD control, which implies that MFAC is able to better compensate for the disturbance torques.
Figure 8 showcases a sample time history out of the 40 obtained by using MFAC.
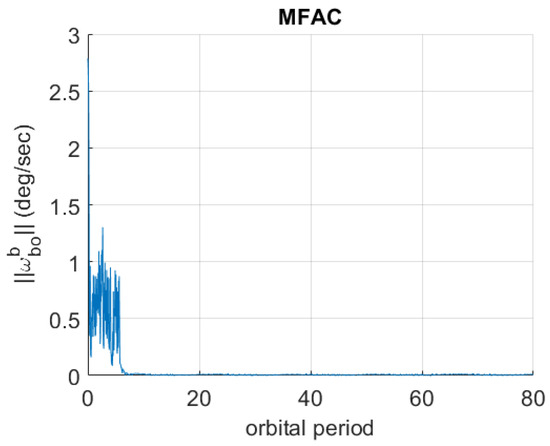
Figure 8.
Sample time history of using MFAC in the realistic scenario.
To evaluate the ability of both MFAC and PD control to make converge to zero, for each simulation run, the maximum value of is determined once a steady-state condition is reached. Table 8 reports the mean values and standard deviations of those maximum values.

Table 8.
Statistics on maximum in steady state.
The statistics show that in this numerical study, PD and MFAC are able to achieve convergence to zero of with comparable accuracy.
Figure 9, Figure 10 and Figure 11 display a sample time behavior of the control magnetic dipole moment generated by magnetorquers using MFAC, out of the 40 time behaviors.
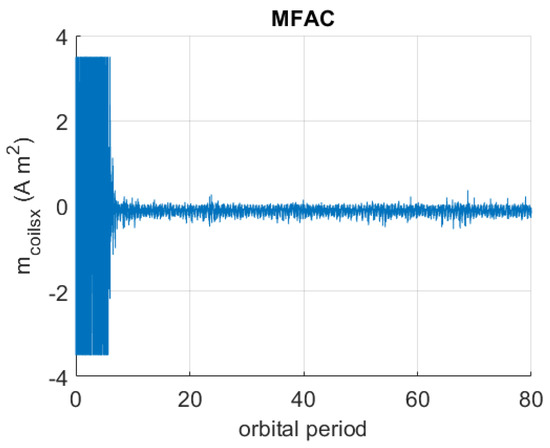
Figure 9.
Sample time history of using MFAC in the realistic scenario.
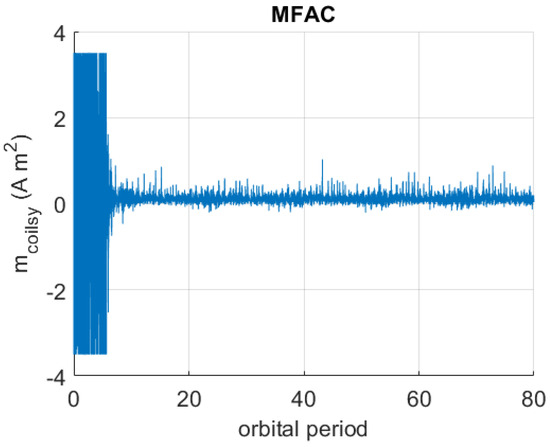
Figure 10.
Sample time history of using MFAC in the realistic scenario.
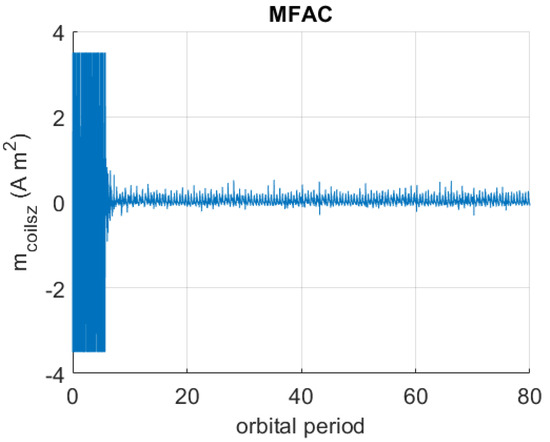
Figure 11.
Sample time history of using MFAC in the realistic scenario.
It is of interest to compare the performances obtained with MFAC and PD control in terms of the energy employed by magnetorquers to stabilize the spacecraft’s attitude. A rough and indirect measure of the latter energy is given by
where denotes the final simulation time, which is set equal to 80 orbital periods. Table 9 reports the mean values and standard deviations of .

Table 9.
Statistics on .
The statistics show that employing MFAC leads to a significant increase in the mean value of . Thus, in this numerical study, MFAC consumes significantly more energy to obtain substantially higher pointing accuracy.
5. Discussion
This work shows the effectiveness of employing FFDL-MFAC for three-axis stabilization of the attitude of a spacecraft pointing to the Earth using only magnetic torque actuators. Numerical simulations for a case study show that the proposed control algorithm is able to achieve a good pointing accuracy starting from a random tumbling condition. A comparative analysis with a model-based PD control reveals the superiority of MFAC in terms of pointing accuracy at the cost of a higher energy consumption. These findings confirm that MFAC is an effective algorithm in spacecraft attitude control.
Author Contributions
Conceptualization, F.C. and M.H.; methodology, F.C. and M.H.; software, F.C. and M.H.; validation, F.C.; formal analysis, F.C.; investigation, F.C. and M.H.; resources, F.C.; data curation, F.C.; writing—original draft preparation, F.C. and M.H.; writing—review and editing, F.C.; visualization, F.C.; supervision, F.C. and A.B.N.; project administration, F.C.; funding acquisition, A.B.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Ministry of Science Research and Technology of Iran.
Data Availability Statement
Data is contained within the present article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FFDL | Full-Form Dynamic Linearization |
| I/O | Input/Output |
| MFAC | Model-Free Adaptive Control |
| PD | Proportional–Derivative |
Appendix A. Full-Form Dynamic Linearization Model-Free Adaptive Control
The goal of this appendix is to recall in a concise form the theoretical framework for full-form dynamic linearization model-free adaptive control, which is employed in this work and is presented in [26].
Model-Free Adaptive Control (MFAC) is a data-driven online control approach that relies on real-time Input/Output (I/O) data and is founded on a data model of the plant being controlled. Specifically, MFAC utilizes dynamic linearization data models rooted in the concept of pseudo-partial derivatives. Three types of data models are employed in MFAC: (1) the Compact Form Dynamic Linearization (CFDL) model, in which only the data of one previous step of the plant control input and the plant output are considered; (2) the Partial Form Dynamic Linearization (PFDL) model, in which only the data of one previous step of the plant output and a window of previous plant control input data are considered; (3) the Full-Form Dynamic Linearization (FFDL) model, in which a window of previous plant control input data and plant output data are considered.
This appendix presents a control obtained with the FFDL-MFAC approach.
Appendix A.1. Dynamic Linearization Data Model ([26] Section 3.3.3)
Consider a class of unknown Multi-Input Multi-Output (MIMO) nonlinear discrete-time plants, where the number of inputs equals the number of outputs
where and are the m-dimensional control input and output, respectively, and are two unknown positive integers, and is an unknown nonlinear function. Equation (A1) is a general description of a nonlinear discrete-time time-invariant plant.
Assumption A1.
The partial derivatives of with respect to all its variables are continuous.
Given two non-negative integers and with , introduce the following notation:
Assumption A2.
Assumption A2 states that the variation in the plant output is constrained by the variations in all possible influential variables, which implies that the output variation must remain finite provided that all relevant variables have finite variations.
Introduce the following notations:
The following theorem holds true.
Theorem A1
([26] Theorem 3.7). Consider the plant in Equation (A1) satisfying Assumptions A1, A2, and . Then, there exists an unknown and bounded matrix such that the plant in Equation (A1) can be represented by the following FFDL data model:
where is called the Pseudo Partitioned Jacobian Matrix (PPJM) in which are matrices.
Appendix A.2. Control Algorithm ([26] Section 5.4.1.1)
Consider the following cost function for the control input
where denotes the desired time behavior for the output, and is a weighting factor. In the cost function, indicates the minimization of the tracking error in next sample, and indicates the minimization of the variation in the control input with respect to the previous sample. By substituting Equation (A5) into Equation (A6), taking the derivative with respect to , and setting it to zero, we obtain
The previous equation includes a matrix inversion which can be computationally expensive and can lead to large numerically errors. Thus, consider the following simplified algorithm for the control input without matrix inversion:
where are weighting factors which are included to add flexibility to the controller.
Appendix A.3. PPJM Estimation Algorithm ([26] Section 5.4.1.2)
The control algorithm in Equation (A8) cannot be employed since it contains the PPJM , which is unknown. Thus, to implement the MFAC controller in practice, it is crucial to design an estimation algorithm for . Introduce the following cost function:
where is a weighting factor, and is the estimation of . The PPJM estimation is provided by an adaptation law which is obtained by substituting Equation (A5) into Equation (A9), taking the derivative respect to and setting it to zero. Thus, the following PPJM adaptation law is obtained:
To avoid matrix inversion, consider the following simplified adaptation law:
where is a weighting factor which is added to obtain more flexibility.
In conclusion, the complete FFDL-MFAC scheme is obtained by employing the control in Equation (A8) with the PPJM matrix replaced by its estimate , which is determined by using the adaptation law in Equation (A10).
To the best of the authors’ knowledge, a stability analysis for FFDL-MFAC applied to MIMO plants is still an open problem in the general case ([26] Section 5.4.1.3).
It is important to note that the behavior of the spacecraft with magnetorquers from the input in Equation (2) to the output in Equation (3) is intrinsically time-varying because of the time-varying nature of both the geomagnetic field along the spacecraft’s orbit and the disturbance torques. Thus, the time-invariant model in Equation (A1) does not apply to the spacecraft with magnetorquers. Nevertheless, in this work, the FFDL-MFAC algorithm is employed to stabilize the spacecraft with magnetorquers, and its effectiveness is validated through numerical simulations. In addition, the authors of FFDL-MFAC reported its capability to deal with time-varying plants ([26] Sections 4.4.2 and 4.5).
References
- Hughes, P.C. Spacecraft Attitude Dynamics; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Sidi, M.J. Spacecraft Dynamics and Control; Cambridge University Press: New York, NY, USA, 1997. [Google Scholar]
- Mahfouz, A.; Pritykin, D.; Biggs, J. Hybrid attitude control for nano-spacecraft: Reaction wheel failure and singularity handling. J. Guid. Control. Dyn. 2021, 44, 548–558. [Google Scholar] [CrossRef]
- Ovchinnikov, M.Y.; Roldugin, D. A survey on active magnetic attitude control algorithms for small satellites. Prog. Aerosp. Sci. 2019, 109, 100546. [Google Scholar] [CrossRef]
- Wiśniewski, R.; Blanke, M. Fully magnetic attitude control for spacecraft subject to gravity gradient. Automatica 1999, 35, 1201–1214. [Google Scholar] [CrossRef]
- Ovchinnikov, M.Y.; Roldugin, D.S.; Ivanov, D.S.; Penkov, V.I. Choosing control parameters for three axis magnetic stabilization in orbital frame. Acta Astronaut. 2015, 116, 74–77. [Google Scholar] [CrossRef]
- Wiśniewski, R. Linear time-varying approach to satellite attitude control using only electromagnetic actuation. J. Guid. Control. Dyn. 2000, 23, 640–647. [Google Scholar] [CrossRef]
- Lovera, M.; De Marchi, E.; Bittanti, S. Periodic attitude control techniques for small satellites with magnetic actuators. IEEE Trans. Control Syst. Technol. 2002, 10, 90–95. [Google Scholar] [CrossRef]
- Pulecchi, T.; Lovera, M.; Varga, A. Optimal Discrete-Time Design of Three-Axis Magnetic Attitude Control Laws. IEEE Trans. Control Syst. Technol. 2010, 18, 714–722. [Google Scholar] [CrossRef]
- Celani, F. Gain Selection for Attitude Stabilization of Earth-Pointing Spacecraft Using Magnetorquers. Aerotec. Missili Spaz. 2021, 100, 15–24. [Google Scholar] [CrossRef]
- Celani, F. Quaternion versus Rotation Matrix Feedback for Spacecraft Attitude Stabilization Using Magnetorquers. Aerospace 2022, 9, 24. [Google Scholar] [CrossRef]
- Lovera, M.; Astolfi, A. Global magnetic attitude control of spacecraft in the presence of gravity gradient. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 796–804. [Google Scholar] [CrossRef]
- Colagrossi, A.; Lavagna, M. Fully magnetic attitude control subsystem for picosat platforms. Adv. Space Res. 2018, 62, 3383–3397. [Google Scholar] [CrossRef]
- Das, S.; Sinha, M.; Kumar, K.; Misra, A. Reconfigurable magnetic attitude control of Earth-pointing satellites. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2010, 224, 1309–1326. [Google Scholar] [CrossRef]
- Psiaki, M.L. Magnetic Torquer Attitude Control via Asymptotic Periodic Linear Quadratic Regulation. J. Guid. Control. Dyn. 2001, 24, 386–394. [Google Scholar] [CrossRef]
- Giri, D.K.; Sinha, M. Robust backstepping magnetic attitude control of satellite subject to unsymmetrical mass properties. J. Spacecr. Rocket. 2019, 56, 298–305. [Google Scholar] [CrossRef]
- Avanzini, G.; de Angelis, E.L.; Giulietti, F. Two-timescale magnetic attitude control of Low-Earth-Orbit spacecraft. Aerosp. Sci. Technol. 2021, 116, 106884. [Google Scholar] [CrossRef]
- Rodriquez-Vazquez, A.L.; Martin-Prats, M.A.; Bernelli-Zazzera, F. Spacecraft magnetic attitude control using approximating sequence Riccati equations. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 3374–3385. [Google Scholar] [CrossRef]
- Hjalmarsson, H. Iterative feedback tuning: An overview. Int. J. Adapt. Control Signal Process. 2002, 16, 373–395. [Google Scholar] [CrossRef]
- Karimi, A.; Mišković, L.; Bonvin, D. Iterative correlation-based controller tuning. Int. J. Adapt. Control Signal Process. 2004, 18, 645–664. [Google Scholar] [CrossRef]
- Campi, M.; Lecchini, A.; Savaresi, S. Virtual reference feedback tuning: A direct method for the design of feedback controllers. Automatica 2002, 38, 1337–1346. [Google Scholar] [CrossRef]
- Johnson, M.A.; Moradi, M.H. (Eds.) PID Control: New Identification and Design Methods; Springer: London, UK, 2005. [Google Scholar]
- Rezayat, F. On the use of an SPSA-based model-free controller in quality improvement. Automatica 1995, 31, 913–915. [Google Scholar] [CrossRef]
- Safonov, M.G.; Tsao, T.C. The unfalsified control concept and learning. IEEE Trans. Autom. Control 1997, 42, 843–847. [Google Scholar] [CrossRef]
- Gupta, M.M.; Jin, L.; Homma, N. Static and Dynamic Neural Networks: From Fundamentals to Advanced Theory; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Hou, Z.; Jin, S. Model Free Adaptive Control: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Heydari, M.; Novinzadeh, A.B.; Tayefi, M. Robust data-driven model-free adaptive control to uncertainties and disturbances for NARMAX systems. Trans. Inst. Meas. Control. 2024. [Google Scholar] [CrossRef]
- Heydari, M.; Novinzadeh, A.B.; Tayefi, M. Anti Wind-Up and Robust Data-Driven Model-Free Adaptive Control for MIMO Nonlinear Discrete-Time Systems. Int. J. Adapt. Control. Signal Process. 2024. [Google Scholar] [CrossRef]
- Das, S.; Sinha, M.; Misra, A.K. Dynamic neural units for adaptive magnetic attitude control of spacecraft. J. Guid. Control. Dyn. 2012, 35, 1280–1291. [Google Scholar] [CrossRef]
- Ziang, L.; Zhengtao, D.; Meihong, W.; Eni, O. Model-free adaptive control for MEA-based post-combustion carbon capture processes. Fuel 2018, 224, 637–643. [Google Scholar] [CrossRef]
- Gao, H.; Ma, G.; Lv, Y.; Guo, Y. Forecasting-based data-driven model-free adaptive sliding mode attitude control of combined spacecraft. Aerosp. Sci. Technol. 2019, 86, 364–374. [Google Scholar] [CrossRef]
- Yulei, L.; Quanquan, J.; Tingpeng, D.; Wen, J. Redefined output model-free adaptive control method and unmanned surface vehicle heading control. IEEE J. Ocean. Eng. 2020, 45, 714–723. [Google Scholar] [CrossRef]
- Duan, L.; Hou, Z.; Yu, X.; Jin, S.; Lu, K. Data-driven model-free adaptive attitude control approach for launch vehicle with virtual reference feedback parameters tuning method. IEEE Access 2019, 7, 54106–54116. [Google Scholar] [CrossRef]
- Shuo, W.; Cong, H.; Guanghui, W. Model free adaptive attitude control method for launch vehicles. In Lecture Notes in Electrical Engineering; Springer Nature: Singapore, 2023; pp. 3587–3593. [Google Scholar] [CrossRef]
- Novinzadeh, A.B.; Heydari, M.; Yaseri, M.R. Model-free adaptive controller design for nonlinear system of an air vehicle pitch channel. Modares Mech. Eng. 2018, 17, 161–171. [Google Scholar]
- Heydari, M.; Darvishpoor, S.; Novinzadeh, A.B.; Roshanian, J. On the performance of the model-free adaptive control for a novel moving-mass controlled flying robot. J. Intell. Robot. Syst. 2024, 110, 79. [Google Scholar] [CrossRef]
- Bu, X.; Hou, Z.; Zhang, H. Data-driven multiagent systems consensus tracking using model free adaptive control. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1514–1524. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Hou, Z.; Tian, T.; Deng, Z.; Li, Z. A novel dual successive projection-based model-free adaptive control method and application to an autonomous car. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3444–3457. [Google Scholar] [CrossRef] [PubMed]
- Shuai, Z.; Ping, Z.; Yongfang, X.; Tianyou, C. Improved model-free adaptive predictive control method for direct data-driven control of a wastewater treatment process with high performance. J. Process Control 2022, 110, 11–23. [Google Scholar] [CrossRef]
- Juan, L.; Yinan, W.; Xiaowei, Z.; Pengyuan, Q. Model free adaptive control of large and flexible wind turbine rotors with controllable flaps. Renew. Energy 2021, 180, 68–82. [Google Scholar] [CrossRef]
- Liu, Z.; Yue, C.; Wu, F.; Wang, F.; Cao, X. Data-driven prescribed performance control for satellite with large rotational component. Adv. Space Res. 2023, 71, 744–755. [Google Scholar] [CrossRef]
- Alken, P.; Thébault, E.; Beggan, C.D.; Amit, H.; Aubert, J.; Baerenzung, J.; Bondar, T.; Brown, W.; Califf, S.; Chambodut, A.; et al. International geomagnetic reference field: The thirteenth generation. Earth Planets Space 2021, 73, 49. [Google Scholar] [CrossRef]
- Bittanti, S.; Colaneri, P. Periodic Systems: Filtering and Control; Springer: London, UK, 2009. [Google Scholar]
- Markley, F.L.; Crassidis, J.L. Fundamentals of Spacecraft Attitude Determination and Control; Springer: New York, NY, USA, 2014. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).