Research on the Dynamic Modeling of Rigid–Flexible Composite Spacecraft Under Fixed Constraints Based on the ANCF
Abstract
1. Introduction
2. Rigid–Flexible Coupling Dynamic Modeling Based on the ANCF
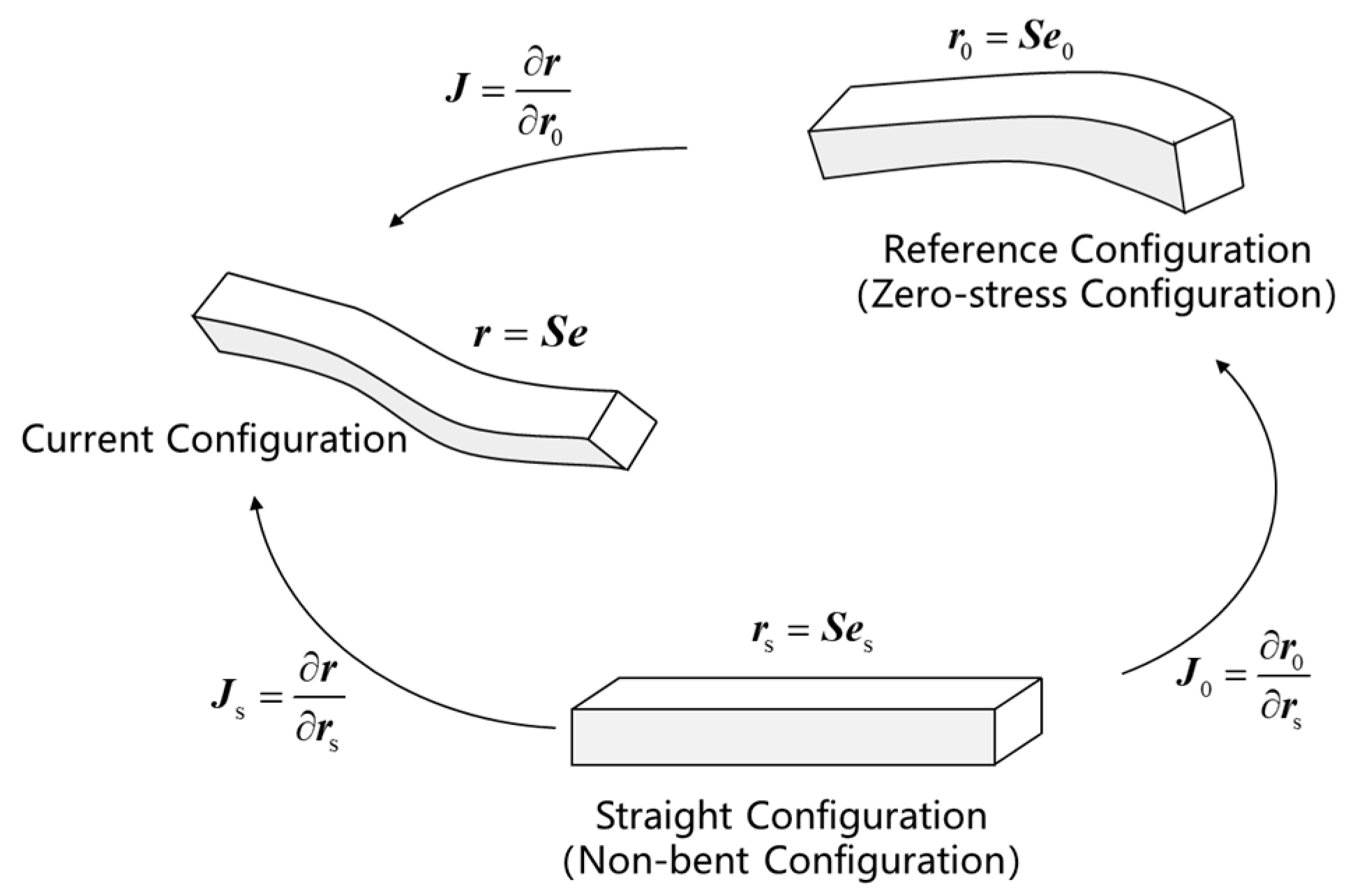
2.1. Dynamic Modeling of Noise Reduction in Beam Elements Based on ANCF
2.2. Dynamic Modeling Based on the Direct Assembly Method
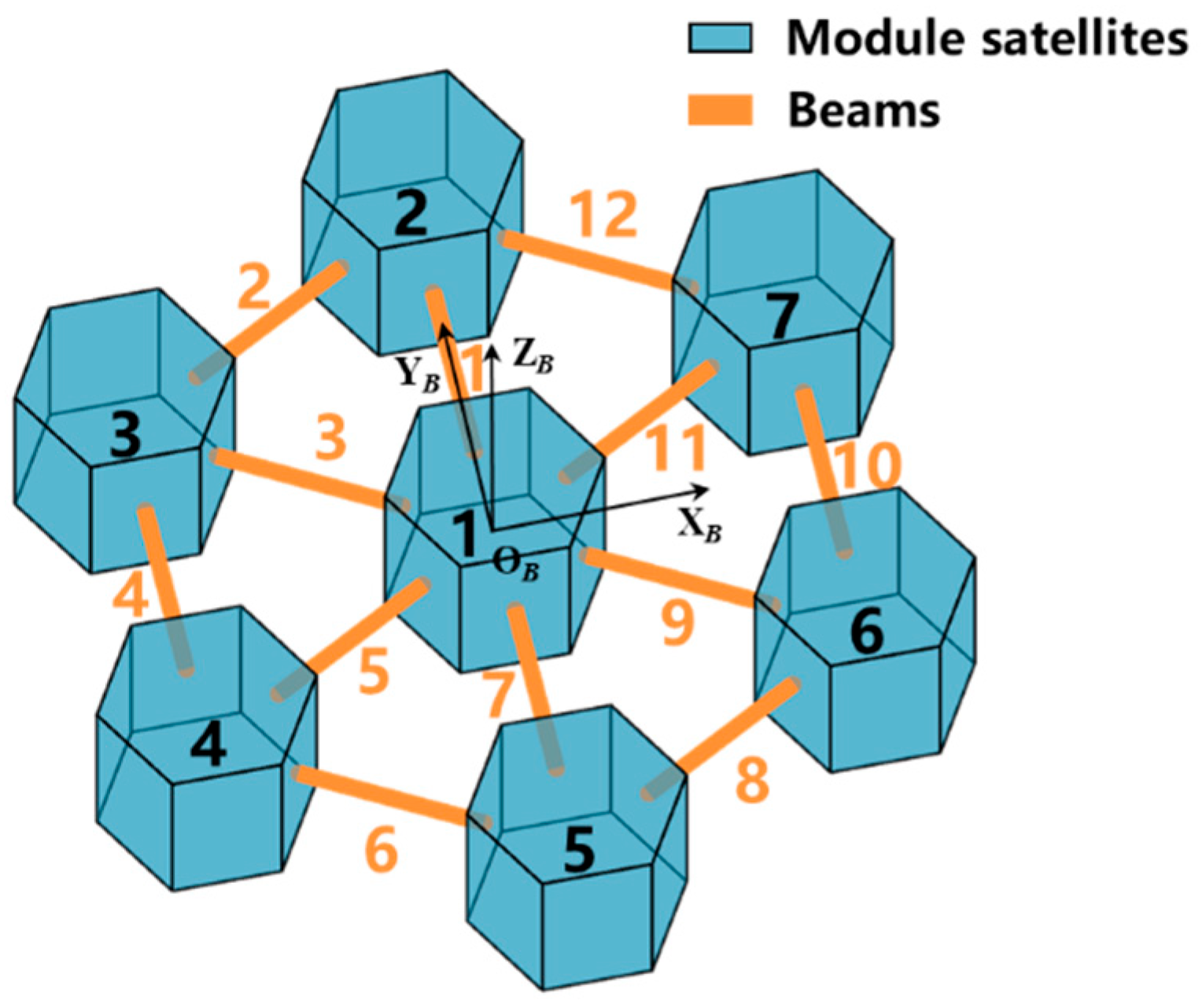
- Comparing Equations (54) and (56) demonstrates that the dynamic equations based on the direct assembly method of the ANCF have lower dimensions than those of the Lagrange multiplier method. Taking the constellation spacecraft with a mesh topology as shown in Figure 1 as an example, Figure 5 presents the relationship between the dynamic dimension and the number of modular satellites.
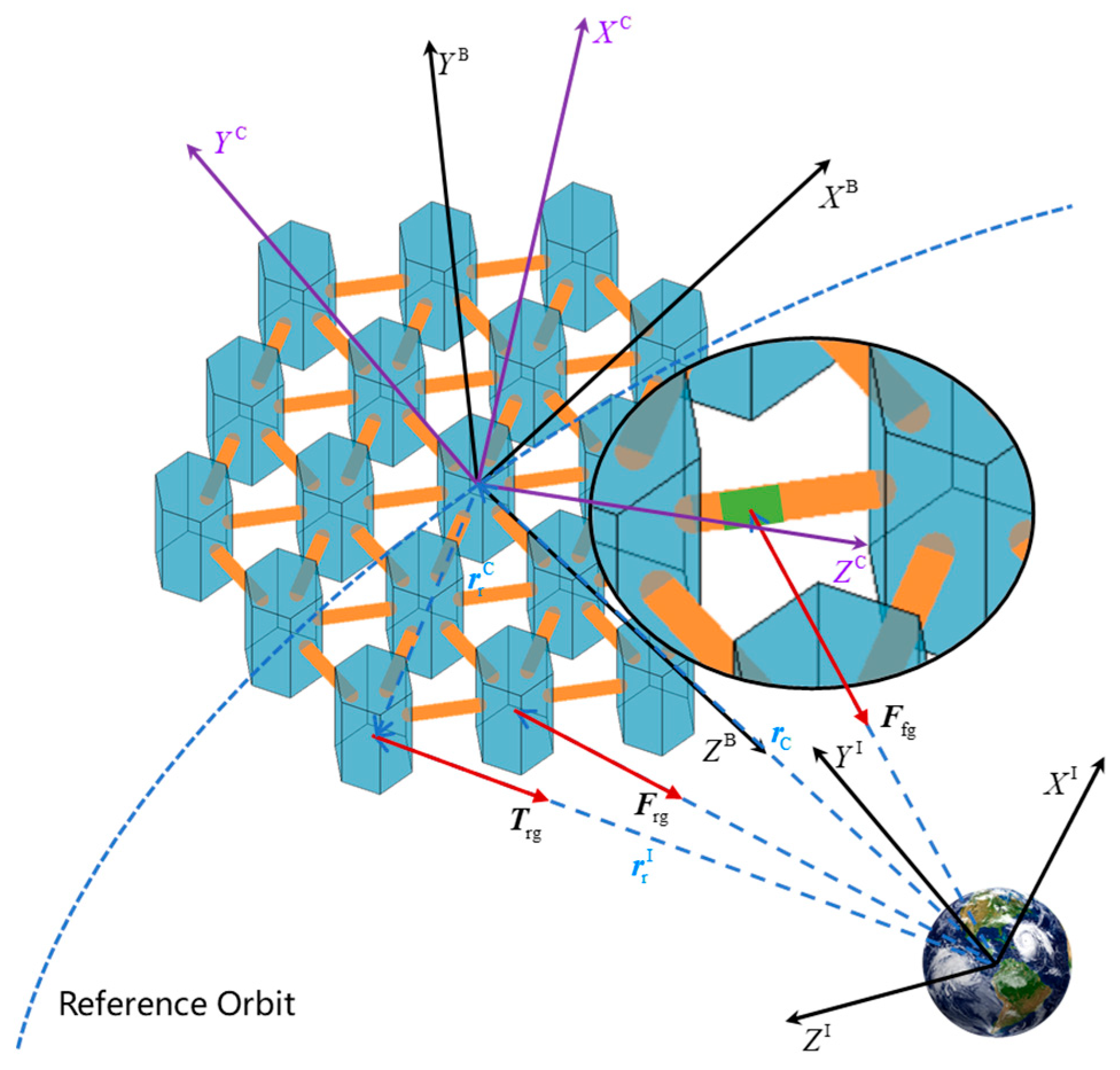
3. Force Analysis of Rigid–Flexible Composites in a Gravitational Field
4. Verification of the Dynamic Response of Rigid–Flexible Composite Structures Through Simulation
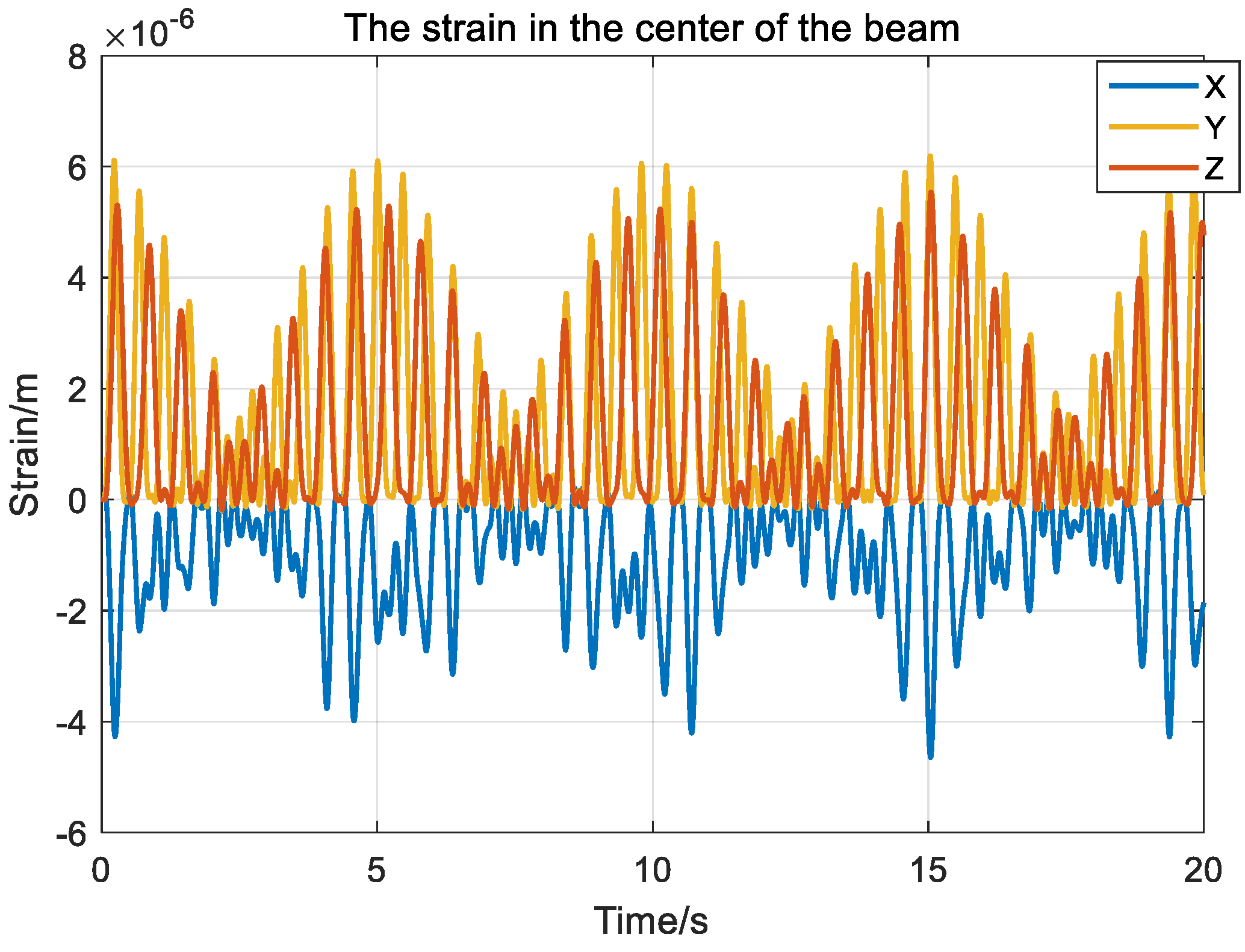
4.1. Analysis of Vibration Response in Dual-Module Composite Structures
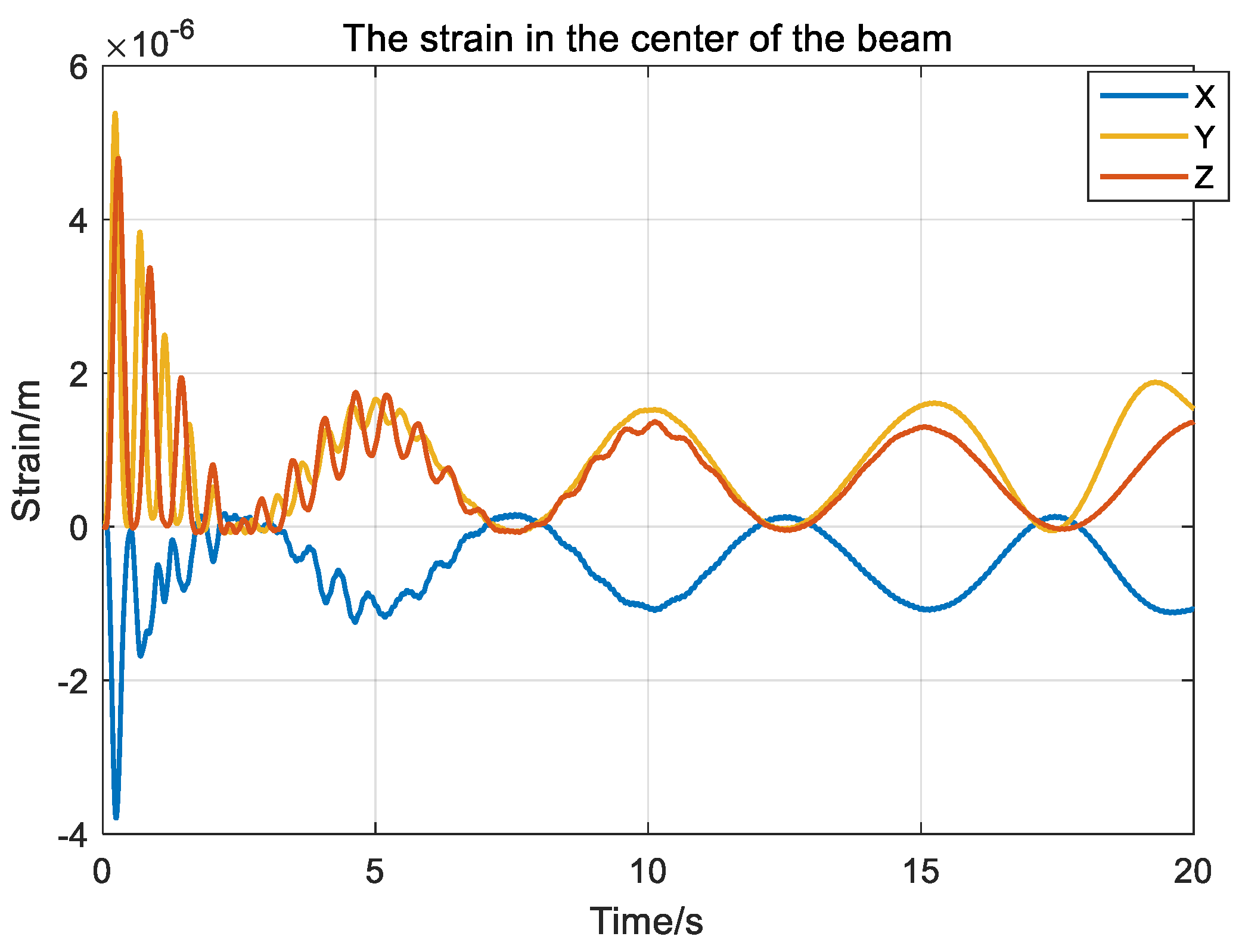
4.2. Analysis of the Impact of the Smoothing Factor on the Vibration of Dual-Module Assemblies
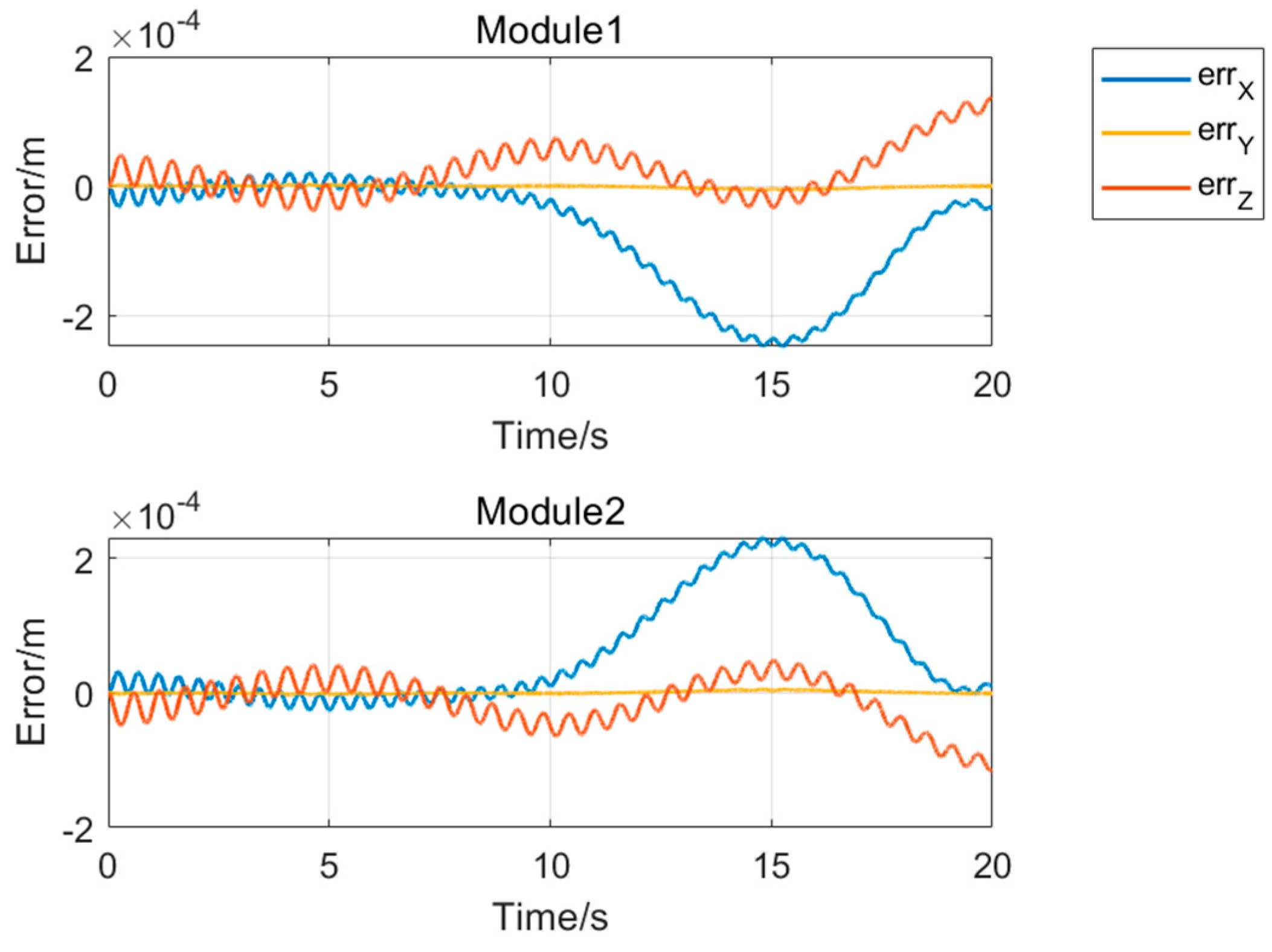
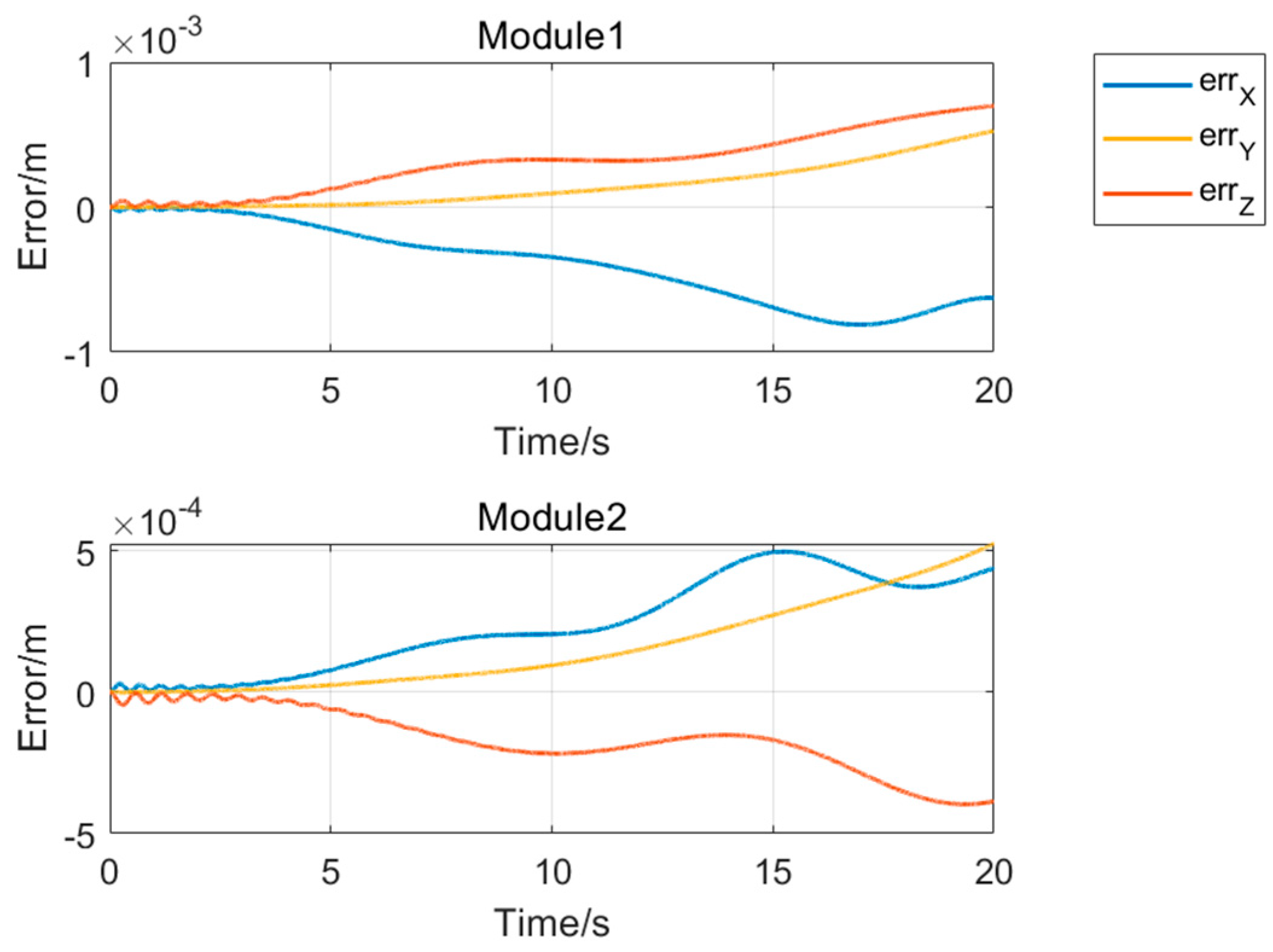
4.3. Vibration Response Analysis of a Seven-Module Assembly in a Gravitational Environment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, G.; Cao, D.; Wei, J.; Cao, Y.; Chen, Z. Study on analytical global modes for a multi-panel structure connected with flexible hinges. Appl. Math. Model. 2021, 91, 1081–1099. [Google Scholar] [CrossRef]
- Wang, E.; Wu, S.; Liu, Y.; Wu, Z.; Liu, X. Distributed vibration control of a large solar power satellite. Astrodynamics 2019, 3, 189–203. [Google Scholar] [CrossRef]
- Shabana, A.A. An Absolute Nodal Coordinate Formulation for the Large Rotation and Deformation Analysis of Flexible Bodies; Technical Report; Department of Mechanical Engineering, University of Illinois at Chicago: Chicago, IL, USA, 1996. [Google Scholar]
- Zwölfer, A.; Gerstmayr, J. The nodal-based floating frame of reference formulation with modal reduction. Acta Mech. 2020, 232, 835–851. [Google Scholar] [CrossRef]
- Sun, J.; Tian, Q.; Hu, H.; Pedersen, N.L. Axially variable-length solid element of absolute nodal coordinate formulation. Acta Mech. Sin. 2019, 35, 653–663. [Google Scholar] [CrossRef]
- Shabana, A.A.; Schwertassek, R. Equivalence of the floating frame of reference approach and finite element formulations. Int. J. Non-Linear Mech. 1998, 33, 417–432. [Google Scholar] [CrossRef]
- Shabana, A.A. Computational Continuum Mechanics, 2nd ed.; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Luo, C.Q.; Sun, J.L.; Wen, H.; Jin, D.P. Dynamics of a tethered satellite formation for space exploration modeled via ANCF. Acta Astronaut. 2020, 177, 882–890. [Google Scholar] [CrossRef]
- Htun, T.Z.; Suzuki, H.; Garcia-Vallejo, D. Dynamic modeling of a radially multilayered tether cable for a remotely-operated underwater vehicle (ROV) based on the absolute nodal coordinate formulation (ANCF). Mech. Mach. Theory 2020, 153, 103961. [Google Scholar] [CrossRef]
- Otsuka, K.; Makihara, K. Absolute Nodal Coordinate Beam Element for Modeling Flexible and Deployable Aerospace Structures. AIAA J. 2019, 57, 1344–1346. [Google Scholar] [CrossRef]
- Westin, C.; Irani, R.A. Efficient semi-implicit numerical integration of ANCF and ALE-ANCF cable models with holonomic constraints. Comput. Mech. 2023, 71, 789–800. [Google Scholar] [CrossRef]
- Desai, C.S.; Kundu, T.; Lei, X. Introductory Finite Element Method. Appl. Mech. Rev. 2002, 55, 284–288. [Google Scholar] [CrossRef]
- Yu, L.; Zhao, Z.; Tang, J.; Ren, G. Integration of absolute nodal elements into multibody system. Nonlinear Dyn. 2010, 62, 931–943. [Google Scholar] [CrossRef]
- Hu, J.; Wang, T. A recursive absolute nodal coordinate formulation with O(n) algorithm complexity. Chin. J. Theor. Appl. Mech. 2016, 48, 1172–1183. [Google Scholar] [CrossRef]
- Kim, E.; Cho, M. Design of a planar multibody dynamic system with ANCF beam elements based on an element-wise stiffness evaluation procedure. Struct. Multidiscip. Optim. 2018, 58, 1095–1107. [Google Scholar] [CrossRef]
- Ren, H.; Zhou, P. Implementation details of DAE integrators for multibody system dynamics. J. Dyn. Control 2021, 19, 1–28. [Google Scholar]
- Yan, Y.; Chen, W.; Wang, C.; Wise, S.M. A second-order energy stable BDF numerical scheme for the Cahn-Hilliard equation. Commun. Comput. Phys. 2018, 23, 572–602. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, R.; Zanoni, A.; Masarati , P. Performance of implicit A-stable time integration methods for multibody system dynamics. Multibody Syst. Dyn. 2022, 54, 263–301. [Google Scholar] [CrossRef]
- Jia, C.; Su, H.; Guo, W.; Masarati, P. An Unconditionally Stable Integration Method for Structural Nonlinear Dynamic Problems. Mathematics 2023, 11, 2987. [Google Scholar] [CrossRef]
- Amiri-Hezaveh, A.; Ostoja-Starzewski, M. A convolutional-iterative solver for nonlinear dynamical systems. Appl. Math. Lett. 2022, 130, 107990. [Google Scholar] [CrossRef]
- Hanafi, M.R.; Babaei, M.; Narjabadifam, P. New Formulation for dynamic analysis of nonlinear time-history of vibrations of structures under earthquake loading. J. Civ. Environ. Eng. 2023, 54, 22–35. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, Y.; Zhang, B.; Xie, F.; Qiu, D. A Time-varying Amplitude and Frequency Description Method of Instantaneous Signal in Power System Based on HHT. In Proceedings of the 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 12–14 May 2023; IEEE: New York, NY, USA, 2023; pp. 1255–1260. [Google Scholar] [CrossRef]
- Qi, Z.; Cao, Y.; Wang, G. Model smoothing methods in numerical analysis of flexible multibody systems. Chin. J. Theor. Appl. Mech. 2018, 50, 863–870. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, X.; Mao, H.; Song, H. Model denoising based on absolute node coordinate method. J. Vib. Shock 2021, 40, 139–146. [Google Scholar]





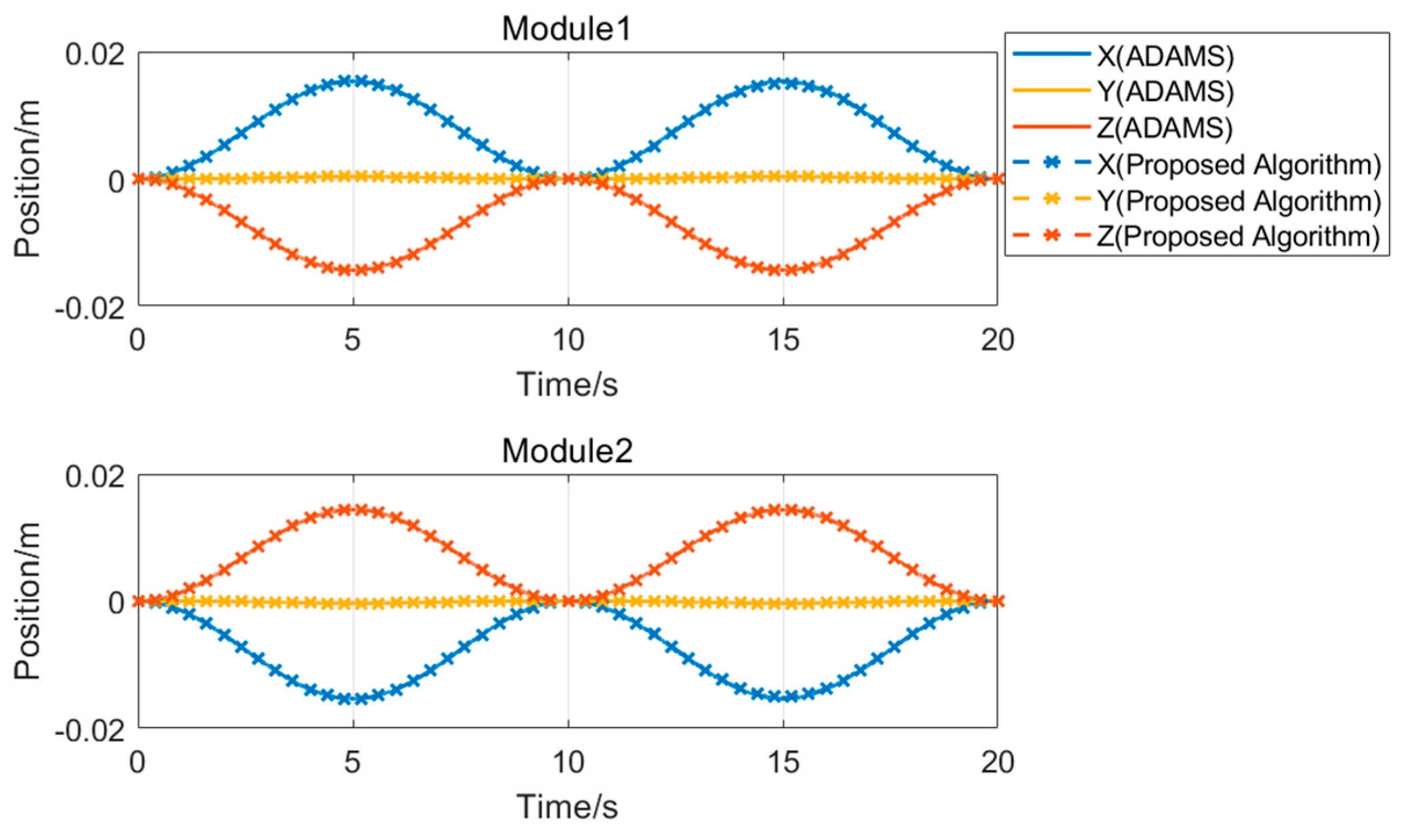
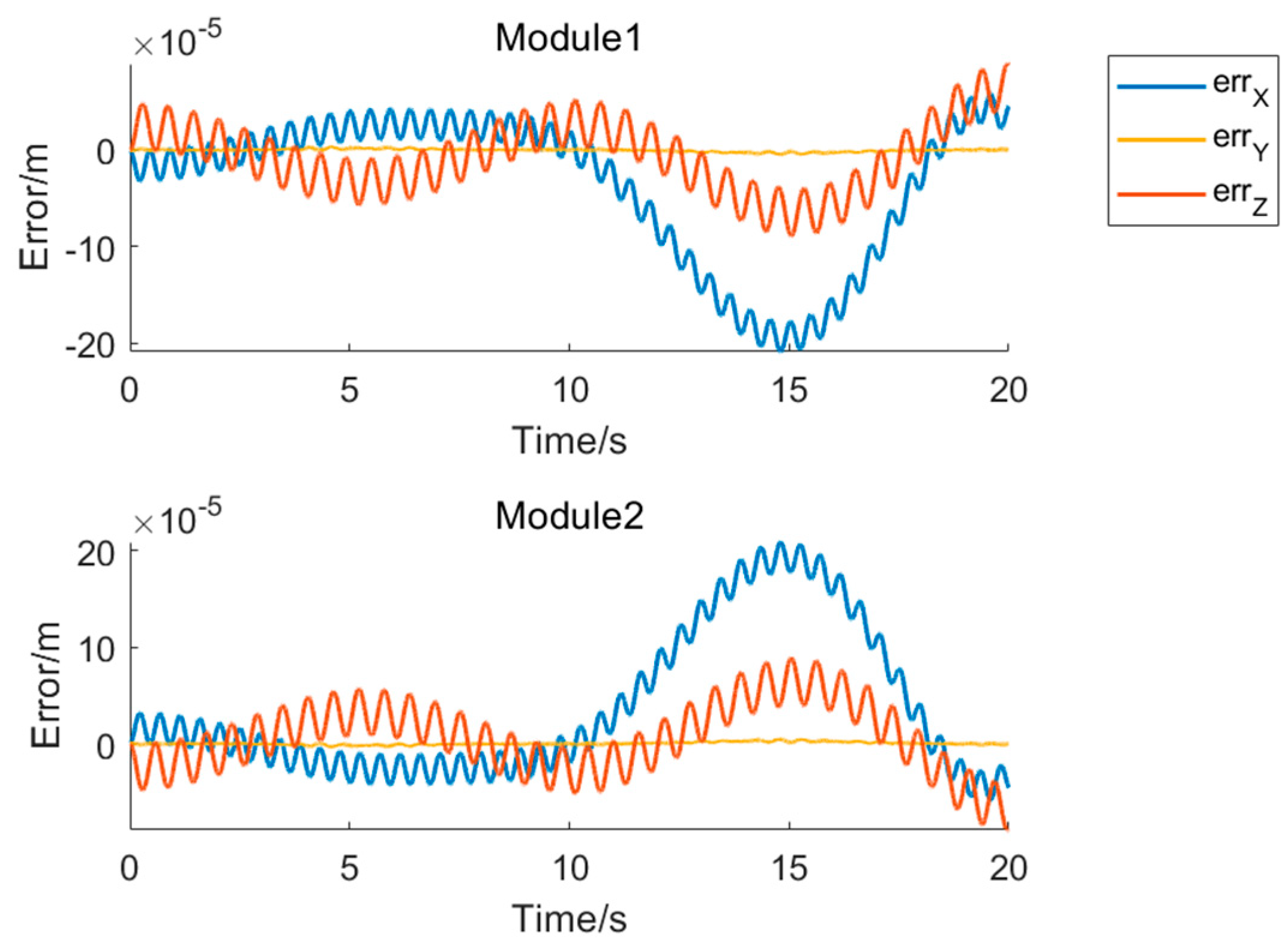






| Parameters | Module 1 | Module 2 | ||||
|---|---|---|---|---|---|---|
| X-Axis | Y-Axis | Z-Axis | X-Axis | Y-Axis | Z-Axis | |
| Mean (m) | −3.63 × 10−5 | −1.17 × 10−7 | −6.63 × 10−6 | 3.63 × 10−5 | 1.17 × 10−7 | 6.63 × 10−6 |
| Variance (m2) | 5.72 × 10−9 | 1.94 × 10−12 | 1.32 × 10−9 | 5.72 × 10−9 | 1.94 × 10−12 | 1.32 × 10−9 |
| Parameters | Module 1 | Module 2 | ||||
|---|---|---|---|---|---|---|
| X-Axis | Y-Axis | Z-Axis | X-Axis | Y-Axis | Z-Axis | |
| Mean (m) | −6.96 × 10−5 | −9.82 × 10−7 | 2.32 × 10−5 | 5.88 × 10−5 | 7.20 × 10−7 | −1.29 × 10−5 |
| Variance (m2) | 7.20 × 10−9 | 3.65 × 10−12 | 1.48 × 10−9 | 6.56 × 10−9 | 3.30 × 10−12 | 1.29 × 10−9 |
| Parameters | Module 1 | Module 2 | ||||
|---|---|---|---|---|---|---|
| X-Axis | Y-Axis | Z-Axis | X-Axis | Y-Axis | Z-Axis | |
| Mean (m) | −3.78 × 10−5 | −9.77 × 10−5 | −5.28 × 10−6 | 3.95 × 10−5 | 9.81 × 10−5 | 5.28 × 10−6 |
| Variance (m2) | 5.80 × 10−9 | 7.55 × 10−9 | 1.32 × 10−9 | 5.89 × 10−9 | 7.80 × 10−9 | 1.32 × 10−9 |
| Smoothing Factor | 0 | 0.00001 | 0.0001 | 0 |
|---|---|---|---|---|
| Integrator | ODE45 | ODE45 | ODE45 | ODE23t |
| CPU Time/s | 16,156.9 | 15,242.3 | 4107.4 | 3517.8 |
| Semi-Major Axis/km | Eccentricity | Inclination/° | RAAN/° | Argument of Perigee/° |
|---|---|---|---|---|
| 6878.137 | 0.001 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Kang, G.; Wu, J.; Xu, C.; Zhou, J.; Tao, X.; Hua, Y. Research on the Dynamic Modeling of Rigid–Flexible Composite Spacecraft Under Fixed Constraints Based on the ANCF. Aerospace 2025, 12, 207. https://doi.org/10.3390/aerospace12030207
Wu J, Kang G, Wu J, Xu C, Zhou J, Tao X, Hua Y. Research on the Dynamic Modeling of Rigid–Flexible Composite Spacecraft Under Fixed Constraints Based on the ANCF. Aerospace. 2025; 12(3):207. https://doi.org/10.3390/aerospace12030207
Chicago/Turabian StyleWu, Jiaqi, Guohua Kang, Junfeng Wu, Chuanxiao Xu, Jiayi Zhou, Xinyong Tao, and Yinmiao Hua. 2025. "Research on the Dynamic Modeling of Rigid–Flexible Composite Spacecraft Under Fixed Constraints Based on the ANCF" Aerospace 12, no. 3: 207. https://doi.org/10.3390/aerospace12030207
APA StyleWu, J., Kang, G., Wu, J., Xu, C., Zhou, J., Tao, X., & Hua, Y. (2025). Research on the Dynamic Modeling of Rigid–Flexible Composite Spacecraft Under Fixed Constraints Based on the ANCF. Aerospace, 12(3), 207. https://doi.org/10.3390/aerospace12030207






