Passive Rotor Noise Reduction Through Axial and Angular Blade Spacing Modulation
Abstract
1. Introduction
- comparing different axial distance ratios for coaxial four-bladed propellers;
- identifying the optimal four-bladed propeller configuration;
- conducting an acoustic analysis to evaluate the A-weighted noise reduction.
2. Methodology: Numerical Tools
2.1. Propeller and Blade Configurations
2.2. Computational Fluid Dynamics Model
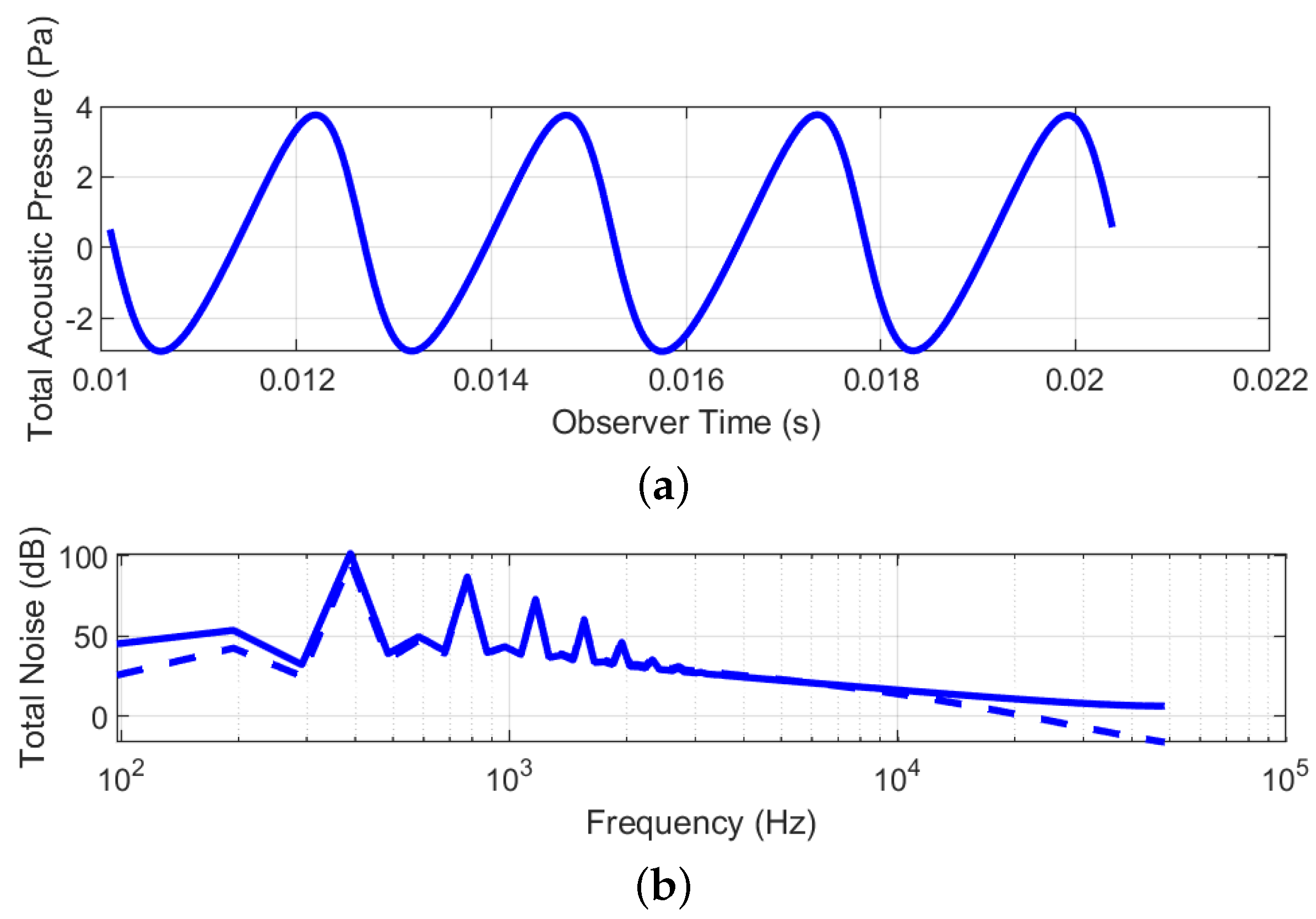
2.3. Aeroacoustic Modeling
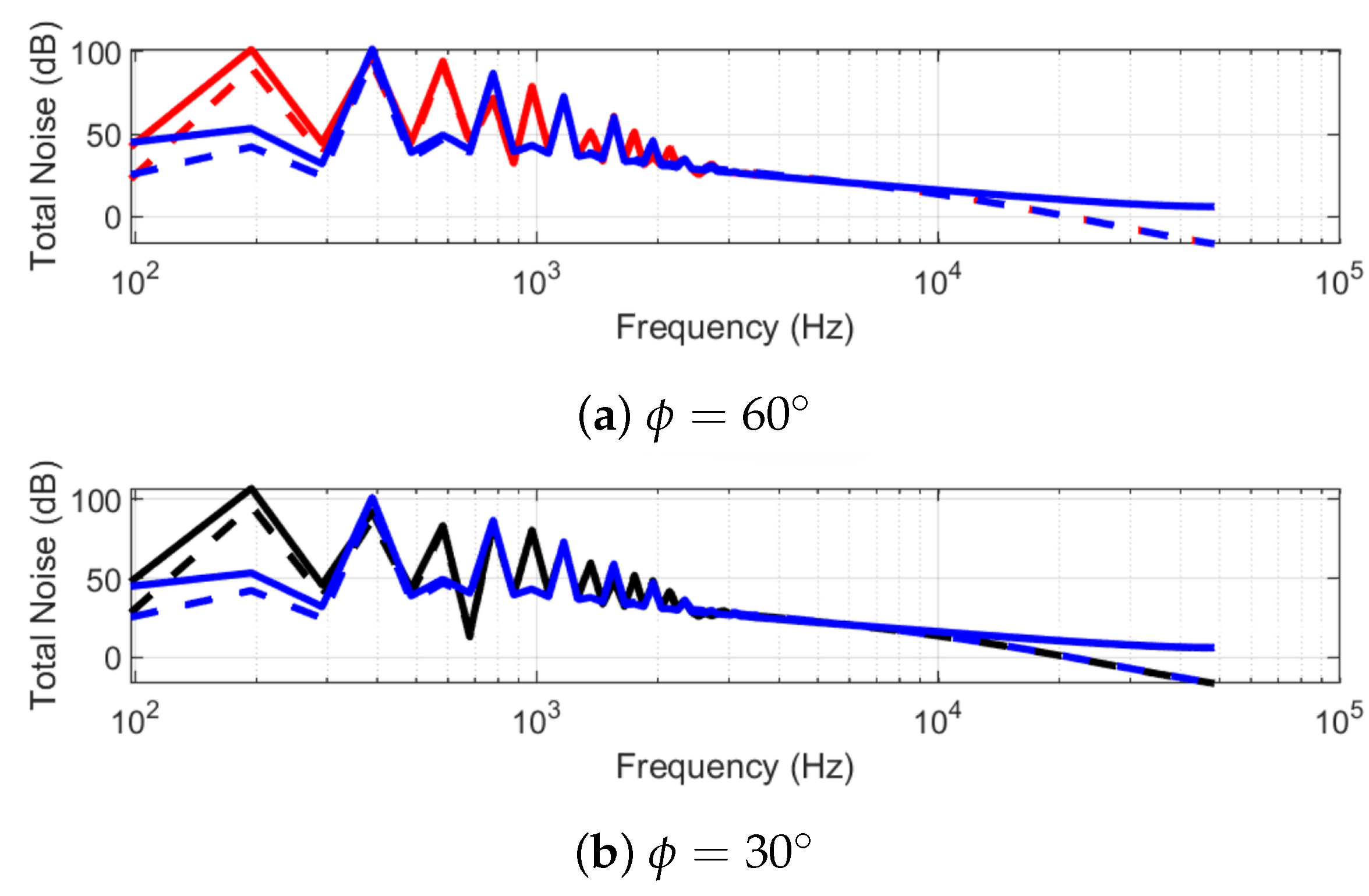
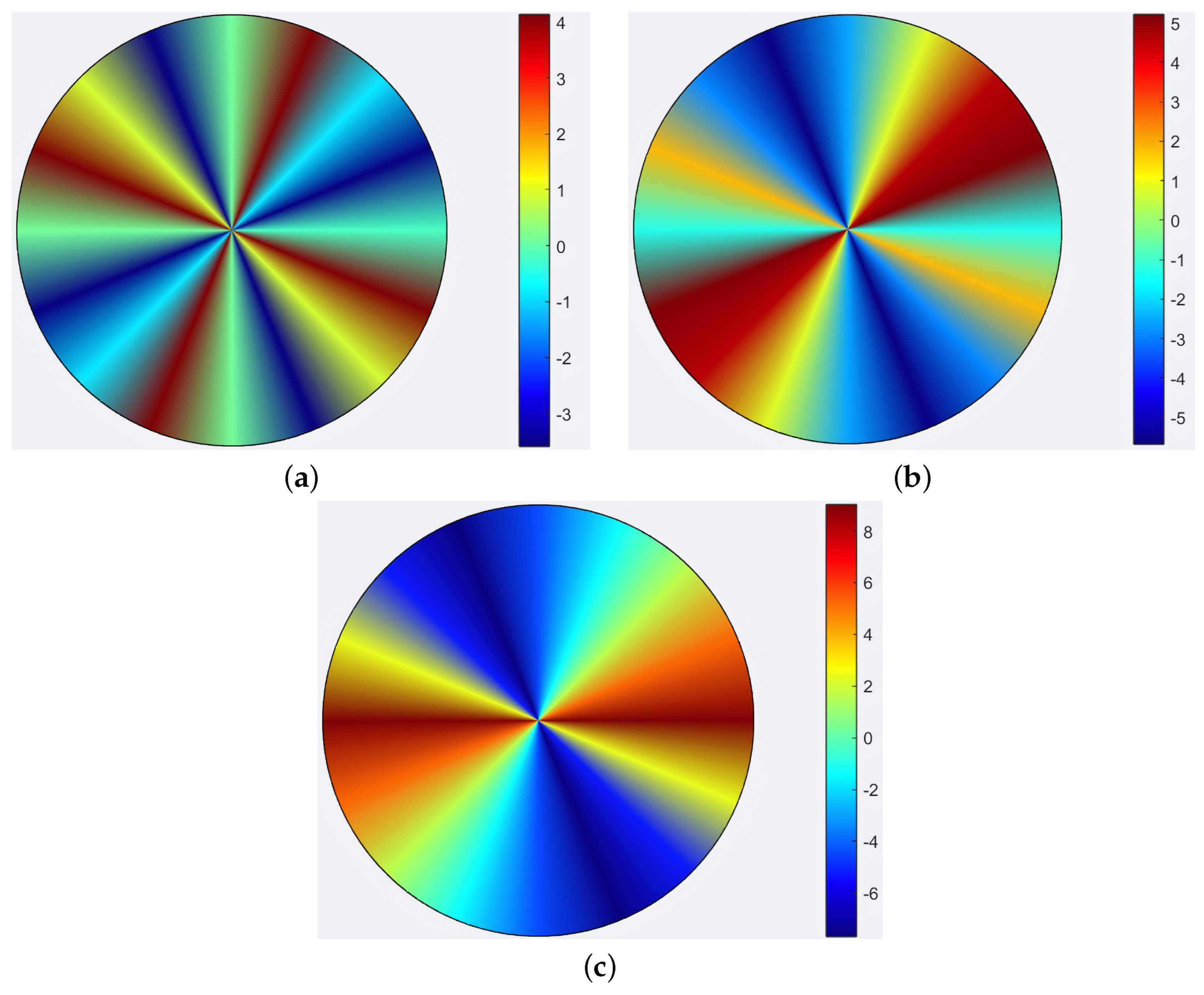
3. Results and Discussion
3.1. CFD Results
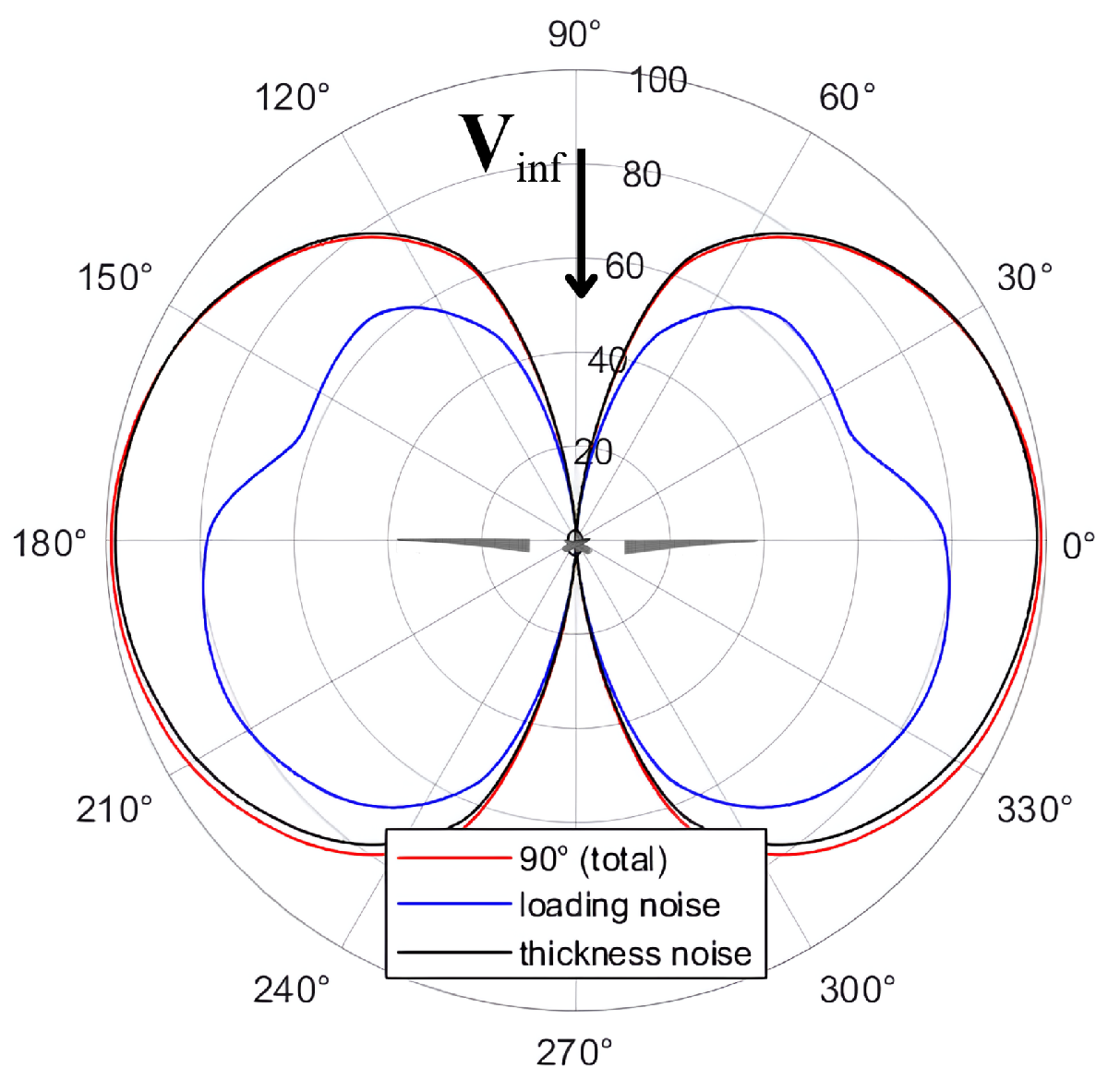
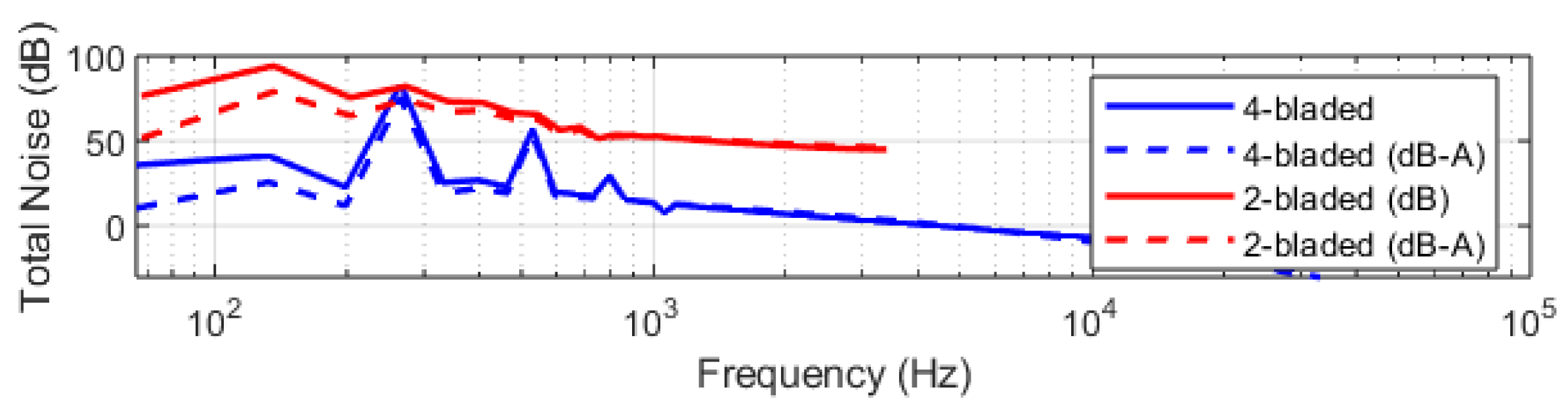
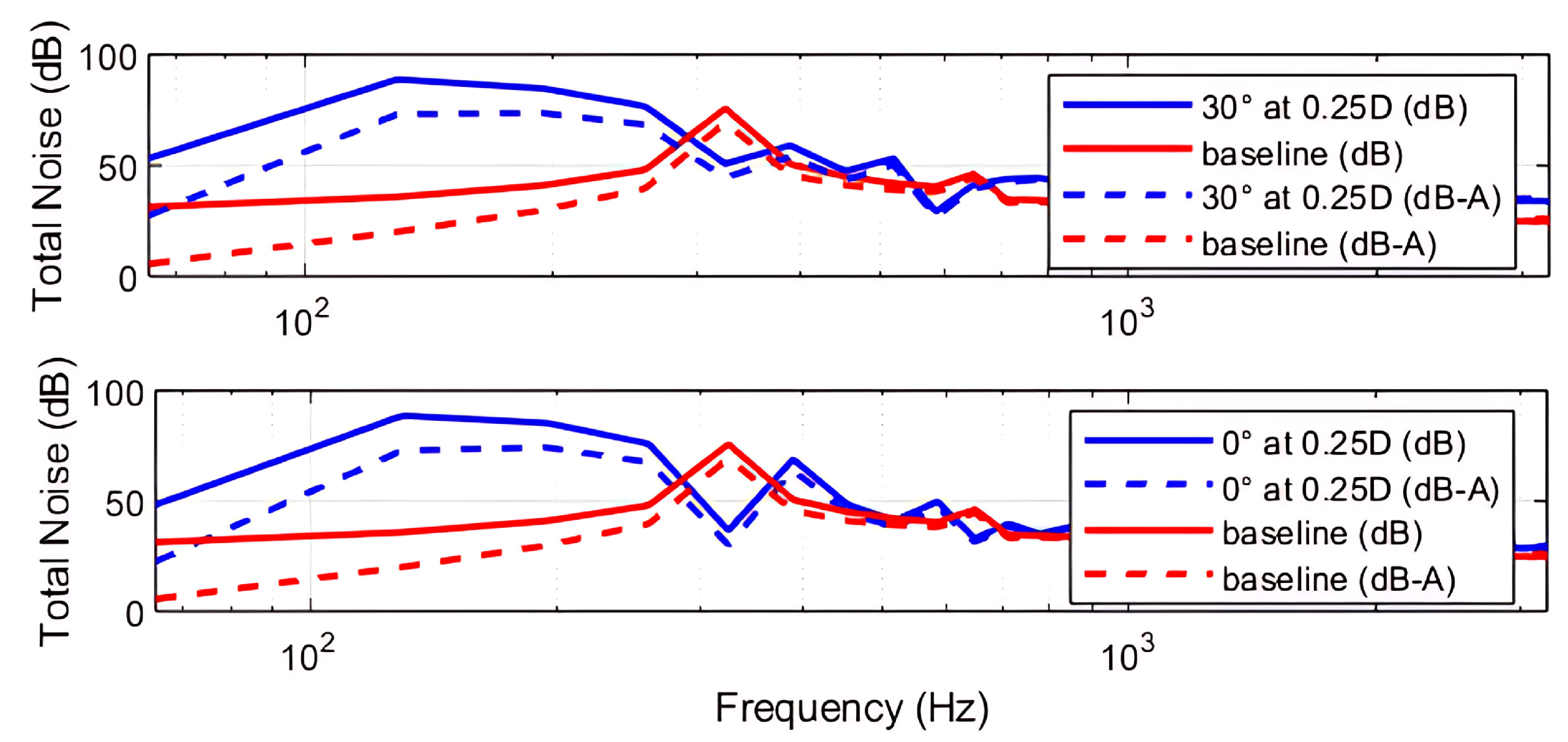
3.2. Aeroacoustic Analysis
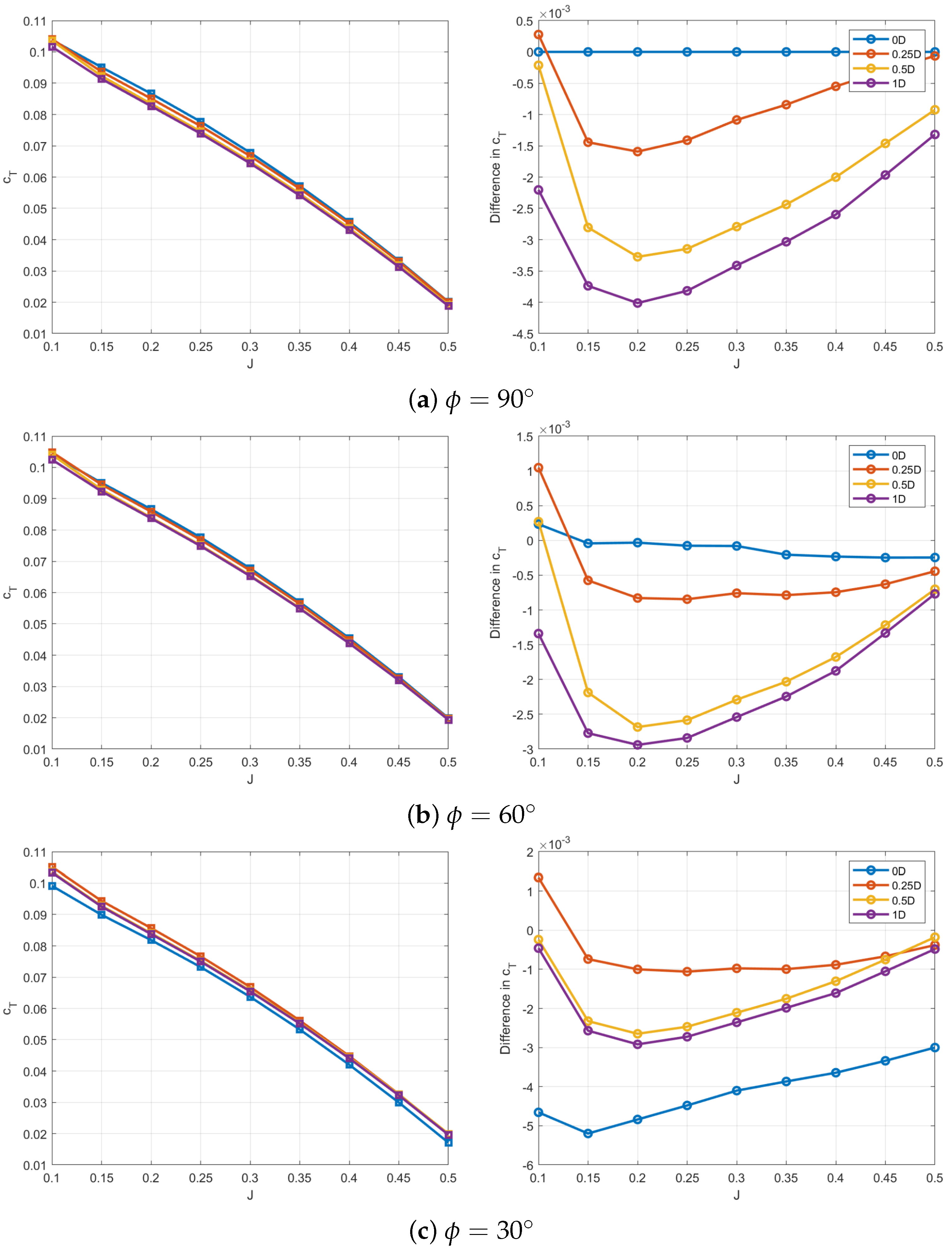
3.2.1. Thrust Coefficient ()
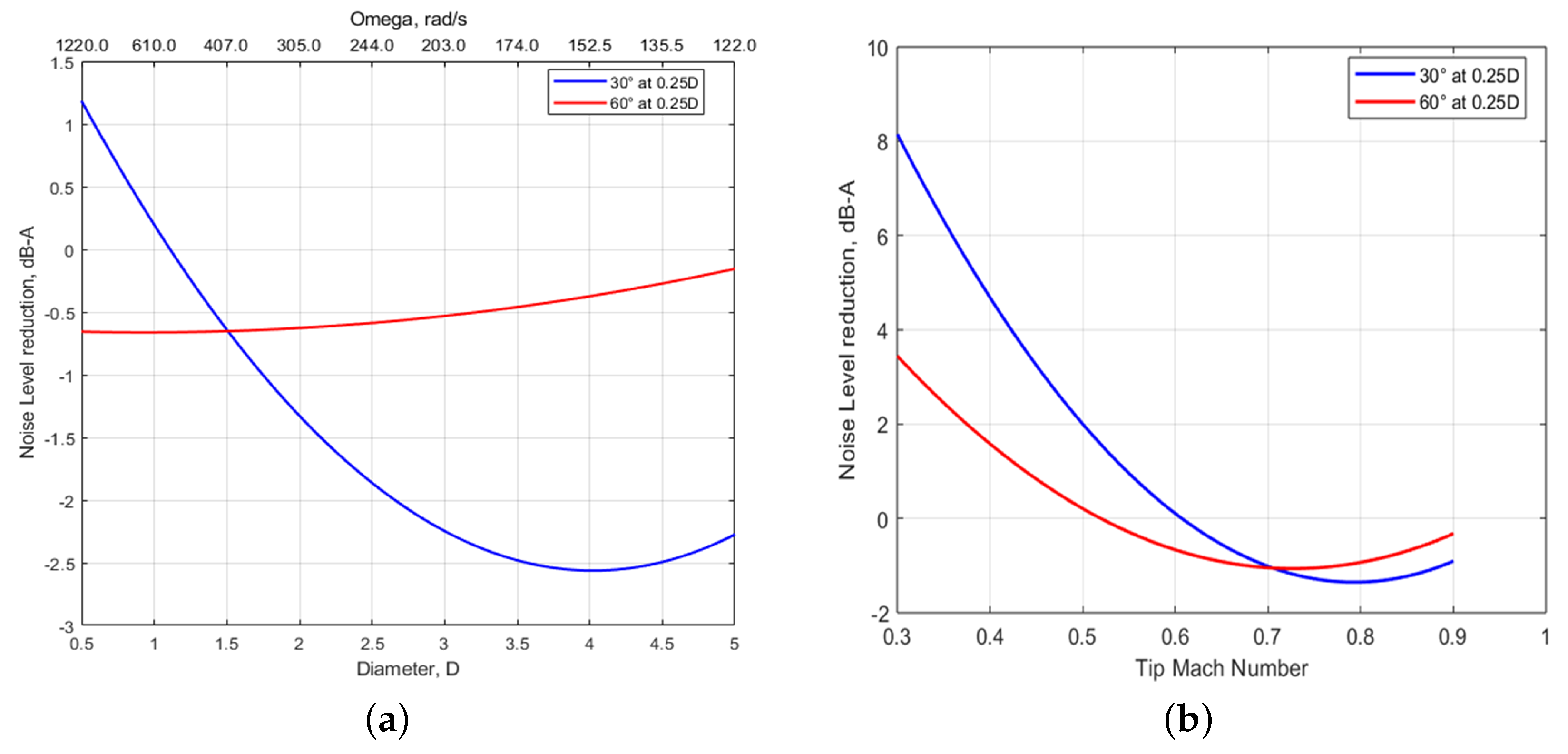
3.2.2. Parametric Study
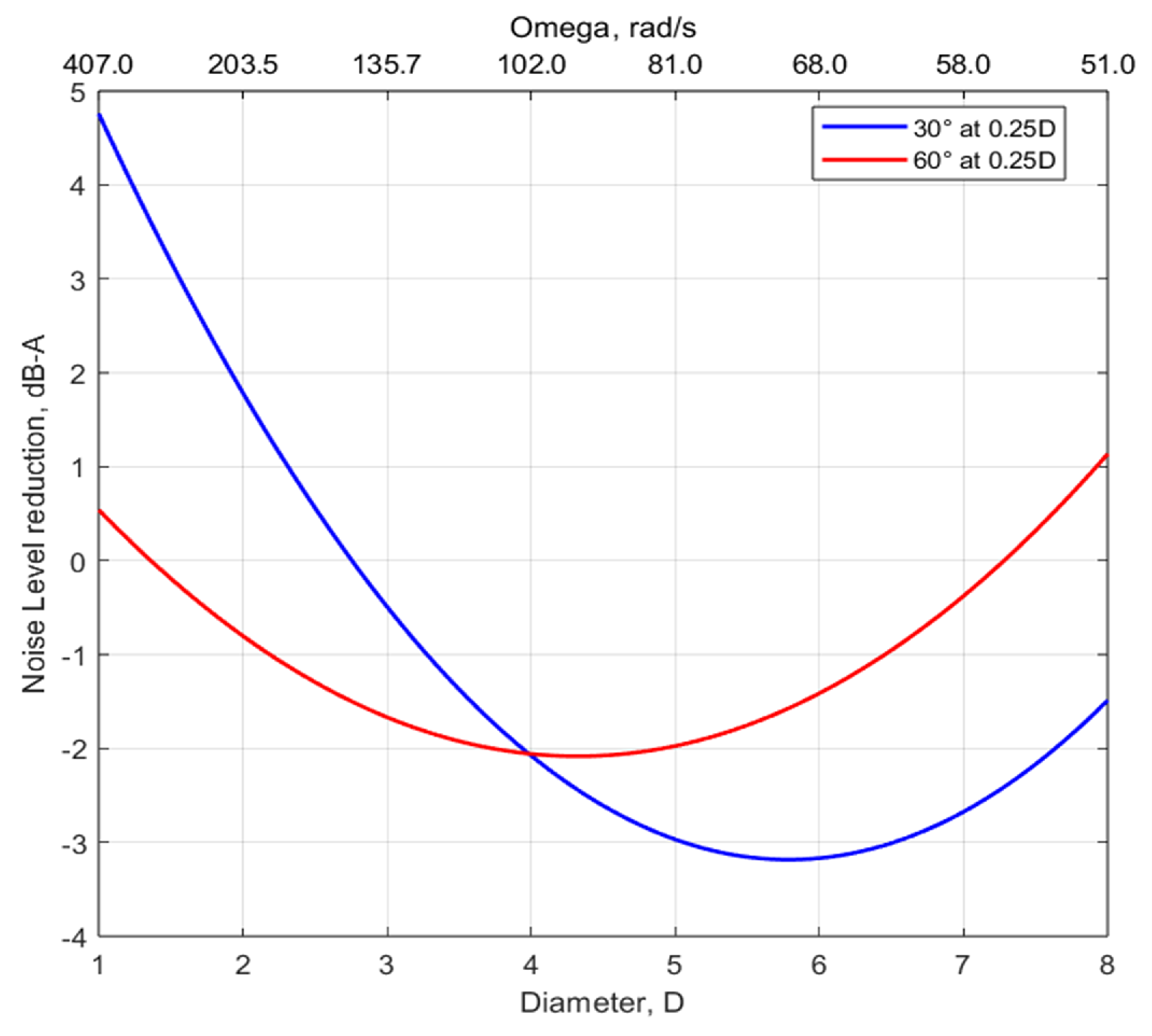
3.3. Five-Bladed Configuration
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Latin Letters | |
| Thrust Coefficient | |
| Torque Coefficient | |
| Freestream Velocity (m/s) | |
| Air Density (kg/m3) | |
| T | Thrust Force (N) |
| Q | Torque (Nm) |
| J | Advance Ratio |
| n | Rotational Speed (revolutions per second) |
| D | Propeller Diameter (m) |
| c | Chord Length (m) |
| r | Distance Between Observer and Source Point (m) |
| Mach Number in the Radiation Direction | |
| Loading Vector in the Radiation Direction | |
| Mach Number Component of the Loading Vector | |
| Greek Letters | |
| Angle of Attack [°] | |
| Blade Twist Angle [°] | |
| Tail Deflection Angle [°] | |
| Damping Ratio | |
| Undamped Natural Frequency (Hz) | |
| Azimuthal Spacing [°] | |
| Subscripts | |
| ac | Aerodynamic Center |
| ∞ | Freestream |
| Operators and Other | |
| First Time Derivative | |
| Perturbation Quantity | |
| Component Normal to a Surface | |
| Normalized Quantity | |
| BPF | Blade Passing Frequency |
| MRF | Moving Reference Frame |
| RANS | Reynolds-Averaged Navier–Stokes |
| RPM | Revolutions per Minute |
| SST | Shear Stress Transport |
| UAV | Unmanned Aerial Vehicle |
| Differential Surface Area Element |
References
- Chen, H.; Kwong, J.C.; Copes, R.; Tu, K.; Villeneuve, P.J.; Van Donkelaar, A.; Hystad, P.; Martin, R.V.; Murray, B.J.; Jessiman, B.; et al. Living near major roads and the incidence of dementia, Parkinson’s disease, and multiple sclerosis: A population-based cohort study. Lancet 2017, 389, 718–726. [Google Scholar] [CrossRef] [PubMed]
- Clark, C.; Paunovic, K. WHO environmental noise guidelines for the European region: A systematic review on environmental noise and quality of life, wellbeing and mental health. Int. J. Environ. Res. Public Health 2018, 15, 2400. [Google Scholar] [CrossRef] [PubMed]
- Lowson, M.V. Noise radiation from V/STOL aircraft. In Proceedings of the International Council of the Aeronautical Sciences, NASA Technical Reports Server (NTRS), Adelaide, Australia, 1 July–31 December 1972; Available online: https://ntrs.nasa.gov/citations/19720057481 (accessed on 1 September 2024).
- Anonymous. Impact of Aircraft Noise on Health. Detailed Review on the Impact of Aircraft Noise on Health Including Sleep Disturbances and Cardiovascular Diseases. SpringerLink. 2018. Available online: https://link.springer.com (accessed on 1 September 2024).
- Anonymous. Drone Noise Emission Characteristics and Noise Effects on Humans—A Systematic Review. Systematic Review of Drone Noise Emissions and Their Health Effects on Humans. PubMed. 2020. Available online: https://pubmed.ncbi.nlm.nih.gov (accessed on 2 September 2024).
- Anonymous. Aviation Noise Impacts: State of the Science. Exploration of the Adverse Health Effects of Aviation Noise. National Center for Biotechnology Information. 2019. Available online: https://www.ncbi.nlm.nih.gov (accessed on 2 September 2024).
- Green, N.; Torija, A.J.; Ramos-Romero, C. Perception of Noise from Unmanned Aircraft Systems: Efficacy of Metrics for Indoor and Outdoor Listener Positions. J. Acoust. Soc. Am. 2024, 155, 915–929. [Google Scholar] [CrossRef] [PubMed]
- Pagano, A.; Barbarino, M.; Casalino, D.; Federico, L. Tonal and Broadband Noise Calculations for Aeroacoustic Optimization of a Pusher Propeller. J. Aircr. 2010, 47, 835–846. [Google Scholar] [CrossRef]
- Chen, J.; Xie, J.; Lee, H.M. Noise Attenuation by Half Flat tip Serrated Trailing Edge in Rotating Blades. J. Phys. Conf. Ser. 2023, 2489, 012022. [Google Scholar] [CrossRef]
- Sinayoko, S.; Azarpeyvand, M.; Lyu, B. Trailing edge noise prediction for rotating serrated blades. In Proceedings of the 20th AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Halimi, A.; Marinus, B.G.; Larbi, S. Analytical prediction of broadband noise from mini-RPA propellers with serrated edges. Int. J. Aeroacoustics 2019, 18, 517–535. [Google Scholar] [CrossRef]
- Ning, Z.; Wlezien, R.; Hu, H. An Experimental Study on Small UAV Propellers with Serrated Trailing Edges. In Proceedings of the 47th AIAA Fluid Dynamics Conference, Denver, CO, USA, 5–9 June 2017. Number AIAA 2017-3813. [Google Scholar]
- Li, Y.; Yang, Y.; Liu, Y.; Wang, Y.; Huang, B.; Li, W. Aerodynamic and Aeroacoustic Analyses of a UAV Propeller with Trailing Edge Serrations. In Proceedings of the ACOUSTICS, Hamburg, Germany, 4–6 October 2018. [Google Scholar]
- Keil, T.H. A Sensitivity Study on the Effect of Blade Sweep on the Trade-Off Between Propeller Efficiency and Noise with Panel Method Analysis. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2021. Available online: https://repository.tudelft.nl/record/uuid:39e67ba0-3409-4069-be3e-f1f12443a9ff (accessed on 7 September 2024).
- de Haan, W. Impact of Blade Sweep on Aerodynamic and Aeroacoustic Performance Optimization of Isolated Propellers. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2021. Available online: https://repository.tudelft.nl/record/uuid:09137b04-f499-47f5-9c17-7334d0ef92ac (accessed on 7 September 2024).
- Wiedemann, A.D. A Study of the Aeroacoustics of Swept Propellers for Small Unmanned Aerial Vehicles. Master’s Thesis, Old Dominion University, Norfolk, VA, USA, 2020. [Google Scholar] [CrossRef]
- Ghodake, D.; Sanjosé, M.; Moreau, S.; Henner, M. Effect of Sweep on Axial Fan Noise Sources Using the Lattice Boltzmann Method. Int. J. Turbomach. Propuls. Power 2022, 7, 34. [Google Scholar] [CrossRef]
- Marinus, B.G. Comparative Study of the Effects of Sweep and Humps on High-Speed Propeller Blades. In Proceedings of the 18th AIAA/CEAS Aeroacoustics Conference (33rd AIAA Aeroacoustics Conference), Colorado Springs, CO, USA, 4–6 June 2012; pp. 1–16. [Google Scholar] [CrossRef]
- Huang, Z.; Yao, H.; Sjögren, O.; Lundbladh, A.; Davidson, L. Aeroacoustic analysis of aerodynamically optimized joined-blade propeller for future electric aircraft at cruise and take-off. Aerosp. Sci. Technol. 2020, 106, 106336. [Google Scholar] [CrossRef]
- Dobrzynski, W. Propeller Noise Reduction by Means of Unsymmetrical Blade-Spacing. J. Sound Vib. 1993, 163, 123–126. [Google Scholar] [CrossRef]
- Kim, T.Y. Reduction of Tonal Propeller Noise by Means of Uneven Blade Spacing. Master’s Thesis, University of California, Irvine, CA, USA, 2016. [Google Scholar]
- Prior, S.D. Reviewing and Investigating the Use of Co-Axial Rotor Systems in Small UAVs. Int. J. Micro Air Veh. 2010, 2, 1–16. [Google Scholar] [CrossRef]
- Tinney, C.E.; Valdez, J.A.; Zhao-Dubuc, Y. Distilling the Acoustics of Stacked Rotors Using Conventional POD with Vold-Kalman Filters. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar] [CrossRef]
- APC Propellers. APC Model Aircraft Propellers. 2024. Available online: https://www.apcprop.com/ (accessed on 2 October 2024).
- ANSYS, Inc. ANSYS Engineering Simulation Software. 2024. Available online: https://www.ansys.com/ (accessed on 2 October 2024).
- Kutty, H.A.; Rajendran, P. 3D CFD Simulation and Experimental Validation of Small APC Slow Flyer Propeller Blade. Aerospace 2017, 4, 10. [Google Scholar] [CrossRef]
- Hennes, C.C.; Lopes, L.V.; Shirey, J.; Cheng, R.; Erwin, J.; Lee, S.; Goldman, B.A.; Botre, M.; Zachos, D.R.; Gan, Z.F.T.; et al. PSU-WOPWOP 3.5.0 User’s Guide; The Pennsylvania State University: University Park, PA, USA, 2022. [Google Scholar]


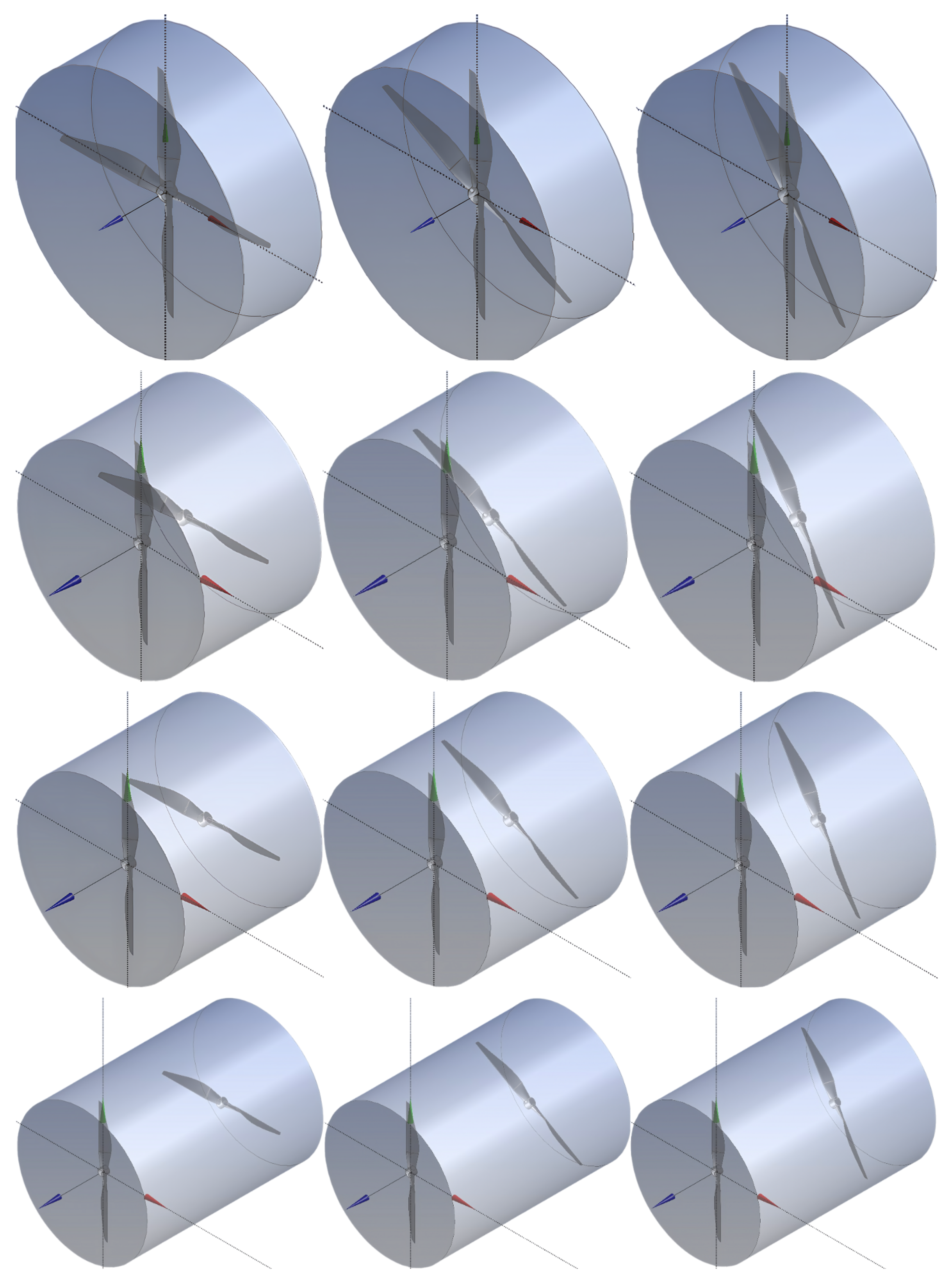
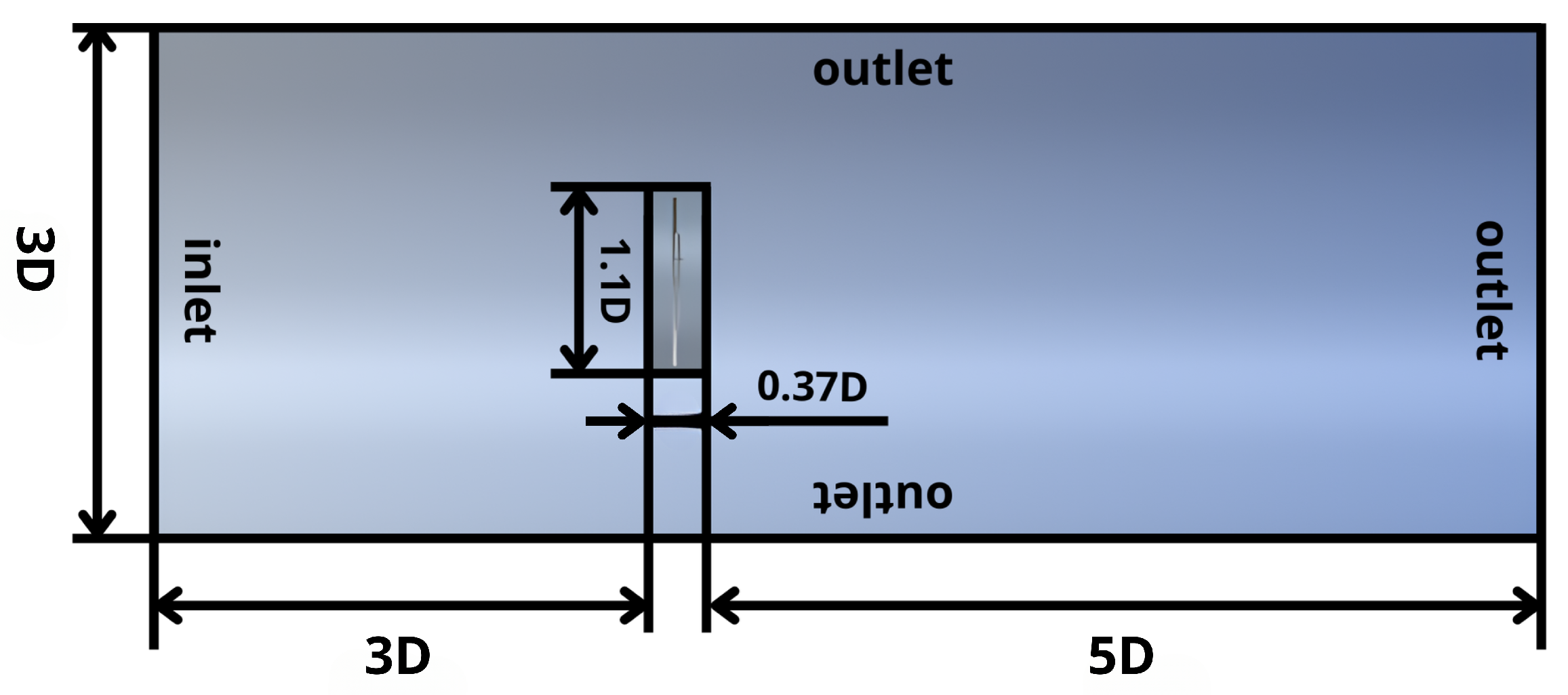
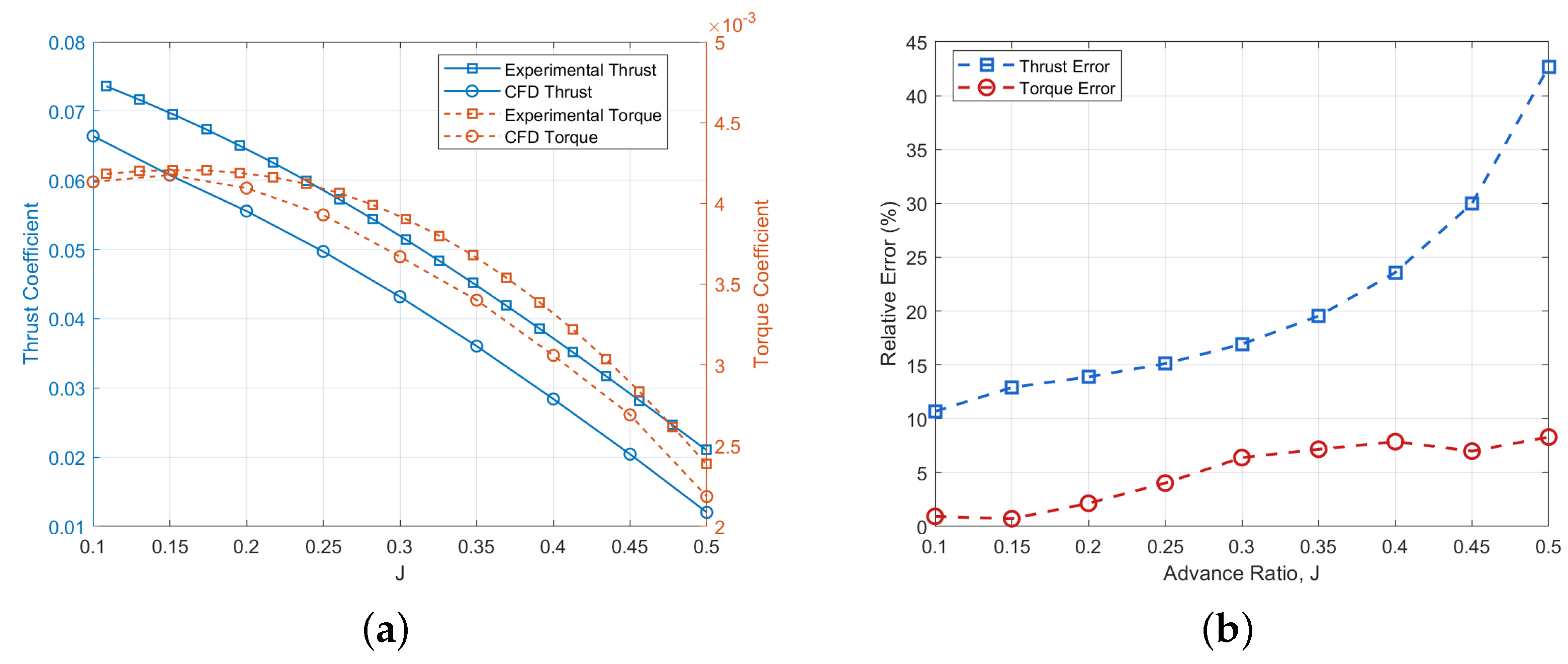
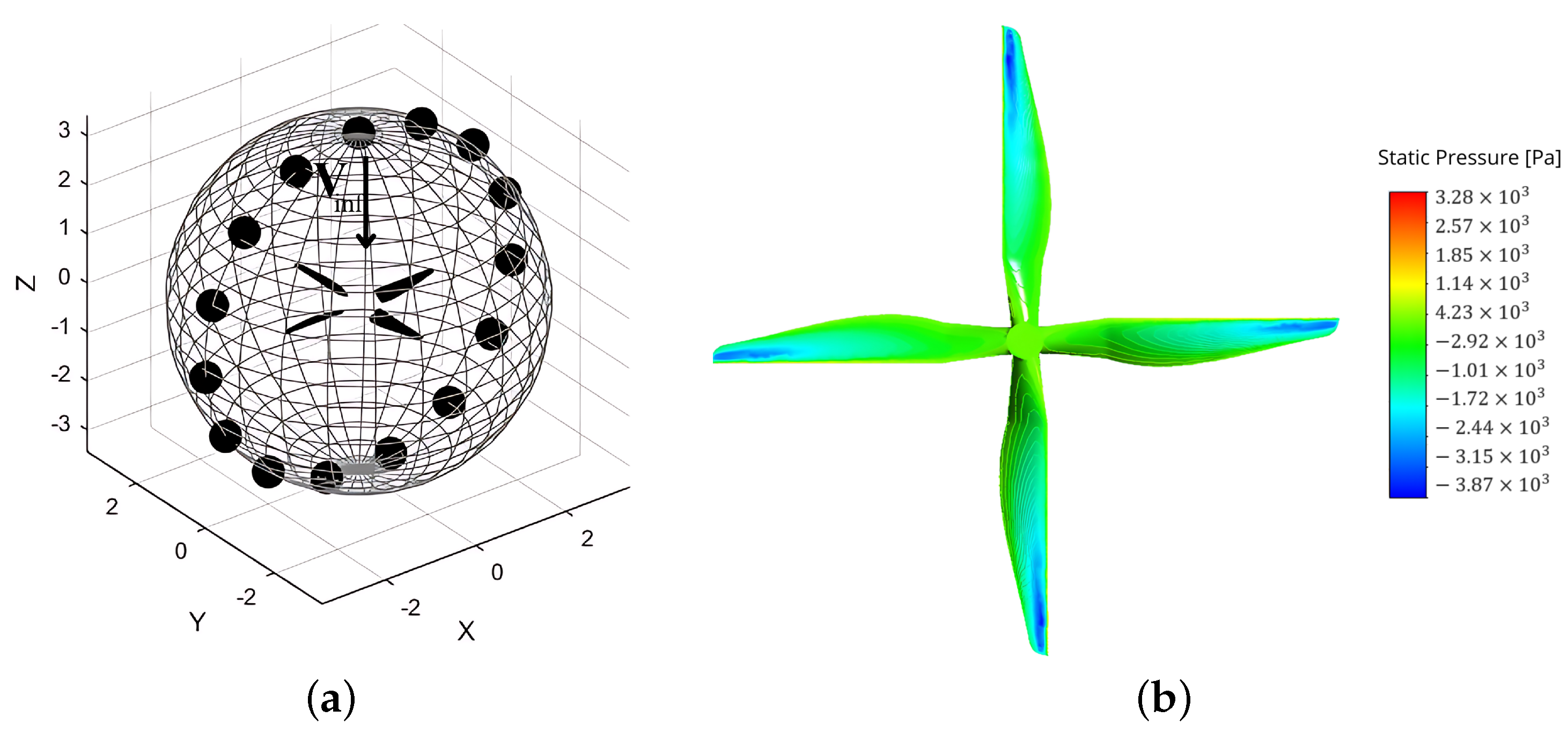



| Configuration | Angular Spacing () | Axial Spacing |
|---|---|---|
| 1–4 | ||
| 5–8 | ||
| 9–12 |
| Cell Count | Thrust Coefficient () | Relative Error (%) |
|---|---|---|
| ∼91,347 | 0.0685 | |
| ∼205,155 | 0.0669 | 2.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arystanbekov, C.; Zhakatayev, A.; Elhadidi, B. Passive Rotor Noise Reduction Through Axial and Angular Blade Spacing Modulation. Aerospace 2025, 12, 167. https://doi.org/10.3390/aerospace12030167
Arystanbekov C, Zhakatayev A, Elhadidi B. Passive Rotor Noise Reduction Through Axial and Angular Blade Spacing Modulation. Aerospace. 2025; 12(3):167. https://doi.org/10.3390/aerospace12030167
Chicago/Turabian StyleArystanbekov, Chingiz, Altay Zhakatayev, and Basman Elhadidi. 2025. "Passive Rotor Noise Reduction Through Axial and Angular Blade Spacing Modulation" Aerospace 12, no. 3: 167. https://doi.org/10.3390/aerospace12030167
APA StyleArystanbekov, C., Zhakatayev, A., & Elhadidi, B. (2025). Passive Rotor Noise Reduction Through Axial and Angular Blade Spacing Modulation. Aerospace, 12(3), 167. https://doi.org/10.3390/aerospace12030167







