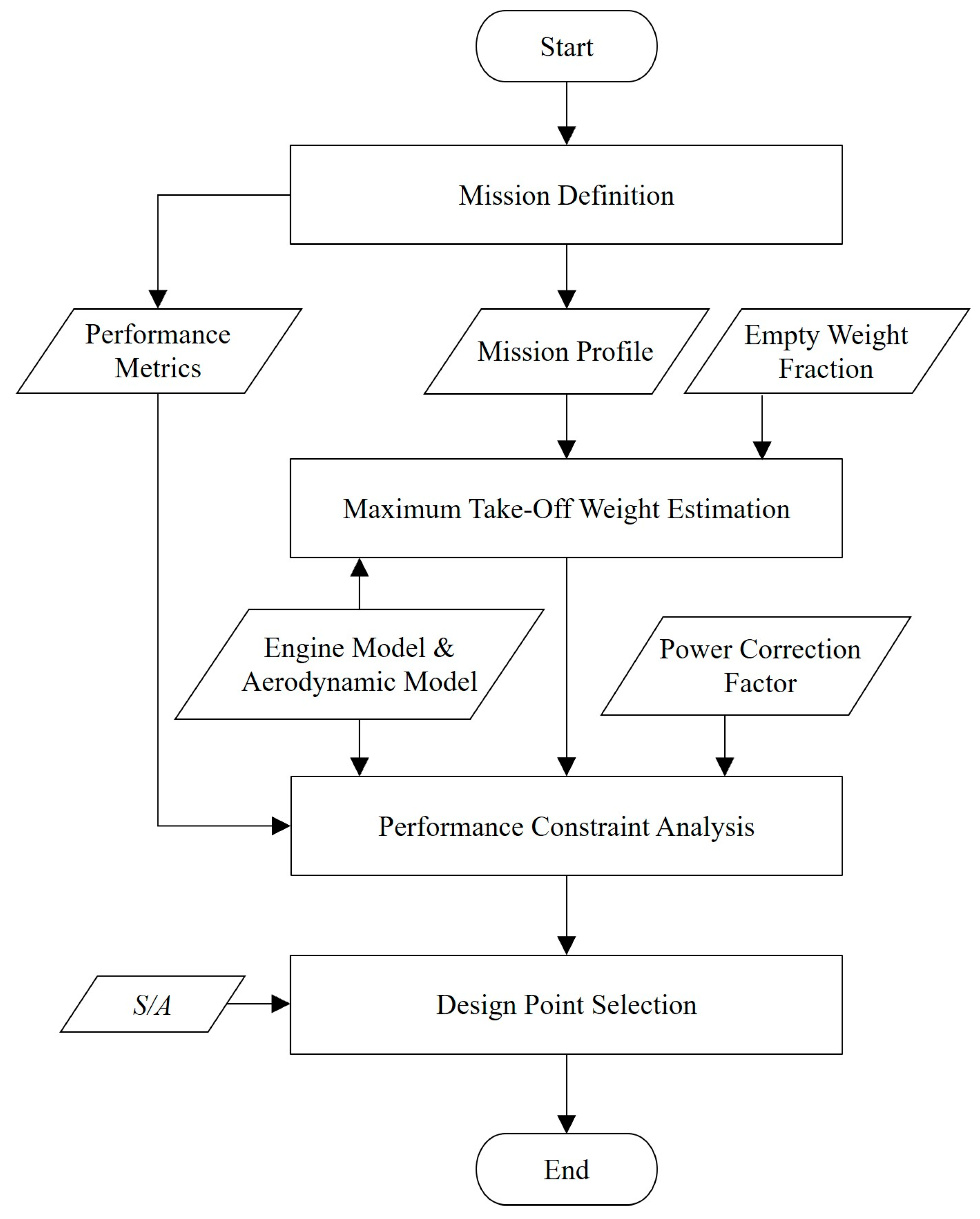
Estimation Method for Basic Parameters of High-Speed Vertical Take-Off and Landing Aircraft
Abstract
1. Introduction
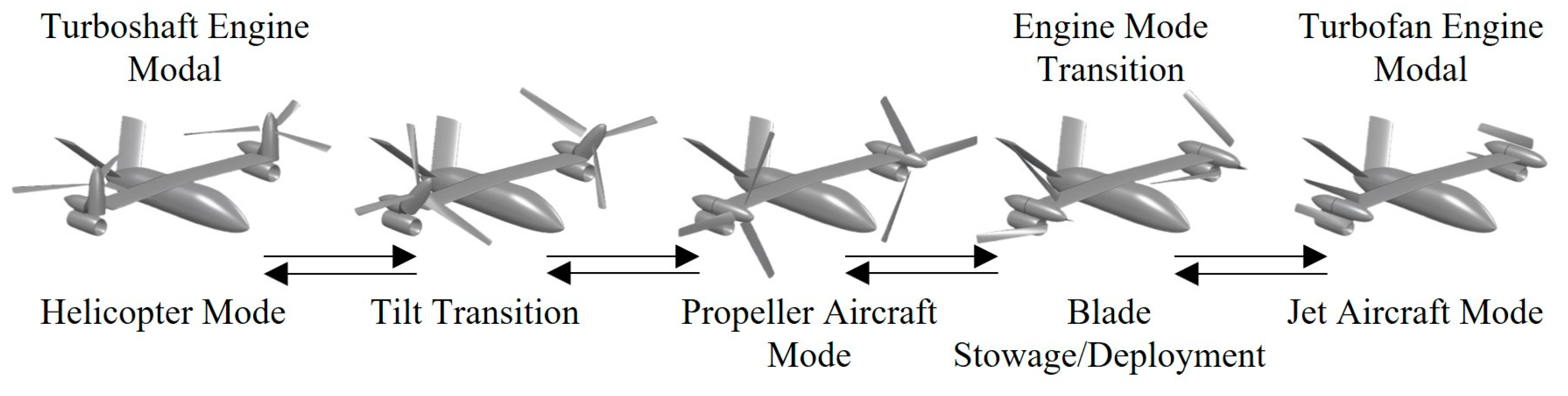
2. Mission Definition
- •
- Helicopter Mode: vertical take-off and landing, hover, climb, and forward flight;
- •
- Fixed-Wing Aircraft Mode (including propeller aircraft mode and jet aircraft mode): climb, turn, cruise, and descent;
- •
- Tilt Transition: mutual transition between helicopter mode and propeller aircraft mode;
- •
- Engine Mode Transition: mutual switching between the engine’s turboshaft and turbofan modes;
- •
- Payload Deployment.
3. Maximum Take-Off Weight Estimation
3.1. Empty Weight
3.2. Fuel Weight
- Vertical Take-off and Climb in Helicopter Mode
- 2.
- Tilt Transition and Engine Mode Transition
- 3.
- Climb in Fixed-Wing Aircraft Mode
- 4.
- Cruise in Fixed-Wing Aircraft Mode
- 5.
- Loiter (or Turn) in Fixed-Wing Aircraft Mode
- 6.
- Descent in Fixed-Wing Aircraft Mode
- 7.
- Payload Deployment
- 8.
- Vertical Landing
4. Preliminary Modeling of Engine and Aerodynamic Characteristics
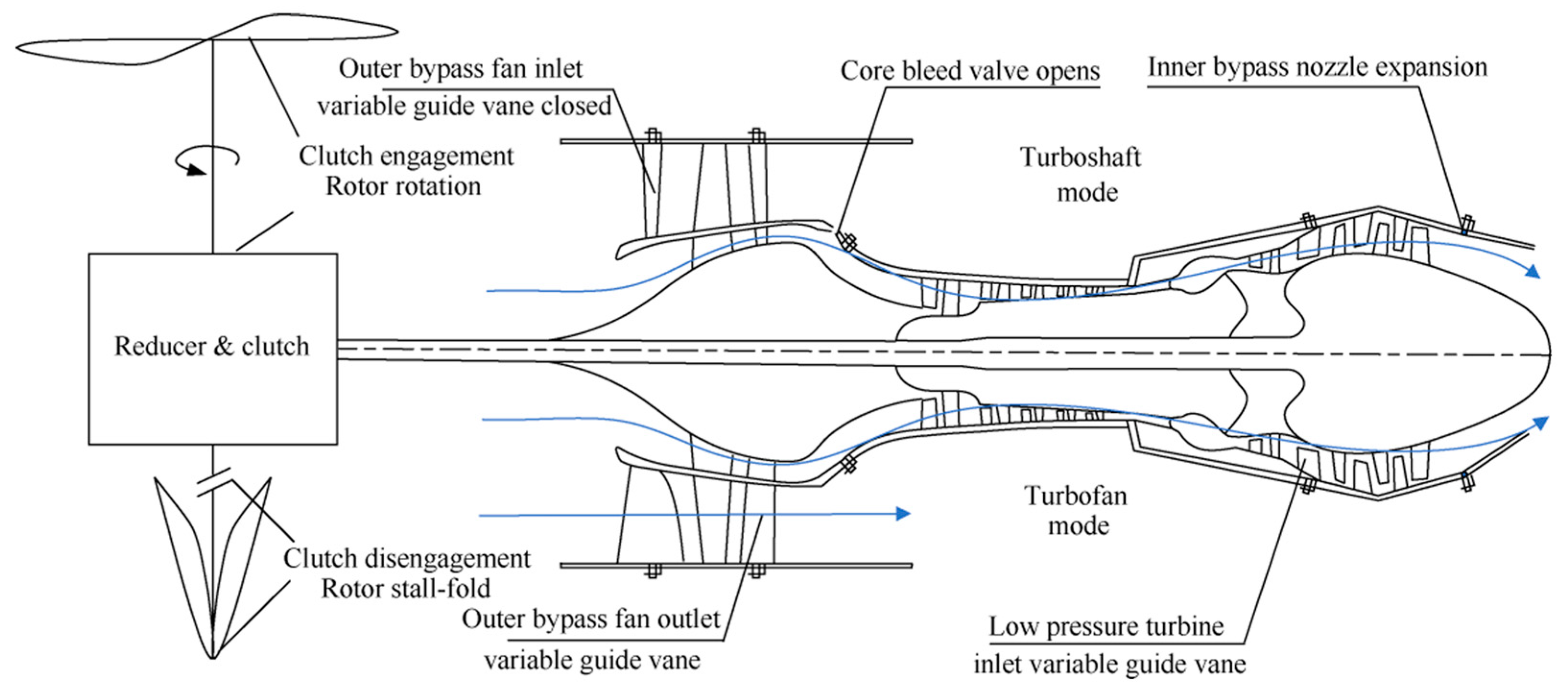
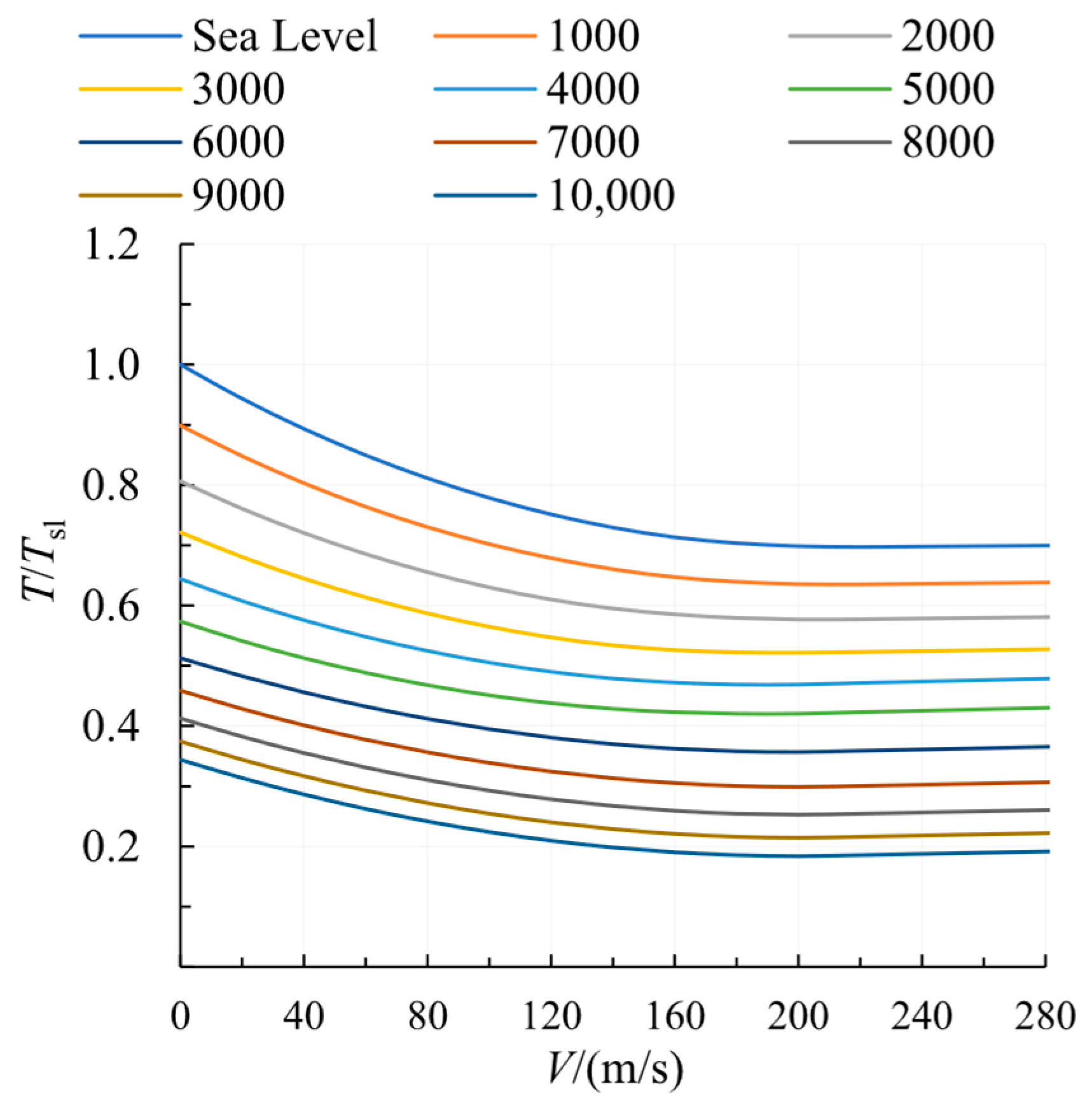
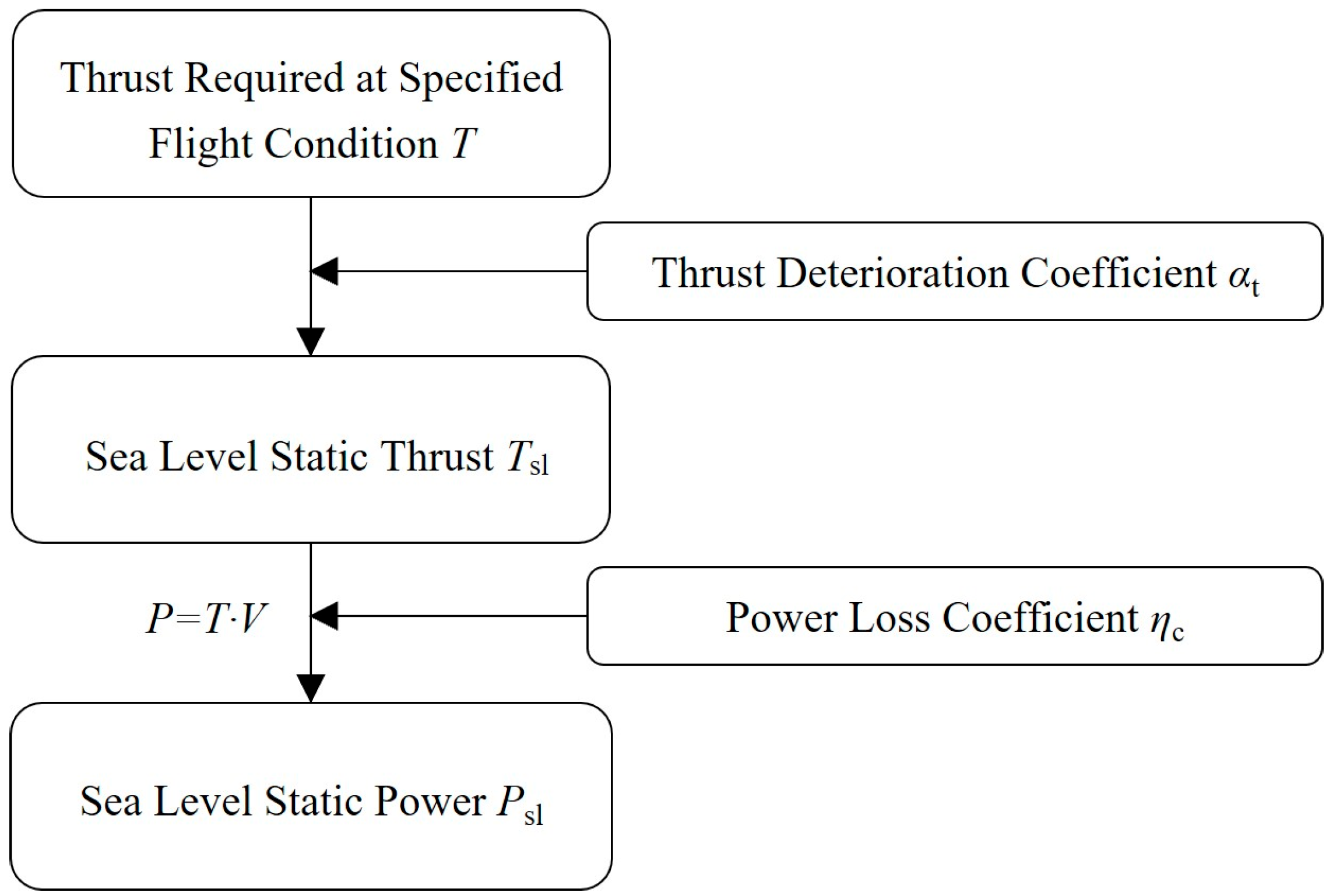
4.1. Engine Model
4.2. Aerodynamic Parameters
5. Performance Constraint Analysis
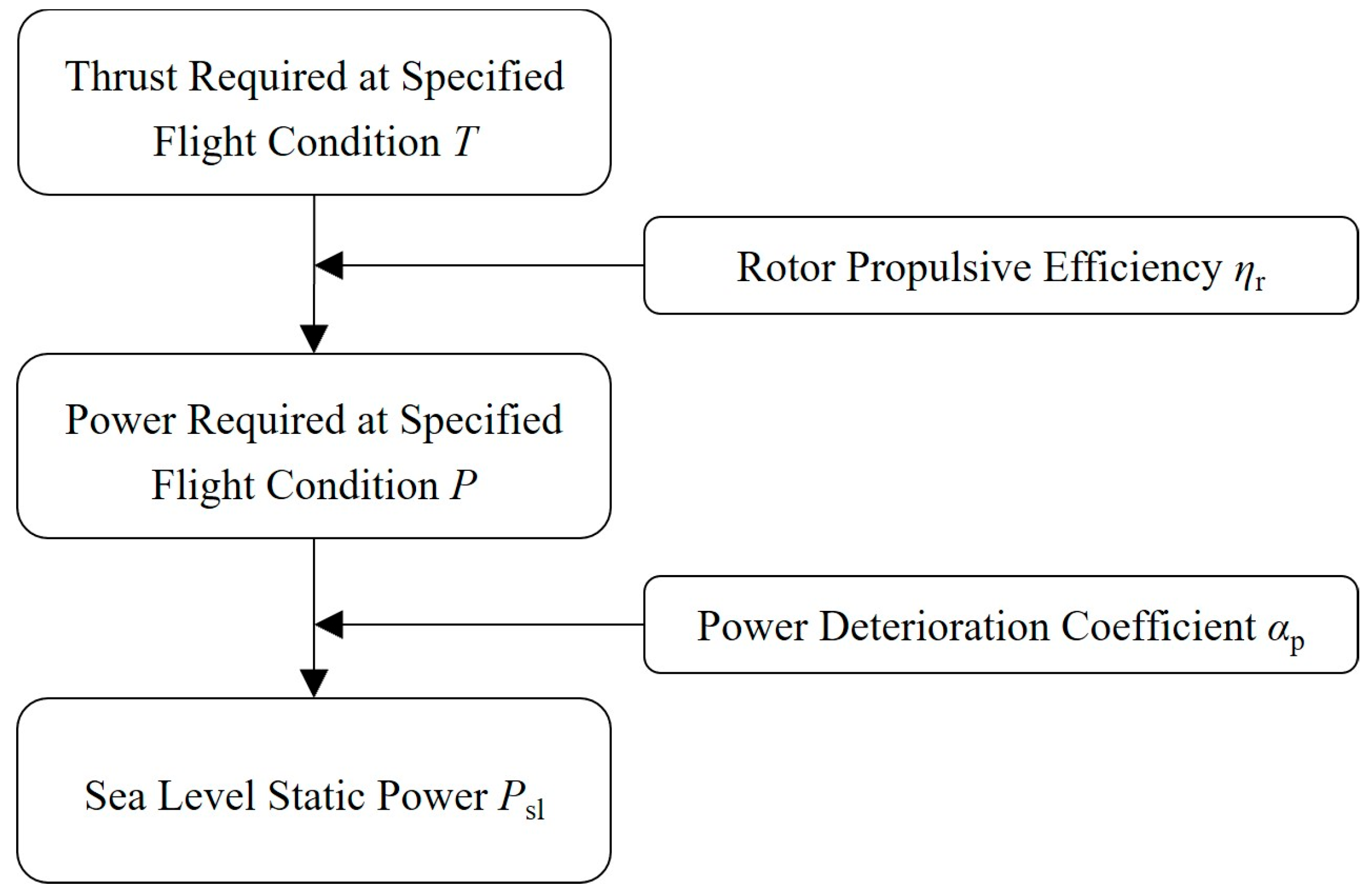
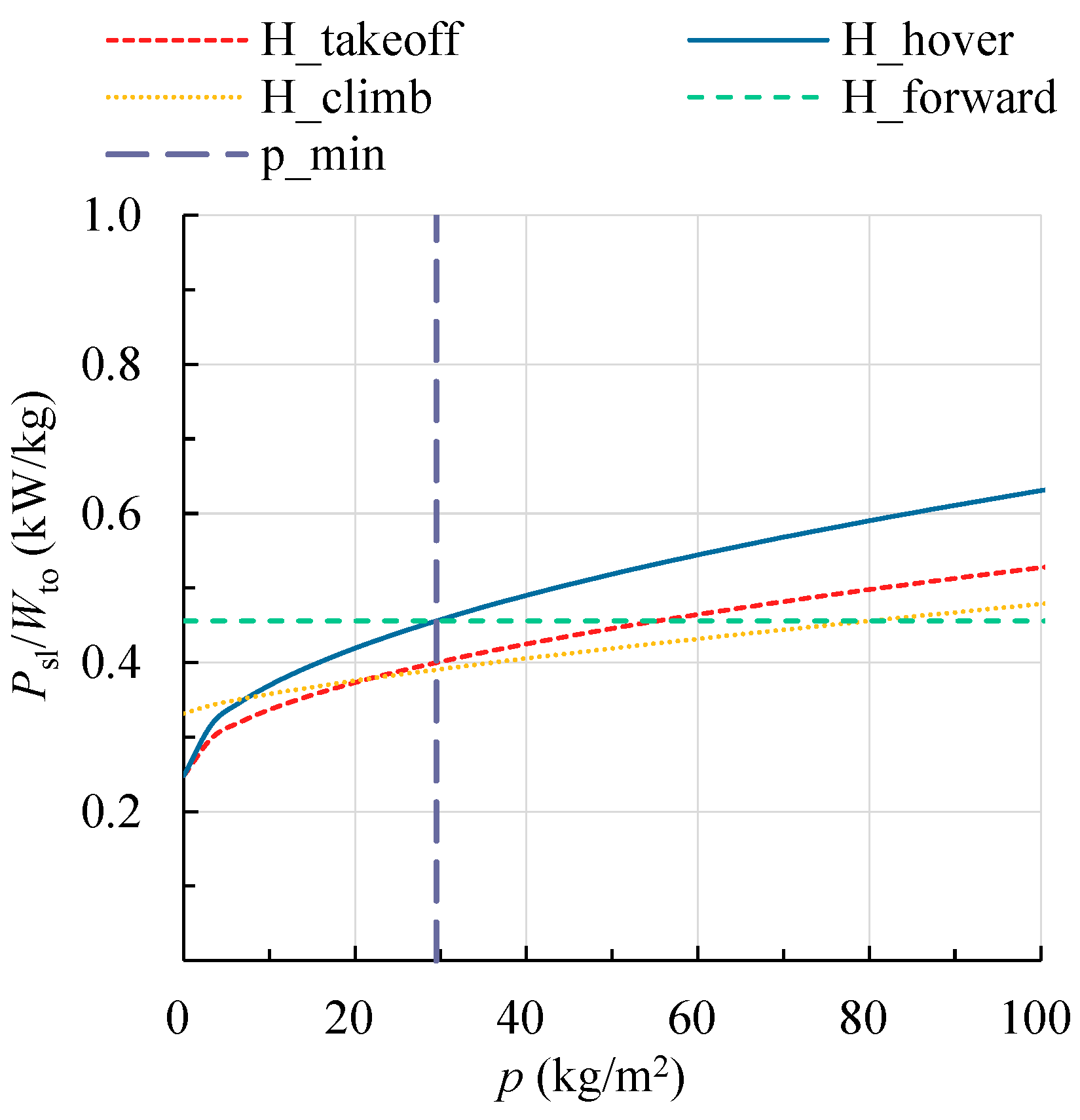
5.1. Helicopter Mode
- Vertical Take-off Requirement
- 2.
- Hover Ceiling
- 3.
- Maximum Rate of Climb
- 4.
- Maximum Forward Speed
- 5.
- Minimum Disk Loading Constraint
5.2. Fixed-Wing Aircraft Mode
- Maximum Rate of Climb
- 2.
- Turning (or Loiter) Radius
- 3.
- Cruise Speed
- 4.
- Maximum Flight Speed
- 5.
- Stall Speed
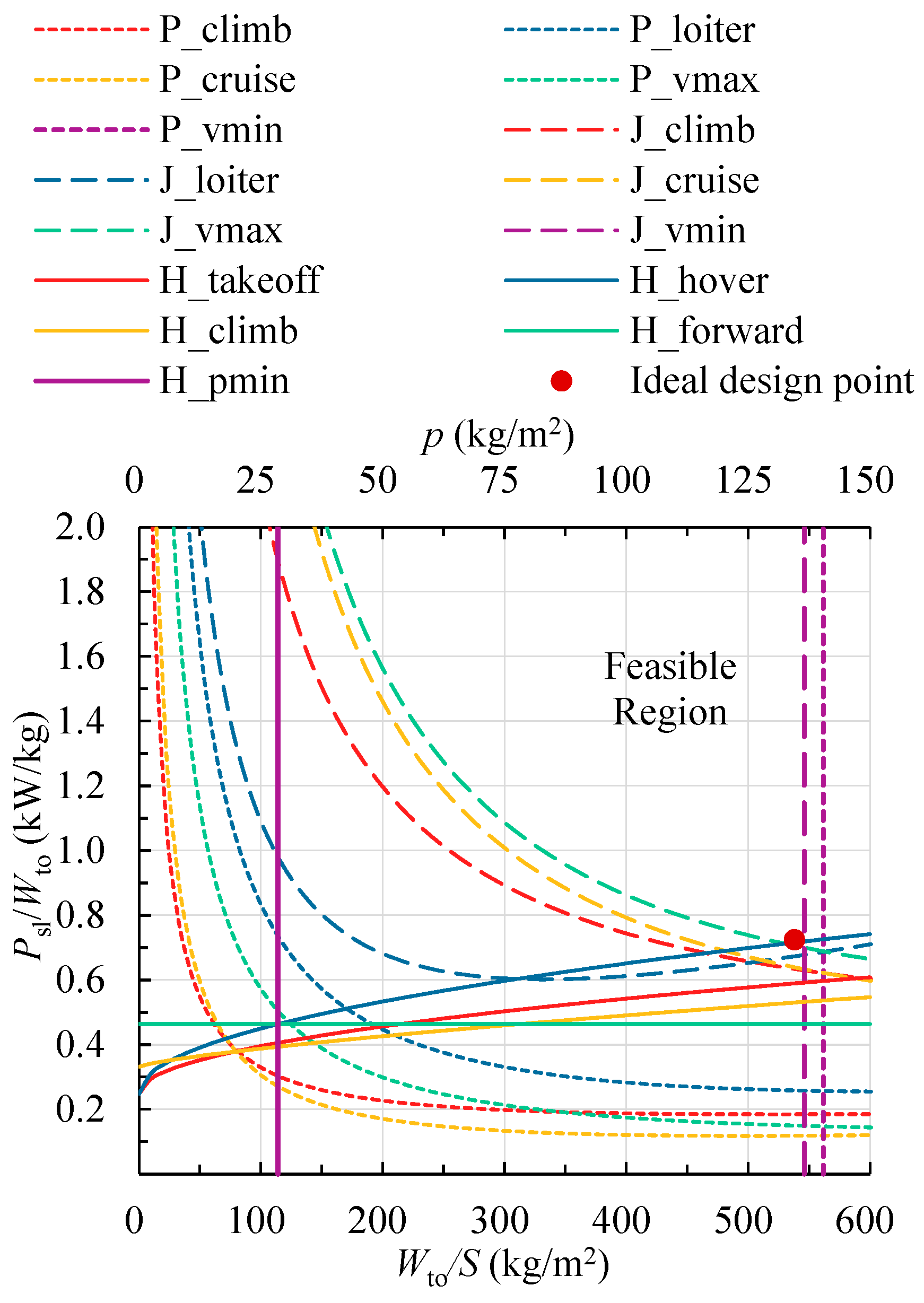
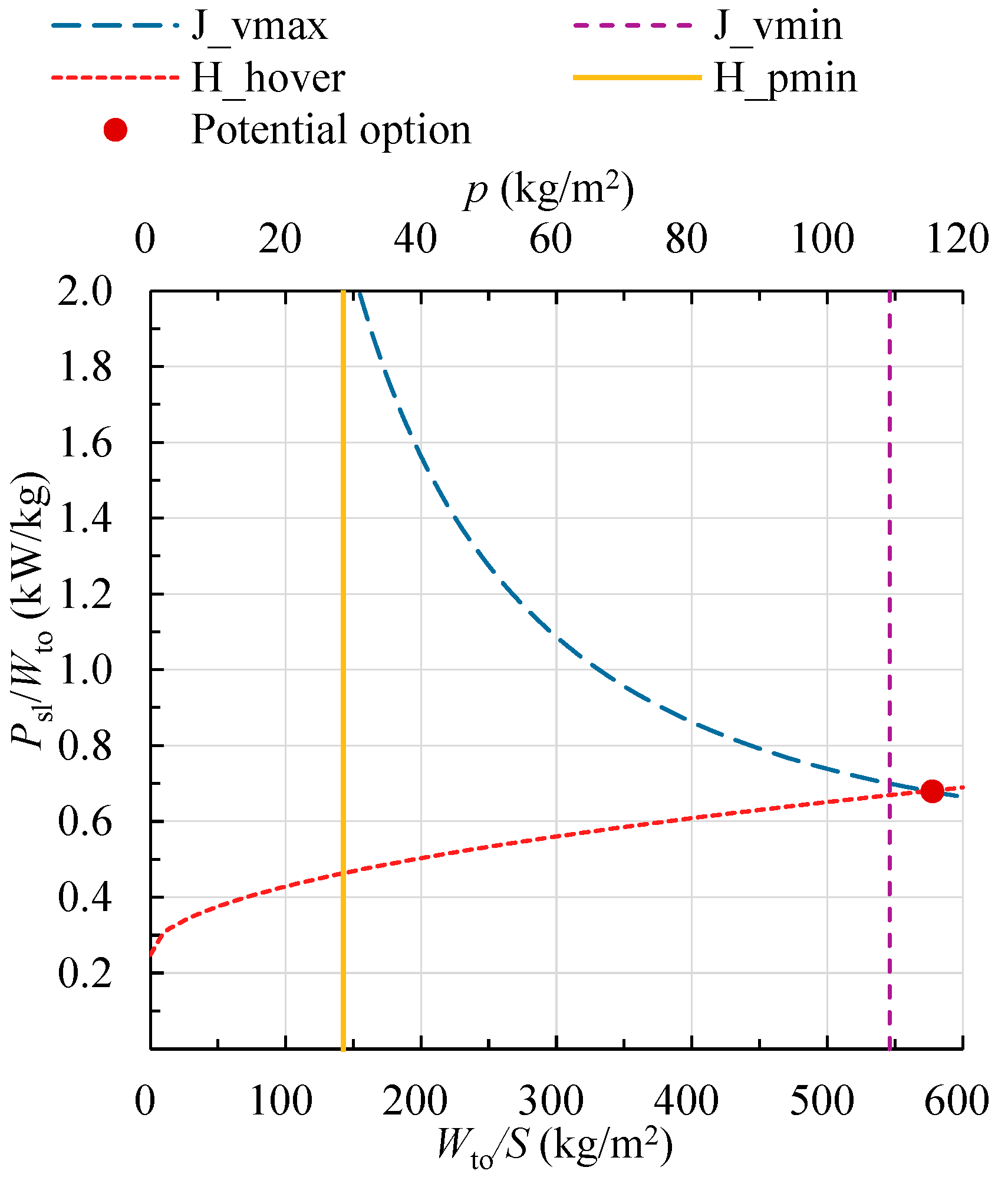
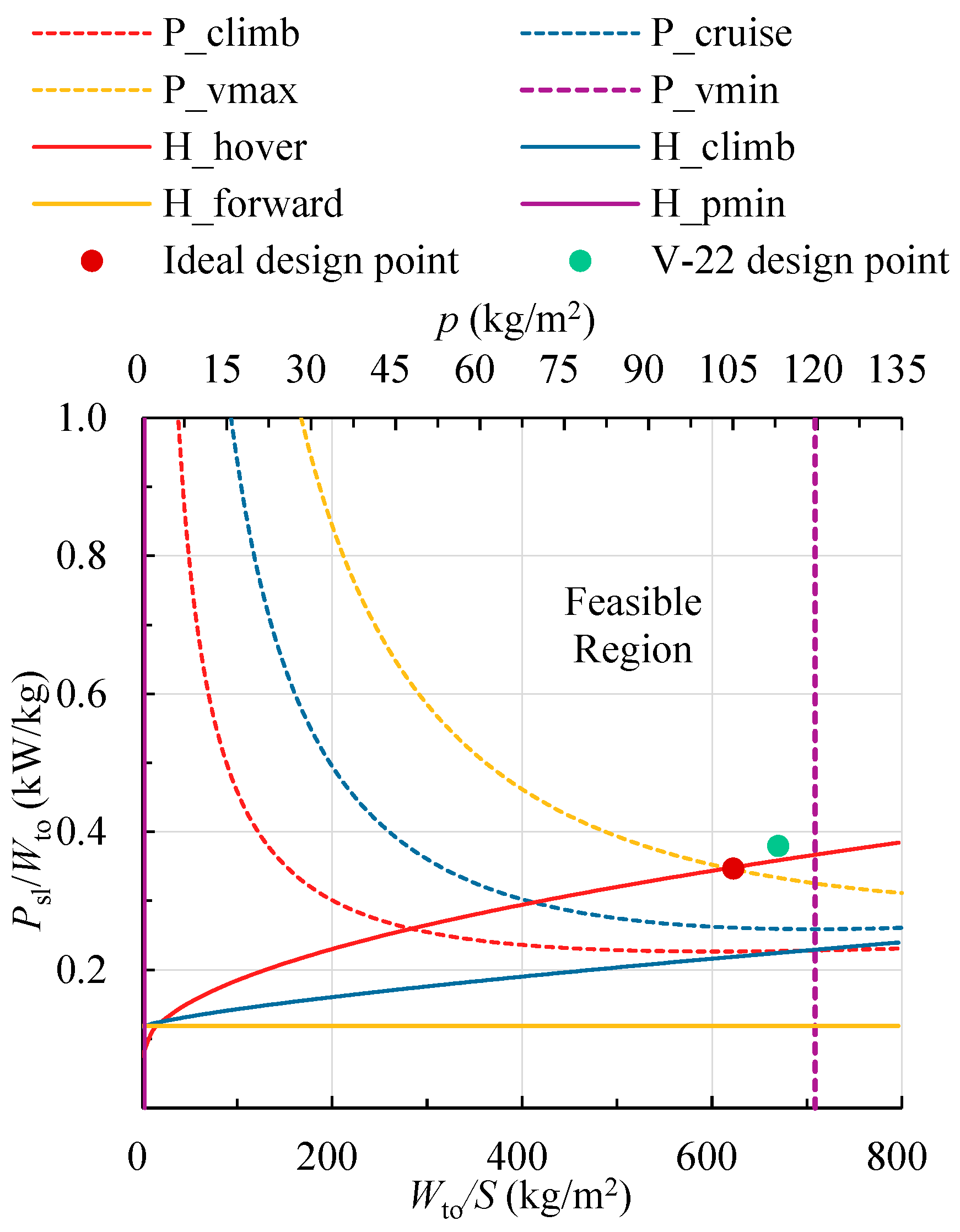
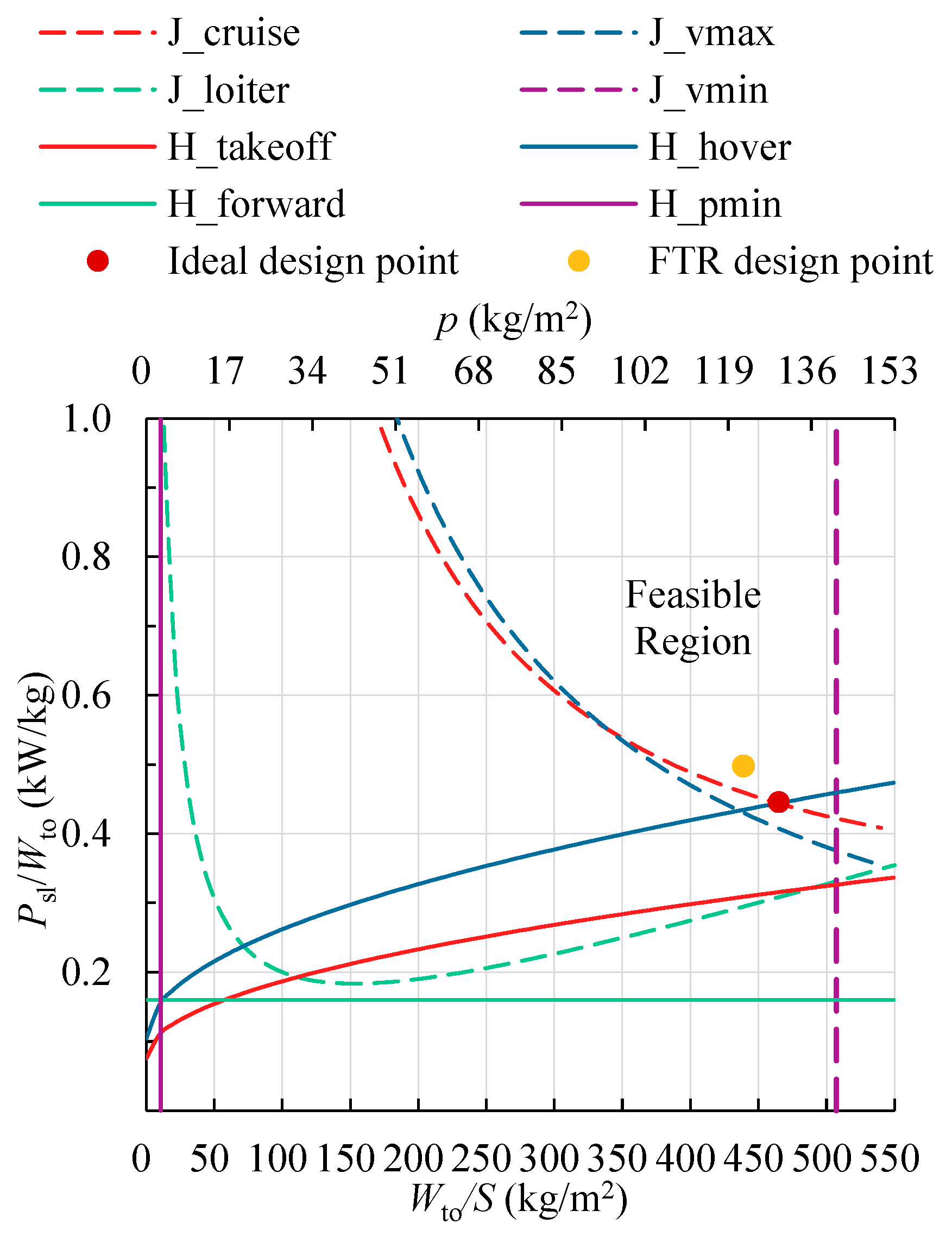
5.3. Comprehensive Constraint Analysis
6. Validation
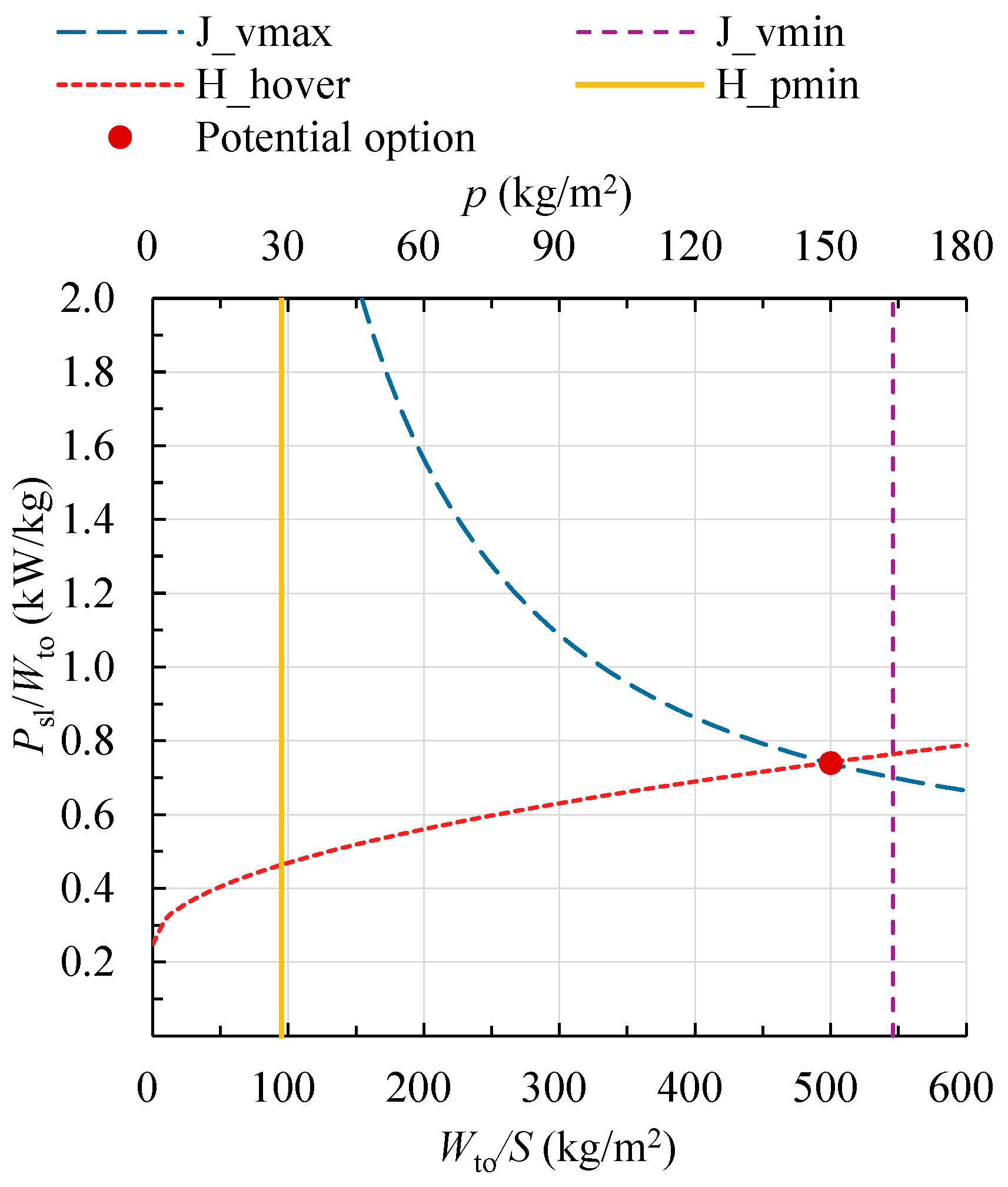
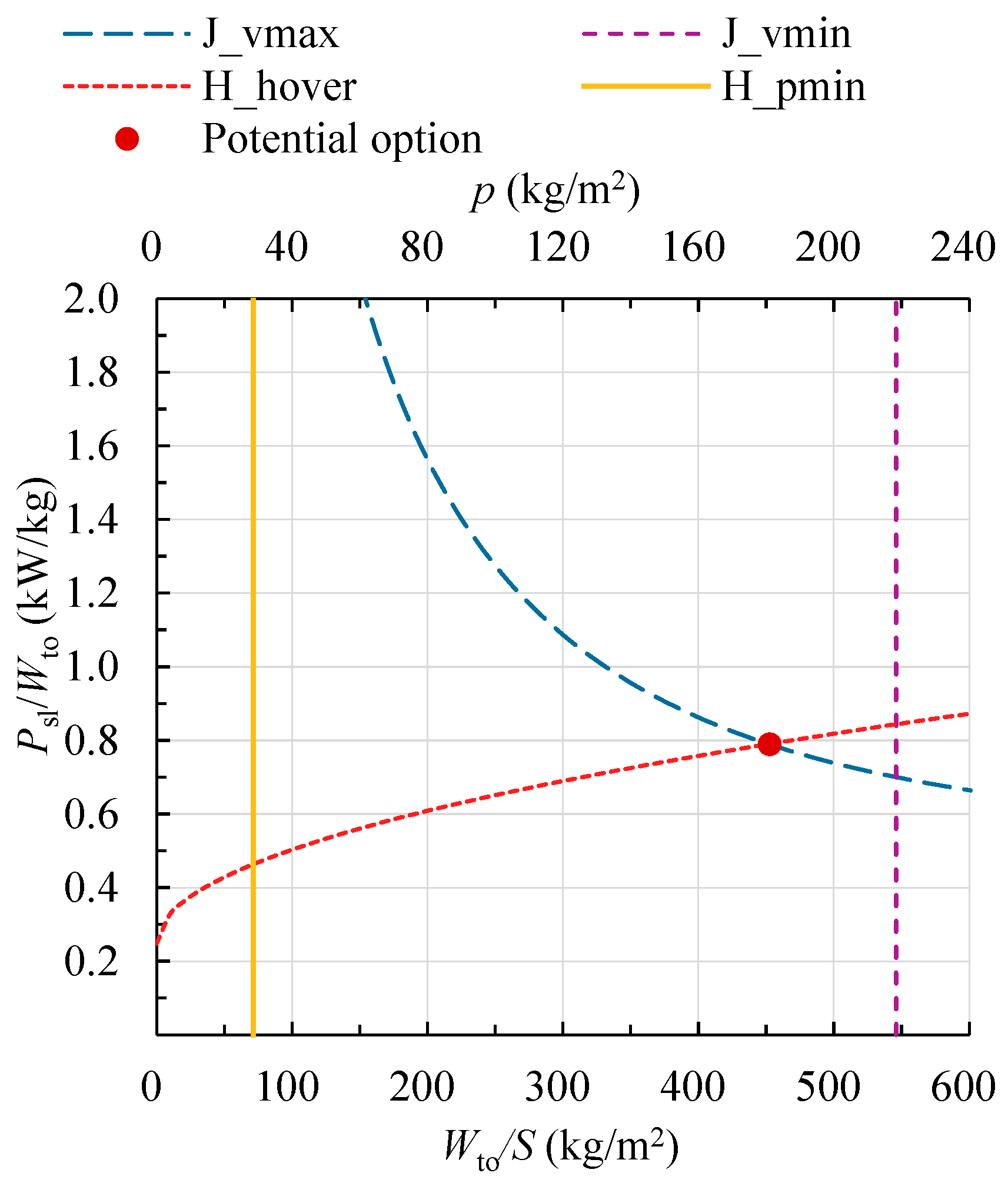
6.1. V-22 Osprey Tiltrotor Aircraft
6.2. High-Speed Folding Rotor Aircraft
6.3. Discussion on Estimation Results
- Evaluation and Quantification of the Difference
- 2.
- The Implications of Selecting the Ideal Design Point
- 3.
- Consequences of Oversizing
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marano, A.D.; Diodati, G.; Paletta, N.; Di Palma, L.; Belardo, M.; Nour, P.A. Structural Scalability Preliminary Studies for the Next Generation Civil Tiltrotor Composite Wing. Aerospace 2023, 10, 478. [Google Scholar] [CrossRef]
- Wu, X. Current status, development trend and countermeasure for high-speed rotorcraft. J. Nanjing Univ. Aeronaut. Astronaut. 2015, 47, 173–179. [Google Scholar] [CrossRef]
- Deng, J. Key technologies and development for high-speed helicopters. Acta Aeronaut. Astronaut. Sin. 2024, 45, 529085. [Google Scholar]
- Ren, C.; Jia, L.; Zhang, P.; Chen, Y.; Yang, J. Fusion algorithm of multi design points for turboshaft-turbofan variable cycle engine scheme design. J. Aerosp. Power 2024, 39, 47–56. [Google Scholar] [CrossRef]
- Tan, M.; Liu, Y. SPRINT promotes the development of HSVTOL Aircraft. Aerosp. Power 2024, 1, 47–49. [Google Scholar]
- Talbot, P.D.; Phillips, J.D.; Totah, J.J. Selected design issues of some high-speed rotorcraft concepts. J. Aircr. 1993, 30, 864–871. [Google Scholar] [CrossRef]
- Davis, J.H. Design Methodology for Developing Concept Independent Rotorcraft Analysis and Design Software. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2007. [Google Scholar]
- Johnson, W. NDARC-NASA Design and Analysis of Rotorcraft Theoretical Basis and Architecture; Technical Report: ARC-E-DAA-TN1109; NASA: Moffett Field, CA, USA, 2010.
- Johnson, W. NDARC-NASA design and analysis of rotorcraft validation and demonstration. In Proceedings of the American Helicopter Society Aeromechanics Specialists Conference, San Francisco, CA, USA, 20–22 January 2010. [Google Scholar]
- Johnson, W. NDARC-NASA Design and Analysis of Rotorcraft; Technical Report: NASA/TP-2015-218751; NASA: Moffett Field, CA, USA, 2017.
- Zhu, Q. General Parameters Optimum Design of Tiltrotor Aircraft. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2011. [Google Scholar]
- Zuo, Z. Tiltrotor Aircraft Conceptual/Preliminary Design and Optimization. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2016. [Google Scholar]
- Zhou, Q.; Li, C. Optimization design of primary parameters for high-speed quad tiltrotor. Helicopter Tech. 2016, 1, 1–6. [Google Scholar]
- Gong, H.; He, W.; Hou, S.; Chen, M.; Yang, Z.; Si, Q.; Zhao, D. Design and Validation of a New Tilting Rotor VTOL Drone: Structural Optimization, Flight Dynamics, and PID Control. Sensors 2025, 25, 3537. [Google Scholar] [CrossRef] [PubMed]
- Xue, L. Research on Aerodynamic/Dynamic Multidisciplinary Design Optimization for Tilt-Rotor Aircraft. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2011. [Google Scholar]
- Li, P.; Zhao, Q. CFD calculations on the interaction flow-field and aerodynamic force of tiltrotor/wing in hover. Acta Aeronaut. Astronaut. Sin. 2014, 2, 80–90. [Google Scholar]
- Wang, Z.; Yang, Y.; Zhao, H.; Wang, X. Aerodynamic optimization design of tiltrotor under multiple flight conditions. Acta Aeronaut. Astronaut. Sin. 2024, 45, 529024. [Google Scholar]
- Savino, A. Multi-Fidelity Aerodynamic Optimization of the Wing Extension of a Tiltrotor Aircraft. Appl. Sci. 2025, 15, 9491. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, X. Enhanced hybrid panel-vortex particle method for aerodynamic analysis of tiltrotor rotor/wing interactions. Acta Aeronaut. Astronaut. Sin. 2025, 46, 165–183. [Google Scholar]
- Raymer, D.P. Aircraft Design: A Conceptual Approach, 6th ed.; AIAA Education Series: Reston, VA, USA, 2018. [Google Scholar]
- Yu, X.; Xu, H.; Luo, D. The Basic Principles of Aircraft Preliminary Design, 1st ed.; Science Press: Beijing, China, 2023. [Google Scholar]
- Nicolai, L.M.; Carichner, G.E. Fundamentals of Aircraft and Airship Design Volume I—Aircraft Design; AIAA Inc.: Reston, VA, USA, 2010. [Google Scholar]
- Padfield, G.D. Helicopter Flight Dynamics: Including a Treatment of Tilt Rotor Aircraft; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2018. [Google Scholar]
- Zhang, C.; Guo, C. Preliminary Design Helicopters; National Defense Industry Press: Beijing, China, 2006. [Google Scholar]
- Wang, S. Helicopter Aeromechanics; Editorial Group for Aviation Professional Textbooks: Beijing, China, 1985. [Google Scholar]
- Johnson, W. Rotorcraft aeromechanics. J. Name J. Am. Helicopter Soc. 2013, 58, 1. [Google Scholar]
- Seddon, J.M. Basic Helicopter Aerodynamics; John Wiley & Sons Inc.: Chichester, UK, 2011. [Google Scholar]
- Edkins, D.P.; Hirschkron, R.; Lee, R. TF-34 Turbofan Quiet Engine Study; Technical Report; General Electric Company Aircraft Engine Group: Lynn, MA, USA; Cincinnati, OH, USA, 1972. [Google Scholar]
- Mcardle, J.G. Outdoor Test Stand Performance of a Convertible Engine with Variable Inlet Guide Vanes for Advanced Rotorcraft Propulsion; Technical Report; NASA Lewis Research Center: Cleveland, OH, USA, 1986. [Google Scholar]
- Ji, C.; Wang, Y.; Wang, Z.; Song, J.; Zhang, H. Serial optimization design method for optimal transfer point of a turboshaft turbofan conversion engine. J. Propuls. Technol. 2025, 46, 259–271. [Google Scholar]
- Bellin, A.I.; Brooks, A. Status Report: DARPA/NASA Convertible Turbofan/Turboshaft Engine Program; V002T02A016; American Society of Mechanical Engineers: New York, NY, USA, 1983. [Google Scholar]
- Li, L.; Bai, J.; Liu, C. A sizing method of all-electric aircraft for conceptual design. J. Aerosp. Power 2022, 37, 2749–2761. [Google Scholar]
- Detore, J.; Conway, S. Technology Needs for High-Speed Rotorcraft; Technical Report: NAS2-13072; NASA Ames Research Center: Moffett Field, CA, USA, 1991.
- CCAR 25-R4; China Civil Aviation Regulations Part 25: Airworthiness Standards for Transport Airplanes. Civil Aviation Administration of China: Beijing, China, 2016; pp. 5–6.
- National Aeronautics and Space Administration. NASA Systems Engineering Handbook, 2nd ed.; NASA: Washington, DC, USA, 2020.
- Bolkcom, C.; Knight, W. V-22 Osprey Tilt-Rotor Aircraft; Congressional Research Service, Library of Congress: Washington, DC, USA, 2001.
- Rosenstein, H.; Clark, R. Aerodynamic development of the V-22 tilt rotor. In Proceedings of the Aircraft Systems, Design and Technology Meeting, Dayton, OH, USA, 20–22 October 1986. [Google Scholar]
- 40th Annual Student Design Competition 2022–2023 Request for Proposals (RFP) High-Speed Vertical Takeoff. 2022. Available online: https://www.prweb.com/releases/the-vertical-flight-society-announces-the-winners-of-the-40th-annual-student-design-competition-301910372.html (accessed on 1 November 2025).



| Weight Parameters | XV-15 | V-22 | AW-609 | V-280 |
|---|---|---|---|---|
| Wto/kg | 6009.2 | 23,860 | 7600 | 14,000 |
| We/kg | 4574 | 15,030 | 4765 | 8200 |
| We/Wto | 0.761 | 0.630 | 0.627 | 0.586 |
| Engine Parameters | TF34-400 | TSFVCE | ||
|---|---|---|---|---|
| Turboshaft | Turbofan | Turboshaft | Turbofan | |
| BPR | 0.53 | 6.22 | 0.579 | 6.4 |
| Tsl/kN | 7.73 | 36.66 | 5.8 | 29.6 |
| Psl/kN | 3930 | 0 | 4300 | 0 |
| Ccruise/(kg/(daN·h)) | - | 0.65 | - | 0.64 |
| Parameters | Value | |
|---|---|---|
| Wing | Aspect ratio | 5.49 |
| Weight | Empty weight coefficient | 0.63 |
| Payload weight/kg | 4360 | |
| Engine | Single engine power/kW | 4586 |
| Specific fuel consumption */(kg/(kW·h)) | 0.255 | |
| Helicopter Mode Performance | Parasite drag coefficient */(m2/N) | 3.6 × 10−5 |
| Figure of merit * | 0.85 | |
| HIGE ceiling/m | 1646 | |
| Max climb speed/(m/s) | 6.8 | |
| Max forward speed/(m/s) | 62 | |
| Rotor tip speed/(m/s) | 241 | |
| Rotor airfoil L/D * | 29 | |
| Propeller Aircraft Mode Performance | Mission radius/km | 722 |
| Cruise L/D * | 7.5 | |
| Zero-lift drag coefficient * | 0.05 | |
| Cruise altitude/m | 4600 | |
| Cruise speed/(m/s) | 123.9 | |
| Max cruise speed/(m/s) | 156.9 | |
| Max rate of climb/(m/s) | 11.8 | |
| Stall speed/(m/s) | 56.9 | |
| Parameters | Actual Value | Estimated Value |
|---|---|---|
| Wto/kg | 23,860 | 23,080.63 |
| We/kg | 15,030 | 14,540.8 |
| Wf/kg | 4470 | 4179.83 |
| S/m2 | 35.49 | 37.32 |
| Wto/S/(kg/m2) | 672.30 | 618.51 |
| A/m2 | 211.37 | 222.12 |
| p/(kg/m2) | 112.88 | 103.91 |
| Psl/kW | 4586 × 2 | 4004 × 2 |
| Psl/Wto/(kW/kg) | 0.384 | 0.347 |
| Parameters | Value | |
|---|---|---|
| Wing | Aspect ratio | 5.33 |
| Weight | Empty weight coefficient | 0.66 |
| Payload weight/kg | 2889 | |
| Helicopter Mode Performance | Parasite drag coefficient */(m2/N) | 2.1 × 10−5 |
| Figure of merit * | 0.8 | |
| HIGE ceiling/m | 1524 | |
| Max forward speed/(m/s) | 67 | |
| Rotor tip speed/(m/s) | 228 | |
| Rotor airfoil L/D * | 28 | |
| Jet Aircraft Mode Performance | Mission radius/km | 648 |
| Cruise L/D * | 10 | |
| Zero-lift drag coefficient * | 0.024 | |
| Cruise altitude/m | 7620 | |
| Cruise speed/(m/s) | 231.4 | |
| Maximum speed at sea level/(m/s) | 246.9 | |
| Turn load factor/g | 1.7 | |
| Stall speed/(m/s) | 62 | |
| Parameters | Actual Value | Estimated Value |
|---|---|---|
| Wto/kg | 23,317.37 | 21,924.80 |
| We/kg | 15,366.35 | 14,470.37 |
| Wf/kg | 4964.57 | 4565.43 |
| S/m2 | 53.05 | 47.11 |
| Wto/S/(kg/m2) | 439.42 | 465.41 |
| A/m2 | 191.10 | 169.59 |
| p/(kg/m2) | 122.06 | 129.28 |
| Psl/kW | 11,610.55 | 9778.46 |
| Psl/Wto/(kW/kg) | 0.498 | 0.446 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Li, Q.; Li, P. Estimation Method for Basic Parameters of High-Speed Vertical Take-Off and Landing Aircraft. Aerospace 2025, 12, 992. https://doi.org/10.3390/aerospace12110992
Wang Y, Li Q, Li P. Estimation Method for Basic Parameters of High-Speed Vertical Take-Off and Landing Aircraft. Aerospace. 2025; 12(11):992. https://doi.org/10.3390/aerospace12110992
Chicago/Turabian StyleWang, Yu, Qihang Li, and Pan Li. 2025. "Estimation Method for Basic Parameters of High-Speed Vertical Take-Off and Landing Aircraft" Aerospace 12, no. 11: 992. https://doi.org/10.3390/aerospace12110992
APA StyleWang, Y., Li, Q., & Li, P. (2025). Estimation Method for Basic Parameters of High-Speed Vertical Take-Off and Landing Aircraft. Aerospace, 12(11), 992. https://doi.org/10.3390/aerospace12110992






