Aerodynamic–Stealth Optimization of an S-Shaped Inlet Based on Co-Kriging and Parameter Dimensionality Reduction

Abstract

Aiming at the challenges of high dimensionality in both design variables and optimization objectives, along with high computational resource consumption in the multi-disciplinary optimization of aerodynamic and stealth performance for an unmanned aerial vehicle (UAV) S-shaped inlet, this paper proposes a multi-objective optimization method that integrates design variable dimensionality reduction and a Co-Kriging multi-fidelity surrogate model. First, the S-shape inlet was defined by utilizing parametric modeling with a total of 11 design variables. Simulations were performed to obtain a subset of samples, and Sobol’ sensitivity analysis was applied to eliminate parameters with minor influence on performance, thereby achieving design variable dimensionality reduction. Subsequently, a Co-Kriging surrogate model was constructed. Based on the Multi-Objective Evolutionary Algorithm Based on Decomposition (MOEA/D) algorithm, multi-objective optimization was carried out with the total pressure recovery coefficient, total pressure distortion coefficient, and the average forward radar cross-section (RCS) as the optimization objectives, yielding a Pareto front solution set. Finally, three optimized inlets were selected from the Pareto front and compared with the original inlet to evaluate their aerodynamic and stealth performance. The results demonstrate that the proposed optimization method balances efficiency and accuracy effectively, significantly increasing the total pressure recovery coefficient while markedly reducing the total pressure distortion coefficient and RCS of the optimized inlet.

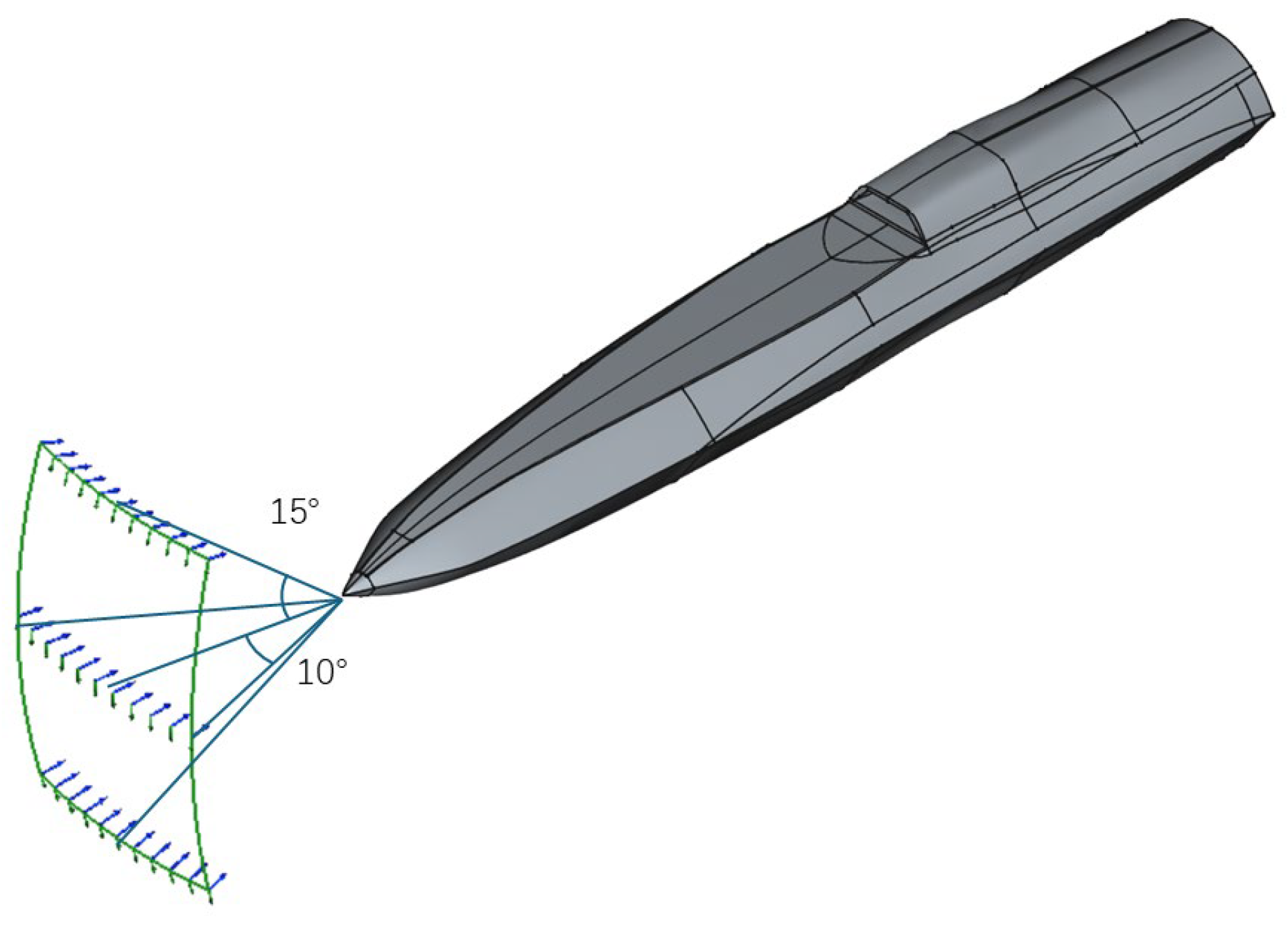
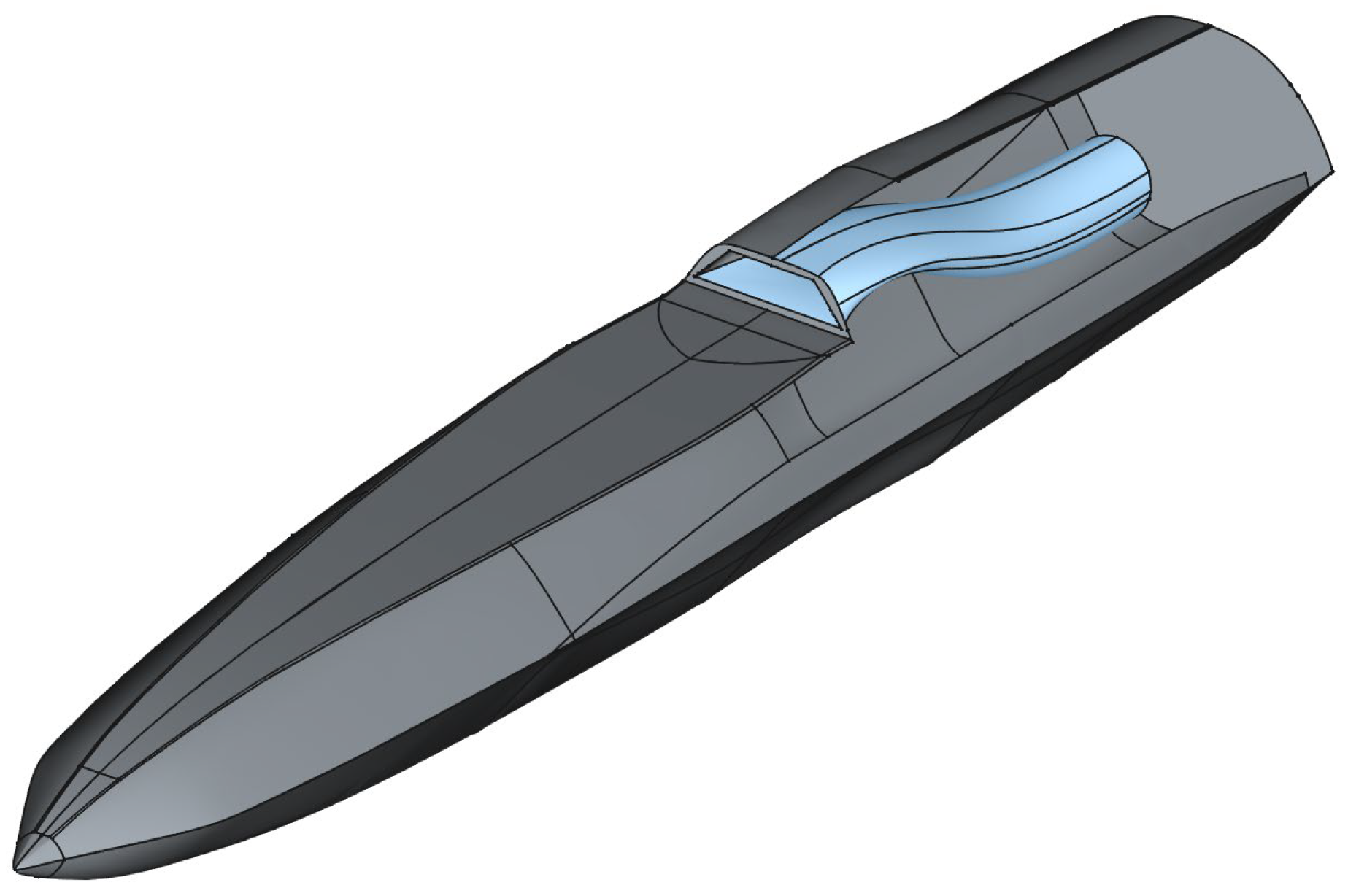
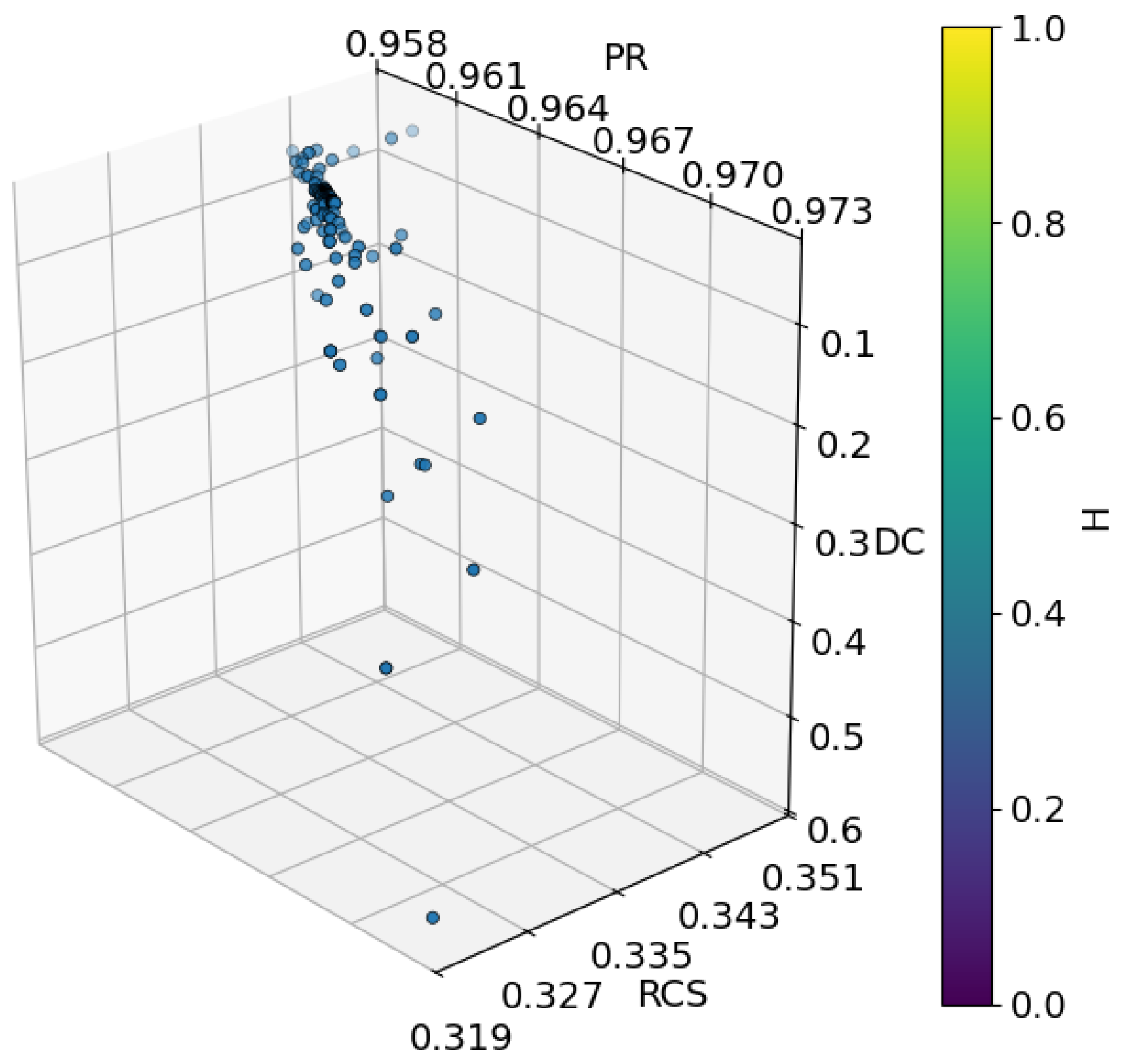
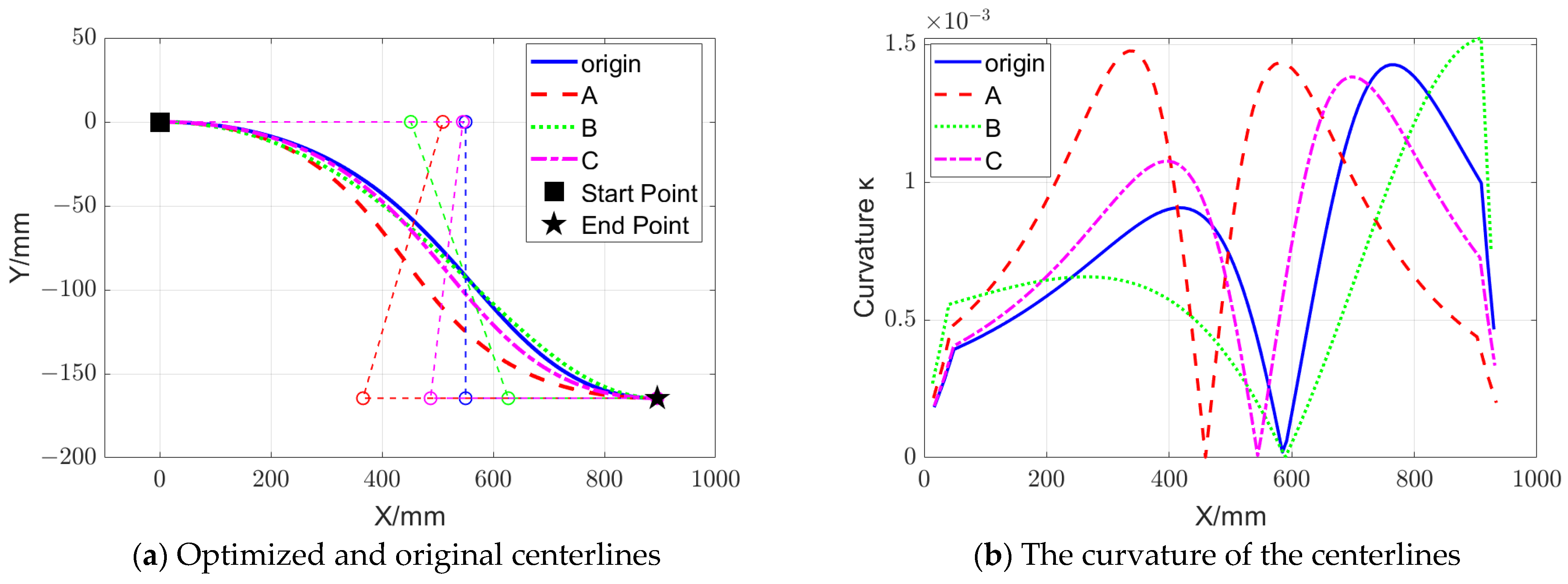
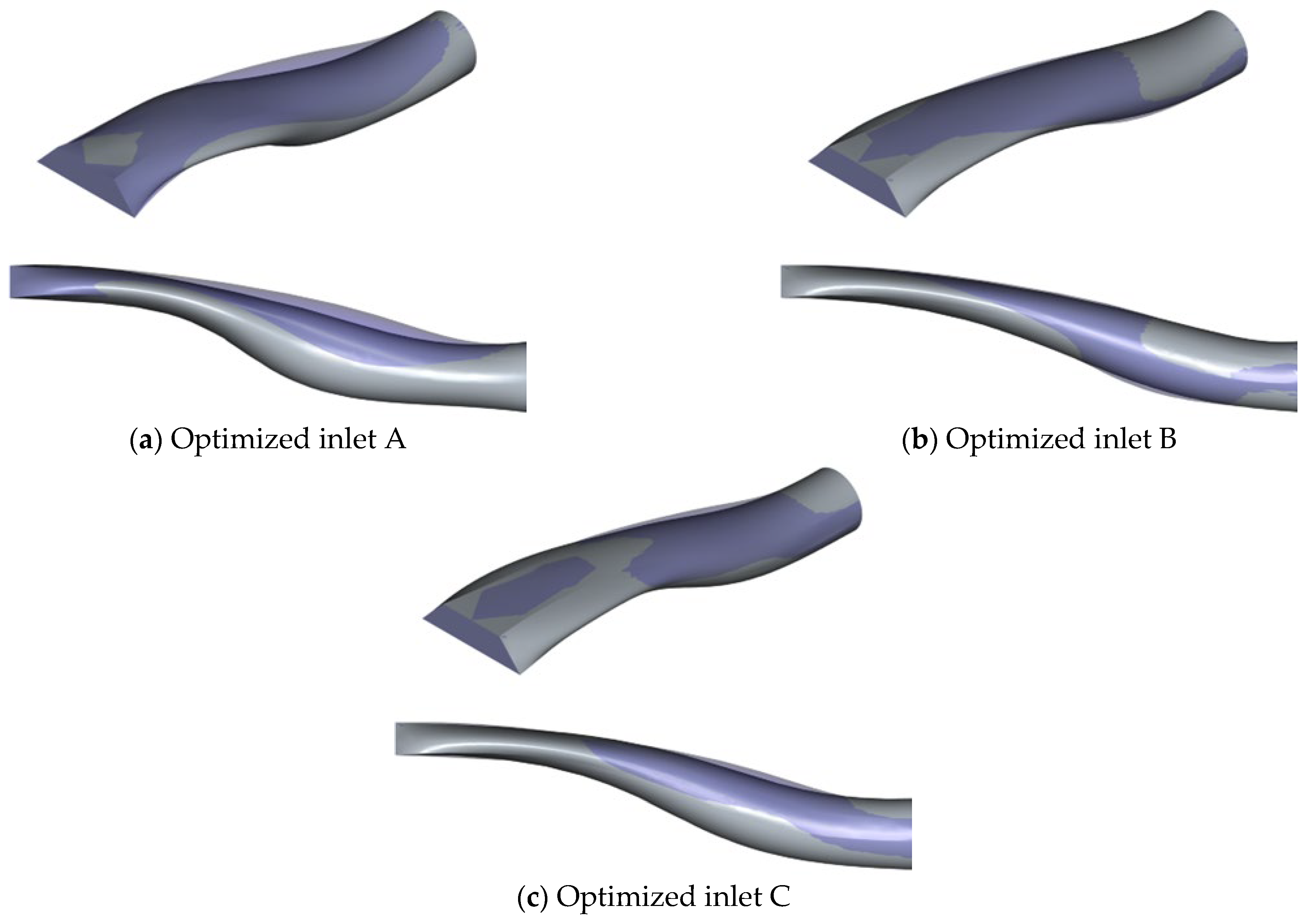
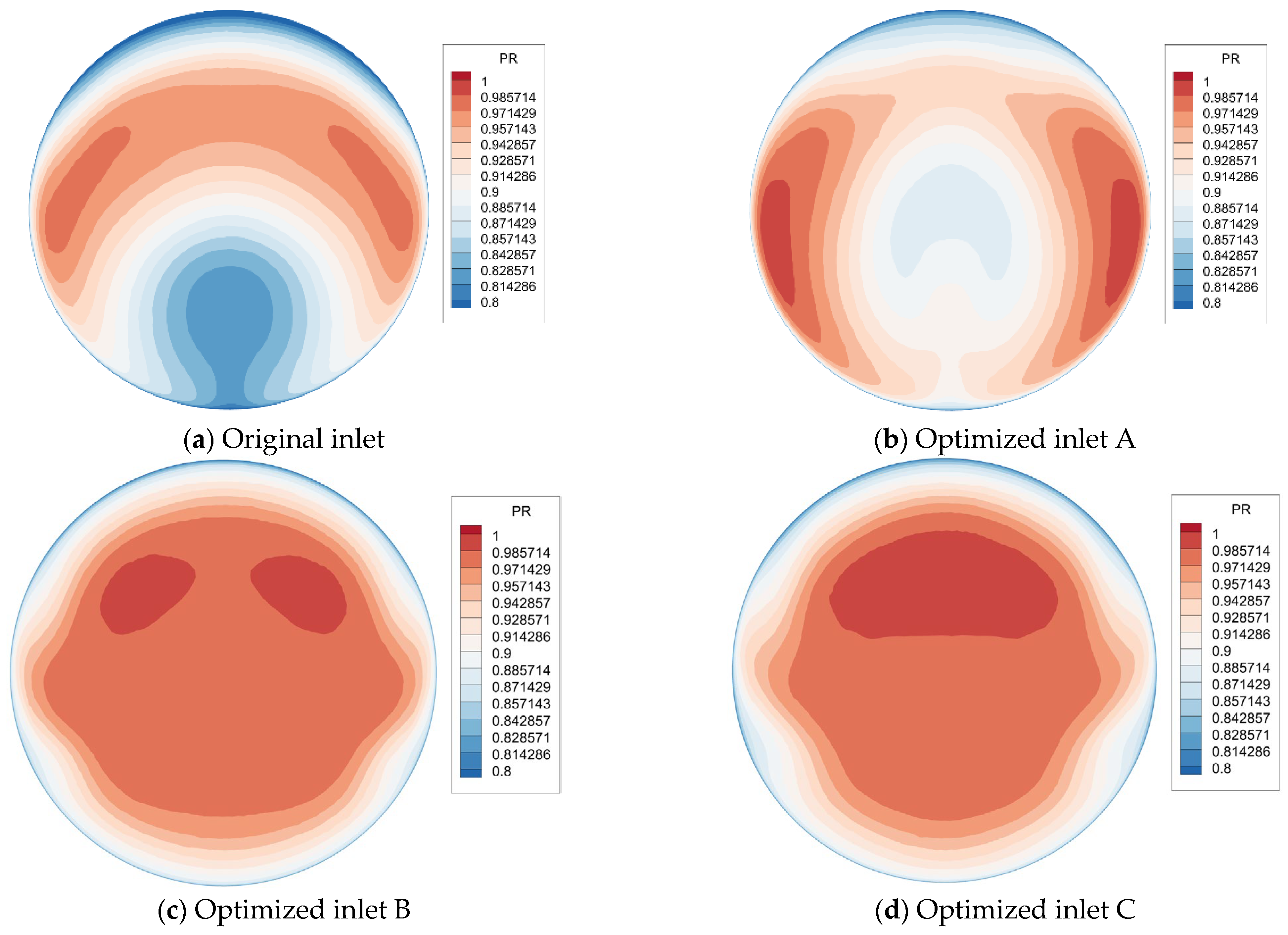
1. Introduction

Aerodynamic and stealth performance are critical metrics for evaluating the overall capabilities of cooperative UAVs [1]. Consequently, they typically employ low-observable designs characterized by smooth, flat, and compact configurations. As an important part of the power system, the inlet not only needs to ensure the recovery of total pressure and flow uniformity at the engine face to provide stable and high-quality air flow for the engine, but also needs to have better stealth performance [2]. The S-shaped inlet has become a typical design for UAV inlets because it effectively conceals the engine blades, a dominant source of radar scattering, and supports a compact integrated layout.

However, the unique structure of S-shaped inlets creates a fundamental design conflict between aerodynamic and stealth performance: although greater curvature and more turns enhance stealth performance, they simultaneously worsen flow distortion and pressure loss at the engine face. Therefore, aerodynamic-stealth optimization design should be carried out to obtain an inlet with superior aerodynamic and stealth performance. High-fidelity evaluations of both aerodynamic and stealth performance are computationally expensive. Surrogate-based optimization methods address this by constructing approximate models to replace time-consuming simulations, thereby significantly enhancing optimization efficiency [3]. 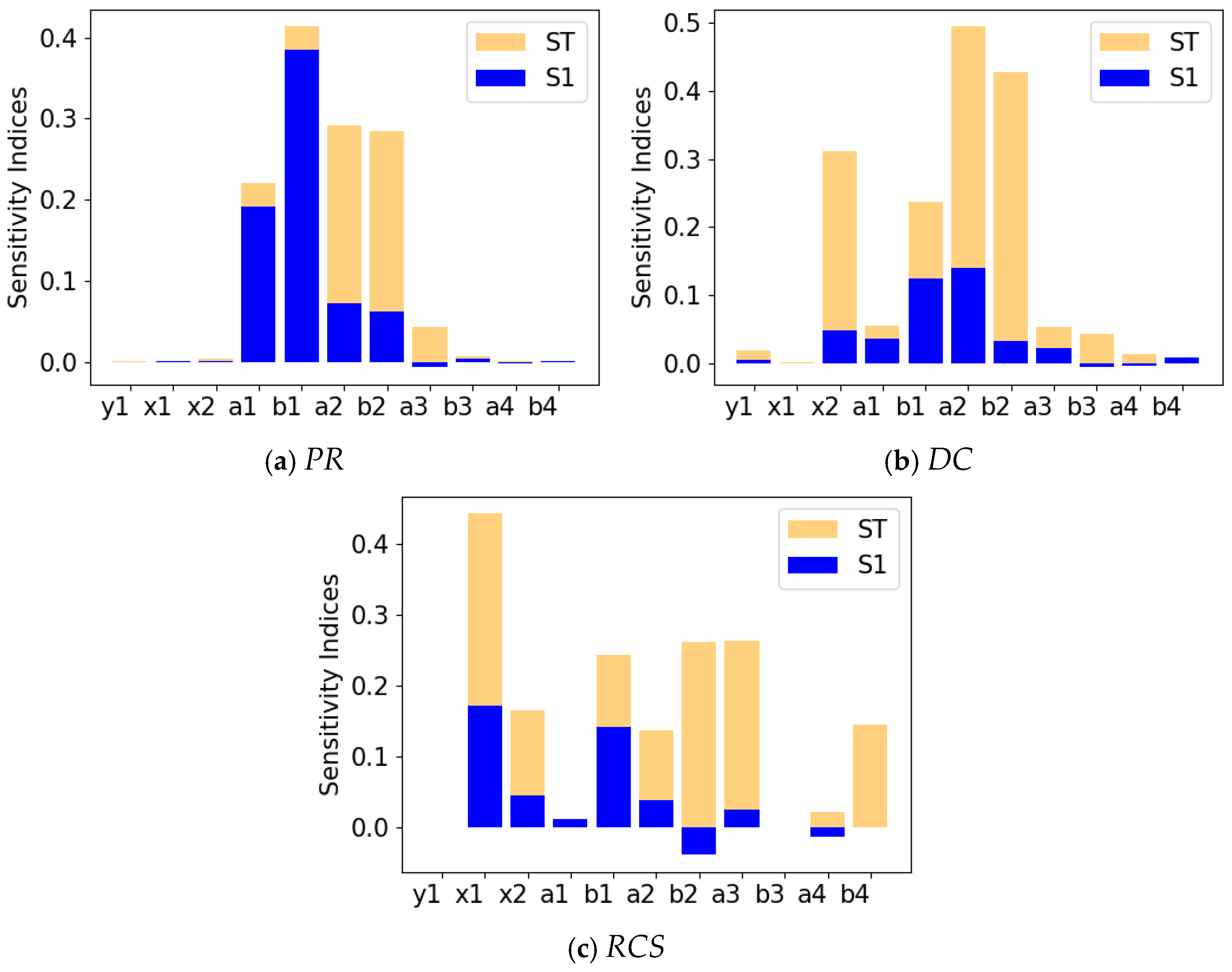As the dimensionality of design variables grows and performance requirements for UAVs become more demanding, a large number of high-fidelity samples are required to adequately cover the design space and ensure the accuracy of traditional surrogate models, thus imposing substantial computational demands [4]. In response to these issues, on the one hand, parameter sensitivity analysis can be used to examine the contribution of input parameters to output parameters of the model, and the design parameters with minor contribution can be eliminated to reduce the dimension of design parameters [5]. On the other hand, a Multi-fidelity Surrogate Model method can be used to fuse a small number of high-fidelity samples and a large number of low-fidelity samples to build a surrogate model with comparable accuracy at a lower computational cost to support the optimization process effectively [6].

From the aspect of inlet optimization, A considerable amount of research has focused on aerodynamic performance. Aniket et al. [7] conducted optimization design of a 915 mm S-shaped inlet at Ma = 0.3. They combined the MOGA-II algorithm with CFD simulations, optimizing the total pressure recovery coefficient (PR) and total pressure distortion coefficient (DC) by adjusting the major and minor axes of elliptical cross-sections. Hyo et al. [8] performed centerline shape optimization for an approximately 1070 mm subsonic S-shaped inlet under conditions of Ma = 0.6 and Re = 2.6 × 10⁶. They constructed a stochastic Kriging model to replace complex simulations, ultimately achieving significant improvements in both PR and DC. Liu Lei et al. [9] carried out design optimization for a 900 mm S-shaped inlet at Ma = 0.53. Through the NSGA algorithm, the optimized inlet showed marked improvement in swirl distortion. Gan [10] employed a modified k-ω SST turbulence model and constructed an RBF surrogate model to optimize an S-shaped inlet at Ma = 0.6. The optimization resulted in a 16.3% reduction in the DC and a 1.1% increase in PR. Zeng Lifang et al. [11] conducted multi-point and multi-objective optimization for a 195 mm S-shaped inlet at Ma = 0.25 and Ma = 0.7. By combining the NSGA-II algorithm with high-fidelity simulations, the performance of the inlet was effectively enhanced.

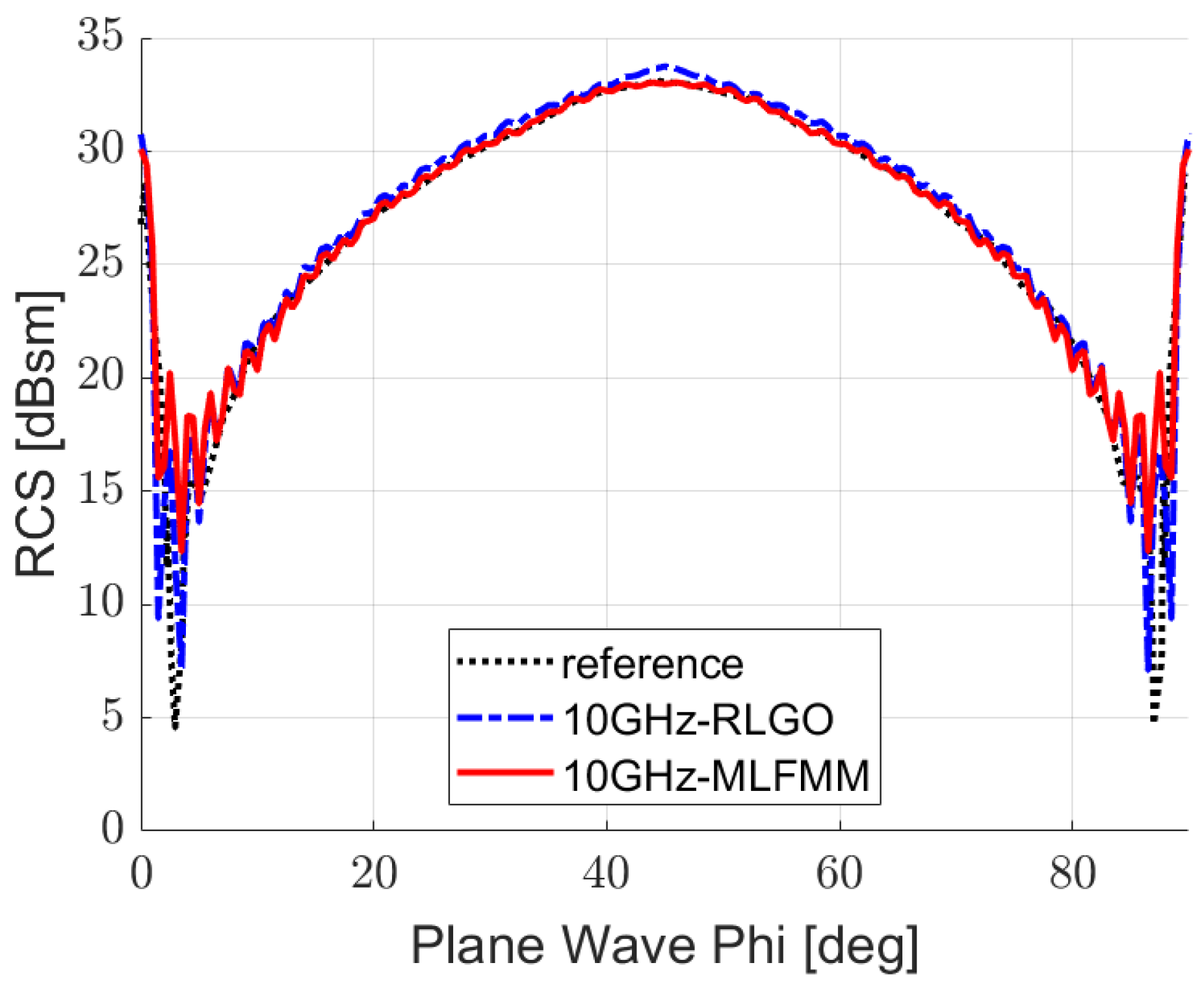
Comparatively, research on the stealth performance of S-shaped inlets is limited. Ji Jinzu et al. [12] tested a series of 850 mm S-shaped inlets with varying curvature and bending configurations at an incident wave frequency of 10 GHz. Based on the dimensional requirements of a conformal inlet for a flying-wing UAV, Zhang Le et al. [13] designed multiple 600 mm S-shaped inlets. The Multi-Level Fast Multipole Method (MLFMM) was employed to calculate their RCS at incident wave frequencies of 1 GHz and 3 GHz. This study revealed favorable cross-sectional area and centerline distribution patterns for the S-shaped inlet that achieve balanced aerodynamic and stealth performance. Deng et al. [14], recognizing that modern aircraft S-shaped inlets must balance both aerodynamic and stealth performance, employed a gradient-based optimization system named NOPT for the design process. The optimization was performed on a 2732 mm S-shaped inlet under the condition of Ma = 0.8 and an incident wave frequency of 600 MHz. The results demonstrated marked improvements: PR increased from 0.8265 to 0.9772, while the DC was significantly reduced from 0.6988 to 0.0235. Furthermore, the average RCS was decreased from 2.2245 m² to 1.2620 m².

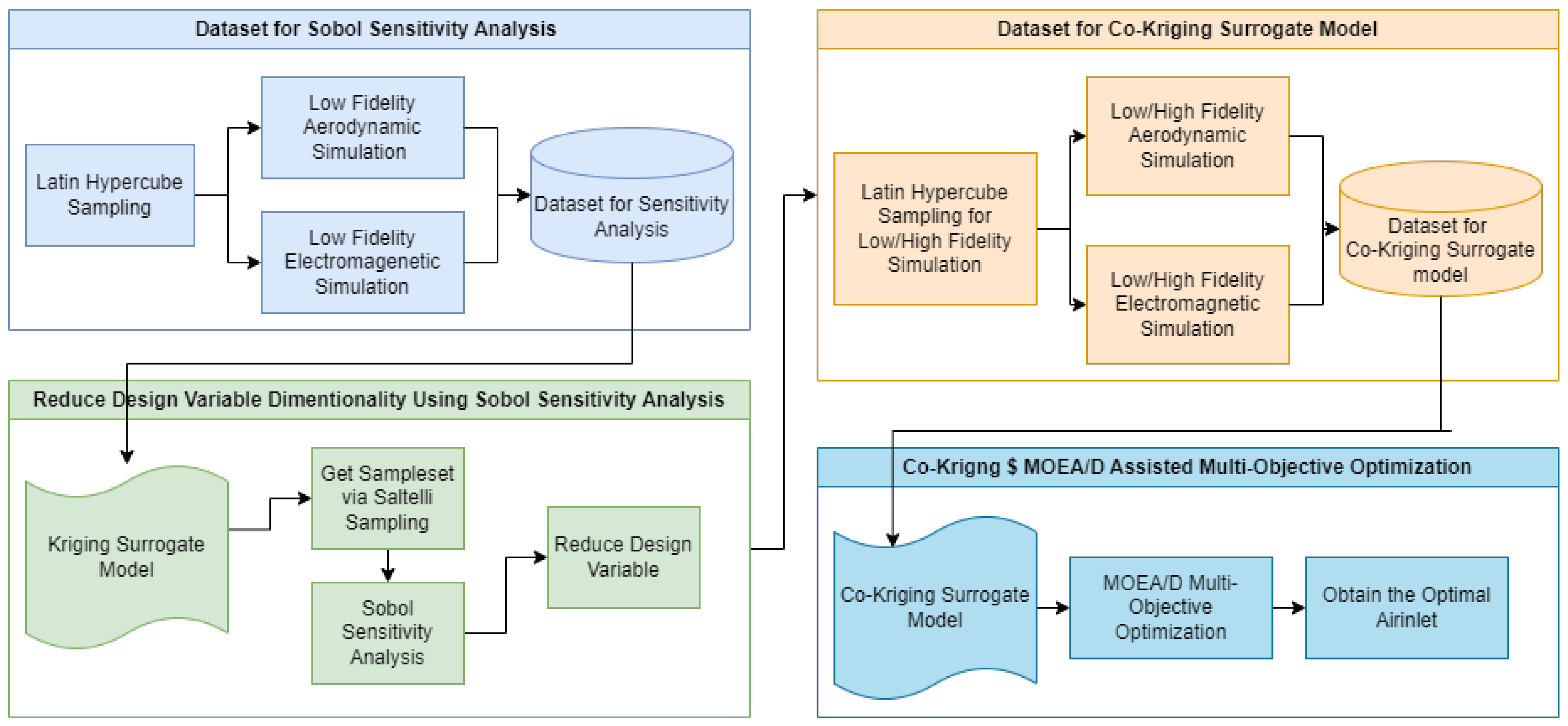
To sum up, most of the existing research focuses on aerodynamics or stealth single discipline and lacks systematic work for aerodynamics and stealth joint optimization. In the evaluation of stealth performance, there is a significant disparity in computational resource consumption between high-fidelity and high-efficiency simulations. On the other hand, stealth characteristics are highly sensitive to geometrical variations. Consequently, blindly employing low-fidelity methods for the sake of efficiency may lead to a substantial discrepancy between the optimized design and its actual performance. The application of variable-fidelity surrogate models to the aerodynamic–stealth coupled optimization of inlets can enhance optimization efficiency while maintaining considerable accuracy. This paper presents a joint optimization of aerodynamics and stealth of the S-shaped inlet. Firstly, a parametric geometric model of the S-shaped inlet is established. The dimensionality of the design space is then reduced through parameter sensitivity analysis. Subsequently, a multi-fidelity surrogate model is constructed and utilized for multi-objective optimization, which efficiently yields an S-shaped inlet with both good aerodynamic and stealth performance.

2. Parametric Modeling and Aerodynamic/Electromagnetic Simulation Methods of Inlets

2.1. Parametric Modeling Method of Inlets

The original inlet design originates from a particular UAV platform. As shown in Figure 1, the entry is a trapezoidal face, and the size is marked as shown in the figure; the engine face is circular, with a diameter of 122.5 mm; axial length of 894.78 mm; and eccentricity of 164.55 mm. The parametric modeling method for the S-shaped inlet is illustrated in Figure 2. Different inlets are constructed by parametrically defining the centerline and four cross-sections. The centerline of the inlet is constructed by the Bezier curve [15], which is determined by three kinds of points: a starting point, an ending point, and a control point. Considering the influence of Bezier curve parameters and curve complexity, the third-order Bezier curve is selected for the centerline construction of the inlet. The starting point and ending point are the center position of the inlet and outlet of the inlet respectively. The centerline shape of the S-shaped inlet is modified by adjusting the coordinates of its two intermediate control points. Elliptical cross-sections are positioned perpendicular to the centerline path at 20% intervals. The cross-sectional shape is controlled by varying the major and minor axes of these ellipses. The design variables are the major and minor axes $a_1~a_4$, $b_1~b_4$ of the four elliptical sections, the $x$ and $y$ coordinates of the Bezier curve control point 1, and the $x$ coordinate of the control point 2. In order to ensure a horizontal outlet, the y coordinate of control point 2 is fixed. The initial values and allowable ranges of these design variables are listed in

Table 1. Initial values and allowable ranges of design variables.

Design Variable	Initial Value/mm	Range/mm
$x_1$	550	[300, 800]
$y_1$	0	[0, 50]
$x_2$	550	[300, 800]
$a_1$	90	[80, 100]
$b_1$	30	[27.5, 32.5]
$a_2$	85	[70, 100]
$b_2$	42.5	[35, 50]
$a_3$	77.5	[75, 80]
$b_3$	60	[55, 65]
$a_4$	70	[65, 70]
$b_4$	60	[60, 65]

.

2.2. Verification of Aerodynamic Simulation Method

The S-shaped inlet model used for verification was adopted from Reference [16]. As shown in Figure 3, the model’s centerline is composed of two 30° circular arcs lying in the same plane, each with a radius of R = 1021 mm. The entrance face radius r₁ is 102 mm, the outlet face radius r₂ is 125.5 mm, and the ends extend outward by 7.5 r_1.

Aerodynamic simulations were conducted by solving the RANS equations. The choice of turbulence model significantly impacts the accuracy of the aerodynamic simulation for S-shaped inlets. Based on a literature survey, the SST k-ω model was selected [17,18]. The verification case was conducted under the following conditions: incoming flow Mach number Ma = 0.6, total pressure p₀ = 101,000 Pa, and total temperature T₀ = 298 K. A pressure-inlet boundary condition was applied at the entrance, and a pressure-outlet boundary condition was applied at the outlet. The pressure coefficient ($C_P$) distribution at cross-section A and PR at cross-section B were examined. The $C_P$ results are summarized in Figure 4. It can be observed that the CFD results agree well with the experimental data. For PR at cross-section B, the experimental data was 0.9655, while the simulation result was 0.9624, demonstrating high accuracy in the simulation. In summary, the CFD results show good agreement with the experimental data, confirming the method’s suitability for subsequent aerodynamic performance evaluation.

A grid independence study was conducted on the original inlet. The computational method followed that described previously. Simulation conditions were set as follows: incoming flow Mach number Ma = 0.6 and 3 km altitude atmospheric condition. The simulation results are presented in Figure 5 and

Table 2. Verification of grid independence of the inlet case.

	Maximum Mesh Size/mm	Maximum Mesh Size/mm	Number of Elements	Time Consumption/s	Mean Total Pressure at Engine Face/Pa
Low-density grid	0.006	0.0006	261,258	513	86,213.098
Medium-density grid	0.004	0.0004	577,416	811	86,156.070
High-density grid	0.003	0.0003	1,027,853	1540	86,136.872

. Figure 5 displays the residual convergence curve for the high-density grid case, showing that all residuals converged below ${10}^{-5}$. Table 2 summarizes the grid information, computational time, and results for three cases with different grid resolutions. It can be observed that the discrepancy between the medium-density and high-density grids is relatively small. The high-density grid required approximately twice the computational time of the medium-density grid and three times that of the low-density grid. Considering the balance between computational efficiency and accuracy, the medium-density grid was employed for sensitivity analysis and low-fidelity aerodynamic calculations, whereas the high-density grid was used for high-fidelity aerodynamic computations.

2.3. Verification of Electromagnetic Simulation Method

Electromagnetic simulation methods include the integral equation method, high-frequency approximation method, and so on. X-band radar is often used as fire control radar, which is the key band to evaluate the stealth performance of a UAV. UAVs belong to an electrically large target in the X-band, so the high-frequency approximation method can ensure certain accuracy and improve efficiency [19]. The integral equation method has high accuracy for geometric models of different shapes and sizes, but it lacks efficiency. Therefore, the MLFMM among the integral equation methods and the Ray Launching Geometric Optics (RL-GO) method, suitable for cavity targets among the high-frequency approximation methods, were selected for accuracy analysis.

The evaluation was conducted using a dihedral corner example, with the model shown in Figure 6. It consists of two square plates with side lengths of 540 mm. Similar to the inlet, incident radar waves can undergo multiple reflections on the dihedral corner, making it suitable for assessing the simulation accuracy of both methods for cavity structures. Simulations were performed under the conditions of a 10 GHz frequency, VV polarization, and an angular range of 0–90°, yielding the RCS distribution results shown in Figure 7. The black dashed line in the figure is the reference result [20]. It can be observed that the MLFMM and RL-GO methods show close agreement within the 10° to 80° range. However, at 45°, the RL-GO method exhibits a noticeable RCS spike.

The computational efficiency of electromagnetic simulation methods is dependent on the object. The high- and low-convergence criteria MLFMM, along with the RL-GO method, were applied to the inlet model studied in this paper. The corresponding computational costs are presented in

Table 3. Calculated consumption of different electromagnetic simulation methods.

Simulation Method	Time Consumption/s	Memory Consumption/GByte
RL-GO	135.328	0.342
MLFMM-low	1903.294	39.942
MLFMM-high	5461.230	110.755

. It was observed that the RL-GO method required significantly less memory and computation time than the MLFMM method, while still maintaining reasonable accuracy for electrically large models. Although both MLFMM methods were computationally expensive, the low-convergence criterion method required approximately 65% less time than its high-convergence criterion counterpart. Considering the balance between efficiency and accuracy, the RL-GO method was selected for parametric sensitivity analysis in the subsequent optimization process, while MLFMM with different convergence criteria was employed as the high- and low-fidelity approach in a multi-fidelity surrogate modeling framework.

3. Optimization Design Framework Based on the Co-Kriging Model and MOEA/D

3.1. Parameter Dimensionality Reduction Based on Sobol’ Sensitivity Analysis

The inlet geometry is defined by 11 design parameters. A proper evaluation of how these parameters affect both aerodynamic and stealth performance provides valuable insight for engineering design and variable reduction. Sobol’ sensitivity analysis is based on the principle of variance decomposition. It decomposes the model under investigation into functions comprising individual input variables and their interactions [21]. The sensitivity indices are then obtained by quantifying how much each variable’s variance contributes to the total output variance.

Due to the large number of samples required for sensitivity analysis, a surrogate modeling approach is employed to inexpensively generate ample sample points. Initially, 135 samples are generated using Latin Hypercube Sampling (LHS) to construct a Kriging surrogate model. Subsequently, a Saltelli sampling sequence with a total of 6500 sample points is generated for the analysis.

3.2. Optimization Method Based on Co-Kriging and MOEA/D

Surrogate models are widely used in aircraft optimization design, as they construct mathematical mappings between input parameters and response values to replace computationally expensive CFD and electromagnetic simulations [22]. This study employs the Co-Kriging surrogate model, an extension of the Kriging model, which integrates simulation data of varying fidelity levels. This approach significantly reduces computational costs while maintaining predictive accuracy and exhibits strong fitting capabilities for highly nonlinear design spaces. In this study, the inlet’s design parameters serve as inputs, while the outputs include PR, DC, and the mean forward-sector RCS values at three pitch angles, collectively used to construct a multi-disciplinary surrogate model.

In terms of optimization methodology, addressing the multi-objective and high-dimensional characteristics inherent in the aerodynamic–stealth optimization of the inlet [23], this study employs the MOEA/D algorithm. This algorithm converts a multi-objective optimization problem into a set of single-objective subproblems. Through information exchange and cooperative evolution among adjacent subproblems, it ensures convergence while maintaining well-distributed solution sets, making it particularly suitable for approximating complex Pareto fronts.

The integration of the Co-Kriging model and the MOEA/D optimization framework provides an effective strategy to address the challenges of high computational cost, high-dimensional design variables, and multiple optimization objectives in the coupled aerodynamic and stealth optimization of inlets. This approach offers strong support for efficient multi-objective cooperative design.

3.3. Optimization Framework and Process Flow

The optimization process in this paper is shown in Figure 8 and can be divided into the following steps:

• First, a database was prepared for Sobol’ sensitivity analysis. Using LHS, 135 sets of inlet design parameters were generated, and corresponding inlet configurations were obtained through parametric modeling techniques. Sensitivity analysis aims to investigate the influence of different design variables on aerodynamic and stealth performance. To save computational resources, only low-fidelity simulations are used here to obtain aerodynamic and stealth performance data.
• Use the data to build a Kriging surrogate model. Use the model to perform Saltelli sampling to obtain a large amount of aerodynamic and stealth data. Use these data for Sobol’ sensitivity analysis and delete design parameters that have little contribution to aerodynamic and stealth performance.
• Perform LHS on the reduced design parameters and perform high- and low-fidelity aerodynamic and electromagnetic simulations, respectively, to obtain the sample points required to build the Co-Kriging surrogate model.

4. S-Shaped Inlet Optimization Design Case

4.1. Optimization Problem Description

The aerodynamic simulation conditions are set at an altitude of 3 km with an entry flow velocity of 0.6 Ma. The two main indicators for evaluating the flow field quality of the inlet are PR and DC [5,24].

PR is used to measure the pressure loss of the fluid after passing through the S-shaped inlet. It is defined as the ratio of the total pressure at the engine face $P_f$ to the total pressure at the entry $P_{f\_in}$:

$$PR=P_f/P_{f\_in}$$

(1)

A higher PR value indicates lower total pressure loss and better inlet performance. According to relevant studies, a 9% increase in total pressure loss can lead to an approximately 15% reduction in engine net thrust [25], demonstrating the critical importance of improving PR.

DC is used to quantify the non-uniformity of the flow field at the engine face, and it is defined as:

$$DC(\theta )=\left|{\displaystyle \frac{P_f-P_{\theta }}{q_f}}\right|$$

(2)

where $P_{\theta }$ represents the minimum value of the average total pressure within a θ-degree sector of the engine face. θ generally ranges from 60° to 90°, and a value of 60° is adopted in this paper; $q_f$ is the average dynamic pressure of the engine face.

The electromagnetic simulation conditions are set at a frequency of 10 GHz with VV polarization. The radar wave incidence direction is shown in Figure 9. The optimization objective is the mean RCS value across the forward azimuthal sector of ±10° at pitch angles of ±15° and 0°. When evaluating the stealth performance of the inlet, the shielding effect of the fuselage on the inlet must be considered. Therefore, a model was constructed, as shown in Figure 10, where a horizontal plane is added at the bottom of the inlet to simulate the specular reflection of electromagnetic waves representing the engine as a strong scattering source.

The aerodynamic–stealth optimization problem is described as follows:

$$\begin{array}{l}\mathrm{minimize}[-PR,DC,\overline{RCS}]\\ \mathrm{subject} \mathrm{to} PR>P{R}_0\\ DC<D{C}_0\\ \overline{RCS}<\overline{RC{S}_0}\\ x\in C\end{array}$$

(3)

The objective is to improve PR, reduce DC, and minimize the RCS at various forward pitch angles through optimization. Since the MOEA/D algorithm cannot explicitly handle constraints, a new metric H is constructed to represent the degree to which the constraints are satisfied:

$$H={\displaystyle \sum _{i=1}^n{m}_i\max (g_i(x),}0)$$

(4)

In the formula, $m_i$ represents the weight value for different constraints, and $g_i(x)$ denotes the value of different constraint functions. During optimization, an H value of 0 indicates that the current optimization objectives satisfy the constraint conditions. Therefore, the optimization problem can be described as:

$$\begin{array}{l}\mathrm{minimize} [-C_l(x),C_d(x),RC{S}_{\pm {20}^{\circ }}(x),H]\\ \mathrm{subject} \mathrm{to} x\in C\end{array}$$

(5)

4.2. Parameter Dimensionality Reduction Method Based on Sobol’ Sensitivity Analysis

Figure 11 shows the Sobol’ first-order index (S1) and total-effect index (ST) obtained through Sobol’ sensitivity analysis, quantifying the effects of the 11 design variables on the three optimization objectives. The yellow bars show ST values. The blue bars show S1 values. Analysis of the results indicates that design variable y1, corresponding to the Y-coordinate of the control point 1 in the Bezier curve, contributes minimally to both aerodynamic and stealth performance variations. Similarly, design variables a4 and b4, which represent the major and minor axes of the elliptical section at the 80% centerline position, demonstrate small effects on aerodynamic performance. Although these parameters provide modest benefits to stealth performance, their ST values remain around 0.1 while maintaining consistently low S1 values. Consequently, these three variables were eliminated from the subsequent multi-fidelity surrogate modeling optimization framework to reduce the dimensionality of the design space.

4.3. Optimization Process Results Display

In this study, 170 low-fidelity samples and 90 high-fidelity samples were selected to construct the Co-Kriging model. For comparison, a conventional Kriging model was constructed using 200 high-fidelity samples. The coefficients of determination (R²) for both surrogate models are presented in

Table 4. Surrogate model evaluation index.

R2 of Different Models	PR	DC	RCS
Co-Kriging R2	0.9880	0.6781	0.7469
Kriging R2	0.9980	0.7515	0.7697

, which indicates that their predictive accuracies are comparable. As indicated by the computational resource data in Table 2 and Table 3, the Co-Kriging model reduces the resource consumption by approximately 20% while achieving similar accuracy, thus demonstrating a significant improvement in modeling efficiency. The constructed Co-Kriging model satisfies the accuracy requirements for optimization.

Optimization was performed using the MOEA/D multi-objective optimization method. The convergence results are shown in Figure 12. The Running Metric was used to evaluate convergence [26]. This metric compares the differences in the objective space between different generations to determine whether the algorithm has converged. The vertical axis represents the difference in the objective space between adjacent generations, denoted by the symbol $\Delta f$, and the horizontal axis represents the number of iterations of the optimization algorithm. The figure shows the change in the objective space difference from generation 0 to 1000. It can be observed that as the number of iterations increases, $\Delta f$ stabilizes near zero, indicating that the algorithm has converged. Figure 13 shows the obtained Pareto front. A three-dimensional coordinate system was constructed using PR, DC, and the mean RCS as the axes. Analysis of the optimized inlets on the Pareto front revealed three types of optimization directions: those focusing primarily on improving aerodynamic performance, those focusing primarily on improving stealth performance, and those balancing both objectives. Three optimized inlets, labeled A, B, and C, were selected from the front for detailed analysis. Their design variable values are listed in

Table 5. Design variable values of optimized S-shaped inlets.

Design Variable	Inlet A	Inlet B	Inlet C
$x_1$	508.9416	451.4498	545.0798
$x_2$	365.4121	626.8626	486.9534
$a_1$	99.2790	100.0000	100.0000
$b_1$	29.6168	31.3518	30.8512
$a_2$	97.4873	82.6225	79.3120
$b_2$	41.7618	43.2969	45.3344
$a_3$	75.0000	75.8012	76.7283
$b_3$	61.8799	57.0476	57.4918

.

5. Analysis of Optimization Results

5.1. Comparison of Optimized Inlet Geometries

Figure 14 shows a comparison of the centerline distributions between the original and optimized inlets. For optimized inlets A and B, the inflection point moves forward, and the curvature of the front segment increases significantly. Compared to the original model, which exhibits a “gentle front and steep rear” shape, the centerlines of the three optimized inlets show a more symmetric variation, presenting a “balanced front-rear gradient” pattern. The change is most pronounced in inlet A. This modification enhances the stealth performance of the inlet, as electromagnetic waves incident within a 20-degree angular domain, reflection occurs earlier, increasing the number of reflections and reducing backward scattering. Meanwhile, optimized inlet C shows no significant change in the location of its inflection point but exhibits an overall reduction in curvature both before and after this point. This results in a smoother centerline, which helps reduce flow separation and reduces flow distortion.

Figure 15 shows the geometric comparison between the three optimized inlets and the original inlet, where the blue parts represent the original inlet. The cross-sectional area changes of the three optimized inlets relative to the original inlet can be visually compared. Among them, the changes in optimized inlet A mainly occur in the middle and rear sections, with a wider lateral expansion and an increased downward curvature, resulting in a more pronounced S-shaped curvature of the inlet. This enhances the shielding of the strong scattering source at the end sections. The cross-sectional area changes of optimized inlets B and C are similar: the cross-sectional area increases in the front and middle sections, while the variation at the inlet part becomes more gradual. This promotes slow diffusion, avoiding the generation of a significant adverse pressure gradient. As a result, the airflow remains closer to the entry velocity when it reaches the first turn, reducing velocity losses caused by area changes.

5.2. Aerodynamic Performance Comparison

The optimized inlets were subjected to CFD simulations again, and the resulting PR and DC are presented in

Table 6. Optimized inlet aerodynamic data.

Inlet	PR	DC
Origin	0.9198	0.3686
A	0.9401	0.1017
B	0.9707	0.0169
C	0.9666	0.0033

. Compared to the original inlet with PR = 0.9198 and DC = 0.3686, all three optimized inlets show significant improvements. Inlets B and C demonstrate notable optimization effects, each exhibiting advantages in PR and DC, respectively. Their PR values reach 0.9707 and 0.9666, representing an improvement of approximately 5%. Both inlets B and C achieved a significant reduction in DC, with a greater reduction observed for inlet C than for inlet B. Inlet A shows a more moderate aerodynamic improvement, with PR = 0.9401, an increase of only 2%. This suggests that the optimization direction for inlet A prioritized stealth performance enhancement over aerodynamic performance improvements. Figure 16 displays the contour plots of PR at the engine face for the original and optimized inlets. Compared to the original inlet, which features large low-pressure zones at the bottom and top, inlets B and C exhibit a more uniform total pressure distribution with a remarkable reduction in the size of low-pressure regions. While the aerodynamic improvement for inlet A is less pronounced than for inlets B and C, it still features a significant expansion of the high-energy fluid regions on both sides and a marked reduction in the low-pressure zone in the bottom region.

Figure 17 illustrates the pathlines for the original and optimized inlets. The original configuration exhibits two distinct vortex structures at the bottom of the second bend and near the tail. Following optimization, the vortex at the bend bottom was significantly reduced in inlets A and C and nearly eliminated in inlet B. In the tail region, the vortex in inlet A shifted upward and increased slightly in size, while those in inlets B and C were almost eliminated.

In practical engineering, S-shaped inlets must operate over a range of Mach numbers. Therefore, the aerodynamic performance of the optimized inlets was further validated under various operating conditions.

Table 7. Inlet aerodynamic performance data under various conditions.

Inlet	Simulation Condition	PR	DC
Origin	Ma = 0.3, 0 km	0.9877	0.1641
	Ma = 0.5, 3 km	0.9620	0.2305
	Ma = 0.7, 3 km	0.8581	0.5263
A	Ma = 0.3, 0 km	0.9874	0.1169
	Ma = 0.5, 3 km	0.9647	0.0900
	Ma = 0.7, 3 km	0.8749	0.1005
B	Ma = 0.3, 0 km	0.9923	0.0037
	Ma = 0.5, 3 km	0.9795	0.0118
	Ma = 0.7, 3 km	0.9470	0.0818
C	Ma = 0.3, 0 km	0.9919	0.0372
	Ma = 0.5, 3 km	0.9775	0.0194
	Ma = 0.7, 3 km	0.9348	0.1746

presents the aerodynamic performance of different inlets under various conditions. It can be observed that as the Mach number increases, PR decreases for both the origin and optimized inlets, following a consistent trend. Compared to the original inlet, optimized inlets B and C demonstrate superior PR values under all three conditions, maintaining PR above 0.93. This indicates the robust and good aerodynamic performance of inlets B and C across the operating range evaluated. In contrast, optimized inlet A shows only a slight improvement at Ma = 0.5 and 0.7, with a slight degradation at Ma = 0.3. This is because the optimization of inlet A prioritized stealth performance, with the design point focused on Ma = 0.6 at 3 km altitude; consequently, its aerodynamic performance saw limited improvement at other conditions. Regarding DC, all three optimized inlets exhibit significant enhancement over the original inlet across all conditions.

5.3. Stealth Performance Comparison

MLFMM simulations were performed again on the optimized inlets, with the results shown in Figure 18 and

Table 8. Optimized inlet RCS data.

Inlet	RCS Mean	RCS Reduction Amplitude
Origin	0.5646
A	0.4303	23.78%
B	0.4607	18.40%
C	0.5253	6.96%

. Figure 18 shows a comparison of the RCS between the three optimized inlets and the original inlet. It can be observed that optimized inlet A achieves the most significant RCS reduction, with notable improvements at pitch angles of 0° and −15°. However, at a pitch angle of 15°, significant reduction only occurs within a small central angular range, while the RCS increases around ±5°. This phenomenon can be attributed to the dominant contribution of terminal specular reflection to RCS at small incidence angles. The optimization strategy of inlet A, which involves moving the centerline inflection point forward and increasing curvature, enhances the shielding of the terminal strong scattering source. As the incident angle increases, reflections from the sidewalls and bottom cavity walls strengthen. The slight contraction of inlet A’s cross-section at the entrance results in stronger electromagnetic scattering around ±5°.

Optimized inlets B and C exhibit some RCS reduction only at pitch angles of 15° and 0°, with minimal reduction in the −5° to 5° angular range and even a slight increase in some parts. This is because the centerline shapes of inlets B and C undergo minor changes, providing limited improvement in shielding the terminal strong scattering source. Outside the ±5° angular range, the outward expansion of the front and middle cross-sections of inlets B and C weakens reflections from the sidewalls and bottom at the entrance. At −15°, inlets B and C show some increase in RCS. However, at this angle, the inlet is shielded by the fuselage, resulting in an overall low RCS. Since the optimization targets the average RCS across three pitch directions, the change at −15° has little impact on the overall average reduction, and the slight increase is negligible for the overall RCS reduction.

Table 8 shows the average RCS values of the optimized inlets. The degree of RCS reduction is greatest for inlet A, followed by B, and smallest for C. Compared with the aerodynamic performance improvements in Table 6, the three optimized inlets emphasize different directions: inlet A focuses on RCS reduction, inlet C prioritizes aerodynamic performance improvement, and inlet B balances both optimization objectives.

6. Conclusions

This study conducted a multi-disciplinary optimization design for an S-shaped inlet integrating aerodynamic and stealth performance. The optimized cases were analyzed in terms of their aerodynamic and stealth characteristics, leading to the following conclusions:

• The multi-objective optimization method that combines design variable dimensionality reduction and the multi-fidelity surrogate model offers significant advantages for computationally expensive problems such as coupled aerodynamic–stealth inlet optimization. Through parameter sensitivity analysis for dimensionality reduction and multi-fidelity surrogate modeling for reduced simulation costs, this approach dramatically reduces computational expenses while maintaining an effective balance between efficiency and accuracy.
• The aerodynamic–stealth optimization framework established in this study proves highly effective. The optimized configurations show notable improvements in both aerodynamic and stealth performance. The three optimized cases also demonstrate three distinct directions for optimizing aerodynamic and stealth performance: Increased centerline curvature to enhance stealth performance by shielding the terminal strong scattering source; reduced centerline curvature and decreased cross-sectional area variation rate at the inlet to improve aerodynamic performance; and a balanced approach with consideration of both aerodynamic and stealth performance.