Predicting Airplane Cabin Temperature Using a Physics-Informed Neural Network Based on a Priori Monotonicity
Abstract
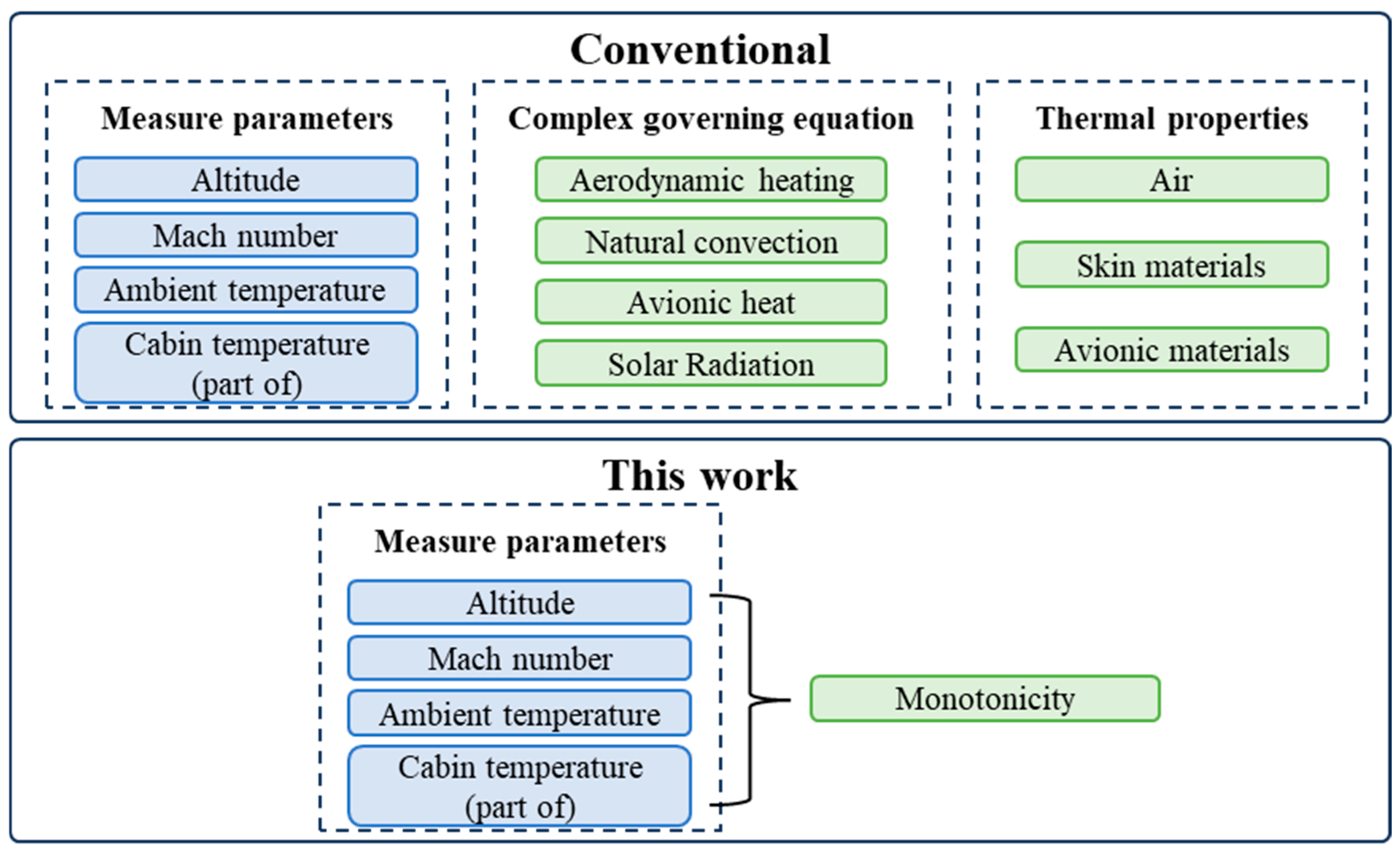
1. Introduction
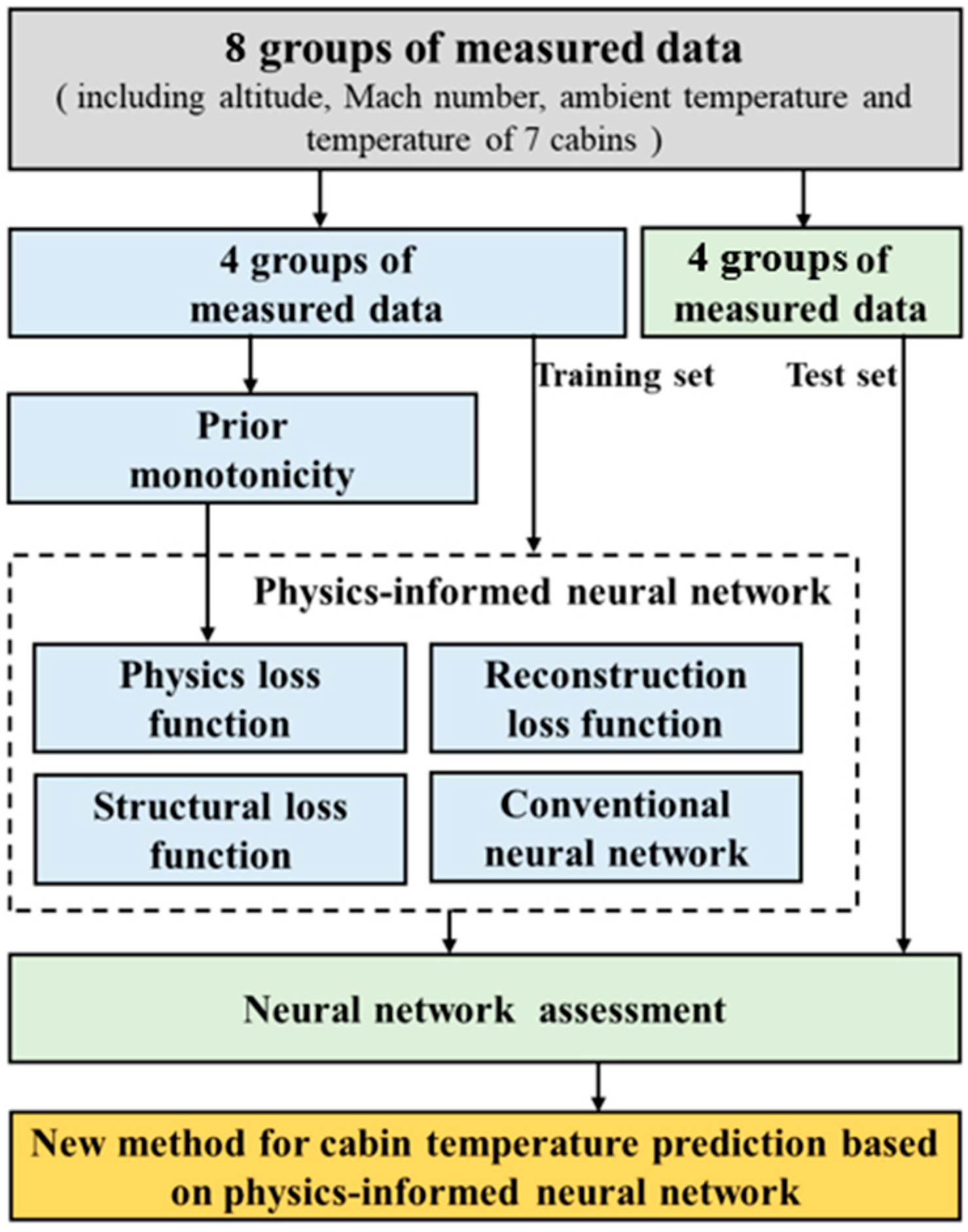
2. Method
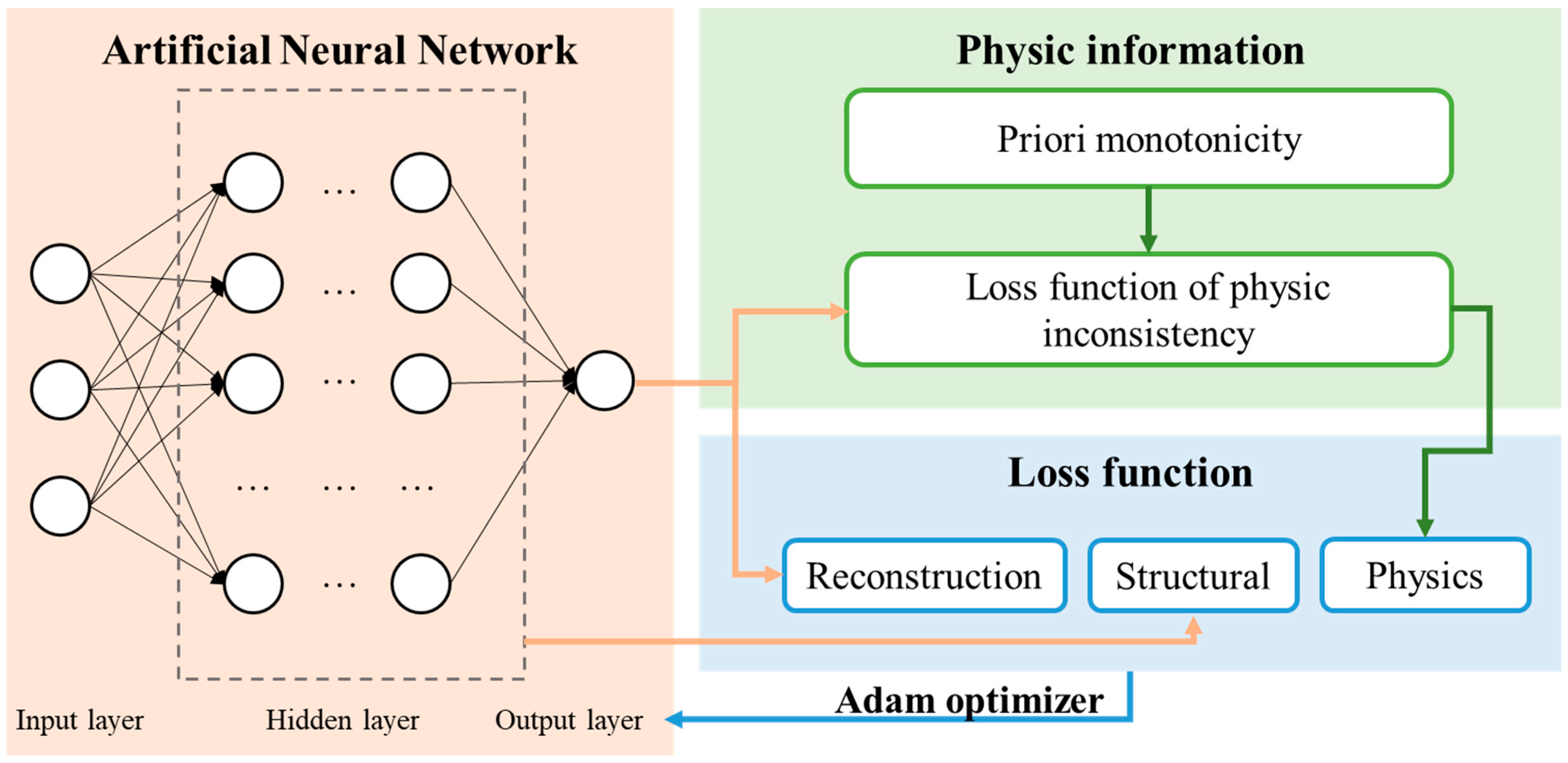
2.1. Development of Physics-Informed Neural Network
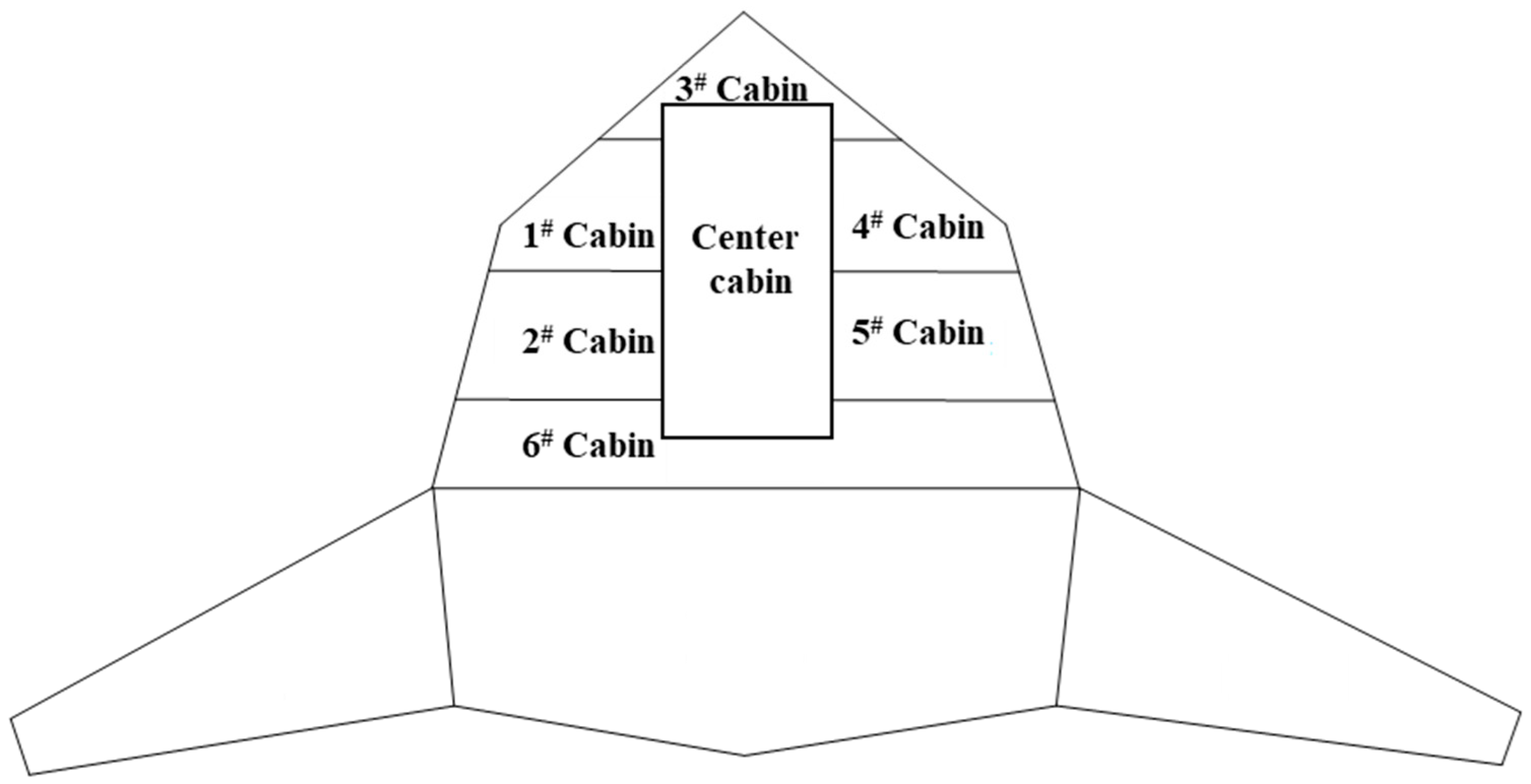
2.2. Experimental Measurement Method
- (1)
- On the ground, configure the data acquisition instrument and check the temperatures of the K-type thermocouple.
- (2)
- Stick the K-type thermocouple on the airplane and fix it with aluminum foil tape.
- (3)
- Configure the time of flight control computer and data acquisition instrument in consensus.
- (4)
- Data sampling during a flight sortie.
- (5)
- Collect flight parameters from the flight control computer, including ambient temperature, flight altitude, and Mach number.
- (6)
- Build a database consisting of flight parameters and cabin temperature.
- (1)
- Instrument Calibration and Verification: All K-type thermocouples were calibrated prior to installation.
- (2)
- System Integration Testing: On the ground, the complete measurement system, including thermocouples, battery, and data acquisition instrument, was fully integrated and tested. This pre-flight check verified the proper functionality and interconnection of all components.
- (3)
- Automated Data Logging: During flight, the data acquisition instrument operated autonomously, disconnected from the computer, to sample temperature data continuously. This approach eliminated potential disruptions from ground equipment and ensured uninterrupted data capture.
- (4)
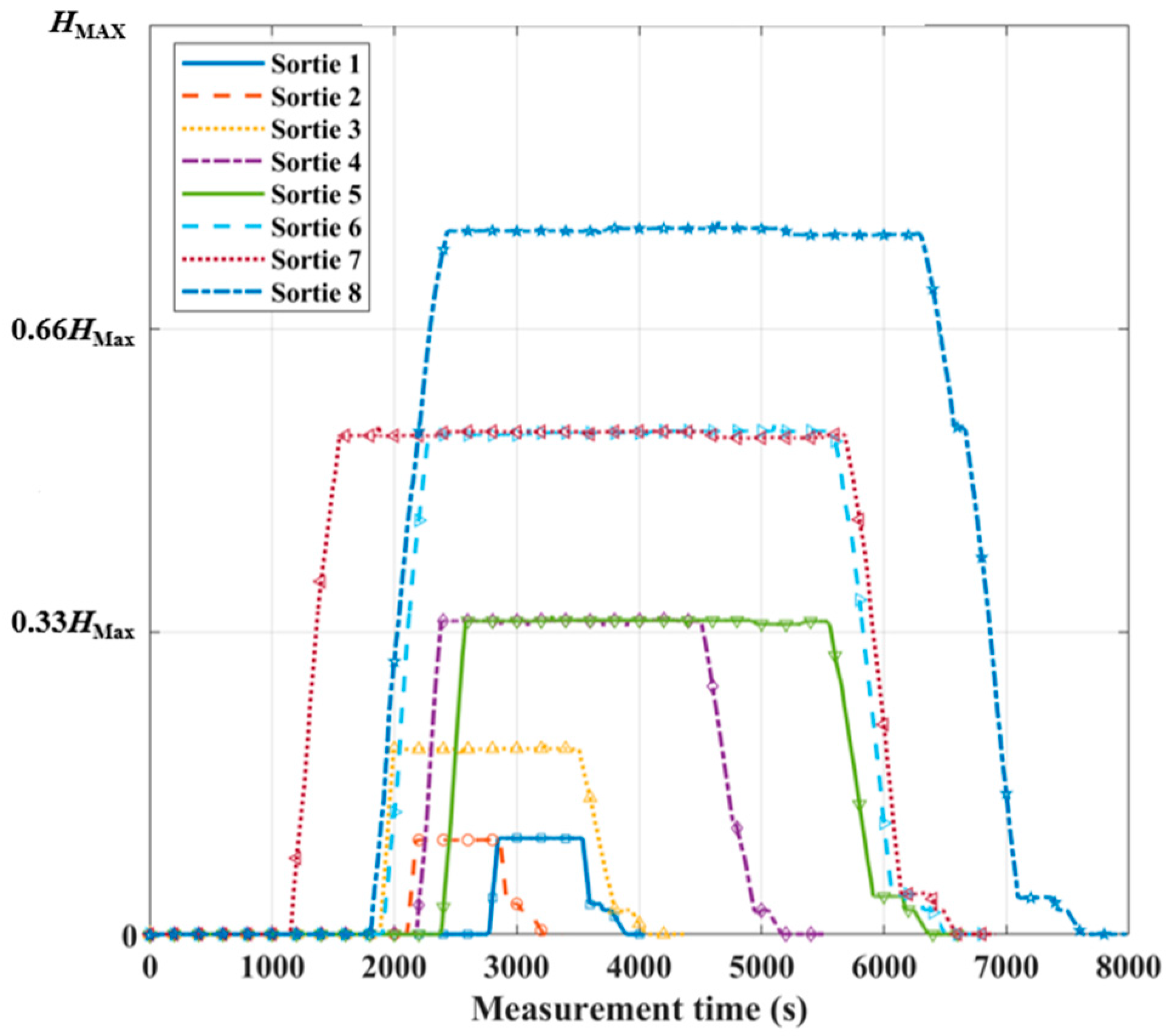
- Data Consistency Checking: Post-flight, a consistency check was performed by comparing data from multiple sources and across different flight sorties. The consistent physical patterns observed across eight separate sorties confirm the reliability and repeatability of the measured data.
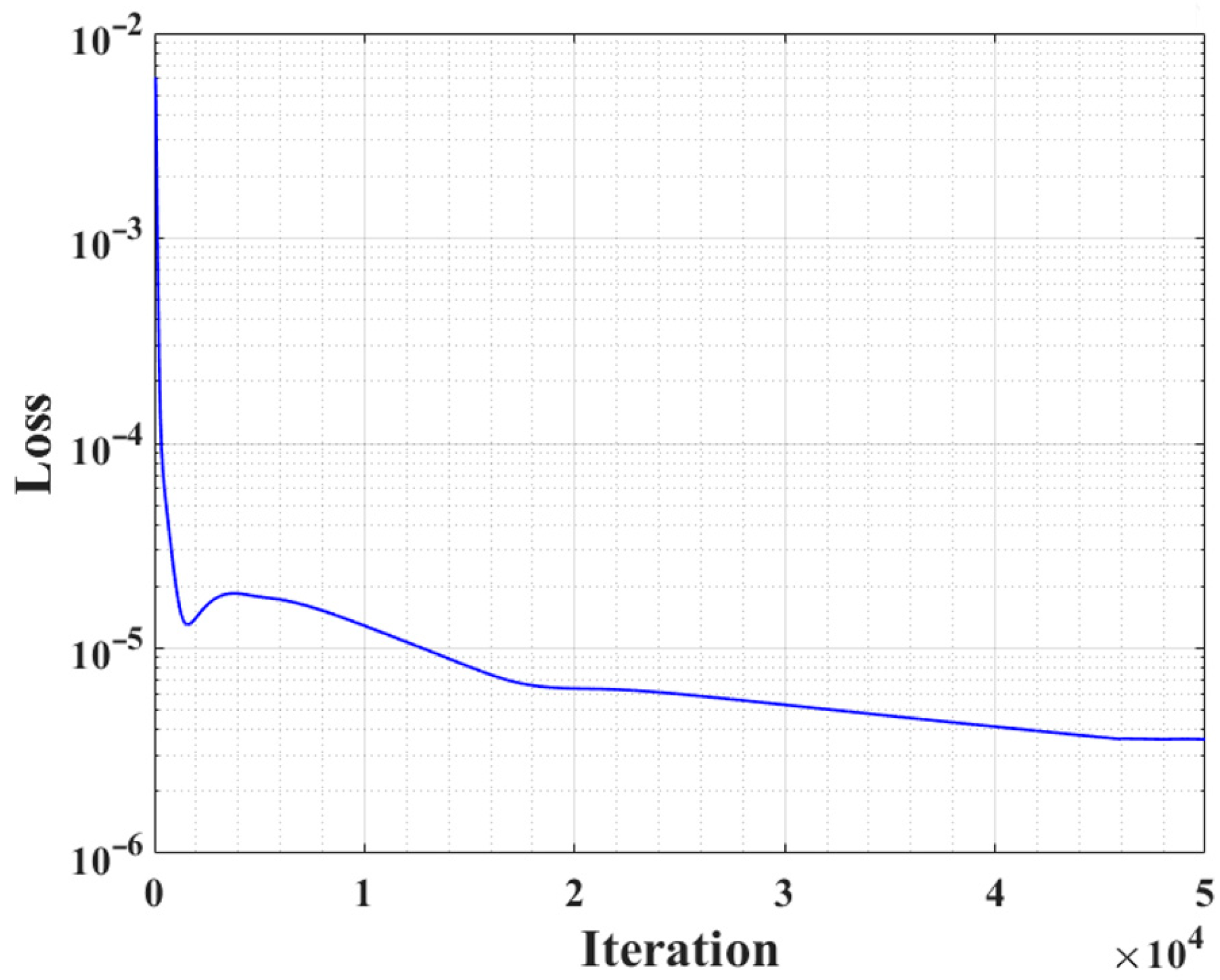
2.3. Training of Physics-Informed Neural Network
3. Result and Discussion
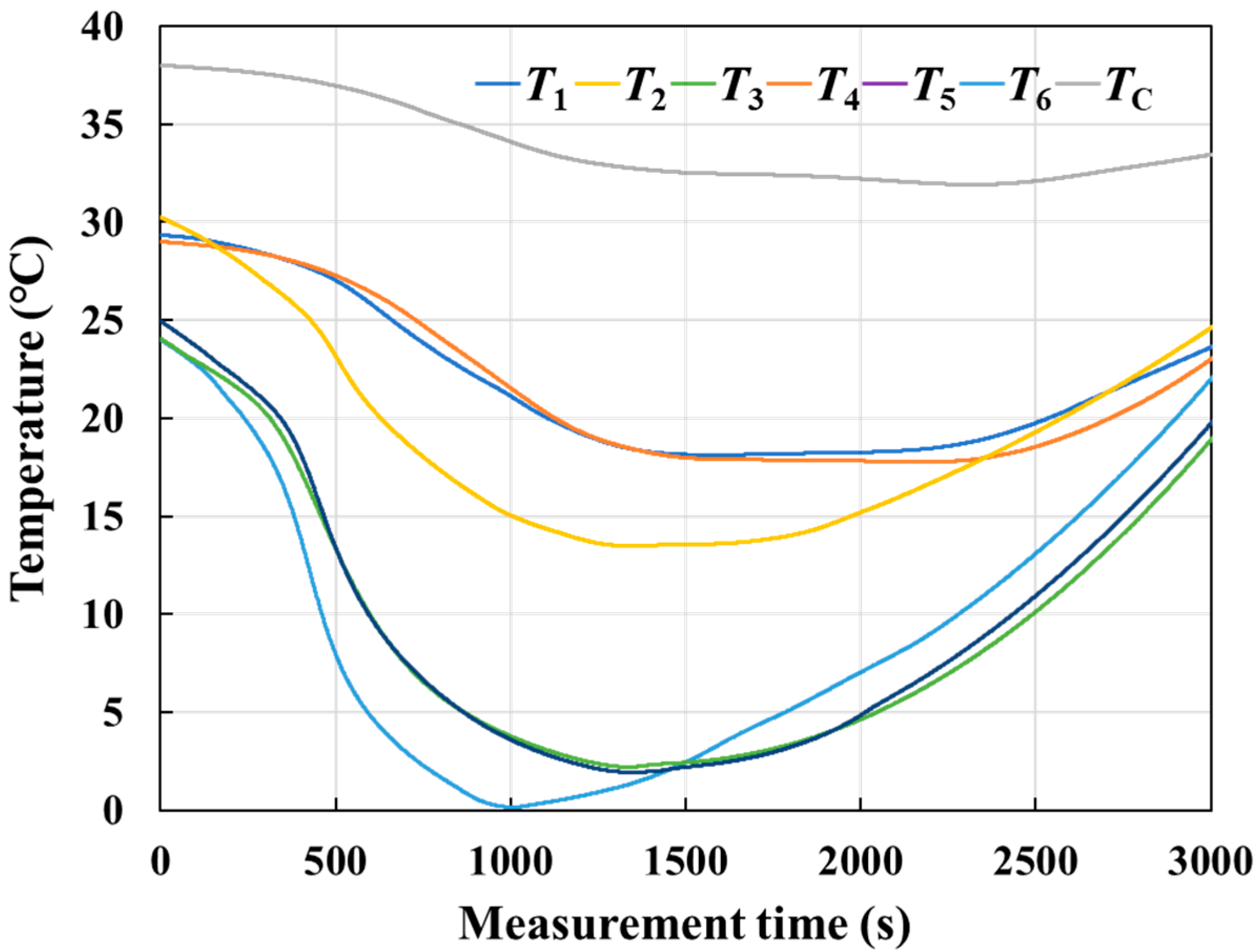
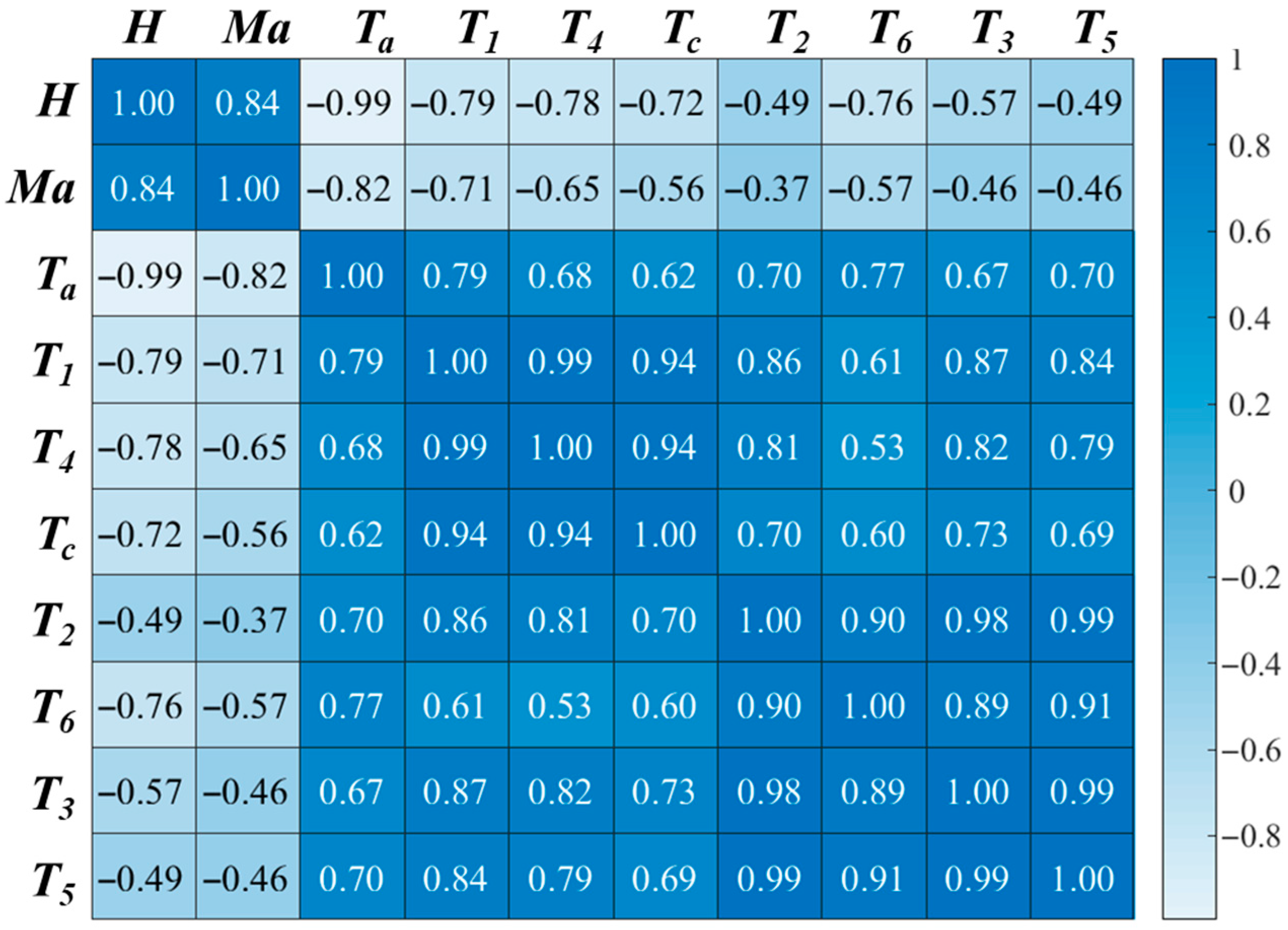
3.1. Analysis of Measurement Result
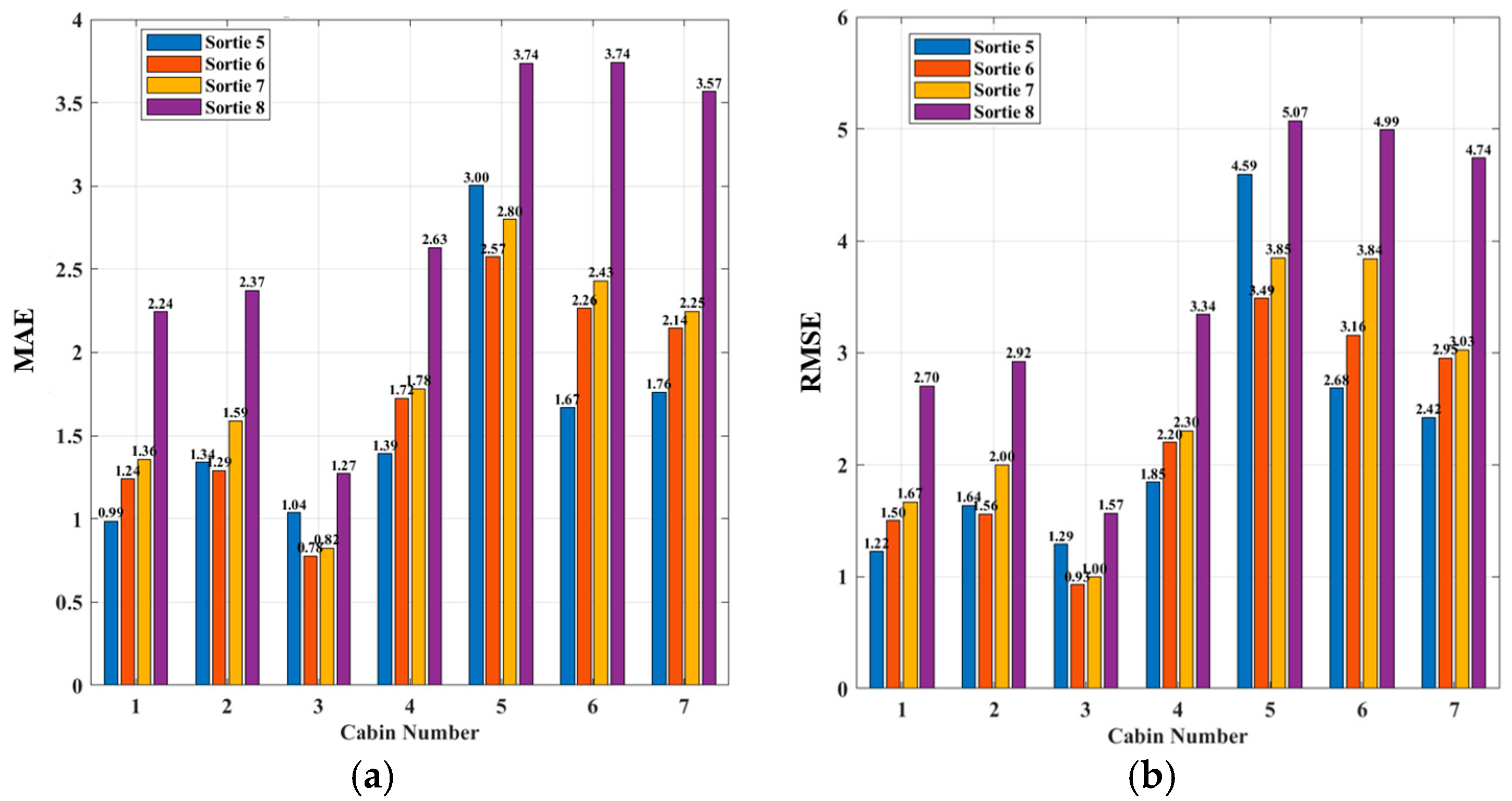
3.2. Prediction Result Analysis of Physics-Informed Neural Network
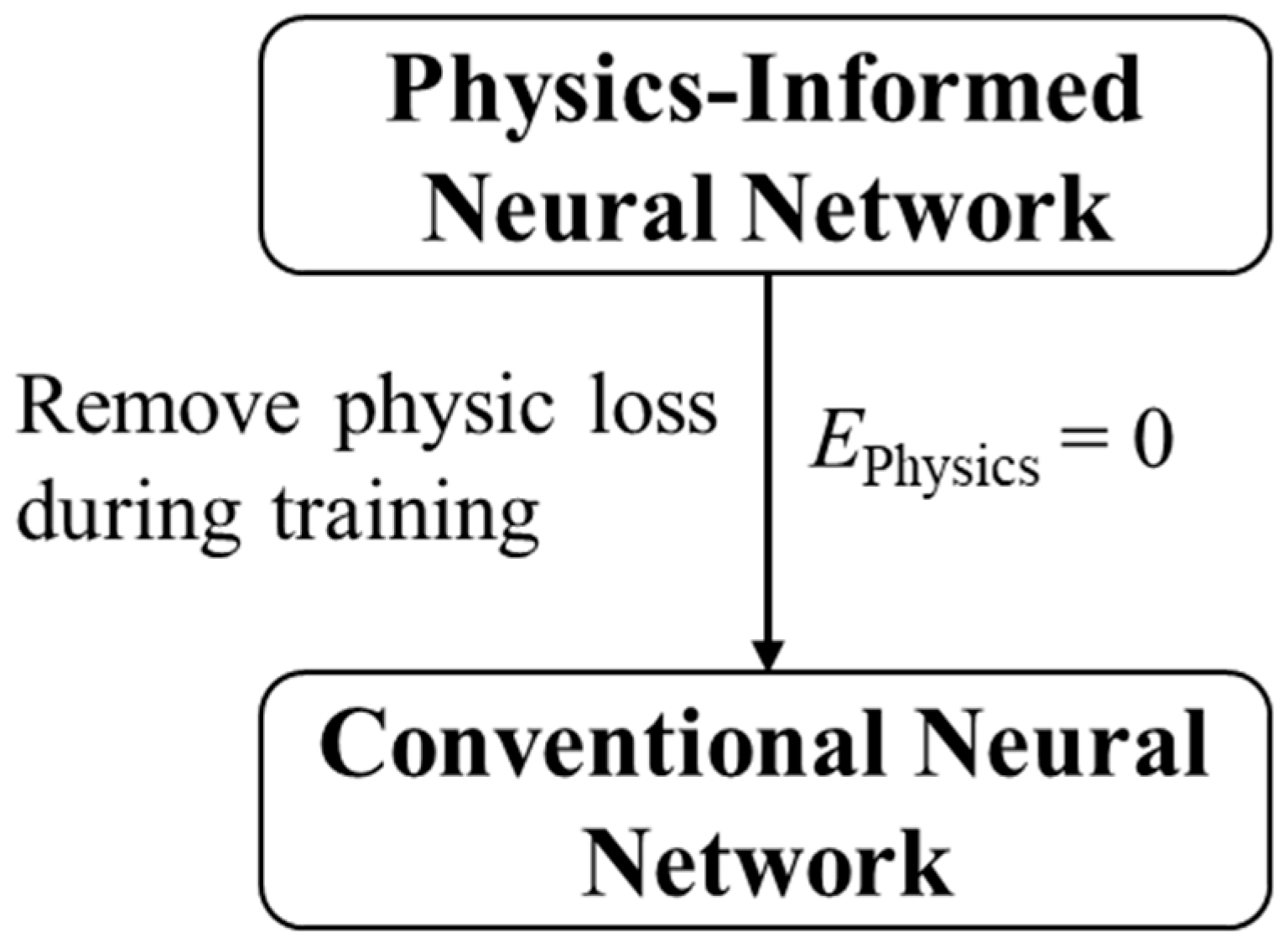
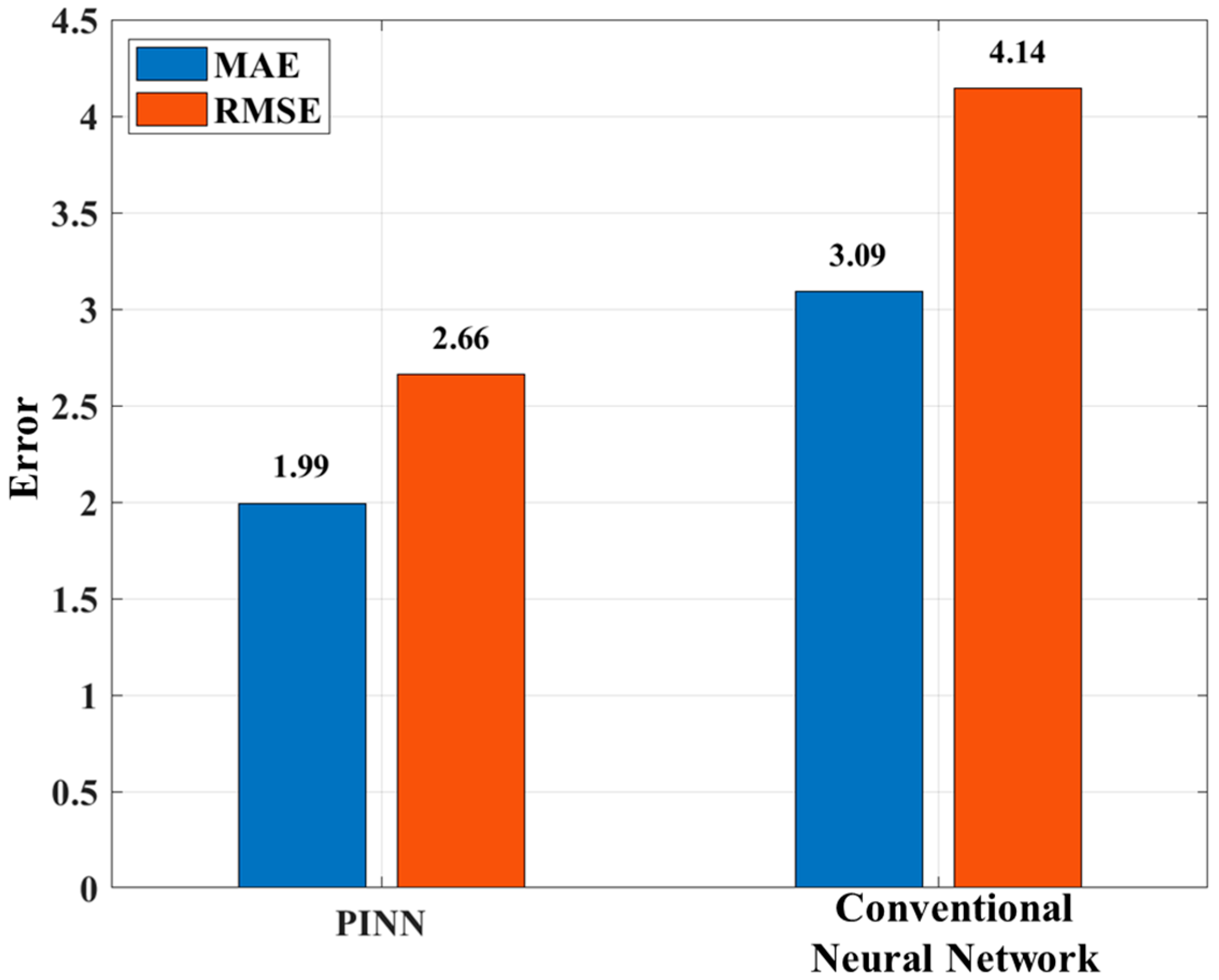
3.3. Comparison with Convention Neural Network
4. Conclusions
- (1)
- Reliable Prediction Accuracy: The proposed model was trained on data from four flight sorties and achieved satisfactory prediction performance when tested on another four separate sorties (sorties 5–8), across seven cabins. The mean absolute error (MAE) across all test cases is 1.6–2.79, demonstrating the model robustness across diverse flight conditions.
- (2)
- Performance Enhancement over Conventional Methods: A comparative analysis with a conventional neural network revealed the substantial benefit of incorporating physical constraints. The PINN framework achieved a 35% reduction in both MAE and RMSE, underscoring the value of the priori monotonicity in guiding the learning process toward physically consistent and accurate solutions.
- (3)
- Practical and Simplified Modeling Method: This approach eliminates the need to derive and solve intricate governing equations for cabin heat transfer, thereby reducing model development complexity and making PINNs more accessible for practical engineering applications in complex systems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Nomenclature | |
| β | Bias |
| E | Error |
| H | Flight altitude |
| L | Loss function |
| m | Monotonicity |
| Ma | Mach number |
| O | Neural network output |
| rho | Pearson correlation coefficient |
| T | Temperature |
| w | Weight |
| Subscripts | |
| a | Ambient |
| c | Center |
| mea | Measured |
| pred | Predicted |
| Abbreviations | |
| Adam | Adaptive moment estimation |
| MAE | Mean absolute error |
| PINN | Physics-informed neural network |
| RMSE | Root mean square error |
| UAV | Unmanned aerial vehicle |
References
- Yan, J.N. Design and Implementation a Measurement System for Aircraft Cabin Heat Comfort Test. In Proceedings of the Asia Conference on Mechanical Engineering and Aerospace Engineering (MEAE), China University of Geosciences, Wuhan, China, 23–25 June 2018. [Google Scholar]
- Zeng, X.J.; Su, X.; Zhang, X.H.; Pan, W.X.; Long, Z.W.; Shen, X. Experimental investigation of convective heat transfer in the aircraft cabin environment at low air pressure. Build. Environ. 2023, 233, 110125. [Google Scholar] [CrossRef]
- Ma, T.; Li, C.R.; Rong, S.L. The study on airborne equipment’s life prediction based on the finite element simulation under comprehensive stress. In Proceedings of the 2nd International Conference on Machine Design and Manufacturing Engineering (ICMDME), Jeju Island, Republic of Korea, 1–2 May 2013; pp. 224–228. [Google Scholar]
- Wróblewski, A.; Macek, A.; Banasiewicz, A.; Gola, S.; Zawislak, M.; Janicka, A. CFD Analysis of the Forced Airflow and Temperature Distribution in the Air-Conditioned Operator’s Cabin of the Stationary Rock Breaker in Underground Mine under Increasing Heat Flux. Energies 2023, 16, 3814. [Google Scholar] [CrossRef]
- Liu, R.X.; Song, J.Z.; Luo, P.J.; Tian, F.F.; Li, W.P. Analysis and prediction of temperature of an assembly frame for aircraft based on BP neural network. Int. J. Comput. Mat. Sci. Eng. 2023, 12, 2350006. [Google Scholar] [CrossRef]
- Chen, G.; Yang, S.; Peng, W.; Duo, L.; Zhang, J.; Liu, X. Transient Temperature Prediction Method for Spacecraft Using Process Neural Network. Spacecr. Eng. 2023, 32, 25–30. [Google Scholar]
- Li, H.; Zhang, J.J.; Cai, L.X.; Li, M.W.; Fu, Y.; Hao, Y.J. The Dynamic Prediction Method for Aircraft Cabin Temperatures Based on Flight Test Data. Aerospace 2024, 11, 755. [Google Scholar] [CrossRef]
- Fei, F.; Wang, D. PTC power control of electric vehicle thermal management system based on neural network feedforward. Appl. Therm. Eng. 2024, 253, 123803. [Google Scholar] [CrossRef]
- Xu, S.T.; Wang, C.H.; Yang, C.X. Optimal Design of Regenerative Cooling Structure Based on Backpropagation Neural Network. J. Thermophys. Heat Transf. 2022, 36, 637–649. [Google Scholar] [CrossRef]
- Verma, A.K.; French, R.H.; Carter, J.L.W. Physics-Informed Network Models: A Data Science Approach to Metal Design. Integr. Mater. Manuf. Innov. 2017, 6, 279–287. [Google Scholar] [CrossRef]
- Cai, K.; Wang, J.Y. Physics-informed neural networks for solving incompressible Navier-Stokes equations in wind engineering. Phys. Fluids 2024, 36, 121303. [Google Scholar] [CrossRef]
- Sun, R.Z.; Jeong, H.; Zhao, J.C.; Gou, Y.X.; Sauret, E.; Li, Z.R.; Gu, Y.T. A physics-informed neural network framework for multi-physics coupling microfluidic problems. Comput. Fluids 2024, 284, 106421. [Google Scholar] [CrossRef]
- Le-Duc, T.; Lee, S.; Nguyen-Xuan, H.; Lee, J. A hierarchically normalized physics-informed neural network for solving differential equations: Application for solid mechanics problems. Eng. Appl. Artif. Intell. 2024, 133, 108400. [Google Scholar] [CrossRef]
- Li, S.L.; Wang, G.; Di, Y.L.; Wang, L.P.; Wang, H.D.; Zhou, Q.J. A physics-informed neural network framework to predict 3D temperature field without labeled data in process of laser metal deposition. Eng. Appl. Artif. Intell. 2023, 120, 105908. [Google Scholar] [CrossRef]
- Zhang, C.; Li, C.G.; Li, X.; Ye, M.; Liu, Z.M. A general Physics-Informed Neural Network approach for deriving fluid flow fields from temperature distribution. Chem. Eng. Sci. 2025, 302, 120950. [Google Scholar] [CrossRef]
- Xia, Y.C.; Meng, Y.G. Physics-Informed Neural Network (PINN) for Solving Frictional Contact Temperature and Inversely Evaluating Relevant Input Parameters. Lubricants 2024, 12, 62. [Google Scholar] [CrossRef]
- Zerrougui, I.; Li, Z.L.; Hissel, D. Physics-Informed Neural Network for modeling and predicting temperature fluctuations in proton exchange membrane electrolysis. Energy AI 2025, 20, 100474. [Google Scholar] [CrossRef]
- Kim, S.; Choi, J.H.; Kim, N.H. Data-driven prognostics with low-fidelity physical information for digital twin: Physics-informed neural network. Struct. Multidiscip. Optim. 2022, 65, 255. [Google Scholar] [CrossRef]
- Ren, S.J.; Wu, S.L.; Weng, Q.H. Physics-informed machine learning methods for biomass gasification modeling by considering monotonic relationships. Bioresour. Technol. 2023, 369, 128472. [Google Scholar] [CrossRef] [PubMed]
- Zhu, B.Y.; Ren, S.J.; Weng, Q.H.; Si, F.Q. A physics-informed neural network that considers monotonic relationships for predicting NOx emissions from coal-fired boilers. Fuel 2024, 364, 131026. [Google Scholar] [CrossRef]
- Utomo, M.S.K.T.S.; Yohana, E.; Mahendra, C.; Utama, I.Y. Analysis of blended winglet parameters on the aerodynamic characteristics of NXXX aircraft using Computational Fluid Dynamics (CFD). Results Eng. 2024, 24, 102901. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, T.; Jin, H. Rapid prediction of airborne gaseous pollutant transport in aircraft cabins based on proper orthogonal decomposition and the Markov chain method. Build. Environ. 2023, 228, 109816. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation Coefficients: Appropriate Use and Interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
- Akoglu, H. User’s guide to correlation coefficients. Turk. J. Emerg. Med. 2018, 18, 91–93. [Google Scholar] [CrossRef] [PubMed]
- Varshney, R.P.; Sharma, D.K. Optimizing Time-Series forecasting using stacked deep learning framework with enhanced adaptive moment estimation and error correction. Expert Syst. Appl. 2024, 249, 123487. [Google Scholar] [CrossRef]
- Zhang, C.X.; Song, D.J.; Huang, C.; Swami, A.; Chawla, N.V.; Assoc Comp, M. Heterogeneous Graph Neural Network. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD), Anchorage, AK, USA, 4–8 August 2019; pp. 793–803. [Google Scholar]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Yang, J.X.; Long, Q. A modification of adaptive moment estimation (adam) for machine learning. J. Ind. Manag. Optim. 2024, 20, 2516–2540. [Google Scholar] [CrossRef]





| Instruments | Models | Parameters |
|---|---|---|
| Data acquisition instrument | KAM-500, ACRA CONTROL | Maximum sample rate: 500 K/s |
| Battery | DH15206, DONGHUA Co., Ltd. | 14.8 V, 6.6 Ah |
| Thermocouple | K-type, DONGHUA Co., Ltd. | Measurement range: −200~200 °C; Accuracy: 0.1 K |
| Parameters | Values |
|---|---|
| Maximum number of iterations | 50,000 |
| Sortie number of training set | 4 |
| Sortie number of test set | 4 |
| Number of hidden layers | 2 |
| Number of nodes per layer | 30 |
| Activation function | Tanh |
| Optimizer | Adam |
| Learning rate | 0.01 |
| Decay rate | 0.005 |
| Mini-batch size | 256 |
| Area | Maximum Temperature/°C | Minimum Temperature/°C | |
|---|---|---|---|
| 1 | Ambient | 35 | −47.1 |
| 2 | Center cabin | 48.6 | 32.9 |
| 3 | 1# cabin | 38.2 | 13.3 |
| 4 | 2# cabin | 39.8 | 4.2 |
| 5 | 3# cabin | 35.1 | −10.1 |
| 6 | 4# cabin | 38 | 13.3 |
| 7 | 5# cabin | 36.2 | −12 |
| 8 | 6# cabin | 36.1 | −12.8 |
| Sortie | Average MAE | Std Dev | Min MAE | Max MAE |
|---|---|---|---|---|
| 5 | 1.60 | 0.68 | 0.99 | 3.00 |
| 6 | 1.72 | 0.65 | 0.78 | 2.57 |
| 7 | 1.86 | 0.68 | 0.82 | 2.80 |
| 8 | 2.79 | 0.93 | 1.27 | 3.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Cai, L.; Zhang, J.; He, Y.; Ren, Z.; Ding, C. Predicting Airplane Cabin Temperature Using a Physics-Informed Neural Network Based on a Priori Monotonicity. Aerospace 2025, 12, 988. https://doi.org/10.3390/aerospace12110988
Liu Z, Cai L, Zhang J, He Y, Ren Z, Ding C. Predicting Airplane Cabin Temperature Using a Physics-Informed Neural Network Based on a Priori Monotonicity. Aerospace. 2025; 12(11):988. https://doi.org/10.3390/aerospace12110988
Chicago/Turabian StyleLiu, Zijian, Liangxu Cai, Jianjun Zhang, Yuheng He, Zhanyong Ren, and Chen Ding. 2025. "Predicting Airplane Cabin Temperature Using a Physics-Informed Neural Network Based on a Priori Monotonicity" Aerospace 12, no. 11: 988. https://doi.org/10.3390/aerospace12110988
APA StyleLiu, Z., Cai, L., Zhang, J., He, Y., Ren, Z., & Ding, C. (2025). Predicting Airplane Cabin Temperature Using a Physics-Informed Neural Network Based on a Priori Monotonicity. Aerospace, 12(11), 988. https://doi.org/10.3390/aerospace12110988






