Design and Research of Lorentz Force Magnetic Levitation Vibration Isolation Platform
Abstract
1. Introduction
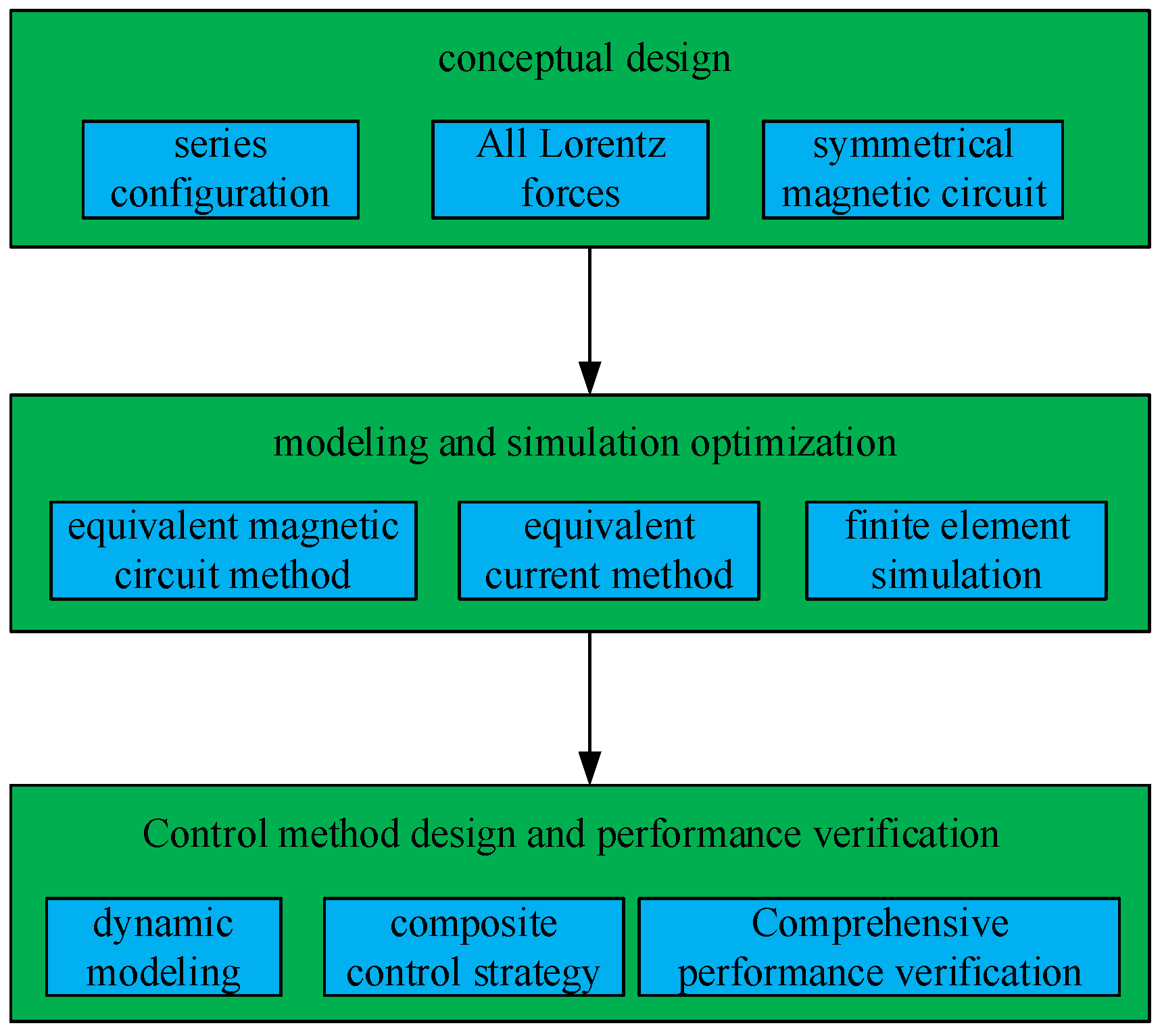
2. Lorenz Force Magnetic Levitation Vibration Isolation Platform Scheme Design and Decoupling Analysis
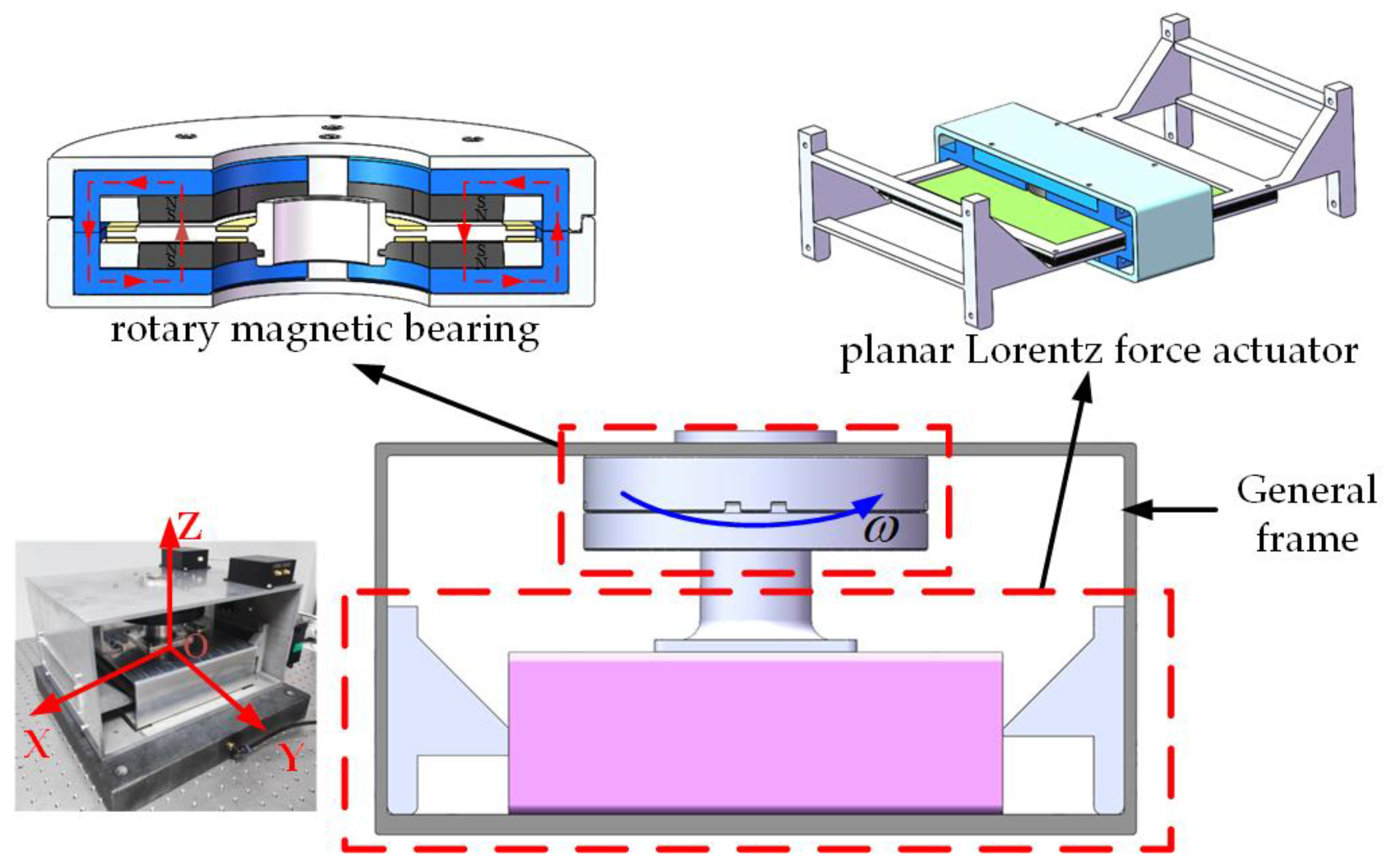
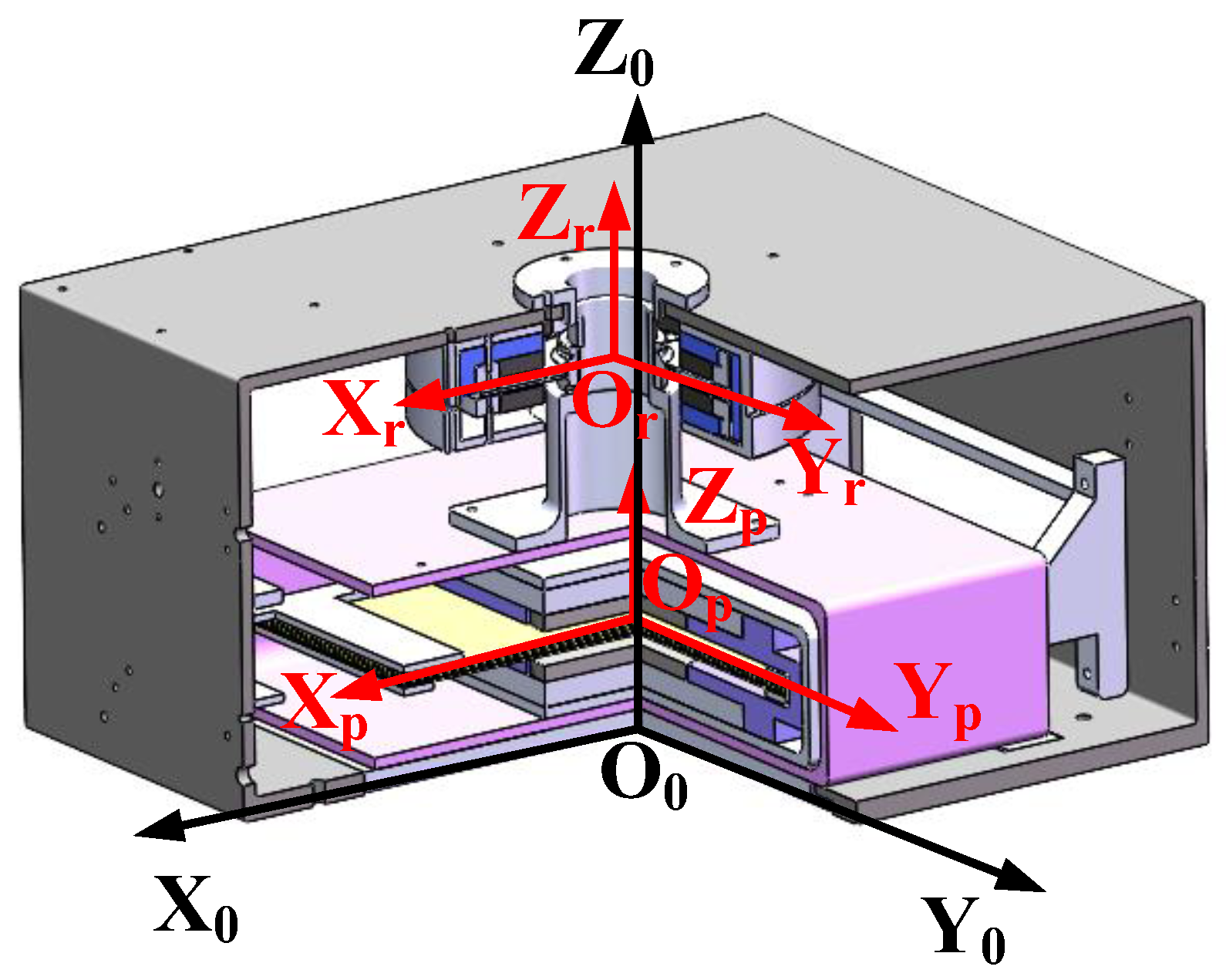
2.1. Overall Structure of Lorentz Force Vibration Isolation Platform
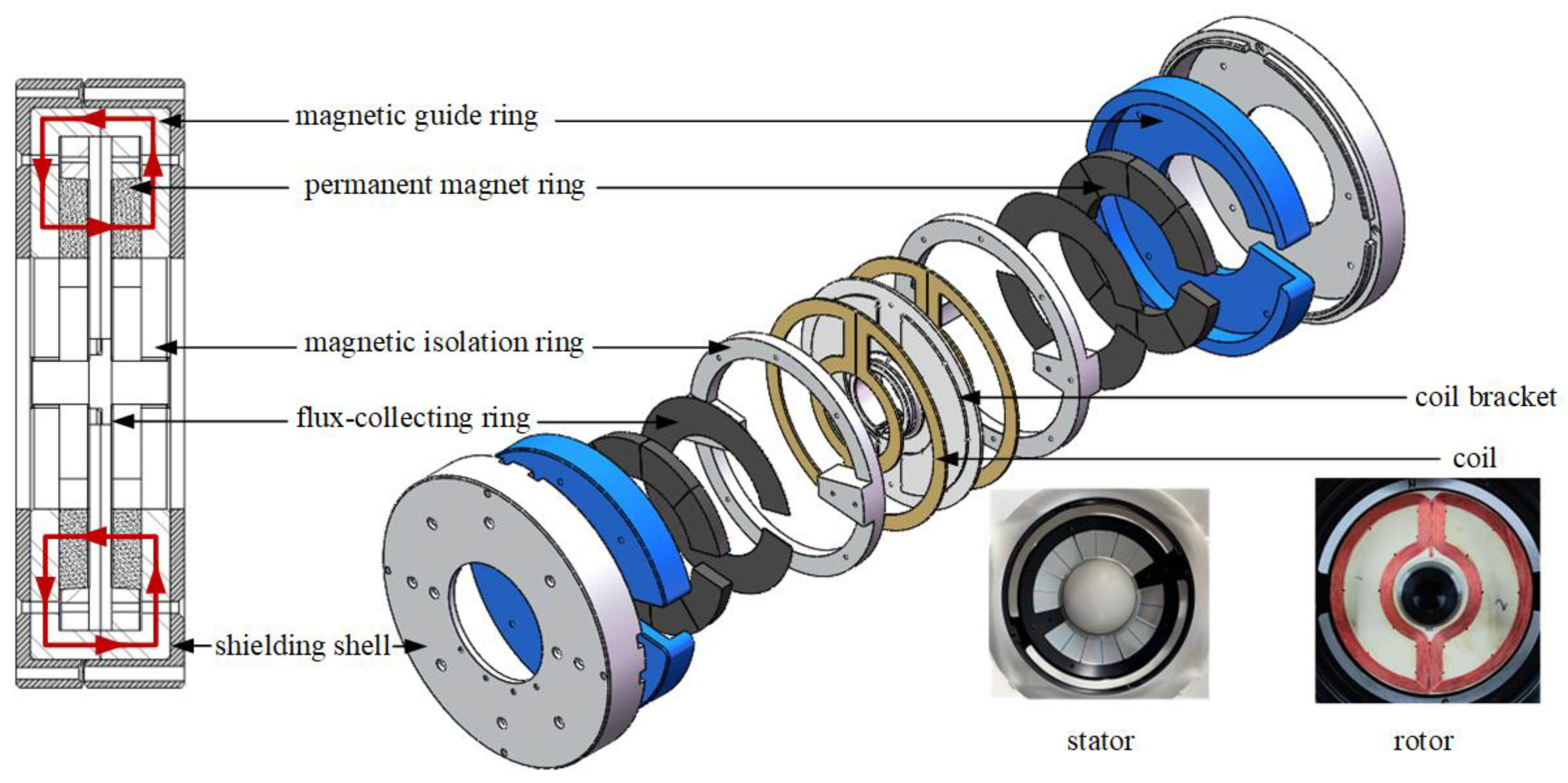
2.2. Design of Rotary Lorentz Force Magnetic Bearing
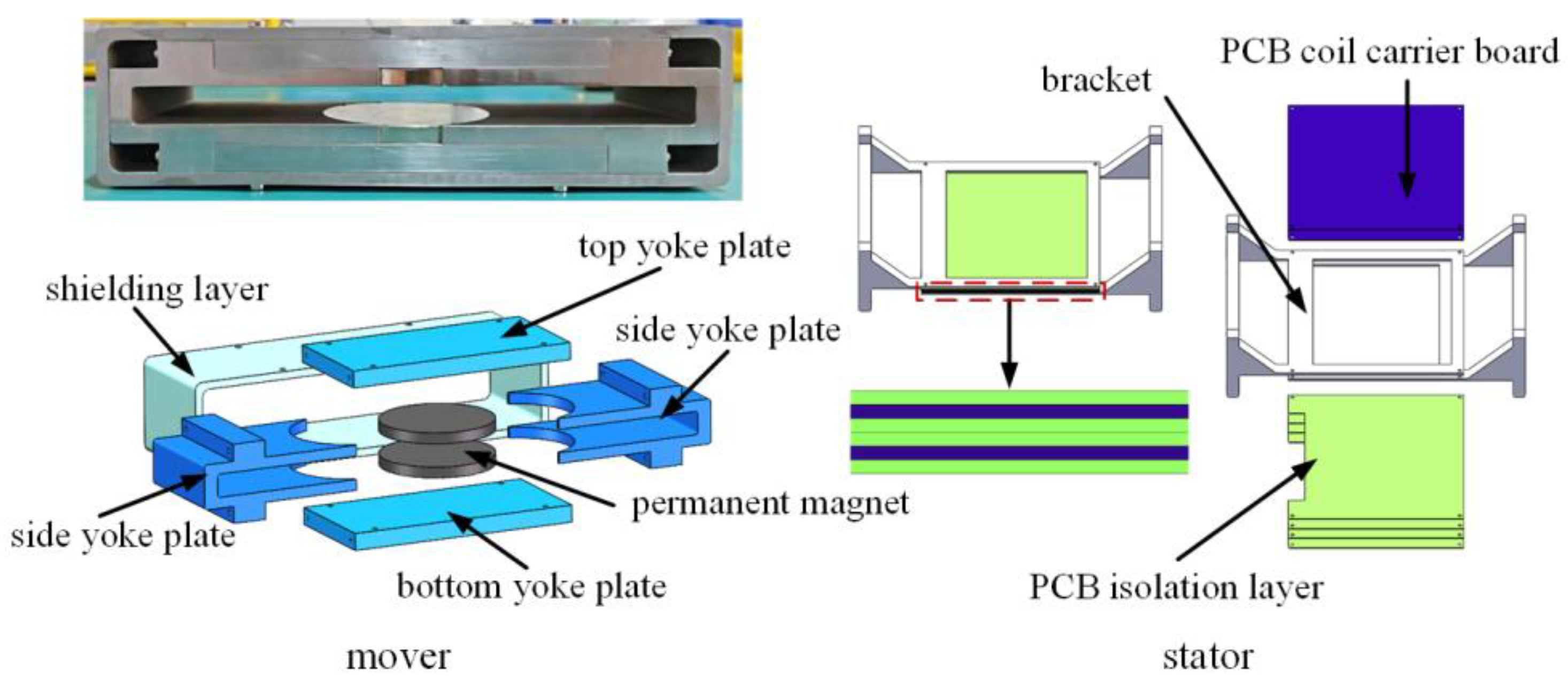
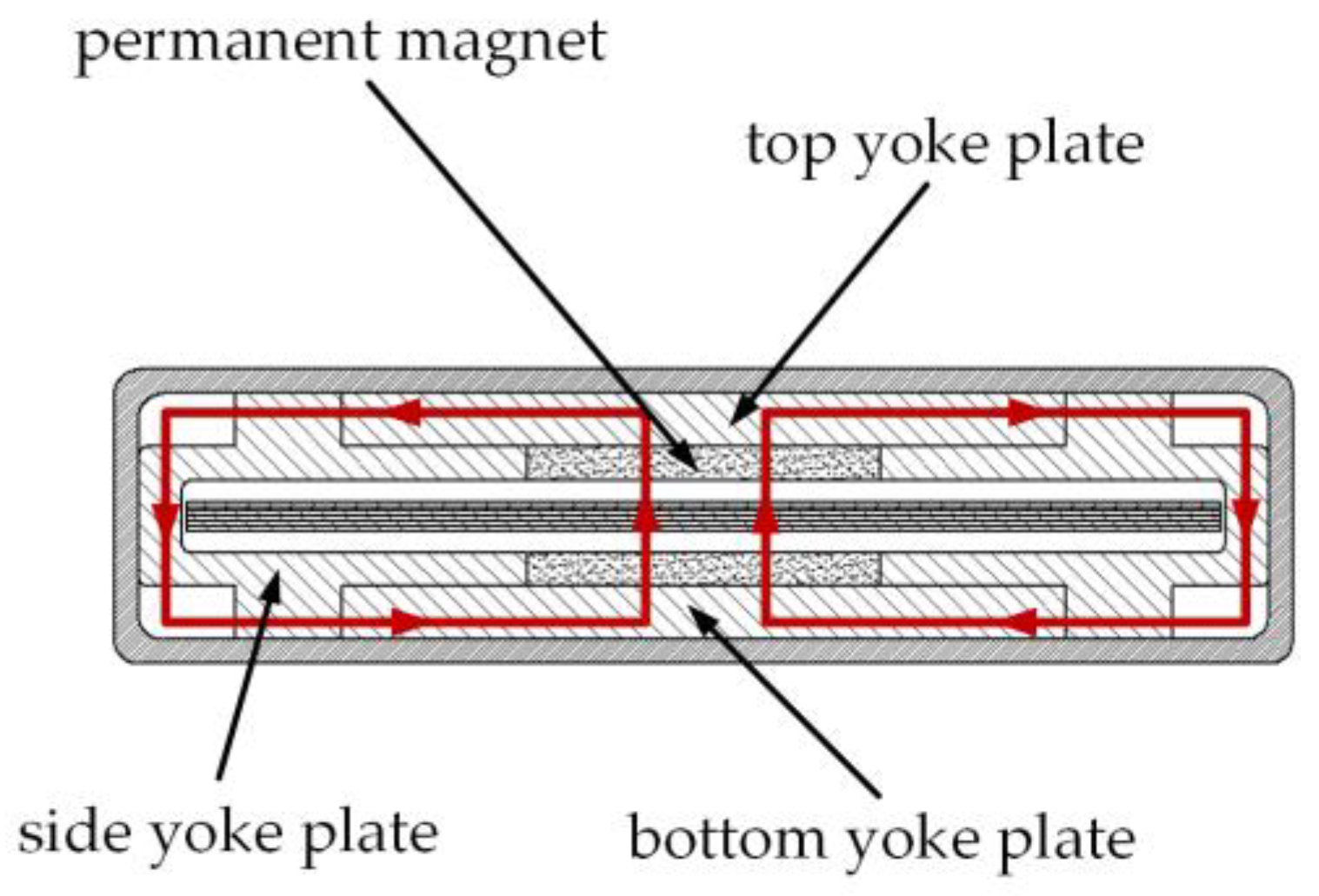
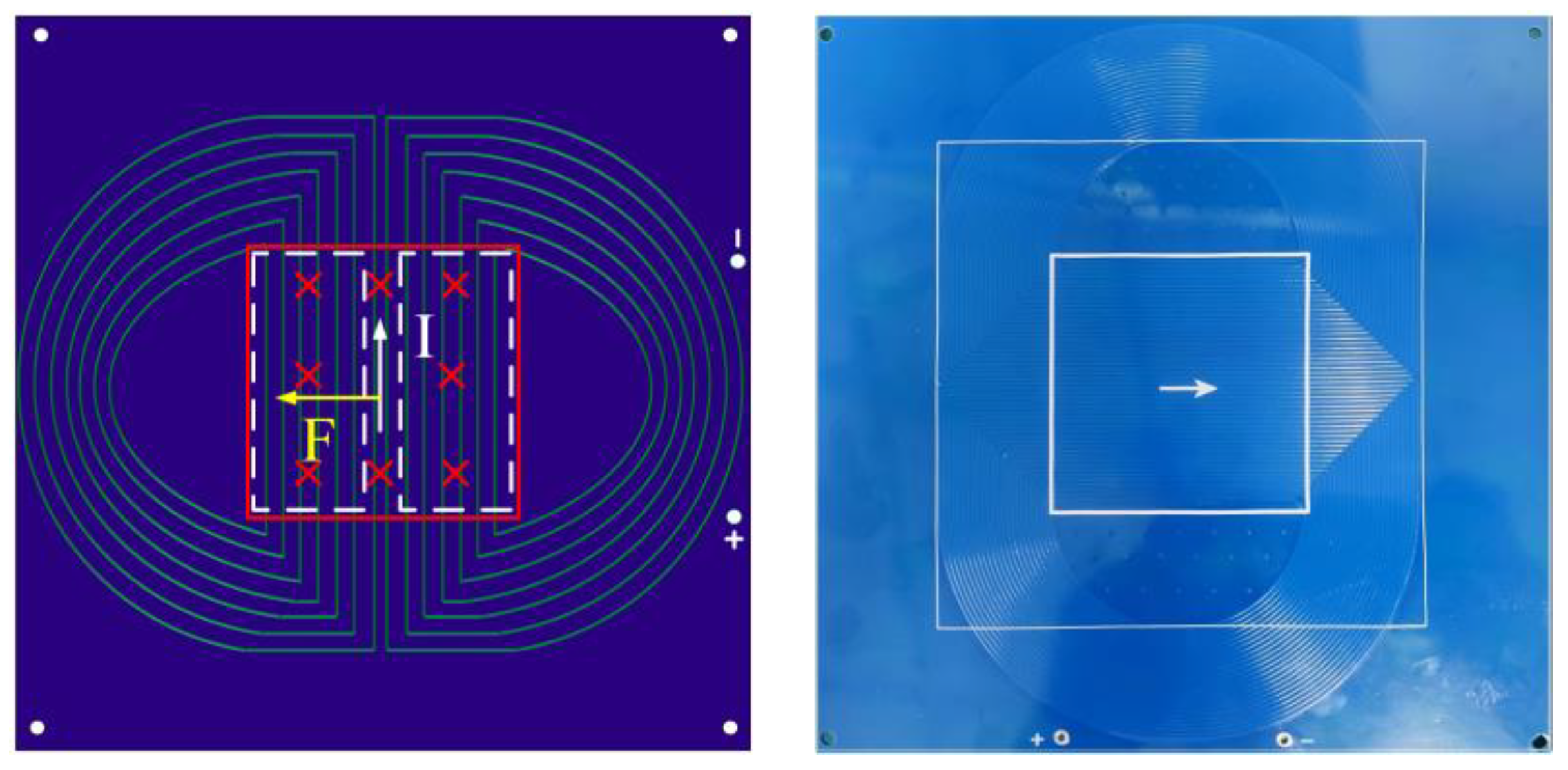
2.3. Design of Planar Lorentz Force Actuator
2.4. Analysis of the Characteristics of the Actuator
2.4.1. Axial High-Precision Magnetic Circuit Symmetrization
2.4.2. Radial Regularized Wiring
2.4.3. Series-Configured Decoupling
3. Magnetic Field Modeling and Steady-State Analysis of Two-Degree-of-Freedom Planar Lorentz Force Actuator
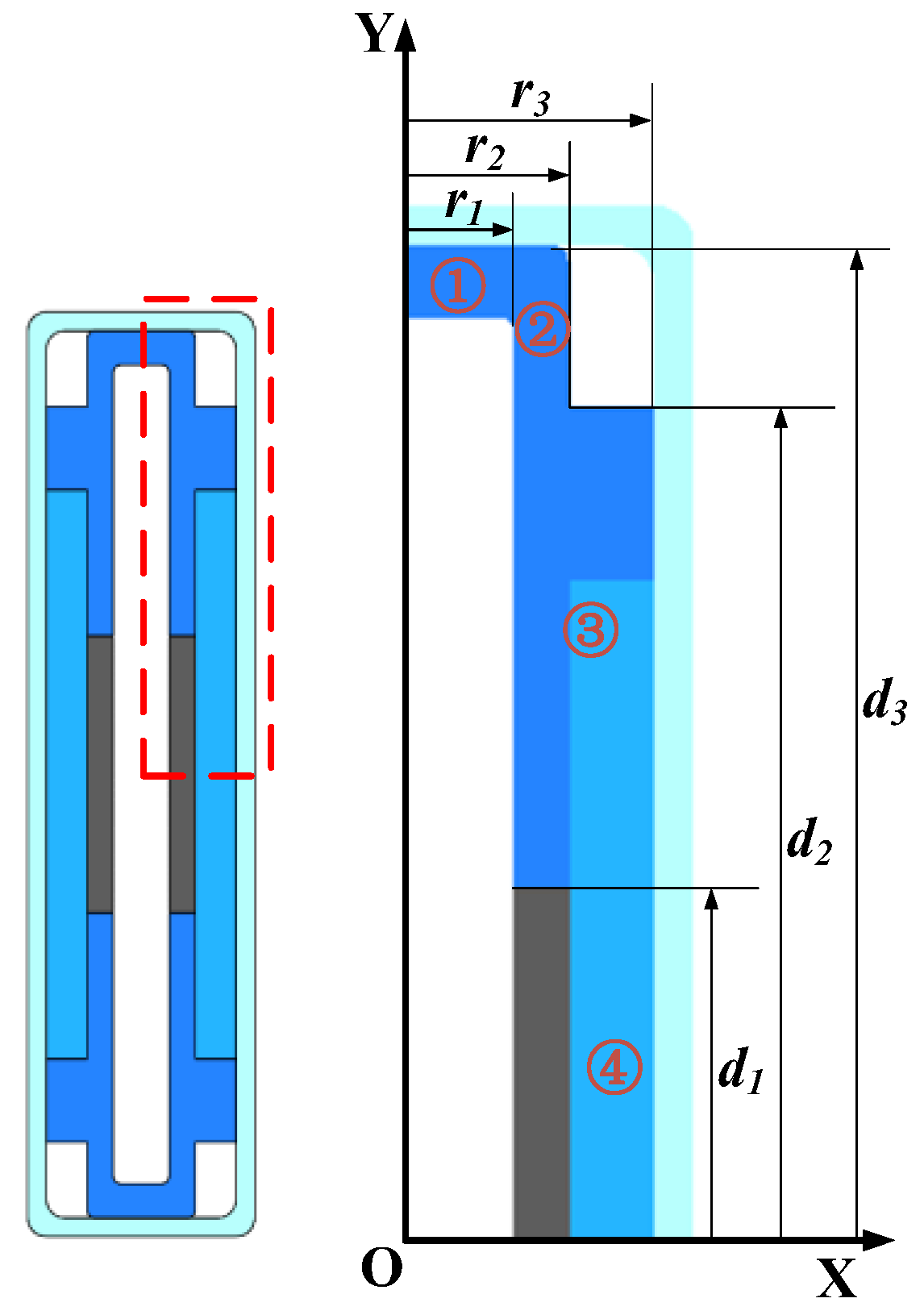
3.1. Establishment and Analysis of Magnetic Circuit Model Based on Equivalent Magnetic Circuit Method
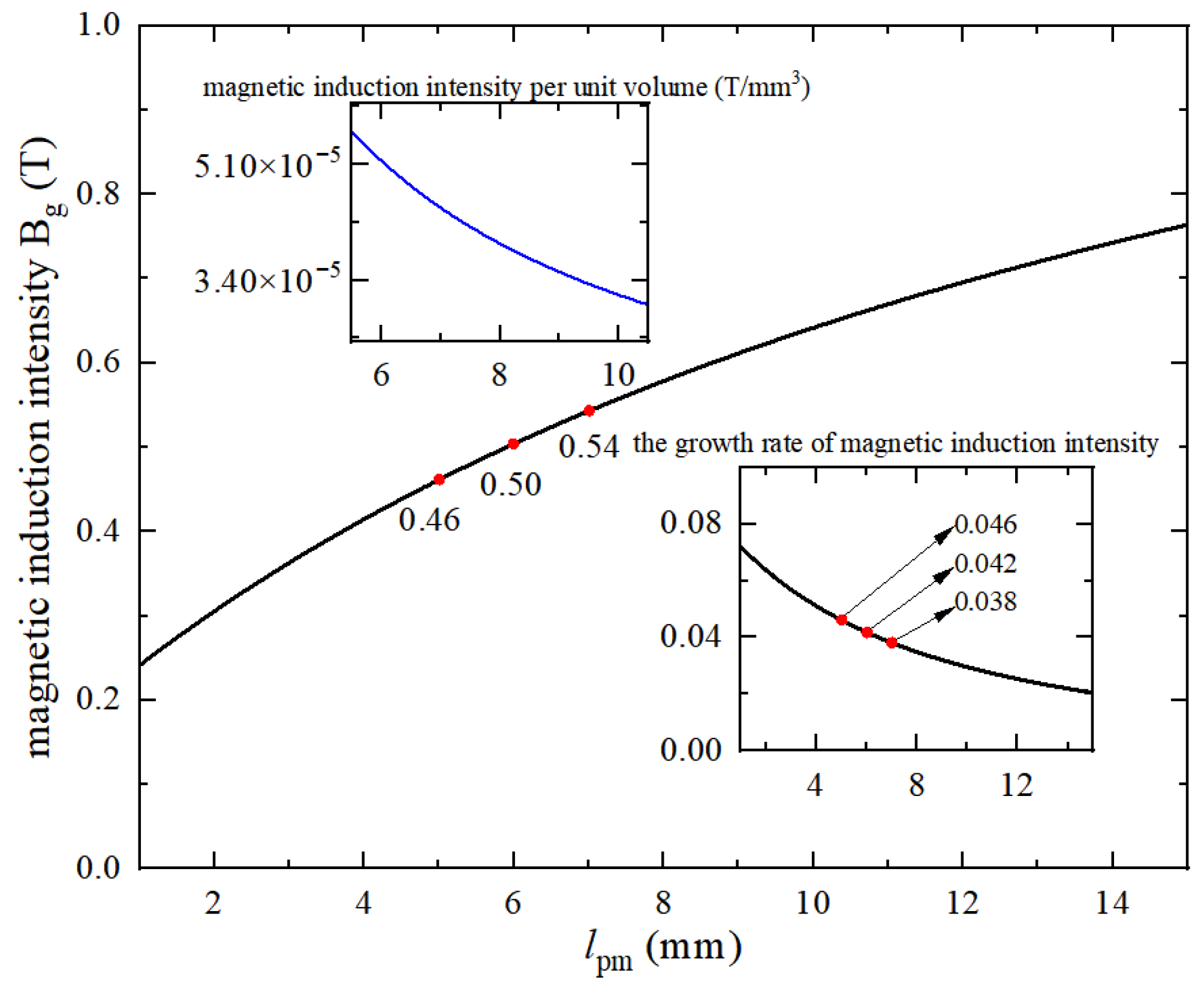
3.2. Establishment and Analysis of Magnetic Field Equivalent Current Model Based on Maxwell’s Principle
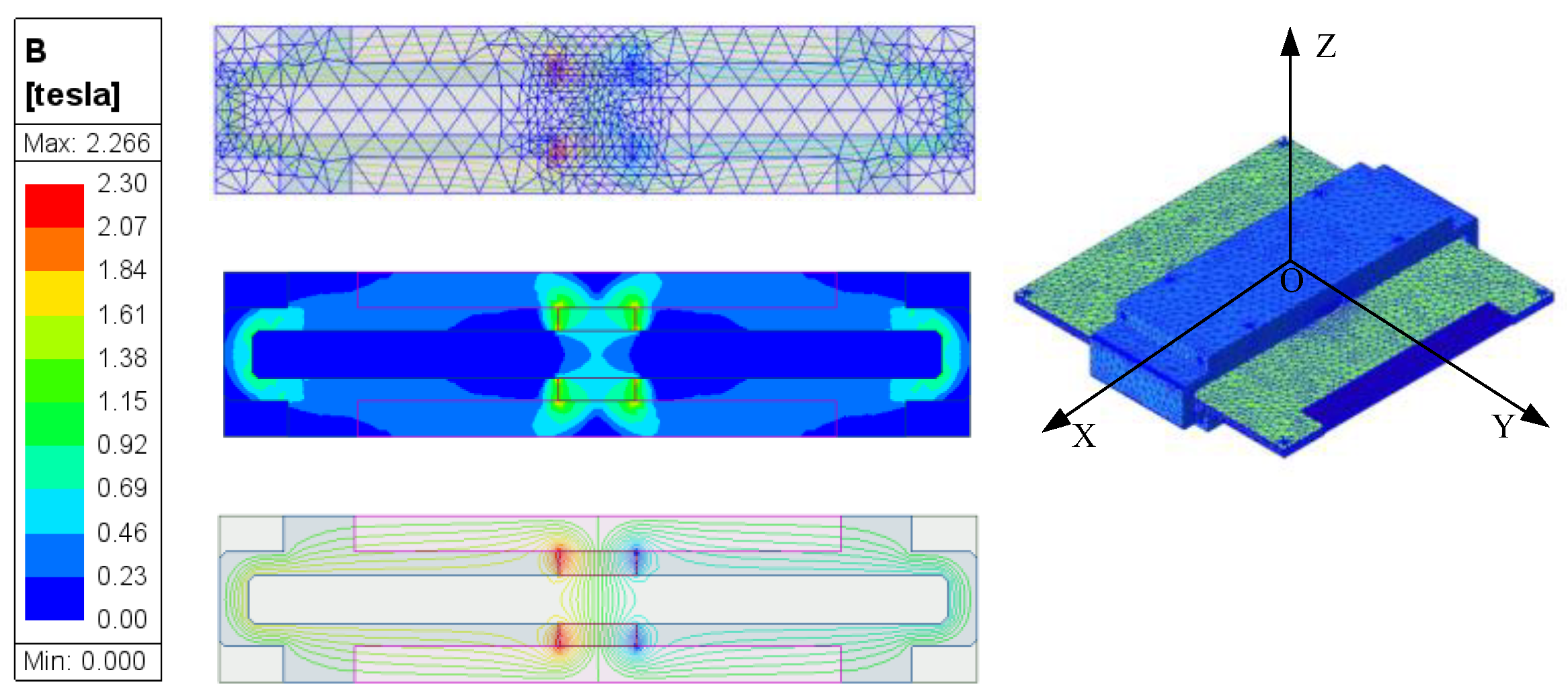
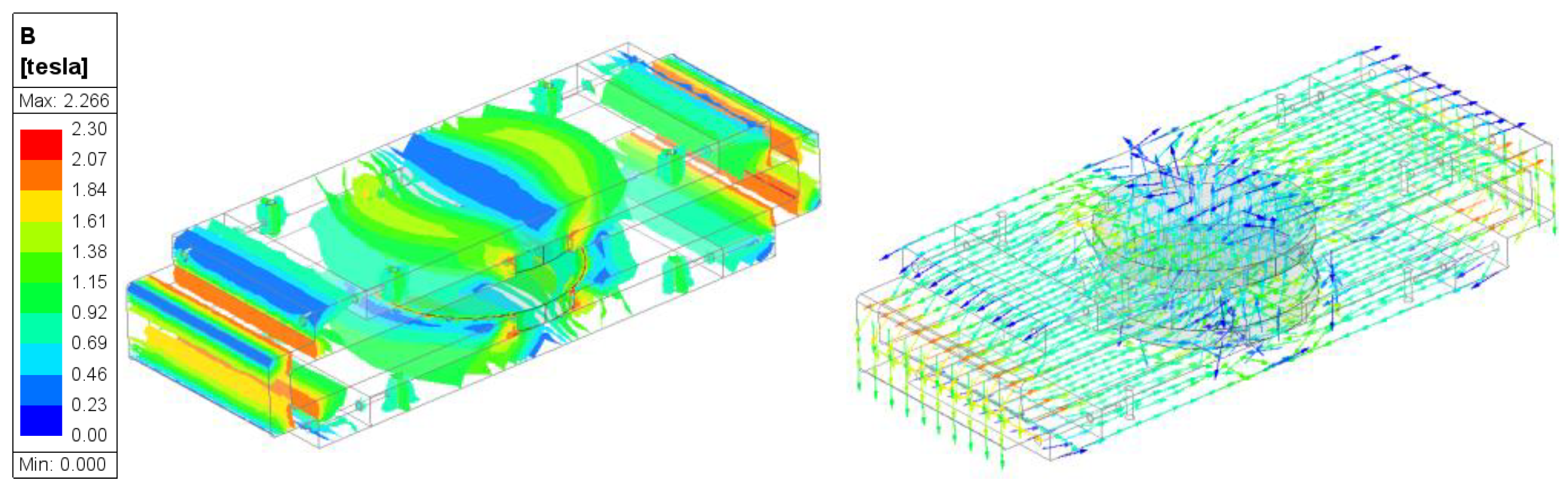
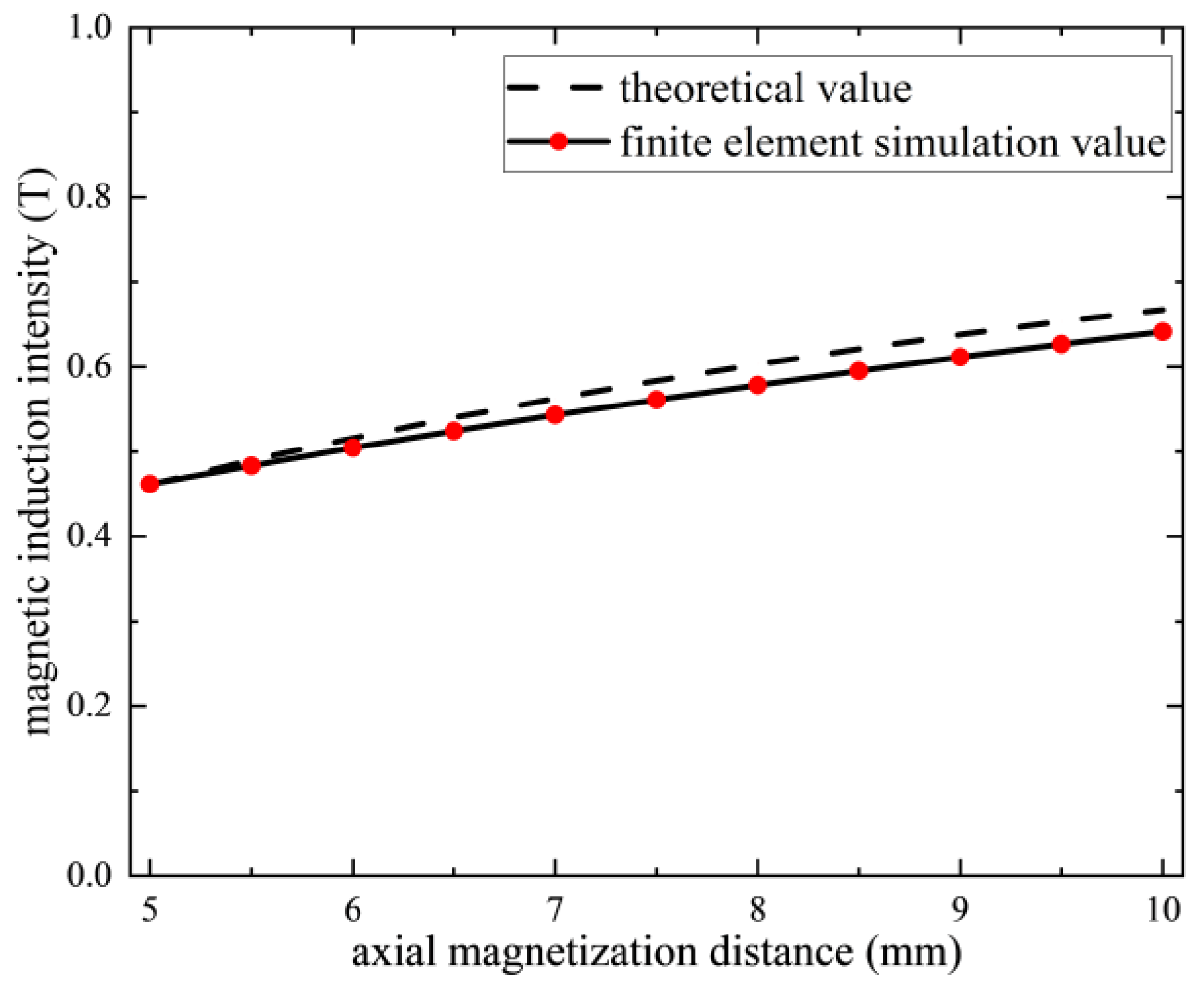
3.3. Finite Element Simulation Analysis
4. Dynamic Coupling Characteristics Analysis and Vibration Isolation Verification of Maglev Active Vibration Isolation Platform
4.1. Mechanism of Mechanical-Magnetic Coupling
4.2. Mathematical Modeling of Coupling Effect
4.3. Coupling Effect Simulation and Vibration Isolation Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, X.B.; Ying, M.X.; Liu, X.T. Review on the Effect and Control Method of Micro-vibration for High-resolution Satellite. Shanghai Aerosp. 2024, 41, 140–147. [Google Scholar] [CrossRef]
- Gao, X.S.; Wang, G.Y.; Guan, S.; Yang, W.T.; Zhang, G.B.; Fan, L.J.; Zhao, Y.; Luo, W.B. Micro-vibration Attenuation Design and Verification for GFDM-1 Satellite. Spacecr. Eng. 2021, 30, 76–85. [Google Scholar] [CrossRef]
- Jiao, X.; Zhang, J.; Li, W.; Wang, Y.; Ma, W.; Zhao, Y. Advances in spacecraft micro-vibration suppression methods. Prog. Aerosp. Sci. 2023, 138, 100898. [Google Scholar] [CrossRef]
- Xing, W.; Tuo, W.; Li, X.; Wang, T.; Yang, C. Micro-vibration suppression and compensation techniques for in-orbit satellite: A review. Chin. J. Aeronaut. 2024, 37, 1–19. [Google Scholar] [CrossRef]
- Du, Y.G.; Wang, X.S.; Wang, Y.L. Research on an all-metal six-degree-of-freedom vibration isolation platform. J. Mech. Eng. 2023, 59, 188–198. [Google Scholar] [CrossRef]
- Geng, Z.J.; Pan, G.G.; Haynes, L.S.; Wada, B.K.; Garba, J.A. An intelligent control system for multiple degree-of-freedom vibration isolation. J. Intell. Mater. Syst. Struct. 1995, 6, 787–800. [Google Scholar] [CrossRef]
- Thayer, D.; Campbell, M.; Vagners, J.; Von Flotow, A. Six-axis vibration isolation system using soft actuators and multiple sensors. J. Spacecr. Rockets 2002, 39, 206–212. [Google Scholar] [CrossRef]
- Chen, H.-J.; Bishop, R.; Agrawal, B. Payload Pointing and Active Vibration Isolation Using Hexapod Platforms. In Proceedings of the American Institute of Aeronautics and Astronautics/American Society of Mechanical Engineers/American Society of Civil Engineers/American Helicopter Society Structures, Structural Dynamics, and Materials Conference, Norfolk, VA, USA, 7–10 April 2003. [Google Scholar] [CrossRef][Green Version]
- Zhang, T.Q. Design and Experimental Study on Micro-Vibration Isolation of Whole Satellite Based on Stewart Platform Configuration Mechanism. Ph.D. Thesis, University of Chinese Academy of Sciences, Changchun, China, 2024. [Google Scholar][Green Version]
- Nawratil, G. A remarkable set of Schönflies-singular planar Stewart Gough platforms. Comput. Aided Geom. Des. 2010, 27, 503–513. [Google Scholar] [CrossRef]
- Wang, J.M.; Kong, Y.F.; Huang, H. Cooperative control for vibration isolation and suppression based on Stewart platform. Vib. Shock 2019, 38, 186–194. [Google Scholar] [CrossRef]
- Hou, Y.; Zeng, D.; Yao, J.; Kang, K.; Lu, L.; Zhao, Y. Optimal design of a hyperstatic Stewart platform-based force/torque sensor with genetic algorithms. Mechatronics 2009, 19, 199–204. [Google Scholar] [CrossRef]
- Yan, J.; He, X.J.; Tang, L. Control method of electromagnetic suspension vibration isolation system. Electro-Opt. Eng. 1999, 26, 18–22. [Google Scholar]
- Carlos, M.G.; Stephen, W.M. Survey of active vibration isolation systems for microgravity applications. J. Spacecr. Rocket. 2000, 37, 586–596. [Google Scholar] [CrossRef]
- Edberg, D.L.; Harduvel, J.T.; Schenck, D.J. Non-Contacting Isolated Stabilized Microgravity Platform System. U.S. Patent US5638303, 10 June 1997. [Google Scholar]
- Whorton, M. Robust control for microgravity vibration isolation system. Spacecr. Rocket. 2005, 42, 152–160. [Google Scholar] [CrossRef]
- Hampton, R.; Calhoun, P.; Whorton, M. Glovebox Integrated Microgravity Isolation Technology: A Linearized State-Space Model. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004. [Google Scholar] [CrossRef]
- Calhoun, P.; Hampton, D. Frequency Weighted H2 Control Design for the Glovebox Integrated Microgravity Isolation Technology. In Proceedings of the American Institute of Aeronautics and Astronautics Guidance, Navigation, and Control Conference and Exhibit, Austin, TX, USA, 11–14 August 2003. [Google Scholar]
- Zhang, W.; Zhao, Y.B.; Liao, H.; Zhao, H.B. Design of an Active-Quiet Isolated and Master-Slave Coordination Controlled Dual-Super Satellite Platform. Shanghai Aerosp. 2014, 31, 7–11+30. [Google Scholar] [CrossRef]
- Zhang, W.; Cheng, W.; You, W.; Chen, X.; Zhang, J.; Li, C.; Fang, C. Levitated-body ultra-high pointing accuracy and stability satellite platform of the CHASE mission. Sci. China Phys. Mech. Astron. 2022, 65, 289604. [Google Scholar] [CrossRef]
- Wu, Q.Q.; Cui, N.; Liu, B.L.; Yue, H.H.; Liu, R.Q. Dynamic model and control strategy of multi-dimensional magnetic levitation vibration isolation system. Acta Aeronaut. Astronaut. Sin. 2019, 40, 153–163. [Google Scholar] [CrossRef]
- Wu, Q.Q.; Yue, H.H.; Liu, R.Q.; Ding, L.; Deng, Z.Q. Parametric design and multiobjective optimization of maglev actuators for active vibration isolation system. Adv. Mech. Eng. 2014, 6, 215358. [Google Scholar] [CrossRef]
- Li, Q.; He, K.D.; Yang, H.J.; Xue, Y.J.; Ma, C.; Wang, T.S.; Liu, L. A study on a low-frequency active vibration isolation platform based on quasi-zero stiffness supporting structures. Vib. Shock 2024, 43, 84–91+117. [Google Scholar] [CrossRef]
- Pang, W.K.; Wang, W.J.; Fan, Y.H.; Li, L.; Yang, Y.; Zhu, H.Y. Design and analysis of double magnetic circuit rotating Lorentz force magnetic bearing. Beijing Univ. Aeronaut. Astronaut. 2024, 1–17. [Google Scholar] [CrossRef]







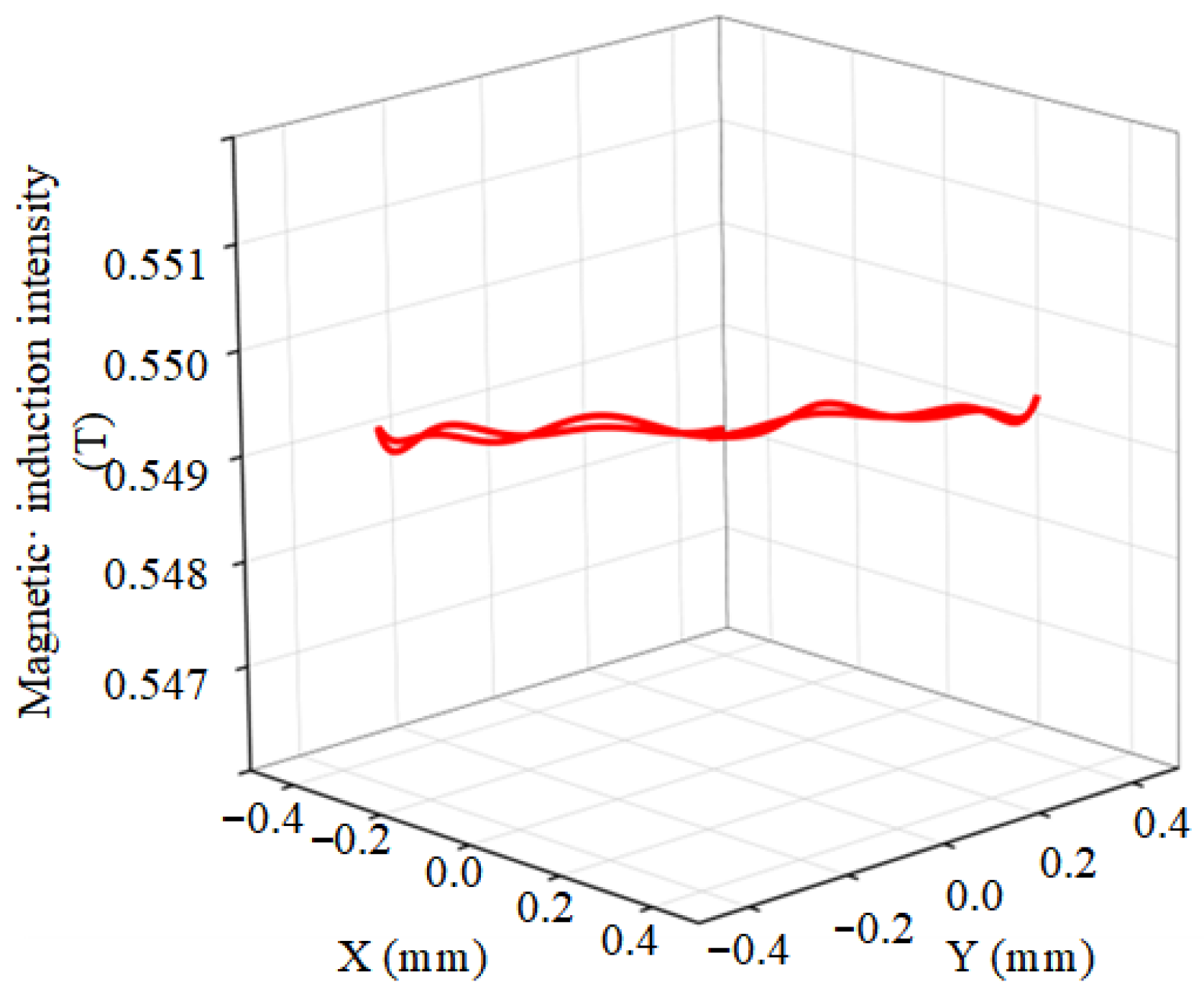
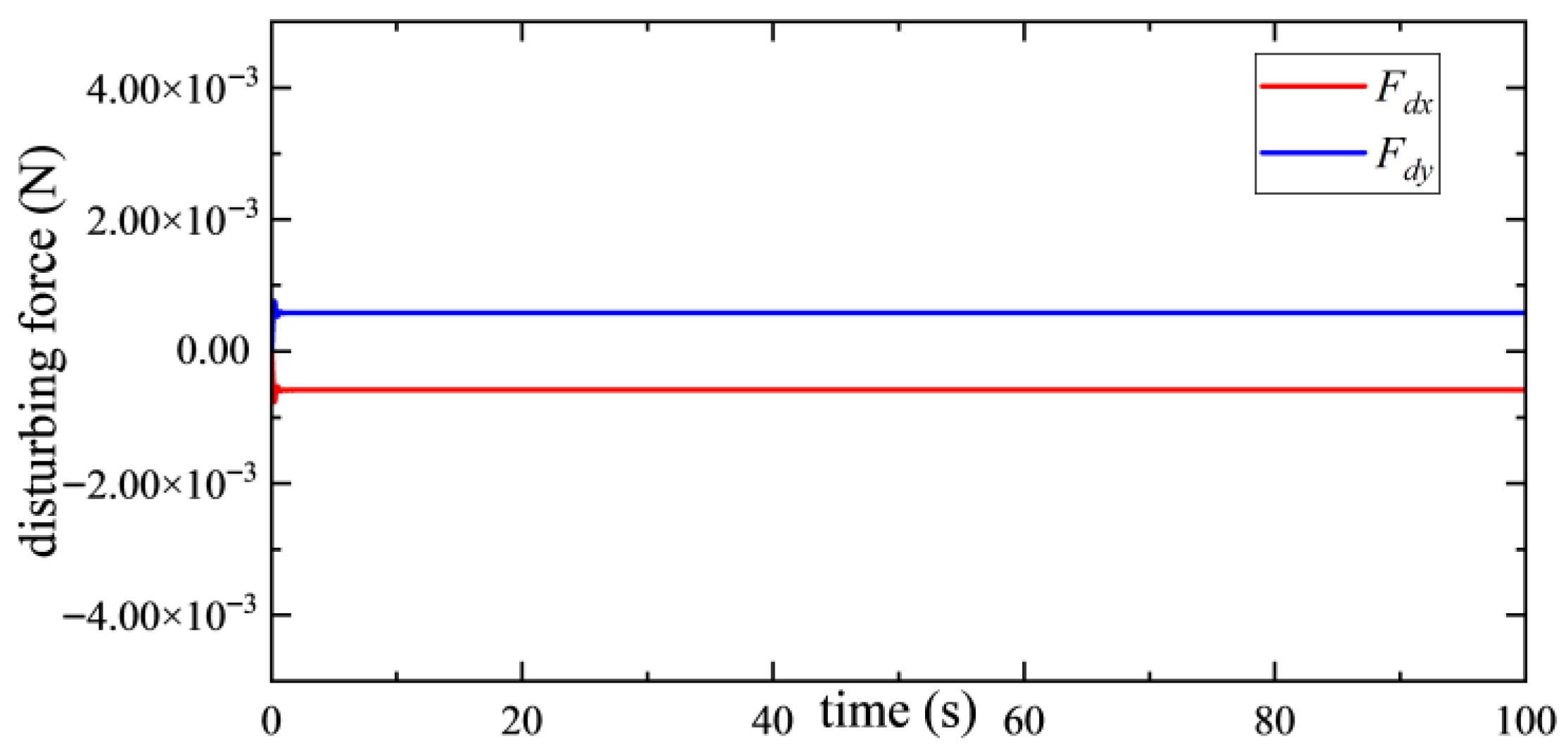
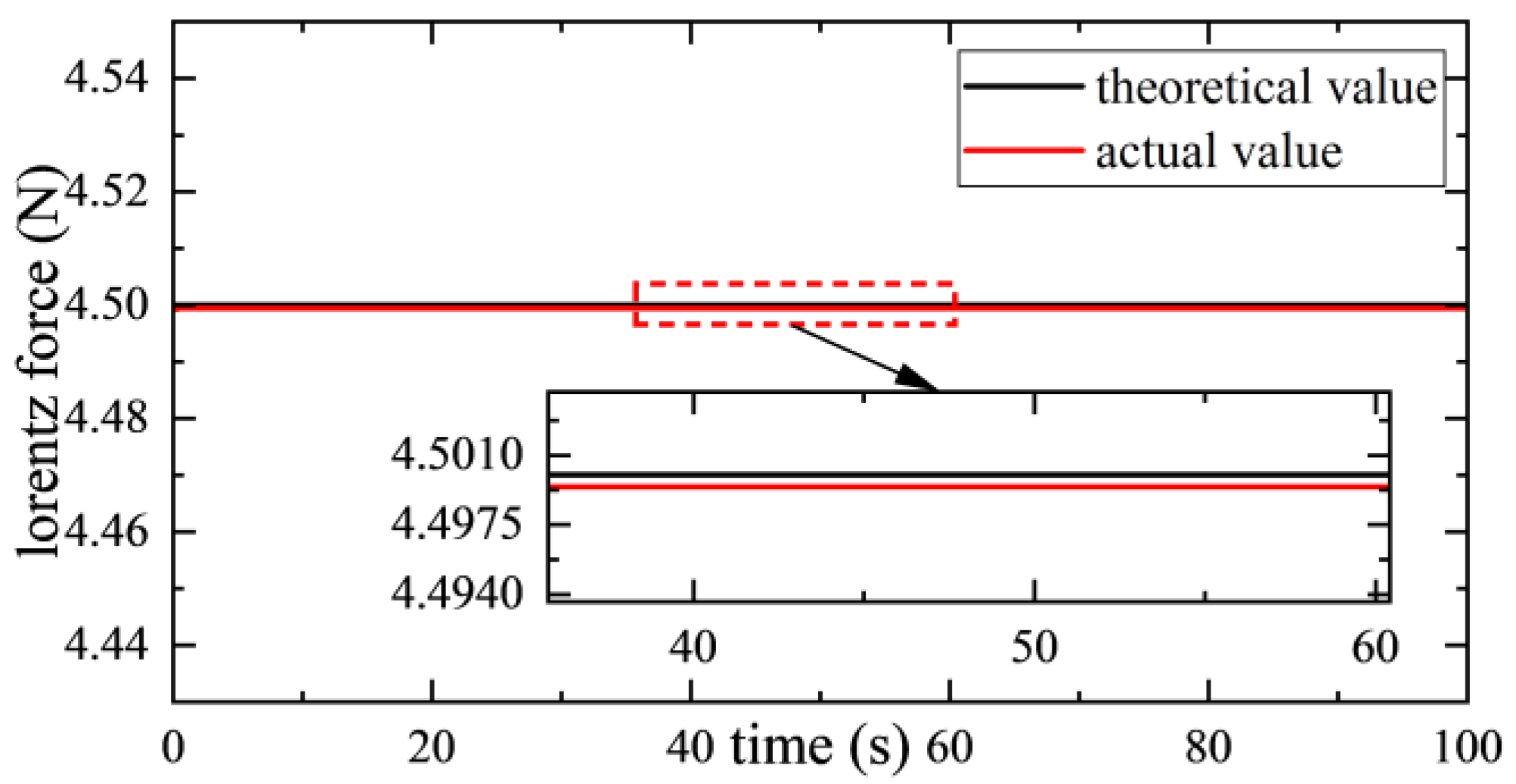

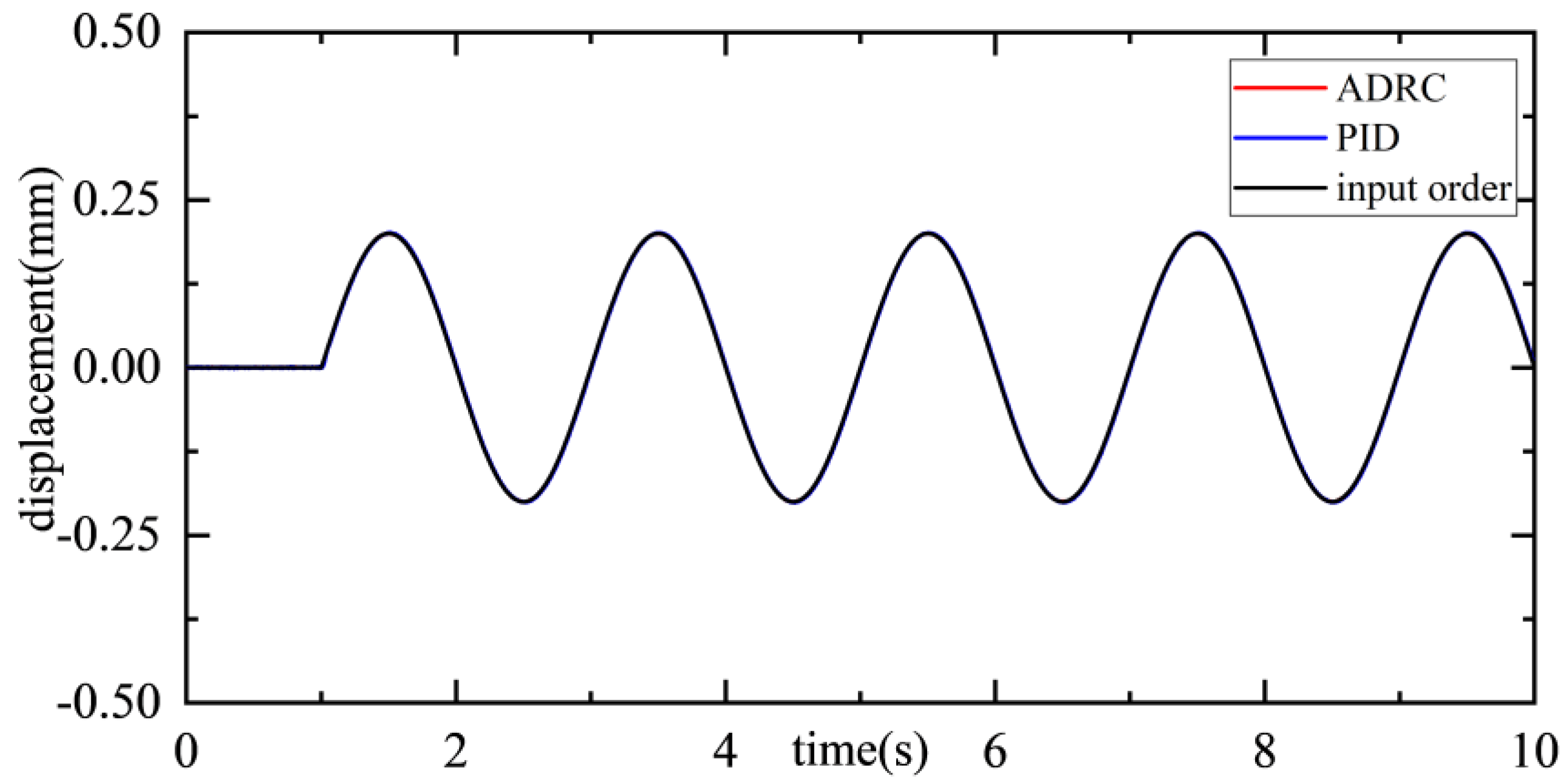
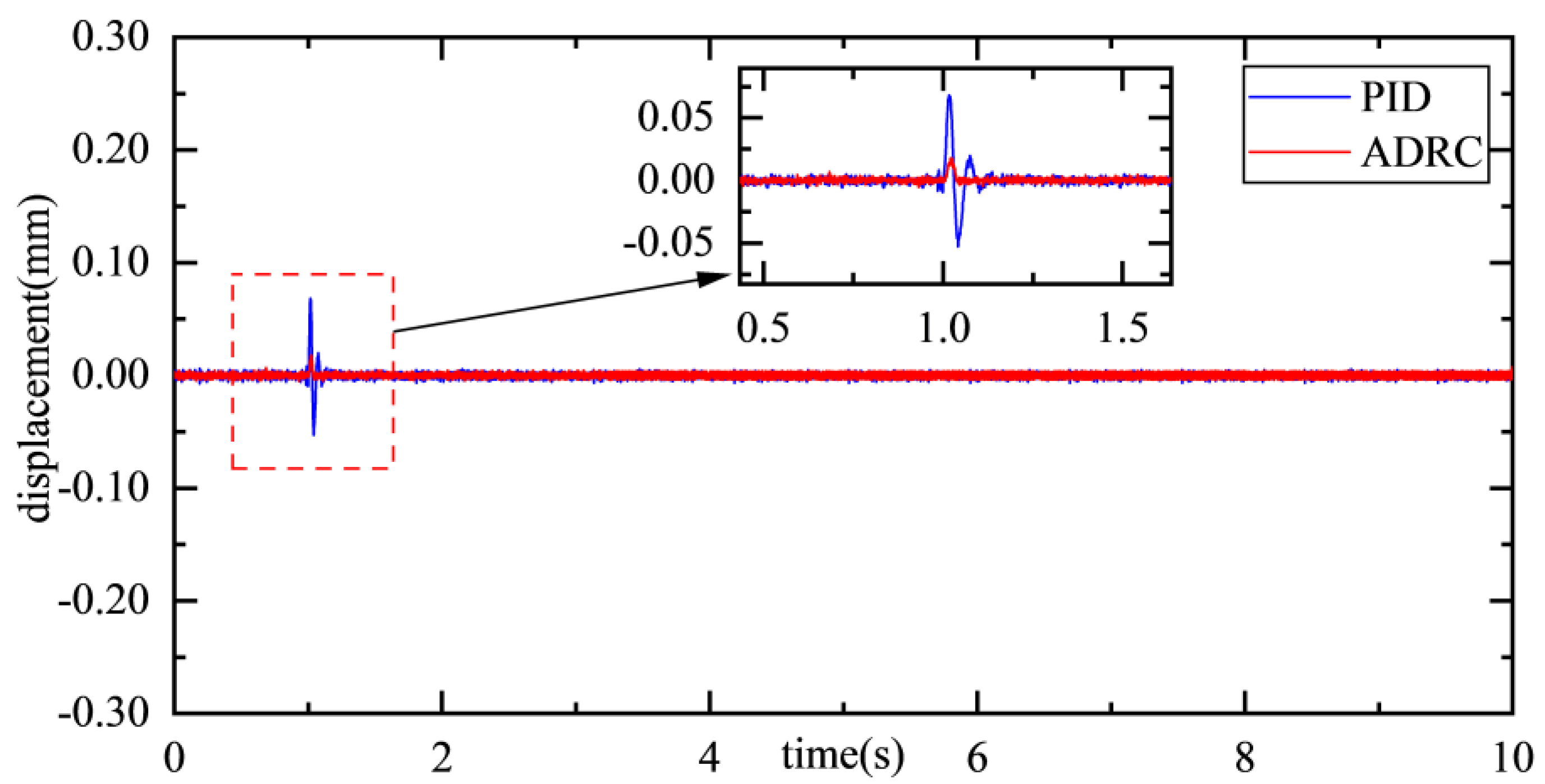
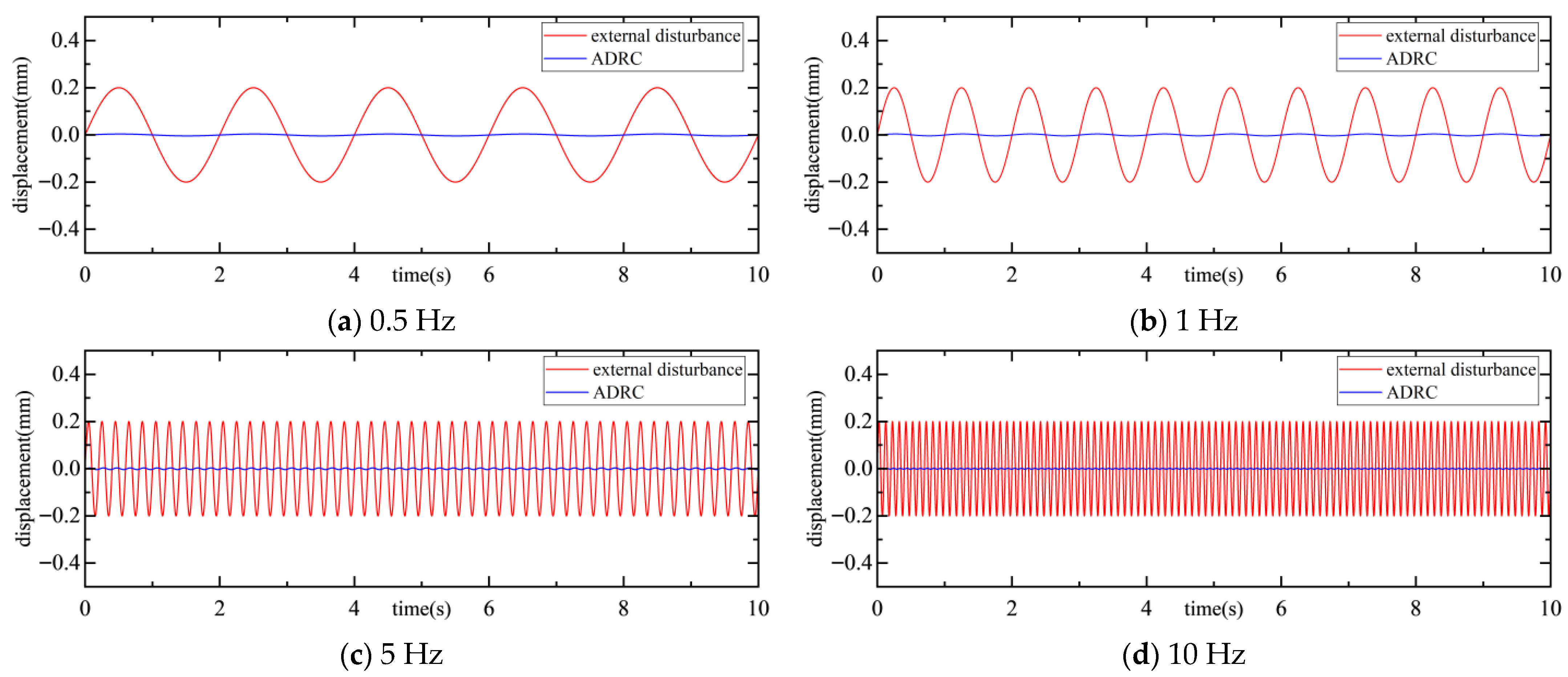

| Name | Principle | Isolation Frequency Bandwidth (Hz) | Vibration Transmissibility (dB) |
|---|---|---|---|
| HAVI | six-bar parallel mechanism/active or passive control | 10–250 | −15 |
| HT/UW | six-bar parallel mechanism/active or passive control | 10–80 | −20 |
| UQP | six-bar parallel mechanism/active or passive control | 5–400 | −40 (50–200 Hz) |
| STABLE/G-LIMIT | Magnetic levitation/active control | 0.01–100 | −34 |
| Parameter | Value |
|---|---|
| body dimension | 376 mm × 310 mm × 193 mm |
| total mass | 35.73 kg |
| isolation frequency bandwidth | 0.5 Hz–100 Hz |
| Material | Remanent Magnetism Br (T) | Coercive Force Hc (kA/m) | Magnetic Energy Product (BH)max (MGOe) | (°C) |
|---|---|---|---|---|
| NdFeB | 1.0–1.4 | 800–2000 | 35–55 | 200 |
| SmCo | 0.8–1.15 | 600–1500 | 20–32 | 350 |
| Ferrite | 0.2–0.4 | 150–300 | 3–5 | 250 |
| AlNiCo | 0.6–1.3 | 50–150 | 5–10 | 550 |
| Material | Saturation Induction Bs (T) | Coercive Force Hc (A/m) | Permeability | (°C) |
|---|---|---|---|---|
| 30Q130 | 2.0 | 10–20 | 1.5–1.8 | 750 |
| DT4C | 2.15 | 70–100 | 3–5 | 770 |
| 1J22 | 2.4 | 120–160 | 3–4 | 940 |
| 1J50 | 1.6 | 4–8 | 10–20 | 500 |
| 1J79 | 0.85 | 1–2 | 50–100 | 460 |
| 1J85 | 0.78 | 0.2–1 | 50–150 | 455 |
| Parameter | Value |
|---|---|
| outer diameter of permanent magnet ring | 57 mm |
| inner diameter of permanent magnet ring | 35 mm |
| circumferential of permanent magnet ring | 140 mm |
| thickness of permanent magnet ring | 8 mm |
| outer diameter of magnetic guide ring | 77 mm |
| inner diameter of magnetic guide ring | 35 mm |
| circumferential of magnetic guide ring | 160° |
| outer diameter of magnetic isolation ring | 69 mm |
| inner diameter of magnetic isolation ring | 57 mm |
| air gap radial distance | 20 mm |
| air gap axial distance | 6 mm |
| outer diameter of coil bracket | 67 mm |
| inner diameter of coil bracket | 18 mm |
| thickness of coil bracket | 5 mm |
| outer diameter of coil outer ring | 65 mm |
| inner diameter of coil outer ring | 57 mm |
| outer diameter of coil inner ring | 34 mm |
| inner diameter of coil inner ring | 24 mm |
| Parameter | Value |
|---|---|
| radius of permanent magnet | 36.5 mm |
| thickness of permanent magnet | 7 mm |
| thickness of air gap | 15 mm |
| length of carrier board | 214 mm |
| thickness of carrier board | 1 mm |
| length of isolation layer | 214 mm |
| thickness of isolation layer | 1 mm |
| thickness of yoke plate | 7 mm |
| thickness of shielding layer | 5 mm |
| Frequency (Hz) | Transmissibility (dB) |
|---|---|
| 0.5 | −34.07 |
| 1 | −34.06 |
| 5 | −35.11 |
| 10 | −38.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Wang, W.; Wang, L.; Yu, C.; Yang, Y. Design and Research of Lorentz Force Magnetic Levitation Vibration Isolation Platform. Aerospace 2025, 12, 965. https://doi.org/10.3390/aerospace12110965
Li B, Wang W, Wang L, Yu C, Yang Y. Design and Research of Lorentz Force Magnetic Levitation Vibration Isolation Platform. Aerospace. 2025; 12(11):965. https://doi.org/10.3390/aerospace12110965
Chicago/Turabian StyleLi, Baiqi, Weijie Wang, Lifen Wang, Chunmiao Yu, and Yanxia Yang. 2025. "Design and Research of Lorentz Force Magnetic Levitation Vibration Isolation Platform" Aerospace 12, no. 11: 965. https://doi.org/10.3390/aerospace12110965
APA StyleLi, B., Wang, W., Wang, L., Yu, C., & Yang, Y. (2025). Design and Research of Lorentz Force Magnetic Levitation Vibration Isolation Platform. Aerospace, 12(11), 965. https://doi.org/10.3390/aerospace12110965





