Non-Iterative Shrinkage-Thresholding-Reconstructed Compressive Acquisition Algorithm for High-Dynamic GNSS Signals

Abstract

Owing to the intrinsic sparsity of GNSS signals in the correlation domain, compressed sensing (CS) is attractive for the rapid acquisition of high-dynamic GNSS signals. However, the compressed measurement-associated noise folding inherently amplifies the pre-measurement noise, leading to an inevitable degradation of acquisition performance. In this paper, a novel CS-based GNSS signal acquisition algorithm is, for the first time, proposed with the efficient suppression of the amplified measurement noise and low computational complexities. The offline developed code phase and frequency bin-compressed matrices in the correlation domain are utilized to obtain a real-time observed matrix, from which the correlation matrix of the GNSS signal is rapidly reconstructed via a denoised back-projection and a non-iterative shrinkage-thresholding (NIST) operation. A detailed theoretical analysis and extensive numerical explorations are undertaken for the algorithm computational complexity, the achievable acquisition performance, and the algorithm performance robustness to various Doppler frequencies. It is shown that, compared with the classic orthogonal matching pursuit (OMP) reconstruction, the NIST reconstruction gives rise to a 3.3 dB improvement in detection sensitivity with a computational complexity increase of <10%. Moreover, the NIST-reconstructed CS acquisition algorithm outperforms the conventional CS acquisition algorithm with frequency serial search (FSS) in terms of both the acquisition performance and the computational complexity. In addition, a variation in the detection sensitivity is observed as low as 1.3 dB over a Doppler frequency range from 100 kHz to 200 kHz.

1. Introduction

As a crucial spatiotemporal infrastructure, the global navigation satellite system (GNSS) provides users with all-weather, full-time, and high-precision information services, including positioning, navigation, and timing (PNT), which plays an important role in the national economy and military defense [1,2,3,4,5]. However, due to the inherent restrictions imposed by the medium Earth orbit (MEO) and geostationary Earth orbit (GEO) satellite constellations, GNSS downlink signals exhibit low received power levels on the ground, significantly degrading the qualities of the PNT services especially in weak-signal environments. Moreover, the low variation in the GNSS satellite geometry prolongs the convergence time for precise point positioning (PPP), which fails to meet the application requirements demanding high real-time performance and precision [6,7]. To address the above-mentioned challenges, multiple navigation augmentation systems emerge, among which low Earth orbit (LEO) navigation augmentation has attracted extensive research interest [1,3,8]. In LEO navigation augmentation systems, GNSS receivers must process the navigation signals broadcast from the LEO satellites. Due to the high orbital velocities of LEO satellites, the reception of GNSS signals is characterized by high dynamics and significant Doppler frequency offsets. Simultaneously, the increasing code phase transition rate necessarily shortens the acquisition window duration and thus increases the acquisition complexities for GNSS signals.

Conventional acquisition algorithms for GNSS signals remain constrained under high-dynamic scenarios with significant Doppler frequency offsets [9,10]. Due to the sliding correlations undertaken across both the code phase and the Doppler frequency, the serial search algorithm entails the exhaustive search intervals [11,12]. Although the replacements of the time domain correlations with the fast Fourier transform (FFT)-based frequency domain multiplications significantly reduce the computational complexities, the parallel frequency or code phase search algorithms still need to perform the one-dimensional serial search, impeding the rapid acquisitions of high-dynamic GNSS signals. Via the segmented time domain correlations and the parallel FFT calculations, the partial match filter (PMF)-FFT algorithm achieves the joint two-dimensional search of both the code phase and Doppler frequency, attracting much interest for high-dynamic application scenarios. However, the scalabilities of the PMF-FFT algorithm are limited by the following two aspects: (1) the search of all code phases is mandatory; (2) both the sampling length of the pseudo-random noise (PRN) code and PMF length impose fundamental restrictions on the achievable acquisition range of Doppler frequency [13,14]. As a direct result, the computational complexity of the PMF-FFT algorithm rises with the increasing length of the PRN code and the extended Doppler frequency offsets.

In recent years, to reduce the number of correlators and minimize the hardware resource consumption, compressed sensing (CS) has garnered extensive investigations for high-dynamic GNSS signal acquisitions. By utilizing the inherent orthogonality of the PRN codes, a code phase matrix-based sparsifying dictionary is developed to enable the rapid compressive acquisitions, in combination with the serial search of Doppler frequency [15,16]. F. Zhou et al. establish an objective function defined by the Frobenius norm of the difference between the Gram matrix and an equiangular tight frame (ETF) matrix and then reduce the column correlations of the random Gaussian measurement matrix using the conjugate gradient method [17,18]. Under the premise of the exhaustive code phase search, K. Wang et al. develop a sparsifying dictionary using both the PMF coefficient matrices and the discrete Fourier transform (DFT) matrices for a compressive PMF-FFT algorithm [19]. Q. Zhang et al. substitute the Walsh–Hadamard matrix for the random measurement matrix and thus alleviate the storage resource consumption required by measurement matrix [20]. To overcome the computational bottleneck of the classic orthogonal matching pursuit (OMP) algorithm for rapidly reconstructing correlation vectors of GNSS signals, the sparsity is redefined by selecting the atom index corresponding to the peak magnitude of the inner products between the updated residual vector and the columns of measurement matrix [21]. Meanwhile, the augmented Lagrangian method (ALM) is also exploited to decompose the signal reconstruction-associated convex optimization problem into several relatively independent subproblems, which are solved iteratively via an alternating direction method of multipliers (ADMM) framework [22].

All the above-mentioned contributions to the CS-based GNSS signal acquisition algorithms primarily focus on the development of sparsifying dictionaries for GNSS signals, the optimizations of measurement matrices, and the reductions in computational complexities for the signal reconstructions. However, noise folding intrinsically occurs in compressed measurements [23,24], where the noise power within the received GNSS signals undergoes considerable amplifications. This severely degrades the reconstruction accuracy and then deteriorates the acquisition performances. In the field of image processing, the iterative shrinkage–thresholding algorithm (ISTA) has been proposed for the signal reconstruction with simultaneously denoising via the eliminations of the small-magnitude coefficients dominated by the noises [25,26,27]. While the fast ISTA (FISTA), incorporating a Nesterov-type momentum for calculating the iteration updates, gives rise to a quadratic improvement of the convergence performance in comparison with ISTA [28], its practical applications in the CS-based GNSS signal acquisitions remains hampered by the following two constraints: (1) the regularization parameter of FISTA lacks the theoretical self-adaptation, necessitating the case-specific tuning via suboptimal heuristics [28,29]; (2) the inherent iterative operations in FISTA inevitably escalate the computational complexities for signal reconstructions.

To suppress the amplified measurement noise and avoid the additional iterative operations associated with ISTA, a novel CS acquisition algorithm is proposed, for the first time, by making use of the non-iterative shrinkage–thresholding (NIST)-enabled reconstruction. This algorithm performs real-time compressed measurements of GNSS signals using the offline developed code phase and frequency bin-compressed matrices. Meanwhile the correlation matrix of the GNSS signal is rapidly reconstructed via a denoised back-projection of the observed matrix, a single-step gradient descent, and a shrinkage–thresholding operation. A detailed theoretical analysis and numerical simulations are undertaken for the algorithm computational complexity, the achievable acquisition performance, and the algorithm robustness to various Doppler frequencies. It is shown that, in comparison with the OMP reconstruction, the NIST reconstruction brings out a detection sensitivity improvement of 3.3 dB with a <10% rise in computational complexity. Furthermore, the NIST-reconstructed CS acquisition algorithm outperforms the conventional CS counterpart with frequency serial search (FSS) in terms of acquisition performance and computational complexity. In addition, a 1.3 dB variation in detection sensitivity is observed for the NIST-reconstructed CS acquisition algorithm over a Doppler frequency range from 100 kHz to 200 kHz.

2. Foundations of CS and ISTA

2.1. Fundamental Theory of CS

The implementation of CS consists of sparse signal representation, compressed measurements, and signal reconstruction. If a signal with a length of N is K-sparse, there exist only $K\left(K\ll N\right)$ non-zero entries while the remaining ones are approximately zeros. A specific measurement matrix can linearly project the high-dimensional sparse signal into a low-dimensional space without losing essential information. Simultaneously, the sparse signal is reconstructed with high probability from the low-dimensional measurements by solving an optimization problem. Therefore, the sampling rate of a sparse signal depends on its sparsity and information structure rather than the signal bandwidth, giving rise to a substantial reduction in the required sampling rate.

If an N-dimensional signal vector $\mathit{x}\in R^N$ exhibits sparsity, it can undergo a compressed measurement via an $M\times N$ measurement matrix $\mathit{\Phi }$ as

$$\mathit{y}=\mathit{\Phi }\mathit{x}$$

(1)

where $\mathit{y}\in R^M$ denotes the observed vector. $M$ is the measurement dimension while $M/N$ is defined as the compression ratio (CR) with $M\ll N$. In practical applications, the signal vector $\mathit{x}$ is generally not sparse and thus a unique mapping between the signal vector x and the observed vector $\mathit{y}$ needs to be established. In order to find such a mapping, the constraint of sparsity on the signal vector $\mathit{x}$ can be utilized [30,31] and the sparse representation of the signal vector $\mathit{x}$ is expressed as

$$\mathit{\theta }=\mathit{\Psi }\mathit{x}$$

(2)

where $\mathit{\Psi }\in R^{N\times N}$ is termed as the sparsifying dictionary. Meanwhile the vector $\mathit{\theta }\in R^N$ is said to be K-sparse in the sparsifying dictionary $\mathit{\Psi }$ if ${‖\mathit{\theta }‖}_0\le K$ with ${‖\cdot ‖}_0$ denoting the number of non-zero elements. With the sparse representation, the compressed measurement of the signal vector $\mathit{x}$ is undertaken as

$$\mathit{y}=\mathit{\Phi }\mathit{\theta }=\mathit{\Phi }\mathit{\Psi }\mathit{x}=\mathit{\Theta }\mathit{x}$$

(3)

where $\mathit{\Theta }$ stands for the sensing matrix which is defined as the product of measurement matrix $\mathit{\Phi }$ and sparsifying dictionary $\mathit{\Psi }$, i.e., $\mathit{\Theta }=\mathit{\Phi }\mathit{\Psi }$. The construction of the sensing matrix $\mathit{\Theta }$ combines the sparse representation and compressed measurement together and thus gives rise to a single linear projection for the compressed measurement of a non-sparse signal vector. When the pre-measurement or signal noise $\mathit{n}\in R^N$ is an additive zero mean Gaussian white noise with a covariance of ${\delta }^2{\mathit{I}}_M$ (here, ${\mathit{I}}_M$ is the identity matrix of relevant dimension), the observed vector $\mathit{y}$ becomes

$$\mathit{y}=\mathit{\Theta }(\mathit{x}+\mathit{n})=\mathit{\Theta }\mathit{x}+\mathit{\Theta }\mathit{n}=\mathit{\Theta }\mathit{x}+\mathit{w}$$

(4)

where $\mathit{w}\in R^N$ is referred to as the measurement noise whose covariance matrix is [23]

$$\begin{array}{cc}\hfill C& =E(\mathit{w}{\mathit{w}}^H)-E(\mathit{w})E({\mathit{w}}^H)\hfill \\ & =E(\mathit{\Theta }\mathit{n}{\mathit{n}}^H{\mathit{\Theta }}^H)\hfill \\ & ={\delta }^2\mathit{\Theta }{\mathit{\Theta }}^H\hfill \end{array}$$

(5)

with ${[\cdot ]}^H$ representing the conjugate transpose operator. Considering that the sensing matrix $\mathit{\Theta }$ is an ETF matrix, $\mathit{\Theta }{\mathit{\Theta }}^H$ equals to $(N/M){\mathit{I}}_M$. As shown in Equation (5), the pre-measurement noise power is amplified by a factor of $N/M$ in the compressed measurement. Since the signal power is kept unchanged, such noise amplification results in severe signal-to-noise ratio (SNR) degradations for the measurements and thus deteriorates the reconstruction performances.

The reconstruction of the sparse vector $\mathit{\theta }$ needs to solve an underdetermined system using both the observed vector $\mathit{y}$ and measurement matrix $\mathit{\Phi }$. Such a solution process of the underdetermined system can be recast as a minimum ℓ₀-norm problem, that is

$$\stackrel{\wedge }{\mathit{\theta }}=\arg \min {‖\mathit{\theta }‖}_{l_0}\hspace{1em}s.t. \mathit{y}=\mathit{\Phi }\mathit{\theta }$$

(6)

where ${‖\cdot ‖}_{l_0}$ denotes the l₀-norm and $\stackrel{\wedge }{\mathit{\theta }}$ is the reconstructed sparse vector. Given the existence of measurement noise $\mathit{w}$ within observed vector $\mathit{y}$, the reconstruction of the sparse vector θ is formulated as an approximation problem, i.e.,

$$\stackrel{\wedge }{\mathit{\theta }}=\arg \min {‖\mathit{\theta }‖}_{l_0}\hspace{1em}s.t. {‖\mathit{y}-\mathit{\Phi }\mathit{\theta }‖}_2^2\le \xi$$

(7)

where $\xi$ is a noise-dependent coefficient. Owing to the discrete and nonconvex natures of ℓ₀-norm, Equation (7) cannot be solved efficiently via the standard convex optimization methods. When the measurement matrix $\mathit{\Phi }$ satisfies the restricted isometry property (RIP), the solution process of the minimum ℓ₀-norm problem is equivalent to that of the minimum ℓ₁-norm problem [32], which is expressed as

$$\stackrel{\wedge }{\mathit{\theta }}=\arg \min {‖\mathit{\theta }‖}_{l_1}\hspace{1em}s.t. {‖\mathit{y}-\mathit{\Phi }\mathit{\theta }‖}_2^2\le \xi$$

(8)

where ${‖\cdot ‖}_{l_1}$ denotes the ℓ₁-norm. Therefore, the nonconvex optimization problem in Equation (7) is ultimately transformed into a convex optimization problem in Equation (8).

2.2. Basic Principles of ISTA

As a sparse reconstruction technique, ISTA is a convex optimization method for solving the linear inverse problems with ℓ₁-regularization. The main idea of ISTA lies in the iterative gradient updates followed by shrinkage–thresholding to achieve the sparse signal approximations. The objective function for solving the linear inverse problems using ISTA is expressed as

$$\widehat{\mathit{x}}=\arg \underset{x}{\min }\left({‖\mathit{\Phi }\mathit{x}-\mathit{y}‖}_2^2+\lambda {‖\mathit{x}‖}_1\right)$$

(9)

where $\lambda >0$ is the regularization parameter, determining the shrinkage threshold. In each iteration of ISTA, the estimate is updated via a shrinkage–thresholding operation [25]. The iterative procedure is formally represented as

$${\mathit{x}}_{k+1}=T_{\lambda \rho }({\mathit{x}}_k-\rho {\mathit{\Phi }}^{\mathrm{T}}(\mathit{\Phi }{\mathit{x}}_k-\mathit{y}))$$

(10)

$$T_{\lambda \rho }(\mathit{x})=sign(\mathit{x})\odot \mathrm{m}\mathrm{a}\mathrm{x}(\left|\mathit{x}\right|-\lambda \rho ,\mathbf{0})$$

(11)

where $T_{\lambda \rho }(\cdot )$ and ${[\cdot ]}^T$ stand for the soft thresholding operator and the transpose operator, respectively. $\rho$ and $k$ are the gradient descent step size and the iteration index. $sign(\cdot )$ is a sign function whilst $\odot$ denotes the Hadamard product. The shrinkage threshold in Equation (11) is determined by the product of the gradient descent step size $\rho$ and the regularization parameter $\lambda$. The iteration terminates when either the number of iterations reaches the preset maximum iteration index or the variation in the estimates $‖{\mathit{x}}_{k+1}-{\mathit{x}}_k‖$ falls below a predefined convergence tolerance. As evident from Equation (11), the shrinkage–thresholding operation sets the coefficients with absolute values below the shrinkage threshold of $\lambda \rho$ to zeros, thus enabling ISTA to effectively suppress the low-energy noises. To ensure the convergence of ISTA, the gradient descent step size $\rho$ is often chosen as the inverse of the Lipschitz constant, i.e., $\rho =1/{‖{\mathit{\Phi }}^T\mathit{\Phi }‖}_2$ [33]. Therefore, the number of ISTA iterations depends critically on both the initial point selection and the regularization parameter $\lambda$. However, in the absence of prior knowledge, ISTA typically initializes at the zero vector whilst the regularization parameter $\lambda$ needs to be manually adjusted through empirical methods, cross-validation, or noise-level-based heuristic rules. These inevitably lead to a slow global convergence rate and a high computational complexity. For example, the typical numbers of ISTA iterations are 800 and 100 for biomedical signal processing [27] and functional magnetic resonance imaging [34], respectively. Such numerous iterations impose a serious challenge for hardware implementations and result in significant processing latency, prohibiting the practical applications of ISTA in highly time-sensitive scenarios such as GNSS signal acquisition. In addition, if the initial point is selected next to a local optimum, ISTA tends to converge to the local optimum rather than the global optimum as the gradient direction exclusively provides the local information [35,36].

3. NIST-Reconstructed Compressive Acquisition Algorithm

3.1. Compressive Acquisition Model for GNSS Signals

A GNSS signal comprises a sinusoidal carrier wave, a PRN code, and a data message. On the satellite side, a GNSS transmitter combines the PRN code and the data message and then modulates them onto the sinusoidal carrier wave for forming the transmitted GNSS signal. At the GNSS receivers, the digital intermediate frequency (IF) signal is produced by the radio frequency (RF) front-end processing procedures including low-noise signal amplification, frequency down-conversion, anti-aliasing filtering, as well as analog-to-digital sampling. Such a digital IF signal is expressed as

$$s(n)=AD(n{T}_s-{\tau }_0)C(n{T}_s-{\tau }_0)e^{j[2\pi (f_{IF}+f_d)n{T}_s+{\phi }_0]}+v(n{T}_s)$$

(12)

where $C(n{T}_s-{\tau }_0)$ and $D(n{T}_s-{\tau }_0)$ are the PRN code and the data message, respectively, with $T_s$ being the sampling period and ${\tau }_0$ representing the code phase delay. Meanwhile $A$ is the carrier amplitude and $f_{IF}$ is the intermediate frequency. $f_d$ is the Doppler frequency generated by the GNSS receiver–satellite relative kinematics. ${\phi }_0$ is the initial phase of the sinusoidal carrier wave. $v(n{T}_s)$ denotes the additive zero mean Gaussian white noise with a variance of ${\delta }^2$. After the digitally controlled oscillator (DCO)-based carrier wiping, the baseband signal correlates with a local reference signal of $C_{LO}(n{T}_s-\tau )e^{-j(2\pi \Delta f_{d}n{T}_s)}$ with $\tau$ being the receiver-generated code phase. The signal acquisition is then achieved by the peak detection and threshold comparison, both of which are illustrated as

$$(\widehat{\tau },{\widehat{f}}_d)=\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}{\left|r\right|}^2$$

(13)

$$r(\tau ,f_d)=⟨C_{LO}(n{T}_s-\tau )e^{-j(2\pi \Delta f_{d}n{T}_s)}, s(n)⟩$$

(14)

where $⟨.,.⟩$ denotes the correlation inner product operation and $\Delta f_d$ is the Doppler search step size.

As shown in Figure 1, different from the conventional CS acquisition algorithms for GNSS signals, the cyclic shifts in the PRN code vector $\mathit{c}=[c_0,c_1,\cdots c_{L-1}]\in R^L$ output from a local PRN code generator are first employed to develop a code phase matrix $\mathit{G}$ as

$${\left.\mathit{G}=\left(\begin{array}{cccc}{c}_0& c_1& \cdots & c_{L-1}\\ c_1& c_2& \cdots & c_0\\ ⋮& ⋮& \ddots & ⋮\\ c_{L-1}& c_0& \cdots & c_{L-2}\end{array}\right.\right)}_{L\times L}$$

(15)

where $L$ is the sampling length of the PRN code. Simultaneously, the Doppler search range $[-F_S,F_S]$ is partitioned into N equal intervals to form the Doppler search vectors ${\mathit{f}}_m\in R^{1\times L}$, which are then synthesized into a frequency offset matrix $\mathit{F}$ of

$$\mathit{F}=\left[\begin{array}{c}{f}_1\\ f_2\\ ⋮\\ f_N\end{array}\right]={\left[\begin{array}{cccc}{e}^{j2\pi T_s{F}_s\left(-1+{\displaystyle \frac{2}{N}}\right)\times 1}& e^{j2\pi T_s{F}_s\left(-1+{\displaystyle \frac{2}{N}}\right)\times 2}& \cdots & e^{j2\pi T_s{F}_s\left(-1+{\displaystyle \frac{2}{N}}\right)\times L}\\ e^{j2\pi T_s{F}_s\left(-1+{\displaystyle \frac{4}{N}}\right)\times 1}& e^{j2\pi T_s{F}_s\left(-1+{\displaystyle \frac{4}{N}}\right)\times 2}& \cdots & e^{j2\pi T_s{F}_s\left(-1+{\displaystyle \frac{4}{N}}\right)\times L}\\ ⋮& ⋮& \ddots & ⋮\\ e^{j2\pi T_s{F}_s\left(-1+{\displaystyle \frac{2N}{N}}\right)\times 1}& e^{j2\pi T_s{F}_s\left(-1+{\displaystyle \frac{2N}{N}}\right)\times 2}& \cdots & e^{j2\pi T_s{F}_s\left(-1+{\displaystyle \frac{2N}{N}}\right)\times L}\end{array}\right]}_{N\times L}$$

(16)

$${\mathit{f}}_m=[e^{j2\pi T_s{F}_s(-1+{\displaystyle \frac{2m}{N}})\times 1},e^{j2\pi T_s{F}_s(-1+{\displaystyle \frac{2m}{N}})\times 2},\cdots e^{j2\pi T_s{F}_s(-1+{\displaystyle \frac{2m}{N}})\times L}]$$

(17)

where $m$ is the Doppler search index with $m=1,2,\dots ,N$. After that, by using code phase matrix $\mathit{G}$, frequency offset matrix $\mathit{F}$, and GNSS signal matrix $\mathit{S}\in R^{L\times L}$, the correlation inner products indicated in Equation (13) are arranged into a correlation matrix $\mathit{X}\in R^{N\times L}$ as

$$\mathit{X}=\mathit{F}(\mathit{G}\odot \mathit{S})$$

(18)

where each column of the GNSS signal matrix $\mathit{S}$ is formed from the received GNSS signal vector $\mathit{r}\in R^L$, i.e., $\mathit{S}=[\mathit{r},\mathit{r},\dots ,\mathit{r}]$ with $\mathit{r}={[s(0),s(1),\dots ,s(L-1)]}^T$. Due to the excellent auto-correlation and cross-correlation characteristics associated with the PRN codes, the column vectors of the correlation matrix $\mathit{X}$ exhibit sparsity when the receiver-generated code phase is aligned to that of the received GNSS signal. Thus, compressed measurements can be performed separately on each column vector of the correlation matrix $\mathit{X}$ using the measurement matrix $\mathit{\Phi }$. Finally, an observed matrix $\mathit{Y}\in R^{M\times L}$ is obtained by

$$\mathit{Y}=\mathit{\Phi }\mathit{X}=\mathit{\Phi }\mathit{F}(\mathit{G}\odot \mathit{S})={\mathit{F}}_{cp}\mathit{H}$$

(19)

where ${\mathit{F}}_{cp}=\mathit{\Phi }\mathit{F}$ and $\mathit{H}=\mathit{G}\odot \mathit{S}$ are referred to as the frequency bin-compressed matrix and the code phase mask matrix, respectively.

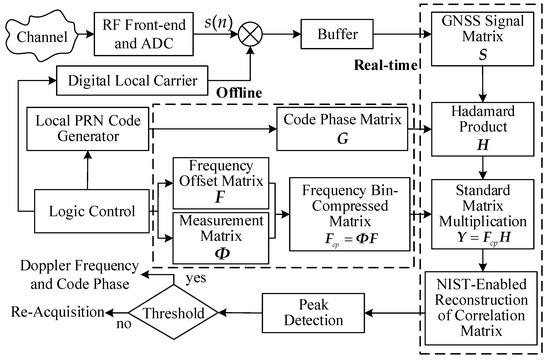
Figure 1. Schematic diagram of CS acquisition algorithm based on NIST-enabled reconstruction.

Since both the code phase matrix $\mathit{G}$ and the frequency bin-compressed matrix ${\mathit{F}}_{cp}$ can be developed offline and prestored in the registers of GNSS receivers, the real-time compressive acquisition of GNSS signals involves the following four procedures: (1) calculating the column-wise Hadamard products between the GNSS signal matrix $\mathit{S}$ and the code phase matrix $\mathit{G}$; (2) performing the standard matrix multiplication between the frequency bin-compressed matrix ${\mathit{F}}_{cp}$ and the code phase mask matrix $\mathit{H}$; (3) employing the measurement matrix $\mathit{\Phi }$ and a reconstruction algorithm to reconstruct the correlation matrix by columns; (4) estimating both the code phase and Doppler frequency in the reconstructed correlation matrix via the peak detection and threshold comparison.

3.2. NIST-Enabled Reconstruction of Correlation Matrix

In contrast to the requirements of ISTA employed in traditional CS applications, the GNSS signal acquisition solely needs to locate the peak position in the correlation matrix $\mathit{X}$ of Equation (18), rather than specifically quantify the actual peak magnitude. As the Gram matrix of the measurement matrix $\mathit{\Phi }$ is approximately an identity matrix under the relaxed ETF constraints [15,37], i.e., ${\mathit{I}}_M\approx {\mathit{\Phi }}^T\mathit{\Phi }$, the identification of the peak in the correlation matrix $\mathit{X}$ can be transformed into the identification of the peak in the back-projection of the observed matrix $\mathit{Y}$. As a result, to avoid both the local convergence issue and the high computational complexity associated with ISTA, an initial correlation matrix is determined by a denoised back-projection of the observed matrix $\mathit{Y}$ whilst a single-step gradient descent along the peak direction of the initial correlation matrix is directly adopted to rapidly reconstruct the correlation matrix $\mathit{X}$. The back-projection of the observed matrix Y is firstly obtained by making use of the measurement matrix $\mathit{\Phi }$, i.e.,

$${\mathit{X}}_{BP}={\mathit{\Phi }}^T\mathit{Y}={\mathit{\Phi }}^T\mathit{\Phi }\mathit{X}$$

(20)

where ${\mathit{X}}_{BP}$ is referred to as the back-projected matrix. After introducing a regularization tuning coefficient (RTC) $\beta$, the regularization parameter $\lambda$ in Equation (9) is determined in combination with the peak magnitude of the back-projected matrix ${\mathit{X}}_{BP}$ as

$$\lambda =\beta \max \left\{\left|x_{BP}^{ij}\right|\right\}$$

(21)

where $x_{BP}^{ij}$ denotes the element at the i-th row and j-th column of the back-projected matrix ${\mathit{X}}_{BP}$. Then, the back-projected matrix ${\mathit{X}}_{BP}$ is subjected to a shrinkage–thresholding operation to yield an initial correlation matrix ${\mathit{X}}_{Init}$, whose elements are given as

$$x_{Init}^{ij}=T_{\lambda }(x_{BP}^{ij})=sign(x_{BP}^{ij})\cdot \mathrm{m}\mathrm{a}\mathrm{x}(\left|x_{BP}^{ij}\right|-\lambda ,0)$$

(22)

where ${\mathit{x}}_{Init}^{ij}$ represents the element at the i-th row and j-th column of the initial correlation matrix ${\mathit{X}}_{Init}$. As the small-magnitude coefficients are removed by the shrinkage–thresholding operation in the initial correlation matrix ${\mathit{X}}_{Init}$, the effective mitigations of the undesirable noise interferences are achieved for the output of the gradient descent. Finally, along the primary peak direction of the initial correlation matrix ${\mathit{X}}_{Init}$, a single-step gradient descent, followed by a shrinkage–thresholding operation and K-sparsification, is performed for each column vector of the initial correlation matrix ${\mathit{X}}_{Init}$ to obtain the reconstructed correlation matrix $\widehat{\mathit{X}}$, i.e.,

$${\mathit{x}}^{*,j}={\mathit{x}}_{init}^{*,j}-\rho ({\mathit{\Phi }}^T(\mathit{\Phi }{\mathit{x}}_{init}^{*,j}-{\mathit{y}}^{*,j}))$$

(23)

$${\widehat{\mathit{x}}}^{*,j}=T_{\lambda \rho }({\mathit{x}}^{*,j})=sign({\mathit{x}}^{*,j})\odot \mathrm{m}\mathrm{a}\mathrm{x}(\left|{\mathit{x}}^{*,j}\right|-\lambda \rho ,\mathbf{0})$$

(24)

where ${\mathit{x}}_{init}^{*,j}$ and ${\widehat{\mathit{x}}}^{*,j}$, with $1\le j\le L$, are the j-th column vectors of the initial correlation matrix ${\mathit{X}}_{Init}$ and the reconstructed correlation matrix $\widehat{\mathit{X}}$, respectively. Here, the gradient descent along the primary peak direction of the initial correlation matrix ${\mathit{X}}_{Init}$ brings about a greater reduction in the data fidelity term, corresponding to the first term on the right side of Equation (9), and thus improves the reconstruction performances. Moreover, since a unique PRN code is assigned to each satellite, a single correlation peak is guaranteed to emerge in ${\widehat{\mathit{x}}}^{*,j}$ when the code phase of the received GNSS signal and the receiver-generated code phase are aligned to each other. This leads to the value of $K$ being set to one for the K-sparsification operations.

The RTC plays a significant role in the achievable acquisition performances of the NIST-reconstructed compressive acquisition algorithm. Equations (21) and (22) show that when the RTC is equal to zero, the value of $\lambda$ is zero and thus the shrinkage–thresholding operation in Equation (22) is not able to suppress the low-energy noises. Simultaneously, when the RTC is set to one, the value of $\lambda$ is equal to the peak magnitude of the back-projected matrix ${\mathit{X}}_{BP}$. This causes the initial correlation matrix ${\mathit{X}}_{Init}$ to become a zero matrix after the shrinkage–thresholding operation. As such, the RTC is confined to a range of (0,1). Meanwhile, the noise suppression capability, resulting from the shrinkage–thresholding operation, enhances with the increasing RTC. However, since the column coherence coefficient of the measurement matrix $\mathit{\Phi }$ is not absolutely equal to zero, the back-projection illustrated in Equation (20) gives rise to an additional coherent interference in the back-projected matrix ${\mathit{X}}_{BP}$ [38]. Under the low-SNR conditions, such an additional coherent interference causes the noise energy peak in the back-projected matrix ${\mathit{X}}_{BP}$ to exceed the correlation peak. In this scenario, the shrinkage threshold is determined by the noise energy peak, which suppresses or even nullifies the correlation peak and consequently generates a false alarm. Therefore, the false alarm probability rises with the increasing RTC. From the preceding analysis, it is evident that the RTC needs to appropriately choose according to the required specifications in practical applications. The detailed procedures of the NIST-reconstructed compressive acquisition algorithm for GNSS signals are manifested in Algorithm 1.

Algorithm 1. Detailed procedures of NIST-reconstructed compressive acquisition algorithm

Input:  Received GNSS signal vector $\mathit{r}={[s(0),s(1),\dots ,s(L-1)]}^T$, Code phase matrix $\mathit{G}$, Frequency bin-compressed matrix ${\mathit{F}}_{cp}$, Measurement matrix $\mathit{\Phi }$, Lipschitz constant, Regularized tuning coefficient $\beta$ Output:  Estimated Doppler frequency ${\widehat{f}}_d$, Estimated code phase $\widehat{\tau }$

Step 1: Construct the GNSS signal matrix $\mathit{S}$ by column-wise stacking of the received GNSS signal vector $\mathit{r}$; Step 2: Calculate the Hadamard product between the GNSS signal matrix $\mathit{S}$ and the code phase matrix $\mathit{G}$; Step 3: Conduct the standard matrix multiplication between frequency bin-compressed matrix ${\mathit{F}}_{cp}$ and the code phase mask matrix $\mathit{H}$ according to Equation (19); Step 4: Back-project the observed matrix $\mathit{Y}$ to obtain the back-projected matrix ${\mathit{X}}_{BP}$ as shown in Equation (20); Step 5: Determine the regularization parameter $\lambda$ by scaling the peak magnitude of the back-projected matrix ${\mathit{X}}_{BP}$ with a regularization tuning coefficient $\beta$; Step 6: Carry out the shrinkage–thresholding operation on the back-projected matrix ${\mathit{X}}_{BP}$ to obtain the initial correlation matrix ${\mathit{X}}_{Init}$ as expressed in Equation (22); Step 7: Perform a single-step gradient descent along the primary peak direction of the initial correlation matrix ${\mathit{X}}_{Init}$, followed by a shrinkage–thresholding operation and then the K-sparsification, for each column vector of the initial correlation matrix ${\mathit{X}}_{Init}$ to yield the reconstructed correlation matrix $\widehat{\mathit{X}}$; Step 8: Detect the peak of the reconstructed correlation matrix $\widehat{\mathit{X}}$.

3.3. Computational Complexity Analysis

The computational complexity of the acquisition algorithm for GNSS signals is primarily determined by the number of multiplication operations. Therefore, this subsection quantifies the computational complexity of the acquisition algorithm by counting the number of the involved multiplication operations. As derived from Figure 1 and Algorithm 1, the computational complexity of the NIST-reconstructed CS acquisition algorithm comprises three parts: the calculation of the Hadamard product between the GNSS signal matrix and the code phase matrix, the generation of the observed matrix, and the reconstruction of correlation matrix via NIST. When the sampling length of the PRN code and the number of Doppler bins are $L$ and $N$, respectively, and the CR equals $M/N$, the numbers of multiplication operations required for the first two parts are $L^2$ and $M{L}^2$, respectively. Meanwhile, the NIST-enabled reconstruction of the correlation matrix contains three procedures involving multiplications, including the back-projection of the observed matrix, the shrinkage–thresholding operation, and the gradient calculation. The corresponding numbers of multiplication operations are $MNL$, $2NL$, and $MNL$, respectively. In addition, the Lipschitz constant can be prestored in registers of GNSS receivers via offline calculations with a negligible computational overhead. As such, the computational complexity of the NIST-reconstructed CS acquisition algorithm is

$$M_1=O(2MNL+2NL+M{L}^2+L^2)$$

(25)

For the classic OMP-enabled reconstruction, when both Doppler frequency and code phase are aligned, the computational complexities associated with the residual update and the calculations of the stopping criteria for the iteration cycle can be ignored [15]. As a result, the multiplication operations of the OMP-enabled reconstruction merely stem from the atomic selections and the calculations of the least-squares solutions, whose numbers of multiplication operations are $MNL$ and $ML$, respectively. The computational complexity of the OMP-reconstructed CS acquisition algorithm, therefore, is

$$M_2=O(MNL+ML+M{L}^2+L^2)$$

(26)

As FISTA achieves fast convergence without compromising the reconstruction performances in comparison with ISTA [28], the FISTA-enabled reconstruction of the correlation matrix is considered here. The multiplication operations are mainly involved in the shrinkage–thresholding operation and the gradient calculation with the corresponding numbers being $MNL$ and $NL$, respectively. Accordingly, if the number of iterations is defined as $I$, the computational complexity of the FISTA-reconstructed CS acquisition algorithm is

$$M_3=O(I(MNL+NL)+M{L}^2+L^2)$$

(27)

The number of multiplication operations of the conventional CS acquisition algorithm with FSS is dominated by the correlation operations and the reconstructions of correlation vectors. When OMP reconstruction is employed, the number of multiplication operations demanded for searching a single Doppler bin is $BL+B$ with $B$ being the measurement length. Then, the computational complexity of the conventional CS acquisition algorithm is

$$M_4=O(2BNL+BN)$$

(28)

Since the computational complexity plays a primary role in the hardware implementations of the acquisition algorithms, a comparison of computational complexity is widely adopted to evaluate the hardware resource consumption for various acquisition algorithms on a specific hardware platform [2,4,5,16,17,18,19,20,22]. For the purpose of clear comparisons, Table 1 lists the computational complexities of various CS acquisition algorithms for GNSS signals. Meanwhile the comparisons of operating characteristics are also illustrated in Table 2.

Table 1. Computational complexities of various CS acquisition algorithms.

Acquisition Algorithm	Computational Complexity
NIST-Recons. CS	$O(2(MNL+NL)+M{L}^2+L^2)$
OMP-Recons. CS	$O(MNL+ML+M{L}^2+L^2)$
FISTA-Recons. CS	$O(I(MNL+NL)+M{L}^2+L^2)$
Conventional CS w/FSS	$O(2BNL+BN)$

Table 2. Comparisons of operating characteristics for various CS acquisition algorithms.

Characteristics	NIST-Recons. CS	OMP-Recons. CS	FISTA-Recons. CS	Conventional CS
Operation Mechanism	Non-Iterative	Iterative	Iterative	Iterative
Memory Requirement	Moderate	Low	High	Moderate
Parameter Tuning	Simple	Simple	Complex	Simple

Given that FISTA still needs iterations to promote the solution sparsity and seek the global optimum, the minimum number of iterations is typically equal to five [34]. As such, it is readily observed from Table 1 that the computational complexity of the NIST-reconstructed CS algorithm is lower than that of the FISTA-reconstructed CS algorithm. However, due to the additional multiplication operations originating from the shrinkage–thresholding operation, a slight increase in the computational complexity of the NIST-reconstructed CS algorithm occurs, in comparison with the OMP-reconstructed CS algorithm. As the sparse representations of the NIST-reconstructed CS algorithm fundamentally differ from the conventional CS algorithm with FSS, a direct comparison of their computational complexities is not obvious in Table 1. The relationship between computational complexity and the number of Doppler bins for various CS algorithms is illustrated in Figure 2, where the sampling length of the PRN code and CR are set to 2046 and 1/2, respectively. As shown in Figure 2, the computational complexity of the NIST-reconstructed CS algorithm is obviously lower than those of the FISTA-reconstructed CS algorithm and the conventional CS algorithm with FSS. When the number of Doppler bins is equal to 256, the computational complexity of the NIST-reconstructed CS algorithm is reduced by 43% and 31%, respectively, compared with the FISTA-reconstructed CS algorithm and the conventional CS algorithm with FSS. However, compared with the OMP-reconstructed CS algorithm, the computational complexity of the proposed algorithm slightly increases by <10%.

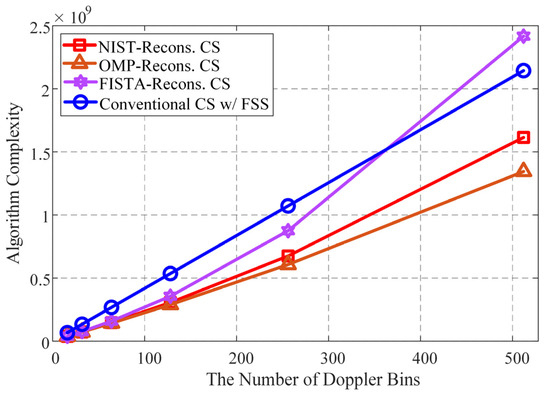
Figure 2. Comparisons of computational complexities for various CS acquisition algorithms.

4. Simulations and Result Discussions

To comprehensively evaluate and exhibit the performance characteristics of the NIST-reconstructed CS algorithm, the L1 C/A code signals, in strict compliance with the interface specification of IS-GPS-200, are adopted to undertake extensive simulation explorations of the acquisition performances for the spread-spectrum signals with a binary phase shift keying (BPSK) modulation. Such a simulation approach has been widely employed for testing the performance of the GNSS signal acquisition algorithms [15,16,17,21,39,40,41]. In the simulations, all the considered Doppler frequencies conform to the JPL Laboratory’s criteria for high-dynamic scenarios [40], with a correlation time of 1 ms. Simultaneously, for comparisons, the acquisition performances are also measured for the OMP- and FISTA-reconstructed CS algorithms, the conventional CS algorithm with FSS, the serial search algorithm, as well as the PMF-FFT algorithm. To ensure the accurate comparisons of the acquisition performances, a random Gaussian matrix is chosen as the measurement matrix for all CS acquisition algorithms whilst the classic decision strategy using the primary-to-secondary peak ratio (PSR) is adopted [40,41]. When calculating the detection probabilities for various acquisition algorithms, 1000 Monte Carlo simulations are performed for each individual SNR and the detection probability is defined as the ratio of the number of successful acquisitions, with both the aligned code phases and the accurately estimated Doppler frequency, to the total number of Monte Carlo simulations.

4.1. Effects of RTC on NIST-Reconstructed CS Acquisition Algorithm

For investigating the effects of RTC on the acquisition performances of the NIST-reconstructed CS algorithm, Figure 3 shows the measured detection probabilities as a function of SNR for different RTCs. In obtaining Figure 3, the CR and Doppler frequency are set to 1/2 and 180 kHz, respectively, whilst the RTC ranges from 0.1 to 0.9 with a step size of 0.2. The decision thresholds of PSR are determined by a false alarm probability of 10⁻⁴. As can be seen from Figure 3, for different RTCs, the detection probabilities exhibit a typical “S”-shaped increase with an SNR rise and increases with the increasing RTCs. When RTCs are equal to 0.1, 0.5, and 0.9, the SNR thresholds at a detection probability of 90% are −23 dB, −24.5 dB, and −26.2 dB, respectively. This is mainly attributed to the enhanced noise suppression capabilities associated with the increasing RTCs. However, as analyzed in Section 3.2, the back-projection of the observed matrix inevitably introduces an additional coherent interference due to the relaxed ETF constraints. Therefore, an increase in RTC leads to a higher false alarm probability, as shown in Figure 4, where the false alarm probabilities versus RTC are illustrated for three representative SNRs. In obtaining Figure 4, each individual false alarm probability is measured via 10⁶ Monte Carlo simulations whilst the false alarm probability is given by the ratio of the number of false acquisitions, with a detected peak accompanied by the misaligned code phases and/or incorrectly estimated Doppler frequency, to the total number of Monte Carlo simulations. As depicted in Figure 4, the RTC gives rise to almost the same developing trends of the false alarm probability for three SNRs, indicating that the effects of RTC on the false alarm probability of the NIST-reconstructed CS algorithm are independent of the received SNR. For a typical SNR of −27 dB, an increase in RTC from 0.3 to 0.9 causes the false alarm probability to rise from 1 × 10⁻⁵ to 4 × 10⁻². Moreover, for a fixed RTC, the false alarm probability increases with the decreasing SNR. This is due to the fact that a lower SNR results in an increased probability of the noise energy peak being misinterpreted as the shrinkage threshold for the shrinkage–thresholding operations. In addition, it is interesting to find that, when RTCs are larger than 0.3, the false alarm probability experiences a nearly linear increase with the growth of the RTC, regardless of the SNR. When the RTC increases from 0.4 to 0.9, the false alarm probability for an SNR of −28 dB (−26 dB) increases from 5 × 10⁻⁴ (4 × 10⁻⁵) to 9 × 10⁻² (1 × 10⁻²). Such a uniform characteristic of the RTC-associated variation in the false alarm probability is desirable for relaxing the design requirements of the GNSS receivers [42].

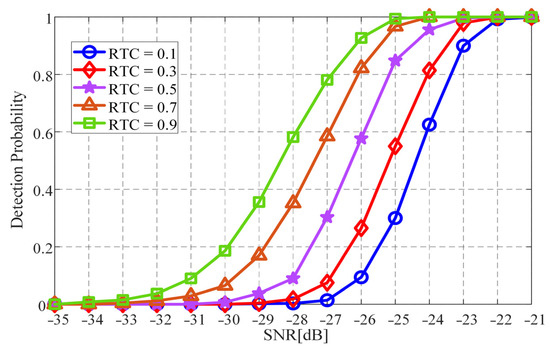
Figure 3. Detection probability versus SNR for various RTCs.

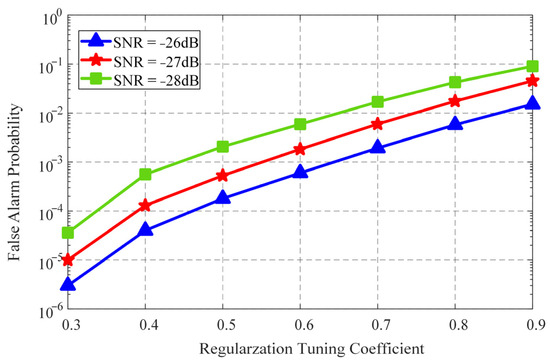
Figure 4. False alarm probability versus RTC for representative SNRs.

To further exhibit the effect mechanism of RTC on the occurrence of false alarms, the relationship between the normalized peak value in the reconstructed correlation matrix and the code phase is illustrated in Figure 5, where the testing code phase delay is set to 100 and the noise energy peak is misinterpreted as the shrinkage threshold for an SNR of −28 dB. As observed from Figure 5, the PSR increases with the increasing RTC, due to the intensified small-value suppression of the shrinkage–thresholding operation with a larger RTC. When the RTC increases from 0.1 to 0.5, the PSR rises from 1 to 1.2. In particular, for a RTC as high as 0.9, the PSR can reach up to 2.8. Such a high PSR leads to a false alarm for a typically adopted decision threshold of PSR [39,43]. Therefore, the RTC can be appropriately selected according to the specific requirements in terms of the detection probability and the false alarm probability. For practical applications that demand high-precision PNT services, including the safe operation and control of high-speed rails, intelligent autonomous control, and crustal deformation monitoring, this demand can be met by increasing the RTC to achieve more precise GNSS signal acquisition. On the contrary, the continuity of PNT services can be enhanced by reducing the RTC for meeting the requirements of GNSS receiver users in practical applications such as smart factories [44]. To balance the acquisition performances of the NIST-reconstructed CS algorithm and facilitate the comparisons among different acquisition algorithms, the RTC is set to 0.5 in the following simulation measurements without losing generality.

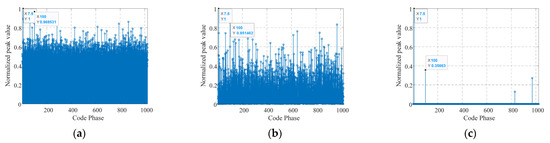
Figure 5. Normalized peak value versus the code phase for various RTCs: (a) RTC = 0.1, PSR = 1; (b) RTC = 0.5, PSR = 1.2; (c) RTC = 0.9, PSR = 2.8.

4.2. Acquisition Performance Evaluations and Comparisons

For a CR of 1/2, Figure 6 depicts the detection probabilities of the CS acquisition algorithms versus SNR for various reconstruction schemes. In obtaining Figure 6, the testing Doppler frequency is 180 kHz and the decision threshold of PSR is set for a false alarm probability of 10⁻⁴. For measuring the detection performances of the FISTA-reconstructed CS algorithm, the number of iterations is chosen as 5, 10, 20, or 30, with the regularization parameter set to the empirical values of 500 and 1500 [28,45]. These parameter selections are subject to comprehensive considerations, in terms of reconstruction performance, the capability of noise suppression, the real-time requirements of GNSS signal acquisition, as well as the effective assessment of the iteration-dependent acquisition performance [28,34,45]. When both Doppler frequency and code phase are aligned, there exists a single correlation peak for a GNSS signal, leading to a sparsity of one in the simulations of the OMP-reconstructed CS algorithm [21]. As can be seen from Figure 6, compared with the OMP-reconstructed CS algorithm, the effective noise suppressions significantly enhance the detection performances of the NIST-reconstructed CS algorithm and thus the SNR threshold of the NIST-reconstructed CS algorithm is reduced by 3.3 dB at a detection probability of 90%. Such a 3.3 dB improvement of detection sensitivity is robust enough to guarantee the successful acquisition of LEO satellite broadcast high-dynamic GNSS signals obstructed by the plywood wall with a typical attenuation of 2.3 dB [46]. For a regularization parameter of 500, the detection performances of the FISTA-reconstructed CS algorithm improve with an increasing number of iterations. However, for the iteration counts of ≥10, the FISTA-reconstructed CS algorithm becomes trapped in a local optimum, leading to a plateau of its detection performances even with the additional iterations. When the regularization parameter of FISTA is changed to 1500, a further improvement of the detection performances after 10 iterations is observed, in comparison with the case involving a regularization parameter of 500. This is contributed to the fact that, similar to ISTA, the reconstruction performance of FISTA is also strongly dependent on the choice of the regularization parameter [28]. It is evident that a 1.9 dB difference in the SNR threshold is still maintained between the NIST- and FISTA-reconstructed CS algorithms even after 10 iterations of FISTA. In addition, the detection performances of the NIST-reconstructed CS algorithm are further measured with the additional operations (AOs) of a gradient descent and the shrinkage–thresholding, expressed as Equations (23) and (24). It can be seen from Figure 6 that the detection performances of the NIST-reconstructed CS algorithm improve with the growth of the number of AOs at the expense of increased computational complexities. This effectively validates the correct selection of gradient direction in the NIST-reconstructed CS algorithm.

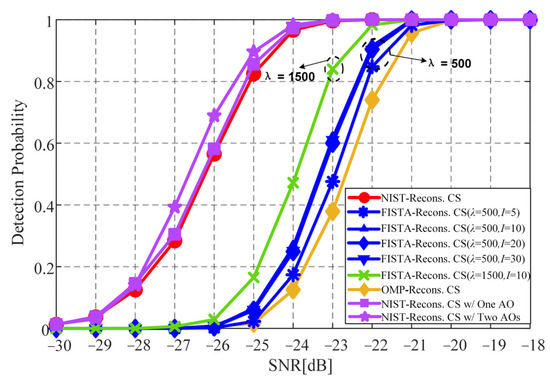
Figure 6. Detection performances of various CS acquisition algorithms.

The detection performances of the NIST-reconstructed CS algorithm are further evaluated for various CRs. For the above-mentioned three CS algorithms and the conventional CS algorithm with FSS, Table 3 lists the SNR thresholds of different CRs at a detection probability of 90%. Here, for the FISTA-reconstructed CS algorithm, the regularization parameter and the number of iterations are set to 500 and 20, respectively. The SNR penalty, defined as the SNR threshold difference between the serial search algorithm and the CS acquisition algorithm considered, is plotted as a function of CR in Figure 7, where the Doppler frequency is set to 180 kHz. It is evident that the SNR penalties of all the four CS algorithms increase with the decreasing CR. This is because the intensified compressed measurements inevitably degrade the reconstruction performances. However, compared with the other three CS algorithms, the NIST-reconstructed CS algorithm experiences the lowest SNR penalties for all the CRs due to its effective noise suppression. For a CR of 1/2, the SNR penalty of the NIST-reconstructed CS algorithm is 3.5 dB, 2.1 dB, and 1.4 dB lower than those of its OMP- and FISTA-counterparts as well as the conventional CS algorithm with FSS, respectively. The acquisition result plots of three CS algorithms are shown in Figure 8, with an SNR of −25 dB and a CR of 1/2. As can be seen from Figure 8, the OMP-reconstructed CS algorithm fails to acquire the GNSS signal whilst successful signal acquisitions are observed for the other two CS algorithms. However, in comparison with the NIST-reconstructed CS algorithm, the FISTA-reconstructed CS algorithm exhibits a reduced PSR.

Table 3. SNR thresholds of CS acquisition algorithms at a detection probability of 90%.

Acquisition Algorithms	CR = 7/8	CR = 6/8	CR = 5/8	CR = 4/8	CR = 3/8	CR = 2/8
NIST-Recons. CS	−26.9 dB	−26 dB	−25.5 dB	−24.4 dB	−23.4 dB	−21.3 dB
OMP-Recons. CS	−23.3 dB	−23 dB	−22 dB	−20.9 dB	−20.2 dB	−17.8 dB
FISTA-Recons. CS	−24.3 dB	−24.2 dB	−23.3 dB	−22.3 dB	−21.8 dB	−19.5 dB
Conventional CS w/FSS	−24.5 dB	−24.2 dB	−23.7 dB	−23 dB	−22.4 dB	−20.5 dB

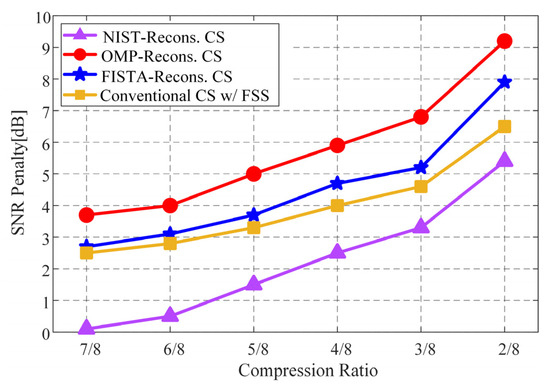
Figure 7. SNR penalty versus CR (relative to the serial search algorithm).

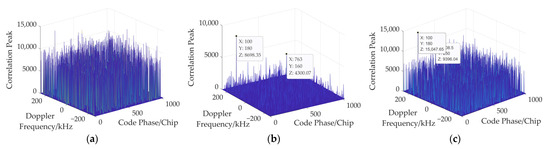
Figure 8. Acquisition results of different CS algorithms: (a) OMP reconstruction; (b) NIST reconstruction; (c) FISTA reconstruction.

Figure 9 presents the comparisons of detection performances between the NIST-reconstructed CS algorithm and the conventional acquisition algorithms, including the serial search algorithm, the conventional CS algorithm with FSS, and the PMF-FFT algorithm. As the main lobe width of the amplitude response of the PMF-FFT output only depends on the PMF length for a fixed sampling length of the PRN code [13,14], a PMF length of eight is employed with a 256 kHz main lobe width in Figure 9. Meanwhile both the number of Doppler frequency bins and the testing Doppler frequency are kept the same for all the algorithms. As can be seen from Figure 9; by exhaustively searching all the code phases and Doppler frequency bins at the cost of increased computational complexity and extended acquisition time, the best detection performance is observed for the serial search algorithm, whose SNR threshold is 2.1 dB lower than that of the NIST-reconstructed CS algorithm at a detection probability of 90%. More importantly, due to the developed compressive acquisition model and the effective noise suppressions for signal reconstructions, the NIST-reconstructed CS algorithm exhibits a 1.5 dB reduction in the SNR threshold at a CR of 1/2, compared with the conventional CS algorithm with FSS. In addition, the NIST-reconstructed CS algorithm achieves 4.4 dB and 1.3 dB gains of the SNR threshold over the PMF-FFT algorithm for the CRs of 1/2 and 1/4, respectively. At an SNR of −25 dB, the acquisition result plots of these four algorithms are depicted in Figure 10. It is clear from Figure 10 that the PMF-FFT algorithm is unable to achieve successful signal acquisition. In contrast, the estimated code phases and Doppler frequencies, detecting from the correlation peaks of both the NIST-reconstructed CS algorithm and the serial search algorithm, remain consistent with those of the testing GNSS signal.

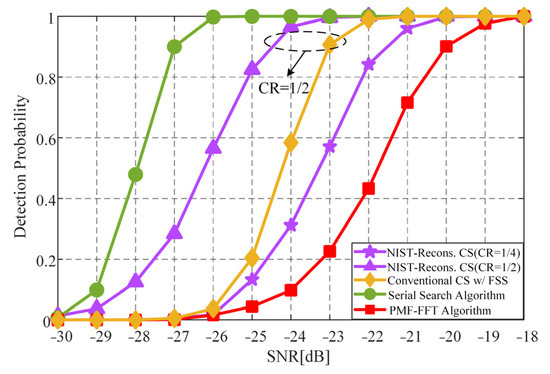
Figure 9. Comparisons of detection performances between NIST-reconstructed CS and conventional acquisition algorithms.

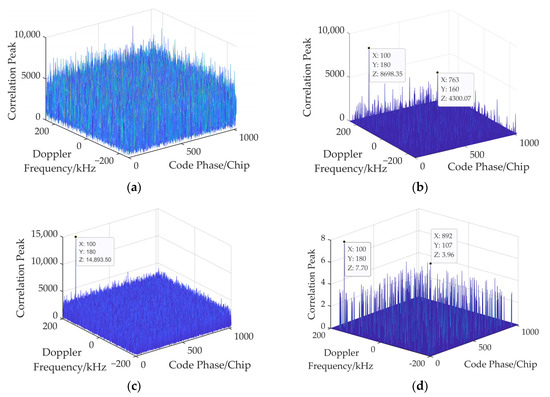
Figure 10. Comparisons of acquisition results between NIST-reconstructed CS and conventional acquisition algorithms: (a) PMF-FFT algorithm; (b) NIST-reconstructed CS algorithm; (c) serial search algorithm; (d) conventional CS algorithm with FSS.

4.3. Robustness of Acquisition Performance to Various Doppler Frequencies

To analyze the robustness of the acquisition performance to different Doppler frequencies, the detection performances of the NIST-reconstructed CS algorithm are measured under the various high-dynamic scenarios with Doppler frequencies ranging from 100 kHz to 200 kHz. Meanwhile, the measurements of the achievable detection performances are also conducted for the CS algorithms with different reconstruction schemes, the conventional CS algorithm with FSS, and the PMF-FFT algorithm for comparisons. Figure 11a shows the Doppler frequency-dependent SNR penalties, which are referred to as the SNR threshold differences between the acquisition of a specific Doppler frequency and that of a 100 kHz Doppler frequency at a detection probability of 90%. In simulating Figure 11a, a CR of 1/2 is exploited for the four CS algorithms whilst the parameter settings of FISTA and PMF-FFT are identical to those adopted in Figure 7 and Figure 9. It can be seen that when the Doppler frequency increases from 100 kHz to 200 kHz, the variations in the SNR penalties are lower than 1.5 dB for all the CS algorithms. In particular, a variation in the SNR penalty is observed as low as 1.3 dB for the NIST-reconstructed CS algorithm. This is inherently contributed to the exhaustive search characteristics for both the code phase and the Doppler frequency within the CS algorithms [11,12]. However, since the amplitude response of the PMF-FFT output exhibits a typical roll-off characteristic, the SNR penalty of the PMF-FFT algorithm increases sharply with the increasing Doppler frequency. Such an excellent performance robustness of the NIST-reconstructed CS algorithm can be further demonstrated in Figure 11b, where the detection probabilities are measured for various Doppler frequencies for an SNR of −25 dB. As shown in Figure 11b, for the Doppler frequencies larger than 160 kHz, the detection probabilities of the PMF-FFT algorithm drop sharply. However, the detection probabilities of the four CS algorithms almost remain stable. Due to its superior noise suppression in the reconstruction of the correlation matrix, the detection probabilities of the NIST-reconstructed CS algorithm are higher than those of other CS algorithms over the whole testing range of the Doppler frequency variation.

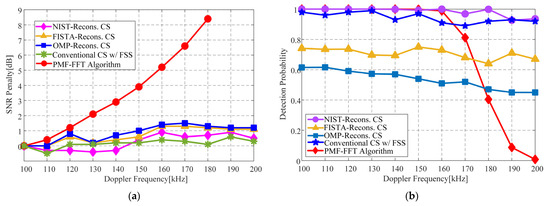
Figure 11. Detection performances for various Doppler frequencies: (a) SNR penalty versus Doppler frequencies for various acquisition algorithms; (b) detection probability versus Doppler frequency at an SNR of −25 dB.

5. Conclusions

By making use of a NIST-enabled rapid reconstruction of the correlation matrix, a novel CS-based GNSS signal acquisition algorithm has been proposed, which performs the compressed measurements of GNSS signals in real time via the offline developed code phase and frequency bin-compressed matrices. Theoretical analyses and numerical simulations have been conducted for computational complexity, achievable acquisition performance, and performance robustness to various Doppler frequencies. It has been shown that, in comparison with the OMP reconstruction, the NIST reconstruction brings out an acquisition performance improvement of 3.3 dB with a <10% increase in computational complexity. Moreover, the proposed algorithm has outperformed the conventional CS algorithm and exhibited a detection sensitivity variation of 1.3 dB over a Doppler frequency range from 100 kHz to 200 kHz. As a result, the proposed algorithm provides a rapid and reliable signal acquisition solution for the design of GNSS receivers operating in high-dynamic and low-SNR scenarios such as urban canyons with LEO navigation augmentation. Since the acquisition performance is highly dependent on the RTC, adaptive RTC tuning schemes warrant in-depth investigations. In our research lab, the hardware implementations of the proposed algorithm are currently undertaken on a commercial field programmable gate array (FPGA) and the detailed experimental results associated with the hardware design and measured GNSS data will be reported elsewhere in due course.