Midcourse Guidance via Variable-Discrete-Scale Sequential Convex Programming

Abstract

To address the challenges of strong nonlinearity, stringent terminal constraints, and the trade-off between computational efficiency and accuracy in the midcourse guidance trajectory optimization problem of aerodynamically controlled interceptors, this paper proposes a variable-discrete-scale sequential convex programming (SCP) method. Firstly, a dynamic model is established by introducing the range domain to replace the traditional time domain, thereby reducing the approximation error of the planned trajectory. Second, to overcome the critical issues of solution space restriction and trajectory divergence caused by terminal equality constraints, a terminal error-proportional relaxation approach is proposed. Subsequently, an improved second-order cone programming (SOCP) formulation is developed through systematic integration of three key techniques: terminal error-proportional relaxation, variable trust region, and path normalization. Finally, an initial trajectory generation algorithm is proposed, upon which a variable-discrete-scale optimization framework is constructed. This framework incorporates a residual-driven discrete-scale adaptation mechanism, which balances discretization errors and computational load. Numerical simulation results indicate that under large discretization scales, the computation time required by the improved SOCP is only about 5.4% of that of GPOPS-II. For small-discretization-scale optimization, the SCP method with the variable discretization framework demonstrates high efficiency, achieving comparable accuracy to GPOPS-II while reducing the computation time to approximately 7.4% of that required by GPOPS-II.

1. Introduction

In recent years, there has been growing interest in high-speed glide vehicles and their interception [1,2]. During the midcourse phase, the interceptor typically employs an aerodynamically controlled reentry-glide mode, which constitutes the longest duration of the engagement and is critical to the success of the interception. The key objective of midcourse guidance is to steer the interceptor toward the predicted intercept point, ensuring optimal reverse-intercept conditions upon entering the terminal phase [3,4]. Hence, designing a midcourse guidance trajectory capable of meeting specific terminal position and angle constraints is essential.

For strict path constraints and terminal constraints, midcourse guidance based on a dynamic model can better design a trajectory than midcourse guidance based on line-of-sight [5,6]. The trajectory planning problem for midcourse guidance can be addressed using indirect methods, direct methods, or intelligent algorithms [7]. According to Pontryagin’s minimum principle, the original optimal control problem is transformed into a multi-point boundary value problem by the indirect method [8,9]. The analytic solution is then derived using the Hamiltonian. The indirect method ensures high accuracy and optimal performance. However, it requires complex derivation and high-quality initial guesses. Additionally, the application of the indirect method is challenging for nonlinear dynamic models with complex constraints [10]. The direct method does not require the explicit derivation of optimality conditions. The continuous problem is transformed into a finite-dimensional parameter optimization problem, which is solved using numerical methods such as nonlinear programming [11,12]. Although the computational time may be longer and algorithmic convergence is not always guaranteed, the direct method has been successfully applied in engineering practice after continuous improvements [13]. Pseudospectral collocation methods, which discretize infinite-dimensional parameters with global polynomials, have attracted much attention [14,15]. For smooth problems, convergence at a quasi-exponential rate can be achieved with only a small number of nodes [16]. Model predictive static programming is classified as a direct method [17,18,19]. It is efficient, and the pseudo-spectral configuration can be used to improve the solution accuracy. Heuristic intelligent algorithms are widely utilized, but their trajectory planning and solution efficiency remain low [20]. In contrast, generative intelligent algorithms (e.g., reinforcement learning) can rapidly address trajectory planning problems. However, pre-training is required, and optimal solutions are difficult to guarantee [21].

Convex optimization algorithms enable the optimal solution to be obtained efficiently, as they exhibit low computational complexity and ensure global optimality [22,23]. The non-convexity of the dynamic model is the main difficulty in its application to guidance problems [24]. The SCP method handles nonlinear systems and non-convex path constraints through the construction of convex subproblems. By means of successive iteration, it approximates the optimal solution of the original problem [25,26]. The solution efficiency and accuracy of SCP are affected by different discretization methods. Currently, three common approaches exist: uniform collocation, pseudospectral collocation, and adaptive methods [27,28,29]. Adaptive methods are generally improved on uniform collocation or pseudospectral collocation. The pseudospectral collocation method employs several mesh refinement strategies. The most common ones are h, p, and hp methods [30,31,32,33]. The h method refines the mesh by increasing the number of subintervals. The p method enhances approximation accuracy by raising the polynomial degree. The hp method combines both strategies. However, the h and hp methods can be theoretically powerful. Yet, their implementation is often complex [34]. Uniform collocation demonstrates significantly higher efficiency than pseudospectral collocation, attributed to the sparser optimization problem structure [35].

The introduction of virtual control and terminal constraint relaxation techniques can mitigate the infeasibility of subproblems caused by strict terminal constraints at the beginning of iterations. Terminal relaxation involves loosening the terminal state, thereby expanding the search range of the terminal state. Regarding terminal position relaxation methods, refs. [29,36] adopted two distinct distance metrics: the absolute difference based on the L1 norm and the squared difference based on the L2 norm, respectively. Meanwhile, ref. [27] utilized the absolute difference form for terminal angle relaxation in its optimization approach. However, infeasibility issues may still arise under stringent terminal conditions. Virtual control techniques [30,37] are often employed in scenarios with rigorous process and terminal constraints, effectively addressing strict terminal constraint problems. Nevertheless, virtual control introduces additional variables in each dynamic equation, significantly increasing computational load compared to terminal relaxation.

Following the aforementioned analysis, a variable-discrete-scale SCP method is proposed to address the non-convex midcourse guidance trajectory planning problem with stringent terminal constraints. The key contributions of this research are outlined below:

(1)

A terminal error-proportional relaxation method is proposed to resolve infeasibility and trajectory divergence under hard terminal constraints. An improved SOCP method is proposed. It is integrated with variable trust region and path normalization techniques.

(2)

A rapid initial trajectory generation method is proposed to enhance the algorithm’s convergence performance and mitigate the artificial infeasibility phenomenon.

(3)

A readily implementable variable-discrete-scale scheme is introduced to overcome the inefficiency in high-precision trajectory computation. The proposed method enhances both accuracy and computational efficiency. Furthermore, an adaptive variable-discrete-scale strategy is proposed to refine the precision-speed trade-off.

The remainder of this paper is organized as follows. Section 2 formulates the optimal control problem for an aerodynamically controlled interceptor in the range domain. Section 3 develops an improved SOCP model. Section 4 presents the implementation of the variable-discrete-scale scheme. Section 5 validates the proposed method under both large discrete-scale and variable-discrete-scale conditions. Section 6 concludes the paper, followed by appendices

2. Problem Formulation

This section establishes an optimal control problem for the midcourse guidance of bank-to-turn aerodynamically controlled interceptors, employing a range-domain formulation in lieu of the time-domain approach and substituting the dual-channel control of angle of attack and bank angle with affine control. In addition, the optimization problem is subject to nonlinear constraints including acceleration, heat flux, and dynamic pressure.

2.1. Dynamics Model

The aerodynamically controlled interceptor in this study employs a bank-to-turn maneuver with angle of attack and bank angle as aerodynamic control inputs. This interceptor cannot rely on an angle-of-attack corridor and its altitude does not necessarily vary monotonically. The dimensionless dynamics of the interceptor over flat ground are described as follows [5,25]:

$$\left\{\begin{array}{l}dh/dt=v\sin \theta \\ dz/dt=v\cos \theta \sin \psi \\ dx/dt=v\cos \theta \cos \psi \\ dv/dt=-D-\sin \theta /r^2\\ d\theta /dt=L\cos \sigma /v+\left(v^2-1/r\right)\cos \theta /\left(vr\right)\\ d\psi /dt=L\sin \sigma /v\cos \theta \end{array}\right.$$

(1)

where $\left(h,z,x\right)$ denotes the position coordinates; $r=1+h$ denotes the distance from the Earth’s center to the interceptor, normalized by the Earth’s radius $r_e$; $v$ denotes the dimensionless relative velocity of the Earth, normalized by $\sqrt{g_0{r}_e}$, $g_0=9.81 \mathrm{m}/{\mathrm{s}}^2$; $\theta$ and $\psi$ represent the trajectory inclination angle and trajectory deflection angle, respectively; and $\sigma$ represents the bank angle.

The dimensionless lift and drag accelerations are $L$ and $D$:

$$L=\rho v^2{r}_e{C}_L\left(\alpha ,Ma\right)S/\left(2m\right)$$

(2)

$$D=\rho v^2{r}_e{C}_D\left(\alpha ,Ma\right)S/\left(2m\right)$$

(3)

where $\rho$ is the atmospheric density, using the exponential model $\rho \left(h\right)={\rho }_0{e}^{-h{r}_e/H}$, ${\rho }_0=1.225 \mathrm{kg}/{\mathrm{m}}^3$, $H=7110 \mathrm{m}$; lift and drag coefficients are represented by $C_L$ and $C_D$, respectively, with both being functions of the angle of attack $\alpha$ and the Mach number $Ma$. $S$ denotes the reference area; $m$ denotes the mass of a vehicle.

To achieve precise trajectory planning and strict constraint satisfaction, this work adopts the range domain for dynamics modeling. The one-to-one correspondence between the range and the geometric flight path allows the state and control variables to be naturally and effectively associated with spatial positions. Figure 1 shows the known initial position $\mathrm{O}(h_0,z_0,x_0)$ and terminal position $\mathrm{T}(h_f,z_f,x_f)$ of the interceptor. The range domain direction is defined along the connecting line from $\mathrm{O}$ to $\mathrm{T}$ in the transverse plane. The trajectory generation problem is transformed into increasing its projection range in the range domain, assuming that the projection range of the interceptor position $\mathrm{A}(h,z,x)$ is $l$.

$$l=\sqrt{{\left(x-x_0\right)}^2+{\left(z-z_0\right)}^2}$$

(4)

The velocity projection of the interceptor in the range domain is

$$v_l=dl/dt=v\cos \theta \cos ({\psi }_p-\psi )$$

(5)

where ${\psi }_p$ is the angle between the range domain direction and the $x$ axis, ${\psi }_p=\arcsin \left({\displaystyle \frac{\left(z_f-z_0\right)}{\sqrt{{\left(z_f-z_0\right)}^2+{\left(x_f-x_0\right)}^2}}}\right)$.

By substituting Equation (3) into Equation (1), the dynamic model can be transformed from the time domain to the range domain.

$$\left\{\begin{array}{l}dh/dl=\tan \theta /\cos ({\psi }_p-\psi )\\ dz/dl=\sin \psi /\cos ({\psi }_p-\psi )\\ dx/dl=\cos \psi /\cos ({\psi }_p-\psi )\\ dv/dl=-D/\left(v\cos \theta \cos ({\psi }_p-\psi )\right)-\tan \theta /\left(r^{2}v\cos ({\psi }_p-\psi )\right)\\ d\theta /dl=L\cos \sigma /\left(v^2\cos \theta \cos ({\psi }_p-\psi )\right)+\left(r{v}^2-1\right)/\left(r^2{v}^2\cos ({\psi }_p-\psi )\right)\\ d\psi /dl=L\sin \sigma /\left(v^2{\cos }^2\theta \cos ({\psi }_p-\psi )\right)\end{array}\right.$$

(6)

2.2. Choice of Control Variable

The dual-channel control model in Equation (6) can be linearized by the affine control variable constructed by the normalized coefficient $\eta$, which is expressed as follows:

$$\dot{\mathit{x}}=F(\mathit{x})+{\rm B}(\mathit{x})\mathit{u}$$

(7)

$$\left\{\begin{array}{l}{u}_1^2+u_2^2=u_3\\ 0\le u_3\le {\overline{u}}_3\\ u_1\tan {\sigma }_{\min }\le u_2\le u_1\tan {\sigma }_{\max }\end{array}\right.$$

(8)

where $\mathit{x}={\left[h,z,x,v,\theta ,\psi \right]}^{\mathrm{T}}$, $\mathit{u}={\left[u_1,u_2,u_3\right]}^{\mathrm{T}}$, and $u_1=\eta \cos \sigma ,u_2=\eta \sin \sigma ,u_3={\eta }^2$; for other details, see Appendix A.

The dimensionless lift and drag accelerations are $L$ and $D$:

$$L=L^{*}\eta ,D=D^{*}\left[1+{\eta }^2\right]/2$$

(9)

where $L^{*}=0.5\rho v^2{r}_e{C}_L^{*}S/m$, $D^{*}=0.5\rho v^2{r}_e{C}_D^{*}S/m$, $C_L^{*}$ and $C_D^{*}$ represent the lift–drag coefficient of the maximum lift–drag ratio, respectively.

2.3. Optimal Control Problem

The path constraint overload, heat flux and dynamic pressure are

$$\left\{\begin{array}{l}n=\sqrt{L^2+D^2}\le n_{\max }\\ \dot{Q}=k_Q{\rho }^{0.5}{\left(v\sqrt{r_e{g}_0}\right)}^{3.15}\le {\dot{Q}}_{\max }\\ q=0.5\rho {\left(v\sqrt{r_e{g}_0}\right)}^2\le q_{\max }\end{array}\right.$$

(10)

Equation (8) can be simplified to be expressed as

$$P_i\left(h,v,u_3\right)-{\overline{P}}_i\le 0,i=1,2,3$$

(11)

where ${\overline{P}}_i$ denotes the upper bound of the i-th path constraint.

The initial state and the ideal terminal state of the interceptor are given as ${\mathit{x}}_0$ and ${\mathit{x}}_f$, respectively. However, the velocity state $v_f$ cannot be accurately estimated. Thus, ${\mathit{x}}_f=\left[h_f,z_f,x_f,{\theta }_f,{\psi }_f\right]$ is set. The corresponding projection ranges for the boundaries are defined as $l_0=0$ and $l_f$, respectively. The initial and terminal boundary conditions of the interceptor are as follows:

$$\mathit{x}\left(l_0\right)={\mathit{x}}_0,\mathit{x}\left(l_f\right)={\mathit{x}}_f$$

(12)

The velocity state $v_f$ can be directly constrained in the objective function, thereby eliminating the need for additional estimation of the velocity term.

$$J_0=-{\kappa }_v{v}_f$$

(13)

where ${\kappa }_v$ is a constant, representing the weight of the speed.

The optimal control problem P0 for midcourse guidance is formulated based on the following: dynamic Equation (7), control constraint (8), path constraint (11), boundary conditions (12), and objective function (13).

P0:

$$\begin{array}{ll}\mathrm{minimize} & J_0=-{\kappa }_v{v}_f\\ \mathrm{subject} \mathrm{to}: & \dot{\mathit{x}}=F(\mathit{x})+{\rm B}(\mathit{x})\mathit{u}\\ & u_1^2+u_2^2=u_3\\ & 0\le u_3\le {\overline{u}}_3\\ & u_1\tan {\sigma }_{\min }\le u_2\le u_1\tan {\sigma }_{\max }\\ & P_i\left(h,v,u_3\right)-{\overline{P}}_i\le 0,i=1,2,3\\ & \mathit{x}\left(l_0\right)={\mathit{x}}_0,\mathit{x}\left(l_f\right)={\mathit{x}}_f\end{array}$$

(14)

3. Improved SOCP Problem Description

In this section, the non-convex optimal control problem is first convexified into an SOCP formulation. Subsequently, equal-scale discretization is performed. Finally, an improved SOCP model is developed to overcome both the stringent terminal constraints and Hessian matrix singularity encountered during the solution.

3.1. SOCP

The non-convexity of the optimal control problem originates from three sources: the affine state equations, path constraints, and control constraints. Through linearization of dynamic equations and path constraints, along with non-destructive convexification of control constraints, the problem can be transformed into an SOCP.

Let $\{{\mathit{x}}^{(k)},{\mathit{u}}^{(k)}\}$ denote the k-th iterative solution of the optimization problem. The dynamic Equation (7) is then linearized with respect to $\{{\mathit{x}}^{(k)},{\mathit{u}}^{(k)}\}$.

$$\dot{\mathit{x}}=A({\mathit{x}}^{(k)},{\mathit{u}}^{(k)})\mathit{x}+{\rm B}({\mathit{x}}^{(k)})\mathit{u}+F({\mathit{x}}^{(k)})-A({\mathit{x}}^{(k)},{\mathit{u}}^{(k)}){\mathit{x}}^{(k)}$$

(15)

where $A({\mathit{x}}^{(k)},{\mathit{u}}^{(k)})={\left.\partial F(\mathit{x})/\partial \mathit{x}\right|}_{\mathit{x}={\mathit{x}}^{(k)}}+{\left.\partial \left[{\rm B}(\mathit{x})\mathit{u}\right]/\partial \mathit{x}\right|}_{\mathit{x}={\mathit{x}}^{(k)},\mathit{u}={\mathit{u}}^{(k)}}$; see Appendix A for details.

The path constraints (11) are linearized with respect to $\{{\mathit{x}}^{(k)},{\mathit{u}}^{(k)}\}$, yielding

$${\dot{P}}_i^{(k)}\cdot \left[h-h^{(k)};v-v^{(k)};u_3-{u_3}^{(k)}\right]+P_i^{(k)}-{\overline{P}}_i\le 0,i=1,2,3$$

(16)

where ${\dot{P}}_j^{(k)}$ represents the derivative of the path constraints with respect to the k-th iteration solution $\{{\mathit{x}}^{(k)},{\mathit{u}}^{(k)}\}$, and ${\overline{P}}_i$ defines the maximum allowable value of the i-th path constraint. To ensure effective linearization, a trust region is introduced.

$$|\mathit{x}-{\mathit{x}}^{(k)}|\le \mathit{\delta }$$

(17)

where $\mathit{\delta }\in {ℝ}^6$ is a constant vector.

The non-convexity in the control constraint arises from the second-order cone constraint (8). This constraint can be non-destructively convexified through control relaxation, as follows:

$$u_1^2+u_2^2\le u_3$$

(18)

The control set is

$$\left\{\begin{array}{l}{u}_1^2+u_2^2\le u_3\\ 0\le u_3\le {\overline{u}}_3\\ u_1\tan {\sigma }_{\min }\le u_2\le u_1\tan {\sigma }_{\max }\end{array}\right.$$

(19)

The control constraint relaxation, being a second-order cone constraint (18), may cause relaxation inaccuracies. To resolve this, a regularization term is incorporated into the objective function as follows [25]:

$$J_1=-{\kappa }_v{v}_f+{\kappa }_{\psi }{\displaystyle {\int }_{l_0}^{l_f}\psi dl}$$

(20)

The optimal control problem P0 is convexified to SOCP, as shown in Problem P1.

P1:

$$\begin{array}{ll}\mathrm{minimize}& -{\kappa }_v{v}_f+{\kappa }_{\psi }{\displaystyle {\int }_{l_0}^{l_f}\psi dl} \\ \mathrm{subject} \mathrm{to}:& \dot{\mathit{x}}=A({\mathit{x}}^{(k)},{\mathit{u}}^{(k)})\mathit{x}+{\rm B}({\mathit{x}}^{(k)})\mathit{u}+F({\mathit{x}}^{(k)})-A({\mathit{x}}^{(k)},{\mathit{u}}^{(k)}){\mathit{x}}^{(k)}\\ & u_1^2+u_2^2\le u_3,0\le u_3\le {\overline{u}}_3,u_1\tan {\sigma }_{\min }\le u_2\le u_1\tan {\sigma }_{\max }\\ & {\dot{P}}_i^{(k)}\cdot \left[h-h^{(k)};v-v^{(k)};u_3-{u_3}^{(k)}\right]+P_i^{(k)}-{\overline{P}}_i\le 0,i=1,2,3\\ & \mathit{x}\left(l_0\right)={\mathit{x}}_0,\mathit{x}\left(l_f\right)={\mathit{x}}_f\\ & \left|\mathit{x}-{\mathit{x}}^{(k)}\right|\le \mathit{\delta }\end{array}$$

(21)

3.2. Discretization

The problem P1 is a continuous-time SOCP. The distance domain $[l_0,l_f]$ is discretized using an equidistant scale in this section. Through this discretization, the infinite-dimensional Problem P1 is transformed into a finite-dimensional SOCP model, with all state constraints being normalized.

The distance domain variable $l$ is an independent variable of Problem P1. Given $N+1$ discrete points, these points are denoted as $[l_0,l_1,\dots ,l_{N-1},l_N]$ and $l_N=l_f$. The discrete scale is represented by $\Delta \mathit{l}=[\Delta l_1,\Delta l_2,\dots ,\Delta l_{N-1},\Delta l_N]$, while the inter-point relationship is characterized by $l_j=l_{j-1}+\Delta l_j$ and $j=1,,2\dots ,N-1,N$. Based on these definitions, the following is obtained:

$${\displaystyle \sum _{j=1}^N\Delta l_j}=l_f-l_0$$

(22)

The dynamic equation is discretized by the trapezoidal method.

$${\mathit{x}}_j={\mathit{x}}_{j-1}+0.5\Delta l_j[(A_{j-1}^{(k)}{\mathit{x}}_{j-1}+{{\rm B}}_{j-1}^{(k)}{\mathit{u}}_{j-1}+C_{j-1}^{(k)})+(A_j^{(k)}{\mathit{x}}_j+{{\rm B}}_j^{(k)}{\mathit{u}}_j+C_j^{(k)})]$$

(23)

where ${\mathit{x}}_j=\mathit{x}\left(l_j\right)$, ${\mathit{u}}_j=\mathit{u}\left(l_j\right)$, $A_j^{(k)}=A({\mathit{x}}_j^{(k)},{\mathit{u}}_j^{(k)})$, ${{\rm B}}_j^{(k)}={\rm B}({\mathit{x}}_j^{(k)})$, $C_j^{(k)}=F({\mathit{x}}_j^{(k)})-A({\mathit{x}}_j^{(k)},{\mathit{u}}_j^{(k)}){\mathit{x}}_j^{(k)}$.

A simplified Equation (23) is available:

$$G_{j-1}{\mathit{x}}_{j-1}+G_j^{*}{\mathit{x}}_j+H_{j-1}{\mathit{u}}_{j-1}+H_j{\mathit{u}}_j=d$$

(24)

where $G_{j-1}=I+0.5\Delta l_j{A}_{j-1}^{(k)}$, $G_j^{*}=-I+0.5\Delta l_j{A}_j^{(k)}$, $H_{j-1}=0.5\Delta l_j{B}_{j-1}^{(k)}$, $H_j=0.5\Delta l_j{B}_j^{(k)}$, $d=0.5\Delta l_j(C_{j-1}^{(k)}+C_j^{(k)})$.

The parameters $\mathit{s}$ and ${\mathit{u}}_p$ are defined as follows: $\mathit{s}={[{\mathit{x}}_0^{\mathrm{T}} {\mathit{x}}_1^{\mathrm{T}}\dots {\mathit{x}}_N^{\mathrm{T}} {\mathit{u}}_0^{\mathrm{T}} {\mathit{u}}_1^{\mathrm{T}}\dots {\mathit{u}}_N^{\mathrm{T}}]}^{\mathrm{T}}$ and ${\mathit{u}}_p={\left[u_{p,1},u_{p,2},u_{p,3}\right]}^{\mathrm{T}},p=0,1,\dots ,N-1,N$. By simplifying the simultaneous Equation (24) and incorporating the initial boundary conditions (12), the equality matrix constraint (25) is obtained.

$$\Gamma \mathit{s}=D$$

(25)

where $\Gamma$ and $D$ represent the coefficient matrix and the constant-term vector of the equation, respectively.

Then, the discretization of the path constraint (16), control constraint (19), trust region (17) and objective function (20) is carried out in turn. The discretized path constraint and control constraint are combined to obtain a second-order cone constraint (24) and inequality matrix constraint (25).

$${\mathit{u}}_{p,1}^2+{\mathit{u}}_{p,2}^2\le {\mathit{u}}_{p,3},p=0,1,\dots ,N-1,N$$

(26)

$$M\mathit{s}\le {\rm T}$$

(27)

where $M$ and ${\rm T}$ represent the inequality coefficient matrix and the inequality constant vector, respectively.

Additional constraints can also be expressed at discrete points. Through this transformation, the SOCP Problem P1 is converted into the discrete formulation P2:

P2:

$$\begin{array}{ll}\mathrm{minimize} & -{\kappa }_v{v}_N+{\kappa }_{\psi }{\displaystyle \sum _{l=l_0}^{l_N}\psi (l)}\\ \mathrm{subject} \mathrm{to}: & \Gamma \mathit{s}=D\\ & M\mathit{s}\le {\rm T}\\ & {\mathit{u}}_{p,1}^2+{\mathit{u}}_{p,2}^2\le {\mathit{u}}_{p,3},p=0,1,\dots ,N-1,N\\ & \mathit{x}\left(l_N\right)={\mathit{x}}_f\\ & \left|\mathit{x}-{\mathit{x}}^{(k)}\right|\le \mathit{\delta }\end{array}$$

(28)

3.3. Improved SOCP

To enhance the convergence speed of the SCP method while addressing stringent terminal constraints and matrix singularity issues, an improved SCP approach is proposed. Key improvements feature terminal error-proportional relaxation, an implemented variable trust region, and path normalization.

3.3.1. Terminal Error-Proportional Relaxation Method

Under complex dynamics and multiple path constraints, strict terminal equality constraints may lead to the non-existence of feasible solutions, and the computational efficiency of handling equality constraints is lower than that of inequality constraints. To address this issue, slack variables are introduced [30]. Due to the significant difference in the numerical ranges between the position states and the angle states, a terminal error proportional relaxation method is proposed based on the physical characteristics of the state variables. This method transforms the hard constraints of strict terminal equalities into soft constraints that gradually converge with slack variables under different weights, overcoming the shrinkage of the feasible solution space and trajectory divergence caused by strict equality constraints.

The relaxed terminal constraint (12) takes the following form:

$$\left\{\begin{array}{l}\left|h\left(l_N\right)-h_f\right|\le c_1{\gamma }_h\\ \left|z\left(l_N\right)-z_f\right|\le c_1{\gamma }_z\\ \left|x\left(l_N\right)-x_f\right|\le c_1{\gamma }_x\\ \left|\theta \left(l_N\right)-{\theta }_f\right|\le c_2{\gamma }_{\theta }\\ \left|\psi \left(l_N\right)-{\psi }_f\right|\le c_2{\gamma }_{\psi }\end{array}\right.$$

(29)

where $c_1$ and $c_2$ represent the coefficients of the relaxation variables of the distance term and the angle term, respectively, which can be selected according to the magnitude of the normalized variables; $\mathit{\gamma }$ is the relaxation variable of the corresponding parameter, and ${\kappa }_{\mathit{\gamma }}{\displaystyle \sum \mathit{\gamma }}$ is added to the objective function to constrain. When $\mathit{\gamma }\to 0$, the effect of the equality constraint $\mathit{x}\left(l_N\right)={\mathit{x}}_f$ can be achieved in the objective function. For ease of expression, the expression (29) can be converted to

$$\left|\mathit{x}\left(l_N\right)-{\mathit{x}}_f\right|\le \mathit{c}\mathit{\gamma }$$

(30)

3.3.2. Variable Trust Region

Compared with fixed trust regions, a variable trust region strategy allows for the expansion of the trust region when poor initial estimates are encountered, thereby facilitating the identification of feasible solutions. As the model solution approaches optimality, the trust region is automatically reduced to accelerate convergence. The variable trust region constraints are formulated as follows:

$$\left|\mathit{x}-{\mathit{x}}^{(k)}\right|\le \lambda \mathit{\delta }$$

(31)

where $\lambda$ is the trust region relaxation variable. Add ${\kappa }_{\lambda }\lambda$ to the objective function to constrain the trust region range.

3.3.3. Path Normalization

The path constraints exhibit a significantly larger magnitude than the state variables, resulting in a substantially greater maximum eigenvalue than minimum eigenvalue in the Hessian matrix. This large condition number, particularly for large-scale problems, causes the matrix determinant to approach zero, leading to near-singularity and potential solution failure. To address this, the path constraints are normalized as follows:

$${\displaystyle \frac{{\dot{P}}_i^{(k)}}{{\overline{P}}_i}}\cdot \left[\mathit{h}-{\mathit{h}}^{(k)};\mathit{v}-{\mathit{v}}^{(k)};{\mathit{u}}_{p,3}-{{\mathit{u}}_{p,3}}^{(k)}\right]+{\displaystyle \frac{P_i^{(k)}}{{\overline{P}}_i}}-I_i\le 0$$

(32)

where $i=1,2,3$ and $p=0,1,\dots ,N-1,N$.

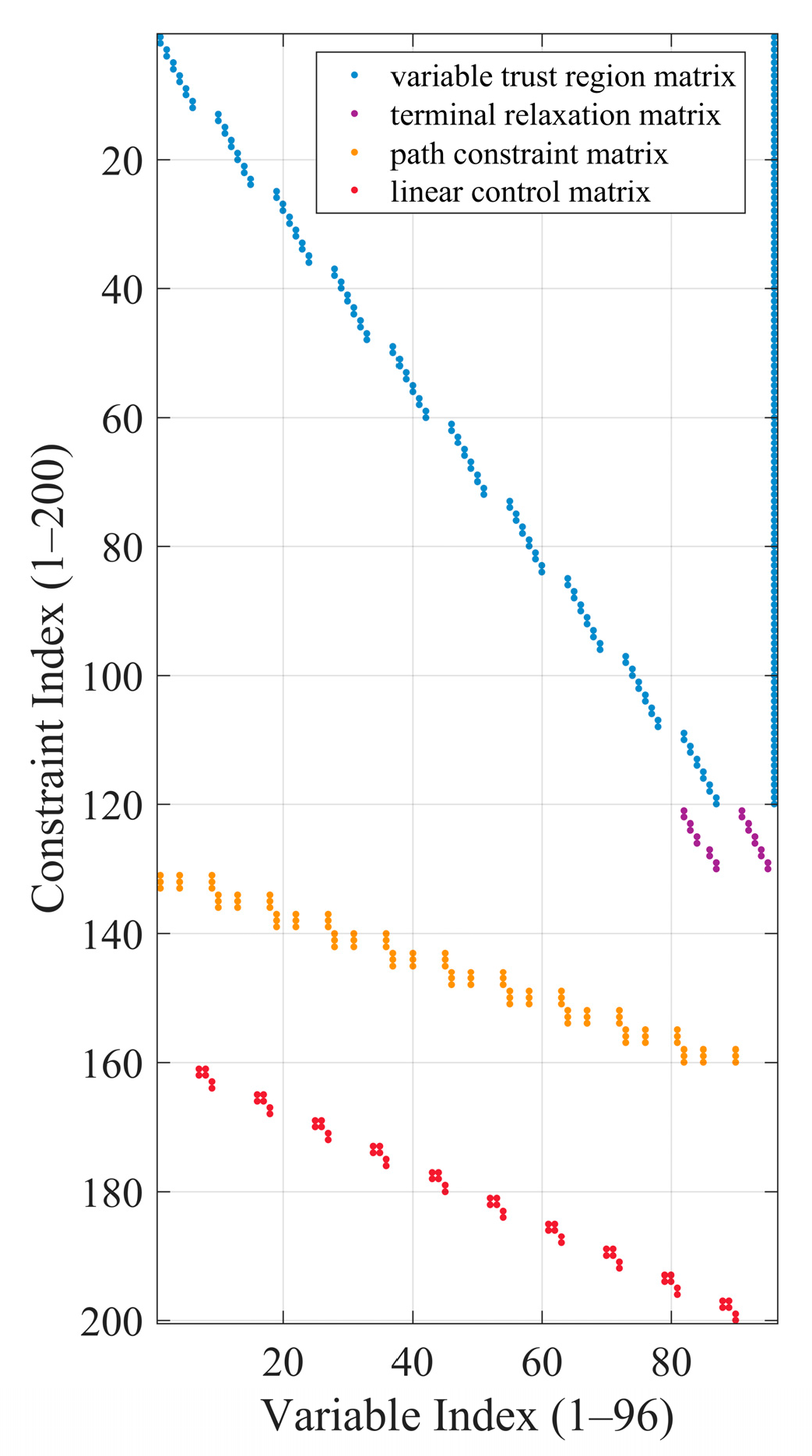
By integrating the terminal-relaxation constraint (30), the variable trust region constraint (31), the path constraint (32), and the inequality matrix constraint (27) under the condition of $\mathit{y}={\left[\begin{array}{ccc}\mathit{s}& \mathit{\gamma }& \lambda \end{array}\right]}^{\mathrm{T}}$, a new inequality matrix constraint is formed. Based on these consolidated constraints, the original SOCP (Problem P2) is transformed into an improved formulation, designated as Problem P3.

P3:

$$\begin{array}{ll}\mathrm{minimize} & -{\kappa }_v{v}_N+{\kappa }_{\psi }{\displaystyle \sum _{l=l_0}^{l_N}\psi (l)}+{\kappa }_{\mathit{\gamma }}{\displaystyle \sum \mathit{\gamma }}+{\kappa }_{\lambda }\lambda \\ \mathrm{subject} \mathrm{to}:& \Gamma \mathit{y}=D\\ & M\mathit{y}\le {\rm T}\\ & {\mathit{u}}_{p,1}^2+{\mathit{u}}_{p,2}^2\le {\mathit{u}}_{p,3},p=0,1,\dots ,N-1,N \end{array}$$

(33)

where the equation coefficient matrix $\Gamma$, constant term vector $D$, inequality coefficient matrix $M$, and inequality constant term vector ${\rm T}$ are provided in Appendix B.

4. Variable-Discrete-Scale SCP

In this section, an initial trajectory generation method is first presented. Subsequently, an SCP framework with a variable discretization scale is proposed. Finally, while maintaining solution accuracy, the computational speed is enhanced through the introduction of a scale adaptation method.

4.1. Initial Trajectory

The initial trajectory is generated using normalized maximum lift coefficients and varying inclination angles. A trajectory group is then obtained by interpolating between the two trajectories nearest to the terminal position in lateral distance. The specific implementation steps are as follows:

Step 1: Select the normalized coefficient ${\overline{\eta }}_{max}$ and bank angle ${\sigma }_i$ as control variables. Assuming that the terminal time $t_{\mathrm{end}}$ is the termination time, the trajectory groups $\tau$ are generated by integrating the interval time $\Delta t$, where ${\sigma }_i$ is selected in $\left[{\sigma }_{\min },{\sigma }_{\max }\right]$ in proportion to $\Delta \sigma$.

Step 2: Select the trajectory ${\tau }_1$ and ${\tau }_2$ that are closest to the terminal position $\mathrm{T}\left(z_f,x_f\right)$ in the trajectory group $\mathit{\tau }$. ${\tau }_1$ and ${\tau }_2$ can be obtained according to the serial numbers of the distance interpolation $\Delta {\tau }_i$ and $\Delta {\tau }_j$ obtained by Equation (34), $\left|i-j\right|=1$. The bank angles corresponding to ${\tau }_1$ and ${\tau }_2$ are ${\sigma }_1$ and ${\sigma }_2$. According to Equation (35), the bank angle ${\sigma }_3$ is obtained.

$$\Delta {\tau }_i=\min [\mathrm{sqrt}{(\mathit{𝒵}-z_f)}^2+{(\mathit{x}-x_f)}^2]$$

(34)

$${\sigma }_3=\left({\sigma }_2\Delta {\tau }_1+{\sigma }_1\Delta {\tau }_2\right)/\left(\Delta {\tau }_1+\Delta {\tau }_2\right)$$

(35)

Step 3: Select ${\overline{\eta }}_{max}$ and bank angle ${\sigma }_3$ as the control quantity and integrate the trajectory. Then, the initial range domain trajectory of the required discrete scale is interpolated.

4.2. SCP with Variable-Discrete-Scale Framework

The variable-discrete-scale method is implemented by first employing a coarse discretization for rapid trajectory solution, followed by conversion to a fine discretization for higher-accuracy results. The SCP with variable-discrete-scale framework is presented in Algorithm 1.

Algorithm 1: SCP with variable-discrete-scale framework

Input: Initial guess trajectory $\{{\mathit{x}}^{(0)},{\mathit{u}}^{(0)}\}$, trust region ${\mathit{\delta }}_{\mathit{x}}$, convergence region ${\mathit{\epsilon }}_{\mathit{x}}$, $N_1$, $N_2$ $k\max$, $e^{+}$, $e^{-}$; Output: $\mathit{x}$ and $\mathit{u}$

For i = 1 to 2           If $i==1$                 Set $k\leftarrow 1$, $N=N_1$;           Else                 Set $k\leftarrow 1$,$N=N_2$;         End If         While $k\le k\max$ do                 Solve problem P3 to get $\mathit{x}$ and $\mathit{u}$;                 If $‖\mathit{x}-{\mathit{x}}^{\left(k\right)}‖\le {\mathit{\epsilon }}_x$ then                     Break;                 Else                 ${\mathit{x}}^{(k+1)}\leftarrow \mathit{x}$;                 Set $k\leftarrow k+1$;                 End If           End While

End For

4.3. Adaptive Variable-Discrete-Scale Algorithm

The SOCP Problem P4 is solved through discrete iterative approximation. The converged iterative solution is discrete, resulting in trajectory integration errors when the control variables are implemented. When the mesh is fixed, the accuracy of the convergence solution depends on the discrete scale. The accuracy, efficiency and convergence speed of the discrete solution are closely related to the grid, convergence accuracy and problem form.

To balance accuracy and convergence, a residual-based adaptive variable-discrete-scale algorithm is proposed. After the k-th iteration converges, the integral terminal state of the j-th discrete scale is

$${\mathit{𝒳}}_j^{(k)}={\displaystyle {\int }_{l_{j-1}^{(k)}}^{l_j^{(k)}}\mathit{f}(\mathit{x},\mathit{u})}\mathrm{d}l$$

(36)

The absolute value of the j-th discrete-scale residual of the i-th state is

$${\mathit{\xi }}_{i,j}^{(k)}=\left|{\mathit{x}}_{i,j}^{(k)}-{\mathit{𝒳}}_{i,j}^{(k)}\right|$$

(37)

Due to varying magnitudes across different states, a uniform error metric cannot be applied. Therefore, the residual is normalized according to each state’s individual scale.

$${\mathit{T}}_i^{(k)}=\max ({\mathit{x}}_i^{(k)})-\min ({\mathit{x}}_i^{(k)})$$

(38)

where ${\mathit{x}}_i^{(k)}$ denotes the i-th state (i = 1, …, 6) of the k-th converged solution, while ${\mathit{T}}_i^{(k)}$ represents the range between the maximum and minimum values in the i-th state of this solution.

The relative residual of the j-th grid of the i-th state is

$${\mathit{e}}_{i,j}^{(k)}={\displaystyle \frac{{\mathit{\xi }}_{i,j}^{(k)}}{{\mathit{T}}_i^{(k)}}}$$

(39)

A large local relative residual indicates strong nonlinearity at the current discrete scale, necessitating increased point density and reduced scale in the region. Conversely, small residuals reflect weak nonlinearity, allowing discrete point reduction and scale enlargement to enhance computational efficiency. Based on this principle, an adaptive variable-discrete-scale strategy is proposed.

Suppose that the allowable lower limit of the local relative residual error is $e^{-}$, the maximum value of the local relative residual error is $\mathit{\zeta }(j)=\max ({\mathit{e}}_j^{(k)})$, and the sequence vector $\mathit{w}$ is

$$\mathit{w}(i)=j,if \mathit{\zeta }(j)<e^{-}$$

(40)

The number of discrete intervals to be processed is the number $a$ of elements in $\mathit{w}$. When condition $a>0$ is met, discrete-scale merging is executed based on relative residuals. The complete procedure is presented in Algorithm 2.

The local discrete interval elimination rule can be defined as scale merging when the sum of adjacent relative residuals falls below the allowable lower limit $e^{-}$. Given an upper limit $e^{+}$ for local relative residuals, the discrete scale reduction rule is specified as follows:

$$p_j=⌈{\displaystyle \frac{\max ({\mathit{e}}_j^{(k)})}{e^{+}}}⌉,if {\mathit{e}}_{i,j}^{(k)}\ge e^{+}$$

(41)

The range domain $\Delta \mathit{l}$ is updated by using $p_j$ scales $\Delta l_j/p_j$ instead of $\Delta l_j$.

The implementation rules for adaptive variable discrete scaling are established by Algorithm 2 and Equation (41), with optimization being performed at large discrete scales.

Algorithm 2: Local discrete interval adjustment algorithm based on relative residuals

Input: $\mathit{\zeta }$, $\mathit{w}$, $\Delta \mathit{l}$, $a$, $e^{-}$, N; Output: Mesh length $\Delta \mathit{l}$; Set $i\leftarrow 1$; While i < $a$ do           If $(\mathit{w}(i+1)\ne \mathit{w}(i)+1)\&\&(\Delta \mathit{l}(\mathit{w}(i\left)\right)\ne 0)$ then                     $\Delta \mathit{l}\left(\mathit{w}\right(i\left)\right)$ ← $\Delta \mathit{l}\left(\mathit{w}\right(i\left)\right)$ + $\Delta \mathit{l}\left(\mathit{w}\right(i)+1)$;                     $\Delta \mathit{l}\left(\mathit{w}\right(i)+1)$ ← 0;                     Set i ← i + 1;           End If           Set k ← i, $\kappa \leftarrow \mathit{\zeta }(\mathit{w}(i))$;           If i < $a$ then                     While $\mathit{w}(i+1)$ = $\mathit{w}\left(i\right)+1$ do                           $\kappa$ ← $\kappa$ + $\mathit{\zeta }(\mathit{w}(i+1))$;                           $\Delta \mathit{l}\left(\mathit{w}\right(i\left)\right)$ ← $\Delta \mathit{l}\left(\mathit{w}\right(i\left)\right)$ + $\Delta \mathit{l}\left(\mathit{w}\right(i+1\left)\right)$;                           $\Delta \mathit{l}\left(\mathit{w}\right(i+1\left)\right)=0$;                           Set i ← i + 1;                           If ($\kappa$ > $e^{-}$)||(i == $a$)||($\mathit{w}(i+1)\ne \mathit{w}\left(i\right)+1$) then                               Set i ← i + 1;                               Break;                           Else If                     End While           Else if End While if (i ≤ $a$) && ($\mathit{w}\left(i\right)$ ≠N) then           $\Delta \mathit{l}\left(\mathit{w}\right(i\left)\right)$ ← $\Delta \mathit{l}\left(\mathit{w}\right(i\left)\right)$ + $\Delta \mathit{l}\left(\mathit{w}\right(i)+1)$;           $\Delta \mathit{l}\left(\mathit{w}\right(i)+1)$ ← 0; End if Return $\Delta \mathit{l}$;

5. Numerical Simulations

The midcourse guidance parameters of the aerodynamically controlled aircraft are as follows: $m=900 \mathrm{kg}$, $S=0.4839 {\mathrm{m}/\mathrm{s}}^2$, $\eta \in \left[0,4.4016\right]$, $\sigma \in \left[-60,60\right]\mathrm{deg}$. The constraint settings of midcourse guidance are as follows: $n_{\max }=5{\mathrm{g}}_0$, ${\dot{Q}}_{\max }=1000 \mathrm{kW}/{\mathrm{m}}^2$, $q_{\max }=150 \mathrm{kpa}$, $k_Q=1.1813\times {10}^{-4}$ for the path constraints in Equation (10); $c_1=0.01$, $c_2=1$ for terminal relaxation in Equation (29); and ${\kappa }_v=0.01$, ${\kappa }_{\psi }=0.1$, ${\kappa }_{\gamma }=100$, ${\kappa }_{\lambda }=0.01$ for the objective function in Equation (33). The parameters generated by the initial trajectory of the range domain are as follows: terminal time $t_{\mathrm{end}}=250 \mathrm{s}$, integration intervals $\Delta t=1 \mathrm{s}$, and bank angle selection increments of $\Delta \sigma =3°$. The initial and ideal terminal conditions are shown in

Table 1. Initial and ideal terminal conditions.

State	$\mathit{h},\mathbf{km}$	$\mathit{z},\mathbf{km}$	$\mathit{x},\mathbf{km}$	$\mathit{v},\mathbf{m}/\mathbf{s}$	$\mathit{\theta },\mathbf{deg}$	$\mathit{\psi },\mathbf{deg}$
${\mathit{x}}_0$	60	0	0	2500	0	0
${\mathit{x}}_f$	25	25	400	-	0	10

. The trust region $\mathit{\delta }=\left[12000/r_{\mathrm{e}},5000/r_{\mathrm{e}},80000/r_{\mathrm{e}},\right.500/\sqrt{g_0{r}_{\mathrm{e}}},$ $\left.20\pi /180,20\pi /180\right]$; ${\mathit{\epsilon }}_0=\left[120/r_{\mathrm{e}},120/r_{\mathrm{e}},800/r_{\mathrm{e}},50/\sqrt{g_0{r}_{\mathrm{e}}},\pi /180,\pi /180\right]$; the convergence region $\mathit{\epsilon }=0.01{\mathit{\epsilon }}_0$. The lower limit $e^{-}$ and upper limit $e^{+}$ for the local relative residual error are set to $2\times {10}^{-4}$ and ${10}^{-2}$, respectively.

All simulations were conducted on a laptop computer with an Intel Core i7-1165G7, 2.80 Ghz, 16 G RAM, and Windows 10 operating system. The subproblems of SCP are solved by ECOS [38] in version 2.0.8.36.

The integral trajectory is obtained by trapezoidal integration on 40,000 equidistant nodes, taking the optimized control sequence as the control quantity. The accuracy of the optimization method is evaluated by comparing the optimization solution with product decomposition and ideal terminal.

5.1. Large Discrete-Scale Optimization

This section first simulates the initial trajectory in the range domain, which serves as the initial guess for the SCP, followed by a large-discretization-scale optimization simulation.

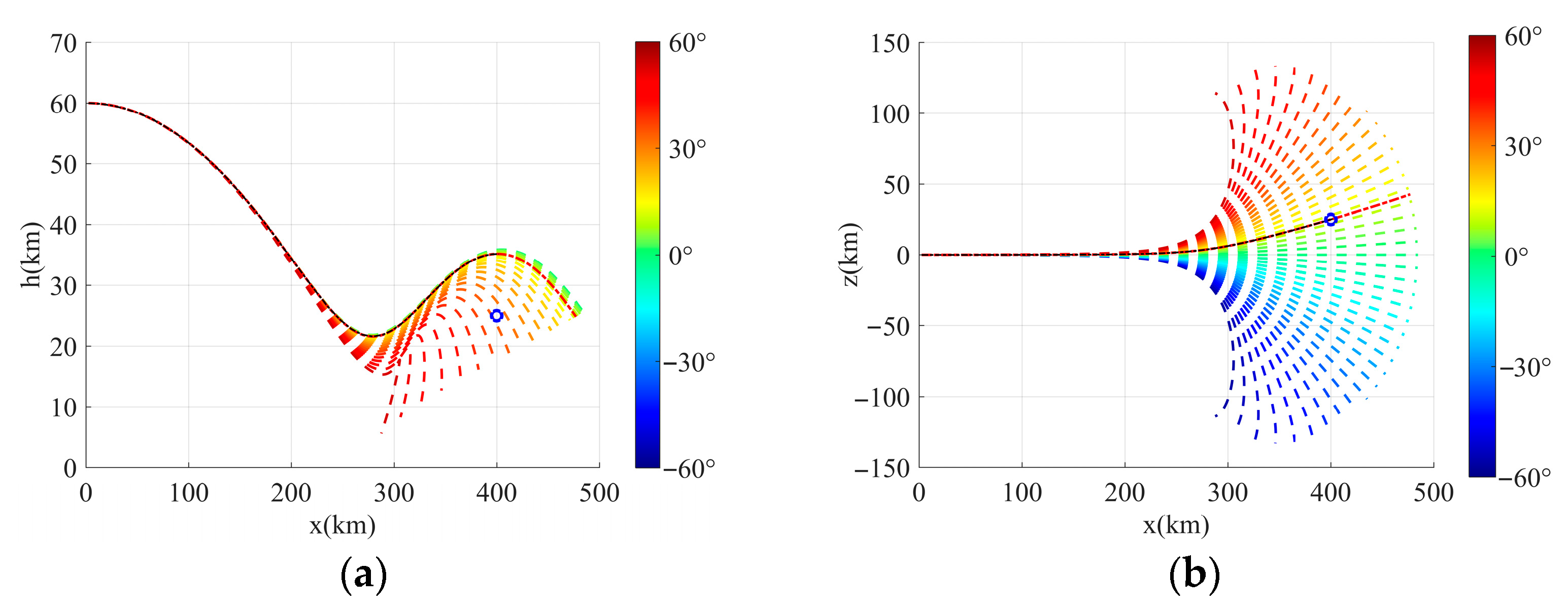
In Figure 2, the generated trajectory cluster, integral trajectory, and interpolated initial range domain trajectory are obtained with a computational time of 0.049 s. The interpolated initial trajectory demonstrates spatial consistency with terminal constraints in the range and longitudinal position, rendering it suitable as an initial iterative solution for SCP.

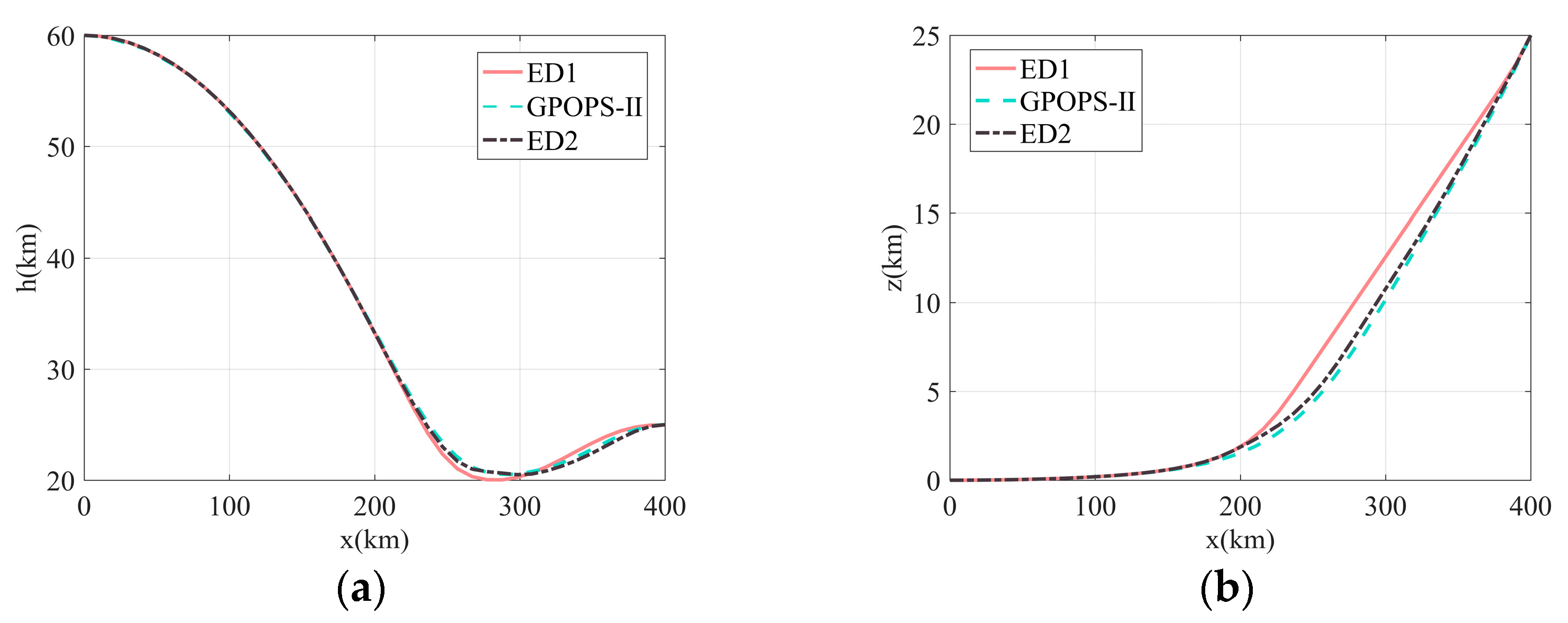
Large-discrete-scale optimization refers to discretizing the midcourse guidance phase into equally spaced large-scale segments for optimization. The optimized results can serve as the first layer of the variable-discrete-scale SCP for midcourse guidance. For comparison, we employ large-discrete-scale SCP (ED1 denotes solving the SOCP with only terminal error proportion relaxation, and ED2 represents solving the improved SOCP and the software GPOPS-II (v5.1) to solve Problem P0.

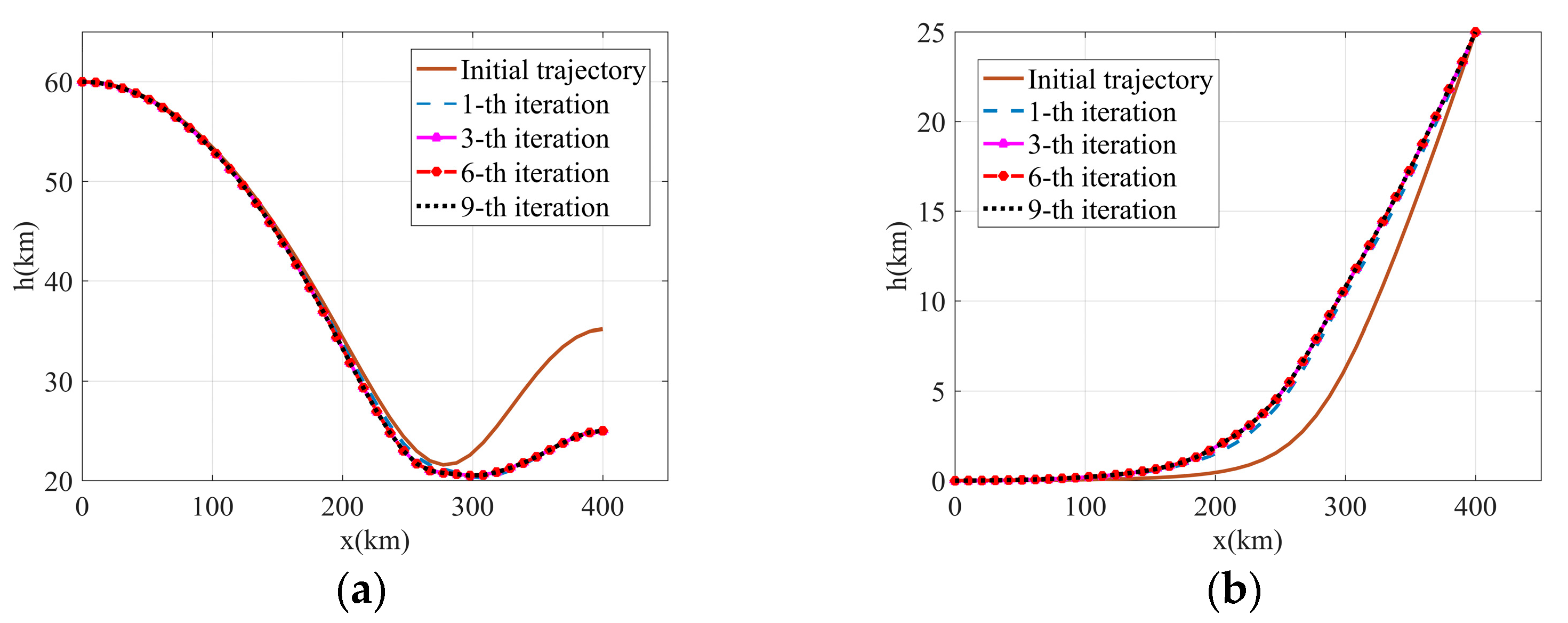
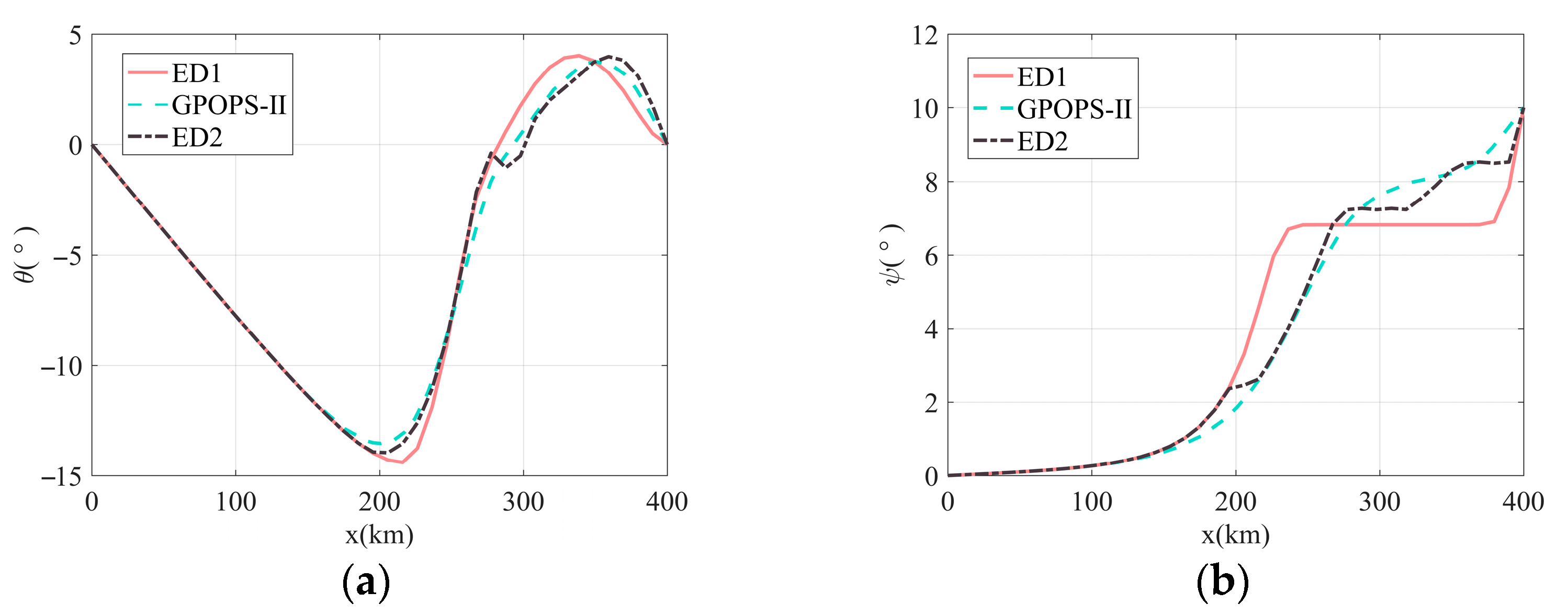
Due to strict constraint conditions, SCP fails to solve the SOCP of the terminal equality constraint (12). Figure 3 presents the convergence after 9 iterations when solving the improved SOCP. The results in Figure 4 and Figure 5 indicate that these three methods have reached the expected terminal state and realized the trajectory planning, which shows the effectiveness of the terminal error proportional relaxation method.

Table 2. Summary and comparison of solutions.

Method	Discrete Point	Iterations	CPU Time (s)
SCP(ED)	40	25	0.796
GPOPS-II	41	-	5.476
SCP(ED2)	40	9	0.296

demonstrates that SCP exhibits significant advantages over GPOPS-II in CPU time for large-scale discrete trajectory optimization, with the improved SOCP solution time accounting for merely 5.4% of that required by GPOPS-II. The computation time for the improved SOCP is 37.2% of that required by the terminal error proportion-relaxed SOCP. The total computation time for the first-layer solution of the variable-discrete-scale SCP in midcourse guidance is 0.345 s.

Table 3. Comparison between optimization results and state integration.

Method	Terminal State Error					Maximum State Error
	$\mathit{h},\mathbf{m}$	$\mathit{z},\mathbf{m}$	$\mathit{x},\mathbf{m}$	$\mathit{\theta },\mathbf{deg}$	$\mathit{\psi },\mathbf{deg}$	$\mathit{h},\mathbf{m}$	$\mathit{z},\mathbf{m}$	$\mathit{x},\mathbf{m}$	$\mathit{\theta },\mathbf{deg}$	$\mathit{\psi },\mathbf{deg}$
SCP(ED1)	61.004	190.088	11.881	0.149	0.051	156.552	200.291	12.518	0.201	0.088
GPOPS-II	58.464	85.749	40.602	0.006	0.069	58.964	85.749	40.602	0.052	0.072
SCP(ED2)	44.892	90.561	5.660	0.140	0.043	131.484	113.965	7.123	0.164	0.081

presents the solution accuracy of different methods for the midcourse guidance problem. The SCP with ED1 yields the poorest accuracy with a maximum state error of approximately 10.9‰. In comparison, GPOPS-II and SCP with ED2 achieve significantly better performance, demonstrating maximum state errors around 7.2‰ and 8.8‰, respectively. The superior accuracy of ED2 compared to both ED1 primarily stems from its normalized path constraints, which exhibit smaller magnitude differences relative to other state constraints. This effectively prevents the neglect of minor constraint errors, thereby enhancing overall solution precision.

5.2. Variable-Discrete-Scale Optimization

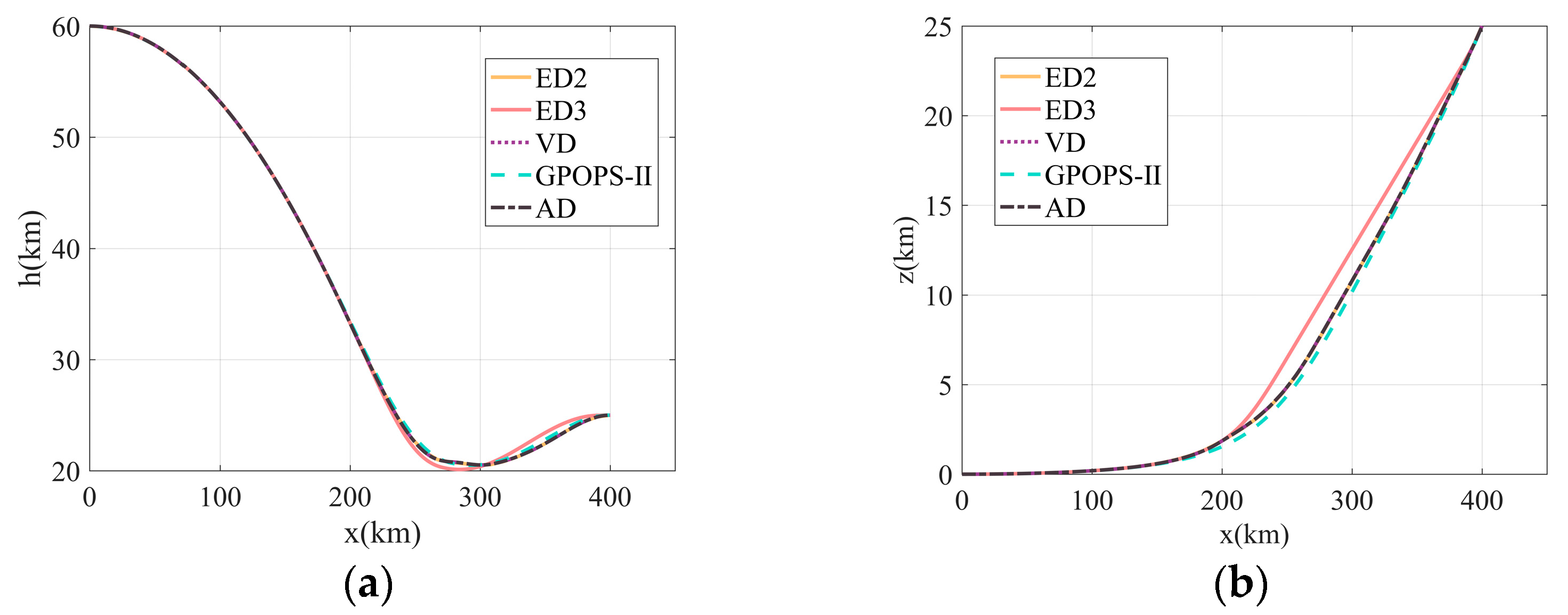
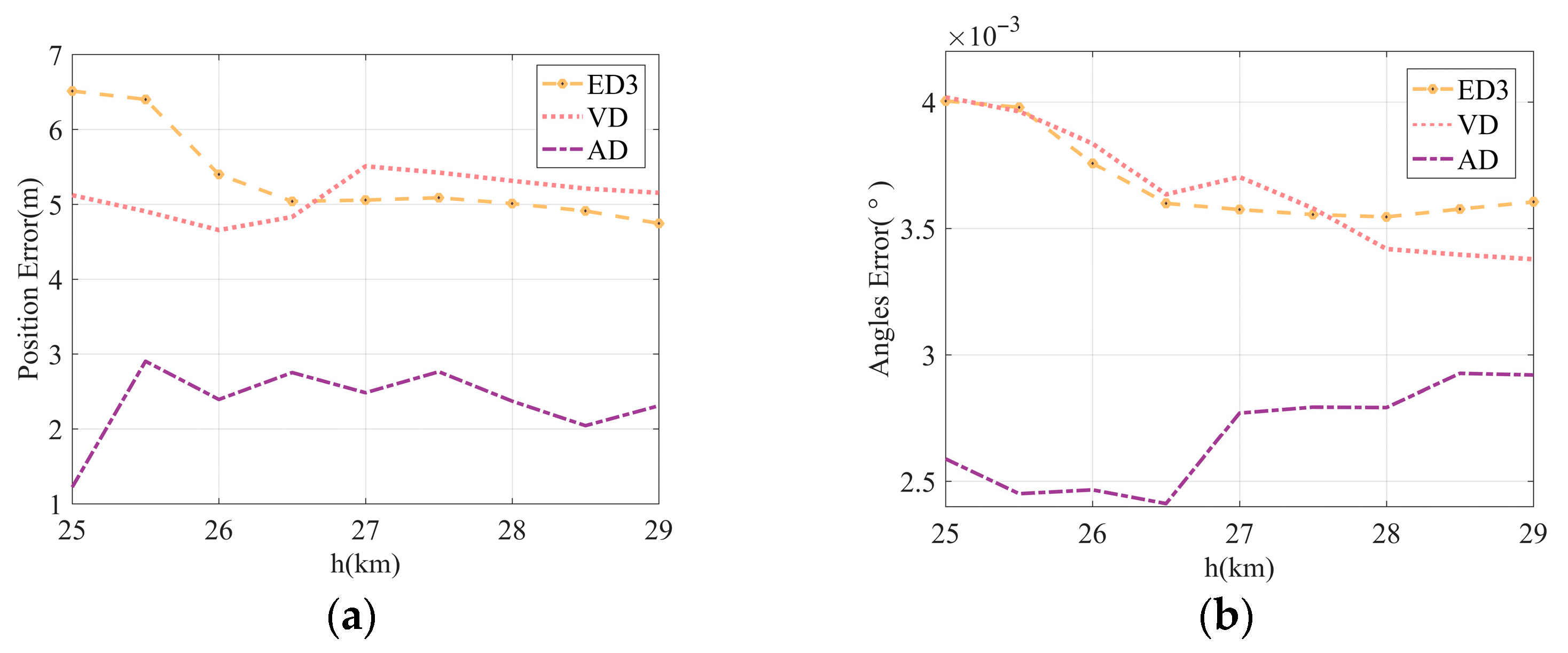
For comparative analysis, we employ improved SOCP-based SCP (where ED3 denotes equidistant small-scale discretization, while VD and AD represent variable-discrete-scale and adaptive variable-discrete-scale optimization, respectively) along with the software GPOPS-II to solve Problem P0. In the variable-discretization-scale simulation of this section, the ED2 solution is employed as an initial guess to further refine the optimization results obtained from the SCP method. Note that the condition ${\kappa }_{\psi }=0.01$ is applied here.

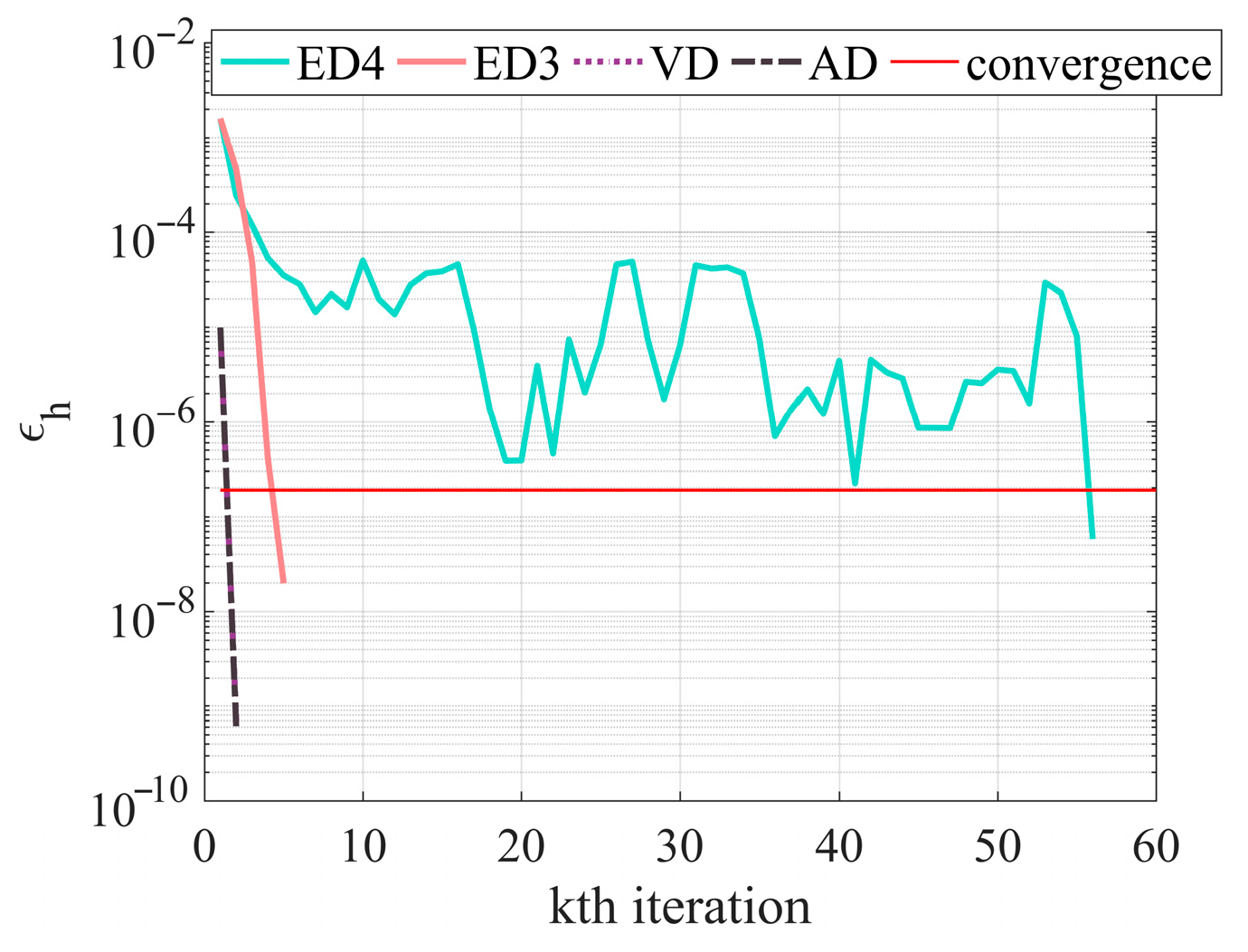
Figure 6 and Figure 7 compare the solving results of different schemes, all of which satisfy the process constraints and achieve the specified terminal states. It is noteworthy that although the SOCP with only terminal error proportional relaxation (named ED4) successfully generates a trajectory, it converges only after 56 iterations.

Figure 8 shows the maximum iteration intervals in altitude for the four SCP solutions. Among them, the SCP of ED4 exhibits significant oscillations and a notably increased number of iterations. This is due to the absence of an acceleration convergence term, as well as the increase in the number of discrete points and the expansion of the matrix scale. Both VD and AD benefit from favorable initial guesses, resulting in reduced maximum iteration intervals.

As can be seen in

Table 4. Simulation results of different methods.

Method	Discrete Point	Iterations	CPU Time (s)
SCP(ED4)	400	56	57.698
SCP(ED3)	400	5	5.364
SCP(VD)	400	2	1.300
GPOPS-II	401	~	22.146
SCP(AD)	399	2	1.298

, for large-scale problems, SCP does not necessarily outperform GPOPS-II in terms of computational efficiency, as observed in ED4. However, compared with GPOPS-II, SCP with convergence acceleration terms, such as ED3, VD, and AD, demonstrates higher computational efficiency. The total computation times for ED4, ED3, VD, and AD are 57.747 s, 5.413 s, 1.645 s, and 1.643 s, respectively. The computation times of the latter three, which employ the improved SOCP formulation, are all less than one-tenth of that of ED4. Among the improved SOCP methods, the total computation times required for VD and AD to successfully generate trajectories account for only 30.39% and 30.35% of that of ED3, respectively, demonstrating the effectiveness of the variable-discrete-scale method.

Table 5. Comparison between optimization results and state integration.

Method	Terminal State Error					Maximum State Error
	$\mathit{h},\mathbf{m}$	$\mathit{z},\mathbf{m}$	$\mathit{x},\mathbf{m}$	${\displaystyle \frac{\mathit{\theta },\mathrm{deg}}{{10}^{-2}}}$	${\displaystyle \frac{\mathit{\psi },\mathrm{deg}}{{10}^{-2}}}$	$\mathit{h},\mathrm{m}$	$\mathit{z},\mathbf{m}$	$\mathit{x},\mathbf{m}$	${\displaystyle \frac{\mathit{\theta },\mathrm{deg}}{{10}^{-2}}}$	${\displaystyle \frac{\mathit{\psi },\mathrm{deg}}{{10}^{-2}}}$
SCP(ED4)	0.972	4.941	0.309	0. 251	0.017	2.287	5.062	0.316	0.325	0.198
SCP(ED3)	0.623	5.539	0.346	0.386	0.014	3.020	5.724	0.355	0.409	0.185
SCP(VD)	0.127	4.699	0.294	0.369	0.033	2.697	4.867	0.303	0.371	0.263
GPOPS-II	0.246	3.979	0.422	0.052	0.223	0.426	3.979	0.422	0.110	0.229
SCP(AD)	0.363	0.808	0.051	0.244	0.015	2.102	3.245	0.128	0.392	0.193

compares the terminal state errors and maximum state errors between the optimization results and the integration results for different methods. The simulation results for SCP(ED4) indicate that an increase in the number of iterations does not necessarily lead to improved accuracy. In terms of position accuracy, the terminal state error of SCP(AD) is the smallest, which is 81.2% higher than that of SCP(ED3) and better than that of GPOPS-II. Furthermore, a strong correlation was observed between the terminal state error and the maximum state error in the range, x (which effectively represents the downrange distance in the simulation), particularly for the terminal position error. When the maximum state error in the range domain is small, the terminal state error also decreases significantly. The underlying mechanism for this phenomenon can be attributed to deviations in the dynamic response over the range domain, which lead to a phase shift in the control profile. This timing-like misalignment accumulates along the flight path, manifesting as lateral or longitudinal deviations in the state trajectory and resulting in peak errors at certain range points, ultimately compromising the convergence accuracy of the terminal state. Collectively, these experiments demonstrate the advantages of the improved SOCP model and the variable discretization scaling strategy in terms of both computational efficiency and solution accuracy.

Figure 9 illustrates the variations in the total terminal position error and total terminal angle error with respect to altitude. Simulation results indicate no clear correlation between terminal state errors and altitude. Among the methods presented in this paper, the improved SOCP method with a VD strategy exhibits terminal state errors comparable to the baseline improved SOCP. In contrast, the AD achieves a significant reduction in terminal errors. This demonstrates that the VD approach, by leveraging a more accurate reference trajectory, enhances computational efficiency without compromising solution accuracy. Furthermore, the AD strategy effectively balances computational cost and precision.

6. Conclusions

This paper presents a variable-discrete-scale SCP for midcourse guidance trajectory design of aerodynamic control interceptors. The improved SOCP model incorporates three key techniques: terminal error relaxation, variable trust region, and path constraint normalization. This integration leads to a reduction in the number of iterations. A variable-discrete-scale optimization framework is proposed to enhance both trajectory solution accuracy and computational efficiency. Numerical simulation results indicate that the proposed method delivers a solution accuracy comparable to GPOPS-II. However, the computational time required is reduced to less than one-tenth of that of GPOPS-II under large discretization scales. For small-scale discretization optimization, an adaptive variable-scale discretization framework is adopted. The proposed algorithm demonstrates a solution accuracy that is comparable to that obtained by GPOPS-II. The computational time required is only 30.4% of that needed by small-scale discretized SCP under the same model. Furthermore, the proposed variable discretization optimization framework exhibits strong versatility for generating high-precision trajectories and is straightforward to implement.

The proposed improved SOCP model employs a variable trust region method to determine the iteration step size, which increases computational complexity and reduces single-iteration efficiency. In the next step, a line search algorithm will be adopted to optimize the step size determination process, thereby improving overall computational efficiency.