Research on Residual Strength and Evaluation Methods of Aircraft Panel Structures with Perforations
Abstract
1. Introduction
2. Tensile Fracture Tests on Panels with Pre-Fabricated Holes (Plain Panels) and Stiffened Panels
3. Analysis of Test Results
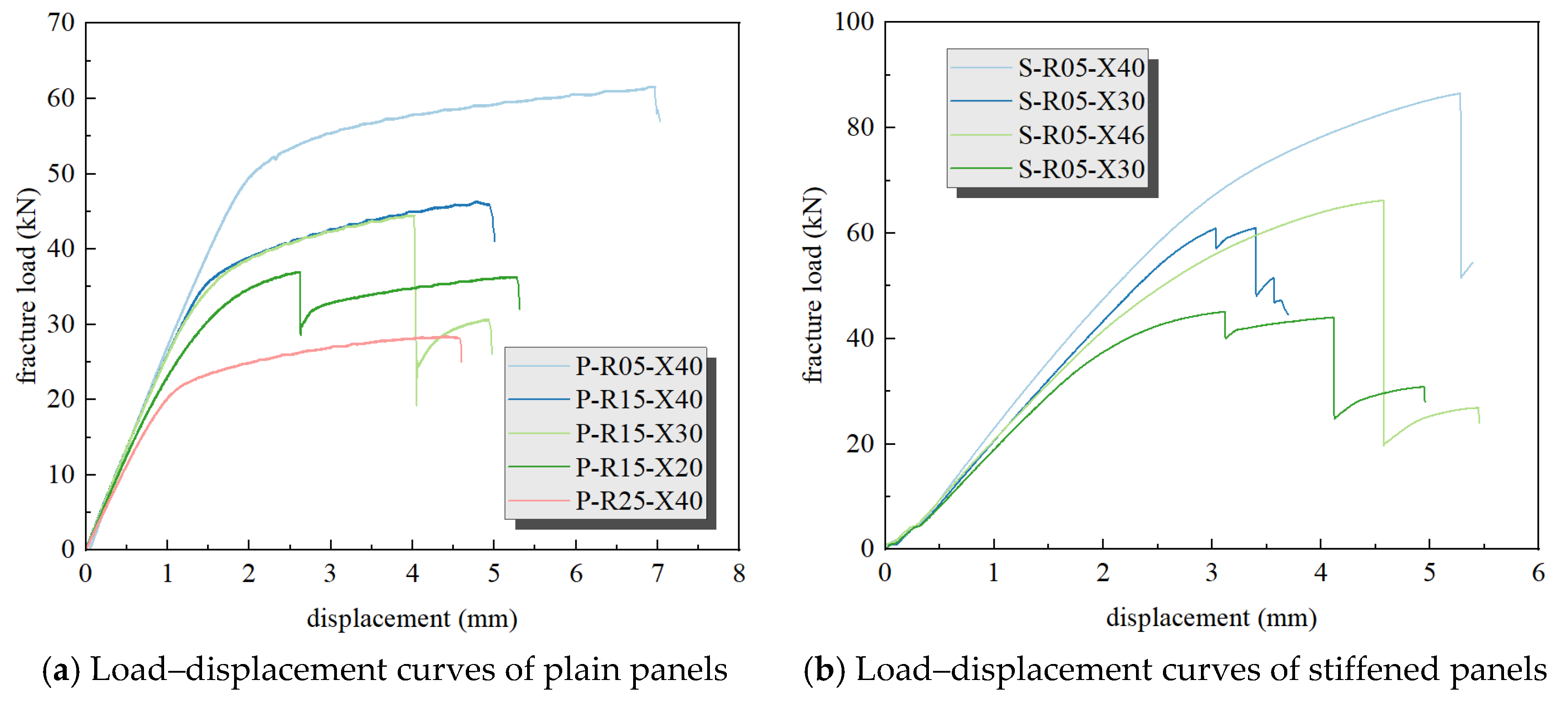
3.1. Analysis of Plain Panel Test Results
3.2. Analysis of Stiffened Panel Test Results
4. Numerical Simulation Setups
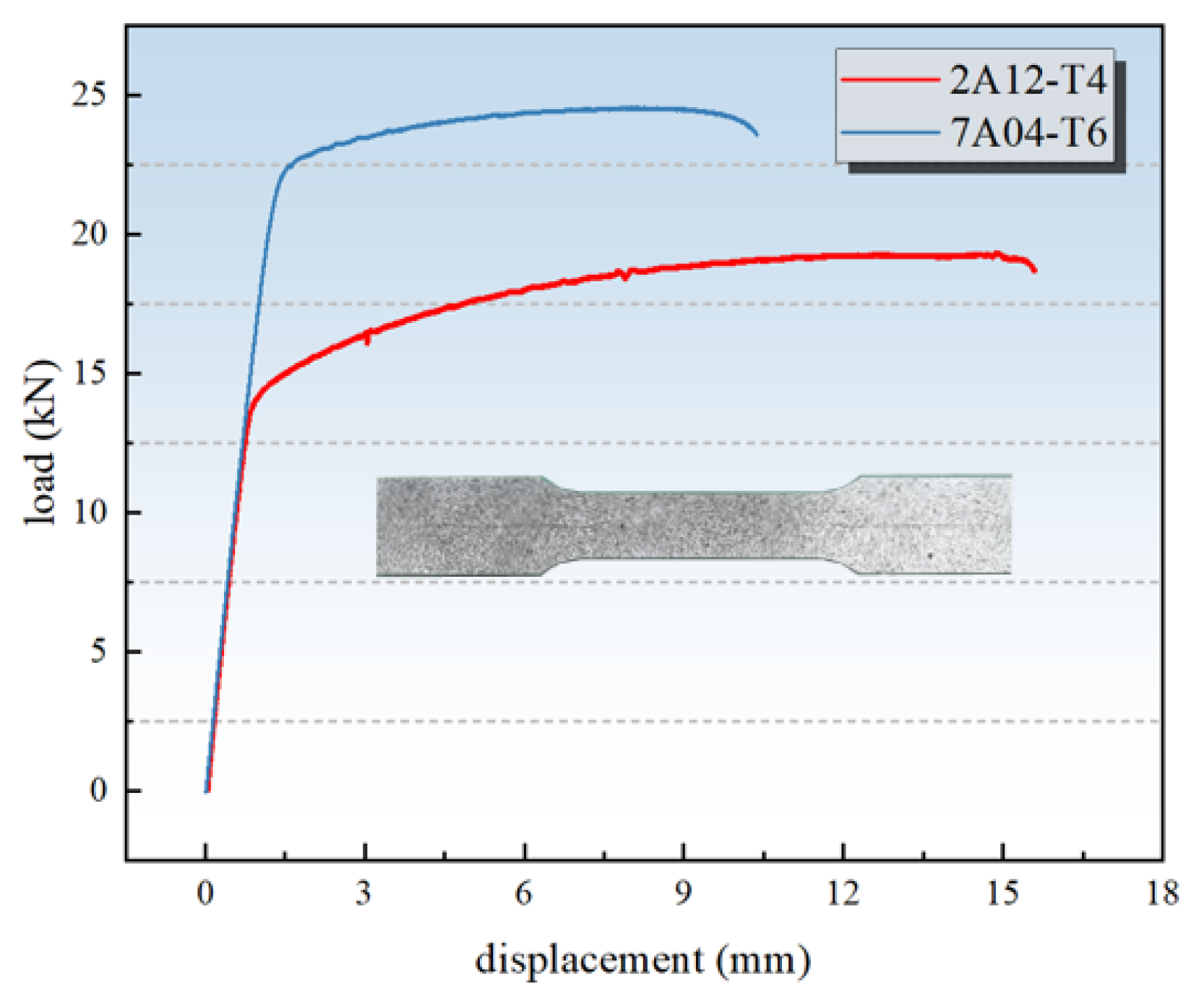
4.1. Material Constitutive
4.2. Model Setups
4.3. Model Validation
4.3.1. Mesh Independence Validation
4.3.2. Comparison Between Experiment and Simulation
4.4. Simulation Result
5. Variation Patterns of Panel Residual Strength
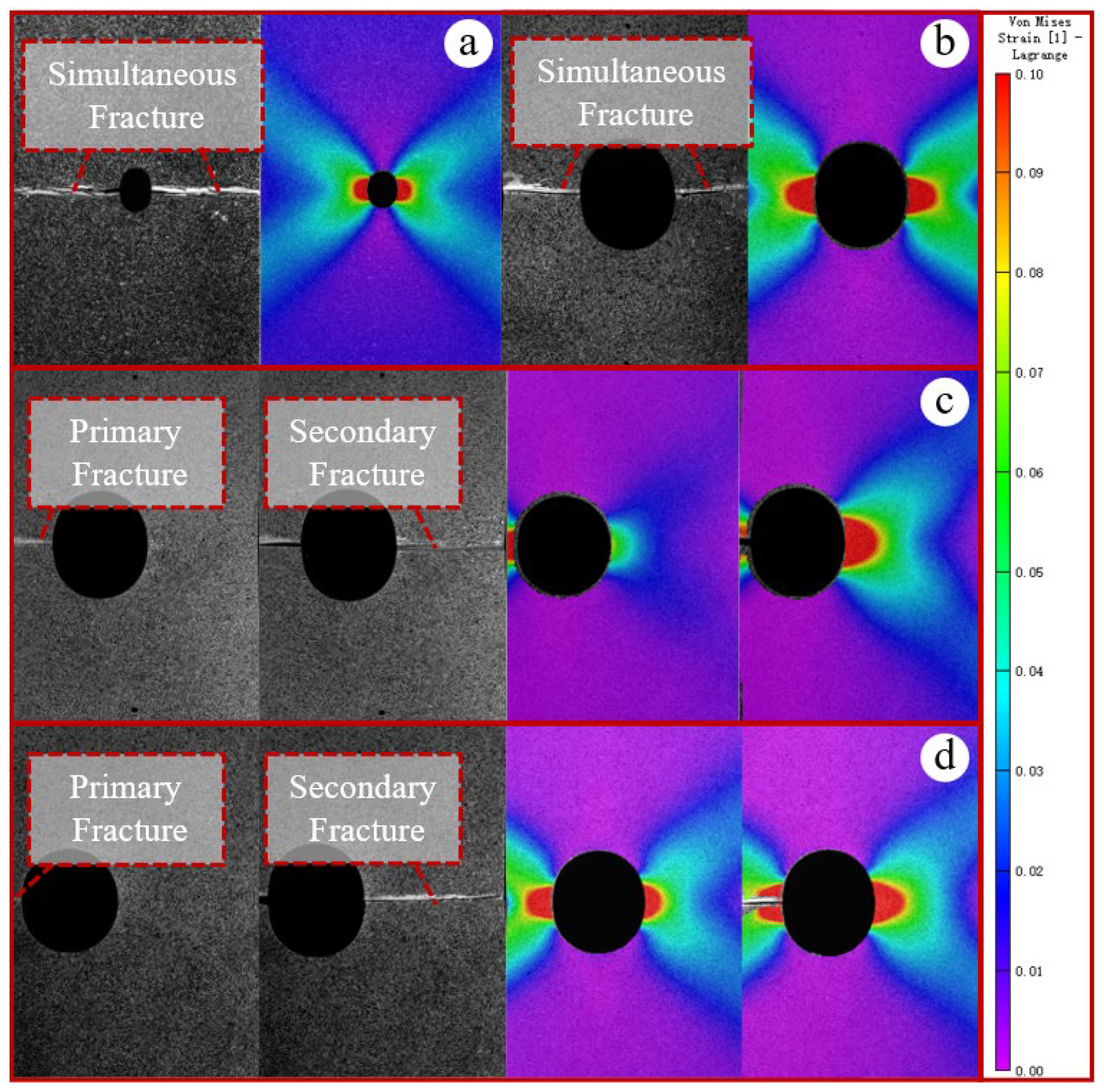
5.1. Fracture Mechanism
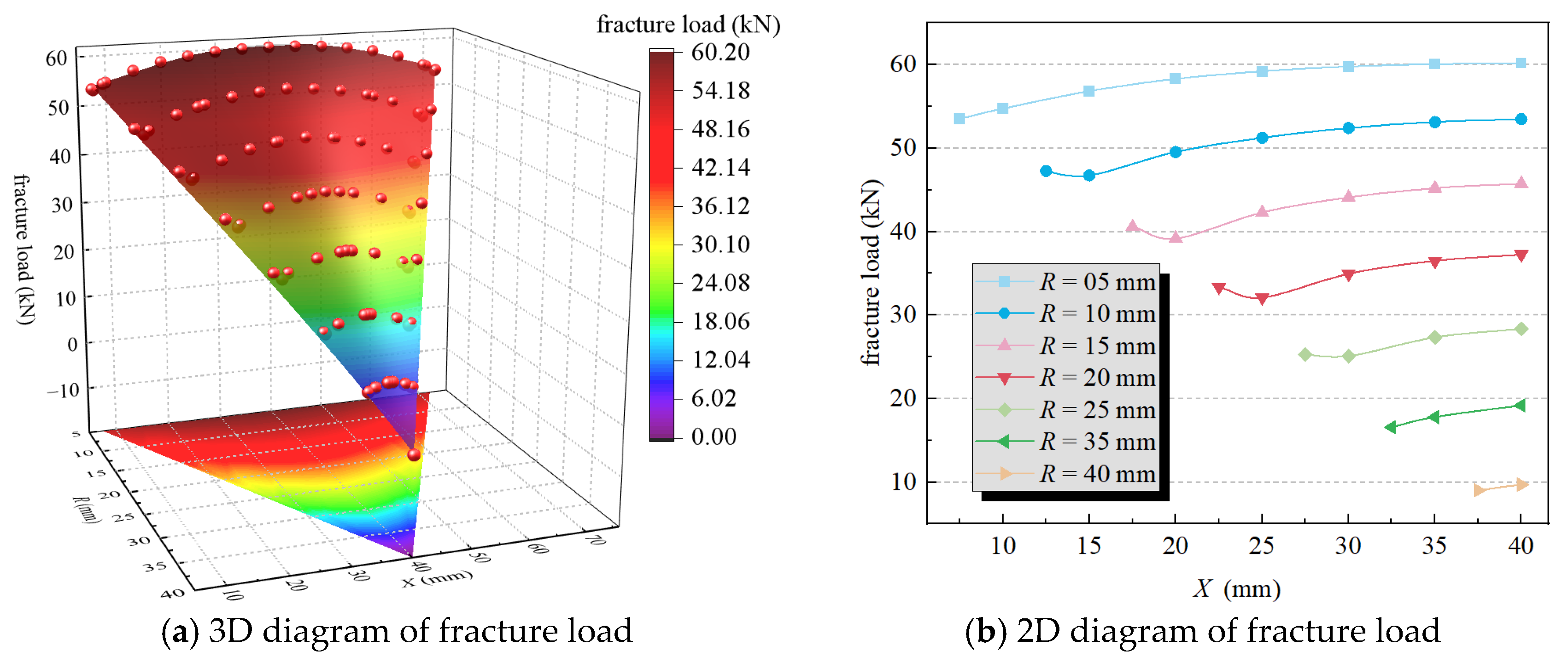
5.2. Simulation Data Analysis
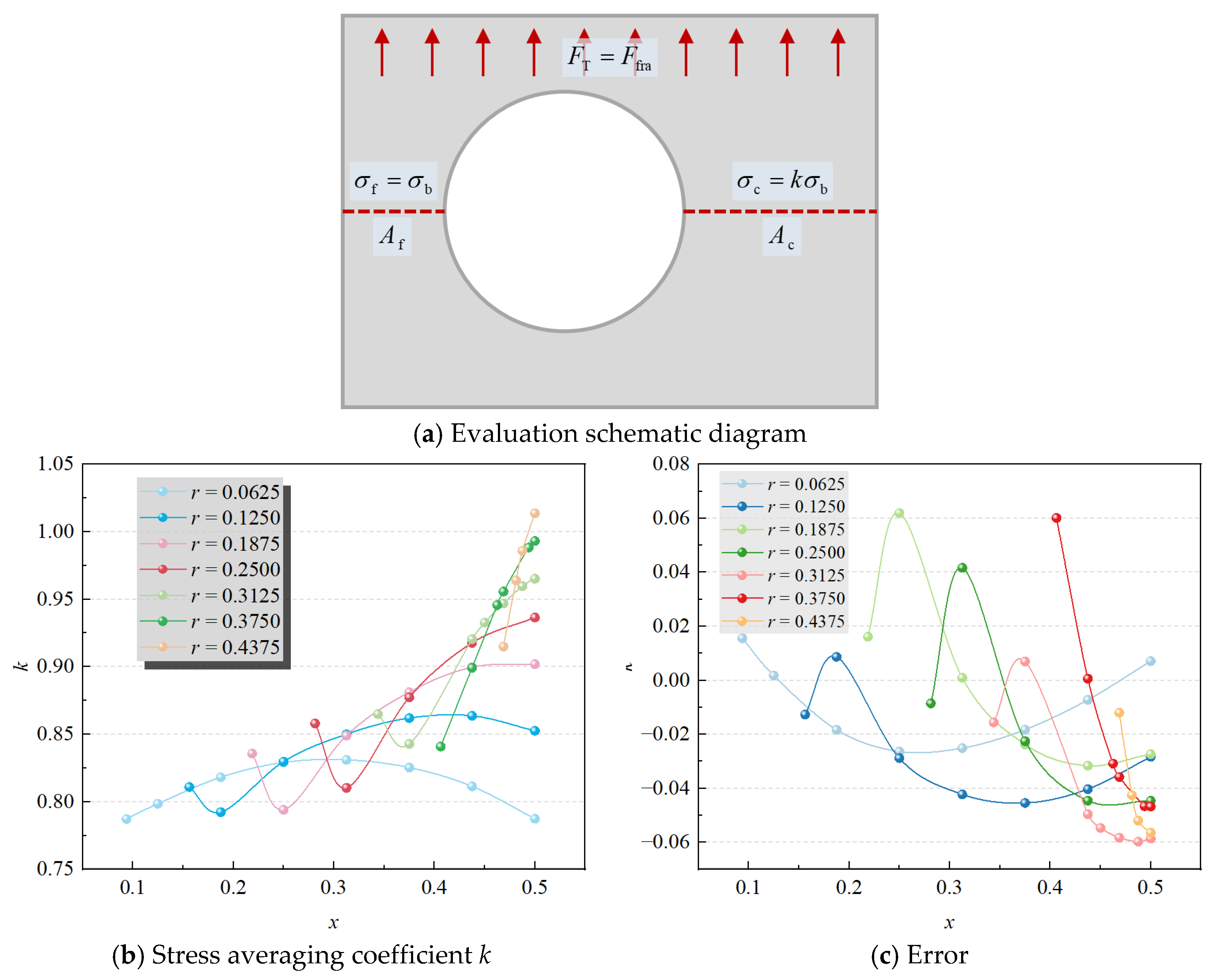
5.3. Evaluation Methods for Fracture Load of Panel Structures
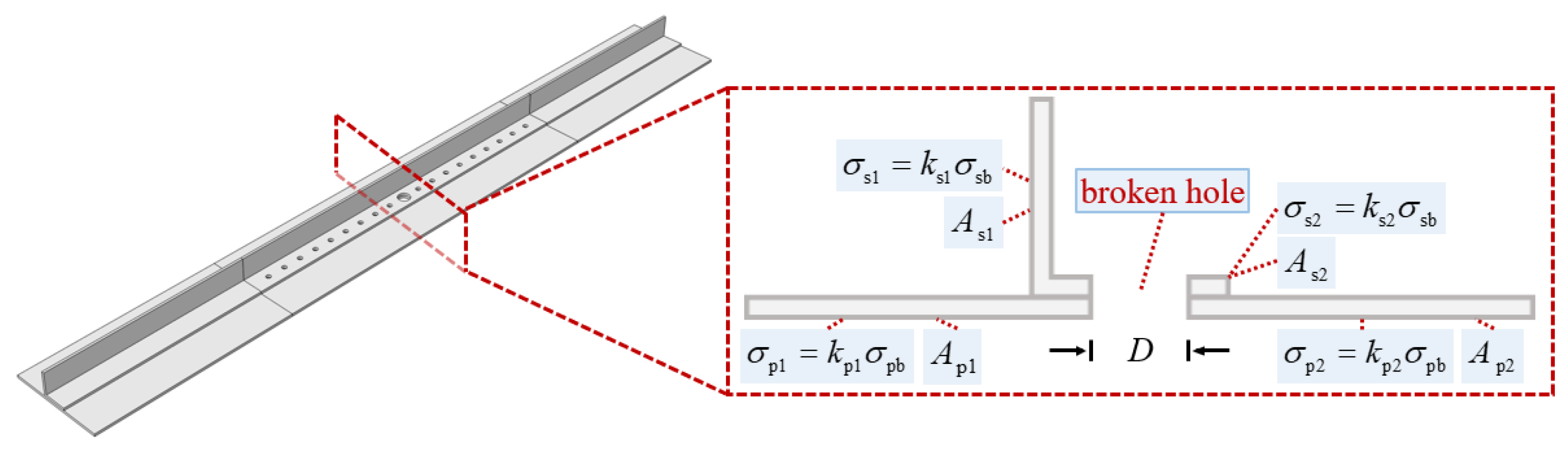
5.4. Evaluation Methods for Fracture Load of Stiffened Panel Structures
6. Conclusions
- For the panel specimen with a central hole, fracture occurs simultaneously on both sides due to uniform loading. In contrast, for the panel specimen with an eccentric hole, asymmetric constraints lead to stress concentration and strain release on the free side, resulting in the free side fracturing first, followed by the constrained side
- The load–displacement curve for the centrally perforated panel exhibits only a single load drop. However, the load–displacement curve for the eccentrically perforated panel shows two load drops due to the sequential fracture of the panel material on either side of the hole. The relationship between these two fracture loads exhibits a dual-peak critical value, Xdual.
- The load–displacement curve for the stiffened panel specimen displays multiple load drops. Because the 7000-series aluminum alloy is more brittle than the 2000-series aluminum alloy, the stiffener fractures first under quasi-static tensile loading. Subsequently, the failure mode of the skin becomes consistent with that of the plain panel.
- The stress distribution is uneven across the two sides of the hole in eccentrically perforated panels. The Net Section Failure Criterion shows significant evaluation errors for these panels. Introducing a stress averaging coefficient (k) to modify the relationship between the Net Section Failure Criterion and the hole’s location and size improve the evaluation accuracy of the residual strength for perforated panels, with the maximum error reduced to 6.19%.
- The modified method of the Net Section Failure Criterion for plain panels was extended to stiffened panels. A stress averaging coefficient was introduced for each sectional region to account for the influence of hole location and size. After this modification across four test conditions, the maximum error was 3.15%
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, B.; Lv, J.; Dang, P. Research on the design factors and assessment for aircraft structures combat survivability. Adv. Aeronaut. Sci. Eng. 2022, 13, 50–58. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, H.; Yu, K. Briefing on Military Aircraft Battle Damage System Assessment. Aviat. Maint. Eng. 2007, 1, 30–33. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, T.; Zhang, H. Damage Evaluation of Typical Aircraft Panel Structure Subjected to High-Speed Fragments. Aerospace 2025, 12, 354. [Google Scholar] [CrossRef]
- Li, Y.; Yang, B.; Cao, C. Analysis of Load-bearing Capacity of Aircraft Thin-wall Parts Damage before and after Riveting Repair. New Technol. New Process 2024, 9, 47–50. [Google Scholar] [CrossRef]
- Zu, G.; Pei, Y.; Hou, P. Review of aircraft battle damage assessment and repair estimation and design technology. Acta Aeronaut. Et Astronaut. Sin. 2020, 41, 87–108. [Google Scholar]
- Li, C.; Li, J.; Wu, Z.; Gao, Y.; Sun, X. Study on key technology requirements analysis for integrity maintenance of typical helicopters. Adv. Aeronaut. Sci. Eng. 2023, 14, 128–137. [Google Scholar]
- Li, S.; Hou, M.; Liu, J.; Li, S.; Liu, Y. Building of the Model Base in ASBDARDSS. J. Air Force Eng. Univ. (Nat. Sci. Ed.) 2006, 7, 3. [Google Scholar]
- Wang, Y.T.; He, Y.T.; Zhang, T.; Fan, X.H.; Zhang, T.Y. Damage analysis of typical structures of aircraft under high-velocity fragments impact. Alex. Eng. J. 2023, 62, 431–443. [Google Scholar] [CrossRef]
- Jia, L.; Yu, N. Research on Repair Process of Damaged Aircraft. Aviat. Maint. Eng. 2022, 10, 94–97. [Google Scholar] [CrossRef]
- Strąg, M.; Świderski, W. Non-destructive inspection of military-designated composite materials with the use of Terahertz imaging. Compos. Struct. 2023, 306, 116588. [Google Scholar] [CrossRef]
- Yao, X.; Zhao, B.; Xuan, S.; Xue, X.; Miao, C.; Yang, H.; Zhou, J. Development of Science and Engineering Technology of Aviation Composite Structural Repair. Aeronaut. Manuf. Technol. 2024, 67, 24–41. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, T.; Zhang, H.; He, Y.; Ma, L.; Ren, A. The Dynamic Response of Aluminum Alloy Plates Subjected to Multiple-Fragment Impacts Under Pre-Tensile Loading: A Numerical Study. Aerospace 2025, 12, 353. [Google Scholar] [CrossRef]
- He, Y.; Zhang, T.; Gou, B. Opinions on the development of military aircraft structural strength based on aircraft structural operational integrity. Adv. Aeronaut. Sci. Eng. 2023, 14, 1–7. [Google Scholar] [CrossRef]
- Yang, H.; Zhu, B.; Gao, Y.; Lei, Y. Effects of penetrating holes on tensile properties of titanium honeycomb core panels with variable cross-section. Aeronaut. Manuf. Technol. 2022, 65, 92–95. [Google Scholar] [CrossRef]
- He, W.; Wang, C.; Wang, S.; Yao, L.; Wu, J.; Xie, D. Tensile mechanical behavior and failure mechanisms of multihole fiber metal laminates—Experimental characterization and numerical prediction. J. Reinf. Plast. Compos. 2020, 39, 499–519. [Google Scholar] [CrossRef]
- Hou, R.; Zhang, J.; Zhou, P.; Tu, M. Residual Strength Analysis of Aircraft LY12 Structure Impacted by Projectile. Aeronaut. Manuf. Technol. 2005, 5, 91–92. [Google Scholar]
- Yao, W.W.; Zhou, P.; Hou, S.L.; Gao, Y.K. Investigation on Residual Strength of Airplane Plate with Smooth Circular Hole. Appl. Mech. Mater. 2013, 2454, 31–34. [Google Scholar] [CrossRef]
- Jia, B.; Liu, P.; Lu, X.; Geng, Y. Analysis and Assessment on Residual Strength of the Non-Collinear Multi-Crack Structures. Mech. Des. Manuf. 2024, 5, 229–233. [Google Scholar] [CrossRef]
- Wang, J.; Callinan, R. Residual strengths of composite structures subjected to ballistic impact. Compos. Struct. 2014, 117, 423–432. [Google Scholar] [CrossRef]
- Beygi, R.; Akhavan-Safar, A.; Carbas, R.; Barbosa, A.Q.; Marques, E.A.S.; da Silva, L.F.M. Utilizing a ductile damage criterion for fracture analysis of a dissimilar aluminum/steel joint made by friction stir welding. Eng. Fract. Mech. 2022, 274, 108775. [Google Scholar] [CrossRef]
- Li, F.; Yuan, H.; Liu, H. Implementation of metal ductile damage criteria in Abaqus FEA. J. Phys. Conf. Ser. 2021, 1906, 012058. [Google Scholar] [CrossRef]
- Chen, G.; Ren, C.; Zhang, P.; Cui, K.; Li, Y. Measurement and finite element simulation of micro-cutting temperatures of tool tip and workpiece. Int. J. Mach. Tools Manuf. 2013, 75, 16–26. [Google Scholar] [CrossRef]
- Liu, C.; Sun, Q.; Liu, Y. Numerical simulation of finite deformation and failure of 2A12 specimens under three-dimensional stress state. Chin. J. Nonferrous Met. 2014, 24, 10. [Google Scholar]
- Yang, J.; Zhang, T.; Kong, C.; Sun, B.; Zhu, R. Application of Python-Based Abaqus Secondary Development in Laser Shock Forming of Aluminum Alloy 6082-T6. Micromachines 2024, 15, 439. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Wang, A.; Wang, L.; Tan, T. Multi-pass roll bending process of asymmetric Z-section profiles based on ABAQUS secondary development. Forg. Stamp. Technol. 2023, 48, 152–161. [Google Scholar] [CrossRef]
- Salih, E.L.; Gardner, L.; Nethercot, D.A. Numerical investigation of net section failure in stainless steel bolted connections. J. Constr. Steel Res. 2010, 66, 1455–1466. [Google Scholar] [CrossRef]
- Jiang, K.; Zhao, O. Net section failure of S690 high-strength steel angle-to-plate connections. J. Struct. Eng. 2022, 148, 04022021. [Google Scholar] [CrossRef]
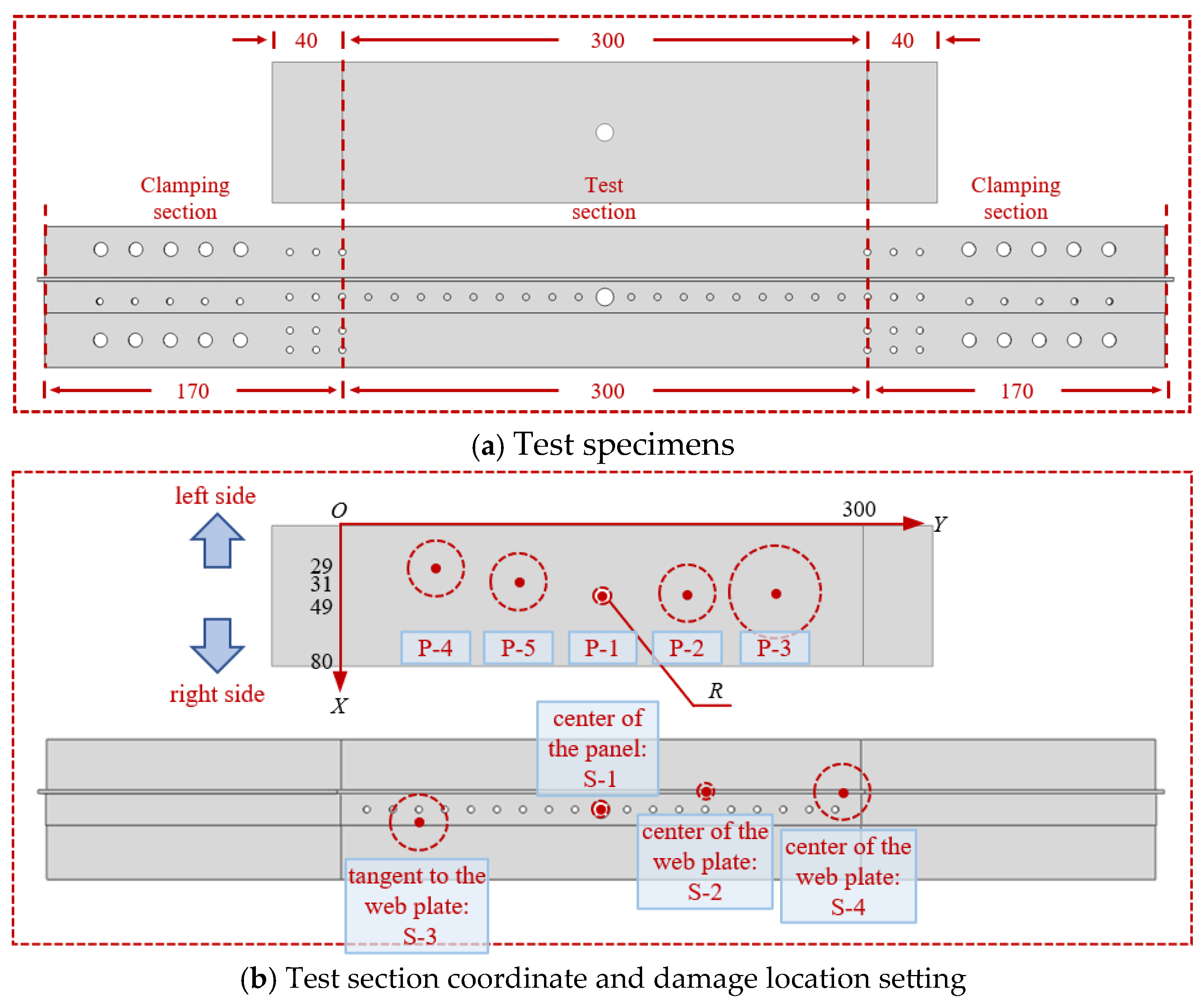


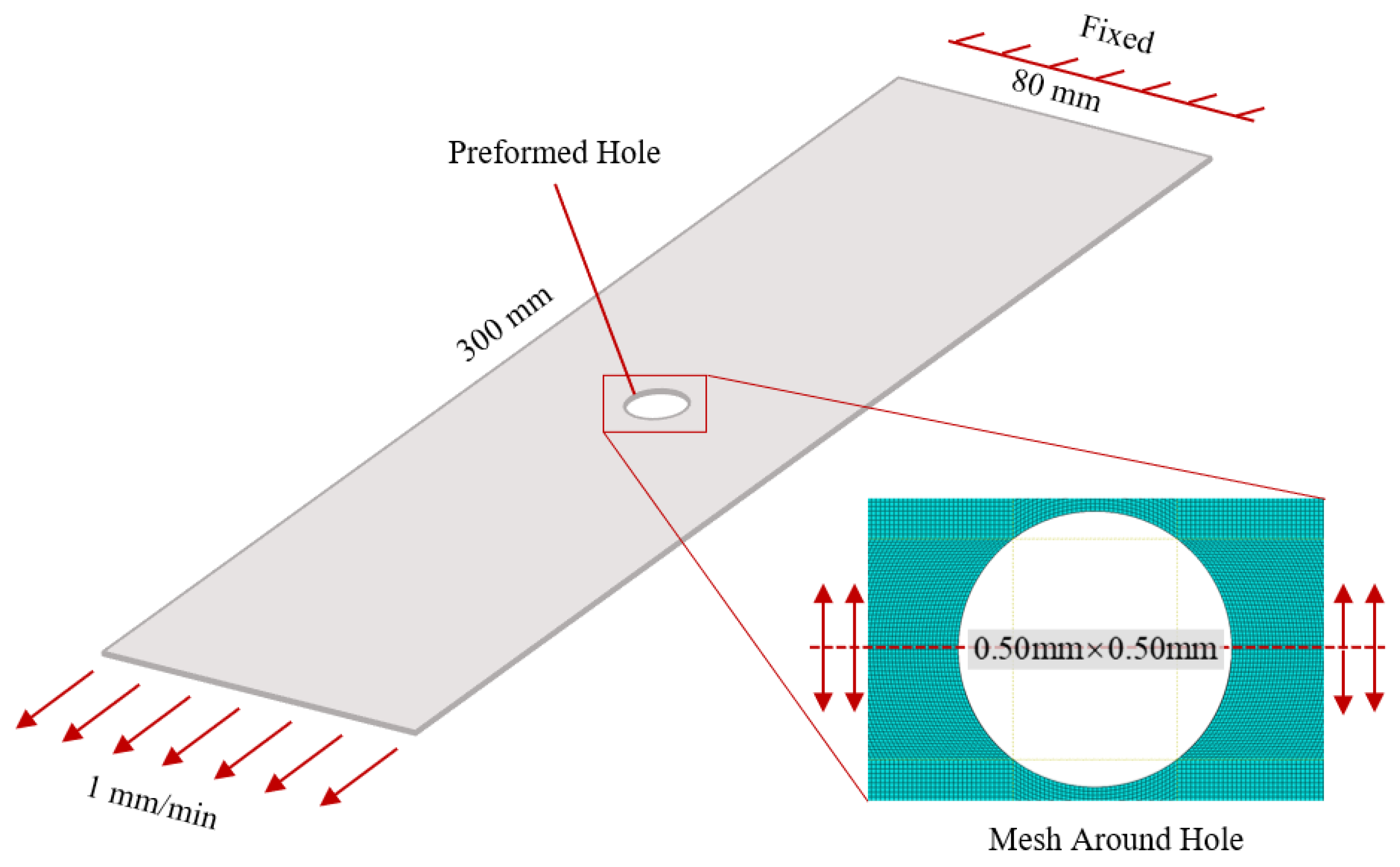

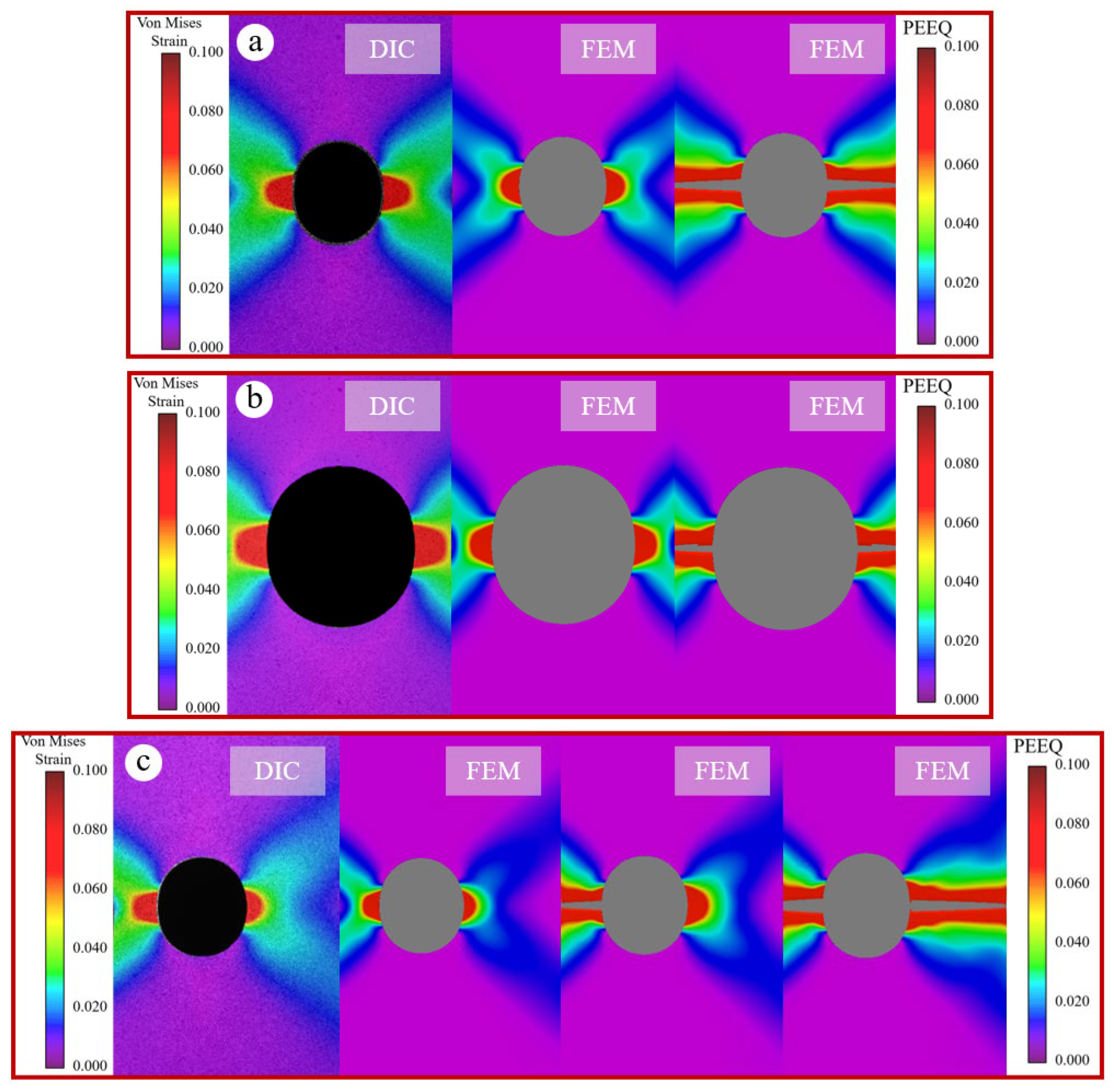
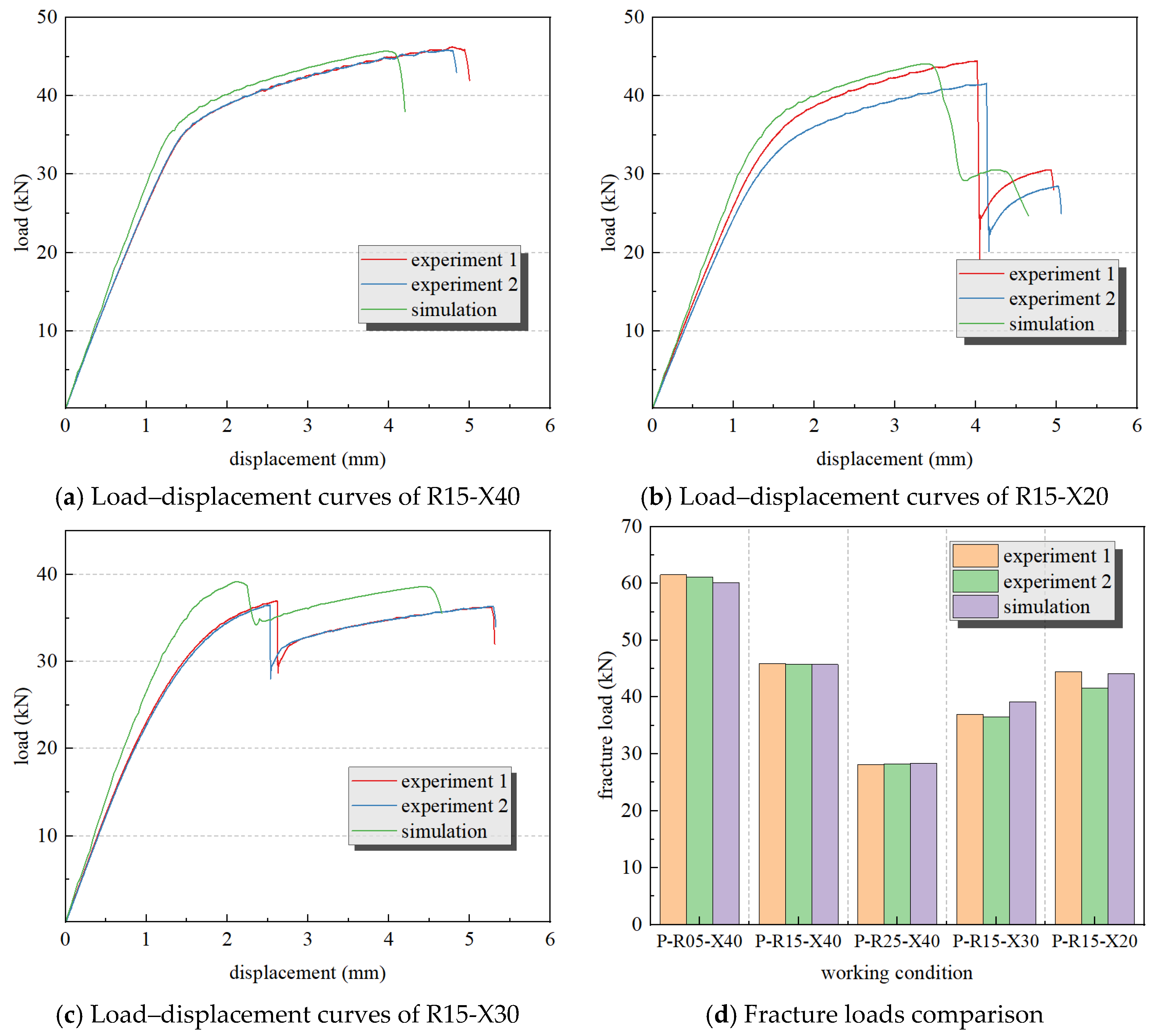
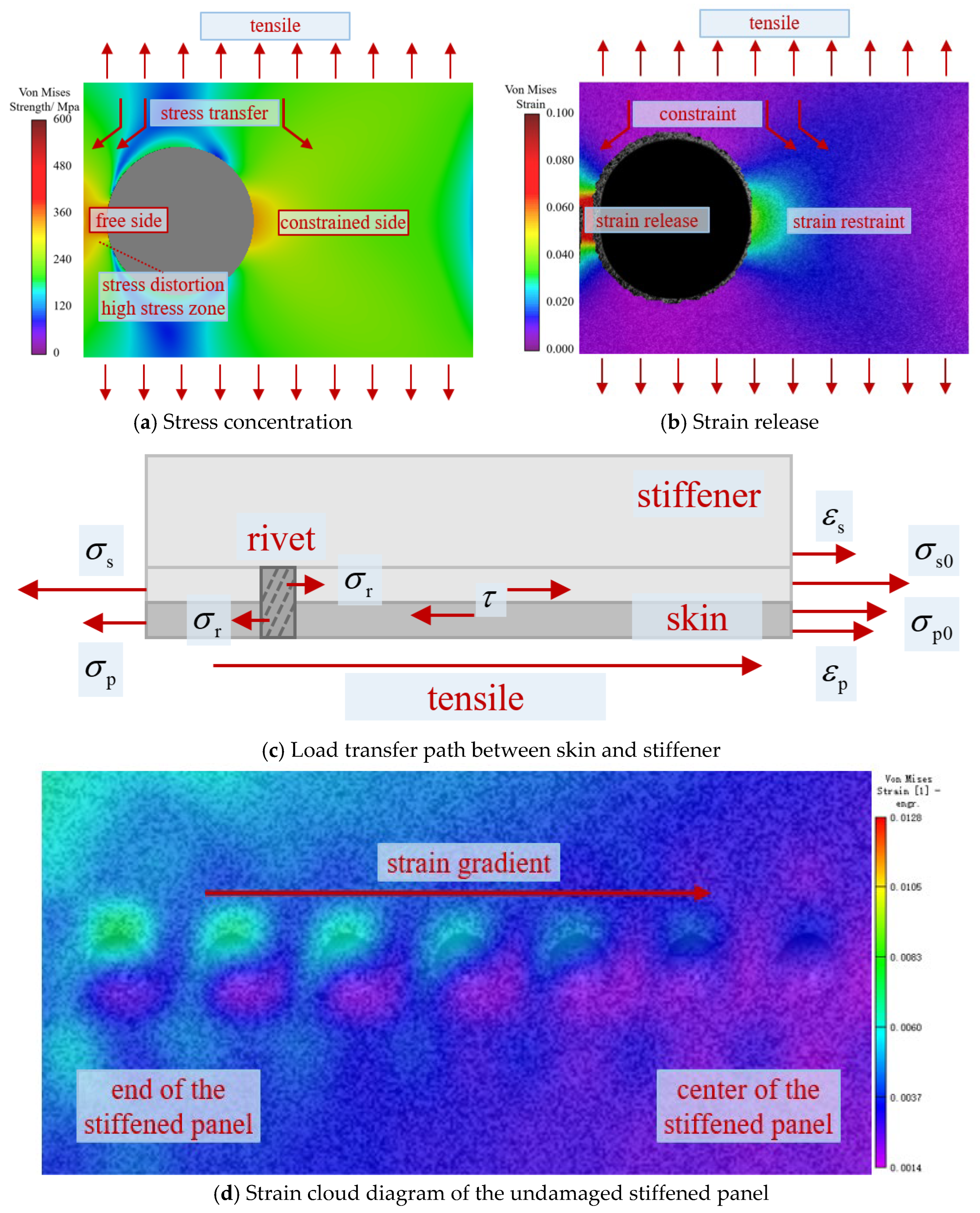
| Test Specimen Numbering | Panel Types | Perforation Radius R/mm | Perforation Center Offset X/mm | Damage Location |
|---|---|---|---|---|
| P-R05-X40 | plain | 5 | 40 | Figure 1b P-1 |
| P-R15-X40 | plain | 15 | 40 | Figure 1b P-2 |
| P-R25-X40 | plain | 25 | 40 | Figure 1b P-3 |
| P-R15-X20 | plain | 15 | 20 | Figure 1b P-4 |
| P-R15-X30 | plain | 15 | 30 | Figure 1b P-5 |
| S-R05-X40 | stiffened | 5 | 40 | Figure 1b S-1 |
| S-R05-X30 | stiffened | 5 | 30 | Figure 1b S-2 |
| S-R15-X46 | stiffened | 15 | 46 | Figure 1b S-3 |
| S-R15-X30 | stiffened | 15 | 30 | Figure 1b S-4 |
| Aluminum Alloy | Elastic Modulus | Poisson’s Ratio | Failure Strain | Tensile Strength |
|---|---|---|---|---|
| 2A12-T4 | 69 GPa | 0.33 | 0.2 | 481 MPa |
| 7A04-T6 | 72 Gpa | 0.33 | 0.14 | 614 MPa |
| Specimen Number | Fracture Load Test Value/kN | Fracture Load Evaluation Value/kN | Error/% |
|---|---|---|---|
| S-R05-X40 | 86.56 | 88.27 | 1.96 |
| S-R05-X30 | 61.02 | 62.21 | 1.96 |
| S-R15-X46 | 66.22 | 68.19 | 2.97 |
| S-R15-X30 | 45.10 | 46.52 | 3.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, A.; Zhang, T.; An, T.; Wang, Y.; Ma, L. Research on Residual Strength and Evaluation Methods of Aircraft Panel Structures with Perforations. Aerospace 2025, 12, 950. https://doi.org/10.3390/aerospace12110950
Ren A, Zhang T, An T, Wang Y, Ma L. Research on Residual Strength and Evaluation Methods of Aircraft Panel Structures with Perforations. Aerospace. 2025; 12(11):950. https://doi.org/10.3390/aerospace12110950
Chicago/Turabian StyleRen, Antai, Teng Zhang, Tao An, Yitao Wang, and Liying Ma. 2025. "Research on Residual Strength and Evaluation Methods of Aircraft Panel Structures with Perforations" Aerospace 12, no. 11: 950. https://doi.org/10.3390/aerospace12110950
APA StyleRen, A., Zhang, T., An, T., Wang, Y., & Ma, L. (2025). Research on Residual Strength and Evaluation Methods of Aircraft Panel Structures with Perforations. Aerospace, 12(11), 950. https://doi.org/10.3390/aerospace12110950





