Abstract
This article outlines a general approach to determining propellant mass requirements for operating a momentum exchange tether (MET), the rotation of which is driven by traditional thrusters for rideshare payload deployments. For payloads flying aboard rideshare launches, some may require unique deployment and ΔV requirements different from those of other payloads, requiring dedicated payload-based propulsion or unique deployment operations. By implementing METs, minimal hardware modification and native deployer-based propulsion can be used to support these unique deployments and expand deployer capabilities. Following initial tether hardware definition, vehicle-agnostic maneuvers for system spin-up, spin-down, and orbit correction maneuvers can be designed, each with their own propellant requirements. The total propellant mass for these maneuvers can contribute to later comparison with other deployment methods, such as motor-driven METs or traditional propulsive maneuvering.
1. Introduction
In recent years, rideshare missions have gained popularity and have delivered large quantities of payloads to orbit, many of which often require unique deployment configurations into specific orbits different from other payloads on shared launches [1]. To execute additional maneuvers specific to a rideshare payload, either the payload itself must implement its own propulsion system to complete its journey to operational orbit after deployment, or its deployer vehicle must execute additional operations which can affect the rest of the deployment sequence for other payloads. One potential design option which may introduce more flexibility in deployer vehicle capabilities while requiring minimal hardware modifications could be to implement thruster-driven momentum exchange tethers (METs) for deploying payloads with unique post-launch ΔV requirements.
This manuscript expands on some of the concepts introduced in Reference [2], which discusses sequential payload deployments utilizing METs from a single deployer vehicle. Focusing on deployer operations, this manuscript introduces a general process, independent of vehicle design, which can be applied to the design process for a multi-payload launch with MET deployment(s). Unlike prior space tether studies which focus primarily on individual tether performance, dynamic modeling, or other tether applications, this work focuses on the generalized propulsion-driven implementation of METs which can be applied to a wide range of deployer architectures. By utilizing propulsion systems native to a launch vehicle upper stage, orbital transfer vehicle, or similar deployer craft, maneuvers associated with system spin-up, spin-down, and optional orbit correction can be executed while requiring minimal deployer orbit adjustments between sequential deployments. This design process represents a new design methodology for MET-based deployment that directly links mechanical tether behavior with propulsive control and propellant mass estimation, which can act as a supporting segment of early MET-associated mission design by quickly determining mass to orbit requirements to be compared among different deployment methods.
In this manuscript, Section 2 provides a brief description of MET technology, along with how and why it could be considered potential rideshare deployment applications. Next, Section 3 describes the methodology of how developing such an MET system in this fashion is declared, defining the overall system geometry, expected maneuvers, and limitations of the analysis performed. The specifics of the design process are then discussed in Section 4, introducing hardware design factors and associated propulsive maneuvers for spin-up, spin-down, and orbit correction operations. From this, initial propellant mass estimates can be made, capable of informing baseline trade studies against other deployment methods introduced in Section 5.
2. Background
2.1. Momentum Exchange Tethers
A MET is a space propulsion concept that relies on the exchange of momentum between a tether-connected payload and deployer. They are not to be confused with electrodynamic tethers or space webs, which operate on different principles. METs involve driven rotation and separation of a tethered system, converting angular momentum into linear momentum upon release and altering the two previously tethered objects’ trajectories [3,4,5]. Operating this system is similar to the concept of a shepherd’s sling spinning and releasing a stone, like in the Biblical story of David and Goliath. There are a variety of different configurations available with options for the location of tether release mechanisms (such as at either the deployer or payload ends of the tether), the quantity of payloads being deployed (such as “asymmetric” single-payload releases or “symmetric” multi-payload releases), or even the use of tethered counterweights to balance a rotating system, variations of which and their applications are described further in References [2,6,7]. A key advantage of METs is their minimal fuel consumption (or complete avoidance thereof in the case of motorized systems), making them attractive for missions with fuel supply and storage constraints. Despite this, they require precise tether management and can be affected by environmental factors in space, mitigations for which have only been demonstrated on a small number of missions, as collectively summarized by Reference [3]. Limitations to space tether development in general are largely due to limited interest, applicability, and resource allocation, as well as unique tether designs needing to be produced for each mission flown. With continued development in the field of space tethers, industry interest in them may return as new applications arise, particularly for various options of multi-payload or rideshare launches and deployments as described by References [2,6,7,8].
One of the key aspects of the MET concept is the driven rotation of the overall system. There are different options for achieving this, with concepts typically either relying on thrusters for larger-scale systems or motorized systems for some smaller-scale systems. Each of these methods have seen application in space from as far back as the Gemini XI mission in 1967 which utilized cold gas thrusters [9], to as recent as the ADRASTEA mission in 2024 which utilized a single electric motor system for dispersing multiple payloads in sequence [10,11]. To contribute to the field of MET development, this manuscript introduces a general approach that can be applied to thruster-driven MET design in determining propellant mass requirements for operations similar to the Gemini XI tether system, which can be helpful in comparing various propulsion methods for payload deployment.
2.2. Potential Application
The primary intended use case for METs being applied in the manner described in this manuscript is for payload deployments on rideshare missions. With these missions, some payloads may require unique and significant additional ΔV beyond what is provided by the upper stage/deployer system delivering it to orbit. Some solutions to unique mission requirements like these involve implementing additional propulsion systems aboard deployed payloads, or with augmented deployment operations executed by the deployer. Adding propulsion systems to payloads can sometimes be difficult to implement, especially for small satellites which may have limitations due to mass, volume, or technical limitations with the hardware itself; nontechnical limitations can include financial, development time, or other resource limitations applied to the payload developers themselves [12,13]. For augmented deployer operations, two general approaches can be pursued: specifically scheduling deployments so payloads with higher ΔV requirements are reserved for late in the deployment sequence, or having the deployer “take a detour” with executing additional maneuvers between deployments. If high-ΔV payloads are reserved for late in the deployment sequence after most/all other payloads aboard the flight have been deployed, the additional ΔV can produced by the deployer, possibly without requiring a return to a prior deployer orbit configuration. If the “detour” option is pursued, the deployer would need to augment its overall velocity (with other payloads still aboard) to match the payload of interest’s ΔV required, deploy it, and then execute an additional maneuver (likely of similar ΔV but in the opposing direction) to return to its prior deployer orbit configuration before continuing on in the deployment sequence for other payloads. Obviously, it can be seen that later scheduling of higher-ΔV payloads would be preferred over the “detour” option, but some scenarios with a wide variety of unique payload needs may introduce difficulties in deployment scheduling.
To offer potential flexibility in propulsion requirements and deployment scheduling, while requiring little additional hardware, METs could be implemented in rideshare missions to support payload and deployer development and operation. By using a concept introduced in Reference [8] to implement a thruster-driven MET with propulsion systems native to the deployer, this system can be used to impart significant ΔV onto a released payload while requiring minimal hardware for the tether itself, and also little linear ΔV being required by the deployer for orbit correction between deployments due to most of the energy/momentum change being sourced from rotation rather than linear motion. Additional hardware required would consist of the tether and mounting hardware at each end, which can be developed with low mass using conventional materials and easily supplemented with deployment/separation hardware used in existing spacecraft dispenser systems. This would require minimal hardware additions to the payload, and those required hardware additions would be simpler than traditional thrusters, thereby supporting payload developers by requiring less resources and development time. For the deployer, minimal hardware and orbit adjustment requirements can enable more flexible payload deployment sequence scheduling and expand upper stage/deployer payload delivery capabilities. With the quantity of small satellites being launched on the rise, as well as an increase in popularity of routine rideshare missions, improvements to capabilities in this part of the satellite and launch market can contribute to the further development of the space industry overall.
3. Methodology
In designing an MET system, three key aspects of the process include development of tether hardware, spin-up and spin-down systems, and orbit correction maneuvering (in the case of an asymmetric release configuration). Tether hardware development is not discussed in detail in this work due to the wide range of factors that are incorporated in that process, but one of the key parameters included here is the length of the tether Ltether, particularly its two components Lpl and Ldep which are the lengths of the tether starting from the overall center of mass and extending out to either the payload or deployer, respectively. This length is critical in determining a driven angular velocity ω at which the system rotates during tether release. Spin-up, spin-down, and orbit correction are each executed propulsively with thrusters native to the deployer, but they do not necessarily all have to use the same set of thrusters. For example, spin-up and spin-down maneuvers could be executed with small RCS thrusters, meanwhile orbit correction could be executed with a primary propulsion system. While thrusters are not the only means to execute MET-specific maneuvers, they are one means which can be approached if trying to minimize the amount of new hardware needing to be developed. For example, if a propulsion-enabled orbital transfer vehicle is selected as the deployer vehicle for an MET deployment scenario, its native propulsion systems could be used rather than needing to also develop a new motor system to drive overall system rotation.
3.1. System Design and Limitations
The general design of the system used in this manuscript is an asymmetric MET system, which involves a deployer on one end of a tether, and a payload on the other end, where upon release, the tether is disconnected from the deployer side. The asymmetric configuration is better aligned for dedicated individual payload deployments with unique orbit requirements, independent of additional payloads or inefficient counterweights required for a symmetric configuration. The maneuver concepts to be discussed can also be applied to other configurations such as those discussed previously in References [2,6,7], which can include asymmetric and symmetric tether systems. It should be noted that symmetric deployments only require spin-up and spin-down maneuvers, meanwhile asymmetric deployments require spin-up, spin-down, and possibly deployer orbit correction maneuvers (discussed further in Section 3.2, Section 4.2 and Section 4.3). Due to the more practical expected usage of asymmetric tether deployments which allow for more precise individual payload positioning without requiring additional payloads or counterweights, asymmetric deployments are discussed throughout the remainder of this text. A visual representation of the system of interest is given in Figure 1, which shows the geometry and velocity profile of the rotating system with attention given to the positions and velocities of deployer and payload ends of the tether.
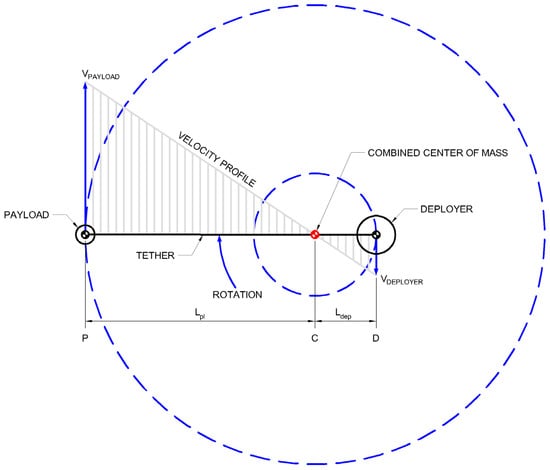
Figure 1.
General geometry of a rotating asymmetric MET system.
This system is designed to not use very long tethers like the kilometers-long systems used in other missions and concepts such as those used in the TSS-1/TSS-1R, SEDS-1/SEDS-2, and YES-2 missions as described in References [14,15,16]. These long tethers were proven to be difficult to manage for reasons including but not limited to deployment dynamics, structural oscillations, and spacecraft alignment, elevating the risk of deployment complications with increasing tether length. With shorter tethers (such as on the order of tens or hundreds of meters), tether handling is more feasible by offering more stable, controllable, and predictable deployment dynamics, lowering deployment failure risks, as described by Reference [17]. Additionally, since smaller tethers which can be assumed to have masses significantly lower than both the payload and deployer, mass and inertial properties of the tether itself are largely neglected in this analysis for the purpose of simplifying baseline propellant estimations, as inclusion of tether-based inertial elements contribute little compared to the inertial elements of the deployer and payload. The tether is assumed to be linear and rigid as in steady-state during rotation due to tension forces by the deployer and payload at each end, and transient effects during spooling/unspooling operations are also not discussed due to dependence on tether extension/retraction hardware, requirements for which can greatly vary design and operation. For this analysis, the only system states utilized in the propellant mass estimation process are when the tether is either stowed or fully extended, and either stationary or rotating at a target rotation rate for release, with tether extension occurring simultaneously with spin-up maneuvering with a theoretical passive unspooling system. Additionally, other hardware-based disturbances such as tether and/or structure elasticity or propellant sloshing are not considered, as these factors are design-specific and can vary greatly from system to system. The only parameters whose changing effects are included other than the stowed/extended states of the tether are change in deployer mass and thus also moment of inertia due to propellant consumption.
3.2. Maneuver Definition
In this analysis, the two primary types of maneuvers discussed are spin-up/spin-down maneuvers for driving/canceling rotation of the system, and orbit correction maneuvers for addressing reactionary linear velocity imparted on the deployer by the release process due to the conservation of linear momentum. Regardless of system design, spin maneuvers are required due to the rotating nature of METs, but orbit correction maneuvers are optional depending on mission requirements and are only required if the deployer must return to its pre-release orbit after an asymmetric release. All idealized maneuver details described in this analysis are executed in a 2D plane local to the MET system, independent of the planetary body being orbited. Additionally, effects from disturbance sources present in the space environment are not considered. This is primarily due to the “quick” expected timelines associated with a MET-based deployment (likely no longer than 1–2 h if maintaining comparable to between-deployment operations for a rideshare deployer), operating on timeframes short enough where these environmental disturbances have negligible impact on the mechanical operation of the system, where these disturbances only have appreciable effect over longer timescales on the order of days or months [18,19].
4. Generalized Design Process
The design process given in this analysis is intended to act as a segment in the overall MET mission design process, taking place between initial tether hardware design and before comparison with other deployment methods. Given a set of associated deployment ΔV, tether length Ltether, and rotation rate ω, MET maneuvers can be defined, and their propellant requirements can support further development comparing mission design options based on required mass to orbit.
To assist in visualization, Figure 2, Figure 3, Figure 4 and Figure 5 depict the states of the overall system through each step of the deployment process, presented as side views looking edge-on to the rotating tether plane of the system depicted in Figure 1. Figure 2 depicts state 0, where the payload is still initially stowed and the system is not rotating. Figure 3 depicts state 1, after the system has executed simultaneous tether extension and spin-up operations, with the tethered payload extended and some amount of propellant having been consumed to drive the rotation. Figure 4 depicts state 2, immediately after tether release, with independent deployer and payload both rotating at the same rate as state 1. Figure 5 depicts state 3, representing the post-spin-down state of the deployer alone, and some amount of propellant having been consumed to cancel the rotation. State 4 can be pursued in the form of a post-deployment orbit correction executed with a simple propellant burn, but this is optional and dependent on future deployer operations in the flight.
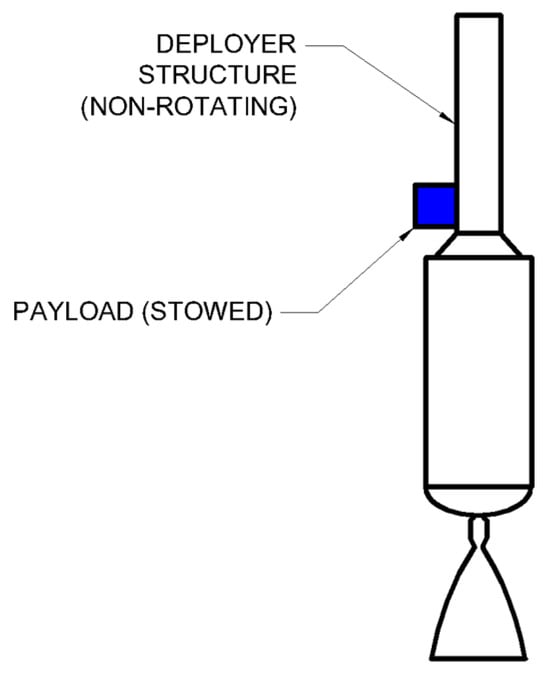
Figure 2.
General mid-deployment geometry of an asymmetric MET system, state 0.
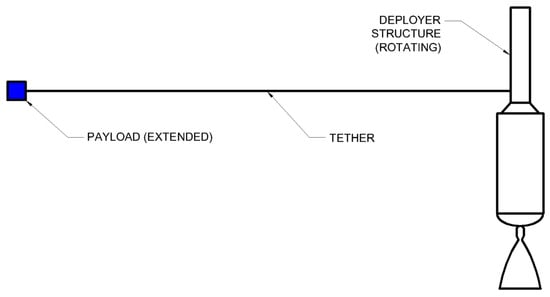
Figure 3.
General mid-deployment geometry of an asymmetric MET system, state 1.
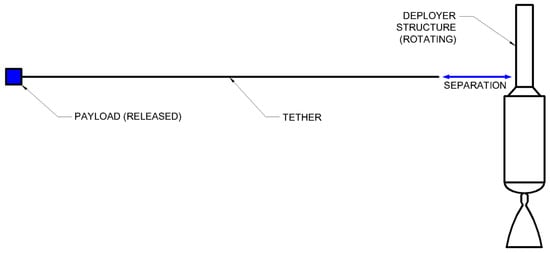
Figure 4.
General mid-deployment geometry of an asymmetric MET system, state 2.
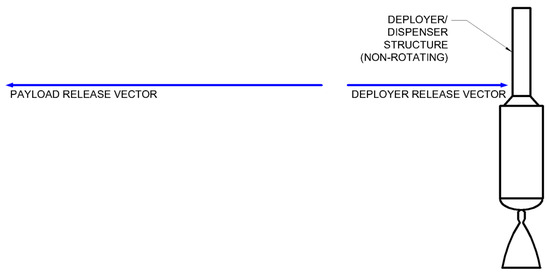
Figure 5.
General mid-deployment geometry of an asymmetric MET system, state 3.
4.1. Tether Hardware Design
While tether hardware design processes are not discussed in detail in this text, a few key properties of the tether must still be defined for this work. Here, tether systems are assumed to be significantly lower mass than both the deployer and the payload, and for initial mission conceptualization and exploring propellant mass requirements, tether mass may be neglected. A key parameter of the tether that must be included in this analysis, however, is the length of the tether. Given a desired ΔVpl to impart on a released payload, either a length Lpl between the payload and the overall system’s center of mass or a target rotation rate ω must be defined, completing the relationship given in Equation (1). Either Lpl or ω can be determined first to guide the determination of the other depending on design needs, but both must be constrained to developer/operator-defined limits. The tether of length Lpl must be suitable for factors including but not limited to staying within tether tensile stress limits, limiting centripetal acceleration experienced by the payload at the end of the tether, and overall tether mass limitations, and ω can be limited to a maximum allowable angular velocity defined by release control limitations and/or vehicle capabilities. In general, it is preferred to have a longer Lpl and lower ω for lower tether stresses and greater ease of release vector control, but for reasons previously mentioned in Section 3.1, it is important to try not to have a tether that is excessively long and difficult to handle. These sources of tether stress and operational limitations are just some of the factors developers ought to consider when creating an MET system, but many other factors may arise from mission-specific needs not discussed in this work.
After a length Lpl is defined, the length of the other segment of the tether on the deployer side Ldep can also easily be determined if the masses of the payload mpl and deployer mdep are also known. Equation (2) approximates Ldep through a simple balance of mass elements on either side of the system’s center of mass, if neglecting the small mass of the tether itself. The mass of the deployer in this equation ought to be the mass of deployer just before tether release, after some amount of propellant mass has been consumed by the prior spin-up maneuver. With tether length and angular velocity parameters now defined, they can be included in calculations for spin-up and spin-down maneuvers which rely on them.
4.2. Spin-Up and Spin-Down Maneuvers
Propellant mass requirements for spin operations can be estimated by calculating the minimum propellant consumption to impart a change in angular momentum of the overall system ΔJ between the rotating and non-rotating states as defined in Equation (3). This allows for estimation of propellant mass from a momentum conservation perspective, assuming thruster location(s) in the system is/are known and are oriented to impart torque in an ideal fashion (where exhaust is directed tangent to the thruster’s rotating path of motion). It should be noted that this process serves as an initial minimum propellant mass estimate for early mission conceptualization, and some thruster arrangements may require more propellant if not aligned to be dedicated solely to spin-axis maneuvering. Starting from derivation of the rocket equation (for convenience given in Equation (4)) [20], the quantity of linear impulse Δp generated from the consumption of propellant mass mprop by a maneuver can be determined using Equation (5). This linear impulse can be combined with the radius of the thruster’s effective moment arm rthruster for rotation about the overall center of mass of the system to produce an expression for the change in angular momentum imparted by the thruster, given in Equation (6). Equations (5) and (6) can then be combined to give an expression for propellant mass mprop consumed to impart a desired change in angular momentum ΔJ, given in Equation (7). In this set of equations, msc is the mass of a spacecraft after a propulsive maneuver having consumed propellant, mprop is the propellant mass consumed by a maneuver, ve is the effective exhaust velocity from the thruster used aboard the spacecraft, Isp is the specific impulse of the thruster, and g0 is the gravitational constant (~9.81 m/s2).
To determine the ΔJ for each spin-up and spin-down maneuver, the local angular momentum of the overall system J must be determined for states before and after each maneuver. For the stationary state before spin-up and the stationary state after spin-down, J = 0. For the rotating states after spin-up and before spin-down however, J can be determined using Equation (8), where Isys is the mass moment of inertia of the system about the axis of rotation, and ω is the angular velocity of the rotating system.
The propellant mass requirements of spin-up and spin-down maneuvers can be estimated once inertial properties of the overall system at pre-release and post-release states are defined. For this, four different inertial states Isys are used, following the convention given in Figure 2, Figure 3, Figure 4 and Figure 5 representing the change in hardware configurations through spin-up and spin-down maneuvers. For state 0, Isys,0 represents the initial moment of inertia of the system, with the payload still stowed and the system not rotating. For state 1, Isys,1 represents the moment of inertia of the rotating system with the tethered payload extended, and some amount of propellant having been consumed to drive the rotation. For state 2, Isys,2 represents the moment of inertia of the rotating deployer, with the tethered payload now released. For state 3, Isys,3 represents the final moment of inertia of the deployer alone, and some amount of propellant having been consumed to cancel the rotation. In states 0 and 3, where the system has no rotation, no angular momentum is present, leaving the primary states of interest being states 1 and 2. This allows for spin-up and spin-down maneuver propellant mass to be estimated using a combination of Equations (7) and (8) with states 1 and 2, resulting in Equations (9) and (10). It should be noted that the specific impulse Isp in these equations has been modified with the addition of the subscript spin to distinguish the operation of thrusters used for spin-up and spin-down maneuvers from those used for later orbit correction maneuvers. Additionally, the thruster effective moment arm radius rthruster has been modified with the additions of the subscripts 1 and 2, where rthruster,1 indicates the radius during state 1, and rthruster,2 indicates the radius during state 2, following the same numbered convention as given in Figure 2, Figure 3, Figure 4 and Figure 5. This is to account for the change in radius rthruster that occurs between states 1 and 2 which is dependent on system geometry and thruster positioning.
For conceptualization, the inertial quantities Isys,1 and Isys,2 can be expanded to include their deployer and payload elements as shown in Equations (11) and (12). Isys can be decomposed into inertial elements for each component of the overall system, and is specific to the design of the deployer, payload, and tether. These elements can be further decomposed into their principal moment of inertia and their parallel axis contributions due to their distance from the overall center of mass. For Isys,1, principal and parallel axis inertial elements are produced for both the deployer and the tethered payload, but for Isys,2, only the principal inertial element for the deployer is required due to the payload having been released, returning the overall center of mass to the center of mass of the deployer itself and no longer producing a parallel axis inertial element.
Additionally, the thruster moment arm radius quantities rthruster,1 and rthruster,2 can be approximated for a minimum propellant mass condition (where the moment arm is maximized to improve thruster effectiveness), given by expressions given in Equations (13) and (14). This would be an arrangement where a thruster could be located to the far right side of the deployer depicted in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5, at a distance rthruster,min to the right from the center of mass of the deployer at station D in Figure 1. The value of rthruster,1 would be composed of the length rthruster,min plus the tether length segment Ldep (the total length of the thruster’s effective moment arm), meanwhile rthruster,2 would be a smaller quantity only consisting of the length rthruster,min (due to the tether being released at this state). It is important to keep in mind, however, that specific thruster positioning (and thus the definitions of rthruster,1 and rthruster,2) is a system-specific matter and requires attention by system developers. Furthermore, alternative thruster configurations may lead to inefficiencies by non-ideal thrust alignment, and may require higher quantities of propellant as a result.
4.3. Orbit Correction Maneuvers
The ideal ΔVdep experienced by the deployer post-release is simply the reaction against the payload being released with ΔVpl due to conservation of linear momentum, as described in Equation (15). If this reactionary velocity change is to be corrected, the general change in mass defined by the rocket equation (Equation (4)) can be simply arranged into the form of Equation (16) and be used to determine the propellant mass mprop,corr required to execute such a correction maneuver when given the released payload’s release velocity ΔVpl and mass mpl, and the deployer’s mass mdep, shown in Equation (17). Following the numbered state convention used previously for the spin-up and spin-down maneuvers, state 4 can be defined as the deployer’s state after the correction burn has been executed. It should be noted that either mdep,3 or mdep,4 should be used, but not mdep,0, mdep,1, or mdep,2. Additionally, the specific impulse Isp in Equation (17) has been modified with the addition of the subscript corr to distinguish the operation of thrusters used for orbit correction maneuvers from those used for prior spin-up and spin-down maneuvers.
4.4. Summation of Propellant Mass Elements
With expressions for propellant mass required for spin-up, spin-down, and orbit correction maneuvers defined, these mass elements can be combined to determine the total propellant mass required for the MET-based deployment process. A general summation of these elements is given in Equation (18), and an expanded form which incorporates expressions from Equations (9)–(14) and (17) is given in Equation (19) where the first braced quantity is the combined propellant mass for spin-up and spin-down maneuvers, and the second braced quantity is the propellant mass for the optional orbit correction maneuver.
Due to Equation (19) having multiple values for mdep and Idep due to propellant consumption between sequential maneuvers, each propellant quantity must be determined individually starting with the last maneuver (orbit correction) and ending with the first maneuver (spin-up), similar in fashion to the process of designing launch vehicle stages beginning with the payload/upper stage and ending with the first stage. The mass of the deployer mdep at each state can be determined using the expressions given in Equations (20)–(23), and associated values of inertial elements Idep at each state ought to be updated according to these mass values and associated design-specific geometry.
To begin the process of propellant calculation, a target end state (state 4) of the deployer must first be defined, having some quantity of propellant remaining in its tank(s) for use in future maneuvers with other payloads. The deployer’s mass at this state mdep,4 can then be used to determine the propellant consumed by orbit correction using Equation (17), and thus also the mass of the deployer before the orbit correction takes place at state 3. The deployer’s mass mdep,3 and moment of inertia Idep,3 at state 3 can then be used to determine the propellant consumed by spin-down using Equation (10) as well as the mass and moment of inertia of the deployer before spin-down at state 2. Transitioning between states 2 and 1, the mdep remains the same, but Idep changes due to the release of the tether and associated change in the center of mass. After this, mdep,1 and Idep,1 can be used to determine the propellant consumed by spin-up using Equation (9) as well as the initial mass mdep,0 and moment of inertia Idep,0 of the deployer. Due to the interrelated nature of mass and inertial properties, if using advanced modeling techniques in the design process, it may be helpful to produce an automated, possibly iterative code which follows this calculation sequence and allows for quick calculations to be made between design changes during development. Due to the dependence on unique design-specific details that are too wide-ranging to concisely discuss here however, such a code is not discussed in this manuscript.
5. Discussion on Comparison with Other Methods
While this process of estimation is just one of many aspects that may be required in developing an MET-based mission, it can still be a helpful exercise which can support comparison with other mission design options. Some examples of this include determining a maximum mass limit to target if choosing to develop a motor-based rotation system, and also comparing against traditional propulsion methods involved with payload deployments. Motor-driven systems (often referred to as motorized momentum exchange tethers, MMETs), induce rotation with a motorized interface between a tether dispenser/attachment section and a counterweight section, resulting in two sections rotating in opposing directions due to the conservation of angular momentum (driven to a speed at which the tether side rotates at a desirable rotation rate for deployment), as described by References [21,22]. Traditional propulsion methods for payload deployments that are discussed here are basic cases of utilizing propulsion on either the deployer or the payload itself, and the associated maneuvers that are required to deliver a payload from the deployer’s orbit to its own destination orbit.
5.1. Motorized Systems
For developing a motorized MET system, there are a wide range of design options that can be pursued, but one of the key aspects of the design that should be kept in mind is the motor system’s mass mmotor. The process of estimating the mass requirements with a thruster-based approach can be used to produce an initial threshold for mass where whichever option (motor or thruster driven) has the lower mass estimate might be preferred as the baseline concept. Since a motorized system can only drive rotation in the system and not perform orbit correction maneuvers, comparison of mass should be performed specifically with only propellant consumed by spin-up and spin-down maneuvers. If a motorized system were chosen, it should satisfy the expression given in Equation (24), where the mass of the motor system mmotor is less than the mass of propellant required for spin-up and spin-down maneuvers.
5.2. Comparison Against Traditional Propulsive Methods
As preferred with any alternative propulsion concept, METs should be compared with existing propulsion methods. Two methods considered in this analysis are where either the payload itself includes its own thruster to satisfy its post-deployment ΔVpl needs, or the deployer executes thrust maneuvers to deliver the whole system to the payload of interest’s required velocity for deployment. Intuitively, it would be expected that payload-based maneuvering might be preferred over the deployer-based maneuvering option due to the lower mass requirements and no need for the deployer having to execute unique operations for a single payload. Some scenarios, however, might require the deployer-based option where payloads might not be able to host their own adequate propulsion systems, such as small satellites.
5.2.1. Payload-Based Propulsion
For payload-based maneuvering, a single thrusting maneuver to impart ΔVpl is required. Equation (16) can be used once more to produce a propellant mass mprop,pl requirement for this maneuver in the form given in Equation (25). Included here is the mass of the thruster hardware mthruster,pl that would need to be included aboard the deployed payload. With mprop,pl and mthruster,pl defined, a comparison with MET mass elements can be made. For completeness, the mass of the tether itself mtether ought to be included, which would be determined by the developer with mission-specific design properties. While prior text in Section 3.1 and Section 4.1 initially neglected tether mass for the purpose of propellant mass estimation, tether mass would still need to be estimated through further design activity (largely defined by tether length, material properties, and cross-sectional profiles selected to handle tether stress conditions). If a thruster-driven MET-based deployment scheme were to be pursued, it ought to satisfy the expression given in Equation (26), where MET mass requirements would be less than payload-based propulsive mass requirements.
5.2.2. Deployer-Based Propulsion (End-Scheduled Deployment)
The process of determining propulsive mass for deployer-based maneuvering is very similar to the payload-based method. For cases where the payload of interest is scheduled for the end of a deployment sequence, the full deployer system acts as the propulsion system required for the payload delivering the same ΔVpl with a single maneuver. Again basing from Equation (16), the propellant mass required for this maneuver is given in Equation (27). In this context, mdep refers to the mass of the deployer system after maneuvering has taken place, allowing deployer propellant mass mprop,dep to be identified.
With mprop,dep defined, a comparison with MET mass elements can be made. Once again, the mass of the tether itself mtether ought to be included (similar to Section 5.2.1); but unlike the payload-based maneuvering method, thruster masses are not included as both options would involve the same thrusters native to the deployer. If a thruster-driven MET-based deployment scheme were to be pursued, it should to satisfy the expression given in Equation (28), where MET mass requirements would be less than deployer-based propellant mass requirements.
5.2.3. Deployer-Based Propulsion (Non-End-Scheduled Deployment)
For cases where unique payload deployments must be executed not at the end of the sequence, but somewhere in the middle, additional operations may be required. The process is very similar to the end-scheduled deployment method, but instead requiring two maneuvers rather than one. Assuming a “round trip” maneuver sequence starting and ending at the same deployer orbit, the deployer would first need to thrust to impart ΔVpl to the full system, deploy the payload, and then thrust back to impart ΔVpl to the full system once again to return to the original deployer orbit. Basing from Equation (16) once again, the propellant mass required for these first and second maneuvers are given in Equations (29) and (30), respectively. In this context, mdep again refers to the mass of the deployer system after maneuvering has taken place, allowing deployer propellant mass elements mprop,dep,1 and mprop,dep,2 to be identified. The total propellant mass based on the summation of Equations (29) and (30) is given in Equation (31).
With mprop,dep defined, a comparison with MET mass elements can again be made. Similarly to the end-scheduled deployer-based maneuvering method, the mass of the tether mtether is included, and thruster masses are not included. If a thruster-driven MET-based deployment scheme were to be pursued, it ought to satisfy the expression previously given in Equation (28), but with mprop,dep determined using Equation (31) rather than Equation (27).
6. Conclusions
As high-volume rideshare missions continue to grow in launch frequency in coming years, deployer vehicles ought to continue supporting payloads which might have unique deployment requirements, but not have to experience added significant system complexity. This work has discussed one potential solution space which could be explored using the propellant mass estimation process given for thruster-driven METs. This process has been described in a way that is vehicle-agnostic, with the only assumptions being that the deployer has native propulsion capabilities for basic linear and rotational maneuvering while in orbit. By focusing on the core basic maneuvers of system spin-up, spin-down, and orbit correction, this methodology enables rapid and flexible mission conceptualization with minimal hardware modifications. The primary contribution of this work is in the establishment of a generalized framework that links deployment requirements, tether geometry, and native deployer-based propulsion systems to estimate the propellant mass required for this alternative method of payload deployment. Following this process, comparisons can be made with other deployment techniques such as motorized METs or traditional thruster-based methods, helping inform early decision-making in rideshare mission design.
Ultimately, this design methodology aims to contribute to the development of new MET systems as well as near-future rideshare deployer vehicles. Continuing work in this area is currently evaluating the integration of thruster-driven METs onto existing deployer vehicles, multi-payload deployments, and larger-scale orbit/mission design for LEO-based applications, included in a forthcoming publication with the 76th International Astronautical Congress [23]. This and adjacent work provides initial insights into the application spaces where METs require less mass to orbit than various types of traditional propulsion systems applied to different sizes of payloads, highlighting cases where METs may be a superior deployment solution. Additional work is in progress that incorporates mass contributions by tether hardware and the time-based performance of MET deployments compared to traditional propulsion, which will be included in future publication(s). Areas of future work that could be explored include but are not limited to investigating transient operations throughout the maneuver types discussed, incorporating high-fidelity tether modeling, mitigating disturbances caused by the environment of space, and applying MET-based deployments to new deployer vehicles and/or payloads. By contributing to these areas, this work intends to support efforts investigating alternative propulsion systems while also contributing directly to in-development/active space technologies, which can affect mission capabilities for spacecraft developers and operators across the modern space industry.
Author Contributions
Conceptualization, B.C.; methodology, B.C.; validation, B.C. and L.D.T.; formal analysis, B.C.; investigation, B.C.; resources, B.C. and L.D.T.; writing—original draft preparation, B.C.; writing—review and editing, B.C. and L.D.T.; supervision, L.D.T.; project administration, B.C. and L.D.T.; funding acquisition, B.C. and L.D.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research is jointly funded by the NASA Alabama Space Grant Consortium (NASA Grant #80NSSC20M0044) and the UAH College of Engineering.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors acknowledge the support from the NASA Alabama Space Grant Consortium and UAH College of Engineering for the research described in this paper.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Kulu, E. Small Launchers—2023 Industry Survey and Market Analysis. In Proceedings of the 74th International Astronautical Congress, Baku, Azerbaijan, 2–6 October 2023. Paper IAC-23-D2.IP.7. [Google Scholar]
- Campbell, B.; Thomas, L.D. Basic Orbit Design and Maneuvers for Satellite Constellations Deployed Using Momentum Exchange Tethers. Aerospace 2024, 11, 182. [Google Scholar] [CrossRef]
- Hoyt, R. Space Tethers: Technology Status and the Way Forward; National Academy of Engineering: Washington, DC, USA, 2010. [Google Scholar]
- Johnson, L.; Khazanov, G.; Gilchrist, B.; Hoyt, R.; Stone, N.; Lee, D.; Elder, C. Space Tethers. J. Space Technol. Sci. 2012, 26, 2–13. [Google Scholar] [CrossRef]
- Johnson, L.; Gilchrist, B.; Estes, R.; Lorenzini, E. Overview of future NASA tether applications. Adv. Space Res. 1999, 24, 1055–1063. [Google Scholar] [CrossRef]
- Campbell, B. Considerations for Satellite Constellation Deployment via Momentum Exchange Tethers. In Proceedings of the 74th International Astronautical Congress, Baku, Azerbaijan, 2–6 October 2023. Paper IAC-23,B6,5,4,x77572. [Google Scholar]
- Campbell, B. Concepts and Considerations for Small Satellite Constellation Deployment via Momentum Exchange Tethers. In Proceedings of the 37th Annual Small Satellite Conference, Logan, UT, USA, 5–10 August 2023. Paper SSC23-WP1-05. [Google Scholar]
- Campbell, B. Design of a Tether Deployment System for Small Satellites. In Proceedings of the American Astronautical Society 16th Wernher von Braun Memorial Symposium, Huntsville, AL, USA, 25–27 October 2023. [Google Scholar]
- Lang, D.D.; Nolting, R.K. Operations with Tethered Space Vehicles. In Proceedings of the Gemini Summary Conference, NASA, SP-138, Houston, TX, USA, 1–2 February 1967. [Google Scholar]
- Campbell, B.; Thomas, L.D. ADRASTEA: A Demonstration of Momentum Exchange Tether Technology for Small Satellites. In Proceedings of the 75th International Astronautical Congress, Milan, Italy, 14–18 October 2024. Paper IAC-24,B4,6A,6,x82924. [Google Scholar]
- Campbell, B.; Chytka, M.; Thomas, L.D. Flight Results from ADRASTEA, a Spaceflight Demonstration of Motorized Momentum Exchange Tethers for Small Satellites. In Proceedings of the 2025 AIAA SciTech Forum, Orlando, FL, USA, 6–10 January 2025. Paper IAC-24,B4,6A,6,x82924. [Google Scholar]
- Crisp, N.; Smith, K.; Hollingsworth, P. Launch and deployment of distributed small satellite systems. Acta Astronaut. 2015, 114, 65–78. [Google Scholar] [CrossRef]
- Curzi, G.; Modenini, D.; Tortora, P. Large constellations of small satellites: A survey of near future challenges and missions. Aerospace 2020, 7, 133. [Google Scholar] [CrossRef]
- Stone, N.H. Unique Results and Lessons Learned From the TSS Missions. In Proceedings of the International Conference on Tethers in Space, Ann Arbor, MI, USA, 24–26 May 2016. M16-5298. [Google Scholar]
- Carroll, J.A. SEDS Deployer Design and Flight Performance. In Proceedings of the American Institute of Aeronautics and Astronautics, Space Programs and Technologies Conference and Exhibit, Huntsville, AL, USA, 21–23 September 1993. Paper 93-4764. [Google Scholar]
- Kruijff, M. Tethers in Space, a Propellantless Propulsion In-Orbit Demonstration. Ph.D. Dissertation, Delft University of Technology, Delft, The Netherlands, 2011. [Google Scholar]
- Mantri, P. Deployment Dynamics of Space Tether Systems. Ph.D. Dissertation, North Carolina State University, Raleigh, NC, USA, 2007. [Google Scholar]
- Nwankwo, V.U.; Denig, W.; Chakrabarti, S.K.; Ajakaiye, M.P.; Fatokun, J.; Akanni, A.W.; Raulin, J.P.; Correia, E.; Enoh, J.E.; Anekwe, P.I. Atmospheric Drag Effects on Modelled Low Earth Orbit (LEO) Satellites during the July 2000 Bastille Day Event in Contrast to an Interval of Geomagnetically Quiet Conditions. In Annales Geophysicae; Copernicus Publications: Göttingen, Germany, 2021; Volume 39, pp. 397–412. [Google Scholar]
- Tolstoj, M. Analysis of Disturbance Torques on Satellites in Low-Earth Orbit Based Upon GRACE. Ph.D. Dissertation, RWTH Aachen University, Aachen, Germany, 2017. [Google Scholar]
- Sutton, G.P.; Biblarz, O. Rocket Propulsion Elements, 9th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Cartmell, M.P.; McKenzie, D.J. A Review of Space Tether Research. Prog. Aerosp. Sci. 2008, 44, 1–21. [Google Scholar] [CrossRef]
- Ziegler, S.W.; Cartmell, M.P. Using Motorized Tethers for Payload Orbital Transfer. AIAA J. Spacecr. Rocket. 2001, 38, 904–913. [Google Scholar] [CrossRef]
- Campbell, B.; Thomas, L.D. Analysis of a Launch Vehicle Upper Stage as a Momentum Exchange Tether Deployer. In Proceedings of the 76th International Astronautical Congress, Sydney, Australia, 29 September–3 October 2025. Paper IAC-25,C4,9,8,x96261; in preparation. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).