Simulation and Experimental Study of Strain Distribution in Composite Materials Considering Impact Velocity and Impact Location
Abstract
1. Introduction
2. Methods
2.1. Finite Element Model
2.2. Material Models
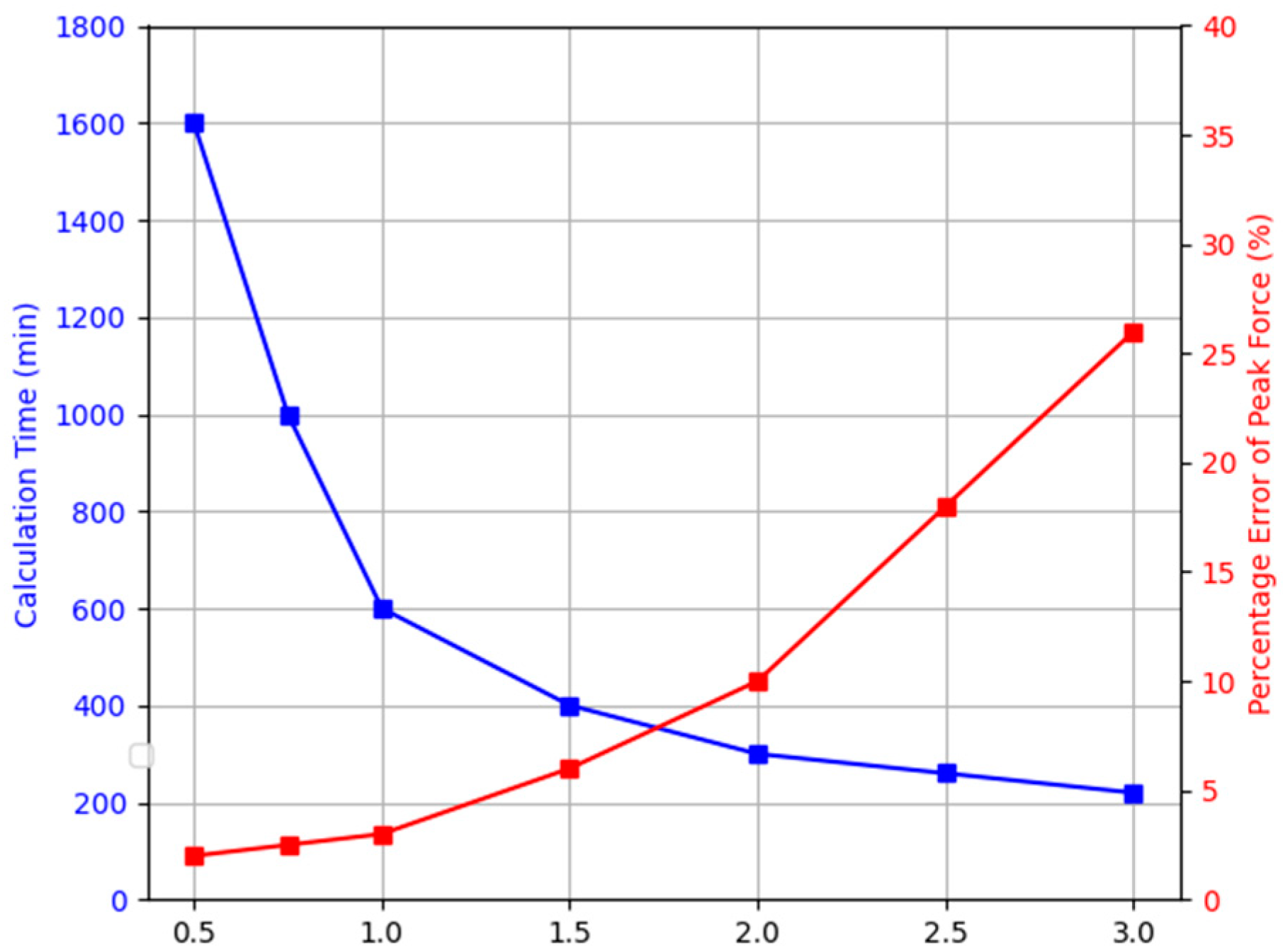
2.3. Simulation Conditions
3. Experiments
3.1. Specimens
3.2. Test System
3.3. Impact Tests
4. Results and Discussion
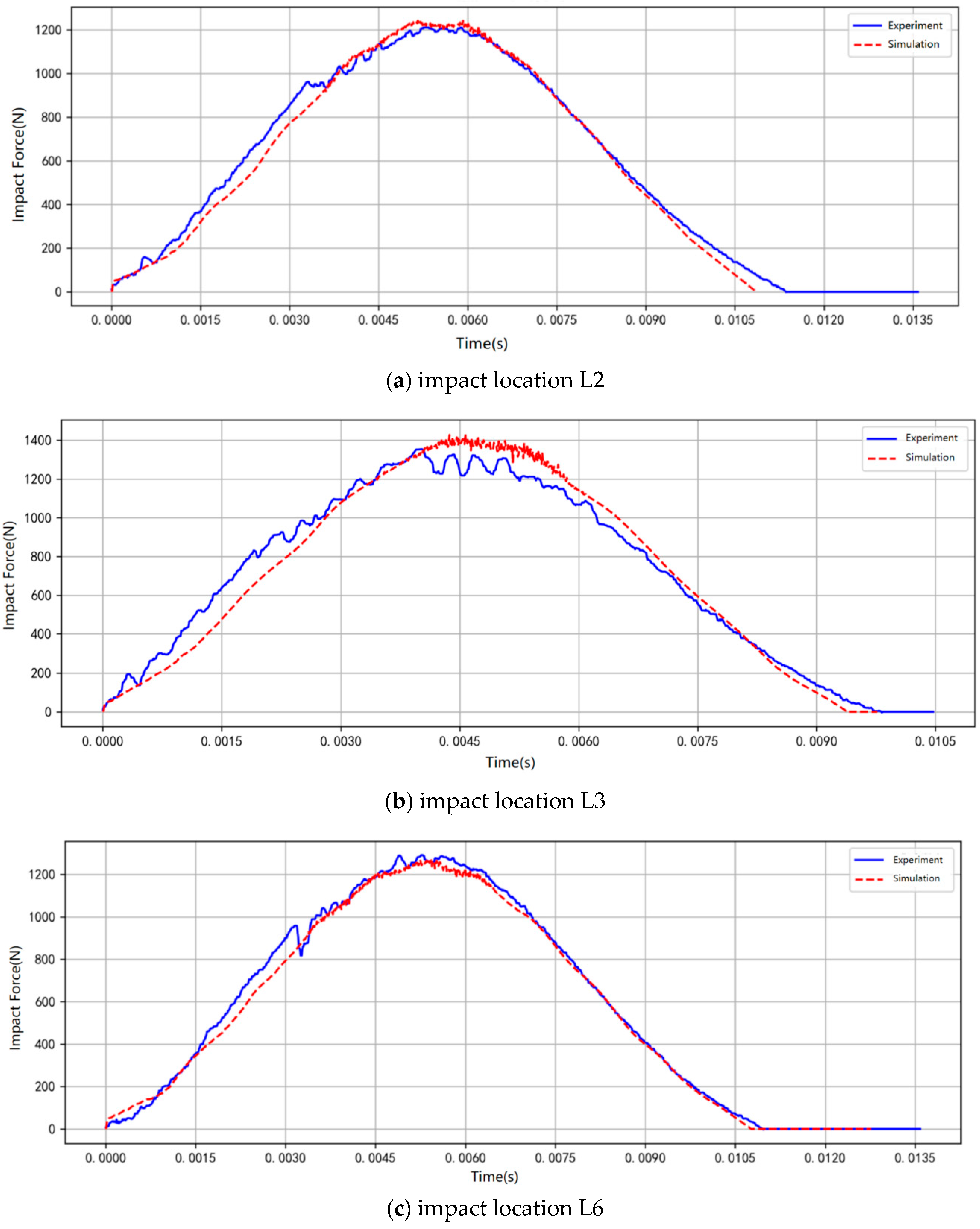
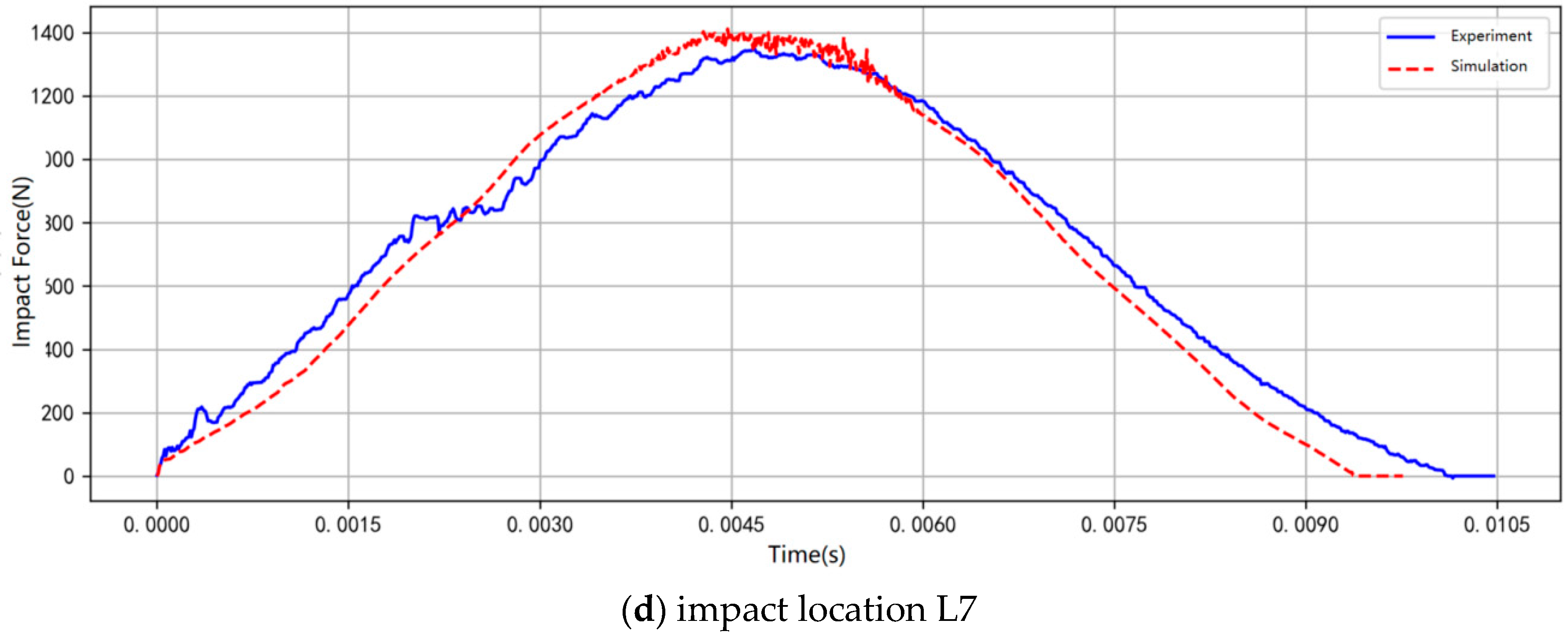
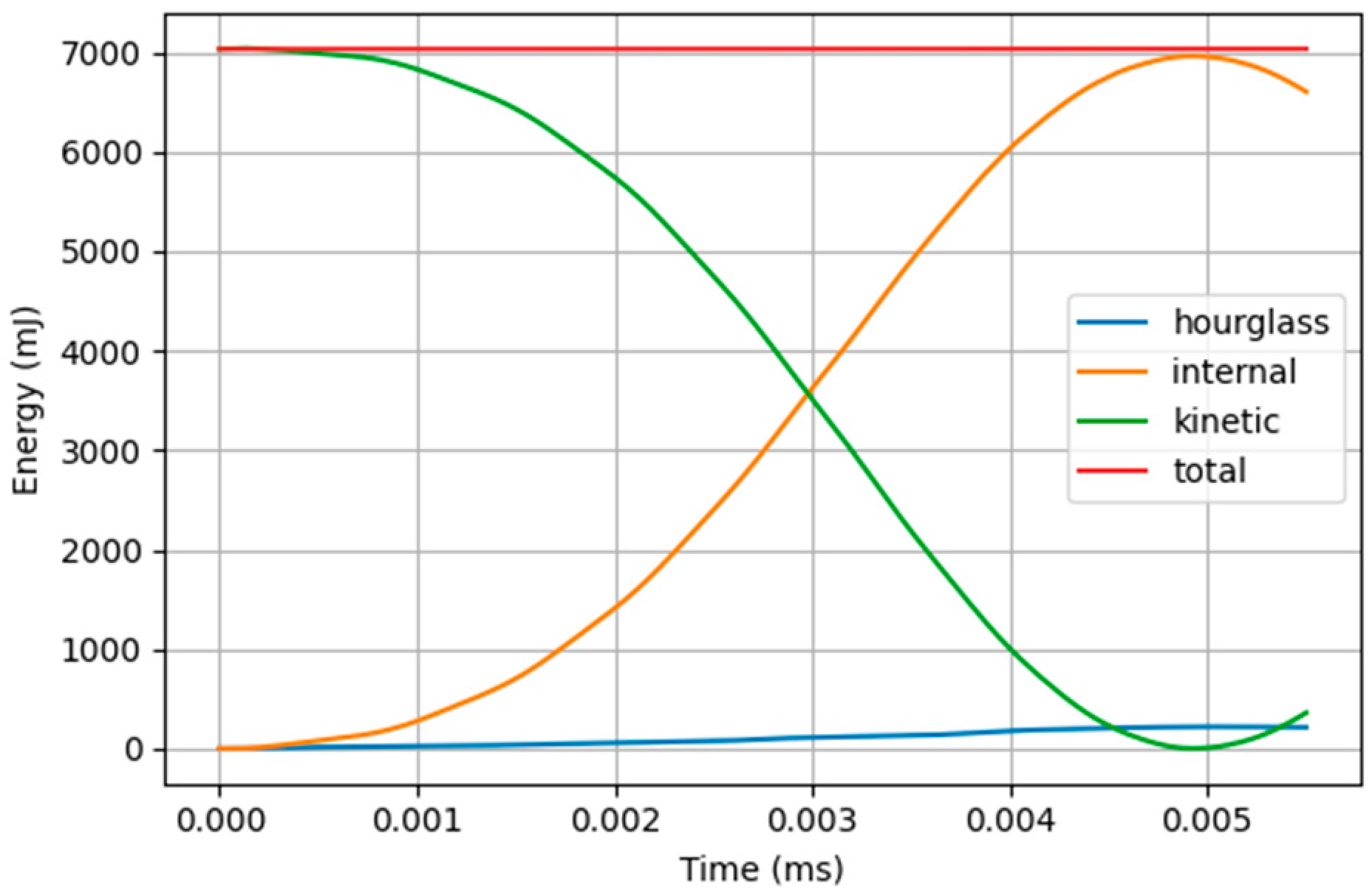
4.1. Simulation Results Verification
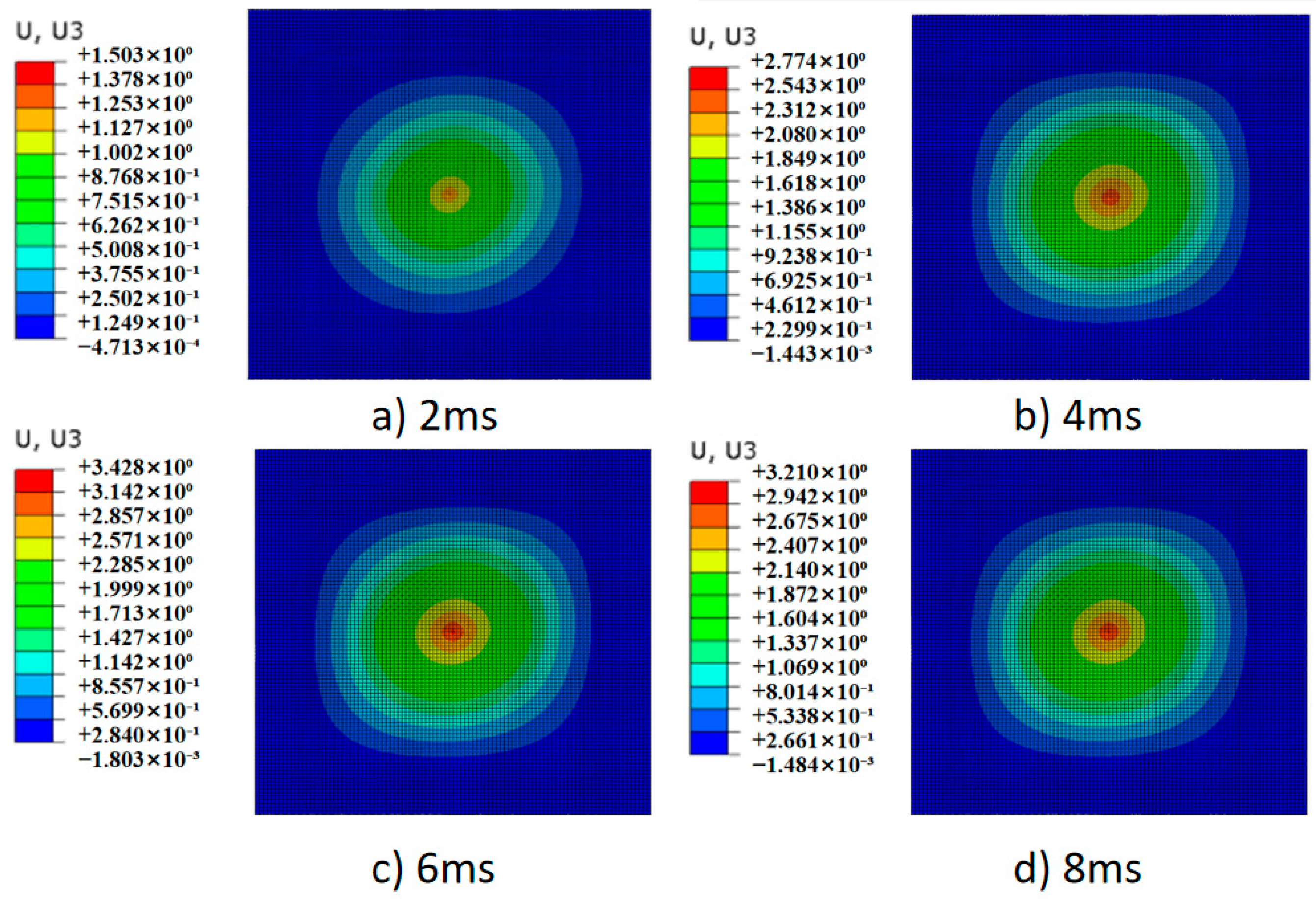
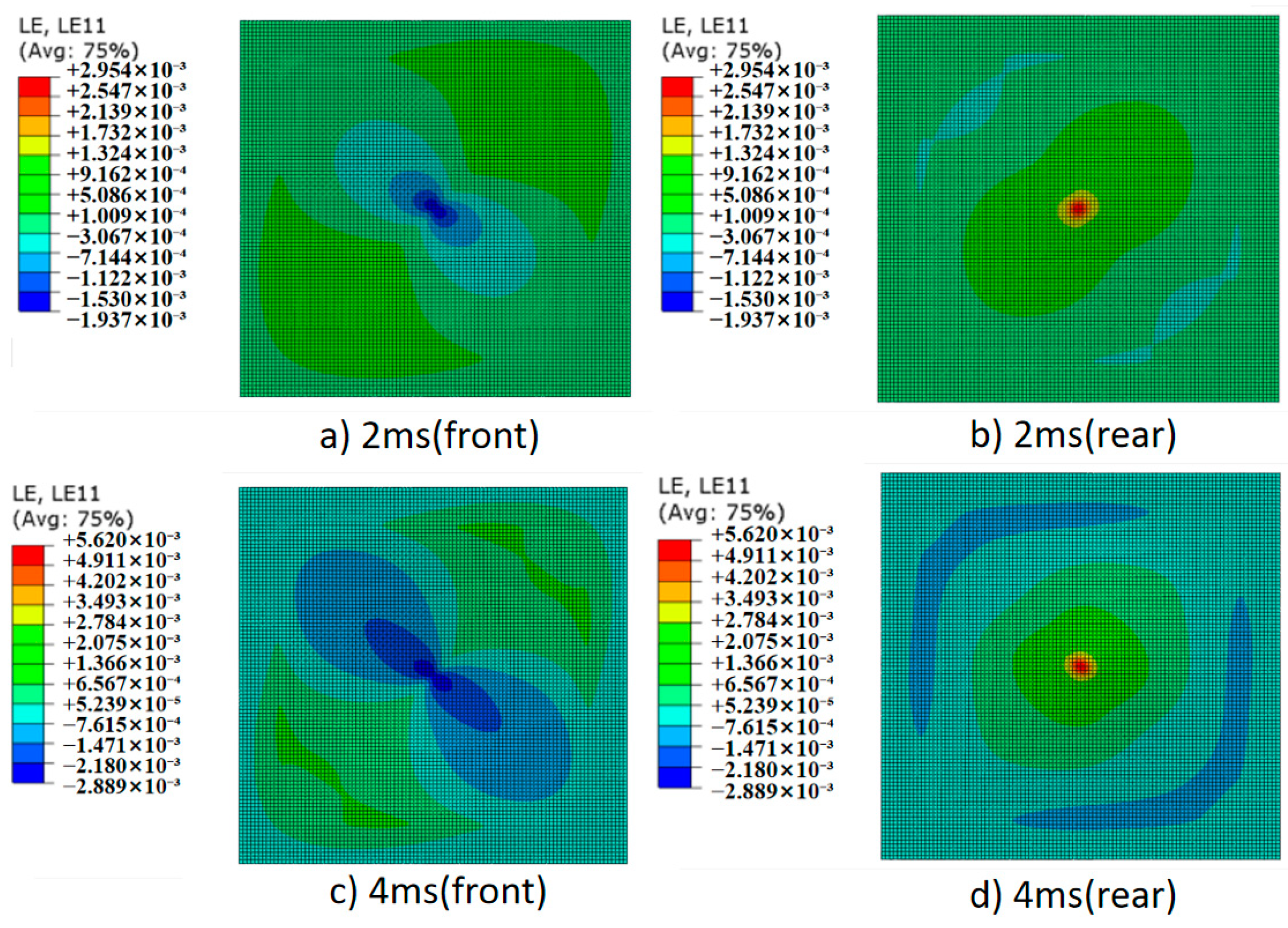
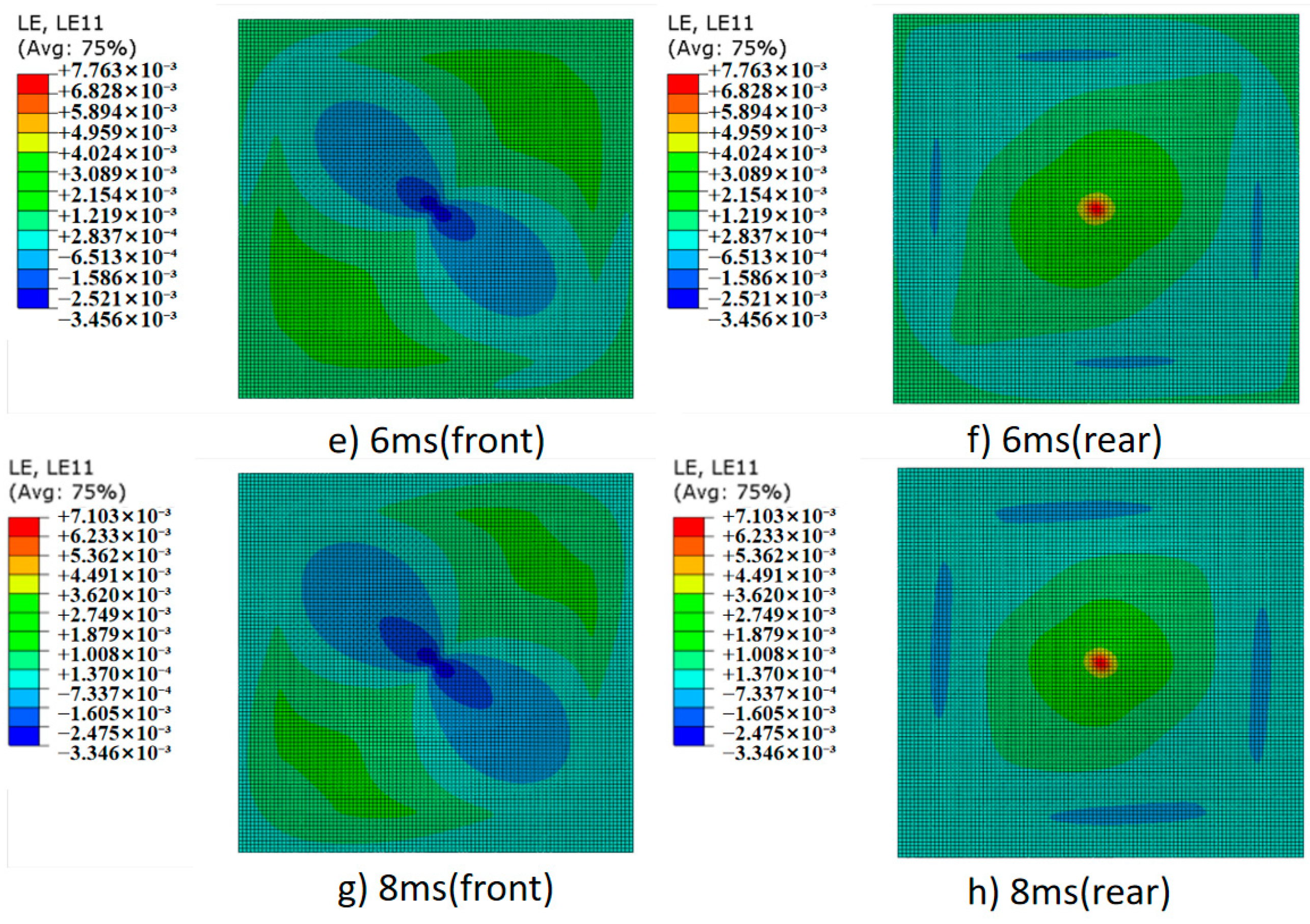
4.2. Impact Response History Analysis
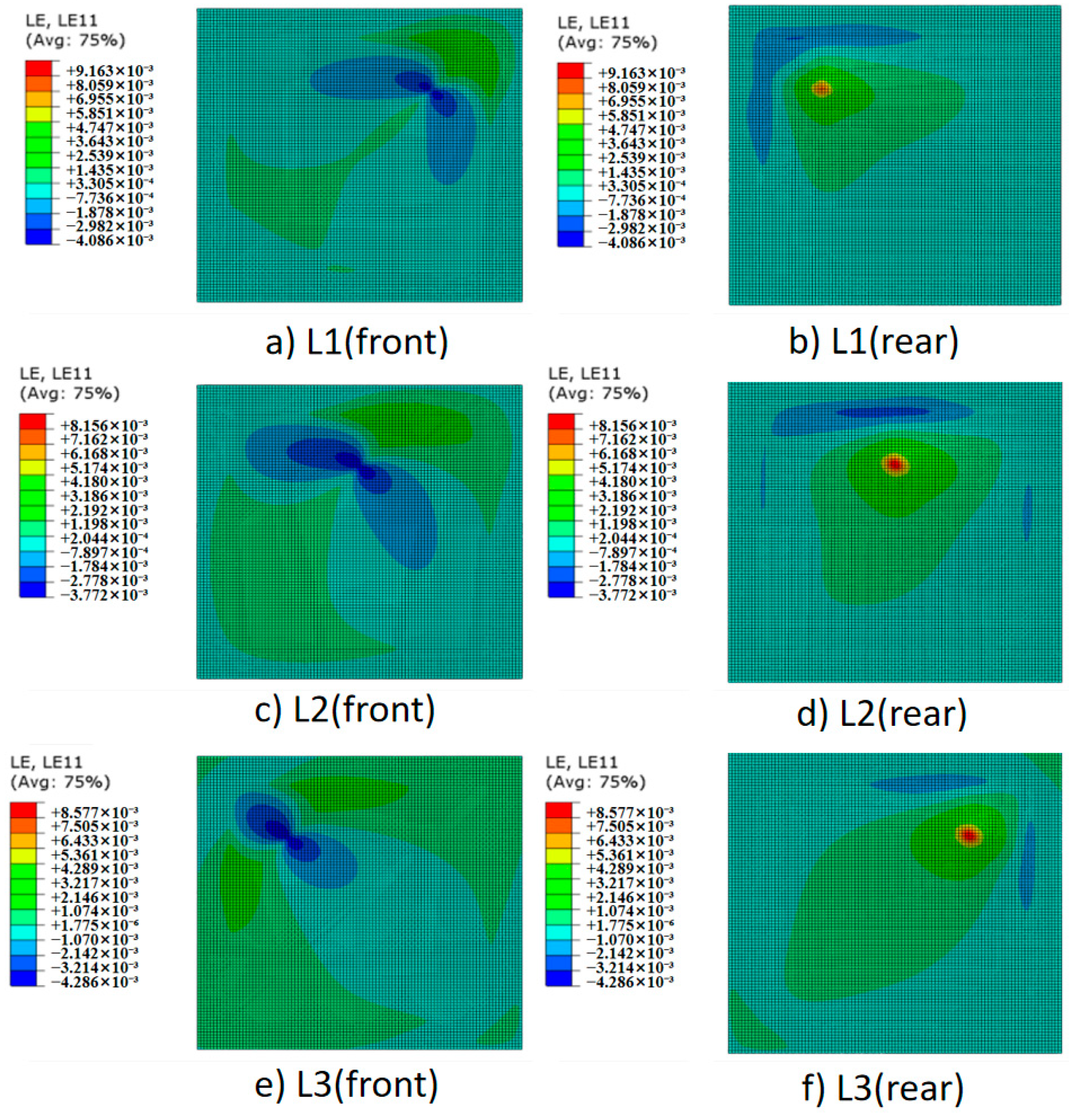
4.3. Impact Response Analysis at Different Locations
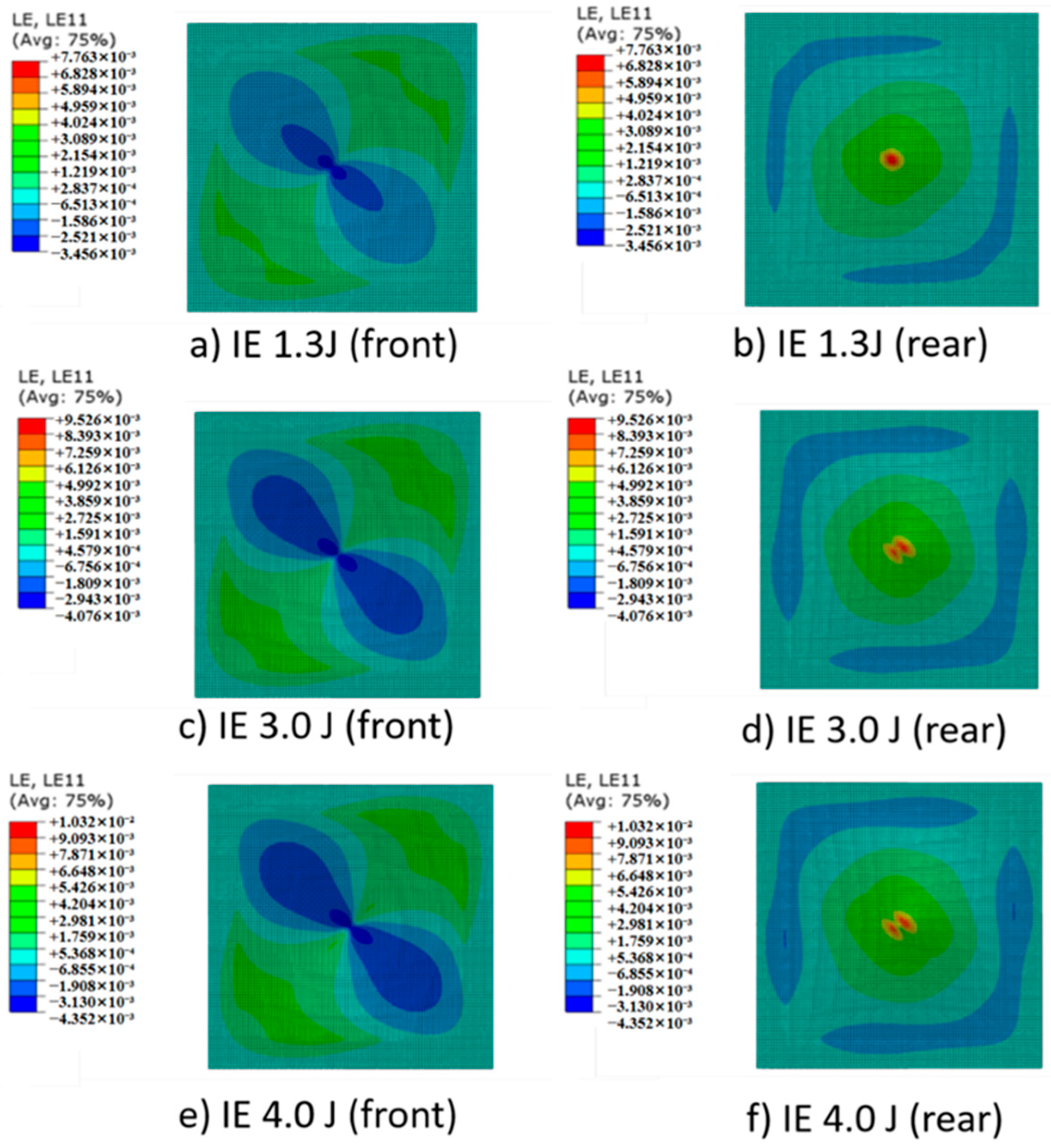
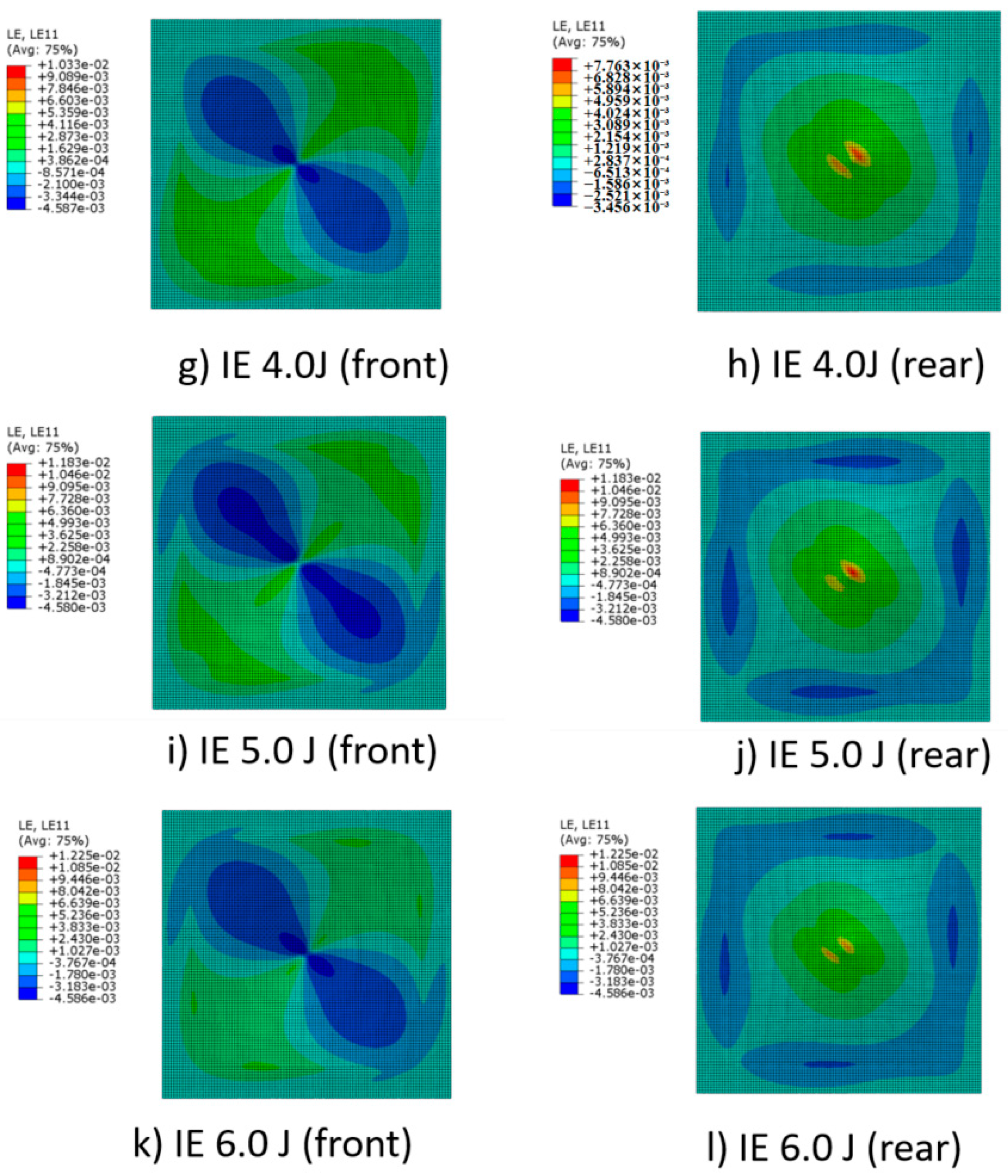
4.4. Impact Response Analysis at Different Energies
4.5. Damage Analysis at Different Energies
5. Conclusions
- (1)
- The proposed simulation modeling approach successfully predicts the impact responses of CLs under low-velocity impacts with high accuracy. The discrepancies between the simulated and experimental peak impact forces and pulse widths were within 5.83% and 4.95%, respectively.
- (2)
- Relative to other impact locations, the strain response at the central point of the CL (impact location 5) was found to be comparatively minimal. Upon impact, this location displayed a larger high-strain area on the rear surface of the laminate, indicating a higher susceptibility to damage and failure.
- (3)
- An increase in IE correlates with a gradual rise in the strain of the CL. The compression strain on the front side shows a less pronounced increase, while the tensile strain on the rear side demonstrates a more significant increase. The strain distribution patterns remain fundamentally consistent across different levels of IE.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, L.; Liu, W.; Wang, Y.; Zhao, Z. Mechanical performance and damage monitoring of CFRP thermoplastic laminates with an open hole repaired by 3D printed patches. Compos. Struct. 2023, 303, 116308. [Google Scholar] [CrossRef]
- Barile, C.; Casavola, C.; Pappalettera, G.; Kannan, V.P. Damage monitoring of carbon fibre reinforced polymer composites using acoustic emission technique and deep learning. Compos. Struct. 2022, 292, 115629. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Y.; Hu, J. Recent advances in the development of aerospace materials. Prog. Aerosp. Sci. 2018, 97, 22–34. [Google Scholar] [CrossRef]
- Thorsson, S.I.; Sringeri, S.P.; Waas, A.M.; Justusson, B.P.; Rassaian, M. Experimental investigation of composite laminates subject to low-velocity edge-on impact and compression after impact. Compos. Struct. 2018, 186, 335–346. [Google Scholar] [CrossRef]
- Habibi, M.; Laperrière, L.; Hassanabadi, H.M. Influence of low-velocity impact on residual tensile properties of nonwoven flax/epoxy composite. Compos. Struct. 2018, 186, 175–182. [Google Scholar] [CrossRef]
- Richardson, M.O.W.; Wisheart, M.J. Review of low-velocity impact properties of composite materials. Compos. Part A Appl. Sci. Manuf. 1996, 27, 1123–1131. [Google Scholar] [CrossRef]
- Bogenfeld, R.; Kreikemeier, J.; Wille, T. Review and benchmark study on the analysis of low-velocity impact on composite laminates. Eng. Fail. Anal. 2018, 86, 72–99. [Google Scholar] [CrossRef]
- Rezasefat, M.; Gonzalez-Jimenez, A.; Giglio, M.; Manes, A. Numerical study on the dynamic progressive failure due to low-velocity repeated impacts in thin CFRP laminated composite plates. Thin Walled Struct. 2021, 167, 108220. [Google Scholar] [CrossRef]
- Aslan, Z.; Karakuzu, R.; Okutan, B. The response of laminated composite plates under low-velocity impact loading. Compos. Struct. 2003, 59, 119–127. [Google Scholar] [CrossRef]
- Zou, D.; Haack, C.; Bishop, P.; Bezabeh, A. Damage criticality and inspection concerns of composite-metallic aircraft structures under blunt impact. In Structural Health Monitoring and Inspection of Advanced Materials, Aerospace, and Civil Infrastructure 2015; SPIE: Bellingham, WA, USA, 2015; Volume 9437. [Google Scholar]
- Zhou, Z.; Sun, W.; Zheng, N.; Tang, L.-C. Experimental and numerical investigation of the energy absorption characteristics of carbon-basalt hybrid fiber reinforced polymer composites under ballistic impact. Compos. Struct. 2024, 335, 118000. [Google Scholar] [CrossRef]
- Thorsson, S.I.; Waas, A.M.; Rassaian, M. Numerical investigation of composite laminates subject to low-velocity edge-on impact and compression after impact. Compos. Struct. 2018, 203, 648–658. [Google Scholar] [CrossRef]
- Canale, G.; Kinawy, M.; Sathujoda, P.; Maligno, A.; Citarella, R.G. Moisture absorption in thick composite plates: Modelling and experiments. Multidiscip. Model. Mater. Struct. 2020, 16, 439–447. [Google Scholar] [CrossRef]
- Zhang, C.; Duodu, E.A.; Gu, J. Finite element modeling of damage development in cross-ply composite laminates subjected to low velocity impact. Compos. Struct. 2017, 173, 219–227. [Google Scholar] [CrossRef]
- Zhang, B.; Ge, J.; Li, B.; Liu, Z.; Liu, S.; Liang, J. A parametric modeling method for 3D woven composites considering realistic meso-structural characteristics. Compos. Sci. Technol. 2024, 257, 110828. [Google Scholar] [CrossRef]
- Xu, W.; Chen, J.; Cui, X.; Wang, D.; Pu, Y. Low-velocity impact analysis and multi-objective optimization of hybrid carbon/basalt fibre reinforced composite laminate. Compos. Struct. 2024, 343, 118305. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X. Simulating low-velocity impact induced delamination in composites by a quasi-static load model with surface-based cohesive contact. Compos. Struct. 2015, 125, 51–57. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X. An efficient approach for predicting low-velocity impact force and damage in composite laminates. Compos. Struct. 2015, 130, 85–94. [Google Scholar] [CrossRef]
- Li, X.; Ma, D.; Liu, H.; Tan, W.; Gong, X.; Zhang, C.; Li, Y. Assessment of failure criteria and damage evolution methods for composite laminates under low-velocity impact. Compos. Struct. 2019, 207, 727–739. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, P.; Wang, S. Finite element analysis of a modified progressive damage model for composite laminates under low-velocity impact. Compos. Struct. 2019, 225, 111113. [Google Scholar] [CrossRef]
- Krueger, R. Virtual crack closure technique: History, approach, and applications. Appl. Mech. Rev. 2004, 57, 109–143. [Google Scholar] [CrossRef]
- Camanho, P.P.; Davila, C.G.; de Moura, M.F. Numerical simulation of mixed-mode progressive delamination in composite materials. J. Compos. Mater. 2003, 37, 1415–1438. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Guo, Y. Analysis of low-velocity impact response and damage characteristics of composite laminates with rigid/soft blunt objects. Polym. Compos. 2025, 46, S660–S677. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, S. A progressive damage model of composite laminates under low-velocity impact. Xibei Gongye Daxue Xuebao/J. Northwest. Polytech. Univ. 2021, 39, 37–45. [Google Scholar] [CrossRef]
- Hashin, Z. Fatigue Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. 1981, 48, 846–852. [Google Scholar] [CrossRef]
- Camanho, P.P.; Matthews, F.L. A progressive damage model for mechanically fastened joints in composite laminates. J. Compos. Mater. 1999, 33, 2248–2280. [Google Scholar] [CrossRef]
- HB6739; General Specifications for Carbon Fiber Prepreg. Aviation Industry Corporation of China (AVIC): Beijing, China, 2003.
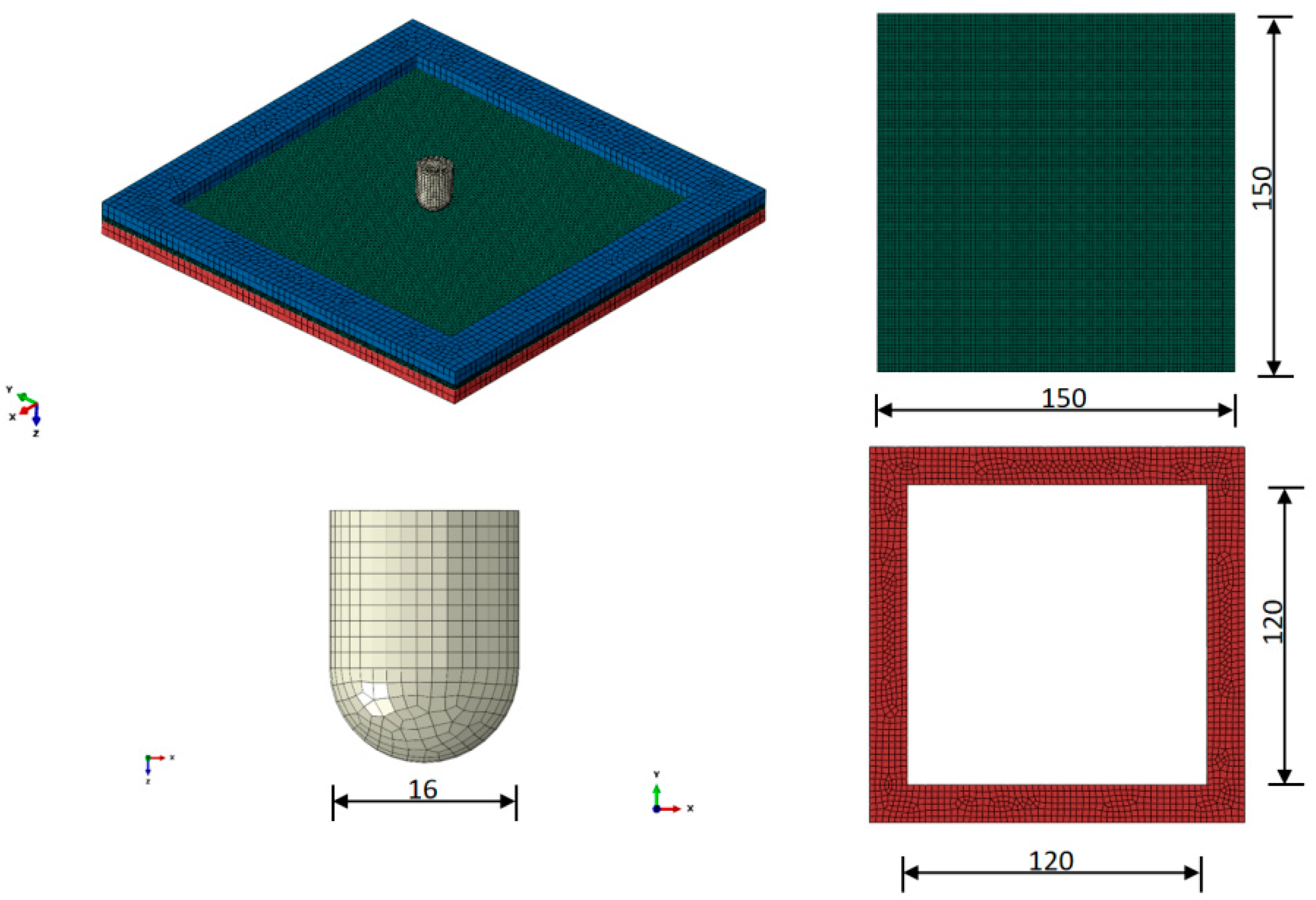




| Parameter | Value |
|---|---|
| ρ/(g/cm3) | 1.792 |
| E11/MPa | 121,000 |
| E22/MPa | 9705 |
| E33/MPa | 9705 |
| ν12 | 0.245 |
| ν13 | 0.245 |
| ν23 | 0.3 |
| G12/MPa | 4330 |
| G13/MPa | 4330 |
| G23/MPa | 3000 |
| Xt/MPa | 1455.20 |
| Xc/MPa | 739.20 |
| Yt/MPa | 41.31 |
| Yc/MPa | 96.80 |
| S12/MPa | 43.92 |
| S13/MPa | 43.92 |
| S23/MPa | 43.92 |
| Parameter | Value |
|---|---|
| E/GPa | 9.82 |
| tn0/MPa | 20.87 |
| ts0/MPa | 37 |
| tt0/MPa | 37 |
| GI/(N/mm) | 0.253 |
| GII/(N/mm) | 1.035 |
| GIII/(N/mm) | 1.035 |
| Parameter | Support Structure | Punch |
|---|---|---|
| ρ/(g/cm3) | 2.80 | 7.83 |
| ν | 0.33 | 0.27 |
| E/GPa | 69 | 193 |
| Test Number | Impact Location | Impact Velocity (m/s) | Punch Mass (kg) | IE (J) |
|---|---|---|---|---|
| 1 | L1 | 0.760, 1.155, 1.333, 1.491, 1.633, 1.764 | 4.50 | 1.30, 3.00, 4.00, 5.00, 6.00, 7.00 |
| 2 | L2 | |||
| 3 | L3 | |||
| 4 | L4 | |||
| 5 | L5 | |||
| 6 | L6 | |||
| 7 | L7 | |||
| 8 | L8 | |||
| 9 | L9 |
| Test Number | Impact Location | Impact Velocity (m/s) | Punch Mass (kg) | IE (J) |
|---|---|---|---|---|
| 1 | L2 | 0.760 | 4.50 | 1.30 |
| 2 | L3 | |||
| 3 | L6 | |||
| 4 | L7 |
| Impact Location | Experiment Results | Simulation Results | Error (%) | |||
|---|---|---|---|---|---|---|
| Impact Force/N | Pulse Widths/ms | Impact Force/N | Pulse Widths/ms | Impact Force/% | Pulse Widths/% | |
| L2 | 1211 | 11.1 | 1241 | 10.9 | 2.53 | 1.80% |
| L3 | 1353 | 10.5 | 1432 | 10.2 | 5.83 | 2.86% |
| L6 | 1291 | 11.2 | 1269 | 11.0 | 4.56 | 1.79% |
| L7 | 1350 | 10.1 | 1411 | 9.6 | 4.55 | 4.95% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, A.; Dong, H.; Cao, K.; Zhang, Y. Simulation and Experimental Study of Strain Distribution in Composite Materials Considering Impact Velocity and Impact Location. Aerospace 2025, 12, 1028. https://doi.org/10.3390/aerospace12111028
Qian A, Dong H, Cao K, Zhang Y. Simulation and Experimental Study of Strain Distribution in Composite Materials Considering Impact Velocity and Impact Location. Aerospace. 2025; 12(11):1028. https://doi.org/10.3390/aerospace12111028
Chicago/Turabian StyleQian, Aibing, Hao Dong, Kang Cao, and Yongjie Zhang. 2025. "Simulation and Experimental Study of Strain Distribution in Composite Materials Considering Impact Velocity and Impact Location" Aerospace 12, no. 11: 1028. https://doi.org/10.3390/aerospace12111028
APA StyleQian, A., Dong, H., Cao, K., & Zhang, Y. (2025). Simulation and Experimental Study of Strain Distribution in Composite Materials Considering Impact Velocity and Impact Location. Aerospace, 12(11), 1028. https://doi.org/10.3390/aerospace12111028






