A Deep Learning Approach to Accelerate MILP Solvers with Application to the Aircraft Routing Problem

Abstract

Large-scale Aircraft Routing Problems (ARPs) remain challenging for standard Branch-and-Bound (B&B) and modern Mixed-Integer Linear Programming (MILP) solvers due to vast search spaces and instance-agnostic heuristics. Methods: We develop a learning-to-accelerate framework centered on a Two-Stage Route Selection Graph Convolutional Network (TRS-GCN) that predicts the importance of flight string variables using structural, LP relaxation, and operational features. Predictions are injected into the solver via three mechanisms: an ML-guided feasibility pump for warm starts, static problem reduction through predictive pruning, and a dynamic hybrid branching rule that blends ML scores with pseudo-costs. A synthetic generator produces realistic ARP instances with seed solutions for robust training. Results: On large instances derived from Bureau of Transportation Statistics data, TRS-GCN-guided static reduction safely pruned up to 49.2% of variables and reduced the time to reach the baseline solver’s 12-h target objective by 52.4%. The dynamic search strategy also yielded more incumbents within fixed time budgets compared with baselines. Conclusion: Integrating TRS-GCN into MILP workflows improves search efficiency for ARPs, offering complementary gains from warm-starting, pruning, and branching without changing the underlying optimality guarantees.

1. Introduction

Over the past few decades, large-scale combinatorial optimization problems in air transportation have been traditionally solved using decomposition techniques such as Column Generation, which remain the state of the art for many industrial applications. However, recent advances in commercial Mixed-Integer Linear Programming (MILP) solvers (e.g., Gurobi, CPLEX) have significantly improved their capability to handle compact formulations even for large-scale problems [1]. Consequently, an increasing number of studies have started to revisit classical decomposition-based approaches and investigate whether high-performance MILP solvers can directly solve large compact models in a competitive way [2]. In this context, a natural next step is to explore how to further accelerate MILP-based solution approaches, by incorporating modern learning techniques to guide and speed up the search process. The present work is conducted precisely under this background: rather than proposing yet another decomposition or heuristic procedure, we focus on accelerating the solution of compact MILP models through deep learning and take a well-known real-world application (aircraft routing) as our testbed.

Due to the large solution space and the combinatorial nature of the problem, the Airline Routing Problem (ARP) is commonly formulated as a SCP (Set Covering Problem: a classical combinatorial optimization problem where the objective is to select the minimum number of subsets from a given collection such that their union covers all the elements) (Barnhart et al., 1998) [3], where each candidate flight sequence (refers to a potential route or series of flight legs that an aircraft could take, often represented by a specific set of flight legs or segments) is represented by a binary decision variable, and the objective is to ensure that all flights are covered by the selected set of variables (Dunbar et al., 2014) [4]. As a critical component of the airline planning process, the ARP has significant implications for downstream decisions, such as crew pairing and fleet utilization, and is essential in maintaining operational efficiency and robustness. However, the vast number of flight strings generated in real-world scenarios often results in substantial computational challenges, even for modern MILP solvers.

Branch-and-Bound (B&B) is a widely used exact algorithm for solving Mixed-Integer Linear Programming (MILP) problems. It systematically explores the solution space by branching on decision variables and bounding the objective function to eliminate infeasible regions. However, B&B can suffer from severe scalability issues, especially when solving large-scale problems with numerous variables. To address these challenges, we propose a Two-Stage Route Selection Graph Convolutional Network (TRS-GCN) that divides the Aircraft Routing Problem (ARP) into two phases. In the first stage, the GCN ranks and selects the most important flight strings based on their interdependencies, reducing the solution space. In the second stage, a heuristic algorithm solves the constraints related to connecting selected flight strings, ensuring a valid and feasible routing solution.

These predicted probabilities are then used to accelerate the B&B solver in three complementary ways:

• Fixing variables with extreme probabilities, which reduces the problem size and limits the search space.
• Providing a high-quality initial solution to enhance the solver’s efficiency and reduce the number of nodes explored.
• Guiding the branching order in a diving-style approach, ensuring that the solver focuses on the areas of the solution space that are most likely to lead to better solutions.

By applying these acceleration strategies to the B&B method, we enable the MILP solver to concentrate on the most promising parts of the solution space, significantly improving computational efficiency while preserving optimality guarantees.

2. Literature Review

Traditional aircraft routing methods can be broadly classified into two main approaches: pure integer linear programming (ILP) formulations and heuristic algorithms augmented with mathematical constraints for practical implementation. Rubin et al. (1973) [5] pioneered set cover models for airline scheduling, blending mathematical rigor with heuristic principles to enable efficient large-scale solutions. Subsequent work by Kabbina et al. (1992) [6] adapted this framework for route allocation, although their single-flight allocation unit resulted in complex cost calculations. A paradigm shift occurred with Barnhart et al. (1998) [3], who introduced flight strings—sequential flight leg sequences operated by individual aircraft. This innovation streamlined maintenance planning while enabling concurrent optimization of fleet assignment and routing through Branch-and-Price algorithms. Hane et al. (1995) [7] extended this integration, developing a dual simplex-based LP relaxation framework with variable aggregation to manage model complexity. Algorithmic advancements continued with Talluri et al. (1998) [8], who formalized the NP-hard 4-Day Maintenance Routing problem, proposing a three-phase heuristic involving flight string generation, greedy assignment, and local search optimization. Cordeau et al. (2001) [9] proposed a unified tabu search heuristic for the Vehicle Routing Problem with Time Windows (VRPTW) and its variants, demonstrating its efficiency and flexibility in solving large-scale instances. Recent innovations (Aydoğan et al., 2023) [10] further advanced conflict-free route optimization in hybrid airspace using constrained simulated annealing. This methodological evolution reflects an increasing emphasis on hybrid approaches that balance computational tractability with real-world operational constraints, leveraging both mathematical programming and metaheuristic strategies to address the inherent complexity of Aircraft Routing Problems.

Recent advancements in machine learning (ML) for combinatorial optimization have been systematically categorized into three frameworks by Bengio et al. (2021) [11]: imitation learning, reinforcement learning (RL), and generative models. Imitation learning employs end-to-end training to replicate expert strategies but suffers from dependency on optimal training data and poor adaptability to dynamic scenarios [12]. RL optimizes decision-making via environmental interactions but faces computational inefficiency and reward design complexity [13]. Generative models (e.g., GANs) explore solution spaces but risk mode collapse and constraint violations [14]. To mitigate these limitations, hybrid algorithms integrating ML with classical optimization methods have emerged, leveraging ML’s flexibility and traditional algorithms’ precision. Prominent applications include (Alvarez et al., 2017) [15] the two-stage ML approach to approximate strong branching decisions in Mixed-Integer Programming (MIP), reducing computational costs while maintaining solution quality. Bartunov et al. (2021) [16] further advanced this by embedding neural networks into MIP solvers via Neural Diving (generating partial solutions) and Neural Branching (optimizing variable selection). Similarly, Paulus et al. (2022) [17] improved cutting plane selection using imitation learning with forward-looking strategies, achieving global optimization in decision-making. In aviation, Ruan et al. (2020) [18] applied RL to aircraft routing, using Q-learning to minimize maintenance costs and scheduling delays. However, challenges persist in graph-based modeling. Zhang et al. (2023) [19] explored the expressive power of Graph Neural Networks (GNNs) by examining their ability to capture graph biconnectivity, offering insights into their capacity for representing complex graph structures. They prove that most popular GNN architectures lack sufficient expressive power under the biconnectivity metric.

In recent years, improvements in MIP solvers’ performance have made it possible to tackle complex optimization problems, leading to a growing body of research focused on using neural networks to accelerate solver computations (Mitrai et al., 2025) [20]. This review paper explores the application of machine learning in accelerating process control and optimization, focusing on how learning algorithm selection and configuration can improve efficiency and address challenges in real-time and scalability for complex systems. Similarly, Khalil et al. (2022) [21] leverage Graph Neural Networks (GNNs) to guide MIP solvers, enhancing decision-making in tasks like node selection and warm-starting, which leads to better efficiency and solution quality. Liu et al. (2024) [22] dynamically adjusted presolving settings through machine learning, significantly speeding up the presolving process and outpacing traditional solvers in terms of speed and solution quality. Lastly, Cai et al. (2025) [23] integrated GNNs with MILP solvers to accelerate motion planning for autonomous systems, particularly in uncertain environments with temporal constraints, further enhancing solver efficiency for real-time tasks. These advancements highlight the growing role of machine learning and hybrid approaches in optimizing the performance of MIP solvers, improving their applicability to large-scale and real-time optimization problems, including those in aviation and autonomous systems.

In recent studies, machine learning has been increasingly applied to vehicle routing problems. For example, Ma et al. (2023) [24] proposed a Flexible Neural k-Opt method that learns to search both feasible and infeasible regions of routing problems, improving solution efficiency. Sobhanan et al. (2023) [25] combined genetic algorithms with a neural cost predictor to solve hierarchical vehicle routing problems, demonstrating the synergy between evolutionary algorithms and deep learning. Additionally, Bogyrbayeva et al. (2022) [26] surveyed various learning-based approaches for solving vehicle routing problems, categorizing them into learning-to-construct, learning-to-search, and learning-to-predict frameworks, which has inspired several advancements in hybrid ML-optimization algorithms.

Table 1. Comparison of our method with related work in the literature.

Reference	Distinction from This Work
Rubin et al. (1973) [5]	This paper first proposed the set covering model, which is applied to the Aircraft Routing Problem. We adopted this model as the foundation for the problem formulation.
Kabbani et al. (1992) [6]	This paper describes the aircraft routing process and solutions used by U.S. airlines in practice. While our work references this article in terms of problem formulation, the solution approach is entirely different.
Barnhart et al. (1998) [3]	We adopted the flight string model but separated the flight string connection constraints from the mathematical model and used a heuristic algorithm to solve them.
Talluri et al. (1998) [8]	We simplified the model’s scale from 4 days to 1 day.
Cordeau et al. (2001) [9]	Compared to the original, we introduced graph partitioning, beam search, and parallel computing strategies, effectively reducing computation time by solving subproblems in parallel.
Bengio et al. (2021) [11]	This paper only provides a general overview of some ideas on combining machine learning with combinatorial optimization. We have further developed these ideas into practical implementations and proposed more detailed solutions.
Alvarez et al. (2017) [15]	We replaced the linear regression model with a Graph Neural Network (GNN) with attention, improved the evaluation function for strong branching, and designed different features specifically for the ARP.
Bartunov et al. (2021) [16]	We adopted the GNN representation for MIP from the original work, but this paper adds a rich feature representation, as the original lacked feature extraction for MIP.
Zhang et al. (2023) [19]	This article demonstrates the necessity of the improvements made to the graph structure in this paper.
Khalil et al. (2022) [21]	We adopted the warm-start strategy but improved the branching node selection method, added a variable reduction strategy, enhanced the neural network model, and changed the prediction output from one-shot to sequential/dynamic.
Cai et al. (2025) [23]	Similarly integrates GNNs and solvers, but their work predicts the solver’s configuration parameters, whereas our work predicts variable importance for branching and reduction.

The following papers address related problems with different methods and are not directly referenced in this work: Hane et al. (1995) [7], Aydoğan et al. (2023) [10], Papagiannis et al. (2024) [12], Yuan et al. (2024) [13], Goodfellow et al. (2020) [14], Paulus et al. (2022) [17], Ruan et al. (2020) [18], Mitrai et al. (2025) [20], Liu et al. (2024) [22], Ma et al. (2023) [24], Sobhanan et al. (2023) [25], and Bogyrbayeva et al. (2022) [26].

summarizes the relationship between our approach and significant related studies. For each key reference, we outline the primary distinction, clarifying how our method adopts, extends, or diverges from existing frameworks.

3. Contribution

In existing MIP solvers, the default presolving and branching strategies are generally adopted without distinguishing between different input instances. However, default settings are not always suitable for all problem instances (previous studies (Hutter et al., 2009 [27]; 2011 [28];) (Lindauer et al., 2022) [29]). This paper presents a single SMAC3, a Bayesian optimization framework proposed for hyperparameter optimization, offering high flexibility and robustness and used to adjust the parameter configurations during the solving process of MIP solvers. Nevertheless, such approaches cannot be tailored to each individual MIP instance, such as the ARP investigated in this study. We argue that the performance of MIP solvers can be significantly improved by designing preprocessing procedures that apply more aggressive strategies in the initial stages to eliminate invalid variables and by utilizing warm-start methods or by incorporating tailored strong branching strategies into the Branch-and-Bound (B&B) search process.

Recent work (Liu, 2024) [22] has pointed out that “an analysis of presolve would be incomplete without an investigation of this effect for particular instances”, which further emphasizes the necessity of developing instance-specific presolve and branching strategies for problems like the ARP. In addition, empirical evidence (Frank et al., 2010) [30] has shown that customized optimization strategies can substantially enhance computational performance.

The primary contributions of this work are fourfold, presenting a comprehensive machine learning-integrated framework for accelerating the solution of the large-scale Aircraft Routing Problem (ARP).

• We propose a novel acceleration method specifically designed for MIP solvers in solving the Aircraft Routing Problem (ARP). This method includes a two-stage modeling strategy integrated with heuristic algorithms, an improved network architecture, an innovative feature extraction approach, and three acceleration strategies (contribution 2) that leverage predicted results to enhance solver performance. At the core of this approach is the Two-Stage Route Selection Graph Convolutional Network (TRS-GCN), a deep learning architecture that formulates variable importance prediction as an autoregressive, sequential task. Unlike traditional static models that predict scores for all variables simultaneously, TRS-GCN generates a ranked sequence, thereby capturing the complex interdependencies inherent in combinatorial optimization. This approach is supported by an enriched feature representation that incorporates problem-specific structural attributes and linear programming-based features.
• We propose three distinct and practical strategies to integrate the model’s predictions into state-of-the-art MIP solvers. These methods target different stages of the solution process: (i) A machine learning-guided feasibility pump (enhances the classical feasibility pump by incorporating machine learning predictions to guide the rounding process) for generating high-quality warm-start solutions enhances the classical feasibility pump by incorporating machine learning predictions to guide the rounding process, improving the efficiency of finding feasible solutions. (ii) A static problem reduction technique prunes low-importance variables based on machine learning predictions before solving, reducing the problem size and improving solver efficiency. (iii) A dynamic hybrid branching strategy that combines machine learning predictions with solver-native pseudo-costs to guide the Branch-and-Bound search. The strategy uses a hybrid branching score, where the machine learning-derived importance score is dynamically weighted with the pseudo-costs as more empirical data becomes available. This approach helps prioritize the most promising variables early in the search process, addressing the cold start problem and improving convergence efficiency.
• To overcome the challenge of data scarcity, we design a novel synthetic ARP instance generator. A key advantage of our generator is its ability to produce realistic, structured problem instances along with corresponding high-quality seed solutions, which drastically reduces the time and effort required to create labeled training data.
• We develop a highly efficient and parallelized flight string generation algorithm using temporal graph partitioning and beam search. This heuristic method enables the rapid construction of the problem’s decision variable space for large-scale, real-world instances, reducing model formulation time by over an order of magnitude compared to conventional enumeration techniques.
• In our experimental study, we constructed test cases using real-world flight data from the publicly available Bureau of Transportation Statistics (BTS) On-Time Performance dataset. All datasets and algorithm implementations used in the experiments are publicly available in a GitHub repository (https://github.com/pyb-107/TRS-GCN, accessed on 3 November 2025), enabling interested researchers to reproduce and further explore the presented results.

4. Methods

The overall framework of the model is shown in Figure 1. The arrows represent the data processing and transformation process, and the orange color in the graph indicates more important nodes. The system integrates deep learning with combinatorial optimization to solve the large-scale Aircraft Routing Problem (ARP) efficiently. The process begins with the training data generation module, which creates feasible ARP instances using a synthetic generator. This generator produces problem instances with structured data, including the incidence matrix, cost vector, and feasible seed solutions. These data are then used to train the Two-Stage Route Selection Graph Convolutional Network (TRS-GCN), which learns to rank flight strings based on their importance to the optimal solution.

In the problem modeling phase, the ARP is represented as a Set Covering Problem (SCP), where each flight string corresponds to a binary decision variable. The problem is formulated as a bipartite graph, linking flight strings to the flights they cover, forming the input for both deep learning and optimization processes. The solving module uses a hybrid approach, combining TRS-GCN predictions with the Gurobi MIP solver. The TRS-GCN ranks flight strings by importance and uses three complementary techniques to accelerate the optimization process: warm-starting, where machine learning-guided feasibility pumps generate high-quality initial solutions; static problem reduction, which prunes low-importance variables; and dynamic search guidance, where TRS-GCN’s predictions guide the branching process.

Through these techniques, the system reduces the solution space, accelerates convergence, and ensures high-quality, near-optimal solutions for large-scale ARP instances. The entire framework efficiently integrates machine learning into the traditional Branch-and-Bound (B&B) method, significantly improving computational performance while maintaining optimality guarantees.

4.1. Model Building

4.1.1. Problem Formulation

We consider the aircraft routing problem over a weekly planning horizon. The input consists of a set of airports, a collection $\mathcal{L}$ of flight strings, and a given number $n^a$ of available airplanes. Some airports are designated as bases, where maintenance operations can be performed. Each flight leg $\mathsf{\ell }\in \mathcal{L}$ is characterized by a departure and arrival airport, along with departure and arrival times, with the natural assumption that the departure time precedes the arrival time.

The routing objective is to construct cyclic schedules for airplanes such that every flight leg is covered exactly once per week without exceeding the available fleet size $n^a$. Additionally, a maintenance constraint is imposed: each aircraft must spend a night in a base at least once every ${\Delta }_{\mathrm{maint}}$ days, where ${\Delta }_{\mathrm{maint}}$ is a fixed parameter. Here, we fix ${\Delta }_{\mathrm{maint}}$ to 1, meaning the scheduling is based on a daily cycle, and after operating for one day, each aircraft must return to a maintenance base.

Formally, an airplane connection is defined as a pair $(\mathsf{\ell },{\mathsf{\ell }}^{\prime })$ of flight strings satisfying the following:

• The arrival airport of ℓ coincides with the departure airport of ${\mathsf{\ell }}^{\prime }$;
• The time interval between the arrival of ℓ and the departure of ${\mathsf{\ell }}^{\prime }$ is above a minimum threshold depending on the airport, time, and fleet.

A route is a cyclic sequence of distinct flight legs ${\mathsf{\ell }}_1,\dots ,{\mathsf{\ell }}_k$ such that consecutive pairs $({\mathsf{\ell }}_i,{\mathsf{\ell }}_{i+1})$ and $({\mathsf{\ell }}_k,{\mathsf{\ell }}_1)$ are airplane connections. Routes may last several weeks, but the operational pattern is repeated weekly. To satisfy the maintenance requirement, an aircraft following a route must visit a base at least once every ${\Delta }_{\mathrm{maint}}$ days. The task is therefore to partition $\mathcal{L}$ into a set of strings that satisfy the maintenance requirement while minimizing the number of airplanes needed, constrained to be less than or equal to $n^a$.

4.1.2. Graph Representation

To model the problem, we introduce a directed graph $D=(V,A)$. Each flight leg $\mathsf{\ell }\in \mathcal{L}$ is duplicated ${\Delta }_{\mathrm{maint}}$ times to capture the number of days since the aircraft last visited a base. Thus, each vertex is denoted by $(\mathsf{\ell },\delta )$, where $\delta \in \left[{\Delta }_{\mathrm{maint}}\right]$.

An arc $((\mathsf{\ell },\delta ),({\mathsf{\ell }}^{\prime },{\delta }^{\prime }))\in A$ exists if $(\mathsf{\ell },{\mathsf{\ell }}^{\prime })$ is an airplane connection and one of the following holds:

1.

ℓ and ${\mathsf{\ell }}^{\prime }$ occur on the same day with $\delta ={\delta }^{\prime }$;

2.

ℓ ends at a base and ${\mathsf{\ell }}^{\prime }$ starts the following day, with ${\delta }^{\prime }=1$;

3.

Otherwise, ${\delta }^{\prime }-\delta \ge 0$ equals the number of days between the arrival of ℓ and the departure of ${\mathsf{\ell }}^{\prime }$.

A cyclic sequence $({\mathsf{\ell }}_1,{\delta }_1),\dots ,({\mathsf{\ell }}_k,{\delta }_k)$ forms a feasible route if it is a cycle in D, meaning that the sequence of legs satisfies the maintenance requirement. If a route violates the maintenance condition, its corresponding sequence cannot form a cycle in D. To restrict fleet usage, we define $A_0\subseteq A$ as the set of arcs crossing a fixed instant within the week. Each cycle crossing this instant corresponds to one aircraft in operation. Thus, bounding the number of arcs in $A_0$ provides control over the total number of airplanes required.

4.1.3. Integer Programming Model

We now state the integer programming formulation. A feasible solution corresponds to selecting a set of vertex-disjoint cycles in D covering all legs in $\mathcal{L}$, while respecting maintenance and fleet constraints.

Feasible solutions of the aircraft routing problem are in one-to-one correspondence with collections $\mathcal{C}$ of vertex-disjoint cycles in D, such that

1.

For each $\mathsf{\ell }\in \mathcal{L}$, exactly one cycle in $\mathcal{C}$ intersects with $V_{\mathsf{\ell }}=\{(\mathsf{\ell },\delta ):\delta \in \left[{\Delta }_{\mathrm{maint}}\right]\}$, and this intersection consists of a single arc;

2.

$\mathcal{C}$ uses at most $n^a$ arcs from $A_0$.

The resulting integer program (AR) is

$$\sum _{a\in {\delta }^{-}\left(v\right)}{x}_a=\sum _{a\in {\delta }^{+}\left(v\right)}{x}_a,\forall v\in V$$

(1)

$$\sum _{a\in {\delta }^{-}\left(V_{\mathsf{\ell }}\right)}{x}_a=1,\forall \mathsf{\ell }\in \mathcal{L}$$

(2)

$$\sum _{a\in A_0}{x}_a\le n^a$$

(3)

$$x_a\in \{0,1\},\forall a\in A$$

(4)

Here, (1) is the flow conservation constraint ensuring the solution consists of cycles; (2) guarantees that each flight leg is covered exactly once; (3) enforces the fleet-size constraint; and (4) ensures integrality.

4.1.4. Flight Leg Matching and String Generation

In order to efficiently enumerate feasible flight strings from the original set of flight legs $\mathcal{L}$, we introduce a hybrid parallel exploration strategy that combines graph partitioning with a beam search [31] procedure. Traditional recursive enumeration algorithms suffer from factorial growth and redundancy due to repeated exploration of common prefixes in the solution space. As the problem size increases, the number of possible solutions expands exponentially, leading to significant computational inefficiency. This redundancy arises from the recursive nature of the search, where shared subpaths are recomputed multiple times. To address this, we propose a hybrid parallel exploration strategy that combines graph partitioning with beam search. This approach constructs a directed connection graph and applies a bounded-width search heuristic, enabling parallel execution and significantly reducing total execution time while preserving solution completeness.

Step 1: Graph Construction: We build a directed graph $G=(V,A)$ in which every vertex represents a flight leg, and an arc $(\mathsf{\ell },{\mathsf{\ell }}^{\prime })$ is added if the arrival of ℓ can be followed by the departure of ${\mathsf{\ell }}^{\prime }$, subject to the minimum turnaround time, aircraft type, and fleet compatibility constraints. Hence, a feasible flight string corresponds to a path in G.

Step 2: Temporal Partitioning: To enable intra-machine parallelization, the graph G is partitioned into k non-overlapping blocks $G_1,\dots ,G_k$ according to the departure time of the flights. Each subgraph $G_i$ contains flights belonging to a specific temporal window and can therefore be processed independently without violating connection feasibility. This partitioning operation reduces the local search space and provides natural boundaries for parallel execution.

Step 3: Beam Search in Each Subgraph: Within each subgraph, we adopt a beam search strategy to construct candidate flight strings. Given a predefined beam width B, only the best B partial strings—as measured by a heuristic score—are retained at each iteration. The heuristic function combines total flight duration, the number of remaining feasible legs, and airline continuity in order to guide the exploration towards promising string extensions while eliminating clearly suboptimal branches.

Step 4: Cross-Block Merging: Upon the completion of local searches in all subgraphs, partial strings from adjacent subgraphs are combined whenever the terminal flight in one string can be connected to the initial flight of a string from the succeeding block. To capture potential long-range connections, the merging procedure is iteratively applied until no further concatenations occur. The complete procedure is summarized in Algorithm 1.

Algorithm 1: Parallel Flight String Generation via Graph Partitioning and Beam Search

Input: $G=(V,A)$: Directed flight connection graph, k: number of temporal partitions, B: beam width Output: $\mathcal{S}$: Set of generated flight strings

The overall procedure offers near linear scalability with respect to the number of CPU cores and has been empirically shown to preserve enumeration quality while reducing the computational cost by more than one order of magnitude compared to conventional depth-first search strategies.

In order to guide the beam search procedure toward promising partial strings, we introduce the following composite scoring function:

$$h\left(S\right)=\alpha ;\mathrm{dur}\left(S\right)+\beta ;\mathrm{con}\left(S\right)-\gamma ;\mathrm{rem}\left(S\right),$$

(5)

where $\mathrm{dur}\left(S\right)$ denotes the cumulative flight duration in the current string, $\mathrm{con}\left(S\right)$ is a continuity indicator that captures airline and airport consistency between consecutive legs, and $\mathrm{rem}\left(S\right)$ denotes the number of yet unvisited legs in the corresponding subgraph that remain compatible with the last flight in S. The constants $\alpha$, $\beta$, and $\gamma$ are tuning parameters calibrated on a small set of representative instances.

Let $n=\left|V\right|$ denote the total number of flight legs and k the number of temporal partitions, so that each subgraph contains approximately $n/k$ vertices. Within one subgraph, the worst-case number of expansions per iteration is bounded by the beam width B and the average out-degree $\overline{d}$ of the graph, yielding

$$T_{\mathrm{local}}=O\left(B,\overline{d},\tau \right),$$

(6)

where $\tau$ denotes the maximum number of iterations in each subgraph. Since the k searches are executed in parallel, the total time associated with local searches remains

$$T_{\mathrm{parallel}}=O\left(B,\overline{d},\tau \right).$$

(7)

During the cross-block concatenation phase, most $O\left(B^2\right)$ string pairs must be evaluated per consecutive block pair, yielding an additional computational effort of

$$T_{\mathrm{merge}}=O\left((k-1),B^2\right).$$

(8)

Combining (7) and (8), the overall run time of the proposed algorithm reads

$$T(n,B,k)=O\left(B,\overline{d},\tau +(k-1),B^2\right),$$

(9)

which is significantly lower than the factorial complexity $O(n!)$ associated with exhaustive enumeration.

4.2. Deep Learning Method

4.2.1. Training Data Generation

The pseudocode of the algorithm is shown in Algorithm A1. The following is an explanation of the symbols and formulas appearing in the pseudocode.

In the training data generation, one of the most crucial aspects is how to collect enough usable training data [32]. For the problem addressed in this study, the data consists of a large number of solvable Set Covering Problems. Regarding the Aircraft Routing Problem, there are several challenges in collecting training data. If public datasets are used to train the model (such as CORLAT, MIPLIB, Google Production Packing, etc.), these datasets suffer from scattered data scales and are randomly generated, with no regularity in the constraint coefficients of the variables. Using these datasets to train the model results in poor fitting for the Aircraft Routing Problem, significantly reducing accuracy.

If real-world data are used for model training, since aircraft routing is typically released on a quarterly basis, even if data from a long time span is collected, the available samples may still be insufficient to fully train the model. In addition, adjacent flight schedules exhibit minimal differences, making overfitting a common issue. Therefore, this paper designs a data generation algorithm that mimics real-world scenarios, generating specific simulated SCP (Set Covering Problem) instances for the Aircraft Routing Problem, where both the problem scale and parameters can be customized.

We design a training data generator for the Aircraft Routing Problem that can generate ARP instances and their corresponding solutions. This generator first builds a covering seed solution and then injects noise columns under hub/time-structured rules. This guarantees feasibility while matching stylized regularities of aircraft routing. For example, hub airports tend to have higher connection rates, so the coefficients for flights connected to hubs are generally higher, reflecting their importance in the system. Similarly, time constraints between flights exhibit patterns, such as common time buckets (e.g., morning, afternoon, evening) with regular sequencing based on typical airline schedules.

Let H be a set of airports with hub weights $w:H\to {\mathbb{R}}_{>0}$ (Zipf-like [33]), and $I=\{1,\dots ,n\}$ be the set of flights. Each flight $i\in I$ has the following properties:

• $(o_i,d_i)\in H\times H$ (origin and destination airports);
• Departure and arrival times $(t_i^{\mathrm{dep}},t_i^{\mathrm{arr}})$;
• A time bucket $b_i\in \{1,\dots ,B\}$ (morning, noon, evening);
• A maintenance flag $m_i\in \{0,1\}$.

The minimum turnaround time is $\Delta >0$. A route S is an ordered subset of I that obeys connectivity and time-monotonicity: for consecutive flights $i<j$ in S, we require $d_i=o_j$ and $t_i^{\mathrm{arr}}+\Delta \le t_j^{\mathrm{dep}}$. The specific process of the algorithm is as follows:

Sample flights with hub/time structure: For each flight, sample the departure airport $o_i$ and the arrival airport $d_i$, with probabilities proportional to $w\left(o_i\right)w\left(d_i\right)$ (reflecting the idea that “hub airports are more likely to be selected,” and $o_i=d_i$ is prohibited to avoid invalid round trips). Sample a time bucket $b_i\in \{1,\dots ,B\}$, and then sample the departure time $t_i^{dep}$ within the bucket; the arrival time is $t_i^{arr}=t_i^{dep}+du{r}_i$, where $du{r}_i\sim \mathrm{Lognormal}({\mu }_{dur},{\sigma }_{dur})$ (log-normal distribution to model flight durations). Select all flights where $m_i=1$ as “maintenance-required flights” (set $m_i=1$), and set $m_i=0$ for others.

Build a feasible seed cover $x^{\star }$: Step 2 aims to construct a feasible seed cover $x^{\star }$ to generate “seed routes” that ensure all flights are covered, thereby forming an initial feasible solution for the Set Covering Problem (SCP). Initially, $J_{\mathrm{seed}}$ (indices of seed routes), U (route nodes), A (incidence matrix with no columns initially), and $Ucv$ (the set of uncovered flights, which initially includes all flights) are initialized. Subsequently, while $Ucv\ne \varnothing$, the procedure iterates to cover all flights: a starting flight $i_0$ is selected from $Ucv$ with a probability proportional to $(\mathrm{deg}\left(v_{i_0}\right)+\alpha )·(w\left(o_{i_0}\right)+w\left(d_{i_0}\right))$, which integrates “flight degree” (the number of connections a flight has) and “hub weights” (the importance of the airport as a hub) to embody the “preferential attachment” mechanism. Preferential attachment is a concept borrowed from network theory, where entities with higher connectivity (in this case, more frequent flight connections) are more likely to be selected. This mechanism mimics the behavior observed in real-world networks, such as airline routes, where hub airports, due to their high connectivity, are more likely to be chosen for flight routes.

The initial route S is initialized as $\left[i_0\right]$, and the route length L is sampled from ${\pi }_{\mathrm{len}}$ to determine the number of flights contained in the route. Following this, subsequent flights are added iteratively: with probability $\beta$, the time bucket of the next flight is restricted to match that of the current flight ℓ; otherwise, this constraint is relaxed. Candidate flights $\mathcal{C}=\{j\in I\setminus S:o_j=d_{\mathsf{\ell }},t_{\mathsf{\ell }}^{\mathrm{arr}}+\Delta \le t_j^{\mathrm{dep}}\}$ (satisfying “origin-destination airport matching and sufficient turnaround time”) are filtered. If $\kappa =1$ and no maintenance-required flight exists in the current route, $\mathcal{C}$ is biased toward flights with $m_j=1$. A candidate flight j is sampled using the score $s\left(j\right)=(deg\left(v_j\right)+\alpha )(w\left(o_j\right)+w\left(d_j\right))exp\{-\gamma (t_j^{\mathrm{dep}}-t_{\mathsf{\ell }}^{\mathrm{arr}})\}$ (which combines flight degree, hub weights, and penalizes longer time intervals) and appended to S. If $\kappa =1$ and no maintenance-required flight is present in the route yet, an attempt is made to append the nearest feasible maintenance-required flight; if this attempt fails, the construction of the current route restarts. Finally, a new route $j^{\star }$ is created to update the incidence matrix A and the set $Ucv$. The seed solution $x^{\star }$ is generated by setting $x_j^{\star }=1$ for seed routes, ensuring that each flight is covered by at least one route (i.e., ${\sum }_j{A}_{ij}{x}_j^{\star }\ge 1$ holds for all i).

Add noise columns for redundancy/realism: Step 3 aims to add noise columns to enhance redundancy and realism, generating additional “noise routes” such that each flight is covered by more routes (closer to the real-world scenario where “one flight has multiple route options”). First, the target degree is set: the “coverage count (degree)” of each flight must satisfy $deg\left(v_i\right)\ge 1+Q_i$, where $Q_i\sim \mathrm{Poisson}\left(q_{\mathrm{dup}}\right)$ (the Poisson distribution controls the number of extra covers). Then, noise routes are generated iteratively until “the number of seed columns + the number of noise columns $\ge p_{\mathrm{target}}$” or “all flights meet the degree requirements”: when generating a noise route $\tilde{S}$, the process is similar to Step 2 but with inflated hub weights $w(·)$, relaxed time-bucket constraint $\beta$, and optionally longer route length L; a new column $\tilde{j}$ is added to update the incidence matrix, mark coverage relationships, and update the degree of flights.

Add noise columns for redundancy/realism: Step 3 aims to add noise columns to enhance redundancy and realism, generating additional “noise routes” such that each flight is covered by more routes (closer to the real-world scenario where “one flight has multiple route options”). The addition of noise routes introduces redundancy by providing multiple possible routes for each flight, reflecting the variety of feasible paths in real-world airline networks. It also improves realism by simulating alternative, less likely routes that might still be valid, thereby better representing the complexity and flexibility of actual flight scheduling. First, the target degree is set: the “coverage count (degree)” of each flight must satisfy $deg\left(v_i\right)\ge 1+Q_i$, where $Q_i\sim \mathrm{Poisson}\left(q_{\mathrm{dup}}\right)$ (the Poisson distribution controls the number of extra covers). Then, noise routes are generated iteratively until “the number of seed columns + the number of noise columns $\ge p_{\mathrm{target}}$” or “all flights meet the degree requirements”: when generating a noise route $\tilde{S}$, the process is similar to Step 2 but with inflated hub weights $w(·)$, relaxed time-bucket constraint $\beta$, and optionally longer route length L; a new column $\tilde{j}$ is added to update the incidence matrix, mark coverage relationships, and update the degree of flights.

Assign costs and control SNR: Step 4 is for assigning costs and controlling the signal-to-noise ratio (SNR), which calculates the cost for each route and scales the cost of noise columns (to make the cost distinction between valid routes and noise routes more reasonable). The base cost formula is

$$c_j={\theta }_0+{\theta }_1\left|S_j\right|+{\theta }_2\sum _{i<i^{\prime }\in S_j}(t_{i^{\prime }}^{\mathrm{dep}}-t_i^{\mathrm{arr}})+{\theta }_3\mathbf{1}[\exists i\in S_j:m_i=1]+{\epsilon }_j,$$

(10)

where $|S_j|$ is the number of flights in route j; ${\sum }_{\begin{array}{c}i\prec i^{\prime }\in S_j\end{array}}\left(t_{i^{\prime }}^{\mathrm{dep}}-t_i^{\mathrm{arr}}\right)$ is the total time interval between consecutive flights in the route; $⊮[·]$ is an indicator function (1 if the route contains a maintenance-required flight, 0 otherwise); ${\epsilon }_j\sim \mathcal{N}(0,{\sigma }^2)$ is noise following a normal distribution (simulating random fluctuations in cost). If j is a noise column ($j\in J_{\mathrm{noise}}$), its cost is scaled as $c_j\leftarrow \rho ·c_j$ ($\rho \ge 1$ makes noise columns more costly, reducing their probability of being selected).

Let $J=\{1,\dots ,p\}$ index the columns, and $A\in {\{0,1\}}^{n\times p}$ be the incidence matrix where $A_{ij}=1$ if $i\in S_j$. The SCP decision vector is $x\in {\{0,1\}}^p$. By construction, we generate a seed cover $x^{\star }$, such that

$$\sum _j{A}_{ij}{x}_j^{\star }\ge 1\forall i.$$

(11)

A signal-to-noise parameter $\rho \ge 1$ scales the costs of noise columns: for $j\in J_{\mathrm{noise}}$, we set $c_j\leftarrow \rho c_j$. An optional maintenance-reach constraint requires every route to include at least one $m_i=1$ flight.

Output: Return the incidence matrix A, cost vector c, and bipartite graph G, along with the feasible seed solution $x^{\star }$.

Bartunov et al. (2017) [16] proposed a method to transform integer linear programming problems into bipartite graph data structures. From the perspective of the Bipartite View, we output a bipartite graph $G=(U,V,E)$, which represents the routes (variable nodes), $V={\left\{v_i\right\}}_{i\in I}$ represents the flights (constraint nodes), and $E=\{(u_j,v_i):A_{ij}=1\}$ is the set of edges that indicate which routes cover which flights.

The seed solution $x^{\star }$ guarantees feasibility. Adding noise columns does not destroy feasibility. The probability of selecting flights depends on the hub weights $w(·)$, which leads to higher degrees for flights connecting to hub airports. The bucket-based sampling process and minimum turnaround time $\Delta$ enforce realistic temporal sequencing. The parameter $\beta$ controls the likelihood of staying within the same time bucket. The parameters $\rho$, $q_{\mathrm{dup}}$, and ${\pi }_{\mathrm{len}}$ jointly control the redundancy and correlation of columns, thus shaping the difficulty of the SCP instance without sacrificing feasibility. The parameter $\kappa =1$ enforces a constraint that every route must contain at least one maintenance flight.

To analyze the complexity, let $\overline{L}=\mathbb{E}\left[\right|S\left|\right]$ denote the average route length and $p\approx p_{\mathrm{target}}$ represent the total number of columns. The complexity of constructing each route is $O(\overline{L}logn)$ as this process involves sampling and feasibility checks. Meanwhile, the overall complexity for generating the entire instance is $O(p\overline{L}logn)$.

4.2.2. Network Structure

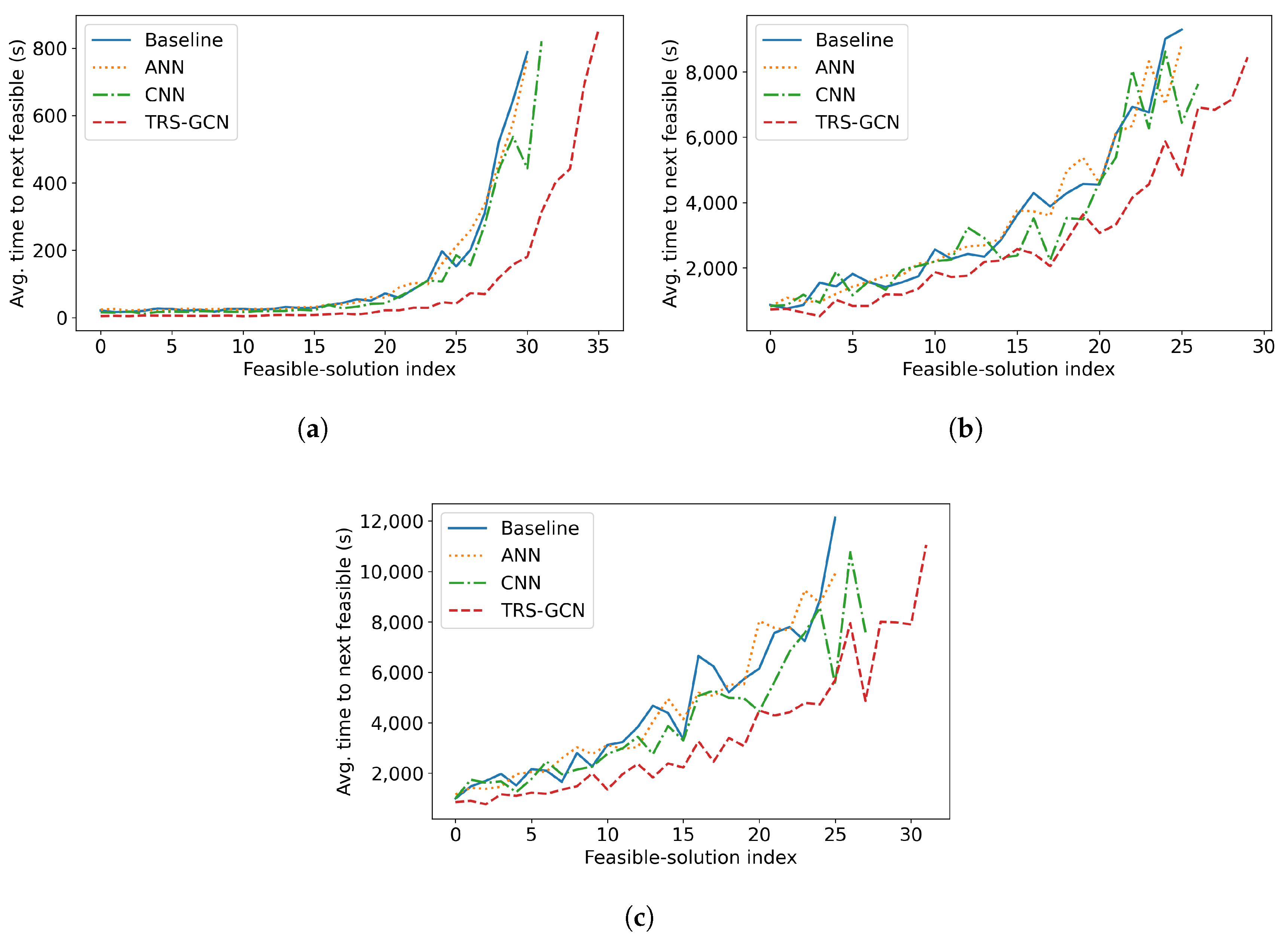
In the hybrid optimization framework for the ARP proposed in this study, the core prediction task associated with the TRS-GCN is the quantification of flight string usefulness. This task aims to accurately determine the probability that a particular flight string will be included in the optimal solution of the ARP (with the imitation target being the optimal solution of generated simulated ARP instances) and its potential to improve the objective function. This task is not only crucial for reducing the variable dimension of Mixed-Integer Programming (MIP) and alleviating enumeration redundancy but also provides a foundation for variable elimination in the subsequent presolve procedure and strong branching ordering in the Branch-and-Bound (B&B) process. The heterogeneous correlation of its multi-modal features (including the newly added linear programming-related mathematical features) has motivated the design of TRS-GCN to adapt to the complex dependency relationships inherent in the problem.

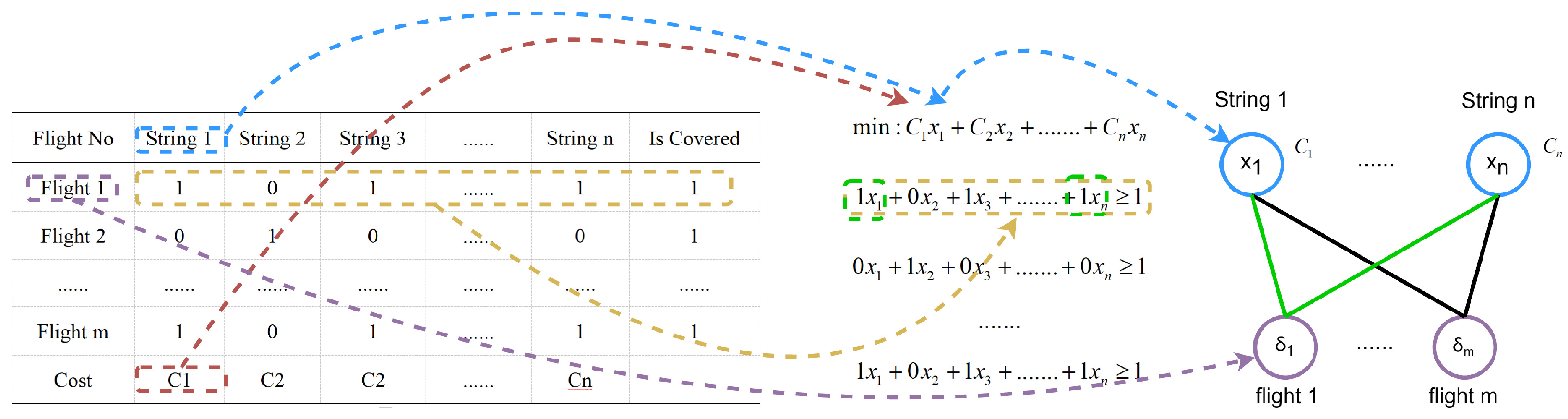
This study retains the traditional bipartite graph for ARPs as the input of the network, as shown in Figure 2, The red represents the objective function coefficients, the blue represents the variables to be allocated, the yellow represents the constraints, and the green represents the coefficients of the constraints. Where the upper layer nodes represent flight strings and the lower layer nodes represent individual flights, with edges denoting inclusion relationships. Unlike traditional methods that use simplistic feature extraction, with objective function coefficients as flight string nodes feature and constraint constants as flight nodes feature, this study identifies limitations in such binary (0/1) edge features. Since the existence of nodes and edges already encodes this binary information, the traditional method lacks sufficient representational depth. To improve this, the study introduces a novel feature extraction approach, categorizing nodes into flight and flight string types and computing tailored feature vectors for each.

These characteristics are defined in

Table A2. Flight (Constraint) Node Features.

Category	Feature	Calculation/Definition
Basic & Time	Airborne duration	$b_i=t_i^{\mathrm{arr}}-t_i^{\mathrm{dep}}$.
	Time-of-day encoding (dep/arr)	$sin\left({\displaystyle \frac{2\pi t}{1440}}\right),cos\left({\displaystyle \frac{2\pi t}{1440}}\right)$ for $t\in \{t_i^{\mathrm{dep}},t_i^{\mathrm{arr}}\}$.
	Day-of-week encoding	$sin\left({\displaystyle \frac{2\pi \mathrm{dow}\left(t_i\right)}{7}}\right),cos\left({\displaystyle \frac{2\pi \mathrm{dow}\left(t_i\right)}{7}}\right)$.
Airport/Hub	Hub indicators (dep/arr)	$⊮\left[\mathrm{airport}\mathrm{is}\mathrm{hub}\right]$ for $a_i^{\mathrm{dep}},a_i^{\mathrm{arr}}$. $\star$
Connectivity	Compat. graph indeg/outdeg	$d_i^{\mathrm{in}},d_i^{\mathrm{out}}$ from the feasibility graph on flights.
	Two-hop reachability	Count of flights reachable within a 6-h window via feasible connections.
	Candidate strings covering i	$\left|\right\{j:a_{ij}=1\left\}\right|$.
	Uniqueness index	$u_i={\displaystyle \frac{1}{1+\left|\right\{j:a_{ij}=1\left\}\right|}}$. $\star$
	Centralities (agg.)	Betweenness/eigenvector centrality (normalized).
	Hub-touch ratio	Fraction of feasible neighbors touching hub airports. $\star$
LP/Price	Dual price	$y_i$.
	Coverage slack	$s_i=1-{\sum }_j{a}_{ij}{x}_j^{\mathrm{LP}}$.
	Complementary gap	$g_i=y_i·s_i$.
	Mean reduced cost (covering)	$\overline{rc}\left(i\right)={\displaystyle \frac{{\sum }_j{a}_{ij}r{c}_j}{{\sum }_j{a}_{ij}}}$.
	Dual quantile rank	Quantile rank of $y_i$ within the instance.
Robustness/Propagation	Buffer means (pre/post)	Mean of feasible pre/post-connection slack over strings containing i. $\star$

$\star$ Denotes ARP-specific or operationally novel features we introduce. All instance-level statistics are standardized (z-score or percentile) within instance to ensure comparability.

and 

Table A3. String (Variable), Edge, and Graph-Level Features.

Category	Feature	Calculation/Definition
String: Scale/Duration	Number of legs	$|S_j|$.
	Total airborne/ground time	${\sum }_{i\in S_j}{b}_i$ and $\sum \mathrm{TAT}$.
	Days crossed	Count of distinct service days covered by $S_j$.
	Max consecutive duty	Max continuous duty duration within $S_j$. $\star$
String: Cost/Composition	Total cost	$c_j$.
	Cost breakdown	Flight-hour/overnight/maintenance insertion components (if available).
String: Turnaround/Robustness	Slack mean/median/min	$\overline{\mathrm{slack}},Q_{0.5}\left(\mathrm{slack}\right),\min \mathrm{slack}$ over $S_j$.
	Tight-connection count	$\#\{k:{\mathrm{slack}}_k^{\left(j\right)}<\Delta +\delta \}$ for small $\delta >0$. $\star$
	Robustness score	${\mathrm{RS}}_j={\min }_k\left({\mathrm{slack}}_k^{\left(j\right)}-Q_{0.9}\left({\mathrm{delay}}_k\right)\right)$. $\star$
String: Scarcity/Price Aggregates	Dual aggregates	${\sum }_{i\in S_j}{y}_i,{\displaystyle \frac{1}{|S_j|}}\sum y_i,\max y_i,\min y_i$.
	Mean uniqueness	$\overline{u}\left(j\right)={\displaystyle \frac{1}{|S_j|}}{\sum }_{i\in S_j}{u}_i$. $\star$
	Mean competition	Mean of $\left|\right\{j^{\prime }:a_{i{j}^{\prime }}=1\left\}\right|$ over $i\in S_j$.
	Coverage-deficit count	$\#\{i\in S_j:s_i>0\}$. $\star$
String: LP/Reduced-Cost	LP value/reduced cost	$x_j^{\mathrm{LP}},r{c}_j$.
	Complement product	$x_j^{\mathrm{LP}}·r{c}_j$.
	Price–cost gap	$c_j-{\sum }_i{a}_{ij}{y}_i=r{c}_j$ (consistency check).
Operational & Base	Base flags (start/end)	$⊮\left[\mathrm{start}\mathrm{at}\mathrm{base}\right],⊮\left[\mathrm{end}\mathrm{at}\mathrm{base}\right]$.
	Overnights/hub share	Count of overnights; share of legs touching hubs.
Edge (String–Flight)	Position index	Normalized index $k/|S_j|$ for leg k in $S_j$.
	Pre/post slack	Slack of predecessor/successor connections if applicable.
	Dual on edge	Carry $y_i$ onto edge $(j,i)$ for attention. $\star$
Graph-Level Context	Size/coverage	$\left|\mathcal{F}\right|=$ #flights, $\left|\mathcal{S}\right|=$ #strings, mean coverage degree.
	Fleet entropy	Entropy of fleet distribution across flights.
	Hub concentration	Share of top-2 hubs in traffic.
	Avg. min turnaround	Instance mean of $\Delta (a,f)$.
	LP–heuristic gap (approx.)	Normalized gap between LP objective and a baseline feasible solution.
	Peak-hour share	Fraction of legs departing in peak time-of-day bands.

$\star$ Denotes ARP-specific or operationally novel features we introduce. All instance-level statistics are standardized (z-score or percentile) within instance to ensure comparability.

, which offer a more informative and problem-specific representation [34]. It is particularly important to emphasize that all feature calculations, especially those related to LP features, can be completed either directly or via the SCIP solver’s API with a time complexity of $O\left(1\right)$ or $O\left(\mathrm{nnz}\right(A\left)\right)$. This ensures that the computation time during the feature extraction phase, prior to solving, is negligible.

To capture solutions close to the optimal one, we define the near-optimal feasible set with tolerance $\epsilon >0$:

$$F_{\epsilon }^{\ast }\left(I\right)=\left\{\mathbf{x}\in {\{0,1\}}^{\left|S\right|}\mid A\mathbf{x}\ge \mathbf{1},{\mathbf{c}}^{\top }\mathbf{x}\le {\mathbf{c}}^{\top }{\mathbf{x}}^{*}+\epsilon \right\}$$

(12)

where $F_{\epsilon }^{\ast }\left(I\right)$ represents the near-optimal feasible set for a given ARP instance I with tolerance $\epsilon$. In this expression, $\mathbf{x}$ is a binary vector representing a solution, where each element indicates whether a flight string is included (1) or excluded (0) from the solution. A is the constraint matrix, $\mathbf{c}$ is the cost vector, and ${\mathbf{x}}^{\ast }$ is the optimal solution vector.

Next, the importance score of flight string s is calculated as a weighted average of its occurrences in near-optimal solutions:

$$b_s\left(I\right)={\displaystyle \frac{{\sum }_{\mathbf{x}\in F_{\epsilon }^{\ast }\left(I\right)}w\left(\mathbf{x}\right)·x_s}{{\sum }_{\mathbf{x}\in F_{\epsilon }^{\ast }\left(I\right)}w\left(\mathbf{x}\right)}}$$

(13)

where $w\left(\mathbf{x}\right)$ is the weight of a solution $\mathbf{x}$, which penalizes higher-cost solutions:

$$w\left(\mathbf{x}\right)=exp\left(-\lambda ({\mathbf{c}}^{\top }\mathbf{x}-{\mathbf{c}}^{\top }{\mathbf{x}}^{\ast })\right)$$

(14)

Here, $b_s\left(I\right)$ is the importance score of flight string s in instance I, reflecting its prevalence in near-optimal solutions. The temperature parameter $\lambda$ controls the sensitivity to the solution’s cost. The binary indicator $x_s$ denotes whether flight string s is included in the solution $\mathbf{x}$.

The vector $\mathbf{b}\left(I\right)={[b_1\left(I\right),\dots ,b_{\left|\mathcal{S}\right|}\left(I\right)]}^{\top }$ encodes the true importance ranking of all flight strings in instance I. From this, we derive the ground-truth sequence of the top-K most important variables, denoted as $Y^{\ast }=(y_1^{\ast },y_2^{\ast },\dots ,y_K^{\ast })$.

Instead of predicting all scores at once in a static manner, the proposed TRS-GCN treats the task of ranking as a sequential decision-making process. Rather than assigning importance scores to all variables simultaneously, the model generates a ranked sequence step by step, selecting the most important variables one at a time. At each step, the model’s choice is influenced by the variables it has already selected, meaning that each decision is conditioned on the previous selections. This autoregressive approach allows the model to learn how the importance of one variable is related to the others, which is especially useful in complex optimization tasks where variables are interdependent.

The TRS-GCN is trained end-to-end by maximizing the likelihood of producing the correct ranking sequence, denoted as $Y^{\ast }$. To achieve this, we minimize the negative log-likelihood of the target sequence. Minimizing the negative log-likelihood is equivalent to minimizing the sum of cross-entropy losses at each decoding step, where cross-entropy measures how much the model’s predicted sequence diverges from the actual ground-truth sequence. The training process uses a set of ARP instances sampled i.i.d. from a distribution $\mathcal{D}$, and the goal is to adjust the model’s parameters to reduce this loss, ultimately learning how to rank the variables most accurately.

$$\underset{\theta \in \Theta }{\min }{\displaystyle \frac{1}{\left|S\right|}}\sum _{I\in S}\mathcal{L}\left(\theta \right)$$

(15)

To address the limitations of static, one-shot prediction models in quantifying variable importance for Mixed-Integer Programming (MIP), we propose the Two-Stage Route Selection Graph Convolutional Network (TRS-GCN). Existing Graph Neural Network (GNN) approaches typically predict scores for all variables simultaneously. While effective, this paradigm does not capture the interdependent nature of variable selection in combinatorial optimization, where the importance of a variable is often conditional on which other variables have been considered.

Inspired by the successes of the encoder–decoder framework in sequence-to-sequence tasks such as machine translation [35] and the autoregressive generation process in time-series forecasting, we reformulate the variable ranking problem as a sequential decision-making task. The core philosophy of TRS-GCN is to first form a holistic understanding of the entire optimization problem and then to autoregressively generate a ranked list of high-importance variables, where each selection is conditioned on the previous selections.

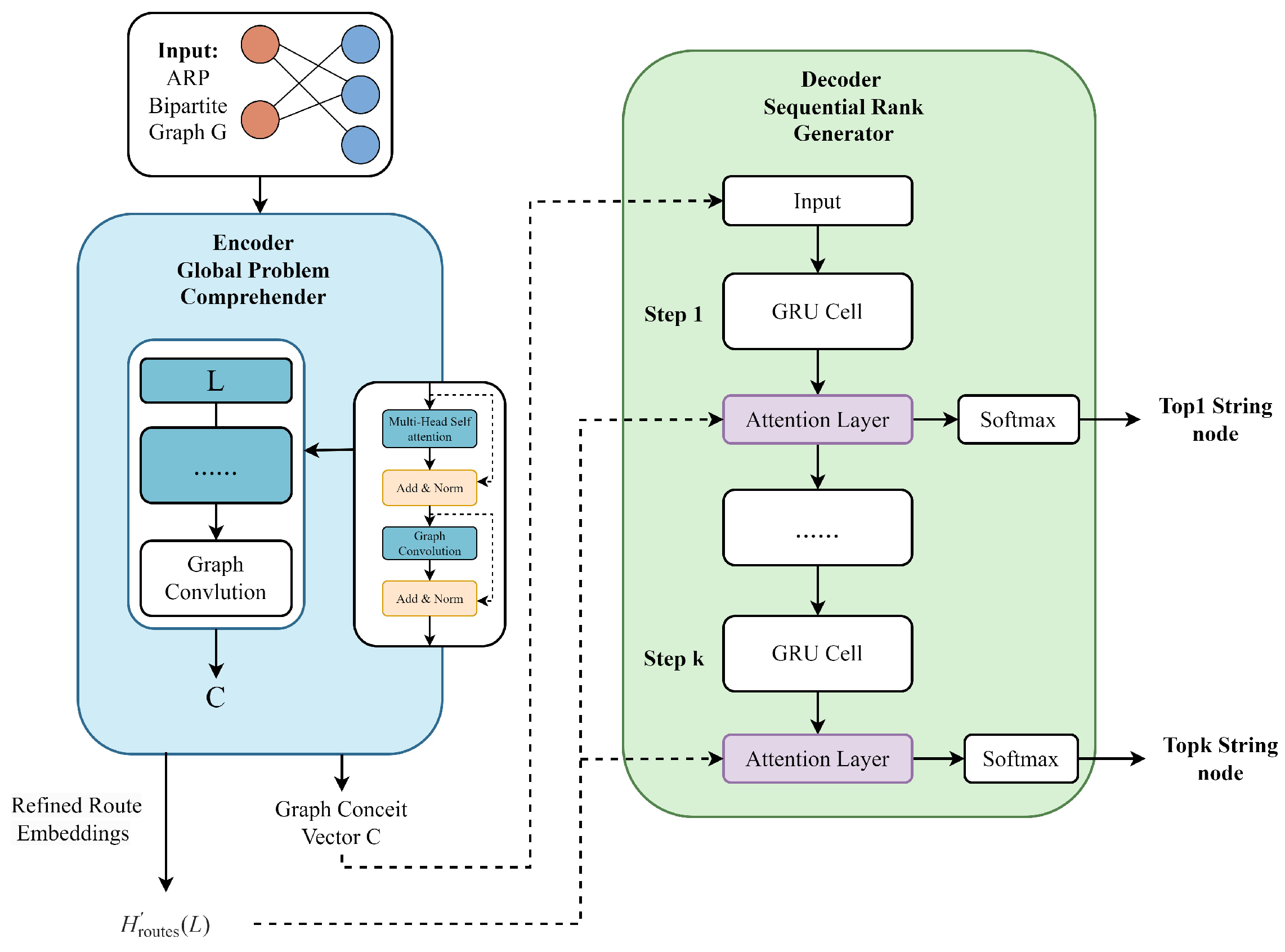
As illustrated in Figure 3, the TRS-GCN architecture is based on an encoder–decoder framework. The encoder, a deep graph neural network, is responsible for comprehending the complex structure and features of the Aircraft Routing Problem (ARP) instance, represented as a bipartite graph. The decoder, a recurrent neural network equipped with an attention mechanism, then utilizes this comprehensive understanding to sequentially identify and rank the most salient variables (flight strings).

4.2.3. Encoder

The encoder aims to learn task-informative, permutation-invariant representations of an ARP instance. Given the bipartite graph $G=(U,V,E)$ with multi-modal node features, it produces context-aware embeddings $\left\{{\mathbf{h}}_i\right\}$ that jointly encode (i) incidence topology and local feasibility signals (e.g., turnaround and maintenance reachability), (ii) global regularities (hubness and temporal order), and (iii) LP-derived cues (such as reduced costs and slacks). A permutation-invariant readout over variable nodes aggregates these embeddings into a global context vector $\mathbf{c}$ that summarizes instance scale and coupling patterns and conditions the decoder. The resulting representations are size-agnostic and capture both long-range dependencies (via attention) and local structure (via graph convolution), providing sufficient statistics for the downstream ranking task.

The input to the encoder is the bipartite graph representation of the ARP instance, where U is the set of variable nodes (flight strings) and V is the set of constraint nodes (flights). Each node $i\in U\cup V$ is associated with a multi-modal feature vector ${\mathbf{x}}_i\in {\mathbb{R}}^{d_{\mathrm{feat}}}$, derived from the categories defined in Table A2 and Table A3.

The encoder is composed of L stacked Hybrid Graph Attention (HGA) layers. Each HGA layer is designed to capture both global, long-range dependencies and local, structural relationships within the graph. An HGA layer consists of two main components followed by a fusion and normalization step:

Multi-Head Graph Self-Attention: To capture global dependencies, we employ a multi-head self-attention mechanism [36], inspired by Graph Attention Networks (GAT) [37]. This allows each node to weigh the importance of all other nodes in the graph when updating its representation. For each attention head k, the attention coefficient $e_{ij}^k$ between node i and node j is computed as

$$e_{ij}^k=\mathrm{LeakyReLU}\left({\mathbf{a}}_k^{\top }[{\mathbf{W}}_k{\mathbf{h}}_i^{\left(l\right)}\parallel {\mathbf{W}}_k{\mathbf{h}}_j^{\left(l\right)}]\right)$$

(16)

where ${\mathbf{h}}_i^{\left(l\right)}$ is the feature vector of node i at layer l, ${\mathbf{W}}_k$ is a learnable weight matrix, ${\mathbf{a}}_k$ is a weight vector for the attention head, and ‖ denotes concatenation. These coefficients are then normalized using the softmax function to obtain attention weights ${\alpha }_{ij}^k$.

Neighborhood Aggregation: Following the self-attention module, a Graph Convolutional Network (GCN) layer [38] is applied to aggregate information from the immediate local neighborhood of each node. This step reinforces the structural relationships encoded by the graph edges. The GCN update rule is given by

$${\mathbf{H}}_{\mathrm{gcn}}^{\left(l\right)}=\mathrm{ReLU}\left({\widehat{\mathbf{D}}}^{-1/2}\widehat{\mathbf{A}}{\widehat{\mathbf{D}}}^{-1/2}{\mathbf{H}}_{\mathrm{attn}}^{\left(l\right)}{\mathbf{W}}_{\mathrm{gcn}}\right)$$

(17)

where ${\mathbf{H}}_{\mathrm{attn}}^{\left(l\right)}$ is the output from the self-attention module, $\widehat{\mathbf{A}}$ is the adjacency matrix with self-loops, and $\widehat{\mathbf{D}}$ is the corresponding degree matrix.

Fusion and Layer Update: The global and local representations are fused, and the layer update is completed with a residual connection [39] and layer normalization [40] to ensure stable training of the deep architecture. The final update for layer l is

$${\mathbf{H}}^{(l+1)}=\mathrm{LayerNorm}({\mathbf{H}}^{\left(l\right)}+\mathrm{MLP}({\mathbf{H}}_{\mathrm{attn}}^{\left(l\right)}+{\mathbf{H}}_{\mathrm{gcn}}^{\left(l\right)}))$$

(18)

After passing through L HGA layers, the encoder produces two outputs:

• A matrix of refined node embeddings ${\mathbf{H}}^{\left(L\right)}\in {\mathbb{R}}^{\left(\right|U|+\left|V\right|)\times d_{\mathrm{model}}}$, containing context-aware representations for all nodes.
• A global context vector $\mathbf{c}\in {\mathbb{R}}^{d_{\mathrm{model}}}$, produced by a graph readout function (e.g., mean pooling) applied to the variable node embeddings ${\mathbf{H}}_U^{\left(L\right)}$. This vector serves as a holistic “fingerprint” of the entire ARP instance.

  $$\mathbf{c}={\displaystyle \frac{1}{\left|U\right|}}\sum _{u\in U}{\mathbf{h}}_u^{\left(L\right)}$$

  (19)

4.2.4. Decoder

The decoder’s objective is to utilize the rich representations learned by the encoder to generate a ranked sequence of the top-K most important variable nodes, denoted by $Y=(y_1,y_2,\dots ,y_K)$. The generation process is autoregressive, meaning the selection of the variable at step t is conditioned on the variables selected in all previous steps. The decoder is implemented as a Gated Recurrent Unit (GRU) [41], coupled with an attention mechanism [42] that dynamically focuses on the most relevant parts of the input problem and generates the ranked sequence one variable at a time over K steps:

Initialization: The initial hidden state of the GRU, ${\mathbf{d}}_0$, is initialized using the global context vector $\mathbf{c}$ from the encoder, via a linear transformation: ${\mathbf{d}}_0=\mathrm{ReLU}\left({\mathbf{W}}_{\mathrm{init}}\mathbf{c}\right)$.

Decoding at Step t (for $\mathit{t}=\mathbf{1},\dots ,\mathit{K}$): The GRU updates its hidden state ${\mathbf{d}}_t=\mathrm{GRU}({\mathbf{d}}_{t-1},{\mathbf{h}}_{y_{t-1}}^{\left(L\right)})$, where ${\mathbf{h}}_{y_{t-1}}^{\left(L\right)}$ is the embedding of the previously selected variable (a special learnable $\langle \mathrm{START}\rangle$ token is used for $t=1$). An attention mechanism then computes a score $e_{t,u}$ for each candidate variable u based on the current decoder state ${\mathbf{d}}_t$ and the encoder outputs ${\mathbf{H}}_U^{\left(L\right)}$:

$$e_{t,u}={\mathbf{v}}_a^{\top }tanh({\mathbf{W}}_a{\mathbf{d}}_t+{\mathbf{U}}_a{\mathbf{h}}_u^{\left(L\right)})$$

(20)

where ${\mathbf{v}}_a,{\mathbf{W}}_a,{\mathbf{U}}_a$ are learnable parameters. The scores are normalized into a probability distribution $p_t$ over all available (not yet selected) variables $U_t^{\prime }$ using a softmax function with masking.

$$p_t\left(u\right)={\displaystyle \frac{exp\left(e_{t,u}\right)}{{\sum }_{u^{\prime }\in U_t^{\prime }}exp\left(e_{t,u^{\prime }}\right)}}$$

(21)

The variable for the current step, $y_t$, is selected from this distribution (e.g., via arg max during inference).

The final output is the ordered sequence $Y=(y_1,y_2,\dots ,y_K)$, representing the predicted ranking of the top-K most important variables.

4.2.5. Training Objective

The TRS-GCN is trained end-to-end by maximizing the likelihood of generating the ground-truth sequence. Let the ground-truth ranking for a given instance be $Y^{\ast }=(y_1^{\ast },y_2^{\ast },\dots ,y_K^{\ast })$, which is derived from the importance scores $\mathbf{b}\left(I\right)$. The training objective is to minimize the negative log-likelihood of the target sequence, which corresponds to minimizing the sum of cross-entropy losses at each decoding step. The loss function $\mathcal{L}\left(\theta \right)$ for a single ARP instance is formulated as

$$\mathcal{L}\left(\theta \right)=-\sum _{t=1}^{K}logp\left(y_t^{\ast }\right|y_1^{\ast },\dots ,y_{t-1}^{\ast };G,\theta )$$

(22)

where $\mathit{\theta }$ denotes the complete set of trainable parameters of TRS-GCN, including the encoder’s projection matrices and attention vectors (e.g., $\{{\mathbf{W}}_k,{\mathbf{a}}_k\}$), GCN and MLP/LayerNorm weights, as well as the decoder’s GRU and attention parameters (${\mathbf{v}}_a,{\mathbf{W}}_a,{\mathbf{U}}_a$), start-token embedding, and output projection head. During training, $\mathit{\theta }$ is updated via gradient-based optimization to maximize the likelihood of $Y^{\ast }$ (not to be confused with data generation cost coefficients ${\theta }_0,{\theta }_1,{\theta }_2,{\theta }_3$). This objective directly encourages the model to learn the stepwise conditional probabilities $p(y_t\mid y_{<t};G,\mathit{\theta })$, thereby effectively training it to perform the ranking task in an autoregressive manner.

4.3. Acceleration Method

Subsequent to the formulation of the Mixed-Integer Program (MIP) and the generation of variable importance scores via the trained machine learning (ML) model, this section systematically investigates three distinct paradigms for leveraging these predictions to accelerate the Gurobi solver. The overarching objective of these methods is to reduce total computation time. However, they differ fundamentally in their point of intervention within the solution process, the associated risk to solution quality—particularly optimality—and their implementation complexity. This section will sequentially dissect the mechanics of these strategies: (1) seeding the search with a high-quality initial solution, (2) statically reducing the problem size through predictive variable pruning, and (3) dynamically guiding the branching decisions to control the search trajectory.

4.3.1. Warm-Starting

Modern commercial solvers for Mixed-Integer Programming (MIP) employ a critical presolve phase to find an initial feasible solution, where the feasibility pump is one of the most commonly used algorithms. In this work, we enhance this established algorithm by integrating predictive guidance from a machine learning model, proposing the Machine Learning-Guided Feasibility Pump (MLFP). The core of this algorithm is the deep integration of the iterative framework of the classical feasibility pump with the variable importance insights derived from a machine learning model. This approach injects problem-specific prior knowledge into the search, guiding it toward more promising regions of the solution space.

Before detailing the procedure, we define the key notation. We consider an MIP of the form $\min \{c^{T}x\mid Ax\le b,x_v\in \{0,1\},\forall v\in I\}$, where I is the index set of binary variables. The feasible region of its linear programming (LP) relaxation, a convex polytope, is denoted by $P=\{x\in {\mathbb{R}}^{\left|V\right|}\mid Ax\le b\}$.

A key input to the algorithm is an importance ranking of all binary variables $v\in I$, as predicted by a pre-trained machine learning model. To apply this ordinal information algorithmically, we first transform the ranking into a normalized numerical score. Let $N=\left|I\right|$ be the total number of binary variables, and let $rank\left(v\right)\in \{1,2,\dots ,N\}$ be the position of variable v in the importance list (where 1 is the most important). The corresponding importance score $I_v$ is obtained via the following linear transformation:

$$I_v=1-{\displaystyle \frac{rank\left(v\right)-1}{N-1}}.$$

(23)

This mapping assigns a score of $I_v=1$ to the top-ranked variable ($rank\left(v\right)=1$), $I_v=0$ to the bottom-ranked variable ($rank\left(v\right)=N$), and linearly distributes the scores for all other variables in between.

This mapping assigns a score of $I_v=1$ to the top-ranked variable ($\mathrm{rank}\left(v\right)=1$) and $I_v=0$ to the bottom-ranked variable ($\mathrm{rank}\left(v\right)=N$). The scores for all other variables are linearly distributed in between. Specifically, the importance score $I_v$ is computed based on the rank of variable v in the list of all variables, where the rank is normalized within the range $[0, 1]$, ensuring that higher-ranked variables receive higher scores.

In iteration k, the algorithm maintains an LP-feasible solution $x^{\left(k\right)}\in P$ and an integer solution ${\tilde{x}}^{\left(k\right)}\in {\{0,1\}}^{\left|I\right|}$. A hyperparameter $\lambda \in [0, 1]$ is used to balance the influence between the LP solution and the ML-derived scores. The weight $\lambda$ allows the algorithm to adjust between prioritizing the feasibility provided by the LP relaxation and the variable importance inferred from the machine learning model, making the optimization process more adaptable and informed.

The specific steps of the algorithm are as follows:

1.

Initialization and LP Relaxation: The algorithm commences by solving the standard LP relaxation of the MIP to obtain an initial solution $x^{\left(0\right)}$. The integrality of this solution is checked. If all binary variables in $x^{\left(0\right)}$ already hold integer values, the solution is LP-optimal and MIP-feasible. The algorithm then terminates and returns this solution. Otherwise, the main iterative loop begins.

2.

ML-Guided Rounding: This step is the core innovation of the algorithm, replacing the information-agnostic rounding procedure of the standard feasibility pump. In each iteration k, a new integer solution ${\tilde{x}}^{(k+1)}$ is constructed with intelligent guidance from both the current LP solution $x^{\left(k\right)}$ and the ranking-derived importance scores $I_v$.

Specifically, a “Tendency Score” $T_v$ is calculated for each binary variable $v\in I$, defined by the convex combination:

$$T_v=\lambda ·x_v^{\left(k\right)}+(1-\lambda )·I_v$$

(24)

This score synthesizes two pieces of information: $x_v^{\left(k\right)}$ reflects the “feasibility pressure” from the current LP relaxation, while $I_v$ represents a quantitative measure of the variable’s relative importance as learned from the problem’s global structure. The new integer assignment is then determined by this score: ${\tilde{x}}_v^{(k+1)}$ is set to 1 if $T_v\ge 0.5$, and 0 otherwise.

3.

Feasibility Check and Projection: After generating the new integer solution ${\tilde{x}}^{(k+1)}$, its feasibility with respect to the linear constraints, $A{\tilde{x}}^{(k+1)}\le b$, is immediately checked. If the solution is feasible, a valid MIP solution has been found, and the algorithm terminates successfully.

If ${\tilde{x}}^{(k+1)}$ is infeasible, the projection step is executed. This step “pumps” the infeasible integer point back to the feasible polytope P by solving an auxiliary LP problem. The objective of this LP is to find a point in P that is closest to ${\tilde{x}}^{(k+1)}$ in terms of the L1-norm (Manhattan distance). The solution to this projection problem becomes the next LP-feasible solution, $x^{(k+1)}$.

4.

Termination and Stagnation Handling: The iterative process terminates under two conditions: (1) a feasible solution is found, as described in Step 2; or (2) a predefined maximum number of iterations, $k_{\max }$, is reached, in which case the algorithm reports failure.

To prevent cycling, a stagnation check is performed. If the same integer solution is generated in consecutive iterations (i.e., ${\tilde{x}}^{(k+1)}={\tilde{x}}^{\left(k\right)}$), a perturbation mechanism is invoked. To maintain the guided nature of the search, this perturbation can prioritize flipping the values of variables with a low importance rank (i.e., a low $I_v$ score), before proceeding to the next iteration.

4.3.2. Static Problem Reduction

This represents a more aggressive, high-risk, high-reward strategy that directly modifies the problem’s mathematical model prior to optimization, acting as an ML-driven presolve technique. The central hypothesis is that variables with extremely low importance scores predicted by the ML model have a negligible probability of being active (i.e., non-zero) in the optimal solution. Based on this assumption, such variables are permanently fixed to zero, effectively removing them from the problem.

This reduction in the number of decision variables can significantly shrink the dimensionality of the constraint matrix. The primary benefit is a reduction in the computational cost of solving the LP relaxation at every single node of the B&B tree. For problems where the number of variables is the principal computational bottleneck, this method can yield orders-of-magnitude improvements in performance.

Implementation: The implementation is typically based on a confidence threshold, $\tau$. First, an ML model is trained to predict the probability that a variable v will be zero in the optimal solution, i.e., $P(x_v=0)$. A high-confidence threshold (e.g., $\tau =0.999$) is selected. Before passing the model to the solver, any variable v where $P(x_v=0)>\tau$ has its upper bound fixed to 0 (i.e., in Gurobi, set it as variable.UB = 0).

While potentially powerful, this strategy carries a profound consequence: the loss of the optimality certificate. When we modify the original problem P into a restricted problem $P^{\prime }$, Gurobi solves $P^{\prime }$. The solver may find the optimal solution for $P^{\prime }$ and provide a mathematical proof of this (i.e., a closed primal–dual gap for $P^{\prime }$). However, this proof is invalid for the original problem P. The feasible region of $P^{\prime }$ is a strict subset of that of P, and consequently, the solution found for $P^{\prime }$ may be suboptimal or even infeasible for P if a critical variable was erroneously pruned.

The risk is highly dependent on the problem’s constraint structure. For problems with “decoupled” constraints (e.g., set covering), removing a low-importance variable is less likely to have catastrophic, non-local effects. Conversely, in problems with tightly coupled global constraints (e.g., network design and scheduling), a single variable might act as a “linchpin.” Its removal, even if its individual score is low, could sever the only feasible path in a long dependency chain, rendering the problem infeasible. This necessitates that the ML model for pruning must not only learn individual variable importance but also implicitly understand the systemic risk of removing a variable, a capability for which graph-based architectures are well-suited.

4.3.3. Dynamic Search

The efficacy of the Branch-and-Bound algorithm is highly dependent on the variable selection strategy. State-of-the-art solvers, such as Gurobi, predominantly rely on pseudo-cost branching, a powerful heuristic that estimates the objective degradation caused by branching on a particular variable. However, this method suffers from a significant “cold start” problem: at the initial stages of the search tree, or for variables that have not been previously selected for branching, historical data is non-existent, rendering pseudo-costs either unknown or unreliable. To mitigate this limitation, we propose a prediction-guided hybrid branching strategy that integrates a priori knowledge from a machine learning model with the solver’s runtime-generated pseudo-costs.

Let $S_i\in [0, 1]$ be the normalized importance score for each integer variable $x_i$, pre-computed by our TRS-GCN, where a higher score indicates a greater predicted importance. The conventional branching score for a candidate variable $x_i$ with a fractional value $f_i$ in the current LP relaxation is based on its pseudo-costs ($P{C}_i^{+},P{C}_i^{-}$). A common formulation for this score is

$${\mathrm{Score}}_{\mathrm{pc}}\left(i\right)=\min (P{C}_i^{+}(f_i-\lfloor f_i\rfloor ),P{C}_i^{-}(\lceil f_i\rceil -f_i))$$

(25)

Our proposed hybrid score, ${\mathrm{Score}}_{\mathrm{hybrid}}\left(i\right)$, incorporates the predictive score $S_i$ through a dynamically weighted formula:

$${\mathrm{Score}}_{\mathrm{hybrid}}\left(i\right)={\alpha }_i·S_i+(1-{\alpha }_i)·{\mathrm{Score}}_{\mathrm{pc}}\left(i\right)$$

(26)

The core of this approach lies in the adaptive weight ${\alpha }_i$, which reflects the confidence in the learned pseudo-costs. This weight is designed to decay as more empirical data becomes available for a variable. Let $N_i$ be the number of times variable $x_i$ has been branched on. We define the weight ${\alpha }_i$ as a decaying function of $N_i$:

$${\alpha }_i=exp(-\lambda N_i)$$

(27)

where $\lambda$ is a decay rate hyperparameter (e.g., $\lambda =0.5$). When a variable has never been branched on ($N_i=0$), ${\alpha }_i=1$, and the branching decision is guided solely by the GCN prediction. As the variable is selected for branching multiple times, $N_i$ increases, causing ${\alpha }_i$ to approach zero. Consequently, the decision-making authority smoothly transitions from our static, pre-trained model to the solver’s dynamic, problem-specific pseudo-costs.

Implementation of this strategy within Gurobi is achieved via its callback mechanism, as direct modification of the internal branching logic is not possible. Specifically, we utilize the ‘MIPNODE’ callback, which is triggered after solving the LP relaxation at each node. Within the callback, we perform the following steps:

1.

Check if the node status is ‘GRB.OPTIMAL’, indicating that the solver is ready to select a branching variable.

2.

Retrieve the LP relaxation solution using ‘getNodeRel()’ to identify all integer variables with fractional values.

3.

For each fractional variable $x_i$, calculate its ${\mathrm{Score}}_{\mathrm{hybrid}}\left(i\right)$. This requires tracking the branching count $N_i$ for each variable externally and querying the solver for its current pseudo-cost estimates.

4.

To influence Gurobi’s branching decision, we dynamically adjust the ‘BranchPriority’ attribute of the candidate variables. The calculated hybrid scores are normalized and mapped to the integer range of ‘BranchPriority’, assigning higher priority to variables with a greater hybrid score.

By setting these priorities before exiting the callback, we guide Gurobi’s sophisticated branching machinery to favor variables that our hybrid model deems most promising, thereby effectively addressing the cold start problem and accelerating the convergence of the search process.

5. Experimental Section

This section presents a comprehensive computational study to systematically evaluate the proposed Two-Stage Route Selection Graph Convolutional Network (TRS-GCN) model and its effectiveness in accelerating the solution process for large-scale Aircraft Routing Problems (ARPs). The experimental design is structured to validate the predictive accuracy of the TRS-GCN model on real-world test instances, to quantify the computational enhancement provided by three proposed acceleration strategies (warm-starting, static problem reduction, and dynamic search) relative to a baseline solver and to establish the model’s superiority by comparing its performance against traditional ANN and CNN architectures.

All experiments were conducted on a server with an Intel Xeon Gold CPU 5118 12 cores, 24 threads, 64 GB RAM, and an NVIDIA 4090 GPU, running Ubuntu 20.04. The software stack included Gurobi v10.1. To ensure robust and reproducible results, we employed a triple-seed protocol for data splitting, network weight initialization, and the MIP solver’s random processes. All reported performance metrics represent the mean ± 95% confidence interval (CI) over three independent runs.

The remainder of this section is organized as follows. We first describe the experimental environment and the procedures for generating both training and testing datasets. We then define the baseline methodology and the metrics used for performance evaluation. Subsequently, the configuration of model hyperparameters is detailed. Finally, we present a thorough analysis of the computational results to systematically answer the research questions posed by our objectives.

5.1. Training Dataset

To train our models, we require a large corpus of structurally realistic ARP instances. Public benchmarks lack the specific constraints of ARPs, while proprietary operational data is scarce and often exhibits low variance, posing a risk of overfitting. We therefore utilize a synthetic instance generator, FR-Gen (Feasible-and-Realistic Generator for ARPs), outlined in Algorithm A1.

This generator produces ARP instances formulated as set covering problems, each accompanied by a guaranteed feasible seed solution $x^{\ast }$. This ensures the generation of solvable, non-trivial problems that reflect key operational complexities. The specific parameterization of the FR-Gen algorithm used in this study is detailed in

Table 2. Parameterization of the FR-Gen algorithm with specific values.

Symbol	Description	Value/Setting
n	Total number of flights (rows/constraints)	Small = 80; medium = 200; large = 400
B	Number of time buckets	19 (05:00–24:00 window with 60 min granularity)
$\Delta$	Minimum turnaround time	45 min
H	Set of airports	$\left|H\right|=16$ with $|H_{\mathrm{hub}}|=4$
$w(·)$	Hub weight function	Hub-spoke share = 0.70; point-to-point share = 0.30
${\pi }_{\mathrm{len}}$	Route length distribution	Truncated Poisson: $\mathrm{Pois}(\lambda =6)$ on $[3,10]$ legs
$\kappa$	Maintenance-required flag	1 (enabled)
$\eta$	Maintenance share	0.08
$\alpha$	PA offset	$1\times {10}^{-3}$
$\beta$	Stay-in-bucket probability	0.62
${\theta }_{0.3}$	Cost parameters	$({\theta }_0,{\theta }_1,{\theta }_2,{\theta }_3)=(0,1.00,0.02,3.00)$
$\rho$	Noise scaler	1.30
$p_{\mathrm{target}}$	Target column count (decision variables)	Small: $120\times 80=9600$ Medium: $140\times 200=28,000$ Large: $160\times 400=64,000$
$q_{\mathrm{dup}}$	Average extra covers	1.8

.

5.2. Testing Dataset

We construct a 300-instance evaluation set from the U.S. DOT Bureau of Transportation Statistics (BTS) On-Time Performance data. Each instance represents a single carrier operating on a single calendar day and is restricted to contiguous U.S. domestic flights. Records are filtered to retain only valid legs: CANCELLED = 0, DIVERTED = 0, complete time fields, and a scheduled local departure within 05:00–24:00. To bound the daily network, we induce an airport subgraph of 8–20 active airports for the chosen carrier and date; flights outside this subgraph are removed, and small disconnected components are discarded to ensure a connected operating network. Duplicate entries with conflicting schedules are resolved by keeping the canonical record. A minimum ground-turn time of 45 min is enforced as a feasibility screen for within-day turnarounds, while cross-midnight arrivals are excluded to avoid inter-day coupling. Instances are then grouped by the total number of daily flights (F) into three scales, with 100 days per group: small ($100\le F\le 150$), medium ($150<F\le 300$), and large ($300<F\le 500$). The distribution of instances across these categories is visualized in the box plot in Figure 4a.

Algorithm 1 is part of the MIP process constructed by the flight scheduling plan. It leverages the testing dataset to generate feasible flight strings by employing parallel processing techniques. The algorithm uses Python 3.8 and several parallelization libraries, including multiprocessing and joblib. The parallelization model employed is shared-memory parallelism, enabling efficient computation across multiple threads within a single machine. The implementation was tested on the three dataset scales (small, medium, large) and compared against baseline methods (Greedy Search and Greedy Search with Caching). The experiments were conducted on a server with an Intel Xeon Gold CPU 5118 (12 cores and 24 threads), 64 GB RAM, and an NVIDIA 4090 GPU, running Ubuntu 20.04. The performance of each algorithm was measured in terms of execution time and the number of generated flight strings across different dataset sizes (small, medium, and large).

As shown in

Table 3. Execution time (average) comparison for different algorithms.

Dataset Scale	Greedy Search (s)	Greedy with Caching (s)	Our Approach (s)
Small	23.2	0.6	1.2
Medium	124.1	11.3	3.6
Large	903.7	32.9	5.6

, our approach consistently outperforms both Greedy Search and Greedy Search with Caching in terms of execution time. Our approach reduces computation time significantly, especially for larger datasets.

Algorithm 1 ultimately outputs the MIP instance to be solved, while the corresponding number of decision variables (n, representing potential aircraft routes) grows in a non-linear, super-linear fashion. The resulting relationship between model constraints and variables is detailed in the scatter plot in Figure 4b. Despite the differences in execution time, the number of generated flight strings and the results remain consistent across all algorithms. This confirms that the parallel method does not sacrifice solution quality for speed, demonstrating its efficiency and scalability for large-scale Aircraft Routing Problems.

5.3. Hyperparameters of Comparative Methods and Baselines

We benchmark the proposed TRS-GCN against two strong non-graph baselines and a fixed solver configuration under identical preprocessing, data splits, and training budgets. To ensure a fair comparison, the proposed TRS-GCN and the two non-graph baselines (ANN and CNN) share the same input feature set, identical optimization schedule (optimizer, learning rate policy, batch size, training epochs, early stopping), and comparable parameter budgets (within $\pm 10\%$ of TRS-GCN). Supervision is unified via a dual-head objective—a listwise ranking loss (${\mathcal{L}}_{\mathrm{list}}$) and a binary cross-entropy (BCE) loss (${\mathcal{L}}_{\mathrm{bce}}$)—together with post hoc probability calibration. The training loss is

$$\mathcal{L}={\lambda }_{\mathrm{rank}}{\mathcal{L}}_{\mathrm{list}}+(1-{\lambda }_{\mathrm{rank}}){\mathcal{L}}_{\mathrm{bce}},{\lambda }_{\mathrm{rank}}=0.7,$$

(28)

and probabilities are calibrated by equal-frequency binning plus isotonic regression. Model selection is conducted on the validation set using macro-AUPRC as the primary criterion, complemented by top-K metrics and calibration quality (ECE/Brier). Solver-side acceleration metrics are evaluated only in downstream experiments to avoid data leakage.

TRS-GCN: The encoder operates on the ARP bipartite graph (string nodes vs. flight nodes), stacking L Hybrid Graph Attention (HGA) layers: multi-head graph self-attention for long-range dependencies, followed by local GCN aggregation; outputs are fused with residual connections and LayerNorm. A readout over variable nodes produces a global context vector $\mathbf{c}$. The decoder is a GRU with additive attention that autoregressively ranks variables with hard masking of previously selected items; teacher forcing decays linearly to stabilize training.

ANN: A 2–3 block multilayer perceptron with blocks of Linear → BN → ReLU → Dropout ($p=0.3$). For sequence-shaped inputs, mean–max pooling is applied before the MLP. Widths are chosen from $\{512,256,(128\left)\right\}$ to align the parameter count with TRS-GCN.

CNN: A temporal 1D-CNN with two stacked stages. Each stage employs parallel kernel branches $\{3,5,7\}$ with residual connections; branch outputs are concatenated and optionally average-pooled between stages. Global mean+max pooling forms per-variable embeddings before the dual-head outputs. Channels are selected from $\{128,256\}$ under the same budget alignment.

Solver Baseline Details: A fixed Gurobi configuration is used across all runs. Concretely, FeasibilityPump is enabled and strengthened; branching uses pseudo-costs (VarBranch = 2); presolve is set to aggressive (presolve = 2); parallelism is limited to the number of physical cores; and node files spill to disk at NodefileStart = 4 GB. We set MIPFocus = 1 for warm-starting comparisons, and MIPFocus $\in \{0,2\}$ when evaluating dynamic search and static reduction. Time budgets are set to 3 h, 6 h, and 12 h for small, medium, and large instances, respectively.

All specific parameter configuration details are shown in

Table 4. Parameterization of the solver baselines.

Symbol	Description	Value/Setting
Version	Solver version	v10.1
Heuristics	Feasibility pump intensity	0.1–0.2 (enabled)
PumpPasses	FP maximum passes	50
InitialIncumbent	Source of first incumbent	feasibility pump (forced for warm-starting validation)
VarBranch	Branching strategy	2 (pseudo-cost; anchor for dynamic search validation)
Presolve	Presolve level	2 (aggressive)
NodefileStart	Nodefile start (GB)	4 GB
MIPFocus	Solver focus	1 (warm-starting); 0/2 (dynamic/static sensitivity)
TimeLimit	Wall-clock limits	$\{3\mathrm{h},6\mathrm{h},12\mathrm{h}\}$

and 

Table A4. Architectural and training hyperparameters for TRS-GCN, ANN, and CNN. “Search Space” indicates validated ranges; “Final” is the configuration used for main results. All models share the same optimizer/schedule for fairness.

Model/Part	Hyperparameter	Search Space	Final
TRS-GCN Encoder (HGA)	#Layers L	$\{3,4,5\}$	4
	Model dim $d_{\mathrm{model}}$	$\{128,256\}$	256
	#Heads h	$\{4,8\}$	8
	Attention dropout $p_{\mathrm{attn}}$	$\{0,0.1\}$	0.1
	Node dropout	$\{0.2,0.3,0.4\}$	0.3
	Normalization	{LayerNorm, BN}	LayerNorm
	Local aggregator	{GCN} (fixed)	GCN
	Fusion MLP width	$\{1\times ,2\times d_{\mathrm{model}}\}$	$2\times d_{\mathrm{model}}$
	Node-type embedding	dim $\{8,16\}$	16
	Readout (variable nodes)	{mean, attn-pool}	mean
TRS-GCN Decoder (Autoregressive)	RNN cell	{GRU, LSTM}	GRU
	Hidden dim $d_{\mathrm{dec}}$	$\{256,384\}$	256
	Attention type	{additive, dot}	additive
	Train seq length K	$\{5,10,20\}$	10
	Init state	${\mathbf{d}}_0=\mathrm{ReLU}\left(W\mathbf{c}\right)$	same
	Teacher forcing	start $\{0.5,0.7\}\to 0.1$	$0.7\to 0.1$ (60% epochs)
	Masking	hard mask selected vars	hard
	Inference	{greedy, top-p}	greedy
ANN (MLP)	#Hidden blocks	$\{2,3\}$	3
	Hidden widths	combos of $[512,256,(128\left)\right]$	$[512,256,128]$
	Block recipe	Linear + BN + ReLU + Dropout	same
	Dropout p	$\{0.2,0.3,0.4\}$	0.3
	Seq pooling	{mean, max, mean + max}	mean + max
	Param budget align	$\pm 10\%$ vs. TRS-GCN	satisfied
CNN (1D Temporal)	#Stages	$\{2,3\}$	2
	Kernel sizes (branches)	$\{3,5,7\}$	$\{3,5,7\}$
	Channels/branch	$\{128,256\}$	256
	Residual connections	{on, off}	on
	Inter-stage pooling	{none, AvgPool}	AvgPool
	Norm/activation	BN + ReLU	same
	Dropout p	$\{0.2,0.3,0.4\}$	0.3
	Global pooling	{mean, max, mean + max}	mean + max
Training (Shared)	Optimizer	{AdamW}	AdamW
	Init LR	$\{1,3,5\}\times {10}^{-4}$	$3\times {10}^{-4}$
	Schedule	Cosine decay + warmup 5	same
	Batch/Max epochs	$\{32,64\}$/100	64/100
	Early stopping (patience)	$\{5,10\}$	10
	Weight decay	$\{1\times {10}^{-5},1\times {10}^{-4}\}$	$1\times {10}^{-4}$
	AMP/grad clip	AMP; clip $\{0.5,1.0\}$	AMP; clip = 1.0
	Label smoothing	$\{0,0.05\}$	0.05
	Supervision weight ${\lambda }_{\mathrm{rank}}$	$\{0.6,0.7,0.8\}$	0.7
	Calibration	{eq.-width/eq.-freq + isotonic}	eq.-freq + isotonic

. All feature computations are obtained pre-solve via solver APIs. Data splits use stratified sampling by flight count to match size distributions across training/validation; results are reported as mean ± 95% CI over three random seeds. When candidates tie on primary metrics, the configuration with lower ECE and fewer parameters is preferred.

5.4. Evaluation Metrics

To rigorously evaluate the efficacy of the proposed TRS-GCN model in accelerating Mixed-Integer Programming (MIP) solver performance, a comprehensive experimental framework was established. The TRS-GCN is benchmarked against two strong non-graph neural network baselines—an Artificial Neural Network (ANN) and a Convolutional Neural Network (CNN). All models were trained and validated on synthetically generated Aircraft Routing Problem (ARP) instances, using a standard 80%/20% split for the training and validation sets, respectively. The training was conducted for a maximum of 100 epochs utilizing the AdamW optimizer. A cosine annealing schedule with a 5-epoch warm-up period was employed for the learning rate, and an early stopping criterion with a patience of 10 epochs was implemented to prevent overfitting. Final evaluation was performed on unseen test sets comprising both synthetic instances and real-world data from the Bureau of Transportation Statistics (BTS), categorized by scale into small, medium, and large.

The evaluation framework is structured into two hierarchical stages: an assessment of the models’ intrinsic predictive accuracy and a subsequent evaluation of their end-to-end impact on solver performance. This is measured across three distinct solver integration strategies, executed under fixed wall-clock time budgets (3 h for small, 6 h for MEDIUM, and 12 h for large instances).

The fundamental capability of the models to differentiate between important and unimportant decision variables is quantified using several metrics. These include the Area Under the ROC Curve (AUC-ROC) for overall classification quality, R-Precision to evaluate the ranking of top-priority variables for warm-starting, the Max Pruning Rate to reflect the potential for safe variable removal, and the False Negative Rate (FNR) to quantify the risk of aggressive pruning.

The tangible impact of model guidance on solver performance is measured using a standardized set of metrics, formally defined in

Table 5. Definitions of solver performance evaluation metrics.

Metric (Symbol)	Description	Goal
R-Precision	Precision within the top-K ranked variables, where K is the number of variables in the optimal solution (variables equal to 1).	↑
Time-to-First-Feasible (TFF)	The wall-clock time (in seconds) required to find the first feasible solution.	↓
GAP@TFF	The solver-defined optimality gap at the instant the first feasible solution appears, measured against the theoretical optimum of the scaled problem via the best valid bound available at TFF.	↓
Time Reduction Rate (TRR)	The percentage reduction in wall-clock time to reach the baseline’s final objective value, $z_{\mathrm{ref}}$.	↑
Primal Integral (PI)	The integral of the (normalized) optimality gap against the theoretical optimum of the scaled problem over the time horizon.	↓
Gap-AUC	The time-averaged Primal Integral.	↓
False-Negative Rate (FNR)	In SPR, during zero-variable pruning, the proportion of optimal-1 variables that were mistakenly removed.	↓
Max Pruning Rate (MPR)	In SPR, the maximum fraction of variables that can be safely pruned while satisfying a false-negative safety budget.	↑
Infeasibility Rate (IFR)	In SPR, the percentage of instances rendered infeasible due to the removal of all optimal solutions.	↓

Note: In this document, the upward arrow (↑) and downward arrow (↓) indicate the goal of maximizing and minimizing the metric, respectively. This notation will be consistent throughout the document and will not be repeated.

. In these definitions, $z\left(t\right)$ denotes the solver’s primal bound at time t, and $z_{\mathrm{ref}}$ represents the best objective value found by the baseline solver within the allocated time budget T.

6. Results

6.1. Model Interpretability and Feature Importance

To elucidate the decision-making process of the TRS-GCN model and to validate our feature engineering strategy, we conducted a comprehensive feature importance analysis. Understanding which features contribute most significantly to the model’s predictive accuracy is paramount for model interpretability and for gaining deeper insights into the structural properties of the Aircraft Routing Problem (ARP). The analysis identifies the key drivers that determine the likelihood of a flight string (i.e., a variable) being included in the optimal solution.

Figure 5 presents a heatmap visualizing the importance scores of the top 20 most influential features, ranked by their mean contribution across small, medium, and large-scale problem instances. The features are sorted in descending order of their average importance, providing a clear hierarchy of their impact. The color intensity corresponds to the normalized importance score, with brighter colors indicating higher predictive power.

The analysis reveals a compelling hierarchy among different categories of features. Notably, features derived from the linear programming (LP) relaxation, such as “Dual price”, “Mean reduced cost (covering)”, and “Complementary gap”, consistently rank as highly influential. This underscores the efficacy of integrating mathematical optimization artifacts into the machine learning model, as these features provide a strong signal regarding a variable’s potential contribution to the objective function. Furthermore, network-theoretic features, including “Centralities (agg.)”, “Compat. graph indeg/outdeg”, and “Two-hop reachability”, demonstrate significant importance. This highlights the TRS-GCN’s ability to effectively leverage the underlying graph structure of the ARP to capture complex interdependencies between flights and flight strings.

Operational features, such as “Airborne duration” and “Curfew flags (dep/arr)” also feature prominently, confirming that the model learns to prioritize variables that satisfy critical real-world constraints. The heatmap also illustrates the relative stability of feature importance across different data scales, although minor variations can be observed. This robustness suggests that the TRS-GCN captures fundamental principles of the ARP that are generalizable across problems of varying complexity. In summary, this analysis not only enhances the transparency of our proposed model but also validates the synergistic combination of features from network topology, mathematical optimization, and operational domains.

6.2. Task-Oriented Performance Evaluation

The ultimate value of a predictive model in this context lies in its ability to accurately guide the solver for specific downstream tasks. We therefore evaluate two complementary goals: identifying high-quality variables for warm-starting and safely pruning irrelevant variables for static problem reduction. The comprehensive results, broken down by dataset and scale, are presented in

Table 6. Task-oriented predictive accuracy for warm-starting and static problem reduction.

Task	Metric	Model	Validation (Synth.)			Test (BTS)
			Small	Medium	Large	Small	Medium	Large
Warm-Starting	R-Precision (%) ↑	TRS-GCN	98.6 ± 0.3	98.2 ± 0.4	97.3 ± 0.4	95.9 ± 0.5	95.2 ± 0.5	94.3 ± 0.6
		CNN	92.1 ± 0.5	91.3 ± 0.6	90.6 ± 0.6	90.9 ± 0.6	90.1 ± 0.7	89.2 ± 0.7
		ANN	89.3 ± 0.6	88.5 ± 0.7	87.7 ± 0.7	88.6 ± 0.7	87.7 ± 0.8	86.8 ± 0.9
Static Problem Reduction	Max Pruning Rate (%) for FNR $\le 5\%$ ↑	TRS-GCN	89.7	86.1	82.3	84.9	81.3	78.1
		CNN	74.6	70.3	65.2	69.8	66.2	60.4
		ANN	59.4	56.5	50.7	55.7	52.3	46.5
	FNR (%) at 20% Pruning ↓	TRS-GCN	0.06	0.09	0.12	0.14	0.17	0.21
		CNN	0.49	0.58	0.71	0.69	0.82	0.93
		ANN	1.09	1.23	1.41	1.17	1.52	1.79
	FNR (%) at 40% Pruning ↓	TRS-GCN	0.53	0.72	1.08	0.88	1.19	1.57
		CNN	2.07	2.76	3.39	3.08	3.27	3.83
		ANN	3.87	4.16	5.37	4.63	5.18	6.11
	FNR (%) at 60% Pruning ↓	TRS-GCN	1.47	1.93	2.38	2.07	2.79	3.41
		CNN	3.87	4.63	4.91	4.76	4.93	5.07
		ANN	5.13	6.24	7.96	6.47	7.73	9.34

Synth.: Synthetic validation data. BTS: Test data from the Bureau of Transportation Statistics. Max Pruning Rate: Maximum percentage of variables that can be removed while $\mathrm{FNR}\le 5\%$. Higher is better (↑). FNR @ X% Pruning: False Negative Rate when the bottom X% of variables are pruned. Lower is better (↓).

.

For warm-starting, we adopt R-Precision to evaluate the model’s ability to rank the true optimal variables at the very top of its prediction list. TRS-GCN remains exceptionally effective on real-world test sets, achieving $\ge 94\%$ R-Precision across scales, providing a high-purity signal for constructing strong initial incumbents and improving the primal bound early in the search.

For static problem reduction, we analyze performance from both benefit and risk perspectives. On benefit, under a strict safety budget of $\mathrm{FNR}\le 5\%$, TRS-GCN enables substantially larger safe pruning than the baselines on BTS test data: Small/medium/large reach 84.9/81.3/78.1%, and on synthetic validation, 89.7/86.1/82.3%. These correspond to a 15–19 percentage-point advantage over the next-best model across scales. On risk, at fixed pruning levels of 20%, 40%, and 60%, TRS-GCN maintains a low false-negative profile.

6.3. MIP Solver Acceleration Performance

This section quantitatively evaluates the efficacy of the three proposed solver–learning integration strategies: warm-starting, static problem reduction (SPR), and dynamic search (hybrid branching). The evaluation is performed on the small, medium, and large (S/M/L) test sets under fixed wall-clock time budgets of 3, 6, and 12 h, respectively. To ensure a controlled and rigorous comparison, we first establish a consistent performance baseline by running the solver with a fixed configuration on each instance. This baseline provides a reference objective value, $z_{\mathrm{ref}}$, and a complete solution trajectory. Subsequently, each ML-guided integration strategy is executed, and its performance is measured against this reference.

6.3.1. Warm-Starting with Feasibility Pump

The objective of the warm-starting strategy is to rapidly generate a high-quality initial incumbent solution, thereby providing the Branch-and-Bound search with a strong primal bound from the outset. To achieve this, we replace the conventional heuristic rounding within the solver’s feasibility pump (FP) with a priority-based rounding scheme informed by the predictive scores from each model (TRS-GCN, CNN, and ANN).

As shown in

Table 7. Warm-starting: TFF and GAP@TFF across S/M/L (median).

Model	Small (3 h)		Medium (6 h)		Large (12 h)
	TFF (s) ↓	GAP@TFF ↓	TFF (s) ↓	GAP@TFF ↓	TFF (s) ↓	GAP@TFF ↓
TRS-GCN	0.64	0.24	3.2	0.31	7.4	0.51
CNN	0.61	0.23	3.3	0.53	7.5	0.56
ANN	0.67	0.24	3.4	0.58	7.6	0.59
Native FP	0.63	0.53	3.3	0.65	7.5	0.83

, TFF is essentially indistinguishable across methods at all scales (sub-second on small, a few seconds on medium, and several seconds on large), indicating that feasibility is found quickly regardless of the warm-start signal. The substantive gains arise in the quality of the first incumbent, measured by GAP@TFF. On small, all ML variants substantially reduce the initial gap relative to the native FP and perform similarly. On medium and large, TRS-GCN consistently provides the strongest initial incumbent, with a clearly lower GAP@TFF than CNN and ANN and a marked improvement over the native FP.

Consistent with the metric definitions in Table 5, warm-starting primarily improves GAP@TFF rather than TFF. In practice, this means that all methods find feasibility at comparable speeds, but TRS-GCN provides a materially stronger initial primal bound, especially on medium and large instances. This higher-quality starting point is expected to propagate downstream, benefiting convergence-oriented metrics such as T1I, PI, and Gap-AUC under fixed time budgets.

6.3.2. Static Problem Reduction (SPR)

We statically prune low-importance variables before solving. We evaluate (i) a prior (oracle) setting that constrains FNR $\le 1\%$ and reports the maximum safe reduction $r_{\max }$ and its speedup, and (ii) posterior (operational) settings with fixed reduction ratios (40%/60%) that expose true FNR/IFR and downstream convergence quality.

Prior results: This analysis evaluates the theoretical maximum performance of static problem reduction (SPR) under a strict safety budget (FNR ≤ 5%), with results summarized in

Table 8. SPR (Prior): Max safe reduction, TRR, and early-stage PI ratios vs. unpruned baseline.

Model	Small			Medium			Large
	$r_{\mathbf{max}}$ (%) ↑	TRR (%) ↑	PI Ratio (×) ↓	$r_{\mathbf{max}}$ (%) ↑	TRR (%) ↑	PI Ratio (×) ↓	$r_{\mathbf{max}}$ (%) ↑	TRR (%) ↑	PI Ratio (×) ↓
TRS-GCN	83.5	—	1.08	57.4	28.6	0.72	49.2	52.4	0.48
CNN	50.1	—	1.13	45.9	2.9	0.97	37.8	23.1	0.79
ANN	37.6	—	1.06	33.8	—	1.12	27.9	13.0	0.88

Notes: “—” indicates that the method did not reach the baseline target $z_{\mathrm{ref}}$ within the budget or could not attain the same theoretical optimum. The PI ratio is measured at fixed horizons: 30 min (small), 1 h (medium), and 3 h (large). The baseline (no-pruning) PI ratio is normalized to $1.00$ at each horizon.

. We assess the maximum safe reduction rate ($r_{\max }$) and its impact on end-to-end performance via the Time Reduction Rate (TRR), as well as on early-stage convergence via the Primal Integral (PI) ratio.

TRS-GCN demonstrates superior capability, achieving the highest safe pruning rates across all scales (small: 83.5%, medium: 57.4%, large: 49.2%), substantially outperforming both the CNN and ANN. This aggressive yet safe reduction translates directly into significant solver acceleration on more complex instances. For medium and large problems, TRS-GCN achieves time savings (TRR) of 28.6% and 52.4%, respectively. It also markedly improves early-stage progress, delivering the best PI ratios (0.72 on medium and 0.48 on large).

On the small instances, a ceiling effect is observed, as the unpruned baseline solver already finds the optimal solution with high efficiency. Consequently, the TRR metric becomes less meaningful (indicated by “—”), and the PI ratios slightly greater than 1.0 suggest that pruning offers no practical benefit for these simpler cases.

Overall, the results confirm that TRS-GCN’s high predictive accuracy enables substantially greater safe problem reduction, leading to the strongest performance gains, with benefits amplifying at larger scales.

Posterior results: In the posterior analysis, we evaluate the operational performance under fixed reduction rates of 40% and 60%, with results shown in

Table 9. SPR (Posterior): Fixed reduction (40%/60%). Risk (FNR/IFR) vs. reward (PI ratio and TRR) and final budget–time gap (%, median). Rows show small/medium/large.

Setting	Model	FNR (%) ↓	IFR (%) ↓	PI Ratio (×) ↓	TRR (%) ↑	Final Gap @ Budget (%) ↓
40%	TRS-GCN	0.14	0.8	0.46	13.8	0.7
		0.33	0.0	0.39	35.1	8.66
		0.60	0.0	0.37	29.1	28.50
	CNN	0.42	2.0	0.57	7.4	1.10
		0.81	1.0	0.46	10.7	8.60
		1.60	0.3	0.42	9.1	28.55
	ANN	0.85	3.6	0.56	-	1.80
		1.62	1.7	0.48	-	8.90
		3.02	0.7	0.40	-	28.80
60%	TRS-GCN	1.24	1.2	0.80	17.4	1.60
		1.88	0.0	0.74	39.0	8.68
		2.36	0.0	0.66	42.2	28.35
	CNN	2.51	7.2	-	-	2.20
		3.66	4.4	0.81	-	9.60
		5.12	2.6	0.70	-	29.40
	ANN	3.94	9.4	-	-	3.10
		5.51	6.9	-	-	10.20
		7.89	4.2	-	-	29.60

Notes: A dash “-” indicates no clear acceleration effect. Concretely, TRR values of $\pm 3\%$ are collapsed to “-” for readability. The PI ratio uses fixed horizons 30 min (small), 1 h (medium), 3 h (large); the no-pruning baseline is $1.00$. Baseline final gaps: Small $=0.00\%$, medium $=8.71\%$, large $=28.77\%$.

. This setting reveals the practical risk–reward trade-off for each model.

At a 40% reduction level, TRS-GCN delivers consistent and significant gains with minimal risk. It achieves the highest Time Reduction Rate (TRR) across all scales (small: 13.8%, medium: 35.1%, large: 29.1%) while maintaining a near-zero Infeasibility Rate (IFR) of 0.0% on Medium and Large instances. This demonstrates a robust ability to accelerate the solver without compromising solution quality. In contrast, both CNN and ANN show much more modest time savings and incur a significantly higher risk, with IFRs reaching up to 3.6%.

When the reduction is increased to 60%, the superiority of TRS-GCN becomes even more apparent. It achieves even greater time savings, with a TRR of up to 42.2% on Large instances, and even improves the final optimality gap compared to the baseline. Most importantly, it maintains perfect feasibility (IFR = 0.0%) on Medium and Large problems. The baseline models, however, become unreliable at this aggressive level; they fail to provide clear acceleration and suffer from a very high Infeasibility Rate (up to 9.4% for ANN), making them impractical for aggressive SPR.

In summary, the posterior results confirm that a 40% to 60% reduction is a highly effective operational window for TRS-GCN, offering substantial solver acceleration with high reliability. The 40% level serves as a safe default, while 60% provides maximum benefit for larger instances where a minimal, controlled risk is acceptable.

6.3.3. Dynamic Search (Hybrid Branching)

This strategy injects ML-derived intelligence directly into the solver’s core Branch-and-Bound search. Branching variables are selected via a time-varying convex combination of the model’s importance score (${\widehat{s}}_v^{\mathrm{ML}}$) and the solver’s native pseudo-cost ($s_v^{\mathrm{PC}}$):

$$s_v\left(t\right)=\lambda \left(t\right){\widehat{s}}_v^{\mathrm{ML}}+\left(1-\lambda \left(t\right)\right)s_v^{\mathrm{PC}},$$

(29)

where the weighting factor $\lambda \left(t\right)=\max \{0,{\lambda }_0{(1-t/T)}^{\gamma }\}$ implements an early guidance, late handover strategy. ML guidance is prioritized early in the search ($\lambda \left(t\right)\approx 1$) and smoothly transitions to the solver’s reliable pseudo-cost branching as time t approaches the budget T.

The efficacy of this approach is evaluated by analyzing the inter-arrival time between consecutively discovered feasible incumbents, as illustrated in Figure 6. The baseline solver exhibits the characteristic exponential increase in time required to find each new incumbent, signifying a diminishing rate of improvement. The performance of the ML-guided strategies is benchmarked against this behavior:

• ANN: The ANN-guided search demonstrates no discernible improvement over the baseline. Its performance curve closely tracks the baseline’s trajectory, indicating no material acceleration in discovering feasible solutions.
• CNN: The CNN-based guidance provides a marginal but consistent benefit. It achieves a slightly lower inter-arrival time, enabling the discovery of approximately 1–2 additional incumbents across all scales within the same time budget.
• TRS-GCN: In stark contrast, the TRS-GCN-guided strategy yields significant and robust acceleration. By consistently maintaining a lower inter-arrival time throughout the search horizon, it discovers a substantially greater number of incumbents. Specifically, within the fixed time limit, it finds approximately five additional solutions on small, four on Medium, and six on large instances.

Figure 6. Dynamic search (hybrid branching): average time between incumbents vs. discovery index. The plots show the feasible solution cadence for (a) small, (b), medium, and (c) large instances. Curves shown for baseline, ANN, CNN, and TRS-GCN.

Figure 6. Dynamic search (hybrid branching): average time between incumbents vs. discovery index. The plots show the feasible solution cadence for (a) small, (b), medium, and (c) large instances. Curves shown for baseline, ANN, CNN, and TRS-GCN.

In conclusion, the results validate that the hybrid branching strategy is highly effective when guided by TRS-GCN. The increased cadence of finding high-quality solutions allows the solver to tighten the primal bound earlier and more frequently, thereby accelerating overall convergence. While the CNN provides minor gains, the ANN fails to offer any practical advantage over the native solver heuristic.

7. Conclusions

This paper addresses the computational challenges of solving large-scale Aircraft Routing Problems (ARPs) by developing a learning-based framework to accelerate modern MILP solvers. We demonstrate that integrating a novel Two-Stage Route Selection Graph Convolutional Network (TRS-GCN) significantly enhances search efficiency, answering our primary research question about the feasibility of using ML-guided acceleration for this class of problems.

Our main findings, based on large-scale, real-world BTS instances, confirm the effectiveness of our approach. The TRS-GCN, which predicts flight string variable importance using structural and LP-based features, provides actionable guidance to the solver. This is realized through three key contributions: an ML-guided feasibility pump for warm-starting, static problem reduction via predictive pruning, and a dynamic hybrid branching rule.

While effective, the framework’s reliance on a synthetic generator for training data is a limitation, as it may not perfectly generalize to the operational idiosyncrasies found in proprietary airline datasets. Additionally, the current study focuses exclusively on the ARP, leaving the applicability of our approach to other MILP structures untested.

These three methods are not mutually exclusive and can be integrated into a sophisticated, multi-stage acceleration workflow. In future research, we aim to combine these algorithms into a comprehensive solution strategy.

Future work should explore the generalizability of the TRS-GCN architecture to other large-scale combinatorial optimization problems, such as crew pairing or vehicle routing. Further research could also investigate the integration of more sophisticated GNN architectures or explore reinforcement learning to dynamically adapt branching and pruning strategies during the search.