A Multi-Scale Airspace Sectorization Framework Based on QTM and HDQN

Abstract

Airspace sectorization is an effective approach to balance increasing air traffic demand and limited airspace resources. It directly impacts the efficiency and safety of airspace operations. Traditional airspace sectorization methods are often based on fixed spatial scales, failing to fully consider the complexity and interrelationships of airspace partitioning across different spatial scales. This makes it challenging to balance large-scale airspace management with local dynamic demands. To address this issue, a multi-scale airspace sectorization framework is proposed, which integrates a multi-resolution grid system and a hierarchical deep reinforcement learning algorithm. First, an airspace grid model is constructed using Quaternary Triangular Mesh (QTM), along with an efficient workload calculation model based on grid encoding. Then, a sector optimization model is developed using hierarchical deep Q-network (HDQN), where the top-level and bottom-level policies coordinate to perform global airspace control area partitioning and local sectorization. The use of multi-resolution grids enhances the interaction efficiency between the reinforcement learning model and the environment. Prior knowledge is also incorporated to enhance training efficiency and effectiveness. Experimental results demonstrate that the proposed framework outperforms traditional models in both computational efficiency and workload balancing performance.

1. Introduction

Airspace is an indispensable and critical resource in modern society. Its efficient management is essential to ensure the safety, efficiency, and sustainability of air transportation. In airspace management, airspace sectors are the basic operational units of air traffic control. They define independent responsibility zones through geographic partitioning. These sectors undertake core functions such as dynamic aircraft monitoring, conflict resolution, and traffic flow coordination. Airspace sectorization is a crucial task for achieving efficient airspace management, and the quality of sectorization directly determines the operational efficiency and safety margins of airspace. Therefore, a well-designed sector structure can dynamically adapt to the spatiotemporal distribution of traffic flow. It balances sector workloads, reduces air traffic controllers’ pressure, and improves airspace resource utilization [1,2]. In recent years, with the rapid growth of air traffic density and flight volumes, rational airspace sectorization has become increasingly important [3,4,5].

Currently, airspace sectorization algorithms can be broadly categorized into two types: those based on traffic flow [6,7,8,9,10,11,12,13,14,15,16,17,18,19] and those based on foundational grids [20,21,22,23,24,25]. Traffic flow-based methods involve preprocessing flight trajectories into graphs, and then applying network, topology, or graph theory techniques for sectorization. However, the data processing and computational procedures involved in these methods are often cumbersome. In foundational grid-based methods, the airspace is initially divided into smaller foundational grids, which are then merged or split according to specific mathematical rules and application contexts to form sectors of varying shapes and sizes. Airspace gridding is a critical element in constructing the foundational framework of digital aviation management, and plays a vital role in enabling the digitalization and intelligent management of airspace sectors [26]. With technological advancements, numerous intelligent algorithms have been applied to the field of airspace management [27,28,29,30,31]. Among these, Mas-Pujol et al. [32] explored the application of image-based multi-agent reinforcement learning techniques to balance the demand and capacity of complex systems such as air traffic management. Marta et al. [33] investigated the use of reinforcement learning for restructuring urban drone airspace environments.

In the aforementioned studies, the spatial scales of the selected research areas vary significantly, ranging from relatively small-scale regions such as cities and Air Traffic Control Centers to larger-scale regions such as continents. For instance, Granberg et al. [34] focused on the terminal control area of Stockholm Arlanda Airport and proposed an airspace sectorization framework based on mixed integer programming, incorporating constraints on various sector geometries. Wong et al. [12] selected the Singapore Flight Information Region as their study area and utilized a non-dominated sorting genetic algorithm to balance air traffic controllers’ monitoring and coordination workloads while maintaining sector shape similarity. Ye et al. [22] conducted their research in the Taiyuan airspace of China, proposing a framework for automated airspace restructuring that employs the Monte Carlo graph-cutting algorithm to smooth irregular sector boundaries formed by grids. Sergeeva et al. [25] studied the French airspace, transforming the dynamic airspace configuration problem into a graph partitioning problem and solving it using a genetic algorithm. Basu et al. [35] applied a one-dimensional solution framework to design a heuristic algorithm for two-dimensional partitioning based on binary space partitioning, with the United States as their study area. Jägare et al. [20] discretized the European airspace into three-dimensional grids and utilized constraint programming to achieve sector planning while ensuring workload balance across sectors and satisfying multiple constraints.

However, these studies on airspace sectorization have primarily focused on sector design at fixed spatial scales, failing to fully consider the complexity and interrelationships of airspace partitioning across different spatial scales. In fact, variations in spatial scale result in different airspace characteristics and management needs. Changes in local airspace sectors may impact the management of surrounding airspace, while adjustments in large-scale airspace sectors can also influence local airspace traffic flows. As an integrated system, the dynamic coupling relationship between local and global airspace needs to be systematically considered in sectorization. Large-scale partitioning faces efficiency bottlenecks when handling local details [36], making it difficult to achieve a balance between fine-grained partitioning and global coordination. Conversely, small-scale partitioning often fails to integrate information from neighboring airspace, affecting the optimization of airspace sectors to achieve better results. Therefore, how to effectively incorporate large-scale information into local airspace sectorization, while achieving fine-grained processing of local areas in large-scale airspace sectorization, has become a critical challenge that urgently needs to be addressed.

To address this challenge, we propose a multi-scale airspace sectorization framework that integrates multi-resolution grids with hierarchical reinforcement learning. This framework divides the airspace into two spatial scales: local target regions and their corresponding larger regions. By leveraging the multi-resolution properties of the Discrete Global Grid System, it achieves multi-scale adaptation of airspace sectorization from local to global levels. Simultaneously, the hierarchical reinforcement learning model enhances the optimization of local airspace sectors through layered decision-making, balancing local and global considerations. First, we construct a globally unified, multi-layered airspace grid model based on the Quaternary Triangular Mesh (QTM). And the workload calculation model based on a spatial grid is extended. Second, we introduce an efficient algorithm for constructing spherical grid Voronoi diagrams to define airspace sectors. Then, we develop a hierarchical deep Q-network (HDQN) reinforcement learning model to optimize sectorization. This model leverages hierarchical structure, multi-resolution grids, and prior knowledge to enhance training efficiency and performance. Finally, real flight data from the Northeastern Chinese airspace is used to experimentally validate the computational efficiency and effectiveness of the proposed framework.

This paper is organized into five Sections. Section 1 introduces the research background. Section 2 provides a detailed explanation of the multi-scale airspace sectorization modeling framework based on QTM and HDQN. Section 3 presents an experimental analysis of the framework’s efficiency and effectiveness. Section 4 offers a discussion and considers future work. Finally, Section 5 concludes the paper.

2. Methodology

Significant differences in spatial scales within airspace management affect both operational demands and decision-making. Local sector adjustments may impact nearby regions. Meanwhile, large-scale changes can influence local traffic distribution. Therefore, airspace sectorization should systematically account for the dynamic coupling between global and local spatial levels. This study focuses on two key questions. One is how to effectively incorporate global spatial information into local sectorization. The other is how to overcome computational bottlenecks while improving the resolution of local optimization and fully leveraging global information. To address these challenges, we propose a multi-scale airspace sectorization framework based on QTM and HDQN. The overall structure of the framework is composed of four core modules, as illustrated in Figure 1.

Module I (Multi-Resolution Discretization of Airspace): This module uses QTM to build multi-resolution grids that discretize continuous airspace into standardized cells. These cells serve as the geometric foundation for sector modeling. High-resolution grids are applied to target regions, while lower-resolution grids cover larger areas, enabling efficient use of computational resources.

Module II (Grid-Based Workload Assessment): This module efficiently assesses sector workloads using the airspace grids. Workloads are discretized and mapped to individual grid cells, providing a structured basis for optimization decisions.

Module III (Grid-Based Voronoi Sector Generation): This module constructs sector structures using grid-based Voronoi diagrams. Each sector comprises multiple grids, and its total workload is calculated by summing the workloads of all corresponding grid cells.

Module IV (Hierarchical Reinforcement Learning Sector Optimization Model): This module constructs an HDQN model, employing a dual-layer policy architecture. The top-level policy determines the partitioning of global airspace, while the bottom-level policy optimizes local sector structures. Adaptive optimization is achieved by dynamically adjusting the positions of Voronoi sites.

Each module is described in detail below.

Figure 1. The framework for airspace sectorization depending on QTM and HDQN.

Figure 1. The framework for airspace sectorization depending on QTM and HDQN.

2.1. Airspace Gridding

The Discrete Global Grid System (DGGS) [26,37,38,39,40,41,42,43,44,45,46,47] is an emerging framework for spatial data modeling. It offers several advantages, including multi-resolution capability, spatial uniformity, and hierarchical structure. These features provide new opportunities for addressing multi-scale airspace sectorization challenges. Its multi-scale design allows flexible adaptation to partitioning needs at various spatial levels. Meanwhile, its regular structure simplifies the division and analysis of complex airspace. Compared to traditional airspace management methods based on administrative boundaries or fixed routes, DGGS improves the efficiency of capacity computation, storage, and indexing, thereby enabling more effective analysis and optimization.

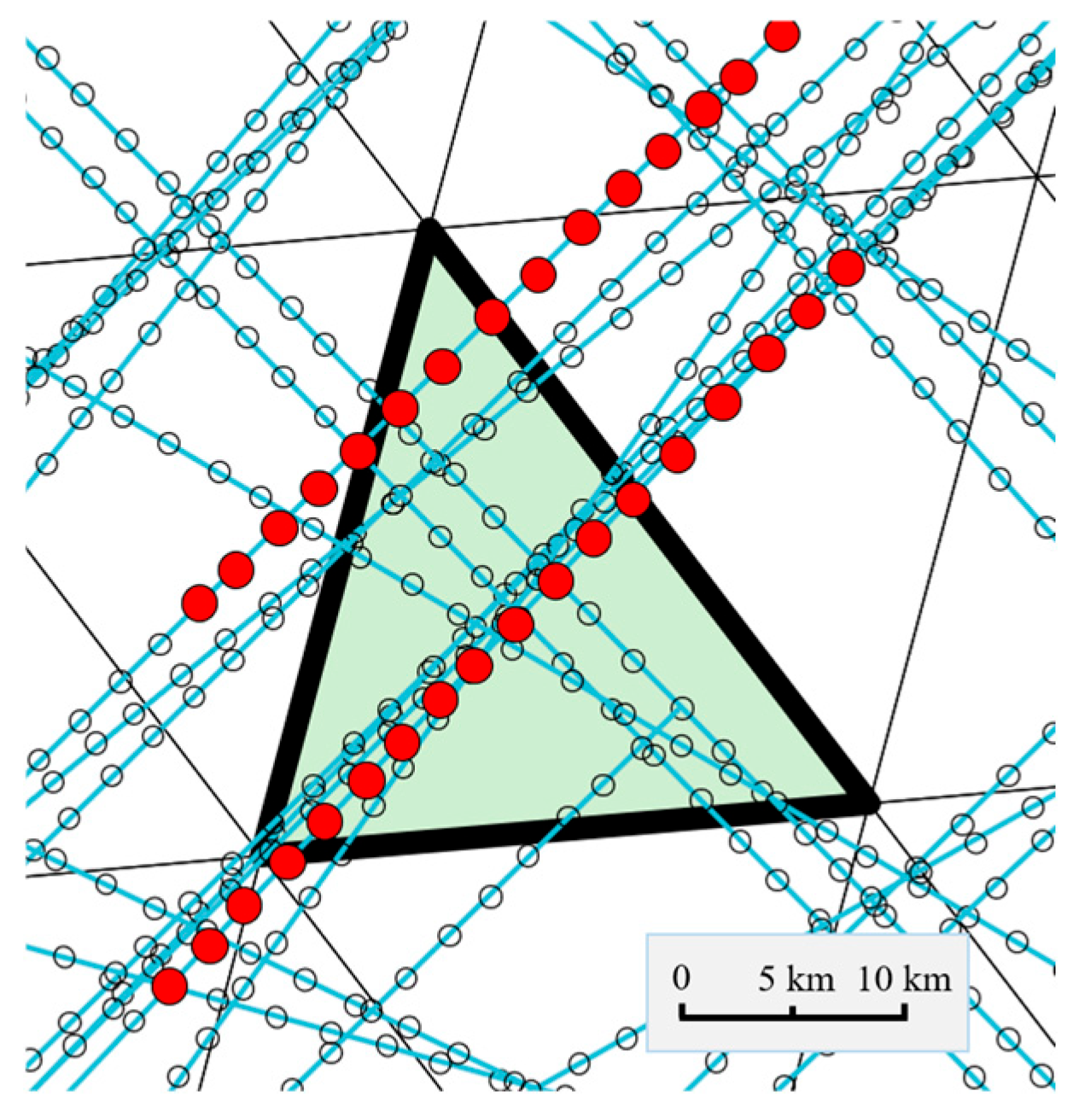
2.1.1. Multi-Resolution Airspace Grid Modeling Based on QTM

In this research, we use the spherical Quadratic Triangular Mesh (QTM) [48], based on the ortho-octahedron as the basis for the foundation of the spherical airspace grids (see Figure 2). QTM is a typical discrete global grid featuring a hierarchical structure, near-uniform resolution, and global consistency. It also supports more accurate boundary fitting [49,50].

The QTM grid is constructed using a direct spherical subdivision approach, where grid points are generated by equally dividing latitude and longitude. These points are then connected using great circle arcs and latitude lines to form the spherical grid. In computation, QTM uses longitude–latitude coordinates and spherical grids as its basis, and projection transformations are applied only for visualization purposes. This approach maintains projection independence and uniformity, effectively avoiding the impact of projection distortions on computational accuracy.

The QTM grid encoding uses a one-dimensional array to represent spherical coordinates. Latitude and longitude coordinates can be efficiently converted into grid codes through a code conversion algorithm. This algorithm refers to a set of rules and formulas for mutual conversion between different global discrete grid codes and geographic coordinates. Detailed conversion rules can be found in [51]. Grid encoding not only avoids the complexity of projection calculations but also enables batch management and efficient indexing of airspace data. It is widely applied throughout all stages of the sectorization process.

2.1.2. Workload Gridding

To establish an optimization model, the workload of air traffic controllers in each sector must be accurately represented. This workload model serves as the core feature of the state vector used in the subsequent reinforcement learning model for sector optimization. Previous studies have proposed numerous workload calculation methods, including physical activity metrics, physiological indicators, controller task simulation models, subjective ratings, and machine learning approaches [11,13,52,53,54,55,56,57,58,59]. However, there is currently no globally accepted definition or standard for airspace sector workload [22]. Existing research generally considers the airspace sector workload to consist of three components [14]: monitoring workload (wl^mon), conflict workload (wl^con), and coordination workload (wl^coo). This study proposes a grid-based airspace workload model by leveraging the grid properties of QTM. It establishes a mapping between ergonomic considerations and mathematical modeling, avoiding complex spatial intersection computations.

(1)

Monitoring Workload Model

The monitoring workload of a sector refers to the workload being proportional to the duration of aircraft flight time within the sector. By using the base grid as an intermediate structure, the workload is allocated to the base grids. After each model iteration updates the sectors, the sector workload is obtained by summing the workloads of its constituent base grids, eliminating the need for recalculation. Assuming sector j consists of n base grids, the monitoring workload of sector j is expressed as:

$$w{l}_j^{mon}={\displaystyle \sum }_{i=1}^{n}ew{l}_i^{mon}$$

(1)

where $ew{l}_i^{mon}$ represents the monitoring workload of base grid i. Assuming there are m trajectories, then:

$$ew{l}_i^{mon}={\displaystyle \sum }_{k=1}^{m}fmo{n}_k^i$$

(2)

where $fmo{n}_k^i$ denotes the function calculating the flight duration of the trajectory k within base grid i. After airspace gridding, the trajectory data are represented as shown in Figure 3. Since each trajectory point is sampled at a fixed time interval, $fmo{n}_k^i$ can be simplified by counting the number of trajectory points within each grid. During this process, the use of grid encoding and conversion algorithms significantly reduces computational time and improves storage and retrieval efficiency. Grid encoding is repeatedly employed throughout this study to enhance efficiency and will not be elaborated further in subsequent sections.

(2)

Conflict Workload Model

The conflict workload of a sector refers to the workload generated by resolving potential conflicts between aircraft within the sector. The grid-based conflict detection algorithm takes advantage of the hierarchical and globally unified encoding of grids. This approach eliminates the need for pairwise distance calculations between aircraft and enables efficient collision detection [60,61], which has been proven to offer higher computational efficiency. Therefore, assume that sector j consists of n base grids, and the conflict workload of sector j is expressed as:

$$w{l}_j^{con}={\displaystyle \sum }_{i=1}^{n}ew{l}_i^{con}$$

(3)

The conflict workload $ew{l}_i^{con}$ of base grid i is determined by checking whether two trajectory points at the same altitude level fall into grid i simultaneously. Specifically, the trajectory point data within the same time interval are converted into a sequence of grid codes. If two trajectories both contain the grid code i, the conflict workload of grid i is incremented by one. The total conflict workload $ew{l}_i^{con}$ is calculated as the sum of conflict occurrences within grid i across all time intervals, as illustrated in Figure 4.

(3)

Coordination Workload Model

The coordination workload of a sector refers to the workload generated by the transfer of control authority for aircraft entering or exiting the sector, measured by the number of aircraft transitioning between sectors. Assuming m trajectories pass through sector j, the coordination workload of sector j is expressed as:

$$w{l}_j^{coo}={\displaystyle \sum }_{k=1}^{m}fco{o}_k^j$$

(4)

where $fco{o}_k^i$ is the function that calculates the number of transitioning aircraft for sector j Specifically, the trajectories are converted into grid code sequences, and if a trajectory passes through sector j and also traverses other sectors, the coordination workload of sector j is incremented by one. Because the coordination workload depends on sector configuration, it must be recalculated whenever sector boundaries are updated.

2.2. Sector Construction Based on DGGS Grid Voronoi Diagrams

The Voronoi diagram is one of the key methods for airspace sectorization [16,23]. It partitions space into multiple Voronoi regions based on spatial distance, where each point in a region is closest to its corresponding generator point. Owing to its natural proximity, dynamic adaptability, and high computational efficiency, the Voronoi diagram has been widely adopted for airspace sectorization. Its dynamic adaptability enables real-time sector boundary updates by adjusting the positions of generator points in response to workload variations. Meanwhile, its global coordination capability ensures seamless coverage and consistent sector management, avoiding boundary overlaps or gaps. Additionally, the convexity and connectivity of Voronoi regions offer structural advantages that are highly beneficial in airspace sectorization. An efficient QTM-based spherical Voronoi diagram generation algorithm is introduced to construct airspace sectors [62], as illustrated in Figure 5. The resulting sectors are represented as collections of base grids within Voronoi regions, with sector boundaries defined by grid boundaries.

The Voronoi diagram is uniquely determined by the spatial distribution of its generator points. The generator point set S is treated as a decision variable for subsequent sector optimization. It consists of k latitude–longitude coordinates, where k represents the number of sectors.

$$S=\left\{\left(Lo{n}_1,La{t}_1\right),\left(Lo{n}_2,La{t}_2\right)\dots \left(Lo{n}_k,La{t}_k\right)\right\}$$

(5)

2.3. Airspace Sector Optimization Strategy Based on Hierarchical Reinforcement Learning

In real-world operations, airspace traffic changes significantly over time, which makes it difficult for static partitioning schemes to maintain long-term workload balance across sectors. To address this issue, we propose an HDQN-based optimization strategy that dynamically adjusts sector boundaries to balance workloads.

2.3.1. HDQN Framework for Airspace Sectorization

HDQN is a deep reinforcement learning algorithm based on hierarchical reinforcement learning. It introduces a hierarchical policy structure to improve learning efficiency and adaptability. The core of HDQN is Q-learning, a value-based reinforcement learning method. In Q-learning, the agent learns an action-value function that estimates the expected cumulative reward of taking action $a$ in state $s$. Through continuous exploration and feedback, the agent gradually updates this function, eventually converging to an optimal policy that maximizes long-term rewards.

The designed HDQN algorithm adopts a two-level hierarchical structure, consisting of a top-level controller and a bottom-level controller, as shown in Figure 6. Specifically, the top-level DQN uses a Voronoi diagram to divide the global airspace into basic control regions. The bottom-level DQN then further partitions each region into multiple sectors. This two-tier structure, built using a recursive multi-level Voronoi diagram, allows the top and bottom DQNs to optimize different levels of the airspace hierarchy, enabling coordinated multi-scale partitioning.

2.3.2. Action Space and State Space

In a multi-level reinforcement learning model for airspace sectorization, the design of the action and state spaces is crucial. It directly affects model performance and decision-making efficiency. The top-level DQN and bottom-level DQN construct their respective state spaces and action spaces for different decision-making layers.

(1)

State Space of the Top-Level DQN

The state set $S$ is utilized to describe the current state of the training environment. In the context of airspace sector optimization, the state space reflects the current partitioning of the airspace sectors. The top-level DQN focuses on macroscopic airspace division. Its state is defined by the spatial distribution of top-level Voronoi generator points, which determine the geometry of each control region. Assuming the airspace is divided into m airspace structural regions, the state space can be expressed as follows:

$$S^T=\left\{\left(Lo{n}_1^T,La{t}_1^T\right),\left(Lo{n}_2^T,La{t}_2^T\right)\dots \left(Lo{n}_m^T,La{t}_m^T\right)\right\}$$

(6)

where $Lo{n}_i^T$ and $La{t}_i^T$ represent the longitude and latitude coordinates of the top-level Voronoi generating point i, respectively.

(2)

The state space of the bottom-level DQN

The bottom-level DQN refines the sector boundaries within the local airspace by adjusting the positions of the bottom-level Voronoi diagram generating points. Its content pertains to the spatial distribution of bottom-level Voronoi boundary points. Assuming a top-level airspace structure area is subdivided into n local sectors, the state space of the bottom-level DQN can be expressed as follows:

$$S^B=\left\{\left(Lo{n}_1^B,La{t}_1^B\right),\left(Lo{n}_2^B,La{t}_2^B\right)\dots \left(Lo{n}_n^B,La{t}_n^B\right)\right\}$$

(7)

(3)

The action space of the top-level DQN

The action space $A$ refers to the set of operations that the agent (the airspace sectorization model) can select under a specific state. The top-level DQN adjusts the positions of Voronoi generator points to indirectly change the shapes of control regions and achieve workload balance across the airspace. Specifically, the actions of the top-level DQN refer to small-range translations of the generator points’ latitude and longitude coordinates in the east, west, south, and north directions. Assuming the airspace is divided into m control areas, the action for each Voronoi generating point can be expressed as:

$$A^T=\left\{\left(\mathrm{\Delta }Lo{n}_1^T,\mathrm{\Delta }La{t}_1^T\right),\left(\mathrm{\Delta }Lo{n}_2^T,\mathrm{\Delta }La{t}_2^T\right)\dots \left(\mathrm{\Delta }Lo{n}_m^T,\mathrm{\Delta }La{t}_m^T\right)\right\}$$

(8)

where $\mathrm{\Delta }Lo{n}_i^T$ and $\mathrm{\Delta }La{t}_i^T$ represent the offsets of the Voronoi generating point i in the longitude and latitude directions, respectively. The absolute values of these offsets, serving as action step sizes, gradually decrease over the course of an Episode.

(4)

The action space of the bottom-level DQN

The action space of the bottom-level DQN refers to the movement operations of the generator points used to construct the Voronoi diagram for local airspace sectorization. Assuming a local sector contains n boundary generating points, the action space of the bottom-level DQN can be expressed as:

$$A^B=\left\{\left(\mathrm{\Delta }Lo{n}_1^B,\mathrm{\Delta }La{t}_1^B\right),\left(\mathrm{\Delta }Lo{n}_2^B,\mathrm{\Delta }La{t}_2^B\right)\dots \left(\mathrm{\Delta }Lo{n}_n^B,\mathrm{\Delta }La{t}_n^B\right)\right\}$$

(9)

In the design of the action space, constraint conditions are imposed to limit the extent of sector boundary adjustments in order to ensure airspace safety (referred to as Constraint 1). The constraint is defined as follows: when a sector boundary adjustment causes the distance between the boundary and high-density flight points to fall below a safety threshold, the agent’s action is considered invalid or unsuccessful. This constraint effectively prevents interference with high-density flight regions during sectorization. The constraint is computed based on the grid as follows:

$$G_h\cup G_b=0$$

(10)

Here, the set of hotspot area grids is denoted as $G_h$, and the set of sector boundary grids is denoted as $G_b$.

2.3.3. Reward Function

The reward function $R$ defines the reward for each task, representing the benefit obtained after executing the task. In the multi-layer reinforcement learning-based airspace sector optimization strategy, designing an appropriate reward function is crucial for guiding the agent to learn and optimize the airspace partitioning strategy. The reward function reflects the quality of airspace sector partitioning based on the workload balancing of the airspace. Workload balancing is represented by the standard deviation of the workload within the sectors, as shown in Equation (11). A smaller standard deviation indicates a smaller difference in traffic control workload among the sectors, implying a higher degree of workload balancing.

$$f_{balance}=\sqrt{{\displaystyle \frac{1}{k}}{\displaystyle \sum }_{i=1}^k{\left(w{l}_i^{mon}+w{l}_i^{con}+w{l}_i^{coo}-\overline{w{l}^{mon}}-\overline{w{l}^{con}}-\overline{w{l}^{coo}}\right)}^2}$$

(11)

(1)

The reward function of the top-level DQN

The reward function of the top-level DQN is designed to optimize the workload balance among control areas while also ensuring reasonable sectorization within the target local airspace. Therefore, in this study, the top-level DQN reward function is defined as the negative standard deviation of the workloads across all top-level control areas minus the standard deviation of the workloads across all sectors within the target local airspace, expressed as:

$$R^T=-f_{balance}^T-f_{balance}^B$$

(12)

where $f_{balance}^T$ represents the standard deviation of the workload across the top-level airspace structural regions; as calculated by Equation (11), while $f_{balance}^B$ denotes the standard deviation of the workload within the sectors of the target local airspace, with the goal of reducing the imbalance in global and local sectorization.

(2)

The reward function of the bottom-level DQN

In the bottom-level DQN, which is primarily responsible for the partitioning and optimization of sectors within local airspace, the design of its reward function takes into account the workload balancing among sectors within the airspace structural region, expressed as:

$$R^B=-f_{balance}^B$$

(13)

2.3.4. Prior Knowledge

The introduction of prior knowledge can effectively reduce model convergence time, enhance the stability of policy learning, and provide more reliable decision-making support in dynamic airspace environments. To further improve computational efficiency and solution quality, domain prior knowledge is incorporated from three aspects: initialization, reward function shaping, and prioritized adjustments [14].

(1)

Initialization

The initialization of the reinforcement learning model has a significant impact on the policy optimization process. To improve learning efficiency, high-density flight grids are identified as clustering centers using the workload computation module. By integrating the spatial distribution of airspace sectors with the clustering characteristics of workload, these clustering centers or the centroids of the original sectors are used as the initial generating sites of the sectoral Voronoi diagram, thereby establishing a well-structured initial state space for the model.

(2)

The plasticity of the reward function

Based on the load-balancing reward mechanism, a minimum safety distance constraint between sector boundaries and high-density flight zones (Constraint 1) is incorporated into the reward function. This guides the agent to quickly learn to avoid placing sector boundaries across densely populated flight areas, which would otherwise lead to invalid actions. When a boundary approaches or crosses a high-density flight zone, a penalty is applied. The reward function is defined as:

$$R=-f_{balance}-f_{boundary}$$

(14)

(3)

Priority Adjustment

To ensure the efficiency of the training process, higher probabilities are assigned to operating in high workload areas during the early stages of training. As the training progresses and the model gradually converges with a certain level of optimization capability, the probabilities of actions become more balanced. This strategy accelerates training while ensuring that airspace planning objectives remain balanced throughout the process.

3. Results

3.1. Experimental Environment

The Northeast airspace in China has a relatively simple structure, with clearly defined sectors and traffic flows. Shenyang, a major central city in the region, oversees an airspace composed of six sectors, known as the Shenyang airspace. This is illustrated in Figure 7. This study selects the Northeast region of China as the research area, with the objective of optimizing the airspace structure of the Shenyang control region.

The flight traffic data used in this study is sourced from FlightAware (https://flightaware.com/ (accessed on 1 May 2024)) and is formatted as ADS-B trajectory point data. Initially, the raw trajectory data are preprocessed, including outlier removal, data cleaning, and time synchronization. Subsequently, the flight traffic is spatially gridded based on the DGGS framework to support subsequent training.

The experimental H-DQN hierarchical reinforcement learning model is structured with the Northeast airspace as the top-level region and the Shenyang airspace as the bottom-level region:

The top-level policy of the model is responsible for the overall airspace partitioning. It divides the Northeast airspace into four control regions: Shenyang, Dalian, Hailar, and Harbin. The top-level state space takes the range of the entire Northeast airspace, and the action space dimension is the number of control regions multiplied by four directions (4 × 4).

The bottom-level policy further refines the airspace partitioning based on the top-level division. Taking the Shenyang Control Region as an example, it is subdivided into six sub-sectors. The state space of the bottom-level policy is confined to the Shenyang control region determined by the top-level policy. Its action space equals the number of subsectors multiplied by four directions (6 × 4).

Considering that the typical width of civil aviation routes is approximately 20 km, the top-layer strategy adopts the 8th-level QTM (with an average side length of about 40 km), while the bottom-layer strategy uses the 9th-level QTM (with an average side length of about 20 km). The 9th-level QTM is also employed for workload calculation.

The algorithm presented in this research is implemented using the Python programming language (version 3.9.0). The spherical reference employed is the WGS84 reference ellipsoid. The hardware environment consists of an 11th Gen Intel(R) Core (TM) i5-1135G7 processor @ 2.40 GHz with 24.0 GB of RAM. For visualization, the Lambert projection is selected.

In the experimental setup, the learning rate for the agent is set to $lr=0.0001$, and the discount factor to $\gamma =0.99$. Each training cycle consists of 200 action steps. For every 10 cycles of training the lower-level policy, one training iteration of the upper-level policy is conducted. After 300 training cycles, the sectorization optimization model is considered fully trained.

3.2. Workload Calculation Efficiency Comparison

The schematic diagram of airspace management workload results based on multi-resolution grids is shown in Figure 8. Different levels of workload are represented by distinct colors, with darker shades indicating higher workload intensities.

In reinforcement learning, the primary consumption of computational resources is concentrated in the interaction process with the environment. In this experiment, this computation mainly involves workload evaluation and Voronoi diagram generation. To evaluate the efficiency of the grid-based approach in calculating airspace management workload, a comparative experiment is conducted. The comparison is made with the traditional airway-based method, which evaluates workload by calculating the number of flights and their dwell time within each sector. The results of the comparative experiment, as shown in Figure 9, demonstrate the significant computational efficiency advantages of the grid-based method. This advantage is mainly due to two features of the grid system. First, grid codes support efficient indexing and high-performance conversion between coordinates and grid codes. Second, batch operations can be applied to all trajectory points within a grid, enabling fast mapping between trajectory data and airspace sectors.

3.3. Effectiveness Comparison Experiment

Figure 10 presents the optimal solution derived from the reinforcement learning training results in this study. The blue regions represent the top-level control areas, with the Shenyang control area further divided into six light-green sectors. Additionally, a series of validation experiments were conducted to demonstrate the superiority of the proposed framework. These experiments include evaluations of the model’s hierarchical structure, the use of multi-resolution grids, and the integration of prior knowledge modules.

(1)

Comparative Experiment between Hierarchical Reinforcement Learning and Single-Layer Reinforcement Learning

This study employs a hierarchical reinforcement learning model. To validate its advantages over single-layer reinforcement learning models in optimizing local airspace, a comparative experiment was designed, as shown in Figure 11. The green curve represents the training results for the Shenyang region using the hierarchical reinforcement learning model. The blue curve denotes the results of applying a single-layer reinforcement learning model exclusively to the Shenyang region. And the red curve illustrates the performance of the Shenyang region when a single-layer reinforcement learning model is trained on the entire Northeast airspace as a whole. All models were tested using identical parameters and training iterations. The experimental results demonstrate that the hierarchical reinforcement learning model achieves better optimization performance and faster convergence than the single-layer models. This confirms the effectiveness and practicality of using a hierarchical structure for airspace sectorization.

(2)

Comparative Experiment on Effectiveness and Efficiency between Multi-Scale Grids and Single-Scale Grids

This study introduces multi-resolution grids into the proposed multi-scale airspace sector planning framework and conducts a comparative experiment with single-resolution grids. As shown in Figure 12a, the training performance of airspace sector optimization using reinforcement learning in the Shenyang region is presented under different grid resolutions. The experimental results indicate that both grid types perform similarly in optimization. However, as illustrated in Figure 12b, single-resolution grids require significantly more training time.

(3)

Comparative Experiment with Incorporation of Prior Knowledge

In the proposed multi-scale airspace sectorization framework, a prior knowledge module is introduced, and its effectiveness is validated through comparative experiments. As shown in Figure 13, the green curve represents the experimental results of incorporating prior knowledge into the reinforcement learning framework, while the blue curve corresponds to the results without prior knowledge. The experimental results demonstrate that integrating prior knowledge significantly improves the model’s convergence speed and training efficiency. It enhances workload balancing and sectorization quality. The primary factors contributing to this improvement include the use of reward shaping and a constrained action space, which help avoid ineffective exploration. In addition, the initial sector structure is optimized through the initialization strategy, further enhancing the model’s performance.

Table 1. Results of the Effectiveness Comparison Experiment.

RL	Grids	Prior Knowledge	Time Per Cycle	Reward
HDQN	multi-resolution	None	6.724 s	−2.67 × 105
Local-region DQN	multi-resolution	None	-	−3.63 × 105
Global-region DQN	multi-resolution	None	-	−4.92 × 105
HDQN	single resolution	None	14.08 s	−2.71 × 105
HDQN	multi-resolution	Yes	-	−1.59 × 105

provides a summary of the results from the effectiveness comparison experiment. The results indicate that the proposed model offers notable advantages in optimization performance, enabled by its hierarchical structure, multi-resolution grids, and the incorporation of prior knowledge.

3.4. Temporal Testing and Validation

To evaluate the adaptability and stability of the proposed multi-scale airspace sector planning framework under dynamic conditions, a temporal testing experiment was designed and conducted. The experiment utilized a pre-trained hierarchical reinforcement learning model to evaluate its performance in airspace sector partitioning under dynamic conditions. Given the significant variations in airspace traffic at different times of the day, the study divided a 24 h period into multiple phases, enabling automatic airspace sector updates based on traffic flow within each phase. Flight traffic data from the Northeast airspace on 24 July 2023 were randomly selected. The data were then divided chronologically into six intervals, each spanning four hours. The workload for each interval was calculated separately. Subsequently, the trained agent was used to perform airspace sector partitioning tests on the data from these six intervals. As shown in Figure 14, the results illustrate how sector partitioning in Shenyang airspace varies across different time intervals. The left vertical axis indicates the workload in each interval, while the right vertical axis shows the standard deviation before and after optimization.

The experimental results demonstrate that the proposed hierarchical reinforcement learning model effectively adapts to dynamic changes in airspace traffic. It achieves more balanced workload distribution across all time intervals and significantly reduces workload fluctuations, thereby validating the model’s dynamic adaptability and stability.

It is worth noting that, to avoid negative impacts on airspace stability due to frequent or large boundary adjustments, a boundary adjustment mechanism (Constraint 2) was incorporated into the reward function. Specifically, the degree of boundary change during each sector update is introduced as a negative reward term, formulated as follows:

$$R=-f_{balance}-f_{boundary}-f_{adjust}$$

(15)

where $f_{balance}$ represents the workload-balancing loss, $f_{boundary}$ is a penalty for sector boundaries nearing high-density flight areas, and $f_{adjust}$ constrains large boundary shifts during optimization. In this experiment, $f_{adjust}$ is defined as $f_{adjust}=100\times N_G$, where $N_G$ is the number of grids that change. This design effectively mitigates excessive and abrupt boundary modifications during the training process, ensuring the continuity and stability of airspace sector partitioning.

Figure 15 illustrates a comparison of the dynamic changes in airspace sector partitioning results across two intervals.

4. Discussion

The research presented in this paper aims to provide an innovative methodology for airspace sector partitioning and offers both theoretical and practical support for addressing complex airspace management challenges. Although significant achievements have been made, several valuable issues remain that warrant further discussion and investigation.

4.1. Airspace Design as a Complex System Problem

Airspace design is a complex systems engineering task. It involves dynamic interactions and optimizations across multiple dimensions and variables. This process not only requires the establishment of an effective theoretical model framework but also necessitates the thorough consideration of various practical constraints in implementation. For researchers, achieving full automation and intelligence in the airspace design process presents both a significant opportunity and a formidable challenge. While notable progress has been made in related research areas, numerous issues remain that warrant further in-depth exploration.

Research addressing this system task encompasses various aspects. Some studies focus on the construction of workload models [63], aiming to accurately reflect the dynamic characteristics of airspace operations. Others emphasize the prediction of airspace management workload [64,65], utilizing historical data and machine learning methods to forecast airspace traffic trends. Additionally, some research concentrates on post-processing procedures for sector partitioning results [16,25], including raster-based vectorization and smoothing of sector boundaries to enhance the practical applicability of the outcomes. Meanwhile, other studies are dedicated to improving optimization algorithms [14], such as genetic algorithms and reinforcement learning methods, to boost sectorization efficiency and effectiveness.

The framework proposed in this study is designed for the preliminary optimization and adjustment of airspace sectors, serving as an integral part of the overall airspace design and management system. As a meta-algorithm, the method presented in this paper demonstrates strong compatibility and scalability, allowing other optimization solutions to be further embedded within it. For instance, vectorization and smoothing algorithms can be introduced in sector boundary handling to reduce irregularities in practical applications. In terms of goal setting, dynamic adjustments can be made according to specific application scenarios. And, by incorporating weighted Voronoi diagrams, differentiated management resources can be allocated to different sectors, thus enabling flexible responses to the demands of complex airspace.

In addition, the experiments in this study primarily aim to balance the workload within the Shenyang Control Area, while also taking into account safety and stability constraints (Constraints 1 and 2). In practical applications, the optimization objectives can be further extended according to specific task requirements—for example, incorporating sector optimization across the entire Northeast airspace as part of a multi-objective optimization task. To this end, a multi-objective optimization framework is designed, with two optimization goals: (1) global airspace optimization involving coordinated scheduling across 16 sectors in the Northeast region; and (2) local airspace optimization focusing on the sectorization of six sectors within the Shenyang Control Area. During the optimization process, a composite reward function is formulated to achieve a trade-off between multi-scale objectives. The reward function is defined as follows:

$$R={\omega }_1{R}_{global}+{\omega }_2{R}_{local}$$

(16)

To quantify the impact of weight allocation on the optimization outcomes, three different sets of weight combinations were configured: (0.3, 0.7), (0.5, 0.5), and (0.7, 0.3). The experimental results are illustrated in Figure 16, where the blue curves represent the overall optimization results for the Northeast airspace, and the green curves correspond to the Shenyang control area. The results demonstrate that when the local weight dominates (Figure 16a, ${\omega }_1=0.3, {\omega }_2=0.7$), the load balancing performance in the Shenyang airspace improved by 24.1% compared to the equal-weight scenario, while the overall structural load balancing index for the Northeast region decreased by 12.5%. Conversely, when the global weight dominates (Figure 16c, ${\omega }_1=0.7, {\omega }_2=0.3$), the overall load balancing improved by 9.98%, but the optimization effect in the Shenyang control area declined by 43.3%. These results confirm the controllability of the optimization direction through weight parameters and provide a theoretical basis for airspace managers to implement differentiated strategies based on task priorities.

However, this study has several limitations that warrant further attention. First, due to data availability, the experimental validation was confined to the Shenyang Control Area and the Northeast China airspace. Future work will aim to apply the proposed framework to broader and more diverse airspace environments to further evaluate its robustness and scalability. Second, the air traffic data used in this study correspond to a specific time window and do not fully account for seasonal variations or operational fluctuations. In cases of unexpected events or extreme weather conditions, this may limit the generalizability of the results to other airspace settings. Third, future improvements could involve incorporating online learning mechanisms to enhance the model’s adaptability to dynamic and evolving traffic scenarios. Lastly, although the proposed framework has demonstrated promising applicability in preliminary airspace sectorization tasks, additional simulations and evaluations tailored to specific operational requirements are still necessary. The integration of human-in-the-loop assessments and real-world field testing will also be crucial to enhancing the framework’s practical reliability and operational value.

4.2. Selection of Base Grids

With the continuous advancement of cutting-edge technologies, the informatization of aviation equipment has triggered a collective technological revolution characterized by digitalization and intelligence, laying the foundation for digital aviation management. Grids can efficiently approximate complex geographical regions, enabling batch management of airspace based on spatial locations and relationships, eliminating the need for pairwise distance calculations between aircraft, and achieving efficient and standardized management processes. Grids provide a highly efficient and flexible approach for processing and managing massive aviation data, addressing the challenges of multi-source spatial data integration and offering high-precision digital support for intelligent airspace management.

In this research, QTM, a representative grid in DGGS, is chosen as the base grid for airspace modelling. In addition to QTM, there are various other grid types. Based on different partitioning methods, commonly used global discrete grid units primarily include spherical triangles, diamonds (quadrilaterals), and hexagons. The subdivision of diamond and triangular grids is relatively straightforward, as the coverage area of the parent cell completely overlaps with its four child cells, as illustrated in Figure 17a and b. In contrast, subdividing hexagonal grids is more complex. It requires determining an initial diamond structure to handle cross-border hexagons, as shown in Figure 17c. Different grids can be converted into one another through one-to-one correspondence. A diamond consists of two triangles, while the conversion rules for hexagons are more intricate, involving the combination and staggered arrangement of multiple triangles to form multiple hexagons, as depicted in Figure 17d.

The spherical QTM chosen in this study exhibits hierarchical, approximately uniform, and globally consistent characteristics, making it the most fundamental spherical grid unit. QTM enables precise boundary fitting and offers better nesting properties and greater flexibility compared to hexagonal grids. Additionally, the initial partitioning of QTM aligns its vertices with key points on the sphere (including the two poles), and its edges coincide with the equator, the prime meridian, and the 90°, 180°, and 270° meridians, facilitating easier localization of points on the sphere. The edges of QTM correspond to lines of latitude, simplifying coordinate transformation with latitude and longitude information, such as aircraft trajectories. Compared to traditional latitude–longitude grids (which suffer from polar distortion and area inequality) and hexagonal grids (which face limitations in hierarchical expansion), QTM demonstrates significant advantages in geometric uniformity, hierarchical continuity, and global coverage.

The experiments in this study employed both level-8 and level-9 QTM grids. Thanks to the multi-scale nature of the proposed framework, it can further reduce the grid resolution to support scalable management of large-scale airspace, while also enabling higher-resolution applications for urban airspace scenarios. By fully leveraging the advantages of multi-resolution grids, the framework achieves a balance between accuracy and efficiency.

This study employs spherical airspace grids to model airspace and represents the partitioned sector results as collections of base grids, where sector boundaries are formed by grid boundaries. However, the process of using grids to represent geographic units inevitably introduces certain errors, primarily manifested in the following two aspects:

First, grids, as basic units, approximate points, lines, and surfaces. The accuracy of representing geographic entities through grids depends on the grid resolution. While finer grids can improve management efficiency and algorithmic precision, they also increase computational time. In practical applications, it is essential to strike a balance between accuracy and computational efficiency.

Second, unlike planar grids, spherical grids cannot achieve complete uniformity. The ratio of the maximum to the minimum cell area of QTM grids on a sphere is approximately 1.86. In the proposed methodological framework, the base grid serves as an intermediate statistical structure, and its shape and size have minimal impact on workload calculations.

Despite these issues, spherical grids still offer significant advantages in airspace management. Their ability to avoid projection distortions enhances the accuracy of spatial representations. Moreover, spherical grid-based models can be flexibly adapted to diverse airspace planning requirements, providing a practical and theoretically sound solution for complex airspace management.

5. Conclusions

5.1. Innovations

Airspace sectorization is a critical issue in airspace management. It directly affects the efficient use of resources, the organization of flight traffic, and the safety of air navigation. To address the limitations of single-scale spatial analysis in airspace sectorization, this study introduces an innovative method based on multi-resolution grids and hierarchical reinforcement learning. The proposed approach enhances workload balancing in local sectorization while improving the computational efficiency of global airspace optimization. This research provides a solid theoretical and practical foundation for future studies and applications in complex airspace management. The main contributions of this research include the following:

(1)

The construction of a QTM-based airspace grid; leveraging the properties and coding of grids, the workload calculation model based on airspace grids has been optimized. Experimental results demonstrate that, compared to traditional methods, the grid-based workload calculation model for airspace management exhibits significant advantages in efficiency.

(2)

A multi-scale airspace sectorization framework is constructed based on multi-resolution grids and hierarchical reinforcement learning models. The framework decomposes the airspace sectorization task into two levels: global control area delineation and local sectorization. These tasks are handled by top-level and bottom-level reinforcement learning strategies, respectively. It considers both global airspace information and local details to improve local sectorization results. It also adopts multi-resolution grids to increase the interaction efficiency between the model and the environment. Furthermore, it incorporates prior knowledge to enhance training efficiency and optimization accuracy. Experimental results show that the framework demonstrates significant advantages in both efficiency and effectiveness.

5.2. Future Work

(1)

This study is based on a two-dimensional spherical space. While much current research focuses on three-dimensional airspace sector partitioning, two-dimensional sector partitioning remains a cutting-edge research problem with significant importance [22]. Future research will explore the potential of multi-scale volumetric grids in dynamic airspace partitioning and integrate them with reinforcement learning algorithms. For instance, three-dimensional grids could be applied in high-density urban flight areas, while planar grids could be used in other regions, thereby enhancing the intelligence level of three-dimensional airspace management.

(2)

Predicting airspace workload changes in advance is another critical focus in airspace management [67]. This study conducts airspace partitioning based on historical data, but in practical applications, adjusting sector partitions based on predicted workloads would be more forward-looking and practical. Therefore, future research will use workload data from airspace grids and apply spatiotemporal convolutional models (e.g., ConvLSTM) to forecast dynamic workload changes. These predictions will support real-time optimization of sector partitioning.