Adaptive Strategy for the Path Planning of Fixed-Wing UAV Swarms in Complex Mountain Terrain via Reinforcement Learning
Abstract
1. Introduction
- (1)
- A novel Reinforcement Learning-guided Hybrid Sparrow Search Algorithm (RLHSSA) is proposed. This algorithm uniquely combines a base metaheuristic (SSA) with a suite of specialized operators and an adaptive RL framework to address complex multi-UAV path planning challenges, offering a more robust and efficient solution than single-strategy or non-adaptive approaches.
- (2)
- Three distinct optimization operators—the Elite-SSA, the Adaptive Differential Perturbation strategy, and the Adaptive Levy Flight strategy—are designed and integrated into the framework. This integration provides a rich set of search behaviors, with Elite-SSA focusing on refined exploitation while the other two operators enhance search diversity and global exploration, thereby mitigating the common issue of premature convergence.
- (3)
- A novel reinforcement learning-based mechanism is developed for the dynamic scheduling of distinct optimization operators within a hybrid metaheuristic. Unlike fixed-strategy or simpler adaptive methods, this mechanism enables the algorithm to intelligently select the most appropriate search behavior for the current optimization phase, leading to a superior exploration–exploitation balance and adaptability.
- (4)
- Comprehensive simulation experiments and comparative studies were conducted to assess the effectiveness of the RLHSSA method against state-of-the-art methods in both threat-free and threatened environments. Our findings demonstrate RLHSSA’s superior effectiveness concerning convergence speed, solution quality, and robustness, particularly in challenging mountainous scenarios.
2. Problem Statement
Path Representation
3. Multi-UAV Cooperative Path Planning
3.1. Flight Distance Cost
3.2. Flight Altitude Cost
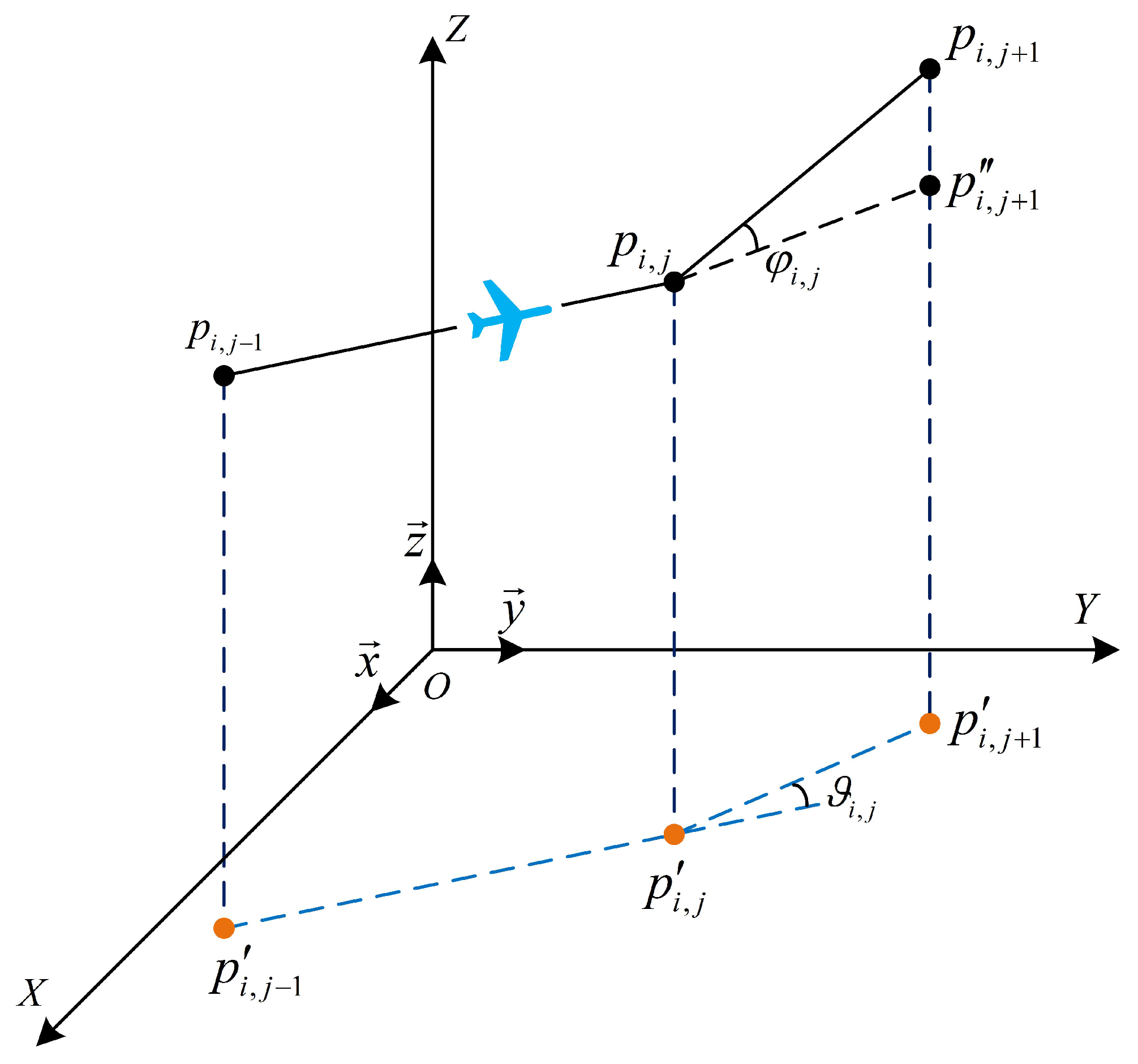
3.3. Path Stability Cost
- (1)
- Turning angle and Climbing angle
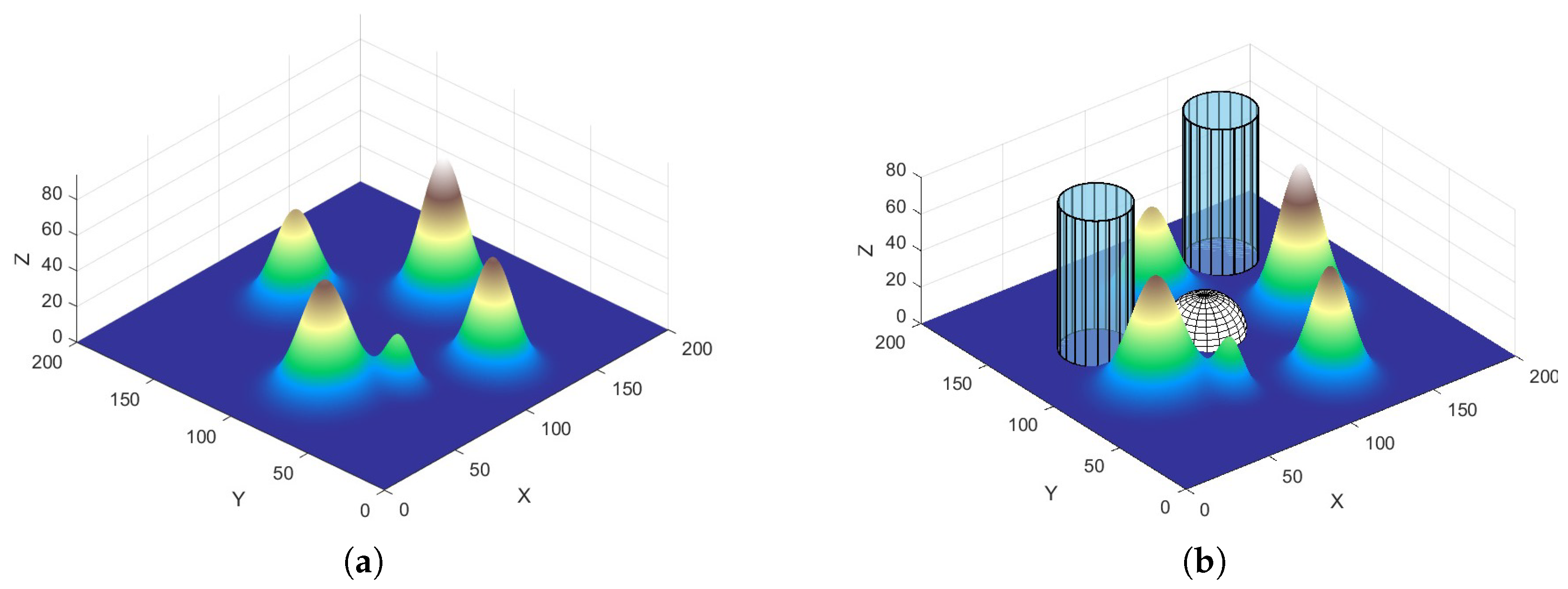
3.4. Path Threat Cost
- (1)
- Enemy threat sources
- (2)
- No-fly zones
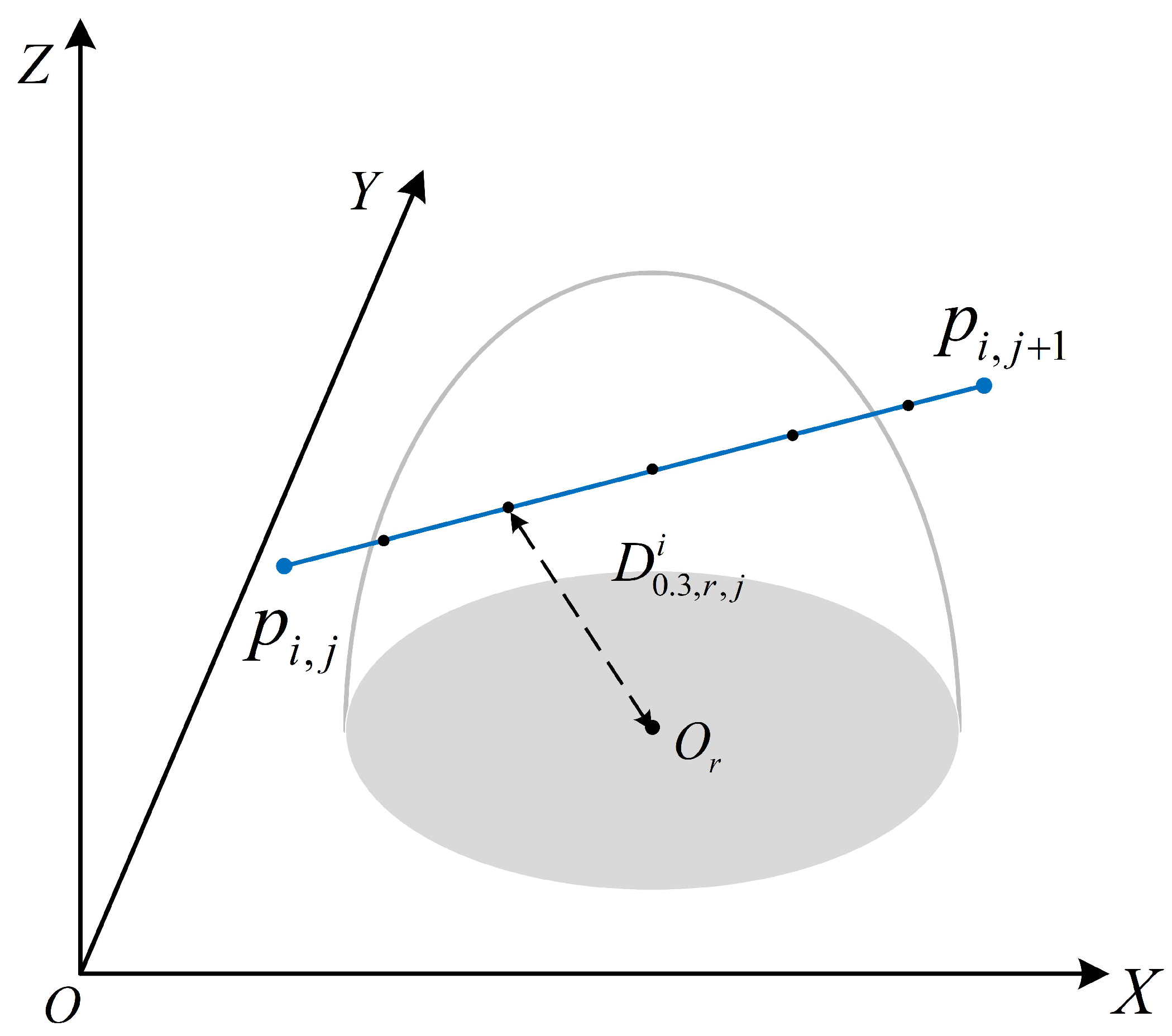
3.5. Terrain Collision Threat Cost
3.6. Multi-UAV Separation Maintenance Cost
3.7. Overall Cost Function
4. The Proposed RLHSSA Algorithm
4.1. Standard SSA
4.2. Proposed Hybrid Optimization Strategies
4.2.1. Elite-SSA
4.2.2. Adaptive Differential Perturbation Strategy
4.2.3. Adaptive Levy Flight Strategy
4.2.4. Reinforcement Learning-Based Strategy Scheduling
- Applying the Elite Sparrow Search Algorithm ().
- Applying the Adaptive Differential Perturbation Strategy ().
- Applying the Adaptive Levy Flight Strategy ().
4.3. Integration of the RLHSSA Algorithm
| Algorithm 1 Pseudocode of the RLHSSA Algorithm |
Initialize 1:
2: Randomly generate initial population positions 3: Set parameters: 4: Define action set 5: Initialize Q-table for all 6: Compute initial fitness for each individual i 7: Initialize personal bests and find the global best Optimize 8: whiledo 9: Determine current state 10: Choose action via -greedy policy on using Equation (40) 11: // Dynamically Scheduled Operator Execution 12: if then 14: else if then 15: Perform Adaptive Differential Perturbation using Equation (34) 16: else 18: end if 19: Evaluate fitness of the new population 20: Update personal bests () and the global best () 21: // Reinforcement Learning Update 22: Compute reward using Equation (41) 23: Observe next state 24: Adjust Q-value using Equation (39) 25: 26: end while 27: Return best solution |
4.4. Cooperative Multi-UAV Path Planning with RLHSSA
5. Simulation Example
5.1. Simulation Environment and Experimental Setup
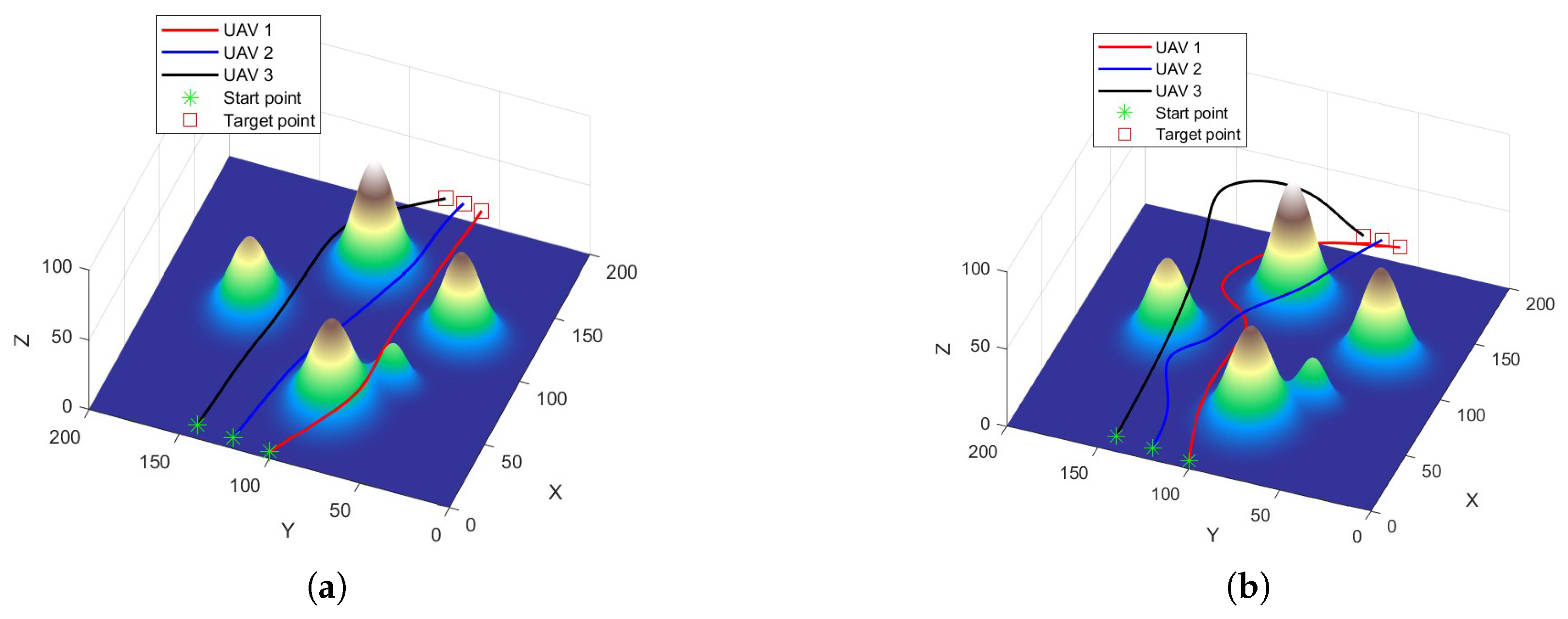
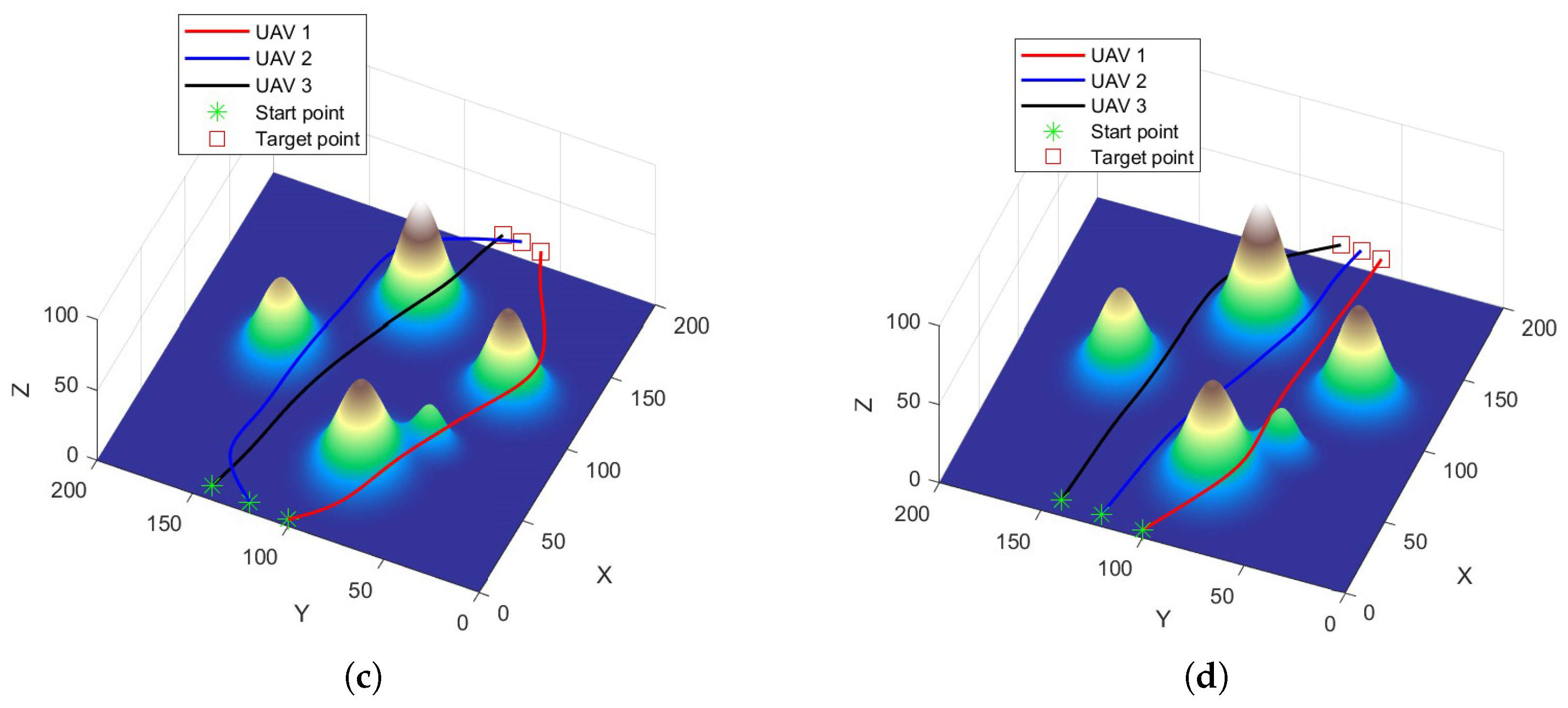
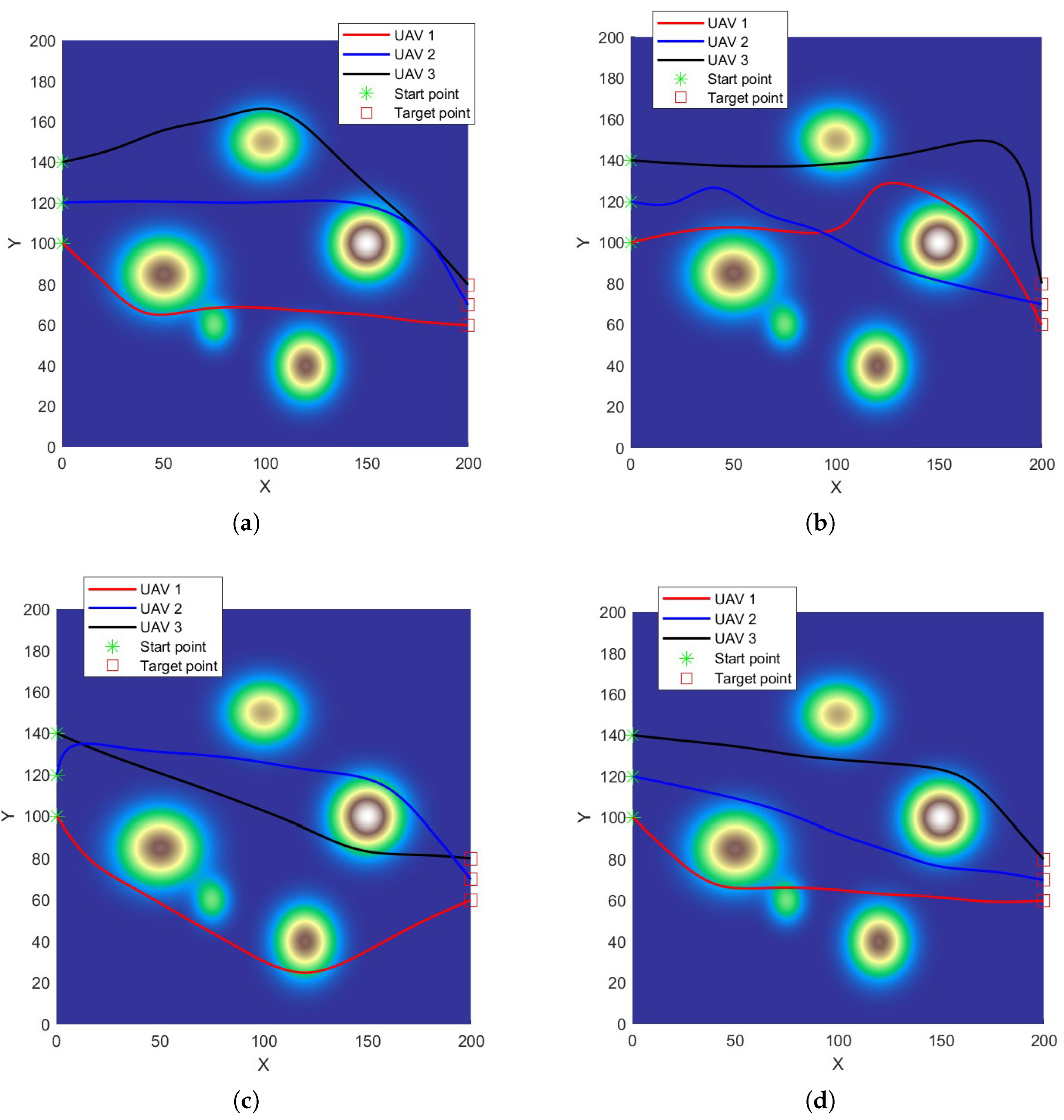
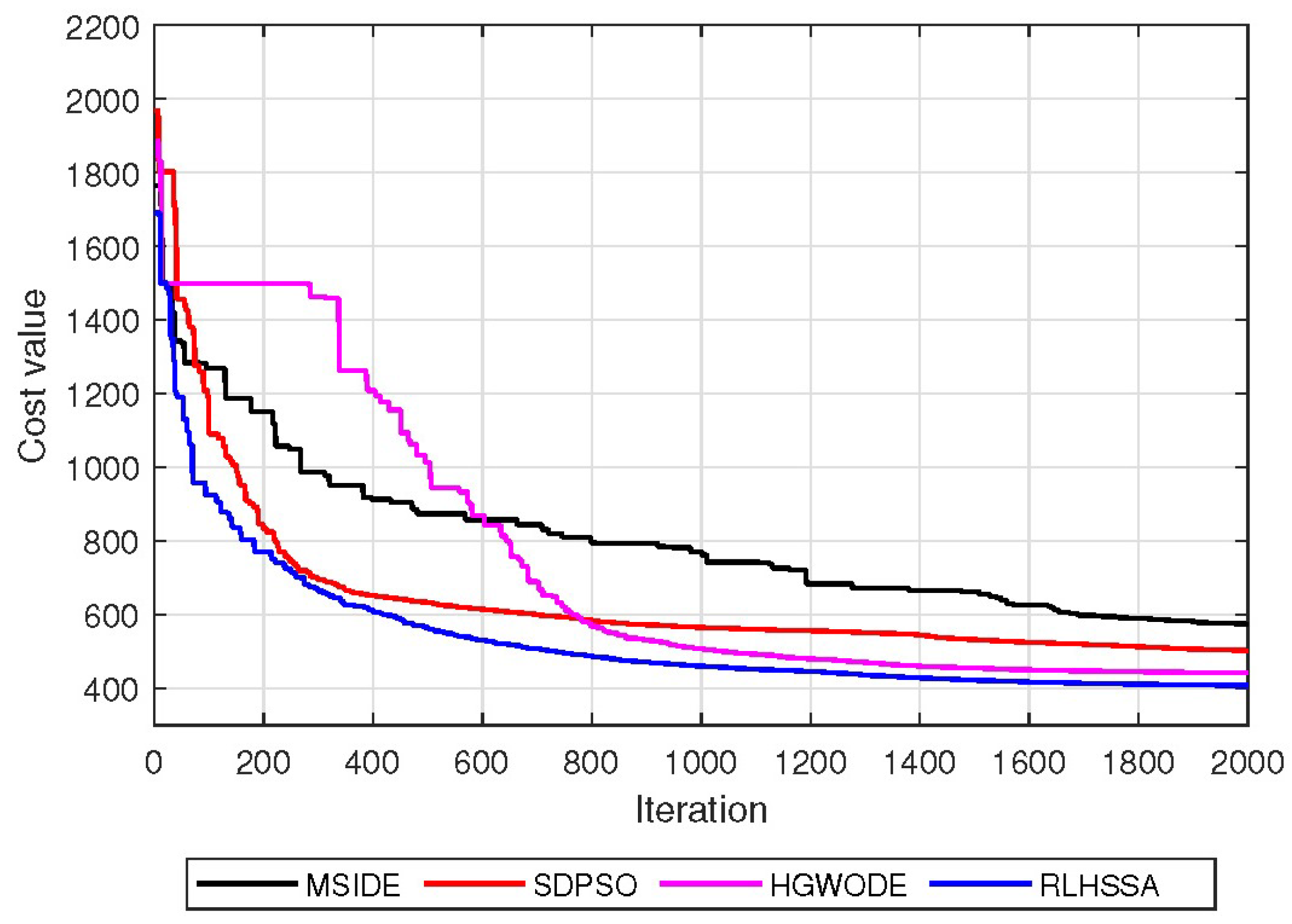
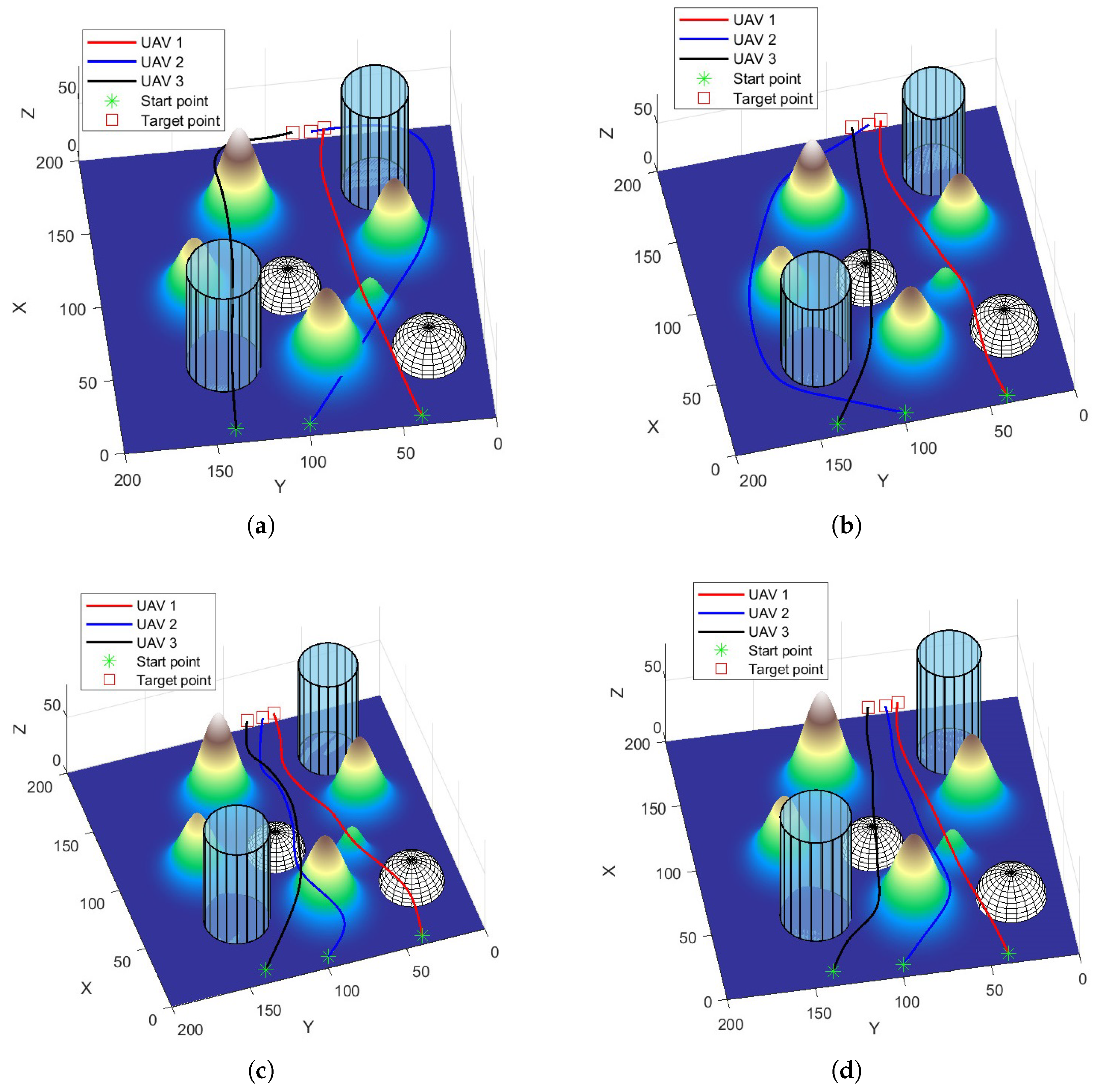
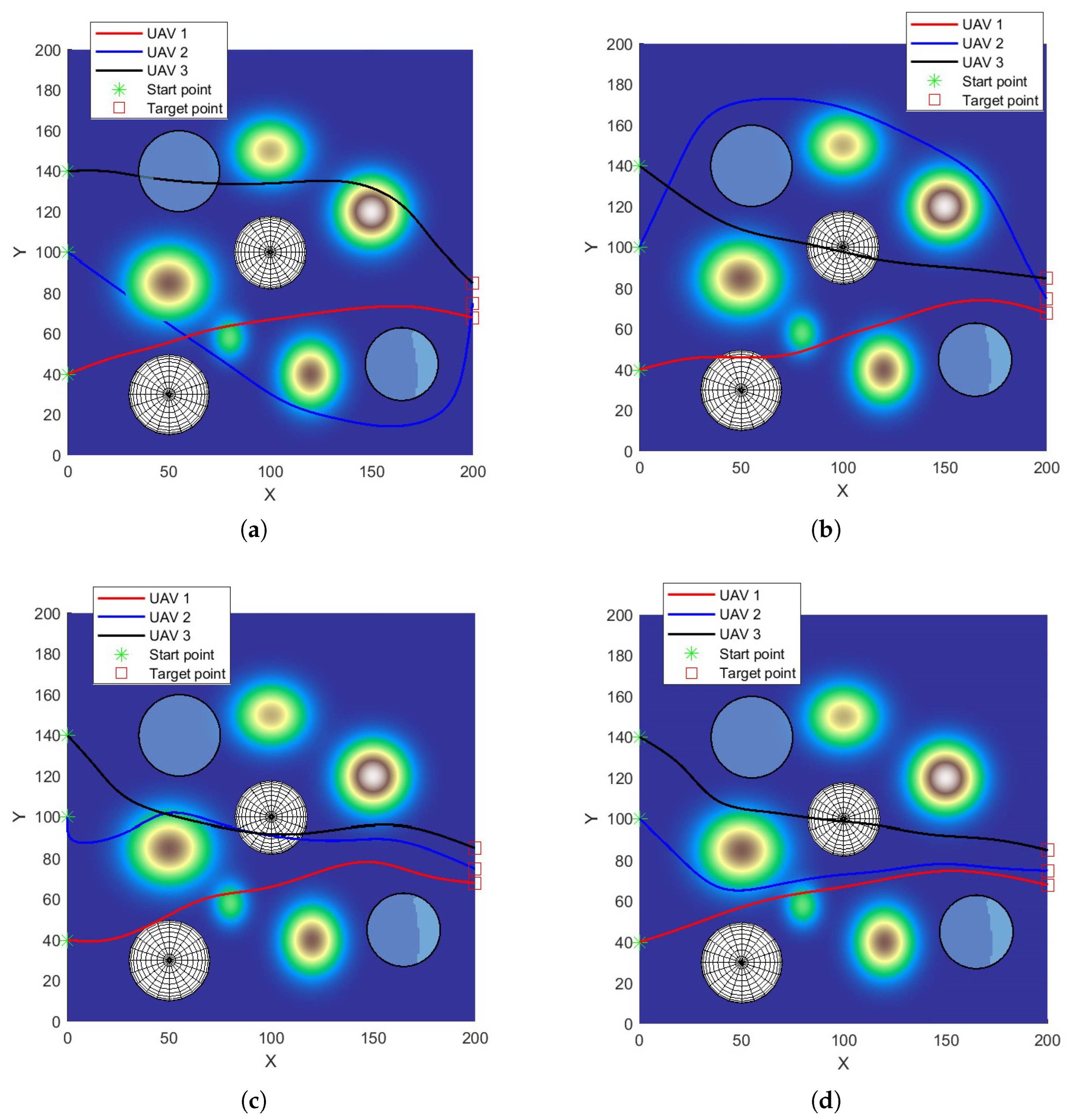
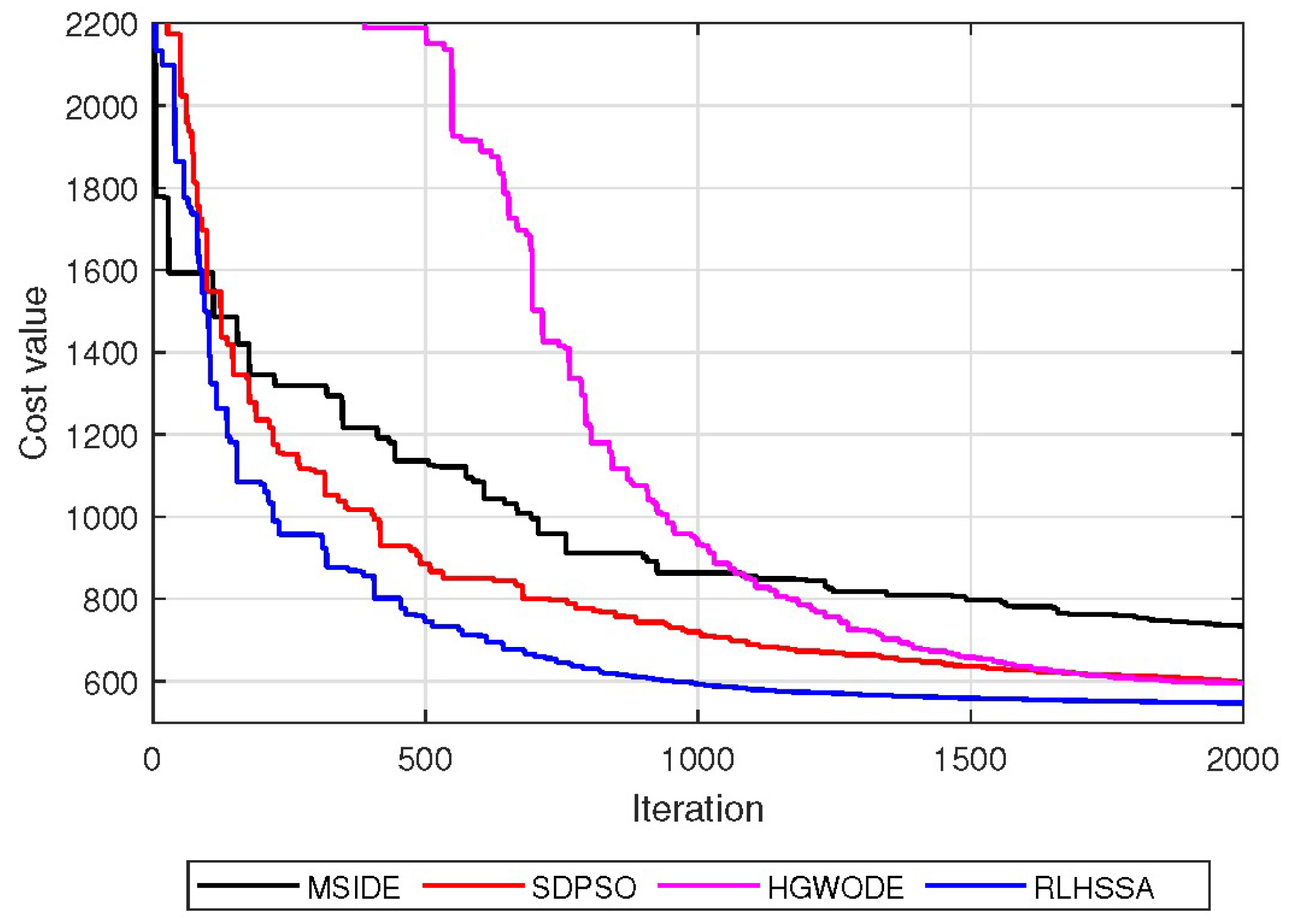
5.2. Simulation Results in Scenario 1
5.3. Simulation Results in Scenario 2
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Skorobogatov, G.; Barrado, C.; Salamí, E. Multiple UAV systems: A survey. Unmanned Syst. 2020, 8, 149–169. [Google Scholar] [CrossRef]
- Erdelj, M.; Natalizio, E.; Chowdhury, K.R.; Akyildiz, I.F. Help from the sky: Leveraging UAVs for disaster management. IEEE Pervas. Comput. 2017, 16, 24–32. [Google Scholar] [CrossRef]
- Wang, K.; Yang, P.; Lv, W.S.; Zhu, L.Y.; Yu, G.M. Current status and development trend of UAV remote sensing applications in the mining industry. Chin. J. Eng. 2020, 42, 1085–1095. [Google Scholar]
- Zhou, X.Y.; Jia, W.; He, R.F.; Sun, W. High-Precision localization tracking and motion state estimation of ground-based moving target utilizing unmanned aerial vehicle high-altitude reconnaissance. Remote Sens. 2025, 17, 735. [Google Scholar] [CrossRef]
- Hong, Y.; Kim, S.; Kwon, Y.; Choi, S.; Cha, J. Safe and Efficient Exploration Path Planning for Unmanned Aerial Vehicle in Forest Environments. Aerospace 2024, 11, 598. [Google Scholar] [CrossRef]
- Yu, X.; Luo, W. Reinforcement learning-based multi-strategy cuckoo search algorithm for 3D UAV path planning. Expert Syst. Appl. 2023, 223, 119910. [Google Scholar] [CrossRef]
- Qadir, Z.; Zafar, M.H.; Moosavi, S.K.R.; Le, K.N.; Mahmud, M.A.P. Autonomous UAV path-planning optimization using metaheuristic approach for predisaster assessment. IEEE Internet Things 2021, 9, 12505–12514. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Sallam, K.M.; Hezam, I.M.; Munasinghe, K.; Jamalipour, A. A multiobjective optimization algorithm for safety and optimality of 3-D route planning in UAV. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 3067–3080. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, R.; Zhao, H.; Li, J.; He, J. Path planning of multiple unmanned aerial vehicles covering multiple regions based on minimum consumption ratio. Aerospace 2023, 10, 93. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, L. A Review on Unmanned Aerial Vehicle Remote Sensing: Platforms, Sensors, Data Processing Methods, and Applications. Drones 2023, 7, 398. [Google Scholar] [CrossRef]
- He, W.J.; Qi, X.G.; Liu, L.F. A novel hybrid particle swarm optimization for multi-UAV cooperate path planning. Appl. Intell. 2021, 51, 7350–7364. [Google Scholar] [CrossRef]
- Xu, L.; Cao, X.B.; Du, W.B.; Li, Y.M. Cooperative path planning optimization for multiple UAVs with communication constraints. Knowl.-Based Syst. 2023, 260, 110164. [Google Scholar] [CrossRef]
- Pan, Z.; Zhang, C.; Xia, Y.; Xiong, H.; Shao, X. An improved artificial potential field method for path planning and formation control of the multi-UAV systems. IEEE T Circuits-II 2021, 69, 1129–1133. [Google Scholar] [CrossRef]
- Wang, W.T.; Li, X.L.; Tian, J. UAV formation path planning for mountainous forest terrain utilizing an artificial rabbit optimizer incorporating reinforcement learning and thermal conduction search strategies. Adv. Eng. Inform. 2024, 62, 102947. [Google Scholar] [CrossRef]
- Sun, B.; Niu, N. Multi-AUVs cooperative path planning in 3D underwater terrain and vortex environments based on improved multi-objective particle swarm optimization algorithm. Ocean Eng. 2024, 311, 118944. [Google Scholar] [CrossRef]
- Xu, C.; Xu, M.; Yin, C. Optimized multi-UAV cooperative path planning under the complex confrontation environment. Comput. Commun. 2020, 162, 196–203. [Google Scholar] [CrossRef]
- Li, Y.; Dong, X.; Ding, Q.; Xiong, Y.; Wang, T. Improved A-STAR algorithm for power line inspection UAV path planning. Energies 2024, 17, 5364. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Li, R.; Chen, H.; Chu, K. Trajectory planning for UAV navigation in dynamic environments with matrix alignment Dijkstra. Soft Comput. 2022, 26, 12599–12610. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, X.; Jiang, W.; Zhang, W. HDP-TSRRT*: A time-space cooperative path planning algorithm for multiple UAVs. Drones 2023, 7, 170. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, J.; Wang, J. Sequential convex programming for nonlinear optimal control problems in UAV path planning. Aerosp. Sci. Technol. 2018, 76, 280–290. [Google Scholar] [CrossRef]
- Wu, Y.; Liang, T.; Gou, J.; Tao, C.; Wang, H. Heterogeneous mission planning for multiple UAV formations via metaheuristic algorithms. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3924–3940. [Google Scholar] [CrossRef]
- Gupta, H.; Verma, O.P. A novel hybrid coyote-particle swarm optimization algorithm for three-dimensional constrained trajectory planning of unmanned aerial vehicle. Appl. Soft Comput. 2023, 147, 110776. [Google Scholar] [CrossRef]
- Ab Wahab, M.N.; Nazir, A.; Khalil, A.; Ho, W.J.; Akbar, M.F.; Noor, M.H.M.; Mohamed, A.S.A. Improved genetic algorithm for mobile robot path planning in static environments. Expert Syst. Appl. 2024, 249, 123762. [Google Scholar] [CrossRef]
- Li, X.; Yu, S. Three-dimensional path planning for AUVs in ocean currents environment based on an improved compression factor particle swarm optimization algorithm. Ocean Eng. 2023, 280, 114610. [Google Scholar] [CrossRef]
- Wang, Z.; Dai, D.; Zeng, Z.; He, D.; Chan, S. Multi-strategy enhanced Grey Wolf Optimizer for global optimization and real world problems. Cluster Comput. 2024, 27, 10671–10715. [Google Scholar] [CrossRef]
- Zhang, M.H.; Han, Y.H.; Chen, S.Y.; Liu, M.X.; He, Z.L.; Pan, N. A multi-strategy improved differential evolution algorithm for UAV 3D trajectory planning in complex mountainous environments. Eng. Appl. Artif. Intel. 2023, 125, 106672. [Google Scholar] [CrossRef]
- Meng, K.; Chen, C.; Wu, T.; Xin, B.; Liang, M.; Deng, F. Evolutionary state estimation-based multi-strategy jellyfish search algorithm for multi-UAV cooperative path planning. IEEE Trans. Intell. Veh. 2024, 10, 2490–2507. [Google Scholar] [CrossRef]
- Wang, F.; Wang, X.; Sun, S. A reinforcement learning level-based particle swarm optimization algorithm for large-scale optimization. Inform. Sci. 2022, 602, 298–312. [Google Scholar] [CrossRef]
- Zhang, S.; Li, Y.; Dong, Q. Autonomous navigation of UAV in multi-obstacle environments based on a deep reinforcement learning approach. Appl. Soft Comput. 2022, 115, 108194. [Google Scholar] [CrossRef]
- Skarka, W.; Ashfaq, R. Hybrid machine learning and reinforcement learning framework for adaptive UAV obstacle avoidance. Aerospace 2024, 11, 870. [Google Scholar] [CrossRef]
- Niu, Y.; Yan, X.; Wang, Y.; Niu, Y. Three-dimensional collaborative path planning for multiple UCAVs based on improved artificial ecosystem optimizer and reinforcement learning. Knowl.-Based Syst. 2023, 276, 110782. [Google Scholar] [CrossRef]
- Qu, C.; Gai, W.; Zhong, M.; Zhang, J. A novel reinforcement learning based grey wolf optimizer algorithm for unmanned aerial vehicles (UAVs) path planning. Appl. Soft Comput. 2020, 89, 106099. [Google Scholar] [CrossRef]
- Jiaqi, S.; Li, T.; Hongtao, Z.; Xiaofeng, L.; Tianying, X. Adaptive multi-UAV path planning method based on improved gray wolf algorithm. Comput. Electr. Eng. 2022, 104, 108377. [Google Scholar] [CrossRef]
- Xue, J.K.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Niu, Y.B.; Yan, X.; Wang, Y.; Niu, Y.Z. Three-dimensional UCAV path planning using a novel modified artificial ecosystem optimizer. Expert Syst. Appl. 2023, 217, 119499. [Google Scholar] [CrossRef]
- Lv, L.; Liu, H.J.; He, R.; Jia, W.; Sun, W. A Novel HGW Optimizer with Enhanced Differential Perturbation for Efficient 3D UAV Path Planning. Drones 2025, 9, 212. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Namazi, M.; Ebrahimi, L.; Abdollahzadeh, B. Advances in sparrow search algorithm: A comprehensive survey. Arch. Comput. Method. E. 2023, 30, 427–455. [Google Scholar] [CrossRef]
- He, Y.; Wang, M. An improved chaos sparrow search algorithm for UAV path planning. Sci. Rep. 2024, 14, 366. [Google Scholar] [CrossRef]
- Amirsadri, S.; Mousavirad, S.J.; Ebrahimpour-Komleh, H. A Levy flight-based grey wolf optimizer combined with back-propagation algorithm for neural network training. Neural Comput. Appl. 2018, 30, 3707–3720. [Google Scholar] [CrossRef]
- Gong, G.M.; Fu, S.W.; Huang, H.S.; Huang, H.F.; Luo, X. Multi-strategy improved snake optimizer based on adaptive lévy flight and dual-lens fusion. Cluster Comput. 2025, 28, 268. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, X.; Zhang, H.; Li, C.; Chen, Z. A reinforcement learning-based hybrid Aquila Optimizer and improved Arithmetic Optimization Algorithm for global optimization. Expert Syst. Appl. 2023, 224, 119898. [Google Scholar] [CrossRef]
- Yu, Z.H.; Si, Z.J.; Li, X.B.; Wang, D.; Song, H.B. A novel hybrid particle swarm optimization algorithm for path planning of UAVs. IEEE Internet Things 2022, 9, 22547–22558. [Google Scholar] [CrossRef]
- Yu, X.B.; Jiang, N.J.; Wang, X.M.; Li, M.Y. A hybrid algorithm based on grey wolf optimizer and differential evolution for UAV path planning. Expert Syst. Appl. 2023, 215, 119327. [Google Scholar] [CrossRef]
- Qu, C.; Gai, W.; Zhang, J.; Zhong, M. A novel hybrid grey wolf optimizer algorithm for unmanned aerial vehicle (UAV) path planning. Knowl.-Based Syst. 2020, 194, 105530. [Google Scholar] [CrossRef]
| State | Action | ||
|---|---|---|---|
| : Elite-SSA | : Diff. Perturbation | : Levy Flight | |
| ⋮ | ⋮ | ⋮ | ⋮ |
| UAV No. | Start Point | Target Point | |
|---|---|---|---|
| Scenario 1 | 1 | (0, 100, 5) | (200, 60, 10) |
| 2 | (0, 120, 8) | (200, 70, 12) | |
| 3 | (0, 140, 10) | (200, 80, 12) | |
| Scenario 2 | 1 | (0, 40, 8) | (200, 68, 8) |
| 2 | (0, 100, 10) | (200, 75, 6) | |
| 3 | (0, 140, 12) | (200, 85, 7) |
| Threat/NFZ | Threat/NFZ Center | Radius | Height | Threat Level |
|---|---|---|---|---|
| Threat | (50, 30, 0) | 20 | – | 10 |
| Threat | (100, 100, 0) | 18 | – | 10 |
| NFZ | (55, 140) | 20 | 80 | – |
| NFZ | (165, 45) | 18 | 80 | – |
| Algorithm | Parameter |
|---|---|
| MSIDE | , , = 0.8 |
| SDPSO | , |
| HGWODE | , |
| RLHSSA | , , = 1.5, |
| Parameter | Description | Value |
|---|---|---|
| Maximum iteration count | 2000 | |
| Population count | 50 | |
| M | waypoint count | 7 |
| UAV operational altitude range | [1, 100] | |
| Max turning angle | ||
| Max climbing angle | ||
| safe-altitude threshold | 15 | |
| Inter-UAV safe distance | 20 |
| NO. | Indicators | MSIDE | SDPSO | HGWODE | RLHSSA |
|---|---|---|---|---|---|
| 1 | Best | 430.0323 | 410.2035 | 405.4126 | 396.3353 |
| 2 | Worst | 586.0367 | 485.3387 | 472.5805 | 416.0802 |
| 3 | Mean | 468.7183 | 434.4157 | 426.9850 | 405.0570 |
| 4 | Std | 43.1114 | 16.7519 | 12.4036 | 4.0826 |
| 5 | SR (%) | 70.0 | 83.33 | 90.0 | 100.0 |
| 6 | 12.48 | 11.87 | 13.32 | 12.81 |
| NO. | Indicators | MSIDE | SDPSO | HGWODE | RLHSSA |
|---|---|---|---|---|---|
| 1 | Best | 625.3503 | 583.6828 | 585.7339 | 570.1830 |
| 2 | Worst | 920.1053 | 832.2043 | 803.0355 | 609.9120 |
| 3 | Mean | 737.2827 | 648.8387 | 625.1940 | 581.4147 |
| 4 | Std | 87.8027 | 62.7768 | 48.3840 | 8.4732 |
| 5 | SR (%) | 60.0 | 76.67 | 86.67 | 100.0 |
| 6 | 15.38 | 13.83 | 15.74 | 14.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, L.; Jia, W.; He, R.; Sun, W. Adaptive Strategy for the Path Planning of Fixed-Wing UAV Swarms in Complex Mountain Terrain via Reinforcement Learning. Aerospace 2025, 12, 1025. https://doi.org/10.3390/aerospace12111025
Lv L, Jia W, He R, Sun W. Adaptive Strategy for the Path Planning of Fixed-Wing UAV Swarms in Complex Mountain Terrain via Reinforcement Learning. Aerospace. 2025; 12(11):1025. https://doi.org/10.3390/aerospace12111025
Chicago/Turabian StyleLv, Lei, Wei Jia, Ruofei He, and Wei Sun. 2025. "Adaptive Strategy for the Path Planning of Fixed-Wing UAV Swarms in Complex Mountain Terrain via Reinforcement Learning" Aerospace 12, no. 11: 1025. https://doi.org/10.3390/aerospace12111025
APA StyleLv, L., Jia, W., He, R., & Sun, W. (2025). Adaptive Strategy for the Path Planning of Fixed-Wing UAV Swarms in Complex Mountain Terrain via Reinforcement Learning. Aerospace, 12(11), 1025. https://doi.org/10.3390/aerospace12111025






