Real-Time Detection of LEO Satellite Orbit Maneuvers Based on Geometric Distance Difference

Abstract

Low Earth orbit (LEO) satellites, characterized by low altitudes, high velocities, and strong ground signal reception, have become an essential and dynamic component of modern global navigation satellite systems (GNSS). However, orbit decay induced by atmospheric drag poses persistent challenges to maintaining stable trajectories. Frequent orbit maneuvers, though necessary to sustain nominal orbits, introduce significant difficulties for precise orbit determination (POD) and navigation augmentation, especially under complex operational conditions. Unlike most existing methods that rely on Two-Line Element (TLE) data—often affected by noise and limited accuracy—this study directly utilizes onboard GNSS observations in combination with real-time precise ephemerides. A novel time-series indicator is proposed, defined as the geometric root-mean-square (RMS) distance between reduced-dynamic and kinematic orbit solutions, which is highly responsive to orbit disturbances. To further enhance robustness, a sliding window-based adaptive thresholding mechanism is developed to dynamically adjust detection thresholds, maintaining sensitivity to maneuvers while suppressing false alarms. The proposed method was validated using eight representative maneuver events from the GRACE-FO satellites (May 2018–June 2022), successfully detecting seven of them. One extremely short-duration maneuver was missed due to the limited number of usable GNSS observations after quality-control filtering. To examine altitude-related applicability, two Sentinel-3A maneuvers were also analyzed, both successfully detected, confirming the method’s effectiveness at higher LEO altitudes. Since the thrust magnitudes and durations of the Sentinel-3A maneuvers are not publicly available, these cases primarily serve to verify applicability rather than to quantify sensitivity. Experimental results show that for GRACE-FO maneuvers, the proposed method achieves near-real-time responsiveness under long-duration, high-thrust conditions, with an average detection delay below 90 s. For Sentinel-3A, detections occurred approximately 7 s earlier than the reported maneuver epochs, a discrepancy attributed to the 30 s observation sampling interval rather than methodological bias. Comparative analysis with representative existing methods, presented in the discussion section, further demonstrates the advantages of the proposed approach in terms of sensitivity, timeliness, and adaptability. Overall, this study presents a practical, efficient, and scalable solution for real-time maneuver detection in LEO satellite missions, contributing to improved GNSS augmentation, space situational awareness, and autonomous orbit control.

1. Introduction

Low Earth Orbit (LEO) satellites, characterized by high signal strength, short signal propagation paths, and dynamic geometric configurations, offer significant potential for enhancing global navigation satellite systems (GNSS) and related navigation services [1,2,3,4,5,6,7]. However, their frequent orbit maneuvers complicate precise orbit determination (POD) and pose challenges to maintaining continuous real-time services.

In recent years, LEO satellites technology has advanced rapidly in communications, navigation, and Earth observation, with LEO-based communication systems becoming the primary driver of large-scale constellation deployment. Governments and commercial entities worldwide are actively developing extensive LEO constellations, leading to an unprecedented surge in the number of operational satellites. By mid-2025, more than 11,700 active satellites were in orbit, with broadband communication constellations in LEO comprising the vast majority. For example, the SpaceX Starlink constellation has deployed approximately 7875 satellites, accounting for nearly 70% of all active satellites. OneWeb operates about 630–650, while Amazon’s Project Kuiper has launched its first 27 satellites and plans to expand to 3232 in the coming years. In China, the G60/Qianfan and GW constellations have each launched over one hundred satellites, with deployment targets reaching tens of thousands by 2035 [8,9].

Table 1. Partial Information on Selected LEO Satellite Constellations.

Constellation Name	Operator/Country	Satellites in Orbit *	Orbit Altitude (km)	Primary Applications	Data Source
Starlink	SpaceX, TX, USA	7875	~550	Broadband communications; navigation augmentation	Jonathan McDowell
OneWeb Eutelsat	Eutelsat OneWeb, London (UK)/Paris (France)	630–650	~1200	Broadband communications; navigation augmentation	OneWeb official website
Kuiper	Amazon, Washington, DC, USA	27 (planned: 3232)	~550	Broadband communications; navigation augmentation	Project Kuiper official website
G60/Qianfan	Shanghai Academy of Spaceflight Technology, Shanghai, China	90 (target: ~1296)	160–2000	Broadband communications; navigation augmentation	Official Chinese space releases; IISS reports
GW	China Satellite Network Group Co., Ltd., Xiong’an, China	>100 (target: several thousand)	500–2000	Broadband communications; navigation augmentation	IISS 2025 report; official sources
Iridium NEXT	Iridium Communications, VA, USA	66 (including spares)	~780	Mobile communications	UCS Database 2025
Orbcomm	Orbcomm, VA, USA	~62	~750–800	Internet of Things (IoT) communications	UCS Database 2025

* Latest publicly available estimates as of 2025. In this table, “navigation augmentation” refers to the potential capability of using communication constellation signals for Positioning, Navigation, and Timing (PNT). Previous studies have shown that the communication signals of Starlink and OneWeb can provide meter-level or higher positioning accuracy as signals of opportunity [10,11,12,13].

summarizes the deployment status of the major LEO communication constellations, including their operators, the number of satellites in orbit, and key orbit parameters. As shown, the rapid expansion of mega-LEO constellations such as Starlink, OneWeb, and Kuiper highlights the accelerating growth of satellites in orbit. While this unprecedented density provides new opportunities for GNSS augmentation and integrated navigation, it also results in more frequent station-keeping and collision-avoidance maneuvers, further increasing the complexity of constellation maintenance and the challenge of timely and reliable maneuver detection.

Due to atmospheric drag and other perturbations [14,15], LEO satellites frequently deviate from their nominal trajectories and require regular orbit maneuvers for safe operations and constellation maintenance. However, maneuver schedules are rarely disclosed, and unexpected thrusts degrade POD accuracy by breaking the consistency of dynamic models [15,16]. For navigation-augmented LEO satellites, such degradation directly threatens service quality and continuity, making real-time maneuver detection a critical technical capability [16].

Extensive research has been conducted worldwide on orbit maneuver detection for LEO satellites. Early studies primarily relied on Two-Line Element (TLE) data analysis, where maneuvers were identified through parameter trends and threshold-based techniques [17,18,19]. Subsequent works enhanced detection capability by applying TLE consistency checks, propagation differences, or simplified perturbation models, which improved performance for high-thrust or routine station-keeping maneuvers but remained sensitive to TLE errors [20,21,22,23,24,25]. More advanced methods have introduced particle filtering [26] and machine learning algorithms such as convolutional LSTM networks, autoencoders, and neural networks [27,28,29,30,31,32,33,34,35], which improved adaptability across datasets but still showed limitations in robustness and real-time performance. In addition, multi-sensor data fusion approaches have been investigated for integration into space cataloging systems [36,37]. For onboard GNSS-based detection, statistical approaches such as the shifting window median absolute deviation have achieved detection accuracy better than 20 s without prior information [38], demonstrating both the real-time feasibility and higher precision of GNSS-based monitoring.

Despite these advances, most existing maneuver detection approaches still rely on TLE data or its derived parameters. However, TLEs suffer from high noise, low accuracy, and the smoothing of orbit perturbations, which prevent them from reliably capturing small-thrust or short-duration maneuvers, especially in large-scale LEO constellations. In comparison, onboard GNSS-based approaches have shown potential for improved accuracy and timeliness than TLE-based methods, but studies applying GNSS observations for maneuver detection in LEO satellites remain limited. Motivated by this gap, this study develops a GNSS-based maneuver detection framework that integrates real-time precise ephemerides with dual-orbit solutions. By constructing a detection indicator from geometric deviations between reduced-dynamic and kinematic POD solutions and applying a sliding window dynamic threshold, the proposed method achieves sensitive and reliable detection of maneuver events.

The key contributions of this study are as follows:

• Extension within GNSS-based detection. A method is proposed that integrates onboard GNSS observations with real-time precise ephemerides, complementing existing SWMAD-based carrier-phase residual approaches [38] by introducing an alternative indicator based on geometric deviations between dual-orbit solutions.
• Novel detection indicator design–A root-mean-square (RMS) metric based on geometric position deviations between reduced-dynamic and kinematic POD solutions is proposed, enabling direct characterization of orbit dynamic changes.

The remainder of this paper is organized as follows: Section 2 describes the LEO POD methods, including kinematic POD and reduced-dynamic POD, and the principle of maneuver detection based on dual-orbit solution differences. Section 3 presents the data sources and processing strategies. Section 4 reports experimental results and evaluates detection performance for different maneuver types. Section 5 concludes the paper and discusses future research directions.

2. Methodology

2.1. LEO Satellite Orbit Determination Methods

LEO satellites usually achieve POD by carrying onboard GNSS receivers, using pseudorange $P_{L,i}^s$ and carrier-phase ${\mathrm{\Phi }}_{L,i}^s$ observations to obtain high-accuracy orbit information. However, the accuracy of GNSS-based POD can still be degraded by observation noise, data outages, or unmodeled orbit maneuvers, which highlights the importance of reliable maneuver detection for maintaining service quality. The observation model is expressed as:

$$P_{L,i}^s={\rho }_L^s+c\left(\delta t_L-\delta t_s\right)+c\left(d_{L,i}-d_i^s\right)+I_{L,i}^s+{\mathrm{\epsilon }}_P,$$

(1)

$${\mathrm{\Phi }}_{L,i}^s={\rho }_L^s+c\left(\delta t_L-\delta t_s\right)+c\left(b_{L,i}-b_i^s\right)-I_{L,i}^s+{\lambda }_i{N}_{L,i}^s+{\mathrm{\epsilon }}_{\mathrm{\Phi }},$$

(2)

where the superscript $s$ denotes the GNSS satellite PRN, the subscripts $L$ and $i$ represent the LEO satellite identifier and frequency index, respectively; ${\rho }_L^s$ is the geometric distance; $\delta t_L$ and $\delta t_s$ are the receiver clock offset of the LEO satellite and the GNSS satellite clock offset, respectively; $d$ and $b$ are the code bias and phase bias, respectively; $I_{L,i}^s$ is the ionospheric delay; ${\lambda }_i{N}_{L,i}^s$ is the integer ambiguity; and ${\mathrm{\epsilon }}_P$ and ${\mathrm{\epsilon }}_{\mathrm{\Phi }}$ are the code and phase observation noise terms, respectively.

Using continuous observations from at least four visible GNSS satellites, along with precise GNSS orbit and clock products, the three-dimensional position and clock offset of a LEO satellite at each epoch can be precisely determined. Since LEO satellites are subject to multiple forces during motion, their acceleration can be decomposed as:

$$a=a_g+a_{ng}+a_m+a_{emp},$$

(3)

where $a_g$ is the acceleration due to the Earth central gravity, Earth gravity field irregularities, N-body perturbations, and tidal effects; $a_{ng}$ is the non-conservative acceleration caused by atmosphere drag, solar radiation pressure, Earth albedo radiation pressure, and thermal radiation; $a_m$ is the thrust acceleration generated during orbit maneuvers; and $a_{emp}$ is the empirical acceleration used to compensate for unmodeled or uncertain perturbations.

During an orbit maneuver, a velocity impulse or continuous thrust generated by the thruster alters the satellite’s velocity magnitude and direction within a very short period, producing a distinct discontinuity in the state vector that describes its position and velocity [11]. If the applied thrust is not accurately modeled in the orbit computation, the acceleration equation lacks the corresponding maneuver term, causing the dynamically propagated orbit to deviate from the satellite’s true trajectory within a short time frame [12]. Moreover, orbit maneuvers are often accompanied by attitude adjustments, antenna re-pointing, and occasional GNSS signal blockages, which may introduce gross errors or data outages in certain epochs [38]. Collectively, these effects disrupt the consistency between dynamically modeled orbit solutions and observation-based solutions, thereby reducing the stability and reliability of precise orbit determination (POD).

In LEO POD, three principal strategies are commonly adopted: purely dynamic POD, kinematic POD, and reduced-dynamic POD. These approaches differ in their dependence on force models and their sensitivity to modeling errors, which directly influence their performance during orbit maneuvers. Purely dynamic POD integrates the satellite trajectory using high-fidelity force models, yielding smooth and continuous orbits but making the results highly sensitive to unmodeled thrust. Consequently, it cannot serve as a reliable basis for maneuver detection. In contrast, kinematic POD determines satellite positions epoch by epoch solely from GNSS observations. This approach rapidly reflects real orbit changes—including maneuvers—but is more susceptible to observation noise and may generate false alarms if applied independently. Reduced-dynamic POD offers a compromise between model fidelity and adaptability by introducing empirical acceleration parameters to compensate for mismodeled forces, thus maintaining orbit continuity under nominal conditions. However, during maneuvers, its solution still deviates because unmodeled thrusts can only be partially absorbed. These complementary characteristics constitute the foundation of the proposed method: by quantifying the geometric discrepancies between kinematic and reduced-dynamic solutions and applying a sliding window adaptive thresholding strategy, orbit maneuvers can be detected with high sensitivity while effectively suppressing false alarms.

2.2. Maneuver Detection Method

To effectively identify orbit maneuver events during the operation of LEO satellites, this study proposes a detection method based on real-time GNSS ephemerides and dual-orbit solution differences. The method constructs a time-series indicator—the geometric distance difference RMS—by quantifying the position differences between reduced-dynamic and kinematic orbit solutions. The reduced-dynamic orbit, derived from the historical POD state and physical force models, exhibits a delayed response to sudden maneuvers. In contrast, the kinematic orbit depends solely on GNSS observations and responds promptly to actual trajectory changes. When a maneuver occurs, the two orbit solutions diverge significantly in geometric position, providing a reliable basis for detecting orbit disturbances. Using real-time GNSS ephemerides as the reference frame, the geometric distance differences between each orbit solution and all visible GNSS satellites are computed at each epoch. The RMS of these differences forms a continuous Difference RMS time series. On this basis, a dynamic and robust threshold is constructed using a sliding window median and median absolute deviation (MAD), enabling effective identification of orbit anomalies while suppressing false detections. Unlike fixed-threshold methods—which lack adaptability to varying noise levels and orbit conditions and are thus prone to false alarms or missed detections—the sliding window approach dynamically adjusts to local statistics. This enhances robustness against outliers while preserving sensitivity to sudden maneuvers. The subsequent sections present in detail the construction of the Difference RMS, the design of the dynamic threshold, and the overall detection workflow.

2.2.1. Geometric Distance Difference Calculation

At each epoch $i$, the LEO satellite position vector ${\overrightarrow{r}}_{dyn,i}^L$ is obtained from the reduced-dynamic method, and the position vector ${\overrightarrow{r}}_{kin,i}^L$ is obtained from the kinematic method. The geometric distance differences between each of these position vectors and the position vector ${\overrightarrow{r}}_i^j$ of the $j$-th visible GNSS satellite are then computed as follows:

$$D_i^j=‖{\overrightarrow{r}}_{dyn,i}^L-{\overrightarrow{r}}_i^j‖-‖{\overrightarrow{r}}_{kin,i}^L-{\overrightarrow{r}}_i^j‖,$$

(4)

where $D_i^j$ represents the geometric distance difference for the $j$-th GNSS satellite at epoch $i$. This difference reflects the discrepancy in spatial position error between the two orbit solutions under the reference ephemeris. When a LEO satellite performs an orbit maneuver, the reduced-dynamic orbit prediction deviates from the actual trajectory due to the unmodeled thrust, causing $D_i^j$ to increase significantly. In the absence of a maneuver, this difference typically remains within a small, stable fluctuation range.

For each epoch $i$, the RMS of the differences for all $M$ visible GNSS satellites is computed to form the RMS time series:

$$p\left(i\right)=\sqrt{{\displaystyle \frac{1}{M}}{\sum }_{j=1}^M{\left(D_i^j\right)}^2},$$

(5)

where $M$ is the number of visible GNSS satellites at each epoch. Before the $p\left(i\right)$ series enters the sliding window statistical detection process, the interquartile range (IQR) method is applied to remove gross errors, thereby mitigating the influence of outliers on subsequent dynamic threshold determination.

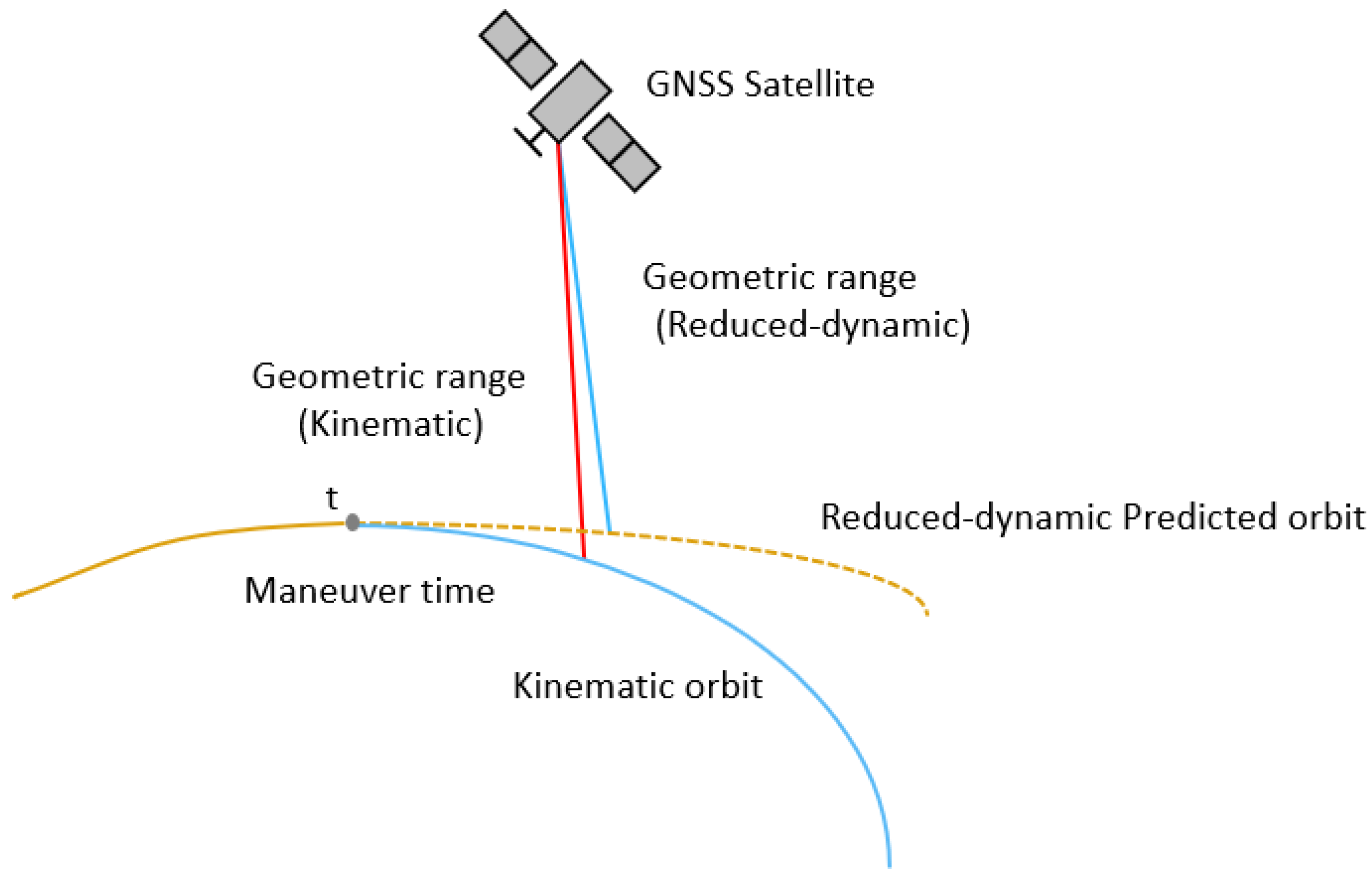
The computation principle is illustrated in Figure 1. After the maneuver start time t, the reduced-dynamic orbit (yellow dashed line) gradually deviates from the kinematic orbit (blue solid line) because the thrust is not modeled in the dynamic equations. This results in differences in the geometric distances from the two orbits to the same GNSS satellite, corresponding to $‖{\overrightarrow{r}}_{dyn,i}^L-{\overrightarrow{r}}_i^j‖$ and $‖{\overrightarrow{r}}_{kin,i}^L-{\overrightarrow{r}}_i^j‖$ in Equation (4). The difference between these distances is $D_i^j$. Taking the RMS of $D_i^j$ across all visible GNSS satellites yields $p\left(i\right)$ in Equation (5). This schematic clearly illustrates the physical meaning of constructing the Difference RMS indicator using geometric distance differences between two orbit solutions and the GNSS satellites.

The orange solid line represents the theoretical trajectories obtained by the two orbit determination methods before the maneuver. The orange dashed line represents the predicted trajectory from the simplified dynamical orbit determination method, and the blue solid line represents the trajectory from the kinematic method (the actual kinematic trajectory is discrete, but is shown here as a continuous curve for clarity). The gray dot indicates the maneuver epoch.

2.2.2. Sliding Window Dynamic Threshold

To enhance the robustness of the maneuver detection algorithm and improve its resistance to outliers, this study introduces a time-varying dynamic threshold based on the sliding window median and the MAD. This adaptive approach adjusts the detection threshold according to local data variations, thereby increasing sensitivity to abrupt changes in the orbit state. It is particularly suitable for onboard GNSS observation data from LEO satellites, which are collected in highly dynamic environments characterized by complex sources and fluctuating data quality. Compared with a fixed-threshold strategy, the proposed method demonstrates stronger robustness, effectively reduces false alarm rates, and has been validated in related studies on GNSS satellite maneuver detection and clock bias anomaly detection, showing good applicability and reliability [38,39,40,41].

To further quantify the implementation of this robust detection strategy, a sliding window statistical model is constructed based on the Difference RMS series. For each sliding window of length n epochs, let the starting index be $i$, and denote the median value within this window as:

$$m\left(i\right)=Median\left\{p\left(k\right)|k=i, i+1, \cdots , i+n-1\right\},$$

(6)

Using this median as the baseline, the scale estimator is defined as:

$$\sigma \left(i\right)={\displaystyle \frac{Median\left(\left|{RMS}_k-m\left(i\right)\right|\right)}{0.6745}},$$

(7)

Here, the sliding window length n is set to the number of epochs corresponding to one orbit period. Considering that the geometric distance difference may couple with disturbances related to the orbit period, an appropriately chosen window length helps capture trend-like features caused by orbit changes while avoiding excessive computational burden. In this study, for a LEO satellite with an orbit period of approximately 90 min and a sampling interval of 30 s, n is set to 180.

Next, the RMS value at epoch $i+n$ is examined. If it satisfies the following equation, the epoch is marked as an outlier.

$$\left|p\left(i+n\right)-m\left(i\right)\right|>\gamma ·\sigma \left(i\right),$$

(8)

where $\gamma$ is an empirical coefficient typically set between 3 and 5 [41], and a value of 4 is used in this study.

To further suppress misdetections caused by random fluctuations or single-point anomalies, a two-point confirmation mechanism is applied as in Equation (9). That is, a maneuver start time is identified only when two consecutive epochs satisfy the anomaly condition:

$$\left\{\begin{array}{c}\left|p\left(i+n\right)-m\left(i\right)\right|>\gamma ·\sigma \left(i\right)\\ \left|p\left(i+n+1\right)-m\left(i+1\right)\right|>\gamma ·\sigma \left(i+1\right)\end{array}\right.$$

(9)

This strategy significantly suppresses false alarms triggered by random noise or isolated anomalies and improves detection stability. In addition, since a large sliding window length n requires sufficient data, when the input data volume is too small to form a complete window, an empirical threshold strategy is used as a supplement: a static Difference RMS threshold is directly set to detect sudden RMS increases in short data spans, thereby improving detection coverage and practicality. Preliminary experiments using the two satellites of the Gravity Recovery and Climate Experiment–Follow On (GRACE-FO) mission show that, during non-maneuver periods, the Difference RMS value is generally within 0.15 m, whereas after maneuvers, the Difference RMS exceeds 0.15 m. Therefore, the static threshold is set to an empirical value of 0.15 m.

2.2.3. Overall Detection Workflow

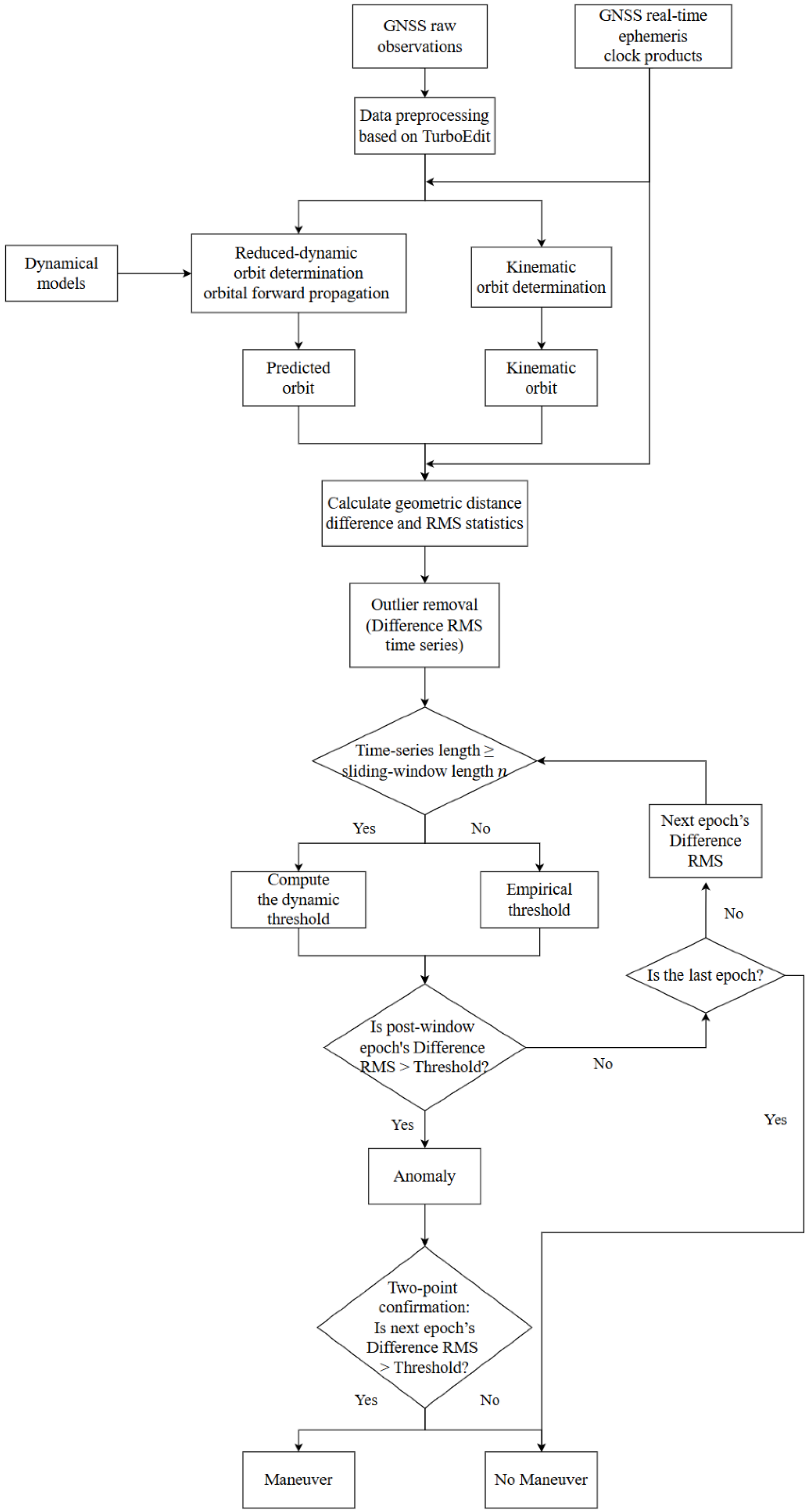
The proposed orbit maneuver detection procedure, which is carried out on the ground based on onboard GNSS observations and real-time precise orbit and clock products, is illustrated in Figure 2. The overall workflow consists of data preprocessing, dual-orbit determination, geometric difference computation, dynamic thresholding, and maneuver confirmation.

First, the onboard GNSS raw observation data of the target LEO satellite, together with real-time precise GNSS orbit and clock products, are obtained. The observation data are then preprocessed, including TurboEdit-based detection of cycle slips, discontinuities, and short continuous-arc segments, as well as gross error removal, to ensure the stability of the orbit solutions. These preprocessing procedures, together with the subsequent IQR-based outlier elimination, serve as observation-domain quality control measures that perform error correction and smoothing, thereby enhancing the reliability of orbit determination under temporarily degraded tracking conditions. Next, parallel orbit-determination chains are established for the reduced-dynamic and kinematic models. On one side, the reduced-dynamic trajectory is generated by propagating the previous orbit arc state using the force models, producing a predicted orbit constrained by the dynamic model. On the other side, the kinematic method independently estimates the three-dimensional position at each epoch, producing a trajectory without dynamic constraints. Using the real-time GNSS ephemerides as the reference, the geometric distances from each of the two trajectories to all visible GNSS satellites are computed. The RMS of these differences is then calculated for each epoch to form a continuous Difference RMS time series. Outliers are removed prior to thresholding to reduce the impact of observation loss-of-lock and other disturbances. Finally, if the time series length meets the predefined sliding window requirement, the dynamic threshold is adaptively constructed from the median and MAD within the window; otherwise, an empirical static threshold is applied. The Difference RMS value of the epoch following the window is tested against the threshold. If it exceeds the threshold, the epoch is flagged as an anomaly; otherwise, it is considered normal. When an anomaly is flagged, the algorithm examines the RMS value at the subsequent epoch: if it also exceeds the threshold, an orbit maneuver event is confirmed; otherwise, the single anomaly is regarded as observation noise or a data disturbance, and no maneuver alarm is triggered.

3. Data and Experimental Strategy

To verify the effectiveness of the proposed method, eight representative orbit maneuver events of the GRACE-FO satellites (GRACE-C and GRACE-D) from 2018 to 2022 and two additional maneuver events of SENTINEL-3A in 2022 are selected for real-data validation of the maneuver detection approach based on the Difference RMS and the sliding window MAD. The GRACE-FO mission is jointly operated by the Jet Propulsion Laboratory (JPL) and the Geoforschungszentrum (GFZ), while SENTINEL-3A is part of the European Copernicus program and operated by ESA in cooperation with EUMETSAT. GRACE-FO flies at an orbit altitude of about 490 km, whereas SENTINEL-3A maintains a higher orbit of approximately 815 km, allowing the influence of orbit altitude on the proposed method to be examined. The two GRACE-FO satellites are processed independently rather than jointly. All selected satellites are equipped with advanced GNSS receivers, providing continuous tracking capability for maneuver detection experiments. External real-time precise orbit and clock products are provided by the Centre National d’Études Spatiales (CNES), with the orbit products sampled every 5 min and the clock products every 5 s, serving as the reference for POD. Recent evaluations against the post-processed precise products from Wuhan University indicate that the CNES real-time GPS orbit and clock products achieve an accuracy of approximately 3 cm and 0.10 ns, respectively, thereby ensuring reliable POD performance during maneuver detection [42].

This study assumes that the user does not have prior knowledge of the thruster ignition timings and relies solely on onboard GNSS observation data and real-time ephemerides to perform independent orbit determination and maneuver detection. The selected maneuver events cover a variety of typical scenarios, with durations ranging from 20 s to 30 min and thrust magnitudes from very small to 0.26 m/s. They were chosen to evaluate the applicability of the proposed method under different maneuver conditions. The selection was made to ensure coverage of representative operational types (including orbit maintenance, attitude adjustment, and orbit-raising cases) and to test the method’s applicability across a wide range of thrust magnitudes and maneuver durations. Some events do not have publicly available thrust parameters, allowing the robustness of the method to be assessed under conditions without prior information. Depending on their duration and thrust magnitude, these events include short-duration low-thrust maneuvers (typically lasting 20 s to 2 min with thrust velocity below 0.01 m/s, usually conducted for orbit maintenance or fine adjustments), medium-thrust maneuvers (lasting 2–10 min with thrust velocity between 0.01 m/s and 0.1 m/s, commonly used for orbit attitude adjustments), and long-duration continuous high-thrust maneuvers (lasting approximately 30 min or longer with thrust velocity exceeding 0.1 m/s, generally performed for orbit-raising or orbit plane transfer missions). During data processing, if observation data are missing for certain epochs, precise-orbit interpolation is applied to maintain the continuity of the Difference RMS series.

The experiment adopts a dual-orbit differencing strategy to construct the detection indicator, establishing both a kinematic orbit determination chain and a reduced-dynamic orbit determination chain. The former directly processes the GNSS observations at each epoch without dynamic constraints, enabling rapid response to trajectory changes caused by maneuvers. The latter propagates the orbit using primary force models combined with periodic empirical acceleration parameters, ensuring trajectory continuity while partially absorbing errors from unmodeled perturbations. The two trajectories agree closely during nominal flight, but exhibit significant geometric differences when a maneuver occurs. Using CNES real-time ephemerides as the reference, the geometric distance differences between the two trajectories and the visible GNSS satellites are computed and their RMS values are calculated to form the Difference RMS series. Potential maneuvers are then automatically identified using the sliding window median and MAD-based dynamic threshold.

Table 2. Data Processing Strategies for Kinematic and Reduced-Dynamic Orbit Determination.

Observation Models
Observations	GPS L1/L2 ionosphere-free code and phase observations
Sampling rate	30 s
Cut-off elevation	1°
GNSS antenna PCO/PCV	IGS14.atx [43]
LEO antenna PCO/PCV	GNV1B products, PCV ignored
GNSS orbit and clock	CNES real-time products
Dynamic Models (Reduced-dynamic)
Earth gravity field	EIGEN_6C (120 × 120) [44]
N-body perturbation	JPL DE405 [45]
Solid earth and pole tides	IERS conventions 2010 [46]
Relativity	IERS conventions 2010 [46]
Ocean tide	FES 2004 [47]
Solar radiation pressure	Box-Wing macro-model
Atmosphere drag	DTM-2020 thermosphere models [48] (estimated every 90 min)
empirical acceleration	Piecewise periodical sine and cosine terms in along-track and cross-track (estimated every 90 min)
Estimator	Batch least-squares estimator

summarizes the observation models, dynamic modeling, and parameter estimation strategies used in the kinematic and reduced-dynamic orbit determination. In the reduced-dynamic solution, empirical acceleration parameters in the along-track and cross-track directions are estimated every 90 min to compensate for unmodeled perturbations, thereby improving the stability of the predicted orbit and the reliability of the detection indicator.

4. Results

Table 3. Detection Results of Selected Maneuver Events for GRACE-FO Satellites.

Satellite	Event Date	Maneuver Duration	ΔV (m/s)	Reference Time	Detection Time	Detection Delay (s)	Maneuver Type
GRACE-C	22 June 2018	49 s	0.007	19:57:34	19:50:00	−454	Short-duration, small-thrust maneuver
	3 November 2021	29 min 50 s	-	04:08:00	04:09:30	90	Long-duration, unknown-thrust maneuver
	22 June 2022	29 min 50 s	0.2645	03:10:05	03:11:30	85	Long-duration high-thrust maneuver
GRACE-D	26 May 2018	6 min 46 s	0.06	00:57:48	00:59:30	102	Medium-duration medium-thrust maneuver
	22 June 2018	1 min 24 s	0.0124	21:37:42	21:38:30	48	Medium-thrust short-duration maneuver
	19 March 2019	17 s	-	13:30:22	13:33:30	188	Short-pulse weak-disturbance maneuver
	3 November 2021	29 min 50 s	-	04:02:30	04:04:00	90	Long-duration, unknown-thrust maneuver
	22 June 2022	29 min 23 s	0.2607	03:10:19	03:12:30	131	Long-duration high-thrust maneuver
Sentinel-3A	13 April 2022	-	-	07:56:37	07:56:30	−7	-
	31 October 2022	-	-	11:20:37	11:20:30	−7	-

lists the basic parameters of each event and the detection results obtained using the proposed method. The maneuver epoch, thrust magnitude, and duration are referenced from the official technical document released by GFZ (ftp://isdcftp.gfz-potsdam.de/grace-fo/DOCUMENTS/TECHNICAL_NOTES/TN-01a-SCE.txt (accessed on 29 September 2025)). for the GRACE-FO satellites, and from the official reference maintained by ILRS (https://ilrs.gsfc.nasa.gov/data_and_products/predictions/maneuver.html, (accessed on 29 September 2025); ftp://ftp.ids-doris.org/pub/ids/satellites/s3aman.txt (accessed on 29 September 2025)) for Sentinel-3A. In this study, the detection time refers to the onset of the satellite’s departure from its nominal trajectory, as identified by the Difference RMS method. The detection latency refers to the time difference between the maneuver start epoch identified by the proposed method and the thruster ignition time recorded in the document, i.e., the official maneuver starts epoch. A positive value indicates that the detection occurs later than the official record, while a negative value indicates that the maneuver is detected in advance.

The results show that the proposed method achieves good responsiveness and stability in medium- to long-duration maneuver scenarios, with most events being effectively detected within 1–2 min. On average, the detection latency was about 118 s for short-duration maneuvers (excluding one abnormal early detection case), 102 s for medium-duration maneuvers, and 99 s for long-duration maneuvers, as summarized in Table 3. Longer maneuvers generally produce more significant orbit deviations, which trigger the indicator response earlier and more reliably than very short-duration cases. Without relying on any prior thrust information, the method demonstrates strong practicality and robustness. However, in certain special cases—such as extremely short-duration thrust or degraded data quality—delayed detection or even early false alarms may occur. In these cases, the main cause was signal interruption or loss of lock, which led to poor-quality observations being discarded during preprocessing (cycle-slip detection and gross-error removal), reducing the number of satellites available for orbit determination and thereby lowering the reliability of the detection. This effect was observed in one out of the eight maneuver events. In addition, the Sentinel-3A case studies were included primarily to verify the applicability of the proposed method across LEO satellites with different orbit altitudes. Both events showed a detection delay of −7 s, which is attributable to the 30 s sampling interval of the observation data. Despite this limitation, the results still confirm the effectiveness of the method for maneuver detection at higher LEO altitudes.

4.1. Typical Case Studies

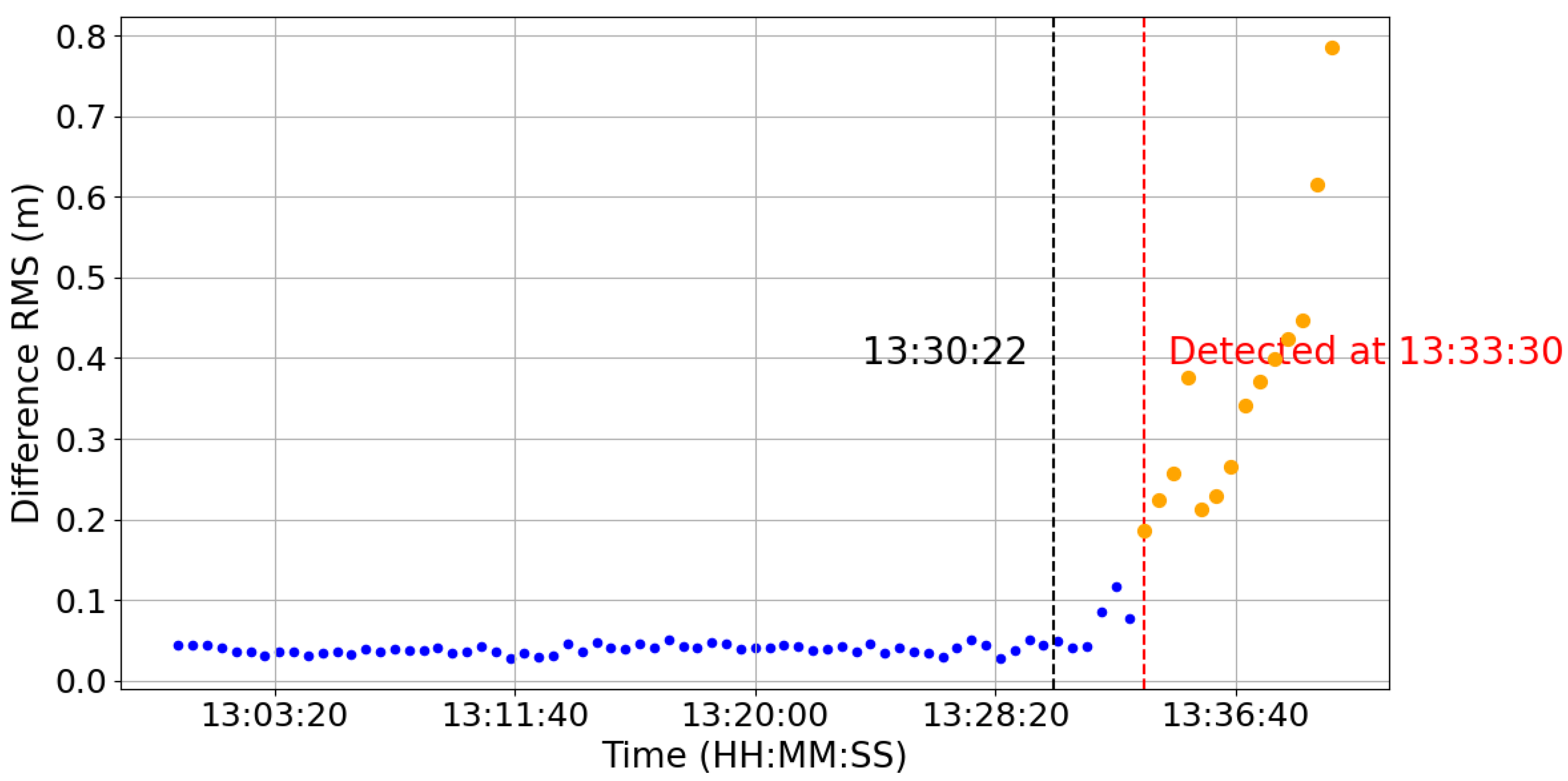
To further evaluate the performance of the method, three representative cases are selected from the eight maneuver events discussed above, covering long-duration high-thrust, medium-duration medium-thrust, and short-duration weak-disturbance scenarios. The detection results for these cases are shown in Figure 3, Figure 4 and Figure 5. In all figures, blue points indicate normal RMS variations, orange points mark maneuver detections by the algorithm, the red dashed line denotes the first detection epoch, and the black dashed line denotes the reference maneuver ignition time.

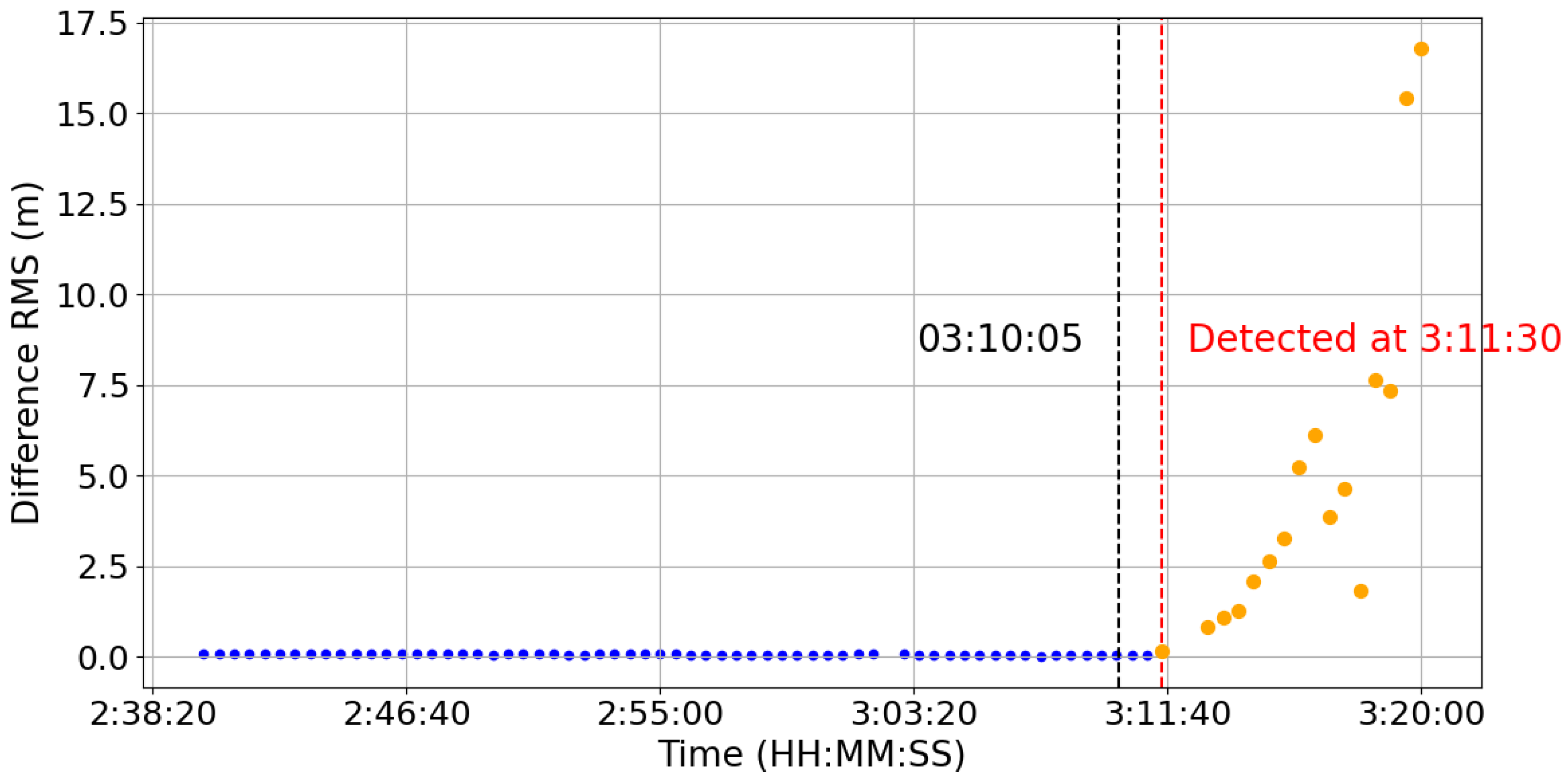
4.1.1. Long-Duration High-Thrust Maneuver

Figure 3 shows a typical orbit adjustment of the GRACE-C satellite on 22 June 2022, with a thrust velocity of 0.2645 m/s and a duration of approximately 30 min. This maneuver was selected for detailed illustration because it is a representative high-thrust, long-duration case that clearly demonstrates the method’s sensitivity and effectiveness in detecting significant orbit deviations. The subsequent case selections follow similar criteria and are therefore not elaborated further. The algorithm successfully detects the maneuver about 85 s after ignition. The RMS curve rises significantly, and the variation trend is consistent with the actual situation, verifying the method’s sensitivity and timeliness under strong-disturbance conditions.

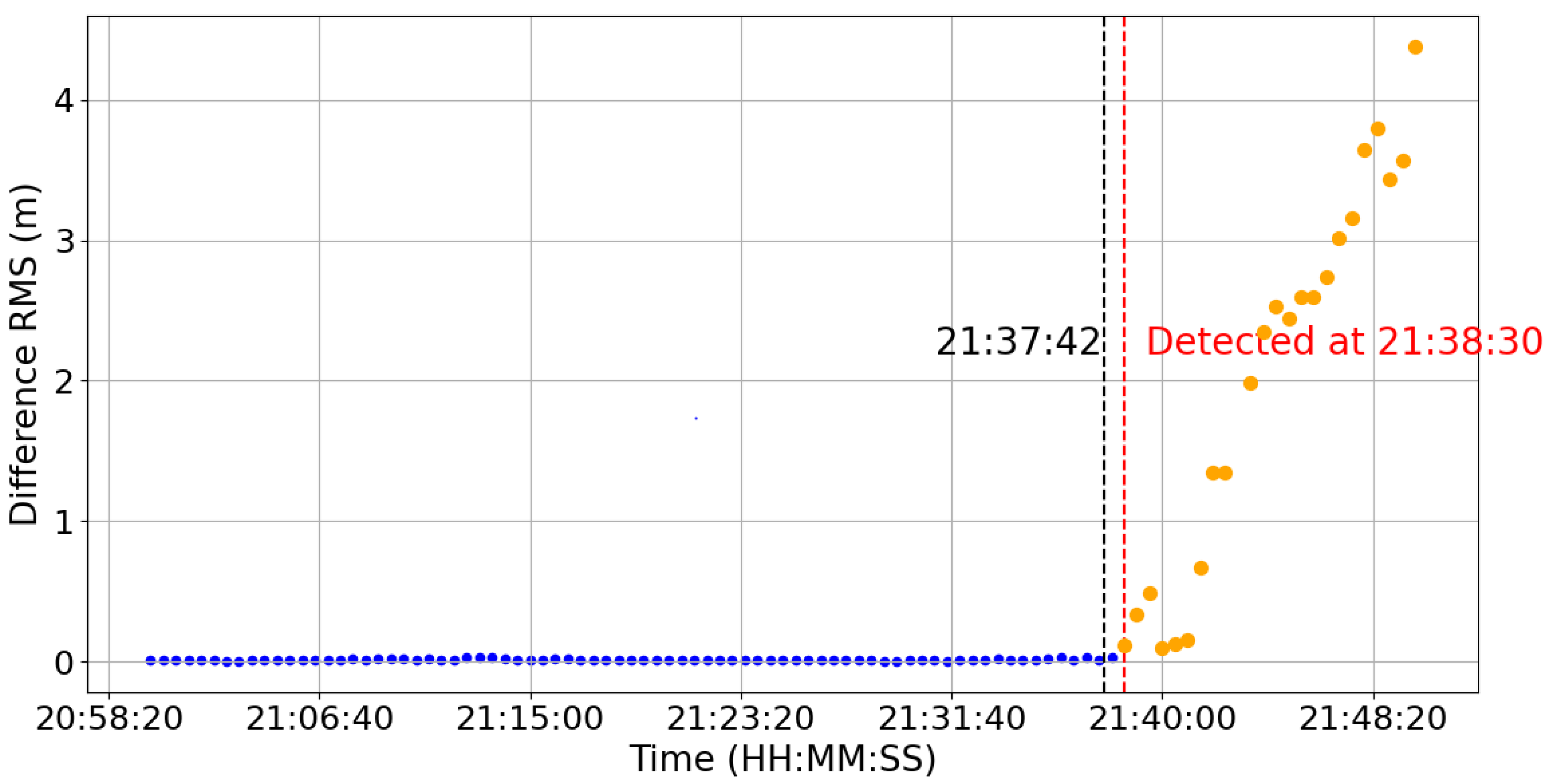
4.1.2. Medium-Thrust Short-Duration Maneuver

Figure 4 presents a medium-thrust maneuver of the GRACE-D satellite on 22 June 2018, with a thrust velocity of 0.0124 m/s and a duration of 84 s. Although the thrust is relatively small, the RMS sequence shows a clear jump before and after the event, and the algorithm responds within 48 s, indicating good sensitivity.

4.1.3. Short-Pulse Weak-Disturbance Maneuver

Figure 5 depicts a 17 s pulse maneuver of the GRACE-D satellite on 19 March 2019. Due to the short duration and low thrust, the RMS curve shows only a slight increase, and the detection delay reaches 188 s. This indicates that, in extremely weak-disturbance scenarios, the method has a certain detection lag, although it can still detect the orbit maneuver.

4.2. Special Cases and False Alarms

Although the method generally achieves high detection accuracy, misclassifications can still occur in certain scenarios. Figure 6 shows a maneuver event of the GRACE-C satellite on 22 June 2018. The actual ignition time is 19:57:34, but the algorithm triggers a maneuver alarm at 19:50:00, leading to a false alarm 7 min and 34 s early.

Further analysis shows that, starting from 19:46, several onboard GNSS observations were flagged as invalid due to temporary tracking discontinuities such as cycle slips or loss of lock. During preprocessing, these observations, although still present in the raw data, were discarded through the TurboEdit quality-control procedure. This algorithmic exclusion reduced the number of available satellites for precise orbit determination, which in turn disturbed the reduced-dynamic POD solution and caused an abnormal early rise in the Difference RMS series, ultimately leading to a premature maneuver detection.

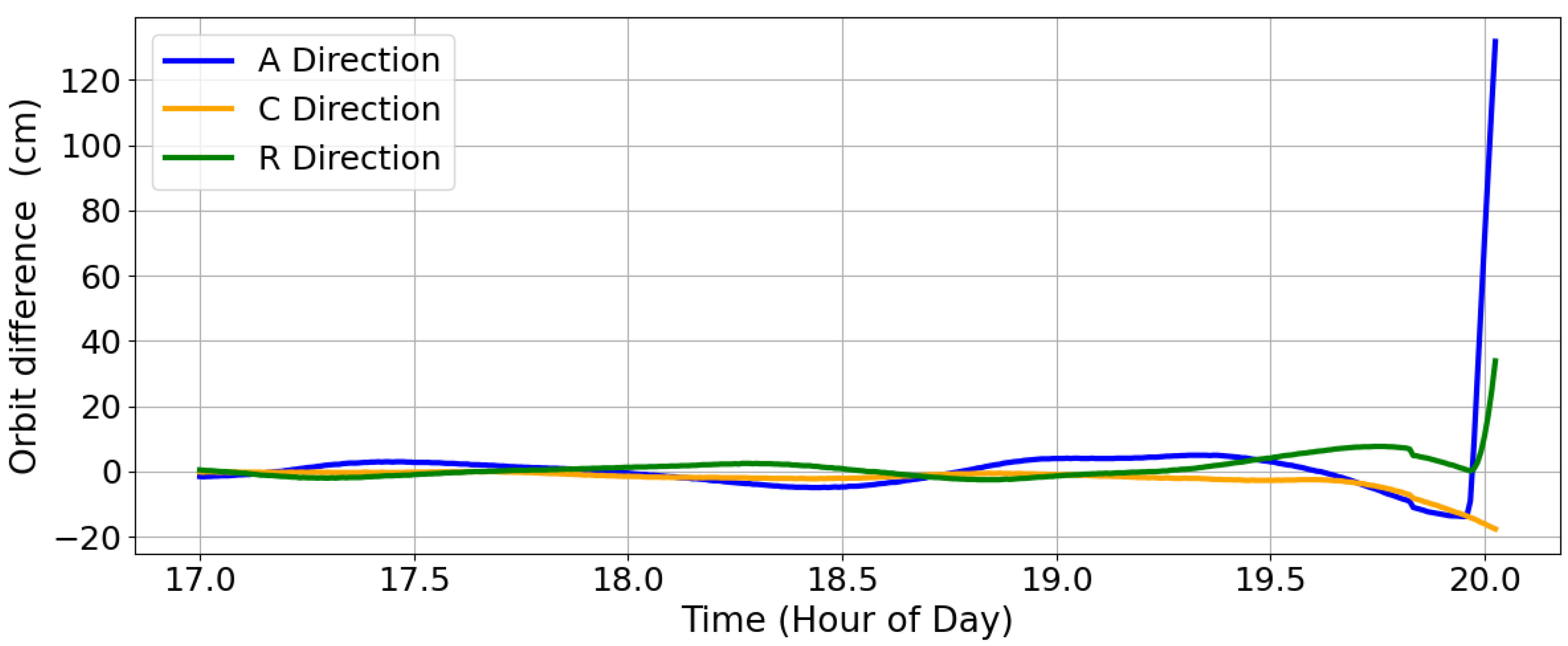
To more intuitively illustrate the change in orbit accuracy, Figure 7 presents the position deviations obtained by differencing the predicted orbit with the precise reference orbit of GRACE-C. The results show a significant increase in orbit differences during the false alarm period, confirming that the misclassification is closely related to the decrease in orbit determination reliability prior to prediction.

This case shows that, while the proposed method achieves good stability and responsiveness for medium- to long-duration maneuvers, unstable observation quality and fluctuations in POD accuracy can cause the Difference RMS to rise prematurely, leading to false alarms. The sliding window dynamic threshold is designed to mitigate such risks by adapting to local noise statistics, thereby reducing sensitivity to random outliers compared with traditional fixed-threshold methods. However, when data quality deteriorates severely—such as when multiple poor-quality observations are discarded and the number of usable satellites drops significantly—the local statistics themselves become distorted. As a consequence, the reduced-dynamic POD solution loses accuracy, which in turn degrades the quality of the orbit prediction. This causes the predicted orbit to diverge from the kinematic reference orbit earlier than the actual maneuver onset, making the Difference RMS indicator cross the threshold in advance and thus triggering a false alarm. In future applications, improving data quality control and optimizing preprocessing strategies to better handle temporary signal degradation may further reduce the likelihood of such false alarms.

4.3. Case Study: Impact of LEO Altitude on Detection Performance

To further evaluate the applicability of the proposed method, we performed additional case studies on the Sentinel-3A satellite, which operates at a higher orbit altitude (~815 km) compared to GRACE-FO (~490 km). The official maneuver epochs for Sentinel-3A were obtained from the International Laser Ranging Service (ILRS) repository (https://ilrs.gsfc.nasa.gov/data_and_products/predictions/maneuver.html (accessed on 29 September 2025)). For Sentinel-3A, only the maneuver epochs are publicly available, while information on thrust magnitude and duration is not provided. Therefore, the validation focuses on comparing the detected maneuver start epochs with the official reference epochs. The results are illustrated in Figure 8 and Figure 9.

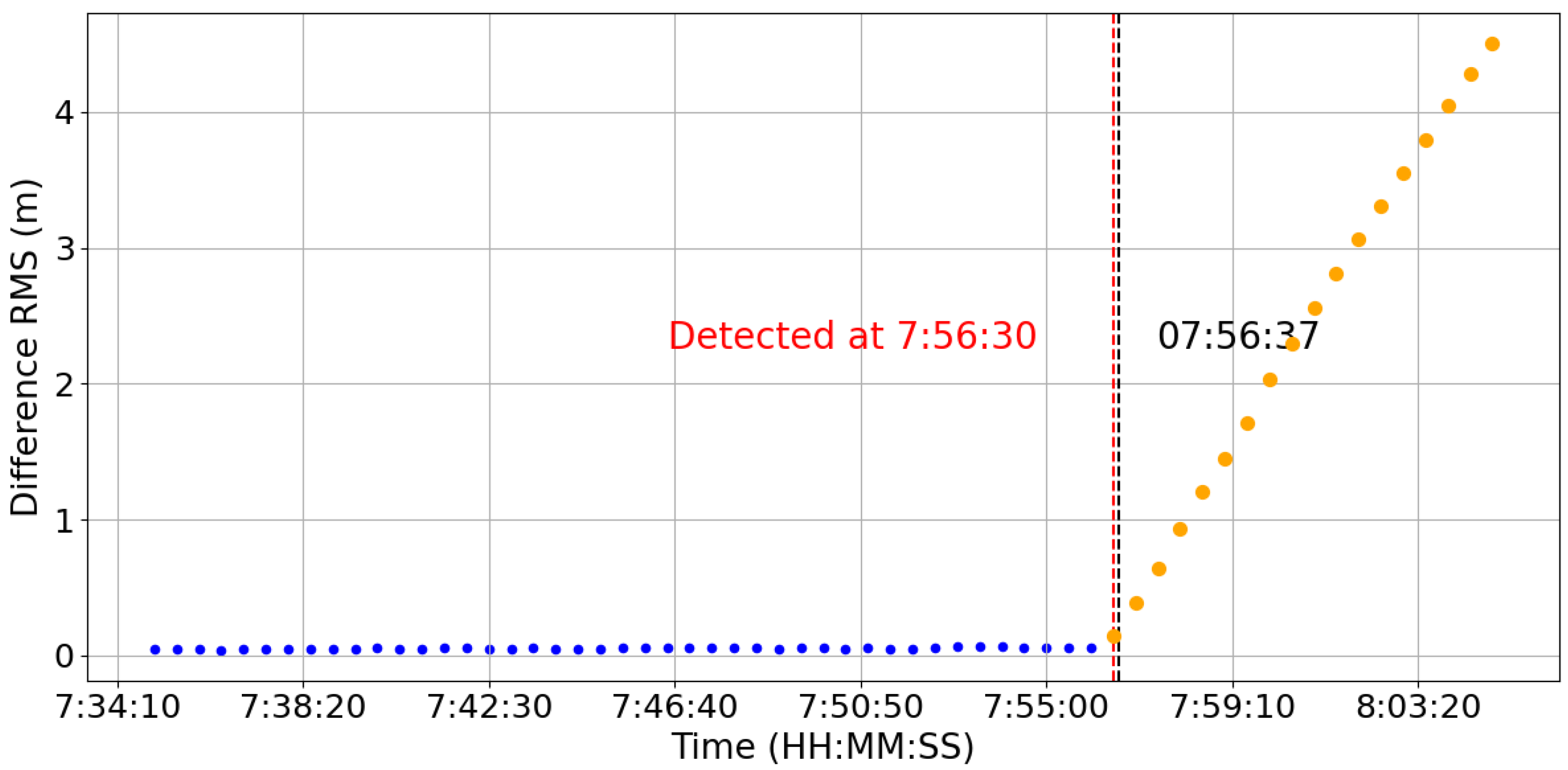
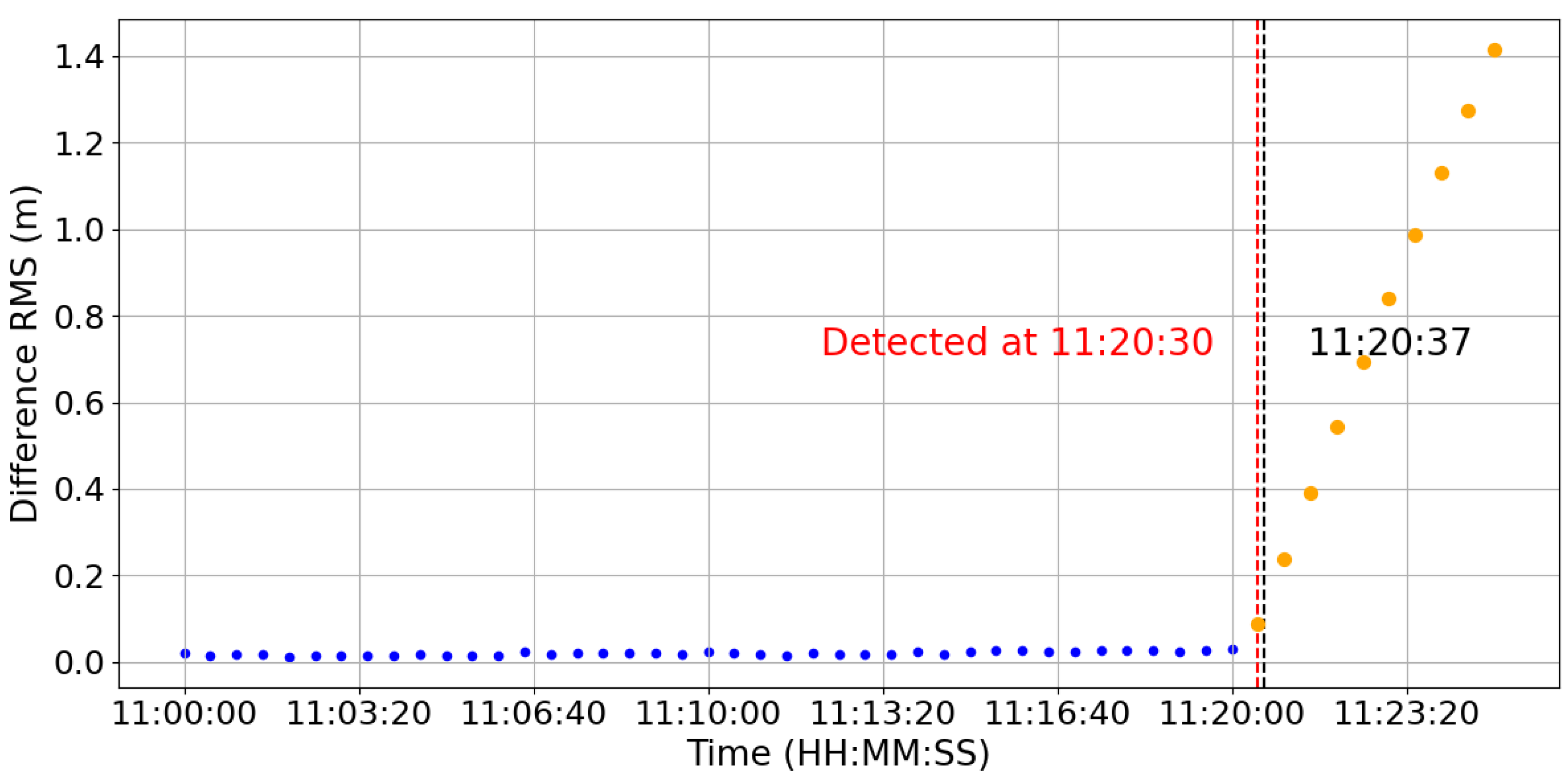
Figure 8 and Figure 9 illustrates the results for two representative maneuver events. The first event occurred on 13 April 2022, at 07:56:37 (Figure 8), and the second event took place on 31 October 2022, at 11:20:37 (Figure 9). In both cases, the Difference RMS indicator exhibited a sharp response immediately after the maneuver, and the proposed method successfully detected the onset of orbit deviation. The detected epochs were 07:56:30 and 11:20:30, respectively, which are both 7 s earlier than the official records. This small discrepancy is caused by the use of GNSS observations with a 30 s sampling interval, which limits the temporal resolution of the detection and leads to a few-second difference from the official ignition time.

Despite this limitation, the results demonstrate that the proposed method remains effective for satellites at different orbit altitudes. In particular, the successful detection of maneuvers for Sentinel-3A confirms that the approach is not restricted to GRACE-FO’s lower orbit regime but can also be applied to higher LEO platforms. This finding highlights the broader applicability of the method for maneuver detection across a wide range of LEO constellations.

5. Discussion

To rigorously evaluate the performance and applicability of the proposed method, we compared it with three representative maneuver detection techniques in terms of detection sensitivity, timeliness, and detection rate (

Table 4. Performance Comparison of Different Orbit Maneuver Detection Methods.

Method	Data Source	Minimum Detectable Thrust (m/s)	Average Detection Delay (s)	Detection Rate
Difference-RMS + Sliding Window MAD	Onboard GNSS observations + real-time precise ephemeris	~0.0124	~90	7/8 events detected
TLE-SGP4 Element Differencing [25]	TLE data	>0.01	Not quantified	100% (tested cases)
TLE + Particle Filtering [26]	TLE data	~0.0002 * (simulation)	Not quantified	High recall (simulation only)
GNSS-SWMAD [38]	Onboard GNSS carrier phase + real-time precise ephemeris	–	<20	High (short-duration maneuvers)

* represents the corresponding values obtained through simulation.

). The following discussion is organized accordingly.

First, regarding detection sensitivity, the TLE-based particle filter method [26] shows the highest theoretical resolution in simulation, being able to detect micro-maneuvers as small as ~0.0002 m/s. This is mainly because (i) the method propagates a large number of “particles” to simulate possible orbit states and continuously updates them with TLE data, which amplifies even subtle perturbations caused by small thrusts; and (ii) the SGP4 model errors were carefully analyzed and treated in advance, preventing them from masking weak maneuver signals. Nevertheless, such performance was only demonstrated in controlled simulations. The TLE-SGP4 element differencing method [25] also exhibits relatively high sensitivity, detecting maneuvers with Δv larger than ~0.01 m/s. However, its performance is strongly constrained by the accuracy of TLE inputs, and the detection thresholds and window lengths in [25] were tuned through trial-and-error for specific satellites, which limits general applicability. By contrast, the proposed GNSS-based method detects maneuvers with thrust levels down to ~0.0124 m/s using real satellite data, without requiring prior thrust information. This demonstrates a practical balance between sensitivity and applicability in real maneuver scenarios.

Second, with respect to detection timeliness, the GNSS-SWMAD method [38] shows the fastest responsiveness, being able to identify short-duration maneuvers within about 20 s due to the direct sensitivity of carrier-phase residuals to orbit deviations. The proposed method achieves an average detection latency of about 90–100 s for medium- and long-duration maneuvers, which ensures minute-level responsiveness while maintaining stability under noisy conditions; this latency partly reflects the use of 30 s sampling observations in our experiments, which inevitably limits responsiveness. In contrast, the two TLE-based methods [25,26] mainly highlight their advantages in terms of sensitivity and detection success rate, but do not explicitly quantify timeliness. Overall, GNSS-based methods show greater potential for real-time maneuver detection of LEO satellites, as they directly exploit onboard observations with higher temporal resolution.

Finally, concerning detection rate, the proposed method successfully detected seven out of eight real-world maneuvers, including some short-pulse events. The TLE-SGP4 differencing method [25] reported 100% success in the TOPEX and Envisat case studies, but this result relied on highly favorable conditions: low-noise TLE data, accurate ground-truth maneuver histories, carefully calibrated thresholds, and maneuvers with sufficiently large Δv signals in non-GEO orbits. Such conditions are not guaranteed, in general, operational scenarios. The particle filter method [26] achieved high recall in simulation, but its effectiveness with real data is limited by TLE accuracy. Both the GNSS-SWMAD method [38] and the proposed approach demonstrated high detection rates under good GNSS tracking quality. However, they share a common limitation: their performance degrades under poor observation conditions, such as cycle slips, signal interruptions, or loss of lock, which may lead to premature or delayed detections. This reflects a general constraint of GNSS-based strategies. In future applications, improving data quality control and optimizing preprocessing strategies to better handle temporary signal degradation may further reduce the likelihood of such false alarms. In addition, complementary measurements such as K-band tracking could also be integrated to enhance overall robustness.

In summary, the proposed method demonstrates a practical balance among sensitivity, timeliness, and detection rate, showing strong potential for operational use in real-time maneuver monitoring. Beyond the GRACE-FO case studies, the Sentinel-3A events further confirm that the method is not limited to lower-altitude LEO but can be effectively extended to higher-altitude missions. This highlights its broader applicability and practical value for diverse LEO satellite operations.

6. Conclusions

This study focuses on the real-time identification of orbit maneuver events for LEO satellites and proposes a detection method based on real-time GNSS ephemerides and dual-orbit solution differences. By constructing a Difference RMS time-series indicator from the geometric position deviations between reduced-dynamic and kinematic POD solutions, and applying a sliding window median and MAD-based dynamic robust threshold, the method achieves high-sensitivity and low false alarm detection of orbit disturbance events without relying on prior thrust information. This design not only ensures adaptability under varying observation conditions but also provides a direct and sensitive characterization of orbit dynamics.

Validation with eight representative maneuver events from multi-year GRACE-FO satellite data confirms that the method maintains strong responsiveness and stability for medium- to long-duration thrust maneuvers, detecting most events within 1–2 min. It also demonstrates effectiveness under medium-thrust and short-duration disturbance conditions, although one short-duration small-thrust event was detected prematurely under degraded observation quality. More generally, degraded GNSS tracking (e.g., cycle slips, signal interruptions, or loss of lock) lowers orbit determination accuracy at earlier epochs, which reduces the fidelity of the propagated orbit and enlarges its discrepancy with the kinematic solution. This effect can distort the Difference-RMS indicator, leading to premature alarms or masking of weak maneuver signals, and thus represents a fundamental limitation of approaches based on onboard GNSS observations. To mitigate this limitation, future work will focus on incorporating complementary observations, such as K-band tracking, to enhance robustness and improve detection reliability under degraded signal conditions. In addition, two case studies from Sentinel-3A further confirm the method’s applicability to higher-altitude LEO satellites, demonstrating its adaptability across different orbit regimes. The results highlight the method’s real-time potential and practical applicability for diverse maneuver scenarios, supporting its use in future LEO constellation operations and GNSS augmentation services.

In addition to achieving minute-level detection latency, the method’s ability to operate without prior maneuver information, its adaptive thresholding mechanism for balancing sensitivity and robustness, and its successful validation on real satellite datasets collectively represent a significant advancement over traditional TLE-based and model-dependent approaches. These advantages position the proposed framework as a promising foundation for operational integration, where higher-rate GNSS observations, multi-sensor data fusion, and advanced post-processing could further improve responsiveness, robustness, and applicability under complex mission conditions. Nevertheless, it should also be acknowledged that the method’s performance may be reduced in extremely short-duration or weak-thrust maneuvers, in severely degraded observation environments, or under rapidly varying atmospheric conditions during extreme space weather events. Addressing these limitations will be an important direction for future research.