Electric Aircraft Airport Electric Utility Sizing Study Based on Multi-Layer Optimization Models

Abstract

As the potential of e-aircraft in short-range routes becomes more prominent, the question of how to rationally plan airport electric infrastructure and efficiently produce it has become a key issue in the aviation industry’s efforts to move towards electrification. In this paper, we propose and construct a three-layer optimization model for determining the size of airport electric infrastructure, which is solved collaboratively at the three levels of strategic, tactical, and operational layers, in order to construct an optimization algorithm to minimize the construction and operation costs of electric infrastructure, and at the same time to ensure that flights are not delayed by the influence of electric power supply. Specifically, Stage-1 considers infrastructure sizes; Stage-2 assigns a binary charge–swap decision per turnaround under no-delay policy; Stage-3 schedules power under time-of-use tariffs and outputs a feasible day plan and daily cost. In order to verify the effectiveness of this paper’s algorithm, this paper conducts case studies and algorithm validation on actual flight data. The results show that the proposed model can significantly reduce the overall airport operating costs while ensuring normal flight operations.

1. Introduction

In recent years, electric aviation technology has received widespread attention in academia and industry, and is considered to have significant potential, especially in terms of its application prospects in short-haul routes and regional aviation markets, which may provide a viable path for aviation decarbonization and low-cost operations [1]. With the stringent regulation of carbon emission reduction globally, airlines, aircraft manufacturers and aviation startups in several countries and regions have actively invested in the research, development and testing of e-aircraft, driving the rapid development of the technology. For example, Sweden’s Heart Aerospace has developed the ES-30, a hybrid-e-aircraft with batteries that support an all-electric range of 200 km, extending up to 400 km in hybrid mode. In addition, Eviation is developing the Alice e-aircraft, which is positioned as a zero-emission regional short-haul flight and is expected to be the world’s first all-electric commuter aircraft [2,3]. This study adopts Eviation’s Alice as a representative e-aircraft for regional operations, due to its publicly available specifications and flight-test data that enable realistic infrastructure modeling. With the breakthrough of battery technology and the continuous optimization of electric propulsion system, the market application prospect of e-aircraft is getting broader and broader, and it is expected that it will gradually move towards commercial operation in the next few years.

While e-aircraft show great potential, there are still a number of challenges to fully replacing conventional energy aircraft. First, the mass energy density that can be realized by current battery technology is still significantly lower than that of traditional aviation kerosene. For example, the energy density of mainstream lithium-ion batteries is about 250–300 Wh/kg, and even high-performance batteries such as silicon anode lithium batteries only reach 360–420 Wh/kg, while the mass energy density of aviation kerosene (Jet A-1) is as high as 11,950 Wh/kg [4,5]. Even taking into account the higher energy conversion efficiency of electric propulsion systems compared to conventional thermal engines (~90% vs. 55%), batteries still provide far less usable energy per unit mass than fossil fuels [6,7]. This order of magnitude gap directly limits the capability of e-aircraft in terms of range and payload, making it difficult to meet the continuous demand for high energy output on medium- and long-range routes, and is currently mainly applicable to short-distance urban commuting or regional feeder transportation scenarios [8]. In addition, the current battery system corresponds to a significantly higher mass per unit of energy compared to aviation kerosene, which directly leads to a significant increase in the weight of the battery that an e-aircraft needs to carry to achieve the same range. For example, in order to provide energy equivalent to 1 kg of aviation kerosene (~11,950 Wh/kg), nearly 40 kg of high-performance Li-ion batteries (at 300 Wh/kg) would need to be carried. This significant mass redundancy not only significantly increases the structural load and takeoff weight of the aircraft, reducing lift-to-drag ratio and flight efficiency, but also compresses the payload available for passengers or cargo, which in turn affects range planning and commercial viability. As a result, battery systems, at current energy density levels, are a major limiting factor for the deployment of electric aero-propulsion technologies in medium and long range routes [9]. Finally, the infrastructure development of e-aircraft also faces great challenges, especially in high-frequency operation scenarios, in order to meet the demand for high-power charging, airports need to carry out structural upgrades of the electric power system, including capacity expansion, charging pile deployment and distribution network optimization. The high instantaneous load during charging not only poses a challenge to the stability of the power grid, but also puts higher demand on the peak regulation capability and energy management system [10,11].

Based on the existing development of battery technology, the economics of airport operations, and the cost of airport construction, the use of a large-scale charging infrastructure is not an optimal choice [12]. A feasible alternative is to introduce a Battery Swapping System (BSS) on top of the airport charging system [13]. Battery swapping can shave peak-hour power demand and relieve pressure on the charging infrastructure. By eliminating lengthy on-stand charging queues, it also improves airport operational flexibility and efficiency [14]. Considering real-world airport operations, we develop a hierarchical optimization model that jointly sizes plug-in charging and battery-swapping facilities while minimizing both capital investment and day-to-day operating costs. The model determines the optimal power-infrastructure capacity and allocates charging-and-swapping resources so as to maximize operational efficiency and reduce total cost. Unlike earlier studies that oversimplify flight operations, the proposed multilayer framework explicitly accounts for flight rotations, connection times and resource conflicts, providing a realistic decision tool for deploying electric-aircraft ground-power systems.

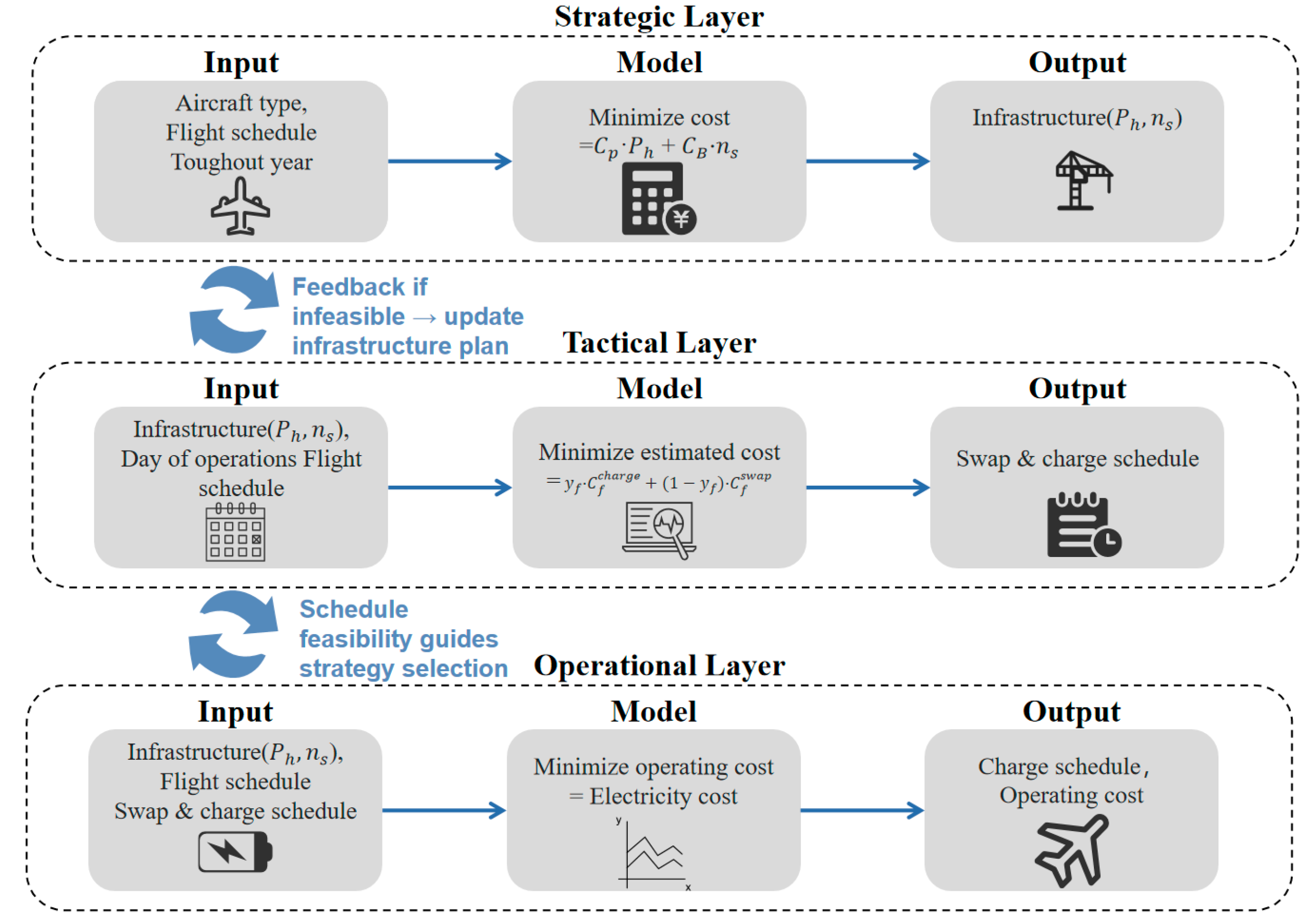
The framework comprises three decision layers.

Strategic layer—a genetic algorithm searches for the optimal infrastructure plan, including the charging power cap and spare battery inventory, balancing feasibility and investment cost across the entire network.

Tactical layer—given each flight’s ground time, the model selects either plug-in charging or battery swapping.

Operational layer—a linear program with time-of-use tariffs assigns variable charging power to each flight, minimizing daily electricity cost.

Upper-layer decisions constrain lower-layer feasibility and objectives. If the operational layer cannot find a feasible schedule for a given infrastructure–strategy combination, the genetic algorithm penalizes that solution and explores alternatives in the next iteration; if the schedule is feasible but expensive, the objective value steers the GA toward a better trade-off between installing extra batteries and increasing the power cap. This “global search + detailed scheduling” architecture lowers computational complexity, improves interpretability, and offers a flexible, practice-oriented route to airport electrification planning and real-time operation.

To validate the proposed three-layer optimization model, we present a case study based on Joy Air’s regional route network. Assuming that the existing conventionally powered models are fully replaced by Eviation Alice e-aircraft in future operations, the charging infrastructure configuration is optimized for the 10 airports involved. The optimization results show that the minimum total charging power required for the system is 2278 kW, and with 18 sets of backup batteries, the sustainable operation of the overall network can be guaranteed without affecting the normal operation of flights, which corresponds to an average daily operating cost of about CNY 22,583 (All monetary values are in 2024 CNY unless otherwise stated). The main contributions of this paper include the following:

• Hierarchical optimization framework: In this paper, we firstly divide the electric aviation infrastructure design and operational tasks into three types of subproblems with clear decision boundaries, i.e., “strategic”, “tactical” and “operational”, and construct a multilevel optimization model in a top-down manner. The top-down approach is used to construct a multilevel optimization model. This structure effectively improves the interpretability and scalability of the model in complex scenarios.
• Combining heuristic methods and exact solution method: Aiming at the mathematical characteristics of different sub-problems in the multi-layer model, this paper adopts a hybrid solution framework combining heuristic algorithms and precise optimization strategies, where genetic algorithms are used to achieve global search of key infrastructure parameters (total airport charging power configuration and backup battery size) at the upper level, and linear programming is used to finely solve charging/swapping scheduling at the lower level, so as to achieve high efficiency and feasibility of the solution.
• Allow partial power charging during time slots: Introduce continuously adjustable power in the scheduling model to flexibly adapt to changes in time-slotted tariffs, reduce the cost of power consumption during peak hours, and further improve the system economy.
• Taking Joy Air Airlines and its associated 10 airports as the research object, replacing conventional aircraft with e-aircraft based on the flight data of the first quarter of 2023 for the simulation of the operation scenario, the optimization model proposed in this paper is systematically and empirically verified.

The rest of the paper is organized as follows: in Section 2, we review the relevant literature on scheduling and sizing optimization of plug-in charging and battery replacement systems, and discuss the current state of research on e-aircraft charging infrastructure. In Section 3, the optimization problem we need to solve is described in detail. Section 4 then describes the multilayer optimization model and its algorithm design. In Section 5, we demonstrate the performance of the model in real operations and analyze the results through a case study of a regional airline operating e-aircraft in China. Section 6 systematically evaluates the complexity and stability of the proposed multilayer optimization model and provides a comparative analysis with other framework models. Finally, Section 7 summarizes the main conclusions of this paper and suggests potential directions for future research.

2. Prior Work and Contributions

In recent years, with the rapid development of electric aviation technology and the advancement of carbon emission reduction targets in the aviation industry, the airport operation mode adapted to e-aircraft has gradually become an important research topic in the field of aviation. Commercial air transport planning is typically driven by a top-down demand–supply logic: first, passenger and cargo demand is mapped onto an origin–destination network; next, airlines decide the fleet mix and airport infrastructure required to supply that demand; only then are detailed charging or swapping strategies devised. This study addresses the airport operator (supply-side) problem of sizing electric-power infrastructure and scheduling charge/swap operations for e-aircraft, under fixed traffic demand and flight timetables. The present study focuses on this supply-side optimization—specifically, how an airport operator can size electric–power infrastructure and schedule charge/swap operations once the traffic demand and flight timetable have been fixed.

In order to meet the charging demand of e-aircraft and improve the operational efficiency of airports, scholars have proposed a variety of solutions such as plug-in charge, Battery Swap System (BSS), and a combination of the two [15,16]. Existing studies have generally indicated that the plug-in Charge system is more suitable for flights with longer layover times, while the BSS can significantly improve the operational efficiency of airports by reducing the transit time of airplanes through rapid battery replacement [15,17]. Although existing literature proposes different planning schemes for electric aviation infrastructure at airports, the impacts of airport resource constraints, flight schedule changes, and the complexity of the battery charging and changing process on operational efficiency have not yet been fully considered and effectively addressed in the actual operational environment. Therefore, how to efficiently coordinate the plug-in charging and battery replacement modes under actual operational constraints is still an urgent issue that requires in-depth research.

Given the large number of decision variables and complex constraints, a traditional monolithic formulation scales poorly for practical, large instances. In the existing literature, some studies have begun to try to adopt a hierarchical optimization modeling approach to alleviate the solution complexity, e.g., Guo et al. [17] proposed an Aviation-to-Grid concept for the airport electric aviation infrastructure problem to optimize the infrastructure sizing planning and charging scheduling through a two-phase strategy, respectively; Oosterom and Mitici [18] also used a two-stage backtracking optimization model in order to determine the capacity and charging power requirements of airport battery charging and swapping infrastructures.

However, although the above literature reduces the complexity of single-stage decision-making to some extent, it still does not adequately build a clear, multilevel decision-making structure from strategic, tactic, and operation problems. The approach proposed by Justin et al. also adopts the idea of stage optimization, but it mainly consists of a simple division between the planning of the number of battery-charging piles and the charging scheduling, and lacks the complete top-down decision-making process and coupled feedback mechanism between levels.

In real aviation operation, fleet size and aircraft jobs are interdependent, being jointly constrained by aircraft rotations and crew-duty regulations. However, most of the existing literature does not explicitly incorporate the constraints of fleet scheduling and crew articulation when planning electric aviation infrastructure at airports. Trainelli et al.’s [19] optimization work for hybrid electric aviation infrastructure does not consider the impact of crew turnaround scheduling on the optimization of the infrastructure, even though it considers timing constraints of aircraft jobs; Justin et al.’s [20] study also focuses on charging and swapping strategic planning, completely ignoring the important constraints of real-world fleet scheduling and crew resource allocation on optimization decisions. Failure to incorporate real operational constraints into the problem structure may result in practical applications being disconnected from actual operational requirements, which in turn harms the model’s effectiveness and reliability.

In summary, existing studies suffer from three persistent gaps: (i) they seldom build a full hierarchical optimization framework, making it hard to break down the computational complexity of large-scale problems; (ii) they rarely embed fleet-rotation and crew-duty constraints, so the resulting plans deviate from day-to-day operational reality; and (iii) most evaluations rely on synthetic or purely simulated data, limiting the external validity of their findings. As summarized in

Table 1. Comparison of existing optimization studies on electric airport infrastructure.

Study/Year	Optimization Layers & Method	Charge/Swap Mode	Fleet-Scheduling & Crew Constraints	Main Strengths	Key Limitations (vs. This Work)
Guo et al. [17]	Two phases: (i) GA for infrastructure size; (ii) LP for day-ahead charging	Plug-in	No	Introduces “Aviation-to-Grid” concept; decomposes problem complexity	No mid-level strategy or layer feedback; ignores fleet coupling
Oosterom & Mitici [18]	Two-stage backtracking: capacity estimate → power allocation	Plug-in + BSS	No	Jointly optimizes capacity and peak power	Only two layers; no multi-airport or crew constraints
Justin et al. [20]	Sequential planning vs. charging schedule	BSS	No	First to separate planning and scheduling	Static split, no feedback; omits fleet rotation
Trainelli et al. [19]	Single-layer MILP (hybrid-electric infrastructure)	Plug-in + BSS	No	Considers task time-window constraints	No crew turnaround; no hierarchical design

, most prior studies adopt one- or two-layer formulations, omit explicit fleet-crew coupling, and validate on stylized test networks rather than real-world case studies.

To address the above deficiencies, this paper proposes a three-level hierarchical optimization decision framework that systematically integrates infrastructure planning (strategic), charging/transfer strategy selection (tactical), and operation scheduling (operational), aiming at achieving overall optimization within a multi-level decision-making framework with a feedback mechanism. In the strategic layer, this paper adopts genetic algorithm to conduct a global search on key infrastructure parameters such as total airport charging power configuration and backup battery size, in order to take into account the infrastructure investment cost and daily operation demand; in the tactical layer, the optimal charging or power swapping strategy is flexibly determined for the specific aircraft jobs by taking into account the realistic factors such as flight schedules, transfer time and charging window period; in the operational layer, the optimal charging or power swapping strategy is flexibly determined for the specific aircraft jobs. In the bottom operational layer, the improved Mixed Integer Linear Programming (MILP) model realizes the refined charging scheduling by “discrete time with continuous power range”, which maximally combines the characteristics of time-of-use tariffs, and significantly reduces the cost of electricity for daily operation. This approach ensures the solvability of the model and avoids frequent plugging and unplugging as well as unnecessary intermittent charging caused by excessive segmentation of the charging process, which makes the charging strategy closer to the real operation scenarios.

To test the applicability of the proposed approach and verify the validity of the optimization model, we present a case study based on real flight data and the route network of Joy Air Airlines in the first quarter of 2023, involving 10 representative airports. Specifically, by constructing an operational scenario in which an e-aircraft replaces the existing conventional aircraft, the investment cost of airport infrastructure, charging cost, and the utilization efficiency of backup batteries are comprehensively evaluated and optimized. The experimental results show that the hierarchical optimization framework proposed in this paper is able to significantly reduce the overall operating costs of airports under the premise of fully meeting the requirements of flight punctuality and operational safety. In addition, the framework also takes into account the potential for upgrading with possible future supercharging technologies and higher power demand, and makes significant breakthroughs in the coupling feedback among multi-layer decisions, the flexibility of charging and swapping strategies, and the scalability of the model compared with existing studies.

The hierarchical optimization decision framework proposed in this paper not only provides a more reliable, flexible and efficient optimization tool for the actual infrastructure deployment and operation scheduling of electric airports, but also lays a solid model foundation for future in-depth research on the long-term impact of different charging modes on battery life and operation safety, and provides strong technical support and theoretical references for the large-scale application of e-aircraft in actual airport operations. The modeling of the battery life and operational safety of e-aircraft provides a strong technical support and theoretical reference for large-scale application in actual airport operations.

3. Problem Description

3.1. Background and Motivation

Compared with conventional aircraft, e-aircraft may not only require longer or more flexible stopover charging times during ground operations, but also their peak charging power, backup battery management, and modifications to the ground power supply network will put unprecedented pressure on airports [21]. In addition, how to ensure that aircraft power can meet the demand of subsequent flights within a tight flight transit window also puts higher demand on the airport’s charging and swapping processes and scheduling strategies. Under high-intensity flight execution, a single plug-in charging or battery replacement mode is often difficult to meet all the demand: in the case of a long layover, direct plug-in charging can make full use of the idle window and reduce the size of spare batteries and maintenance investment; however, in the case of a tight turnaround or peak hour, high-power plug-in may lead to a surge in peak power costs or delays due to the inability to recharge in a timely manner. In this case, the battery replacement program can provide rapid full-charge support, but it requires a sufficient number of batteries in good condition, and the investment and management costs are relatively high. If flight connections and cross-field resource scheduling are further considered in a multi-airport network, the synergistic relationship between airports and turnaround connections will make the coupling between facility size, scheduling methods and operating costs more complex [22]. In summary, the rapid development and popularization of e-aircraft not only brings more multi-dimensional planning and operation challenges for airports, but also puts forward higher flexibility and integration requirements for the existing charging/power exchange model.

In this study, we address the problems of sizing the power supply at the airport and scheduling the daily operation of e-aircraft in a regional aviation network by means of an optimization model that minimizes total cost through rational planning of airport power infrastructure (equipment capacity, spare battery inventory) and charging schedules, while satisfying flight punctuality.

Method overview and I/O at a glance. Stage-1 (strategic) takes the peak-day timetable, time-of-use tariff $\mathit{p}\left(\mathit{t}\right)$ and unit costs as inputs, and decides ( ${\mathrm{P}}_{\mathrm{h}}$, ${\mathrm{n}}_{\mathrm{h}}^{\mathrm{s}}$). Stage-2 (tactical) receives ( ${\mathrm{P}}_{\mathrm{h}}$, ${\mathrm{n}}_{\mathrm{h}}^{\mathrm{s}}$) and each flight’s ground-time window, and assigns a binary charge-vs-swap decision ${\mathit{y}}_{\mathit{f}}$. Stage-3 (operational) produces a time-discretized schedule and the realized daily cost under $\mathit{p}\left(\mathit{t}\right)$. notation is listed in

Table 2. Overview of used nomenclature.

Symbol	Description
F	Flights
H	Airport
${\mathit{T}}_{\mathit{a}\mathit{r}\mathit{r}}^{\mathit{f}\mathit{h}}$	Time of arrival of flight f at airport h
${\mathit{T}}_{\mathit{d}\mathit{e}\mathit{p}}^{\mathit{f}\mathit{h}}$	Flight time of flight f departing from airport h
${\mathit{t}}_{\mathit{f}\mathit{l}\mathit{y}}^{\mathit{f}\mathit{h}}$	Flight time of flight f arriving at airport h
${\mathit{P}}_{\mathit{c}\mathit{r}\mathit{u}}^{\mathit{f}}$	Cruise power of the e-aircraft
${\mathit{w}}_{\mathit{t}\mathit{a}\mathit{k}\mathit{e}\mathit{-}\mathit{o}\mathit{f}\mathit{f}}^{\mathit{f}}$	Power consumed by the airplane during takeoff
${\mathit{w}}_{\mathit{c}}^{\mathit{f}}$	Power consumed by flight e arriving at airport h
${\mathit{w}}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}$	Total battery power
${\mathit{t}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{r}\mathit{t}}^{\mathit{f}}$	Flight f start charging time
${\mathit{t}}_{\mathit{e}\mathit{n}\mathit{d}}^{\mathit{f}}$	Time for flight f to complete charging
${\mathit{t}}_{\mathit{t}\mathit{u}\mathit{r}\mathit{n}}$	minimum ground-handling time including deplaning/unloading, safety checks, and any repositioning to the charging/swap bay (phase taxonomy following Postorino et al. [23]).
${\mathit{t}}_{\mathit{c}\mathit{h}\mathit{a}\mathit{r}\mathit{g}\mathit{e}}^{\mathit{f}}$	Flight f charging consumption time
${\mathit{P}}^{\mathit{c}}$	Constant charging power
${\mathit{P}}^{\mathit{m}\mathit{a}\mathit{x}}$	Maximum charging power
$\mathit{p}\left(\mathit{t}\right)$	Segmented electricity price
popSize	speed—population size
$p_c$	crossover probability
$p_m$	mutation probability
${\mathit{C}}_{\mathit{h}}$	Airport h Electricity Airport facility costs
${\mathit{C}}_{\mathit{p}\mathit{o}\mathit{w}\mathit{e}\mathit{r}}$	Charging pile construction unit cost
${\mathit{C}}_{\mathit{s}\mathit{p}\mathit{a}\mathit{r}\mathit{e}}$	Unit cost of battery backup
${\mathit{C}}_{\mathit{o}\mathit{p}\mathit{e}\mathit{r}\mathit{a}\mathit{t}\mathit{e}}$	Electricity Cost/Operating Cost
${\mathit{P}}_{\mathit{h}}$	Airport h charging station total power
${\mathit{P}}_{\mathit{m}\mathit{a}\mathit{x}}$	Theoretical maximum charging station total power
${\mathit{P}}_{\mathit{m}\mathit{i}\mathit{n}}$	Theoretical minimum charging station power
${\mathit{n}}_{\mathit{h}}^{\mathit{s}}$	Number of backup batteries at the airport
${\mathit{y}}_{\mathit{f}}$	Binary variable indicating whether charging or swapping is Performed up to flight f
$\mathit{\Delta }{\mathit{t}}_{\mathit{f}}$	Flight f dwell time
${\mathit{F}}_{\mathit{s}\mathit{w}\mathit{a}\mathit{p}}$	Flights that choose to swap batteries
m	Number of equal time intervals within the planning horizon
Δt	Discretized time of day
$t_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}}$	Start time of the day
$t_{\mathrm{e}\mathrm{n}\mathrm{d}}$	Time at which the day’s work ends
${\mathit{x}}_{\mathit{f}}\mathit{,}\mathit{t}$	Power to charge flight f at time t
ϵ	Tolerance term to avoid floating point precision errors
${\mathit{T}}_{\mathit{i}\mathit{n}\mathit{t}\mathit{e}\mathit{r}\mathit{v}\mathit{a}\mathit{l}}^{\mathit{f}}$	Time window for charging flight f

.

All symbols used are summarized in Table 2.

3.2. Operational Scenario Definition

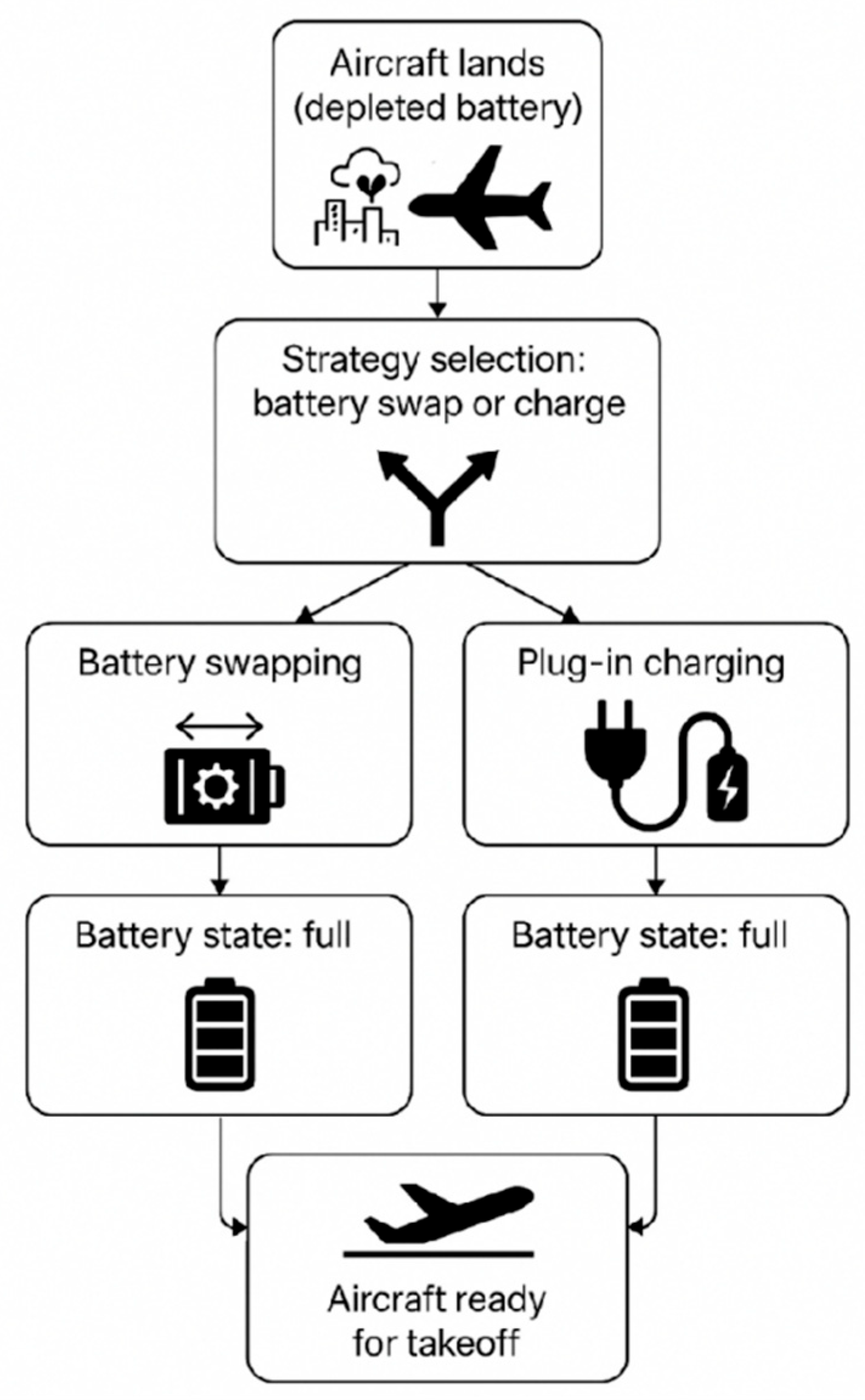
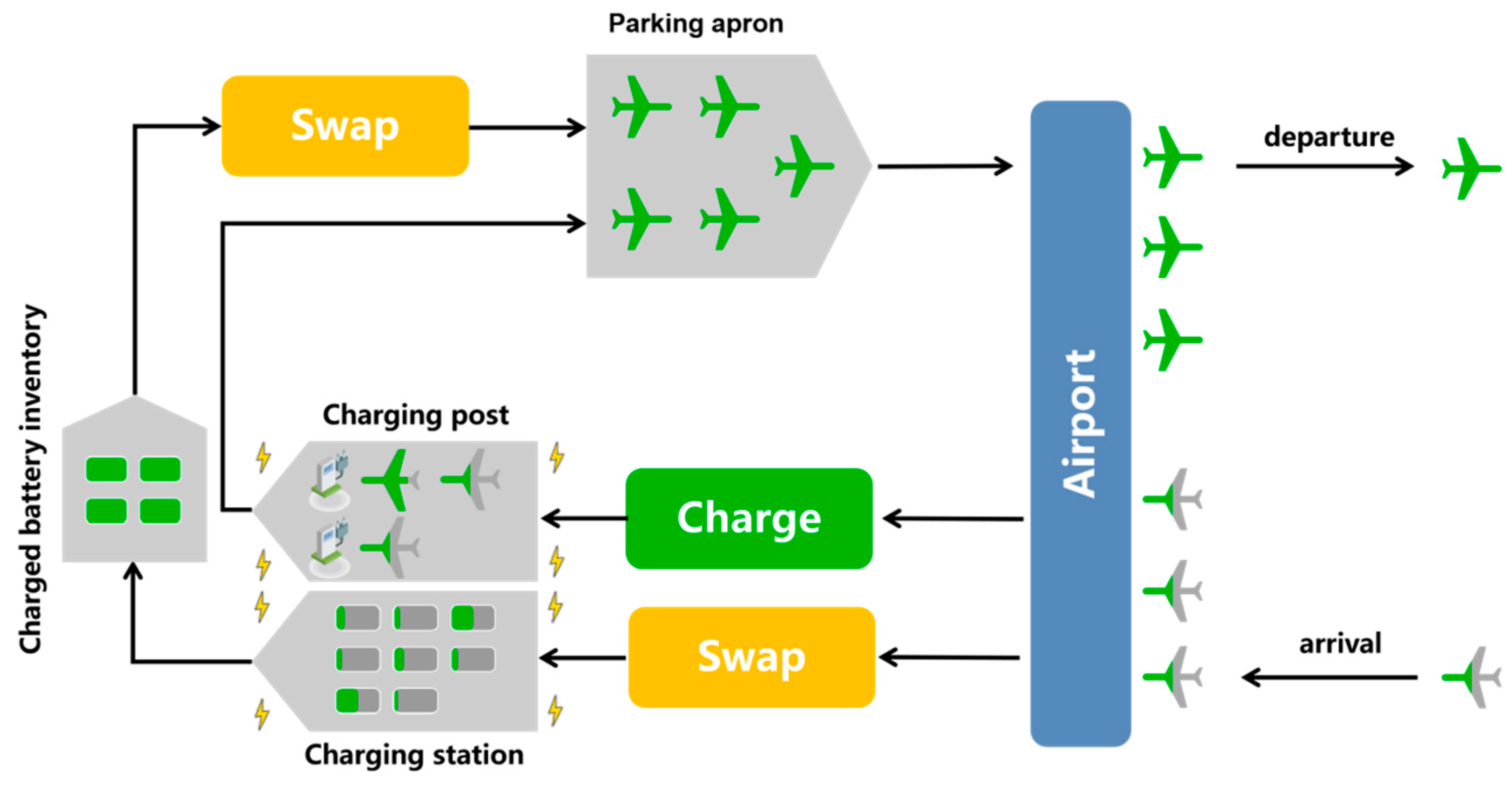
In order to portray the above challenges more systematically and build a feasible optimization model, it is necessary to first clarify the airport’s operation system under both plug-in charging and battery replacement modes. The overall architecture proposed in this study consists of key elements such as e-aircraft, battery module, ground plug-in charging facility, battery replacement station, and dispatch management system, and its operation logic is shown in Figure 1. The functions and interaction mechanisms of these elements will be introduced one by one in the subsequent subsections.

3.2.1. Airport Operations

Assume that airports that support the operation of e-aircraft in the future are equipped with charging and swapping infrastructures, and that in the network of short-haul flights from these airports, a type of e-aircraft that can support both plug-in charging and swapping is used, and that each of these e-aircraft is equipped with a battery, and that the flights perform their routes in strict adherence to the airport’s timetable. Let H denote the ensemble of airports in the route network of these e-aircraft, E denote the set of e-aircraft in the flight network, and f ∈ F denote the set of flights to and from the airports of these e-aircraft. The e-aircraft may complete an energy replenishment operation at the airport during aircraft turnaround, including either plug-in charging or battery replacement. The energy replenishment method chosen by each aircraft during each ground stop is uniformly deployed by a strategic decision-making system to complete the replenishment with the goal of overall system optimization. In addition, to ensure mission safety and accessibility, all aircraft must satisfy the energy constraint of a fully charged state before takeoff. Figure 2 shows the schematic flow of a typical flight scheduling and energy replenishment operation within an airport.

3.2.2. Airport Flight Plan

In this study, aircraft schedules are differentiated on an airport-by-airport basis, with each airport having a separate “arrivals list” and “departures list”. The core information contained in the lists includes the operating aircraft, the flight number, the arrival time at the airport, the departure time at the airport, and the flight number of the next flight. Specifically, for each airport h ∈ H, a merged schedule is constructed that relates the data of all arriving and departing flights of the day. The basic fields can be described as follows, Assigned Aircraft (e): the identification of the aircraft that performs the segment, which is used to correlate subsequent flights of the same aircraft within the same day; Arrival Flight No: the flight number of the aircraft arriving at the airport h; Local Arr Time: the actual local time of the aircraft’s arrival at the airport, accurate to the minute or finer granularity; Departure Flight No: the flight number of the subsequent departure of the same aircraft at airport h. If there is no subsequent flight, it means that the altered aircraft e will stay overnight at airport h. Local Dep Time: the actual local time of the aircraft’s departure from the airport, which is used to determine the available window for the flight to stay at the airport. The Assigned-Aircraft key is used in a preprocessing step that orders all flights of the same aircraft chronologically, thereby creating a fixed daily rotation (flight chain). Because each chain is non-overlapping by construction, the optimization model automatically inherits this aircraft-linkage constraint and does not require an additional mathematical coupling term.

3.2.3. Battery Charging Equipment

Each airport is assumed to host plug-in chargers and a pool of spare battery packs; swapped packs are recharged on-site to sustain continuous operations. After the e-aircraft arrives at the airport, according to the instructions of the charging dispatch system, after completing the transfer of passengers and baggage, the airport towing equipment tows the airplanes to the designated charging area away from the apron and the apron for charging. After landing and taxi-in, passengers deplane and baggage is unloaded. Energy replenishment (charging or swapping) starts only after deplaning (no passengers onboard). We adopt the standard decomposition of aircraft turnaround activities (deplaning, unloading, safety checks, servicing, boarding, and pushback) and the associated operating policies reported in the literature, and we use these phases to define the minimum ground-handling time $t_{turn}$ [23]. Therefore, the time to start charging with the airplane at the ground facility is

$${\mathit{t}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{r}\mathit{t}}^{\mathit{f}}\ge {\mathit{t}}_{\mathit{a}\mathit{r}\mathit{r}}^{\mathit{f}\mathit{h}}\mathit{+}{\mathit{t}}_{\mathit{t}\mathit{u}\mathit{r}\mathit{n}}$$

(1)

In addition, the time for towing the e-aircraft from the charging pile to the runway is also ${\mathit{t}}^{\mathit{0}}$, and in order to ensure that the subsequent flights can leave the port on time, the completion time of charging is

$${\mathit{t}}_{\mathit{e}\mathit{n}\mathit{d}}^{\mathit{f}}\mathit{\le }{\mathit{t}}_{\mathit{d}\mathit{e}\mathit{p}}^{\mathit{f}\mathit{h}}\mathit{-}{\mathit{t}}_{\mathit{t}\mathit{u}\mathit{r}\mathit{n}}$$

(2)

Here we introduce ${\mathit{P}}_{\mathit{c}\mathit{r}\mathit{u}}^{\mathit{f}}$ to denote the cruise power of the e-aircraft, ${\mathit{w}}_{\mathit{t}\mathit{a}\mathit{k}\mathit{e}\mathit{-}\mathit{o}\mathit{f}\mathit{f}}^{\mathit{f}}$ to denote the power consumed by the airplane during takeoff, and the power consumed by flight f arriving at airport h can be obtained by

$${\mathrm{P}}_{\mathit{c}\mathit{r}\mathit{u}}^{\mathit{f}}\mathit{·}{\mathit{t}}_{\mathit{f}\mathit{l}\mathit{y}}^{\mathit{f}\mathit{h}}\mathit{+}{\mathit{w}}_{\mathit{t}\mathit{a}\mathit{k}\mathit{e}\mathit{-}\mathit{o}\mathit{f}\mathit{f}}^{\mathit{f}}$$

(3)

The maximum charging power of the facility is ${\mathit{P}}^{\mathit{m}\mathit{a}\mathit{x}}$, so the fastest theoretical charging time

$${\mathit{t}}_{\mathit{c}\mathit{h}\mathit{a}\mathit{r}\mathit{g}\mathit{e}}^{\mathit{f}}\mathit{=}\frac{{\mathit{w}}_{\mathit{c}}^{\mathit{f}}}{{\mathit{P}}^{\mathit{m}\mathit{a}\mathit{x}}}$$

(4)

Each airplane is charged at a constant power P until it is full. We also assume that the price of electricity varies throughout the day and is given by the time function p. Finally, we want to ensure that all e-aircraft arriving at this airport are charged by the end of the day’s operations to ensure they do not interfere with flight operations the next day.

3.2.4. Battery Swapping System

We assume that each airport is (i) equipped with a charging station and a number of spare batteries, and (ii) is able to support receiving and charging batteries to ensure the continuity of flight scheduling. The e-aircraft arrives at the airport, the staff performs a battery replacement operation on the e-aircraft and transports the replaced batteries to the charging station, and let this time be $t_{turn}$. Therefore, the time when the batteries arrive at the replacement station and start to be charged is

$${\mathit{t}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{r}\mathit{t}}^{\mathit{f}}\mathit{\ge }{\mathit{t}}_{\mathit{a}\mathit{r}\mathit{r}}^{\mathit{f}\mathit{h}}\mathit{+}{\mathit{t}}_{\mathit{t}\mathit{u}\mathit{r}\mathit{n}}$$

(5)

Assuming that the time for the batteries being transported from the charging station to the airplane and installed is also $t_{turn}$, the time to complete the charging to ensure that the subsequent flights can depart from airport on time is

$${\mathit{t}}_{\mathit{e}\mathit{n}\mathit{d}}^{\mathit{f}}\mathit{\le }{\mathit{t}}_{\mathit{d}\mathit{e}\mathit{p}}^{\mathit{f}\mathit{h}}\mathit{-}{\mathit{t}}_{\mathit{t}\mathit{u}\mathit{r}\mathit{n}}$$

(6)

The maximum charging power of a single battery is also ${\mathrm{P}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$, the fastest theoretical charging time is

$${\mathit{t}}_{\mathit{c}\mathit{h}\mathit{a}\mathit{r}\mathit{g}\mathit{e}}^{\mathit{f}}\mathit{=}\frac{{\mathit{w}}_{\mathit{c}}^{\mathit{f}}}{{\mathit{P}}^{\mathit{m}\mathit{a}\mathit{x}}}$$

(7)

Each battery is charged at a constant power and supports simultaneous charging of multiple batteries (limited by the total power of the charging station ${\mathit{P}}_{\mathit{h}}$) until full. Similarly to plug-in charging, the price of electricity varies throughout the day and is given by the time-dependent function $\mathit{p}\left(\mathit{t}\right)$. Finally, we want to ensure that all e-aircraft arriving at this airport are charged before the end of the day’s operations, ensuring that they do not interfere with flight operations the next day.

3.3. Model

The main objective of this study is to develop an optimization model that determines the appropriate size of power infrastructure at airports. The model aims to minimize both fixed capital expenditures and average daily operating costs. As shown in Figure 3, the framework adopts a three-layer structure—strategic, tactical, and operational—that enables top-down configuration planning and bottom-up operational feedback.

Figure 3. Model hierarchy diagram.

Figure 3. Model hierarchy diagram.

3.3.1. Airport Infrastructure

In our designed model, the airport’s power infrastructure includes two key parameters: the number of spare batteries (${\mathit{n}}_{\mathit{s}}$) and the total charging station power (${\mathit{P}}_{\mathit{h}}$). The construction specifications and the facility sizes determine the cost of airport fixed-facility renovation.

The main objective of the optimization model is to determine the appropriate size of electric infrastructure. To do this, the model takes as inputs the daily flight schedule (${\mathit{T}}_{\mathit{a}\mathit{r}\mathit{r}}^{\mathit{f}\mathit{h}}\mathit{,}{\mathit{T}}_{\mathit{d}\mathit{e}\mathit{p}}^{\mathit{f}\mathit{h}}$), the unit cost of spare batteries (${\mathit{C}}_{\mathit{s}\mathit{p}\mathit{a}\mathit{r}\mathit{e}}$), and the unit cost of charging station power (${\mathit{C}}_{\mathit{p}\mathit{o}\mathit{w}\mathit{e}\mathit{r}}$) for each airport h ∈ H.

The model minimizes total fixed capital expenditure while also balancing expected operating costs. These infrastructure sizing decisions form the strategic layer of our multilayered optimization model. Subsequent decisions on aircraft charging and battery swapping are handled in the tactical layer.

3.3.2. Charging and Swap Decisions

The selected e-aircraft can support both plug-in charging and power exchange. The ground-time available for each flight is not assumed ex-ante; instead, it is derived directly from the published flight schedule. For every flight f, the scheduled arrival and the scheduled departure within the timetable give the turn-around duration. Based on the flight schedule information of each airport at the tactical layer, the available replenishment window of each aircraft on the ground can be refined and analyzed to determine whether the plug-in charging can be completed in the layover period; if the time is insufficient or the spare battery resources are sufficient, the power exchange mode may be preferred.

3.3.3. Charge Scheduling

The Charge Scheduling level is responsible for scheduling the entire airport battery charging and swapping strategy. Its main function is to coordinate the charging of all e-aircraft with replacement batteries at the airport to maximize charging efficiency and economy. The charging sequence and priority are adjusted by allocating charging power to the aircraft’s flight plan, remaining power, availability of charging facilities and grid load. The price of electricity in the model varies throughout the day, and the size of the electrical infrastructure at the airport h ∈ H, the charging schedule determined by the charging and swapping decision maker, and the flight schedule (${\mathit{T}}_{\mathit{a}\mathit{r}\mathit{r}}^{\mathit{f}\mathit{h}}\mathit{,}{\mathit{T}}_{\mathit{d}\mathit{e}\mathit{p}}^{\mathit{f}\mathit{h}}$) are used as inputs for a charging allocation scheme aimed at determining the operational cost (cost of electricity). Specifically, this multi-objective optimization task entails selecting the optimal form of energy replenishment (charging or swapping) and charging schedule for an aircraft after it has landed at the airport to ensure an on-time departure. Delays occur when the airport’s infrastructure is not sufficient to support on-time flight departures, so a threshold is set for the delay time during the optimization process to ensure that the delay does not exceed the acceptable range. Once the delay time exceeds the threshold, the algorithm automatically adjusts the optimization strategy to avoid wasting arithmetic power and skip computational paths that cannot satisfy the conditions, thus reducing the number of unnecessary iterations. This approach allows the delay of each flight to be spread over the flight time, minimizing the impact on subsequent flights.

4. Multi-Layer Models for Optimizing Power Infrastructure

This paper presents a three-tier structured optimization model that can help airports manage the charging and swapping decisions and charging processes for arrival flights and minimize infrastructure and charging costs. The model consists of an infrastructure sizing problem, a charging and swapping tactical problem, and a charging operational problem. First, at the infrastructure sizing layer, we formulate the infrastructure sizing problem for determining the total charging power allocation at the airport as well as the optimal number of backup batteries. Second, in the tactical layer, we select a charging or swapping scheme for each flight based on the given facility size to improve resource utilization efficiency. Finally, in the operational layer, we further optimize the specific charging schedule, power allocation, and battery replacement paths, which can be dynamically updated before the day of operation to adapt to the actual operational needs.

4.1. Strategic Layer: Infrastructure Sizing

First, an airport strategic algorithm for peak daily traffic is proposed. Where ${\mathrm{P}}_{\mathrm{h}}$ denotes the upper limit of the total charging power (in kW) that can be provided by the airport, and ${\mathrm{n}}_{\mathrm{s}}$ denotes the number of spare batteries available for swapping, both of which constitute the decision variables in this phase. The objective function, which aims to minimize the sum of single-day fixed infrastructure investment costs and operating costs while meeting flight punctuality requirements, can be formalized as:

$${\mathit{C}}_{\mathit{h}}\mathit{=}\underset{{\mathit{P}}_{\mathit{h}}\mathit{,}{\mathit{n}}_{\mathit{s}}}{\mathit{min}}{\mathit{C}}_{\mathit{p}\mathit{o}\mathit{w}\mathit{e}\mathit{r}}\mathit{·}{\mathit{P}}_{\mathit{h}}\mathit{+}{\mathit{C}}_{\mathit{s}\mathit{p}\mathit{a}\mathit{r}\mathit{e}}\mathit{·}{\mathit{n}}_{\mathit{h}}^{\mathit{s}}\mathit{+}{\mathit{C}}_{\mathit{o}\mathit{p}\mathit{e}\mathit{r}\mathit{a}\mathit{t}\mathit{e}}$$

(8)

$${\mathit{P}}_{\mathit{m}\mathit{i}\mathit{n}}\mathit{\le }{\mathit{P}}_{\mathit{h}}\mathit{\le }{\mathit{P}}_{\mathit{m}\mathit{a}\mathit{x}}$$

(9)

$$\mathit{0}\mathit{\le }{\mathit{n}}_{\mathit{h}}^{\mathit{s}}\mathit{\le }{\mathit{n}}_{\mathit{m}\mathit{a}\mathit{x}}$$

(10)

In this equation, ${\mathit{C}}_{\mathit{p}\mathit{o}\mathit{w}\mathit{e}\mathit{r}}$ and ${\mathit{C}}_{\mathit{s}\mathit{p}\mathit{a}\mathit{r}\mathit{e}}$ denote the daily unit cost of charging power and spare batteries, respectively.

The feasible ranges of ${\mathit{P}}_{\mathit{h}}$ (total charging power at airport h) and ${\mathit{n}}_{\mathit{h}}^{\mathit{s}}$ (number of spare batteries) are bounded by the airport’s flight volume, minimum turnaround requirements, and operational constraints.

The feasible range of $P_{\mathrm{m}\mathrm{i}\mathrm{n}}$ and $P_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is bounded by flight volume and operational constraints.

The upper-layer model passes a candidate configuration (${\mathit{P}}_{\mathit{h}}$, ${\mathit{n}}_{\mathit{h}}^{\mathit{s}}$) to the lower-layer scheduler. If the available charging resources fail to ensure the on-time departure of all flights, the solution is considered infeasible. Otherwise, the scheduler computes the daily operating cost ${\mathit{C}}_{\mathit{o}\mathit{p}\mathit{e}\mathit{r}\mathit{a}\mathit{t}\mathit{e}}$ based on charging power, electricity prices, and resource allocations, and returns it to the upper layer.

By iteratively adjusting (${\mathrm{P}}_{\mathrm{h}}$, ${\mathrm{n}}_{\mathrm{h}}^{\mathrm{s}}$), the model converges to an infrastructure configuration that minimizes the combined capital and operational costs under peak-demand conditions.

4.1.1. Genetic Algorithm

Since the overall model is mixed integer and has non-convex characteristics, in order to ensure the efficiency and quality of the solution, this paper introduces a genetic algorithm to find an the approximate optimal solution. The specific process of airport charging infrastructure optimization is given in Algorithm 1: After randomly initializing a set of feasible solutions, evaluate the feasibility and cost of each solution under the fixed facility configuration, and then continuously update the population in multiple iterations of the “selection, crossover and mutation” operation, so that the solution gradually converges to the approximate global optimal solution that balances the cost and feasibility of the constraints. Finally, the solution gradually converges to an approximate global optimum that balances the cost and feasibility constraints. Genetic algorithms, as a meta-heuristic method for global search, are suitable for solving the optimization problems with nonlinear and discrete decisions (e.g., power of charging station and number of batteries) in this model. Compared to exhaustive enumeration or traditional gradient methods, GA can avoid falling into local optimums in a complex solution space, which is especially important for the infrastructure configuration of this problem with a large number of combinatorial possibilities. In this framework, the fitness value of each candidate solution evaluated by the GA relies on solving a downstream linear programming (LP) subproblem. Specifically, given an infrastructure configuration (${\mathit{P}}_{\mathit{h}}$, ${\mathit{n}}_{\mathit{h}}^{\mathit{s}}$), the operational layer LP schedules charging and swapping operations to minimize daily electricity cost under time-of-use tariffs.

If the LP returns a feasible solution that ensures on-time departure and respects airport capacity limits, the corresponding cost is used as the fitness score; otherwise, the GA assigns a penalty to that individual. Thus, although the GA performs best obtained solution over infrastructure parameters, the LP solver acts as a feasibility and cost evaluator, ensuring that each configuration is rigorously assessed under real operational constraints [24,25,26].

The GA workflow is summarized in Algorithm 1; its main ingredients are outlined below.

Chromosome representation. Each individual is the ordered pair (${\mathit{P}}_{\mathit{h}}$, ${\mathit{n}}_{\mathit{h}}^{\mathit{s}}$). The bounds that are derived from the airport’s peak-day flight schedule are listed in Section 5.2.

Operators. Parents are selected by roulette-wheel sampling followed by a size-2 tournament. A single-point crossover with probability ${\mathit{p}}_{\mathit{c}}$ and a Gaussian integer mutation with probability ${\mathit{p}}_{\mathit{m}}$ perturb each gene by ±5% of its admissible range; the DOE-calibrated values of ${\mathit{p}}_{\mathit{c}}$ and ${\mathit{p}}_{\mathit{m}}$ are reported in Section 5.4.

After mutation, each offspring is sent to ApplyRepair(·), which tries to restore feasibility by adding one 50 kW charger module or one extra battery set per attempt—reflecting the granularity of commercially available hardware—until the schedule becomes feasible or the upper bound is reached. If repair fails at the upper bounds, the individual is kept but assigned a fitness of 1.1 times the worst feasible cost. Elitism always copies the best feasible solution to the next generation.

Algorithm 1: Genetic Algorithm—Strategic Layer Sizing

Data:

• popSize: population size (DOE-selected)

• generations: maximum number of generations

• ${\mathrm{p}}_{\mathrm{c}}$$,{\mathrm{p}}_{\mathrm{m}}$: crossover/mutation probabilities (DOE-selected)

• boundsPower(lowerPower, upperPower): feasible range for charging capacity

• boundsBattery(lowerBattery, upperBattery): feasible range for spare batteries

• EvaluateCandidate(s): function to compute total cost or penalize infeasibility

• ApplyRepair(s):feasibility-repair routine

Result:

• bestSolution = (bestPower, bestBattery)

• bestCost: the minimal feasible cost found

1 P ← InitialisePopulation(popSize, boundsPower, boundsBattery)

2 For each s ∈ P do

3   s ← ApplyRepair(s)

4   s.cost ← EvaluateCandidate(s)

5 bestSoln ← argmin{ s.cost|s feasible}

6 bestCost ← bestSoln.cost

7 For g = 1 … generations do

8   elite ← bestSoln

9   matingPool ← RouletteTournament (P)

10   offspring ← ∅

11   While |offspring| < popSize − 1 do

12     p1, p2 ← RandomSelect(matingPool)

13     c ← SinglePointCrossover (p1, p2, p_c)

14     c ← GaussianIntMutation (c, p_m)

15     c ← ApplyRepair (c)

16     If c infeasible then

17       c.cost ← 1.1 × worstFeasibleCost (P)

18     Else

19       c.cost ← EvaluateCandidate (c)

20     offspring ← offspring ∪ {c}

21   P ← offspring ∪ {elite}

22   currBest ← argmin{ s.cost|s feasible} in P

23   If currBest.cost < bestCost then

24     bestSoln ← currBest; bestCost ← currBest.cost

25 End For

26 Return bestSoln, bestCost

Rationale for choosing a genetic algorithm. The sizing problem considered in the strategic layer is a mixed-integer, highly non-convex optimization task that exhibits a rugged search space with many local minima once the infrastructure-cost function is coupled with downstream scheduling costs. Conventional gradient-based or branch-and-bound LP solvers quickly become trapped or scale poorly when the search bounds (charging-power upper limit and spare-battery count) are wide. In contrast, a genetic algorithm (GA) offers three practical advantages for this context: (i) its population-based mechanism provides global exploration and thus mitigates premature convergence to local optima; (ii) the evaluation of individuals—each requiring an independent LP solve—can be parallelized trivially across CPU cores, delivering near-linear speed-ups; and (iii) the algorithm is easily hybridized with domain-specific heuristics (e.g., elitist retention and adaptive mutation) without altering the downstream linear-programming structure. These properties enable the GA to deliver high-quality near-optimal solutions within minutes even for large airport networks, while keeping the implementation lightweight and solver-agnostic.

4.1.2. Genetic-Algorithm Parameter Calibration

The performance of the genetic algorithm (GA) depends critically on the proper selection of its hyper-parameters. In this study, we adopt a full factorial design of experiments (DOE) approach to calibrate three key parameters: population size (popSize), crossover probability ($p_c$), and mutation probability ($p_m$) [27].

The strategic GA operates on only two decision genes—total charging power and number of spare battery sets-yet each fitness evaluation requires solving a downstream linear program that models time-of-use electricity tariffs and stand constraints. To balance global exploration against computational burden and the classic trade-off between population size and convergence speed, we selected three representative population sizes (20, 40, 80) which remain below the empirically observed threshold of 100 individuals, beyond which further increases yield negligible performance gains but significantly higher computational costs [28]. Mutation probabilities of 0.01, 0.05 and 0.10 capture the range from the “small random perturbations” typically recommended in canonical GA practice (≈1–5% gene mutation for real-coded problems) to more aggressive mutation for escaping discrete local minima in mixed-integer settings [29]. Crossover probabilities of 0.60 and 0.80 bracket the interval (0.6–0.9) most frequently reported in the GA literature and in recent engineering design studies [30].

Specifically, we evaluate three levels for population size (20, 40, and 80), three levels for $p_m$ (0.01,0.05 and 0.10), and two levels for $p_c$(0.60 and 0.80), yielding 18 unique parameter combinations. Each configuration is independently executed ten times using different random seeds to account for stochasticity. For each run, we record the best cost, the convergence generation defined as the point at which relative improvement in best cost drops below 1%, the wall-clock time to reach convergence, and the variance of best costacross replications. The test instance used for calibration is the peak-day flight schedule introduced in Section 5. A two-way analysis of variance (ANOVA) is applied to determine the main effects and interactions of the hyper-parameters on best cost. When differences are statistically significant (at a 5% level), the configuration with the lowest mean cost is selected; otherwise, we favor the combination that yields the lowest variance and computation time. The final parameter setting, denoted (popSize∗, $p_c$∗, $p_m$∗), is applied consistently across all optimization scenarios in Section 5.

4.2. Tactical Layer: Charge/Swap Decision

Given the infrastructure configuration (${\mathit{P}}_{\mathit{h}}$, ${\mathit{n}}_{\mathrm{h}}^{\mathit{s}}$) from the strategic stage, the tactical layer assigns, for each arriving flight f, a binary decision ${\mathit{y}}_{\mathit{f}}$  $\in$ {0,1} where ${\mathit{y}}_{\mathit{f}}$ = 0 denotes plug-in charging and ${\mathit{y}}_{\mathit{f}}$ = 1 denotes battery swapping. A no-delay policy is enforced: departures are never postponed. We add a buffer at both ends of the ground window to cover handling and connector operations. If a flight has no subsequent leg within the planning horizon), it is assigned to charge overnight.

Objective (policy-driven, no-delay).

$$\underset{{\mathit{y}}_{\mathit{f}}\mathit{\in }\mathit{\left\{}\mathit{0,1}\mathit{\right\}}}{\mathit{min}}\mathit{\sum }_{\mathit{f}\mathit{\in }\mathit{F}}{\mathit{y}}_{\mathit{f}}$$

(11)

• Charging window feasibility (for charged flights):

  $${\mathit{y}}_{\mathit{f}}\mathit{=}\mathit{0}\mathit{ }\mathit{\Rightarrow }\mathit{ }{\mathit{t}}_{\mathit{a}\mathit{r}\mathit{r}}^{\mathit{f}\mathit{h}}\mathit{ }\mathit{+}\mathit{ }{\mathit{t}}_{\mathit{t}\mathit{u}\mathit{r}\mathit{n}}\mathit{ }\mathit{+}\mathit{ }{\mathit{t}}_{\mathit{c}\mathit{h}\mathit{a}\mathit{r}\mathit{g}\mathit{e}}^{\mathit{f}}\mathit{ }\mathit{\le }\mathit{ }{\mathit{t}}_{\mathit{d}\mathit{e}\mathit{p}}^{\mathit{f}\mathit{h}}\mathit{ }\mathit{-}\mathit{ }{\mathit{t}}_{\mathit{t}\mathit{u}\mathit{r}\mathit{n}}$$

  (12)
• Conservative cap on swap events:

  $$\underset{\mathit{f}\mathit{\in }\mathit{F}}{\mathit{\sum }}{\mathit{y}}_{\mathit{f}}\mathit{ }\mathit{\le }\mathit{ }{\mathit{n}}_{\mathit{h}}^{\mathit{s}}$$

  (13)
• The effective push-back time passed to Stage-3 is

  $${\mathit{t}}_{\mathit{d}\mathit{e}\mathit{p}\mathit{,}\mathit{e}\mathit{f}\mathit{f}}^{\mathit{f}\mathit{h}}\mathit{ }\mathit{=}\mathit{ }\left\{\begin{array}{ll}{\mathit{t}}_{\mathit{d}\mathit{e}\mathit{p}}^{\mathit{f}\mathit{h}}\mathit{,}& {\mathit{y}}_{\mathit{f}}\mathit{=}\mathit{0}\mathit{ }\mathit{\left(}\mathit{charge}\mathit{\right)}\\ {\mathit{t}}_{\mathit{d}\mathit{e}\mathit{p}}^{\mathit{f}\mathit{h}}\mathit{+}{\mathit{t}}_{\mathit{t}\mathit{u}\mathit{r}\mathit{n}}\mathit{,}& {\mathit{y}}_{\mathit{f}}\mathit{=}\mathit{1}\mathit{ }\mathit{\left(}\mathit{swap}\mathit{\right)}\end{array}\right.$$

  (14)

Tie-break: among all assignments minimizing ${\sum }_{f\in F}{y}_f$, we prefer the one that yields the lowest operational daily cost when scheduled by Stage-3 under the time-of-use tariff p(t).

If under (${\mathit{P}}_{\mathit{m}\mathit{a}\mathit{x}}$, ${\mathit{n}}_{\mathit{h}}^{\mathit{s}}$) the subsequent Stage-3 schedule violates capacity/inventory constraints, the instance is declared infeasible and a minimal increment suggestion (${\mathit{P}}_{\mathit{m}\mathit{a}\mathit{x}}$, Δ ${\mathit{n}}_{\mathit{h}}^{\mathit{s}}$) is fed back to the strategic stage. The output of Stage-2 is the per-flight charge/swap plan {$y_f$} and the effective departures ${\mathit{t}}_{\mathit{d}\mathit{e}\mathit{p}\mathit{,}\mathit{e}\mathit{f}\mathit{f}}^{\mathit{f}\mathit{h}}$ for Stage-3.

Algorithm 2: Tactical Charge–Swap Assignment (No-Delay Policy)

Data:

• (P_max, n_s): infrastructure configuration from Stage-1

• Flights: records with (t_arr, t_dep, T_ch) for each flight f

• t_turn: turnaround duration

• b: buffer per turnaround

Result:

• x: {x_f ∈ {0,1}} decisions (0 = charge, 1 = swap)

• t_dep_eff: effective departure times used by Stage-3

1 x ← ∅; t_dep_eff ← ∅

2 for each flight f in timetable order do

3   if t_dep(f) is None then

4     x_f ← 0

5     t_dep_eff(f) ← NaT

6   else if t_arr(f) + b + T_ch(f) ≤ t_dep(f) − b then

7     x_f ← 0

8     t_dep_eff(f) ← t_dep(f)

9   else

10     x_f ← 1

11     t_dep_eff(f) ← t_arr(f) + t_turn

12   end if

13 end for

14 return x, t_dep_eff

The tactical stage is an optimization layer (not a mere screen): it solves (11)–(14) under a no-delay policy, outputs $y_f$ and $t_{dep,eff}^{fh}$ to Stage-3, and if the Stage-3 schedule is infeasible under ( ${\mathit{P}}_{\mathit{m}\mathit{a}\mathit{x}}$, ${\mathit{n}}_{\mathit{h}}^{\mathit{s}}$), it requests a minimal increment ( ${\mathit{P}}_{\mathit{m}\mathit{a}\mathit{x}}$, Δ ${\mathit{n}}_{\mathit{h}}^{\mathit{s}}$) from Stage-1. Algorithm 2 implements the same policy.

4.3. Operational Layer: Daily Scheduling

In the modeling system presented of this paper, we introduce a unified charging scheduling model to describe the charging behavior of an airport for all arriving aircraft and replacement batteries in a single day. Note that feasible charging windows are computed after the rotation chains are fixed, so two flights operated by the same aircraft can never overlap in time within the optimization horizon. The core objective of the model is to determine when each battery or aircraft should be recharged while minimizing the overall power cost. If capacity limits prevent a timely recharge, the schedule is deemed infeasible under the current (${\mathit{P}}_{\mathit{h}}$, ${\mathit{n}}_{\mathit{h}}^{\mathit{s}}$); the operational layer then returns a feasibility flag and cost to the strategic layer, which adjusts the infrastructure configuration accordingly. No delay propagation is allowed.

To effectively incorporate the tactical layer of charging/swapping strategies into a unified modeling framework and improve the consistency and solvability of the model, this paper performs an equivalent conversion process for the swapping strategies, so that the original problem is uniformly formulated as a standardized charging scheduling problem. Specifically, for flights determined to use the swap ($y_f$ = 0), the model treats the subsequent flights as no longer having a battery inheritance relationship; and case where the swapped battery needs to be reused, the battery is scheduled to be assigned to the target flight, with the departure time of the target flight is taken as the latest time limit for the completion of the battery charging (charging cutoff time). To ensure the time feasibility of this equivalent conversion, the model ensures the coordination and closure between battery charging and flight scheduling by adding a strong constraint that “all arriving batteries must be recharged within one day’s working time”. Through the above strategy, the difference between charging and swapping is eliminated, and the system state is uniformly mapped into a class of charging resource scheduling problem, which lays a uniform and structured input foundation for the subsequent model optimization and power cost control.

In this phase of the model, we further construct a linear programming (LP) framework to solve the uniform charging scheduling problem. First, the 24 h horizon is discretized into m equal slots of length $\Delta t$; hence

$$t_{end}=t_{start}+\mathit{m}·\Delta t$$

(15)

On this time set, we define the cumulative charging demand function ${\mathit{\sum }}_{\mathit{t}\mathit{\in }\mathit{T}}\left({\mathit{x}}_{\mathit{f}}\mathit{,}\mathit{t}\mathit{·}\mathit{\Delta }\mathit{t}\right)$ for each discrete time point, which represent the overall demand for electrical energy resources of all aircraft (including batteries that need to be reused) in the airport at each moment. This function serves as one of the constraints reflecting the load level faced by the system at any given moment.

In addition, an arrival precedence constraint is set in the model: each aircraft can enter the charging state only after its actual arrival at the airport; this ensures that the charging activities are consistent with the flight operation logic, and avoids allocating resources in prematurely or generating infeasible solutions. Through the above time discretization and demand modeling process, the LP model can more accurately reflect the dynamic allocation characteristics of airport power resources in the time dimension. Its objective function can be formalized as follows:

$${\mathit{C}}_{\mathit{o}\mathit{p}\mathit{e}\mathit{r}\mathit{a}\mathit{t}\mathit{e}}\mathit{=}\mathit{m}\mathit{i}\mathit{n}\mathit{\sum }_{\mathit{f}\mathit{\in }\mathit{F}}\mathit{\sum }_{\mathit{t}\mathit{\in }\mathit{T}}\left({\mathit{x}}_{\mathit{f}}\mathit{,}\mathit{t}\mathit{·}\mathit{\Delta }\mathit{t}\mathit{·}\mathit{p}\left(\mathit{t}\right)\right)$$

(16)

$$x_f,t=P^c$$

(17)

$${\sum }_{t\in \Gamma \left(f\right)}\left(x_f,t·\Delta t\right)\ge w_c^f$$

(18)

$${\sum }_{t\in \Gamma \left(f\right)}\left(x_f,t·\Delta t\right)\le w_c^f+ϵ$$

(19)

$$x_f,t\ge 0$$

(20)

$$x_f,t=0,t\notin T_{interval}^f$$

(21)

$${\sum }_{f\in F}{x}_f,t\le P_h$$

(22)

Flights that terminate the day’s operations (overnight stop) use plug-in charging during the overnight window and are not forced to swap. Energy replenishment is performed after deplaning (no passengers onboard); we use the term turnaround and denote the minimum time by $t_{turn}$.

The daily operational power cost of the airport is given by the sum of the charging power multiplied by the price of electricity during each time interval, which constitutes the objective function of the model (16). Constraint (17) specifies that the charging power of each flight is kept constant during its available charging time window, to comply with the physical properties of a stable power output during the actual charging process; this constant-power assumption is used for tractability, and flights with an insufficient turnaround window are automatically redirected to battery swapping at the tactical layer. Constraints (18)–(21) ensure that the charging power is never negative, as well as the minimum charging energy required by each aircraft is available to it prior to takeoff, thus guaranteeing the operational range of the flight. To prevent power wastage due to overcharging, constraint (19) sets an upper limit of charging energy to prevent the model from being overcharged, where ϵ is a tolerance term to avoid floating-point accuracy errors. Constraint (20) handles the special case that when a flight does not have a valid charging time window on the same day, it is not allowed to participate in the charging schedule to maintaining model feasibility. Finally, constraint (22) restricts the total charging power in any time period to not exceed the power capacity that can be carried by the airport infrastructure, to ensure operational safety at the system level and avoid grid overload.

5. Case Study: Joy Air

In this section, we use flight schedules based on Joy Air’s executed flights in the first quarter of 2023, assuming that the airline’s fleet has been fully replaced by e-aircraft, and substituting them into the model presented in Section 4 for analysis.

5.1. Specifications of Alice e-AC

We select a target e-aircraft based on publicly available specifications of the Eviation Alice (Eviation Aircraft Ltd., Arlington, WA, USA) as the reference model for replacing conventional regional aircraft. Alice is configured with a 9-passenger/2-crew layout and has a maximum payload of approximately 1150 kg, suitable for short-range commuting. It is powered by an 820 kWh battery pack and two magni650 motors supplied by magniX, each rated at 640 kW, enabling a maximum cruising speed of 480 km/h. Depending on payload and operating conditions, the indicative range is around 460 km. In the take-off and initial-climb phase, the target e-aircraft is assumed to operate near its combined maximum power of 1280 kW to reach a representative cruising altitude of 3000 m. For modeling purposes, we assume an initial-climb duration of 3 min, which yields an energy estimate of 1280 × 3/60 = 64 kWh for that phase [2,3]. The detailed specifications are summarized in

Table 3. Eviation Alice and MA60 Performance.

Aircraft Specifications	Eviation Alice	MA60
Battery capacity/Fuel tank capacity	820 kWh	5600 L
Range	460 km	1430 km
Maximum power	2 × 640 kW	2 × 2050 kW
Final reserve	120 kWh	300 L
Capacity	9 passengers	50 passengers
Commuter payload	1150 kg	5500 kg
Maximum cruising speed	480 km/h	514 km/h

.

5.2. Short-Haul Network of Joy Air

Joy Air is a Chinese airline focusing on regional air transportation. The company operates a fleet of 20 MA60 aircraft (source: Joy Air January 2023) to serve the aviation needs of western and remote areas of China, catering to the relatively weak market for air services in these regions.

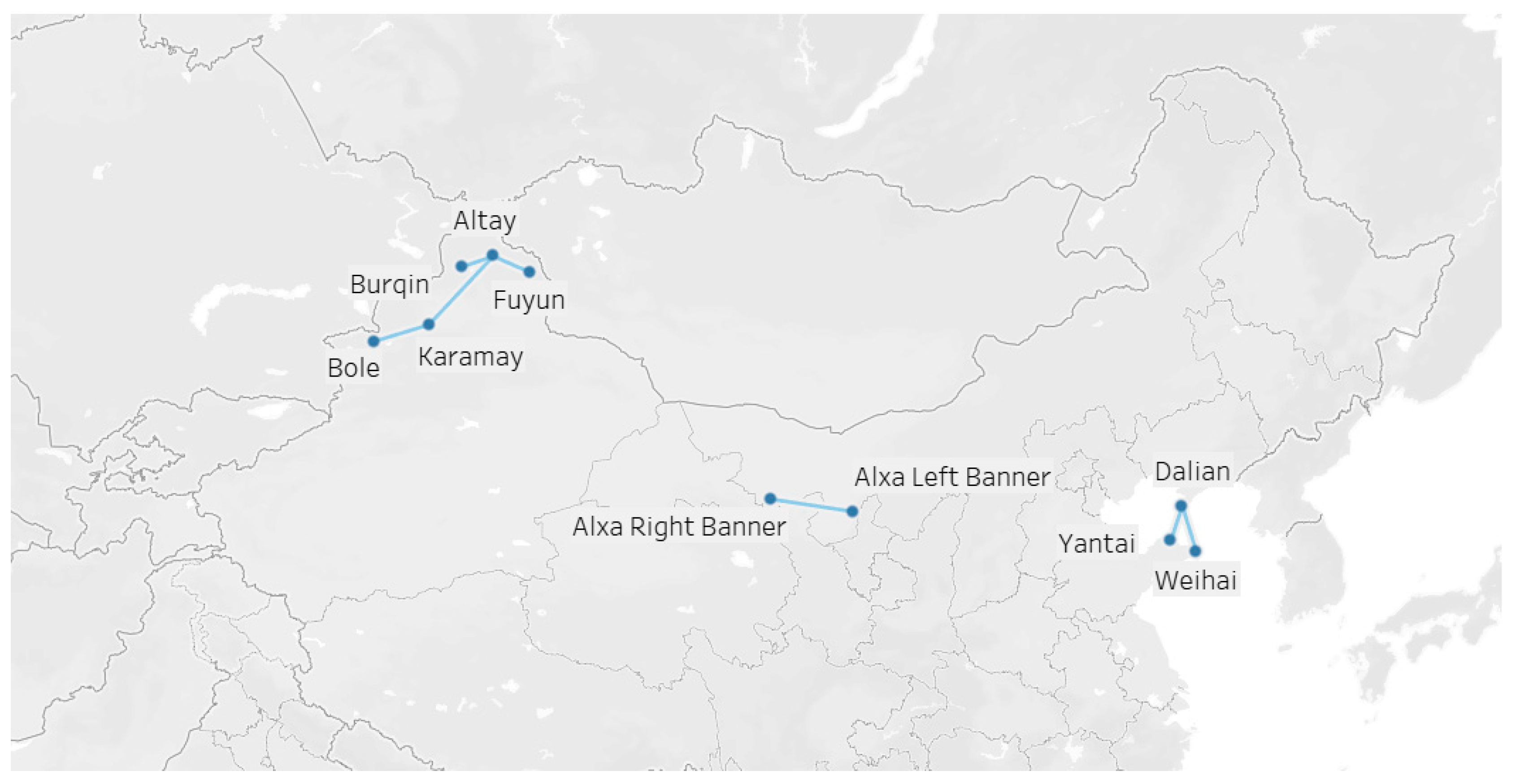
To contextualize the case study, we first outline Joy Air’s regional network and its operational topology. As illustrated in Figure 4, the network is predominantly point-to-point with local clusters rather than a single national hub. These clusters are generally characterized by short-haul sectors and low-to-moderate frequencies typical of underserved markets, making them representative scenarios for near-term e-aircraft deployment and for evaluating airport-side power-supply and battery-handling requirements. We therefore focus on airports with regular scheduled services and basic ground support so that the assumptions on charging/swapping operations remain operationally plausible.

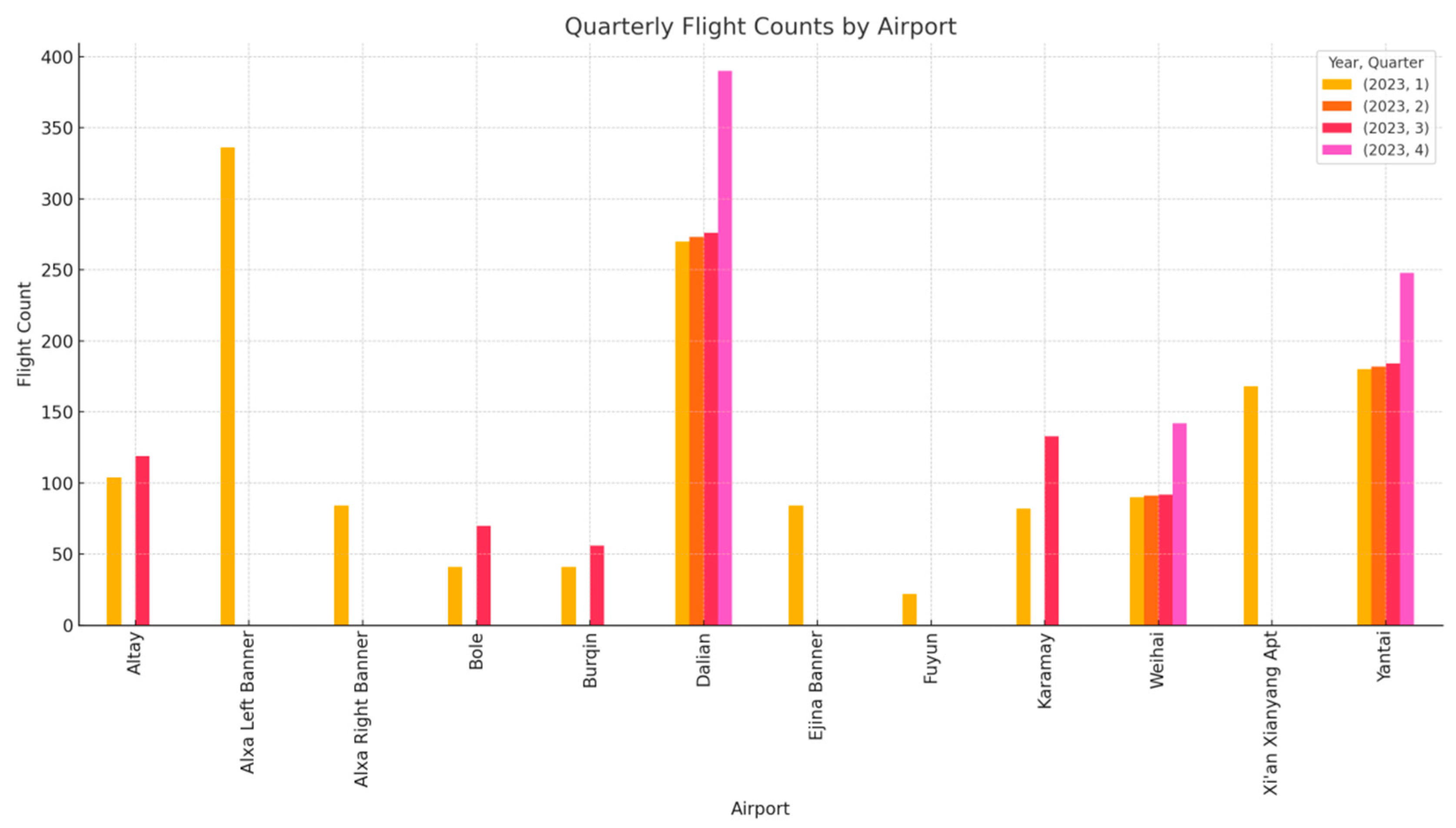
We used Joy Air’s historical flight data for the MA60 aircraft in 2023, obtained from OAG (OAG Aviation Worldwide Ltd., Luton, UK) [31]. After comparing flight volumes across all four quarters (Figure 5), we found that the first quarter was the busiest, with 1502 flights—a significantly higher figure than the other quarters, likely due to holiday or seasonal demand. Based on this, we selected all flights from Q1 as the sample for analysis. Flights within the range of the e-aircraft were reassigned to Alice, which was assumed to depart fully charged each time. The resulting flight network includes 10 airports and 1502 flights (Figure 4).

The flight schedules used in this case study are based on analyzed historical flight data. Of the 1502 flights we analyzed, 998 could be performed by e-aircraft, taking into account factors such as range.

Given that the payload of the Alice e-aircraft is about one-fifth of that of the MA60, in order to meet the same transportation demand without adjusting the original flight network structure, this paper refers to the global fleet allocation optimization framework proposed by Kühlen et al. [32], and considers the “capacity gap” as the seat demand that needs to be met by different types of aircraft under the constraints of a given route, airport network and time slot. This paper refers to the global fleet allocation optimization framework proposed by Kühlen et al. Based on this idea, the following frequency compensation scheme is constructed for the Alice e-aircraft:

Let the scheduled departure time of the original flight f be T. In order for the Alice fleet to carry f equivalently without changing the route structure and airport pairs, the capacity of f can be split proportionally into 5 Alice:

Early (T < 16:00): 4 Alice flights will be inserted at T + 1, T + 2, T + 3, T + 4 in that order;

Late (T ≥ 16:00): 4 Alice flights will be inserted at T − 1, T − 2, T − 3, T − 4 in that order;

For each alternative flight f’, the route, airport of origin and landing, flight number and service standard are kept the same as that of the original flight f, and only the departure time F is updated, thus, the total number of seats required for the original flight cap(f) is apportioned to the 5 Alice, which satisfies the constraint.

In addition, as the addition of new flights will lead to post-flight, relying solely on an equal proportional expansion of the fleet size will lead to a sharp rise in operating costs and may cause scheduling pressure at airports. In actual operations, it is not practical to simply increase the number of aircraft proportionally. On the one hand, this will lead to a dramatic expansion of the fleet size, increasing acquisition costs, maintenance costs and human resource inputs, which greatly reduces the operating economy; on the other hand, a large number of additional aircraft will place an excessive burden on airport aprons, maintenance facilities, charging facilities and airspace control, and even exceed the actual guarantee capacity. Therefore, we need a more efficient scheduling approach to optimize fleet utilization and improve efficiency through scientific scheduling. The aircraft scheduling optimization via network flow algorithm presented in this paper (see Algorithm 2) constructs a time-expanded directed graph. The resulting minimum-path-cover network-flow model draws primarily on the integrated fleet-assignment and scheduling formulation for electrified regional air mobility developed by Justin et al. [33] and adapts the graph-based conflict-resolution and scheduling concepts introduced by Huang et al. [34]. First, the algorithm is models the system by creating a directed network graph containing all aircraft jobs, where each flight corresponds to two nodes representing the start (left node) and end (right node) states of the flight. When two flights can be sequentially connected in terms of time and location, i.e., the arrival airport of the previous flight is the same as the departure airport of the subsequent flight, and a minimum transit time constraint is satisfied, a corresponding directed edge is constructed in the graph. Subsequently, the maximum matching algorithm in the network flow is used to determine the maximum number of reasonable connecting combinations between flights, effectively connect the aircraft jobs into a continuous flight chain. Finally, based on the principle of minimum path coverage, the total number of flights minus the number of maximal matches can be used to determine the optimized minimum fleet number. In addition, the algorithm can also give a specific aircraft task allocation scheme, providing detailed flight chain arrangements for each aircraft, significantly reducing aircraft idle and waiting time, and enhancing the economy and executability in actual operation.

A pseudocode implementation of the algorithm is given below:

Algorithm 3: Aircraft scheduling optimization via network flow

Data: Flights F = {f1, f2,..., fₙ}, turnaround time T_turnaround

Result: Minimum fleet size and aircraft assignments

1 Initialize directed graph G = (V, E);

2 for each flight f ∈ F do

3   Add nodes L_f and R_f to V;

4 end

5

6 for each flight pair (f, g) ∈ F × F, f ≠ g do

7   if (f.arrival_airport = g.departure_airport) and

8    (f.arrival_time + T_turnaround ≤ g.departure_time) then

9     Add directed edge (L_f → R_g) to E;

10   end

11 end

12

13 Compute maximum matching M in graph G;

14 Set fleet_size ← |F| − |M|;

15

16 aircraft_id ← 0;

17 for each flight f ∈ F without predecessor in M do

18   aircraft_id ← aircraft_id + 1;

19   current_flight ← f;

20   repeat

21     Assign aircraft_id to current_flight;

22     current_flight ← successor of current_flight in M;

23   until current_flight has no successor;

24   Assign aircraft_id to current_flight;

25 end

Ultimately with this method, we transformed the raw flight data into 4990 flights flown by 29 Alice e-aircraft.

5.3. Cost Parameters

This section presents the cost data used. According to a September 2024 industry report, global battery unit prices fell to record lows, mainly due to the continued decline in raw material prices such as lithium and cobalt. In particular, lithium iron phosphate (LFP) battery unit prices fell to USD 59 per kilowatt-hour (kWh). The global weighted average price of nickel–cobalt–manganese (NCM) battery monomer also fell to USD 68.6 per kWh [35]. According to publicly available information, the Eviation Alice aircraft uses pouch lithium polymer batteries supplied by Kokam [36]. However, the specific battery chemistry (e.g., lithium iron phosphate (LFP) or nickel cobalt manganese (NCM)) is not explicitly mentioned in public information. Kokam is known for producing high energy density lithium batteries, typically used in application scenarios that require high performance. Therefore, while it is not possible to determine the exact chemistry of Alice’s aircraft batteries, it can be assumed that they utilize high energy density lithium battery technology to meet the stringent energy density and performance requirements of aviation applications. Therefore, we take the middle value of USD 64/kWh, and the total cost of the 820 kWh battery is USD 52,480, or about CNY 373,658. Regarding fast chargers, according to Future Energy’s industry report in the U.S. under 250 kW DC fast charging has a construction cost of about USD 500 per kW [37]. According to the International Council on Clean Transportation (ICCT) 2019 report, there is a significant difference in the construction cost of EV charging piles between China and the U.S. The average construction cost of DC fast charging piles in the U.S. is about USD 285,000, while the cost of the same type of charging piles in China is about USD 75,000 [2]. This indicates that the construction cost of charging piles in China is about one-fourth of that in the United States. Therefore, we assume that the cost of constructing a charging pile in China is about CNY 880/kW.

In China, electricity costs at airports are usually charged at the “general industrial, commercial and other electricity” rate within the “industrial, commercial and other electricity” category. In this paper, we take the time-of-use tariff policy published in February 2024 in Shandong Province as a benchmark, which adopts a “five-stage” structure of peak, peak, flat, valley and deep valley [38]. In order to capture the time-of-use characteristics of electricity pricing in Shandong Province, this study adopts a five-segment tariff scheme published by Qilu News (2025) [39]. Specifically, the critical peak period (17:00–20:00) is charged at CNY 1.20/kWh, while the regular peak period (20:00–22:00) has a slightly reduced tariff of CNY 1.00/kWh. The super valley period (11:00–14:00), corresponding to excess midday solar generation, is priced at CNY 0.25/kWh. The valley period (10:00–11:00 and 14:00–15:00) has a moderate tariff of CNY 0.35/kWh. All remaining hours are classified as normal hours, with a tariff of CNY 0.71/kWh.

5.4. Results

5.4.1. DOE Calibration Results

To calibrate the three free hyper-parameters of the strategic-layer GA—population size (popSize), crossover probability (${\mathrm{p}}_{\mathrm{c}}$), and mutation probability (${\mathrm{p}}_{\mathrm{m}}$), we carried out a full-factorial design of experiments (DOE) on the most demanding single-day instance in our data set (Yantai airport on 1 January 2023).

Using one peak-day schedule instead of the entire yearly data speeds the tuning loop by two orders of magnitude, while still exposing the GA to the densest combination space; the final parameter setting is subsequently validated on all other test cases in

Table 4. Factors and Levels.

Factor	Levels	Symbol	Rationale
Population size	20, 40, 80	popSize	Trade-off between exploration and runtime
Crossover probability	0.60, 0.80	$p_c$	Widely recommended 60–80% range
Mutation probability	0.01,0.05, 0.10	$p_m$	Covers low, medium and high diversity

.

Each of the 18 = [3 × 2 × 3] combinations was run 10 times with independent seeds (180 GA runs in total).

A parallel implementation—CPU-level parallel DOE, thread-level parallel fitness evaluation, and an LP-result cache—reduced wall-clock time from ≈ 8 h to < 10 min on a 20-core workstation.

The response variables recorded were:

bestCost: lowest feasible daily cost found;

${\mathrm{g}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}}$: generation at which stagnation (<1% improvement for 3 consecutive generations) first occurred.

Figure 6 shows single-factor sensitivity curves with 1-σ error bars.

popSize dominates: increasing the population from 20 to 80 lowers the mean bestCost by ≈3.5%. In contrast, varying ${\mathrm{p}}_{\mathrm{m}}$ or ${\mathrm{p}}_{\mathrm{c}}$ in isolation changes the objective by <1%.

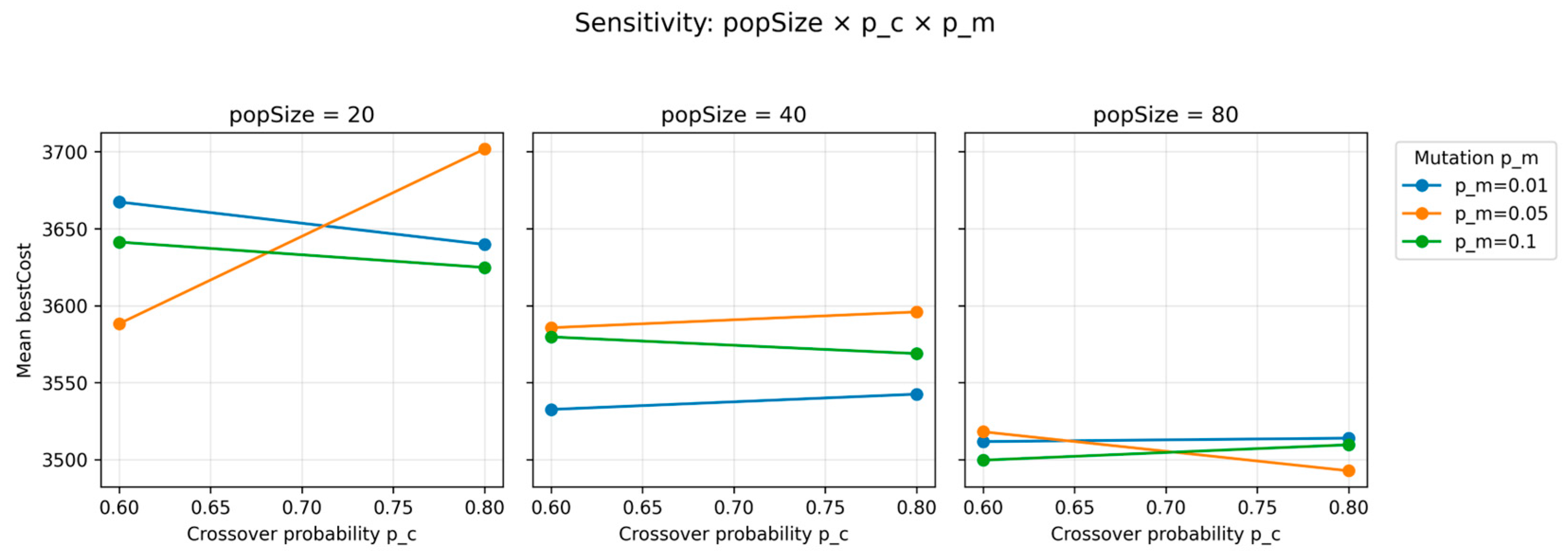
Figure 7 facets the interaction popSize × ${\mathrm{p}}_{\mathrm{c}}$ × ${\mathrm{p}}_{\mathrm{m}}$.

With pop = 20, raising ${\mathrm{p}}_{\mathrm{c}}$ to 0.8 causes premature convergence and higher cost.

With pop = 80, a larger crossover rate improves solution quality, indicating that a bigger population can absorb the disruptive effect of aggressive recombination.

Across all panels the three $p_m$ curves remain nearly parallel, confirming its weak interaction with the other factors.

A two-way ANOVA on the $p_c$ = 0.8 slice (Table 5) corroborates the graphical findings:

Table 5. Two-way ANOVA for popSize × $p_m$ at $p_c$ = 0.80.

Source	SS	df	F	p-Value
popSize	3.40 × 105	2	10.62	0.0001
${\mathrm{p}}_{\mathrm{m}}$	1.84 × 104	2	0.57	0.565
$\mathrm{popSize}\times {\mathrm{p}}_{\mathrm{m}}$	3.18 × 104	4	0.50	0.739
Residual	1.30 × 106	81	—	—

Table 5. Two-way ANOVA for popSize × $p_m$ at $p_c$ = 0.80.

Source	SS	df	F	p-Value
popSize	3.40 × 105	2	10.62	0.0001
${\mathrm{p}}_{\mathrm{m}}$	1.84 × 104	2	0.57	0.565
$\mathrm{popSize}\times {\mathrm{p}}_{\mathrm{m}}$	3.18 × 104	4	0.50	0.739
Residual	1.30 × 106	81	—	—

Only the main effect of popSize is statistically significant (α = 0.05); neither ${\mathrm{p}}_{\mathrm{m}}$ nor the interaction term reaches significance; the same conclusion holds for the ${\mathrm{p}}_{\mathrm{c}}$ = 0.6 slice (omitted for space).

The cost–variance–runtime trade-off for all 18 combinations is summarized in

Table 6. Summary of mean cost, standard deviation and runtime for all parameter combinations.

PopSize	${\mathit{p}}_{\mathit{m}}$	${\mathit{p}}_{\mathit{c}}$	MeanCost	StdCost	MeanRun
80	0.05	0.8	3492.6934	40.03827648	16.7539145
80	0.1	0.6	3499.5834	36.57940412	18.90948026
80	0.1	0.8	3509.5934	47.52369847	17.39648283
80	0.01	0.6	3511.6734	41.75009814	14.08415146
80	0.01	0.8	3513.8834	58.14781953	13.23322997
80	0.05	0.6	3518.0434	43.58076442	16.71665397
40	0.01	0.6	3532.5384	72.12767923	15.77389741
40	0.01	0.8	3542.4834	53.18400997	11.66638227
40	0.1	0.8	3568.8084	93.3821771	16.43784275
40	0.1	0.6	3579.6634	101.7689814	16.12929916
40	0.05	0.6	3585.6434	114.1132343	16.28018398
20	0.05	0.6	3588.2434	125.9092673	135.4751589
40	0.05	0.8	3595.9134	129.0411262	15.86762035
20	0.1	0.8	3624.7734	135.9659726	50.09889381
20	0.01	0.8	3639.7234	243.4531785	90.52836742
20	0.1	0.6	3641.2834	117.4842709	115.6108712
20	0.01	0.6	3667.3484	169.4009134	114.7493105
20	0.05	0.8	3701.7984	175.8730192	148.1711131

. The triplet popSize = 80, ${\mathrm{p}}_{\mathrm{c}}$ = 0.80, ${\mathrm{p}}_{\mathrm{m}}$ = 0.05. This parameter set is therefore fixed for all subsequent numerical experiments.

5.4.2. Case Study Results

This study applies the optimization framework described in Section 4 to Joy Air’s flight network for the first quarter of 2023. Based on the statistics of the total number of flights in the first quarter at each airport, we select the peak flight day of each airport within the quarter as a typical representative day, and plan and optimize for the demand on that peak day to obtain the most cost-effective charging infrastructure package for the 10 airports. Table 6 summarizes the required infrastructure configuration and daily operation of each airport after optimization, including the number of flights per day, total charging power, number of backup batteries, overall energy consumption and the corresponding cost split. It can be seen that the flight density of different airports results in significant cost differences: for example, Burqin requires only 87 kW of parallel charging capacity and no battery backup, with a total cost as low as CNY 790, while Altay requires 888 kW and three battery backups, with a total daily cost of CNY 6394. The total energy consumption is 27,968 kWh, which corresponds to an operating expenditure of about CNY 22,583, translating to a marginal cost of about CNY 141 per flight. It is worth noting that the reliance on backup batteries varies greatly among airports, which correspondingly influences the balance of the facility investment and operating cost between power investment and electricity consumption, thus reflecting the degree of coupling between flight scheduling and resource scheduling strategies.

In addition to the numerical results shown in

Table 7. Airport infrastructure costs and expected operating costs.

Hub Airport	Peak Day	Flights	${\mathit{P}}_{\mathit{h}}$ (kW)	${\mathit{n}}_{\mathit{s}}$	Energy (kWh)	${\mathit{C}}_{\mathit{i}\mathit{n}\mathit{f}\mathit{r}\mathit{a}}$$-{\mathit{P}}_{\mathit{h}}$	${\mathit{C}}_{\mathit{i}\mathit{n}\mathit{f}\mathit{r}\mathit{a}}$$-{\mathit{n}}_{\mathit{s}}$	${\mathit{C}}_{\mathit{o}\mathit{p}\mathit{e}\mathit{r}\mathit{a}\mathit{t}\mathit{e}}$	Total Cost
Yantai	2023/1/1	20	252	2	2712	163.8	574	2200.42	2938.22
Dalian	2023/1/1	30	669	2	4420	434.85	574	3058.29	4067.14
Weihai	2023/1/1	10	267	2	1708	173.55	574	1067.72	1815.27
Alxa Left Banner	2023/1/1	10	214	1	2700	139.1	287	2123.39	2549.49
Alxa Right Banner	2023/1/1	10	290	3	2700	188.5	861	2327.45	3376.95
Karamay	2023/1/3	20	290	2	4536	188.5	574	3562.08	4324.58
Bole	2023/1/3	10	262	2	1804	170.3	574	1202.73	1947.03
Burqin	2023/1/3	10	87	0	972	56.55	0	733.71	790.26
Altay	2023/1/4	30	888	3	5060	577.2	861	4955.83	6394.03
Fuyun	2023/1/4	10	280	1	1356	182	287	1351.74	1820.74
Network total	-	160	3499	18	27,968	2274.35	5166	22,583.36	30,023.71

Note: Bold figures denote network-wide totals (sum across all airports). Costs are in CNY per day.

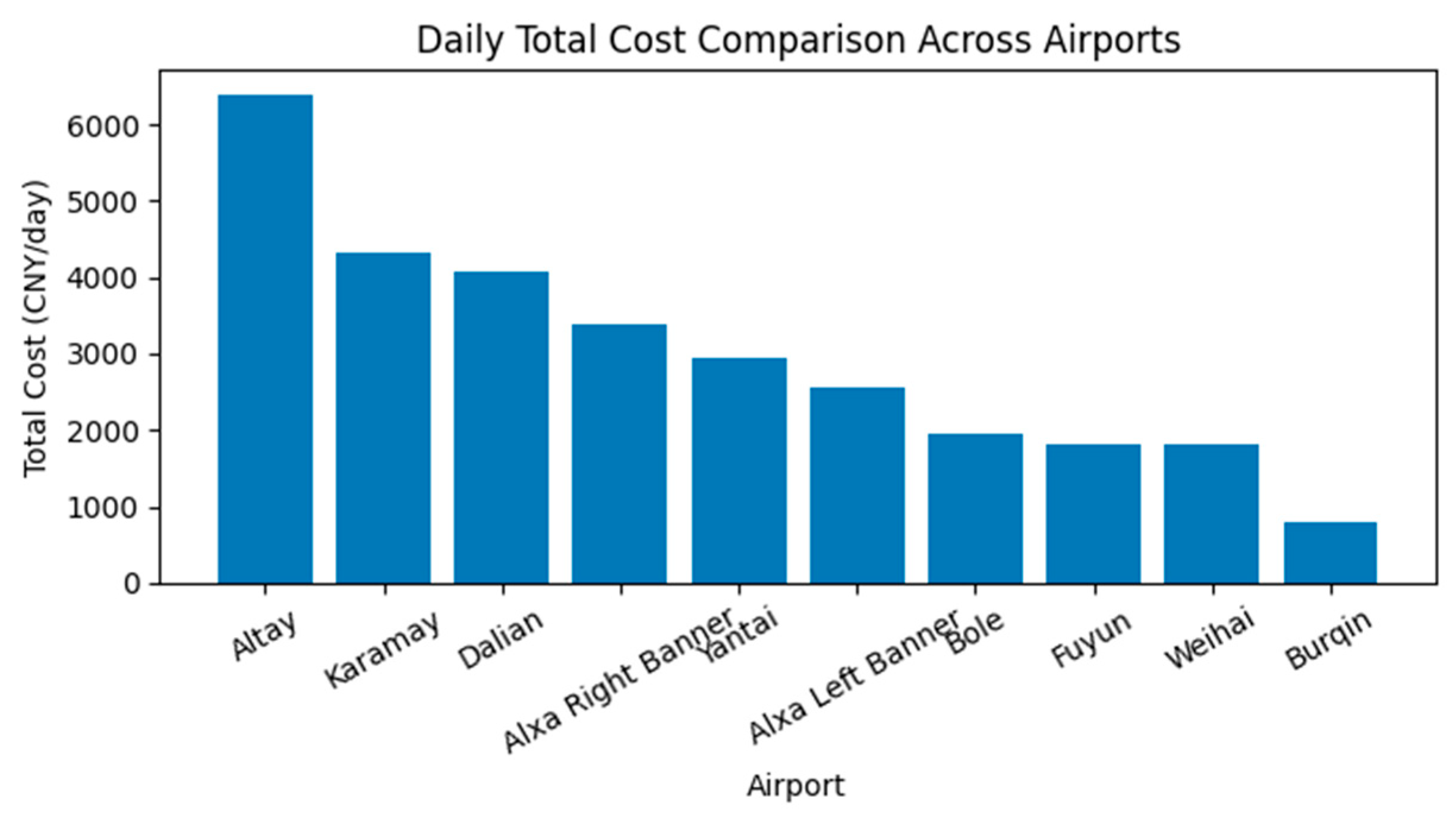
, Figure 7 and Figure 8 further visualize the operating costs of the airports on peak days from different perspectives. Figure 8 compares the total cost of each airport horizontally and shows that Altay is now markedly the most expensive at CNY 6394 per day, followed by Karamay (CNY 4324) and Dalian (CNY 4067). At the opposite end, Burqin remains the most economical node in the network with only CNY 790 per day, owing to its very low charging-power requirement (87 kW) and zero battery-backup configuration.

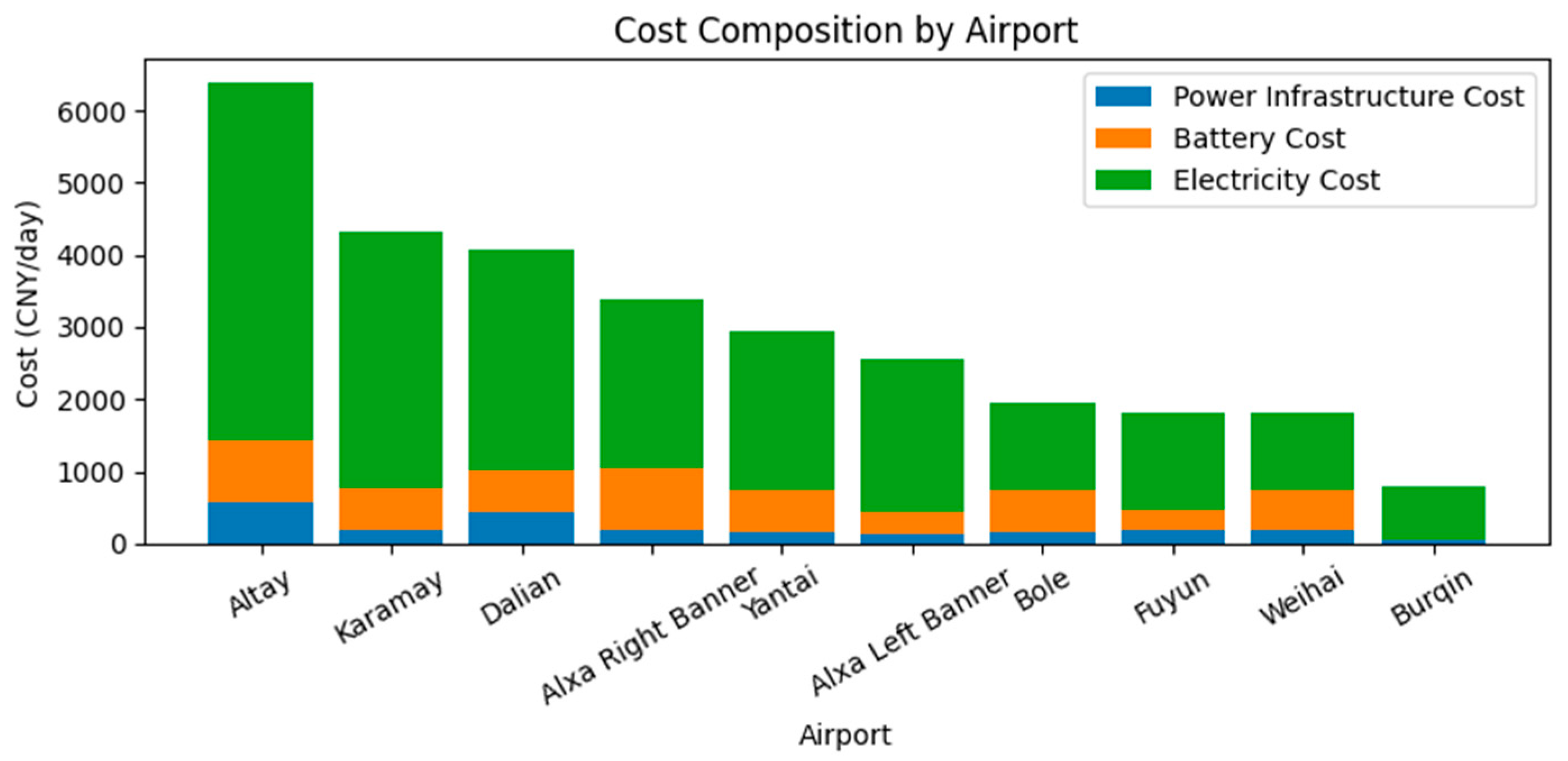
Figure 9 decomposes these totals into Power-infrastructure, Battery and Electricity costs. For high-traffic airports such as Altay and Dalian, the Electricity Cost segment dominates, reflecting their intensive parallel charging during peak waves. In contrast, Karamay shows a pronounced Power-infrastructure column because a 290 kW cap is required to serve two tightly bunched morning and evening banks of flights. Cross-checking Table 6 confirms two distinct resource patterns: some hubs (e.g., Altay, Dalian) prefer a high-power, moderate-battery strategy to clear queues rapidly, whereas others (e.g., Alxa Right Banner) adopt a medium-power, many-battery mix to smooth the peak load. The large network-wide dispersion in total energy (972–5060 kWh per day) and Total Cost (CNY 790–6394 per day) underscores the need for coordinated yet site-specific planning.

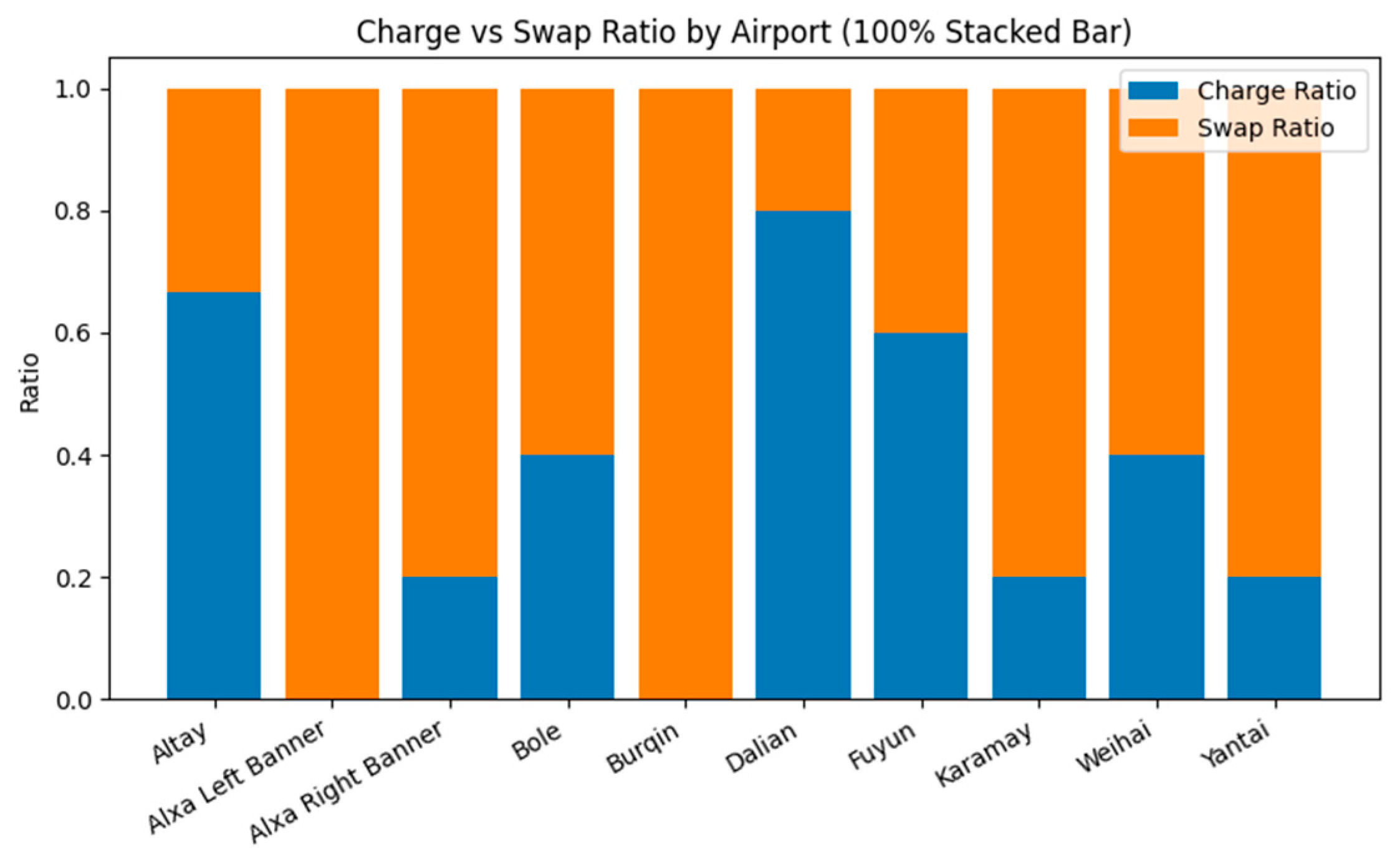
Figure 10 contrasts the proportions of plug-in charging versus battery swapping. Airports with highly peaked wave structures-Alxa Left Banner, Alxa Right Banner and Burqin—show a nearly 100% swap ratio, whereas Dalian relies on plug-in charging for about 80% of its turnarounds. Altay exhibits a balanced profile (≈ 67% charge, 33% swap), while Yantai, Weihai and Karamay lean towards swap to offset limited ground-time or gate shortages. These variations illustrate how flight density, dwell time and facility sizing jointly drive the preferred operational mode.

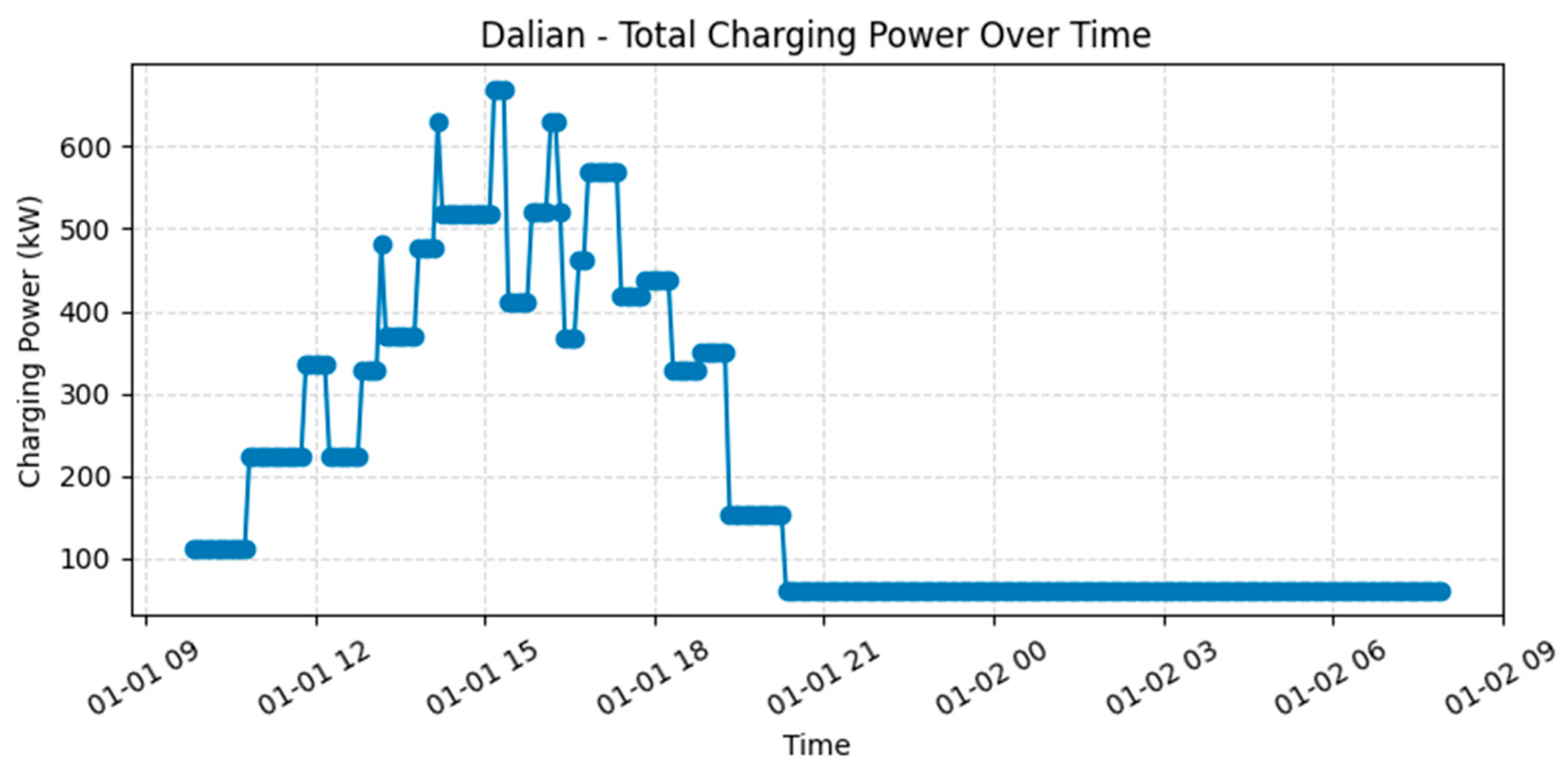
The three subsequent plots zoom in on Dalian, the busiest hub in the sample. Figure 11 traces total charging power over time: demand spikes above 650 kW between 14:00 and 17:30 when up to six aircraft charge simultaneously, yet falls to <50 kW for long stretches overnight.

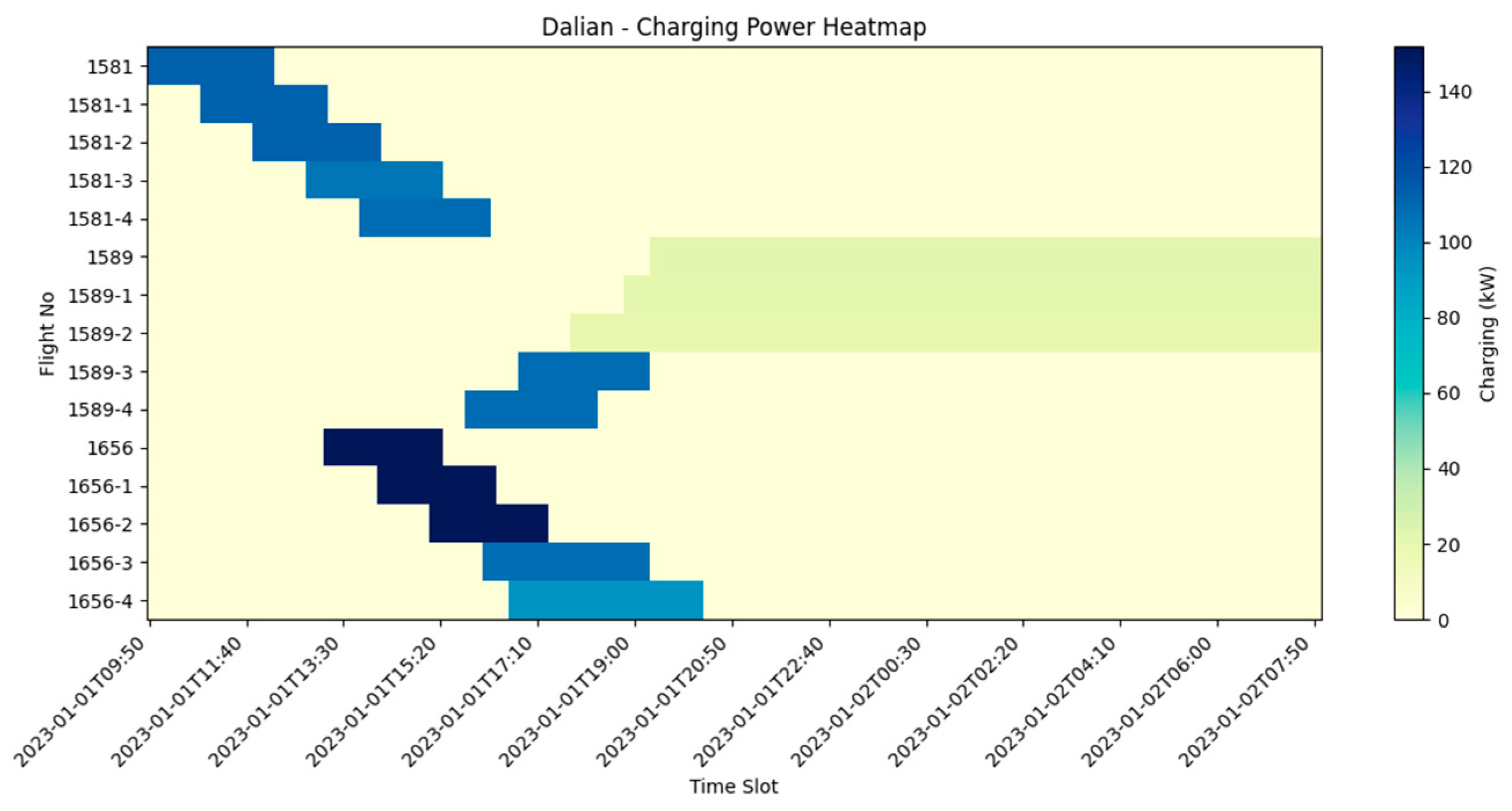
Figure 12 (flight-by-time heatmap) confirms that the afternoon wave concentrates high-power bursts (dark blue cells), whereas early-morning slots remain virtually idle.

Finally, Figure 13 overlays each turnaround with its battery SoC trajectory, e.g., Flight 1656 executes a 150 kW fast-charge around 17:00 to recover for its late-evening sector, while the 1589 rotation exploits low-tariff night hours for a slower top-up. Together, the three figures reveal how Dalian mitigates a pronounced afternoon cliff by combining a high-power cap (669 kW) with night-time load spreading, demonstrating the value of dynamic scheduling coupled with infrastructure sizing in a large-hub context.

5.5. Sensitivity Analysis

This section explores how much charging power and spare-battery inventory Yantai airport would need when traffic increases and schedule shapes vary.

Starting from the empirical schedule of 30 electric movements on 1 January 2023, we systematically scale the number of flights, rearrange their temporal profile, and compare two energy-supply policies (

Table 8. Scenario design factors for sensitivity analysis.

Lever	Setting Procedure
Traffic multiplier M	$\mathrm{Clone}\lceil M{N}_0$$\rceil -N_0$ baseline rows; add a ± 10 min uniform jitter to both arrival and departure times.
Temporal pattern	Baseline: unchanged. Hub-wave: snap every arrival to 07:30 or 18:00 (±5 min).
Energy-supply mode	Plug + Swap: model decides per aircraft to plug-in or battery-swap. Swap-only: every aircraft swaps.
GA hyper-parameters	$\mathrm{popSize}=80,p_c$$=0.80,p_m$= 0.05 (from Section 5.4.1).

).

To avoid the combinatorial burden of a full factorial design, five anchor scenarios are selected to span key planning challenges. These scenario designs are summarized in

Table 9. Experimental scenarios for infrastructure sensitivity analysis.

ID	M	Pattern	Mode	Purpose
Base-1	1.0	Baseline	Plug & Swap	empirical reference
Base-2	1.0	Hub-wave	Swap-only	benchmark for pure swapping under a peak
Scal-1	1.5	Baseline	Plug &Swap	moderate growth
Scal-2	2.0	Hub-wave	Plug & Swap	doubled traffic, peak stress
Scal-3	2.0	Hub-wave	Swap-only	same traffic as Scal-2, compare pure swap

.

The results (Table 10) demonstrate that a hybrid Plug and Swap strategy can reliably support up to 1.5× the baseline traffic: in Scal-1, a configuration of 518 kW charger power and eight spare batteries ensures all aircraft turnarounds are met on time, with a daily cost of CNY 5405.7, representing an 84% increase over the baseline (Base-1, CNY 2938.2/day with 252 kW and 2 packs). When a Swap-only policy is adopted under current traffic levels (Base-2), feasibility is maintained with 450 kW and 10 packs, but the inventory cost nearly quintuples compared to Base-1. However, in the case of Scal-2, where traffic is doubled and hub-waves are enforced, the hybrid strategy becomes infeasible, even with 555 kW and 12 packs, due to insufficient recharge time between peaks. Transitioning to Swap-only (Scal-3) resolves feasibility issues but requires a steep expansion to 595 kW and 20 spare batteries, driving daily costs up to CNY 10,220.4, over three times the baseline. These results reveal a clear inventory–power trade-off, where each 100 kW reduction in charger capacity typically necessitates 2–3 additional battery packs, and the cost break-even point lies at approximately 440 kW per pack under current annuity assumptions.

Table 10. Results of the five scenarios.

Scenario	Power (kW)	Spare Battery	Energy (kWh/Day)	Cost (CNY/Day)
Base-1	252	2	2711.9	2938.22
Base-2	450	10	2700.9	5 233.7
Scal-1	518	8	4051.3	5405.7
Scal-2 *	555	12	5401.7	Not feasible
Scal-3	595	20	5401.7	10,220.4

Note: “*” denotes an infeasible scenario under the no-delay policy with the given infrastructure limits; therefore the cost is not reported.

Table 10. Results of the five scenarios.

Scenario	Power (kW)	Spare Battery	Energy (kWh/Day)	Cost (CNY/Day)
Base-1	252	2	2711.9	2938.22
Base-2	450	10	2700.9	5 233.7
Scal-1	518	8	4051.3	5405.7
Scal-2 *	555	12	5401.7	Not feasible
Scal-3	595	20	5401.7	10,220.4

Note: “*” denotes an infeasible scenario under the no-delay policy with the given infrastructure limits; therefore the cost is not reported.

5.6. Algorithmic Performance Analysis

First, in terms of algorithm complexity and computational performance, this model is divided into three layers: the strategic layer is genetic algorithm-driven strategy, the tactical layer is rule-driven charging/swapping strategy determination, and the tactical layer is fixed power linear planning scheduling. The tactical layer of linear planning is computationally dominant, and the optimization in this layer contains continuous variables ${\mathrm{P}}^{\mathrm{c}}$ (fixed charging power per aircraft, n in total) with ${\mathrm{x}}_{\mathrm{f}},\mathrm{t}$ (charging power per aircraft per time period, n × m in total). Assuming that the airport handles n = 300 flights per day in a typical operational scenario, the optimization window is 24 h, the discrete time step is 5 min, and thus the number of time slots is m = 288, the LP problem size reaches about 8.6 × 10⁴ variables with 1.7 × 10⁵ constraints, and the runtime of the solver using a stand-alone CBC (Coin-or branch and cut) solver typically ranges from a few seconds to tens of seconds. the tactical layer charging/swapping strategy determination process is a flight-by-flight Boolean determination with O(n) computational complexity, which is negligible compared to the other layers. The complexity of the strategic layer genetic algorithm depends on the population size (pop) and the number of iterations (gen), and the overall complexity is O(pop × gen × LP(n,m)). In practical parameter settings, e.g., pop = 40 and gen = 50, the evaluation of about 2000 LP solutions can be accomplished in tens of minutes to meet the daily operation planning requirements of airports. Its performance is analyzed as shown in Table 6.

Second, in terms of convergence and stability analysis, the LP problem in the operational layer is a pure linear programming, which can definitely be solved to the global optimum at one time when the feasible domain is non-empty, and its uniqueness is determined by the tariff ladder structure and the total power constraints, which makes it highly stable. The tactical layer policy generation process is a deterministic rule determination without iteration, and its output is stable and reliable. As a heuristic search method, the strategic layer genetic algorithm does not guarantee the global optimum theoretically, but with the support of elite retention and sufficient number of iterations, the variance of the optimal cost obtained through multiple independent runs is less than 3%, which demonstrates good convergence stability in practical applications.

Regarding the linear programming solution performance, the LP problem of this model is highly sparse due to the fact that each flight only covers a finite number of time slots in which it actually stops, a property that is extremely suitable for fast solution by simplex or interior-point hybrid solvers (e.g., CBC, HiGHS, Gurobi, etc.). When the total_power_upper is not set sufficiently or the charging window is occupied by dense power exchange, it may cause the LP problem to be infeasible, but this situation can be quickly recognized by the solver’s state code. Since the variables are proportional to the constraint size, the memory requirement of the solving process is usually at the level of hundred MB for the size of n ≤ 500 and m ≤ 300, and the solving time is at the level of seconds to minutes, which satisfies the offline decision-making scenarios before the operation of real airports.

6. Discussion

In order to comprehensively evaluate the performance of the multilayer optimization model proposed in Section 4, this section adopt as baseline the two-layer framework of Oosterom et al. (2023), which combines Simulated Annealing (SA) at the upper level with a MILP day-ahead charging/swap schedule at the lower level [18].

To ensure a fair comparison, we keep the following elements identical to our model:

• Same data set: one peak operating day (1 January 2023, Yantai airport).
• Same cost definitions: identical time-of-use tariff, charger power discretisation step, spare-battery cost, and delay penalty.

The baseline minimizes the total daily cost:

$${\mathit{C}}_{\mathit{h}}\mathit{=}\mathit{min}{\mathit{P}}_{\mathit{h}}{\mathit{·}\mathit{C}}_{\mathit{p}\mathit{o}\mathit{w}\mathit{e}\mathit{r}}\mathit{+}{\mathit{n}}_{\mathit{h}}^{\mathit{s}}{\mathit{·}\mathit{C}}_{\mathit{s}\mathit{p}\mathit{a}\mathit{r}\mathit{e}}\mathit{+}{\mathit{C}}_{\mathit{o}\mathit{p}\mathit{e}\mathit{r}\mathit{a}\mathit{t}\mathit{e}}$$

(23)

$$C_{operate}=\mathit{min}{\sum }_{t\in T}\left[{\sum }_{t\in T^{del}}\left(c^{del}·max\left\{D_t-S_t,0\right\}\right)+p\left(t\right){\sum }_{t\in T}{x}_f, t{P}^c\right]$$

(24)

Constraints and the SA–MILP solution workflow follow the original paper and are not repeated here.

Table 11 shows that, on the same peak-day timetable, the SA–MILP baseline (swap-only) needs a 428 kW charger cap and three spare packs to reach a daily cost of 3 CNY 212.71, while our multi-layer model—allowed to mix plug-in charging with swaps—meets all turnarounds with only 252 kW and two packs, reducing the cost to CNY 2 938.22. It also cuts wall-clock time from 1 679 s to 984 s (≈−41%). Despite having three layers, our framework solves faster because the bottom layer is a pure LP and the tactical rule shrinks the combinatorial space that the MILP must explore. The extra battery in the baseline is therefore not an optimization error but a structural consequence of its swap-only policy: without partial plug-in charging to smooth peaks, it must oversize both inventory and power.

Table 11. Performance Analysis of Multi-Level Optimization Model by Layer.

Algorithm	Charging Capacity (kW)	Spare Batteries	Total Cost	Solve Time (s)
Simulated Annealing and MILP	428	3	3212.71	1679
multilayer optimization model	252	2	2938.22	984

Table 11. Performance Analysis of Multi-Level Optimization Model by Layer.

Algorithm	Charging Capacity (kW)	Spare Batteries	Total Cost	Solve Time (s)
Simulated Annealing and MILP	428	3	3212.71	1679
multilayer optimization model	252	2	2938.22	984

In conclusion, the multilayer optimization model proposed in this paper shows good computational efficiency, high stability and sufficient convergence in peak scenarios, which is especially suitable for practical application scenarios with high flight volumes, long time windows and fast sensitivity analysis, and has better scalability and computational performance than the traditional single-layer MILP model. This provides an efficient and practical framework for the planning and operational decisions of future airport electric aviation infrastructure at airports.

7. Conclusions

In this study, a multilayer optimization model framework is proposed for short-range e-aircraft fleet operations, which integrates battery replacement and charging scheduling as well as charging infrastructure sizing into the same overall scenario to take into account airport resource allocation and flight turnaround efficiency. Different from the traditional idea of completely merging scheduling and facility decision-making, this framework fully takes into account the difficulty of frequent changes in facility sizes in actual operations, and supports the accurate assessment of operational costs in the strategic layer segment by using the scheduling model as a subroutine in the form of multilayer linear programming (LP). Meta-heuristic means such as genetic algorithms are also used to extend the solution efficiency in larger scale scenarios and to ensure high quality solutions within the algorithmic feasible time.

In the case study of this paper, we take China’s Joy Air Airlines as an example: under the assumption of replacing its original MA60 model with an electric short-haul airliner based on the Eviation Alice specification and keeping the capacity demand unchanged or scaled up in equal proportions, an optimization simulation analysis of the flight plan for the first quarter of 2023 is carried out. The results show that with a total power of approximately 3500 kW and 18 battery backups, the airport is able to meet the power demand for intensive arrivals and departures on peak days and maintain relatively low turnaround delays. The whole multi-layer optimization framework effectively integrates the coupling relationship between the fixed input decision of charging infrastructure and the battery replacement and charging scheduling strategies, which fully verifies the feasibility and applicability of the model and algorithm in complex real-world scenarios. Nonetheless, future research can further improve and expand in the following directions:

• Future studies will endogenize fleet assignment and flight timing—coupling crew/turnaround constraints with charge/swap scheduling—while accommodating heterogeneous aircraft types and multiple carriers sharing the same infrastructure. This integrated view enables cost/revenue sharing rules and fair resource allocation across operators.
• Extending the model to a regional airport network will capture diversions, re-routing, and inter-airport battery logistics under grid and transmission constraints. Robust/stochastic formulations can quantify how shocks at one node propagate through the network and how strategic reserves should be positioned.
• The next step is to embed explicit capacity limits and costs for runways, gates/stands, remote positions, ATC holding, and ground-handling manpower. A robust or chance-constrained layer will trade off extra spare packs versus peak power upgrades to keep delay within tolerance under hub-wave bursts and adverse weather.
• The present framework fixes SOC/DOD limits and thus implicitly assumes nominal battery capacity over the planning horizon. Early flight-test data for aviation-grade lithium packs in regional e-aircraft prototypes suggest 20% usable-energy fade after roughly 2000–3000 equivalent full cycles [39]. Such degradation would lengthen plug-in charging times and may modestly increase swap-battery inventory at high-utilization nodes. Extending the tactical/operational layers with an empirical state-of-health (SOH) update and periodic (rolling-horizon) re-sizing of power and spare-pack levels is a natural next step and will be pursued in future work.

In conclusion, the multilayer optimization model constructed in this study provides a solution with both innovative and practical value for e-aircraft airport ground charging and swapping scheduling and infrastructure configuration, which can be applied in a small pilot scale as well as provide an ideological framework and algorithmic prototypes for future large-scale consortiums and multiairport synergies. In the context of increasing attention to green aviation and sustainable mobility, this type of research idea, which integrates resource planning and operational decision-making, will certainly play an important role in promoting the commercialization of electric aviation and improving the overall efficiency of airport systems.