Fixed-Time Attitude Control for a Flexible Space-Tethered Satellite via a Nonsingular Terminal Sliding-Mode Controller
Abstract
1. Introduction
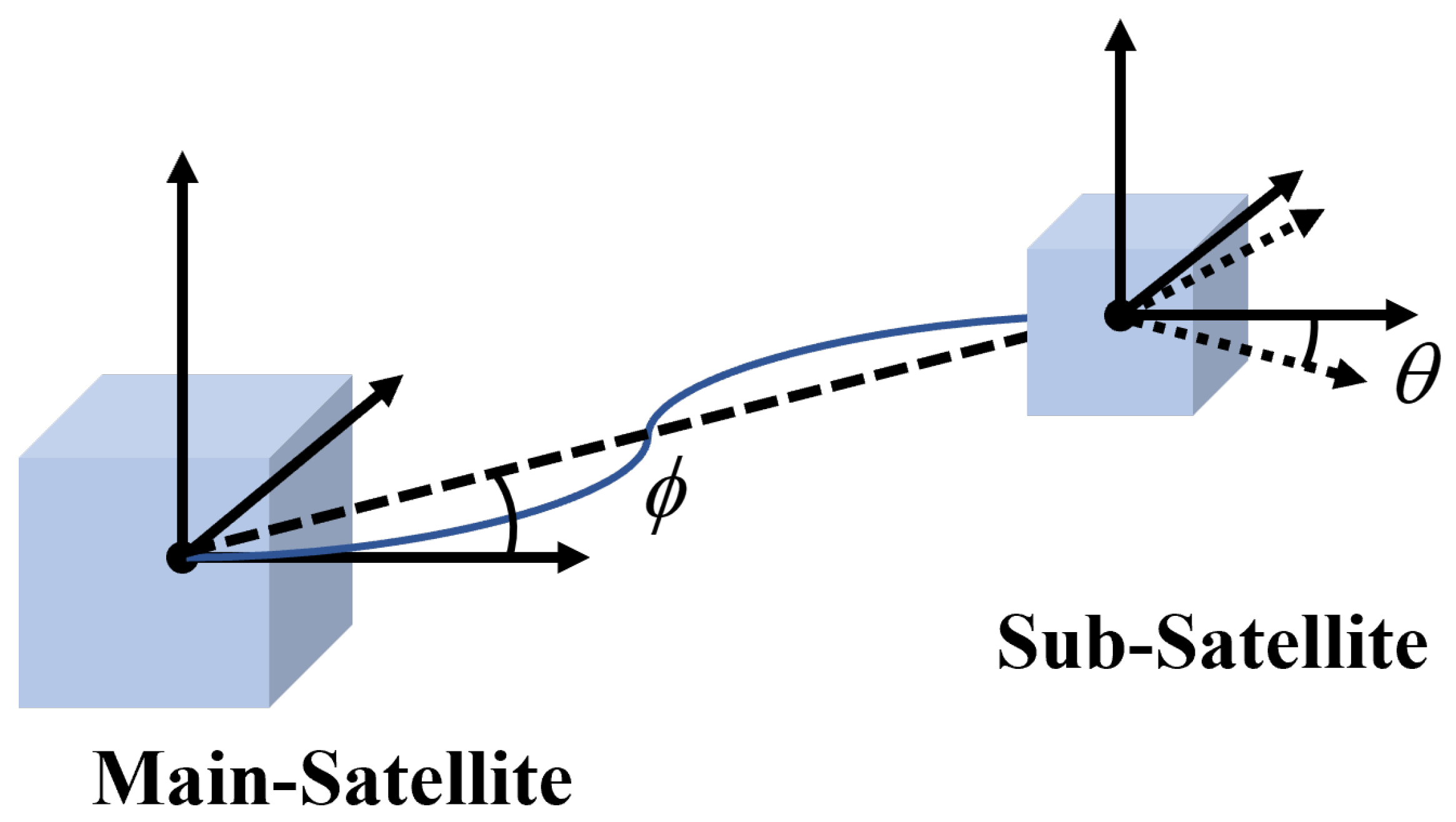
2. Flexible Dynamic Model of STS
3. Controller Design
3.1. Preliminaries and Simplified Model
3.1.1. Fixed-Time-Stable
3.1.2. RBFNN Approximation
3.1.3. Simplified Model
3.2. Fixed-Time NTSM Controller
3.3. Stability Analysis
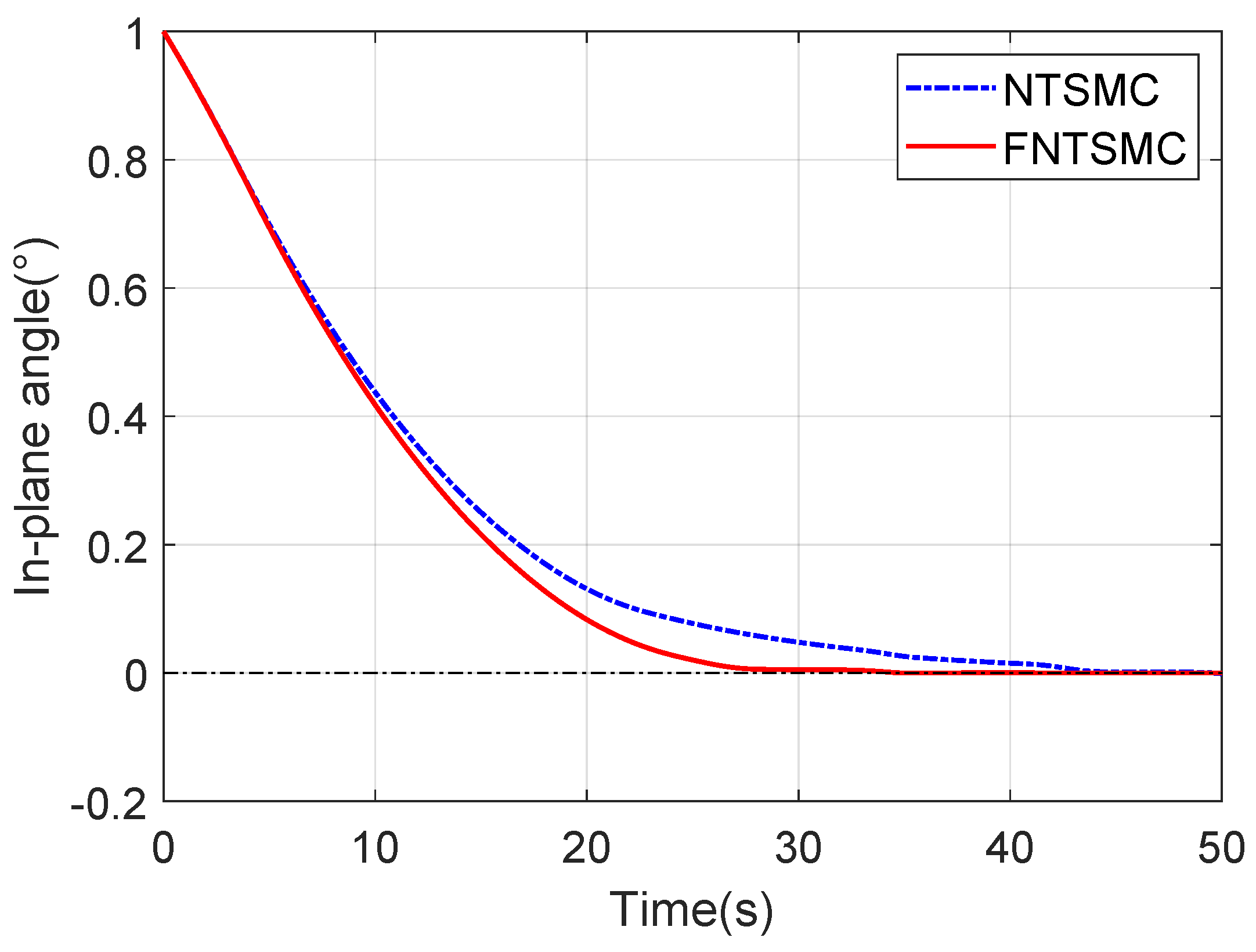
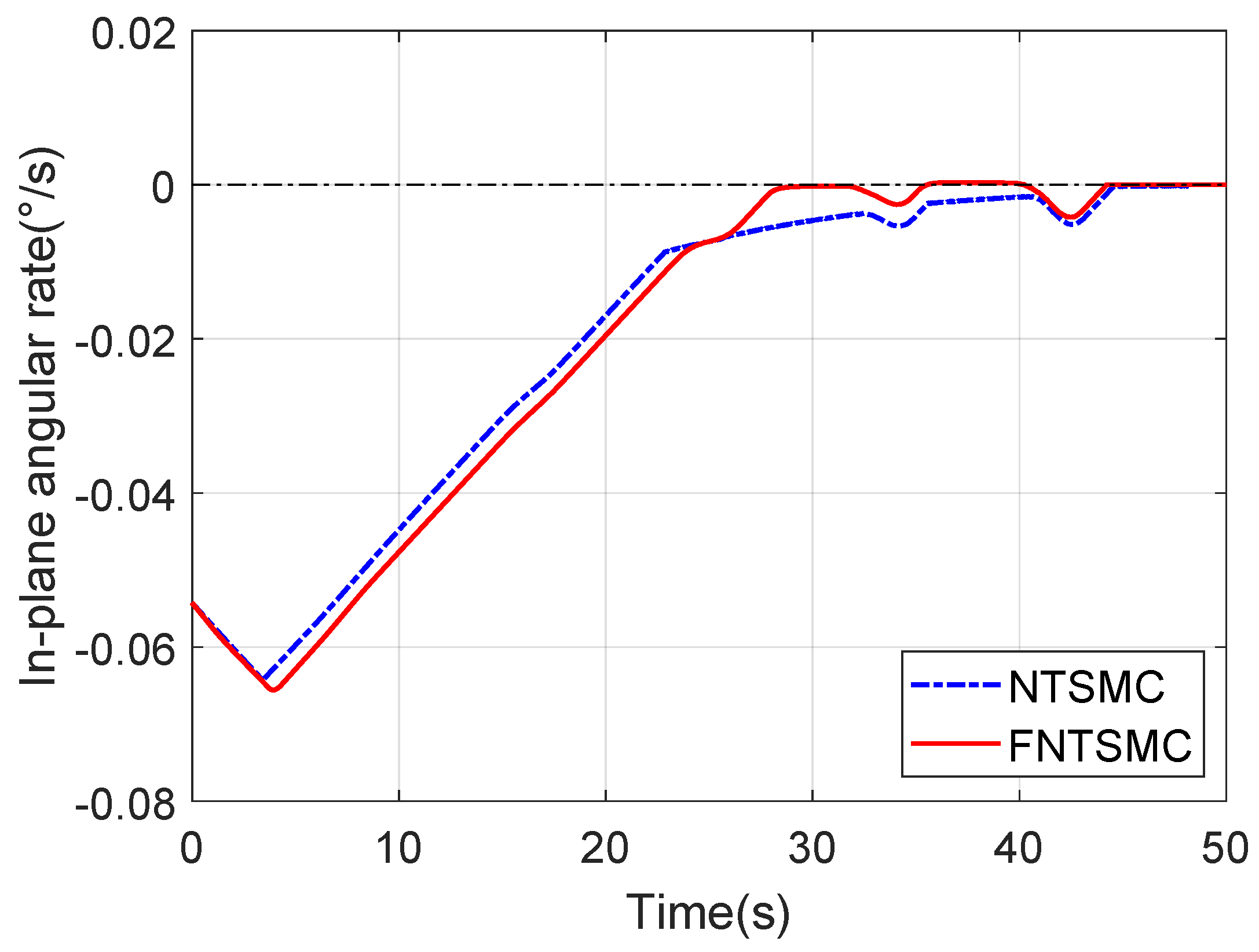
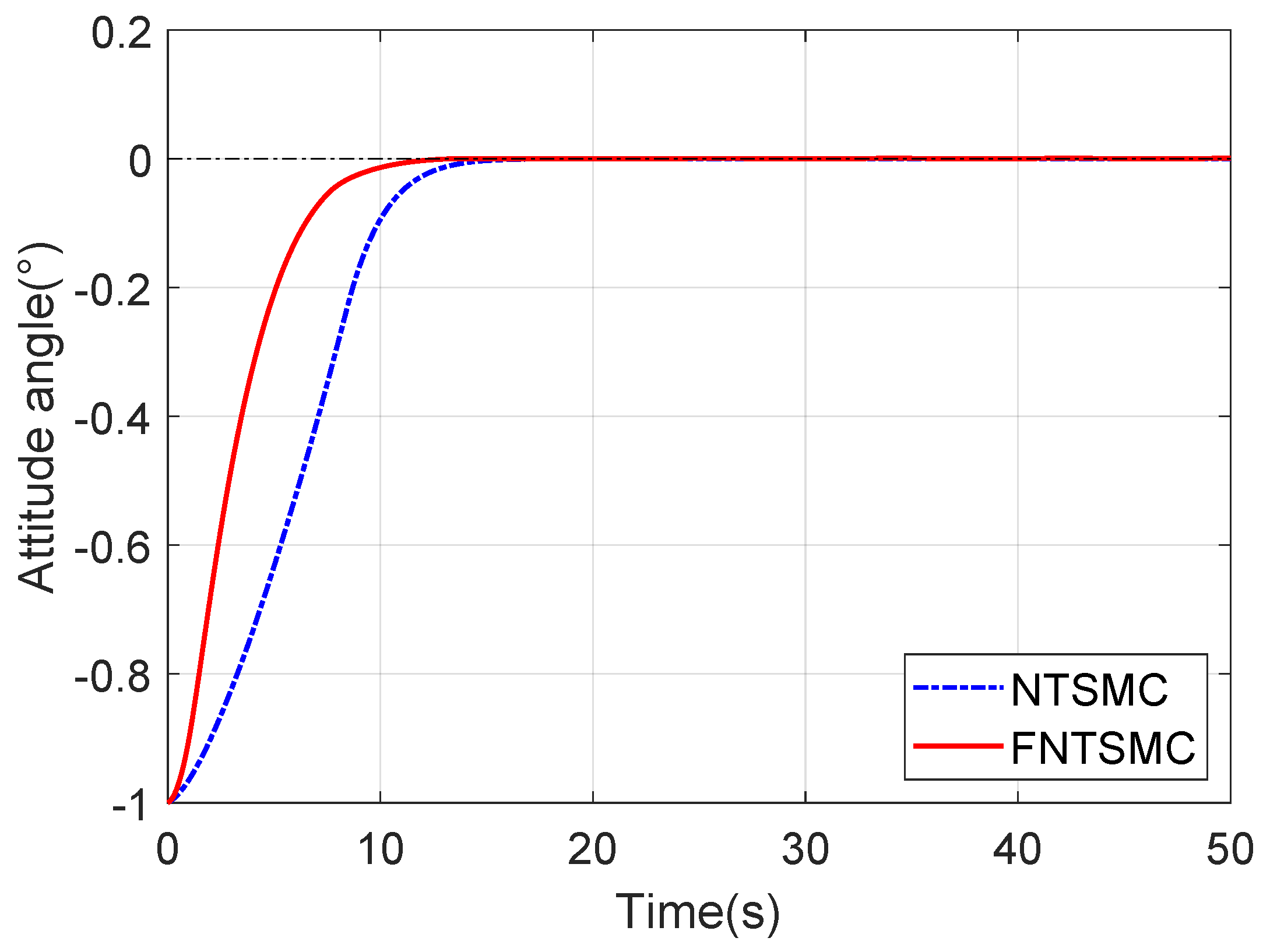
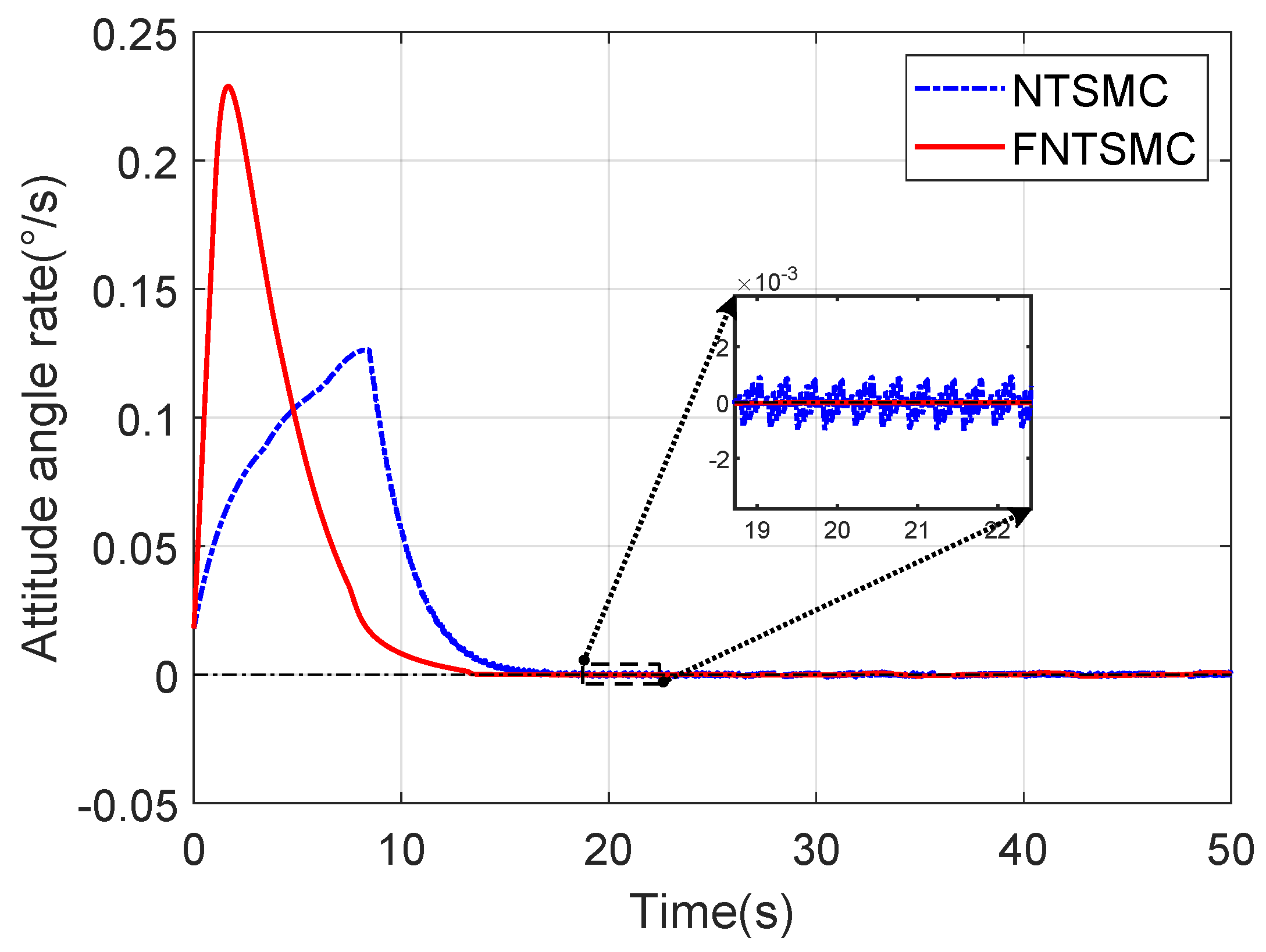
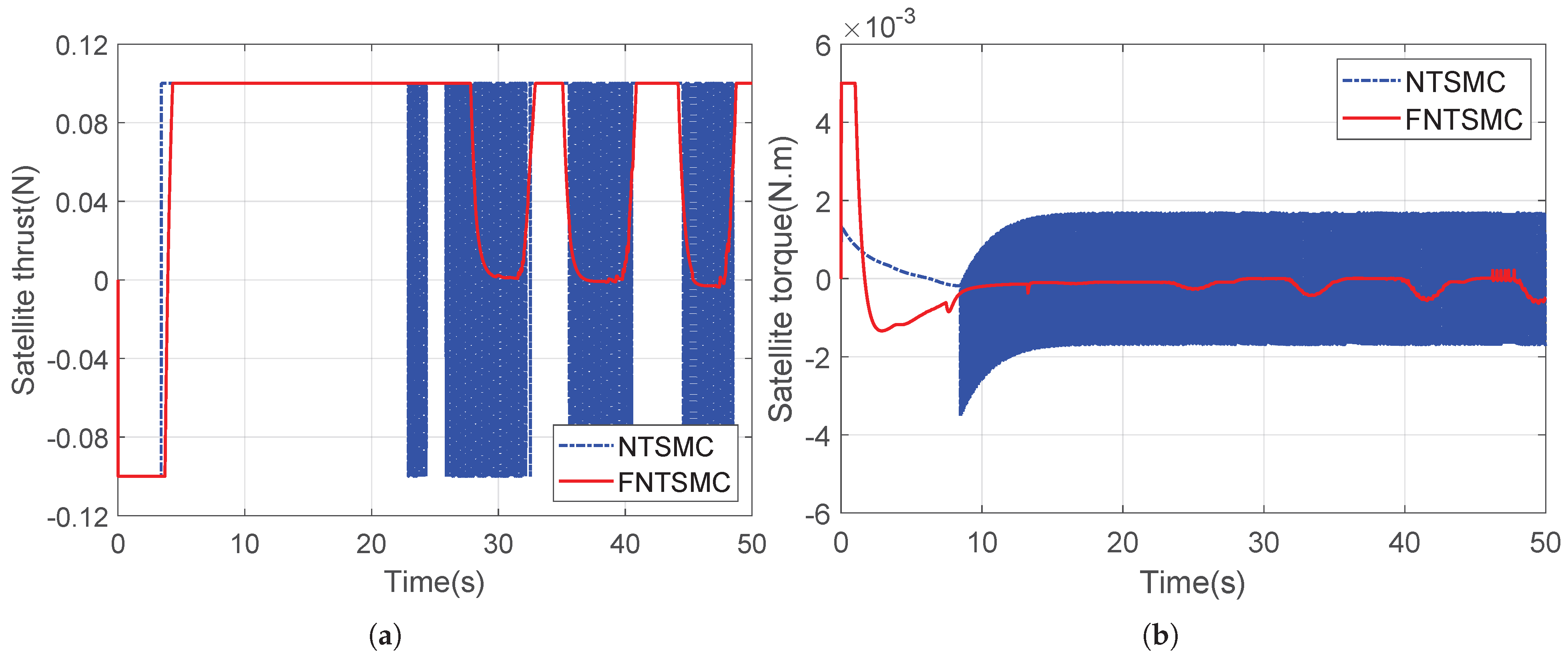
4. Simulation Result
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, P.; Zhang, F.; Chen, L.; Meng, Z.; Zhang, Y.; Liu, Z.; Hu, Y. A Review of Space Tether in New Applications. Nonlinear Dyn. 2018, 94, 1–19. [Google Scholar] [CrossRef]
- Ma, Z.; Huang, P.; Ahn, C.K. Learning-Based Control for Deployment of Tethered Space Robot via Sliding Mode and Zero-Sum Game. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 1457–1461. [Google Scholar] [CrossRef]
- Xu, S.; Wen, H.; Huang, Z.; Jin, D. A Fuzzy Control Scheme for Deployment of Space Tethered System with Tension Constraint. Aerosp. Sci. Technol. 2020, 106, 106143. [Google Scholar] [CrossRef]
- Su, B.; Zhang, F.; Huang, P. Stability Research of a Triangular Tethered Satellite Formation: Dynamics, Filtering, and Control. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5240–5255. [Google Scholar] [CrossRef]
- Yu, B.S.; Dai, P.B. Deployment Dynamics of a Tape-Shaped Tethered Satellite. J. Aerosp. Eng. 2022, 35, 04022044. [Google Scholar] [CrossRef]
- Williams, P.; Trivailo, P. Dynamics of Circularly Towed Aerial Cable Systems, Part I: Optimal Configurations and Their Stability. J. Guid. Control. Dyn. 2007, 30, 753–765. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, Z.; Zhang, Q.; Zeng, M.; Li, S. Dynamics and Control of a Tethered Space-Tug System Using Takagi-Sugeno Fuzzy Methods. Aerosp. Sci. Technol. 2019, 87, 289–299. [Google Scholar] [CrossRef]
- Tirop, P.; Jingrui, Z. Review of Control Methods and Strategies of Space Tether Satellites. Am. J. Traffic Transp. Eng. 2019, 4, 137. [Google Scholar] [CrossRef]
- Kojima, H.; Trivailo, P.M. Model Predictive Tether-Deployment Control for Precise Landing of Tethered Reentry Body. Adv. Space Res. 2019, 64, 1537–1548. [Google Scholar] [CrossRef]
- Vafamand, N. Adaptive Robust Neural-Network-Based Backstepping Control of Tethered Satellites with Additive Stochastic Noise. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3922–3930. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, P.; Zhang, F. Dynamic Modeling and Super-Twisting Sliding Mode Control for Tethered Space Robot. Acta Astronaut. 2018, 143, 310–321. [Google Scholar] [CrossRef]
- Jin, D.P.; Wen, H.; Chen, H. Nonlinear Resonance of a Subsatellite on a Short Constant Tether. Nonlinear Dyn. 2013, 71, 479–488. [Google Scholar] [CrossRef]
- Luo, C.; Wen, H.; Jin, D. Deployment of Flexible Space Tether System with Satellite Attitude Stabilization. Acta Astronaut. 2019, 160, 240–250. [Google Scholar] [CrossRef]
- Yu, B.; Jin, D.; Wen, H. Analytical Deployment Control Law for a Flexible Tethered Satellite System. Aerosp. Sci. Technol. 2017, 66, 294–303. [Google Scholar] [CrossRef]
- Hu, W.; Huai, Y.; Xu, M.; Deng, Z. Coupling Dynamic Characteristics of Simplified Model for Tethered Satellite System. Acta Mech. Sin. 2021, 37, 1245–1254. [Google Scholar] [CrossRef]
- Lim, J.; Chung, J. Dynamic Analysis of a Tethered Satellite System for Space Debris Capture. Nonlinear Dyn. 2018, 94, 2391–2408. [Google Scholar] [CrossRef]
- Bai, Z.; Jiang, X.; Fu, X. Investigation of the Retrieval Dynamics of the Tethered Satellites Using ANCF-ALE Variable-Length Element. IEEE Trans. Aerosp. Electron. Syst. 2022, 59, 1980–1988. [Google Scholar] [CrossRef]
- Kristiansen, K.U.; Palmer, P.L.; Roberts, R.M. Numerical Modelling of Elastic Space Tethers. Celest. Mech. Dyn. Astron. 2012, 113, 235–254. [Google Scholar] [CrossRef]
- Li, G.Q.; Zhu, Z.H. Long-Term Dynamic Modeling of Tethered Spacecraft Using Nodal Position Finite Element Method and Symplectic Integration. Celest. Mech. Dyn. Astron. 2015, 123, 363–386. [Google Scholar] [CrossRef]
- Gao, F.; Li, J.; Dong, F.; Ji, Y.; Sun, G. Dynamic Modeling and Control Strategy for Tethered Satellite Systems in Orbital Debris Management. Acta Mech. Sin. 2025, 41, 524262. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhu, Z.H. Computational Control Framework for Tethered Space Systems Using Finite Element Method. Acta Astronaut. 2025, 228, 595–606. [Google Scholar] [CrossRef]
- Ghorbani, H.; Vatankhah, R.; Farid, M. Adaptive Nonsingular Fast Terminal Sliding Mode Controller Design for a Smart Flexible Satellite in General Planar Motion. Aerosp. Sci. Technol. 2021, 119, 107100. [Google Scholar] [CrossRef]
- Lu, K.; Xia, Y. Adaptive Attitude Tracking Control for Rigid Spacecraft with Finite-Time Convergence. Automatica 2013, 49, 3591–3599. [Google Scholar] [CrossRef]
- Cao, L.; Xiao, B.; Golestani, M. Robust Fixed-Time Attitude Stabilization Control of Flexible Spacecraft with Actuator Uncertainty. Nonlinear Dyn. 2020, 100, 2505–2519. [Google Scholar] [CrossRef]
- Tao, X.; Zhang, F.; Huang, B.; Shen, G.; Huang, P. Fixed-Time Sliding Mode Coordinated Deployment Control for Space Triangle Tethered Formation System. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 1351–1363. [Google Scholar] [CrossRef]
- Li, A.-j.; Tian, H.-c.; Wang, C.-q. Fixed-Time Terminal Sliding Mode Control of Spinning Tether System for Artificial Gravity Environment in High Eccentricity Orbit. Acta Astronaut. 2020, 177, 834–841. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, F.; Liu, M.; Chen, X. Fractional-Order Robust Fixed-Time Sliding Mode Control for Deployment of Tethered Satellite. Acta Astronaut. 2023, 209, 172–178. [Google Scholar] [CrossRef]
- Huang, S.J.; Huang, K.S.; Chiou, K.C. Development and Application of a Novel Radial Basis Function Sliding Mode Controller. Mechatronics 2003, 13, 313–329. [Google Scholar] [CrossRef]
- Sun, Y.; Gao, Y.; Zhao, Y.; Liu, Z.; Wang, J.; Kuang, J.; Yan, F.; Liu, J. Neural Network-Based Tracking Control of Uncertain Robotic Systems: Predefined-Time Nonsingular Terminal Sliding-Mode Approach. IEEE Trans. Ind. Electron. 2022, 69, 10510–10520. [Google Scholar] [CrossRef]
- Guo, S.; Li, D.; Meng, Y.; Fan, C. Task Space Control of Free-Floating Space Robots Using Constrained Adaptive RBF-NTSM. Sci. China-Technol. Sci. 2014, 57, 828–837. [Google Scholar] [CrossRef]
- Li, X.; Sun, G.; Xue, C. Fractional-Order Deployment Control of Space Tethered Satellite via Adaptive Super-Twisting Sliding Mode. Aerosp. Sci. Technol. 2022, 121, 107390. [Google Scholar] [CrossRef]
- Zhong, R.; Xu, S. Neural-Network-Based Terminal Sliding-Mode Control for Thrust Regulation of a Tethered Space-Tug. Astrodynamics 2018, 2, 175–185. [Google Scholar] [CrossRef]
- Ji, Y.; Xing, Y. A Three-Sub-Step Composite Method for the Analysis of Rigid Body Rotations with Euler Parameters. Nonlinear Dyn. 2023, 111, 14309–14333. [Google Scholar] [CrossRef]
- Andrieu, V.; Praly, L.; Astolfi, A. Homogeneous Approximation, Recursive Observer Design, and Output Feedback. SIAM J. Control Optim. 2008, 47, 1814–1850. [Google Scholar] [CrossRef]
- Deng, H.; Krstic, M. Output-Feedback Stochastic Nonlinear Stabilization. IEEE Trans. Autom. Control 1999, 44, 328–333. [Google Scholar] [CrossRef]
- Tian, B.; Zuo, Z.; Yan, X.; Wang, H. A Fixed-Time Output Feedback Control Scheme for Double Integrator Systems. Automatica 2017, 80, 17–24. [Google Scholar] [CrossRef]

| Description | Parameters | Values |
|---|---|---|
| Main satellite mass | 1000 kg | |
| Sub-satellite mass | 10 kg | |
| Tether length | 100 m | |
| Sub-satellite dimension | a | 1 m |
| Parameters | Values |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, C.; Shi, Q.; Zheng, H.; Huan, B.; Yao, W.; Wang, Y.; Shao, X. Fixed-Time Attitude Control for a Flexible Space-Tethered Satellite via a Nonsingular Terminal Sliding-Mode Controller. Aerospace 2025, 12, 907. https://doi.org/10.3390/aerospace12100907
Xue C, Shi Q, Zheng H, Huan B, Yao W, Wang Y, Shao X. Fixed-Time Attitude Control for a Flexible Space-Tethered Satellite via a Nonsingular Terminal Sliding-Mode Controller. Aerospace. 2025; 12(10):907. https://doi.org/10.3390/aerospace12100907
Chicago/Turabian StyleXue, Cong, Qiao Shi, Hecun Zheng, Baizheng Huan, Weiran Yao, Yankun Wang, and Xiangyu Shao. 2025. "Fixed-Time Attitude Control for a Flexible Space-Tethered Satellite via a Nonsingular Terminal Sliding-Mode Controller" Aerospace 12, no. 10: 907. https://doi.org/10.3390/aerospace12100907
APA StyleXue, C., Shi, Q., Zheng, H., Huan, B., Yao, W., Wang, Y., & Shao, X. (2025). Fixed-Time Attitude Control for a Flexible Space-Tethered Satellite via a Nonsingular Terminal Sliding-Mode Controller. Aerospace, 12(10), 907. https://doi.org/10.3390/aerospace12100907


_Zhu.png)




