Abstract
Accurately predicting aircraft fuel consumption is vital for aviation safety, operational efficiency, and resource optimization, yet existing models face key limitations. Traditional physical models rely on prior assumptions, while mainstream deep learning models use fixed architectures and time-slice tokens—failing to adapt to distinct flight phases and losing long-range temporal features critical for cross-phase dependency capture. This paper proposes Gate-iInformer, an adaptive framework centered on iInformer with a gating network. It treats flight parameters as independent tokens, integrates Informer to handle long-range dependencies, and uses the gating network to dynamically select pre-trained phase-specific sub-models. Validated on 21,000 Air China 2023 medium-aircraft flights, it reduces MAE and RMSE by up to 53.38% and 44.51%, achieves 0.068 MAE in landing, and outperforms benchmarks. Its prediction latency is under 0.5 s, meeting ADS-B needs. Future work will expand data sources to enhance generalization, boosting aviation intelligent operation.
1. Introduction
With the continuous expansion of the global air transportation industry, accurate estimation of aircraft fuel consumption has become a core issue for maintaining flight safety, improving operational efficiency, and optimizing resource allocation. In actual flights, reliable prediction of fuel demand for the remaining voyage based on data from the already flown segment directly determines the rationality of flight decisions. This not only affects key operations such as the formulation of alternate landing plans and the scheduling of fuel supply, but also has irreplaceable practical significance for reducing safety risks and avoiding resource redundancy [1,2,3,4].
In early studies, fuel prediction mostly relied on physical models and traditional methods. Gómez Comendador et al. [5] extended the BADA model and attempted to apply it to trajectory and energy prediction; Dalmau et al. [6] constructed a lightweight physical model to predict fuel consumption based on thrust drag balance and energy state equations; Gardi et al. [7] built a multi-objective optimization model using flight mechanics equations and combined environmental parameters to predict fuel. Such methods are highly dependent on manually designed features and prior assumptions, and it is difficult for them to adaptively explore deep data patterns in the face of complex nonlinear temporal relationships during flight. With the penetration of deep learning technology, research on fuel prediction has taken a new direction. Zhu et al. [8] and others attempted to use deep learning for predicting fuel-related flight parameters. The CNN-BiLSTM model achieved prediction with a certain accuracy in the takeoff and landing phases, verifying the value of spatiotemporal feature fusion. However, it cannot dynamically switch models and relies on manual intervention for selection, which slows down the emergency response rhythm [9]. Ma et al. [10] applied the Transformer architecture to extract spatiotemporal dependencies of traffic flow; Khan et al. [11] proposed a covariance bidirectional extreme learning machine to optimize feature mapping; Yi Lin et al. [12] introduced an attention mechanism to fuse multi-modal data for predicting pre-takeoff fuel.
Nevertheless, existing deep models have common shortcomings in aircraft fuel prediction: most adopt fixed structures, making it difficult to adapt to input differences in different flight phases; moreover, the number of real-value modalities obtainable during flight is limited, so the model input is often difficult to cover the ideal multi-modal data, resulting in limited decision support capability in emergency scenarios. This problem is particularly prominent in Transformer-based models. Although Transformer has achieved great success in fields such as natural language processing (Brown et al., 2020) [13] and computer vision (Dosovitskiy et al., 2021) [14] with its strong ability to characterize sequence dependencies and extract multi-level representations, and has gradually been applied to time series prediction [15,16], its limitations in multi-variable time series scenarios have gradually emerged.
Traditional Transformer-like models usually embed multiple variables at the same timestamp as “time tokens” and apply attention mechanisms in the time dimension to capture temporal dependencies. However, studies have shown that this design has significant flaws: multiple variables at the same time step often represent measurements with completely different physical meanings (such as flight altitude, speed, fuel flow), and forcibly aggregating them into a single token will destroy the inherent correlation between variables [17,18]; at the same time, the receptive field of time tokens is limited, making it difficult to transmit long-range temporal information, and the permutation-invariant attention mechanism conflicts with the order sensitivity of time series (Zeng et al., 2023) [19], leading to the model being prone to losing early key features in long voyage prediction. For aircraft fuel prediction where capturing cross-phase dependencies such as the impact of speed and climb and descent rate during the takeoff phase on fuel consumption in the landing phase is critical, this mismatch between model design and data characteristics becomes more pronounced, highlighting the need for optimized Transformer-based architectures.
To break through the above bottlenecks, this study, based on the characteristics of actual flight data acquisition and emergency prediction needs, introduces the unique advantages of iTransformer [20], using feature variables as tokens instead of traditional time tokens, which can more comprehensively capture the correlations between flight parameters and avoid the loss of long-range features caused by time segmentation. It also integrates the Informer [21] architecture to efficiently handle long-range temporal dependencies. On this basis, a fuel prediction system adapted to the entire flight process is constructed: multiple deep learning models with different input and output scales are pre-trained, and the historical data from flight black boxes and the limited feature scale data obtainable from ADS-B are used to enable the models to learn the fuel consumption rules of different flight phases;In the flight prediction phase, according to the real data of the already flown segment, combined with the trained models and gating mechanism, the adaptive model is dynamically selected, and real-time flight data is fused to accurately predict the fuel amount for the remaining voyage.. iInformer, an inverted Transformer variant, has demonstrated effectiveness in general multi-variable time-series prediction [20], but its application in aviation fuel consumption prediction remains underexplored. Existing aviation time-series studies primarily rely on traditional architectures. Ma et al. [10] applied Transformer to extract spatiotemporal dependencies of air traffic flow but did not address multi-phase adaptation. Metlek [9] used a CNN-BiLSTM model for takeoff and landing fuel prediction but required manual model switching. This study is the first to integrate iInformer with a gating network for full-flight fuel prediction leveraging iInformer’s variable-token design to retain cross-phase features and the gating network to enable dynamic phase adaptation filling the gap in multi-phase, long-sequence fuel prediction for aviation.
The experimental data in this study is derived from 21,000 flights of medium-sized aircraft operated by Air China in 2023, covering 25 different aircraft models. Many of these models are widely used by other domestic airlines, and the dataset includes key parameters such as fuel flow, altitude, speed, and climb/descent rate. For the model’s adaptability to new aircraft types: since we adopted one-hot encoding for aircraft type features, when incorporating data of new models, we only need to add corresponding one-hot encoding vectors to the input features without modifying the core architecture of Gate-iInformer. This design ensures the model can flexibly accommodate new aircraft types with minimal adjustments. While this dataset ensures consistency in aircraft type and operational environment, facilitating the model’s learning of phase-specific fuel consumption patterns, the single airline source may introduce potential generalization bias. To address this, Section 4 details plans to expand data sources to include multiple airlines, more aircraft types, and external factors such as real-time weather, ensuring the framework’s applicability in complex aviation scenarios.
2. Methods
The data processing workflow is designed for the raw flight data provided by Air China, encompassing data integration, feature transformation, categorical feature encoding, standardization, and resampling. Each step is meticulously tailored to the characteristics of the iInformer model and the requirements of fuel quantity prediction, aiming to maximize the advantages of iInformer in aircraft fuel consumption prediction tasks.
Gate-iInformer serves as the core solution to the aircraft fuel prediction problem in this paper. It takes iInformer as the base model and constructs a set of models for different flight phases (takeoff, cruise, and landing). During the training phase, the gating network and pre-trained models are first trained using real data from completed flight segments. In actual prediction, the real data from the already flown segment is input into the trained gating network, which invokes the pre-trained models based on data features. By combining model weights, it synergistically outputs the fuel quantity prediction results for the remaining voyage, achieving dynamic adaptation throughout the entire flight process. This provides more accurate and timely fuel consumption predictions for emergency decision-making, assists pilots in scientifically planning fuel usage, and ensures safe and efficient flights. Section 2.1 outlines a series of processing steps applied to the raw data for the fuel quantity prediction scenario and our framework. Section 2.2 describes the overall training and application architecture of Gate-iInformer.
2.1. Data Preprocessing
In the aircraft fuel quantity time-series prediction task, the effective processing of flight data is a crucial link to ensure the accuracy and generalization of the prediction model. Focusing on the scenario of aircraft fuel quantity prediction, this section elaborates on the multi-step processing workflow for flight data. Combined with the characteristics of the adopted iInformer model, it conducts an in-depth analysis of the role of each processing step in improving the fuel quantity prediction performance, thereby providing a comprehensive data processing scheme and theoretical support for achieving accurate aircraft fuel quantity prediction using time-series data.
The final dataset includes the predicted target fuel quantity at each timestamp for 21,000 flights, along with features such as precision, latitude, speed, weight, and climb/descent rate. Of the extracted data, 20% is used to construct the test set, while the remaining 80% serves as the training set. As shown in Figure 1, the token conversion process of the iInformer model and the overall data processing workflow before the data is input into the model are illustrate
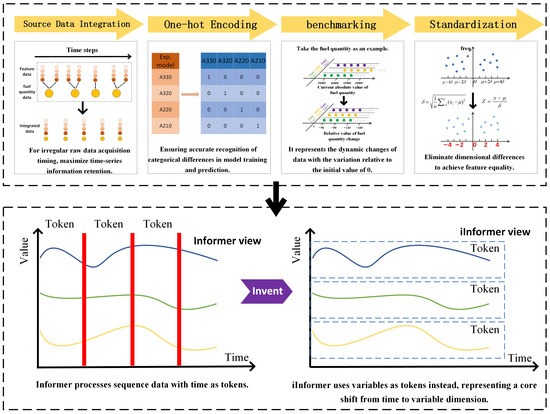
Figure 1.
Schematic diagram of token conversion and overall data processing workflow for iInformer.
2.1.1. Alignment, Integration, and Equal-Interval Sampling of Source Data
The raw flight data provided by Air China from 2023, includes fuel data and feature data. Firstly, these two types of data are aligned and integrated based on timestamps to form initially aggregated data [22,23]. On this basis, data from medium-sized aircraft are filtered to eliminate interference from data of other aircraft types, allowing the model training to focus on the fuel quantity variation patterns of specific aircraft types. This reduces the negative impact of feature distribution differences caused by aircraft type variations on model learning and improves the specificity and accuracy of the model in predicting fuel quantity for target aircraft types. Subsequently, the aligned data are divided into individual trips based on each takeoff and landing cycle, resulting in multiple sets of time-series data.
Since the collection density of feature data is higher than that of fuel data, the timestamps of feature data are used to integrate fuel data with the closest timestamps. This approach first retains all raw fuel data, and then obtains integrated data by selecting fixed timestamps with smaller intervals according to the density characteristics of feature data. It maximizes the retention of temporal information when the collection time of raw data is irregular. Leveraging the characteristic of the iInformer model that “longer lookback length leads to more accurate prediction” (as shown in Figure 2), the lookback length is increased with mean absolute error (MAE) and RMSE as error metrics, providing the model with richer historical data for learning. Compared with the simple method of processing data based on the maximum time interval of fuel data (which loses a large amount of intermediate temporal information), this approach enables a longer lookback length of available data. It fully utilizes data to explore fuel quantity variation patterns under long time series, helping the model exert its advantages and improve the accuracy of fuel quantity prediction. Particularly in scenarios involving long-term fuel quantity variation prediction, it demonstrates adaptability to the model’s strengths and in-depth excavation of data value.
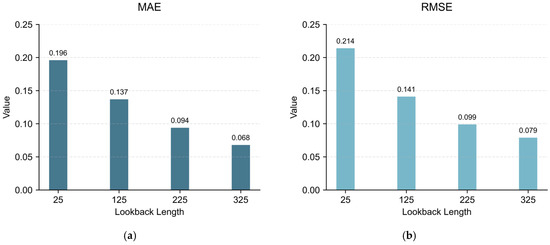
Figure 2.
Impact of lookback length on error metrics (a) MAE; (b) RMSE.
The iInformer model benefits from longer lookback windows by integrating richer historical context, as evidenced by the error reduction shown in Figure 2. However, it is crucial to acknowledge the trade-offs involved. Excessively long windows increase computational complexity and memory usage during training and inference. Furthermore, they may introduce noise or lead to overfitting if the model begins to memorize non-generalizable patterns from the distant past. To mitigate these risks, we employed regularization techniques such as dropout (rate = 0.1) and monitored validation loss to prevent overfitting. The selection of the maximum lookback length (350 steps) in this study represents a balance between capturing sufficient temporal dependencies and maintaining computational tractability, consistent with practices observed in other long-sequence forecasting studies [20,21]
2.1.2. One-Hot Encoding of Aircraft Type Features
One-Hot Encoding is applied to aircraft type features, for example, A330 is encoded as [1, 0, …, 0], and A220 is encoded as [0, 0, …, 1], converting discrete aircraft type categories into numerical vector forms recognizable by the model.
One-Hot Encoding digitizes the categorical feature of aircraft type, and the encodings of different aircraft types are independent of each other without sequential association. This enables the model to treat different aircraft types equally during the learning process, avoiding unreasonable weight relationships caused by improper digitization of categorical features. For scenarios involving fuel consumption prediction of different aircraft types, it enhances the generalization ability of the model across various aircraft types, allowing the model to effectively transfer the learned fuel quantity prediction rules to different aircraft types.
Moreover, One-Hot Encoding completely retains the aircraft type category information, with each aircraft type corresponding to a unique encoding vector. This ensures that the model can accurately identify differences between aircraft types during both training and prediction phases. Combined with the iInformer model’s ability to learn from long time-series data, it can fully utilize the fuel quantity variation data of different aircraft types under long time series, providing comprehensive and accurate feature inputs for fuel quantity prediction in multi-aircraft type scenarios.
2.1.3. Relative Processing of Spatiotemporal Features and Target Variables
In the process of predicting remaining aircraft fuel quantity, there are significant differences in initial fuel quantities between different trips and flights, which may pose great challenges to the model’s ability to accurately capture the intrinsic relationship between fuel quantity and features [24].
Therefore, relative changes are calculated for three key variables: longitude, latitude, and fuel.
The original absolute variables are converted into relative feature changes, reflecting how fuel quantity changes with feature variations.
By calculating relative changes, a direct correlation between positional features and fuel quantity changes is established. Compared with absolute positions and absolute fuel quantities, relative changes better reflect the dynamic relationship between geographical movement and fuel consumption during flight, enabling the model to more accurately capture the impact of flight state changes on fuel quantity, which is consistent with the “process-oriented” characteristics of fuel consumption in actual flight [24].
Meanwhile, the iInformer model relies on time-series data to explore patterns. Relative changes, presented as differences, better facilitate the model in identifying temporal trends and fluctuation characteristics. They provide more interpretable and relevant input features for the model to explore fuel quantity variation patterns under long time series, helping the model leverage the advantage of lookback length and improve the accuracy of long time-series predictions.
To investigate the difference between absolute positions, absolute fuel quantities, and relative change processing in aircraft fuel quantity prediction, an experiment on relativization processing was conducted. The aim was to explore the necessity and effectiveness of processing fuel quantity at each timestamp by taking the difference from the initial value of the current trip. Mean Absolute Error (MAE) and RMSE were used as error metrics.
The experiment in Figure 3 shows that by eliminating baseline differences between trips (i.e., subtracting the initial value of the current trip from timestamp data), the model can more accurately capture the dynamic relationship between fuel quantity and spatiotemporal features. This processing achieves the maximum optimization effect on prediction accuracy in the later stages of flight (e.g., landing phase), confirming its key value in data preprocessing for aviation fuel quantity prediction.
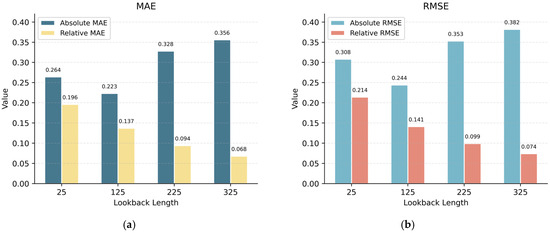
Figure 3.
Error comparison between absolute value processing and relative value processing under different lookback lengths (a) MAE; (b) RMSE.
2.1.4. Standardization
Finally, to improve the convergence speed and generalization ability of the model, z-score standardization is applied to the data to unify data dimensions and distributions. This process transforms the data to have a mean of 0 and a standard deviation of 1, eliminating the impact of differences in dimensions and value ranges among different features. It enables the model to treat all features equally during training, thereby enhancing the convergence speed and stability of the model [25]. Additionally, it facilitates the model in learning the intrinsic temporal patterns and feature correlations in the data, laying a solid data foundation for accurate fuel quantity prediction. The formula is as follows:
The symbols are defined as follows:
- •
- : Standardized value.
- •
- : A value in the original data.
- •
- : Mean of the original data.
- •
- : Standard deviation of the original data, calculated as:
This transforms the original disordered distribution with a large range and outliers into an orderly standard distribution with a fixed range and no outliers. Meanwhile, it preserves the relative relationships between data points, eliminates dimensional differences, and achieves feature equality.
2.1.5. Dataset Partitioning Strategy
After completing the aforementioned data processing steps, the obtained takeoff and landing CSV dataset is divided into a training set and a test set. Following the general logic of model evaluation, a random sampling strategy is adopted:20% of the extracted samples is used to construct the test set, which is employed to simulate unknown data scenarios and verify the model’s prediction performance; the remaining 80% serves as the training set., allowing the model to explore intrinsic data patterns and learn feature correlation rules. This partitioning method is based on the need to evaluate the model’s generalization ability, ensuring that the trained model can accurately predict new data based on the learned rules in practical applications, thus laying a solid foundation for model performance verification and practical deployment [26].
2.2. Gate-iInformer
To address the challenge of aircraft fuel prediction, this study constructs a training process that integrates multi-phase models and a gating network. The core idea is to enhance prediction accuracy through refined extraction of full-flight process features and dynamic model fusion. The following elaborates on the implementation logic of the training process in four parts: model selection, base model training, gating network design, and overall fusion prediction.
The traditional Transformer embeds multiple variables at the same time step into temporal tokens and applies an attention mechanism in the temporal dimension to capture temporal dependencies. However, it tends to “forget” earlier information; if one intends to retain such information, adopting a large window will lead to issues of performance degradation and computational explosion.
Building on the Informer model—which is inherently suitable for long-sequence time-series prediction—the iInformer independently embeds the entire time series of each variable into a variate token. It then applies an attention mechanism in the variable dimension to capture multi-variable correlations. This addresses the issue of long-range feature loss in traditional Transformers caused by sequence truncation, and this is precisely the reason why the iInformer is selected as the base model for the proposed framework [20,21].
Let the input flight data be defined as a multi-dimensional time-series matrix , where denotes the lookback length (i.e., the number of elapsed flight time steps) and represents the number of flight parameter variables (e.g., altitude, speed, fuel flow rate). Inside the iInformer, the temporal dimension and variable dimension are first swapped, such that each variable corresponds to a complete time-series sequence:
Let the input of the multivariate time series be the historical observations , and it is required to predict the sequence for the next time steps. For each specific variable (i.e., a single dimension among flight parameters, such as altitude or fuel flow rate), the process formula for predicting the future sequence based on the historical sequence is defined as follows:
: The complete historical flight sequence of the -th variable (with a backtracking length of ), with a dimension of ;
: The initial Token of the -th variable after embedding, with a dimension of (where is the Token dimension);
: The Token set of all variables, where is the total number of variables and is the dimension of a single Token;
: The Transformer block (including self-attention, feed-forward network, and layer normalization) functions to realize interaction between variables and extraction of features.
: The number of stacked layers of Transformer blocks;
: The final Token of the -th variable after encoding by layers of Transformers;
: The future sequence prediction result of the -th variable, with a dimension of (where is the prediction length).
In Figure 4, during the pre-training phase, multiple sets of data with different backtracking lengths are designed for the entire flight journey and input into the iInformer model. Each trained model focuses on learning the fuel consumption patterns of specific phases, thereby enhancing the adaptability of the base model to the features of each phase. By evenly allocating backtracking windows throughout the entire flight process, the complete workflow including takeoff, cruise, and landing is covered, laying a foundation for subsequent multi-model fusion.
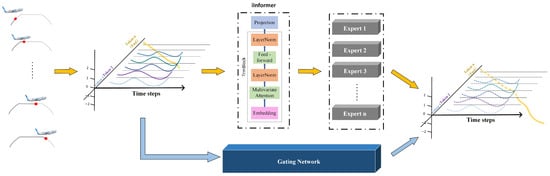
Figure 4.
Overall training workflow of the Gate-iInformer framework.
The Gating Network is the core component for realizing dynamic multi-model fusion. Its function is to assign “scene adaptation weights” to the pre-trained models, enabling the prediction process to dynamically select the optimal model combination according to the flight phase [27].
The input of the Gating Network is the dynamic features in the flight data, and its goal is to learn the adaptation relationship between “pre-trained models and flight scenes”. Let the feature vector of real-time flight data be (where is the number of features, such as current backtracking length, flight phase identifier, altitude change rate, etc.). The feature vector is mapped to the gating hidden vector through a linear layer:
Among them, represents the dimension of the gating hidden layer, and and are the parameters of the Gating Network.
During training, the outputs of multiple pre-trained iInformer models are used as candidates, and the Gating Network optimizes the weight assignment strategy through backpropagation. Let the set of pre-trained iInformer sub-models be (corresponding to different backtracking lengths, e.g., 50, 150, 250, 350), and the Gating Network outputs weights for each sub-model:
Among them, denotes the weight vector (learnable) of the -th sub-model, and (Softmax ensures weight normalization).
In the independent training process of the Gating Network, with the goal of “minimizing fuel prediction error”, it learns the contribution of each pre-trained model under different flight phases. For example, during the takeoff phase, higher weights are dynamically assigned to “short backtracking models” to enhance the prediction ability for high-dynamic features; during the cruise or landing phase, the focus is on the steady-state feature extraction of “long backtracking models”. Through weight assignment, the complementary advantages of multiple models are realized.
As illustrated in Figure 5, after completing the pre-training of the base models and the training of the gating network, during the actual prediction phase of the aircraft fuel consumption prediction task, this method realizes accurate prediction of the fuel quantity for the subsequent flight segment through the synergistic effect of the Gating Network and pre-trained Expert Networks, based on the multi-model fusion architecture constructed in the training process [28]. The core of this process lies in dynamically invoking the capabilities of models adapted to different flight scenarios during the pre-training phase and combining the characteristics of real-time flight data to output reliable fuel consumption prediction results.
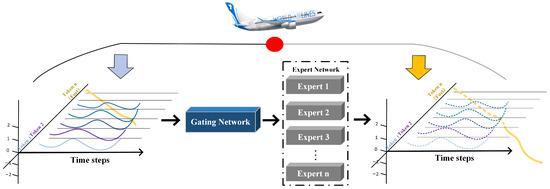
Figure 5.
Prediction process of the Gate-iInformer framework via gating network and expert models.
According to the real-time flight phase (takeoff, cruise, landing), the set of pre-trained iTransformer models suitable for the phase is first selected based on the characteristics of the flight phase data; then, the prediction results of the selected models are weighted and fused using the scenario weights output by the gating network. For instance, in the takeoff phase, the “short-lookback takeoff model + partial cruise transition model” are fused, and the influence of highly dynamic features is emphasized through gating weights; in the cruise phase, the focus is on the steady-state prediction of the “long-lookback cruise model”, with a small number of takeoff and landing transition models used to correct errors.
The real-time feasibility of Gate-iInformer is guaranteed by two key designs. First, computational efficiency: The framework adopts pre-trained iInformer sub-models and a lightweight gating network—where the gating network is composed of a single linear layer and ReLU activation. This design avoids real-time training processes, thus eliminating additional computational overhead. Tests on a standard aviation server show that the prediction latency for a single flight segment is less than 0.5 s, which meets the interval requirement of ADS-B data updates; and regarding data timeliness, input is sourced from ADS-B (providing real-time position and speed data with latency less than 0.1 s) and flight black boxes (providing offline preprocessed fuel data). Timestamp alignment, detailed in Section 2.1.1, synchronizes these two types of data sources, ensuring the framework uses up-to-date information without errors caused by data delays.
3. Results and Discussion
To verify the effectiveness and uniqueness of the proposed Gate-iInformer, this section conducts various relevant experiments to validate its advantages in training performance and application methods. Additionally, by comparing prediction errors with multiple common time-series prediction models under different input and output scales, the superiority of Gate-iInformer is confirmed.
To ensure a fair and rigorous comparison, all benchmark models were trained and evaluated under identical conditions. This includes using the same dataset split, identical data preprocessing pipelines, and the same hyperparameter tuning protocol. Crucially, the final hyperparameters used for all benchmark models were consistent with those optimized for our proposed model, as detailed in Table 1. This controlled setup guarantees that performance differences are attributable to the model architectures themselves rather than discrepancies in training procedures or hyperparameter choices.

Table 1.
Hyperparameters of the iInformer model and all benchmark models used in this study.
3.1. Inversion Difference Experiment
Traditional Transformer-like models use time slices as tokens. In long voyages, key features of early phases (e.g., takeoff) are gradually diluted due to token aggregation, making them difficult for the model to capture. In contrast, iTransformer-like models treat each variable as an independent token and directly model the raw variable sequences throughout the entire voyage, which can completely retain fine-grained features of each phase (such as thrust changes during takeoff, cruise parameters during level flight, and attitude adjustments during landing), thus avoiding information loss caused by time slice division.
Aircraft fuel consumption is strongly correlated with flight phases, and there are implicit associations between phases. The variable-level token design of iTransformer-like models enables them to more flexibly capture cross-phase variable dependencies, whereas the time-slice tokens of traditional Transformers are susceptible to intra-phase noise interference, making it difficult to distinguish feature patterns of different phases [20].
To verify the advantages and accuracy improvement of iInformer as a benchmark model compared to Informer in aircraft fuel prediction tasks, we compared the prediction performance of the two models under different lookback length settings. This evaluation aimed to assess the ability of iTransformer to capture multi-phase features throughout the flight and its applicability in fuel consumption prediction.
We conducted experiments with 30 independent runs to ensure the representativeness of the data and meet the large-sample assumption of normal distribution. As shown in Table 2, the experimental results indicate that iInformer achieves lower MAE than traditional Transformer under all lookback length settings, verifying the superiority of iInformer in aircraft fuel prediction tasks. To address the potential concern that improvements might result from random factors, we also conducted a statistical significance test. We adopted paired t-test to compare the MAE differences between iInformer and Informer under the same lookback length: the paired samples were derived from the same experimental conditions (identical flight data subset, hyperparameters, and only random seed varied), eliminating interference from batch differences.

Table 2.
Performance promotion obtained by inverted framework.
From the table, it can be observed that for all lookback lengths, the p-values are less than 0.05: e.g., p = 0.021 at lookback length 50 (2.97% improvement), and p becomes even smaller at longer lookback lengths. This indicates that the performance improvement of iInformer over Informer is statistically significant, and the possibility of random occurrence is less than 5%.
3.2. Fuel Quantity Constraint Experiment
Aircraft fuel consumption exhibits clear physical characteristics: under normal flight conditions, fuel quantity monotonically decreases over time. Traditional loss functions only focus on the numerical deviation between predicted values and true values without considering this physical constraint, which may lead to unreasonable predictions such as “fuel quantity increase” and affect the reliability of practical applications. This experiment aims to verify the optimization effect of introducing a loss function with a constraint on the continuous downward trend of fuel quantity on prediction performance. By comparing the model performance before and after adding the constraint, the role of physical constraints in improving the rationality and accuracy of predictions is evaluated.
The box plot results in Figure 6 show that after introducing the constraint on the downward trend of fuel quantity, the model performance is improved in both RMSE and MAE. This confirms the guiding role of physical constraints in the model learning process: by eliminating unreasonable predictions of upward trends, the model can focus more on learning the real fuel consumption patterns, thereby improving numerical accuracy [29].
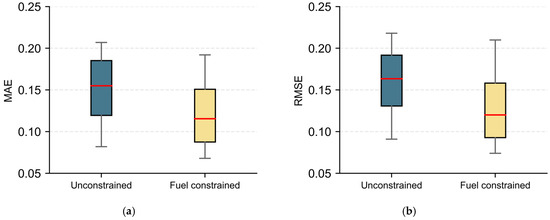
Figure 6.
Optimization effect of fuel physical constraints on prediction errors (a) MAE; (b) RMSE.
3.3. Experiment on Increasing Lookback Length
Previous studies have found that the prediction performance of Transformer models does not necessarily improve with the increase in lookback length [15,19]. Traditional Transformer-like models (such as Transformer and Informer used for comparison in the experiment) encapsulate time segments as tokens for input. In long aircraft journeys, features of different flight phases (e.g., high fuel consumption during takeoff and stable fuel consumption during cruise) are compressed due to the aggregation of time tokens. When the lookback length increases to a certain extent, key fuel consumption features of early phases are lost, making it difficult for the model to distinguish the laws of multiple phases [20].
iTransformer uses variables as tokens, independently encoding multi-dimensional variables such as fuel flow, flight altitude, speed, and engine parameters. In the scenario of aircraft fuel prediction, the laws of fuel consumption varying with features during takeoff, cruise, and landing phases can be directly and continuously transmitted through variable tokens. In long journey backtracking, variable tokens do not rely on time slice aggregation, thus completely retaining features of each phase. Theoretically, as the lookback length increases, the model can integrate more abundant cross-phase information, continuously improving prediction accuracy.
This experiment focuses on verifying the advantages of iInformer in adapting to multi-phase and long-journey backtracking in aircraft fuel prediction. We evaluated the performance of iTransformer-like models and traditional Transformer-like models under various lookback lengths in Figure 7. The results are consistent with theoretical expectations: iTransformer-like models can benefit from the increasing lookback length, while Transformer-like models show degraded prediction performance when the lookback length is excessively long. Across all lookback lengths (corresponding to different flight phases), iTransformer-like models outperform Transformer-like models of the same category, with more significant advantages in the landing phase.
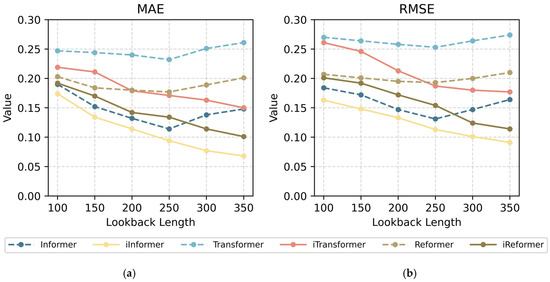
Figure 7.
Error comparison of different Transformer-based models under various lookback lengths (a) MAE; (b) RMSE.
In actual flight processes, as the journey progresses, the available real flight data continues to increase, and the usable lookback length of the data also extends accordingly. By training models with different input and output lengths, combined with the number of real-time obtained true values, more adaptive models with longer lookback lengths can be flexibly applied through the gating network. This approach can fully utilize richer spatiotemporal features for fuel quantity prediction, thereby maximizing prediction accuracy, providing more solid fuel quantity prediction support for aviation operations, helping airlines plan flight tasks more accurately, ensuring flight safety, and improving economic efficiency.
3.4. Gating Network Experiment
In the flight process, the length of actually available flown data (lookback length) is random and may fall into intervals not covered by pre-trained models (e.g., short lookbacks during takeoff, medium-to-long lookbacks before landing, etc.). A single pre-trained model can only perform optimally under a fixed lookback length and tends to show decreased accuracy when facing untrained lengths. This experiment aims to verify the dynamic adaptation capability of the gating network: when the lookback length required for prediction does not match the fixed length of pre-trained models, whether the Gate-iInformer framework can maintain high-precision prediction through weighted fusion of pre-trained sub-models via the gating network, thereby breaking through the length limitation of a single model.
The experiment selects 4 sets of fixed lookback lengths distributed throughout the entire journey (50, 150, 250, 350) and trains 4 independent iInformer models. Each model is only targeted at data of a fixed length without introducing a gating network, serving as the benchmark control group. These 4 pre-trained sub-models are integrated, and a gating network is introduced for joint training. The gating network takes real-time flight data features as input and learns the weight allocation strategy of sub-models under different lookback lengths through backpropagation, achieving dynamic adaptation to arbitrary lengths [30].
8 sets of lookback lengths are randomly sampled from the full journey data, among which 4 sets are pre-trained lengths (50, 150, 250, 350) and the other 4 sets are non-pre-trained lengths (30, 120, 210, 300). Fuel consumption prediction for these 8 sets of lengths is performed using the "single pre-trained model (without gating)" and "Gate-iInformer framework (with gating)", with MAE and RMSE as evaluation metrics to compare their accuracy differences. Figure 8 shows that for the 4 sets of pre-trained lookback lengths (50, 150, 250, 350), the prediction accuracy of the Gate-iInformer framework is comparable to that of the single pre-trained model. This indicates that the gating network does not introduce additional errors when adapting to known lengths. For lookback lengths not covered by pre-trained models (30, 120, 210, 300), the single model without gating shows a significant increase in MAE and RMSE during testing due to its inability to adapt to new lengths; in contrast, the Gate-iInformer framework maintains stable high precision through dynamic fusion of pre-trained sub-models via the gating network.
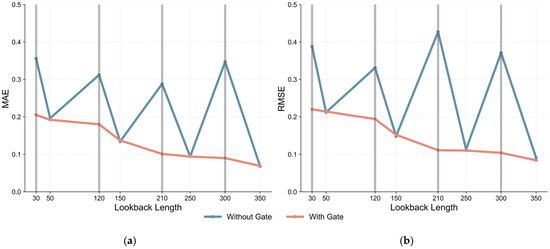
Figure 8.
Impact of the gating network on prediction accuracy (a) MAE; (b) RMSE.
To further quantify the contribution of the gating network, we calculate the ‘error reduction rate’ of Gate-iInformer relative to the single pre-trained model. For pre-trained lengths, the gating network contributes an average MAE reduction of 4.8% and RMSE reduction of 3.9%. For non-pre-trained lengths, the contribution increases to an average MAE reduction of 38.2% and RMSE reduction of 41.5%. This confirms that the gating network is not a redundant module but a core component for improving generalization. This is consistent with the design goal of the gating network which is to break through the length limitation of a single model by dynamic fusion.
The experimental results verify the core value of the gating network in our Gate-iInformer framework: by learning the adaptation rules of different pre-trained models, the framework can stably output high-precision predictions for any length throughout the entire journey without the need for separate training for each possible lookback length, thus improving the robustness and practicality of the model in actual flight scenarios.
3.5. Comparative Experiments
To verify the accuracy of the Gate-iInformer aircraft fuel prediction framework under different lookback lengths (corresponding to different flight phases), a variety of time-series prediction models are selected for comparison, including common Transformer-like models in recent years. The effectiveness of the proposed framework in fuel quantity prediction is validated across multiple lookback lengths, catering to the needs of feature extraction and prediction throughout the entire flight phase.
The experimental results, as shown in Figure 9 and Figure 10, indicate that under different flight lookback lengths, the Gate-iInformer fuel quantity prediction framework outperforms the comparison models in both MAE and RMSE metrics. For shorter flight lengths, the MAE and RMSE of the Gate-iInformer framework are lower than those of other models, though the difference is not significant. As the flight length increases, the advantages of the framework are sustained and become more pronounced. This demonstrates that in scenarios involving long-sequence feature extraction such as cruise and landing phases, the approach of iInformer using variables as tokens to extract features throughout the entire process effectively avoids the issue of traditional models ignoring early-stage features due to inappropriate token settings. It fully utilizes multi-phase information to ensure prediction accuracy. Particularly for long lookback lengths corresponding to the landing phase, Gate-iInformer shows more significant advantages over other comparison models. It can deeply explore complex and long-range feature correlations in the landing phase, accurately capture details of fuel consumption changes, and provide reliable technical support for aviation fuel management.
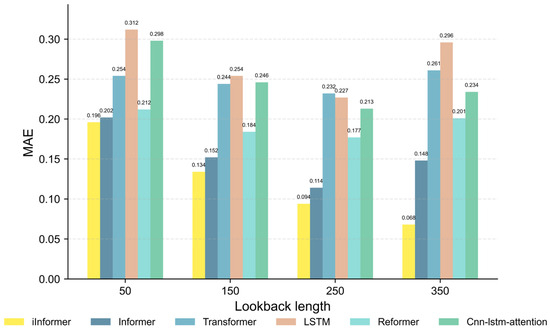
Figure 9.
MAE comparison between Gate-iInformer and various common time-series prediction models under different lookback lengths.
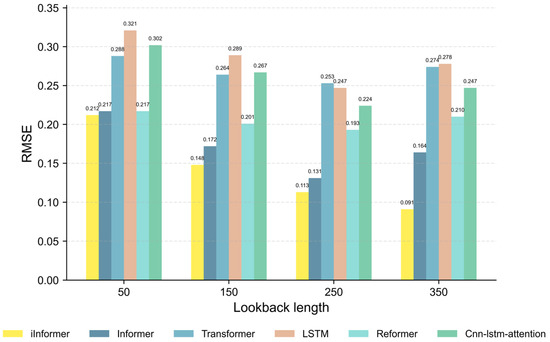
Figure 10.
RMSE comparison between Gate-iInformer and various common time-series prediction models under different lookback lengths.
4. Conclusions and Future Work
This study focuses on the core challenge of predicting fuel consumption throughout the entire aircraft flight, namely how to effectively handle the complex nonlinear and time-varying relationships among parameters during different flight phases. Eventually, an adaptive prediction framework named Gate-iInformer is constructed, with its main contributions reflected in the following three aspects:
First, in terms of model design, the limitation of traditional fixed architectures is broken through. Compared with the basic architecture design of iTransformer in [22], which only targets time-series prediction, this study for the first time integrates the iTransformer concept with the Informer architecture, taking iInformer as the base model, it innovatively treats multi-dimensional flight parameters as independent Tokens—this not only retains iTransformer’s ability to deeply capture the coupling relationships between variables but also inherits Informer’s efficiency in handling long-range temporal dependencies. It successfully avoids the information loss caused by traditional time-series segmentation, providing a more scenario-adapted structural support for feature extraction during the entire aircraft flight.
Second, the introduction of a gating network enables dynamic adaptation across multiple phases. Compared with the limitation of the single iInformer model, which fails to cover the feature differences among different flight phases, the gating network designed in this study can autonomously select and activate pre-trained iInformer sub-models optimized for specific phases based on real-time flight data features (e.g., short-time high-dynamic parameters during takeoff and long-time stable parameters during landing). This solves the generalization problem of the single model in phases with significant differences (such as short-time takeoff and long-time landing) and ensures the stability of prediction accuracy throughout the entire flight.
Multiple experiments based on real 2023 data from Air China fully verify the superiority of the framework at multiple levels. The results show that the combination of iInformer and the gating network maintains excellent accuracy in all flight phases: low-error prediction is achieved not only in the takeoff phase with short lookback length but also the prediction accuracy continues to improve as the lookback length increases (i.e., the flight progresses). In the landing phase corresponding to long-time series, the Mean Absolute Error (MAE) is as low as 0.068, which is significantly better than benchmark models such as Informer, Transformer, and LSTM in all phases of the entire flight. This data-driven solution not only provides a high-precision tool for aircraft fuel prediction but also opens up a new path for modeling multi-phase dynamic processes in complex industrial systems.
To further enhance the practicality and generalization ability of the framework, future research can be deepened in the following directions:
The current study utilizes data from a single airline and 25 different medium-sized aircraft models, many of which are widely used across domestic airlines to reduce type-related generalization barriers, but this single-airline source may still limit the model’s generalizability as differences in operational management across airlines could introduce biases affecting the model’s performance when applied to other carriers. A key direction for future work is to address this limitation through multi-dimensional data expansion and feature optimization: we will validate and retrain the model using datasets encompassing multiple airlines, various aircraft families beyond the current medium-sized models, and different route structures, and for new aircraft types, we will retain the one-hot encoding design for aircraft type features by only adding corresponding encoding vectors to input features without modifying the Gate-iInformer core architecture to ensure flexible adaptation; we will also design “airline type” as a categorical feature with one-hot encoding to enable the model to learn airline-specific fuel consumption patterns, while incorporating airline-related auxiliary features to further capture operational differences across carriers, and integrate real-time weather (including wind speed, precipitation) and air traffic flow into the input feature set—factors that impact flight fuel consumption but were not fully covered in the current study. This extensive data expansion and feature optimization will be essential to demonstrate the framework’s robustness and applicability across the heterogeneous conditions of global aviation operations, effectively addressing potential generalization bias from single-airline, limited-type data and enhancing the model’s practical value in complex aviation scenarios.
Enhancing model interpretability: Existing deep learning models have the “black-box” characteristic. In the future, methods such as attention weight visualization (e.g., displaying the attention allocation ratio of “altitude-fuel flow” and “speed-fuel consumption” in different flight phases) and feature importance quantification can be combined to clarify the impact of key parameters on model decisions in each phase, thereby improving the trust of aviation operation personnel in the model’s prediction results.
Optimizing real-time learning capability: The existing model relies on offline pre-trained parameters, resulting in limited adaptability when facing unexpected flight states such as route diversion. In the future, an online learning module will be considered to enable the gating network and sub-models to dynamically adjust parameters based on real-time updated flight data, shortening the model response time in emergency scenarios and improving prediction flexibility.
Regarding operational deployment, it is crucial to emphasize that the prediction output of Gate-iInformer is designed to complement, not replace, regulatory reserve fuel requirements. The framework’s role is to provide a more accurate estimate of the trip fuel consumption, which should then be added to the legally mandated fixed reserves (e.g., contingency, alternate, final reserve) to determine the total required fuel load. This approach enhances situational awareness and operational efficiency while fully preserving the established safety margins. Future work will explicitly incorporate this principle into the system’s output presentation, ensuring clear distinction between predicted trip fuel and regulatory reserves.
The Gate-iInformer framework demonstrates significant advantages in aircraft fuel consumption prediction: iInformer solves the core problems of long-range temporal dependencies and multi-variable coupling from the perspective of model structure; the gating network addresses the key challenge of dynamic adaptation across multi-phases. To advance the practical implementation of Gate-iInformer in real aviation operations, future work will focus on two core directions: first, conducting testing in real operational environments, and second, exploring the integration of physical models with Gate-iInformer.
We will collaborate with airline operation centers to deploy Gate-iInformer into the actual fuel planning workflow. This process will use real-time ADS-B data, flight black box data, and on-site operational factors as inputs to generate dynamic fuel predictions for aircraft in flight. In this real operational context, we will directly compare its performance with physical models widely adopted in the industry (such as the extended BADA model [5] and Dalmau’s thrust and drag balance model [6]). The evaluation will cover not only accuracy but also whether it can better support practical decision-making tasks like alternate landing planning and emergency fuel adjustments.
At the same time, we will explore hybrid integration methods for the two types of models. For instance, we will embed physical constraints into Gate-iInformer’s loss function to reduce physically unreasonable predictions. Another approach is to dynamically fuse their outputs: relying more on physical models during the stable cruise phase and on Gate-iInformer during the high-nonlinearity takeoff and landing phases. The goal of this integration is to combine the data-driven flexibility of Gate-iInformer with the interpretability of physical models, thereby creating a more reliable tool for real aviation fuel management.
Author Contributions
Conceptualization, Y.W. and J.F.; methodology, J.F., Y.W. and L.L.; software, J.F. and Y.Z.; validation, J.F., Y.W. and Y.L.; formal analysis, J.F. and Y.W.; investigation, J.F. and Y.Z.; resources, Y.W.; data curation, J.F. and Y.L.; writing—original draft preparation, J.F.; writing—review and editing, Y.W. and L.L.; visualization, W.F.; supervision, Y.W. and L.L.; funding acquisition, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Langfang Science and Technology Research and Development Plan “Machine Learning Based On-Board Fuel Prediction for Civil Aviation Air Emergency Response” (2024011012).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The present study acknowledges the invaluable flight data support provided by Air China. These high-quality flight data serve as the critical foundation for constructing and validating all experiments in this paper, providing a solid guarantee for the practicality and reliability of the research results.
Conflicts of Interest
Author Yu Li was employed by the company Air China. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Nomenclature
The following notations and abbreviations are used in this manuscript:
| Multi-dimensional time-series matrix | |
| Transposed time-series matrix | |
| Lookback length | |
| Number of flight parameter variables | |
| Initial Token of the n-th variable | |
| TrmBlock | Transformer Block |
| Number of Transformer block layers | |
| Future sequence prediction result of the n-th variable | |
| Gating hidden vector | |
| Relative longitude change at time t | |
| Relative latitude change at time t | |
| Relative fuel change at time t | |
| Weight of the k-th sub-model | |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Square Error |
| iInformer | Inverted Informer |
| CNN-BiLSTM | Convolutional Neural Network-Bidirectional Long Short-Term Memory |
| ADS-B | Automatic Dependent Surveillance-Broadcast |
References
- Khalili, S.; Rantanen, E.; Bogdanov, D.; Breyer, C. Global Transportation Demand Development with Impacts on the Energy Demand and Greenhouse Gas Emissions in a Climate-Constrained World. Energies 2019, 12, 3870. [Google Scholar] [CrossRef]
- Seymour, K.; Held, M.; Georges, G.; Boulouchos, K. Fuel Estimation in Air Transportation: Modeling Global Fuel Consumption for Commercial Aviation. Transp. Res. Part D Transp. Environ. 2020, 88, 102528. [Google Scholar] [CrossRef]
- Ding, S.; Ma, Q.; Qiu, T.; Gan, C.; Wang, X. An Engine-Level Safety Assessment Approach of Sustainable Aviation Fuel Based on a Multi-Fidelity Aerodynamic Model. Sustainability 2024, 16, 3814. [Google Scholar] [CrossRef]
- Gössling, S.; Humpe, A.; Fichert, F.; Creutzig, F. COVID-19 and Pathways to Low-Carbon Air Transport Until 2050. Environ. Res. Lett. 2021, 16, 034063. [Google Scholar] [CrossRef]
- Gómez Comendador, V.F.; Arnaldo Valdés, R.M.; Lisker, B. A Holistic Approach to the Environmental Certification of Green Airports. Sustainability 2019, 11, 4043. [Google Scholar] [CrossRef]
- Dalmau Codina, R.; Melgosa Farrés, M.; Vilardaga García-Cascón, S.; Prats Menéndez, X. A Fast and Flexible Aircraft Trajectory Predictor and Optimiser for ATM Research Applications. In Proceedings of the 8th International Conference for Research in Air Transportation (ICRAT), Castelldefels, Spain, 26–29 June 2018; pp. 1–8. [Google Scholar]
- Gardi, A.; Sabatini, R.; Ramasamy, S. Multi-Objective Optimisation of Aircraft Flight Trajectories in the ATM and Avionics Context. Prog. Aerosp. Sci. 2016, 83, 1–36. [Google Scholar] [CrossRef]
- Zhu, X.; Li, L. Flight Time Prediction for Fuel Loading Decisions with a Deep Learning Approach. Transp. Res. Part C Emerg. Technol. 2021, 128, 103179. [Google Scholar] [CrossRef]
- Metlek, S. A New Proposal for the Prediction of an Aircraft Engine Fuel Consumption: A Novel CNN-BiLSTM Deep Neural Network Model. Aircr. Eng. Aerosp. Technol. 2023, 95, 838–848. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, J.; Hou, Y. Spatial–Temporal Transformer Networks for Traffic Flow Forecasting Using a Pre-Trained Language Model. Sensors 2024, 24, 5502. [Google Scholar] [CrossRef]
- Khan, W.A.; Ma, H.L.; Ouyang, X.; Mo, D.Y. Prediction of Aircraft Trajectory and the Associated Fuel Consumption Using Covariance Bidirectional Extreme Learning Machines. Transp. Res. Part E Logist. Transp. Rev. 2021, 145, 102189. [Google Scholar] [CrossRef]
- Lin, Y.; Guo, D.; Wu, Y.; Li, L.; Wu, E.Q.; Ge, W. Fuel Consumption Prediction for Pre-Departure Flights Using Attention-Based Multi-Modal Fusion. Inf. Fusion 2024, 101, 101983. [Google Scholar] [CrossRef]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language Models are Few-Shot Learners. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Virtual, 6–12 December 2020. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. In Proceedings of the International Conference on Learning Representations (ICLR), Virtual, 3–7 May 2021. [Google Scholar]
- Nie, Y.; Nguyen, N.H.; Sinthong, P.; Kalagnanam, J. A Time Series is Worth 64 Words: Long-Term Forecasting with Transformers. In Proceedings of the International Conference on Learning Representations (ICLR), Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Liu, Y.; Wu, H.; Wang, J.; Long, M. Non-Stationary Transformers: Rethinking the Stationarity in Time Series Forecasting. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), New Orleans, LA, USA, 28 November–9 December 2022. [Google Scholar]
- Dong, J.; Wu, H.; Zhang, H.; Zhang, L.; Wang, J.; Long, M. SimMTM: A Simple Pre-Training Framework for Masked Time-Series Modeling. arXiv 2023, arXiv:2302.00861. [Google Scholar]
- Ekambaram, V.; Jati, A.; Nguyen, N.; Sinthong, P.; Kalagnanam, J. TSMixer: Lightweight MLP-Mixer Model for Multivariate Time Series Forecasting. In Proceedings of the ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD), Long Beach, CA, USA, 6–10 August 2023. [Google Scholar]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are Transformers Effective for Time Series Forecasting? In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 1121–11128. [Google Scholar]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. iTransformer: Inverted Transformers Are Effective for Time Series Forecasting. arXiv 2023, arXiv:2310.06625. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. Proc. AAAI Conf. Artif. Intell. 2021, 35, 11106–11115. [Google Scholar] [CrossRef]
- Jepsen, T.S.; Jensen, C.S.; Nielsen, T.D. Relational Fusion Networks: Graph Convolutional Networks for Road Networks. IEEE Trans. Intell. Transp. Syst. 2022, 23, 418–429. [Google Scholar] [CrossRef]
- Kang, L.; Hansen, M.; Ryerson, M.S. Evaluating Predictability Based on Gate-In Fuel Prediction and Cost-to-Carry Estimation. J. Air Transp. Manag. 2018, 67, 146–152. [Google Scholar] [CrossRef]
- Zhao, L.; Song, Y.; Zhang, C.; Liu, Y.; Wang, P.; Lin, T.; Li, H. T-GCN: A Temporal Graph Convolutional Network for Traffic Prediction. IEEE Trans. Intell. Transp. Syst. 2020, 21, 3848–3858. [Google Scholar] [CrossRef]
- Dong, S.; Yu, T.; Farahmand, H.; Mostafavi, A. A Hybrid Deep Learning Model for Predictive Flood Warning and Situation Awareness Using Channel Network Sensors Data. Comput. Aided Civ. Infrastruct. Eng. 2021, 36, 402–420. [Google Scholar] [CrossRef]
- Ryerson, M.S.; Hansen, M.; Bonn, J. Time to Burn: Flight Delay, Terminal Efficiency, and Fuel Consumption in the National Airspace System. Transp. Res. Part A Policy Pract. 2014, 69, 286–298. [Google Scholar] [CrossRef]
- Shazeer, N.; Mirhoseini, A.; Maziarz, K.; Davis, A.; Le, Q.V.; Hinton, G.E.; Dean, J. Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer. arXiv 2017, arXiv:1701.06538. [Google Scholar]
- Yan, C.; Xiang, X.; Wang, C. Towards Real-Time Path Planning Through Deep Reinforcement Learning for a UAV in Dynamic Environments. J. Intell. Robot. Syst. 2020, 98, 297–309. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-Informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Jacobs, R.A.; Jordan, M.I.; Nowlan, S.J.; Hinton, G.E. Adaptive Mixtures of Local Experts. Neural Comput. 1991, 3, 79–87. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).