An Interval Analysis Method for Uncertain Multi-Objective Optimization of Solid Propellant Formulations
Abstract
1. Introduction
1.1. Traditional Methods for Formulation Optimization
1.2. Artificial Intelligence-Based Methods for Formulation Optimization
1.3. MOEA/D and Large Language Models
1.4. Uncertainty Analysis Methods
1.5. Contributions and Highlights
2. Methods
2.1. Calculation of Formulation Performance
2.2. Transformation of Unconstrained Uncertain Multi-Objective Optimization Problems
2.2.1. Processing Methods for Unconstrained Uncertain Objective Functions
2.2.2. Processing Methods for Uncertain Multi-Objective Function
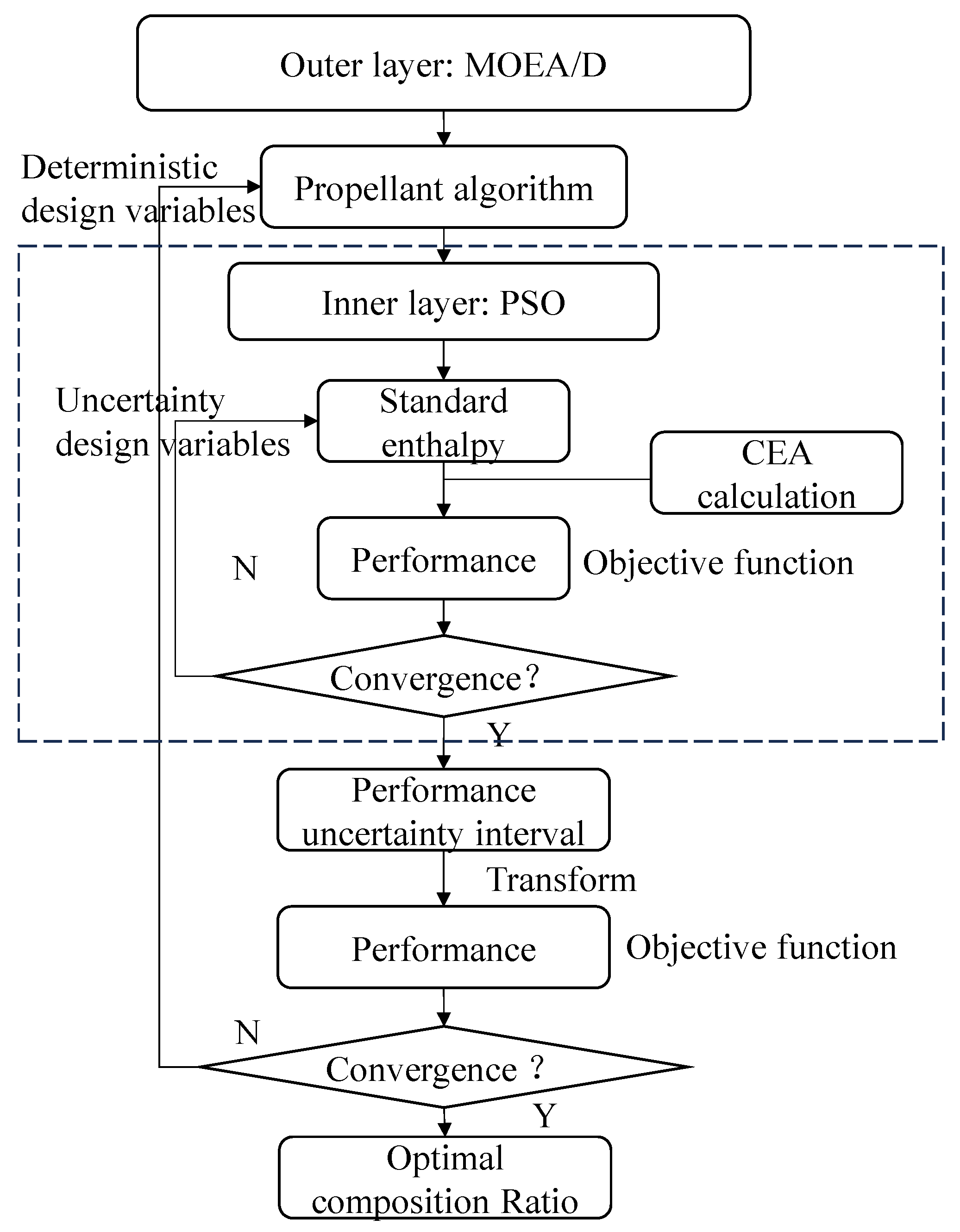
2.3. Uncertain Multi-Objective Optimization Model for Solid Propellants
- (1)
- Randomly select the mass fraction of each propellant component, and carry out inner layer optimization under this component mass fraction.
- (2)
- In the inner layer, the design variable is the standard enthalpy, and the target is to find the best and the worst performance of the propellant under a fixed formulation. The performance of the propellant can be calculated using the RocketCEA 1.2.0. And the PSO algorithm is applied to obtain the best and the worst performance, respectively. The settings of PSO are shown in Table 4. The best and the worst values form the uncertainty interval of the performance.
- (3)
- The uncertainty interval will be transformed to deterministic performance using Equation (8).
- (4)
- In the outer layer, the design variable is the mass fraction of the component, and the target is to find the best deterministic performance using the MOEA/D-LLM algorithm. The settings of MOEA/D-LLM are shown in Table 5.
2.4. Case Study on Solid Propellant Optimization
- The preparation of the NEPE propellant:Firstly, place AP in a vacuum drying oven at 60 °C with a vacuum of 0.06 MPa for 4 h. Place the metal fuel in the same vacuum oven for 2 h. Place HTPB, PEG, and NG in a vacuum drying oven at 105 °C for dehydration for 10 h. The dried reagents are stored in sealed containers.Secondly, weigh out the required masses of the three liquid reagents (HTPB, PEG, and NG) according to the component ratios. Pour the liquid reagents into a beaker and place the beaker in a water bath at 50 °C. The resulting mixture was stirred with a high shear homogenizer HG-15D (Daihan Scientific, Seoul, Republic of Korea) at 5000 rpm for 30 min.After thorough mixing, place the mixture into a 50 °C vacuum drying oven and allow it to stand for 1 h to defoam.Thirdly, mix curing agents, adhesives, and additives evenly. Add aluminum powder, AP, and HMX in sequence for mixing. For each solid filler, it needs to be mixed evenly before adding another one, and repeat the above steps until all raw materials are added. Mix and stir the propellant for another 30 min. At this stage, the mixture appears as a dark gray, opaque slurry with a certain degree of fluidity.Fourthly, remove the beaker from the 50 °C water bath and place it in a 50 °C vacuum drying oven. Allow it to stand for 4 h to eliminate bubbles from the propellant slurry. Pour the propellant slurry into a PTFE mold coated with release agent. Place the PTFE mold in a drying oven at 50 °C with a vacuum of 0.06 MPa. Dry for 7 days until the sample solidifies into a cylindrical solid. At this stage, the propellant sample has a compact structure with good elasticity. Demold the propellant from the PTFE mold using a glass rod.Finally, use a ceramic knife to cut it into a flake with a diameter of 10 mm and a thickness of 1 mm.
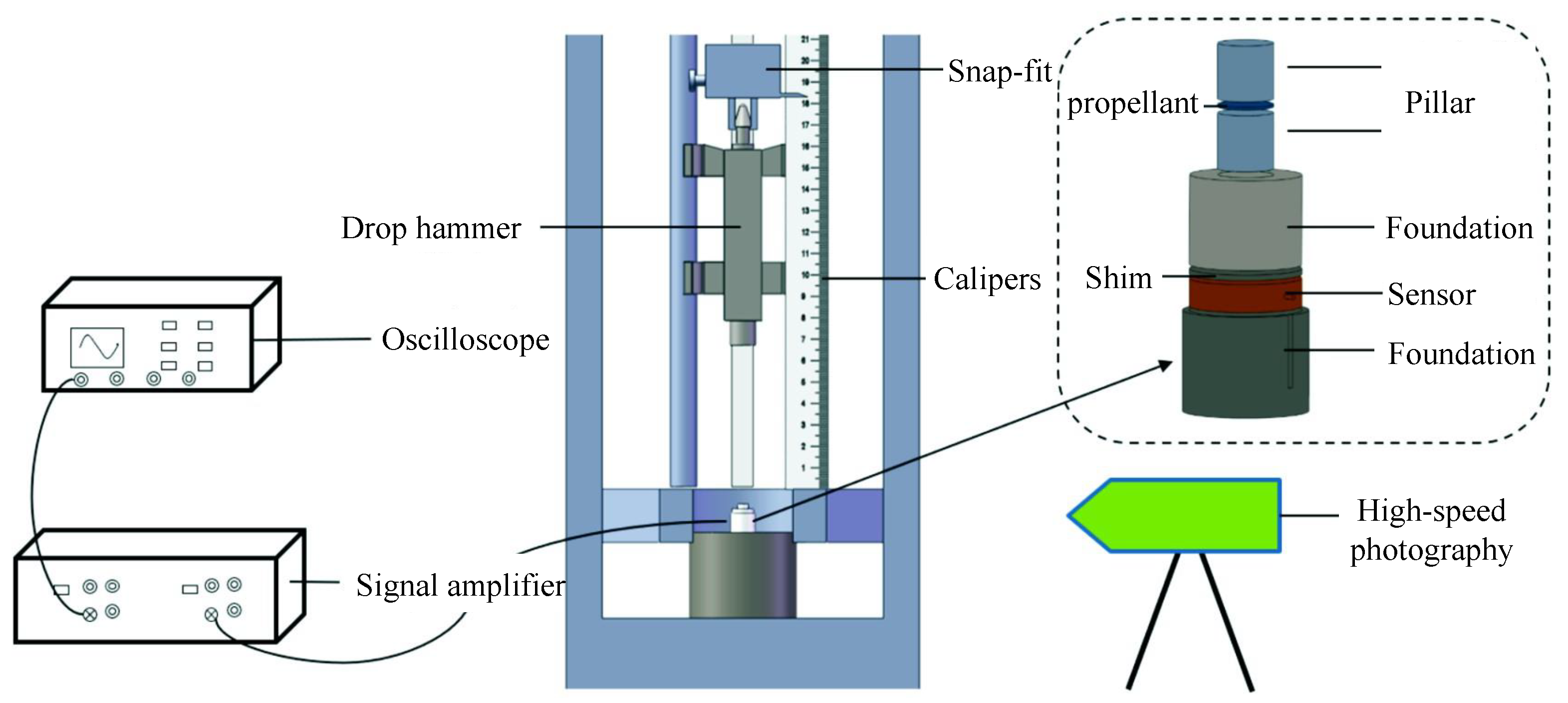
- The impact sensitivity test: The impact sensitivity test is a safety procedure that assesses the mechanical sensitivity of solid rocket propellants. It typically involves a drop-weight test, where a known weight is dropped from varying heights onto a sample. The goal is to determine the critical impact energy required to cause ignition or explosion. The standard is based on the “Test method for drop weight impact sensitivity of composite solid propellants (QJ3039-1998)” [42]. If decomposition, combustion, or explosion occurs in the solid propellant, it is judged as explosion; otherwise, it is judged as a non-explosion. For example, in Figure 3a, localized ignition occurs within the circled area, while in Figure 3b,c, visible smoke is ejected outward from the circled area. These two phenomena can indicate that the sample has exploded.In this paper, the impact sensitivity of the NEPE propellant is based on the characteristic drop height values under a 2 kg drop hammer. The drop hammer device is shown in Figure 4. The entire impact process of the propellant is recorded using a high-speed camera.First, select an appropriate step size (0.05 logarithmic units of drop height) to calculate the height increment/decrement.Second, determine the initial drop height by the Drop-Weight Impact Test. Adjust the drop hammer height after each test based on whether ignition occurs.Finally, conduct 25 experiments per sample group and record the explosion/non-explosion in each trial.
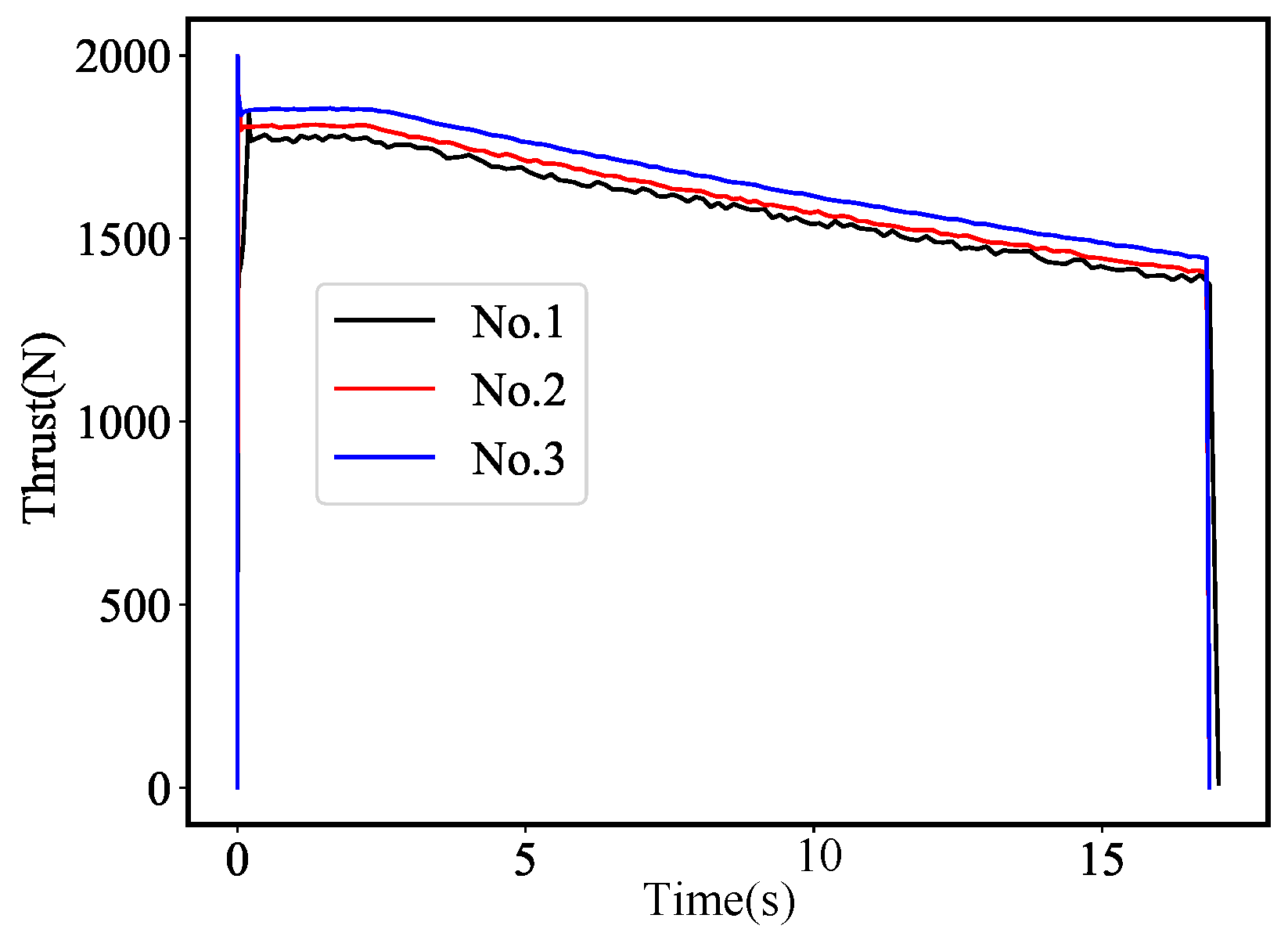
- Ground hot-fire test: To calculate the specific impulse of the experiment, a ground hot-fire test of an end-burning solid rocket motor was conducted. The parameters of the solid rocket motor used in the test are provided in Table 8.
- and from the combustion gas of the NEPE propellant is tested via the EDTA titration method and acid–base titration [43].Firstly, weigh the m = 0.2 g sample and fuse with sodium carbonate. Dissolve the melt in hydrochloric acid and dilute to 250 mL. Transfer 25 mL aliquot, add excess EDTA standard solution (0.05 mol/L), and boil for 3 min to complex .After cooling, adjust the aliquot to pH 5.5 using an acetate-ammonium buffer, add a PAN indicator, and titrate with zinc acetate standard solution ( = 0.025 mol/L) to purple endpoint (record as ).Add 10 mL potassium fluoride solution (200 g/L), boil for 2 min to release Al-EDTA complex, and back-titrate at 80 °C with zinc acetate until purple reappears (record as ). can be calculated by Equation (15).In acid–base titration for HCl, the sample ( = 10 mL) is added with phenolphthalein, then titrated with NaOH solution ( = 0.1 mol/L) to the endpoint (phenolphthalein: colorless to pink at pH 8.3). can be calculated by Equation (16).
3. Results and Discussions
3.1. NEPE Solid Propellant
3.1.1. Validation for the Impact Sensitivity Factor Model
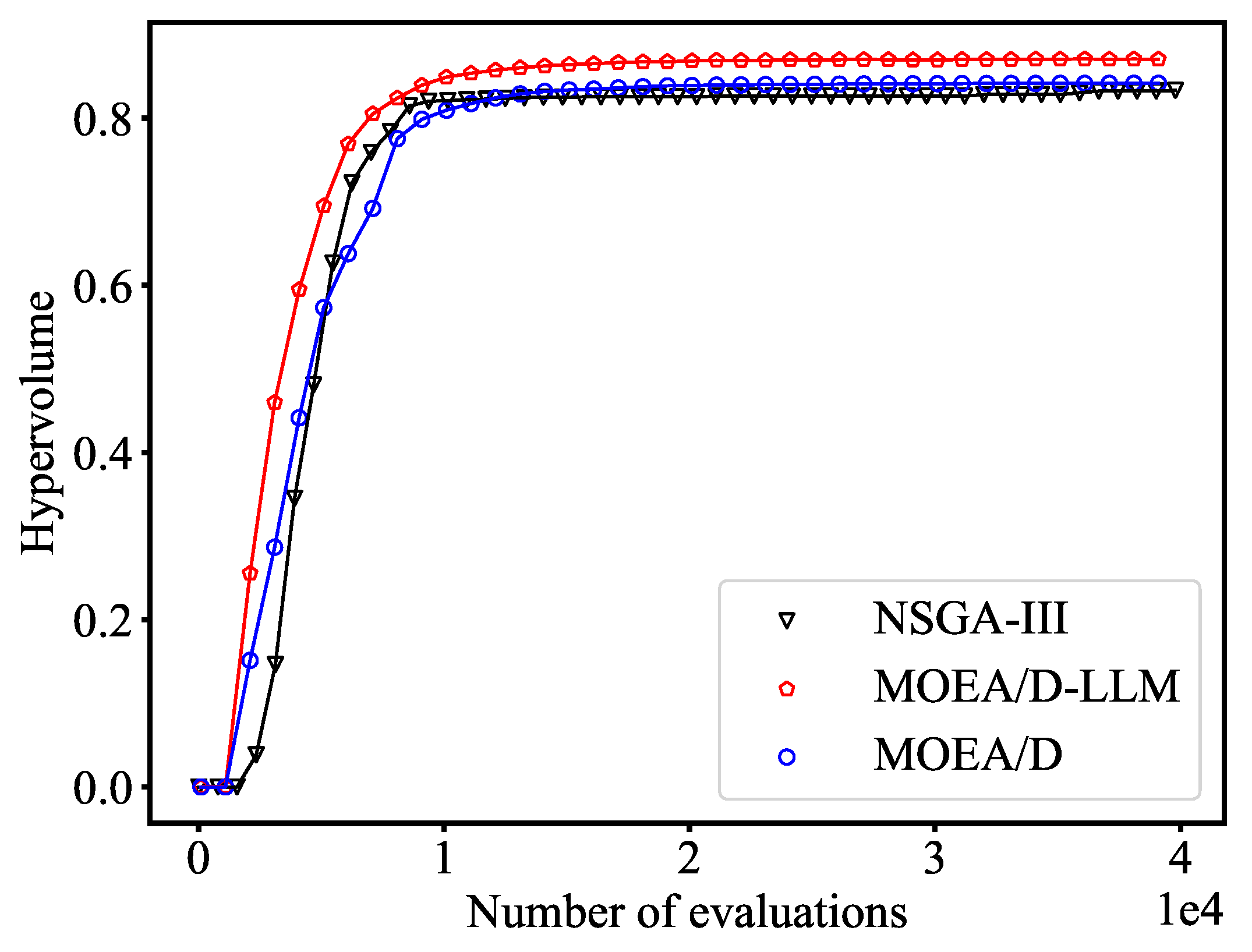
3.1.2. Validation for the MOEA/D-LLM
3.1.3. Validation for the Interval Uncertain Method
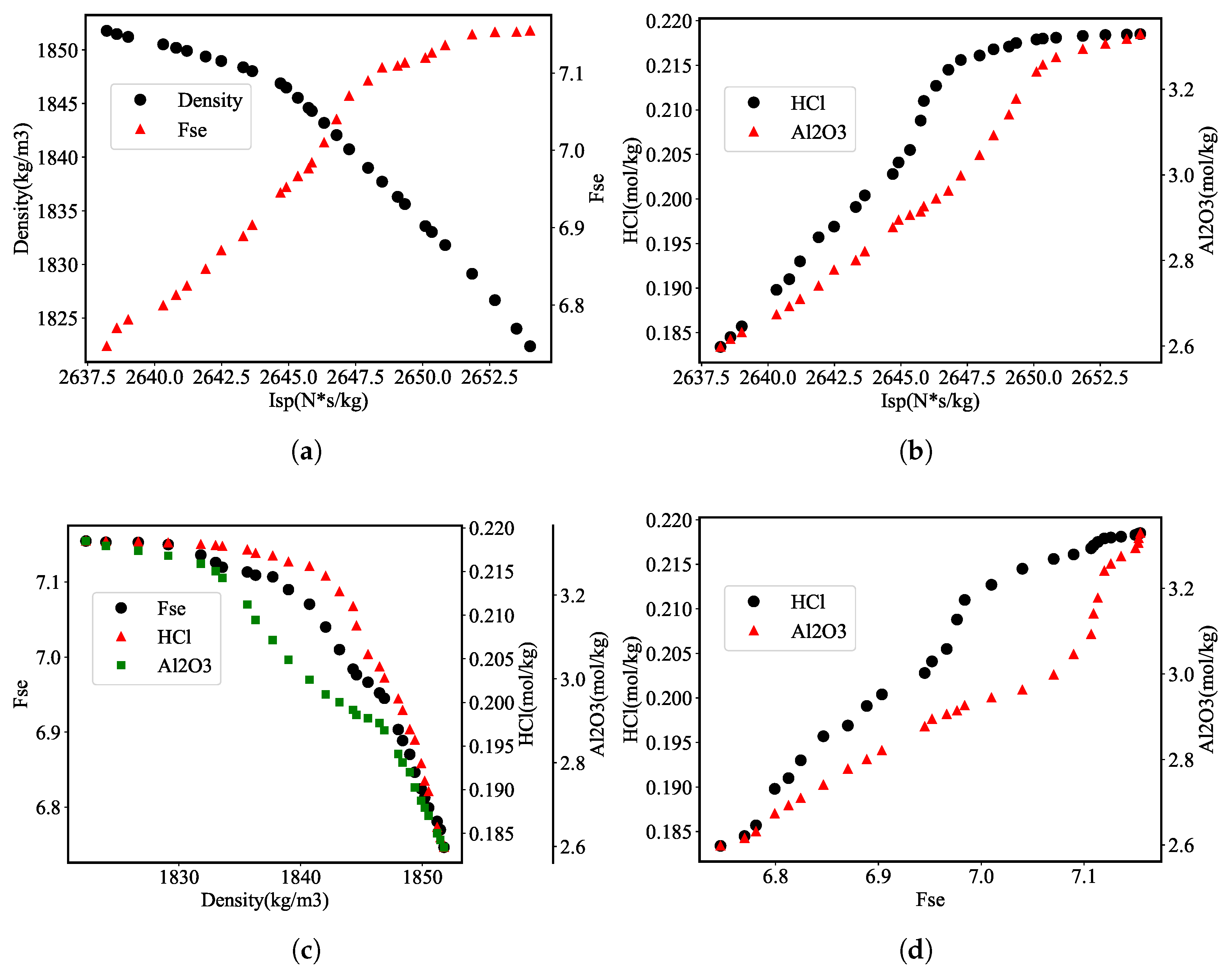
3.1.4. Optimization Results of NEPE Propellant
3.2. HTPB Solid Propellant
4. Conclusions
- (1)
- The optimization results of ZDTs and UFs show that MOEA/D-LLM has the best HV value and the fasted convergence speed compared to NSGA-II and MOEA/D. MOEA/D-LLM achieves approximately a 4.0% improvement in hypervolume values compared to MOEA/D. For the NEPE propellant optimization case, MOEA/D-LLM reduces the computational time by about 13.05% and enhances hypervolume values by around 2.7% compared to MOEA/D.
- (2)
- The interval uncertain method avoids establishing a surrogate model compared to PCE, and it has better calculation accuracy than the PCE method.
- (3)
- The performance of the NEPE and HTPB propellant is improved using the optimization model we proposed. For NEPE, the specific impulse increases by 1.11%, the generation of aluminum oxide and hydrogen chloride decreases by approximately 18.43% and 16.40%, respectively, and the impact sensitivity is reduced by about 1.67%. For HTPB, the generation of aluminum oxide and hydrogen chloride is reduced by 20.54% and 5.07%, respectively. The specific impulse increases by 0.61%, the density improves by 1.48%, and the impact sensitivity is reduced by 1.82%.
- (4)
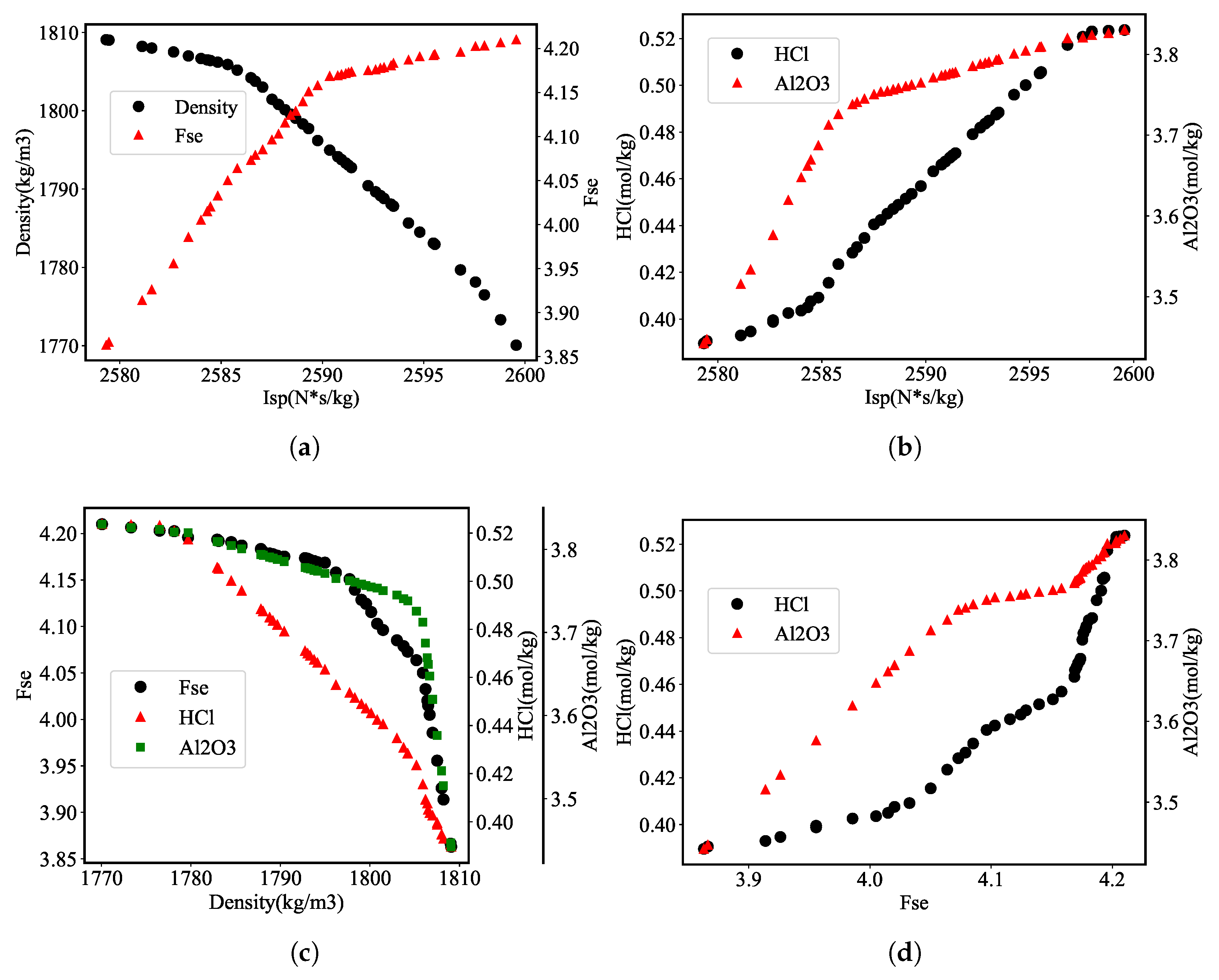
- When the optimal specific impulse value is raised, there is a trend of the optimal density value decreasing and the optimal impact sensitivity factor value, , and , production increasing. Designers can choose the appropriate propellant ratio according to experience and demand.
- (5)
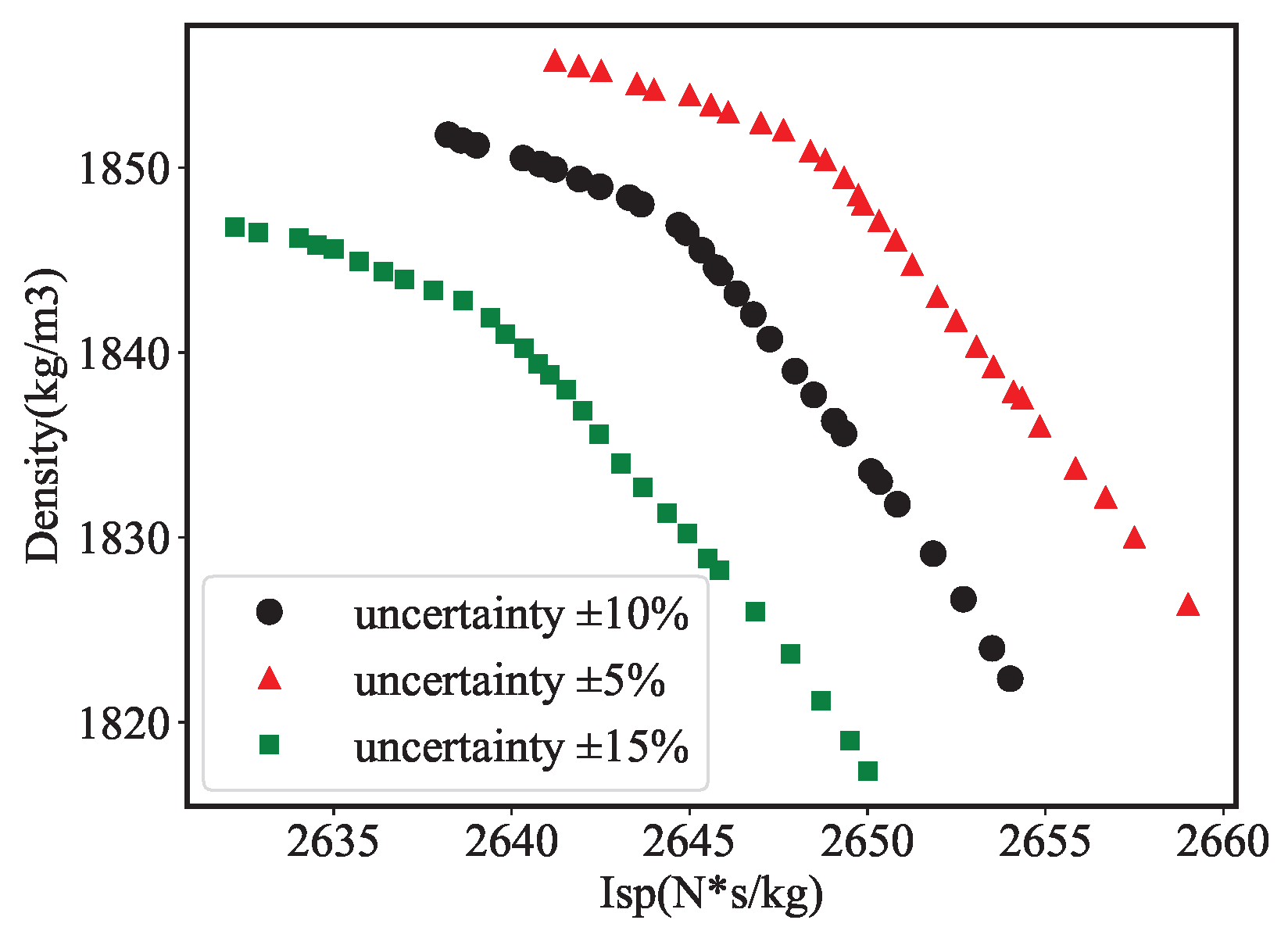
- When the uncertainty level of the standard heat of formation of each propellant component is increased, the uncertainty interval radius of each performance index gradually increases. When the weight coefficient in the MOEA/D algorithm is increased, the uncertainty interval radius of each performance index gradually decreases, but at the same time, the performance will also decline. Designers can adjust the weight coefficient and uncertainty level of the MOEA/D algorithm according to the actual optimization robustness requirements. When more emphasis is placed on the robustness of propellant performance, designers should appropriately increase the uncertainty level of the propellant property parameters and decrease the weighting coefficient of MOEA/D. In contrast, if higher performance propellants are desired, it is necessary to reduce the level of uncertainty and increase the weight coefficient of MOEA/D while ensuring minimal propellant losses.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pang, A.; Wu, J.; Xu, H.; Wu, F. Development of Advanced Low Signature Characteristics Propellant. Chin. J. Solid Mech. 2003, 26, 43–50. [Google Scholar] [CrossRef]
- Wang, Z.; Pang, A.; He, J.; Lei, Q. Application and Development of Energetic Compounds in Solid Propellant. J. Solid Rocket Technol. 2025, 48, 1–8. [Google Scholar] [CrossRef]
- Dong, W.; Zhao, H.; Geng, G.; Li, M. Computer-aided Conceptual Design Method of Double-base Solid Propellant Formulation. Chin. J. Energetic Mater. 2017, 25, 1018–1024. [Google Scholar] [CrossRef]
- Tian, D. Graphical Method for Calculating the Performance of Smokeless Propellant. Acta Armam. 1980, 4, 11. [Google Scholar]
- Swaminathan, V.; Madhavan, N.; Chacko, C. A Penalty Function Approach to the Optimization of Chemical Propellant Systems using the fletcher-powell algorithm. Propellants Explos. Pyrotech. 1982, 7, 96–99. [Google Scholar] [CrossRef]
- Tian, D. Optimization and Design of Solid Propellant Formulations, 3rd ed.; National Defense Industry Press: Beijing, China, 2013; pp. 1–95. [Google Scholar]
- Yu, Z.; Yao, W.; Fu, X.; Wei, H.; Tan, G. Theoretical Study on Formulation Optimization for Multi-Index Solid Propellant. Trans. Beijing Inst. Technol. 2017, 37, 1310–1314. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, Y.; Zhao, F. Intelligent Design for the Burning Rate of MDB Propellants Containing RDX. Chin. J. Explos. Propell. 2022, 45, 814–820. [Google Scholar] [CrossRef]
- Klinger, D.; Casey, A.; Manship, T.; Son, S. Prediction of Solid Propellant Burning Rate Characteristics Using Machine Learning Techniques. Propellants Explos. Pyrotech. 2023, 48, e202200267. [Google Scholar] [CrossRef]
- Tian, D. Optimization Design Method of Solid Propellant Formulation and Its Software System. Chin. J. Explos. Propell. 2014, 37, 1–23. [Google Scholar] [CrossRef]
- Fan, L.; Pan, G.; Ou, Y.; Chen, X.; Feng, G. Application of Genetic Algorithm-Support Vector Machine in Formula Optimization of Mg/PTFE Fuel Rich Propellant. J. Propul. Technol. 2012, 33, 620–624. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, W. Improved Particle Swarm Algorithm to Lower Signature Characteristics of Solid Propellant. Comput. Eng. Appl. 2017, 53, 136–141. [Google Scholar] [CrossRef]
- Hao, Y.; Zhao, C.; Zhang, Y.; Cao, Y.; Li, Z. Constrained Multi-objective Optimization Problems: Methodologies, Algorithms and Applications. Knowl.-Based Syst. 2024, 299, 11198. [Google Scholar] [CrossRef]
- Zhou, W.; Liu, B.; Zhang, Y.; Ma, Y.; Wang, X. Multi-objective Optimization for HTPB Propellant Breaking Process by Submerged Cavitating Water Jet. Chin. J. Explos. Propell. 2022, 45, 227–284. [Google Scholar] [CrossRef]
- Liu, C.; Wang, B.; Ma, Y. Multi-objective Optimization Design of High-rise Diagrid Structure Based on Non-dominated Sorting Genetic Algorithm II. J. Build. Eng. 2025, 108, 112801. [Google Scholar] [CrossRef]
- Li, Y.; Lei, J.; Ren, S. Multi-objective Optimization and Machine Learning for the Temperature Distribution Measurement Using Acoustic Tomography. Appl. Therm. Eng. 2025, 277, 127113. [Google Scholar] [CrossRef]
- Nishi, Y.; Konno, K. Multi-objective Optimization Design Method for Single-blade Centrifugal Pump Impellers to Improve Performance and Reduce Radial Thrust. Eur. J. Mech. B-Fluids 2025, 114, 204311. [Google Scholar] [CrossRef]
- Ma, Y.; Li, M.; Wang, M. Improve Thermal Efficiency And Reduce NOx Emission of Circulating Fluidized Bed Boiler Based on Multi-objective Optimization Framework. Therm. Sci. Eng. Prog. 2025, 64, 103753. [Google Scholar] [CrossRef]
- Peng, W.; Zhang, Q. A Decomposition-based Multi-objective Particle Swarm Optimization Algorithm for Continuous Optimization Problems. In Proceedings of the 2008 IEEE International Conference on Granular Computing, Hangzhou, China, 26–28 August 2008. [Google Scholar] [CrossRef]
- Xue, Y.; Cai, X.; Neri, F. A multi-objective evolutionary algorithm with interval based initialization and self-adaptive crossover operator for large-scale feature selection in classification. Appl. Soft Comput. 2022, 127, 109420. [Google Scholar] [CrossRef]
- Lin, A.; Yu, P.; Cheng, S.; Xing, L. One-to-one ensemble mechanism for decomposition-based multi-Objective optimization. Swarm Evol. Comput. 2022, 68, 101007. [Google Scholar] [CrossRef]
- Katharine, S. GPT-4 is Here: What Scientists Think. Nature 2023, 615, 773. [Google Scholar] [CrossRef]
- Thiago, R.; Felix, L.; Stefan, M. Large Language Model-assisted Surrogate Modelling for Engineering Optimization. In Proceedings of the 2nd IEEE Conference on Artificial Intelligence, Marina Bay Sands, Singapore, 25–27 June 2024. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, Q. Hyperparameter Optimization of Object Detection Networks Based on Large Language Models. In Proceedings of the 50th Annual Conference of the IEEE Industrial Electronics Society, Chicago, IL, USA, 3–6 November 2024. [Google Scholar] [CrossRef]
- Hameed, S.; Qolomany, B.; Belhaouari, S.B.; Abdallah, M.; Qadir, J.; Al-Fuqaha, A. Large Language Model Enhanced Particle Swarm Optimization for Hyperparameter Tuning for Deep Learning Models. IEEE Open J. Comput. Soc. 2025, 6, 574–585. [Google Scholar] [CrossRef]
- Lange, R.; Schaul, T.; Chen, Y.; Zahavy, T.; Dalibard, V.; Lu, C.; Singh, S.; Flennerhag, S. Discovering Evolution Strategies via Meta-Black-Box Optimization. In Proceedings of the Companion Conference on Genetic and Evolutionary Computation, New York, NY, USA, 29–30 July 2023. [Google Scholar] [CrossRef]
- Xiong, F.; Li, Z.; Liu, Y.; Xia, H. A Review of Characterization Methods for Parameter Uncertainty in Engineering Design Based on Numerical Simulation. Acta Aeronaut. Astronaut. Sin. 2023, 44, 92–123. [Google Scholar] [CrossRef]
- Li, M.; Zhao, F.; Xu, S.; Gao, X.; Yi, J. Comparison of Three Kinds of Energy Calculation Programs in Formulation Design of Solid Propellants. Chin. J. Explos. Propell. 2013, 36, 73–77. [Google Scholar] [CrossRef]
- Liu, J.; Yang, G.; Wang, L.; Xue, L. Interval Uncertainty Analysis of Ultra-light Artillery Firing Process Based on Polynomial Chaos Expansion. J. Vib. Shock 2025, 44, 132–139. [Google Scholar] [CrossRef]
- Mahmoud, H.; Sharaf, M.; El-Meligy, M. An Adaptive Robust Optimization Model for Transmission Expansion Planning Considering Uncertain Intervals. Int. J. Electr. Power Energy Syst. 2024, 157, 109821. [Google Scholar] [CrossRef]
- Yao, X.; Wang, F.; Yuan, J.; Wang, X. Path Planning for Autonomous Underwater Vehicles Based on Interval Optimization in Uncertain Flow Fields. Ocean Eng. 2021, 234, 108675. [Google Scholar] [CrossRef]
- Chen, Y.; Zhong, R.; Wang, Q.; Chen, L.; Qin, B. Free Vibration Analysis and Multi-objective Robust Optimization of Three-dimensional Pyramidal Rruss Core Sandwich Plates with Interval Uncertain Parameters. Eur. J. Mech. A-Solids 2024, 108, 105401. [Google Scholar] [CrossRef]
- Moore, R. Methods and Applications of Interval Analysis, 3rd ed.; Prentice-Hall Inc.: London, UK, 1979; pp. 1–50. [Google Scholar]
- Gao, S. Theoretical Prediction of Sensitivity of Mixed Explosives. Master’s Thesis, North University of China, Taiyuan, China, 2011. [Google Scholar]
- Huang, S. Research on Mechanical Sensitivity Prediction Model of Composite Explosives. Master’s Thesis, North University of China, Taiyuan, China, 2013. [Google Scholar]
- Michalchuk, A.; Hemingway, J.; Morrison, C. Predicting the impact sensitivities of energetic materials through zone-center phonon up-pumping. J. Chem. Phys. 2021, 154, 064105. [Google Scholar] [CrossRef] [PubMed]
- Rice, B.; Hare, J. A Quantum Mechanical Investigation of the Relation between Impact Sensitivity and the Charge Distribution in Energetic Molecules. J. Phys. Chem. 2002, 106, 1770–1783. [Google Scholar] [CrossRef]
- Mathieu, D. Sensitivity of Energetic Materials: Theoretical Relationships to Detonation Performance and Molecular Structure. Ind. Eng. Chem. Res. 2017, 56, 8191–8201. [Google Scholar] [CrossRef]
- Wang, S. An Approach for Predicting Propellant Stability and Sensitivity to Impact ETC Based on Propellant Compositions. J. East China Inst. Technol. 1993, 1, 64–69. [Google Scholar]
- Jiang, C.; Han, X.; Liu, G.; Liu, G. A Nonlinear Interval Number Programming Method for Uncertain Optimization Problems. Eur. J. Oper. Res. 2008, 188, 1–13. [Google Scholar] [CrossRef]
- Yao, S.; Liu, F.; Lin, X.; Lu, Z.; Wang, Z.; Zhang, Q. Multi-Objective Evolution of Heuristic Using Large Language Model. In Proceedings of the 9th Annual AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025. [Google Scholar] [CrossRef]
- QJ 3039-1998; Test Method for Drop Weight Impact Sensitivity of Composite Solid Propellants. Industry Standard-Aerospace: Beijing, China, 1997.
- Li, X.; Cao, L.; Peng, W.; Zhao, S.; Liu, M. A Study on Diffusion of HCl and Al2O3 in solid rocket motor combustion-gas. J. Propul. Technol. 1994, 1, 45–51. [Google Scholar] [CrossRef]
- Cheng, X.; Zhao, X.; Li, J. Effect of Al on Sensitivity of NEPE Propellant. Chin. J. Energet. Mater. 2013, 21, 61–63. [Google Scholar] [CrossRef]
- Xie, W.; Zhao, Y.; Zhang, W.; Liu, Y.; Fan, X. Sensitivity and Stability Improvements of NEPE Propellantsby Inclusion of FOX-7. J. Explos. Propell. 2018, 43, 308–314. [Google Scholar] [CrossRef]
- Song, X.; Gao, X.; Kou, Y.; Yu, Z.; Wang, Y.; An, C.; Li, F. Thermolysis and sensitivities of solid propellants using characterized nano oxidizers involving energy performance evaluation. FirePhysChem 2022, 2, 323–333. [Google Scholar] [CrossRef]


| Parameter Name | Value |
|---|---|
| Number of subproblems (N) | 200 for bi-objective, 300 for tri-objective |
| Number of weight vectors in neighborhood (T) | N/10 |
| Maximum number of evaluations () | 200,000 for ZDT, 300,000 for UF |
| Crossover probability () | 1.0 |
| Mutation probability () | 0.9 |
| Neighborhood selection probability () | 0.9 |
| Number of individuals (l) | 10 |
| Number of new individuals (s) | 2 |
| LLM | GPT-4o |
| Problem | NSGA-II | MOEA/D | MOEA/D-LLM |
|---|---|---|---|
| ZDT1 | 0.7220 | 0.7224 | 0.7222 |
| ZDT2 | 0.4466 | 0.4470 | 0.4468 |
| ZDT3 | 0.6004 | 0.5996 | 0.5996 |
| ZDT4 | 0.7192 | 0.7191 | 0.7207 |
| ZDT6 | 0.3899 | 0.3901 | 0.3901 |
| UF1 | 0.6087 | 0.5534 | 0.7201 |
| UF2 | 0.6916 | 0.6849 | 0.7136 |
| UF3 | 0.4611 | 0.3713 | 0.7111 |
| UF4 | 0.3912 | 0.3650 | 0.4023 |
| UF5 | 0.2647 | 0.1570 | 0.2690 |
| UF6 | 0.3491 | 0.1895 | 0.3132 |
| UF7 | 0.4980 | 0.2855 | 0.5785 |
| UF8 | 0.3143 | 0.3891 | 0.4681 |
| UF9 | 0.5988 | 0.5932 | 0.6751 |
| Problem | NSGA-II | MOEA/D | MOEA/D-LLM |
|---|---|---|---|
| ZDT1 | 172.03 s | 128.88 s | 132.45 s |
| ZDT2 | 175.67 s | 129.92 s | 131.62 s |
| ZDT3 | 179.48 s | 140.51 s | 140.38 s |
| ZDT4 | 165.45 s | 123.21 s | 114.72 s |
| ZDT6 | 164.82 s | 124.44 s | 115.60 s |
| UF1 | 185.88 s | 152.20 s | 140.56 s |
| UF2 | 180.63 s | 146.86 s | 139.22 s |
| UF3 | 176.19 s | 138.21 s | 130.32 s |
| UF4 | 178.89 s | 138.32 s | 128.03 s |
| UF5 | 175.55 s | 140.53 s | 131.17 s |
| UF6 | 180.72 s | 134.45 s | 135.68 s |
| UF7 | 171.39 s | 129.95 s | 121.14 s |
| UF8 | 169.94 s | 132.46 s | 127.32 s |
| UF9 | 178.92 s | 134.66 s | 122.67 s |
| Parameter Name | Value |
|---|---|
| Number of particles () | 100 |
| Maximum number of evaluations () | 200 |
| Initial inertia weight () | 0.9 |
| Final inertia weight () | 0.1 |
| Cognitive factor () | 1.5 |
| Social factor () | 1.5 |
| Max velocity () | 2 |
| Parameter Name | Value |
|---|---|
| Number of weight vectors in neighborhood (T) | 10 |
| Maximum number of evaluations () | 40,000 |
| Crossover probability () | 1.0 |
| Mutation probability () | 0.9 |
| Neighborhood selection probability () | 0.9 |
| Number of individuals (l) | 10 |
| Number of new individuals (s) | 2 |
| Component | Density /(kg/m3) | Impact Sensitivity Factor | Mass Fraction Boundary | Standard Enthalpy /(kcal/mol) |
|---|---|---|---|---|
| PEG | 1130 | 10 | [5%, 10%] | −109.89 |
| NG | 1600 | 1 | [7%, 11%] | −64.65 |
| BTTN | 1520 | 4.5 | [7%, 11%] | −98.90 |
| AP | 1950 | 1.5 | [10%, 20%] | −69.36 |
| Al | 2700 | 9 | [10%, 20%] | - |
| HMX | 1900 | 3 | [35%, 45%] | 17.87 |
| TPB | 1590 | 10 | [0%, 3%] | 112.04 |
| Component | Density/(kg/m3) | Impact Sensitivity Factor | Mass Fraction Boundary | Standard Enthalpy /(kcal/mol) |
|---|---|---|---|---|
| HTPB | 0.92 | 10 | [8%, 15%] | −4.06 |
| AP | 1.95 | 1.5 | [60%, 80%] | −69.36 |
| Al | 2.70 | 9 | [12%, 18%] | - |
| 1.59 | 10 | [0%, 3%] | −197.00 |
| Name of the Parameters | Value |
|---|---|
| Throat diameter of the nozzle | 0.014 m |
| Nozzle expansion ratio | 13 |
| Throat ablation rate | 0.2 mm/s |
| The initiation time of nozzle ablation | 2 s |
| The mass of the propellant | 10.23 kg |
| PEG/% | NG/% | BTTN/% | AP/% | Al/% | HMX/% | TPB/% | Ours/J | Experiment/J |
|---|---|---|---|---|---|---|---|---|
| 9.20 | 9.60 | 10.60 | 16.00 | 6.00 | 48.00 | 0.60 | 6.23 | 6.31 |
| 9.20 | 9.60 | 10.60 | 16.00 | 16.00 | 38.00 | 0.60 | 6.93 | 6.78 |
| 9.20 | 9.60 | 10.60 | 16.00 | 24.00 | 30.00 | 0.60 | 7.25 | 7.41 |
| /(N·s·kg−1) | /% | /% | |
|---|---|---|---|
| Ours | 2639.59 | 7.44 | 14.01 |
| Reference [45] | 2639.80 | 7.50 | 14.00 |
| Algorithm Name | Mean HV ± Std | Best HV | Worst HV |
|---|---|---|---|
| NSGA-III | 0.815 ± 0.032 | 0.862 | 0.760 |
| MOEA/D | 0.822 ± 0.028 | 0.868 | 0.765 |
| MOEA/D-LLM | 0.847 ± 0.019 | 0.880 | 0.800 |
| The Order of PCE | The Total Number of Samples | Prediction/ (N·s·kg−1) | Actual Value/ (N·s·kg−1) | Relative Error |
|---|---|---|---|---|
| 4 | 1820 | 2646.42 | 2643.17 | 0.1228% |
| 5 | 6188 | 2644.65 | 2644.88 | 0.0087% |
| 6 | 18,563 | 2645.29 | 2645.12 | 0.0064% |
| Uncertain Level | Maximum Interval of /(N·s·kg−1) | Maximum Interval of /(mol/kg) | Maximum Interval of /(mol/kg) |
|---|---|---|---|
| ±5% | [2635.74, 2639.11] | [4.26, 4.39] | [0.2406, 0.2458] |
| ±10% | [2628.34, 2635.75] | [3.93, 4.03] | [0.2553, 0.2625] |
| ±15% | [2625.66, 2637.86] | [3.85, 3.91] | [0.2542, 0.2656] |
| Weight | Maximum Interval of /(N·s·kg−1) | Maximum Interval of /(mol/kg) | Maximum Interval of /(mol/kg) |
|---|---|---|---|
| 0 | [2649.44, 2658.41] | [4.68, 5.21] | [0.195, 0.241] |
| 0.25 | [2645.21, 2652.08] | [4.62, 4.86] | [0.190, 0.224] |
| 0.5 | [2643.47, 2648.88] | [4.60, 4.75] | [0.189, 0.213] |
| 0.75 | [2640.95, 2644.69] | [4.56, 4.66] | [0.187, 0.196] |
| 1 | [2638.03, 2640.52] | [4.50, 4.61] | [0.182, 0.188] |
| Index | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| PEG | 6.89% | 6.69% | 7.21% | 6.87% | 7.55% |
| NG | 8.52% | 10.61% | 9.84% | 8.14% | 10.58% |
| BTTN | 9.84% | 6.94% | 7.04% | 7.36% | 8.36% |
| AP | 14.36% | 13.38% | 16.79% | 15.13% | 14.69% |
| Al | 20.25% | 18.54% | 18.34% | 19.29% | 21.01% |
| HMX | 39.61% | 41.14% | 40.21% | 40.77% | 37.34% |
| TPB | 0.54% | 2.71% | 0.48% | 2.43% | 0.47% |
| Formulation | /(N·s·kg−1) | /(kg/m3) | /mol/kg | /mol/kg | |
|---|---|---|---|---|---|
| NO.1 Exp. | 2610.33 (0.000) | 1851.00 | 2.591 | 0.177 | 7.289 J |
| NO.1 Sim. | 2638.10 (0.000) | 1851.92 | 2.601 | 0.183 | 7.340 J |
| NO.2 Exp. | 2624.05 (0.484) | 1849.00 | 2.892 | 0.203 | 7.146 J |
| NO.2 Sim. | 2642.50 (0.483) | 1849.05 | 2.883 | 0.198 | 7.281 J |
| NO.3 Exp. | 2638.67 (1.000) | 1841.00 | 3.290 | 0.209 | 7.149 J |
| NO.3 Sim. | 2647.20 (1.000) | 1840.92 | 3.273 | 0.216 | 7.222 J |
| [45] Exp. | 2609.80 | 1866.97 | 2.778 | 0.250 | 6.990 J |
| Index | HTPB | AP | Al | |
|---|---|---|---|---|
| 1 | 11.43% | 71.87% | 13.78% | 2.92% |
| 2 | 11.98% | 71.02% | 15.11% | 1.91% |
| 3 | 12.44% | 71.00% | 15.66% | 0.86% |
| 4 | 12.84% | 70.31% | 15.98% | 1.86% |
| 5 | 12.51% | 70.05% | 17.01% | 0.43% |
| Scheme | /(N·s·kg−1) | /J | /(mol/kg) | /(mol/kg) | /(kg/m3) |
|---|---|---|---|---|---|
| 1 | 2578.79 | 3.76 | 3.29 | 0.47 | 1808.82 |
| 2 | 2585.78 | 4.06 | 3.73 | 0.43 | 1805.62 |
| 3 | 2586.88 | 4.05 | 3.74 | 0.43 | 1803.78 |
| 4 | 2588.17 | 4.05 | 3.75 | 0.44 | 1802.75 |
| 5 | 2599.56 | 3.95 | 3.81 | 0.42 | 1770.01 |
| Uncertainty Level | Maximum Interval of /(N·s·kg−1) | Maximum Interval of /(mol/kg) | Maximum Interval of /(mol/kg) |
|---|---|---|---|
| ±5% | [2594.74, 2605.11] | [3.76, 3.99] | [0.4956, 0.5058] |
| ±10% | [2690.34, 2695.75] | [3.70, 3.77] | [0.4653, 0.4725] |
| ±15% | [2684.66, 2688.86] | [3.45, 3.51] | [0.4042, 0.4096] |
| Formulation | /(N·s·kg−1) | /kg/m3 | /(mol/kg) | /(mol/kg) | /J |
|---|---|---|---|---|---|
| Reference [46] | 2572.50 | 1776.38 | 6.800 | 9.100 | 3.83 |
| Ours | 2588.17 | 1802.75 | 6.455 | 7.231 | 3.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, J.; Wei, R.; Bao, F.; Hou, X. An Interval Analysis Method for Uncertain Multi-Objective Optimization of Solid Propellant Formulations. Aerospace 2025, 12, 865. https://doi.org/10.3390/aerospace12100865
Ren J, Wei R, Bao F, Hou X. An Interval Analysis Method for Uncertain Multi-Objective Optimization of Solid Propellant Formulations. Aerospace. 2025; 12(10):865. https://doi.org/10.3390/aerospace12100865
Chicago/Turabian StyleRen, Jiaren, Ran Wei, Futing Bao, and Xiao Hou. 2025. "An Interval Analysis Method for Uncertain Multi-Objective Optimization of Solid Propellant Formulations" Aerospace 12, no. 10: 865. https://doi.org/10.3390/aerospace12100865
APA StyleRen, J., Wei, R., Bao, F., & Hou, X. (2025). An Interval Analysis Method for Uncertain Multi-Objective Optimization of Solid Propellant Formulations. Aerospace, 12(10), 865. https://doi.org/10.3390/aerospace12100865






