A Class of Pursuit Problems in 3D Space via Noncooperative Stochastic Differential Games
Abstract
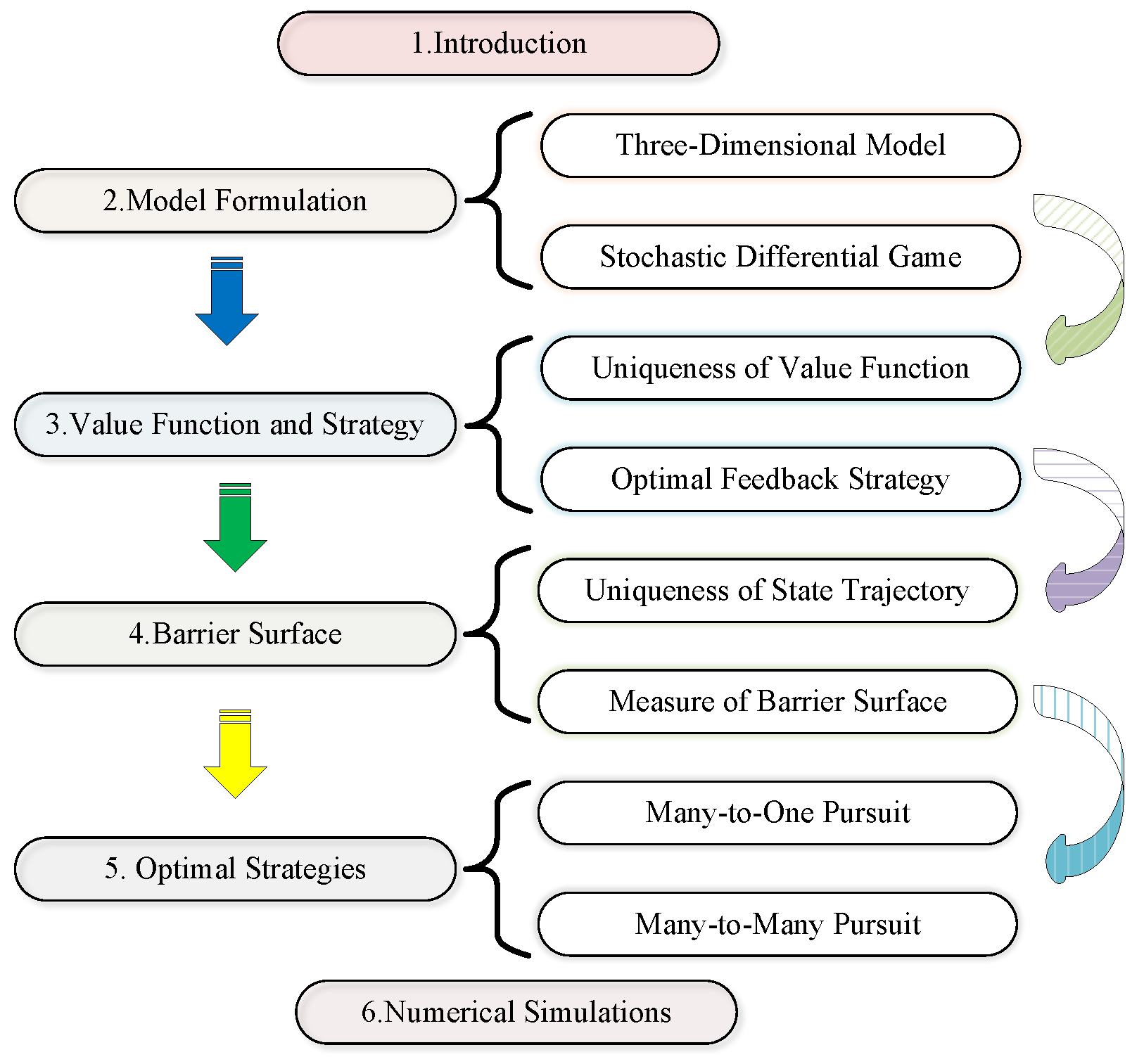
1. Introduction
- 1.
- This work extends previous studies (e.g., Qi et al. (2024) in [10]) by addressing pursuit problems in many-to-one and many-to-many scenarios, with initial applications in missile interception. Building on the system dynamics introduced in Section 2.2, we derive the optimal strategies for high-dimensional systems through a system of partial differential equations.
- 2.
- In Section 2 presents a rigorous analysis proving the uniqueness of the value function under bounded control inputs. A novel polynomial value function is introduced, which plays a critical role in ensuring the stability and scalability of the proposed framework.
- 3.
- Leveraging the uniqueness of the value function, we further establish in Section 5 the uniqueness of state trajectories within the pursuit problem. Additionally, we analyze the barrier surface separating the pursuit region and the termination set, demonstrating that its Lebesgue measure is zero. This result is crucial for ensuring the feasibility of optimal strategies in practical scenarios.
2. Many-to-One Pursuits Problem in Stochastic Differential Games
2.1. Notation
2.2. Problem Formulation
- , . There exist positive constants , , and such that:
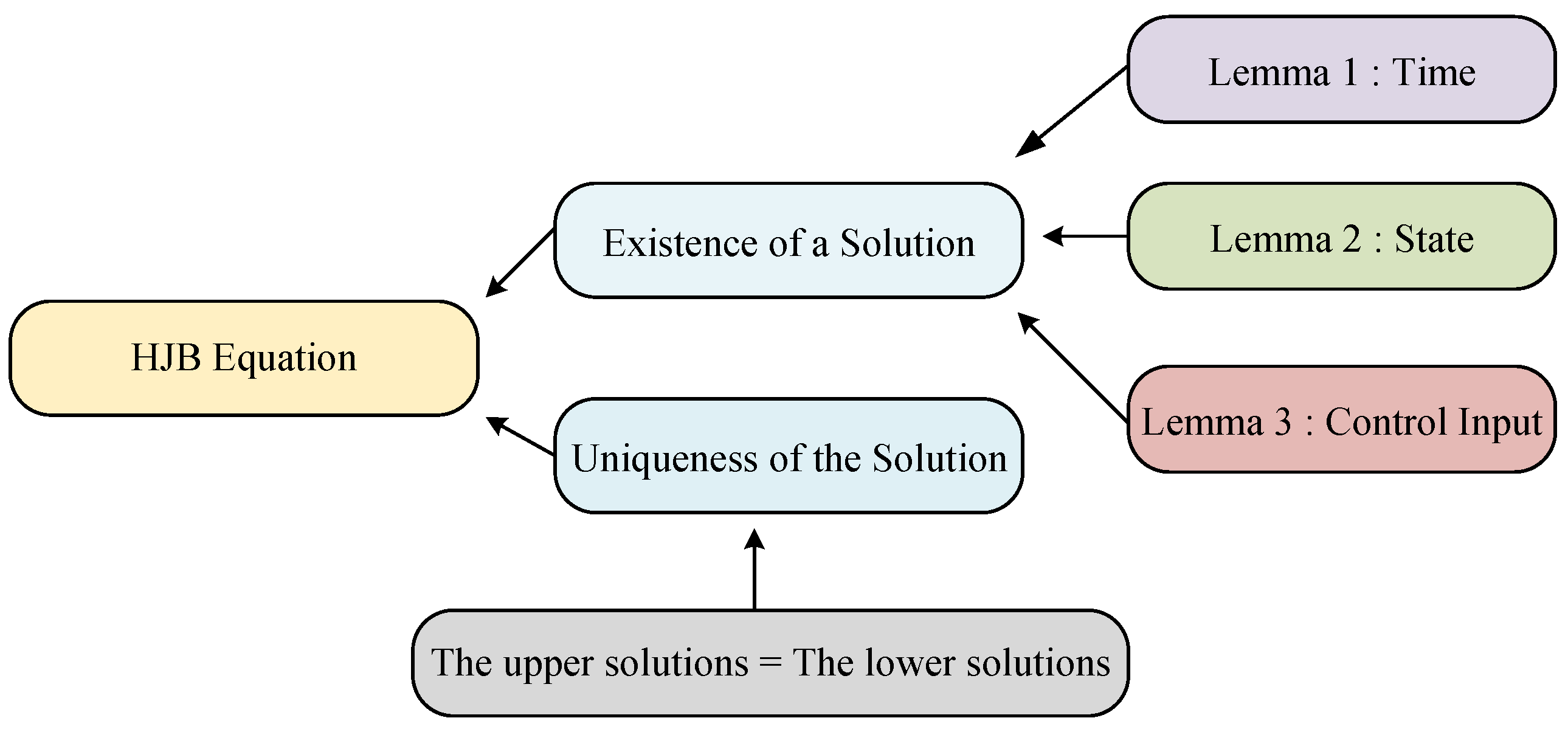
3. The Optimal Feedback Strategies
- Lemma 1: Proves that time is Lipschitz continuous, ensuring stability with respect to temporal variations.
- Lemma 2: Shows that the state is Lipschitz continuous, accounting for the relationship between states and dynamics.
- Lemma 3: Demonstrates that the control inputs are Lipschitz continuous under bounded constraints, ensuring consistency of input–output relationships.
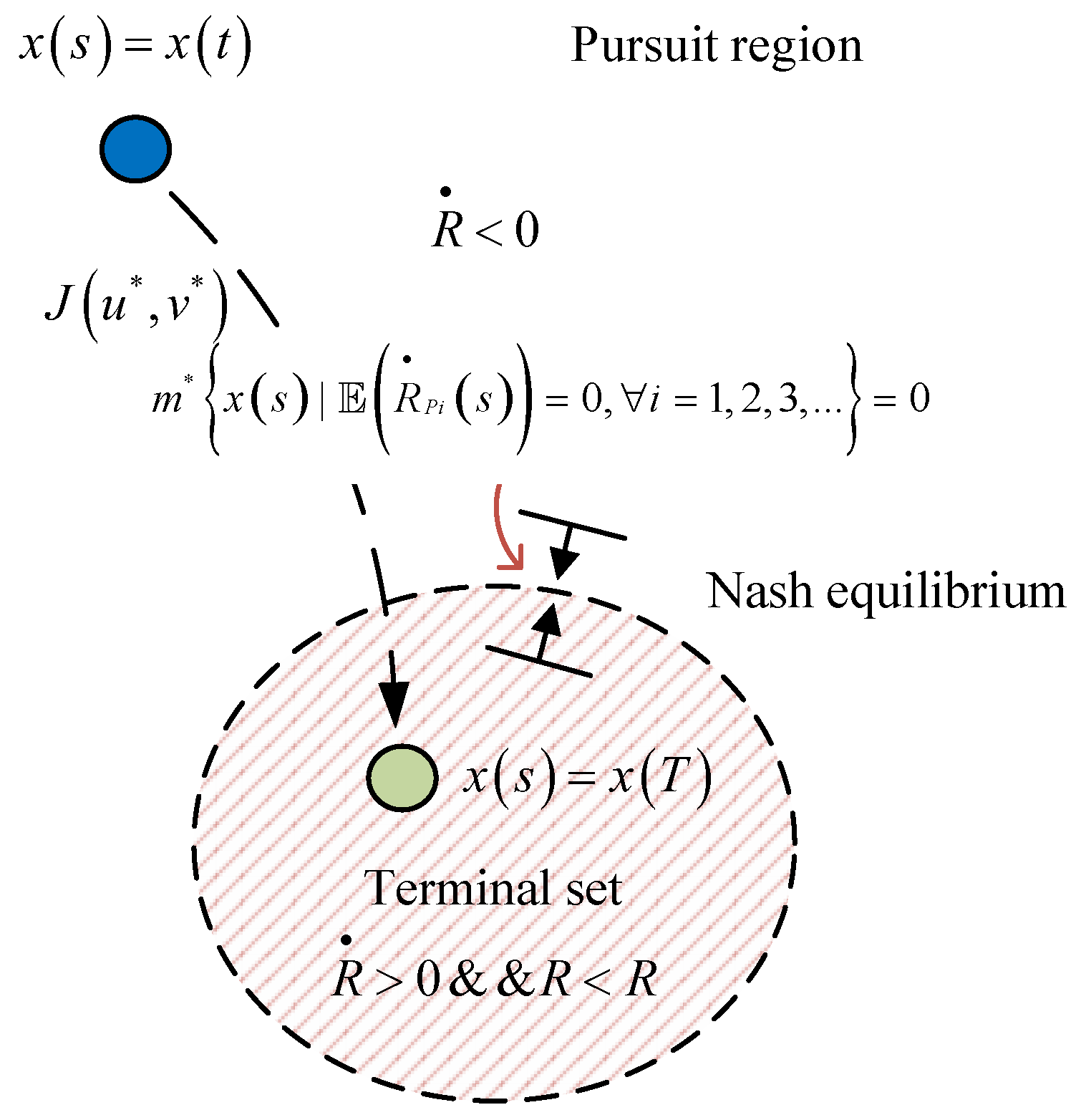
4. The Barrier Surface in the Stochastic Differential Game
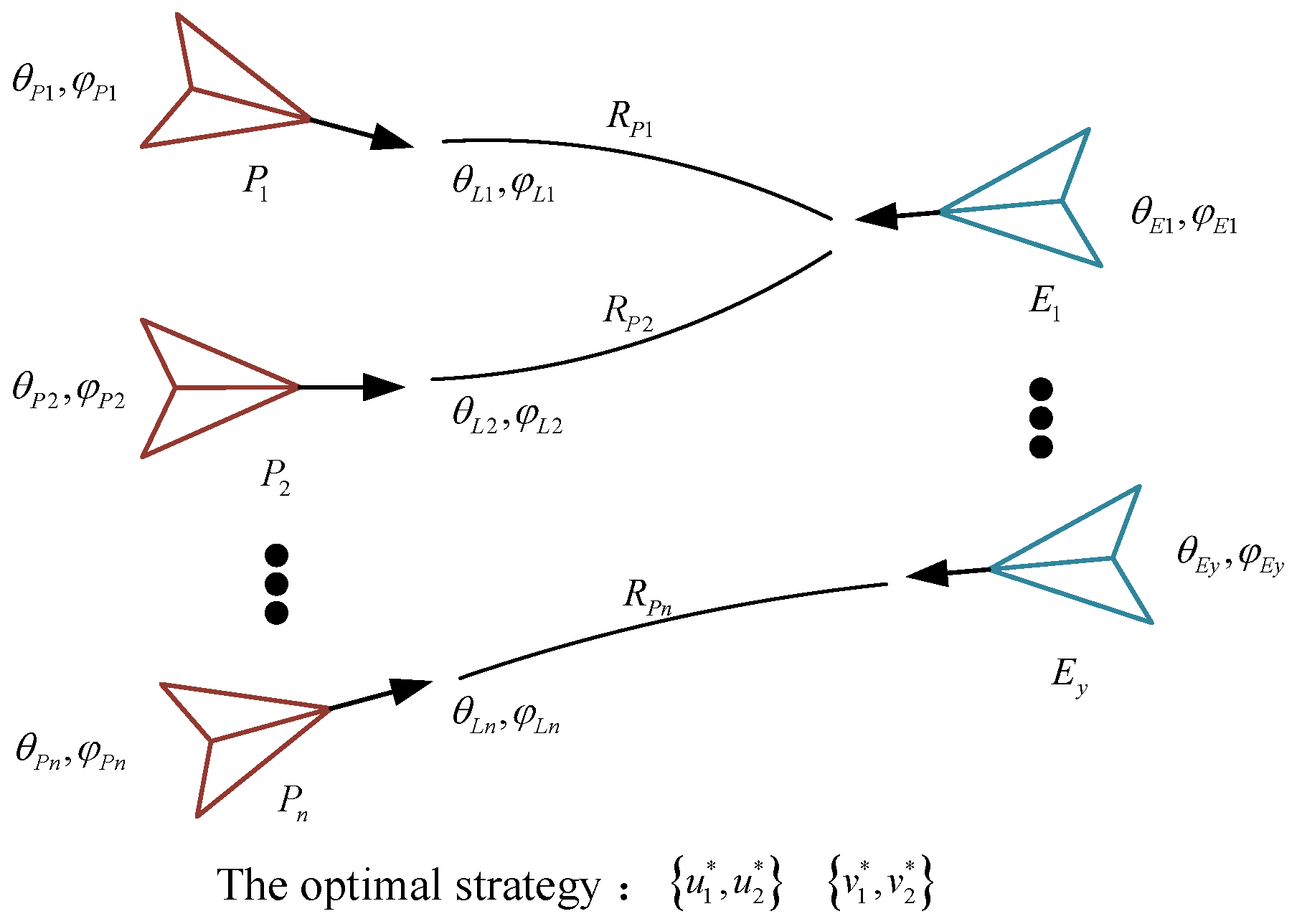
5. The Multiple Pursuers and Evaders in a Stochastic Differential Game
- Step 1: Dividing the n pursuers into groups, with each group corresponding to a respective number of evaders denoted by y.
- Step 2: Substituting the information of the pursuers into the system Equation (8), where and . The status includes the following:
- Step 3: Calculating the parameters of the value function based on the equation.
- Step 4: Solving for the optimal closed-loop feedback strategies based on FBSDEs.
- Step 5: Implementing the optimal strategies into the motion equations for the pursuers to capture the evaders.
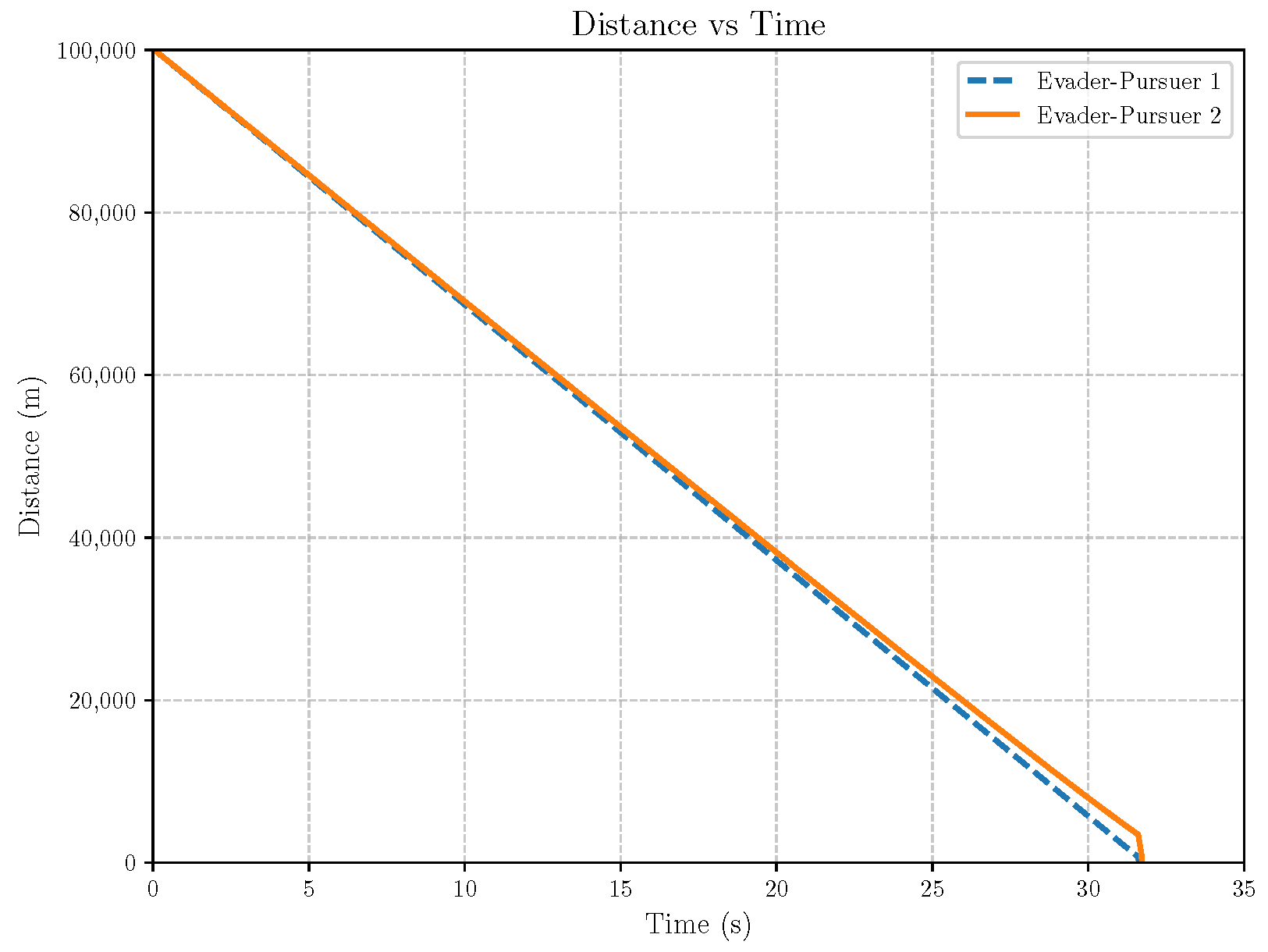
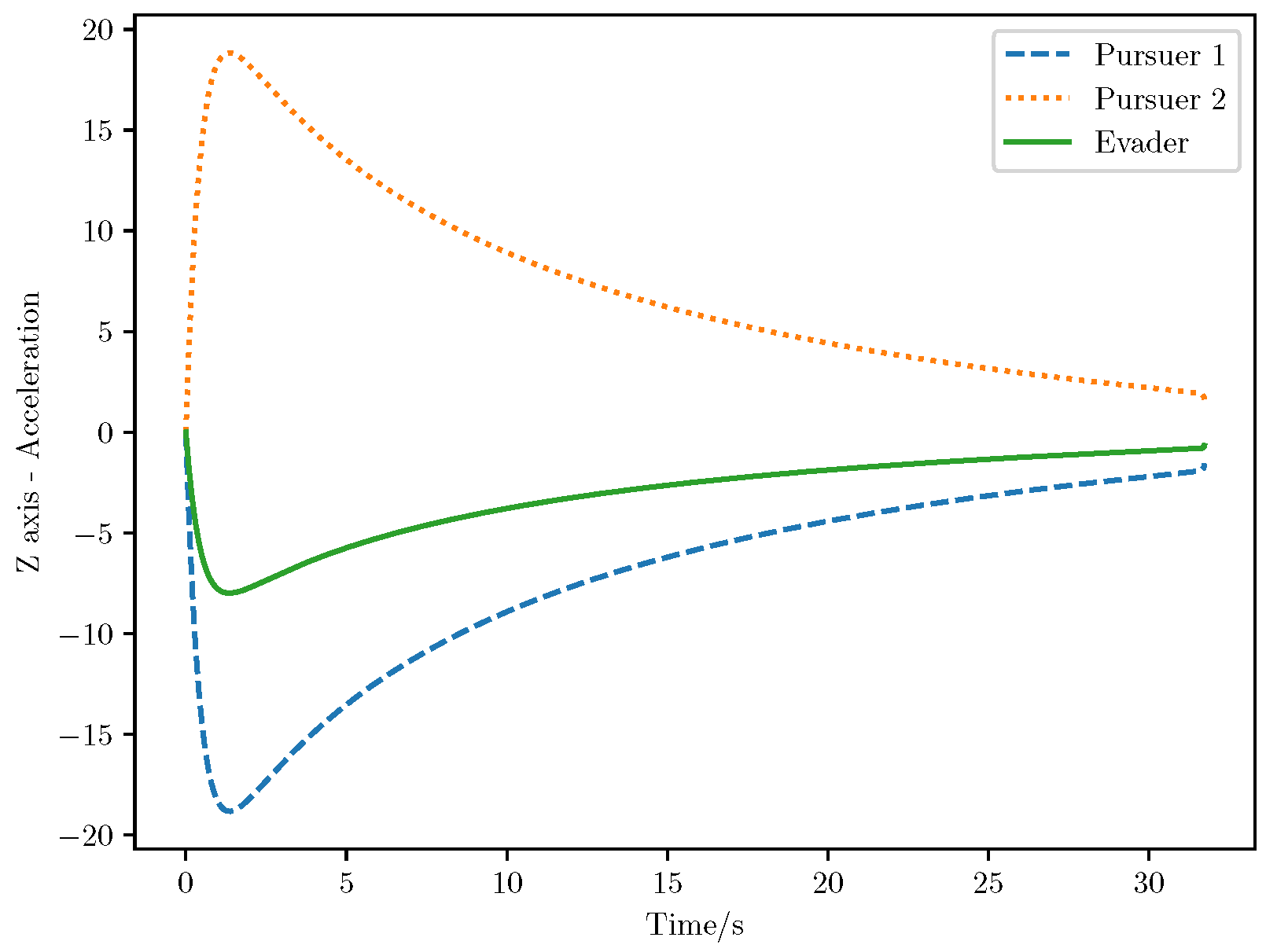
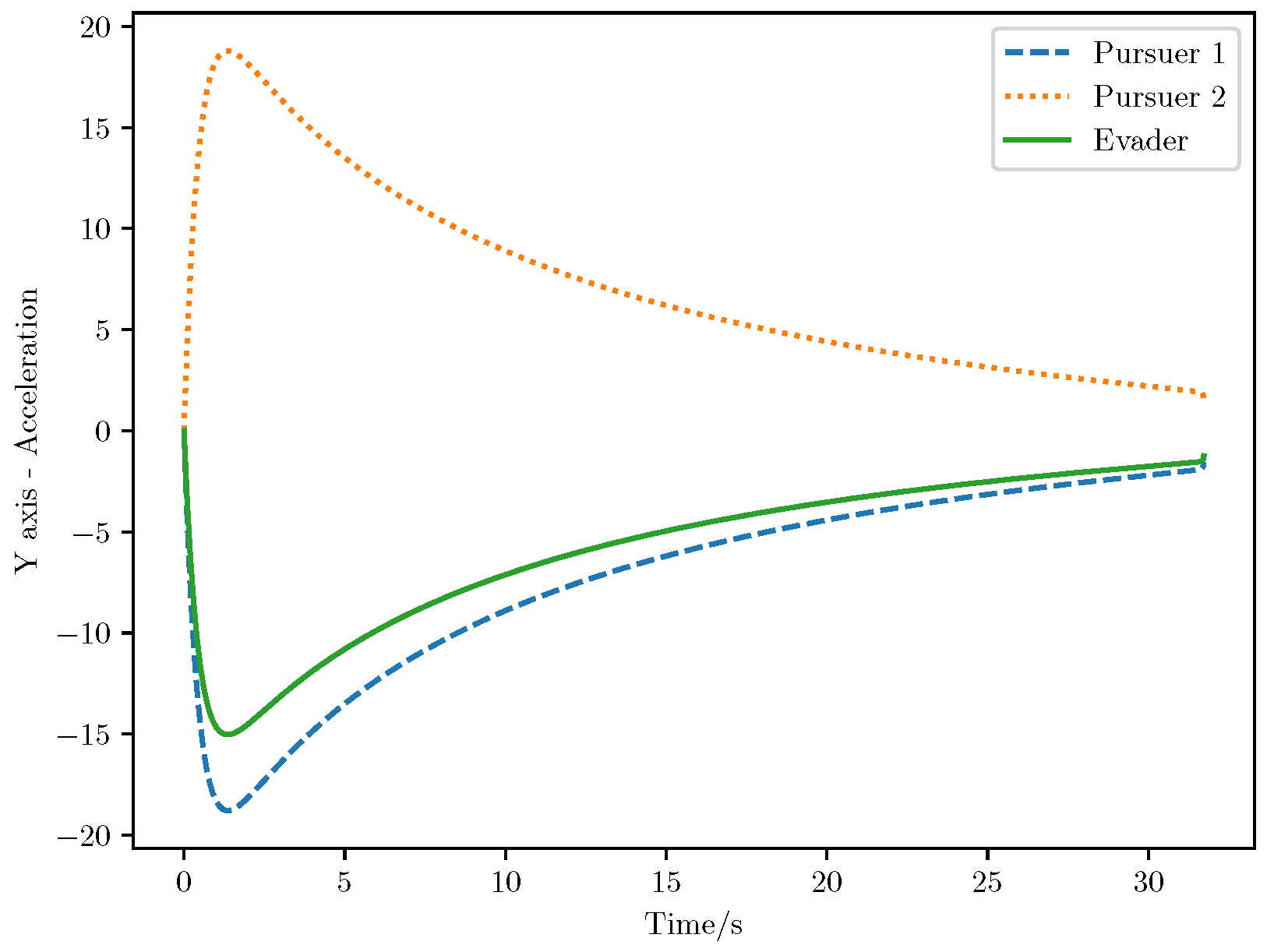
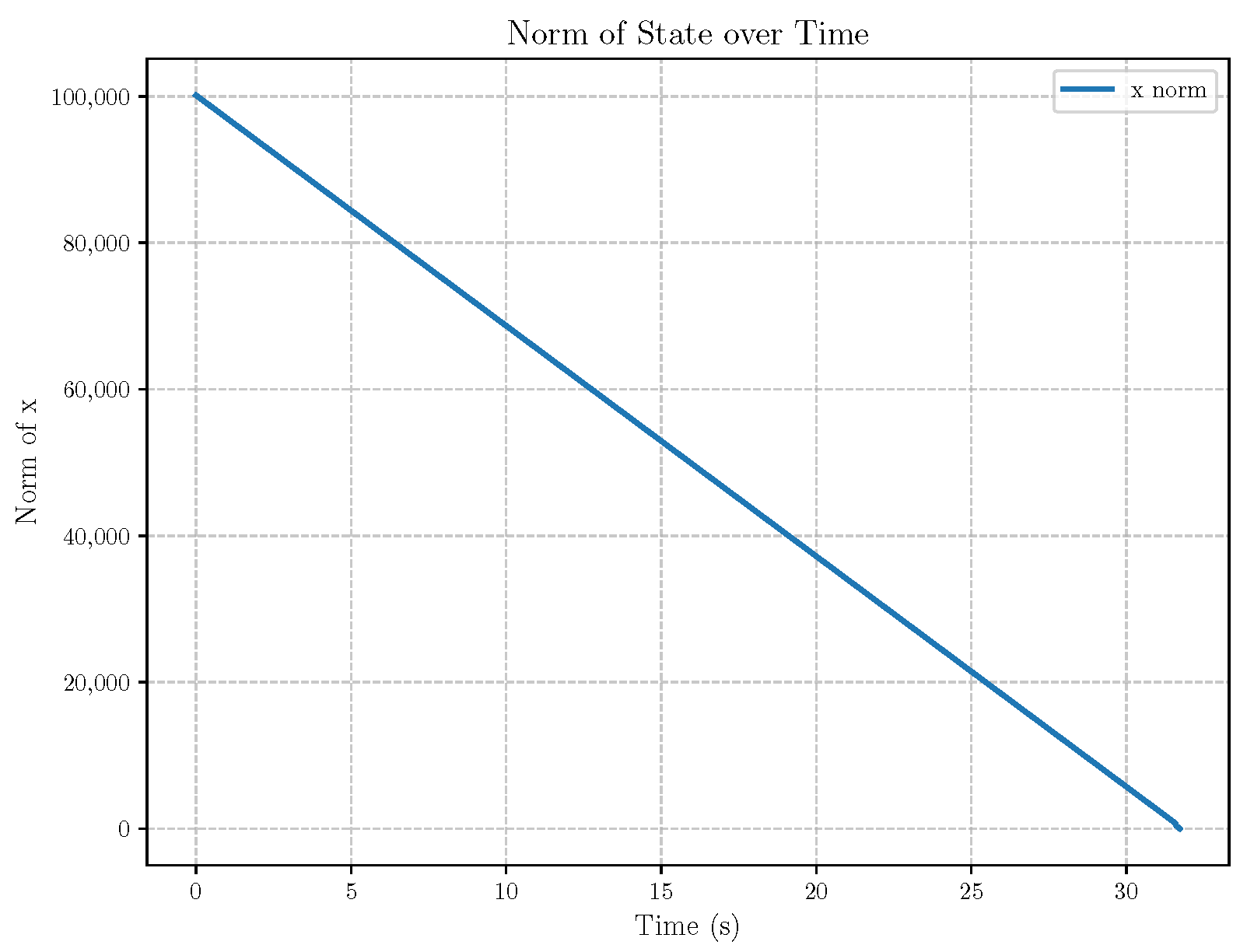
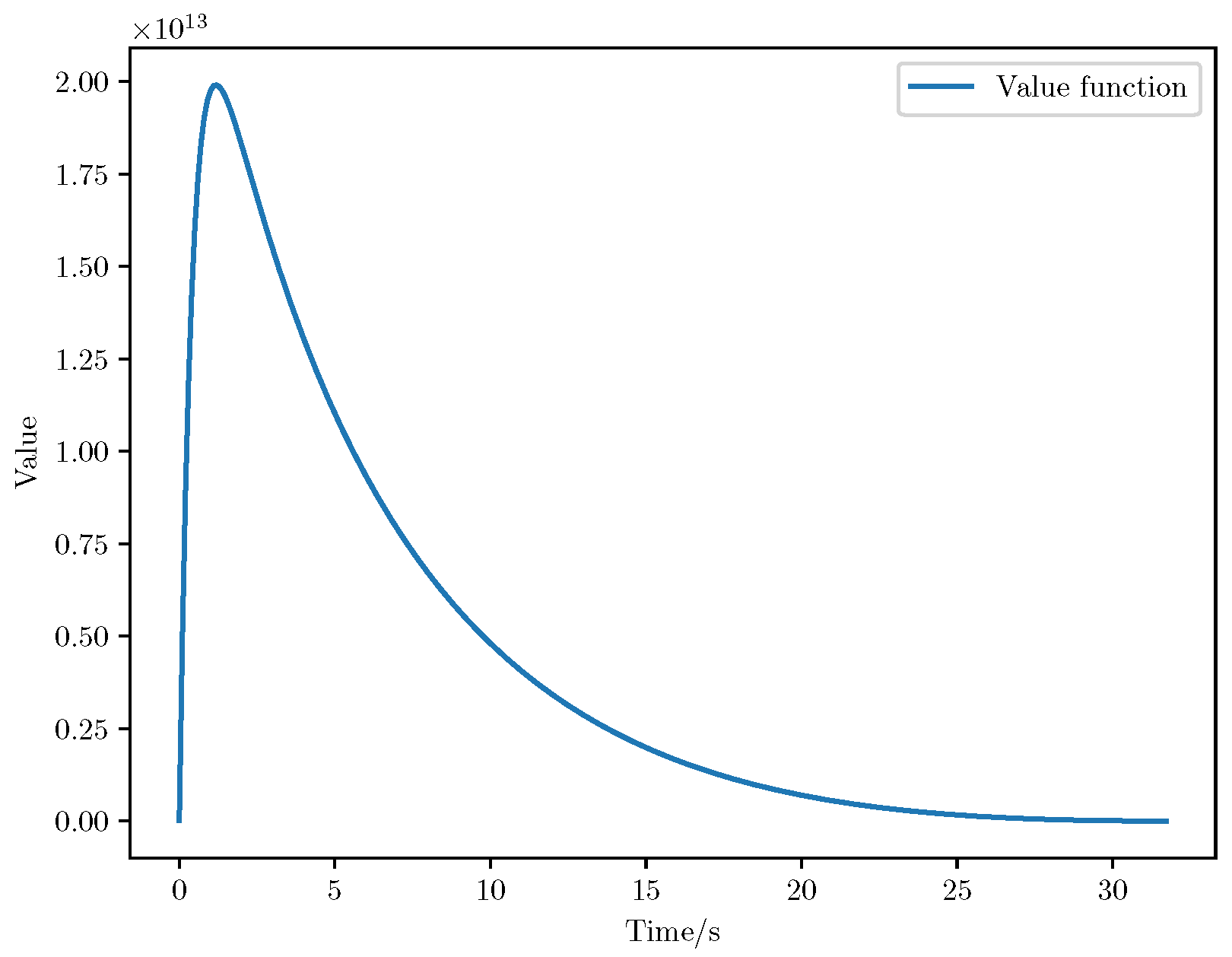
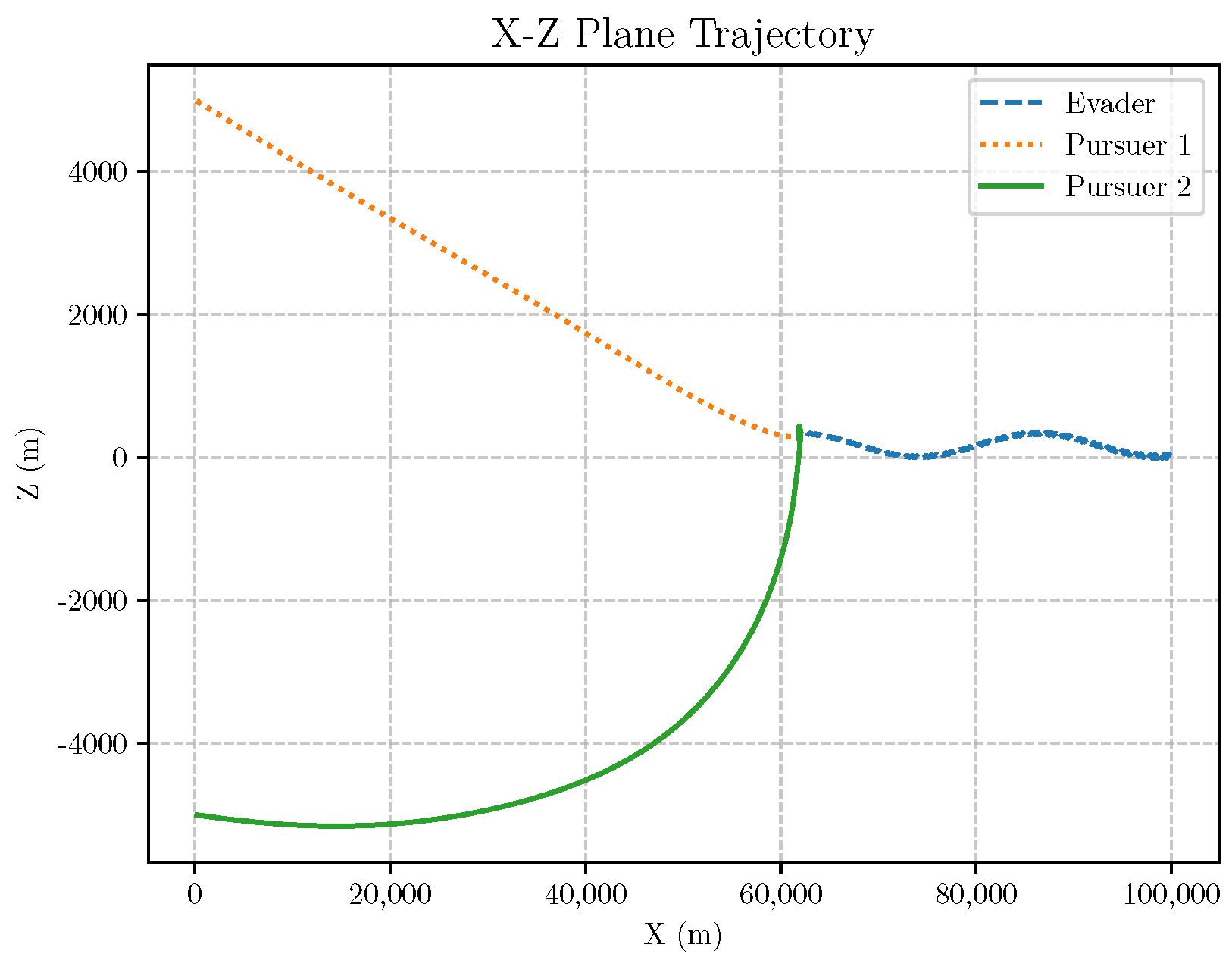
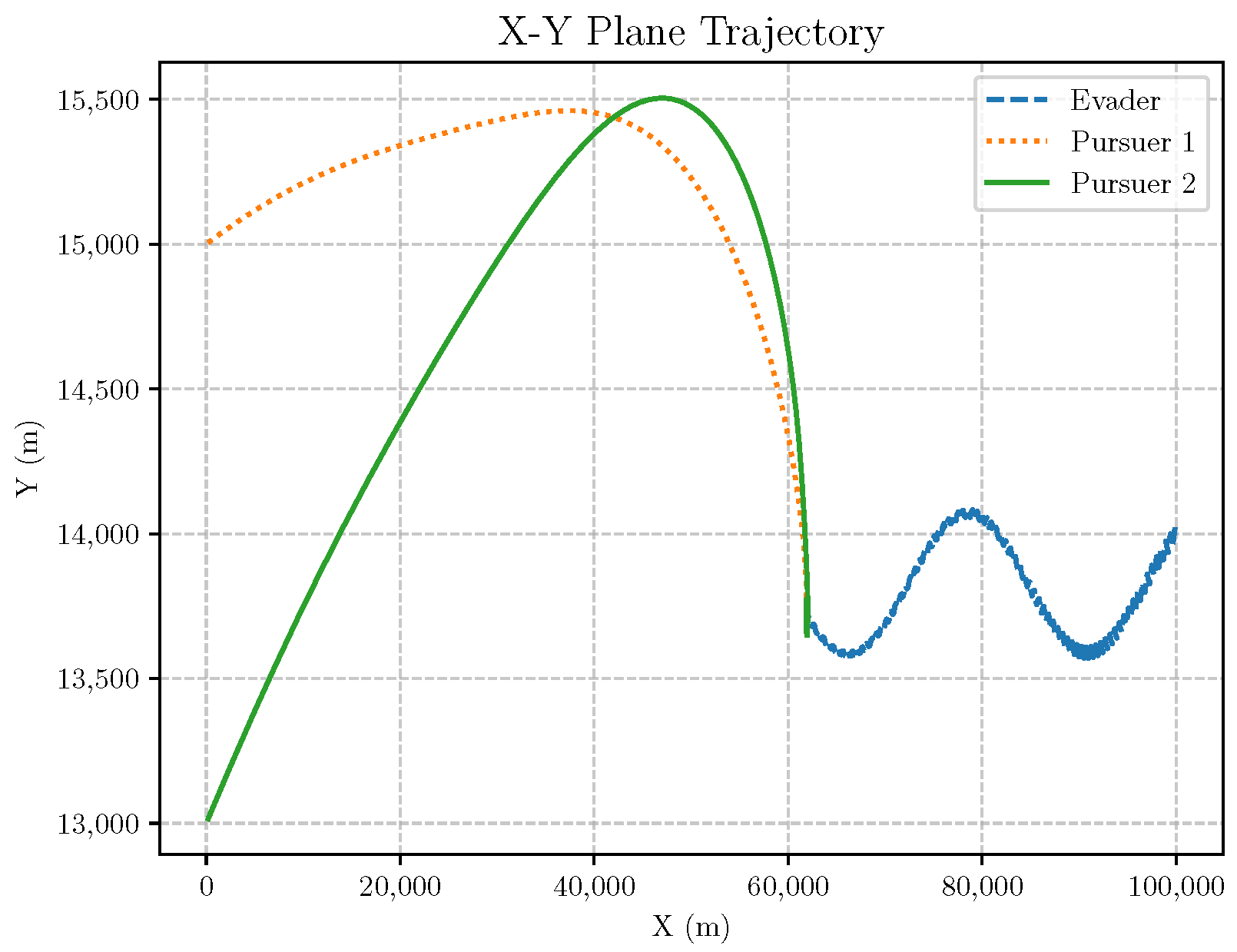
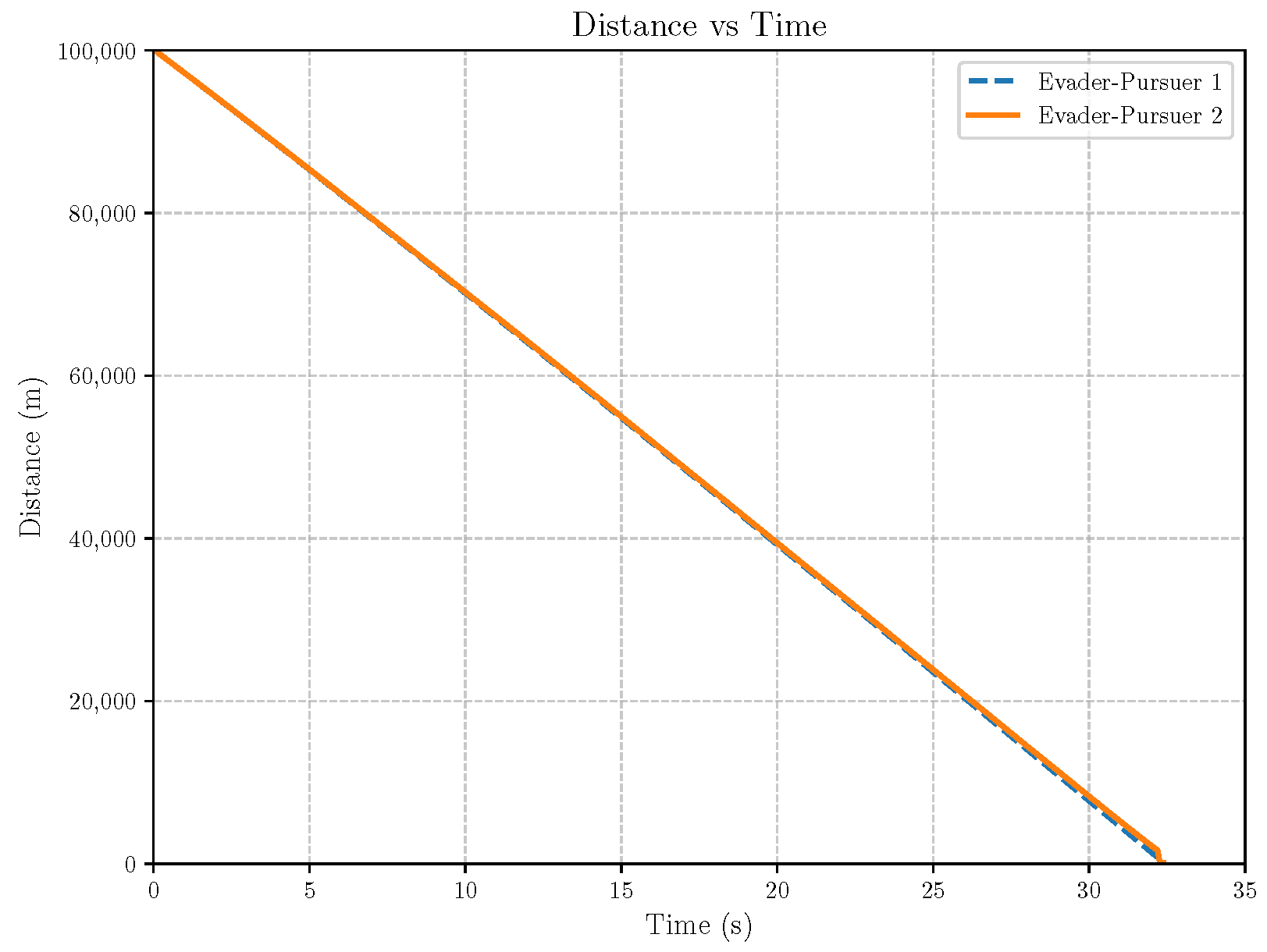
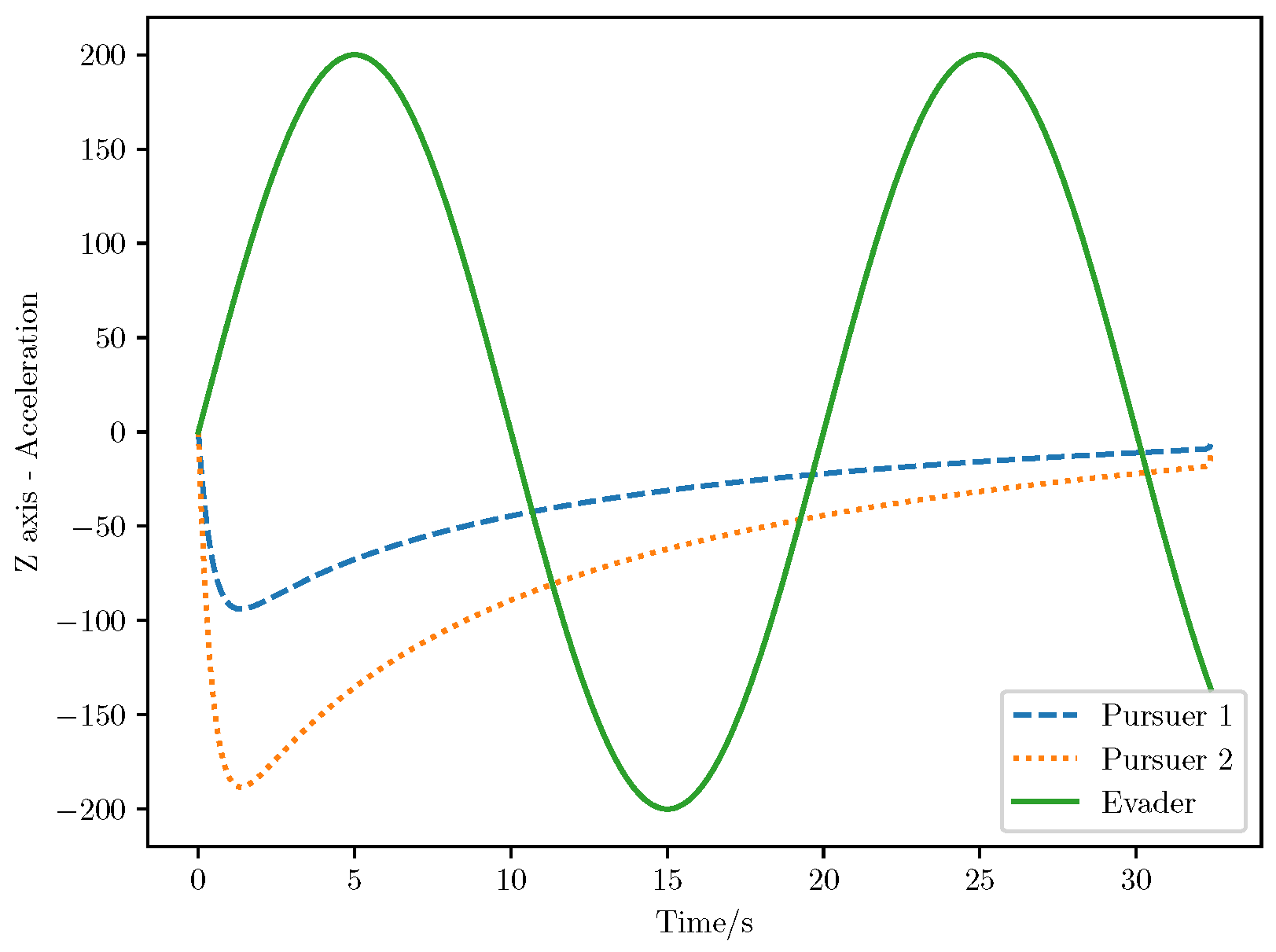
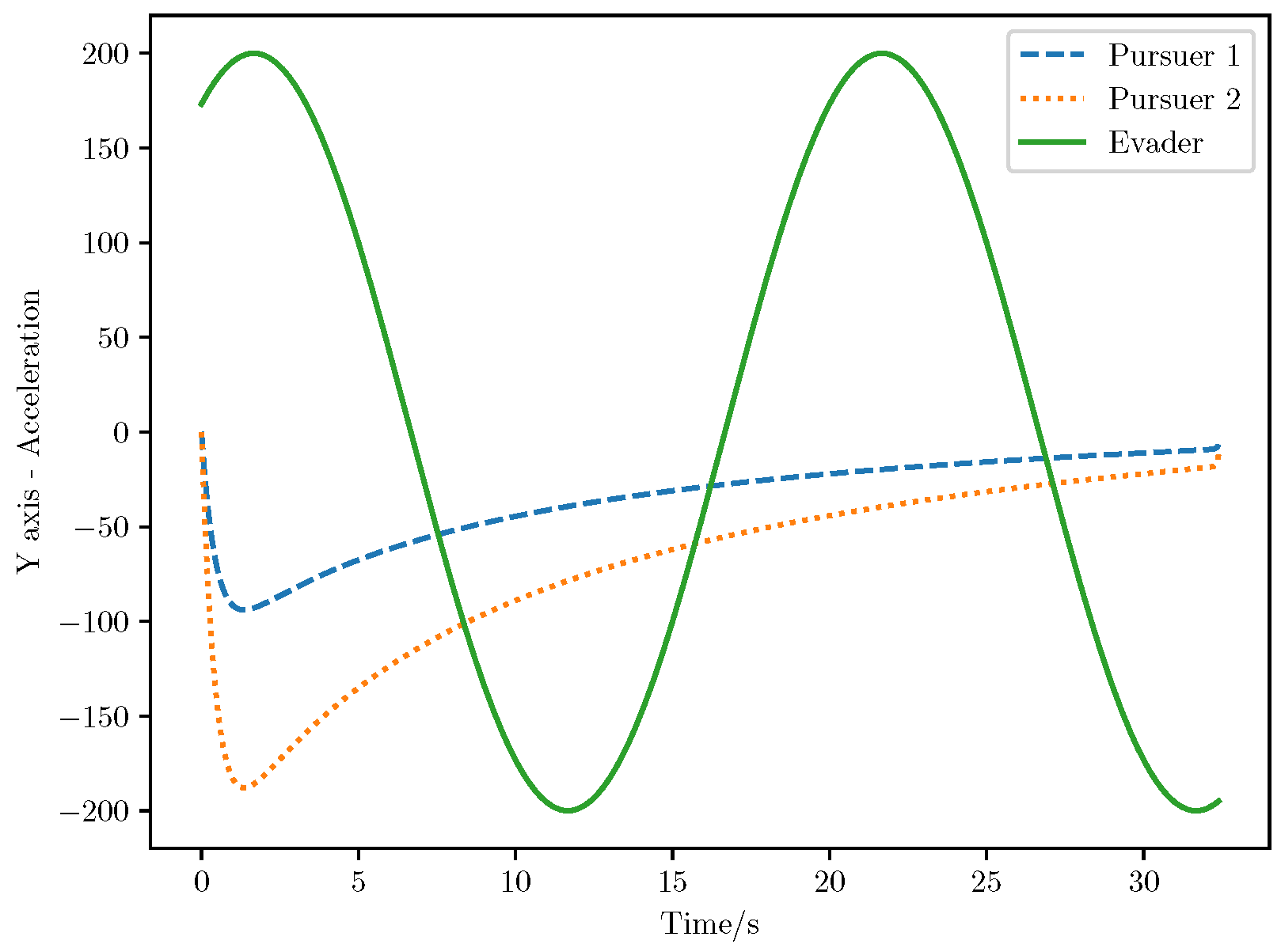
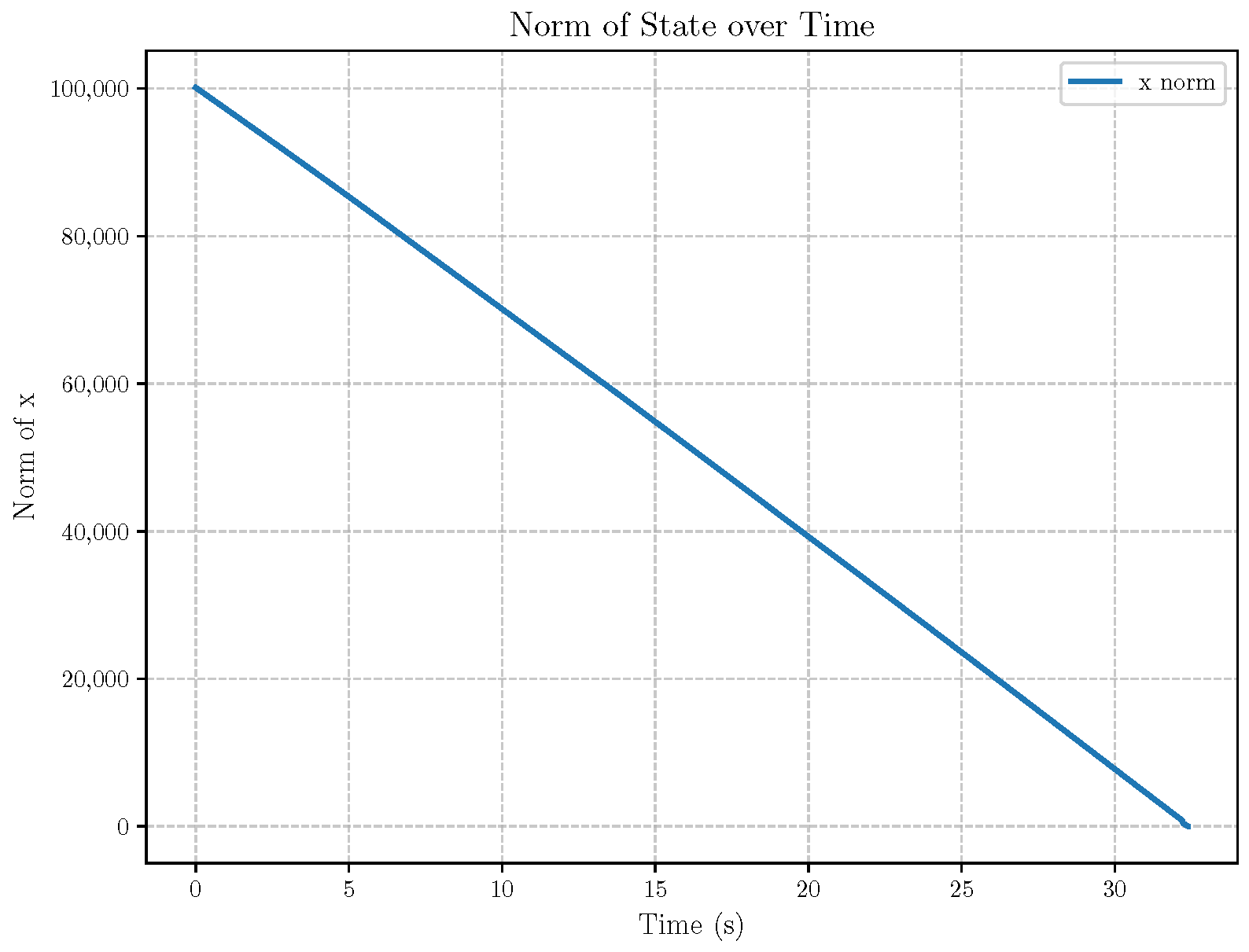
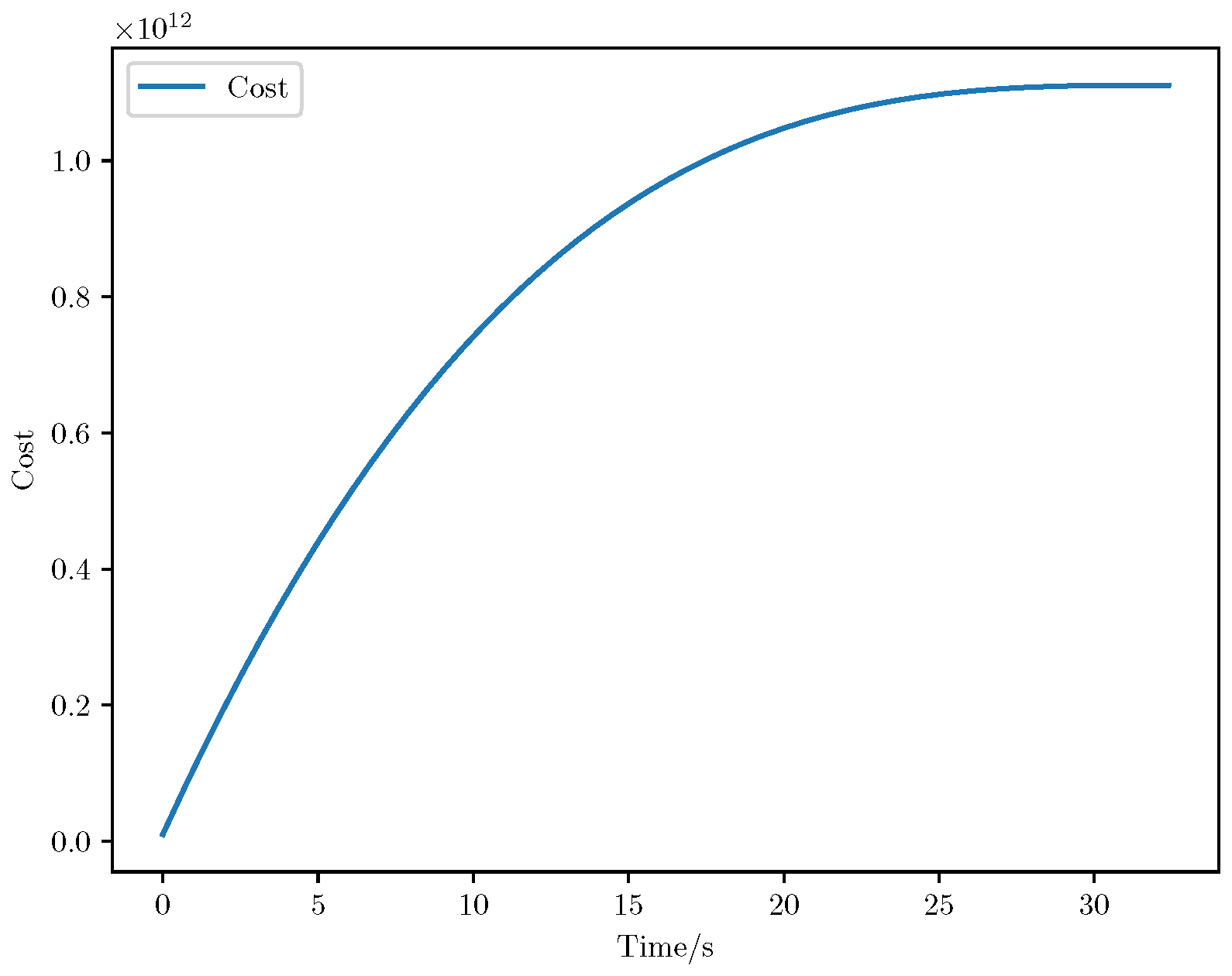
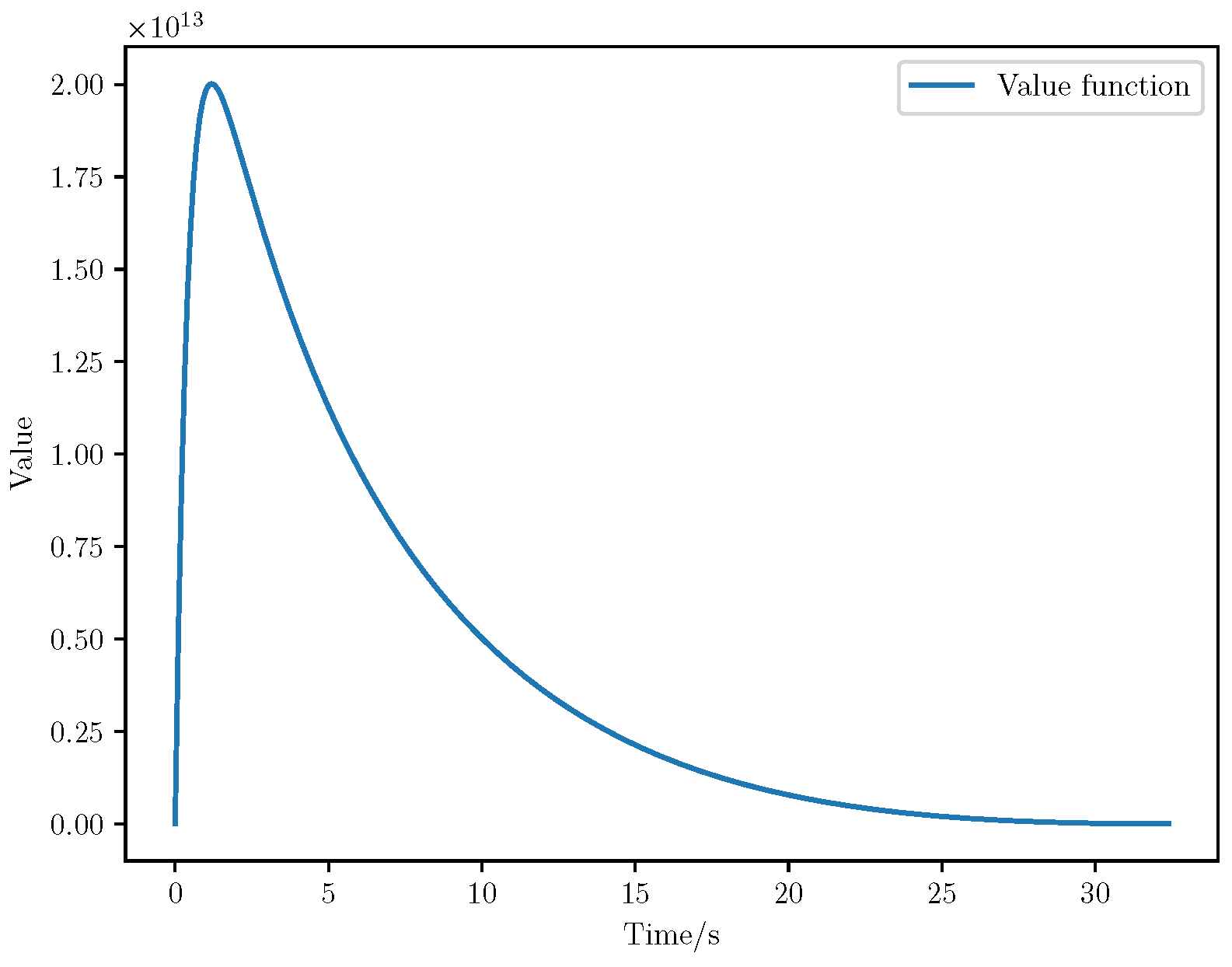
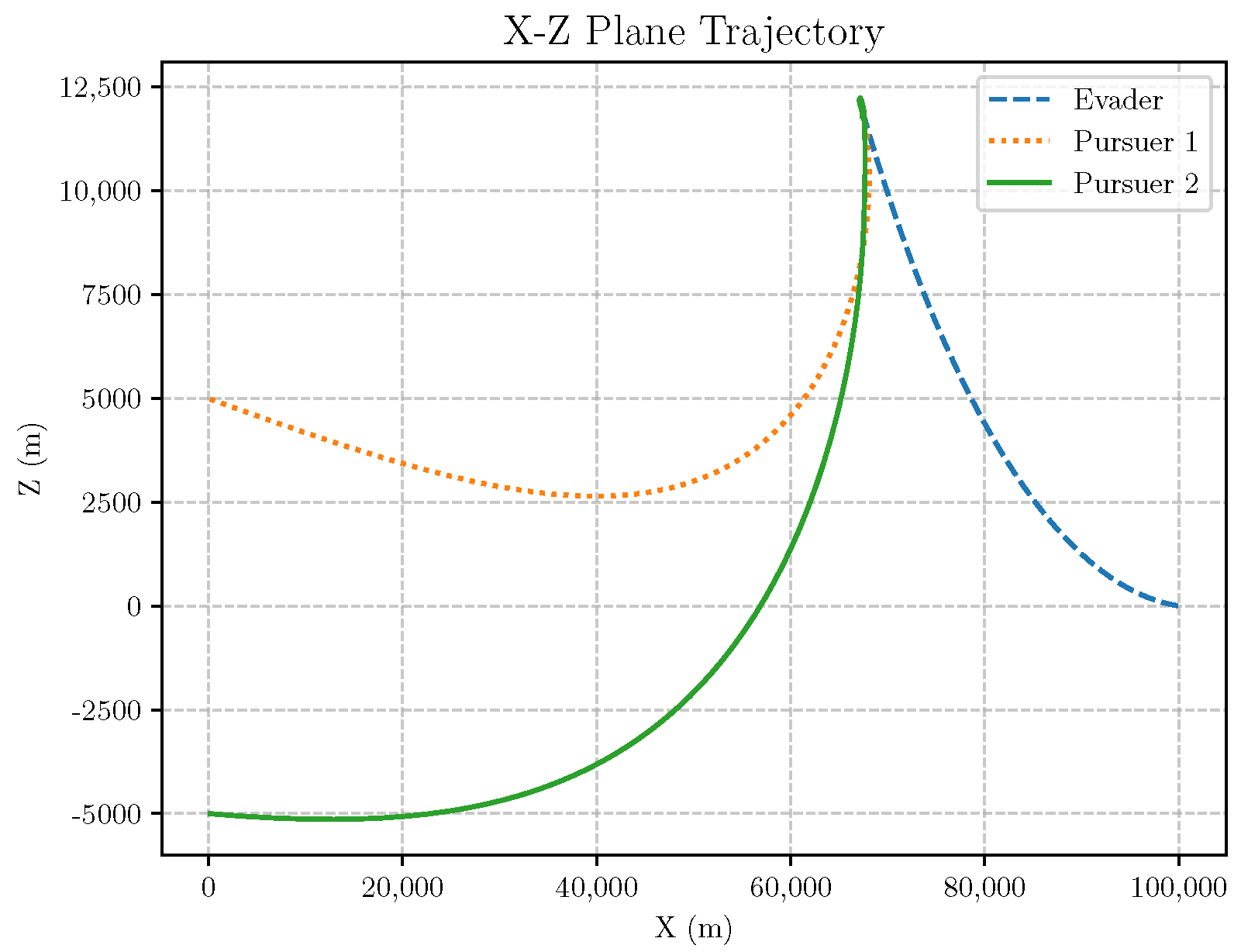
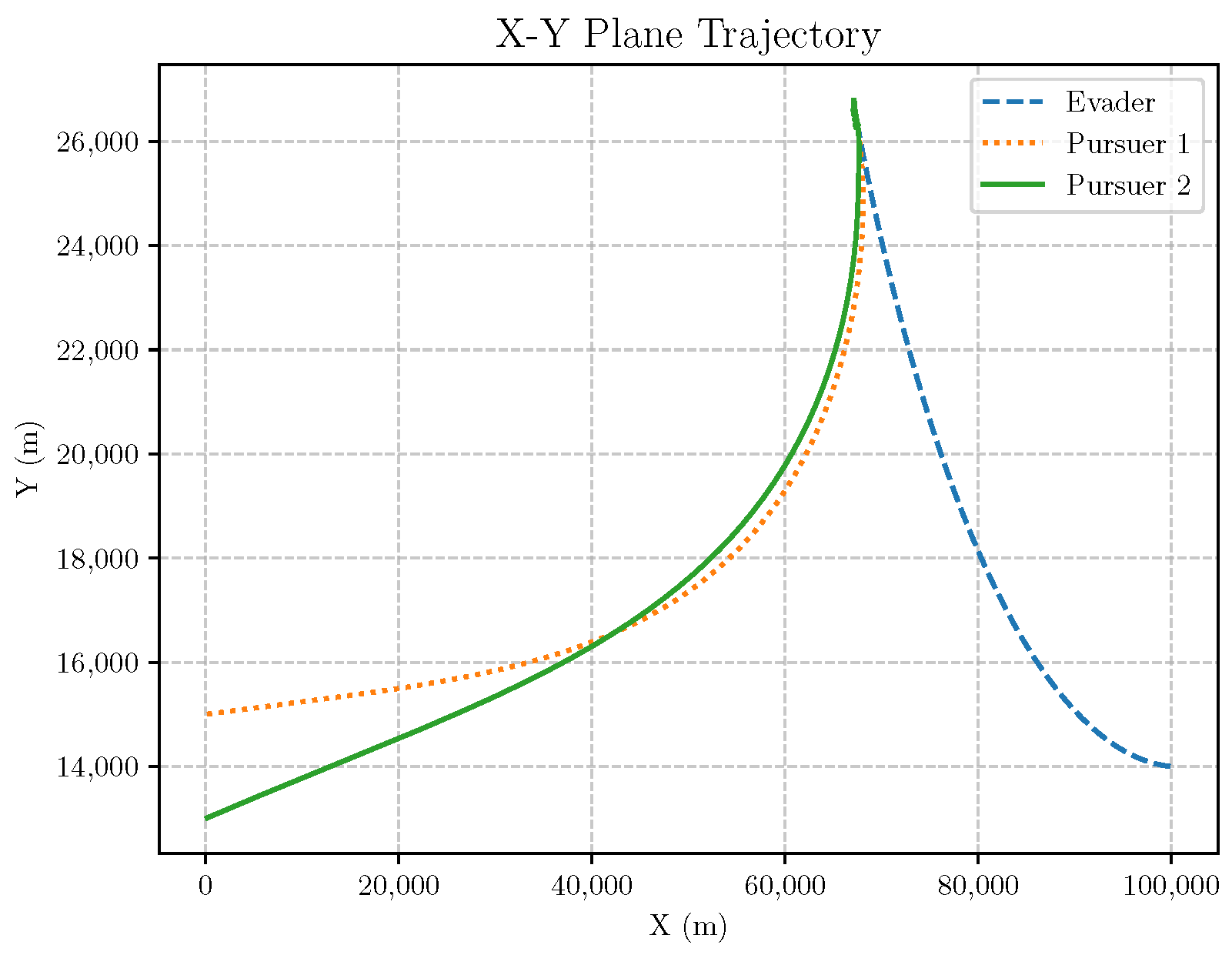
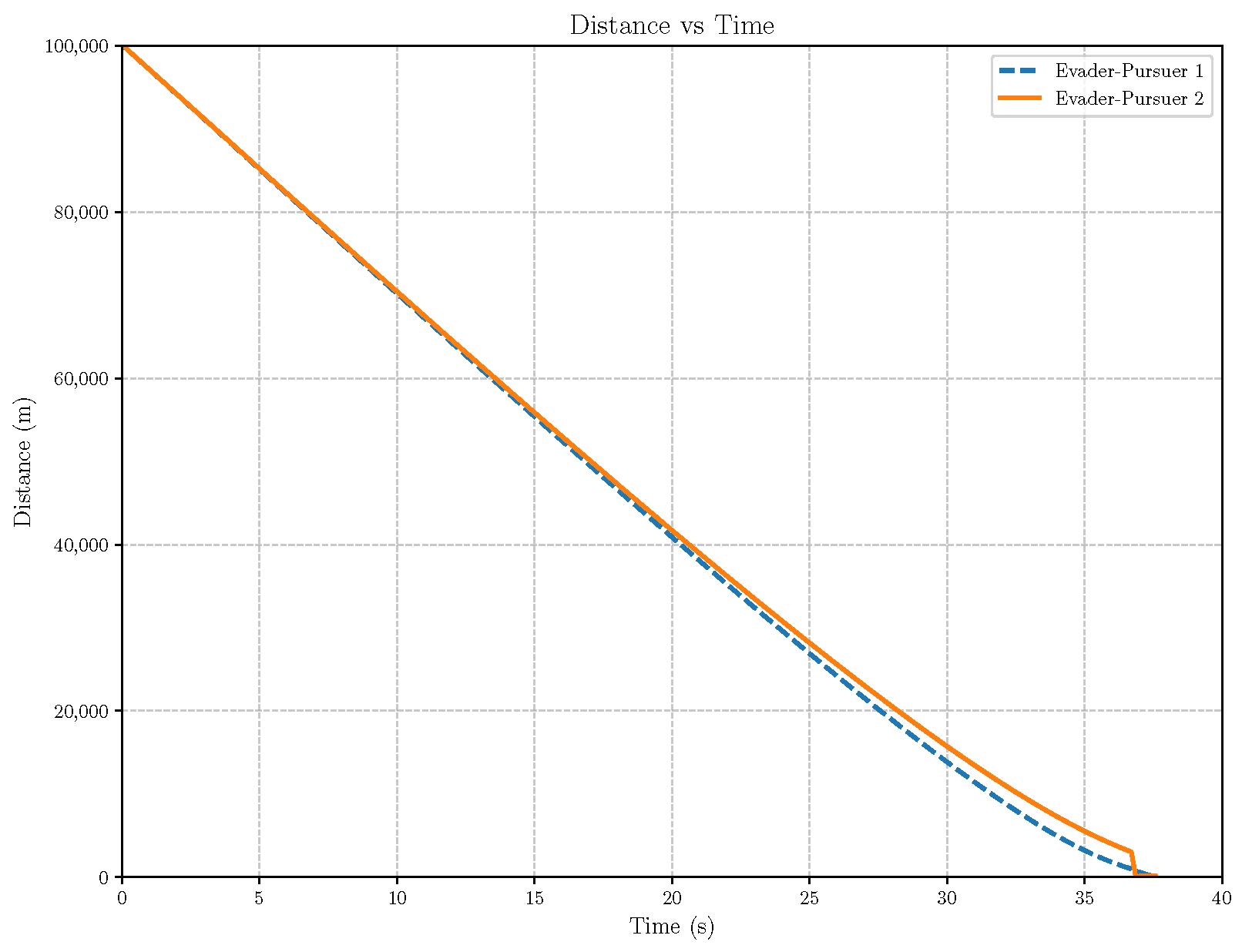
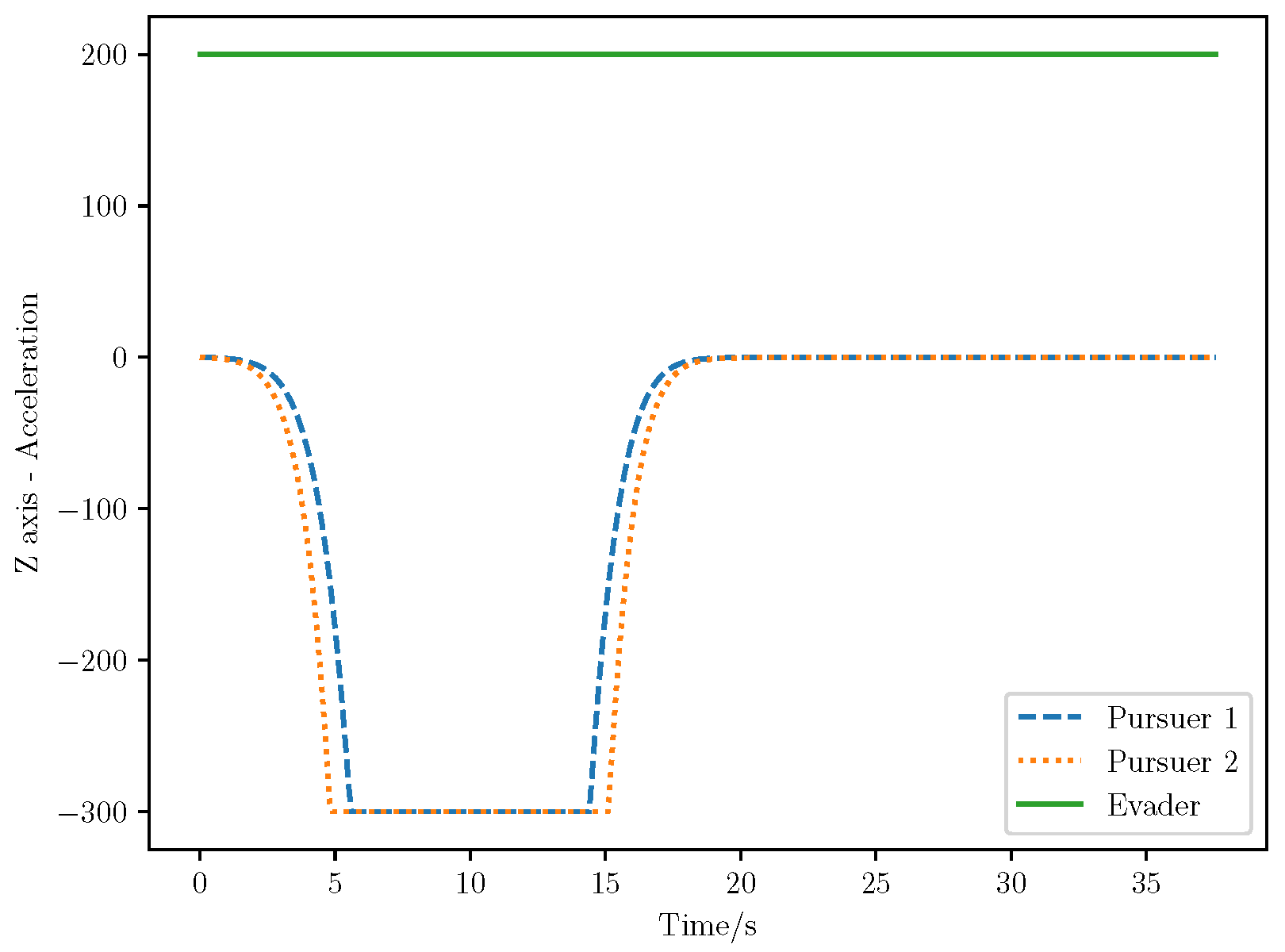
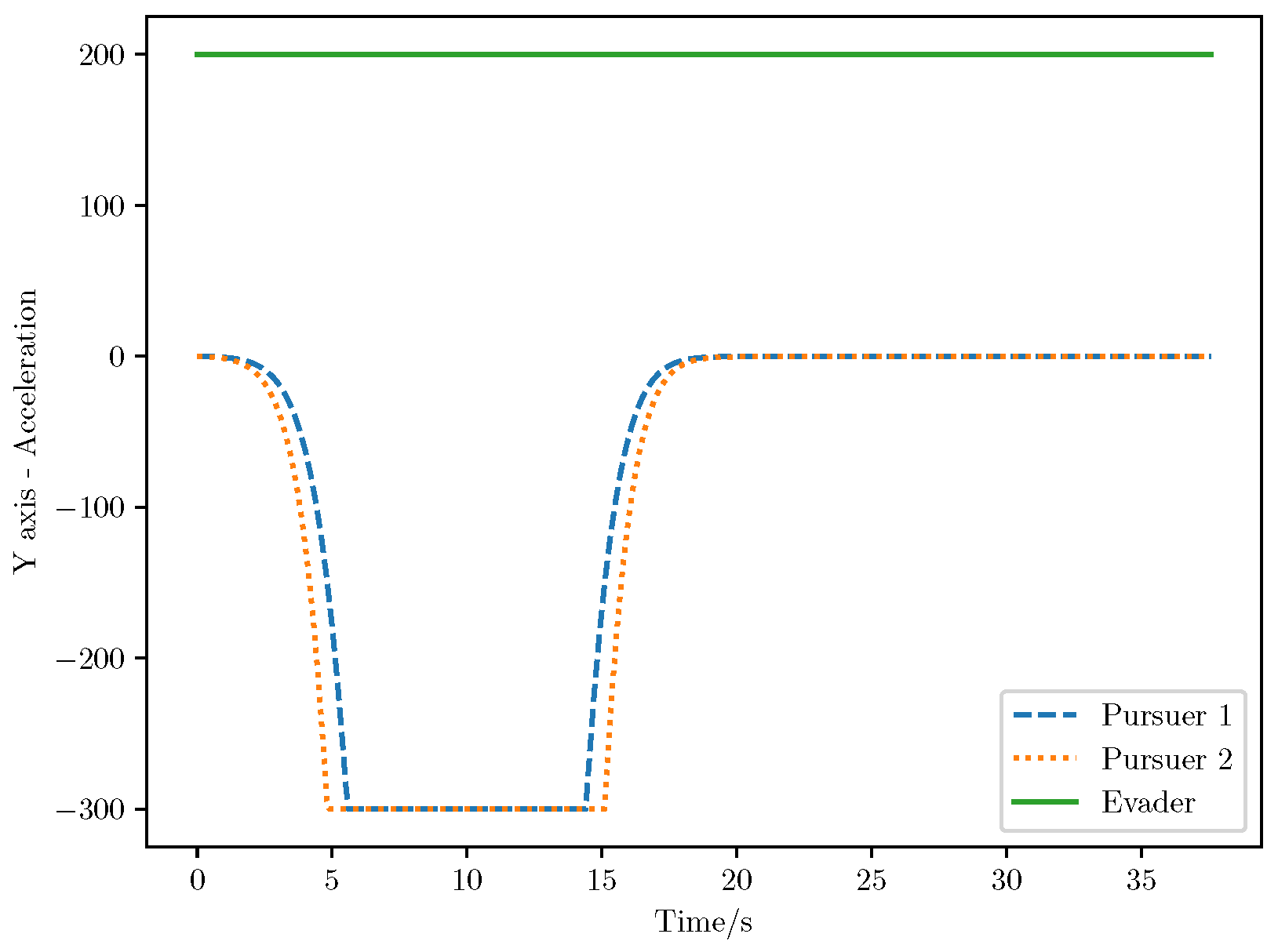
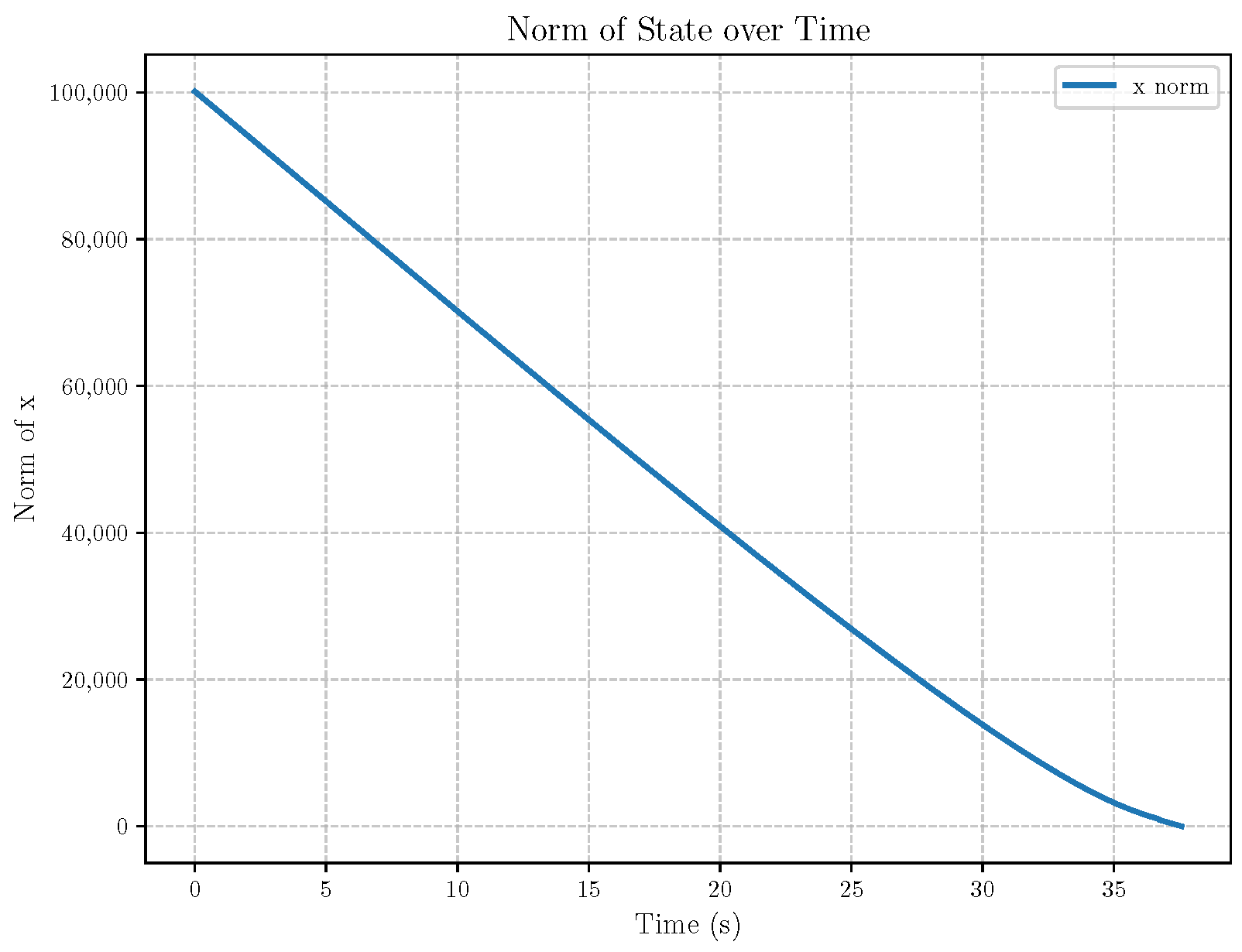
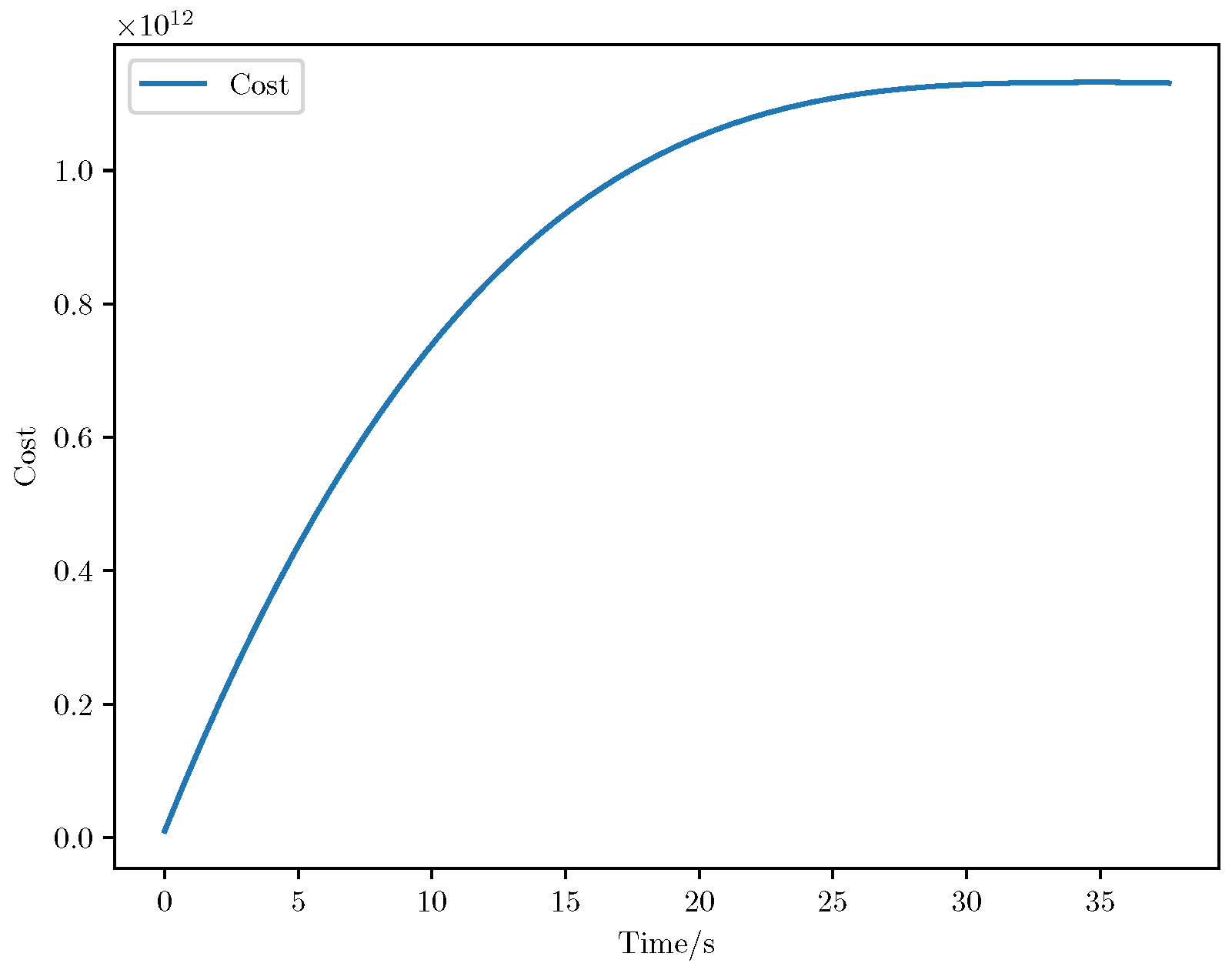
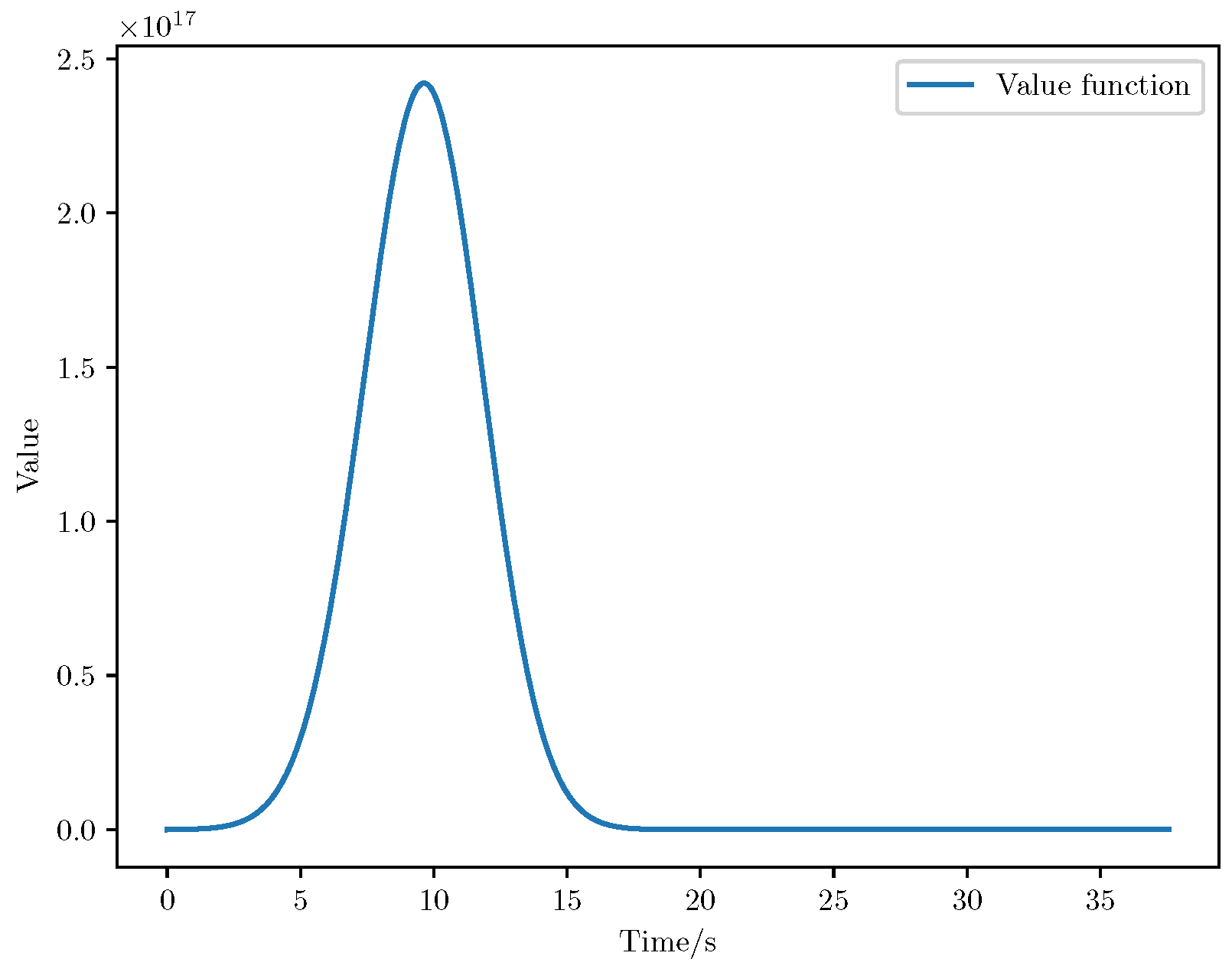
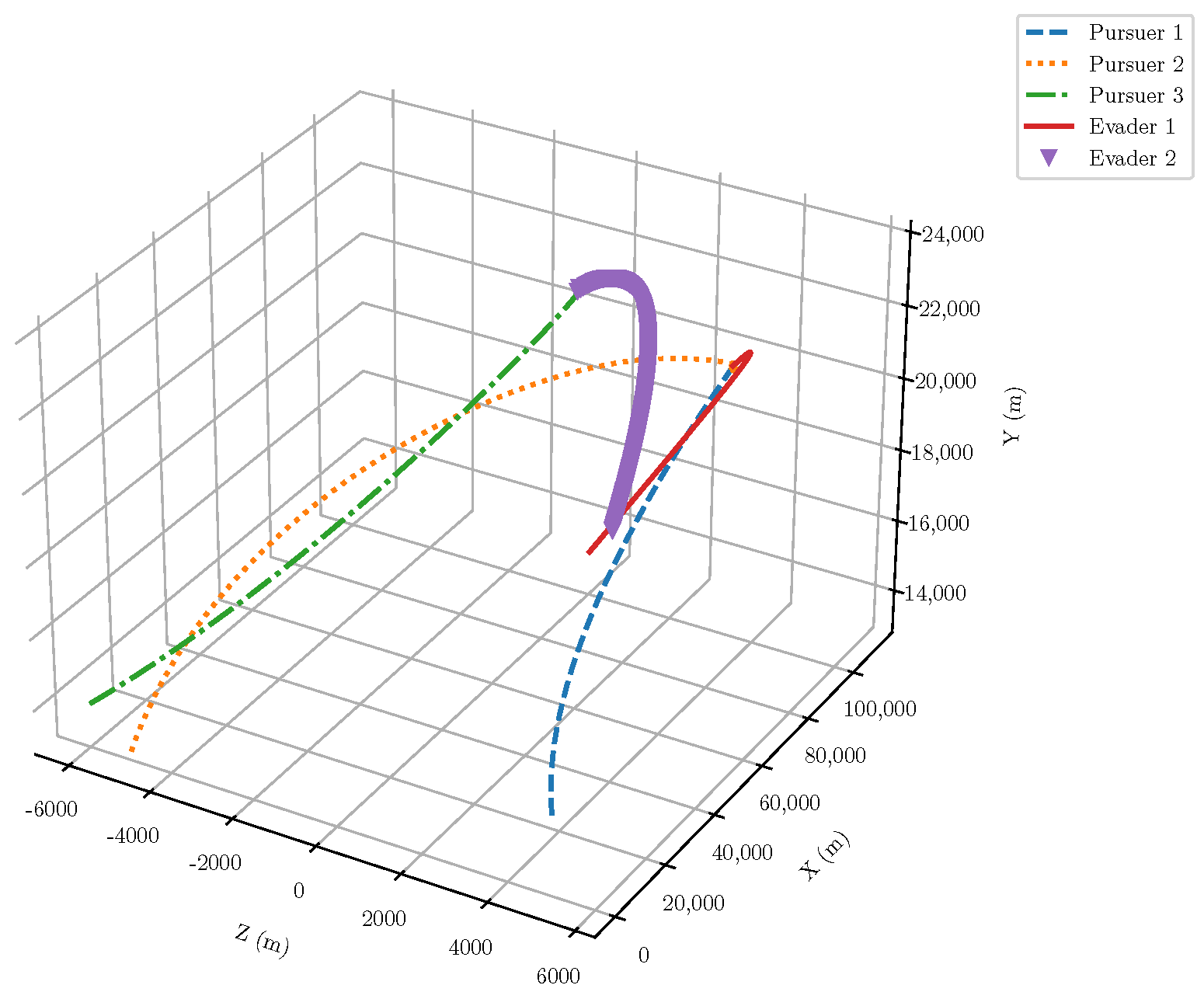
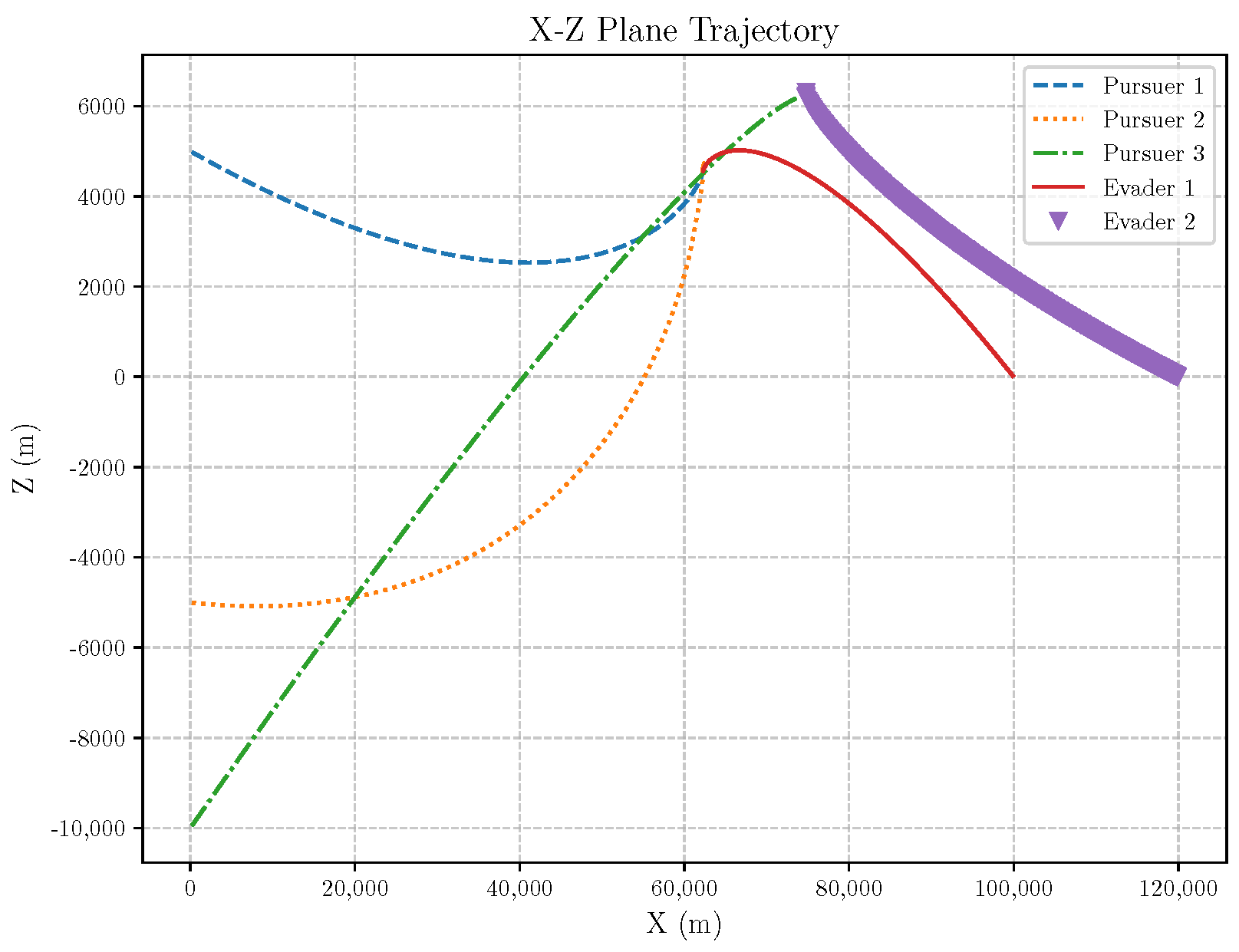
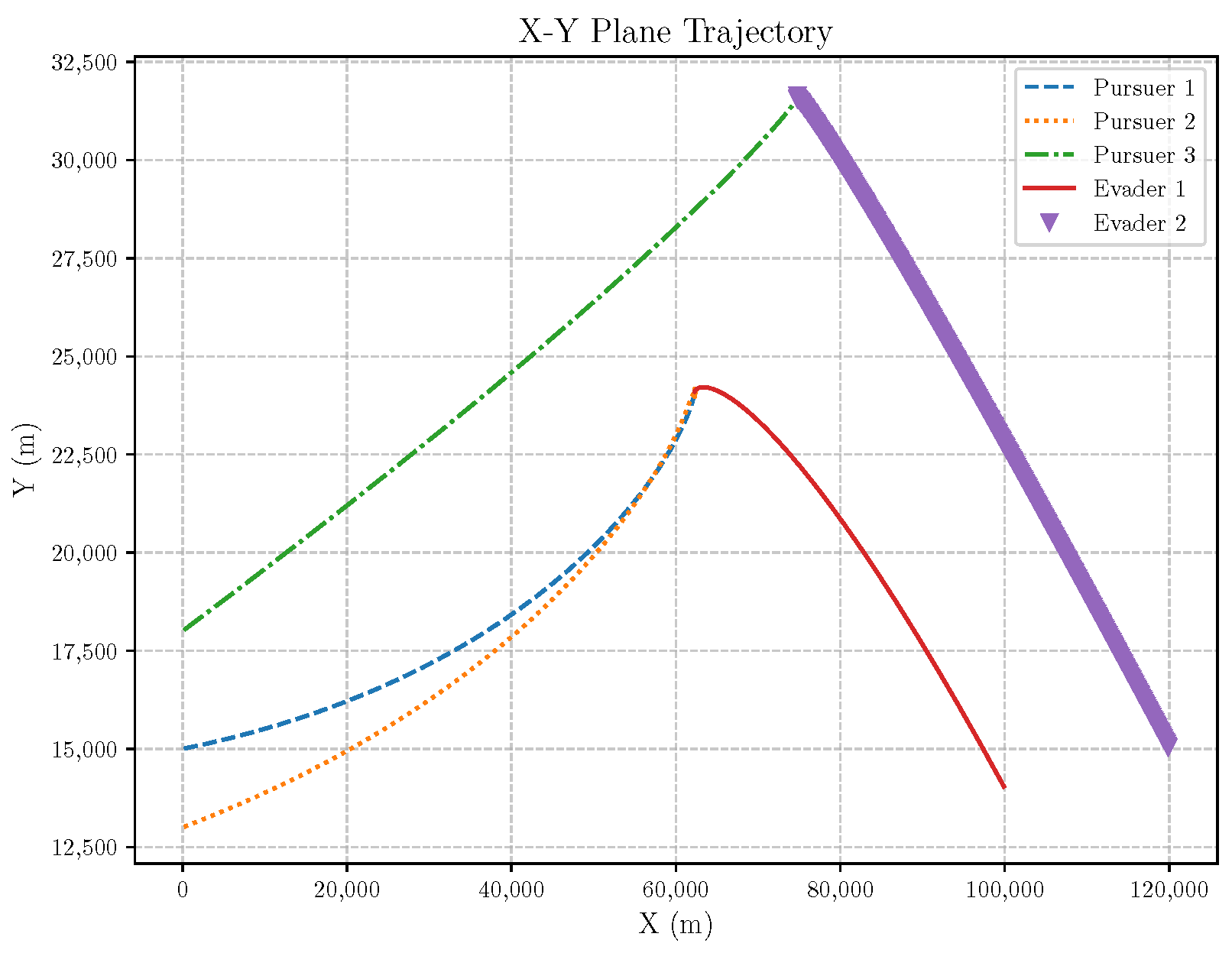
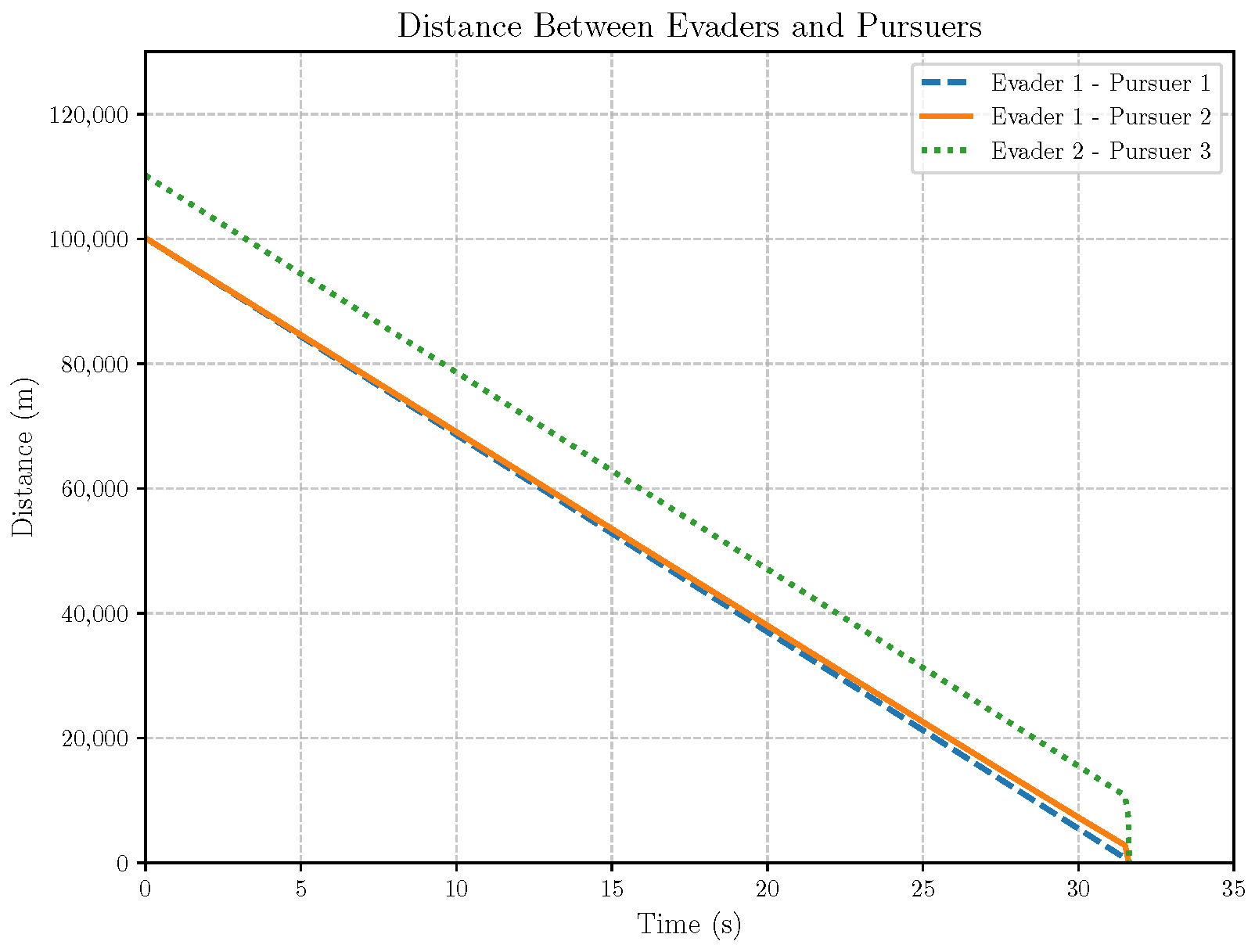
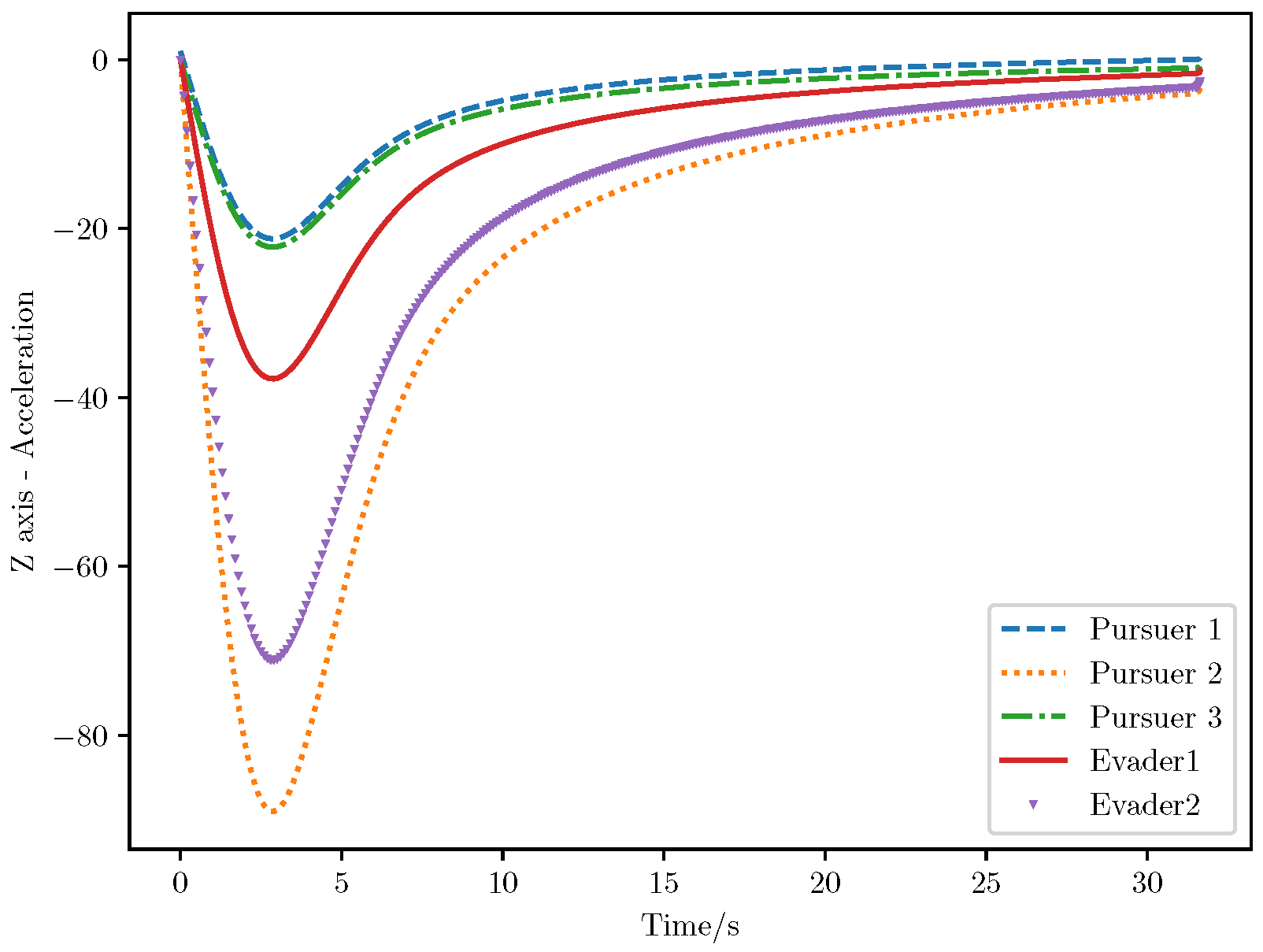
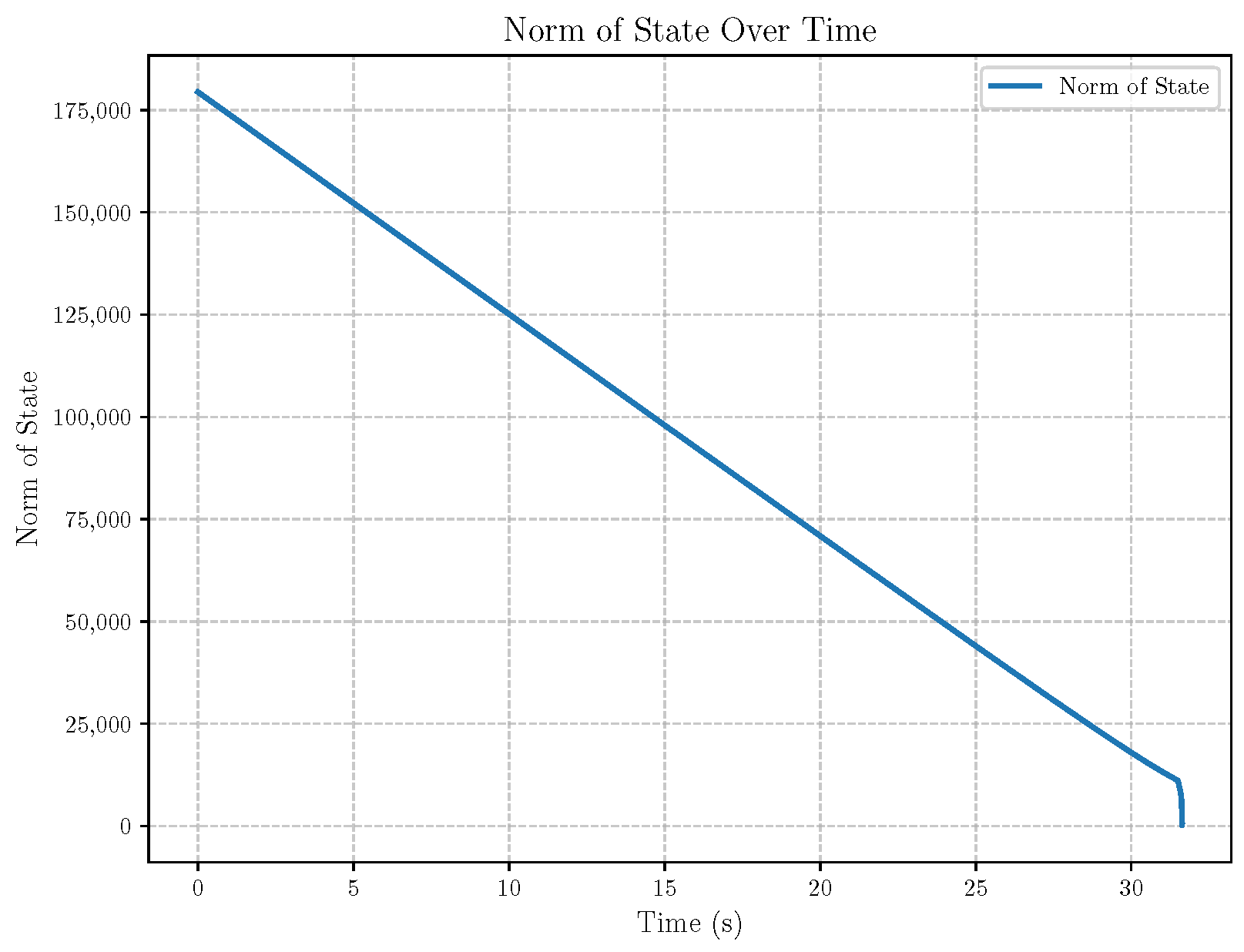
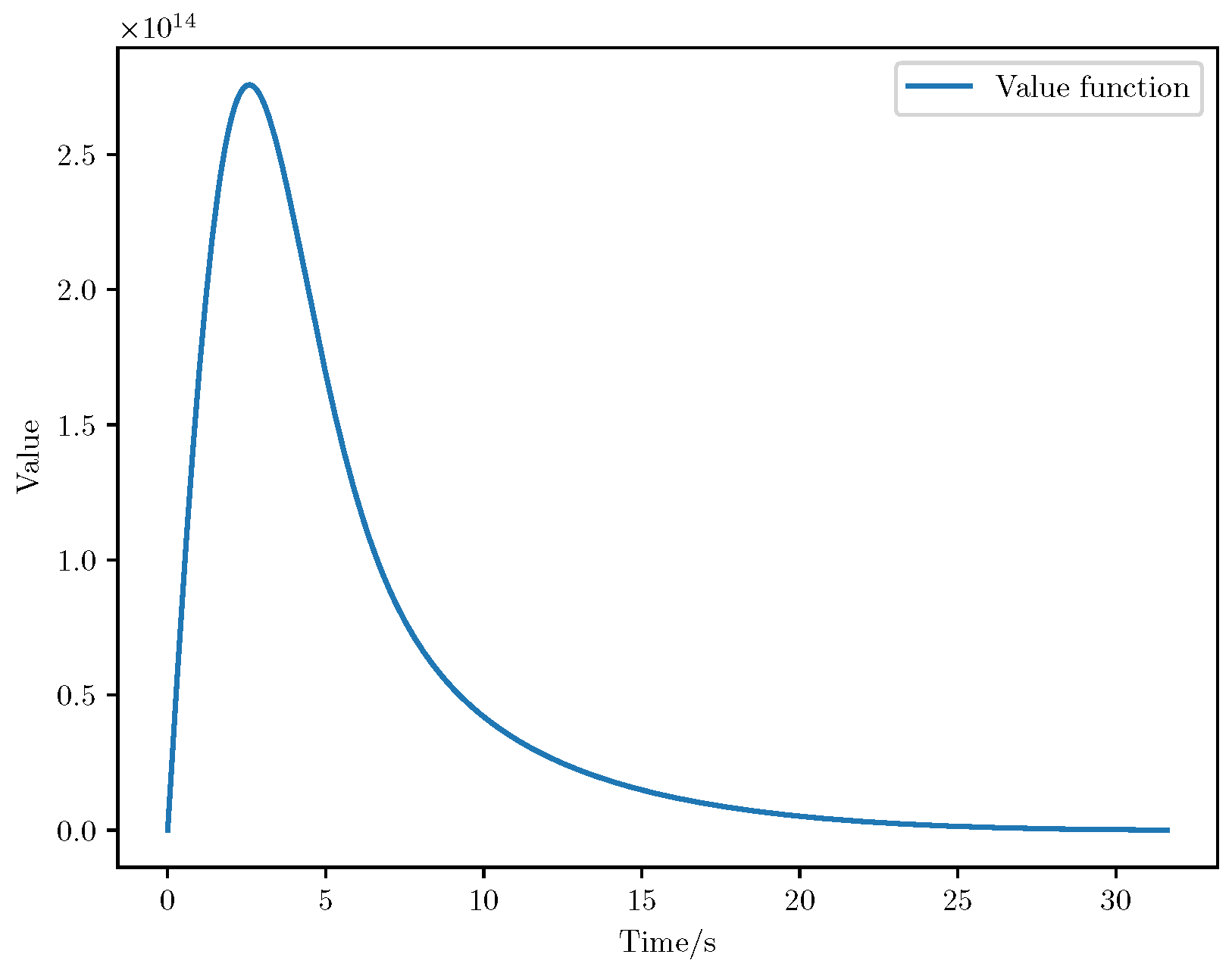
6. Numerical Analysis
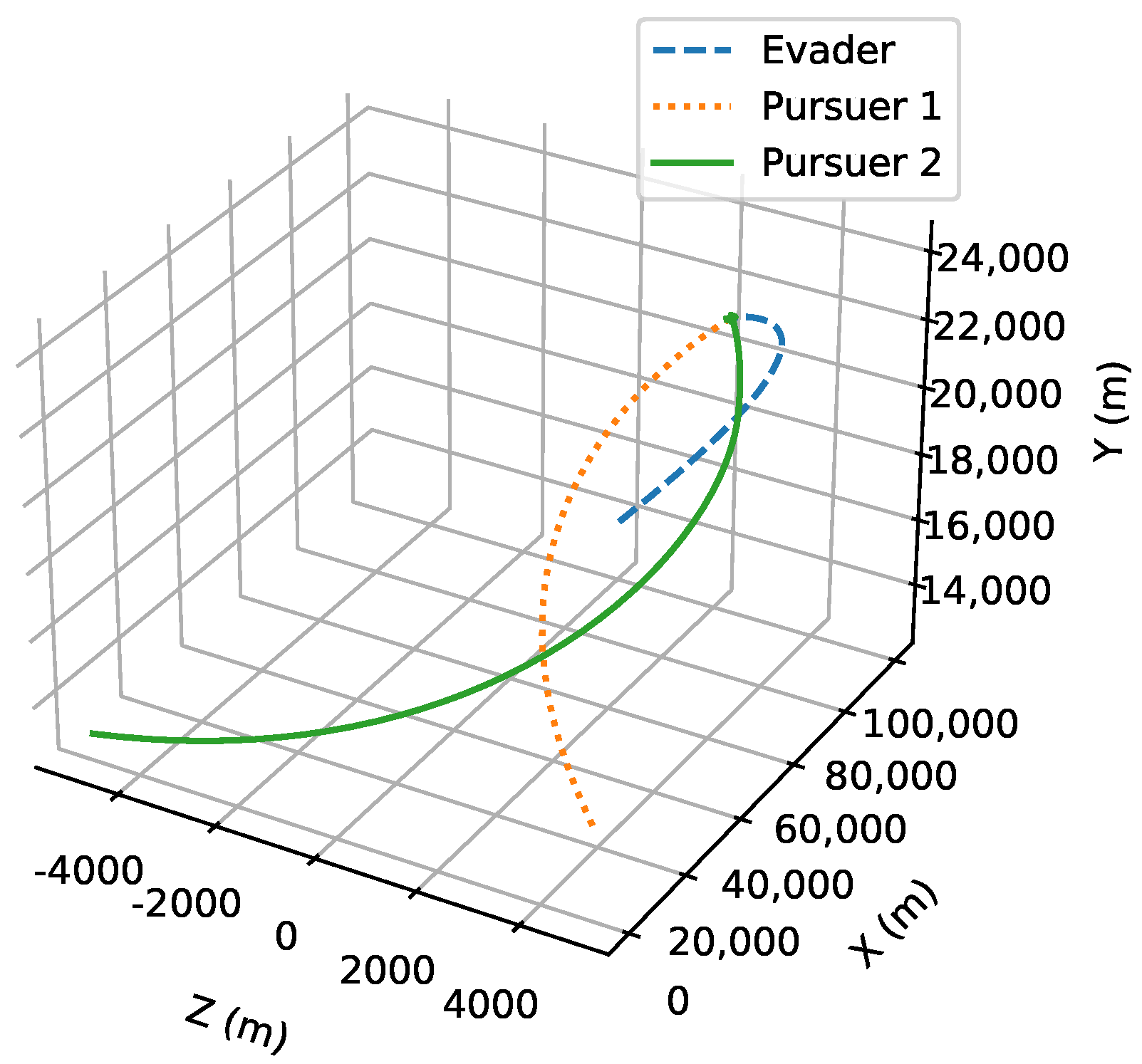
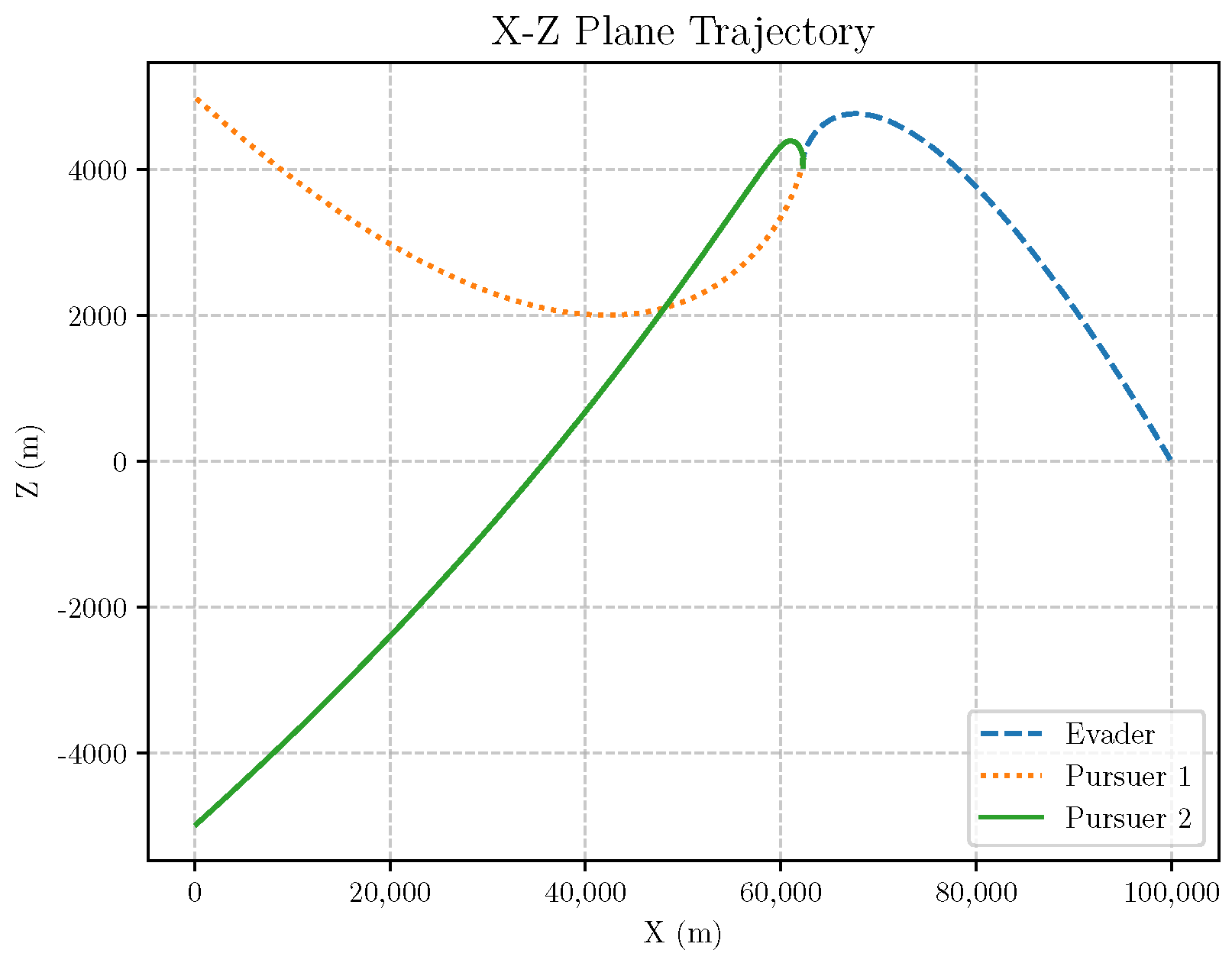
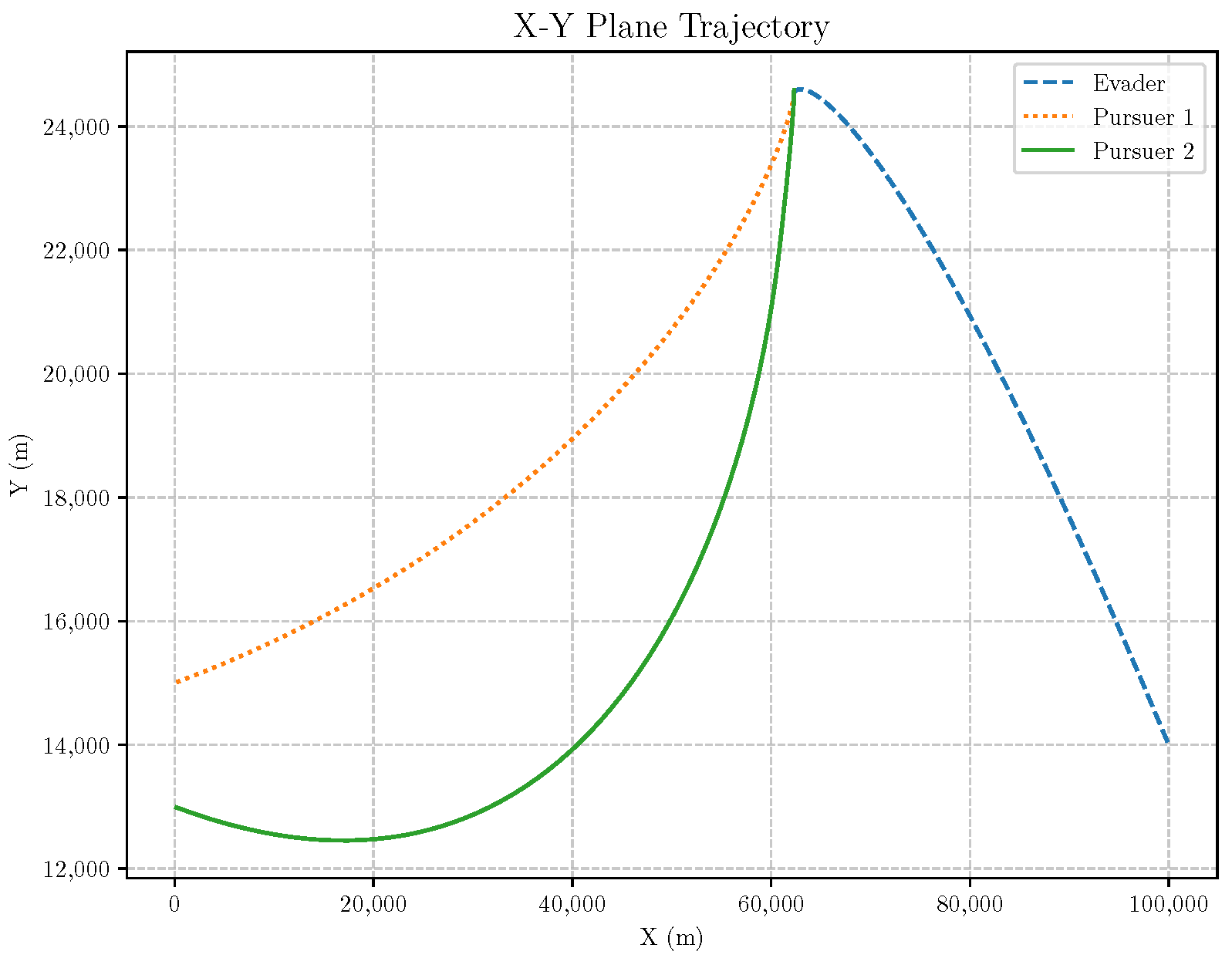
- Initial positions: The initial position of pursuer is [0, 15,000, 5000] m, while that of is [0, 13,000, −5000] m. The initial position of the evader E is [100,000, 14,000, 0] m.
- Initial velocities: The pursuers’ velocities are set to 3000 m/s and 3500 m/s, respectively, while the evader’s velocity is 2000 m/s.
- Acceleration limits: The maximum normal accelerations are 30 g for the pursuers and 20 g for the evader (g = 9.81 m/s2).
- Flight path angles: The initial flight path angles for the pursuers are set to −4° (elevation) and 4° (azimuth). The evader’s initial angles are 10° (elevation) and 170° (azimuth).
- Time step: A time interval of 0.1s was used for numerical integration.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Isaacs, R. Differential Games I, II, III, IV; Research Memoranda; RAND Corporation: Santa Monica, CA, USA, 1954. [Google Scholar]
- Basar, T.; Olsder, G.J. Dynamic Noncooperative Game Theory, 2nd ed.; SIAM: Philadelphia, PA, USA, 1999. [Google Scholar]
- Bagchi, A. Stackelberg Differential Games in Economic Models; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Smith, J.M. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar] [CrossRef]
- Yeung, D.W.K.; Petrosyan, L.A. Cooperative Stochastic Differential Games; Springer: New York, NY, USA, 2006. [Google Scholar]
- Ho, Y.C.; Bryson, A.; Baron, S. Differential games and optimal pursuit-evasion strategies. IEEE Trans. Autom. Control 1965, 10, 385–389. [Google Scholar] [CrossRef]
- Bernhard, P. Linear-quadratic, two-person, zero-sum differential games: Necessary and sufficient conditions. J. Optim. Theory Appl. 1979, 27, 51–69. [Google Scholar] [CrossRef]
- Liu, N.; Guo, L. Adaptive Stabilization of Noncooperative Stochastic Differential Games. SIAM J. Control Optim. 2024, 62, 1317–1342. [Google Scholar] [CrossRef]
- Engwerds, J.C.; van den Broek, W.A.; Schumacher, J.M. Feedback Nash equilibria in uncertain infinite time horizon differential games. In Proceedings of the 14th International Symposium of Mathematical Theory of Networks and Systems, Perpignan, France, 19–23 June 2000; pp. 1–6. [Google Scholar]
- Huang, Q.; Shi, J. Mixed leadership stochastic differential game in feedback information pattern with applications. Automatica 2024, 160, 111425. [Google Scholar] [CrossRef]
- Xie, T.H.; Feng, X.W.; Huang, J.H. Mixed linear quadratic stochastic differential leader-follower game with input constraint. Appl. Math. Optim. 2021, 84, S215–S251. [Google Scholar] [CrossRef]
- Moon, J. Linear-quadratic stochastic leader-follower differential games for Markov jump-diffusion models. Automatica 2023, 147, 110713. [Google Scholar] [CrossRef]
- Lv, S. Two-player zero-sum stochastic differential games with regime switching. Automatica 2020, 114, 108819. [Google Scholar] [CrossRef]
- Moon, J. A sufficient condition for linear-quadratic stochastic zero-sum differential games for Markov jump systems. IEEE Trans. Autom. Control 2019, 64, 1619–1626. [Google Scholar] [CrossRef]
- Sun, H.; Yan, L.; Li, L. Linear-quadratic stochastic differential games with Markov jumps and multiplicative noise: Infinite-time case. Int. J. Innov. Comput. Appl. 2015, 11, 349–361. [Google Scholar]
- Zhang, C.; Li, F. Non-zero sum differential game for stochastic Markovian jump systems with partially unknown transition probabilities. J. Frankl. Inst. 2021, 358, 7528–7558. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, H.; Fu, M.; Liang, Y. Decentralized strategies for finite population linear-quadratic-Gaussian games and teams. Automatica 2022, 148, 110789. [Google Scholar] [CrossRef]
- Luo, G.; Zhang, H.; He, H.; Jin, Y.; Cui, Y. Mean field theory-based multi-agent adversarial cooperative learning. IEEE Trans. Cybern. 2020, 50, 5052–5065. [Google Scholar]
- Bensoussan, A.; Chen, S.K.; Chutani, A.; Sethi, S.P.; Siu, C.C.; Yam, S.C.P. Feedback Stackelberg-Nash equilibria in mixed leadership games with an application to cooperative advertising. SIAM J. Control Optim. 2019, 57, 3413–3444. [Google Scholar] [CrossRef]
- Huang, J.; Qiu, Z.; Wang, S.; Wu, Z. Linear quadratic mean-field game-team analysis: A mixed coalition approach. Automatica 2024, 159, 111358. [Google Scholar] [CrossRef]
- Liu, N.; Guo, L. Stochastic Adaptive Linear Quadratic Differential Games. IEEE Trans. Autom. Control 2022, 69, 1066–1073. [Google Scholar] [CrossRef]
- Hamadène, S. Nonzero sum linear-quadratic stochastic differential games with time-inconsistent coefficients. SIAM J. Control Optim. 1999, 37, 460–485. [Google Scholar]
- Sun, J.; Yong, J. Linear quadratic stochastic differential games: Open-loop and closed loop saddle points. SIAM J. Control Optim. 2014, 52, 4082–4121. [Google Scholar] [CrossRef]
- Yu, Z. An optimal feedback control-strategy pair for zero-sum linear-quadratic stochastic differential game: The Riccati equation approach. SIAM J. Control Optim. 2015, 53, 2141–2167. [Google Scholar] [CrossRef]
- Miller, E.; Pham, H. Linear-quadratic McKean-Vlasov stochastic differential games. In Modeling, Stochastic Control, Optimization, and Applications; Springer: Berlin/Heidelberg, Germany, 2019; Volume 164, pp. 451–481. [Google Scholar] [CrossRef]
- Sun, J. Two-person zero-sum stochastic linear-quadratic differential games. SIAM J. Control Optim. 2021, 59, 1804–1829. [Google Scholar] [CrossRef]
- Chang, D.; Xiao, H. Linear quadratic nonzero sum differential games with asymmetric information. Math. Probl. Eng. 2014, 2014, 262314. [Google Scholar] [CrossRef]
- Shi, J.; Wang, G.; Xiong, J. Leader-follower stochastic differential game with asymmetric information and applications. Automatica 2016, 63, 60–73. [Google Scholar] [CrossRef]
- Nourian, M.; Caines, P.E. ϵ-Nash Mean Field Game Theory for Nonlinear Stochastic Dynamical Systems with Major and Minor Agents. arXiv 2012, arXiv:1209.5684. [Google Scholar]
- Goldys, B.; Yang, J.; Zhou, Z. Singular perturbation of zero-sum linear-quadratic stochastic differential games. SIAM J. Control Optim. 2022, 60, 48–80. [Google Scholar] [CrossRef]
- Shi, Q.H. A Verification Theorem for Stackelberg Stochastic Differential Games in Feedback Information Pattern. arXiv 2021, arXiv:2108.06498. [Google Scholar]
- Zheng, Y.; Shi, J. A linear-quadratic partially observed Stackelberg stochastic differential game with application. Appl. Math. Comput. 2022, 420, 126819. [Google Scholar] [CrossRef]
- Song, S.H.; Ha, I.J. A Lyapunov-like approach to performance analysis of 3-dimensional pure png laws. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 238–248. [Google Scholar] [CrossRef]
- Song, J.; Zhang, X.; Wang, L. Impact Angle Constrained Guidance against Non-maneuvering Targets. AIAA J. Guid. Control Dyn. 2023, 46, 1556–1565. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Guo, J. A Review of Missile Interception Techniques. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2341–2357. [Google Scholar]
- Li, B.; Zhang, W.; Sun, Z. Guidance for Intercepting High-Speed Maneuvering Targets. J. Guid. Control Dyn. 2021, 44, 2282–2293. [Google Scholar]
- Wang, L.; Zhou, J. Nonlinear Missile Guidance and Control; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Chen, Q.; Zhou, X. Design of Optimal Missile Guidance Law Using LQR. Control Eng. Pract. 2019, 83, 62–73. [Google Scholar] [CrossRef]

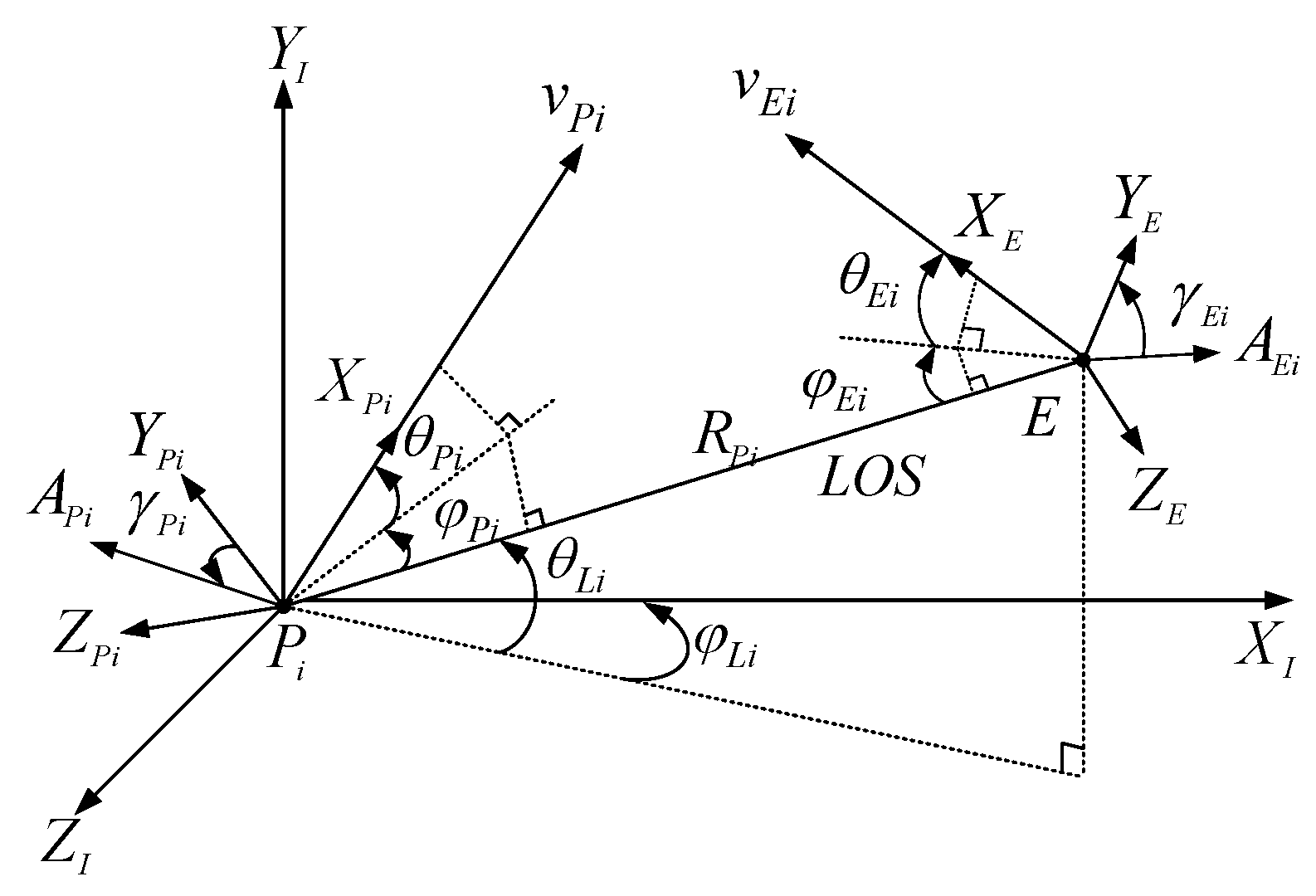





| Symbol | Description | Coordinate System |
|---|---|---|
| Inertial reference coordinate system | Inertial | |
| Line-of-sight (LOS) coordinate system | LOS | |
| Velocity coordinate system of the i-th pursuer | Pursuer | |
| Velocity of the i-th evader | Evader | |
| Velocity of the i-th pursuer | Pursuer | |
| Acceleration of the i-th pursuer | Pursuer | |
| Acceleration of the i-th evader | Evader | |
| Angle between the acceleration of the i-th pursuer and axis | Pursuer | |
| Angle between the acceleration of the i-th evader and axis | Evader | |
| Distance between the i-th pursuer and the evader | Spatial | |
| LOS angles between the evader and the i-th pursuer relative to the inertial reference coordinate system | LOS | |
| Elevation and azimuth angles of relative to the LOS coordinate system from pointing toward E | Pursuer | |
| Elevation and azimuth angles of relative to the LOS coordinate system from pointing toward | Evader | |
| Projections of the pursuer’s normal acceleration on the and axes in the velocity coordinate system | Pursuer | |
| Projections of the evader’s normal acceleration on the and axes in the velocity coordinate system | Evader |
| Item | Environment |
|---|---|
| Development language | Python |
| Library | Numpy |
| Disk capacity | 2 T |
| RAM | 32 G |
| CPU | i7 2.2 GHZ |
| OS | Ubantu 16.04 |
| Parameter | Value |
|---|---|
| Initial distance | 100,000 |
| Evader initial elevation angle | (elevation) and (azimuth) |
| Evader initial azimuth angle | (elevation) and (azimuth) |
| Iteration time | 0.1–0.5 s |
| Maximum normal acceleration | 20–40 g |
| 100 experiments | 98 successful, 2 failed |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.; Zhou, D.; He, Z. A Class of Pursuit Problems in 3D Space via Noncooperative Stochastic Differential Games. Aerospace 2025, 12, 50. https://doi.org/10.3390/aerospace12010050
Bai Y, Zhou D, He Z. A Class of Pursuit Problems in 3D Space via Noncooperative Stochastic Differential Games. Aerospace. 2025; 12(1):50. https://doi.org/10.3390/aerospace12010050
Chicago/Turabian StyleBai, Yu, Di Zhou, and Zhen He. 2025. "A Class of Pursuit Problems in 3D Space via Noncooperative Stochastic Differential Games" Aerospace 12, no. 1: 50. https://doi.org/10.3390/aerospace12010050
APA StyleBai, Y., Zhou, D., & He, Z. (2025). A Class of Pursuit Problems in 3D Space via Noncooperative Stochastic Differential Games. Aerospace, 12(1), 50. https://doi.org/10.3390/aerospace12010050






