Abstract
As an emerging rapid manufacturing technology, 3D printing has been widely applied in numerous fields such as aerospace, shipbuilding, and wind power, by virtue of its advantage in efficiently fabricating components with complex structures and integrated functions. In response to the problems of poor mechanical properties and difficulty in selecting process parameters for fused deposition modeling (FDM), this paper analyzed the principle of FDM and proposed a parameter optimization method based on a Kriging and Cuckoo Search (CS) algorithm aimed at improving the mechanical properties of 3D printed polylactic acid (PLA) parts. Firstly, by analyzing FDM principle and its main parameters, printing speed and temperature were selected as research elements, and tensile strength as the mechanical performance index. Latin hypercube sampling (LHS) was integrated to generate a limited experimental sample set. Secondly, a Kriging-based prediction model for mechanical properties was constructed by learning sample data, and the nonlinear mapping relationship between process parameters and tensile strength was obtained. Then, using the combinations of speed and temperature as design variables and maximizing tensile strength as the optimization objective, an optimization model was established, and the optimal process parameters were searched by CS. The optimal printing velocity was 31 mm/s and printing temperature was 225 °C, and the corresponding maximum tensile strength was 38.27 MPa. Finally, compared to the test data, the relative prediction error of Kriging model was 0.62%, and the optimal strength (38.27 MPa) increased by about 12.7% compared to the average value (33.97 MPa) of experimental data. It can be seen that the Kriging model is effective, and the tensile strength of parts printed under the optimal process parameters is significantly improved.
1. Introduction
Different from conventional processes such as subtractive manufacturing (i.e., milling or drilling) and formative manufacturing (i.e., casting or forging), additive manufacturing, also referred to as rapid prototyping [1] and 3D printing [2], is a revolutionary manufacturing technique based on digital models that utilizes adhesive materials such as metals, polymers, or composites to construct structures with complex shapes through depositing material layer by layer. Due to not being limited by the shape of parts and forming molds or tools, 3D printing products have a short development cycle and low cost. Currently, 3D printing has received tremendous attention in transportation, aerospace, industrial equipment, medical, and other fields [3].
Fused deposition modeling (FDM) is a commonly utilized 3D printing technique. It heats and extrudes filaments via a small nozzle along a computer-controlled route to manufacture polymer components with shapes varying from simple to complex. To improve the performance of FDM, it is essential to appropriately configure input parameters like printing speed and orientation, layer thickness, nozzle and substrate temperatures, and infill percentage and pattern, along with other parameters [3,4]. Rodríguez-Reyna et al. [5] and Cheng et al. [6] conducted optimization and statistical analyses regarding the influence of printing parameters such as infill percentage, printing direction, layer thickness, printing speed, and nozzle temperature on the tensile stress and elastic modulus of FDM parts printed with polylactic acid (PLA), acrylonitrile-butadiene-styrene copolymer (ABS), nylon with carbon fiber, and recycled carbon fiber-reinforced PLA by applying the Design of Experiments (DOE) method. Portoacă et al. [7] and Pereira et al. [8] also utilized the DOE technique to examine the impact of process parameters (infill percentage, layer thickness, printing speed, infill pattern, and printing material) on the tensile, compressive, and bending properties of ABS and PLA parts. Alzyod et al. [9] employed a Variance Analysis (ANOVA), means, and signal-to-noise (S/N) ratio graphs to explore the correlation between the residual stress of ABS-printed samples and three printing parameters, namely printing orientation, raster angle, and infill pattern. Wang et al. [10] carried out uni-axial tensile tests and dynamic mechanical analyses to describe the tensile properties and dynamic mechanical properties of FDM-printed PLA which were under different process parameters, specifically including printing angle, layer thickness, infill percentage, and nozzle temperature. Khosravani et al. [11] performed compact tension (CT) tests on 3D-printed PLA and ABS parts fabricated by FDM to study the effects of printing speed, layer thickness, and printing direction on tensile strength and fracture toughness and enhanced their mechanical properties. Two quadratic mathematical models were put forward by Algarni et al. [12] to demonstrate the effect of three printing process variables, namely raster angle, layer thickness, and infill density, on two outputs, that is, the strength at fracture and strain behavior of PLA-printed specimens. Orthogonal experiments were adopted by Huang et al. [13], Mani et al. [14], and Sahoo et al. [15] to investigate process parameters like layer thickness, printing speed, raster angle, and building orientation regarding their effects on the mechanical properties, surface quality, and micro-structure of samples in FDM. The above studies conducted a large number of experiments through trial and error and then selected better process parameters in discrete intervals. Its disadvantage is that the results are not optimal, and the experimental cost is huge.
Combining DOE and NSGA-II, Kafshgar et al. [16] and Long et al. [17] conducted multi-objective optimization studies on the process parameters of 3D-printed PLA and continuous flax-fiber-reinforced composites and provided the optimal 3D printing process parameters. Similarly combining DOE with grey wolf algorithm (GWO), Fountas et al. [18] studied five important FDM parameters (layer thickness, infill percentage, deposition angle, printing speed, and printing temperature) and their effect on the response of flexural strength. Patil et al. [19] investigated the impacts of layer thickness, printing speed, infill percentage, and infill pattern on surface roughness, printing time, and the length of consumed filaments. Additionally, a multi-objective optimization framework was put forward to optimize the parameters of FDM for PLA printing by combining orthogonal experiments with grey correlation analysis. Furthermore, Dusanapudi et al. [20] combined orthogonal experiments, grey relational analysis, and genetic algorithm (GA) to study the effects of extrusion multiplier, nozzle temperature, and layer thickness on the mechanical properties and porosity of acrylonitrile-butadiene-styrene copolymer (ABS) FDM parts and acquired the optimal combination of process parameters. Singh et al. [21] studied the influence of the printing process parameters of FDM, namely nozzle diameter, build orientation, raster pattern, layer height, and print speed, on the tensile strength, build time, material consumption, and surface roughness of 3D-printed PLA. Moreover, an Artificial Neural Network (ANN) prediction model was developed to predict the relevant responses with the minimum error. Similarly, in order to achieve multi-objective optimization of conflicting performance responses, namely specific energy, scrap weight, and surface roughness depending on the constraints of printing parameters, namely infill percentage, layer thickness, printing speed, and extruder temperature, Poonia et al. [22] integrated GA to provide a Pareto solution and utilized an analytical hierarchal process (AHP) to determine the weights of the three objectives and techniques for order preference by similarity to the ideal solution to obtain the most preferred solution. In order to enhance the shape accuracy of FDM parts, Yang et al. conducted research on a comparison between Kriging and neural networks [23], as well as a comparison between Cuckoo Search (CS), GA, and PSO. The authors of [24,25] proposed a deformation control-oriented optimization method for the process parameters of FDM of PLA. However, there is still little research on combining surrogate models and evolutionary algorithms to optimize printing speed and temperature in order to improve the mechanical properties of FDM parts.
In this paper, printing velocity and nozzle temperature are the parameters employed for examination, while tensile strength acts as the response index for analysis. Subsequently, an optimization framework based on the Kriging method and CS algorithm is put forward to optimize the process parameters of FDM for the printing of PLA parts. By integrating Latin hypercube sampling (LHS) with an experimental analysis to generate sample data, a Kriging model is constructed based on this sample data for predicting tensile strength. Then, based on the Kriging forecast model, CS is utilized to seek out the optimal solution. The proposed method plays a significant role in enhancing the mechanical properties of 3D-printed polymer components and facilitating the in-depth application of 3D printing technology.
2. Problem Formulation
2.1. FDM Principle and Process Parameters
The main materials of FDM are filaments such as PLA, ABS, and nylon. During printing, the filament is rolled in two feeding rods and sent to the printing nozzle through a feeding mechanism. At this time, the material is heated, melted, and extruded. The nozzle first moves along the cross-sectional contour of the workpiece and then moves along the internal CNC filling trajectory. The extruded material quickly solidifies, with each layer adhering to each other and stacked layer by layer, ultimately forming a solid workpiece. The printing principle of FDM is shown in Figure 1.
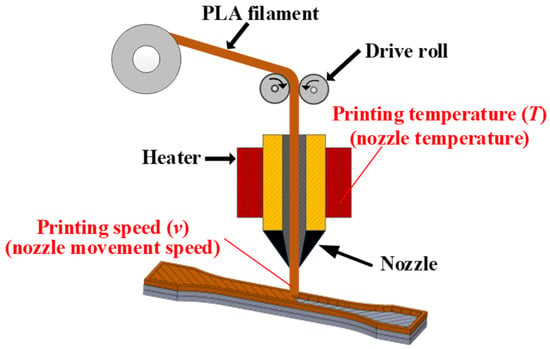
Figure 1.
FDM printing principle.
In FDM, the poor mechanical properties of the printed part are a major bottleneck in the development and application of 3D printing. And, printing speed and temperature have a significant impact on the mechanical properties of FDM parts. In this article, these two parameters are taken as the research objects to explore the mechanism of influence of the printing parameters on the mechanical properties.
Printing speed (v) refers to the nozzle movement speed during printing. If the speed is too low, it will reduce printing efficiency and increase printing time. At the same time, if the material stays in the nozzle for too long, it will lead to excessive heating. If the speed is too high, the surface of the workpiece is prone to wire drawing, which affects the surface quality and cannot guarantee machining accuracy.
Printing temperature (T) refers to the nozzle temperature during 3D printing. If the temperature is too low, it will prevent the material from fully melting, reduce its adhesion, and prevent it from bonding to the hot bed. A peeling phenomenon may also occur between layers, reducing the mechanical properties and easily causing nozzle blockage. If the temperature is too high, it will cause the material to lean towards a liquid state during extrusion, making it difficult to effectively control the filling trajectory and lead to molding failure.
2.2. Optimization Model
In this paper, printing speed (v) and temperature (T) printing were taken as design variables, and the objective function was to maximize the tensile strength (σ). Thus, the objective optimization problem can be formulated as follows:
Here, X denotes the design variables that characterize different combinations of process parameters. v and T represent printing speed and printing temperature, respectively. U(X) denotes the objective function, which is the tensile strength, represented by σ. Ω1 and Ω2 represent the reasonable range of v and T, respectively. In this paper, and .
3. Kriging and CS
3.1. Kriging
Kriging is a type of interpolation function model based on statistical discipline and is widely used as a popular type of surrogate model for approximating expensive black box functions in engineering design and optimization. When predicting the information of a certain point, it is necessary to estimate unknown information about the point by linearly combining the information in a certain range of the point, and it is not affected by random error. The Kriging model has good global convergence and high fitting accuracy and has high nonlinear approximation ability. Kriging model y(x) can be expressed as the sum of a parameterized linear regression model and a non-parametric random process [26]:
Here, is polynomial regression function; is the corresponding weight coefficient vector; f(x) is the basis function for the input parameter x; and z(x) is the estimated error of the system, which is a random distribution with a covariance and a mean of 0, where σ2 is the variance and is the correlation function of hyperparameter θ, which is used to characterize the spatial correlation between sample points xi and xj. Its mathematical expression is as follows:
where m is the number of pre-designed variables; dk is the Euclidean distance of sample point k; and θk is a hyperparameter. There are many forms of correlation function . The commonly used correlation functions in the Kriging proxy model are the exponential function, Gaussian function, cubic function, spherical function, and spline function.
3.2. CS
The Cuckoo Search algorithm is a swarm intelligence optimization algorithm as well as a novel meta-heuristic search algorithm. It boasts several advantages, such as having a small number of parameters, being easy to operate, being simple to implement, possessing excellent random search paths, and having powerful optimization capability. Its concept is founded on two strategies: cuckoo’s nest parasitism and the Lévy flight mechanism. By seeking the optimal nest through random walks for hatching its own eggs, an efficient optimization pattern can be achieved. The CS algorithm employs nests to symbolize solutions. In the simplest scenario, there is one egg in each nest, and the cuckoo’s egg stands for a new solution. The goal is to substitute less favorable solutions with new and potentially better ones. The algorithm is predicated on three idealized rules: (1) Each cuckoo lays an egg and puts it in a randomly chosen nest. (2) The nests containing eggs of the highest quality will be retained and passed down to the next generation. (3) The number of nests is fixed, and the probability that the cuckoo’s eggs are discovered is .
A balanced combination of local random walks and global random walks is used in the algorithm [27], which is controlled by the switching parameter Pa.
- (1)
- Local random walks can be written as
- (2)
- Global random walk flight using levy:
4. Proposed Method
To effectively solve the problem of selecting 3D printing process parameters, improve the mechanical properties of the parts, and reduce experimental costs, this paper proposes a process parameter optimization method that combines Kriging and CS. Latin hypercube sampling (LHS) is a method of approximating random sampling from multivariate parameter distributions and can ensure that each of the input variables has all portions of its range represented [28]. Therefore, LHS is used to generate a limited number of training and testing samples, and then, the mechanical strength of the printed specimens corresponding to each sample point is calculated through sample printing and performance experiments, thereby generating a Kriging training and testing sample set. At this point, in order to improve the recognition accuracy of the prediction model, the input sample data are normalized:
Here, is the input sample corresponding to the i-th set of process parameters; xmin and xmax are the minimum and maximum values of the sample. Based on the normalized sample data, a Kriging prediction model is established. By conducting a small number of experiments to generate a limited sample set, the experimental cost is reduced and the process design efficiency is improved. Combining the CS algorithm to search for the optimal process parameters and obtain the corresponding optimal mechanical properties, the specific process is shown in Figure 2, where the yellow part represents the establishment of the Kriging prediction model, and the blue part represents the parameter optimization by CS.
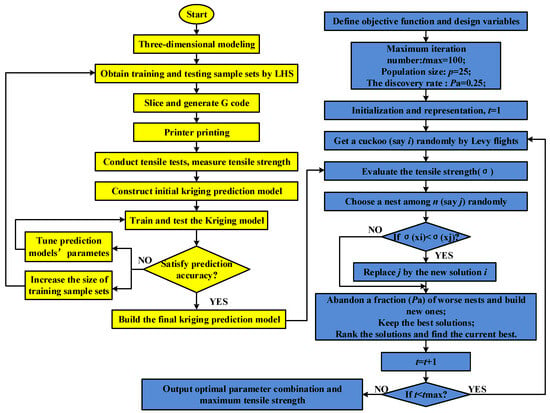
Figure 2.
Flow chart for optimizing FDM process parameters based on Kriging and CS.
5. Case Study
5.1. Experimental Process
PLA is a biodegradable thermoplastic polymer with good thermal stability. In this paper, the PLA filament (from Shenzhen Aurora Technology Co., Ltd., Shenzhen, China) was printed by a commercial 3D printing machine (from Aurora™). The experimental specimens were prepared according to ISO 527-1:2019 [29], and the specific parameters are illustrated in Figure 3. The printing temperature and printing speed were generated as research variables by LHS. The other printing parameters used in this paper are listed in Table 1.
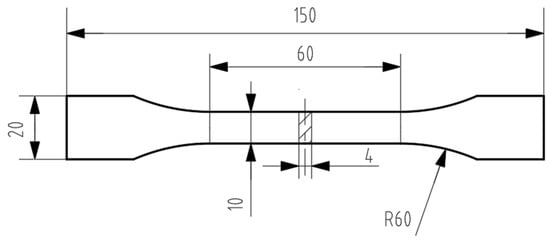
Figure 3.
Dog-bone-shaped specimens and dimensions.

Table 1.
Fixed FDM process parameters.
The tensile strength of various samples was measured using a Microcomputer controlled electronic universal testing machine (TEM104C, Shenzhen Wance Testing Machine Co., Ltd., Shenzhen, China), as shown in Figure 4. The load cell used was an American AiLogics force sensor (Model: DBSL-1t). And, the PLA specimens after tension are shown in Figure 5.

Figure 4.
Tensile test.

Figure 5.
PLA specimens after tension.
5.2. Result Analysis
Using printing speed and nozzle temperature as design variables, LHS was used to generate 40 sets of process parameter combinations. In total, 30 sets were randomly selected as training samples, and the remaining 10 sets were used as test samples to test the accuracy of the surrogate model. Three samples were printed for each set of process parameter combinations, and tensile experiments were conducted sequentially. The tensile strength was measured, and the average value was calculated. The experimental results are shown in Appendix A. According to the modeling process shown in Figure 2, a suitable Kriging prediction model was constructed using the MATLAB R2018a platform. Figure 6 shows the tensile strength response surface of the workpiece under different printing speeds and nozzle temperature combinations. It can be observed that for any given different process parameters (T and v) within a continuous interval, the corresponding tensile strength can be obtained on the response surface. Figure 7 illustrates the comparison between the output curve of the Kriging prediction model and that of the test samples, with a relative prediction error of 0.62%.
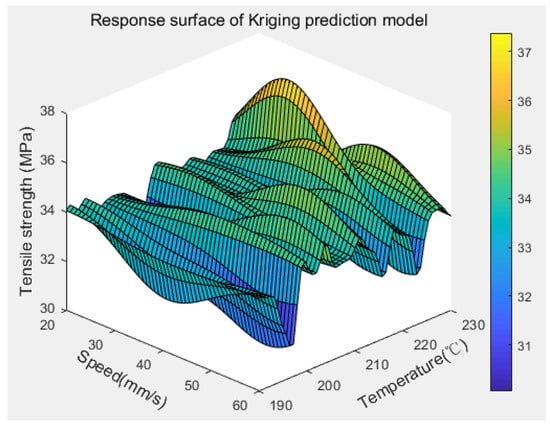
Figure 6.
Kriging response surface.
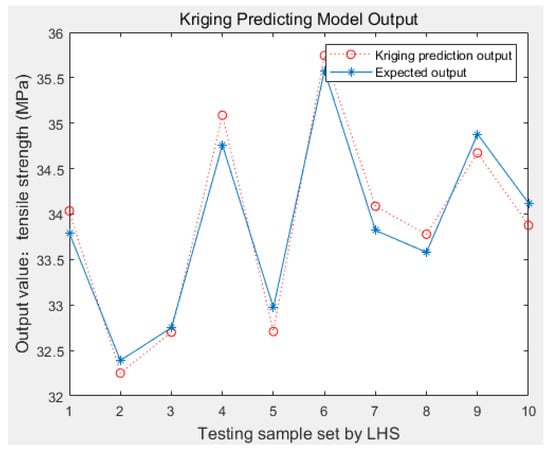
Figure 7.
The predicted and expected values of Kriging.
On the basis of Kriging response surface, with printing speed and nozzle temperature as design variables and maximizing the tensile strength of printed parts (minimizing the negative number of tensile strengths in this case) as the goal, combined with the CS algorithm for search and optimization, the convergence curve shown in Figure 8 was obtained. In CS, the discovery probability was 0.25, the population size was 25, and the maximum number of iterations was 100. The optimal result was that the printing speed was 31 mm/s, the printing temperature was 225 °C, and the corresponding tensile strength under this printing parameter combination was the maximum, with a value of 37.47 MPa.
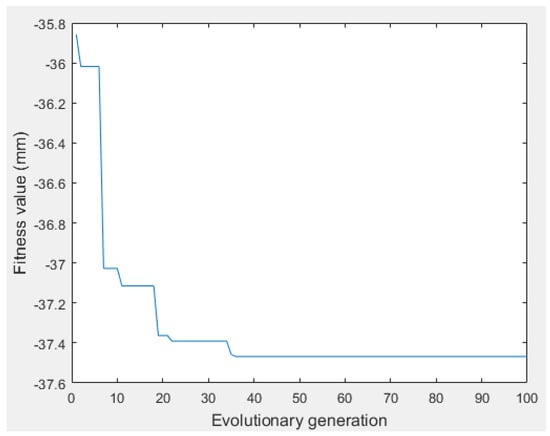
Figure 8.
Convergence curve of tensile strength by CS.
For the purpose of conducting further comparative analysis and validating the optimization outcome, experimental verification was performed on the tensile strength of PLA components under the optimal FDM process parameters. The comparison results are presented in Table 2, and it can be observed that the result acquired by the proposed method is in close conformity with that from the experiment, and the ultimately relative error (2.09%) falls within the scope of the common engineering accuracy precision (5%). The optimal strength (38.27 MPa) increased by about 12.7% compared to the average value (33.97 MPa) of 40 sets of experimental data.

Table 2.
Optimization results and validation.
6. Conclusions
In this paper, a methodology that integrates CS with Kriging for devising and majorizing the FDM process parameters was developed and verified. Compared with the majority of experimental approaches, the proposed surrogate model can effectively illustrate the impact of process parameters on the performance within a continuous range. The consequence of the project demonstrates that the proposed means is more effective, and it can cut down the experimental cost and enhance the efficiency of the optimization of FDM process parameters.
The optimal process parameters obtained in this paper were as follows: the printing velocity was 31 mm/s, the printing temperature was 225 °C, and the corresponding maximum tensile strength was 37.47 MPa. Meanwhile, thanks to the high degree of accuracy of the Kriging method and the CS as well as the merit of having few parameters that need to be finely adjusted, the proposed method has great capability and can be extended and used in the performance-improvement-oriented optimization of process parameters.
Author Contributions
Methodology, Y.Y.; Validation, B.X.; Formal analysis, B.Y.; Investigation, Y.Y., Y.W. and C.W.; Data curation, B.Y.; Writing—original draft, Y.Y. and Y.W.; Writing—review & editing, C.W.; Visualization, Y.W. and B.X.; Supervision, C.W. and B.Y.; Funding acquisition, Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the College Student Innovation and Entrepreneurship Training Program Project (Grant No. 138) and Key Lab. of Manufacturing Equipment of Shaanxi Province, (Grant No. JXZZZB-2022-05).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
The following gives the training and testing samples generated by Latin hypercube sampling and experimental measurements for the case study.

Table A1.
Training data set for Kriging.
Table A1.
Training data set for Kriging.
| No. | X | σ(X) (MPa) | |
|---|---|---|---|
| v (mm/s) | T (°C) | ||
| 1 | 34 | 196 | 31.97 |
| 2 | 54 | 223 | 31.83 |
| 3 | 48 | 205 | 33.79 |
| 4 | 40 | 211 | 34.91 |
| 5 | 56 | 199 | 34.55 |
| 6 | 28 | 216 | 34.25 |
| 7 | 52 | 204 | 35.29 |
| 8 | 49 | 218 | 34.88 |
| 9 | 35 | 220 | 34.43 |
| 10 | 42 | 222 | 35.76 |
| 11 | 25 | 209 | 34.68 |
| 12 | 22 | 194 | 34.22 |
| 13 | 40 | 200 | 34.82 |
| 14 | 53 | 226 | 34.62 |
| 15 | 60 | 195 | 32.15 |
| 16 | 28 | 225 | 37.22 |
| 17 | 44 | 213 | 33.95 |
| 18 | 37 | 228 | 34.65 |
| 19 | 21 | 191 | 34.18 |
| 20 | 32 | 208 | 34.39 |
| 21 | 35 | 219 | 33.58 |
| 22 | 30 | 207 | 33.56 |
| 23 | 44 | 228 | 35.77 |
| 24 | 55 | 197 | 30.71 |
| 25 | 25 | 225 | 36.55 |
| 26 | 39 | 192 | 31.69 |
| 27 | 47 | 211 | 35.63 |
| 28 | 49 | 202 | 33.8 |
| 29 | 58 | 216 | 32.44 |
| 30 | 23 | 205 | 29.97 |

Table A2.
Testing data set for Kriging.
Table A2.
Testing data set for Kriging.
| No. | X | σ(X) (MPa) | |
|---|---|---|---|
| v (mm/s) | T (°C) | ||
| 1 | 27 | 215 | 33.79 |
| 2 | 31 | 206 | 32.39 |
| 3 | 38 | 193 | 32.75 |
| 4 | 51 | 227 | 34.76 |
| 5 | 57 | 198 | 32.97 |
| 6 | 29 | 224 | 35.58 |
| 7 | 36 | 217 | 33.82 |
| 8 | 45 | 214 | 33.58 |
| 9 | 52 | 203 | 34.88 |
| 10 | 58 | 201 | 34.12 |
References
- Huang, S.H.; Liu, P.; Mokasdar, A.; Hou, L. Additive manufacturing and its societal impact: A literature review. Int. J. Adv. Manuf. Technol. 2013, 67, 1191–1203. [Google Scholar] [CrossRef]
- Conner, B.P.; Manogharan, G.P.; Martof, A.N.; Rodomsky, L.M.; Rodomsky, C.M.; Jordan, D.C.; Limperos, J.W. Making sense of 3-D printing: Creating a map of additive manufacturing products and services. Addit. Manuf. 2014, 1–4, 64–76. [Google Scholar] [CrossRef]
- Mengesha Medibew, T. A Comprehensive Review on the Optimization of the Fused Deposition Modeling Process Parameter for Better Tensile Strength of PLA-Printed Parts. Adv. Mater. Sci. Eng. 2022, 2022, 5490831. [Google Scholar] [CrossRef]
- Dey, A.; Yodo, N. A Systematic Survey of FDM Process Parameter Optimization and Their Influence on Part Characteristics. J. Manuf. Mater. Process. 2019, 3, 64. [Google Scholar] [CrossRef]
- Rodríguez-Reyna, S.L.; Mata, C.; Díaz-Aguilera, J.H.; Acevedo-Parra, H.R.; Tapia, F. Mechanical properties optimization for PLA, ABS and Nylon + CF manufactured by 3D FDM printing. Mater. Today Commun. 2022, 33, 104774. [Google Scholar] [CrossRef]
- Cheng, H.; Tang, M.; Zhang, J.; Wang, H.; Zhou, J.; Wang, Q.; Qian, Z. Effects of rCF attributes and FDM-3D printing parameters on the mechanical properties of rCFRP. Compos. Part B Eng. 2024, 270, 111122. [Google Scholar] [CrossRef]
- Portoacă, A.I.; Ripeanu, R.G.; Diniță, A.; Tănase, M. Optimization of 3D Printing Parameters for Enhanced Surface Quality and Wear Resistance. Polymers 2023, 15, 3419. [Google Scholar] [CrossRef]
- Pereira, R.J.R.; de Almeida, F.A.; Gomes, G.F. A multiobjective optimization parameters applied to additive manufacturing: DOE-based approach to 3D printing. Structures 2023, 55, 1710–1731. [Google Scholar] [CrossRef]
- Alzyod, H.; Borbas, L.; Ficzere, P. Rapid prediction and optimization of the impact of printing parameters on the residual stress of FDM-ABS parts using L27 orthogonal array design and FEA. Mater. Today Proc. 2023, 93, 583–588. [Google Scholar] [CrossRef]
- Wang, S.; Ma, Y.; Deng, Z.; Zhang, S.; Cai, J. Effects of fused deposition modeling process parameters on tensile, dynamic mechanical properties of 3D printed polylactic acid materials. Polym. Test. 2020, 86, 106483. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Sadeghian, H.; Ayatollahi, M.R.; Reinicke, T. Optimization of fracture toughness in 3D-printed parts: Experiments and numerical simulations. Compos. Struct. 2024, 329, 117766. [Google Scholar] [CrossRef]
- Algarni, M. Tensile strength and strain behavior study and modeling of PLA printed parts with optimized AM parameters. Procedia Struct. Integr. 2023, 51, 185–191. [Google Scholar] [CrossRef]
- Huang, B.; Meng, S.; He, H.; Jia, Y.; Xu, Y.; Huang, H. Study of processing parameters in fused deposition modeling based on mechanical properties of acrylonitrile-butadiene-styrene filament. Polym. Eng. Sci. 2019, 59, 120–128. [Google Scholar] [CrossRef]
- Mani, M.; Karthikeyan, A.G.; Kalaiselvan, K.; Muthusamy, P.; Muruganandhan, P. Optimization of FDM 3-D printer process parameters for surface roughness and mechanical properties using PLA material. Mater. Today Proc. 2022, 66, 1926–1931. [Google Scholar] [CrossRef]
- Sahoo, S.; Sutar, H.; Senapati, P.; Mohanto, B.S.; Dhal, P.R.; Baral, S.K. Experimental investigation and optimization of the FDM process using PLA. Mater. Today Proc. 2023, 74, 843–847. [Google Scholar] [CrossRef]
- Kafshgar, A.R.; Rostami, S.; Aliha, M.R.M.; Berto, F. Optimization of Properties for 3D Printed PLA Material Using Taguchi, ANOVA and Multi-Objective Methodologies. Procedia Struct. Integr. 2021, 34, 71–77. [Google Scholar] [CrossRef]
- Long, Y.; Zhang, Z.; Yan, C.; Huang, Z.; Fu, K.; Li, Y. Multi-objective optimization for improving printing efficiency and mechanical properties of 3D-printed continuous plant fibre composites. Compos. Commun. 2022, 35, 101283. [Google Scholar] [CrossRef]
- Fountas, N.A.; Papantoniou, I.; Kechagias, J.D.; Manolakos, D.E.; Vaxevanidis, N.M. Modeling and optimization of flexural properties of FDM-processed PET-G specimens using RSM and GWO algorithm. Eng. Fail. Anal. 2022, 138, 106340. [Google Scholar] [CrossRef]
- Patil, P.; Singh, D.; Raykar, S.J.; Bhamu, J. Multi-objective optimization of process parameters of Fused Deposition Modeling (FDM) for printing Polylactic Acid (PLA) polymer components. Mater. Today Proc. 2021, 45, 4880–4885. [Google Scholar] [CrossRef]
- Dusanapudi, S.; Krupakaran, R.L.; Srinivas, A.; Nikhil, K.S.; Vamshi, T. Optimization and experimental analysis of mechanical properties and porosity on FDM based 3D printed ABS sample. Mater. Today Proc. 2023; in press. [Google Scholar] [CrossRef]
- Singh, J.; Goyal, K.K.; Kumar, R.; Gupta, V. Development of artificial intelligence-based neural network prediction model for responses of additive manufactured polylactic acid parts. Polym. Compos. 2022, 43, 5623–5639. [Google Scholar] [CrossRef]
- Poonia, V.; Kumar, R.; Kulshrestha, R.; Sangwan, K.S. Optimization of Specific Energy, Scrap, and Surface Roughness in 3D Printing Using Integrated ANN-GA Approach. Procedia CIRP 2023, 116, 324–329. [Google Scholar] [CrossRef]
- Yang, B.; Wang, Z.; Yang, Y.; Kang, Y.; Li, X. Optimum fixture locating layout for sheet metal part by integrating kriging with cuckoo search algorithm. Int. J. Adv. Manuf. Technol. 2017, 91, 327–340. [Google Scholar] [CrossRef]
- Yang, B.; Wang, Z.; Yang, Y.; Kang, Y.; Li, C. Optimization of fixture locating layout for sheet metal part by cuckoo search algorithm combined with finite element analysis. Adv. Mech. Eng. 2017, 9, 168781401770483. [Google Scholar] [CrossRef]
- Yang, Y.; Dai, X.; Yang, B.; Zou, P.; Gao, F.; Duan, J.; Wang, C. Optimization of polylactic acid 3D printing parameters based on support vector regression and cuckoo search. Polym. Eng. Sci. 2023, 63, 3243–3253. [Google Scholar] [CrossRef]
- Nielsen, H.B.; Lophaven, S.N.; Sondergaard, J. DACE, a MATLAB Kriging Toolbox. Informatics and Mathematical Modelling; Technical University of Denmark, DTU: Lyngby, Denmark, 2002. [Google Scholar]
- Yang, X.S.; Deb, S. Engineering optimisation by cuckoo search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330–343. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A compari son of three methods for selecting values of input vari ables in the analysis of output from a computer code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- ISO 527-1-2019; Plastics—Determination of Tensile Properties—Part 1: General Principles. ISO: Geneva, Switzerland, 2019.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).