End-to-End Deep-Learning-Based Surrogate Modeling for Supersonic Airfoil Shape Optimization
Abstract
1. Introduction
- a novel, end-to-end DL-based SM trained on openly accessible subsonic and transonic airfoil geometric data to predict aerodynamic coefficients from airfoil coordinates, for guiding the optimization routine in supersonic conditions;
- an InfoGAN trained to represent an aerodynamically valid design space that includes shapes suited for subsonic, transonic and supersonic conditions;
- a modular, real-time-capable optimization framework that integrates the SM with the generative design space representation, enabling rapid ASO for supersonic conditions.
2. Methodology
2.1. Overview
2.2. Airfoil Geometry Parameterization
2.3. Aerodynamic Coefficients Surrogate Modeling
2.4. Optimization Algorithm
3. Numerical Results and Discussion
3.1. Problem Formulation
3.2. DL Models Development
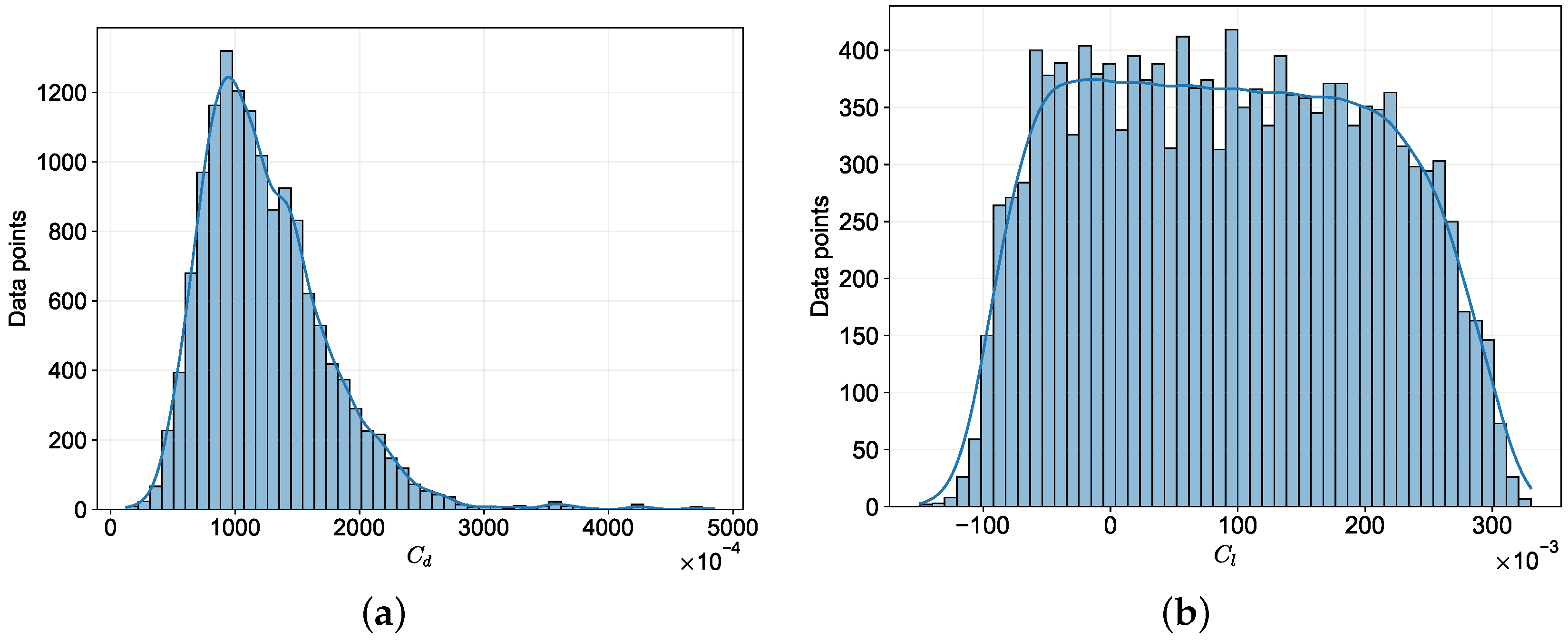
3.2.1. Data Collection
3.2.2. Dataset Splitting
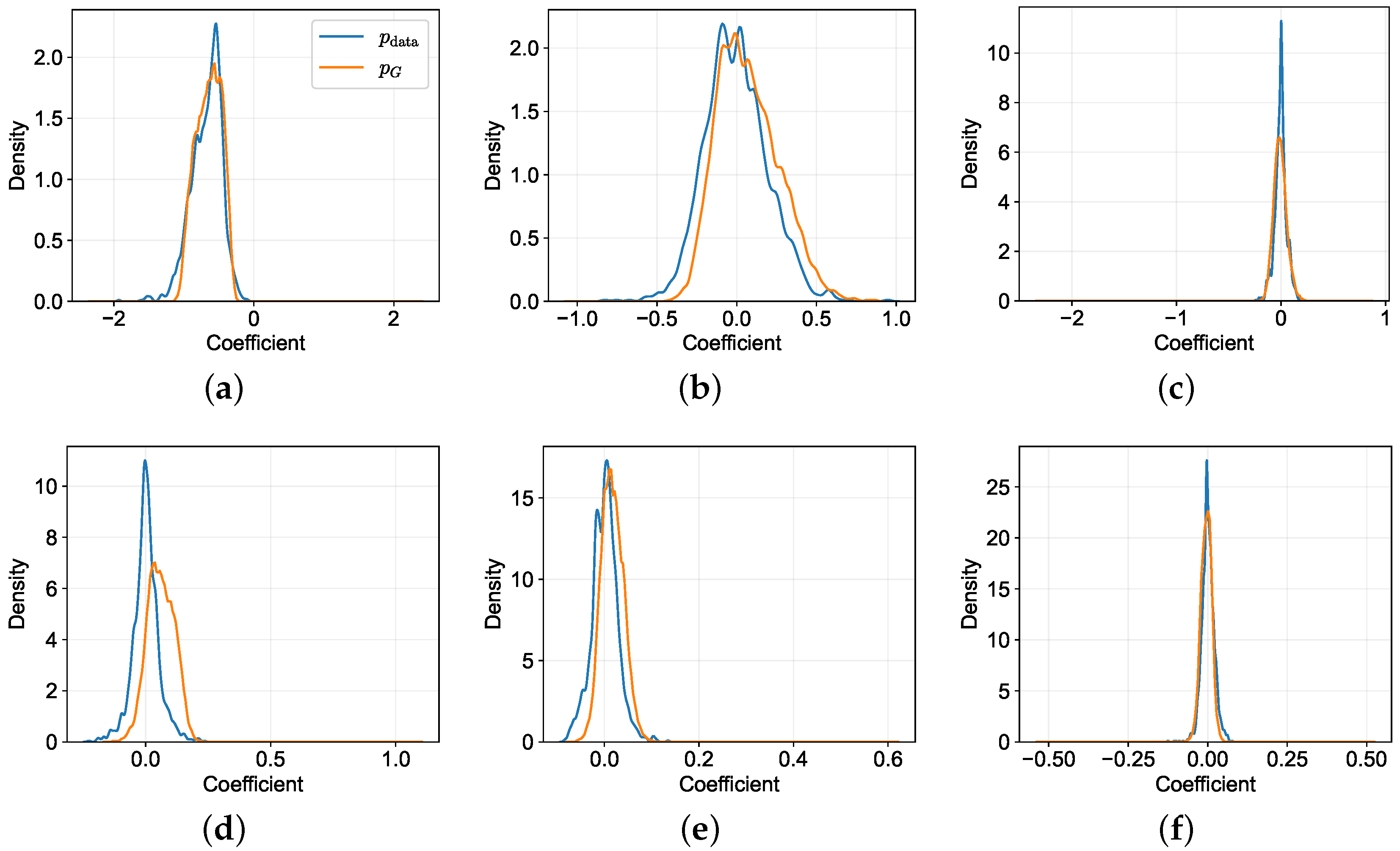
3.2.3. InfoGAN Training
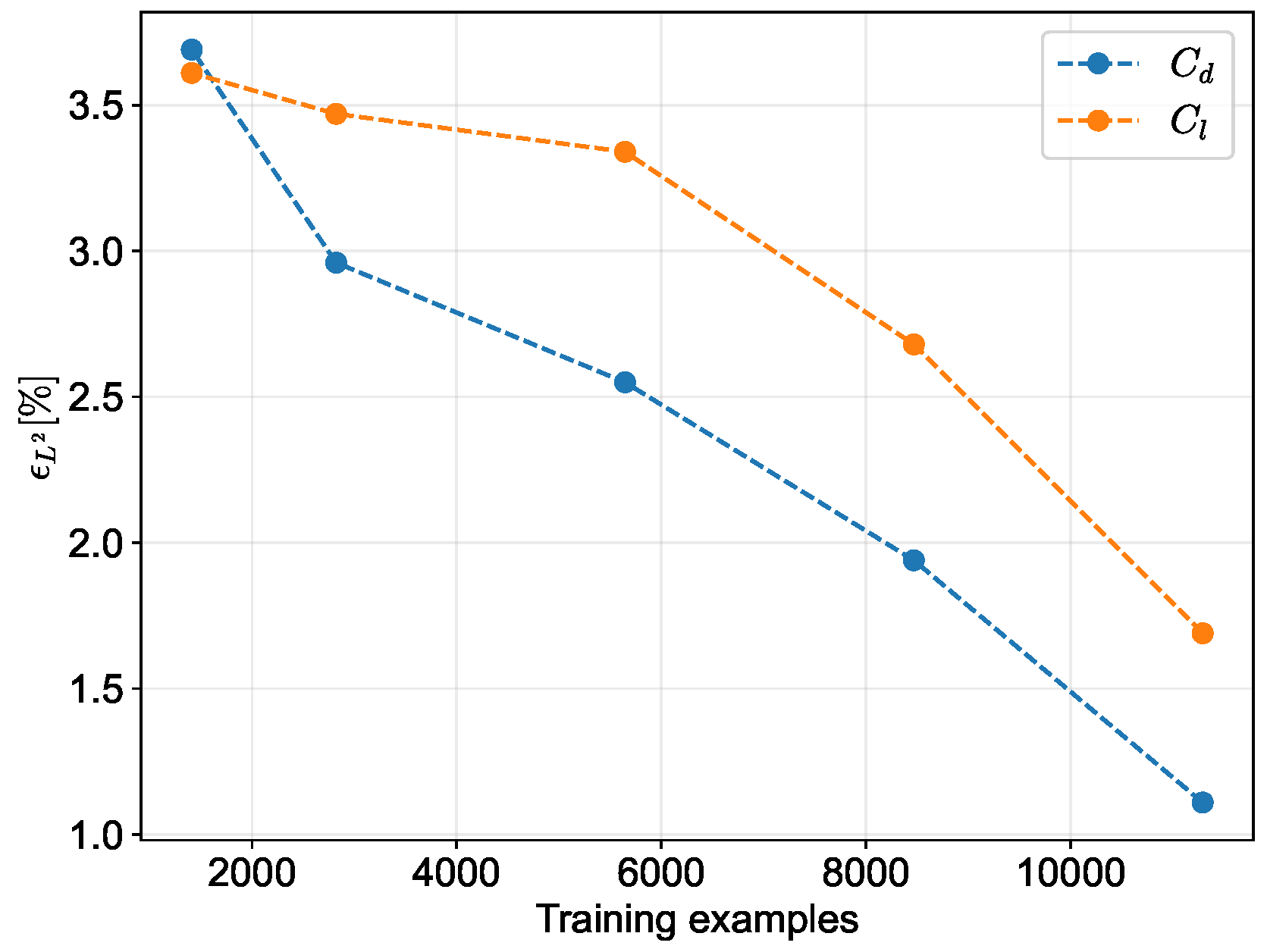
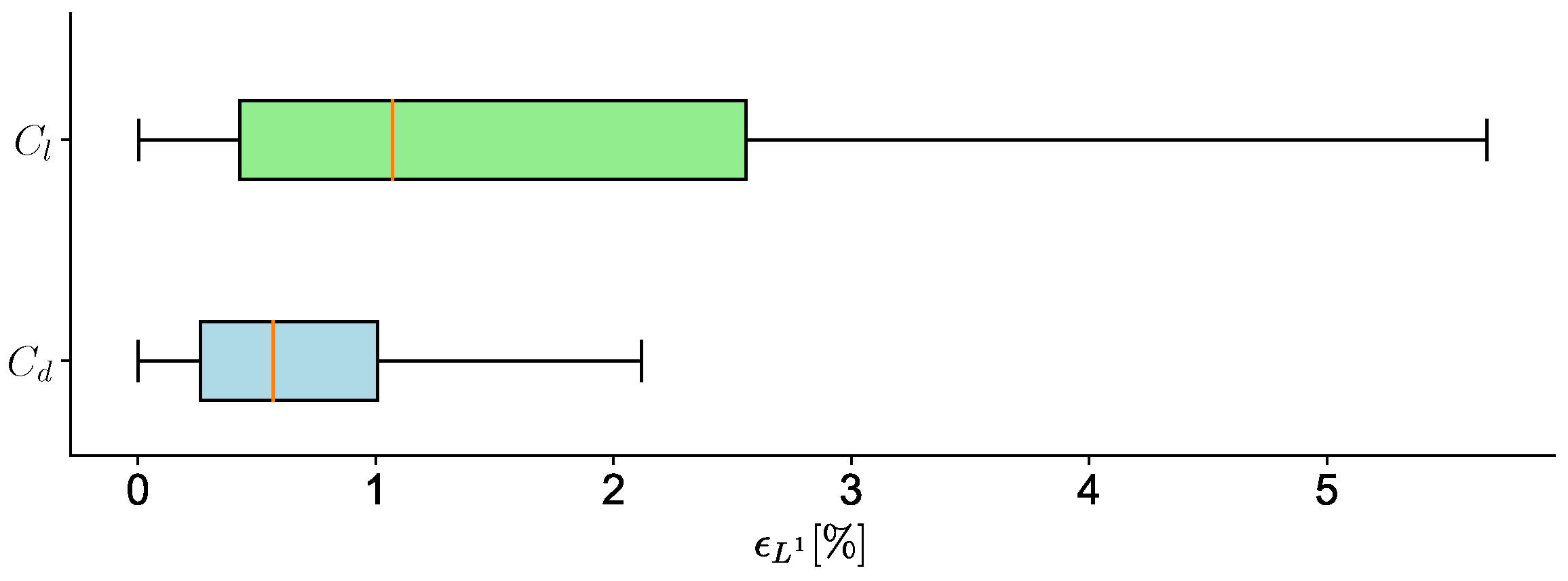
3.2.4. SM Training
3.3. GA Development
3.4. Aerodynamic Drag Minimization
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jameson, A.; Vassberg, J. Computational Fluid Dynamics for Aerodynamic Design: Its Current and Duture Impact. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001. [Google Scholar] [CrossRef]
- Li, J.; Du, X.; Martins, J.R. Machine learning in aerodynamic shape optimization. Prog. Aerosp. Sci. 2022, 134, 100849. [Google Scholar] [CrossRef]
- Peng, W.; Zhang, Y.; Desmarais, M. Deep neural network for airfoil optimization. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA and Virtual, 3–7 January 2022. [Google Scholar] [CrossRef]
- Martins, J.R.R.A.; Ning, A. Engineering Design Optimization; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar] [CrossRef]
- He, X.; Li, J.; Mader, C.A.; Yildirim, A.; Martins, J.R. Robust aerodynamic shape optimization–From a circle to an airfoil. Aerosp. Sci. Technol. 2019, 87, 48–61. [Google Scholar] [CrossRef]
- Chen, W.; Chiu, K.; Fuge, M.D. Airfoil Design Parameterization and Optimization using Bézier Generative Adversarial Networks. AIAA J. 2020, 58, 4723–4735. [Google Scholar] [CrossRef]
- Du, X.; He, P.; Martins, J.R. Rapid airfoil design optimization via neural networks-based parameterization and surrogate modeling. Aerosp. Sci. Technol. 2021, 113, 106701. [Google Scholar] [CrossRef]
- Masters, D.A.; Taylor, N.J.; Rendall, T.C.S.; Allen, C.B.; Poole, D.J. Geometric Comparison of Aerofoil Shape Parameterization Methods. AIAA J. 2017, 55, 1575–1589. [Google Scholar] [CrossRef]
- Toal, D.J.; Bressloff, N.W.; Keane, A.J.; Holden, C.M. Geometric Filtration Using Proper Orthogonal Decomposition for Aerodynamic Design Optimization. AIAA J. 2010, 48, 916–928. [Google Scholar] [CrossRef]
- Poole, D.J.; Allen, C.B.; Rendall, T.C. Metric-Based Mathematical Derivation of Efficient Airfoil Design Variables. AIAA J. 2015, 53, 1349–1361. [Google Scholar] [CrossRef]
- Li, J.; Bouhlel, M.A.; Martins, J.R.R.A. Data-Based Approach for Fast Airfoil Analysis and Optimization. AIAA J. 2019, 57, 581–596. [Google Scholar] [CrossRef]
- Bouhlel, M.A.; He, S.; Martins, J.R. Scalable gradient–enhanced artificial neural networks for airfoil shape design in the subsonic and transonic regimes. Struct. Multidiscip. Optim. 2020, 61, 1363–1376. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M. Data-based approach for wing shape design optimization. Aerosp. Sci. Technol. 2021, 112, 106639. [Google Scholar] [CrossRef]
- Yonekura, K.; Suzuki, K. Data-driven design exploration method using conditional variational autoencoder for airfoil design. Struct. Multidiscip. Optim. 2021, 64, 613–624. [Google Scholar] [CrossRef]
- Wang, Y.; Shimada, K.; Farimani, A.B. Airfoil GAN: Encoding and Synthesizing Airfoils for Aerodynamic-aware Shape Optimization. arXiv 2021, arXiv:2101.04757. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M.; Tay, C.M.J.; Liu, N.; Cui, Y.; Chew, S.C.; Khoo, B.C. Low-Reynolds-number airfoil design optimization using deep-learning-based tailored airfoil modes. Aerosp. Sci. Technol. 2022, 121, 107309. [Google Scholar] [CrossRef]
- Li, J.; He, S.; Martins, J.R. Data-driven constraint approach to ensure low-speed performance in transonic aerodynamic shape optimization. Aerosp. Sci. Technol. 2019, 92, 536–550. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M.; Martins, J.R.; Shu, C. Efficient Aerodynamic Shape Optimization with Deep-Learning-Based Geometric Filtering. AIAA J. 2020, 58, 4243–4259. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M. On deep-learning-based geometric filtering in aerodynamic shape optimization. Aerosp. Sci. Technol. 2021, 112, 106603. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M. Adjoint-Free Aerodynamic Shape Optimization of the Common Research Model Wing. AIAA J. 2021, 59, 1990–2000. [Google Scholar] [CrossRef]
- Krige, D.G. A statistical approach to some basic mine valuation problems on the Witwatersrand. J. S. Afr. Inst. Min. Metall. 1951, 52, 119–139. [Google Scholar]
- Laurenceau, J.; Sagaut, P. Building Efficient Response Surfaces of Aerodynamic Functions with Kriging and Cokriging. AIAA J. 2008, 46, 498–507. [Google Scholar] [CrossRef]
- Han, Z.H.; Görtz, S. Hierarchical Kriging Model for Variable-Fidelity Surrogate Modeling. AIAA J. 2012, 50, 1885–1896. [Google Scholar] [CrossRef]
- Nagawkar, J.; Leifsson, L.T.; Du, X. Applications of Polynomial Chaos-Based Cokriging to Aerodynamic Design Optimization Benchmark Problems. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Zhang, X.; Xie, F.; Ji, T.; Zhu, Z.; Zheng, Y. Multi-fidelity deep neural network surrogate model for aerodynamic shape optimization. Comput. Methods Appl. Mech. Eng. 2021, 373, 113485. [Google Scholar] [CrossRef]
- Zhang, Y.; Sung, W.J.; Mavris, D.N. Application of Convolutional Neural Network to Predict Airfoil Lift Coefficient. In Proceedings of the 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Peng, W.; Zhang, Y.; Desmarais, M. Spatial Convolution Neural Network for Efficient Prediction of Aerodynamic Coefficients. In Proceedings of the AIAA Scitech 2021 Forum, Virtual Event, 11–21 January 2021. [Google Scholar] [CrossRef]
- Selig, M. UIUC Airfoil Data Site. 1996. Available online: https://m-selig.ae.illinois.edu/ads.html (accessed on 30 May 2023).
- Sekar, V.; Zhang, M.; Shu, C.; Khoo, B.C. Inverse Design of Airfoil Using a Deep Convolutional Neural Network. AIAA J. 2019, 57, 993–1003. [Google Scholar] [CrossRef]
- Du, X.; Martins, J.R.; O’Leary-Roseberry, T.; Chaudhuri, A.; Ghattas, O.; Willcox, K.E. Learning Optimal Aerodynamic Designs through Multi-Fidelity Reduced-Dimensional Neural Networks. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA and Online, 23–27 January 2023. [Google Scholar] [CrossRef]
- Chen, X.; Duan, Y.; Houthooft, R.; Schulman, J.; Sutskever, I.; Abbeel, P. InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets. In Proceedings of the 30th International Conference on Neural Information Processing Systems (NIPS 2016), Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Lambe, A.B.; Martins, J.R. Extensions to the design structure matrix for the description of multidisciplinary design, analysis, and optimization processes. Struct. Multidiscip. Optim. 2012, 46, 273–284. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Martins, J.R. Aerodynamic design optimization: Challenges and perspectives. Comput. Fluids 2022, 239, 105391. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on International Conference on Machine Learning (ICML’15), Lille, France, 6–11 July 2015. [Google Scholar]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier nonlinearities improve neural network acoustic models. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef]
- Yeniay, Ö. Penalty Function Methods for Constrained Optimization with Genetic Algorithms. Math. Comput. Appl. 2005, 10, 45–56. [Google Scholar] [CrossRef]
- Secco, N.R.; Kenway, G.K.W.; He, P.; Mader, C.; Martins, J.R.R.A. Efficient Mesh Generation and Deformation for Aerodynamic Shape Optimization. AIAA J. 2021, 59, 1151–1168. [Google Scholar] [CrossRef]
- Yildirim, A.; Kenway, G.K.; Mader, C.A.; Martins, J.R. A Jacobian-free approximate Newton–Krylov startup strategy for RANS simulations. J. Comput. Phys. 2019, 397, 108741. [Google Scholar] [CrossRef]
- Mader, C.A.; Kenway, G.K.W.; Yildirim, A.; Martins, J.R.R.A. ADflow: An Open-Source Computational Fluid Dynamics Solver for Aerodynamic and Multidisciplinary Optimization. J. Aerosp. Inf. Syst. 2020, 17, 508–527. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef]
- Palaniappan, K.; Jameson, A. An Analysis of Bodies Having Minimum Pressure Drag in Supersonic Flow: Exploring the Nonlinear Domain. In Proceedings of the Computational Fluid Dynamics 2004: Proceedings of the Third International Conference on Computational Fluid Dynamics, ICCFD3, Toronto, ON, Canada, 12–16 July 2004. [Google Scholar] [CrossRef]
- Siegler, J.; Ren, J.; Leifsson, L.; Koziel, S.; Bekasiewicz, A. Supersonic airfoil shape optimization by variable-fidelity models and manifold mapping. Procedia Comput. Sci. 2016, 80, 1103–1113. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks. arXiv 2016, arXiv:1511.06434. [Google Scholar] [CrossRef]
- Jarrett, K.; Kavukcuoglu, K.; Ranzato, M.; LeCun, Y. What is the best multi-stage architecture for object recognition? In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision (ICCV), Kyoto, Japan, 29 September–2 October 2009. [Google Scholar]
- Gretton, A.; Borgwardt, K.M.; Rasch, M.J.; Schölkopf, B.; Smola, A. A kernel two-sample test. J. Mach. Learn. Res. 2012, 13, 723–773. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the 30th Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 4–9 December 2019. [Google Scholar]
- Lepine, J.; Guibault, F.; Trepanier, J.Y.; Pepin, F. Optimized Nonuniform Rational B-Spline Geometrical Representation for Aerodynamic Design of Wings. AIAA J. 2001, 39, 2033–2041. [Google Scholar] [CrossRef]
- Wang, Q.; Ma, Y.; Zhao, K.; Tian, Y. A Comprehensive Survey of Loss Functions in Machine Learning. Ann. Data Sci. 2022, 9, 187–212. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic Gradient Descent with Warm Restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar] [CrossRef]
- Anderson, J.D. Fundamentals of Aerodynamics; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Gad, A.F. PyGAD: An Intuitive Genetic Algorithm Python Library. arXiv 2021, arXiv:2106.06158. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- Kraft, D. A Software Package for Sequential Quadratic Programming; Technical Report DFVLR-FB 88-28; Deutsche Forschungs- und Versuchsanstalt für Luft- und Raumfahrt: Bavaria, Germany, 1988. [Google Scholar]
- Sederberg, T.W.; Parry, S.R. Free-Form Deformation of Solid Geometric Models. In Proceedings of the 13th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH 86, New York, NY, USA, 18–22 August 1986; pp. 151–160. [Google Scholar] [CrossRef]
- Kenway, G.K.; Mader, C.A.; He, P.; Martins, J.R. Effective adjoint approaches for computational fluid dynamics. Prog. Aerosp. Sci. 2019, 110, 100542. [Google Scholar] [CrossRef]









| Nodes in Off-Wall Direction | Number of Cells | Counts | Counts | Extrapolated Relative Error | CPU Time [s] |
|---|---|---|---|---|---|
| 2048 | 499,468 | 55.07 | 973.7 | 0.01% | 2.4 × |
| 512 | 124,684 | 55.09 | 974.0 | 0.04% | 2.3 × |
| 128 | 30,988 | 55.14 | 975.9 | 0.23% | 8.7 × |
| Richardson extrapolation | - | 973.2 | - | - | |
| Study | Model | Flight Condition | Training Samples | Modeling Variables | Application | Results RMSE (Counts) | NRMSE | |
|---|---|---|---|---|---|---|---|---|
| Nagawkar et al. [24] | PC-Cokriging | Transonic | 1074 | 8 | - | 6.00 | 2.5% | |
| Subsonic | 81,000 | 16 | 0.26 %, 0.15% | - | - | |||
| Li et al. [11] | GE-KPLS | Transonic | 32,400 | 10 | , | 0.83%, 0.40% | - | - |
| Subsonic | 42,039 | 16 | 0.32%, 0.19% | - | - | |||
| Bouhlel et al. [12] | MLP | Transonic | 4120 | 10 | , | 0.48%, 0.28% | - | - |
| Subsonic | 45,696 | 29 | 2.26%, 2.34% | 2.77, 12.90 | 0.9%, 0.9% | |||
| Du et al. [7] | MLP | Transonic | 39,505 | 29 | , | 4.65%, 2.87% | 8.76, 16.13 | 1.5%, 1.5% |
| Zhang et al. [26] | CNN | Transonic | 1600 | 2403 | - | 70.71 | - | |
| Proposed | CNN | Supersonic | 11,290 | 257 | , | 1.11%, 1.69% | 15.50, 2.42 | 0.4%, 0.5% |
| Configuration | Test MSE | Number of Parameters |
|---|---|---|
| MLP | 1.20 × | 0.077 M |
| CNN + Pooling | 6.70 × | 0.630 M |
| Early fusion | 5.54 × | 1.450 M |
| Without residual | 1.41 × | 0.474 M |
| Proposed | 4.73 × | 0.507 M |
| (Counts) | |||||||
|---|---|---|---|---|---|---|---|
| Optimal Airfoil | Theory | CFD | SM | Theory | CFD | SM | |
| Biconvex | 4.82° | 0.194 | 0.200 | 0.193 | 465.5 | 483.6 | 487.9 |
| CFD | 4.99° | 0.201 | 0.200 | 0.200 | 600.0 | 473.2 | 432.8 |
| SM | 5.44° | 0.219 | 0.200 | 0.207 | 572.4 | 482.1 | 400.2 |
| Optimal Aerofoil | Theory | SM | Theory | SM |
|---|---|---|---|---|
| Biconvex | −3.00% | −3.50% | −3.74% | 0.89% |
| CFD | 0.50% | 0.00% | 26.80% | −8.54% |
| SM | 9.50% | 3.50% | 18.73% | −16.99% |
| Optimal Airfoil | (Counts) | Deviation | CPU Time [s] | CPU Time Deviation |
|---|---|---|---|---|
| CFD | 473.2 | - | 5.8 × | - |
| SM | 482.1 | 1.88% | 1.9 × | −99.97% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereira, D.; Afonso, F.; Lau, F. End-to-End Deep-Learning-Based Surrogate Modeling for Supersonic Airfoil Shape Optimization. Aerospace 2025, 12, 389. https://doi.org/10.3390/aerospace12050389
Pereira D, Afonso F, Lau F. End-to-End Deep-Learning-Based Surrogate Modeling for Supersonic Airfoil Shape Optimization. Aerospace. 2025; 12(5):389. https://doi.org/10.3390/aerospace12050389
Chicago/Turabian StylePereira, Diogo, Frederico Afonso, and Fernando Lau. 2025. "End-to-End Deep-Learning-Based Surrogate Modeling for Supersonic Airfoil Shape Optimization" Aerospace 12, no. 5: 389. https://doi.org/10.3390/aerospace12050389
APA StylePereira, D., Afonso, F., & Lau, F. (2025). End-to-End Deep-Learning-Based Surrogate Modeling for Supersonic Airfoil Shape Optimization. Aerospace, 12(5), 389. https://doi.org/10.3390/aerospace12050389







