Abstract
In response to the rapid growth of air passenger and cargo transportation services and the sharp increase in congestion at various airports, it is necessary to optimize the allocation of flight schedules. On the basis of reducing the total airport delay time and ensuring the total deviation of flight schedules applied by airlines, it is necessary to consider finely configuring flight schedules with slot coordination parameters, introducing a 5 min slot coordination parameter, and optimizing airport flight schedules in different time periods. This article considers factors such as flight schedule uniqueness, corridor flow restrictions, and time adjustment range limitations to establish a three-objective flight-schedule refinement configuration model, which is solved using the NSGA-II algorithm based on the entropy weight method. Taking Beijing Capital International Airport as an example, the optimized results show that the total flight delay was reduced from 4130 min to 1142 min, and the original delay of 389 flights was reduced to 283 flights. Therefore, flight schedule optimization considering the fine-grained configuration of slot coordination parameters can effectively reduce airport delays, fully utilize time resources, and reduce waste of time slot resources.
1. Introduction
Airports providing commercial passenger services can be categorized into three classes based on their congestion levels [1]. Level 1 airports are characterized by “airport infrastructure capacity generally being sufficient to meet user demand”. Level 2 airports may experience congestion at certain times of the day, week, or season, which can be managed through schedule adjustments agreed upon by airlines and service providers. Level 3 airports require all airlines and other aircraft operators to obtain slots allocated by a coordinator to arrive or depart during the slot allocation periods. Level 3 airports, also known as coordinated airports, necessitate the establishment of slot coordination parameters for slot allocation. Slot coordination parameters refer to the number of flight slots that can be allocated within a specific hour or 15 min interval, within the airport’s capacity standards [2].
With the continuous development of China’s economy and the vigorous promotion of the construction of a strong civil aviation nation, the demand for civil aviation travel among the populace is gradually increasing. Consequently, the passenger throughput and the number of flight movements at transportation airports are also increasing year by year. According to the “2023 Civil Aviation Industry Development Statistical Bulletin” issued by the Civil Aviation Administration of China, in 2023, the passenger throughput of Chinese civil aviation transportation airports reached 1.26 billion passengers, representing a 142.2% increase compared to the previous year. The number of flight movements reached 11.71 million, a 63.7% increase over the previous year. The civil aviation industry maintains a strategic development approach of “controlling total volume and adjusting structure” to ensure the steady progress of the industry. However, China’s civil aviation industry also faces many challenges, such as limited airport support capabilities, constrained air route resources, the uneven regional development of the aviation industry, a shortage of flight slots at busy airports, and severe flight delays. Due to the limited resources of flight slots, airport operational support capabilities, and airport capacity within a certain period, the increase in the number of airport flights correspondingly prolongs flight delay times, reducing the operational efficiency of airports.
In the context of resource scarcity, flight slot optimization is a feasible and effective method to reduce flight delays and improve airport operational efficiency. Through flight slot optimization, airport resources and flight slots can be utilized reasonably and efficiently, preemptively alleviating periods that may cause flight delays, thereby enhancing the operational efficiency of air traffic. Against this backdrop, this paper takes Beijing Capital International Airport as an example to conduct an optimization study of flight slots based on the airport’s operational capabilities and delay characteristics. The significance of this study is as follows:
Theoretical Value: busy airports exhibit distinct temporal characteristics and peak periods for flight arrivals and departures. By analyzing flight delay characteristics and considering constraints such as airport capacity, operational capabilities, and connectivity capabilities, a scientifically constructed flight slot optimization model provides a reference for adjusting the flight slot resources of busy airports.
Practical Value: currently, major busy airports commonly face flight delay issues. Reasonable adjustments to airport flight slots can alleviate delay problems, reduce losses for airlines, decrease congestion during air traffic peak periods, and lessen the workload of air traffic controllers. This paper conducts a statistical analysis on the planned flight resource allocation and actual operational flight data of Beijing Capital International Airport, constructing a targeted flight slot optimization model to reduce delays caused by unreasonable flight schedules and improve airport operational efficiency.
2. Literature Review
Internationally, the primary method for flight slot allocation is slot coordination, which aims to strategically align airports, air traffic control units, and airlines to achieve an optimal balance between demand and capacity. To enable the global aviation industry to utilize a unified standard for managing and coordinating airport slot resources, the International Air Transport Association (IATA), Airports Council International (ACI), and the Worldwide Airport Coordinators Group (WWACG) jointly issued the Worldwide Airport Slot Guidelines (WASG). This guideline, renamed from the Worldwide Slot Guidelines (WSG) in 2020, has been applied to major aviation hub airports globally. The latest edition updates the definitions of airport classifications, demand-capacity management, and slot allocation principles [3]. Jacquillat combined the primary interventions for managing airport demand and capacity, fundamental policies, analytical tools for managerial and operational decisions, as well as policy and practice guidelines derived from recent research, yielding three types of insights. These include the dependence of airport capacity on available infrastructure and operational procedures, sensitivity to demand and capacity variations, the impact of scheduling mechanisms on existing practices, and a perspective on the development and management of global airport systems [4].
In China, the Civil Aviation Administration of China (CAAC) first announced the hourly capacity standards and coordinated time periods for 21 domestic coordinated airports on 1 November 2011. In April 2018, the CAAC released the Flight Slot Management Measures, which clarified the slot coordination parameters, including the number of flight slots available within an hour or 15 min interval [5], thereby institutionalizing and standardizing slot management. Subsequently, Wang Wei [6], Pan Weijun [7], and Wang Yanjun [8] explored the general characteristics and rules of airport slot resource allocation, proposed flight slot allocation processes, and elaborated on slot coordination parameters. Their research primarily employed administrative methods, examining methods for slot resource allocation and presenting key technical issues related to slot resource optimization and allocation across single airports, multiple airports, and airport clusters. Zhou Shibo [9], Feng Huilin [10], and Tang Xiaoyi [11] divided flight slot allocation into primary and secondary market allocations, summarizing optimization models for primary market allocation based on administrative distribution and two market-based primary market allocation methods: slot auctions and congestion pricing.
The primary objective of flight slot optimization is to alleviate the transportation pressure during peak hours at large, busy airports by optimizing flight schedules, effectively utilizing limited spatio-temporal resources, and improving operational efficiency. The earliest flight slot optimization methods were considered in conjunction with ground holding strategies. By altering the planned departure times of flights, ground holding strategies were used to replace predictable in-flight delays in cases where delays were unavoidable. As the research on slot allocation and optimization technologies deepened, scholars domestically and internationally established flight slot optimization models from various perspectives based on different optimization goals, building on the foundation of ground holding strategies.
Stojkovic proposed a model for optimizing flight slots, which can be used to solve real-time problems with linear, piecewise convex, or smooth convex objective functions for the largest airlines [12]. Zografos attempted to allocate slot resources at congested airports and optimized slot allocation using a linear relaxation algorithm for integer programming problems. By minimizing the discrepancy between requested and allocated slots, the model better adapted coordinated airports to airline preferences. A sensitivity analysis of the model’s results highlighted the importance of slot coordination parameters and their impact on allocation efficiency [13]. Ribeiro proposed a multi-objective, priority-based slot allocation model (PSAM). This model provides optimal slot allocation solutions for large airports while adhering to the priorities stipulated by IATA guidelines and the capacity limits published by airports [14]. Subsequently, Jorge built an optimization-based decision support tool on the foundation of Ribeiro’s PSAM to assist slot coordinators in primary slot allocation [15]. Dixit proposed a game-theoretic model and designed a mechanism design solution for fair slot allocation at congested airports [16].
Research on flight slot optimization in China started relatively late. Scholars such as Yang Xinhai [17,18], Feng Xin [19], Wang Mengdie [20], Xu Chen [21], Ke Yuchen [22], and Zuo Jiejun [23] established flight scheduling models based on route networks and flight slots, minimum costs, the benefits of domestic and international flights, and flight transfer efficiency. They used genetic algorithms, improved squeaky wheel optimization, particle swarm optimization, and other methods to optimize flight slot allocation.
Currently, research related to flight slot allocation is still in its initial stages. Slot coordination parameters are divided into only two units (1 h and 15 min), with six reference parameters, such as arrivals and departures, considered throughout the day, which is relatively simplistic. This paper proposes a refined division of airport slot coordination parameters, increasing the division units to three by adding a 5 min coordination parameter. Additionally, the reference parameters are expanded to 24 h, with capacity values assigned at different times of the day. Considering the minimization of total airport delay and the minimization of the sum of squared errors between airlines’ requested and allocated slots, we incorporate refined slot coordination parameters into the objective function and establish a three-objective flight slot refinement model. The model is solved using the NSGA-II algorithm based on the entropy weight method. To validate the model’s effectiveness, optimization is conducted using Beijing Capital International Airport as a case study, aiming to precisely utilize slot resources, improve slot resource utilization rates, and reduce wastage of slot resources.
3. Problem Description and Assumptions
The refined allocation of airport slot resources can be succinctly described as follows: Considering the maximum support capacity, safety restrictions, and flight connection requirements of restricted units such as the terminal area and major route points at the airport, slot coordination parameters are set for different time periods to determine the optimal takeoff and landing times for each flight. On one hand, it is necessary to adjust flights during time periods that exceed the operational capacity to optimize the distribution of flight slots across different periods. On the other hand, it is also essential to consider factors such as the market economic benefits of civil aviation transportation, operational costs, and passenger and cargo demand. The aim is to minimize the extent and scope of slot adjustments to reduce the impact on related sectors such as air carriers.
An airport is a huge resource integration entity, including runway resources, airspace resources, airline resources, crew members, environmental energy, etc. Coordinating and optimizing flight schedules is just one of many resources, and in addition to objective factors, there may also be special situations such as manual adjustments or emergency landings. It is necessary to control the impact of other resources on the optimization objectives of this article and minimize the interference of other factors. To ensure the rigor of the issues described above, the following assumptions are made before constructing the refined allocation model for airport slot resources:
Assumption 1.
Airport resources are unlimited.
Assumption 2.
Aircraft rotations, maintenance schedules, and crew allocations remain unchanged, with only flight slots being allocated.
Assumption 3.
Only regular flights are considered for slot allocation, excluding special cases such as charter flights and extra flights.
Assumption 4.
The number of parking positions allocated by ATC (Air Traffic Control) equals the original flight parking positions, and airlines do not consider canceling flights. There are no parking space constraints at the airport.
Assumption 5.
Flights can only be delayed or on time, not advanced.
4. Fine-Grained Configuration Model for Airport Flight Schedules
4.1. Time Division
The number of flight takeoffs and landings within a day exhibits significant temporal heterogeneity with hourly variations, manifesting as a coexistence of peaks and troughs in a fluctuating pattern. This temporal heterogeneity indicates substantial differences in airport flight traffic during different time periods. To make flight slot allocation more precise and targeted, this paper categorizes time periods within a day based on flight traffic into golden periods, peak periods, and off-peak periods. The peak periods are further subdivided into inbound peak periods and outbound peak periods.
During peak periods, the number of inbound and outbound flights typically reaches the maximum values set by the slot coordination parameters for inbound and outbound times, indicating that airport resource utilization is at its highest during these periods. Conversely, during golden periods, the total number of flights often reaches the maximum value of the overall slot coordination parameters, signifying the highest concentration and intensity of overall flight traffic. In contrast, flight numbers during off-peak periods have a considerable margin relative to the slot coordination parameters, with fewer flights, thereby generally negating the need for slot coordination in these periods.
In light of this temporal heterogeneity, the focus of this paper is on optimizing flight slots during peak and golden periods to enhance operational efficiency at the airport while ensuring flight safety and punctuality. Our aim is to provide superior service to airlines and passengers. By analyzing the slot arrangements for inbound and outbound flights during peak periods, this study ensures optimal utilization of airport resources during these times, avoiding excessive congestion. For the golden periods, the focus will be on optimizing overall flight traffic to ensure efficient and orderly takeoffs and landings. As for the off-peak periods, given the lower number of flights and resource utilization, the existing slot settings will be retained without further optimization.
4.2. Symbol Explanation
We explain the key symbols, variables, and parameters of the model in this chapter, as shown in Table 1.

Table 1.
Symbols for the refined configuration model.
4.3. Objective Functions
Decision variables: Decision variable is a 0–1 variable, if the i-th flight is assigned to the j-th slot, ; if the i-th flight is not assigned to the j-th slot, .
Objective 1: Efficiency Assurance: Minimization of Total Flight Delay Time
Flight delays directly result in time and economic losses for both the airport and passengers. Therefore, to minimize these losses, it is essential to reduce the total flight delay time while satisfying various constraints. By adopting this approach, it is possible to achieve the objective of efficiency while maintaining the overall optimality of resource allocation. The specific expression for Objective Function (1) is as follows:
In Equation (1), , which means the flight sequence, , which means the slot sequence. Starting from 6:00 to 24:00, there are a total of 216 minimum time slots, .
Note: If the optimized time is less than the time that needs to be optimized, then , which is considered a delay of 0.
Objective 2: Fairness Assurance: Minimization of the Sum of Squared Errors of Total Flight Time Shifts
For air carriers, adjustments to flight schedules may result in shift losses, subsequently affecting economic benefits and increasing operational costs. Therefore, fairness demands that the requested flight times remain as unaltered as possible or that any adjustments are kept within a minimal range. To achieve this objective, it is necessary to make minimal changes to the original flight schedules while satisfying various constraints, thereby minimizing the sum of squared errors of total flight time shifts. By adopting this approach, it is possible to achieve the objective of fairness while maintaining the overall optimality of resource allocation. The specific expression for Objective Function (2) is as follows:
Objective 3: Refined Allocation of Slot Coordination Parameters: Minimization of the Total Exceedance of Airport Capacity Limits
The 15 min and 60 min slot coordination parameters at airports are insufficient to fully utilize flight slot resources. Therefore, this chapter introduces a 5 min slot coordination parameter and refines the allocation of flight slots by time periods. Based on the daily flight flow characteristics, the day is divided into four periods: off-peak, morning peak, golden period, and evening peak. The slot coordination parameters are fine-tuned for different periods to maximize the reduction in slot resource wastage. Given the lower number of flights during off-peak hours, the focus is on applying slot coordination parameter limitations primarily during the morning and evening peaks, as well as the golden period:
- Morning Peak Period
- b.
- Evening Peak Period
- c.
- Golden Period
Due to the excessive limitations of slot coordination parameters, these are combined into a single objective function for ease of calculation, aiming to ensure that airport slot capacity does not exceed the values of the respective slot coordination parameters to the greatest extent possible. The specific expression of Objective Function (3) is as follows:
4.4. Constraint Conditions
1. Flight Slot Uniqueness Constraint:
where each flight must be assigned one and only one slot.
2. Slot Range Constraint:
where slot adjustments must be within an acceptable range.
3. Corridor Flow Constraint:
where it is necessary to ensure that the entry and exit of flights through corridor points are not congested. Corridor points are critical airway points for flights entering and exiting the airport terminal area. Optimization is required for corridor points during periods that do not meet capacity constraints to avoid congestion caused by concentrated arrivals or departures in a single direction.
4. Minimum Turnaround Time for Consecutive Flights Constraint:
To ensure the stability of the scheduled flight times, it is necessary to ensure that aircraft connections and passenger itineraries do not change. It is assumed that the impact of different aircraft types on the model algorithm can be ignored, so the minimum turnaround time for consecutive flights is the same for all types of aircraft.
5. Model Solution
5.1. Multi-Objective Optimization Algorithm (NSGA-II)
NSGA-II (non-dominated sorting genetic algorithm II) is a multi-objective optimization method based on genetic algorithms. It addresses multi-objective optimization problems by finding a set of approximate non-dominated solutions while maintaining diversity within the solution set. The algorithm was proposed by Kalyanmoy Deb et al. in 2002 and solves issues related to computational complexity, non-dominated sorting, and parameter settings inherent in NSGA (non-dominated sorting genetic algorithm) [24].
1. Fast Non-dominated Sorting Strategy:
NSGA-II performs a fast non-dominated sorting process to stratify the population. It divides the population into several different fronts according to the dominance level of each individual. Individuals within each front are non-dominated by individuals in other fronts. Parameters is set to indicate the number of individuals that dominate a given individual , and is set to represent the set of individuals that a given individual dominates. The specific operations are as follows:
a. Establish set , which includes all individuals not dominated by any other individuals.
b. For each individual in , determine the remaining individuals it can dominate, place them into a set , and update the dominance count for each individual in . If becomes zero, add the individual to the next front .
c. Assign a non-dominated rank of 1 to individuals in .
d. Repeat the above steps for individuals in and subsequent fronts to form different levels of Pareto sets.
2. Crowding Distance:
To maintain population diversity, the algorithm introduces the calculation of crowding distance, which measures the density of solutions surrounding an individual. A larger crowding distance indicates a larger space around the individual. For the i-th individual, let the crowding distance be ,. The crowding distance is the perimeter of the smallest rectangle containing the individual but excluding other individuals. represent the i−1-th and i+1-th individual’s values for the m-th objective function.
3. Elitism Strategy:
NSGA-II combines parent and offspring populations and selects the next generation based on non-dominated sorting and crowding distance, ensuring the inheritance of superior genes. Let represent the parent population and represent the offspring population. The new population is formed by combining and . The combined population is sorted by Pareto rank from low to high, followed by crowding distance from large to small. Individuals with a higher crowding distance are prioritized and added to the parent population until it reaches the desired size N.
In this paper, the tournament selection method is used, where two individuals are randomly selected each time, and their rank and crowding distance are recorded. Individuals with higher rank are preferred; if ranks are the same, those with larger crowding distances are preferred. A simulated binary crossover and polynomial mutation are applied, using real number encoding.
5.2. Solution Steps
The steps of the NSGA-II algorithm are illustrated in Figure 1.
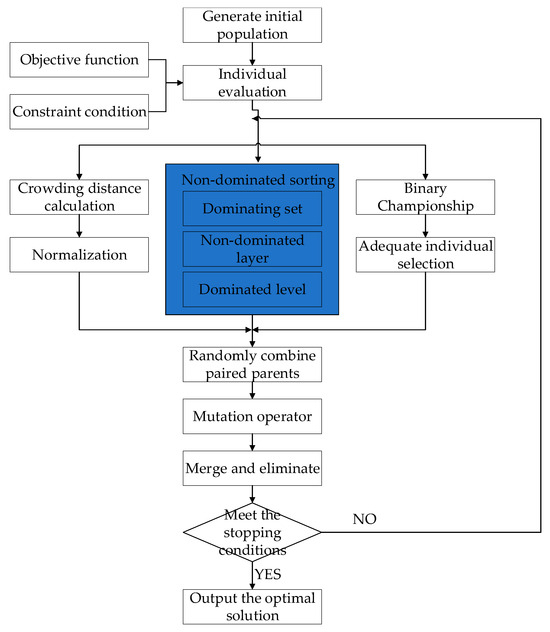
Figure 1.
The Flow of the NSGA-II algorithm.
- Initialization:
Generate a random population as the initial set of solutions.
- 2.
- Evaluation:
Calculate the objective values and constraints for each individual.
- 3.
- Non-dominated Sorting:
Perform non-dominated sorting on the current population based on the dominance relationships of individuals.
- 4.
- Crowding Distance:
Compute the crowding distance for each non-dominated front.
- 5.
- Selection:
Use binary tournament selection based on non-dominated rank and crowding distance to select individuals.
- 6.
- Crossover and Mutation:
Generate the next generation population through crossover and mutation operations. In this study, simulated binary crossover and polynomial mutation are used, with real number encoding.
- 7.
- Merging and Elimination:
Merge the parent and offspring populations, and then select superior individuals based on dominance rank and crowding distance to form the new parent population.
- 8.
- Iteration:
Repeat steps 3–7 until the stopping condition is met (usually a predefined number of iterations or a satisfactory solution is found).
5.3. Pareto Optimal Solution Based on Entropy Weight Method
When solving multi-objective optimization problems using NSGA-II, a set of Pareto optimal solutions is typically obtained. Generally, individuals select the most satisfactory solution from the Pareto set based on their subjective preferences as the final solution for the multi-objective optimization. Different subjective preferences can lead to variations in the choice of the optimal solution. To reduce the subjectivity that may arise from manually harmonizing objectives in this paper, the entropy weight method [25] is introduced to calculate the objective weights when selecting objectives. The principle is described as follows [26].
Assume the number of Pareto optimal solutions is and the number of evaluation criteria is . Let be the j-th evaluation criterion for the i-th solution to be evaluated. Dimensionless processing is performed to obtain , as follows:
The weight for the i-th solution under the j-th evaluation criterion is calculated as follows:
The entropy value for the j-th criterion is then calculated as:
The weight for the j-th criterion is given by:
Therefore, the total objective function value for the i-th solution is:
Using Equation (22), compute the total objective function value for each configuration at different time points, and select the configuration with the minimum total objective function value as the optimal solution for the refined allocation of airport flight schedules.
6. Case Study
6.1. Data Source
Analysis of flight scheduling at major airports reveals that during busy operational periods, not every time slot is scheduled based on the maximum hourly takeoff and landing capacity. For example, on a busy day in August 2023 at Beijing Capital International Airport, a total of 1131 flights were executed. The hourly arrival and departure traffic flow is illustrated in Figure 2. By calculating the ratio of the total daily volume to the hourly flow, the equivalent daily hours are obtained, reflecting the utilization level of the airport’s time slots, as shown in Figure 3. From Figure 3, it can be observed that the equivalent daily hours during 1:00–6:00 are relatively high, indicating significant available capacity for time slot utilization. The utilization of time slots during the remaining hours is relatively tight, approaching saturation.
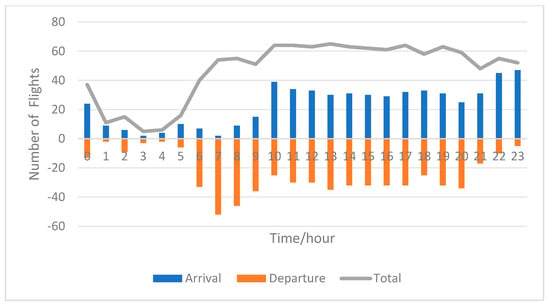
Figure 2.
Hourly arrival and departure traffic flow.
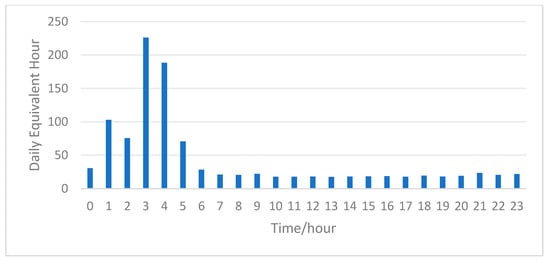
Figure 3.
Daily equivalent hour.
Based on the actual operational conditions at Beijing Capital International Airport, a day can be divided into four periods. The 0:00–6:00 period is designated as the off-peak period, characterized by a low number and density of flights, predominantly consisting of international, transfer, and cargo flights. The 7:00–9:00 period is identified as the departure peak period, with the number of departing flights fluctuating between 40 and 60, making it a critical period for the refined allocation of time slot resources due to the high demand. The 22:00–00:00 period is marked as the arrival peak period, with the number of arriving flights ranging between 40 and 50, resulting in a concentrated flight schedule. The remaining periods have a total traffic flow exceeding 40 flights, classified as the golden periods, during which the number of flights is generally high, accounting for 58.3% of the total, making this the primary period for time slot resource allocation.
To alleviate the pressure during the departure and arrival peak periods and to make full use of the time slot resources, this study proposes to extend the departure peak to 4 h and the arrival peak to 3 h. This approach is intended to achieve a flexible adjustment and refined allocation of time slots. The final distribution structure of flight time slot resources at Beijing Capital International Airport is presented in Table 2.

Table 2.
Distribution structure of flight schedule resources.
Due to the limited number of flights during off-peak periods, which do not significantly affect the daily operations of the airport, this paper conducts a further analysis of departure peaks, arrival peaks, and prime time (06:00–24:00) by examining 15 min and 5 min intervals of departure and arrival traffic, as illustrated in Figure 4 and Figure 5. The analysis reveals considerable fluctuations and substantial differences between peaks and troughs in 15 min and 5 min intervals of departure and arrival traffic, indicating an uneven utilization of slot resources and highlighting substantial potential for improvement.
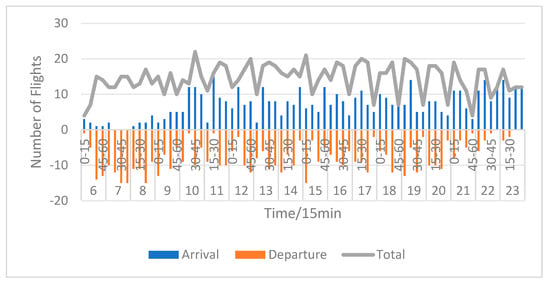
Figure 4.
The 15 min arrival and departure traffic flow.
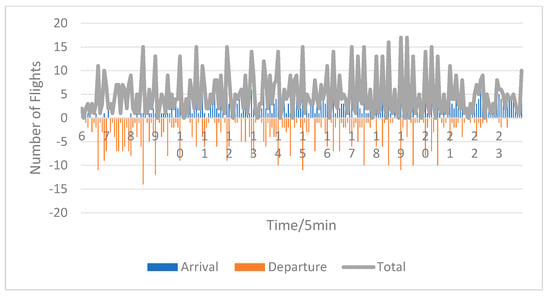
Figure 5.
The 5 min arrival and departure traffic flow.
6.2. Result Analysis
Based on the refined flight schedule allocation model, the minimum turnaround time for consecutive flights at the airport is set to 90 min. Using the NSGA-II algorithm, the population size is set to 1000, the number of iterations to 500, ,,,,,,,, , the crossover rate to 0.7, and the mutation rate to 0.3. The problem is solved using Matlab R2021b software. The changes in the objective functions with the number of iterations are shown in Figure 6, and the Pareto optimal set is illustrated in Figure 7.
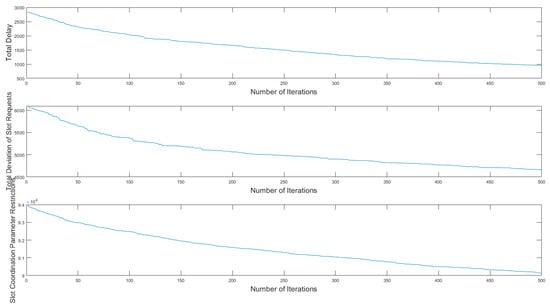
Figure 6.
The variation in each objective function with the number of iterations.
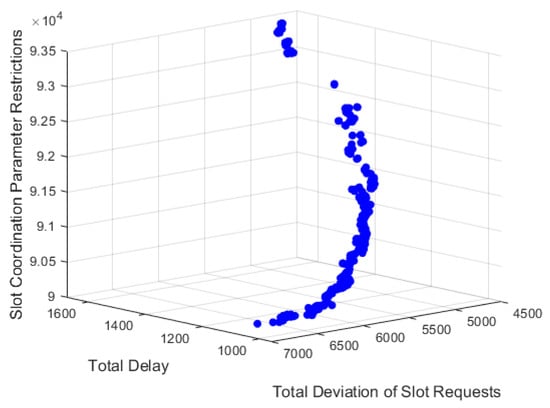
Figure 7.
Pareto diagram.
From the perspective of the three objective functions—total delay time, total deviation of slot requests, and time slot coordination parameter restrictions—all objective functions converge to their minimum values around the 495th iteration, achieving optimal results. The Pareto diagram is shown in Figure 7, where the blue dots represent the optimal solution. Due to the complexity of the three objective functions, it is not possible to directly obtain the most suitable solution in the graph. Therefore, this paper uses the entropy weight method to calculate optimal results, part of which are shown in Table 3. Some departure peak flights are selected, drawing a time slot configuration diagram before and after optimization, as shown in Figure 8. After optimization, the total delay time is reduced from 4130 min to 1142 min; the sum of squared errors for total deviation of slot requests decreases from 6056 to 5297, reducing the number of delayed flights from 389 to 283; and the time slot coordination parameter restriction value decreases from 93,931 to 91,695. All three objectives have been significantly optimized.

Table 3.
Partial optimization results.
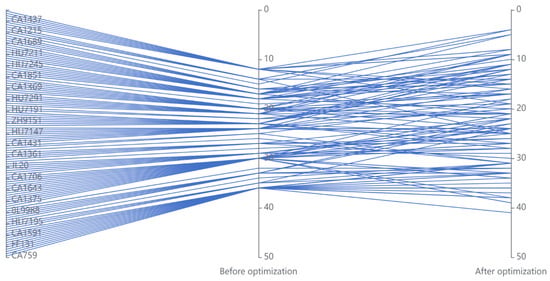
Figure 8.
Comparison of optimization results for departure peak flights.
Further analysis of the optimized results revealing the hourly, 15 min, and 5 min arrival and departure flows post-optimization are depicted in Figure 9, Figure 10 and Figure 11. Compared to pre-optimization, the optimized flight schedules strictly adhere to the hourly time slot coordination parameter restrictions, with minor deviations in some 15 min intervals, aligning with the actual airport operations. Introducing the 5 min time slot coordination parameter restrictions, the maximum number of flight arrivals and departures in a single time slot decreases from 17 to 11, not exceeding the coordination parameter limits. As shown in Figure 11, the original flight schedule had highly concentrated flight arrivals and departures in 5 min intervals, with a significant number exceeding operational capacity and being in an overloaded state. For example, from 11:55 to 12:00, there were 15 arrivals and departures, while from 11:50 to 11:55, there was only 1; after optimization, the number of arrivals and departures from 11:55 to 12:00 was 11, and from 11:50 to 11:55 was 5, thus improving the utilization of time slot resources in other intervals without exceeding the coordination parameter limits.
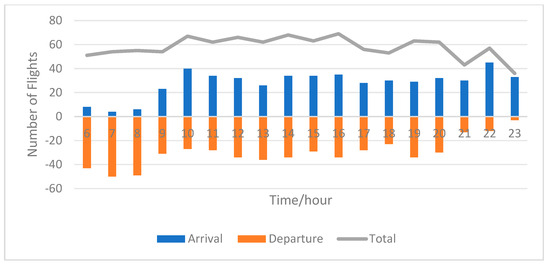
Figure 9.
Optimized hourly arrival and departure traffic flow.
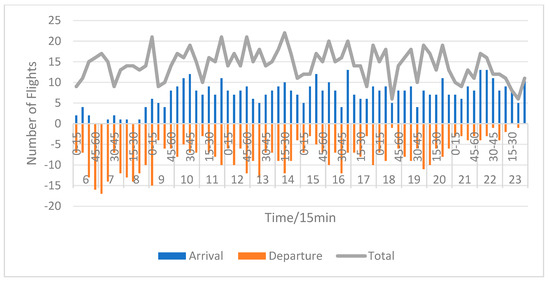
Figure 10.
Optimized 15 min arrival and departure traffic flow.
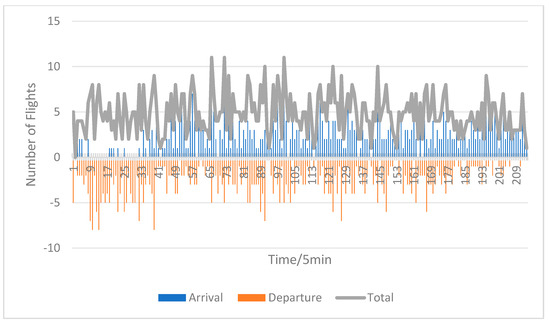
Figure 11.
Optimized 5 min arrival and departure traffic flow.
Additionally, for the 216 five-minute time slots throughout the day, the standard deviation of the number of time slots in the original flight schedule was 4.21, compared to 2.24 after optimization. This further indicates that the original flight schedule had significant fluctuations in the number of flights per time slot, while the optimized schedule showed significantly reduced volatility, with more stable flight timings and a more balanced overall distribution of time slots. The optimization results are evident, effectively enhancing the utilization of airport time slot resources and achieving a peak-shaving and valley-filling effect.
Similarly, the optimized flight schedule did not achieve a completely uniform distribution of time slots throughout the day. Even after optimization, there will still be peak and valley trends, although the magnitude is reduced. While distributing flights uniformly throughout the day can minimize delays for any given number of flights, a completely flat flight schedule would result in a greater total adjustment of flight times compared to the solution presented in this paper. Therefore, this optimization method retains the characteristic variations in flight times but with smaller fluctuations than in the original schedule, thus meeting capacity constraints with minimal adjustments to the original flight plan. This optimized schedule better aligns with the needs of airlines and potential passengers than a perfectly flat version.
Next, the distribution of the number of arrivals and departures in 5 min intervals for each direction before and after optimization is illustrated in Figure 12 and Figure 13. It can be observed that the number of flights in peak periods significantly decreases after optimization: the peak for arrivals was adjusted from 7 flights to 4 flights, and the peak for departures was reduced from 7 flights to 4 flights, aligning with operational capacity constraints. In the original plan, there were large fluctuations in the number of flights within 5 min intervals, especially during morning and evening peak periods. Some flights were overly concentrated, with flight schedules for the RUSDO and DUGEB directions exceeding the operational capacity limits for single directions, making it difficult to ensure timely arrivals and departures in actual operations. However, the optimized schedule not only met the overall operational capacity constraints but also balanced the number of arrivals and departures, leading to a more reasonable allocation of flight time slot resources for each direction.
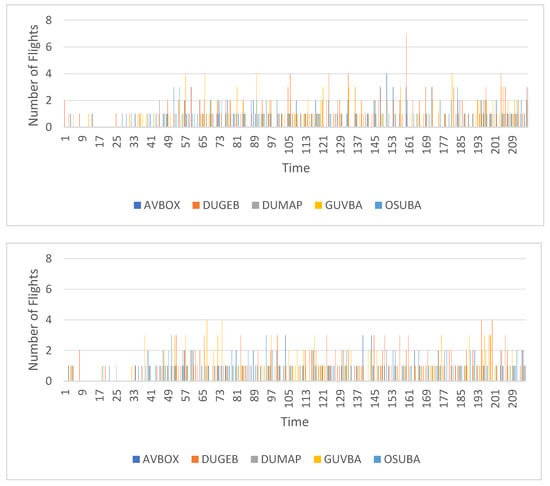
Figure 12.
Comparison of the number of arrival flights in 5 min time slots in all directions before and after optimization.
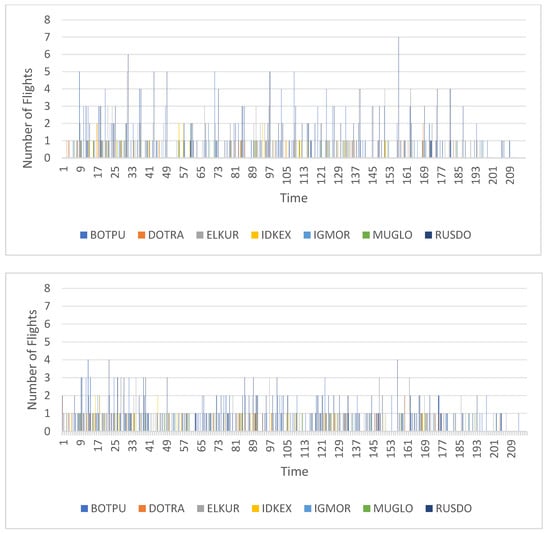
Figure 13.
Comparison of the number of departure flights in 5 min time slots in all directions before and after optimization.
In summary, the refined allocation method for airport flight schedule resources optimizes the distribution by aligning flight demand with overall operational capacity and directional constraints. By finely adjusting the flight schedule distribution, smoothing out peaks and filling valleys, this method ensures compliance with airport and airspace resource limitations, thus achieving a balance between flight demand and supply. This approach not only reduces the likelihood of planned flight delays but also promotes the smooth operation of arriving and departing flights.
7. Conclusions
This paper considers the refined allocation of time coordination parameters, introducing a 5 min time coordination parameter constraint in addition to the hourly and 15 min constraints, and optimizes airport flight schedules by time periods. A tri-objective flight schedule refinement model is established, taking into account constraints such as the uniqueness of flight times, corridor flow constraints, and time range constraints. The model is solved using the entropy weight-based NSGA-II algorithm. Taking Beijing Capital International Airport as an example, the results show that this method optimizes all three objectives to a certain extent. By reducing delays and deviations in flight schedule requests, the refined allocation of time coordination parameters can lead to a more even distribution of flight schedules, making better use of flight times. This validates the effectiveness of the model and effectively reduces the waste of time slot resources.
The contributions and the novelty of this paper is as follows:
1. Creatively introducing five-minute time coordination parameters for a more refined configuration of time capacity. The previously coordinated parameters of 1 h and 15 min cannot meet the increasingly busy airport operations. By introducing a five-minute time coordination parameter limitation, the scheduling of flight schedules can be more refined, which can scientifically reduce flight delays and improve the utilization of time resources at the planning level.
2. Assigning time coordination parameters in different time periods. Previously, the time coordination parameters were only uniform values. In this article, time periods were divided into prime-time periods, morning rush hour periods, evening rush hour periods, and off-peak periods. Different time coordination parameters were configured for different time periods to maximize the utilization of flight time and avoid unnecessary delays and flight time waste.
3. Taking into account efficiency and fairness, a three objective time optimization model was established by simultaneously incorporating parameter constraints for 1 h, 15 min, and 5 min into the time objectives. Previous studies mostly focused on single objective and dual objective optimization. This article integrates airport, airline, and passenger demands, and introduces time coordination parameter values into the model to more comprehensively solve the problem of flight schedule optimization.
The separation problem was not considered in this model. This article aims to arrange the schedule reasonably from the perspective of planned flights and use delay as an important judgment indicator, with a focus on schedule arrangement and traffic control. The separation problem is also an important cause of flight congestion, and it is necessary to conduct more in-depth research on it. Meanwhile, comparing with more advanced optimization algorithms will become a further focus in the future. It is better to consider incorporating multiple different algorithms and further analyzing and comparing them with the NSGA-II algorithm in various outcome indicators.
Author Contributions
Conceptualization, J.Y. and B.J.; methodology, J.Y. and M.H.; software, J.Y.; data analysis, J.Y.; data curation, J.Y. and Z.Z.; writing—original draft preparation, J.Y.; writing—review and editing, J.Y.; visualization, J.Y. All authors have read and agreed to the published version of this manuscript.
Funding
This research was funded by National Key Research and Development Program (2022YFB2602401).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
We thank the State Key Laboratory of Air Traffic Management System for supporting this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Odoni, A.R. A Review of Certain Aspects of the Slot Allocation Process at Level 3 Airports under Regulation 95/93; MIT Libraries: Cambridge, MA, USA, 2020. [Google Scholar]
- Wang, Y. Secondary trading of airport slots: Issues and challenges. Chin. J. Aeronaut. 2023, 36, 1–12. [Google Scholar] [CrossRef]
- ACI; IATA; WWACG. Worldwide Airport Slot Guidelines (WASG); IATA: Geneva, Switzerland, 2020. [Google Scholar]
- Jacquillat, A.; Odoni, A.R. A roadmap toward airport demand and capacity management. Transp. Res. Part A Policy Pract. 2018, 114, 168–185. [Google Scholar] [CrossRef]
- Civil Aviation Administration of China. Civil Aviation Flight Slot Management Measures; Civil Aviation Administration of China: Beijing, China, 2018. [Google Scholar]
- Wang, W.; Wang, C. A Spatio-Temporal Network Model for Slot Allocation in Hub Airports: A Case Study of Beijing Capital International Airport. Acta Geogr. Sin. 2013, 68, 762–774. [Google Scholar]
- Pan, W.; Lu, G. Research on Multi-Factor Weight Determination Method for Slot Allocation. Autom. Technol. Appl. 2015, 34, 19–23. [Google Scholar]
- Wang, Y.; Shui, X.; Wang, M. Advances and Challenges in Slot Resource Management at Airports. J. Beihang Univ. 2024, 50, 1065–1076. [Google Scholar]
- Zhou, S. Comparative Study on Flight Slot Allocation Models. Logist. Technol. 2023, 46, 102–106. [Google Scholar]
- Feng, H.; Hu, R.; Wang, D. Research Progress on Optimization Models for Primary Market Allocation of Flight Slots. J. Transp. Eng. Inf. 2022, 20, 42–58. [Google Scholar]
- Tang, X.; Chen, M.; Hu, H. Research on Issues Related to Market-Based Allocation of Flight Slot Resources. Civ. Aviat. Manag. 2021, 2, 11–16. [Google Scholar]
- Stojkovic, G.; Soumis, F.; Desrosiers, J. An optimization model for a real-time flight scheduling problem. Transp. Res. Part A Policy Pract. 2002, 36, 779–788. [Google Scholar] [CrossRef]
- Zografos, K.G.; Salouras, Y.; Madas, M. Dealing with the efficient allocation of scarce resources at congested airports. Transp. Res. Part C Emerg. Technol. 2012, 21, 244–256. [Google Scholar] [CrossRef]
- Ribeiro, N.A.; Jacquillat, A.; Antunes, P. An optimization approach for airport slot allocation under IATA guidelines. Transp. Res. Part B Methodol. 2018, 112, 132–156. [Google Scholar] [CrossRef]
- Jorge, D. Towards a decision-support tool for airport slot allocation: Application to Guarulhos (Sao Paulo, Brazil). J. Air Transp. Manag. 2021, 93, 102048. [Google Scholar] [CrossRef]
- Dixit, A.K.; Shakya, G.; Jakhar, S.K. Algorithmic mechanism design for egalitarian and congestion-aware airport slot allocation. Transp. Res. Part E Logist. Transp. Rev. 2023, 169, 102971. [Google Scholar] [CrossRef]
- Yang, X.; Qi, L.; Zhai, W. Optimization allocation of flight schedule resources and evaluation of delay levels. J. Henan Univ. Sci. Technol. (Nat. Sci. Ed.) 2016, 37, 19–23. [Google Scholar]
- Yang, X.; Pei, Y. Research on airline route and flight optimization based on bilevel programming. Aviat. Comput. Technol. 2018, 48, 1–7. [Google Scholar]
- Feng, X.; Xia, H.; Feng, Y. Optimization Design and System Implementation of Flight Timetable Based on Minimum Cost. Comput. Mod. 2017, 1, 106–110. [Google Scholar]
- Wang, M.; Hu, M.; Zhao, Z. Research on Flight Schedule Optimization Based on Acceptable Adjustment Levels. J. Wuhan Univ. Technol. (Transp. Sci. Eng. Ed.) 2019, 43, 671–675+681. [Google Scholar]
- Xu, C.; Liu, J.; Dong, X. Research on Airport Flight Schedule Optimization Based on Flight Characteristics. Aviat. Comput. Technol. 2019, 49, 96–101. [Google Scholar]
- Ke, Y.; Hu, M.; Yang, L. Strategic Flight Schedule Optimization Technology for Actual Operations. Sci. Technol. Eng. 2021, 21, 4260–4265. [Google Scholar]
- Zuo, J.; Wang, Q.; Zhong, Q. Optimization of Departure Flight Schedule Based on Genetic Algorithm. Comput. Simul. 2022, 39, 23–28. [Google Scholar]
- Hu, Y. Research on Path Optimization of Urban Domestic Waste Removal Vehicles Based on Improved NSGA-II. Master’s thesis, Anhui University of Technology, Anhui, China, 2022. [Google Scholar]
- Wang, J.; Sun, Y.; Kang, J. Evaluation of competitive of power enterprises based on entropy and improved TOPSIS. J. North China Electr. Power Univ. 2010, 37, 61–64. [Google Scholar]
- Jia, Z.; Zhao, L. Comprehensive evaluation of power quality based on the model of entropy weight and unascertained measure. Power Syst. Prot. Control. 2010, 38, 33–37. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).