Consensus SE(3)-Constrained Extended Kalman Filter for Close Proximity Orbital Relative Pose Estimation
Abstract
1. Introduction
2. Spacecraft Dynamics on
2.1. Pose Kinematics
2.2. Satellite Dynamics
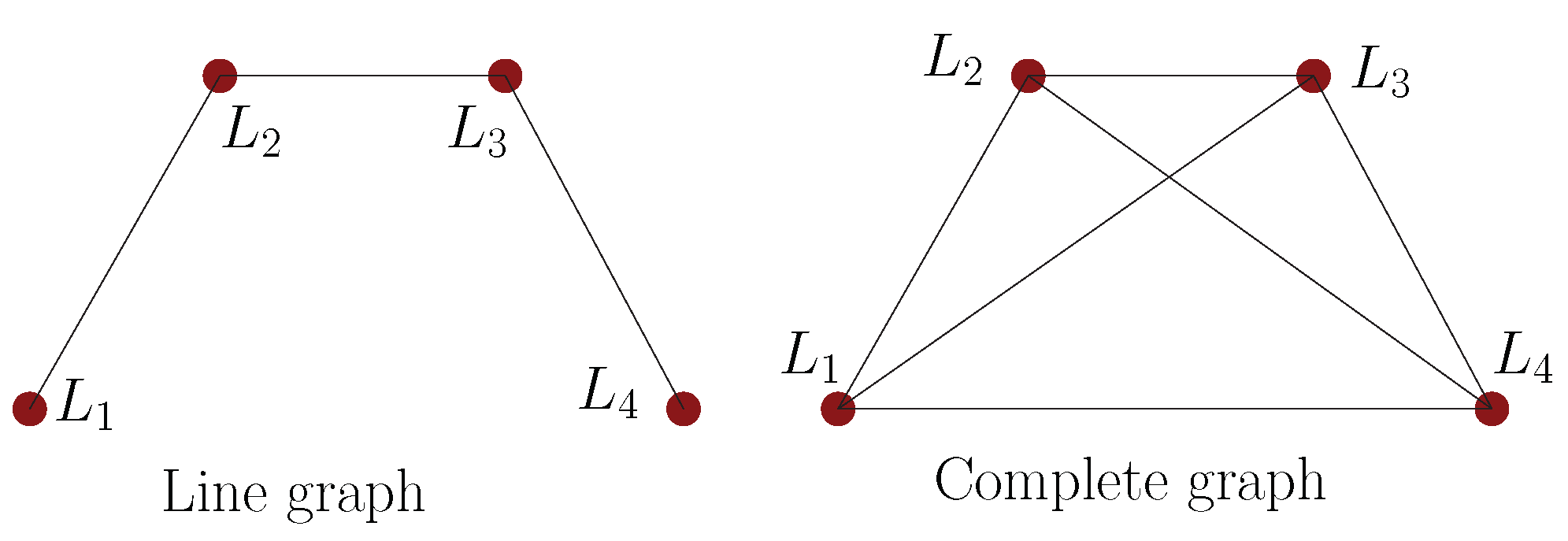
2.3. Communication Graph
3. Problem Statement for Proximity Operations
- (i)
- Four chief satellites and one deputy satellite is in formation, as shown in Figure 3.
- (ii)
- Chief satellite orbital elements and its attitude are known perfectly at all times.
- (iii)
- The objective is to estimate the deputy satellite— information—using the filters that are running in each chief satellite.
- (iv)
- The deputy satellite has attitude sensors for estimating C in Equation (1). This information along with its velocities is shared with each chief satellite for running the filter.
- (v)
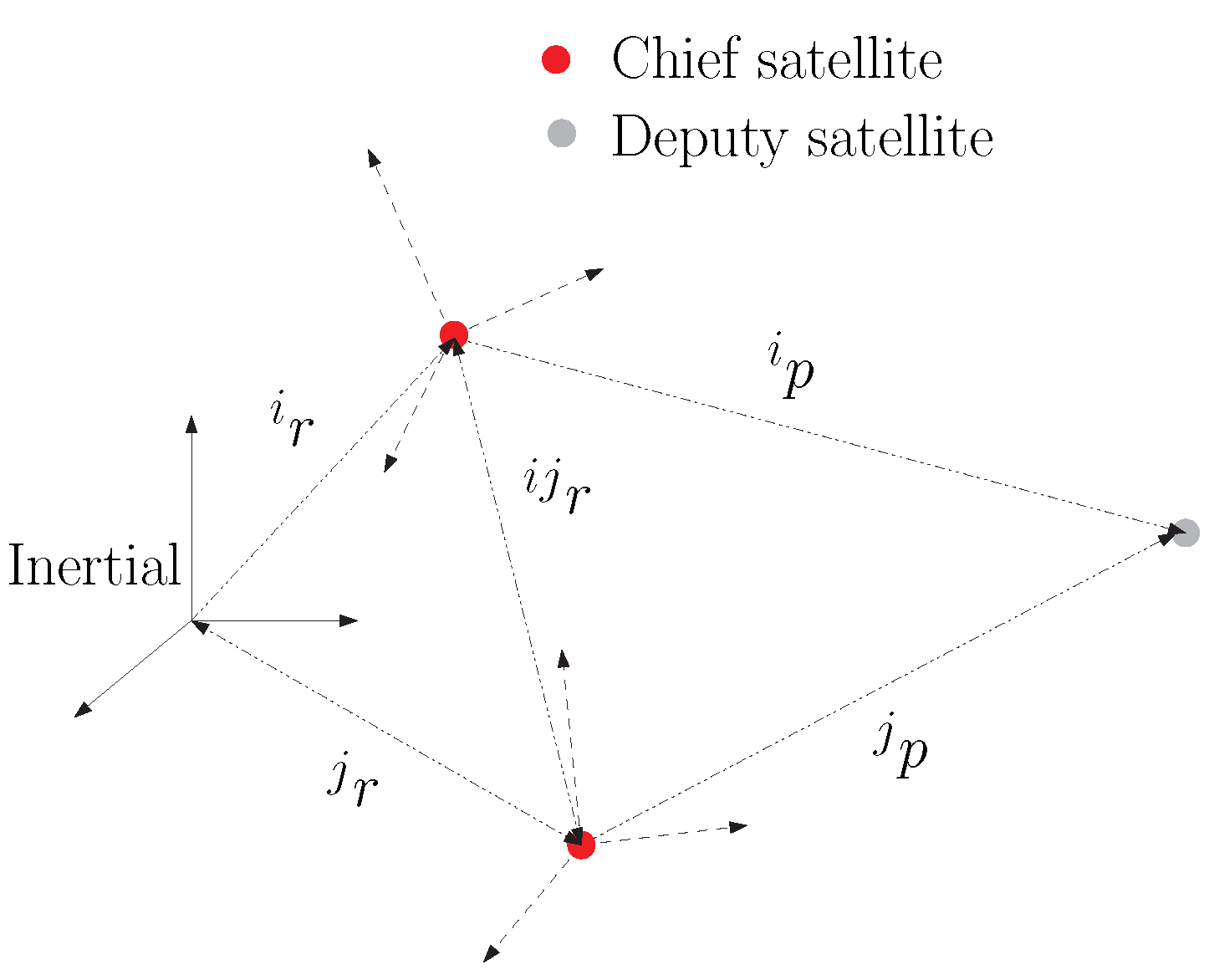
- Chief satellites have a LIDAR sensor, which measures its range from the deputy satellite. This is used to estimate the p in the g-matrix.
- (vi)
- For consensus estimation, each chief satellite state is shared in the communication network.
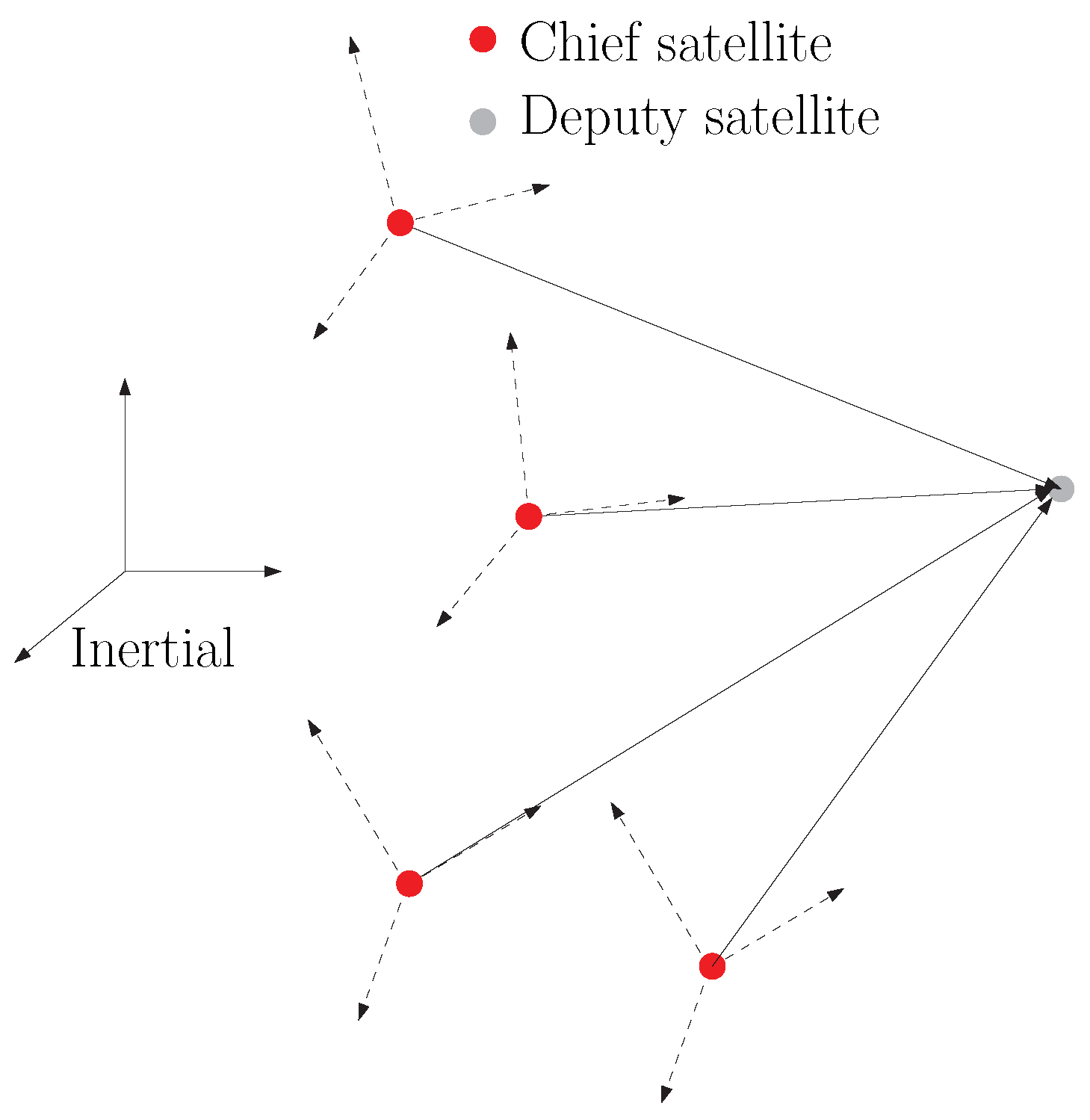
Measurement Model
4. Consensus Continuous-Discrete -Constrained Extended Kalman Filter
4.1. Continuous-Discrete Time SE(3)-EKF Structure
4.2. Continuous-Discrete Time SE(3)-EKF Error Dynamics
4.3. Discrete Time SE(3)-EKF Gain Selection
5. Discretized Variational Integration
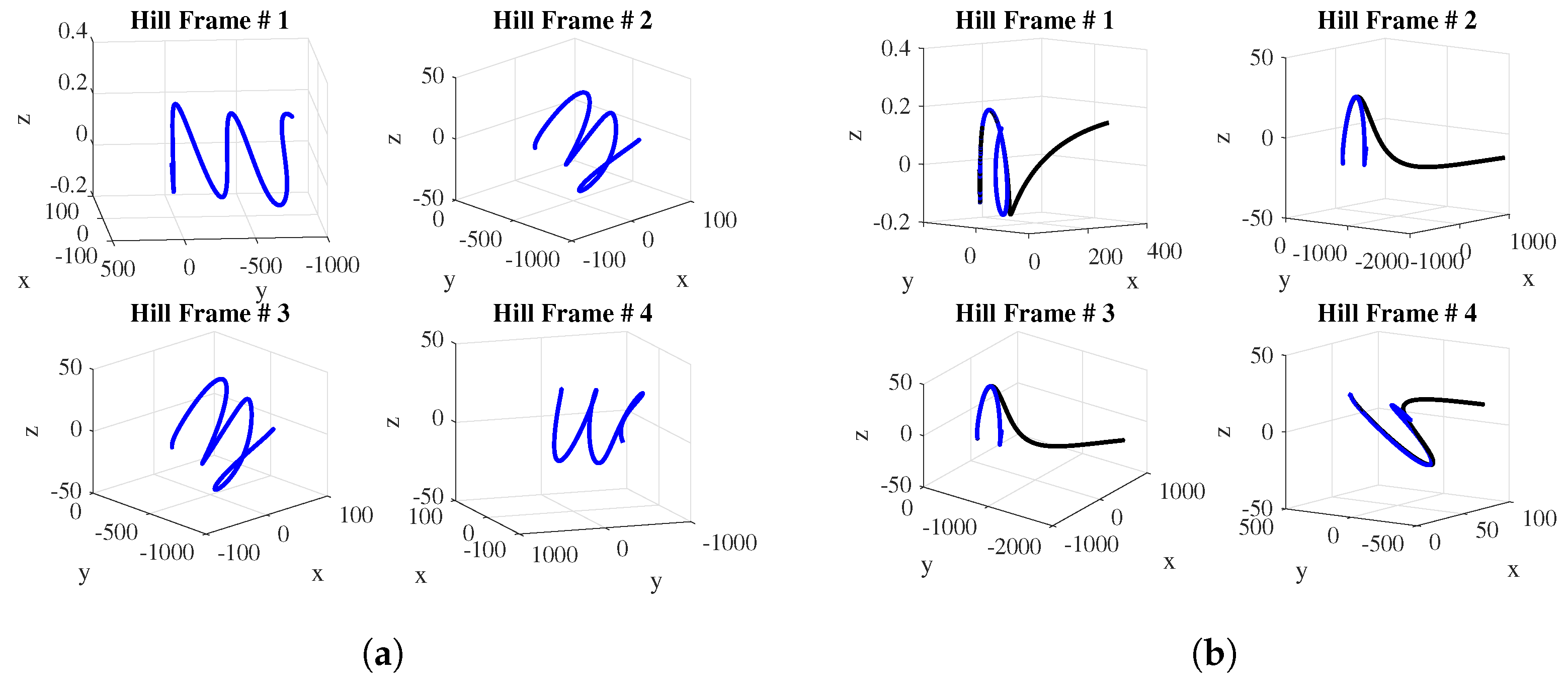
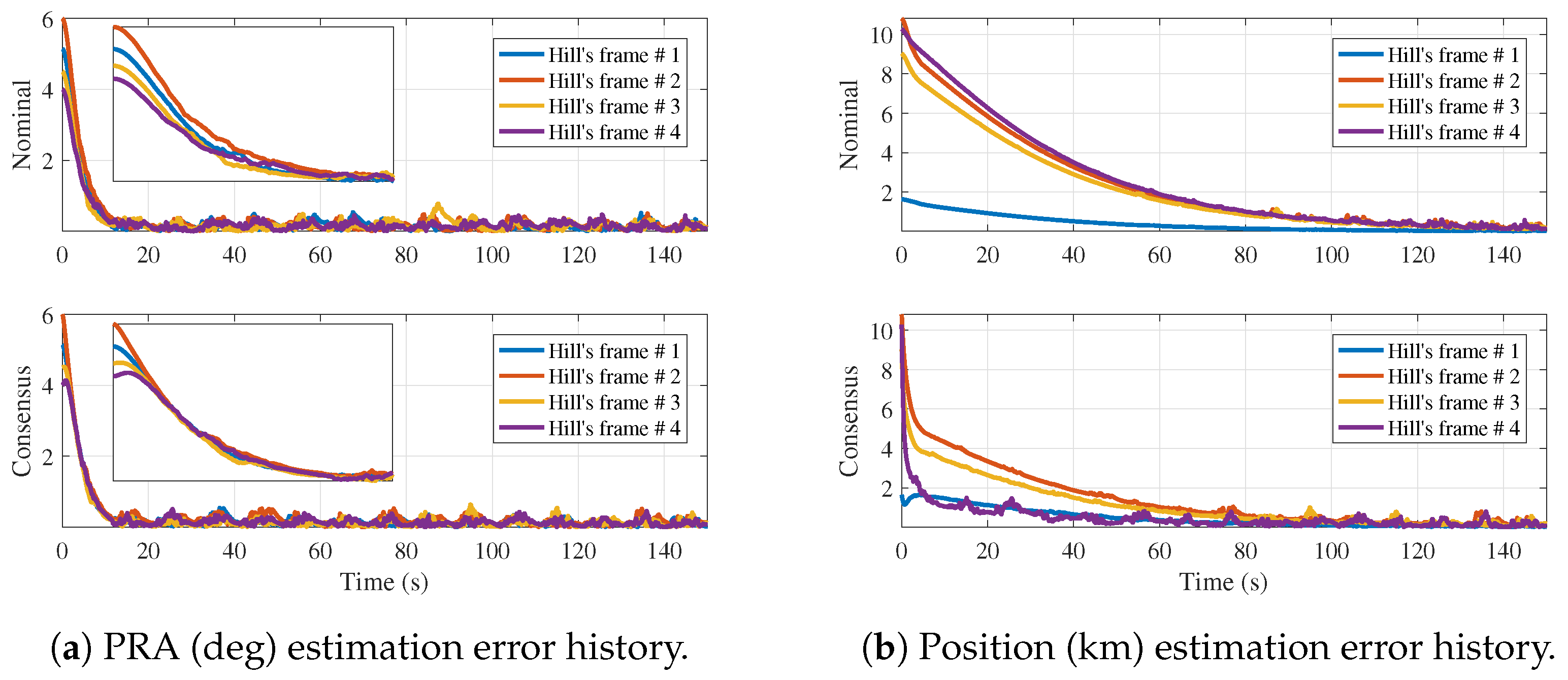
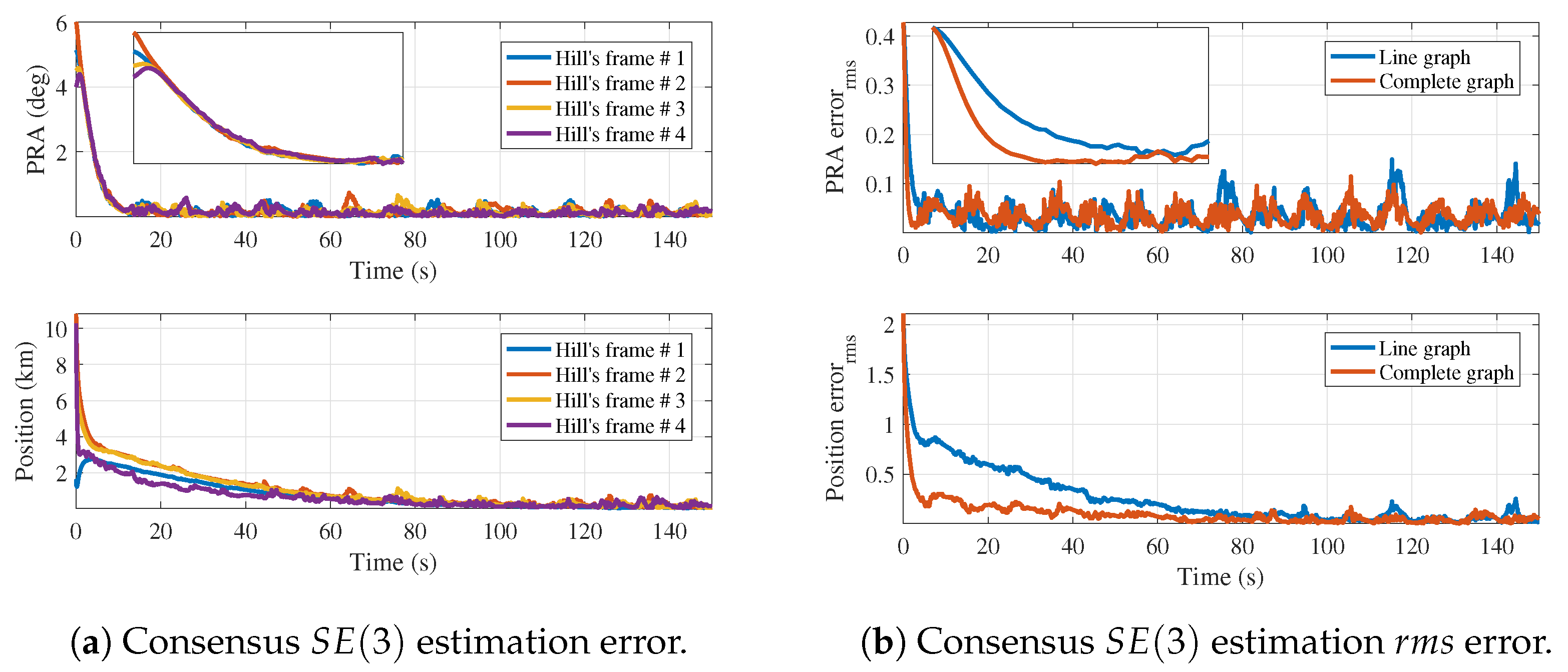
6. Numerical Simulation
Effects of Additional Communication Links
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schilling, K. I-3D: Formations of small satellites. In Nanosatellites: Space and Ground Technologies, Operations and Economics; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2020; pp. 327–339. [Google Scholar]
- Kaiser, M.; Gans, N.; Dixon, W. Vision-based estimation for guidance, navigation, and control of an aerial vehicle. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1064–1077. [Google Scholar] [CrossRef]
- Liu, C.; Hu, W. Relative pose estimation for cylinder-shaped spacecrafts using single image. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 3036–3056. [Google Scholar] [CrossRef]
- Opromolla, R.; Fasano, G.; Rufino, G.; Grassi, M. Pose estimation for spacecraft relative navigation using model-based algorithms. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 431–447. [Google Scholar] [CrossRef]
- Kim, S.G.; Crassidis, J.L.; Cheng, Y.; Fosbury, A.M.; Junkins, J.L. Kalman filtering for relative spacecraft attitude and position estimation. J. Guid. Control Dyn. 2007, 30, 133–143. [Google Scholar] [CrossRef]
- Bar-Itzhack, I.Y.; Idan, M. Recursive attitude determination from vector observations Euler angle estimation. J. Guid. Control Dyn. 1987, 10, 152–157. [Google Scholar] [CrossRef]
- Gui, H.; De Ruiter, A.H. Quaternion invariant extended Kalman filtering for spacecraft attitude estimation. J. Guid. Control Dyn. 2018, 41, 863–878. [Google Scholar] [CrossRef]
- Hemingway, E.G.; O’Reilly, O.M. Perspectives on Euler angle singularities, gimbal lock, and the orthogonality of applied forces and applied moments. Multibody Syst. Dyn. 2018, 44, 31–56. [Google Scholar] [CrossRef]
- Markley, F.L. Attitude filtering on SO(3). J. Astronaut. Sci. 2006, 54, 391–413. [Google Scholar] [CrossRef]
- Izadi, M.; Sanyal, A.K. Rigid body attitude estimation based on the Lagrange-D’Alembert principle. Automatica 2014, 50, 2570–2577. [Google Scholar] [CrossRef]
- Chaturvedi, N.A.; Sanyal, A.K.; McClamroch, N.H. Rigid-body attitude control. IEEE Control Syst. Mag. 2011, 31, 30–51. [Google Scholar]
- Varadarajan, V.S. Lie Groups, Lie Algebras, and Their Representations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 102. [Google Scholar]
- Sanyal, A.K.; Izadi, M.; Bohn, J. An observer for rigid body motion with almost global finite-time convergence. In Proceedings of the ASME Dynamic Systems and Control Conference. American Society of Mechanical Engineers Digital Collection 2014, San Antonio, TX, USA, 22–24 October 2014. [Google Scholar]
- Izadi, M.; Sanyal, A.K. Rigid body pose estimation based on the Lagrange-D’Alembert principle. Automatica 2016, 71, 78–88. [Google Scholar] [CrossRef]
- Stanković, S.S.; Stankovic, M.S.; Stipanovic, D.M. Decentralized parameter estimation by consensus based stochastic approximation. IEEE Trans. Autom. Control 2010, 56, 531–543. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Distributed Kalman filter with embedded consensus filters. In Proceedings of the 44th Conference on Decision and Control, Seville, Spain, 15 December 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 8179–8184. [Google Scholar]
- Olfati-Saber, R. Distributed Kalman filtering for sensor networks. In Proceedings of the 46th Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 5492–5498. [Google Scholar]
- Kar, S.; Moura, J.M. Gossip and distributed Kalman filtering: Weak consensus under weak detectability. IEEE Trans. Signal Process. 2010, 59, 1766–1784. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Kalman-consensus filter: Optimality, stability, and performance. In Proceedings of the Conference on Decision and Control IEEE 2009, Shanghai, China, 15–18 December 2009; pp. 7036–7042. [Google Scholar]
- Li, W.; Jia, Y. Distributed consensus filtering for discrete-time nonlinear systems with non-Gaussian noise. Signal Process. 2012, 92, 2464–2470. [Google Scholar] [CrossRef]
- Battistelli, G.; Chisci, L. Stability of consensus extended Kalman filter for distributed state estimation. Automatica 2016, 68, 169–178. [Google Scholar] [CrossRef]
- Wang, J.; Butcher, E.A.; Yucelen, T. Space-based relative orbit estimation using information sharing and the consensus Kalman filter. J. Guid. Control Dyn. 2019, 42, 491–507. [Google Scholar] [CrossRef]
- Mathavaraj, S.; Butcher, E. SE(3)-Constrained Extended Kalman Filtering for Rigid Body Pose Estimation. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2482–2492. [Google Scholar] [CrossRef]
- De Ruiter, A.H.; Forbes, J.R. Discrete-time SO(n)-constrained Kalman filtering. J. Guid. Control Dyn. 2017, 40, 28–37. [Google Scholar] [CrossRef]
- Hill, G.W. Researches in lunar theory. Am. J. Math. 1878, 1, 5–26,29–147,245–260. [Google Scholar] [CrossRef]
- Clohessy, W.H.; Wiltshire, R.S. Terminal guidance for satellite rendezvous. J. Aerosp. Sci. 1960, 27, 653–658,674. [Google Scholar] [CrossRef]
- Alfriend, K.; Vadali, S.R.; Gurfil, P.; How, J.; Brege, L. Spacecraft Formation Flying: Dynamics, Control, and Navigation; Elsevier Astrodynamics Series; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Park, H.E.; Park, S.Y.; Choi, K.H. Satellite formation reconfiguration & station keeping using SDRE technique. Aerosp. Sci. Technol. 2011, 15, 440–452. [Google Scholar]
- Schaub, H.; Junkins, J.L. Analytical Mechanics of Space Systems; American Institute of Aeronautics and Astronautics: Las Vegas, NV, USA, 2009. [Google Scholar]
- Black, H.D. A passive system for determining the attitude of a satellite. AIAA J. 1964, 2, 1350–1351. [Google Scholar] [CrossRef]
- Wang, J.; Butcher, E.A.; Lovell, T.A. Ambiguous orbits in elliptic chief spacecraft relative orbit estimation with range-only measurements. J. Spacecr. Rocket. 2019, 56, 708–724. [Google Scholar] [CrossRef]
- Stadter, P.; Chacos, A.; Heins, R.; Moore, G.; Olsen, E.; Asher, M. Confluence of navigation, communication, and control in distributed spacecraft systems. In Proceedings of the Aerospace Conference IEEE 2001, Big Sky, MT, USA, 10–17 March 2001; Volume 2, pp. 2–563. [Google Scholar]
- Schmidt, S.F. The Kalman filter—Its recognition and development for aerospace applications. J. Guid. Control 1981, 4, 4–7. [Google Scholar] [CrossRef]
- Furuta, K. Alternative solution of discrete-time Kalman filter. Syst. Control Lett. 1994, 22, 429–435. [Google Scholar] [CrossRef]
- Hargrave, P. A tutorial introduction to Kalman filtering. In Proceedings of the IEE colloquium on Kalman Filters: Introduction, Applications and Future Fevelopments 1989, London, UK, 21 February 1989; p. 1. [Google Scholar]
- Zanetti, R.; Majji, M.; Bishop, R.H.; Mortari, D. Norm-constrained Kalman filtering. J. Guid. Control Dyn. 2009, 32, 1458–1465. [Google Scholar] [CrossRef]
- Lee, T. Computational Geometric Mechanics and Control of Rigid Bodies. Ph.D. Thesis, The University of Michigan, Ann Arbor, MI, USA, 2008. [Google Scholar]
- Mathavaraj, S.; Padhi, R. Satellite Formation Flying: High Precision Guidance using Optimal and Adaptive Control Techniques; Springer Nature: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Scharnagl, J. Distributed Guidance, Navigation and Control for Satellite Formation Flying Missions. Ph.D. Thesis, Universität Würzburg, Würzburg, Germany, 2022. [Google Scholar]

| Satellite | , km | |||||
|---|---|---|---|---|---|---|
| Second, chief | 0 | 0 | 0 | 0 | ||
| Third chief | 0 | 0 | 0 | 0 | ||
| Four chief | 0 | 0 | 0 | 0 | ||
| Deputy | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mathavaraj, S.; Butcher, E.A. Consensus SE(3)-Constrained Extended Kalman Filter for Close Proximity Orbital Relative Pose Estimation. Aerospace 2024, 11, 762. https://doi.org/10.3390/aerospace11090762
Mathavaraj S, Butcher EA. Consensus SE(3)-Constrained Extended Kalman Filter for Close Proximity Orbital Relative Pose Estimation. Aerospace. 2024; 11(9):762. https://doi.org/10.3390/aerospace11090762
Chicago/Turabian StyleMathavaraj, S., and Eric A. Butcher. 2024. "Consensus SE(3)-Constrained Extended Kalman Filter for Close Proximity Orbital Relative Pose Estimation" Aerospace 11, no. 9: 762. https://doi.org/10.3390/aerospace11090762
APA StyleMathavaraj, S., & Butcher, E. A. (2024). Consensus SE(3)-Constrained Extended Kalman Filter for Close Proximity Orbital Relative Pose Estimation. Aerospace, 11(9), 762. https://doi.org/10.3390/aerospace11090762





