A Neural Network with Physical Mechanism for Predicting Airport Aviation Noise
Abstract
1. Introduction
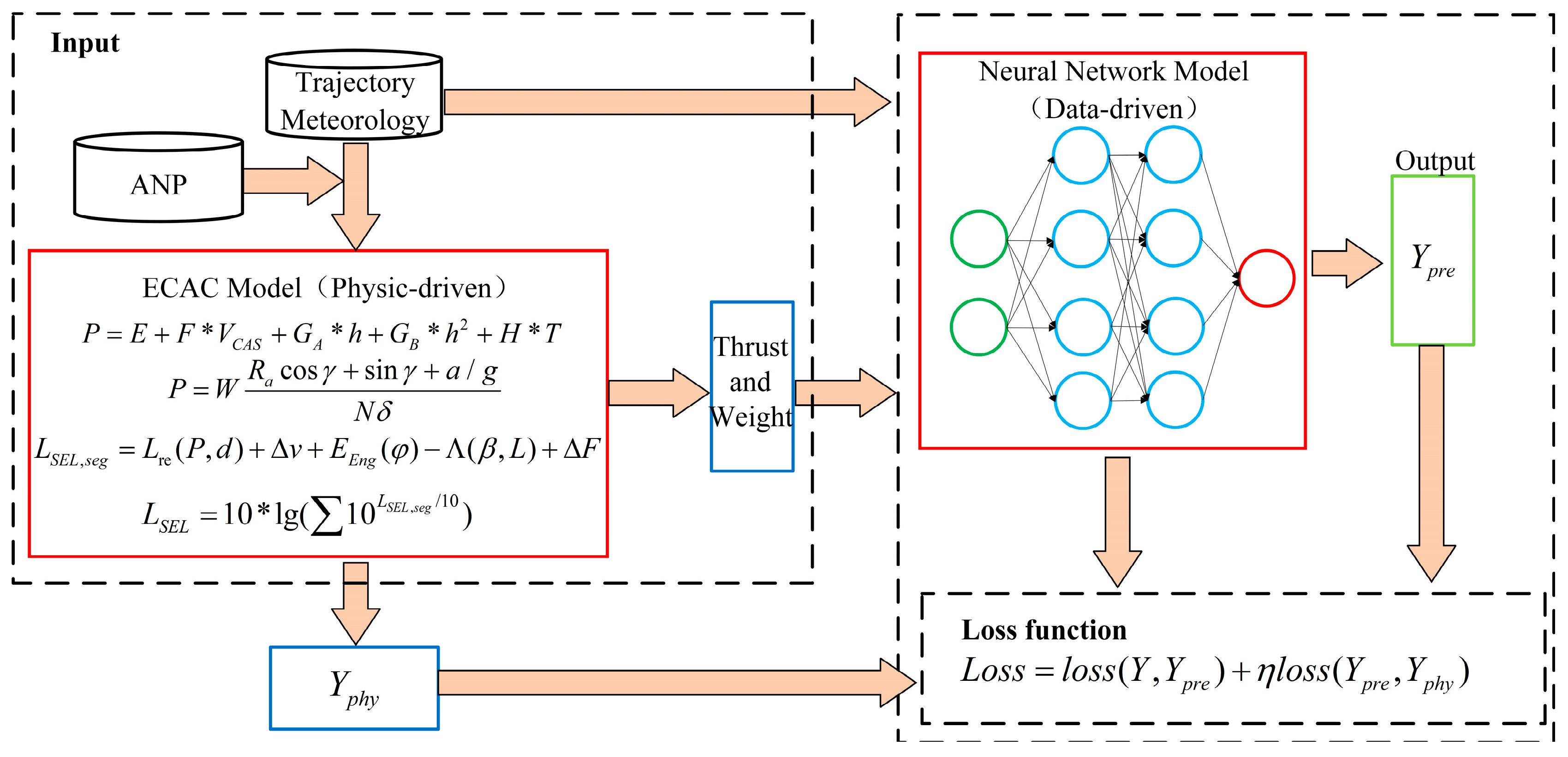
2. Methodology
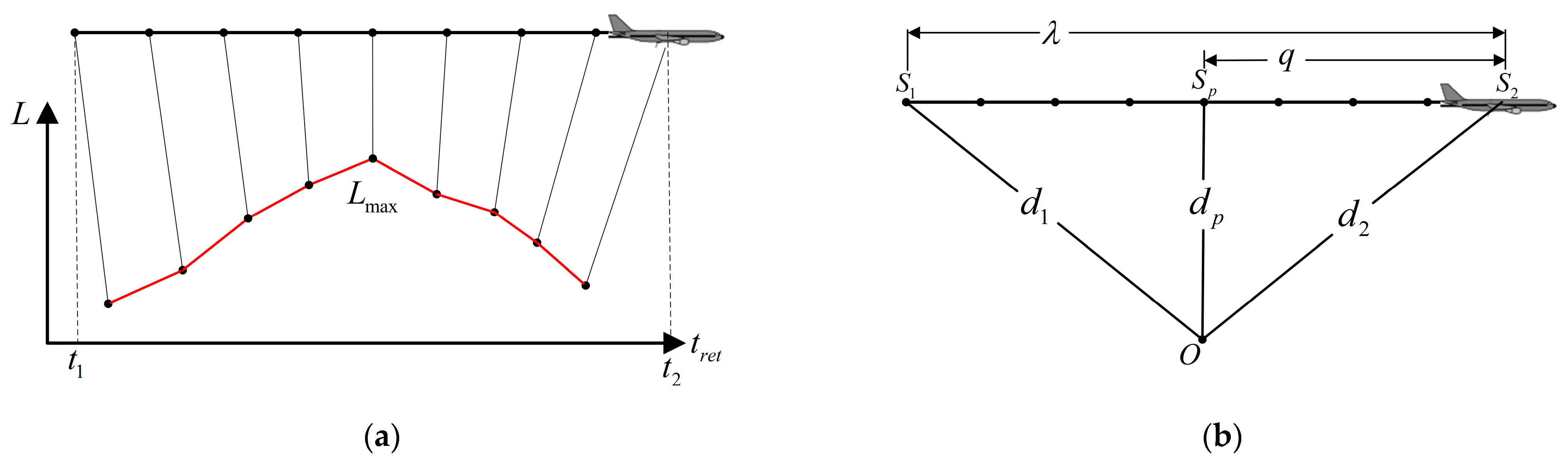
2.1. ECAC Model
- The propagation of aviation noise remains isotropic.
- The aircraft engine power, climb or descent angle, flap settings, and other flight states remain unchanged in each segmented track, i.e., the flight state is updated once per track segment.
- The ground is a constant single medium with negligible noise absorption.
2.2. Neural Networks
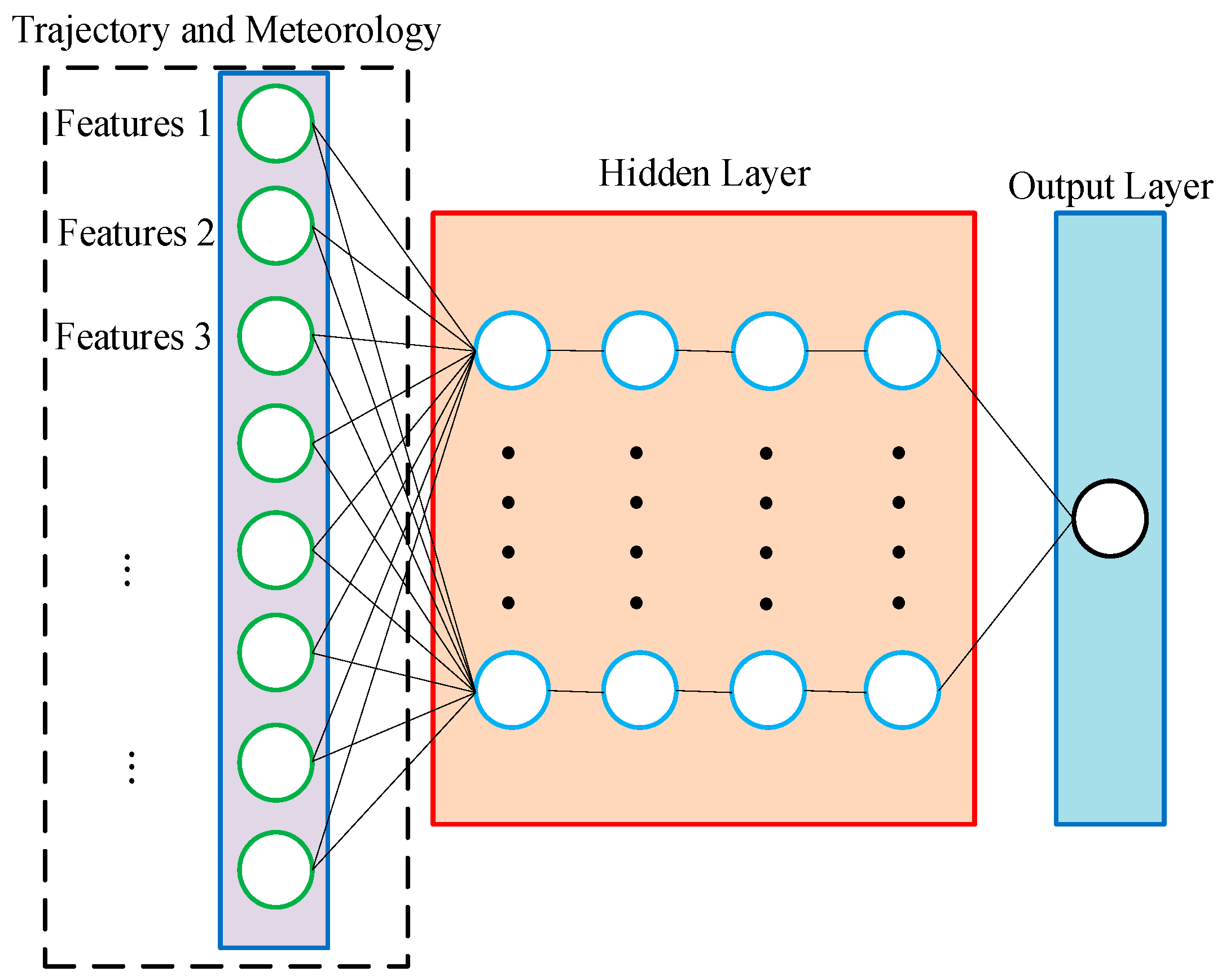
2.2.1. Input Features
- Flight trajectory
- 2.
- Meteorological data
- 3.
- Engine thrust and aircraft weight
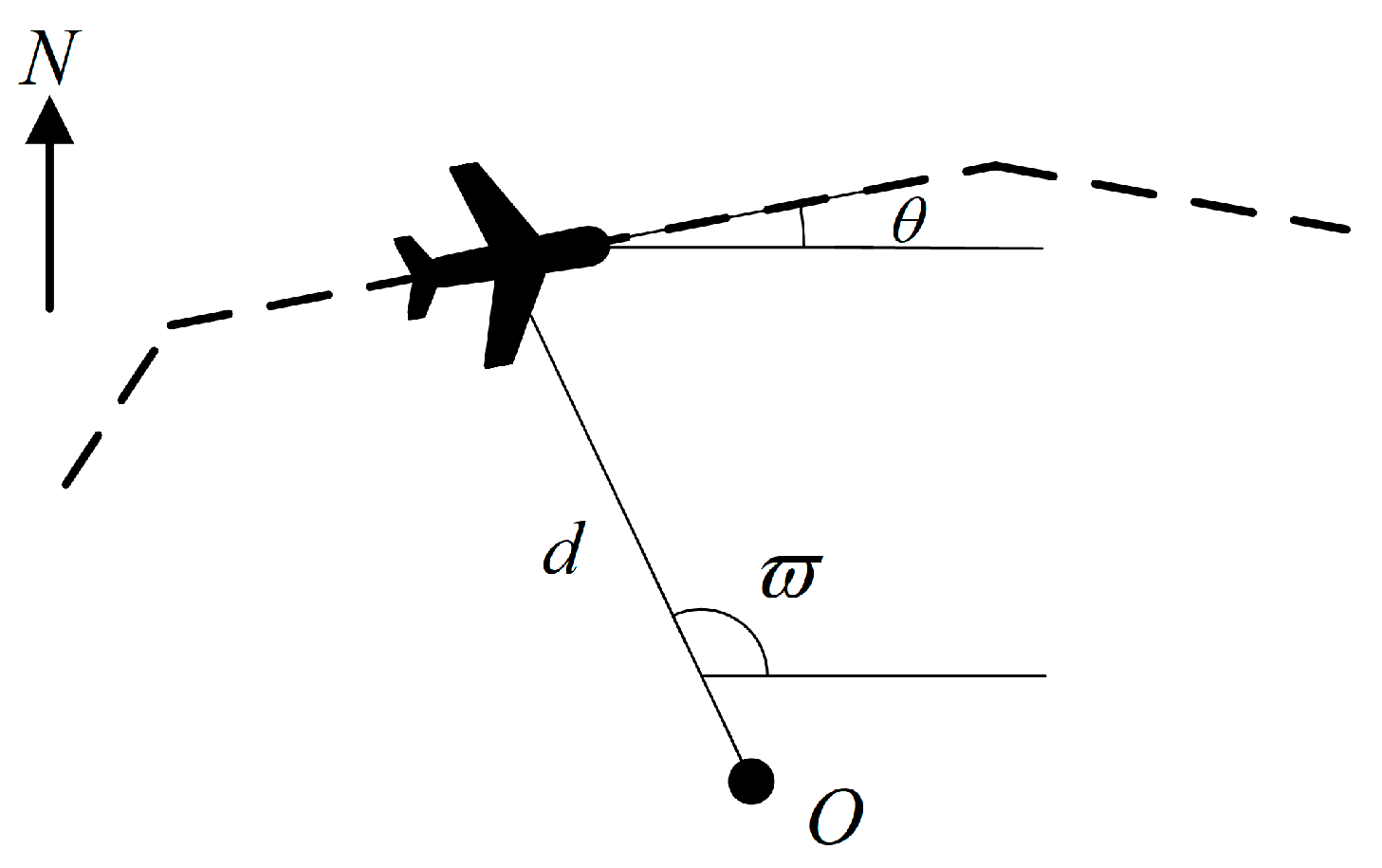
- Slant distance d and azimuth angle . Aircraft position relative to a ground observer.
- Ground-speed v and heading of the aircraft
- Arrival or departure. Indication of the operation type of the flight
- Airport temperature, humidity, and atmospheric pressure at the nearest 1 min time
- Wind speed and direction at the nearest 2 min time
- Engine thrust and aircraft weight constructed using ECAC model
2.2.2. Neural Network
- DNN model
- 2.
- HPNN model
- 3.
- PGNN model
2.3. Implementation
| Algorithm 1: ECAC-based single-event noise prediction algorithms |
| Input: 1. Standardized trajectory , includes monitoring time, longitude, latitude, altitude, ground speed, flight number and heading 2. Meteorological feature datasets includes temperature, atmospheric pressure, relative humidity, wind speed and direction 3. ANP Database Process: 1. Determine the coordinates of ground monitoring observation points 2. Match() // Match NPD curves 3. // Update to correct the NPD curve 4. for i1 to do ; // Calculate engine thrust ; // Calculate aircraft weight ; // Calculate Sound Exposure Level using ECAC end for Output: ECAC model-calculated single-event noise sound exposure levels |
| Algorithm 2: Implementation steps of DNN algorithm |
| Input: 1. Standardized trajectory , includes monitoring time, longitude, latitude, altitude, ground speed, flight number and heading 2. Meteorological feature datasets includes temperature, atmospheric pressure, relative humidity, wind speed and direction 3. Number of hidden layers 4. Number of neurons in each hidden layer Loss function construction: The loss function of the DNN is to calculate the mean square error between the output value of the model and the true value Output: DNN model-calculated single-event noise sound exposure levels |
| Algorithm 3: Implementation steps of HPNN algorithm |
| Input: 1. Standardized trajectory , includes monitoring time, longitude, latitude, altitude, ground speed, flight number and heading 2. Meteorological feature datasets includes temperature, atmospheric pressure, relative humidity, wind speed and direction 3. Number of hidden layers 4. Number of neurons in each hidden layer 5. ECAC model-calculated single-event noise sound exposure levels Loss function construction: The loss function of HPNN is the same as that of DNN, which calculates the mean square error between the model output value and the true value . Output: HPNN model-calculated single-event noise sound exposure levels |
| Algorithm 4: Implementation steps of PGNN algorithm |
| Input: 1. Standardized trajectory , includes monitoring time, longitude, latitude, altitude, ground speed, flight number and heading 2. Meteorological feature datasets includes temperature, atmospheric pressure, relative humidity, wind speed and direction 3. Number of hidden layers 4. Number of neurons in each hidden layer 5. ECAC model-calculated single-event noise sound exposure levels 6. Physical constraint weight Loss function construction: Add physical condition constraints to the loss function of the original HPNN model to guide the model to optimize in the direction of physical consistency and obtain the loss function . Output: PGNN model-calculated single-event noise sound exposure levels |
| Algorithm 5: The training process of DNN, HPNN, and PGNN |
| 1. Back propagation optimization is performed with the goal of minimizing the loss function construction. The Adam optimizer is used to update the model weight parameters and continuously adjust the parameters to optimize the model. By using a K-fold cross-validation method (specifically set to k = 5), we iteratively train the model using the training set data. In each round of cross-validation, the model is trained on a training subset and evaluated on a validation subset. 2. If the error metrics obtained after cross-validation meet the expected performance criteria, this indicates that the model training is complete and meets the predefined accuracy requirements. Conversely, if the error does not meet expectations, we will repeat the training and optimization steps of the model until we obtain results that satisfy the desired training model performance. |
3. Validation
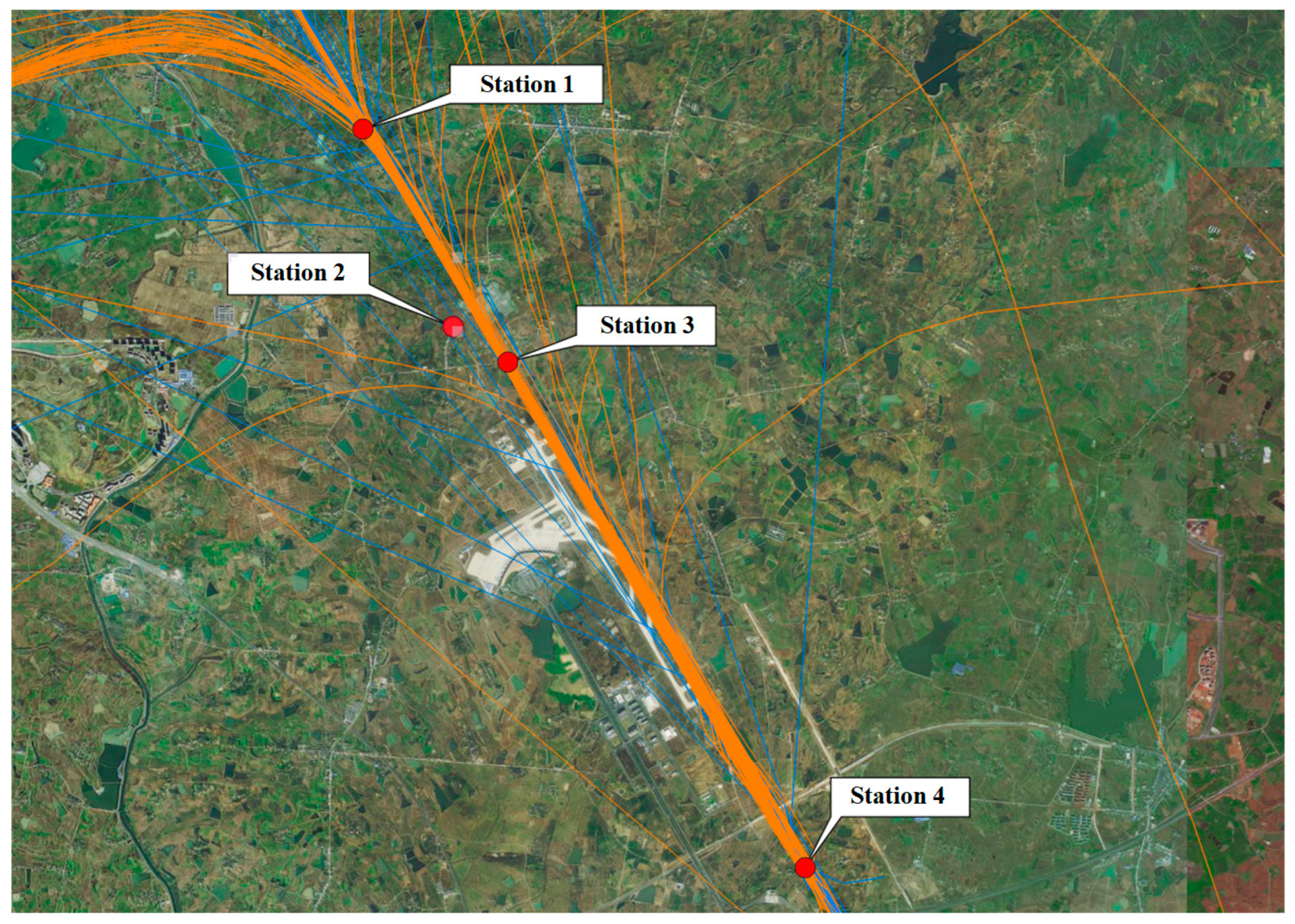
3.1. Data Description
3.2. Evaluation Metrics
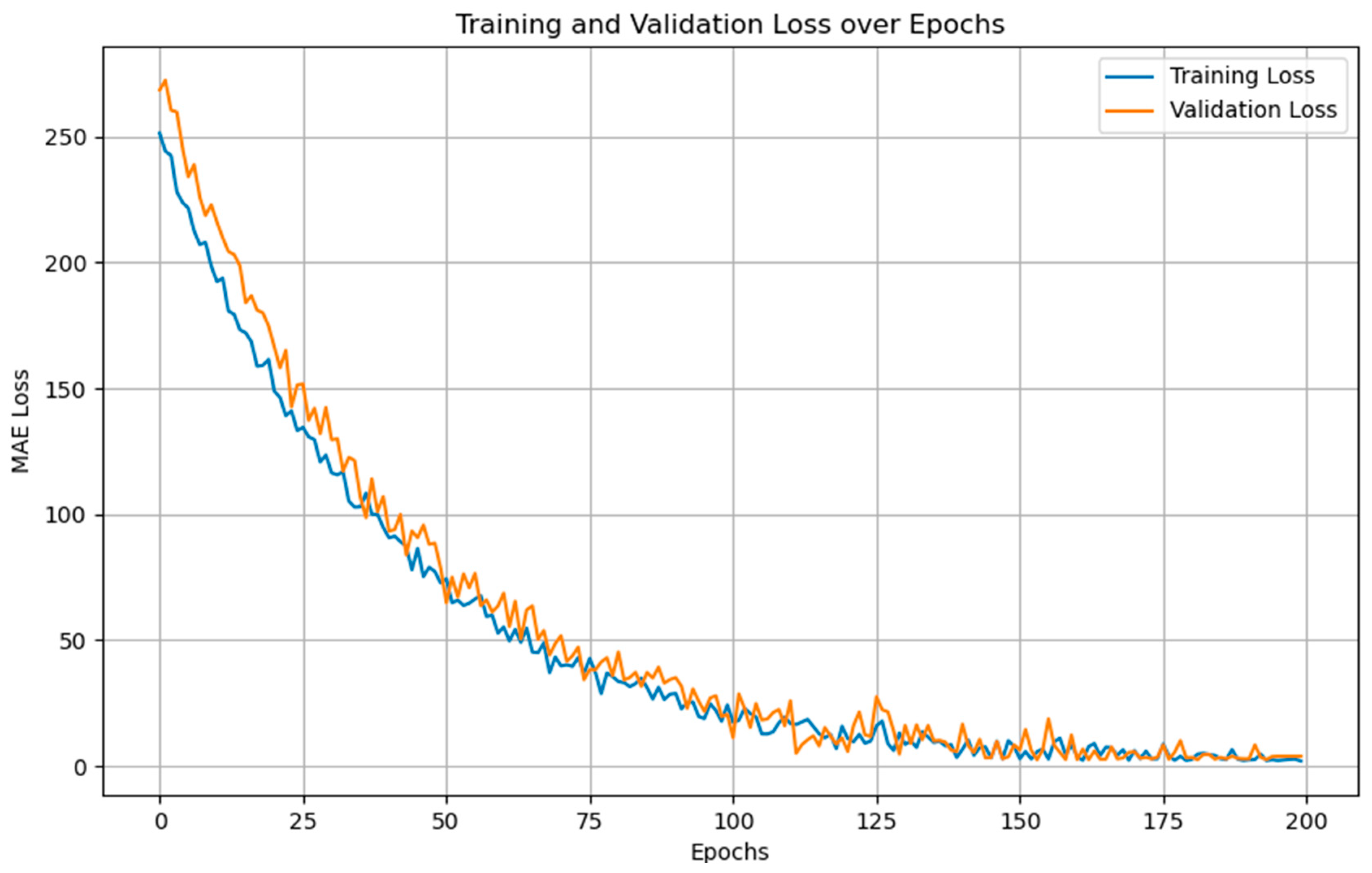
3.3. Model Training and Experimental Design
- Physically driven ECAC model;
- DNN neural network model, which uses trajectory and meteorological features as inputs and monitored noise information as labels;
- HPNN model, which adds ECAC physical output characteristics as input to the DNN model;
- PGNN model, which incorporates physical laws into a modified loss function based on the HPNN framework to guide the entire training process.
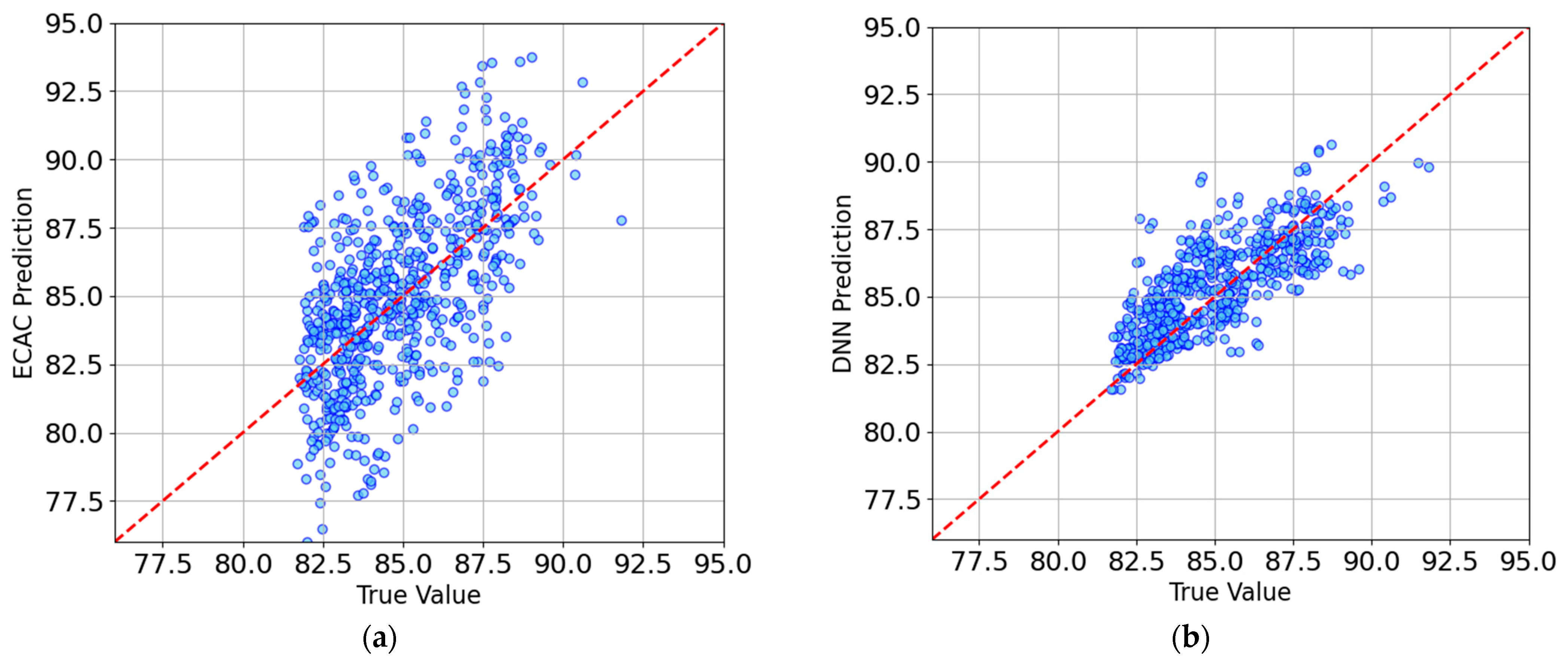
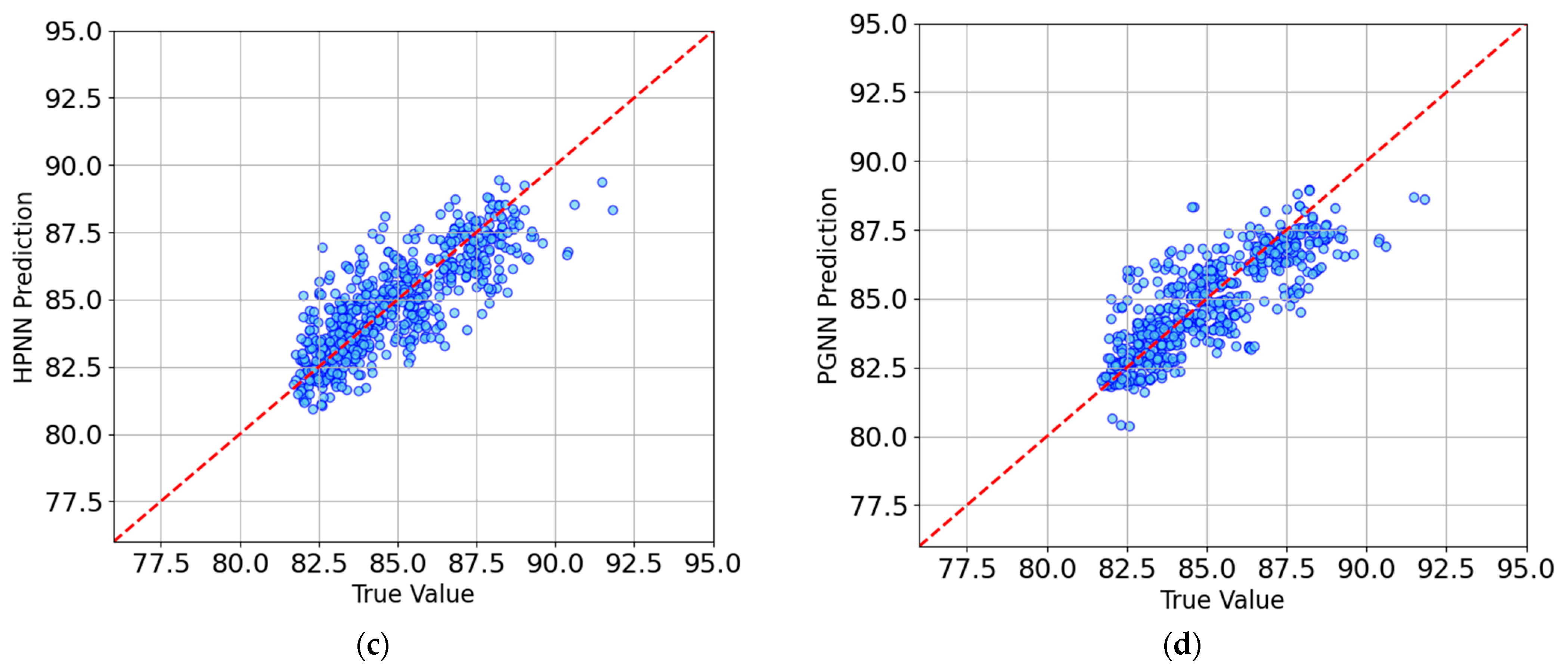
3.4. Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jackson, D.C.; Rindfleisch, T.C.; Alonso, J.J. A system for measurement and analysis of aircraft noise impacts. Eng. Proc. 2021, 13, 6. [Google Scholar] [CrossRef]
- Pretto, M.; Giannattasio, P.; De Gennaro, M.; Zanon, A.; Kühnelt, H. Web data for computing real-world noise from civil aviation. Transp. Res. Part D Transp. Environ. 2019, 69, 224–249. [Google Scholar] [CrossRef]
- Pretto, M.; Giannattasio, P.; De Gennaro, M.; Zanon, A.; Kuehnelt, H. Forecasts of future scenarios for airport noise based on collection and processing of web data. Eur. Transp. Res. Rev. 2020, 12, 4. [Google Scholar] [CrossRef]
- Feng, H.; Zhou, Y.; Zeng, W.; Ding, C. Review on metrics and prediction methods of civil aviation noise. Int. J. Aeronaut. Space Sci. 2023, 24, 1199–1213. [Google Scholar] [CrossRef]
- Gao, Z.; Mavris, D.N. Statistics and machine learning in aviation environmental impact analysis: A survey of recent progress. Aerospace 2022, 9, 750. [Google Scholar] [CrossRef]
- Pretto, M.; Giannattasio, P.; De Gennaro, M. Mixed analysis-synthesis approach for estimating airport noise from civil air traffic. Transp. Res. Part D Transp. Environ. 2022, 106, 103248. [Google Scholar] [CrossRef]
- Bertsch, L.; Sanders, L.; Thomas, R.H.; LeGriffon, I.; June, J.C.; Clark, I.A.; Lorteau, M. Comparative assessment of aircraft system noise simulation tools. J. Aircr. 2021, 58, 867–884. [Google Scholar] [CrossRef]
- Revoredo, T.; Mora-Camino, F.; Slama, J. A two-step approach for the prediction of dynamic aircraft noise impact. Aerosp. Sci. Technol. 2016, 59, 122–131. [Google Scholar] [CrossRef]
- Lukić, M.; Gavran, D.; Fric, S.; Ilić, V.; Vranjevac, S.; Trpčevski, F. Prediction of aircraft noise using machine learning. In Proceedings of the 27th International Congress on Sound and Vibration, Online, 11–16 July 2021. [Google Scholar]
- Barron, A.R. Universal approximation bounds for superpositions of a sigmoidal function. IEEE Trans. Inf. Theory 1993, 39, 930–945. [Google Scholar] [CrossRef]
- Feng, H.; Zhou, Y.; Ding, C.; Zeng, W.; Guo, W. Aircraft Noise Prediction Based on Machine Learning Model. Trans. Nanjing Univ. Aeronaut. Astronaut. 2023, 40, 54–61. [Google Scholar]
- Vabalas, A.; Gowen, E.; Poliakoff, E.; Casson, A.J. Machine learning algorithm validation with a limited sample size. PLoS ONE 2019, 14, e0224365. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.; Willard, J.; Karpatne, A.; Read, J.S.; Zwart, J.A.; Steinbach, M.; Kumar, V. Physics-guided machine learning for scientific discovery: An application in simulating lake temperature profiles. ACM/IMS Trans. Data Sci. 2021, 2, 1–26. [Google Scholar] [CrossRef]
- Zhou, H.; Qiu, Y.; Feng, Y.; Liu, J. Power prediction of wind turbine in the wake using hybrid physical process and machine learning models. Renew. Energy 2022, 198, 568–586. [Google Scholar] [CrossRef]
- June, J.C.; Thomas, R.H.; Guo, Y. System Noise Prediction Uncertainty Quantification for a Hybrid Wing–Body Transport Concept. AIAA J. 2020, 58, 1157–1170. [Google Scholar] [CrossRef]
- Gabrielian, A.B.; Puranik, T.G.; Bendarkar, M.V.; Kirby, M.; Mavris, D.; Monteiro, D. Noise model validation using real world operations data. In Proceedings of the 2021 AIAA Aviation and Aeronautics Forum and Exposition, Online, 2–6 August 2021; p. 2136. [Google Scholar]
- Simons, D.G.; Besnea, I.; Mohammadloo, T.H.; Melkert, J.A.; Snellen, M. Comparative assessment of measured and modelled aircraft noise around Amsterdam Airport Schiphol. Transp. Res. Part D Transp. Environ. 2022, 105, 103216. [Google Scholar] [CrossRef]
- Thomas, R.H.; Burley, C.L.; Guo, Y. Progress of aircraft system noise assessment with uncertainty quantification for the environmentally responsible aviation project. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May 2016; p. 3040. [Google Scholar]
- von Rueden, L.; Mayer, S.; Sifa, R.; Bauckhage, C.; Garcke, J. Combining machine learning and simulation to a hybrid modelling approach: Current and future directions. In Proceedings of the Advances in Intelligent Data Analysis XVIII: 18th International Symposium on Intelligent Data Analysis, IDA 2020, Konstanz, Germany, 27–29 April 2020; Proceedings 18. pp. 548–560. [Google Scholar]
- Jurj, S.L.; Grundt, D.; Werner, T.; Borchers, P.; Rothemann, K.; Möhlmann, E. Increasing the safety of adaptive cruise control using physics-guided reinforcement learning. Energies 2021, 14, 7572. [Google Scholar] [CrossRef]
- Monaco, S.; Apiletti, D.; Malnati, G. Theory-guided deep learning algorithms: An experimental evaluation. Electronics 2022, 11, 2850. [Google Scholar] [CrossRef]
- Murphy, C.P.; Kerekes, J.P. Physics-guided neural network for predicting chemical signatures. Appl. Opt. 2021, 60, 3176–3181. [Google Scholar] [CrossRef]
- Changdar, S.; Bhaumik, B.; De, S. Physics-based smart model for prediction of viscosity of nanofluids containing nanoparticles using deep learning. J. Comput. Des. Eng. 2021, 8, 600–614. [Google Scholar] [CrossRef]
- Karpatne, A.; Atluri, G.; Faghmous, J.H.; Steinbach, M.; Banerjee, A.; Ganguly, A.; Shekhar, S.; Samatova, N.; Kumar, V. Theory-guided data science: A new paradigm for scientific discovery from data. IEEE Trans. Knowl. Data Eng. 2017, 29, 2318–2331. [Google Scholar] [CrossRef]
- Uzun, M.; Demirezen, M.U.; Inalhan, G. Physics guided deep learning for data-driven aircraft fuel consumption modeling. Aerospace 2021, 8, 44. [Google Scholar] [CrossRef]
- Bode, M.; Gauding, M.; Lian, Z.; Denker, D.; Davidovic, M.; Kleinheinz, K.; Jitsev, J.; Pitsch, H. Using physics-informed enhanced super-resolution generative adversarial networks for subfilter modeling in turbulent reactive flows. Proc. Combust. Inst. 2021, 38, 2617–2625. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, F. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Cang, R.; Li, H.; Yao, H.; Jiao, Y.; Ren, Y. Improving direct physical properties prediction of heterogeneous materials from imaging data via convolutional neural network and a morphology-aware generative model. Comput. Mater. Sci. 2018, 150, 212–221. [Google Scholar] [CrossRef]
- Sadowski, P.; Fooshee, D.; Subrahmanya, N.; Baldi, P. Synergies between quantum mechanics and machine learning in reaction prediction. J. Chem. Inf. Model. 2016, 56, 2125–2128. [Google Scholar] [CrossRef]
- Yazdani, A.; Lu, L.; Raissi, M.; Karniadakis, G.E. Systems biology informed deep learning for inferring parameters and hidden dynamics. PLoS Comput. Biol. 2020, 16, e1007575. [Google Scholar] [CrossRef]
- Bernardo, J.E.; Kirby, M.; Mavris, D. Development of a rapid fleet-level noise computation model. J. Aircr. 2015, 52, 721–733. [Google Scholar] [CrossRef]
- Kim, S.; Lim, D.; Lee, K. Reduced-order modeling applied to the aviation environmental design tool for rapid noise prediction. J. Aerosp. Eng. 2018, 31, 04018056. [Google Scholar] [CrossRef]
- Ecac, E. CEAC DOC. 29: Report on standard method of computing noise contours around civil airports, volume 2: Technical guide. In Proceedings of the European Civil Aviation Conference (ECAC), Neuilly-sur-Seine, France, 3 September 2016. [Google Scholar]
- Zaporozhets, O.; Levchenko, L. Accuracy of noise-power-distance definition on results of single aircraft noise event calculation. Aerospace 2021, 8, 121. [Google Scholar] [CrossRef]
- International Civil Aviation Organization. Recommended Method for Computing Noise Contours Around Airports, 2nd ed.; International Civil Aviation Organization: Montreal, QC, Canada, 2018. [Google Scholar]
- Torija, A.J.; Self, R.H. Aircraft classification for efficient modelling of environmental noise impact of aviation. J. Air Transp. Manag. 2018, 67, 157–168. [Google Scholar] [CrossRef]
- Synodinos, A.P.; Self, R.H.; Torija, A.J. Framework for predicting noise–power–distance curves for novel aircraft designs. J. Aircr. 2018, 55, 781–791. [Google Scholar] [CrossRef]
- Boeker, E.R.; Dinges, E.; He, B.; Fleming, G.; Roof, C.J.; Gerbi, P.J.; Rapoza, A.S.; Hermann, J. Integrated Noise Model (INM) Version 7.0 Technical Manual; Federal Aviation Administration; Office of Environment and Energy: Fairfax County, VA, USA, 2008.
- Lee, C.B.E.; Downs, R.; Gorshkov, S.; Hansen, A.; Koopmann, J.; Thrasher, T. Aviation Environmental Design Tool (AEDT) Version 3e Technical Manual; DOT-VNTSC-FAA-22-04; Federal Aviation Administration; Office of Environment and Energy: Fairfax County, VA, USA, 2022.
- Berton, J.J. Aircraft Noise and Performance Data for a Notional Supersonic Business Jet. In Proceedings of the 28th AIAA/CEAS Aeroacoustics 2022 Conference, Southampton, UK, 14–17 June 2022; p. 3078. [Google Scholar]
- Thomas, J.L.; Hansman, R.J. Modeling, assessment, and flight demonstration of delayed deceleration approaches for community noise reduction. In Proceedings of the 2020 AIAA Aviation and Aeronautics Forum and Exposition, Online, 15–19 June 2020; p. 2874. [Google Scholar]
- Rodríguez-Díaz, A.; Adenso-Díaz, B.; González-Torre, P.L. A review of the impact of noise restrictions at airports. Transp. Res. Part D Transp. Environ. 2017, 50, 144–153. [Google Scholar] [CrossRef]
- Berton, J.J. Simultaneous use of ground reflection and lateral attenuation noise models. J. Aircr. 2022, 59, 536–543. [Google Scholar] [CrossRef]
- Tenney, A.S.; Glauser, M.N.; Lewalle, J. A deep learning approach to jet noise prediction. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 1736. [Google Scholar]
- Zellmann, C.; Schäffer, B.; Wunderli, J.-M.; Isermann, U.; Paschereit, C. Aircraft noise emission model accounting for aircraft flight parameters. J. Aircr. 2018, 55, 682–695. [Google Scholar] [CrossRef]
- Vela, A.E.; Oleyaei-Motlagh, Y. Ground level aviation noise prediction: A sequence to sequence modeling approach using LSTM recurrent neural networks. In Proceedings of the 2020 AIAA/IEEE 39th Digital Avionics Systems Conference (DASC), Online, 11–15 October 2020; pp. 1–8. [Google Scholar]
- Campos, L.M. On physical aeroacoustics with some implications for low-noise aircraft design and airport operations. Aerospace 2015, 2, 17–90. [Google Scholar] [CrossRef]
- Isermann, U.; Bertsch, L. Aircraft noise immission modeling. CEAS Aeronaut. J. 2019, 10, 287–311. [Google Scholar] [CrossRef]
- Gagliardi, P.; Teti, L.; Licitra, G. A statistical evaluation on flight operational characteristics affecting aircraft noise during take-off. Appl. Acoust. 2018, 134, 8–15. [Google Scholar] [CrossRef]
- Torija, A.J.; Self, R.H.; Flindell, I.H. Airport noise modelling for strategic environmental impact assessment of aviation. Appl. Acoust. 2018, 132, 49–57. [Google Scholar] [CrossRef]
- Chen, T.; Chen, H. Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to dynamical systems. IEEE Trans. Neural Netw. 1995, 6, 911–917. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]


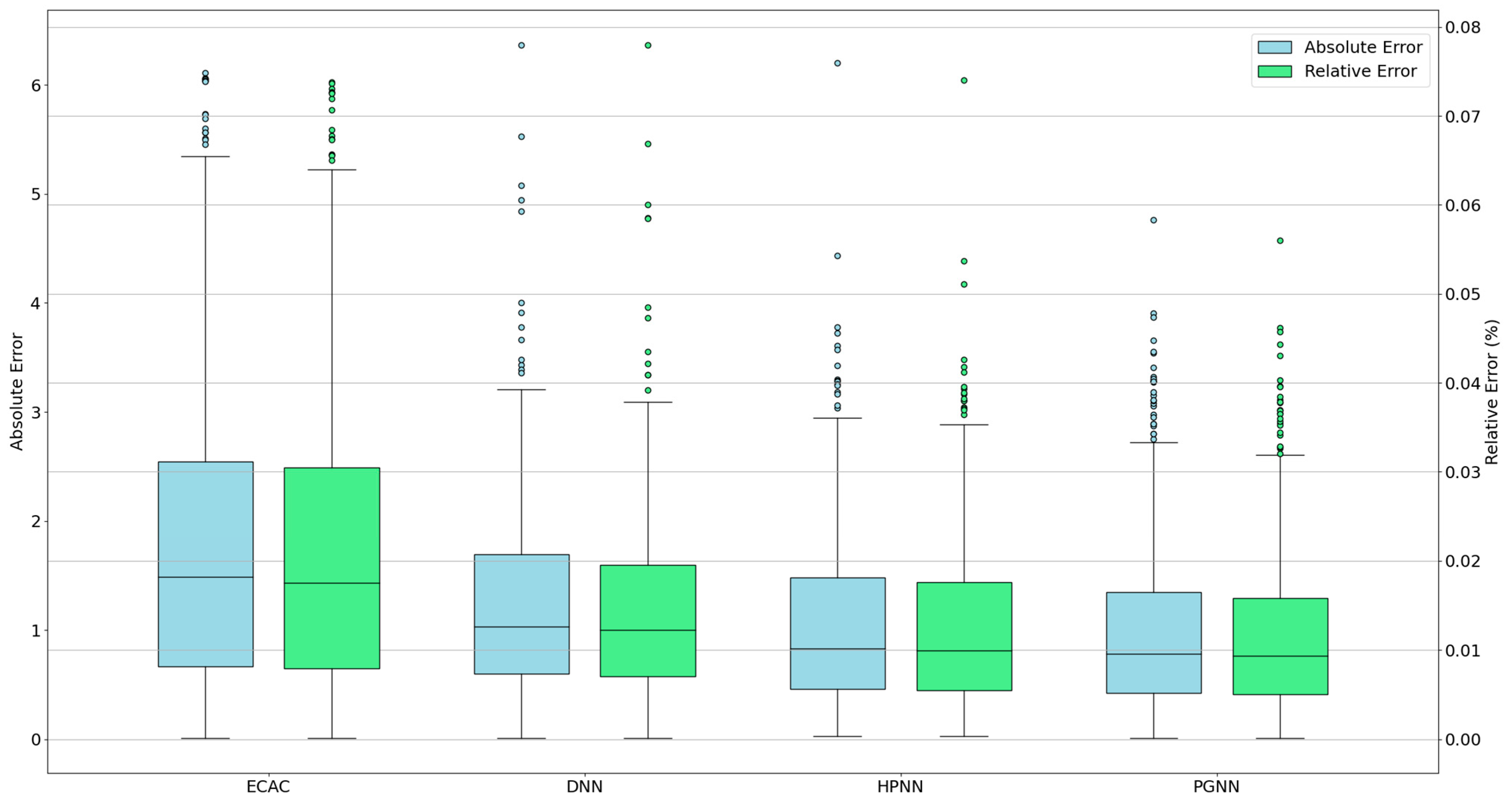
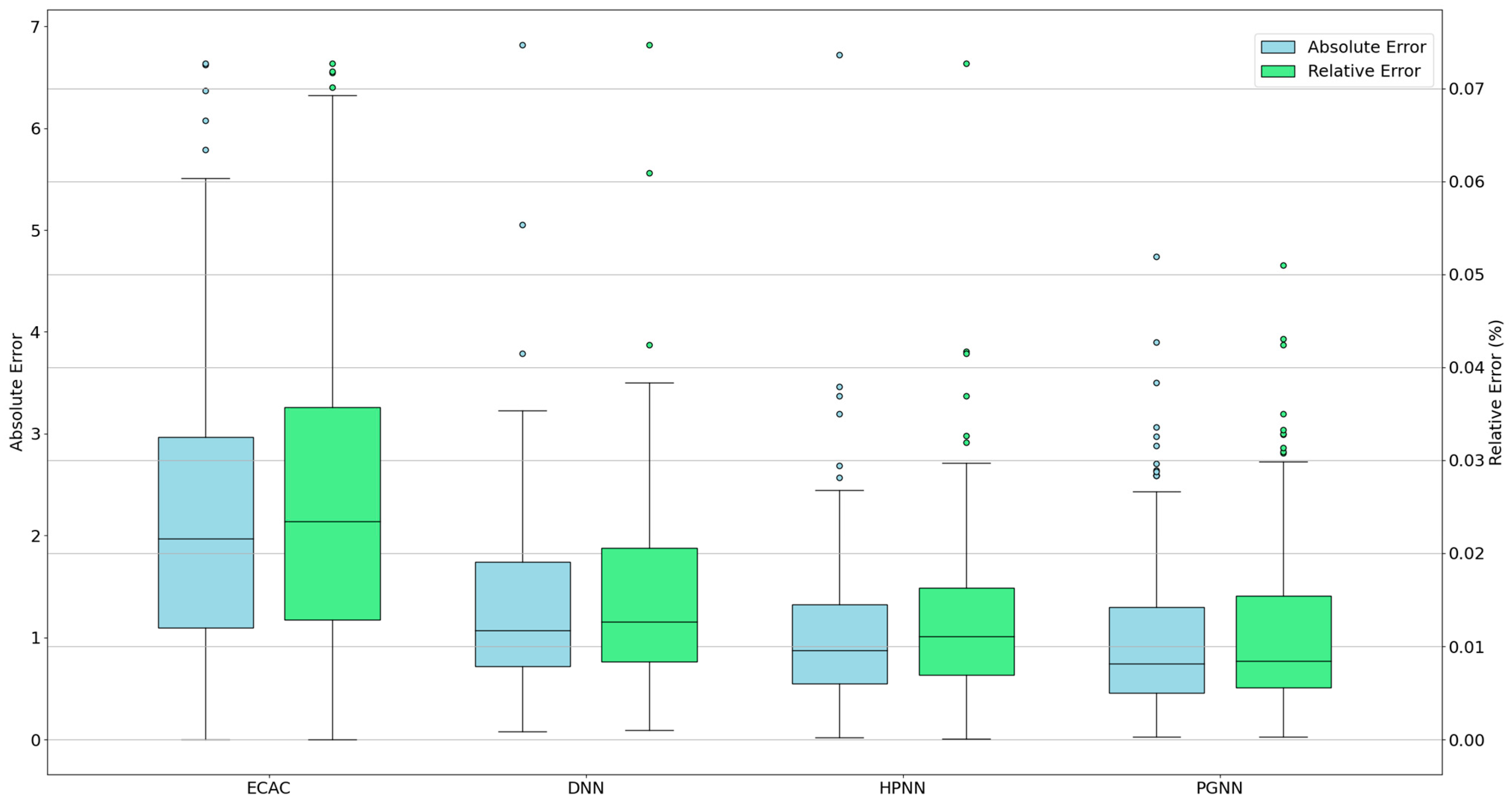
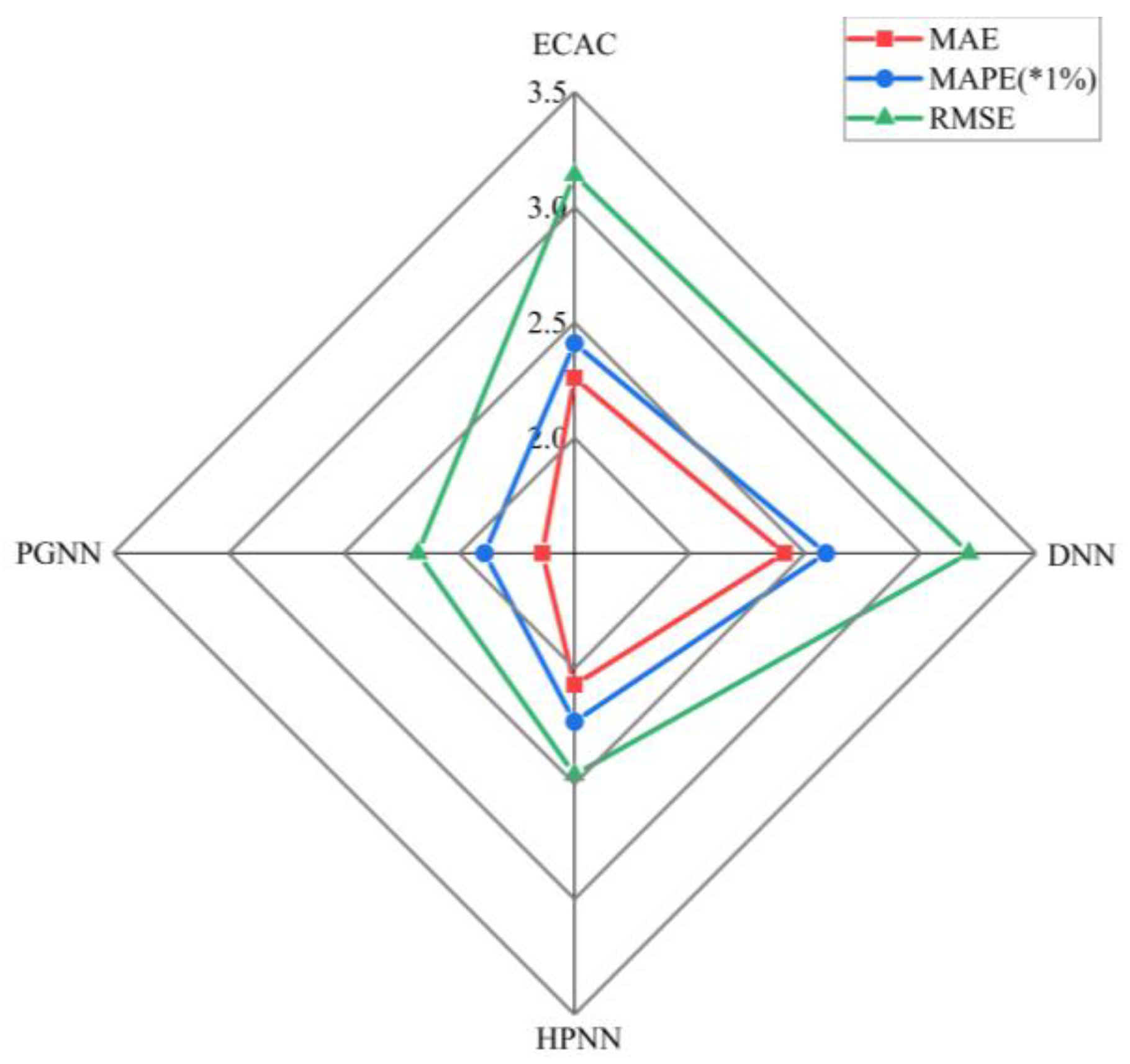
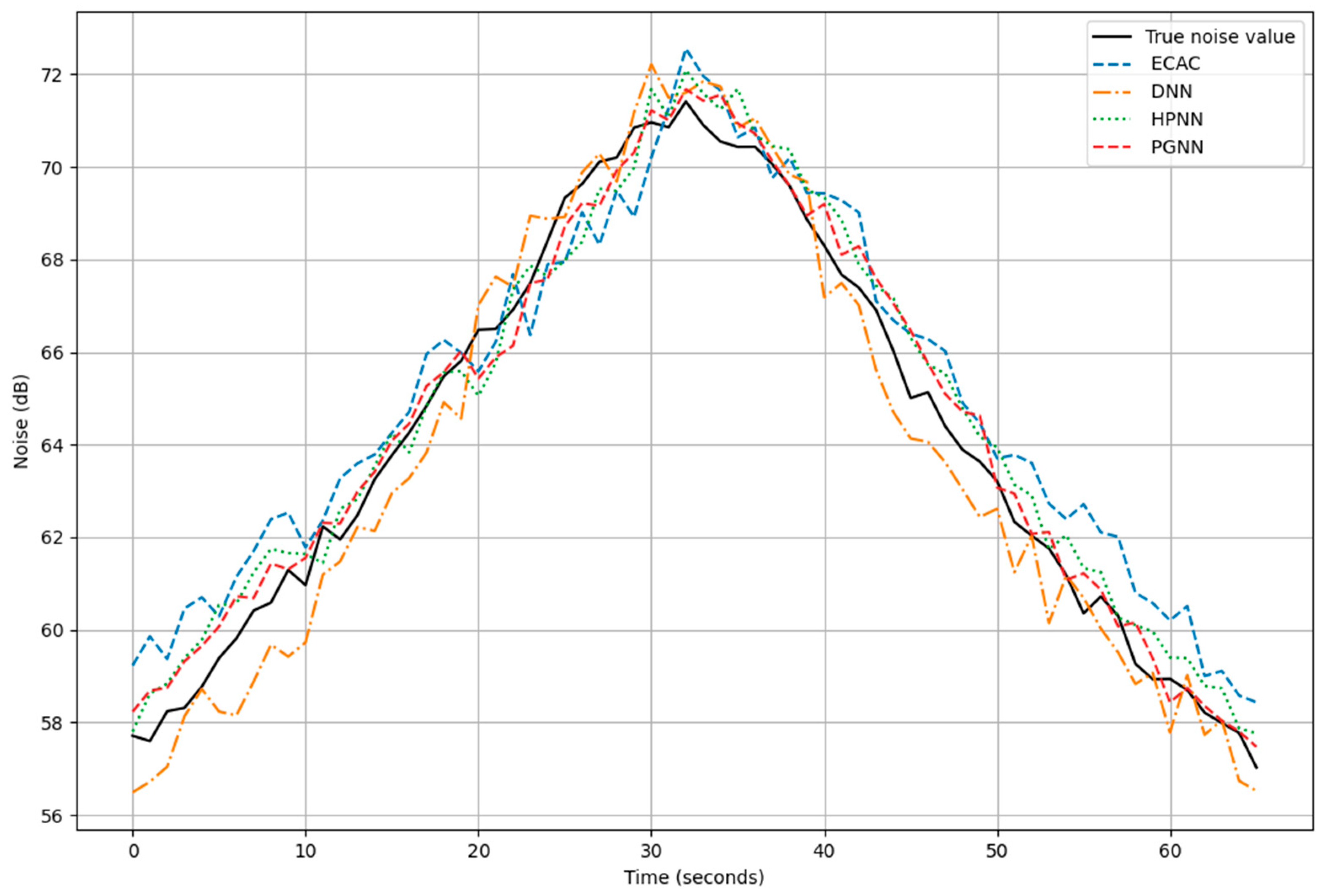
| Stage Length | Great Circle Distance (NM) | Weight (lb) |
|---|---|---|
| 1 | 0–500 | 429,900 |
| 2 | 500–1000 | 442,400 |
| 3 | 1000–1500 | 456,100 |
| 4 | 1500–2500 | 483,100 |
| 5 | 2500–3500 | 516,400 |
| 6 | 3500–4500 | 551,700 |
| 7 | 4500–5500 | 589,400 |
| 8 | 5500–6500 | 629,500 |
| 9 | 6500+ | 656,000 |
| Attribute Name | Attribute Meaning |
|---|---|
| Monitoring time | The point in time at which aircraft trajectory information is collected |
| Longitude | The longitude of the aircraft in a spherical space coordinate system |
| Latitude | The latitude of the aircraft in the spatial spherical coordinate system |
| Altitude | The barometric altitude of the aircraft |
| Ground speed | The projected ground speed of the aircraft |
| Flight number | Exclusive number of the flight |
| Heading | The direction of travel of the aircraft |
| Model. | Hidden Layers | Neurons | η |
|---|---|---|---|
| DNN | 3 | [64, 64, 32] | — |
| HPNN | 3 | [128, 64, 32] | — |
| PGNN | 3 | [128, 64, 32] | 0.31 |
| Model | MAE | MAPE | RMSE |
|---|---|---|---|
| ECAC | 2.24 | 2.39% | 3.11 |
| DNN | 1.26 | 1.54% | 1.57 |
| HPNN | 1.03 | 1.23% | 1.33 |
| PGNN | 0.98 | 1.17% | 1.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, D.; Peng, J.; Ding, C. A Neural Network with Physical Mechanism for Predicting Airport Aviation Noise. Aerospace 2024, 11, 747. https://doi.org/10.3390/aerospace11090747
Zhu D, Peng J, Ding C. A Neural Network with Physical Mechanism for Predicting Airport Aviation Noise. Aerospace. 2024; 11(9):747. https://doi.org/10.3390/aerospace11090747
Chicago/Turabian StyleZhu, Dan, Jiayu Peng, and Cong Ding. 2024. "A Neural Network with Physical Mechanism for Predicting Airport Aviation Noise" Aerospace 11, no. 9: 747. https://doi.org/10.3390/aerospace11090747
APA StyleZhu, D., Peng, J., & Ding, C. (2024). A Neural Network with Physical Mechanism for Predicting Airport Aviation Noise. Aerospace, 11(9), 747. https://doi.org/10.3390/aerospace11090747





