Abstract
The metal fibre surface combustion structure has the characteristics of strong thermal matching ability, short response time, and strong shape adaptability. It has more advantages in the thermal test of complex hypersonic vehicle surface inlet, leading edge, etc. In this paper, a method of aerodynamic thermal simulation test based on metal fibre surface combustion is proposed. The aim of the study was to create a uniform target heat flow on the inner wall surface of a cylindrical specimen by matching the gas jet flow rate and the geometry of the combustion surface. The research adopted the optimisation design method based on the surrogate model to establish the numerical calculation model of a metal fibre combustion jet heating cylinder specimen. One hundred sample points were obtained through Latin hypercube sampling, and a database of design parameters and heat flux was established through numerical simulation. The kriging surrogate model and the non-dominated sequencing genetic optimisation algorithm with elite strategy were adopted. A bi-objective optimisation design was carried out with the optimisation objective of the coincidence between the predicted and the target heat flux on the inner wall of the specimen. The results showed that the average relative errors of heat flow density on the specimen surface were 8.8% and 6% through the leave-one-out cross-validation strategy and the validation of six test sample points, respectively. The relative error values in most regions were within 5%, which indicates that the established kriging surrogate model has high prediction accuracy. Under the optimal solution conditions, the numerical calculation results of the heat flow on the inner wall of the specimen were in good agreement with the target heat flow values, with an average relative error of less than 5% and a maximum value of less than 8%. These results show that the optimisation design method based on the kriging surrogate model can effectively match the thermal test parameters of metal fibre combustion structures.
1. Introduction
The hypersonic vehicle inlet, leading edge, wing rudder structure, and other key parts form a complex surface design. In the process of a hypersonic flight, the surface heat load distribution gradient is large. At the same time, due to the flight process, hypersonic vehicles often manoeuvre or ultra-manoeuvre orbit changes, have thermal loads with a high impact rate, and have non-linear characteristics. These aspects make the vehicle structure face a serious stress overrun, so a full-scale structural thermal test needs to be carried out. Such extreme working conditions make it very difficult to accurately simulate the aerodynamic thermal environment in ground tests.
Over the years, various kinds of ground test systems have been developed at home and abroad to simulate aerodynamic heat by radiation or convection, such as quartz lamps, electric arcs, high-temperature gas burners, etc., so that the technical parameters of the test, such as the temperature, size, and time, are constantly improved.
The NASA Dryden Flight Research Centre, the NASA Flight Load Laboratory, the Russian National Institute of Aerodynamics, and other institutions have conducted research on quartz lamp heaters to achieve a high temperature of more than 1800 K for a long time [1,2]. The thermal test control system developed by Wu Dafang et al. realises the automatic tracking of the preset temperature curve on the surface of the material or structure by adjusting the electric power of the infrared radiant heater. Here, the maximum temperature reaches more than 2000 K, the tracking error between the control curve and the preset curve is not more than 1.5%, and the system control accuracy is high [3,4,5].
NASA Ames conducted the X-33 local large structure investigation using the IHF arc wind tunnel [6]. The Italian Centre for Aerospace Research (CIRA) carried out a thermal assessment of the HYFLEX vehicle nose cone model using the Scirocco arc wind tunnel. China Aerodynamic Research and Development Centre (CIRA) conducted a large number of evaluation tests on key hypersonic vehicle components, such as the leading-edge structure, wave-transparent structure, wing/rudder rotating parts, etc., using arc wind tunnels and achieved satisfactory simulation results [7].
The feasibility and method of high-temperature gas flow testing for typical specimens have been studied in the literature [8]. The research results show that under the premise of existing heating technology, the method of high-temperature gas heating can simulate the stationary heat flow density and stationary temperature on the surface of the specimen under real flight conditions and can simulate the temperature distribution on the surface of the specimen within a certain range of accuracy.
However, the existing testing methods still have certain shortcomings for the thermal testing requirements of complex structures. On the one hand, it is difficult to combine the ability to simulate large-gradient heat flow distribution on the surface with the ability to simulate non-linear, time-varying heat flow with a high impact rate. From the perspective of traditional testing methods, high-temperature wind tunnels are mostly used to achieve non-steady thermal environment simulation in the form of stepped thermal power rise and fall, which makes it difficult to accurately simulate rapid changes in the complex non-linear thermal environment. With quartz lamps and other radiant heating equipment, although the control of the electrical control performance is excellent and they can achieve simulation of high-impact non-linear, time-varying heat flow, it is difficult to accurately simulate the structure of the surface of large-gradient heat flow distribution. On the other hand, due to the installation form of the test system, it is difficult to adapt to the load of heat flow on the surface of large complex structures. Traditional high-temperature wind tunnel specimen size is limited, so it is difficult to achieve the full-size simulation of components. With quartz lamps and other radiant heating equipment, it is difficult to adapt to the complex aerodynamic shape. The high-temperature gas flow test method improves the aerodynamic thermal simulation capability of complex structures to a certain extent, but for specific structures and working conditions, such as inlet structures, there are still problems of insufficient impact rate and poor adaptability [9].
In this study, an aerodynamic thermal simulation test method based on metal fibre surface combustion is proposed. In this method, metal fibre is used as the attachment surface for combustion, and a pre-mixed homogeneous air–fuel mixture is burned on the surface of the metal fibre fabric to simulate the aerodynamic heating process of the hypersonic vehicle by heating the test specimen by radiation and convection. This method has the ability to simulate high-impact-rate, non-linear, time-varying heat flow; adapt to complex structural profiles; and simulate large-gradient heat flow distributions. For a cylinder specimen, the radial jet heating characteristics are analysed, and structural improvement of the combustion surface is proposed. Furthermore, a kriging surrogate model is established, and a non-dominated sorting genetic algorithm (NSGA-II) with an elite strategy is used to perform bi-objective optimisation, complete the matching design of the thermal test parameters, and obtain reasonable values of the test parameters. This study lays the foundation for carrying out a thermal test of the combustion structure of metal fibre surfaces.
2. Thermal Test Method for the Combustion Structure of Metal Fibre Surfaces
Metal fibre surface combustion is a fully pre-mixed combustion method with metal fibre as the attachment surface. It has high combustion thermal intensity, a large adjustment range, a short response time, and excellent shape adaptability [10]. This paper proposes a structural thermal test method based on metal fibre surface combustion, which makes use of the above characteristics to provide a new solution to the problem of aerodynamic thermal simulation of complex structures.
The thermal test apparatus of the metal fibre surface combustion structure, as shown in Figure 1, consists of a fuel supply subsystem, an air supply subsystem, a combustion subsystem, a measurement subsystem, and a control subsystem. The metal fibre can be an iron–chromium–aluminium alloy with a 2 mm thick braid layer.
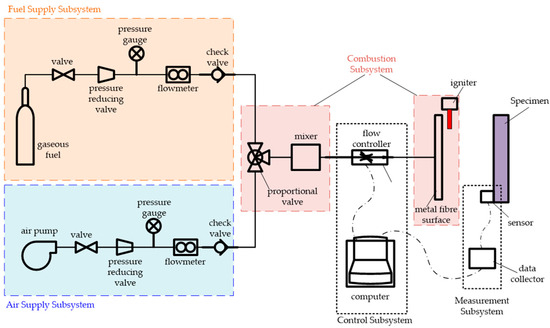
Figure 1.
Schematic of the thermal test device for the metal fibre surface burning structure.
The fuel supply subsystem is used to provide the specified fuel flow rate to the combustion subsystem and consists of a gaseous fuel source, a manual valve, a pressure-reducing valve, a pressure gauge, a flowmeter, and a check valve. The air supply subsystem is used to provide the specified flow rate of air to the combustion subsystem, which has a similar composition to the fuel supply system. The combustion subsystem is used to mix the gaseous fuel and air and combust on the surface of the metal fibre. It consists of a proportional valve, a mixer, an igniter, and a combustion surface. The proportional valve is used to control the proportion of gaseous fuel and air supplied to the combustion subsystem. The mixer is used to evenly mix the gaseous fuel and air in a confined space. The igniter is used to initiate combustion of the air–fuel mixture. The combustion surface is made of metal fibre and is used to provide support for the flame. The measurement subsystem is used to measure the temperature and surface heat flow of the specimen in real time during the test and to provide measured parameters to the control subsystem, which consists of a sensor and a data collector. The control subsystem is used to control the heat flow in real time during the test and consists of a computer and a flow controller. By controlling the flow controller through the computer, the air–fuel mixture flow is adjusted to control the heat flow, which automatically follows the preset target value of the heat flow and achieves loading with a fast impact rate and large non-linear, time-varying heat flow. The metal fibre burning head can be made into different shapes to meet the testing requirements of specimens with different appearances. In addition, the metal fibre burning surface can be divided into zones so that the heating intensity can be independently controlled according to the different surface heat flow requirements of different areas of the specimen, thus realising simulation of the heat flow gradient.
For a cylindrical specimen, the metal fibre combustion surface can be formed into a cylindrical shape so that the gas flow is injected radially against the inner wall surface of the specimen, as shown in Figure 2.
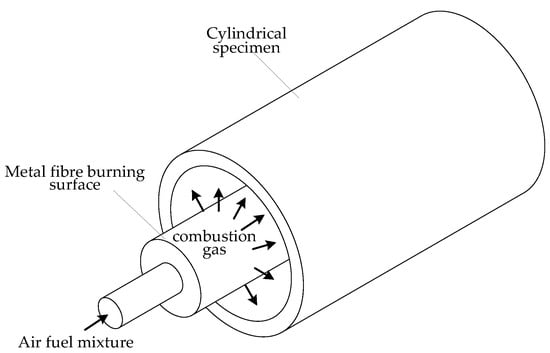
Figure 2.
Schematic diagram of the gas radial jet for a cylindrical specimen.
3. Radial Jet Heating Performance of Cylindrical Combustion Surface
3.1. Numerical Calculation Model
The hypersonic vehicle inlet generates severe temperature gradient and temperature shock effects under aerodynamic heating, which leads to large thermal stresses in its structure [11,12]. For example, a hypersonic vehicle inlet is simplified into a cylindrical type for a particular inlet structure, as shown in Figure 3. The radial length of the cylindrical sample is L = 175 mm, the inner diameter of the sample is D2 = 139 mm, the thickness of the sample is h = 10 mm, and the outer diameter of the combustion surface is D1 = 75 mm for the preliminary design.
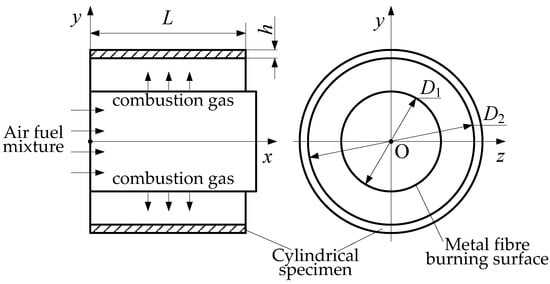
Figure 3.
Profile drawing of the simplified cylinder specimen of the air inlet.
In this study, the commercial software Fluent was used for numerical calculations with a semisymmetric model, and the grid model is shown in Figure 4. Three sets of coarse (2 million), dense (3.5 million), and precision (4.5 million) grids were used to perform the grid-independent validation. The turbulence model was based on the standard k-ε two-equation model, and the wall function was treated with an enhanced wall treatment to keep y+ around 1. In Figure 5, the density distribution of the heat flow at the wall surface under different grid sizes is shown. The deviation between the dense grid and the precision grid calculation results was small, and 3.5 million grids were selected for calculation in this study.

Figure 4.
Mesh structure of the computational model.
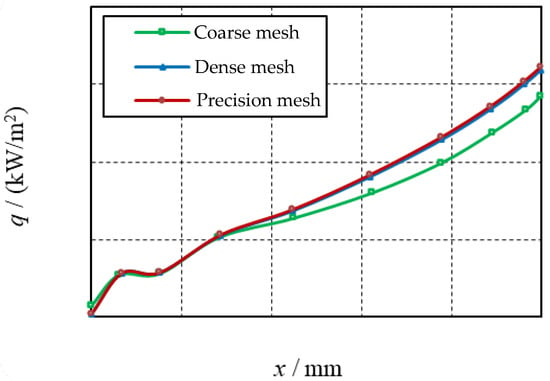
Figure 5.
Heat flux at the inner wall surface of the specimen with different mesh volumes.
High-temperature burning gas is produced by the combustion of methane in air. Assuming a fuel equivalence ratio of 1, the methane was completely burnt. NOx and other trace gases were omitted, so the main components of the gas were N2, CO2, and H2O. To improve the accuracy of the numerical calculations, the variation of the physical parameters with temperature must be taken into account [13]. The constant pressure specific heat capacity, thermal conductivity, and kinetic viscosity were calculated using the fitting function of temperature [14]. According to the physical parameters of each gas phase component, the variation of physical parameters of the combustion gas mixtures with temperature was obtained as shown in Table 1.

Table 1.
Physical properties of combustion gas.
The combustion gas temperature was set at 1700 K, and the surface temperature of the metal fibre was set at 1100 K [15]. The calculation of the heat flow on the specimen surface under different working conditions was carried out by changing the incoming flow rate. The surface temperature and heat flow distribution of the specimen was analysed by taking into account one of the working conditions, the combustion gas temperature distribution of the domain between the inner surface of the specimen and the surface of the metal fibre, as shown in Figure 6. The distribution of the heat flow was avoided in the cylindrical specimen, as shown in Figure 7.
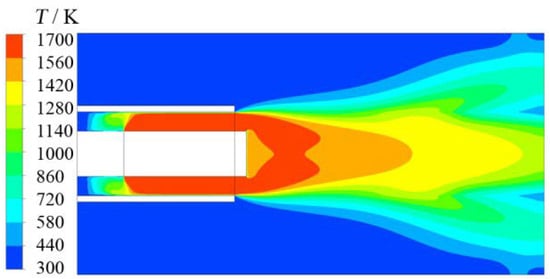
Figure 6.
The temperature distribution of combustion gas on the symmetry plane.
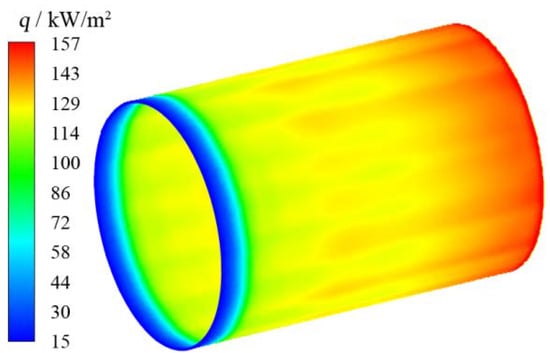
Figure 7.
The heat flux distribution on the inner surface of the cylindrical specimen.
3.2. Calculation Result Analysis
When both the combustion surface and the specimen wall were cylindrical, it can be seen from the above heat flow distribution cloud diagram that the heat flow on the specimen surface increased along the axial direction of gas flow, and the heat flow near the exit position was the largest. Through the optimised design of the cylindrical combustion parameters, the difference between the calculated and target heat flow was still significant. The results indicated that the axial heat flow gradient was significant when the combustion surface was parallel to the specimen surface. As the flow was radial from the combustion surface to the inner wall surface of the specimen, the flowrate increased from the origin to the x-direction, which made it difficult to achieve uniform heat flow.
In order to obtain a specified rate of uniform heat flow on the surface of the specimen, the structure of the combustion surface was improved by adopting a conical combustion surface, as shown in Figure 8, so that the distance between the combustion surface and the surface of the specimen increased axially to gradually expand the flow path, thus avoiding the uneven distribution of heat flow caused by the increase in the flow rate. For the radial jet heating scheme of the conical combustion surface, the parameters that affect the magnitude and uniformity of the heat flow on the specimen include the air–fuel mixture flow rate G, the diameter of the top surface of the conical combustion surface D11, and the diameter of the bottom surface D12 [16]. Therefore, this study took these three parameters as the optimisation design variables. The optimisation objective was the consistency between the inner wall surface heat flow and the target heat flow. The optimisation was performed to obtain the optimal test solution.
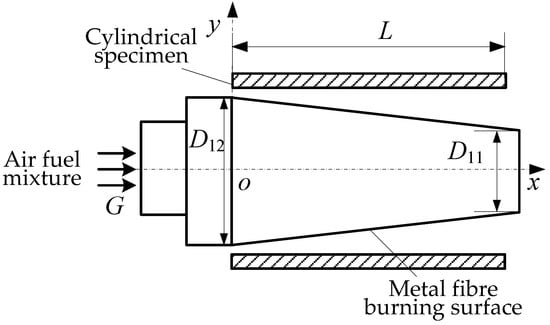
Figure 8.
Radial jet heating of cylindrical specimens with conical combustion surface.
4. Surrogate Model and Optimisation Method
The radial jet heating characteristics of the conical combustion surface are complex, and it is difficult to obtain the relationship between the heat flow distribution and the optimisation variables by analytical methods or empirical formulae. An iterative optimisation based solely on CFD numerical calculations requires a large number of calculations, which is not efficient. The use of the surrogate model instead of the original numerical analysis model for iterative optimisation has the characteristics of high accuracy and good robustness [17,18], which can greatly improve the computational efficiency when applied to the design of a radial jet heating system for conical combustion surface optimisation.
4.1. Experimental Design Method
Experimental design methods are used to reasonably distribute the design sample points to be simulated in the design space, which is an important statistical method in the optimisation process loop. Among the commonly used experimental design methods, the Latin hypercube design method is characterised by good spatial homogeneity and coverage and can obtain a large amount of information required for constructing a surrogate model with a smaller number of simulations.
The Latin hypercube design method uses a stratified sampling method, and Equation (1) shows the method of generating the design points for its trials. Here, i denotes the ith trial, p denotes the pth design variable, n is the number of sample points, π is the independent random permutation of π, and U is the random number in the interval [0, 1].
In this study, the lhsdesign function in Matlab R2014a was used to optimise the sampling method, i.e., for the optimal Latin hypercubic sampling method, the standard parameter of lhsdesign function sampling was set to maximin, and the number of iterations was 100 times.
4.2. Kriging Surrogate Modelling Approach
In the matching design of thermal test conditions and specimen surface heat flow, the surrogate model can be used to obtain the surrogate relationship between thermal test conditions (design variables) and specimen surface heat flow (system response), which can be used as a substitute for direct CFD analysis and improve the optimisation design efficiency of parameter matching under the premise of ensuring credibility of the analysis. Commonly used surrogate modelling methods include the response surface model, the radial basis function model, and the kriging model. Among them, it is easier to obtain ideal fitting results with the kriging model when solving problems with a high degree of non-linearity [19]. Therefore, this study adopted the kriging method to establish the surrogate model.
The kriging model is a method for finding linearly optimal, unbiased interpolation estimates for data points distributed in space, and its mathematical expression can be expressed as follows:
where g(X) is the global approximation model on the matrix X within the design space, and z(X) is a stochastic process with zero mean, σ2 variance, and non-zero covariance.
The covariance matrix of z(X) can be expressed as follows:
where R is the correlation matrix, R is the correlation function, and i = 1, 2, …, n, j = 1, 2, …, n (n is the number of sample points). R is a symmetric matrix, and its diagonal element is 1. R takes the Gaussian correlation function, which can be expressed as follows:
where m is the number of design variables, and θ is the vector of unknown correlation parameters.
Introducing the correlation vector,
The kriging model can be expressed as follows:
where β is the unknown parameter, σ2 and R are both functions of θ, and y is an n-dimensional column vector consisting of the response values of the sample points .
β and σ2 can be obtained by least squares estimation. The relevant parameter θ can be obtained by optimising the great likelihood estimation.
4.3. Bi-Objective Optimisation Method
In this study, the objective was to obtain a uniform heat flow on the inner wall surface of a cylindrical specimen of a certain size, so the heat flow distribution on the surface of the cylindrical specimen predicted by the simulation must be as similar as possible to that of the objective. The cylindrical specimen is divided into two segments along the axial direction on an average basis so that the average relative errors of the heat flow in these two segments are minimised by matching the conical combustion surfaces. Therefore, the objective function can be expressed as follows:
where denotes the average relative error of heat flow on the inner wall surface of the specimen with the x coordinate range of (0, 1/2L], as shown in Figure 8, and denotes the average relative error of heat flow on the inner wall surface of the specimen with the x coordinate range of (1/2L, L]. The average relative error value can be calculated by Equation (8):
where is the target heat flow on the inner wall surface of the specimen, is the predicted heat flow on the surface of the specimen, and N is the number of nodes on the surface of the specimen in the calculation region.
denotes the optimised design variable matrix, which consists of three adjustable parameters in the thermal test:
where G is the airflow rate in kg/s, D11 is the diameter of the top surface of the conical burning surface in mm, and D12 is the diameter of the bottom surface in mm.
Considering that the diameter of the inner wall surface of the cylindrical specimen was 139 mm and the combustion surface was conical, the range of values of the design optimisation variables are listed in Table 2.

Table 2.
Value range of design variables.
For the above bi-objective optimisation problem, this study adopted the non-dominated sorting genetic algorithm (NSGA-II) [20] with an elite strategy to carry out the optimisation design. The computational flow is shown in Figure 9. First, initial parent populations (G = 1, where G is the number of population generations) were randomly generated within the range of values of the optimisation variables. Then, the parent population generated offspring populations of the same size. The parent and offspring populations were merged to form a population of size 2N. The newly generated population was subjected to non-dominated fast sorting, and the degree of crowding was calculated for all individuals in this population of size 2N. According to the degree of crowding relationship between the individuals and the degree of crowding of the individuals, the appropriate individuals were selected to form a new parent population of size N. The new parent population was then selected by the traditional genetic algorithm (NSGA). Then, the crossover, mutation, etc. of the traditional genetic algorithm (NSGA) was used to generate a child population of size N, which was merged with its parent population. The above non-dominated fast sorting process was repeated until the number of population generations was equal to the preset number of generations.
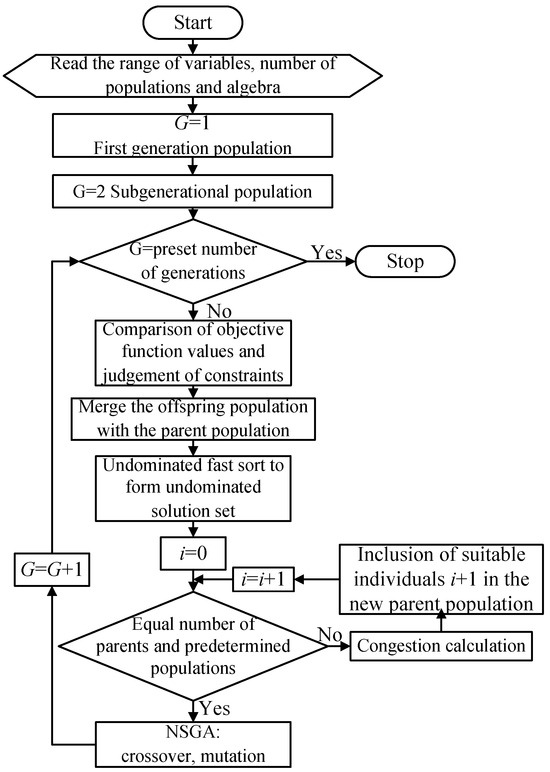
Figure 9.
Flow chart of the NSGA-II algorithm.
The bi-objective optimisation of the experimental simulation accuracy was performed using NSGA-II by setting the initial population and finally obtaining the constraint-compliant and relatively optimal solution set through selection, crossover, and mutation operations. The relevant parameters during the NSGA-II operations are listed in Table 3.

Table 3.
Parameter settings of the NSGA-II algorithm.
4.4. Flow of Optimised Design Based on the Kriging Surrogate Model
Figure 10 shows the flow chart of the design method for matching the thermal test parameters of metal fibre surface combustion structures based on the kriging surrogate model and dual-objective optimisation design. It mainly includes the experimental design, construction of a design scheme for matching the test parameters, construction of the surrogate model for the heat flow on the inner wall surface of the specimen, accuracy analysis of the surrogate model, and bi-objective optimisation design.
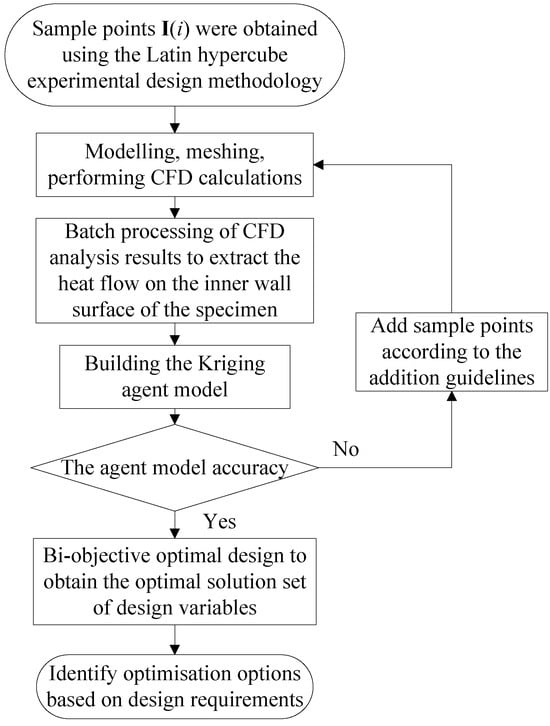
Figure 10.
Flow chart of parameter optimisation based on the surrogate model.
First, the Latin hypercubic test design method was applied to sample the design variables in the determined design space to ensure the homogeneity and orthogonality of the sample points in the design space, and the sample point set I(i) was established. According to the values of the sample points, the geometric model of the corresponding test program was established, the grid was divided, and CFD solution batch processing was carried out.
The CFD results were analysed to obtain the heat flow distribution on the inner wall of the cylindrical specimen corresponding to each sample point, and the kriging surrogate model was constructed based on the set of sample points and the corresponding heat flow results. The accuracy of the constructed surrogate model was analysed; if the accuracy did not meet the requirements, the number of sample points was increased according to the point addition criterion, and the surrogate model was reconstructed until it met the accuracy requirements.
Finally, the optimal design was carried out to obtain the optimal solution set. The optimal values of the design variables were selected according to the design requirements, and the optimal design of the parameters based on the surrogate model was completed.
In the above step, the average relative error and correlation coefficient were used to quantitatively evaluate the accuracy of the surrogate model, and for each sample point, the average relative error was calculated by Equation (8), where the CFD calculation was taken as the target heat flow. The correlation coefficient was calculated by Equation (10):
where is the heat flow on the surface of the specimen calculated by CFD. i = 1, 2, …, A, and A is the number of nodes on the surface of the specimen in the numerical calculation model.
5. Optimisation Results and Analysis
5.1. Kriging Surrogate Model Establishment
According to the range of the design variables shown in Table 2, one hundred initial sample points were obtained by the Latin hypercube test design method. The CFD numerical calculation of one hundred working conditions was completed as the input conditions of the kriging surrogate model.
The DACE toolbox of Matlab software was used to establish the kriging surrogate model for the heat flow density at each node of the specimen surface in the design space, the heat flow error at the stationary point, and the heat flow error in the flat zone. The Gaussian correlation function was used for the correlation function. The anisotropic effect was considered, and each design variable was individually assigned θ value in the range of [0.1, 20] with an initial value of 10.
5.2. Kriging Surrogate Model Accuracy Analysis
The evaluation criteria for the accuracy of the kriging surrogate model include the average relative error, the root mean square error, and the correlation coefficient. In this study, the average relative error was calculated using the leave-one-out cross-validation strategy, i.e., the ith sample point was taken as the test point, and the heat flow value was obtained by substituting it into the kriging model constructed by the remaining 99 sample points. This calculation was performed for all sample points. Figure 11 shows the relative error value of the specimen surface at each sample point calculated by the leave-one-out method. The average relative error value of all sample points was 8.8%, and the relative error value is within 5% in most areas. A few sample points had larger relative error values near the exit position of the specimen, which was due to the sudden expansion of the flow channel at the exit position. The flow field changed drastically, and the degree of non-linearity was high, resulting in a relatively low accuracy of the surrogate model.
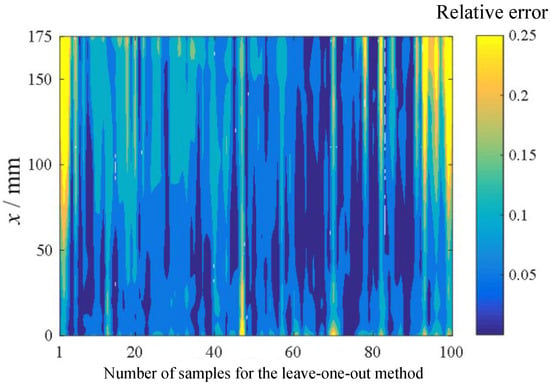
Figure 11.
Relative error of the specimen surface by the leave-one-out cross-validation strategy.
In addition, six sample points were randomly taken in the design space listed in Table 2 using the Latin hypercube experimental design method to evaluate the accuracy of the developed kriging surrogate model. The values of the sample points are given in Table 4.

Table 4.
Values of the test samples.
Taking the No.1 test sample as an example for analysis, the relative error between the CFD calculation results of heat flow on the surface of the specimen and the prediction results of the surrogate model under the case is shown in Figure 12. The prediction results of the surrogate model were in good agreement with the CFD calculation results, and the maximum relative error value did not exceed 7%. For further quantitative analysis, the average relative errors and correlation coefficients of the test sample points were calculated, as shown in Table 5. The average relative error values of the six test conditions were less than 6%, and the correlation coefficients were more than 90%.
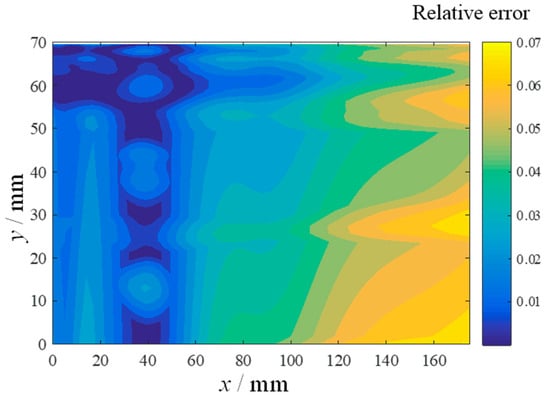
Figure 12.
Relative error of surface heat flux of the No.1 test sample.

Table 5.
Errors of the test samples.
According to the leave-one-out cross-validation strategy and the test sample test, the prediction accuracy of the kriging surrogate model developed in this study is high enough to satisfy the engineering design requirements without adding more sample points.
5.3. Optimisation Results
In this study, the heat flow value of the inner wall surface of the cylindrical specimen, Q = 0.13 MW/m2, was taken as the test simulation objective for analysis, and test parameter adjustment was carried out according to the optimisation design process described in Figure 10. Because the dual-objective function cannot reach the optimal solution at the same time, a Pareto optimal solution set is used in the optimal design result, which corresponds to the frontier curve in the objective space. The solutions in the Pareto optimal solution set all have better objective function values than those corresponding to feasible solutions outside the solution set. The Pareto optimal solution set in this study is shown in Figure 13. In the optimisation, it is necessary to minimise the relative error of the surface heat flow in both the front and back of the specimen, corresponding to the horizontal and vertical coordinates, respectively.
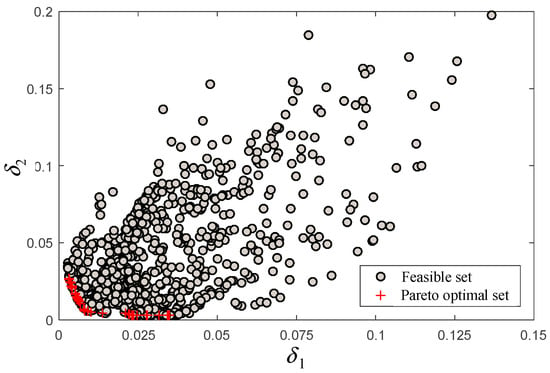
Figure 13.
Objective space of a feasible solution.
As shown in Figure 13, the optimal solutions are mainly distributed in the boundary region of the target space near the coordinate origin. Without any additional conditions, all Pareto optimal solutions were equivalent. For the cylindrical specimen, the relative error values of the surface heat flow should be minimised in both the front and back segments, which means that the distance from the optimal solution to the origin of the coordinates is minimised. Based on this evaluation criteria, the optimal solutions were further screened.
The distance Δ of the Pareto optimal solution relative to the coordinate origin was calculated by Equation (11):
The selected Pareto optimal solutions with Δ less than 2% are listed in Table 6.

Table 6.
Pareto optimal solution and distance from the coordinate origin.
According to the distance of the optimal solution relative to the coordinate origin listed in Table 6, point No. 1968, which was closest to the coordinate origin, was selected as the optimal solution and further checked.
5.4. Validation of the Optimisation Results
Optimal solution No. 1968 was used to verify the results of the optimisation, i.e., . The heat flux distribution on the inner surface of the specimen calculated by CFD for optimal solution conditions is shown in Figure 14, which shows a significant improvement in uniformity compared to the heat flux distribution of the cylindrical metal fibre in Figure 7.

Figure 14.
Heat flux distribution on the cylindrical specimen for the optimal solution.
Firstly, the accuracy of the surrogate model for the optimal solution was verified. The relative error values between the CFD calculation results of the heat flow on the inner wall surface of the specimen and the prediction results of the surrogate model under the conditions of the optimal solution are shown in Figure 15. As can be seen from Figure 15, in the specimen, the inlet and outlet positions of the runner size changed greatly. The calculation of the relative error was correspondingly large, but the maximum value did not exceed 8%. The average relative error value of the heat flow density on the whole surface of the specimen was 5.5%. The prediction results were more consistent with the CFD results, and the correlation coefficient between the two was more than 90%. The above analysis results show that the surrogate model established in this paper has a high accuracy and can be used as an alternative to CFD calculation in the optimisation design of parameter matching.
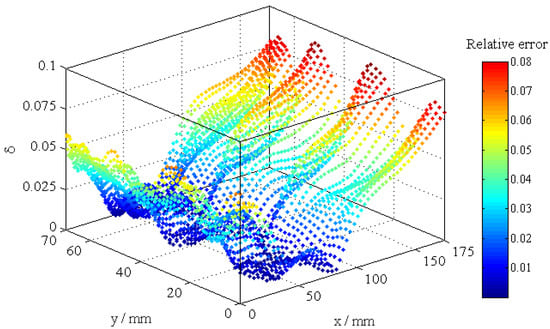
Figure 15.
Relative error of surface heat flux at optimum condition.
Furthermore, to analyse the agreement between the optimum solution and the optimisation objective, the relative error of the heat flux density on the inner wall surface of the specimen under the optimum solution with respect to the optimisation objective is shown in Figure 16. The relative error was larger at the position of the specimen inlet and outlet, but the maximum value was less than 8%, and the average relative error value of the heat flow density on the whole specimen surface was 4.9%. It can be seen that the conical combustion surface under the combustion test condition of the metal fibre surface can well simulate the heat flow distribution under the given condition. In addition, by establishing the kriging surrogate model for metal fibre combustion heating and adopting the non-dominated sorting genetic algorithm (NSGA-II) optimisation method with elite strategy, the test parameters corresponding to the given condition can be efficiently adjusted.
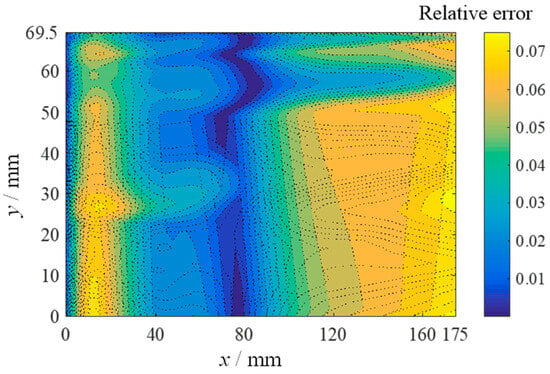
Figure 16.
Comparison between surface heat flux and target value at optimum condition.
6. Conclusions
For the cylindrical specimen thermal test, an aerodynamic thermal simulation test method for the combustion of conical metal fibre surfaces is proposed in this paper in order to form a uniform target heat flux on the inner surface. The kriging agent model and the non-dominated sorted genetic optimisation algorithm with elite strategy were employed to optimise the fitting design of the test parameters, and the following conclusions were drawn:
- The kriging surrogate model established using Latin hypercubic sampling has high accuracy. The average relative error of all samples was 8.8% as calculated by the leave-one-out cross-validation strategy, and the relative error value was within 5% in most regions, which can meet the requirements of engineering design.
- The accuracy of the surrogate model was further verified by six test samples. The average relative error value of the six test conditions was less than 6%, and the correlation coefficient was greater than 90%. This indicates that the established kriging surrogate model has a high prediction accuracy for optimisation design.
- For the optimal solution obtained by the optimisation design, the average relative error between the prediction results of the proxy model and the CFD calculation results was 5.5%, which appears to be a satisfactory arrangement. This indicates that the surrogate model can be used instead of numerous CFD calculations to find the optimum parameterised design. Meanwhile, the average relative error value between the CFD calculation results and the target heat flux under the optimal solution was 4.9%. Consequently, the optimal test parameters obtained by the kriging surrogate model-based optimisation design can provide the conical combustion surface with a uniform heat flux distribution on the inner surface of the cylindrical specimen.
Author Contributions
Conceptualisation, B.Q., R.A. and S.D.; methodology, B.Q.; software, R.A.; validation, B.Q., R.A. and R.W.; formal analysis, B.Q.; investigation, B.Q., R.A. and Y.Z.; resources, B.Q., R.A. and S.D.; data curation, R.A. and D.Y.; writing—original draft preparation, B.Q. and R.A.; writing—review and editing, B.Q.; visualisation, R.A. and Y.Z.; supervision, S.D. and D.Y.; project administration, B.Q. and R.W.; funding acquisition, B.Q. and R.A.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (11902026).
Data Availability Statement
Due to the limitations of the Ethics Review Committee, these data cannot be made public to protect the privacy and confidential information of the subjects. The data presented in this study are available upon request from the corresponding author.
Acknowledgments
The authors would like to sincerely thank the relevant organisations and institutions for their support of this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, X.; Fu, B. Thermal test technique of complex structure of hypersonic aircraft. Acta Aeronaut. Astronaut. Sin. 2016, 37, 73–79. [Google Scholar]
- Wu, D.; Lin, L.; Ren, H.; Zhu, F. Fracture performance test of wave transparent brittle materials of hypersonic vehicle under high-heat-flow thermal shock. Acta Aeronaut. Astronaut. Sin. 2019, 40, 210–219. [Google Scholar]
- Wu, D.; Zhou, A.; Zheng, L.; Pan, B.; Wang, Y. Thermal protection performance of metallic honeycomb panel structure at transient thermal shock environment. J. Aerosp. Power 2014, 29, 1261–1271. [Google Scholar]
- Wu, D.; Shang, L.; Gao, Z.; Pu, Y. Experimental Research on Thermal-Insulation Performance under High-Temperature/Oxidation and Time-Varying Environment up to 1700 °C. J. Astronaut. 2015, 36, 1083–1092. [Google Scholar]
- Wu, D.; Wu, S.; Wang, Y.; Gao, Z.; Yang, J. High-speed and accurate non-linear calibration of temperature sensors for transient aerodynamic heating experiments. Trans. Inst. Meas. Control 2014, 36, 845–852. [Google Scholar] [CrossRef]
- Polsky, S.; Venkatapathy, E.; Prabhu, D.K. Arc-jet semi-elliptical nozzle simulations and validation in support of X-33 TPS testing. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998. [Google Scholar]
- Zhang, S.; Yang, Y.; Wang, M.; Ma, P. Studies and applications of thermal/wave-transmission test technique in arc-heated wind tunnel. Acta Aerodyn. Sin. 2017, 35, 141–145. [Google Scholar]
- Cai, C.; Li, Y.; Dong, S. Compound sliding-mode predictive control for a temperature system of high-speed heat-airflow wind tunnel. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 228, 1869–1879. [Google Scholar] [CrossRef]
- Cai, C.; Li, Y.; Dong, S. Experimental Study on Gas Temperature Control for a High-Speed Heat-Airflow Wind Tunnel. J. Aerosp. Eng. 2016, 29, 04016054. [Google Scholar] [CrossRef]
- Diamantis, D.; Mastorakos, E.; Goussis, D. Simulations of premixed combustion in porous media. Combust. Theory Model. 2002, 6, 383–411. [Google Scholar] [CrossRef]
- Dai, G.Y.; Jia, H.Y.; Zeng, L.; Liu, L.; Qiu, B. Effects of Fluid-Thermal-Structural Coupling on Inlet Parameters of Hypersonic Intake. J. Propuls. Technol. 2018, 39, 1267–1274. [Google Scholar]
- Frauholz, S.; Hosters, N.; Reinartz, B.U.; Behr, M. Fluid-Structure Interaction in the Context of a Scramjet Intake. In Proceedings of the 44th AIAA Fluid Dynamics Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Kai, X.; Li, Y.; Dong, S. Temperature distribution of a test specimen with high-speed heat air-flow passing through. Therm. Sci. 2018, 22, 2527–2538. [Google Scholar]
- Wu, R.; Nie, W.; Cai, H. Numerical simulation of flow field characteristics of UDMH/NTO rocket engine plume. J. Aerosp. Power 2018, 33, 952–960. [Google Scholar]
- Chen, X.; Cao, Z.; Fu, B.; Xu, X.; Yan, H.; Wang, P.; Zhang, H. Adding-point strategy for surrogate-based reduced-order hypersonic aerothermodynamic modeling based on fuzzy clustering. J. Spacecr. Rocket. 2021, 58, 244–253. [Google Scholar] [CrossRef]
- Wang, R.; Qi, B.; Zhou, Y.; Dong, S. Numerical Investigation on Combustion and Heating Characteristics of Metal Fiber Burner. Energies 2023, 16, 4301. [Google Scholar] [CrossRef]
- Leonardi, S.; Viskata, R.; Gore, J. Radiation and thermal performance measurements of a metal fiber burner. J. Quant. Spectrosc. Radiat. Transf. 2002, 73, 491–501. [Google Scholar] [CrossRef]
- Yi, C.; Liu, Y.; Cao, R. Shape parameters optimization of hypersonic vehicle based on surrogate model. J. Aerosp. Power 2019, 34, 2354–2365. [Google Scholar]
- Mu, X.; Yao, W.; Yu, X.; Liu, K. A survey of surrogate models used in MDO. Chin. J. Comput. Mech. 2005, 22, 608–612. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multi-objective genetic algorithm: Nsga-ii. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).