Advanced UAV Design Optimization Through Deep Learning-Based Surrogate Models
Abstract
1. Introduction
1.1. Overview of Aircraft Design
1.2. Design from the Perspective of Unmanned Aerial Vehicles
1.3. Design Solutions Using Machine Learning
2. Conceptual Framework
- Combines DNNs with multiobjective genetic algorithms for rapid UAV design optimization, speeding up the process by over three orders of magnitude.
- Develops a multidisciplinary framework integrating aerodynamics, structural analysis, radar cross section, and propulsion for comprehensive UAV evaluation.
- Utilizes physics-informed feature engineering for accurate surrogate models, predicting key UAV metrics with high precision.
- Optimizes UAV designs for specific missions by addressing distinct operational needs.
3. Methodology
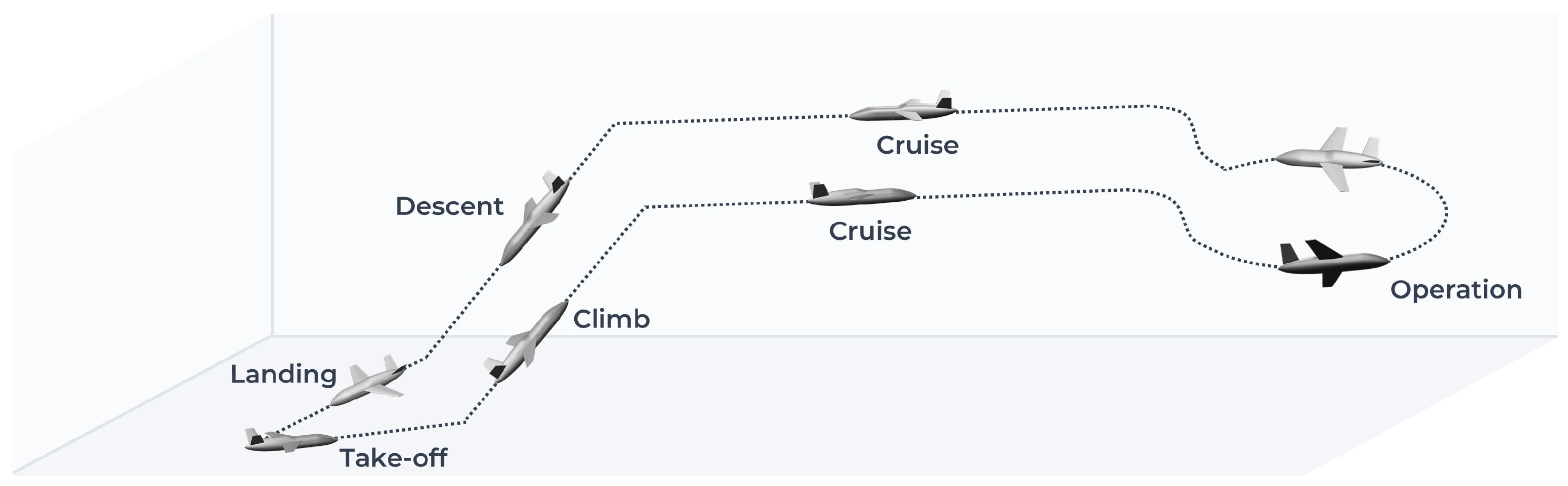
3.1. Initial Sizing Algorithm
- Stall speed : minimum speed for maintaining level flight.
- Maximum speed : highest achievable speed in level flight.
- Rate of climb : defines how quickly an aircraft gains height.
- Take-off run distance : distance required for take-off.
- Ceiling altitude : maximum altitude for sustained level flight.
3.2. Aircraft Model
3.2.1. Aerodynamics
| Approach | Primary Use | Accuracy (Average) | Computation Time | Examples |
|---|---|---|---|---|
| Semi-empirical methods | Conceptual design | Seconds on a PC | DATCOM, ESDU, AAA, RDS, etc. | |
| Potential flow methods | Preliminary design | Seconds/minutes on a PC | VSPAero, PANAir, AVL, XFOIL, etc. | |
| CFD methods | Detailed design | Hours/days/weeks on a WS/HPC | SU2, Fluent, USM3D, OpenFOAM, etc. |
3.2.2. Radar Cross Section
3.2.3. Structures
3.2.4. Propulsion
3.2.5. Weight
3.3. Artificial Neural Network Modeling
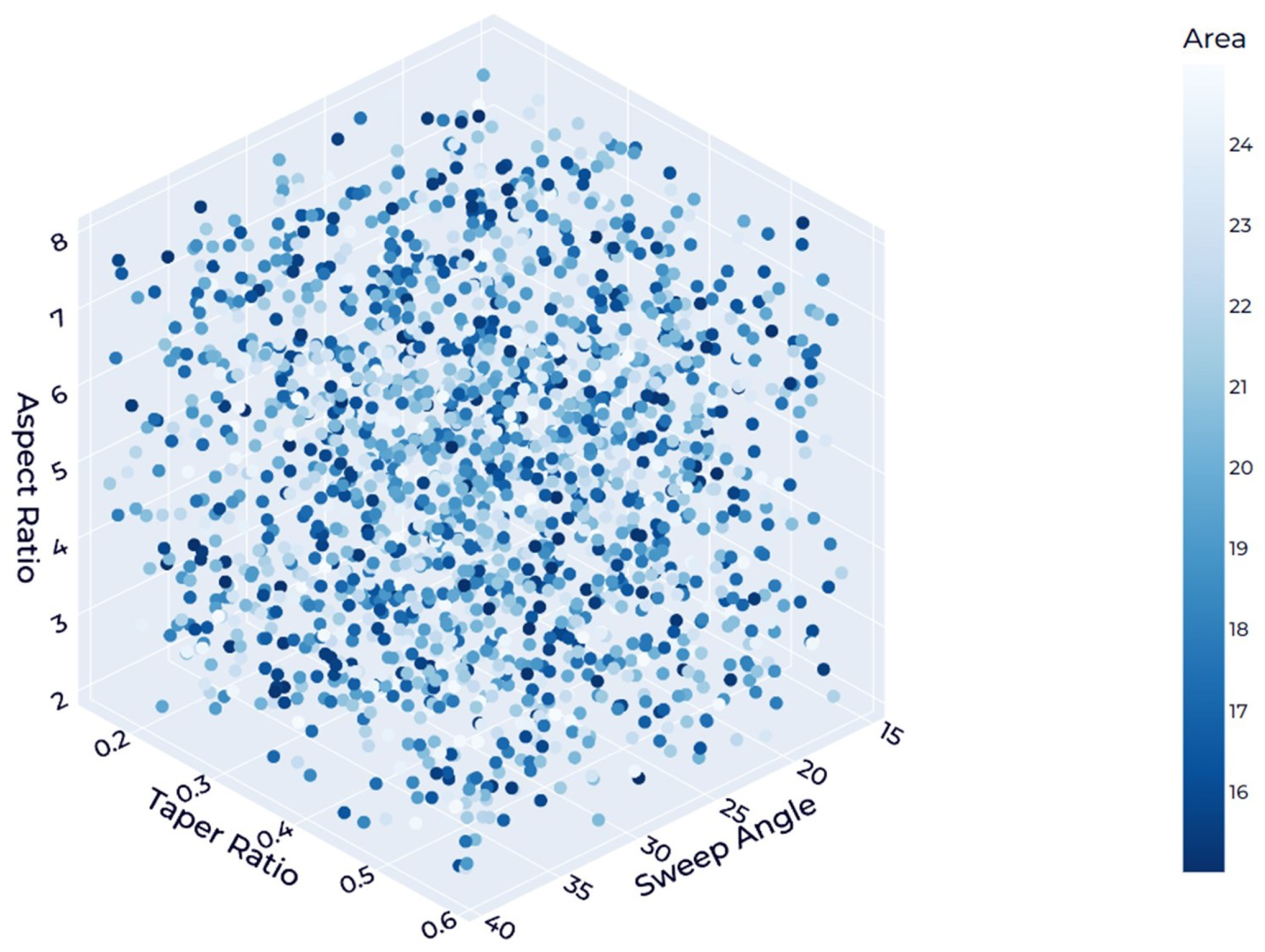
3.3.1. Data Generation and Sampling
| Algorithm 1 Design space generation algorithm. | |
| Input: , | |
| Output: | |
| 1: | procedure DesignSpace(, ) |
| 2: | Initialize VSP API |
| 3: | Define physical and environmental parameters |
| 4: | |
| 5: | |
| 6: | for do |
| 7: | |
| 8: | Define wing geometry using |
| 9: | Define tail geometry using |
| 10: | Define fuselage geometry using |
| 11: | Set geometry using wing, tail, fuselage |
| 12: | Update VSP model |
| 13: | |
| 14: | AerodynamicsPerformance |
| 15: | |
| 16: | StructuralPerformance |
| 17: | |
| 18: | RadarCrossSectionPerformance |
| 19: | Weights |
| 20: | |
| 21: | end for |
| 22: | |
| 23: | return |
| 24: | end procedure |
| 25: | procedure AerodynamicsPerformance() |
| 26: | |
| 27: | Run aerodynamics analysis |
| 28: | return |
| 29: | end procedure |
| 30: | procedure StructuralPerformance() |
| 31: | if component = wing or tail then |
| 32: | |
| 33: | Run structural analysis |
| 34: | Optimize |
| 35: | else |
| 36: | Calculate |
| 37: | end if |
| 38: | |
| 39: | return |
| 40: | end procedure |
| 41: | procedure RadarCrossSectionPerformance() |
| 42: | |
| 43: | Run RCS analysis |
| 44: | return |
| 45: | end procedure |
| 46: | procedure Weights() |
| 47: | Run weights analysis |
| 48: | return |
| 49: | end procedure |
3.3.2. Physics-Informed Feature Engineering
3.3.3. Multilayer Perceptron-Based Network Architecture
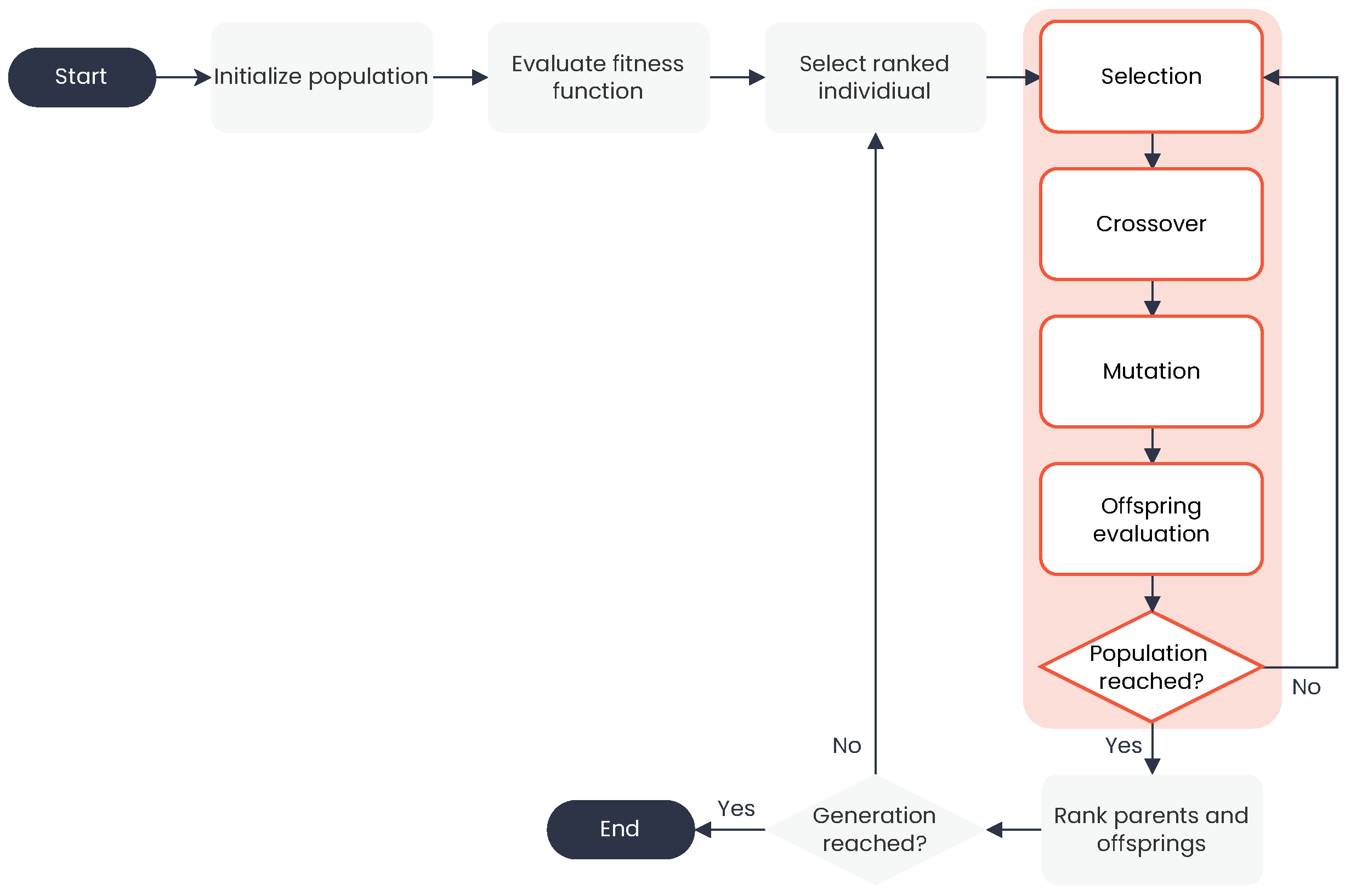
3.4. Multiobjective Genetic Algorithm
4. Application of the Model
- Maximum take-off weight: 3000 kg
- Payload weight: 500 kg
- Cruise speed: 0.7 Mach
- Endurance: 5 h
- Range: 3000 NM
- Maximum altitude: 45,000 ft
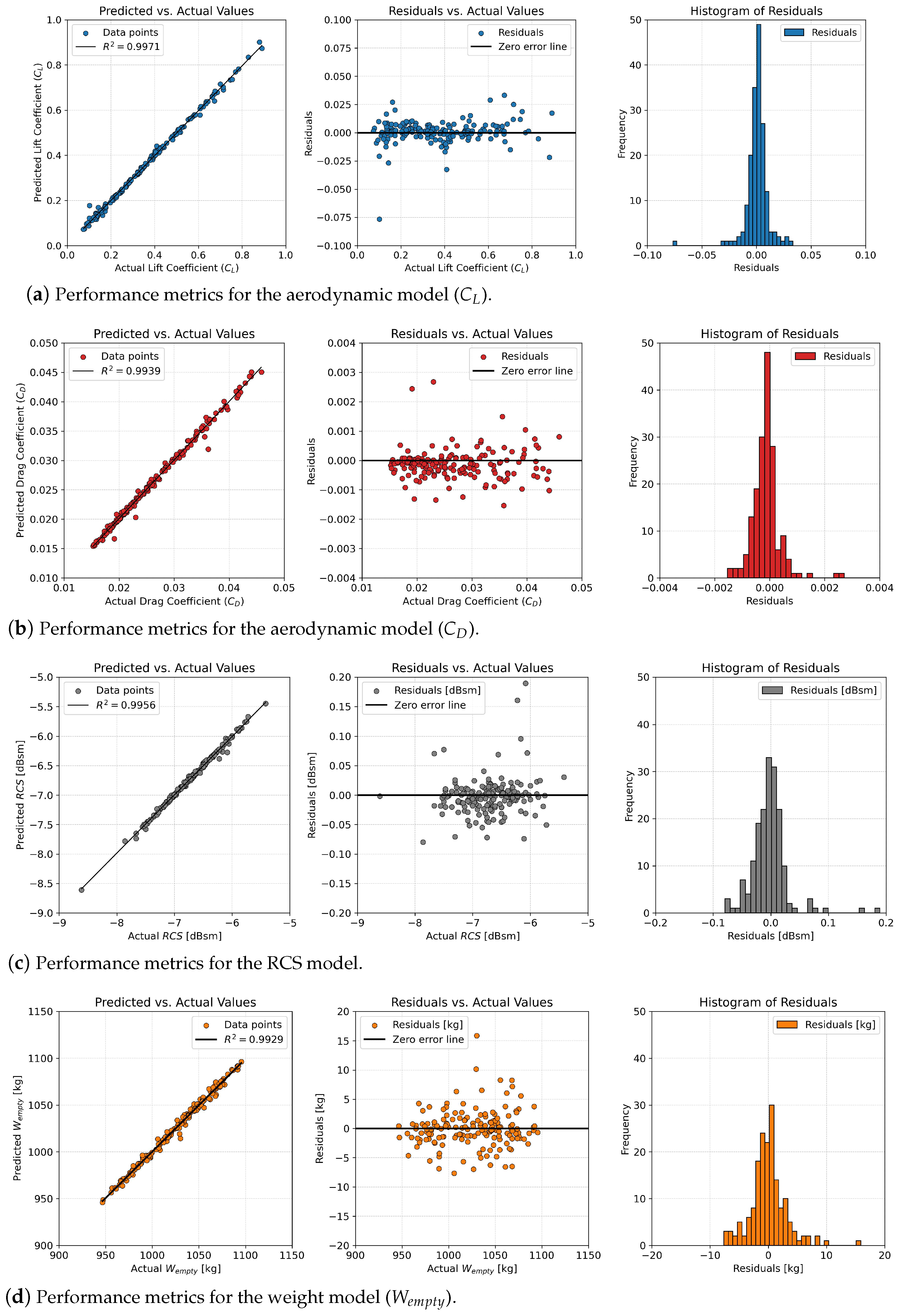
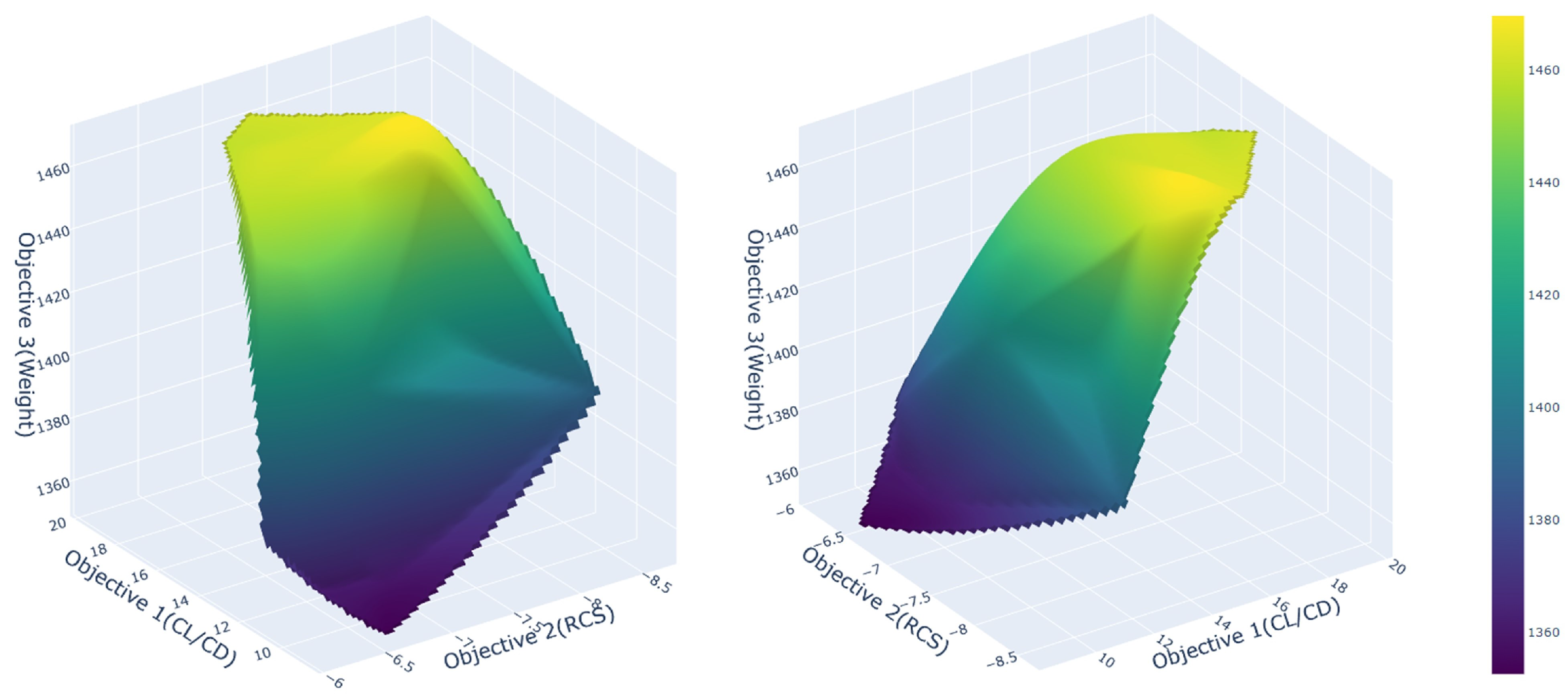
5. Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CAD | Computer-aided design |
| CAP | Combat air patrol |
| CFD | Computational fluid dynamics |
| EW | Electronic warfare |
| FEM | Finite element method |
| FoM | Figure of merit |
| DNN | Deep neural network |
| ISR | Intelligence, surveillance and reconnaissance |
| LCC | Life-cycle costing |
| LHS | Latin hypercube sampling |
| MDO | Multidisciplinary design optimization |
| MTOW | Maximum take-off weight |
| PM | Panel method |
| PO | Physical optics |
| RCS | Radar cross section |
| RF | Radio frequency |
| ROM | Reduced order model |
| SEAD | Suppression of Enemy Air Defenses |
| SFC | Specific fuel consumption |
| UAS | Unmanned aerial system |
| UAV | Unmanned aerial vehicle |
| UCAV | Unmanned combat aerial vehicle |
| VLM | Vortex lattice method |
| Nomenclature | |
| Angle of attack | |
| Sweep angle | |
| Aspect ratio | |
| Reference span | |
| Taper ratio | |
| Lift coefficient | |
| Drag coefficient | |
| Moment coefficient | |
| M | Mach number |
| Reynolds number | |
| Reference wing area | |
| Air density | |
| Dynamic viscosity | |
| Free stream velocity | |
| Hydraulic diameter | |
| f | Fineness ratio |
| T | Thrust |
| Radar cross section | |
| Empty weight | |
| Root chord length | |
| Tip chord length | |
| Aerodynamic loads | |
| Number of neurons in the l-th layer | |
| Nonlinear activation function of the l-th layer | |
| Input to the l-th layer | |
| Weights of the l-th layer | |
| Biases of the l-th layer | |
| Output of the l-th layer | |
| Model parameters (weights and biases) | |
| Sigmoid activation function | |
| Learning rate | |
| N | Number of layers |
References
- Cummings, R.M.; Mason, W.H.; Morton, S.A.; McDaniel, D.R. Applied Computational Aerodynamics: A Modern Engineering Approach; Cambridge Aerospace Series; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar] [CrossRef]
- Jungo, A.; Zhang, M.; Vos, J.B.; Rizzi, A. Benchmarking New CEASIOM with CPACS adoption for aerodynamic analysis and flight simulation. Aircr. Eng. Aerosp. Technol. 2018, 90, 613–626. [Google Scholar] [CrossRef]
- Roskam, J. Airplane Design; DARcorporation: St. Lawrence, KS, USA, 1985. [Google Scholar]
- Raymer, D. Aircraft Design: A Conceptual Approach; American Institute of Aeronautics and Astronautics Inc.: Las Vegas, NV, USA, 2012. [Google Scholar]
- Sadraey, M.H. Aircraft Design: A Systems Engineering Approach; Aerospace Series; John Wiley and Sons: Chichester, UK, 2013. [Google Scholar] [CrossRef]
- de Weck, O.; Willcox, K. Multidisciplinary System Design Optimization. 2003. Available online: https://ocw.mit.edu/courses/ids-338j-multidisciplinary-system-design-optimization-spring-2010/ (accessed on 10 June 2022).
- Roth, G.L.; Altman, A. Re-imagining Engineering Conceptual Design for Aerospace. In Proceedings of the AIAA AVIATION 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022; p. 3880. [Google Scholar]
- Liao, P.; Song, W.; Du, P.; Feng, F.; Zhang, Y. Aerodynamic Intelligent Topology Design (AITD)-A Future Technology for Exploring the New Concept Configuration of Aircraft. Aerospace 2023, 10, 46. [Google Scholar] [CrossRef]
- Asimov, I. I, Robot; Doubleday: New York, NY, USA, 1950. [Google Scholar]
- Stanisław, L. The Invincible; Seabury Press: New York, NY, USA, 1973. [Google Scholar]
- Humphreys, C.; Cobb, R.; Jacques, D.; Reeger, J. Optimal Mission Path for the Uninhabited Loyal Wingman. In Proceedings of the 16th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Dallas, TX, USA, 22–26 June 2015; p. 2792. [Google Scholar]
- Stensrud, R.; Mikkelsen, B.; Betten, S.; Valaker, S. A proposal for a simple evaluation method in support of the initial concept phase assessing a future unmanned Loyal Wingman for Royal Norwegian Air Force (RNoAF). In Proceedings of the 38th International Symposium on Military Operational Research (38 ISMOR), Online, 20–21 July 2021. [Google Scholar]
- Harper, J. The Rise of Skyborg: Air Force Betting on New Robotic Wingman. Natl. Def. 2020. Available online: https://www.nationaldefensemagazine.org/articles/2020/9/25/air-force-betting-on-new-robotic-wingman#:~:text=The%20Rise%20of%20Skyborg%3A%20Air%20Force%20Betting%20on%20New%20Robotic%20Wingman&text=The%20next%20year%20will%20be,will%20soon%20undergo%20operational%20experimentation (accessed on 11 August 2024).
- Gunzinger, M.; Autenried, L. Understanding the Promise of Skyborg and Low-Cost Attritable Unmanned Aerial Vehicles. Mitchell Inst. Policy Pap. 2020, 24. Available online: https://mitchellaerospacepower.org/understanding-the-promise-of-skyborg-and-low-cost-attritable-unmanned-aerial-vehicles/ (accessed on 11 August 2024).
- Reim, G. Analysis: US Air Force eyes adoption of ‘Loyal Wingman’ UAVs. Flight Glob. 2018. Available online: https://www.flightglobal.com/analysis/analysis-us-air-force-eyes-adoption-of-loyal-wingman-uavs/129330.article (accessed on 11 August 2024).
- Smith, A.; Rogers, M. F-35 Sustainment: DOD Needs to Cut Billions in Estimated Costs to Achieve Affordability; U.S. Government Accountability Office: Washington, DC, USA, 2021.
- Colombi, J.; Bentz, B.; Recker, R.; Lucas, B.; Freels, J. Attritable design trades: Reliability and cost implications for unmanned aircraft. In Proceedings of the 2017 Annual IEEE International Systems Conference (SysCon), Montreal, QC, Canada, 24–27 April 2017; IEEE: New York, NY, USA, 2017; pp. 1–8. [Google Scholar]
- Pittaway, N. Boeing details MQ-28A payload ground test phase. Aust. Def. Mag. 2022. Available online: https://www.australiandefence.com.au/defence/air/boeing-details-mq-28a-payload-ground-test-phase#:~:text=A%20variety%20of%20payloads%20will,of%20the%20aircraft%27s%20removable%20nose (accessed on 11 August 2024).
- Newdick, T. The United Kingdom Has Chosen Who Will Build Its First Prototype Loyal Wingman Combat Drone. Drive Warzone 2021. Available online: https://www.thedrive.com/the-war-zone/42134/the-united-kingdom-has-chosen-who-will-build-its-first-prototype-loyal-wingman-combat-drone (accessed on 11 August 2024).
- Aviation Week. EADS Barracuda. Available online: https://aviationweek.com/defense-space/eads-cassidian-eyes-further-barracuda-uav-flights (accessed on 26 May 2024).
- 96th Test Wing, 40th Flight Test Squadron. Kratos XQ-58. Photo by Master Sgt. Tristan McIntire. Available online: https://www.flightglobal.com/military-uavs/usmc-completes-first-test-flight-with-autonomous-xq-58/155257.article (accessed on 26 May 2024).
- Australian Defense Department. MQ-28 Loyal Wingman. Available online: https://aviationweek.com/shownews/farnborough-airshow/boeings-phantom-works-wants-untethered-loyal-wingman (accessed on 26 May 2024).
- Anadolu Images. Baykar Kizilelma. Available online: https://www.aa.com.tr/tr/bilim-teknoloji/bayraktar-kizilelma-ilk-ucusunu-gerceklestirdi/2763872 (accessed on 26 May 2024).
- General Atomics. XQ-67A Off Board Sensing Station Maiden Flight over Palmdale, California. Available online: https://www.dvidshub.net/image/8275788/afrls-xq-67a-makes-1st-successful-flight (accessed on 26 May 2024).
- Qinetiq. Qinetiq Derives Collaborative UAS from Banshee Target. Credit: Qinetiq. Available online: https://aviationweek.com/defense-space/aircraft-propulsion/qinetiq-derives-collaborative-uas-banshee-target (accessed on 26 May 2024).
- BAE Systems. UAS Concepts. 2023. Available online: https://www.baesystems.com/en/product/uas-concepts (accessed on 26 May 2024).
- Air & Space Forces Magazine. Anduril and General Atomics to Develop New Collaborative Combat Aircraft for Air Force. The Anduril “Fury” Autonomous Aircraft on April 24. Courtesy Photo. Available online: https://www.airandspaceforces.com/cca-contract-winners-to-be-announced-imminently/ (accessed on 11 August 2024).
- Sobieszczanski-Sobieski, J. Multidisciplinary design optimization: An emerging new engineering discipline. In Advances in Structural Optimization; Springer: Berlin/Heidelberg, Germany, 1995; pp. 483–496. [Google Scholar]
- Nguyen, N.V.; Choi, S.M.; Kim, W.S.; Lee, J.W.; Kim, S.; Neufeld, D.; Byun, Y.H. Multidisciplinary unmanned combat air vehicle system design using multi-fidelity model. Aerosp. Sci. Technol. 2013, 26, 200–210. [Google Scholar] [CrossRef]
- Karali, H.; Inalhan, G.; Umut Demirezen, M.; Adil Yukselen, M. A new nonlinear lifting line method for aerodynamic analysis and deep learning modeling of small unmanned aerial vehicles. Int. J. Micro Air Veh. 2021, 13, 17568293211016817. [Google Scholar] [CrossRef]
- Ng, L.W.; Willcox, K.E. Multifidelity approaches for optimization under uncertainty. Int. J. Numer. Methods Eng. 2014, 100, 746–772. [Google Scholar] [CrossRef]
- Brunton, S.L.; Nathan Kutz, J.; Manohar, K.; Aravkin, A.Y.; Morgansen, K.; Klemisch, J.; Goebel, N.; Buttrick, J.; Poskin, J.; Blom-Schieber, A.W.; et al. Data-driven aerospace engineering: Reframing the industry with machine learning. AIAA J. 2021, 59, 2820–2847. [Google Scholar] [CrossRef]
- AIAA Digital Engineering Integration Committee. Digital Twin: Definition & Value—An AIAA and AIA Position Paper; AIAA: Reston, VA, USA, 2020. [Google Scholar]
- Dantas de Jesus Ferreira, J.A.; Secco, N.R. Decision tree classifiers for unmanned aircraft configuration selection. Aircr. Eng. Aerosp. Technol. 2021, 93, 1122–1132. [Google Scholar] [CrossRef]
- Sharma, R.S.; Hosder, S. Investigation of aircraft design space exploration with machine learning. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 & 19–21 January 2021; p. 0114. [Google Scholar]
- Oroumieh, M.A.A.; Malaek, S.M.B.; Ashrafizaadeh, M.; Taheri, S.M. Aircraft design cycle time reduction using artificial intelligence. Aerosp. Sci. Technol. 2013, 26, 244–258. [Google Scholar] [CrossRef]
- Boutemedjet, A.; Samardžić, M.; Rebhi, L.; Rajić, Z.; Mouada, T. UAV aerodynamic design involving genetic algorithm and artificial neural network for wing preliminary computation. Aerosp. Sci. Technol. 2019, 84, 464–483. [Google Scholar] [CrossRef]
- Setayandeh, M.R. Surrogate model–based robust multidisciplinary design optimization of an unmanned aerial vehicle. J. Aerosp. Eng. 2021, 34, 04021029. [Google Scholar] [CrossRef]
- Bekemeyer, P.; Bertram, A.; Hines Chaves, D.A.; Dias Ribeiro, M.; Garbo, A.; Kiener, A.; Sabater, C.; Stradtner, M.; Wassing, S.; Widhalm, M.; et al. Data-driven aerodynamic modeling using the DLR SMARTy toolbox. In Proceedings of the AIAA Aviation 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022; p. 3899. [Google Scholar]
- Sharma, R.S.; Hosder, S. Mission-Driven Inverse Design of Blended Wing Body Aircraft with Machine Learning. Aerospace 2024, 11, 137. [Google Scholar] [CrossRef]
- Wu, P.; Yuan, W.; Ji, L.; Zhou, L.; Zhou, Z.; Feng, W.; Guo, Y. Missile aerodynamic shape optimization design using deep neural networks. Aerosp. Sci. Technol. 2022, 126, 107640. [Google Scholar] [CrossRef]
- Yan, X.; Zhu, J.; Kuang, M.; Wang, X. Aerodynamic shape optimization using a novel optimizer based on machine learning techniques. Aerosp. Sci. Technol. 2019, 86, 826–835. [Google Scholar] [CrossRef]
- Li, J.; Du, X.; Martins, J.R. Machine learning in aerodynamic shape optimization. Prog. Aerosp. Sci. 2022, 134, 100849. [Google Scholar] [CrossRef]
- Bouhlel, M.A.; He, S.; Martins, J.R. Scalable gradient–enhanced artificial neural networks for airfoil shape design in the subsonic and transonic regimes. Struct. Multidiscip. Optim. 2020, 61, 1363–1376. [Google Scholar] [CrossRef]
- Du, X.; He, P.; Martins, J.R. A B-spline-based generative adversarial network model for fast interactive airfoil aerodynamic optimization. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 2128. [Google Scholar]
- Li, J.; Zhang, M. Data-based approach for wing shape design optimization. Aerosp. Sci. Technol. 2021, 112, 106639. [Google Scholar] [CrossRef]
- Barnhart, S.A.; Narayanan, B.; Gunasekaran, S. Blown wing aerodynamic coefficient predictions using traditional machine learning and data science approaches. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 & 19–21 January 2021; p. 0616. [Google Scholar]
- Yuan, Y.; Dongli, M.; Muqing, Y.; Zhang, L.; Yang, G. Adaptive-surrogate-based robust optimization of transonic natural laminar flow nacelle. Chin. J. Aeronaut. 2021, 34, 36–52. [Google Scholar]
- Yu, B.; Xie, L.; Wang, F. An improved deep convolutional neural network to predict airfoil lift coefficient. In Proceedings of the International Conference on Aerospace System Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2019; pp. 275–286. [Google Scholar]
- Zhang, Y.; Sung, W.J.; Mavris, D.N. Application of convolutional neural network to predict airfoil lift coefficient. In Proceedings of the 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 8–12 January 2018; p. 1903. [Google Scholar]
- Wu, M.Y.; Yuan, X.Y.; Chen, Z.H.; Wu, W.T.; Hua, Y.; Aubry, N. Airfoil shape optimization using genetic algorithm coupled deep neural networks. Phys. Fluids 2023, 35, 085140. [Google Scholar] [CrossRef]
- Keane, A.J.; Voutchkov, I.I. Surrogate approaches for aerodynamic section performance modeling. AIAA J. 2020, 58, 16–24. [Google Scholar] [CrossRef]
- Karali, H.; Inalhan, G.; Tsourdos, A. AI-Based Multifidelity Surrogate Models to Develop Next Generation Modular UCAVs. In Proceedings of the AIAA Scitech 2023 Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar] [CrossRef]
- Karali, H.; Inalhan, G.; Tsourdos, A. AI-driven Unmanned Aerial System Conceptual Design with Configuration Selection. In Proceedings of the 2023 IEEE Conference on Artificial Intelligence (CAI), Santa Clara, CA, USA, 5–6 June 2023; IEEE: New York, NY, USA, 2023; pp. 83–84. [Google Scholar] [CrossRef]
- Karali, H.; Inalhan, G.; Tsourdos, A. AI-Driven Multidisciplinary Conceptual Design of Unmanned Aerial Vehicles. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024; p. 1708. [Google Scholar] [CrossRef]
- Roskam, J.; Lan, C.T.E. Airplane Aerodynamics and Performance; DARcorporation: St. Lawrence, KS, USA, 1997. [Google Scholar]
- Pratt & Whitney Canada. JT15D Turbofan Engine. Available online: https://airandspace.si.edu/collection-objects/pratt-whitney-canada-jt15d-1turbofan-engine-cutaway/nasm_A19780210000 (accessed on 7 August 2024).
- Pratt & Whitney Canada. PW617 Turbofan Engine. Available online: https://www.prattwhitney.com/en/products/business-aviation-engines/pw600 (accessed on 7 August 2024).
- Pratt & Whitney Canada. PW545B Turbofan Engine. Available online: https://www.prattwhitney.com/en/products/business-aviation-engines/pw500 (accessed on 7 August 2024).
- Pratt & Whitney Canada. PW610F Turbofan Engine. Available online: https://www.prattwhitney.com/en/products/business-aviation-engines/pw600 (accessed on 7 August 2024).
- Pratt & Whitney Canada. PW615F Turbofan Engine. Available online: https://www.prattwhitney.com/en/products/business-aviation-engines/pw600 (accessed on 7 August 2024).
- GE Honda. GE Honda HF120 Turbofan Engine. Available online: https://www.geaviation.com (accessed on 7 August 2024).
- Ivchenko Progress. AI-25TL Turbofan Engine. Available online: http://uecrus.com (accessed on 7 August 2024).
- Williams International. FJ33 Turbofan Engine. Available online: https://www.williams-int.com/products/ (accessed on 7 August 2024).
- Williams International. FJ44-4 Turbofan Engine. Available online: https://www.williams-int.com/products/ (accessed on 7 August 2024).
- Honeywell Aerospace. TFE731-2 Turbofan Engine. Available online: https://aerospace.honeywell.com/us/en/products-and-services/product/hardware-and-systems/engines/tfe731 (accessed on 7 August 2024).
- Katz, J.; Plotkin, A. Low-Speed Aerodynamics, 2nd ed.; Cambridge Aerospace Series; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar] [CrossRef]
- Erickson, L.L. Panel Methods: An Introduction; Technical Publication NASA-TP-2995, NASA Technical Paper 2995 December 1990; NASA Ames Research Center: Moffett Field, CA, USA, 1990. [Google Scholar]
- Karali, H.; Demirezen, U.M.; Yukselen, M.A.; Inalhan, G. A novel physics informed deep learning method for simulation-based modelling. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 & 19–21 January 2021; p. 0177. [Google Scholar] [CrossRef]
- Karakoc, A.; Kaya, H. A multi-objective multi-disciplinary optimization approach for NATO AVT 251 UCAV–MULDICON. In Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018; p. 3001. [Google Scholar]
- Fourikis, N. Advanced Array Systems, Applications and RF Technologies; Academic Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Chung, S.S.M.; Tuan, S.C. Radar Cross Section Simulation of XQ-58 Valkyrie Like CAD Model. In Proceedings of the 2020 International Workshop on Electromagnetics: Applications and Student Innovation Competition (iWEM), Makung, Taiwan, 26–28 August 2020; IEEE: New York, NY, USA, 2020; pp. 1–2. [Google Scholar]
- Leung, S.; Liang, C.p.; Tao, X.f.; Li, F.f.; Poo, Y.; Wu, R.x. Broadband radar cross section reduction by an absorptive metasurface based on a magnetic absorbing material. Opt. Express 2021, 29, 33536–33547. [Google Scholar] [CrossRef] [PubMed]
- Kapoulas, I.K.; Hatziefremidis, A.; Baldoukas, A.; Valamontes, E.S.; Statharas, J. Small Fixed-Wing UAV Radar Cross-Section Signature Investigation and Detection and Classification of Distance Estimation Using Realistic Parameters of a Commercial Anti-Drone System. Drones 2023, 7, 39. [Google Scholar] [CrossRef]
- Peng, Z.; Li, C.; Uysal, F. Modern Radar for Automotive Applications; Institution of Engineering and Technology: Stevenage, UK, 2022. [Google Scholar]
- Peng, Z. Rookiepeng/Radarsimpy. 2022. Available online: https://zenodo.org/records/6792269 (accessed on 11 August 2024).
- Jasa, J.P.; Hwang, J.T.; Martins, J.R. Open-source coupled aerostructural optimization using Python. Struct. Multidiscip. Optim. 2018, 57, 1815–1827. [Google Scholar] [CrossRef]
- Bouhlel, M.A.; Hwang, J.T.; Bartoli, N.; Lafage, R.; Morlier, J.; Martins, J.R.R.A. A Python surrogate modeling framework with derivatives. Adv. Eng. Softw. 2019, 135, 102662. [Google Scholar] [CrossRef]
- McDonald, R.A. Advanced modeling in OpenVSP. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, DC, USA, 13–17 June 2016; p. 3282. [Google Scholar]
- McDonald, R.A.; Gloudemans, J.R. Open Vehicle Sketch Pad: An Open Source Parametric Geometry and Analysis Tool for Conceptual Aircraft Design. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 0004. [Google Scholar]
- Freedman, D.; Pisani, R.; Purves, R. Statistics (International Student Edition); WW Norton & Company: New York, NY, USA, 2007. [Google Scholar]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Engineering Sciences Data Unit. Lift-Curve Slope and Aerodynamic Centre Position of Wings in Inviscid Subsonic Flow; Technical Report ESDU 70011; As at Amendment I; ESDU International: London, UK, 1970. [Google Scholar]
- Engineering Sciences Data Unit. Wing Angle of Attack for Zero Lift at Subcritical Mach Numbers; Technical Report ESDU 87031; As at Amendment A; ESDU International: London, UK, 1987. [Google Scholar]
- ESDU International. Lift-Curve Slope of Swept and Tapered Wings; Technical Memorandum ESDU AERO W.01.01.01, Issued March 1953, with Amendments A to D, October 1989; ESDU International: London, UK, 2001. [Google Scholar]
- Lowry, J.; Polhamus, E. A Method for Predicting Lift Increments Due to Flap Deflections at Low Angles of Attack in Incompressible Flow. Technical Note Technical NACA-TN-3911, 1 August 1957. [Google Scholar]
- ESDU International. Wing Lift-Curve Slope in Inviscid Subsonic Flow: Improvements to the Helmbold-Diederich Equation and Comparison with Data from ESDU 70011; Technical Memorandum TM 169; ESDU International: London, UK, 2012. [Google Scholar]
- Zaheer, M.; Reddi, S.J.; Sachan, D.; Kale, S.; Kumar, S. Adaptive Methods for Nonconvex Optimization. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; Volume 31. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Blank, J.; Deb, K. pymoo: Multi-objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]







| Engine | Length (mm) | Diameter (mm) | Dry Weight (kg) | Maximum Thrust (kN) |
|---|---|---|---|---|
| Pratt Whitney Canada PW610F | 1153 | 704 | 115.7 | 4.22 |
| Pratt Whitney Canada PW615F | 1258 | 750 | 140 | 6.49 |
| Williams FJ33 | 976 | 466 | 140 | 8.21 |
| Pratt Whitney Canada PW617 | 1360 | 750 | 172 | 8.41 |
| GE Honda HF120 | 1510 | 660 | 211.3 | 9.10 |
| Pratt Whitney Canada JT15D | 1531 | 685.8 | 285.7 | 13.57 |
| Honeywell TFE731-2 | 1844 | 1041 | 184 | 15.57 |
| Williams FJ44-4 | 1340 | 640 | 298 | 16.00 |
| Ivchenko AI-25TL | 1494 | 611.6 | 350 | 16.90 |
| Pratt Whitney Canada 545B | 1742 | 693.4 | 376.5 | 17.58 |
| Parameter | Symbol | Units | Minimum | Maximum | |
|---|---|---|---|---|---|
| Wing | Wing area | A | 15 | 25 | |
| Aspect ratio | − | 2 | 8 | ||
| Taper ratio | − | 0.2 | 0.6 | ||
| Sweep | ° | 15 | 40 | ||
| Length | l | m | 5 | 15 | |
| Hydraulic diameter | m | 1 | 2 | ||
| Fuselage | Fineness ratio | f | − | 2.5 | 15 |
| Engine | Thrust | T | kN | 5 | 20 |
| Angle of attack | ° | 0 | 4 | ||
| Mach number | M | − | 0.6 | 0.8 | |
| Flow condition | Reynolds number | − |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karali, H.; Inalhan, G.; Tsourdos, A. Advanced UAV Design Optimization Through Deep Learning-Based Surrogate Models. Aerospace 2024, 11, 669. https://doi.org/10.3390/aerospace11080669
Karali H, Inalhan G, Tsourdos A. Advanced UAV Design Optimization Through Deep Learning-Based Surrogate Models. Aerospace. 2024; 11(8):669. https://doi.org/10.3390/aerospace11080669
Chicago/Turabian StyleKarali, Hasan, Gokhan Inalhan, and Antonios Tsourdos. 2024. "Advanced UAV Design Optimization Through Deep Learning-Based Surrogate Models" Aerospace 11, no. 8: 669. https://doi.org/10.3390/aerospace11080669
APA StyleKarali, H., Inalhan, G., & Tsourdos, A. (2024). Advanced UAV Design Optimization Through Deep Learning-Based Surrogate Models. Aerospace, 11(8), 669. https://doi.org/10.3390/aerospace11080669








