Abstract
The internal losses in the tip clearance region strongly influence the compressor performance and its operational range. Previous research proved that passive wall treatments with circumferential grooves in axial compressors effectively increase the compressor stall margin. The vortex generated inside the circumferential grooves creates a resistance to the flow that leaks into the tip clearance region of the compressor. However, most works found in the literature on circumferential grooves in axial compressors deal only with high-performance single-stage axial compressors. Therefore, there is a need to investigate and analyze the behavior of circumferential grooves in a multi-stage environment. In the present work, a passive wall treatment with circumferential grooves was implemented in a multi-stage axial compressor. Different configurations of circumferential grooves were created at the casing of the first and second rotor rows used in a four-stage axial flow compressor. Numerical simulations were performed to evaluate the influence of the circumferential grooves on the performance of a multi-stage axial compressor. The results obtained after the simulations for the different circumferential groove configurations were compared with the results obtained for the compressor without casing treatment (smooth wall) for different rotational speeds. Furthermore, the complete compressor map characteristics were simulated for the different casing treatment configurations, and the results were compared with the compressor characteristics of the smooth wall case. The passive wall treatment with circumferential grooves produced changes in the multi-stage axial compressor flow field, especially in the tip clearance region, improving the compressor stability mainly for part load speeds.
1. Introduction
Tip clearance has a strong influence on the performance of turbomachines. Large tip clearances cause a loss of turbomachine performance and a reduction in its operational range [1,2,3,4]. In this region, the flow that leaks between the blade tip and the casing from the blade pressure side to the suction side, known as tip leakage flow, does not participate in the energy generation process, thus, being a source of losses in the compressor flow [5,6]. Moreover, the tip leakage flow interacts with the main flow and other vortex structures, contributing to the formation and strengthening of the tip leakage vortex. The degradation of the tip leakage vortex greatly influences the occurrence of the compressor stall [7,8,9,10].
Various studies have emerged in the last decades seeking to reduce the effect of losses in the tip clearance region and, thus, increase the stall margin of the compressors. The techniques used for this purpose can be classified into two large groups: active and passive. Tip injection is an example of a widely studied active technique [11,12,13]. The passive techniques, known as passive wall treatments, consist of modifications to the casing above the blade rotor rows. Among them, the most employed are the circumferential grooves and the axial slots [14,15,16,17,18].
Circumferential groove casing treatments have obtained significant improvements in the stall margin in works found in the literature. Mao et al. [19] achieved a 5.1% improvement in the stall margin with circumferential grooves in a counter-rotating axial compressor. Rolfes et al. [20] investigated the influence of three casing treatment configurations of circumferential grooves on the stall margin. They reached a 3–5.6% reduction in the stall mass flow of a low-speed axial compressor.
Previous works studied the mechanisms involved in the stall margin improvement achieved with casing treatments [21,22]. Rabe and Hah [23] suggested that the circumferential grooves change the flow incidence angle on the blade pressure side at the blade leading edge, which delays the stall in the compressor. Xingen et al. [24] investigated a five circumferential groove casing treatment. They observed that, by changing the flow path in the tip clearance region, the circumferential grooves induced the tip leakage vortex formation in a more backward position than in the configuration without casing treatment, which caused the delay of the onset of the stall.
In addition, works investigating the influence of the geometrical parameters of the circumferential grooves on compressor performance can be found in the literature. In the work of Sakuma et al. [25], the position and depth of a single circumferential groove were evaluated in a transonic axial compressor. The results showed an optimum location of the circumferential groove near the blade leading edge (but not above), and that deeper grooves present better performance than shallow grooves. Mirzabozorg et al. [26] analyzed the width of the circumferential grooves. If the width of the groove is large, it can adversely affect the compressor stall margin. On the other hand, medium-width grooves can very effectively enhance the stall margin. Nevertheless, the circumferential groove casing treatment implementation should be studied for each compressor design. Lin et al. [27] investigated the position of the circumferential grooves in the casing of an axial fan stage, concluding that grooves placed upstream of the blade leading edge or downstream of the blade trailing edge could cause a penalty in the compressor stall margin. Lin also found an optimum location for the circumferential groove around 20% of the blade axial chord downstream of the leading edge.
In recent years, some researchers have evaluated the influence of the casing treatments on the compressor stall margin for multi-stage axial compressors [20,23,28,29]. Nevertheless, most applied the casing treatments only in the first blade rotor row. Hence, there is a need to study the behavior of casing treatments created at the casing of different blade rotor rows in a multi-stage axial compressor.
In the present work, a passive wall treatment with circumferential grooves was implemented at the casing located in the first and second rotor rows of a four-stage axial compressor to assess its influence on the compressor stall margin. For that purpose, 3D flow simulations of Computational Fluid Dynamics (CFD) based on the Reynolds-Averaged Navier–Stokes (RANS) equations were performed for the smooth wall case and then for the compressor with the casing treatment to evaluate the flow field of the multi-stage compressor. Different configurations of circumferential grooves were evaluated for different rotational speeds.
2. Description of the Casing Treatment
Circumferential groove casing treatments were created at the first and second blade rotor rows of the casing of a multi-stage axial compressor for aeronautical applications. (Figure 1). This compressor is a four-stage turbomachine that operates with an aggressive transonic flow at the inlet. More details corresponding to the characteristics of the compressor can be found in previous works [30,31].

Figure 1.
Meridional view of the geometry model of the four-stages axial compressor.
First, circumferential grooves were created at the casing of the first blade rotor row. After that, the circumferential grooves were created at the casing of the second blade rotor row. For the creation of the circumferential groove geometries, different parameters were defined: width (w), depth (d), location of the first circumferential groove (L1), space between grooves (s), and the number of circumferential grooves. Figure 2 presents the parameters commonly used to define a geometry of circumferential groove.
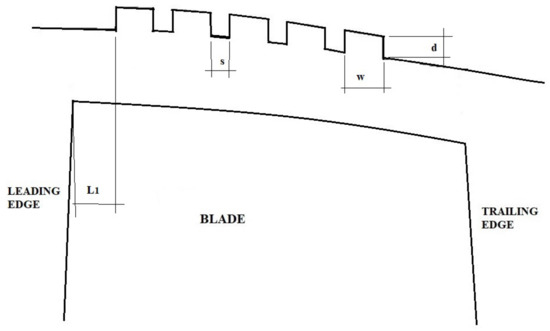
Figure 2.
The main parameters employed in creating the circumferential groove geometries.
2.1. Circumferential Grooves at the Casing of the First Blade Rotor Row
In this work, six different geometries of circumferential grooves were created at the casing of the first blade rotor row. All geometries have a width of 10% cx and a space of 5% cx between the circumferential grooves. The other parameters were varied to evaluate their influence on the compressor performance. Previous research has shown the significant impact that the depth of grooves has on the performance of circumferential grooves. The number of circumferential grooves was chosen to assess which circumferential grooves, installed near the leading or trailing edge, have the most influence on improving the compressor stall margin. Five geometries have the first circumferential groove located at 10% of cx. In the sixth geometry, the first circumferential groove is located above the blade leading edge (0% cx). The main characteristics of the circumferential grooves created at the casing of the first rotor row are summarized in Table 1.

Table 1.
Main parameters of the circumferential grooves placed at the casing of the first rotor row.
2.2. Circumferential Grooves at the Casing of the Second Blade Rotor Row
After the numerical simulations of the compressor with the circumferential grooves placed at the casing of the first blade rotor row, more circumferential groove geometries were created at the casing of the second blade rotor row. The geometries created for the second blade rotor row follow the same logic described in the previous section. Nevertheless, as the groove parameters are dimensioned based on the blade tip axial chord, the circumferential grooves do not have the exact dimensions. Four geometries were created at the casing of the second blade rotor row. These geometries were simulated in combination with geometries at the casing of the first rotor described in the previous section (Figure 3). Table 2 summarizes the main parameters of these geometries.
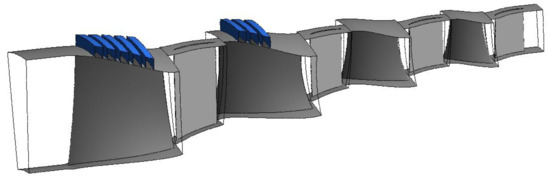
Figure 3.
Circumferential grooves installed on first and second blade rotor rows of the four-stage axial compressor.

Table 2.
Main parameters of the circumferential grooves placed at the casing of the second rotor row.
3. Numerical 3D Flow Calculations
3.1. Numerical Scheme Settings
The CFX solver developed by ANSYS® v. 2020 R1 (Canonsburg, PA, USA) was employed for the numerical simulations. The compressor map characteristics were computed by varying the static pressure at the outlet, beginning with a low value to represent a point near the choke condition [9]. The stall point is considered where the last converged point for a rotational speed is reached [24,32]. The RANS equations were solved during the steady-state simulations. The Rhie–Chow discretization method [33] was employed for the mass terms. For the convection terms from momentum equations, a high-resolution second-order scheme was applied. This high resolution uses the MUSCL (Monotonic Upstream-centered Scheme for Conservation Laws) with limiter functions to determine the discretization order based on the existence of discontinuities in the flow field. The two-equation k-ω Shear Stress Transport (SST) turbulence model, developed by Menter [34] was chosen to calculate the eddy viscosity. This turbulence model is suitable for turbomachine flow simulations, mainly when the flow boundary-layer detachment is present, as is the case of high-performance axial compressors. For this reason, it is the model employed to determine the flow eddy viscosity, also following the previous works performed in references [30,31]. By the way, the use of the SST turbulence model is part of the best practices in numerical simulations of turbomachines.
The boundary conditions set on the compressor inlet were total pressure, total temperature, turbulent intensity, and the flow angles. At the walls, the non-slip condition was set. At the outlet, the spanwise distribution of the static pressure was calculated through the radial equilibrium equation. Mixing-plane interfaces were established between the compressor stages, and the rotational periodicity was set in the blade-to-blade direction to save computational time, avoiding the full 3D geometry turbomachine flow simulation.
The decay and stabilization of the Root Mean Square (RMS) residuals from RANS equations were observed during the numerical simulations as convergence criteria. The RMS residuals values of continuity and momentum are lower than 10−4. The global continuity, momentum and energy imbalances in the entire computational domain should be less than 0.01%. Figure 4 shows the RMS residuals of the RANS equations for the smooth wall case. Other parameters like pressure ratio, mass flows at the inlet and outlet, compressor efficiency, and mass imbalance at the compressor inlet and outlet (Figure 5) were also monitored.
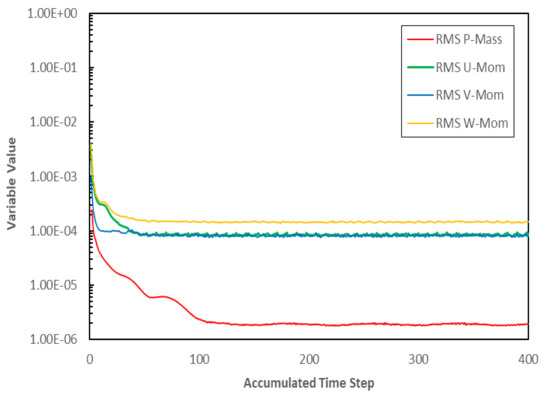
Figure 4.
RMS residuals of the RANS equations for the smooth wall case.
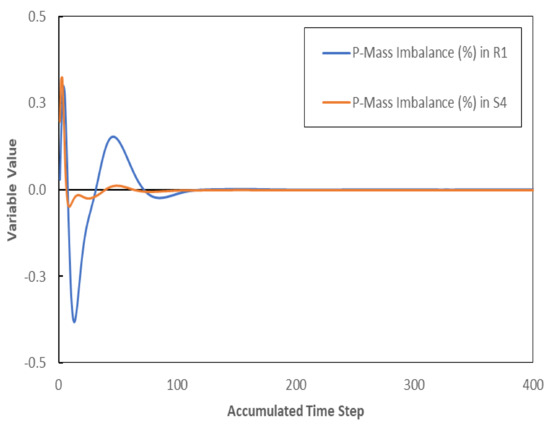
Figure 5.
Mass imbalance at the inlet and outlet.
3.2. Mesh Generation and Its Evaluation
To generate the mesh, an unstructured mesh with tetrahedral elements was generated using the commercial software ICEM CFD developed by ANSYS® v. 2020 R1. Prism elements were placed on all walls to adequately capture the viscous effects of the boundary layer (Figure 6).
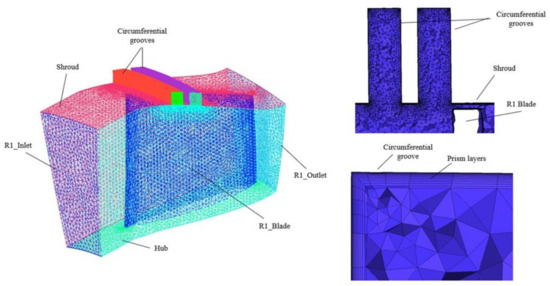
Figure 6.
Unstructured mesh of the R1 blade with two circumferential grooves and details of the mesh and prism layers inside the grooves.
Three different meshes were computed to study the mesh independence. The present work only includes the results obtained for the mesh independence for the case with one circumferential groove. The main parameters of these three meshes are shown in Table 3. In meshes 2 and 3, the number of prism layers in the circumferential grooves was limited to 15 to improve the mesh quality.

Table 3.
Main parameters of the meshes for the mesh independence study.
The compressor map characteristics for the design-point rotational speed (N = 1.0) were obtained from the simulations for the three meshes, as presented in Figure 7. The behavior of the three curves and the values obtained were similar. For this reason, mesh 1 was chosen to compute the rest of the simulations.
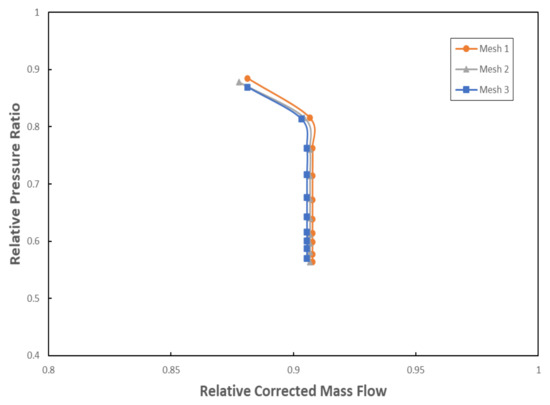
Figure 7.
Compressor map characteristics (relative pressure ratio) for N = 1.0% for the casing treatment with circumferential grooves.
4. Results
Numerical simulations were performed to calculate the compressor maps of the different casing treatment configurations and evaluate their influence on the flow. To assess the performance of the different passive wall treatments, the following equation was employed to calculate the variation of the compressor stall margin:
First, the compressor map for the smooth wall case was calculated. After that, the compressor map with the circumferential grooves at the first blade rotor row was computed and compared to the smooth wall case. Finally, the compressor map with the circumferential grooves at the second blade rotor row was calculated and compared to the smooth wall case.
4.1. Circumferential Grooves Located at the Casing of the First Blade Rotor Row
4.1.1. Analysis of the Circumferential Groove Depth
First, the influence of the circumferential groove depth was analyzed. To that end, three geometries of the circumferential grooves were studied. The three geometries have two circumferential grooves, and the other parameters were fixed and can be seen in Table 1. The three geometries have a depth of 2 mm (R1_d2_G2), 6 mm (R1_d6_G2), and 10 mm (R1_d10_G2), respectively.
In Figure 8, the compressor maps obtained for these geometries are plotted against the compressor map of the smooth wall case. Some improvements can be observed for different rotational speeds. First, all geometries improved the stall margin for low rotational speeds, N = 0.60 and N = 0.65. Furthermore, a significant extension of the stall margin for N = 0.90 occurred with the implementation of the deeper circumferential grooves at the casing of the first rotor row. Figure 9 and Figure 10 show a close-up of the stall margin improvements using casing treatment, for different part-load compressor speeds.
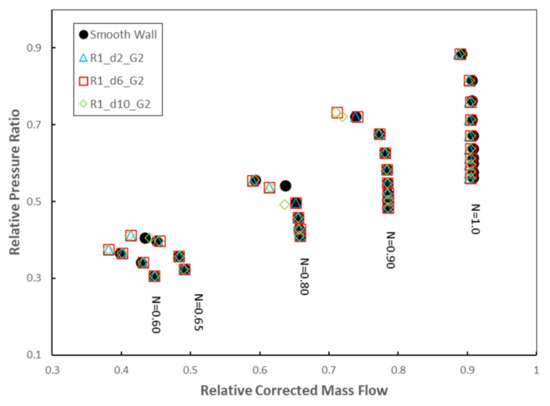
Figure 8.
Compressor map for the casing treatments at R1 and the smooth wall case: depth analysis.
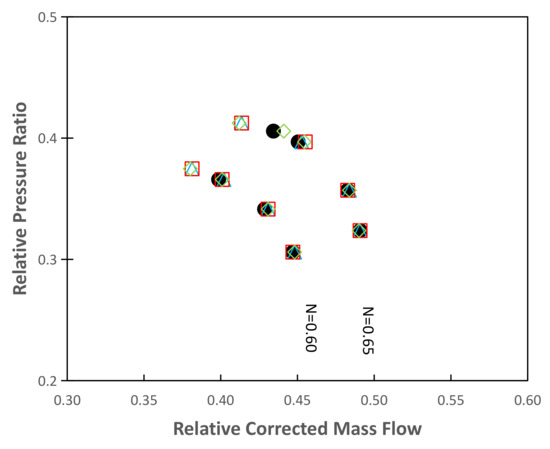
Figure 9.
Compressor map for the casing treatments at R1 and the smooth wall case: depth analysis—N = 0.60 and N = 0.65.
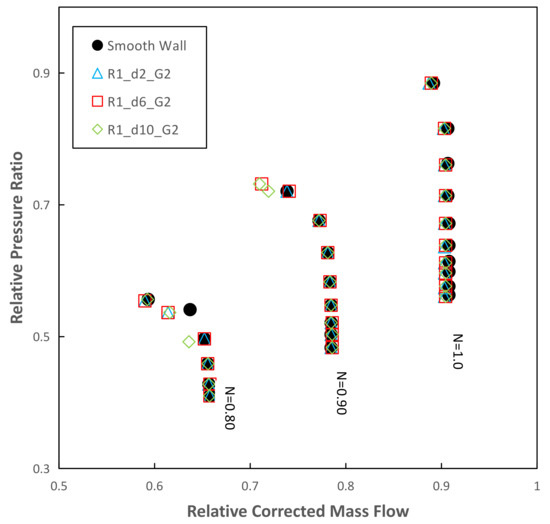
Figure 10.
Compressor map for the casing treatments at R1 and the smooth wall case: depth analysis—N = 0.80, N = 0.90 and N = 1.0.
Table 4 shows the variations of the stall margin and the isentropic peak efficiency of the three cases of circumferential grooves compared to the compressor without casing treatment. All geometries achieved an extension of the stall margin for low rotational speeds, N = 0.60 and N = 0.65. The stall margin increase is more significant than 7% in all cases. The main difference occurs for the N = 0.90 design rotational speed. In both cases, the geometries with deeper circumferential grooves (R1_d6_G2 and R1_d10_G2) reach a variation of over 5% of the stall margin with respect to the smooth wall case. However, for the geometry of shallower circumferential grooves (R1_d2_G2), which is a significant variation of the stall margin, was not achieved. Figure 11 shows a comparison of the entropy generation at the tip clearance with the installation of the circumferential grooves for the rotational speed N = 0.90. As the depth of the circumferential grooves increases, the entropy generation in the tip clearance region also increases.

Table 4.
Stall margin and peak efficiency variation of the circumferential grooves placed at the casing of the first rotor row.
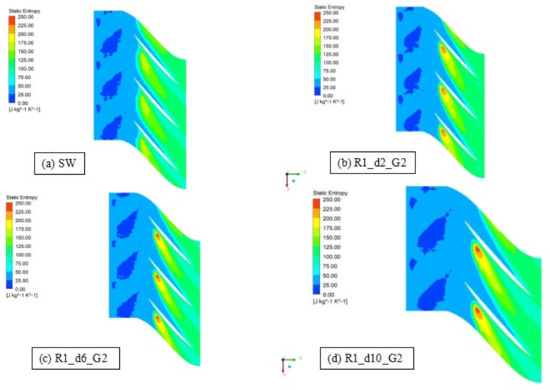
Figure 11.
Entropy contours for N = 0.90 for the casing treatment with circumferential grooves installed at the casing of the first blade rotor row at 0.95 blade span at near stall condition.
Figure 12 shows the pressure distribution at the R1 blade tip for N = 0.90 design rotational speed at stall mass flow. The pressure is diminished between 10% and 30% of the blade chord in the cases with circumferential grooves. This decrease is more significant in the case of the geometry with 6 mm circumferential grooves (R1_d6_G2).
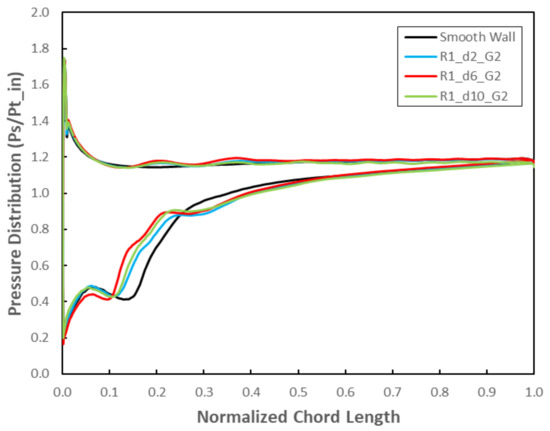
Figure 12.
Pressure distribution at R1 blade tip for N = 0.90 design rotational speed at near stall condition.
Figure 13 compares the smooth wall case and the circumferential groove casing treatment of the Relative Mach number contours at the tip of the R1 blade for N = 0.90. The tip leakage vortex expansion into the blade passage is reduced with the introduction of the circumferential grooves. This reduction helps to stabilize the flow in the blade tip region, contributing to the delay of the compressor stall. This reduction is more significant in the case of the geometry with circumferential grooves 6 mm depth (R1_d6_G2). Figure 14 compares the smooth wall case and the circumferential groove casing treatment of the static pressure contours at the tip of the R1 blade for N = 0.90.
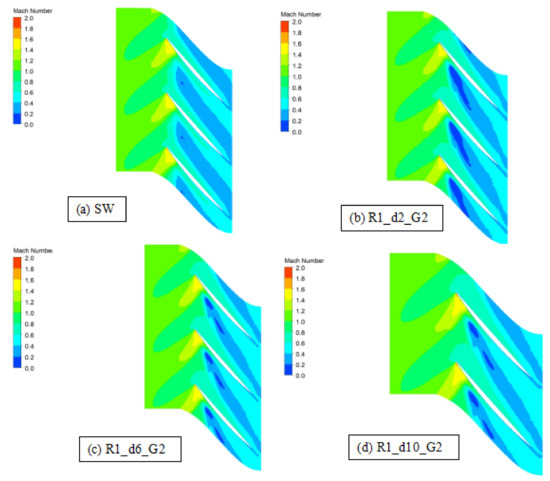
Figure 13.
Relative Mach number contours for N = 0.90 for the casing treatment with circumferential grooves installed at the casing of the first blade rotor row at 0.95 blade span at near stall condition.
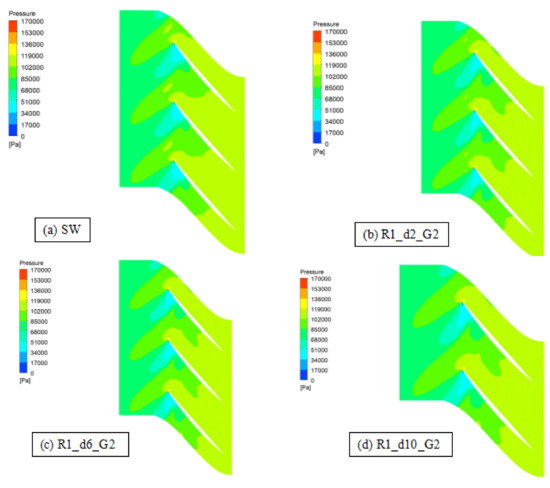
Figure 14.
Static contours for N = 0.90 for the casing treatment with circumferential grooves installed at the casing of the first blade rotor row at 0.95 blade span at near stall condition.
For the N = 0.60 design rotational speed, Figure 15 shows a comparison of relative pressure contours in blade-to-blade planes at near-stall condition. With the addition of the circumferential grooves, the low-pressure associated with the tip leakage vortex is reduced, especially in the case with deeper circumferential grooves (R1_d6_G2). The flow enters the circumferential grooves, where vortices are generated that reduce the leakage effect between the blade sides. The flow inside the grooves enters the mainstream in a more forward position interacting with the tip leakage vortex (TLV) (Figure 16). This reduction of the TLV effect delays the onset of the stall; thus, the compressor stall margin is extended.
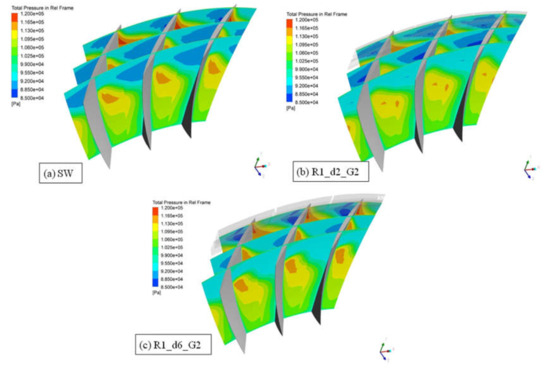
Figure 15.
Relative Total Pressure contours for N = 0.60 in blade-to-blade planes at near-stall condition.
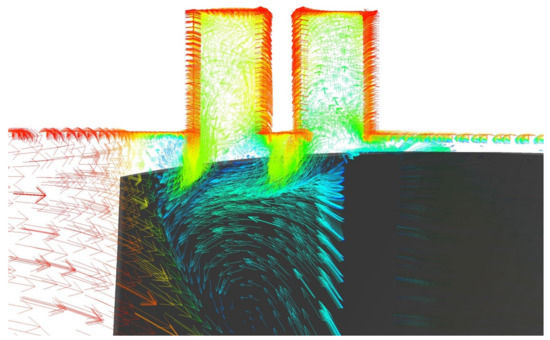
Figure 16.
Velocity vectors inside the circumferential grooves for N = 0.60 at near-stall condition (R1_d6_G2).
4.1.2. Number of Circumferential Groove Analysis
In this section, the number of circumferential grooves was increased from two to five in two of the geometries previously presented (R1_d2_G2 and R1_d6_G2) to evaluate the influence of increasing the number of circumferential grooves on the compressor performance.
The characteristic maps of the compressor for the new geometries (R1_d2_G5 and R1_d6_G5) in comparison with the smooth wall case and the two circumferential groove geometries are shown in Figure 17. In Table 5 and Table 6, the variations of the stall margin and the peak isentropic efficiency with respect to the smooth wall case are reported. Figure 18 and Figure 19 show a close-up of the stall margin improvements using casing treatment, for different part-load compressor speeds.
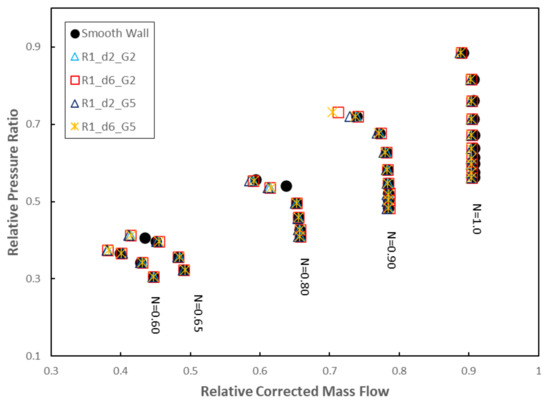
Figure 17.
Compressor map for the casing treatments at R1 and the smooth wall case: number of grooves analysis.

Table 5.
Stall margin and peak efficiency variation of the circumferential grooves: R1_d2_G2 and R1_d2_G5.

Table 6.
Stall margin and peak efficiency variation of the circumferential grooves: R1_d6_G2 and R1_d6_G5.
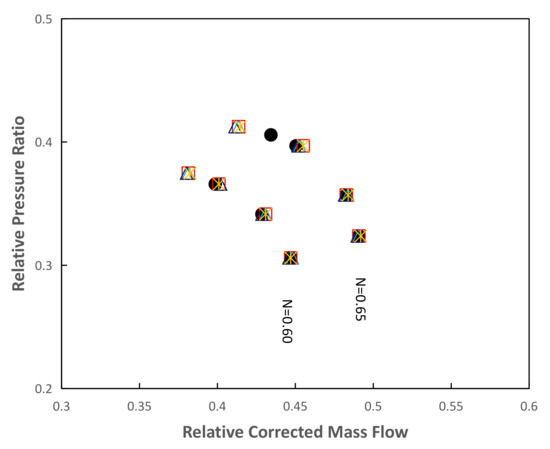
Figure 18.
Compressor map for the casing treatments at R1 and the smooth wall case: number of grooves analysis—N = 0.60 and N = 0.65.
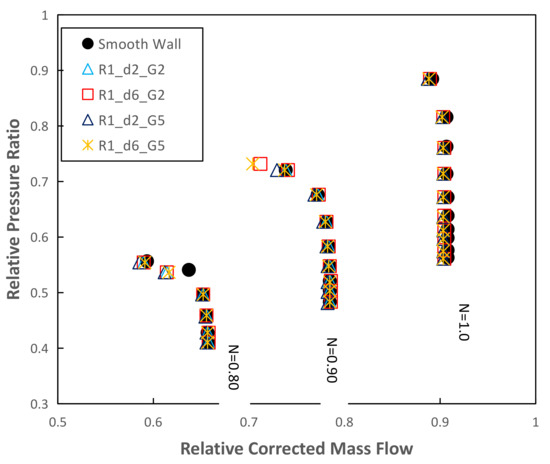
Figure 19.
Compressor map for the casing treatments at R1 and the smooth wall case: number of grooves analysis—N = 0.80, N = 0.90, and N = 1.0.
As described before, the four circumferential grooves perform well for low rotational speeds. Nevertheless, for the N = 0.90 design rotational speed, only the two geometries with deeper circumferential grooves (R1_d6_G2 and R1_d6_G5) achieved a significant extension of the stall margin, indicating that the depth of the circumferential grooves has a more substantial influence on the compressor performance than the number of circumferential grooves. With the increase in the number of circumferential grooves, the stall margin improved with respect to the geometries with two circumferential grooves, however, with a more significant efficiency penalty.
In Figure 20, the static pressure distribution at the blade tip is shown for the corrected rotational speed N = 0.90. Again, the pressure is reduced between 10 and 30% of the blade chord in the cases with circumferential grooves. Regarding the number of grooves, the pressure is reduced in this region compared to the geometries with only two circumferential grooves. However, the two geometries with deeper circumferential grooves have greater effect.
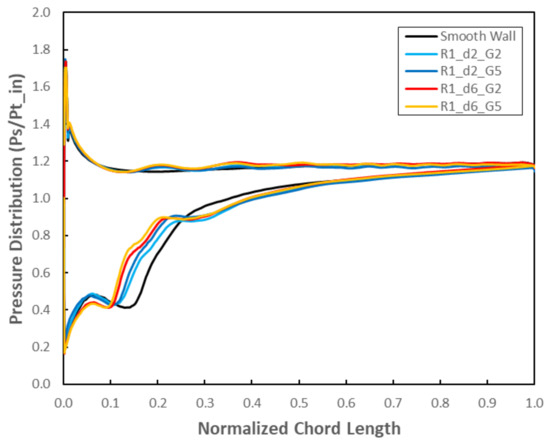
Figure 20.
Pressure distribution at 0.95 blade span for N = 0.90 design rotational speed at near stall condition: number of grooves analysis.
The spread of the tip leakage vortex into the passage is reduced when the circumferential grooves are installed. The addition of three more circumferential grooves in R1_d6_G5 does not lead to significant variations regarding the TLV when compared to the geometry with only two circumferential grooves, R1_d6_G2 (Figure 21). The two circumferential grooves located in a more forward position have a greater influence on the tip leakage vortex.
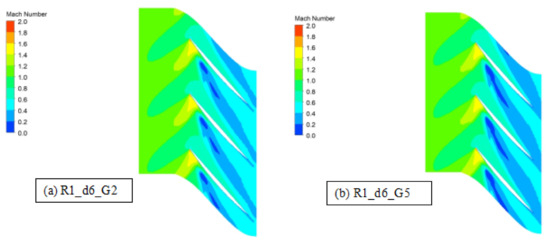
Figure 21.
Relative Mach number contours for N = 0.90 at 0.95 blade span at near stall condition: R1_d6_G2 and R1_d6_G5.
In the compressor with the R1_d2_G5 geometry installed, the tip leakage flow is reduced in the region covered between the third and fifth circumferential groove (Figure 22). That reduction weakens the tip leakage vortex, which consequently delays the onset of the compressor stall at N = 0.60 design rotational speed.
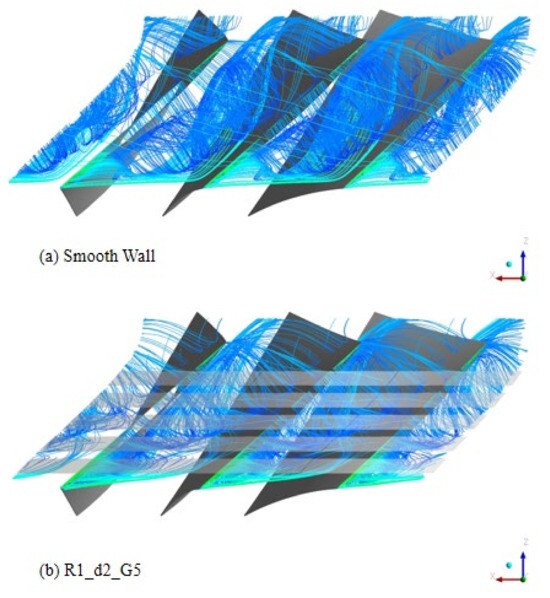
Figure 22.
Tip leakage vortex streamlines for the smooth wall case and R1_d2_G5 at N = 0.60 at stall mass flow.
4.1.3. First Circumferential Groove Location Analysis
Finally, the position of the first circumferential groove was changed to assess the effect of this parameter on the compressor stall margin. The first circumferential groove was moved above the leading edge (0% cx). This new geometry (R1_L1_0_G2) has two circumferential grooves with 6 mm depth as the R1_d6_G2 geometry. The compressor map and the results obtained for the stall margin and peak isentropic efficiency variation are presented in Figure 23 and Table 7, respectively. Figure 24 and Figure 25 show a close-up of the stall margin improvements using casing treatment, for different part-load compressor speeds.
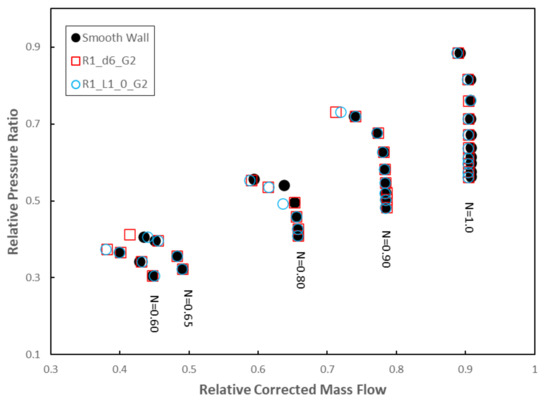
Figure 23.
Compressor map for the casing treatments at R1 and the smooth wall case: first groove location analysis.

Table 7.
Stall margin and peak efficiency variation of the circumferential grooves: R1_d6_G2 and R1_L1_0_G2.
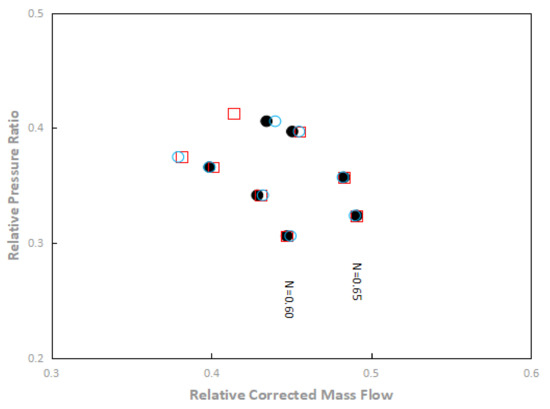
Figure 24.
Compressor map for the casing treatments at R1 and the smooth wall case: first groove location analysis—N = 0.60 and N = 0.65.
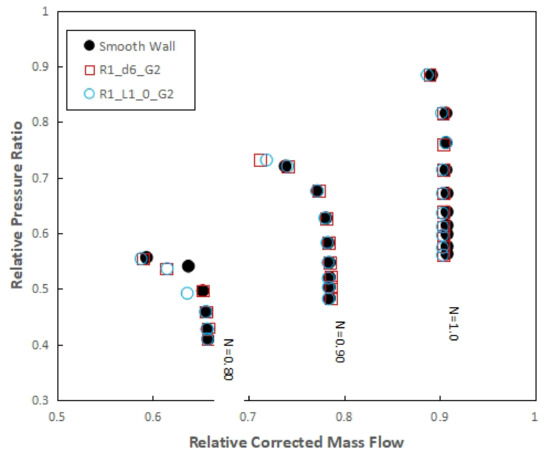
Figure 25.
Compressor map for the casing treatments at R1 and the smooth wall case: first groove location analysis—N = 0.80, N = 0.90, and N = 1.0.
With the first circumferential located above the blade leading edge, the stall margin extension is slightly greater than in the case where the first circumferential groove is placed at 10% of cx for the N = 0.60 design rotational speed. Still, for the N = 0.90 design rotational speed, the increase in stall margin with respect to the smooth wall case, is smaller. For the peak isentropic efficiency variation, the results obtained are similar to those obtained for the R1_d6_G2 geometry. Table 8 shows the variations of the stall margin and the isentropic peak efficiency of the three cases of circumferential grooves with respect to the compressor without casing treatment.

Table 8.
Stall margin and peak efficiency variation of the circumferential grooves: R1_G5_R2_G2 and R1_G5_R2_G3.
Both geometries presented a good performance in extending the compressor stall margin. For N = 0.90 design rotational speed, the circumferential grooves of the R1_L1_0_G2 geometry reduce the leakage flow coming from the blade pressure side, weakening the formation of the leakage vortex (Figure 26). However, the reduction of the pressure distribution (Figure 27) is less than the one obtained for the R1_d6_G2 geometry.
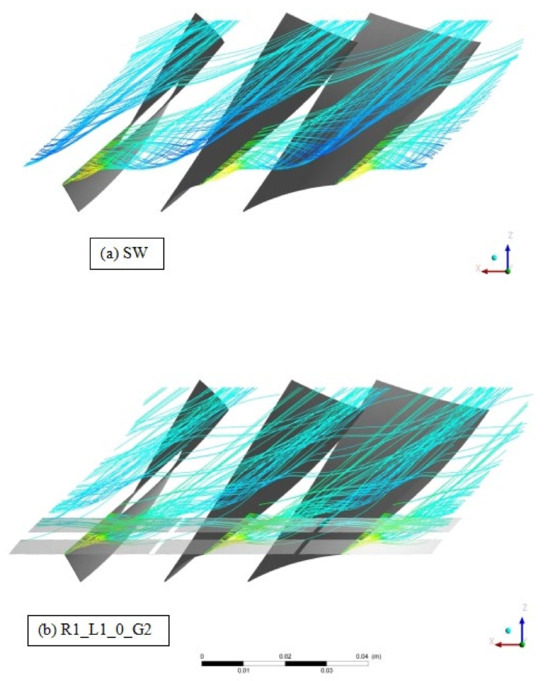
Figure 26.
Tip leakage vortex streamlines for the smooth wall case and R1_L1_0_G2 at N = 0.90 at stall mass flow.
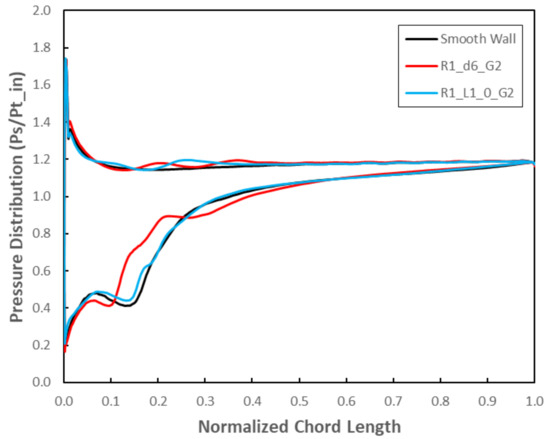
Figure 27.
Pressure distribution at 0.95 blade span for N = 0.90 design rotational speed at near stall condition: first groove location analysis.
4.2. Circumferential Grooves Located at the Casing of the Second Blade Rotor Row
After the study of the performance of the circumferential grooves at the casing of the first blade rotor row, circumferential grooves were created at the casing of the second blade rotor row. The performance of circumferential grooves to improve the stall margin was evaluated for cases with combinations of circumferential grooves on the first and second blade rotor rows. Four circumferential groove geometries were studied: two with five circumferential grooves at the first rotor and two and three circumferential grooves at the second rotor (R1_G5_R2_G2 and R1_G5_R2_G3), one with two circumferential grooves at R1 and R2 (R1_G2_R2_G2), and the last one with five grooves at R1 and three at R2, but with the first circumferential groove at R2 located at −5% of cx (R2_L1-5).
The compressor maps of these casing treatment configurations are shown in Figure 28. Table 8 and Table 9 present the variations of the stall margin and the isentropic peak efficiency of the three circumferential groove cases with respect to the compressor without casing treatment. A remarkable extension of the compressor stall margin for N = 0.60 rotational speed occurred in all cases with circumferential grooves at the casing of R1 and R2. The four geometries managed to extend the stall margin above 7% (R1_G5_R2_G2 and R2_L1-5) or 8% (R1_G5_R2_G3 and R1_G2_R2_G2) when compared to the smooth wall case. Nevertheless, none of these circumferential groove geometries obtained a significant improvement of stall margin for the other rotational speeds.
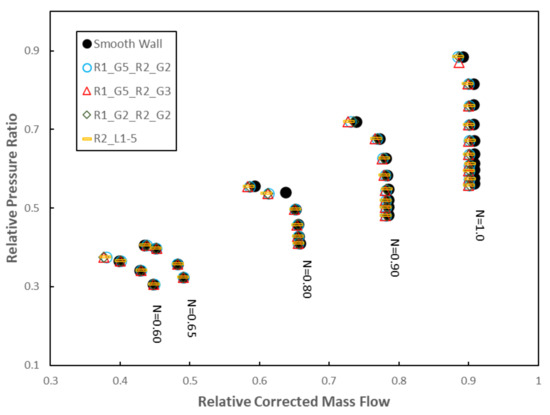
Figure 28.
Compressor map for the casing treatments at R2 and the smooth wall case.

Table 9.
Stall margin and peak efficiency variation of the circumferential grooves: R1_G2_R2_G2 and R2_L1_-5.
At N = 0.60 corrected rotational speed, the development of the tip leakage vortex at near stall condition occurs in the first blade rotor (R1) region between 75 and 80% of the blade span (Figure 29). Figure 30 and Figure 31 show Mach number contours at 0.75 and 0.80 blade span, respectively, at N = 0.60 for the smooth wall case and the R1_G2_R2_G2 case. The circumferential grooves installed at the first blade rotor row diminished the effect of the tip leakage vortex development observed for the smooth wall case. This contributes to the delay of the compressor stall and, hence, the extension of the compressor stall margin.
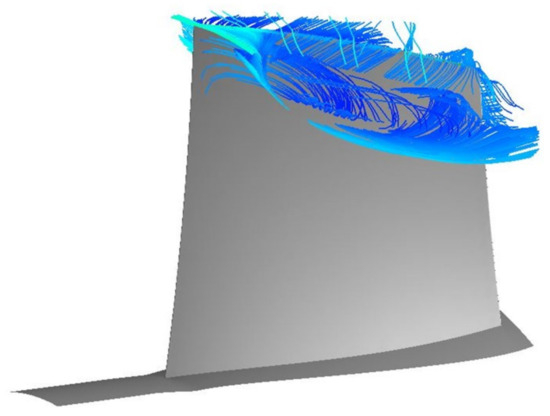
Figure 29.
The tip leakage vortex development for the smooth wall case at N = 0.60 at near stall condition.
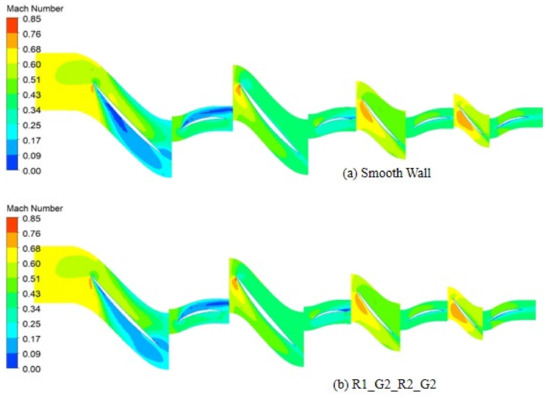
Figure 30.
Mach number contours at 0.75 blade span at N = 0.60 for the smooth wall case and R1_G2_R2_G2 at near stall condition.
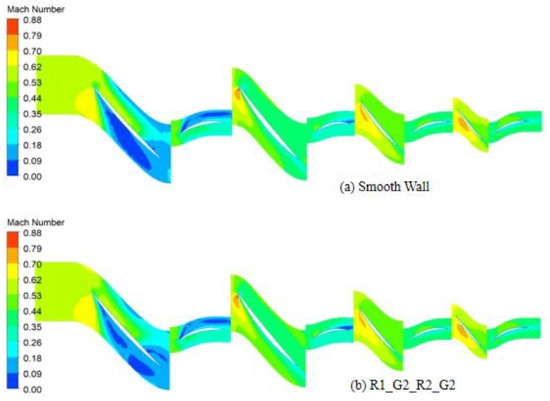
Figure 31.
Mach number contours at 0.80 blade span at N = 0.60 for the smooth wall case and R1_G2_R2_G2 at near stall condition.
5. Conclusions
The objective of the present work was to evaluate the influence of a casing treatment with circumferential grooves on the compressor map of a high-performance multi-stage axial compressor. To that end, different geometries of circumferential grooves were created at the casing of the first and second blade rotor rows of a four-stage axial compressor. Parameters of the circumferential grooves were evaluated to assess their influence on the compressor stall margin. 3D CFD simulations were computed to obtain the compressor map characteristics and to evaluate the flow field of the axial compressor for the different cases. The results obtained were compared with the results obtained for the compressor without casing treatment (smooth wall case).
First, the study of some groove parameters was conducted for circumferential grooves placed at the casing of the first blade rotor row. The influence on the compressor stall margin of the depth (d), the number of circumferential grooves, and the location of the first circumferential grooves (L1) were evaluated. The circumferential grooves with deeper circumferential grooves presented a significant influence on the extension of the stall margin. The geometry with two circumferential grooves with 6 mm depth achieve an improvement in the stall margin of 7.07% for N = 0.60, and the geometry with five circumferential grooves with 6 mm depth achieved an improvement in the stall margin of 6.69% for N = 0.90. Regarding the number of circumferential grooves, the five circumferential geometries performed better than the ones with only two circumferential grooves, however, with a greater penalty in isentropic efficiency. Finally, the location of the first groove was moved forward to 0% of cx (above the blade leading edge). This geometry (R1_L1_0_G2) obtained improvements of 7.72% and 4.49% in the stall margin for N = 0.60% and N = 0.90%, respectively.
Finally, circumferential grooves were created at the casing of the second blade rotor row. These new geometries improved the compressor stall margin for the N = 0.60 rotational speeds in more than 7% for all cases. However, for the other rotational speeds, this improvement was less for the geometries created only at the casing of the first blade rotor row. This demonstrates that the casing treatments are interesting in the front compressor stages, even to improve or enhance the compressor operation with stall inception, in which the compressor stability is affected. Furthermore, with the use of variable geometry technique, the undesirable flow behaviors should be treated at the compressor inlet, improving its alignment and features from the machine inlet until its outlet region.
Author Contributions
Conceptualization, J.T.T., C.B. and D.F.C.; methodology, R.B.D., J.T.T. and D.F.C.; validation, R.B.D. and J.T.T.; investigation, R.B.D.; writing—original draft preparation, R.B.D.; writing—review and editing, J.T.T., D.F.C., C.B. and F.J.d.S.S.; supervision, J.T.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Council for Scientific and Technological Development (CNPq) and AVIBRAS Aerospace Industry. Grant number: 141634/2019-7.
Data Availability Statement
Data are available on request due to restrictions. Due to privacy, the data presented in this study are available on request from the authors.
Acknowledgments
The authors would like to thank the National Council for Scientific and Technological Development (CNPq) and AVIBRAS Aerospace Industry for supporting this research conducted at the Turbomachines Department of the Aeronautics Institute of Technology (ITA).
Conflicts of Interest
Author Diogo Ferraz Cavalca was employed by the company Avibras Aerospace Industry. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.
Abbreviations
| CFD | Computational Fluid Dynamics |
| CT | Casing treatment |
| N | Rotational speed |
| PR | Pressure ratio |
| RANS | Reynolds-Averaged Navier–Stokes |
| RMS | Root Mean Square |
| SM | Stall margin |
| SST | Shear Stress Transport |
| SW | Smooth wall |
| Nomenclature | |
| Cw | Tangential velocity |
| cx | Blade tip axial chord |
| k | Turbulent kinetic energy |
| Stall mass flow | |
| ηis,peak | Isentropic efficiency at peak condition |
| ρ | Density |
| p | Pressure |
| r | Radius |
| ω | Turbulent dissipation rate |
| y+ | Non-dimensional wall distance |
References
- Zhong, J.; Han, S.; Lu, H.; Kan, X. Effect of tip geometry and tip clearance on aerodynamic performance of a linear compressor cascade. Chin. J. Aeronaut. 2013, 26, 583–593. [Google Scholar] [CrossRef]
- Berdanier, R.A.; Smith, N.R.; Young, A.M.; Key, N.L. Effects of Tip Clearance on Stall Inception in a Multistage Compressor. J. Propuls. Power 2018, 34, 308–317. [Google Scholar] [CrossRef]
- Gourdain, N.; Leboeuf, F. Unsteady Simulation of an Axial Compressor Stage with Casing and Blade Passive Treatments. ASME J. Turbomach. 2009, 131, 021013. [Google Scholar] [CrossRef]
- Yoon, S.; Cargill, P. Casing Treatment: Its Potential and Limitations. ASME J. Turbomach. 2023, 145, 041011. [Google Scholar] [CrossRef]
- Booth, T.C.; Dodge, P.R.; Hepworth, H.K. Rotor-Tip Leakage: Part I—Basic Methodology. J. Eng. Power 1982, 104, 154–161. [Google Scholar] [CrossRef]
- Wadia, A.R.; Booth, T.C. Rotor-Tip Leakage: Part II—Design Optimization Through Viscous Analysis and Experiment. J. Eng. Power 1982, 104, 162–169. [Google Scholar] [CrossRef]
- Adamczyk, J.J.; Celestina, M.L.; Greitzer, E.M. The Role of Tip Clearance in High-Speed Fan Stall. J. Turbomach 1993, 115, 28–38. [Google Scholar] [CrossRef]
- Furukawa, M.; Inoue, M.; Saiki, K.; Yamada, K. The Role of Tip Leakage Vortex Breakdown in Compressor Rotor Aerodynamics. J. Turbomach 1999, 121, 469–480. [Google Scholar] [CrossRef]
- Chen, H.; Huang, X.; Shi, K.; Fu, S.; Ross, M.; Bennington, M.A.; Cameron, J.D.; Morris, S.C.; McNulty, S.; Wadia, A. A Computational Fluid Dynamics Study of Circumferential Groove Casing Treatment in a Transonic Axial Compressor. J. Turbomach. 2014, 136, 031003. [Google Scholar] [CrossRef]
- Kau, H.-P.; Brignole, G.; Wilke, I. Designing a Casing Treatment for a Transonic Axal Compressor; Lecture Series; von Karman Institute for Fluid Dynamics: Sint-Genesius-Rode, Belgium, 2006. [Google Scholar]
- Wang, W.; Chu, W.; Zhang, H.; Kuang, H. Experimental and numerical study of tip injection in a subsonic axial flow compressor. Chin. J. Aeronaut. 2017, 30, 907–917. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Du, J.; Zhang, H.; Nie, C. Implementation of stability-enhancement with tip air injection in a multi-stage axial flow compressor. Aerosp. Sci. Technol. 2021, 113, 106646. [Google Scholar] [CrossRef]
- Yoon, S.; Cargill, P. Casing Treatment: Its Potential and Limitations. In Volume 10A: Turbomachinery—Axial Flow Fan and Compressor Aerodynamics, Proceedings of ASME Turbo Expo 2022: Turbomachinery Technical Conference and Exposition, Rotterdam, The Netherlands, 13–17 June 2022; American Society of Mechanical Engineers: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Alone, D.B.; Kumar, S.S.; Shobhavathy, M.; Mudipalli, J.R.R.; Pradeep, A.; Ramamurthy, S.; Iyengar, V.S. Experimental assessment on effect of lower porosities of bend skewed casing treatment on the performance of high speed compressor stage with tip critical rotor characteristics. Aerosp. Sci. Technol. 2017, 60, 193–202. [Google Scholar] [CrossRef]
- Lu, B.; Zhu, M.; Teng, J.; Qiang, X. Design optimization of axial slot casing treatment in a highly-loaded mixed-flow compressor. Aerosp. Sci. Technol. 2020, 107, 106262. [Google Scholar] [CrossRef]
- Lu, B.; Zhu, M.; Teng, J.; Qiang, X. Design strategy of axial slot casing treatment for a transonic compressor rotor based on parametric analysis. Aerosp. Sci. Technol. 2021, 119, 107142. [Google Scholar] [CrossRef]
- Du, J.; Qiu, J.; Zhang, Q.; Ba, D.; Maroldt, N.; Seume, J.R. Unsteady Interaction Mechanisms of Axial-Slot Casing Treatment with Tip Region Flow in a Highly-Loaded Mixed-Flow Compressor. J. Eng. Gas. Turbine Power 2022, 144, 091001. [Google Scholar] [CrossRef]
- Legras, G.; Gourdain, N.; Sicot, F.; Roumeas, M. Time Spectral Calculation of a Casing Treatment Configuration for a High Pressure Compressor. In Proceedings of the 8th European Turbomachinery Conference, Graz, Austria, 23–27 March 2009. [Google Scholar]
- Mao, X.; Liu, B.; Zhao, H. Numerical analysis of the circumferential grooves casing treatment in a counter-rotating axial flow compressor. Appl. Therm. Eng. 2018, 130, 29–39. [Google Scholar] [CrossRef]
- Rolfes, M.; Lange, M.; Vogeler, K.; Mailach, R. Experimental and Numerical Investigation of a Circumferential Groove Casing Treatment in a Low-Speed Axial Research Compressor at Different Tip Clearances. J. Turbomach. 2017, 139, 121009. [Google Scholar] [CrossRef]
- Smith, G.D.J.; Cumpsty, N.A. Flow Phenomena in Compressor Casing Treatment. J. Eng. Gas. Turbine Power 1984, 106, 532–541. [Google Scholar] [CrossRef]
- Legras, G.; Gourdain, N.; Trebinjac, I. Numerical analysis of the tip leakage flow field in a transonic axial compressor with circumferential casing treatment. J. Therm. Sci. 2010, 19, 198–205. [Google Scholar] [CrossRef]
- Rabe, D.C.; Hah, C. Application of Casing Circumferential Grooves for Improved Stall Margin in a Transonic Axial Compressor. In Proceedings of the ASME Turbo Expo 2002: Power for Land, Sea, and Air, Amsterdam, The Netherlands, 3–6 June 2002; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2002; pp. 1141–1153. [Google Scholar] [CrossRef]
- Lu, X.; Chu, W.; Zhu, J.; Wu, Y. Mechanism of the interaction between casing treatment and tip leakage flow in a subsonic axial compressor. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2006; pp. 79–90. [Google Scholar] [CrossRef]
- Sakuma, Y.; Watanabe, T.; Himeno, T.; Kato, D.; Murooka, T.; Shuto, Y. Numerical Analysis of Flow in a Transonic Compressor with a Single Circumferential Casing Groove: Influence of Groove Location and Depth on Flow Instability. J. Turbomach. 2014, 136, 031017. [Google Scholar] [CrossRef]
- Mirzabozorg, M.A.S.; Bazazzadeh, M.; Hamzezade, M. Numerical Study on the Effect of Single Shallow Circumferential Groove Casing Treatment on the Flow Field and the Stability of a Transonic Compressor. J. Appl. Fluid. Mech. 2017, 10, 257–265. [Google Scholar] [CrossRef]
- Lin, W.; Sreenivas, K.; Webster, R.S.; Hyams, D.G. Effect of Casing Groove Locations on the Performance of an Axial Flow Stage. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, San Jose, CA, USA, 14–17 July 2013; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2013. [Google Scholar] [CrossRef]
- Shabbir, A.; Adamczyk, J.J. Flow Mechanism for Stall Margin Improvement due to Circumferential Casing Grooves on Axial Compressors. J. Turbomach. 2005, 127, 708–717. [Google Scholar] [CrossRef]
- Hathaway, M.D. Passive Endwall Treatments for Enhancing Stability; NASA/TM-2007-214409, ARL-TR-3878; NASA: Washington, DC, USA, 2007.
- Silva, L.M.; Tomita, J.T.; Bringhenti, C.; Whitacker, L.H.L.; Almeida, L.E.N.; Cavalca, D.F. A Small Jet Engine Preliminary Design and its Performance Calculations. In Proceedings of the 24th ISABE Conference, Canberra, Australia, 22–27 September 2019. [Google Scholar]
- Diaz, R.B.; Tomita, J.T.; Bringhenti, C.; Cavalca, D.F. Improvements in a Multistage Axial-Flow Compressor Design and its Operation on a Small Gas Turbine Performance. In Proceedings of the 25th ISABE Conference, Ottawa, ON, Canada, 25–30 September 2022. [Google Scholar]
- Qiang, X.-Q.; Zhu, M.-M.; Teng, J.-F. Effect of circumferential grooves casing treatment on tip leakage flow and loss in a transonic mixed-flow compressor. J. Theor. Appl. Mech. 2013, 51, 903–913. [Google Scholar]
- Rhie, C.M.; Chow, W.L. Numerical study of the turbulent flow past an airfoil with trailing edge separation. AIAA J. 1983, 21, 1525–1532. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).