Size-Dependent Finite Element Analysis of Functionally Graded Flexoelectric Shell Structures Based on Consistent Couple Stress Theory
Abstract
1. Introduction
2. Basic Governing Equations
2.1. The Flexoelectricity Model Based on Consistent Couple Stress Theory
2.2. Equivalent Material Properties of Functionally Graded Materials
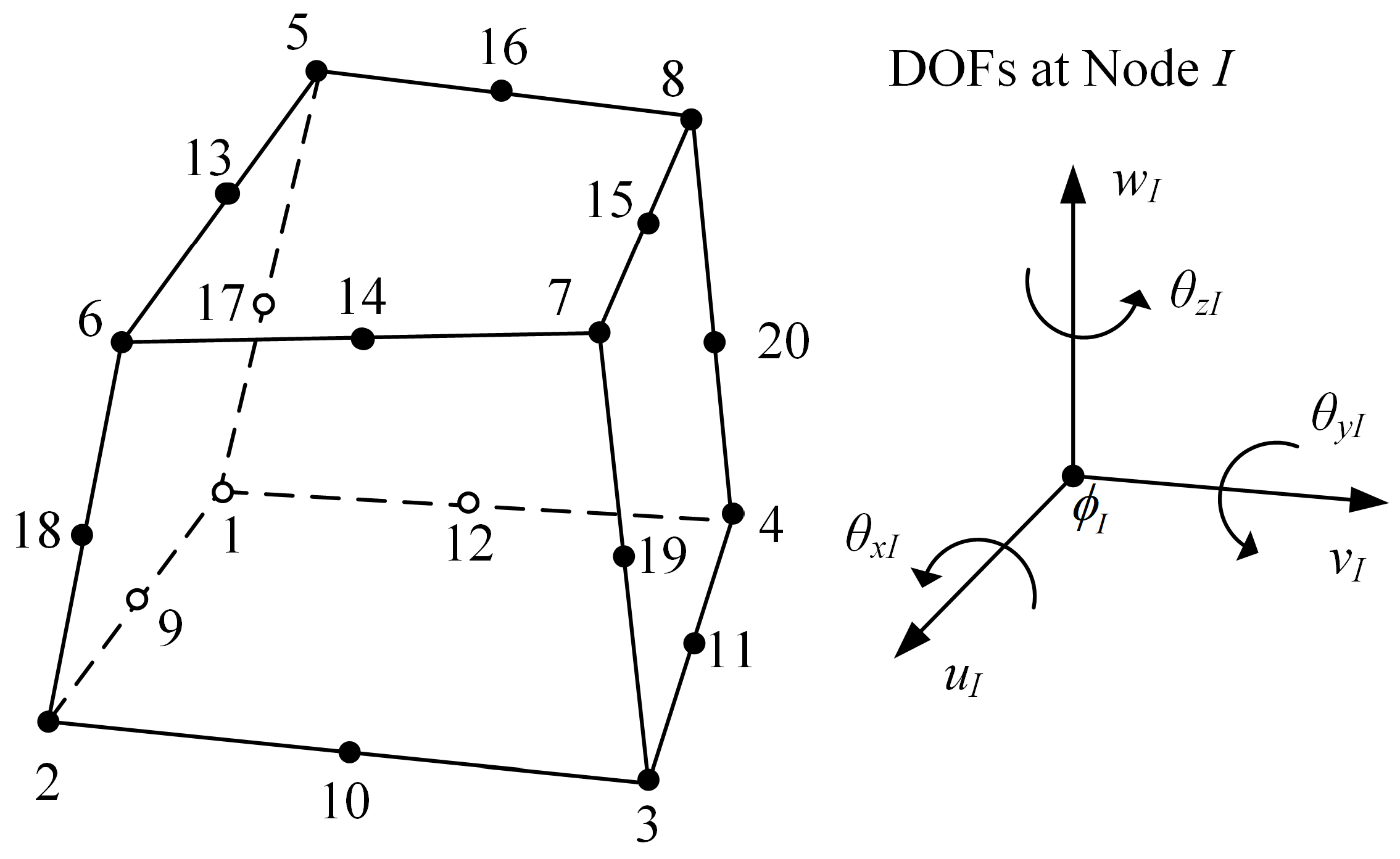
3. Element Formulation
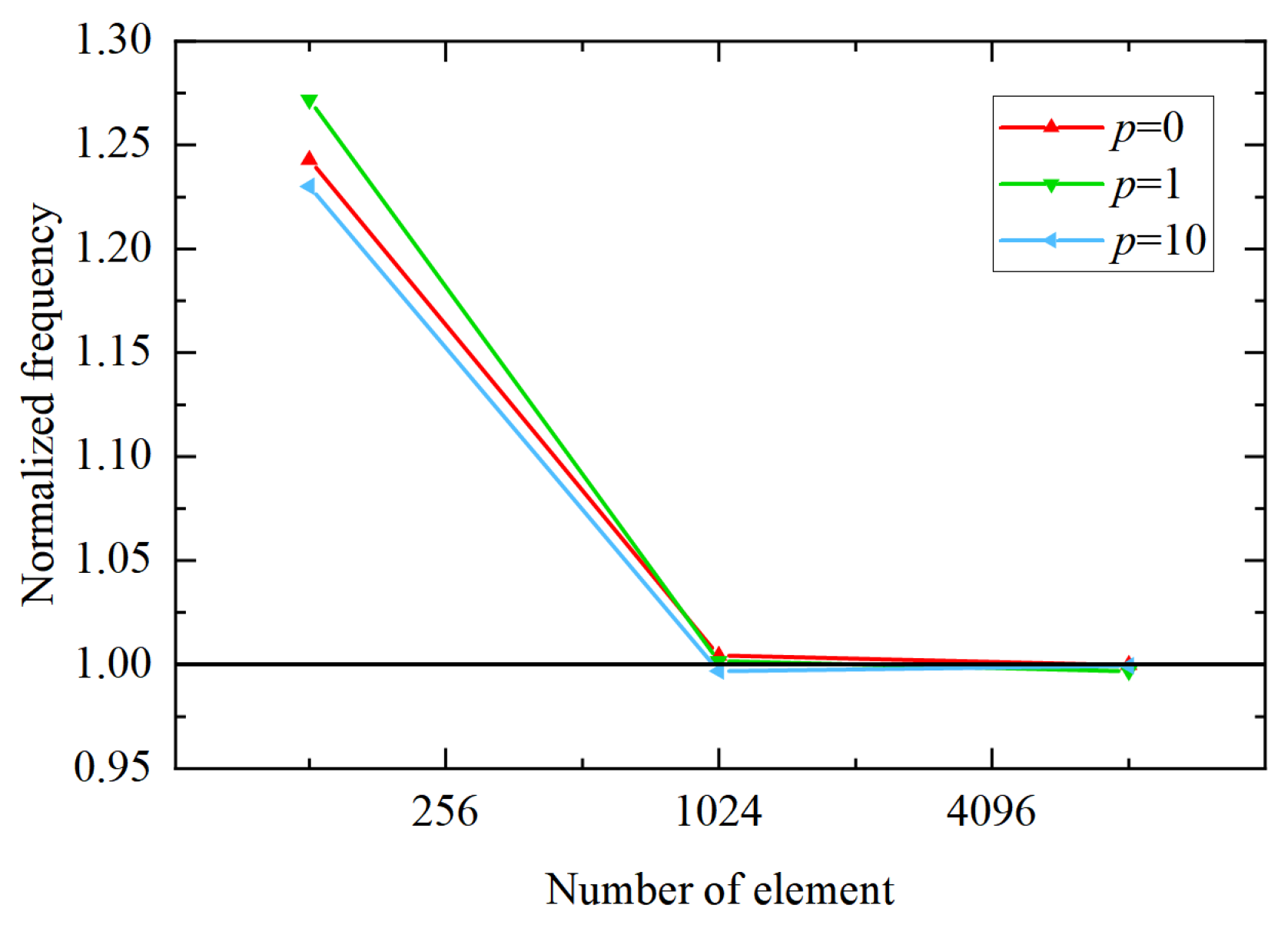
4. Numerical Tests
4.1. Static Analysis
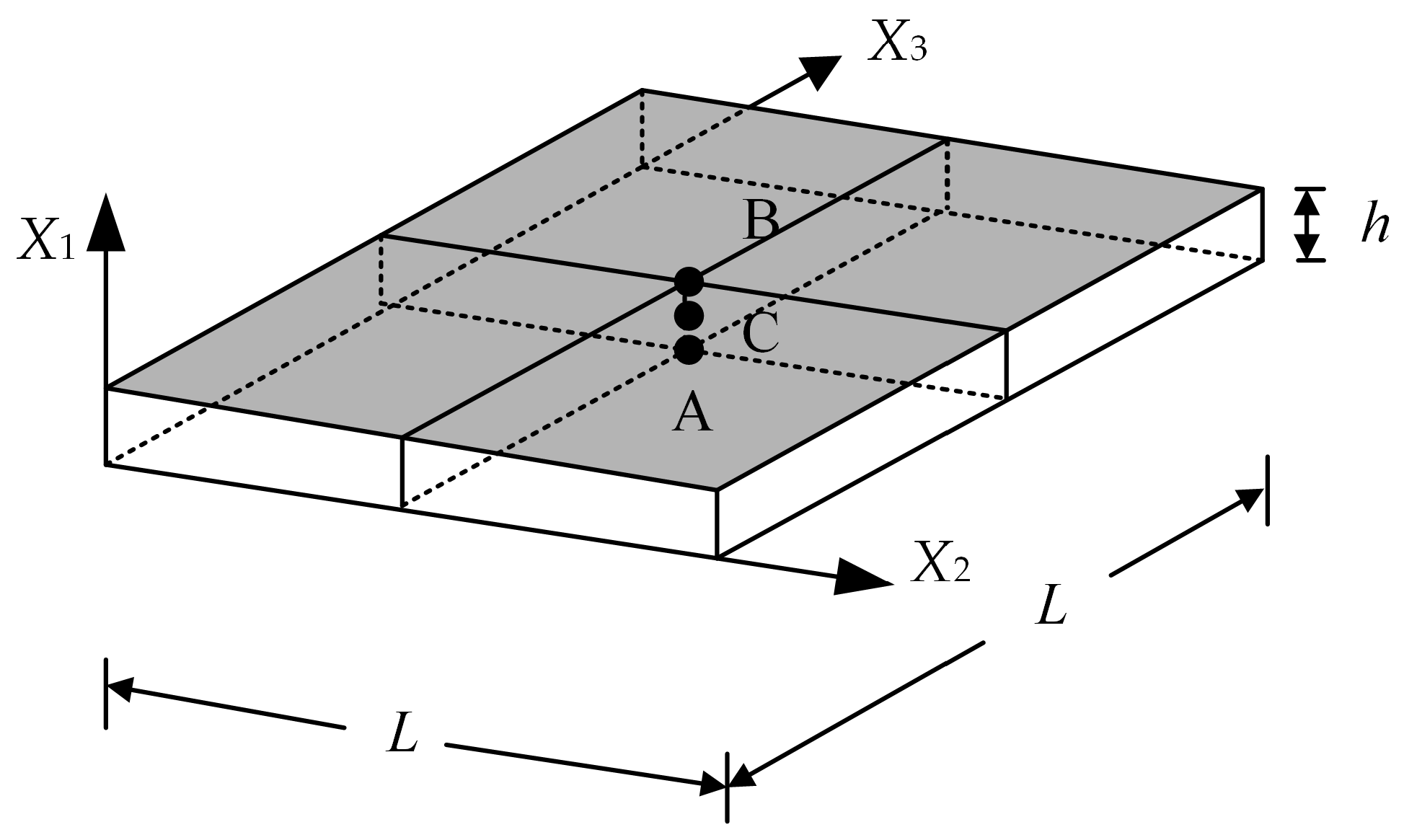
4.1.1. The Square Functionally Graded Microplate without Flexoelectricity
4.1.2. Functionally Graded Flexoelectric Microplate
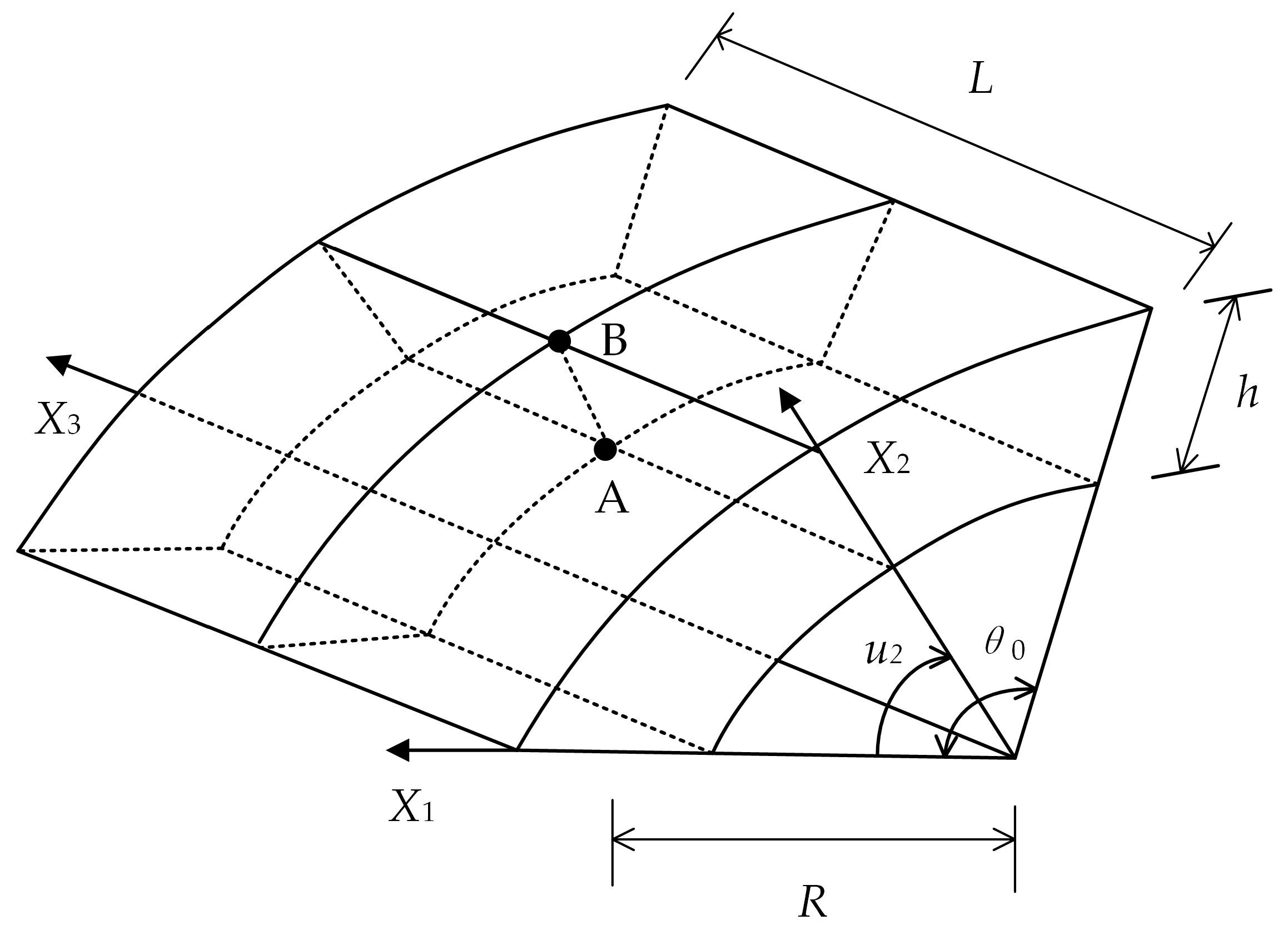
4.1.3. Functionally Graded Flexoelectric Cylindrical Micro-Shell
4.2. Free Vibration Analysis
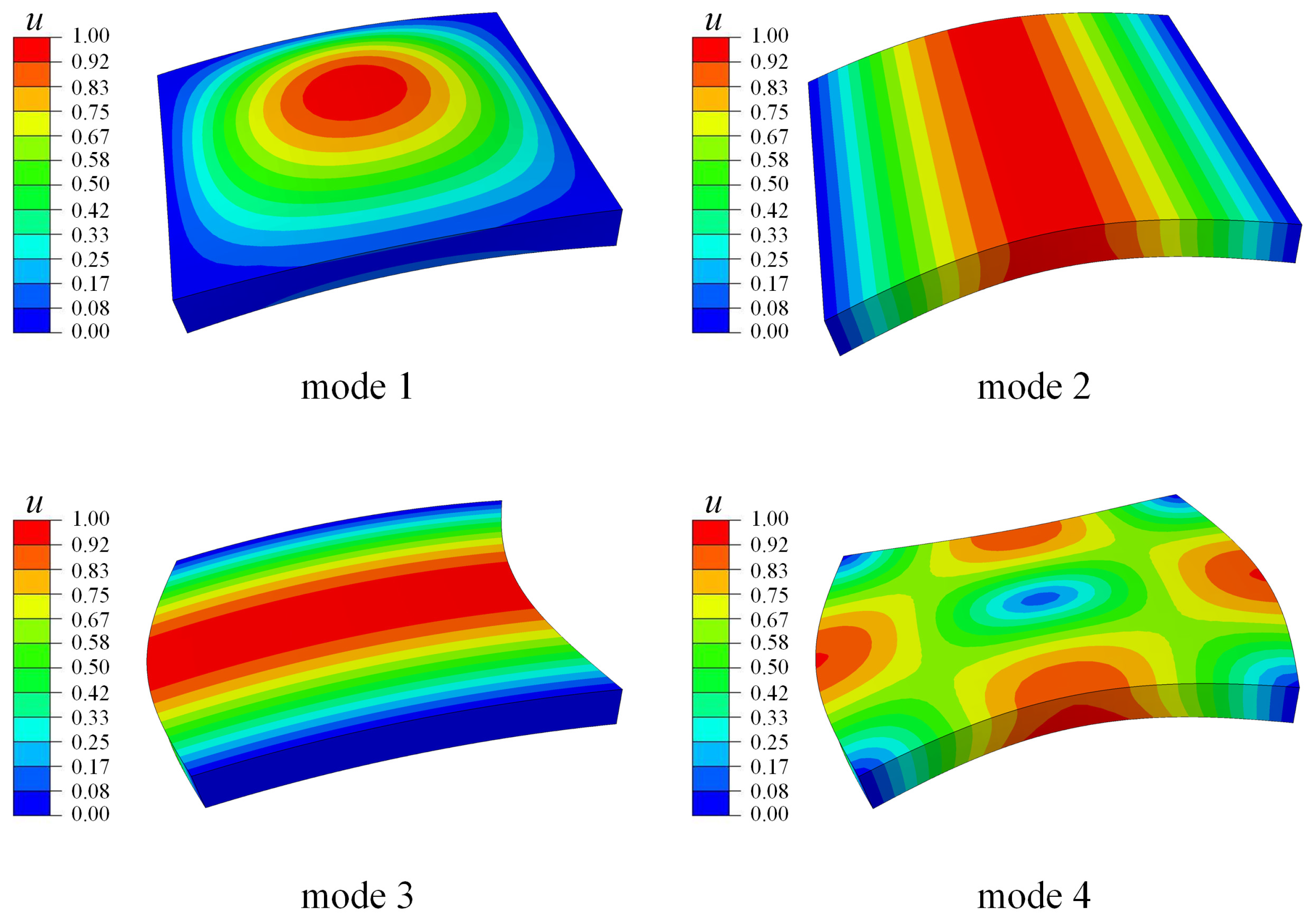
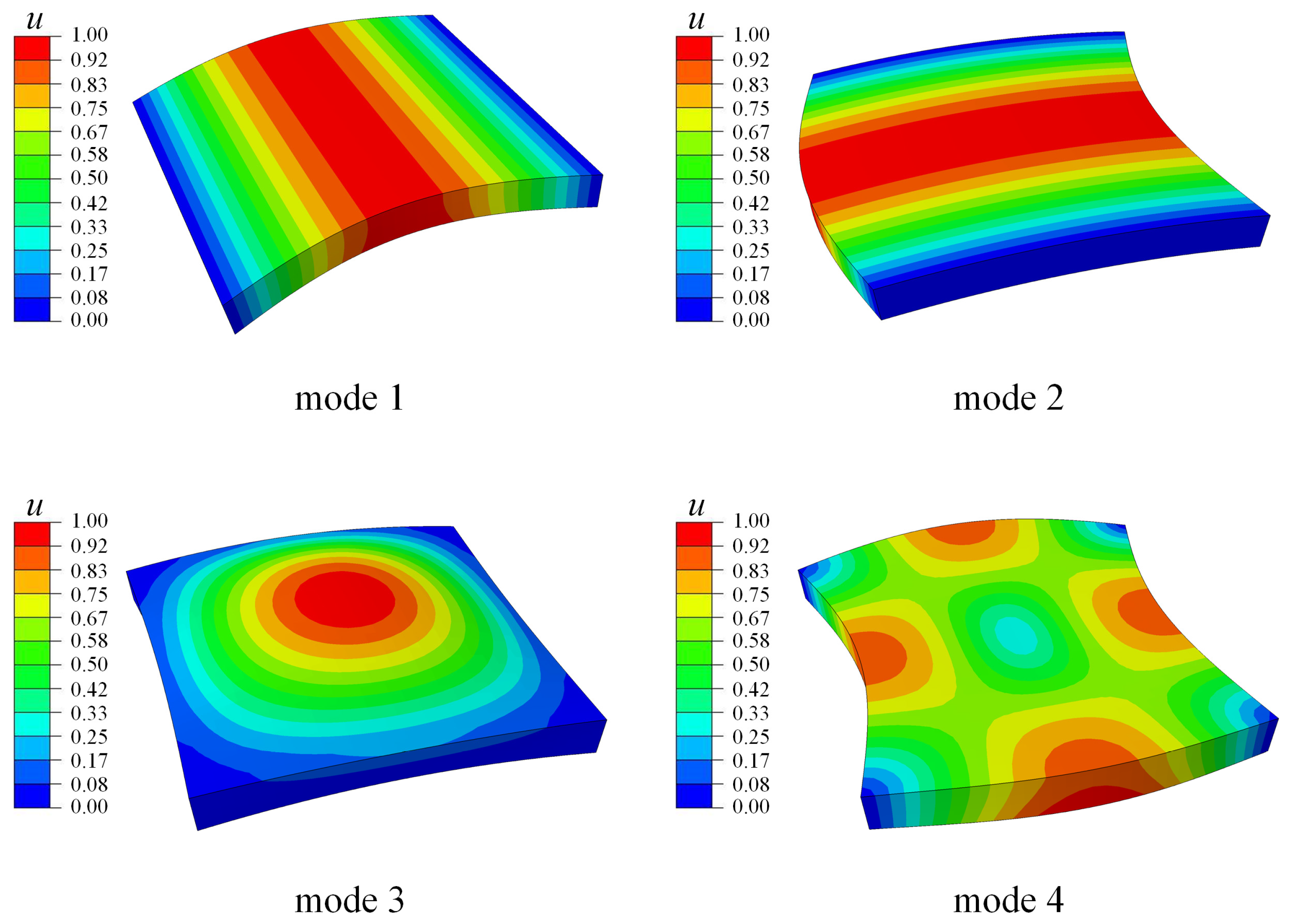
4.2.1. The Square Functionally Graded Microplate without Flexoelectricity
4.2.2. Functionally Graded Flexoelectric Microplate
4.2.3. Functionally Graded Flexoelectric Cylindrical Micro-Shell
5. Conclusions
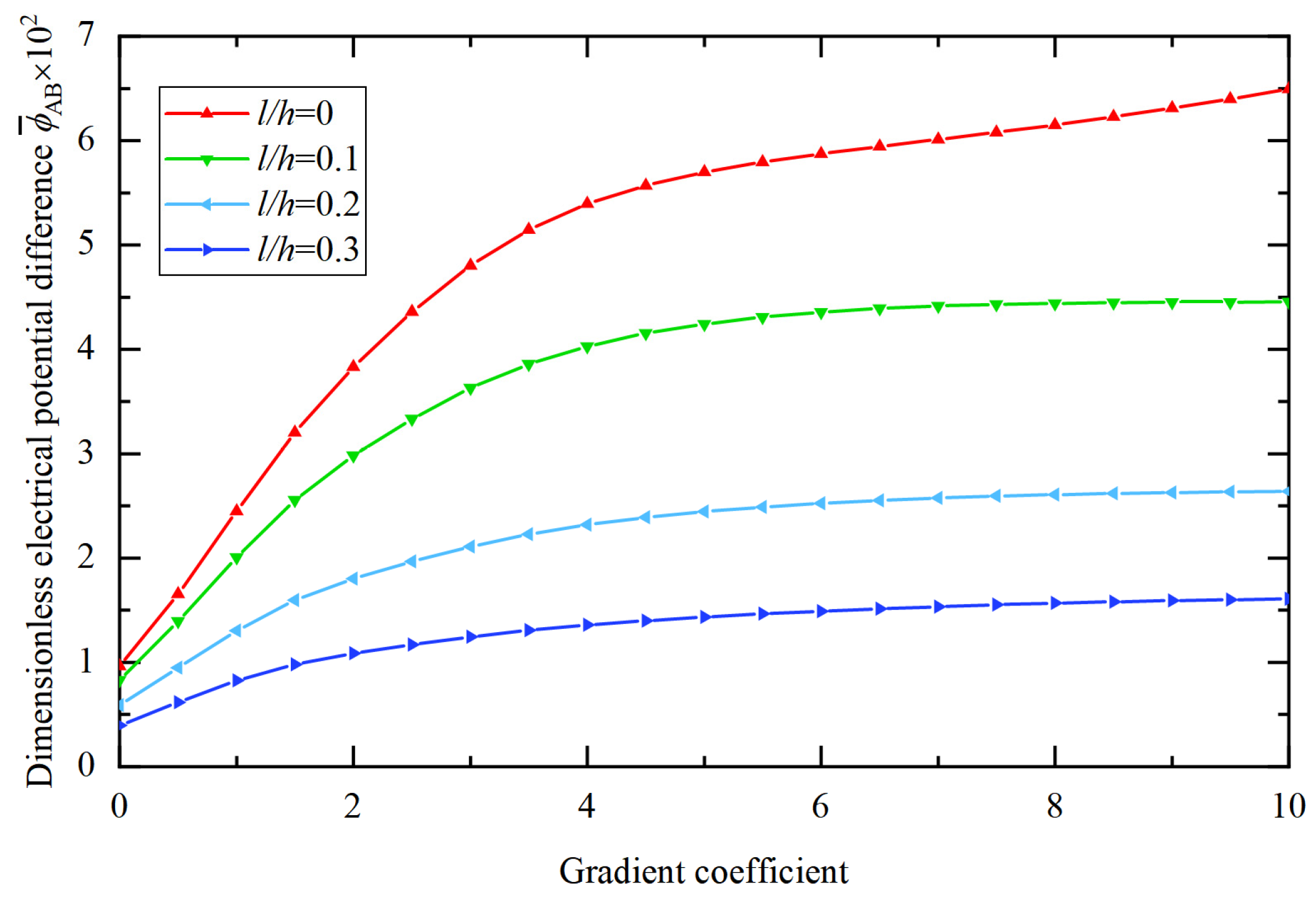
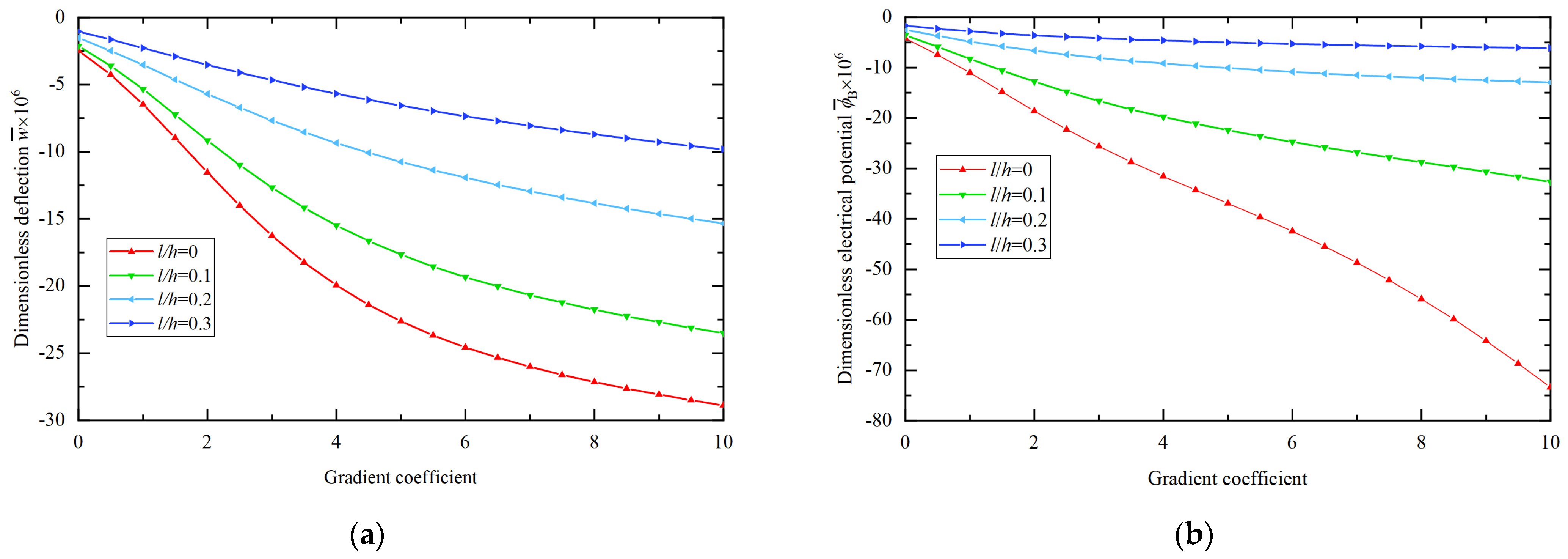
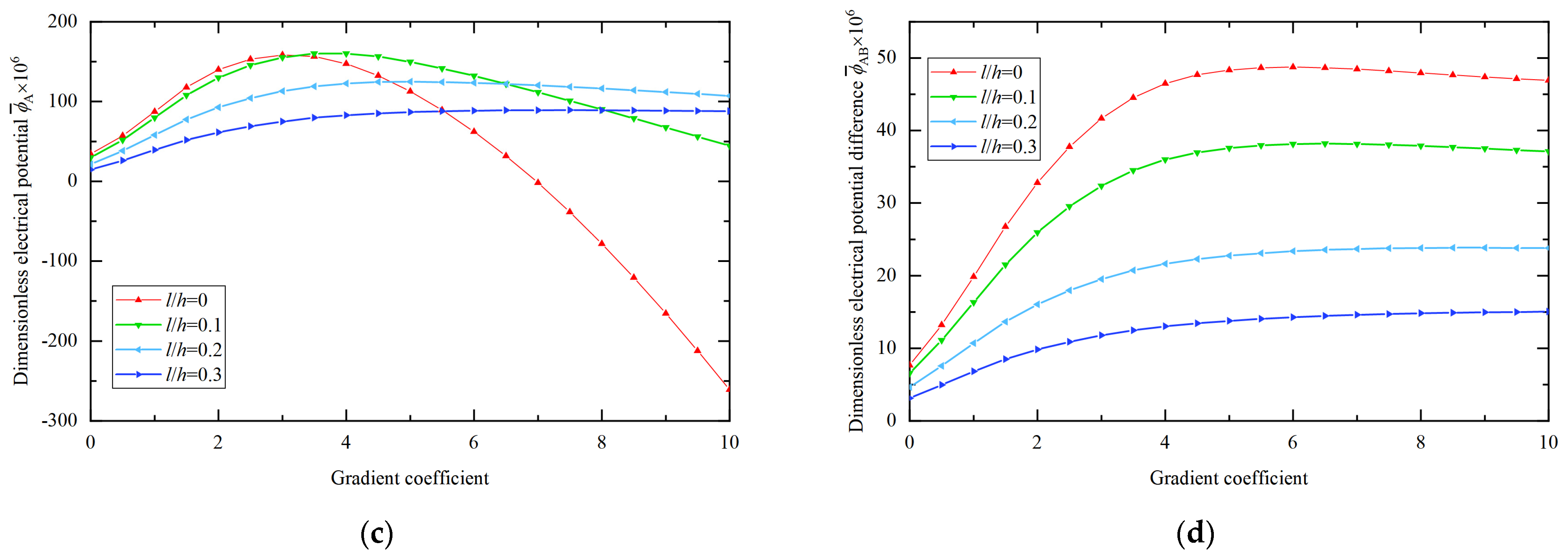
- In the static analysis of the BaTiO3/PVDF microplate subjected to mechanical loads, an increase in the gradient coefficient results in an increase in the central deflection of the microplate and the electric potential difference between the upper and lower center points. This is due to the fact that the increase in the gradient coefficient leads to a lower volume fraction of BaTiO3 and a higher volume fraction of PVDF, which decreases the overall stiffness of the microplate. When the magnitude of the applied loads remains constant, the central deflection of the microplate increases.
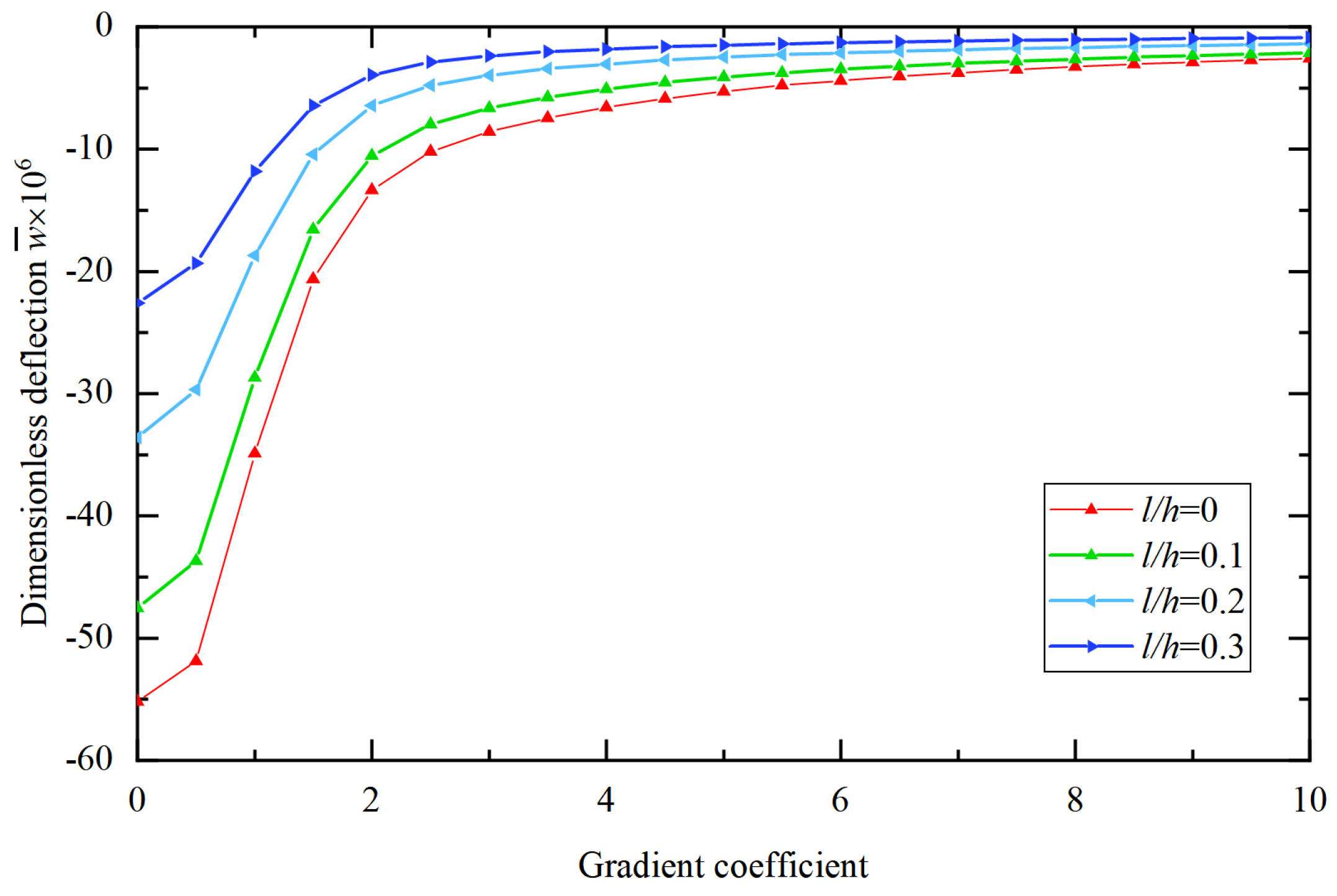
- In the static analysis of the BaTiO3/PVDF microplate subjected to electrical loads, an increase in the gradient coefficient leads to a decrease in the central deflection of the microplate. The increase in the gradient coefficient results in a lower volume fraction of BaTiO3 and a higher volume fraction of PVDF, which decreases the overall flexoelectric parameter and stiffness of the microplate. Furthermore, the reduction in the overall flexoelectric parameter has a greater impact on the deflection than the reduction in the overall stiffness. When the magnitude of the applied voltages remains constant, the central deflection of the microplate decreases.
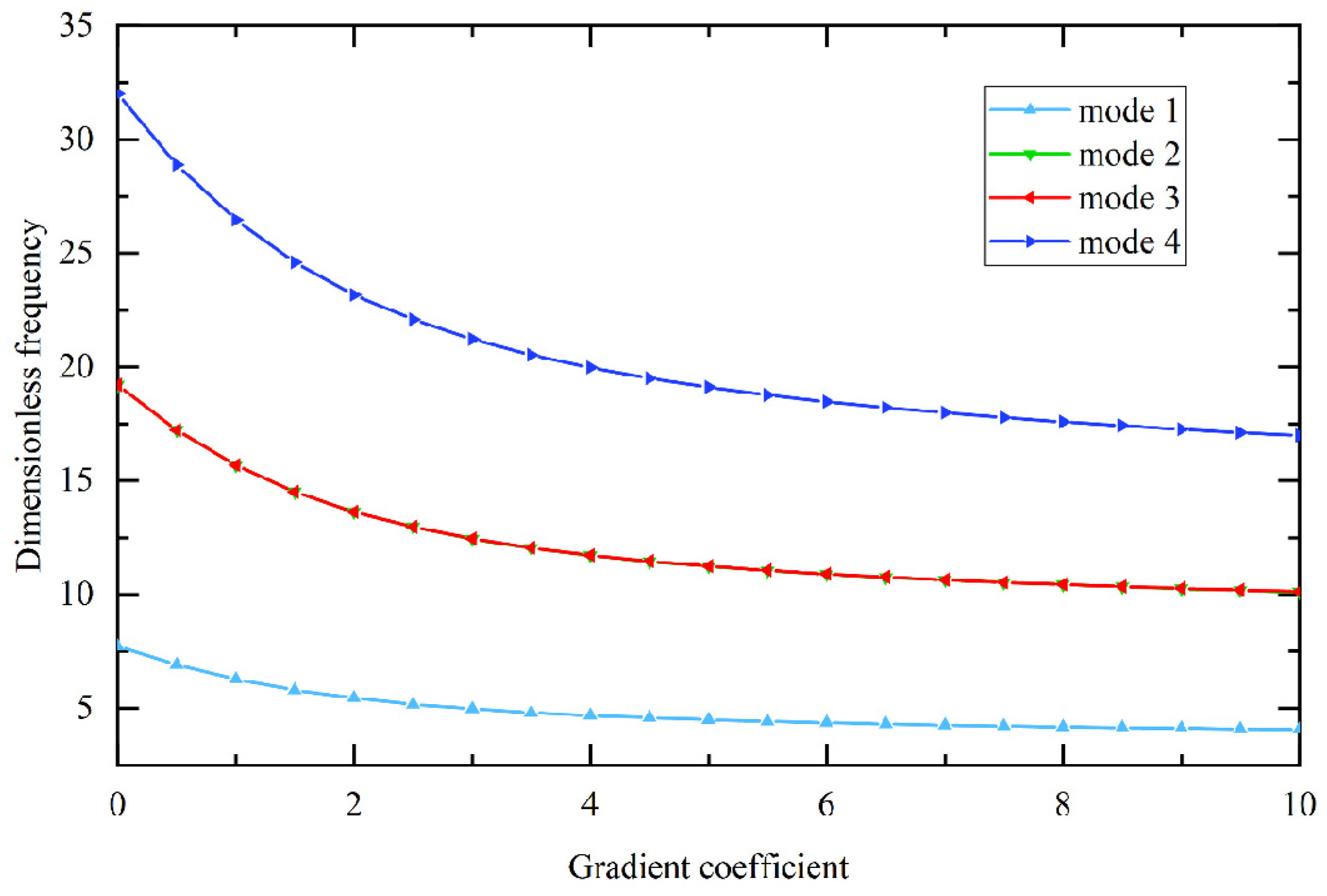
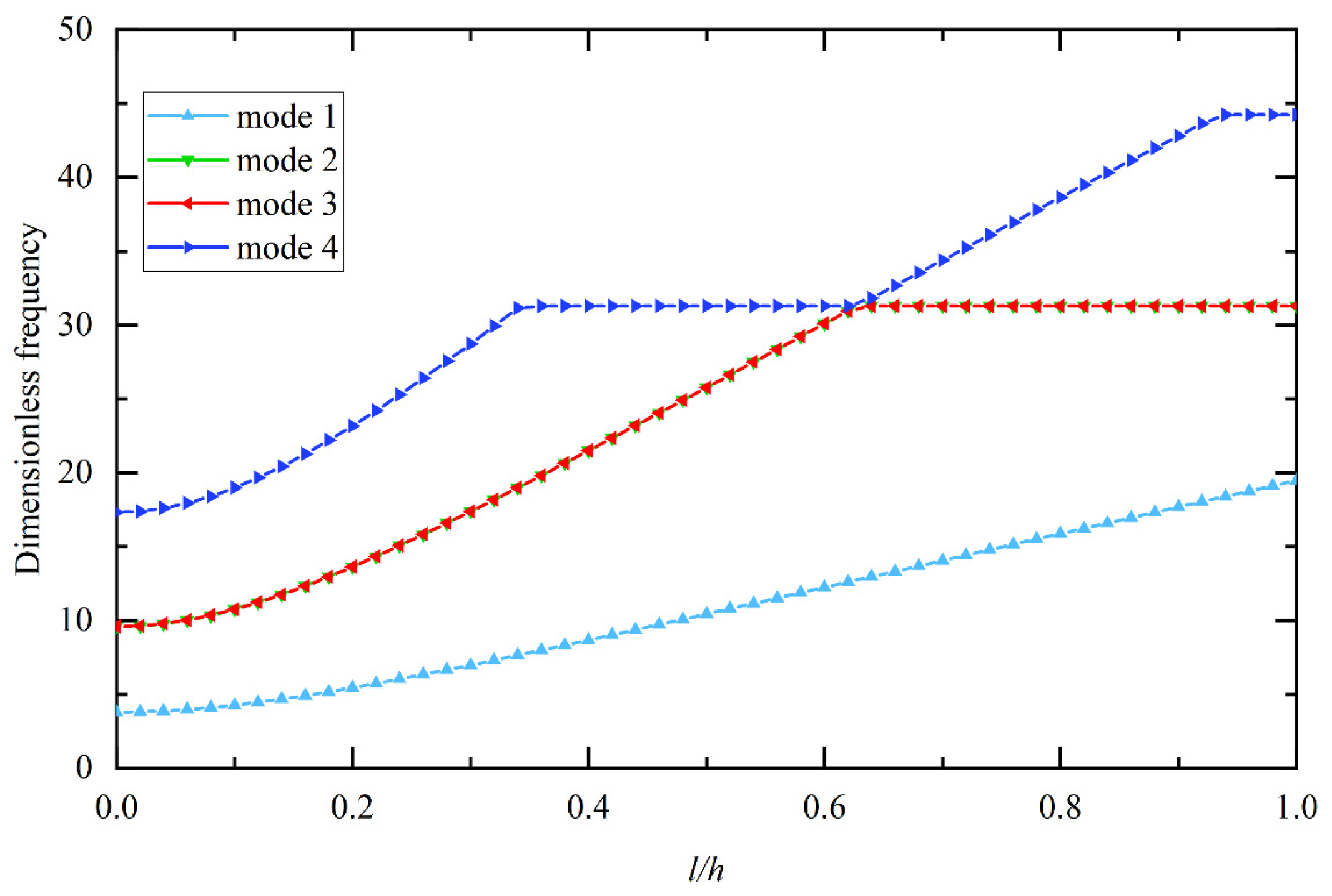
- In the free vibration analysis of BaTiO3/PVDF plates and shells, the natural frequency gradually decreases as the gradient coefficient increases. In addition, as the material length scale parameter increases, the bending stiffness increases, resulting in a gradual increase in the natural frequency of the out-of-plane modes. The in-plane modes are much less affected, resulting in mode switching.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Chen, X.; Liu, J.; Li, Q. The smart morphing winglet driven by the piezoelectric Macro Fiber Composite actuator. Aeronaut. J. 2022, 126, 830–847. [Google Scholar] [CrossRef]
- Kochersberger, K.B.; Ohanian, O.J.; Probst, T.; Gelhausen, P.A. Design and flight test of the generic micro-aerial vehicle (GenMAV) utilizing piezoelectric conformal flight control actuation. J. Intell. Mater. Syst. Struct. 2017, 28, 2793–2809. [Google Scholar] [CrossRef]
- Rouaix, C.; Jiménez-Navarro, C.; Carvalho, M.; Raibaudo, C.; Abou-Khalil, J.; Marouf, A.; Hoarau, Y.; Harran, G.; Hunt, J.C.R.; Hangan, H.; et al. Electroactive morphing effects on the aerodynamic performance through wobulation around an A320 wing with vibrating trailing edge at high Reynolds number. J. Fluids Struct. 2023, 123, 27. [Google Scholar] [CrossRef]
- Resta, R. Towards a Bulk Theory of Flexoelectricity. Phys. Rev. Lett. 2010, 105, 4. [Google Scholar] [CrossRef] [PubMed]
- Krichen, S.; Sharma, P. Flexoelectricity: A Perspective on an Unusual Electromechanical Coupling. J. Appl. Mech.-Trans. ASME 2016, 83, 5. [Google Scholar] [CrossRef]
- Sharma, N.D.; Landis, C.M.; Sharma, P. Piezoelectric thin-film superlattices without using piezoelectric materials. J. Appl. Phys. 2010, 108, 9. [Google Scholar] [CrossRef]
- Sharma, N.D.; Maranganti, R.; Sharma, P. On the possibility of piezoelectric nanocomposites without using piezoelectric materials. J. Mech. Phys. Solids 2007, 55, 2328–2350. [Google Scholar] [CrossRef]
- Mao, S.; Purohit, P.K. Insights Into Flexoelectric Solids From Strain-Gradient Elasticity. J. Appl. Mech.-Trans. ASME 2014, 81, 10. [Google Scholar] [CrossRef]
- Mao, S.; Purohit, P.K. Defects in flexoelectric solids. J. Mech. Phys. Solids 2015, 84, 95–115. [Google Scholar] [CrossRef]
- Shen, S.P.; Hu, S.L. A theory of flexoelectricity with surface effect for elastic dielectrics. J. Mech. Phys. Solids 2010, 58, 665–677. [Google Scholar] [CrossRef]
- Wang, G.F.; Yu, S.W.; Feng, X.Q. A piezoelectric constitutive theory with rotation gradient effects. Eur. J. Mech. A-Solids 2004, 23, 455–466. [Google Scholar] [CrossRef]
- Qu, Y.L.; Zhang, G.Y.; Fan, Y.M.; Jin, F. A non-classical theory of elastic dielectrics incorporating couple stress and quadrupole effects: Part I—Reconsideration of curvature-based flexoelectricity theory. Math. Mech. Solids 2021, 26, 1647–1659. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R. Size-dependent piezoelectricity. Int. J. Solids Struct. 2013, 50, 2781–2791. [Google Scholar] [CrossRef]
- Abbaspour, F.; Arvin, H. Vibration and thermal buckling analyses of three-layered centrosymmetric piezoelectric microplates based on the modified consistent couple stress theory. J. Vib. Control 2020, 26, 1253–1265. [Google Scholar] [CrossRef]
- Dehkordi, S.F.; Beni, Y.T. Electro-mechanical free vibration of single-walled piezoelectric/flexoelectric nano cones using consistent couple stress theory. Int. J. Mech. Sci. 2017, 128, 125–139. [Google Scholar] [CrossRef]
- Wu, C.P.; Lu, Y.A. A Hermite-Family C1 Finite Layer Method for the Three-Dimensional Free Vibration Analysis of Exponentially Graded Piezoelectric Microplates Based on the Consistent Couple Stress Theory. Int. J. Struct. Stab. Dyn. 2023, 23, 41. [Google Scholar] [CrossRef]
- Nguyen, B.H.; Nanthakumar, S.S.; Zhuang, X.; Wriggers, P.; Jiang, X.; Rabczuk, T. Dynamic flexoelectric effect on piezoelectric nanostructures. Eur. J. Mech. A-Solids 2018, 71, 404–409. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, L.Y. Size-dependent bending and vibration behaviour of piezoelectric nanobeams due to flexoelectricity. J. Phys. D-Appl. Phys. 2013, 46, 7. [Google Scholar] [CrossRef]
- Yue, Y.M.; Xue, K.Y.; Chen, T. A micro scale Timoshenko beam model for piezoelectricity with flexoelectricity and surface effects. Compos. Struct. 2016, 136, 278–286. [Google Scholar] [CrossRef]
- Zhang, R.Z.; Liang, X.; Shen, S.P. A Timoshenko dielectric beam model with flexoelectric effect. Meccanica 2016, 51, 1181–1188. [Google Scholar] [CrossRef]
- Chu, L.L.; Dui, G.S.; Ju, C.J. Flexoelectric effect on the bending and vibration responses of functionally graded piezoelectric nanobeams based on general modified strain gradient theory. Compos. Struct. 2018, 186, 39–49. [Google Scholar] [CrossRef]
- Mehralian, F.; Beni, Y.T. Size-dependent torsional buckling analysis of functionally graded cylindrical shell. Compos. Part B-Eng. 2016, 94, 11–25. [Google Scholar] [CrossRef]
- Sadeghi, H.; Baghani, M.; Naghdabadi, R. Strain gradient elasticity solution for functionally graded micro-cylinders. Int. J. Eng. Sci. 2012, 50, 22–30. [Google Scholar] [CrossRef][Green Version]
- Xin, L.B.; Dui, G.S.; Yang, S.Y.; Zhang, J.M. An elasticity solution for functionally graded thick-walled tube subjected to internal pressure. Int. J. Mech. Sci. 2014, 89, 344–349. [Google Scholar] [CrossRef]
- Shariyat, M. Nonlinear transient stress and wave propagation analyses of the FGM thick cylinders, employing a unified generalized thermoelasticity theory. Int. J. Mech. Sci. 2012, 65, 24–37. [Google Scholar] [CrossRef]
- Zheng, Y.C.; Chu, L.L.; Dui, G.S.; Zhu, X. Modeling and simulation of functionally graded flexoelectric micro-cylinders based on the mixed finite element method. Appl. Phys. A-Mater. Sci. Process. 2021, 127, 16. [Google Scholar] [CrossRef]
- Abdalla, H.M.A.; Casagrande, D.; De Bona, F. Analysis of Stress Concentration in Functionally Graded Plates with Linearly Increasing Young’s Modulus. Materials 2023, 16, 6882. [Google Scholar] [CrossRef] [PubMed]
- Krpensky, A.; Hruska, V.; Bednarik, M. Elastic P-wave manipulation utilizing functionally graded parallel plate gradient refractive index structures. Wave Motion 2023, 122, 13. [Google Scholar] [CrossRef]
- Beni, Y.T. Size-dependent electromechanical bending, buckling, and free vibration analysis of functionally graded piezoelectric nanobeams. J. Intell. Mater. Syst. Struct. 2016, 27, 2199–2215. [Google Scholar] [CrossRef]
- Chu, L.L.; Li, Y.B.; Dui, G.S. Size-dependent electromechanical coupling in functionally graded flexoelectric nanocylinders. Acta Mech. 2019, 230, 3071–3086. [Google Scholar] [CrossRef]
- Mao, S.; Purohit, P.K.; Aravas, N. Mixed finite-element formulations in piezoelectricity and flexoelectricity. Proc. R. Soc. A-Math. Phys. Eng. Sci. 2016, 472, 19. [Google Scholar] [CrossRef] [PubMed]
- Deng, F.; Deng, Q.; Yu, W.S.; Shen, S.P. Mixed Finite Elements for Flexoelectric Solids. J. Appl. Mech.-Trans. ASME 2017, 84, 12. [Google Scholar] [CrossRef]
- Deng, F.; Deng, Q.; Shen, S.P. A Three-Dimensional Mixed Finite Element for Flexoelectricity. J. Appl. Mech.-Trans. ASME 2018, 85, 10. [Google Scholar] [CrossRef]
- Yvonnet, J.; Liu, L.P. A numerical framework for modeling flexoelectricity and Maxwell stress in soft dielectrics at finite strains. Comput. Methods Appl. Mech. Eng. 2017, 313, 450–482. [Google Scholar] [CrossRef]
- Darrall, B.T.; Hadjesfandiari, A.R.; Dargush, G.F. Size-dependent piezoelectricity: A 2D finite element formulation for electric field-mean curvature coupling in dielectrics. Eur. J. Mech. A-Solids 2015, 49, 308–320. [Google Scholar] [CrossRef]
- Poya, R.; Gil, A.J.; Ortigosa, R.; Palma, R. On a family of numerical models for couple stress based flexoelectricity for continua and beams. J. Mech. Phys. Solids 2019, 125, 613–652. [Google Scholar] [CrossRef]
- Thai, T.Q.; Rabczuk, T.; Zhuang, X.Y. A large deformation isogeometric approach for flexoelectricity and soft materials. Comput. Methods Appl. Mech. Eng. 2018, 341, 718–739. [Google Scholar] [CrossRef]
- Ghasemi, H.; Park, H.S.; Zhuang, X.Y.; Rabczuk, T. Three-Dimensional Isogeometric Analysis of Flexoelectricity with MATLAB Implementation. CMC-Comput. Mater. Contin. 2020, 65, 1157–1179. [Google Scholar] [CrossRef]
- Thai, T.Q.; Zhuang, X.Y.; Park, H.S.; Rabczuk, T. A staggered explicit-implicit isogeometric formulation for large deformation flexoelectricity. Eng. Anal. Bound. Elem. 2021, 122, 1–12. [Google Scholar] [CrossRef]
- Chen, X.; Yao, S.; Yvonnet, J. Dynamic analysis of flexoelectric systems in the frequency domain with isogeometric analysis. Comput. Mech. 2023, 71, 353–366. [Google Scholar] [CrossRef]
- Ray, M.C. Mesh free model of nanobeam integrated with a flexoelectric actuator layer. Compos. Struct. 2017, 159, 63–71. [Google Scholar] [CrossRef]
- Basutkar, R.; Sidhardh, S.; Ray, M.C. Static analysis of flexoelectric nanobeams incorporating surface effects using element free Galerkin method. Eur. J. Mech. A-Solids 2019, 76, 13–24. [Google Scholar] [CrossRef]
- He, B.; Javvaji, B.; Zhuang, X. Characterizing Flexoelectricity in Composite Material Using the Element-Free Galerkin Method. Energies 2019, 12, 271. [Google Scholar] [CrossRef]
- Shang, Y.; Deng, Z.; Cen, S.; Li, C.F. Penalty hexahedral element formulation for flexoelectric solids based on consistent couple stress theory. Int. J. Numer. Methods Eng. 2024, 125, 30. [Google Scholar] [CrossRef]
- Rajendran, S.; Liew, K.M. A novel unsymmetric 8-node plane element immune to mesh distortion under a quadratic displacement field. Int. J. Numer. Methods Eng. 2003, 58, 1713–1748. [Google Scholar] [CrossRef]
- Shang, Y.; Li, C.F.; Jia, K.Y. 8-node hexahedral unsymmetric element with rotation degrees of freedom for modified couple stress elasticity. Int. J. Numer. Methods Eng. 2020, 121, 2683–2700. [Google Scholar] [CrossRef]
- Li, Z.; Cen, S.; Li, C.F. Extension of the unsymmetric 8-node hexahedral solid element US-ATFH8 to geometrically nonlinear analysis. Eng. Comput. 2021, 38, 3219–3253. [Google Scholar] [CrossRef]
- Nobili, A. Asymptotically consistent size-dependent plate models based on the couple-stress theory with micro-inertia. Eur. J. Mech. A-Solids 2021, 89, 10. [Google Scholar] [CrossRef]
- Chu, B.J.; Salem, D.R. Flexoelectricity in several thermoplastic and thermosetting polymers. Appl. Phys. Lett. 2012, 101, 4. [Google Scholar] [CrossRef]
- Deng, Q.; Kammoun, M.; Erturk, A.; Sharma, P. Nanoscale flexoelectric energy harvesting. Int. J. Solids Struct. 2014, 51, 3218–3225. [Google Scholar] [CrossRef]
- Wu, C.P.; Hsu, C.H. A three-dimensional weak formulation for stress, deformation, and free vibration analyses of functionally graded microscale plates based on the consistent couple stress theory. Compos. Struct. 2022, 296, 23. [Google Scholar] [CrossRef]
- Wu, C.P.; Lu, Y.A. 3D static bending analysis of functionally graded piezoelectric microplates resting on an elastic medium subjected to electro-mechanical loads using a size-dependent Hermitian C2 finite layer method based on the consistent couple stress theory. Mech. Based Des. Struct. Mach. 2023, 52, 3799–3841. [Google Scholar] [CrossRef]
- Thai, H.T.; Choi, D.H. Size-dependent functionally graded Kirchhoff and Mindlin plate models based on a modified couple stress theory. Compos. Struct. 2013, 95, 142–153. [Google Scholar] [CrossRef]


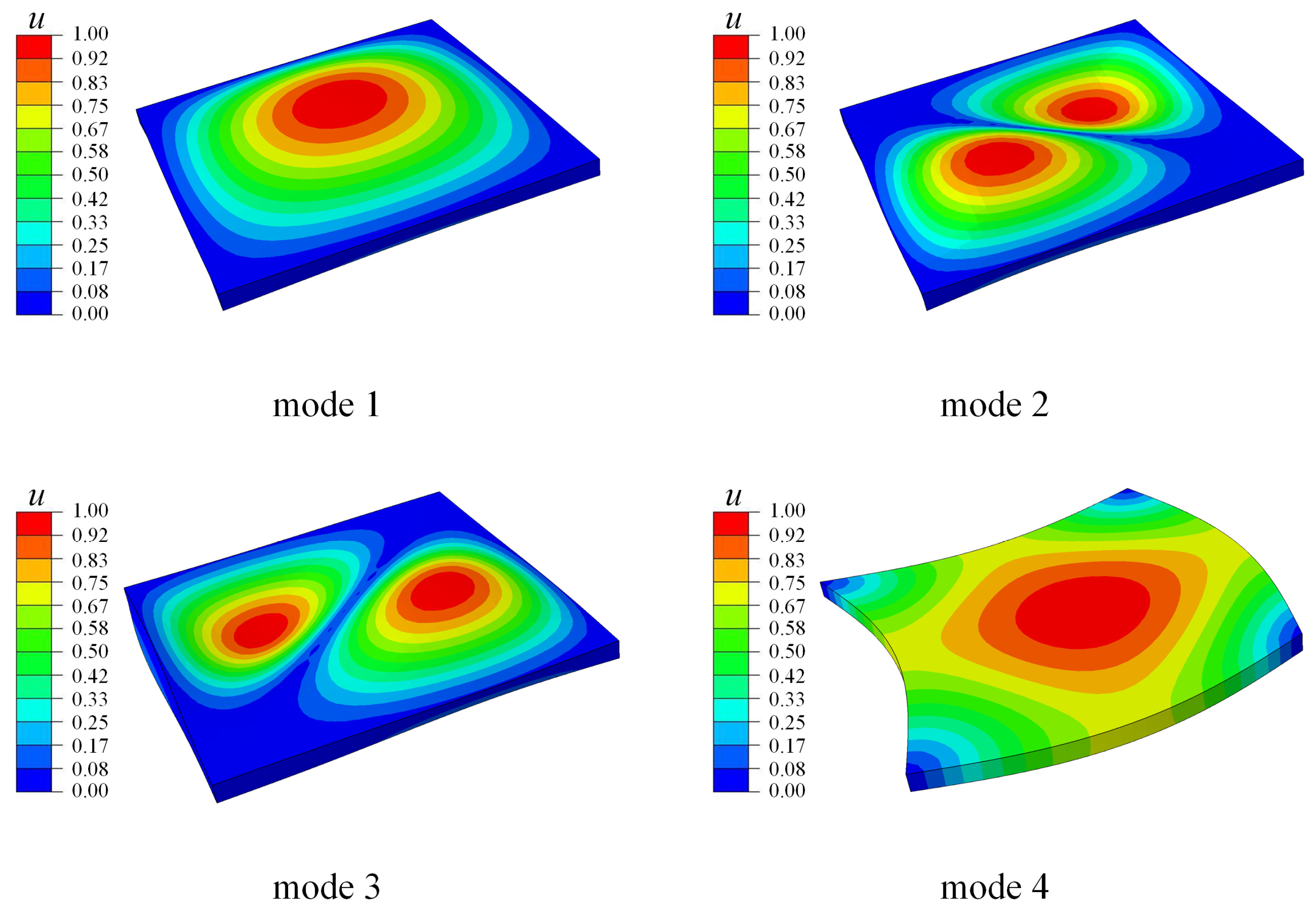

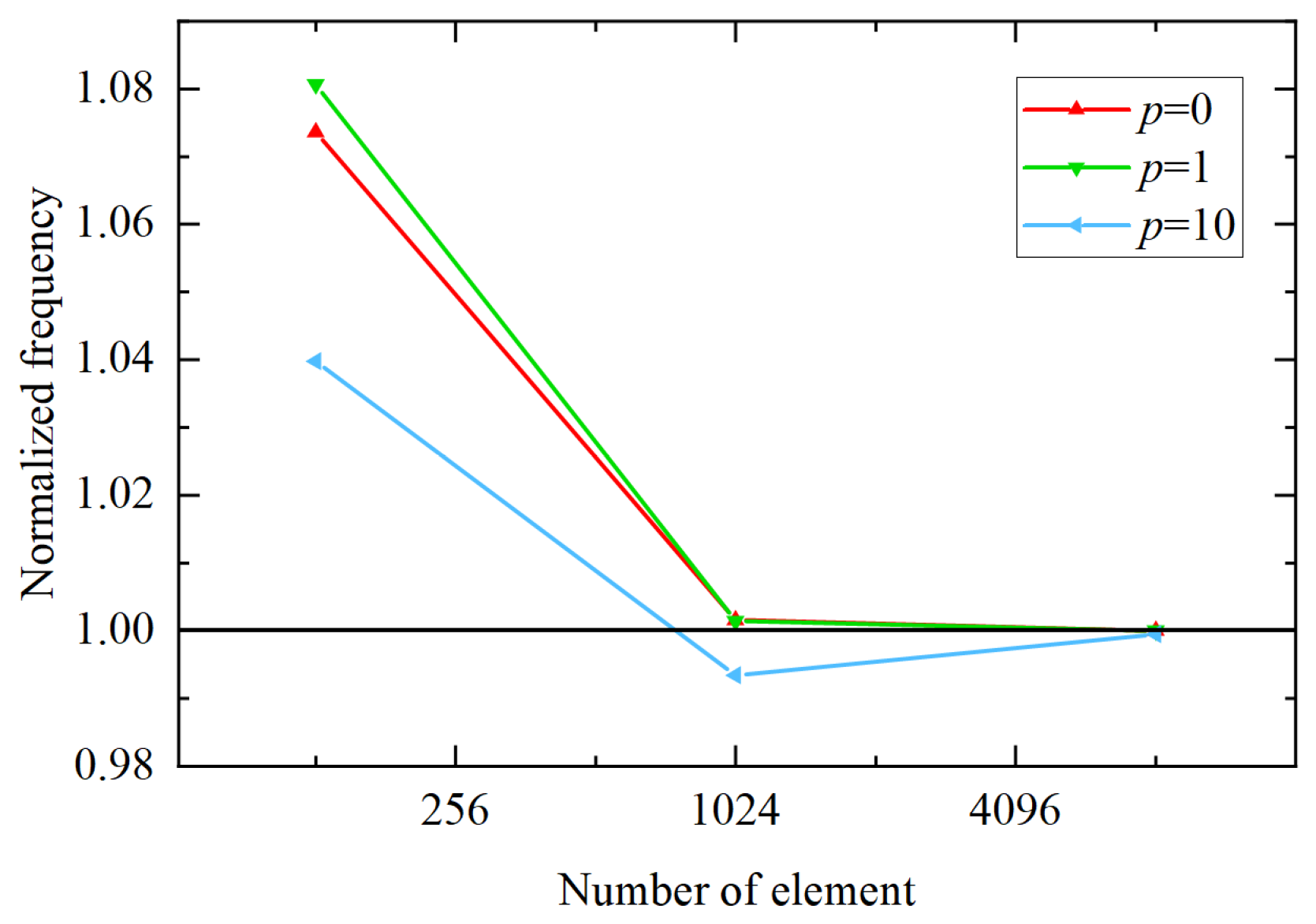
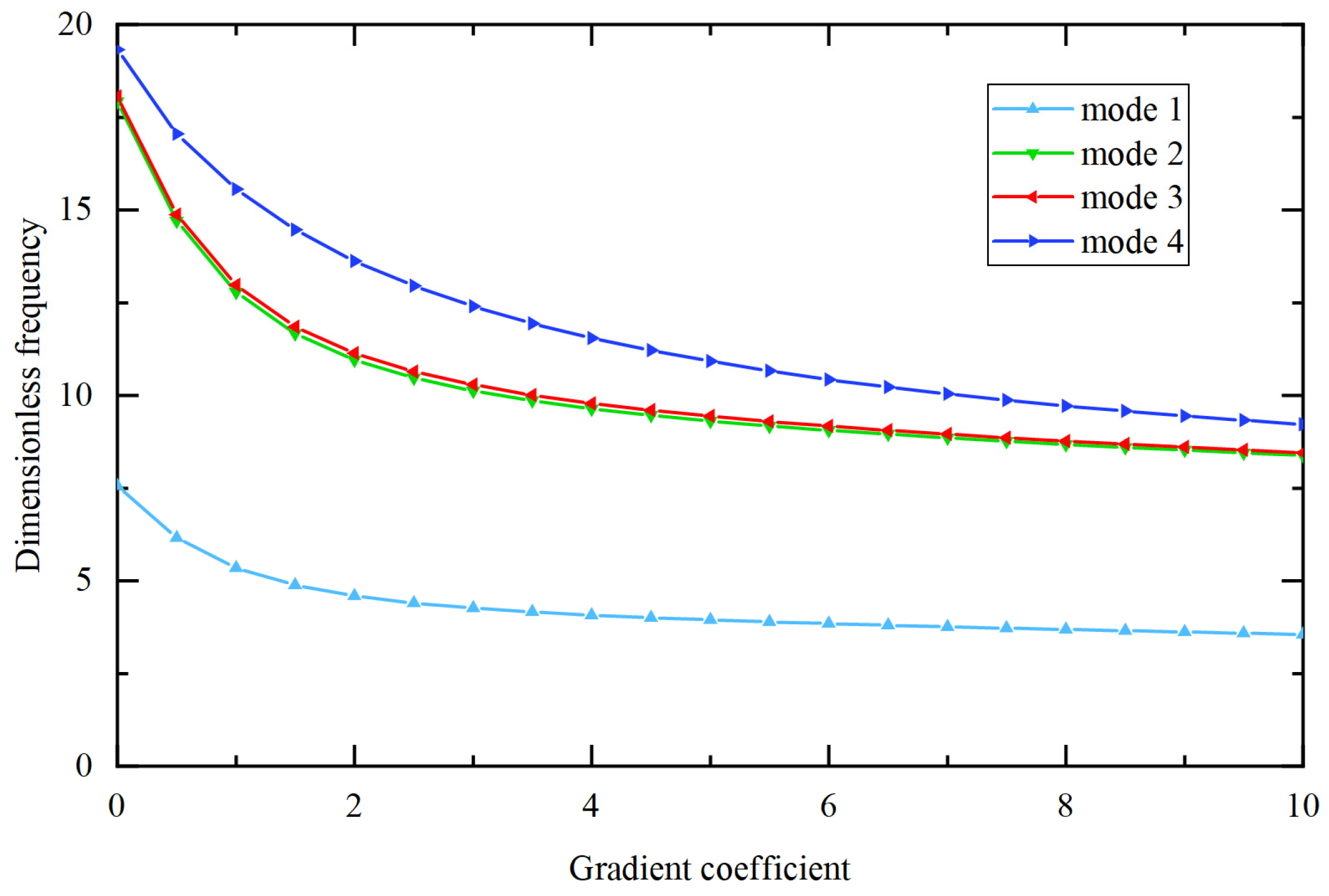
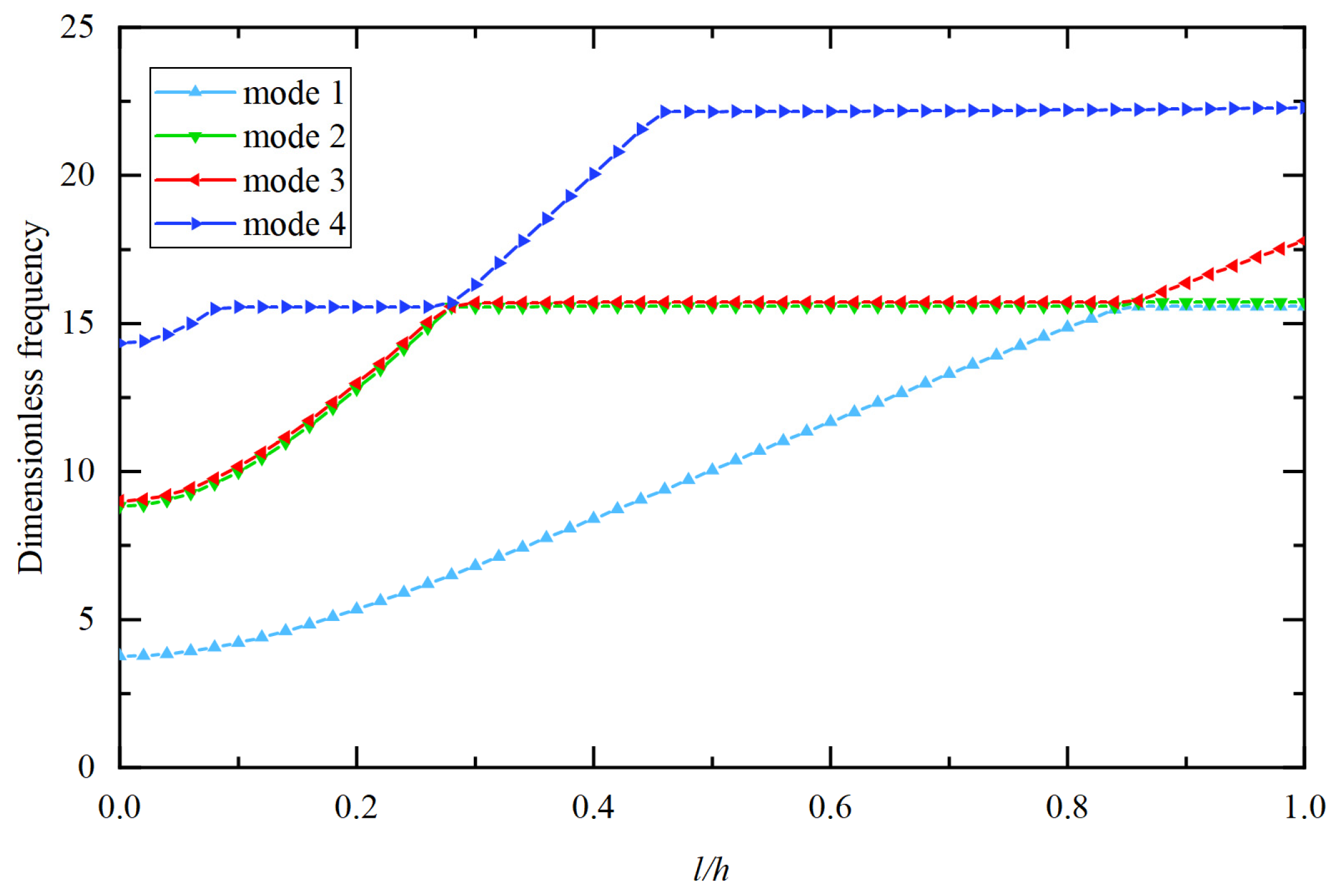

| Materials | (GPa) | (C/m) | (F/m) | (kg/m3) | |
|---|---|---|---|---|---|
| BaTiO3 | 113.7 | 0.325 | 1.0 × 10−5 | 1.24 × 10−8 | 6017 |
| PVDF | 3.7 | 0.38 1 | 1.3 × 10−8 | 8.15 × 10−11 | 1780 |
| Mesh | 2 × 10 × 10 | 4 × 20 × 20 | 8 × 40 × 40 | Ref [51] |
|---|---|---|---|---|
| p = 0, l/h = 0.1 | 0.1985 | 0.2415 | 0.2427 | 0.2428 |
| p = 0, l/h = 0.4 | 0.0719 | 0.0770 | 0.0772 | 0.0773 |
| p = 1, l/h = 0.1 | 0.3801 | 0.4712 | 0.4735 | 0.4738 |
| p = 1, l/h = 0.4 | 0.1266 | 0.1358 | 0.1361 | 0.1362 |
| p = 10, l/h = 0.1 | 0.7401 | 0.8404 | 0.8322 | 0.8315 |
| p = 10, l/h = 0.4 | 0.2752 | 0.2886 | 0.2876 | 0.2875 |
| Mesh | 2 × 10 × 10 | 4 × 20 × 20 | 8 × 40 × 40 | Ref [51] |
|---|---|---|---|---|
| p = 1, l/h = 0.1 | 0.3578 | 0.4624 | 0.4713 | 0.4738 |
| p = 1, l/h = 0.4 | 0.1240 | 0.1351 | 0.1359 | 0.1362 |
| p = 10, l/h = 0.1 | 0.9647 | 0.9495 | 0.8635 | 0.8315 |
| p = 10, l/h = 0.4 | 0.3474 | 0.3154 | 0.2950 | 0.2875 |
| Mesh | 2 × 8 × 8 | 4 × 16 × 16 | 8 × 32 × 32 | 16 × 32 × 32 | Ref [16] |
|---|---|---|---|---|---|
| p = 0, l/h = 0 | 6.5475 | 5.9510 | 5.9412 | 5.9412 | 5.9412 |
| p = 0, l/h = 0.2 | 8.0040 | 7.5202 | 7.5109 | 7.5106 | 7.5102 |
| p = 0, l/h = 0.4 | 11.1795 | 10.8598 | 10.8527 | 10.8521 | 10.8517 |
| p = 1, l/h = 0 | 5.9098 | 5.2825 | 5.2739 | 5.2740 | 5.2740 |
| p = 1, l/h = 0.2 | 7.5084 | 7.0218 | 7.0146 | 7.0145 | 7.0142 |
| p = 1, l/h = 0.4 | 10.8576 | 10.5568 | 10.5532 | 10.5532 | 10.5531 |
| p = 10, l/h = 0 | 6.3395 | 6.0488 | 6.1097 | 6.1158 | 6.1163 |
| p = 10, l/h = 0.2 | 7.8208 | 7.6102 | 7.6679 | 7.6749 | 7.6763 |
| p = 10, l/h = 0.4 | 10.9750 | 10.8893 | 10.9526 | 10.9636 | 10.9675 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Z.; Shang, Y. Size-Dependent Finite Element Analysis of Functionally Graded Flexoelectric Shell Structures Based on Consistent Couple Stress Theory. Aerospace 2024, 11, 661. https://doi.org/10.3390/aerospace11080661
Deng Z, Shang Y. Size-Dependent Finite Element Analysis of Functionally Graded Flexoelectric Shell Structures Based on Consistent Couple Stress Theory. Aerospace. 2024; 11(8):661. https://doi.org/10.3390/aerospace11080661
Chicago/Turabian StyleDeng, Zhuo, and Yan Shang. 2024. "Size-Dependent Finite Element Analysis of Functionally Graded Flexoelectric Shell Structures Based on Consistent Couple Stress Theory" Aerospace 11, no. 8: 661. https://doi.org/10.3390/aerospace11080661
APA StyleDeng, Z., & Shang, Y. (2024). Size-Dependent Finite Element Analysis of Functionally Graded Flexoelectric Shell Structures Based on Consistent Couple Stress Theory. Aerospace, 11(8), 661. https://doi.org/10.3390/aerospace11080661






