An Intelligent Bait Delivery Control Method for Flight Vehicle Evasion Based on Reinforcement Learning
Abstract
1. Introduction
2. Relative Motion Model of Aircraft-Bait-Incoming Missile
2.1. Motion Modeling of Aircraft, Incoming Missile, and Bait
2.2. Relative Motion Model between Incoming Missile and Target
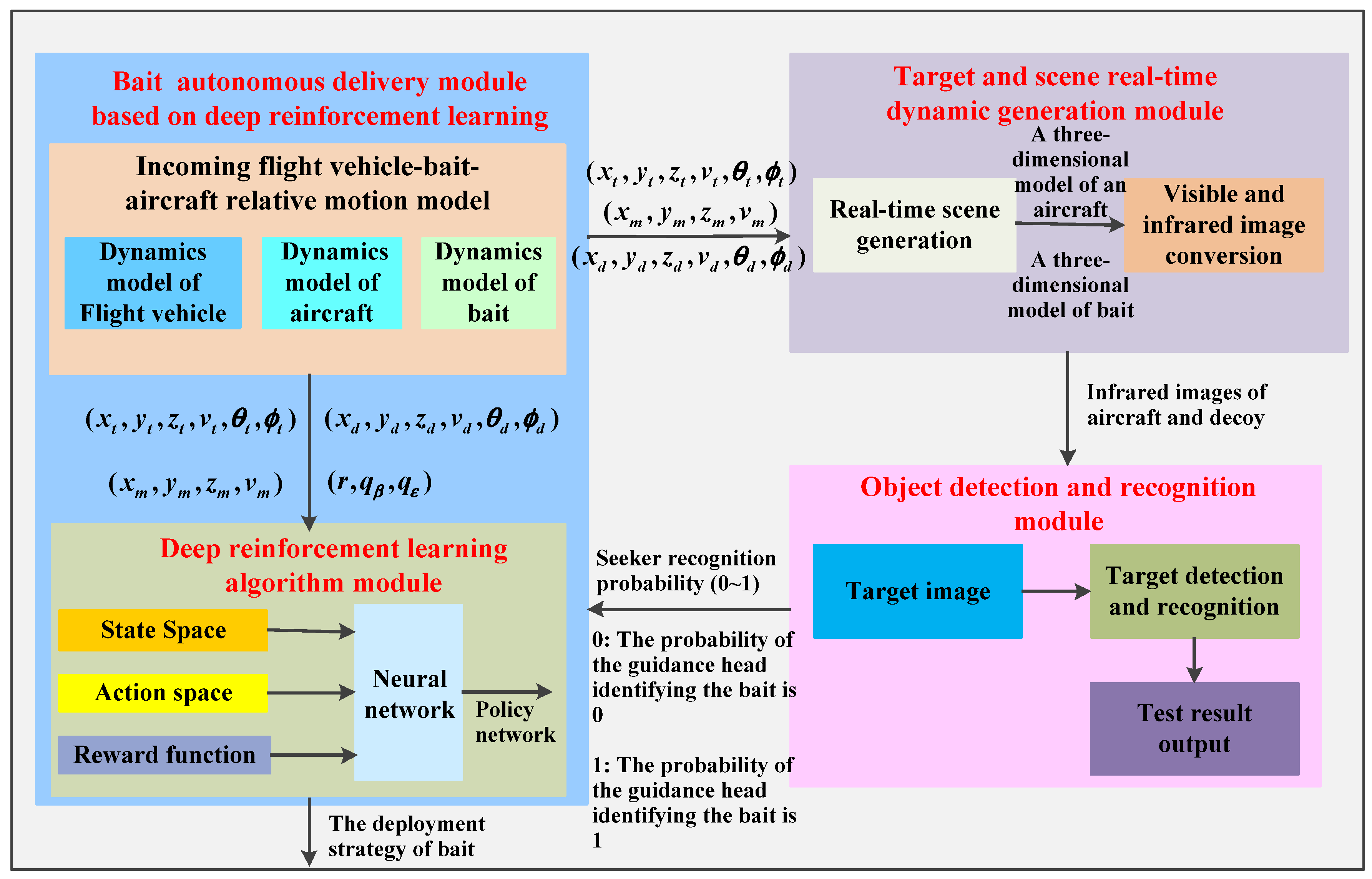
3. Design of Adversarial Defense Framework for Incoming Missile
3.1. Overall Framework Design
3.2. Bait Delivery Model Based on Deep Reinforcement Learning
3.2.1. State Space and Action Space Design
3.2.2. Probability of State Transition
3.2.3. Reward Function Design
3.3. Identification Model of Incoming Missile Seeker
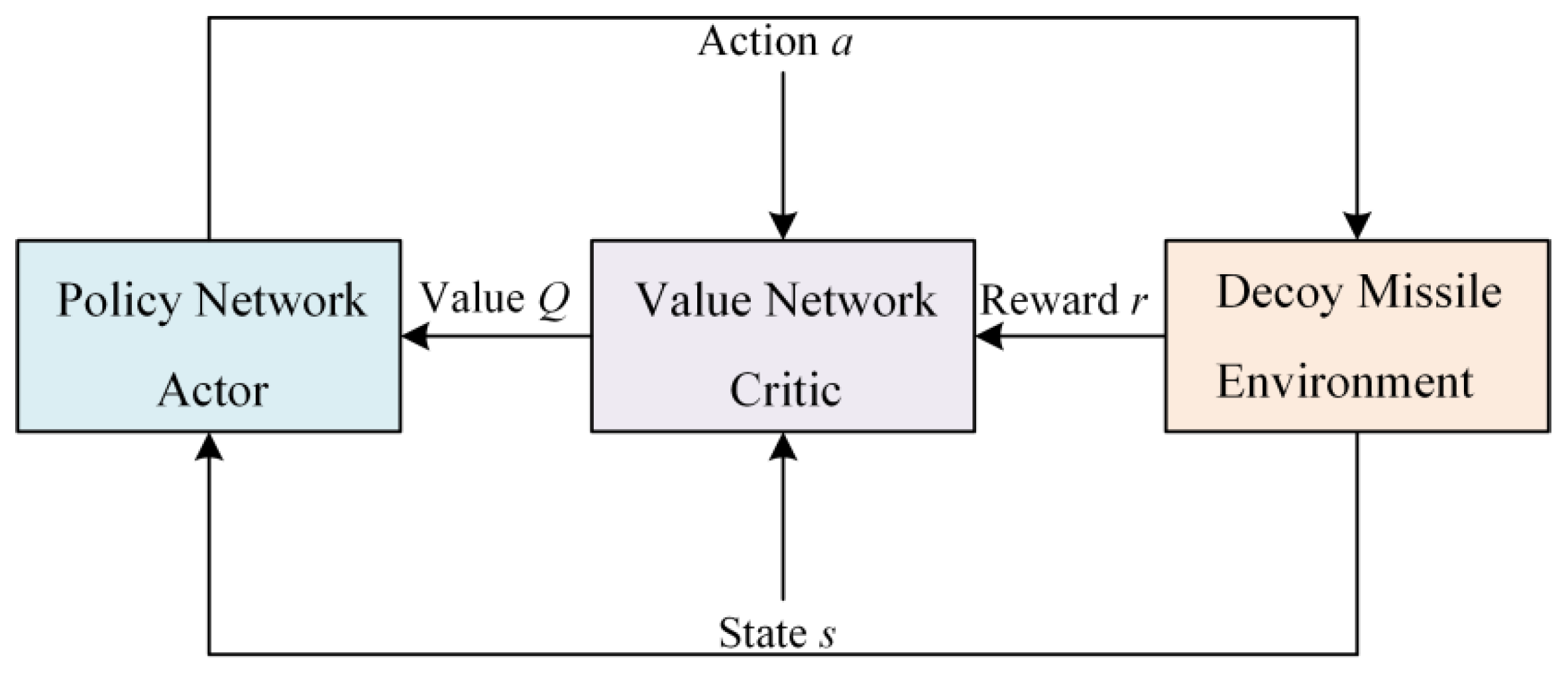
4. Deep Reinforcement Learning Algorithms
4.1. DDPG Algorithm
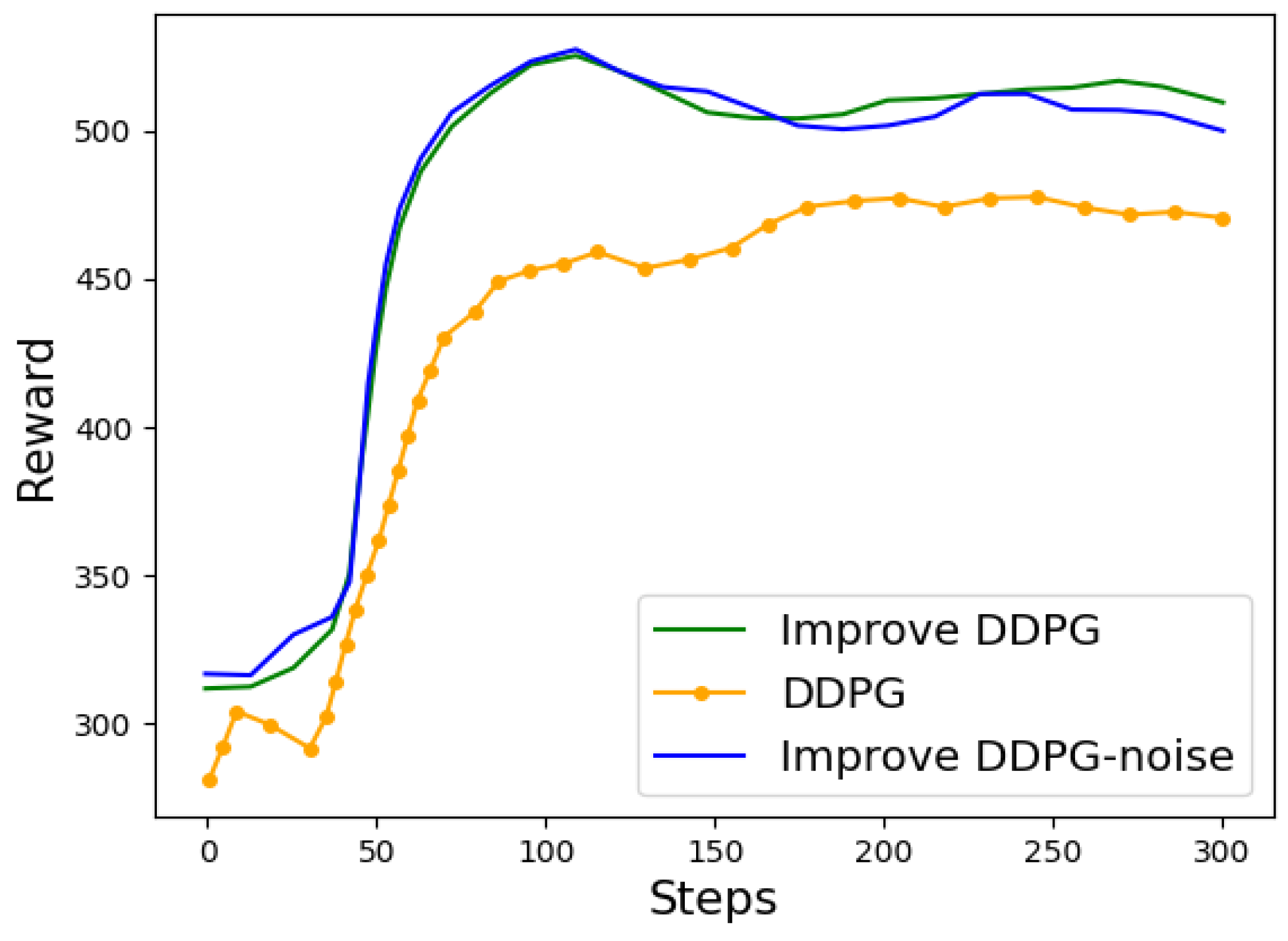
4.2. Improved DDPG Algorithm
5. Simulation Verification and Analysis
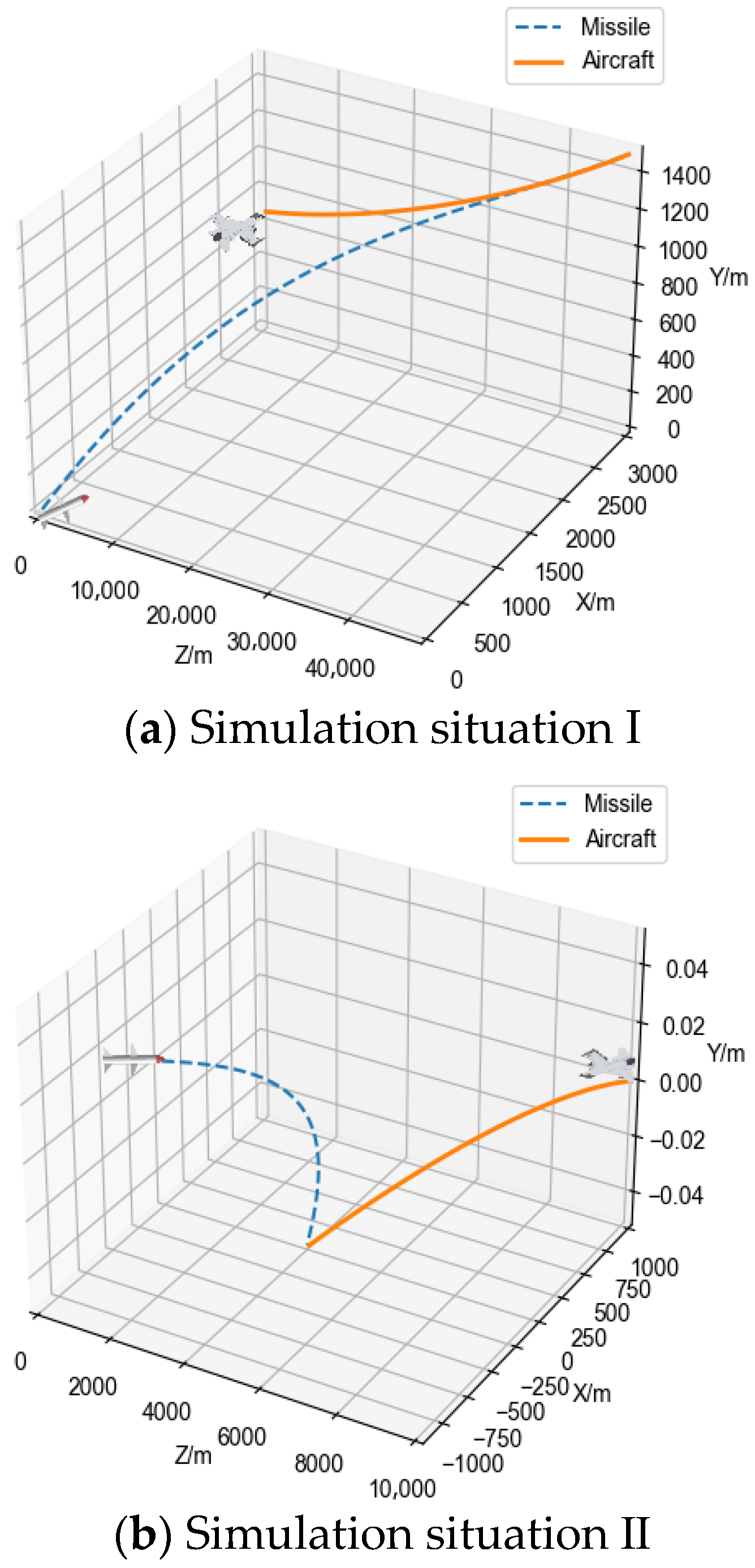
5.1. Simulation Scenario Setting and Platform Construction
5.2. Setting Simulation Parameters
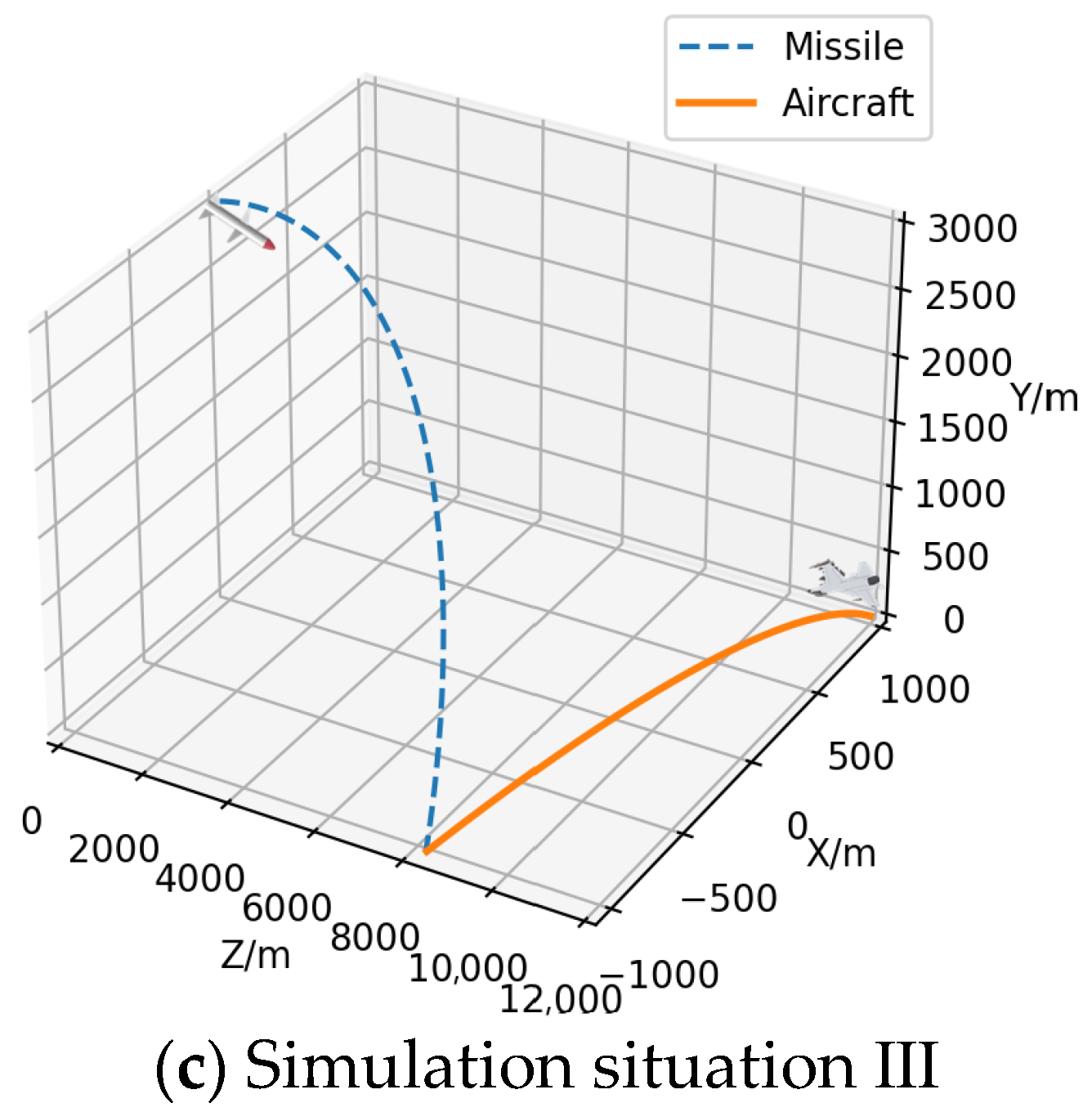
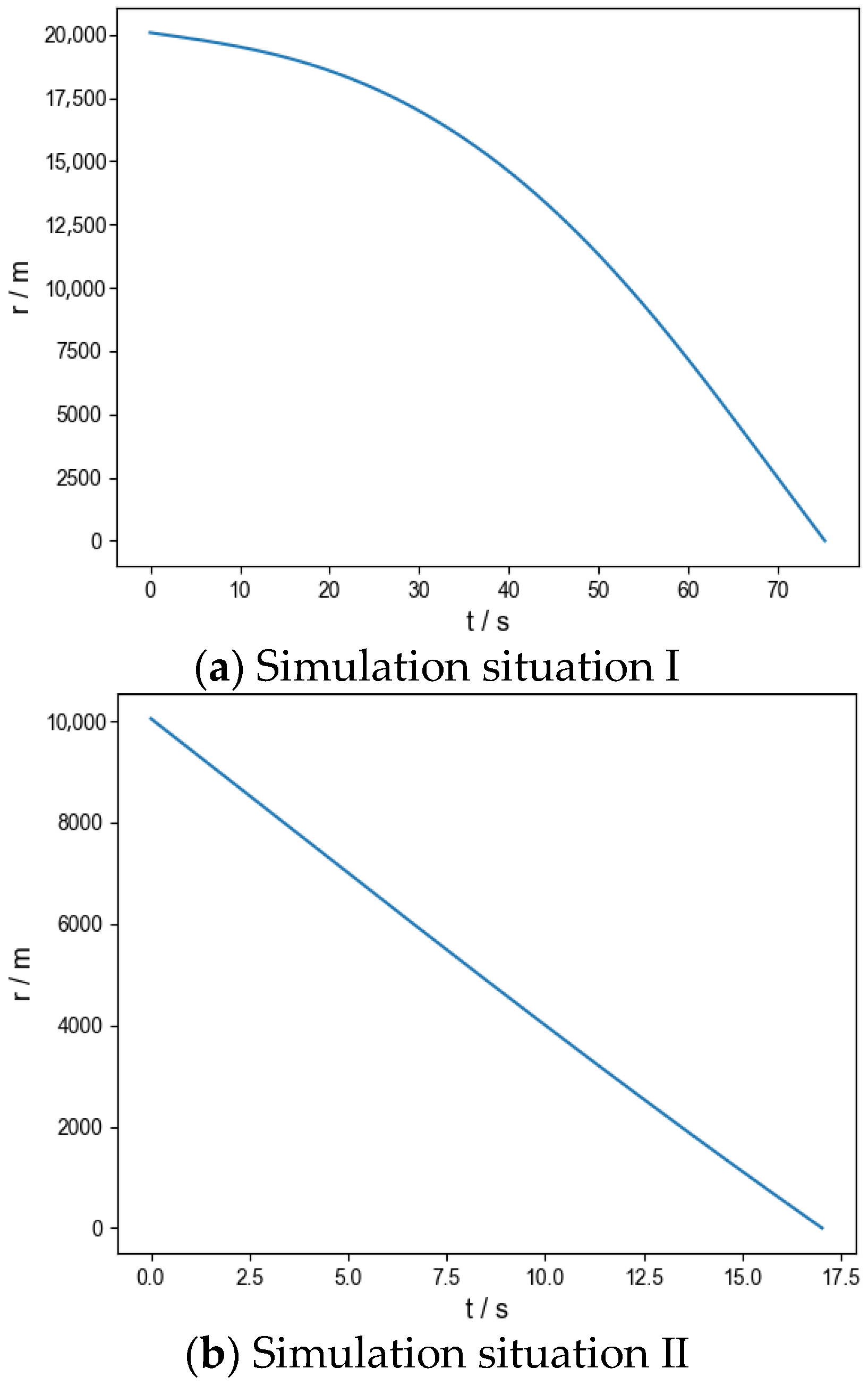
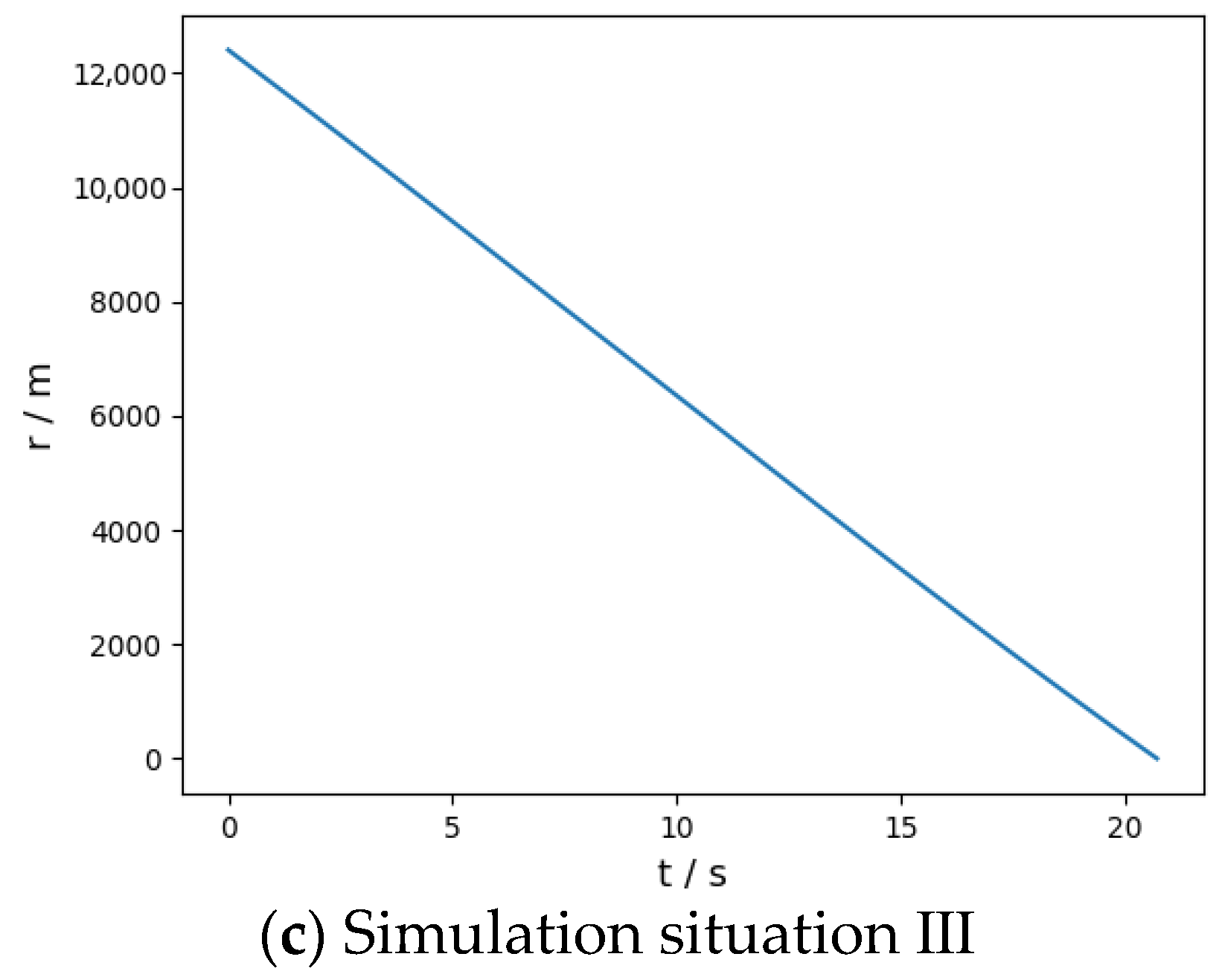
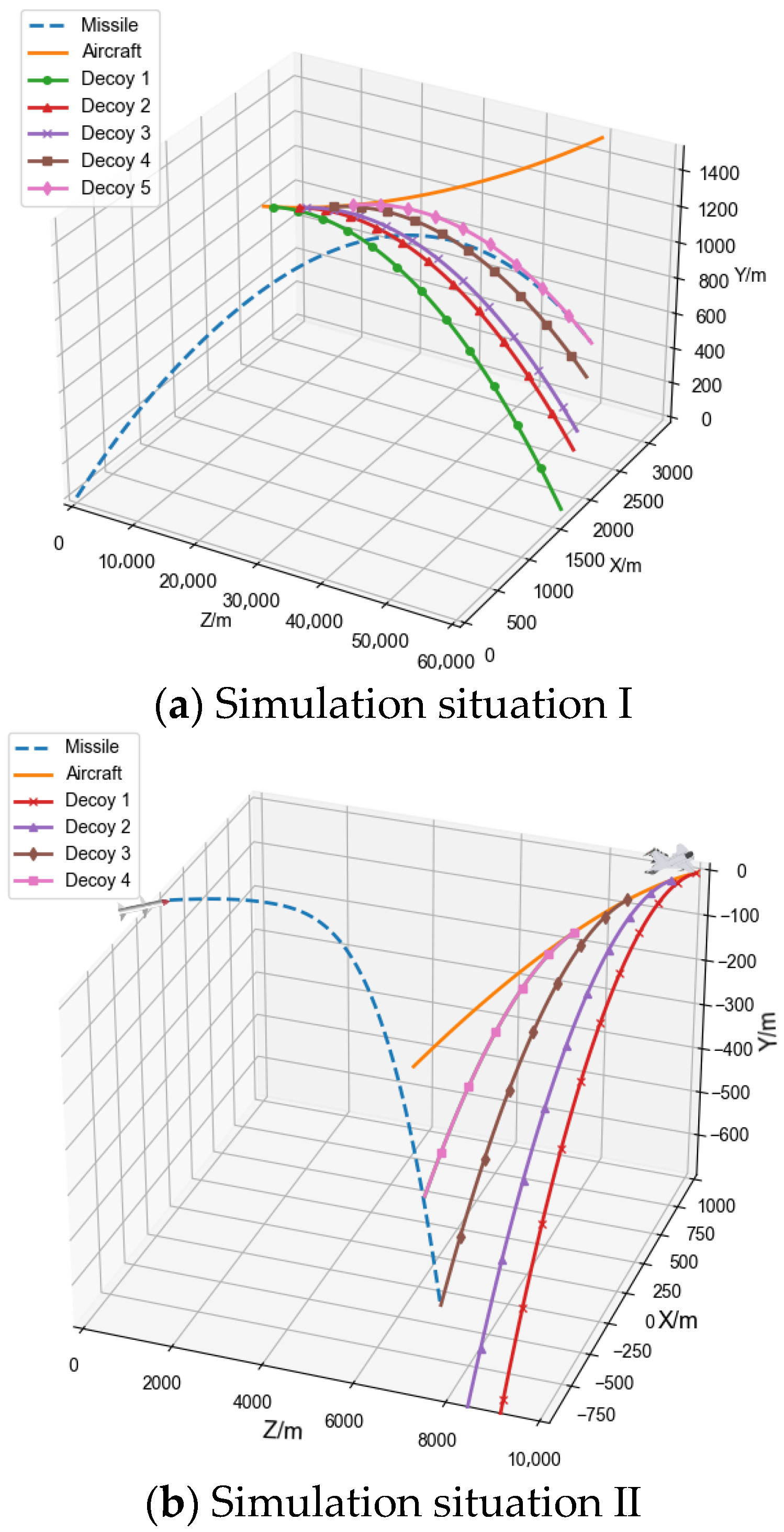
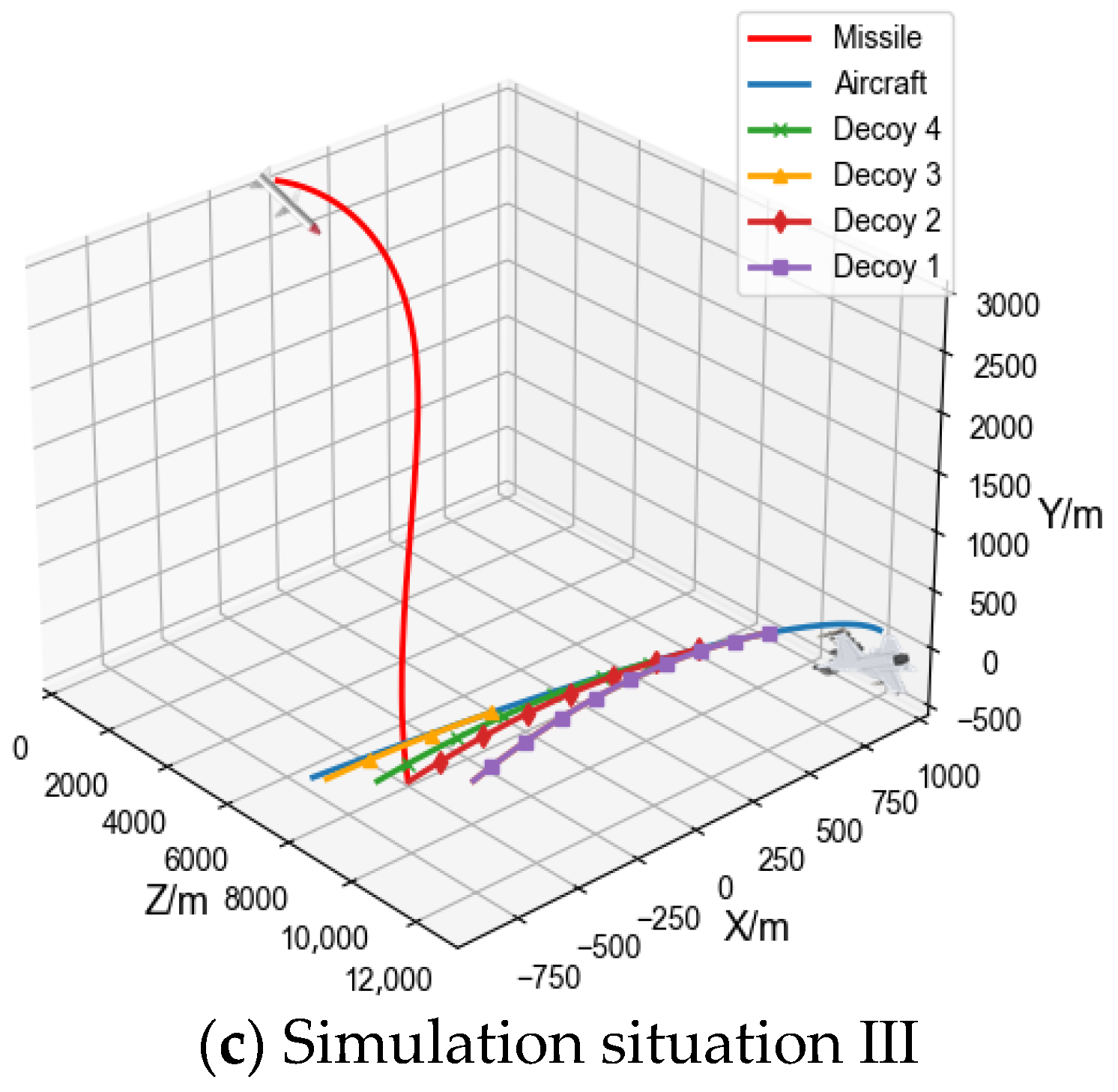
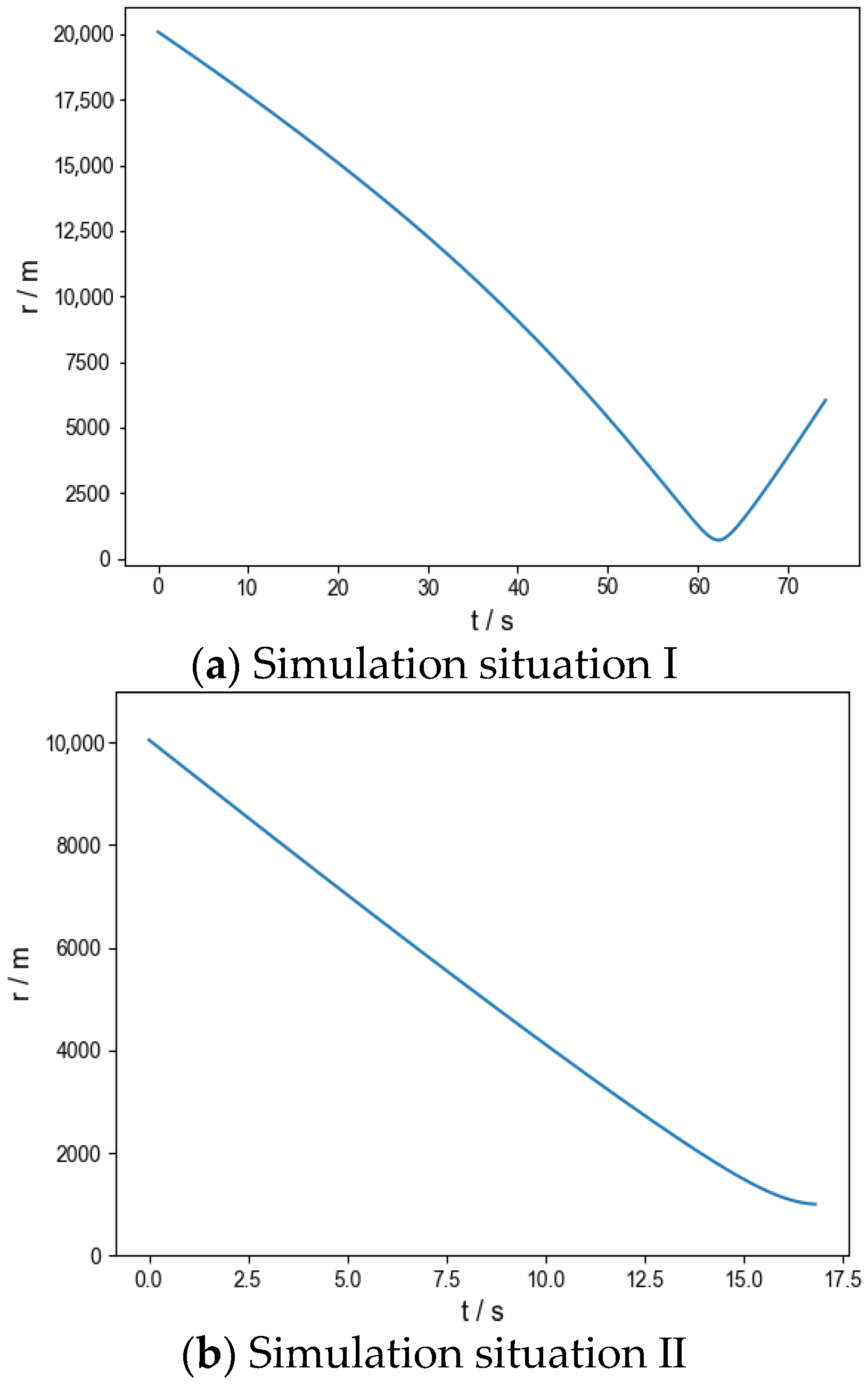
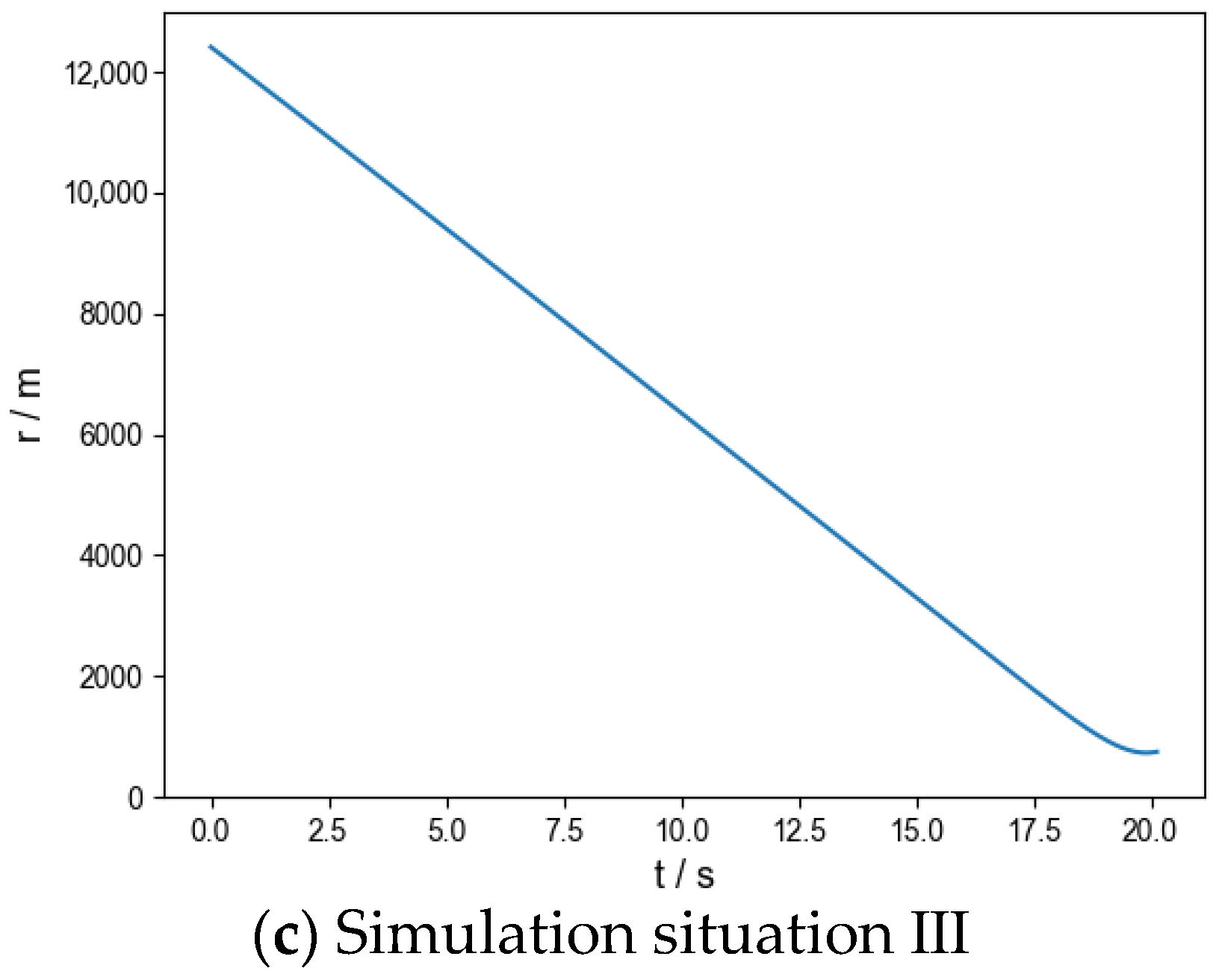
5.3. Analysis of Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nowak, J.; Achimowicz, J.; Ogonowski, K.; Biernacki, R. Protection of air transport against acts of unlawful interference: What’s next. Saf. Def. 2020, 2, 75–88. [Google Scholar]
- Wang, R.F.; Wu, W.D.; Zhang, Y.P. Summarizotion of defense measures for the IR guided flight vehicle. Laser Infrared 2006, 12, 1103–1105. [Google Scholar]
- Hu, Z.H.; Chen, K.; Yan, J. Research on control parameters of infrared bait delivery device. Infrared Laser Eng. 2008, 37, 396–399. [Google Scholar] [CrossRef]
- Shen, T.; Li, F.; Song, M.M. Modeling and simulation of infrared surface source interference based on SE-Work-Bench. Aerosp. Electron. Work. 2019, 39, 6–10. [Google Scholar]
- Yang, S.; Wang, B.; Yi, X.; Yu, H.; Li, J.; Zhou, H. Infrared baits recognition method based on dual-band information fusion. Infrared Phys. Technol. 2014, 67, 542–546. [Google Scholar] [CrossRef]
- Chen, S.H.; Zhu, N.Y.; Chen, N.; Ma, X.J.; Liu, J. Infrared radiation characteristics test of aircraft and research on infrared bait delivery. Infrared Technol. 2021, 43, 949–953. [Google Scholar]
- Zhang, N.; Chen, C.S.; Sun, J.G.; Liang, X.C. Research on infrared air-to-air flight vehicle based on barrel roll maneuver and bait projection. Infrared Technol. 2022, 44, 236–248. [Google Scholar]
- Huang, S.C.; Li, W.M.; Li, W. Two-sided optimal decision model used for ballistic flight vehicle attack-defense. J. Airf. Eng. Univ. Nat. Sci. Ed. 2007, 8, 23–25. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement learning: An introduction. IEEE Trans. Neural Netw. 1998, 9, 1054. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, M.; Skelton, R.E. Markov data-based reference tracking control to tensegrity morphing airfoils. Eng. Struct. 2023, 291, 116430. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, M.; Majji, M.; Skelton, R.E. Q-Markov covariance equivalent realizations for unstable and marginally stable systems. Mech. Syst. Signal Process. 2023, 196, 110343. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, M.; Skelton, R.E. A Markov data-based approach to system identification and output error covariance analysis for tensegrity structures. Nonlinear Dyn. 2024, 112, 7215–7231. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, X.; Liu, H. Impact time control guidance law with time-varying velocity based on deep reinforcement learning. Aerosp. Sci. Technol. 2023, 142, 108603. [Google Scholar] [CrossRef]
- Aslan, E.; Arserim, M.A.; Uçar, A. Development of push-recovery control system for humanoid robots using deep reinforcement learning. Ain Shams Eng. J. 2023, 14, 102167. [Google Scholar] [CrossRef]
- Lee, G.; Kim, K.; Jang, J. Real-time path planning of controllable UAV by subgoals using goal-conditioned reinforcement learning. Appl. Soft Comput. 2023, 146, 110660. [Google Scholar] [CrossRef]
- Fan, X.L.; Li, D.; Zhang, W.; Wang, J.Z.; Guo, J.W. Flight vehicle evasion decision training based on deep reinforcement learning. Electron. Opt. Control 2021, 28, 81–85. [Google Scholar]
- Deng, T.B.; Huang, H.; Fang, Y.W.; Yan, J.; Cheng, H.Y. Reinforcement learning-based flight vehicle terminal guidance of maneuvering targets with baits. Chin. J. Aeronaut. 2023, 36, 309–324. [Google Scholar] [CrossRef]
- Qiu, X.Q.; Lai, P.; Gao, C.S.; Jing, W.X. Recorded recurrent deep reinforcement learning guidance laws for intercepting endoatmospheric maneuvering flight vehicles. Def. Technol. 2024, 31, 457–470. [Google Scholar] [CrossRef]
- Qian, X.F.; Lin, R.X.; Zhao, Y.N. Aircraft Flight Mechanics; Beijing Institute of Technology Press: Beijing, China, 2012; pp. 102–110. [Google Scholar]
- Tang, S.J.; Yang, B.E.; Xu, L.F.; Zhang, Y. Research on anti-interference technology based on target and infrared bait projectile motion mode. Aerosp. Shanghai 2017, 34, 44–49. [Google Scholar]
- Sigaud, O.; Buffet, O. Markov decision processes in artificial intelligence. In Markov Processes & Controlled Markov Chains; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Howard, M. Multi-Agent Machine Learning: A Reinforcement Approach; China Machine Press: Beijing, China, 2017. [Google Scholar]
- Ma, X.P.; Zhao, L.Y. Overview of research status of key technologies of infrared seeker at home and abroad. Aviat. Weapons 2018, 3, 3–10. [Google Scholar]
- Bai, H.Y.; Zhou, Y.X.; Zheng, P.; Guo, H.W.; Li, Z.M.; Hu, K. A Real-Time Dynamic Generation System and Method for Target and Scene Used in Image Seeker. CN202010103846.3, 28 July 2020. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Vosoogh, A.; Sorkherizi, M.S.; Zaman, A.U.; Yang, J.; Kishk, A.A. An integrated Ka-Band diplexer-antenna array module based on gap waveguide technology with simple mechanical assembly and no electrical contact requirements. IEEE Trans. Microw. Theory Tech. 2018, 66, 962–972. [Google Scholar] [CrossRef]


| Improved DDPG Algorithm |
|---|
|
| Name | Parameter | Value |
|---|---|---|
| Simulation Situation I | Initial position of aircraft (m) | |
| Initial position of missile (m) | ||
| Initial speed of aircraft (m·s−1) | ||
| Initial velocity of missile (m·s−1) | ||
| Initial azimuth angle of missile (rad) | ||
| Simulation Situation II | Initial position of aircraft (m) | |
| Initial position of missile (m) | ||
| Initial speed of aircraft (m·s−1) | ||
| Initial velocity of missile (m·s−1) | ||
| Initial azimuth angle of missile (rad) | ||
| Simulation Situation Ⅲ | Initial position of aircraft (m) | |
| Initial position of missile (m) | ||
| Initial speed of aircraft (m·s−1) | ||
| Initial velocity of missile (m·s−1) | ||
| Initial azimuth angle of missile (rad) |
| Name | Value |
|---|---|
| Actor and critic learning rate | 0.0003 |
| Discount factor | 0.99 |
| Experience pool | 1 × 107 |
| Sample rate of experience pool II | 0.05 |
| Number of batch samples | 256 |
| Maximum steps | 400 |
| Optimizer | Adam |
| Name | Value |
|---|---|
| GPU | NVIDIA Pascal architecture with 256 NVIDIA CUDA cores |
| CPU | Dual core Denver 2, 64 bit CPU and quad core ARM A57 Complex |
| Memory | 8 GB 128 bit LPDDR4 |
| Storage space | 32 GB eMMC 5.1 |
| Connect | Gigabit Ethernet |
| Size | 87 mm × 50 mm |
| Simulation Situation | Name | Bait Type | The Number of Baits Dropped | Bait Drop Position /m | Bait Drop Angle /rad | Average Miss Distance/m | Escape Success Rate/% | Decision Time for PC/ms | Decision Time for Nvidia Jetson TX2/ms |
|---|---|---|---|---|---|---|---|---|---|
| I | Release without bait | _ | _ | _ | _ | 0.5 | 0.3 | _ | _ |
| Bait release | Point source bait | 5 | (1025.1, 1500.0, 21,234.9) | (0.8, −0.02) | 670.2 | 96.8 | 2.5 | 12.5 | |
| (1081.3, 1499.9, 24,013.3) | (1.1, −0.02) | ||||||||
| (1106.5, 1500.0, 25,248.2) | (1.2, −0.01) | ||||||||
| (1162.7, 1499.9, 28,026.7) | (1.4, −0.01) | ||||||||
| (1206.6, 1500.0, 30,187.8) | (1.6, −0.01) | ||||||||
| II | Release without bait | _ | _ | _ | _ | 0.2 | 0.24 | _ | _ |
| Bait release | Point source bait | 4 | (993.9, −0.1, 9969.1) | (−0.7, −0.02) | 1000.0 | 97.2 | 2.5 | 12.5 | |
| (890.1, 0.0, 9573.2) | (−1.1, −0.02) | ||||||||
| (656.5, 0.0, 8988.7) | (−1.6, −0.01) | ||||||||
| (302.1, 0.0, 8394.1) | (−2.1, −0.01) | ||||||||
| III | Release without bait | _ | _ | _ | _ | 0.6 | 0.4 | _ | _ |
| Bait release | Point source bait | 4 | (719.6, −0.01, 10,491.0) | (−1.3, −0.01) | 750.5 | 96.0 | 2.5 | 12.5 | |
| (481.0, −0.08, 9977.2) | (−1.7, −0.02) | ||||||||
| (−281.2, −0.1, 8979.7) | (−2.6, −0.02) | ||||||||
| (301.8, −0.06, 9680.7) | (−2.0, −0.02) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, S.; Wang, Z.; Bai, H.; Yu, C.; Deng, T.; Sun, R. An Intelligent Bait Delivery Control Method for Flight Vehicle Evasion Based on Reinforcement Learning. Aerospace 2024, 11, 653. https://doi.org/10.3390/aerospace11080653
Xue S, Wang Z, Bai H, Yu C, Deng T, Sun R. An Intelligent Bait Delivery Control Method for Flight Vehicle Evasion Based on Reinforcement Learning. Aerospace. 2024; 11(8):653. https://doi.org/10.3390/aerospace11080653
Chicago/Turabian StyleXue, Shuai, Zhaolei Wang, Hongyang Bai, Chunmei Yu, Tianyu Deng, and Ruisheng Sun. 2024. "An Intelligent Bait Delivery Control Method for Flight Vehicle Evasion Based on Reinforcement Learning" Aerospace 11, no. 8: 653. https://doi.org/10.3390/aerospace11080653
APA StyleXue, S., Wang, Z., Bai, H., Yu, C., Deng, T., & Sun, R. (2024). An Intelligent Bait Delivery Control Method for Flight Vehicle Evasion Based on Reinforcement Learning. Aerospace, 11(8), 653. https://doi.org/10.3390/aerospace11080653






