Investigation of the Film Cooling Performance of Laminated SiC_fSiC Composite Plates

Abstract

Silicon carbide fiber-reinforced silicon carbide matrix ceramic composites (SiC_f/SiC) are extensively utilized in high-temperature resistant materials in the aerospace industry. This study investigated the influence of stacking structure on the performance of SiC_f/SiC laminated composite plates with film cooling. Initially, the thermal conductivity of cross-piled SiC_f/SiC composites was determined using the laser flash analysis (LFA) method and differential scanning calorimetry (DSC) method. Subsequently, a representative volume element (RVE) model that reflected the stacking structure was established. The anisotropic thermal conductivity of the unidirectional SiC_f/SiC layer was calculated using numerical methods and experimental results. Finally, numerical simulations were carried out to assess the film cooling effectiveness of various stacking sequences and layers. The results showed that the thermal conductivity values predicted by the RVE model for the laminated composite aligned well with the experimental results, and the unidirectional SiC_f/SiC composite thermal conductivities at different temperatures were obtained. The stacking sequence impacted the temperature distribution near the film hole, with the [0-90-0] structure exhibiting a more pronounced effect on film cooling performance compared with the [0-90] and [0-90-90-0] structures. The performance of the film cooling in the laminated SiC_f/SiC composites was consistent across all stacking layers [0-90]₁, [0-90]₂, and [0-90]₃. The maximum difference in overall cooling efficiency was 1.7% between [0-90-0]₁ and [0-90]₁ and [0-90-90-0]₁

1. Introduction

Fiber-reinforced ceramic composites (CFCCs) have emerged as a rapidly developing material with extensive applications in various aerospace fields [1,2]. Among the CFCCs, SiC_f/SiC composites are utilized in aerospace, nuclear energy, and other industries due to their high temperature resistance, wear resistance, oxidation resistance, and excellent mechanical properties at high temperatures [3,4]. SiC_f/SiC composites have higher operating temperatures than traditional nickel-based high-temperature alloys. To further enhance the capabilities of SiC_f/SiC composites, commercial-grade prepreg–MI and CVI-SMI SiC_f/SiC composites have been developed, achieving a temperature capability of 1316 °C. Ongoing research and development efforts aim to push the temperature capability of SiC_f/SiC composites to reach 1755 °C [5]. However, with an increase in the inlet temperature of the turbine, cooling is still necessary for specific applications in aircraft engines to ensure the safe operation of the hot end parts of the CFCC. NASA applied gas film cooling technology to CFCC blades, successfully passing 50 h of steady state and 102 thermal cycling tests between 1173 K and 1713 K [6].

Film cooling is a simple and efficient cooling technology for hot-end components that has been successfully applied to CFCC components [7]. Predicting cooling efficiency and internal temperature is necessary for designing CFCC components. Several researchers have conducted studies to investigate the film-cooling performance of CFCC components. Carol E. Bryant [8,9] used conjugate heat transfer computational simulations to evaluate the effect of anisotropy on the overall cooling effectiveness of the leading edge region of a turbine component and a plate. The study found that thermal conductivity anisotropy significantly influenced the resulting overall effectiveness of film cooling. Tu Zecan [10,11] studied the cooling performance of film cooling holes in unidirectional CFCC panels. Research showed that the anisotropic thermal conductivity can affect the heat transfer process within gas film cooling systems. Specifically, the heat transfer ability is enhanced in the direction of toughening, affecting the average cooling efficiency and temperature distribution of walls covered by the gas film.

Furthermore, the fiber distribution and microstructure of CFCC materials can also impact film cooling performance [12]. Zhao X. [13] investigated the effect of the relative position of holes and braided fibers on the cooling performance of 2.5D braided CFCC flat plates. Their study showed that the interference between the film-cooling holes and the fibers influenced the temperature distribution of the flat plate. The weaving structure around the film hole significantly impacted the heat transfer path, temperature field, and temperature gradient distribution near the gas film hole. Zhu Ailin [14] established a full-size calculation model reflecting the internal mesoscale structure of CFCC plates. The geometric parameter, the braided angle of the braided structure, was changed in different models. Their study showed that the fiber bundles inside the CFCC plate were the main heat transfer channels due to their relatively higher thermal conductivity. However, the influence of the braided angle was relatively weak in the downstream region away from the holes. The research above indicated that the thermal conductivity characteristics in CFCC materials were significant for the film performance.

Determining the effective thermal performance of CFCC materials as non-uniform materials has long been an interesting issue. The thermal conductivity of fiber-reinforced ceramic matrix composites is anisotropic due to the different components, proportions, and manufacturing processes in CFCC materials. To measure or estimate the thermal performance of composite materials, researchers have developed various methods for measuring the thermal conductivity of anisotropic materials based on methods for measuring the thermal conductivity of isotropic materials. Zhang Hui [14] compared the anisotropic thermal conductivity of CFCC materials measured by the one-dimensional steady-state, TPS transient plane, and hot wire methods. The maximum deviation of the steady-state measurement method compared with that of the transient thermal conductivity measurement was 18.1%. Diana Vitiello et al. [15] compared the thermal conductivity measurement of insulating boards and refractory clay bricks using the heat flux meter, laser flash, hot plate, and hot wire methods. The deviation of the three measurement methods was within 10%. The material’s equivalent thermal conductivity can be obtained by experimental measurement. However, the measurement ignores the fiber’s stacking structure of the CFCC. The thermal conductivity was the effective thermal conductivity (ETC).

Due to the continuous development of materials’ internal woven fiber structure, woven fiber structure composites have evolved from UD and laminar to 2D, 2.5D, and 3D woven structures. However, current research usually considers the thermal conductivity of CFCC as a homogeneous anisotropic material. As a heterogeneous material, the thermal conductivity of CFCC is different from that of homogeneous materials. Although early scholars developed different homogenization methods for CFCC materials, the final progress was attributed to numerical methods [16]. Researchers have begun to shift the prediction method for the thermal conductivity of CFCC materials toward numerical methods based on the representative volume element (RVE) model and establish RVE models at different scales based on the internal structural characteristics of the material. The current numerical method was used to predict the efficient thermal conductivity and study the behavior of the thermal conductivity of CFCC materials. Y. Liu et al. [17] proposed a numerical model at three scales based on the 3D geometric reconstructions. It was developed to investigate the thermal conductivities of different structural C/SiC composites. The mesoscale unit cell model comprised woven yarns and an out-of-yarn SiC matrix for the composites. The proposed model was validated using available analytical and experimental results. Zheng Sun et al. [17] proposed microscale, void/matrix, and mesoscale representing volume element (RVE) models to investigate the thermal conductivity behaviors of composites with different preformation architectures. The mesoscale model consisted of fiber yarns and a matrix. The RVE model at the fiber bundle scale was used to predict the thermal conductivity and study the internal thermal conductivity behavior of CFCC materials.

The literature above showed that SiC_f/SiC composites as CFCCs have been applied in hot-end components. The characteristic of thermal transfer was significant for the SiC_f/SiC composites. Although some researchers have found that CFCC materials’ fiber direction impacts the material’s film cooling, there is still a lack of research on the influence of the layering structures of the SiC_f/SiC composites on the cooling performance of film cooling. In addition, the thermal conductivity of a SiC_f/SiC was published in this study.

This study established a micrometer-scale RVE model reflecting the laminated composites’ stacking structures. Numerical simulation methods combined with experimental measurements were used to obtain the thermal conductivity of cross-piled SiC_f/SiC composites and the unidirectional SiC_f/SiC composites at 373 K–973 K. On this basis, the gas film cooling performance of SiC_f/SiC composite plates with different layer structures was studied. This study will provide a reference for the thermal structure design of laminated composites.

2. The Thermal Conductivity of the SiC_f/SiC

2.1. Material

The laminated composites of SiC_f/SiC studied in this paper were manufactured by the melt infiltration (MI) process. The manufacture of SiC-based composites is quite widespread. Currently, different methods are employed to produce them. The most efficient method, taking into account the cost/performance ratio, is reactive melt infiltration [18]. For cross-piled laminated composites, the stacking structure can be changed by different fiber cross proportions and the number of stacking layers. Stacked SiC fibers were wetted with phenolic resin to transform into SiC prepregs. The prepregs were obtained as green bodies via thermal curing of the phenolic resin. The green bodies were subsequently pyrolyzed to convert phenolic resin into a carbon source, which was used for the silicon infiltration process to form a SiC matrix by the reaction of carbon with silicon.

The SiC fibers of the material were cross-piled, as shown in Figure 1. The thicknesses along the z-direction were 0.79 mm, 0.65 mm, 0.74 mm, 0.66 mm, 0.51 mm, and 0.35 mm. The fibers used in the composites were second-generation SiC fibers, with an average fiber diameter of 10.9 μm. The volume fraction of fibers in the matrix was 24.0%.

The laminated composites were assembled using fibrous layers and combined with matrix materials. The unidirectional layer with the same orientation of fibers was considered homogeneous, and the thermal conductivity was anisotropic. The thermal conductivity geometry models of thermal conductivity and the film cooling plate were established, as shown in Figure 2. Figure 2a shows the representative volume element (RVE) model. The RVE model was established according to the cross-section photo. The RVE model was the cube. The length l was 3.7 mm. The z direction was the through-thickness direction of the RVE model. The x and y directions were the in-plane direction of the RVE model, and the x direction had more axis-direction unidirectional composites than the y direction. Figure 2b presents the model of a plate with a film cooling hole. The model is the same as that in the literature [19]. The plate included the stacking structure of the laminated composite. The diameter of the air film hole D was 2.4 mm, and the angle of the air film hole was 90°. The thickness of the flat plate H was 3.3 mm. The height of the mainstream and cold-air areas was 7.5D, and the distance from the center of the air film hole to the upstream and downstream boundaries was 7.5D and 15.5D. The stacking orientation of both models was the in-plane direction.

2.2. Anisotropic Thermal Conductivity

The thermal conductivity of laminated composites is anisotropic, and a second-order tensor can represent the anisotropic thermal conductivity. Currently, based on the homogenization assumption, researchers can use numerical simulation and experimental measurements to obtain the thermal conductivity of laminated composites.

$$\mathit{K}=\left[\begin{array}{ccc}{\mathit{k}}_{\mathit{x}}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\mathit{k}}_{\mathit{y}}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& {\mathit{k}}_{\mathit{z}}\end{array}\right]$$

(1)

2.3. Measure

The thermal diffusivity was measured using the laser flash analysis method (LFA 500, Linseis, Selb, Germany), and the specific heat capacity of the sample was measured using the differential scanning calorimetry (DSC) method (Setaram, Themes one, Caluire, France). After testing was completed, the thermal conductivity of the sample was calculated using the thermal diffusivity equation. The thermal conductivity (K) was calculated according to the equation: k_i = α∙Cp∙ρ, where i is the x, y, z, ρ is the specimen density, Cp is the specific heat capacity, and α is the thermal diffusivity. As shown in Figure 3, samples with a diameter of 12.7 mm were used to measure the thermal diffusivity.

2.4. Analysis of Thermal Conductivity

Simulation of thermal conductivity was carried out using the finite element method (FEM). The finite element method in the RVE model of the SiCf/SiC composites can predict the thermal conductivity of laminated composites. The contact thermal resistance between the layers of the RVE model was ignored, and only the influence of thermal conductivity on the temperature distribution of the RVE model was considered.

The through-thickness direction of the thermal conductivity of the SiC_f/SiC was the z-axis direction of the RVE model. The in-plane direction was the orientation of the x-axis and y-axis. For any direction of the thermal conductivity in the FEM, the faces of orientation were uniform temperature, and the temperature difference was 1 K. The other surfaces were adiabatic. The thermal conductivity of the transverse direction of the unidirectional composites was experimental. The thermal conductivity in the axis direction was predicted. The experimental thermal conductivity in the in-plane direction verified the predicted thermal conductivity. The effective thermal conductivity was calculated using the equation k_i = q_i∙l/∆t, where q is the heat flow density, l is the length, and ∆t is the temperature difference.

The difference in temperature on the two faces resulted in heat flux. Figure 4 shows the temperature and heat flow density distribution of the RVE model at 373 K in the x, y, and z directions. The temperature was uniform along the orientation of the difference of temperature. The heat flow density was different between layers in the x-axis direction and y-axis direction. The heat flow density in the fiber axis direction was more significant than that in the transverse direction. However, the heat flow density in the z-axis direction was uniform. The results showed that the heat flow in the fiber axis direction was more significant than that in the transverse direction.

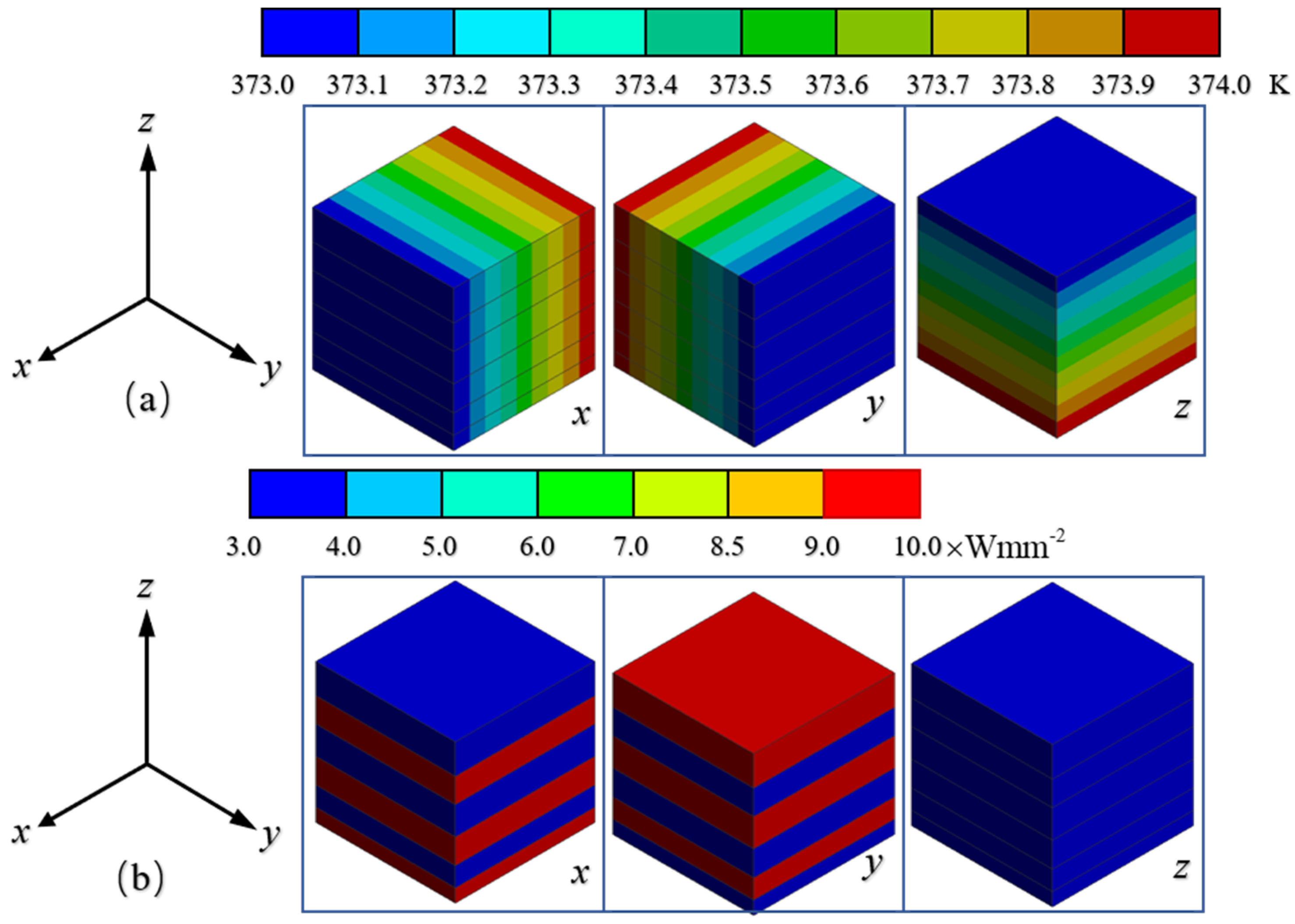
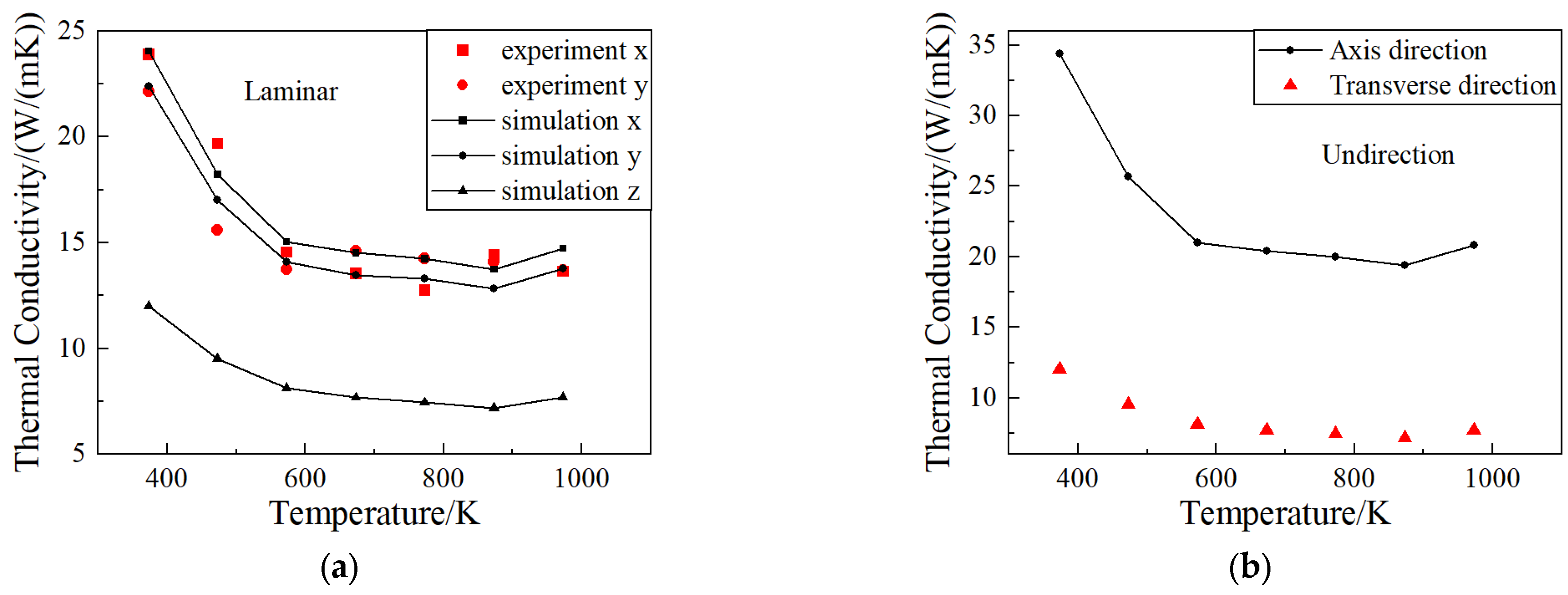
2.5. Result of Thermal Conductivity

Figure 5 shows the thermal conductivity of the SiC_f/SiC ranging from 373 K to 973 K. The thermal conductivity in the in-plane direction of the laminated composites and the transverse direction of the unidirectional composites were measured. The thermal conductivity in the through-thickness direction of the laminated composites and the fiber axis direction of the unidirectional composts were predicted by the numerical method. The thermal conductivity determined by measurement and simulation had great fitness. Therefore, the simulation can indicate the laminated composites and the unidirectional composites. The maximum relative error between the measured and predicted values was 7%, so this numerical prediction model can predict the in-plane anisotropic thermal conductivity of the material.

The result for the thermal conductivity showed that it decreased from 373 K to 573 K and remained unchanged from 573 K to 973 K. The thermal conductivity of the in-plane direction of laminated composts was almost equal. The in-plane direction and the thermal conductivity of the thickness direction were about two times those in the in-plane direction. The thermal conductivities at 373 K were 12.0 W/(mK), 22.4 W/(mK) and 23.9 W/(mK), respectively. The thermal conductivity of unidirectional composites in the fiber axis direction was about three times that in the transverse direction. The thermal conductivities of the unidirectional composites at 373 K were 12.0 W/(mK) and 34.4 W/(mK).

The thermal conductivity of laminated composites throughout the thickness direction and unidirectional composites in the transverse direction were equal. The laminated composites along the fibers’ axis direction resulted in heat transfer channels, which will influence the heat flow.

3. Influence of Stacking Sequence and Layers on Film Cooling

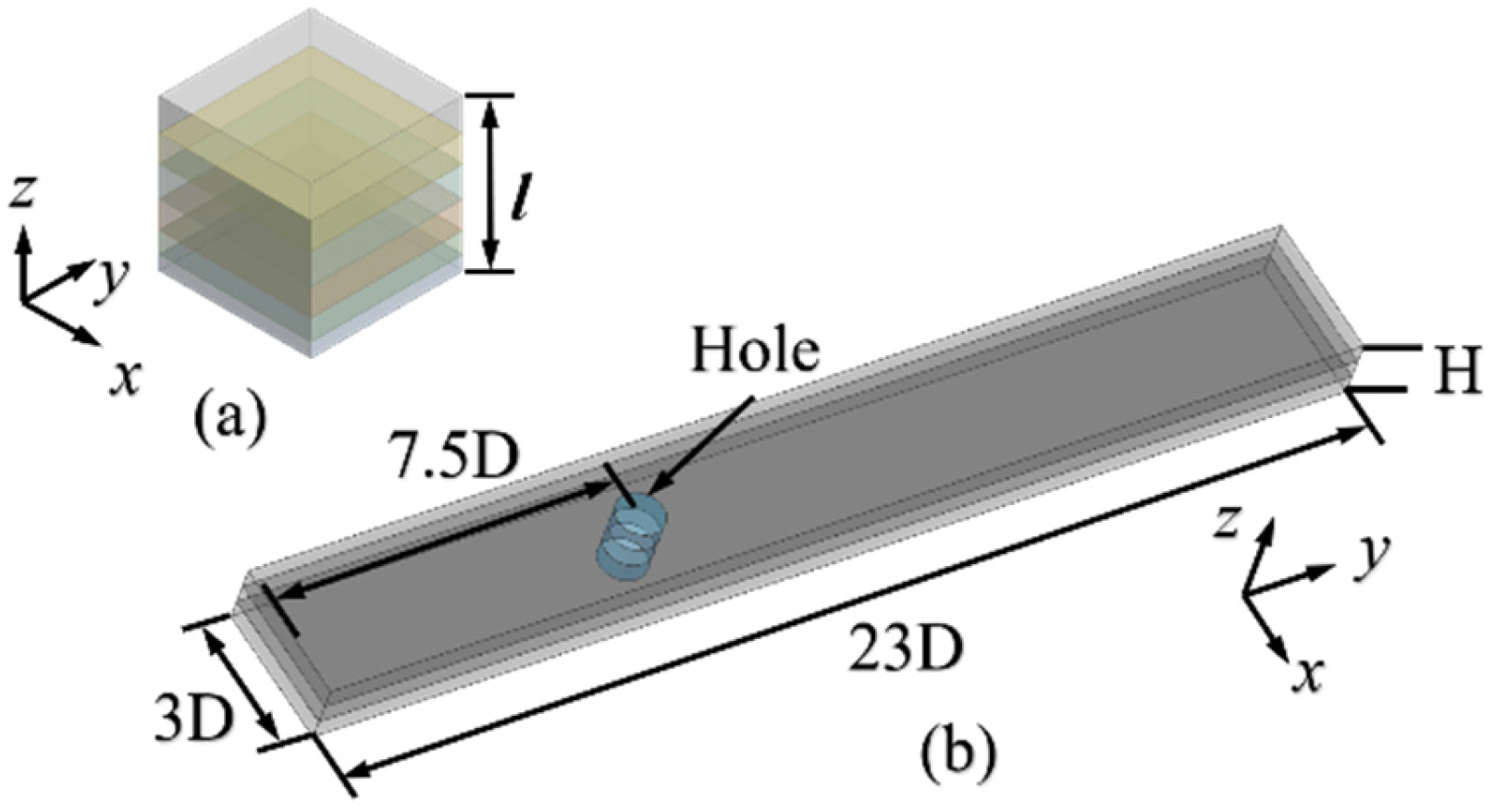
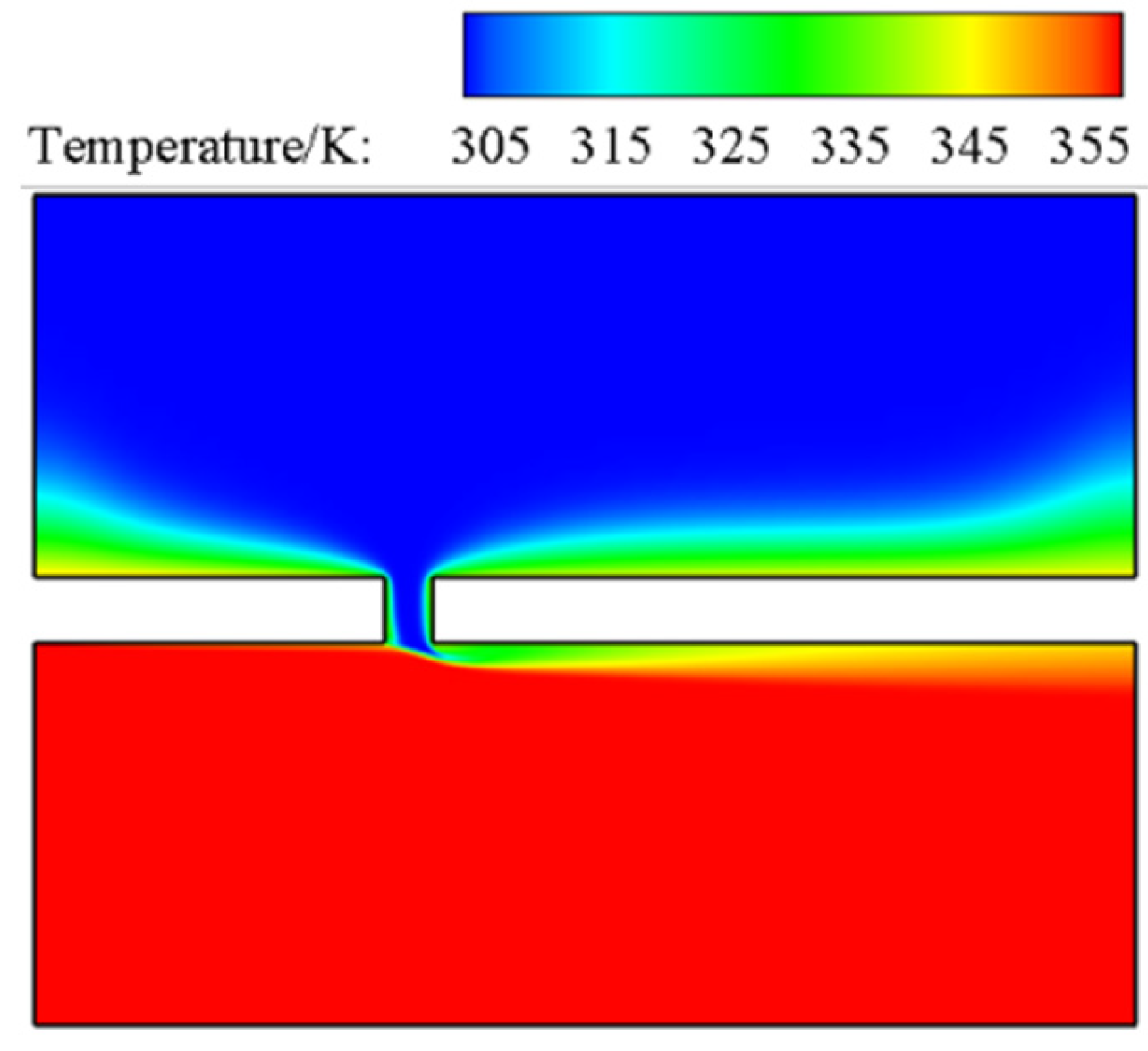
3.1. Simulation Model

Figure 6 shows the numerical model of the flat plate with a film-cooling hole. The model included a film-cooling hole, mainstream flow region, coolant flow region, and laminated composite plates. The plate’s material was laminated SiC fibers reinforced with SiC matrix composites. The thickness of the flat plate H was 3.3 mm. The length of the mainstream flow region and coolant flow region was 8D.

The thermal conductivity of laminated composites in the thickness direction was equal to that in the transverse direction of unidirectional composites. The stacking structure was the main factor influencing the heat flow distribution. Therefore, the film cooling performance of the laminated composites needs to be studied. This paper considers three stacking sequences and three stacking layers, as shown in

Table 1. Stacking structure of the simulation.

	Case 1	Case 2	Case 3	Case 4	Case 5	Case 6	Case 7	Case 8	Case 9	Case 10
Stacking structure	[0/90]1	[90/0]1	[0/90/0]1	[90/0/90]1	[0/90/90/0]1	[90/0/0/90]1	[0/90]2	[90/0]2	[0/90]3	[90/0]3

. Three typical layer structures of 0-90, 0-90-0, and 0-90-90-0 were considered. In addition, 0-90 stacking sequences with a single layer, two, and three layers were considered. In addition, each stacking sequence had two directions in the through-thickness direction. Considering the influence of fiber direction on film cooling at the mainstream angle, the fiber direction of each structure was rotated by 90°. The numerical simulation of the layered flat-plate model is shown in the table below.

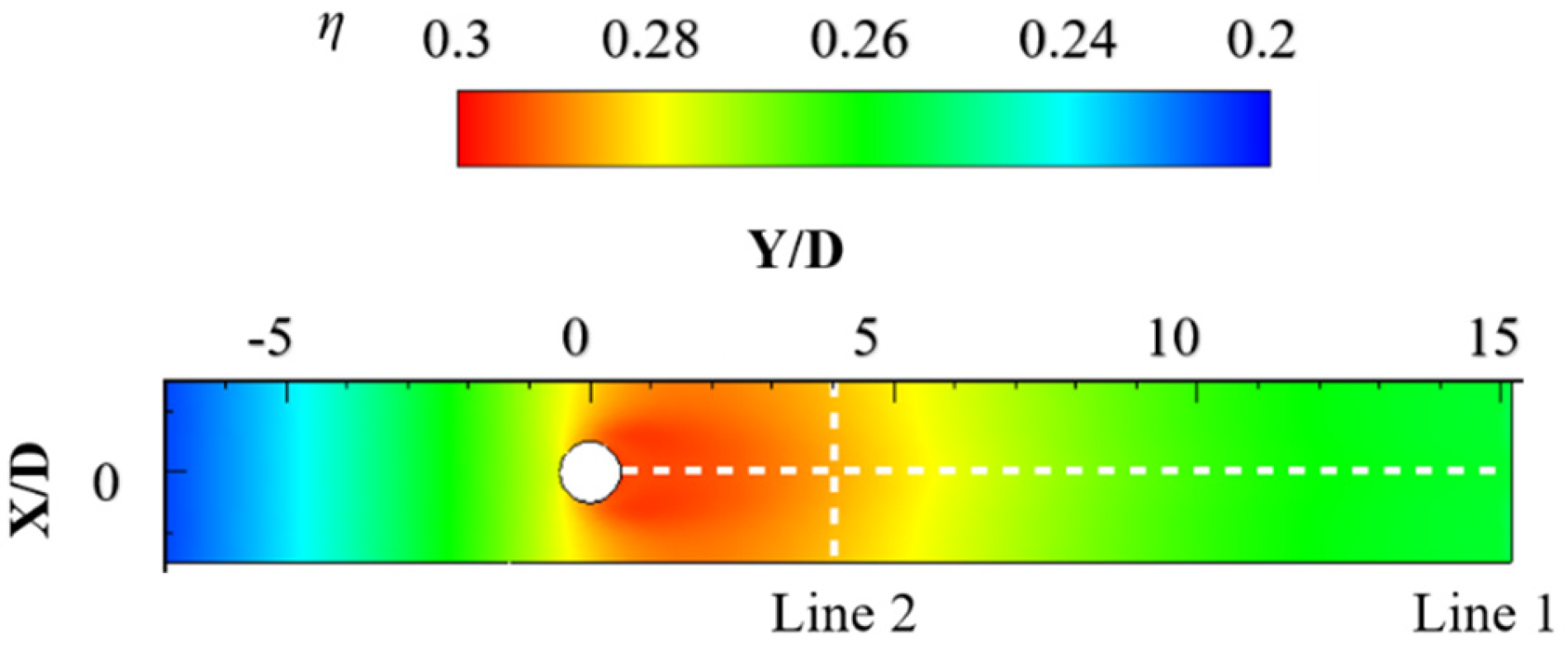
3.2. Boundary Conditions and Parameter Definitions

As shown in Figure 6, the inlet of the mainstream was the velocity inlet. The velocity of the inlet was 20 m/s, the temperature was 360 K, and the turbulence intensity was 0.2%. The mainstream outlet was a pressure outlet at 1 atm. The inlet of the coolant flow was the velocity inlet, with a flow rate of 0.04823 m/s and a temperature of 300 K. The boundary on both sides of the mainstream was periodic, and the other walls were non-slip adiabatic. Conjugate heat transfer numerical simulation was performed on the solid and fluid domains.

This study selects two positions to compare the effects of different stacking sequences and layers. The temperature distribution at the center section of the divergent hole, the comprehensive cooling efficiency, and the hot side wall X/D = 4 and Y/D = 0 curves downstream of the divergent hole were compared.

The blowing ratio (Br) is defined as:

$$\mathrm{Br}={\displaystyle \frac{{\rho }_{\mathrm{c}}{u}_{\mathrm{c}}}{{\rho }_{\infty }{u}_{\infty }}}$$

(2)

where ρ_∞ and ρ_c are the densities of the mainstream and the coolant at the inlet of the film-cooling hole.

To analyze the performance of the film cooling, the overall cooling efficiency is defined as:

$$\eta ={\displaystyle \frac{T_{\infty }-T_W}{T_{\infty }-T_C}}$$

(3)

where T_∞ and T_c are the temperatures at the mainstream inlet and the coolant inlet, respectively; and T_w is the temperature on the hot-side wall.

To analyze the temperature gradient, relative temperature gradient ε is introduced, as shown in Equation (4):

$$\epsilon ={\displaystyle \frac{T_{grad}H}{T_{\infty }-T_C}}$$

(4)

where T_grad is the temperature gradient.

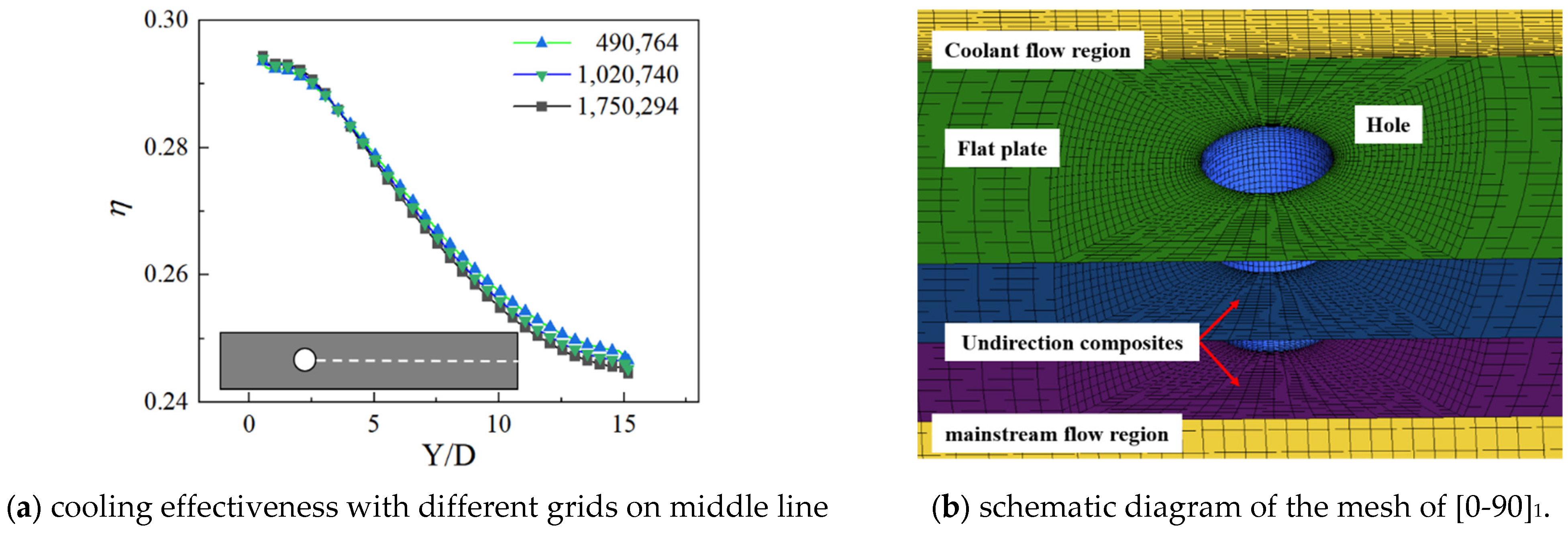
3.3. Mesh Independent

The simulation was carried out using the computational fluid dynamics (CFD). The numerical simulation model used in this article was validated. In the verification model, the standard k-ε model, the standard k-ω model, and the SST model were used. According to experiment results in the literature [20], the turbulence model of this study was compared. The temperature was verified using the dimensionless temperature cooling effectiveness. Figure 7 shows the cooling effectiveness on the centerline of the film-cooling hole downstream; both the k-ω and SST models could better match the experimental results. Therefore, the calculation was performed using the SST model in this study.

The entire computational domain was divided using the hexahedral mesh. This article divided three grids with meshes of 490,764, 1,020,740, and 1,750,294. Figure 8a shows the cooling effectiveness on the centerline of the film-cooling hole downstream when these three models were used for calculation. The result shows that, when the number of meshes was changed from 490,764 to 1,750,294, the overall cooling efficiency was less than 1%. Therefore, the grid with 1,020,740 meshes was used in the simulation, as shown in Figure 8a. The grid growth rate near the flat plate was 1.1, and the grid growth rate on other walls was 1.2. The height of the first-layer grid was 0.02 mm, ensuring that the y+ was around 1. The number of grids in the calculation result domain was independent.

4. Result and Discussion

For the film-cooling of the flat plate, the fluid exchanged the heat with the wall on the flat plate. The characteristics of the fluid were significant for cooling performance. Figure 9 shows the temperature distribution on the cross-section at X = 0. The coolant flow passed through the hole, and a film of coolant was found near the hot wall downstream of the hole. Figure 10 shows the distribution of the comprehensive cooling efficiency. The film performance was highest near the hole. To study the influence of the different stacking structures of the film-cooling holes on the temperature field and heat transfer path of the plate, the cross-section at X = 0 on the center of the film-cooling hole was selected. To analyze the cooling performance of the hot-side wall clearly, two special lines (as shown in Figure 9) were introduced, namely line 1 (centerline of the outflow) and line 2 (X/D = 4).

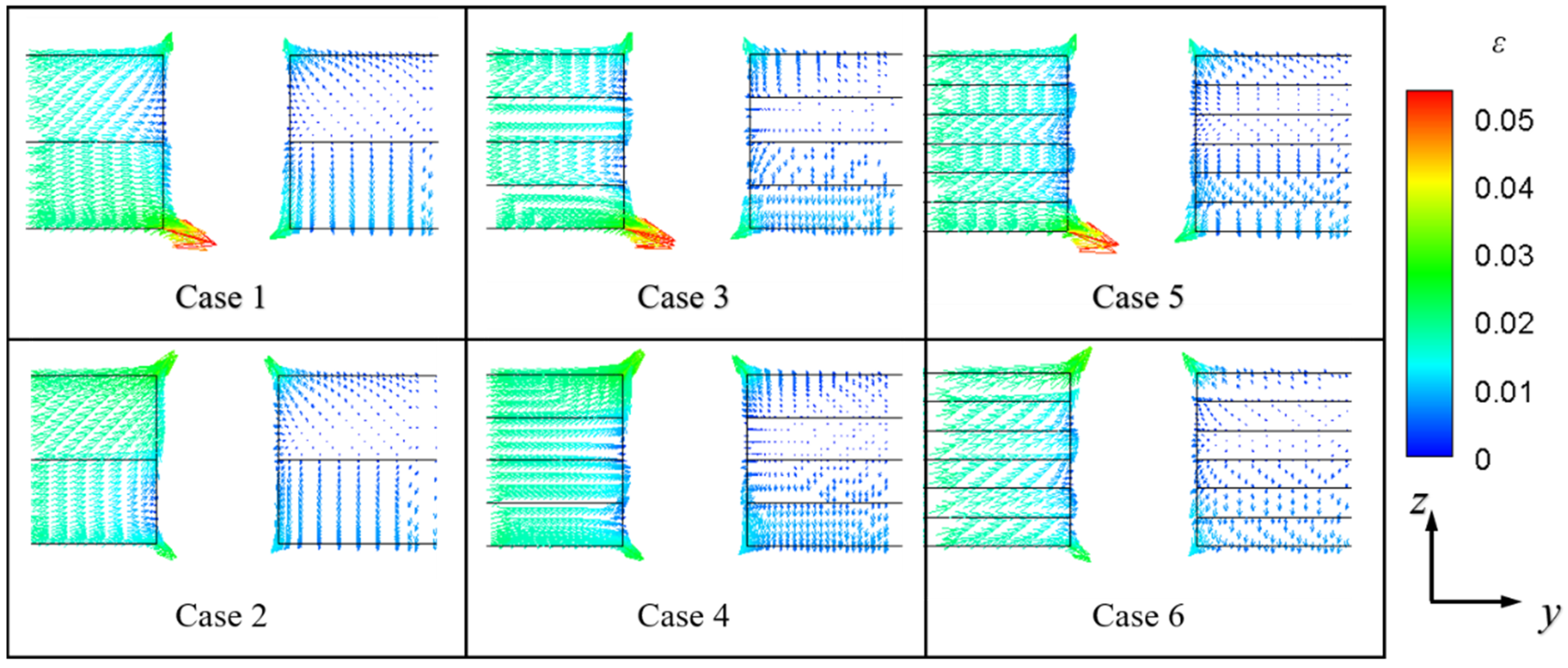
4.1. Influence of Stacking Sequence

Figure 11 shows the distribution of η on the hot side for different stacking sequences (cases 1–6). In Figure 11a, the η distribution is shown on line 1, where η decreases with Y. The η values were different in the downstream (0D–3D) of the film hole, and the maximum η (case 4) was 1.7% greater than the minimum η (case 1, 2, 5, 6). η exhibited similar values downstream of the film hole (3D–15.5D). Figure 11b shows the η distribution on line 2. The η distribution at the X = 0 position was the highest and it was the lowest on both sides. The η of cases 1, 2, 5, and 6 was almost the same. Cases 1, 2, 5, and 6 had nearly identical η values, while case 3 had the lowest and case 4 had the highest value.

Different internal structures and conjugate heat transfer with the cooling film caused variations in the overall cooling efficiency on the hot-side wall. The distribution of the overall cooling efficiency on the hot-side wall varied based on the laminated sequence. [0-90]₁ and [0-90-90-0]₁ showed similar distributions, while [0-90-0]₁ differed near the film hole. Additionally, the overall cooling efficiency of [0-90-0]₁ was sensitive to the flow direction.

Figure 12 shows the temperature distribution of cross-section X = 0 for different stacking sequences (cases 1–6). The temperature distribution near the hole upstream varied, with two low-temperature areas on each side, except for cases 3 and 5. Cases 4 and 5 exhibited lower temperatures than 3 and 6 in these areas. Downstream of the hole, the temperature distribution was consistent. When fibers were oriented in the y direction near the wall, temperatures were higher than those when fibers were oriented in the vertical y direction. The trend was obvious between case 3 and case 4. In the middle of the hole, the temperature approached the higher temperature in the flat plate. This trend was evident in cases like case 3 and case 5.

Due to the flow and heat transfer characteristics near the film hole, two low-temperature areas were observed at the inlet and outlet of the film hole. Different fiber directions can impact the temperature distribution of fibers close to the film hole. Temperatures increased when fibers aligned with the mainstream direction and decreased when they were perpendicular. The coupling effect resulted in temperature distributions. [0-90]_1, [0-90-0]_1, and [0-90-90-0]₁ exhibited nearly similar temperature distribution downstream of the film hole, while [0-90-0]₁ showed distinct temperatures.

Considering that the comprehensive cooling effect near the film hole was significantly affected by the stacking sequence and the complex temperature distribution, an analysis was conducted on the heat flow direction near the film hole. The heat flux direction indicated how heat moved within the flat plate. Figure 13 shows the heat flux direction for different stacking sequences (cases 1–6). In each case, four high-heat-flux positions were on the four corners of the cross-section. Heat moved from the hot side of the plate toward the film hole and was then dissipated through convective heat transfer on the surface. Significant heat exchange occurred at both the hole’s inlet and outlet, with minimal heat flow occurring at its center. Additionally, there were variations in heat flow direction among different cases.

The coolant film on the hot side isolated the flat plate near the hole from the high-temperature mainstream. As this effect weakened, heat from the mainstream flowed into the flat plate. The heat energy was lost from the wall of the film hole and the cold side on the flat plate. The flow characteristics at the inlet and outlet of the film hole led to significant heat exchange. The stacking layer influenced the thermal conductivity near the wall, causing changes in the heat flow direction around the film hole.

The analysis of the film cooling efficiency and temperature distribution for three typical stacking sequences revealed that different stacking sequences could impact heat transfer near the film hole, leading to varying temperature distributions. This influenced the cooling efficiency of the flat plate. The maximum difference was 1.7% between [0-90-0]₁ and [0-90]₁ and [0-90-90-0]₁. [0-90]₁ and [0-90-90-0]₁ showed similar distributions, while that in [0-90-0]₁ differed near the film hole. Additionally, the overall cooling efficiency of [0-90-0]₁ was sensitive to the flow direction.

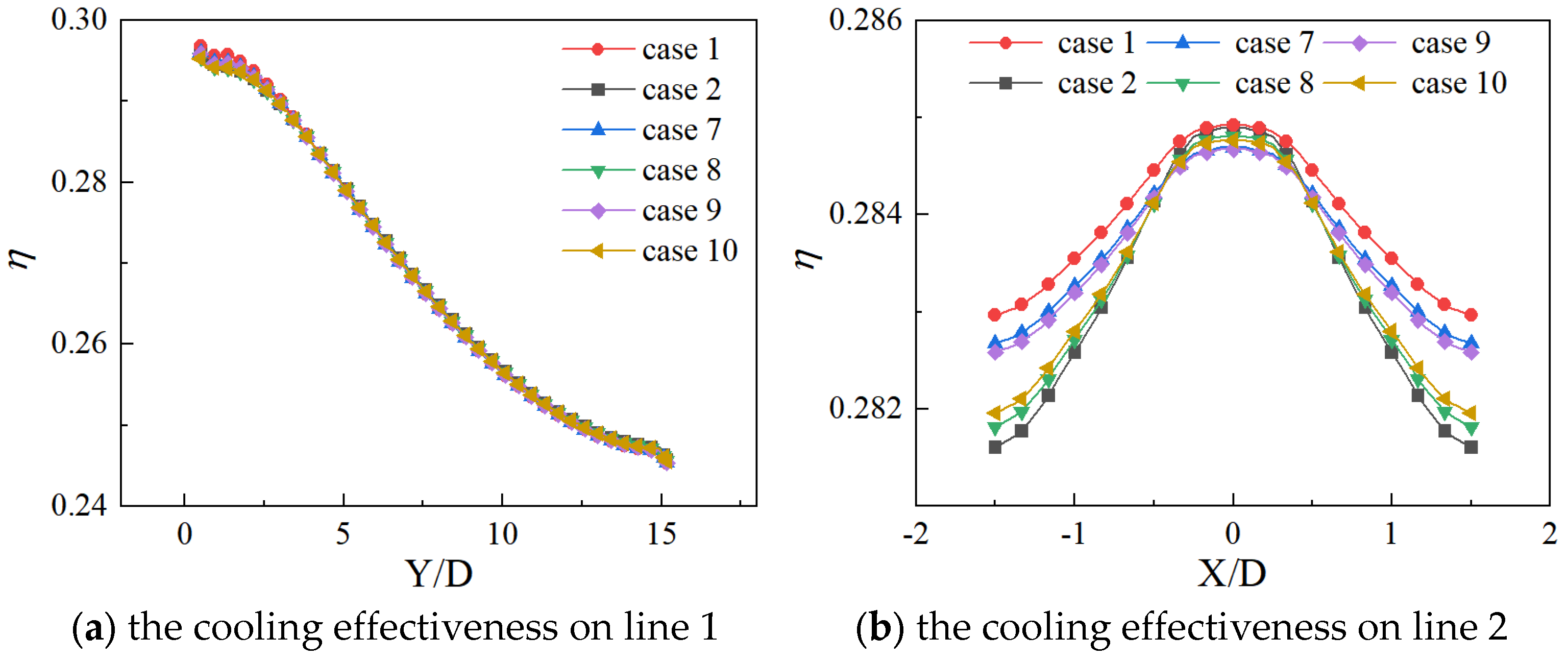
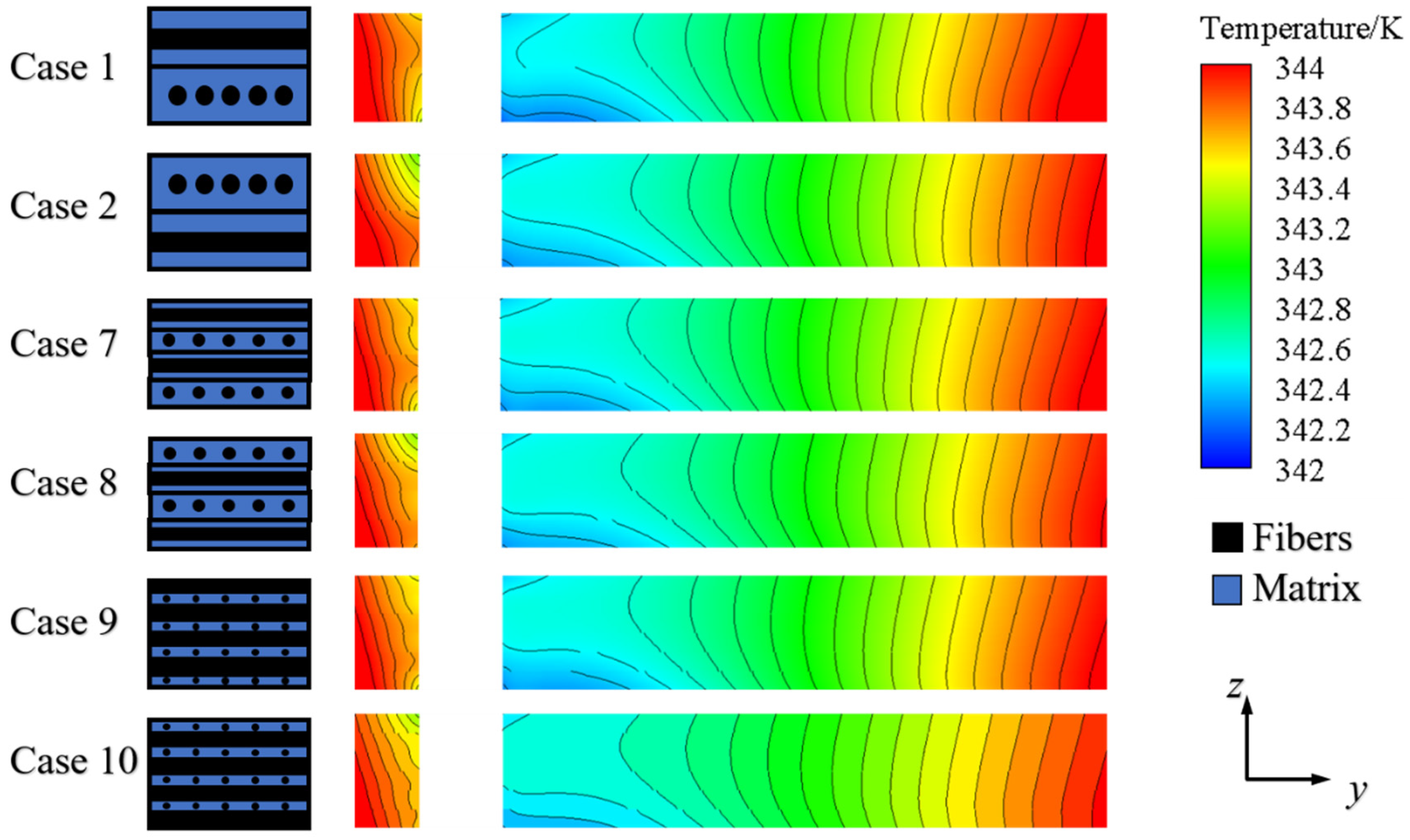
4.2. Influence of Stacking Layers

Figure 14 shows the distribution of η on the hot side for different stacking layers (cases 1, 2, and 7–10). Figure 14a shows the η distribution on line 1, and Figure 14b shows the η distribution on line 2. The overall cooling effectiveness on the hot side was consistent. η decreased along line 1. η at the X = 0 position was the highest and gradually reduced towards the sides. η remained constant between positions −0.5D and 0.5D. The η values of cases 1, 7, and 9 were slightly higher than those of cases 2, 8, and 10 at other positions along line 2.

Figure 15 shows the temperature distribution of cross-section X = 0 for different stacking layers (cases 1, 2, and 7–10). The temperature distribution varied upstream of the hole, but remained consistent downstream. Near the hole, a distinct low-temperature region formed on the cold flow side. Cases 2, 8, and 10 exhibited lower temperatures in this area compared with cases 1, 7, and 9. The extent of the cold region decreased with additional layers while the temperatures elsewhere remained constant. When fibers were oriented along the y direction near the wall, the temperature was higher than that when they were oriented vertically. A clear difference was observed between cases 1 and 2. When fibers aligned with the mainstream flow direction, a cold area formed upstream of the hole wall. However, aligning them vertically reduced this effect significantly.

Considering that the comprehensive cooling effect near the film hole was significantly affected by the stacking layers and the complex temperature distribution, an analysis was conducted on the heat flow direction near the film hole. Figure 16 shows the heat flux direction for different stacking layers (cases 1, 2, and 7–10). In each case, four high-heat-flux positions were observed on the four corners of the cross-section. Heat moved from the hot side of the plate toward the film hole and was then dissipated through convective heat transfer on the surface. Significant heat exchange occurred at both the hole’s inlet and outlet, with minimal heat flow occurring at its center. The heat flow in the middle of the hole was lower. The direction was different in different cases. Additionally, there were variations in the heat flow direction among different cases.

Due to the flow characteristics at the inlet and outlet positions, there was significant heat exchange at the inlet and outlet positions of the gas film hole. Due to the influence of the layering method on the thermal conductivity direction near the wall, there was a certain change in the direction of heat flow near the gas film hole.

The analysis of the film cooling efficiency and temperature distribution for three typical stacking layers revealed that different stacking layers impacted heat transfer near the hole. Still, the influence on the comprehensive cooling efficiency was slight. The film cooling efficiencies of [0-90]₁, [0-90]₂, and [0-90]₃ were almost identical.

The amount of heat carried away significantly increased at the film hole’s inlet and outlet when the fiber layer direction near the wall was perpendicular to it. This suggested that different stacking sequences and layers can affect the temperature distribution around a flat plate. However, different stacking sequences had a certain impact on the performance of film cooling around the film hole. The maximum difference in the overall cooling efficiency was 1.7% between [0-90-0]₁ and [0-90]₁ and [0-90-90-0]₁. [0-90]₁ and [0-90-90-0]₁ showed similar distributions near the film hole. The influence of stacking layers on the performance of the film cooling was negligible.

5. Conclusions

This study measured the thermal conductivity of laminated composites and unidirectional composites of SiCf/SiC. The relationship of thermal conductivity between the laminated composite and the unidirectional composites was studied using the RVE model. Moreover, the influence of different stacking sequences and layers on the film-cooling performance over laminated composite plates was numerically investigated. The conclusions could be drawn as follows:

• The microscale RVE model predicted the thermal conductivity of SiC_f/SiC composites well. In the range of 373 K to 973 K, the thermal conductivity of SiC_f/SiC composites gradually decreased with increasing temperature, and the difference in out-of-plane thermal conductivity was slight. The in-plane thermal conductivity was about twice that in the thickness direction. The thermal conductivity in the fiber direction was about three times that in the transverse direction for the unidirectional SiC_f/SiC composites. At 373 K, the in-plane thermal conductivities of the laminated SiC_f/SiC composites were 22.4 W/(mK) and 24.0 W/(mK), and the out-of-plane thermal conductivity was 12.0 W/(mK). The thermal conductivities of the unidirectional SiC_f/SiC composites were 12.0 W/(mK) and 34.4 W/(mK).
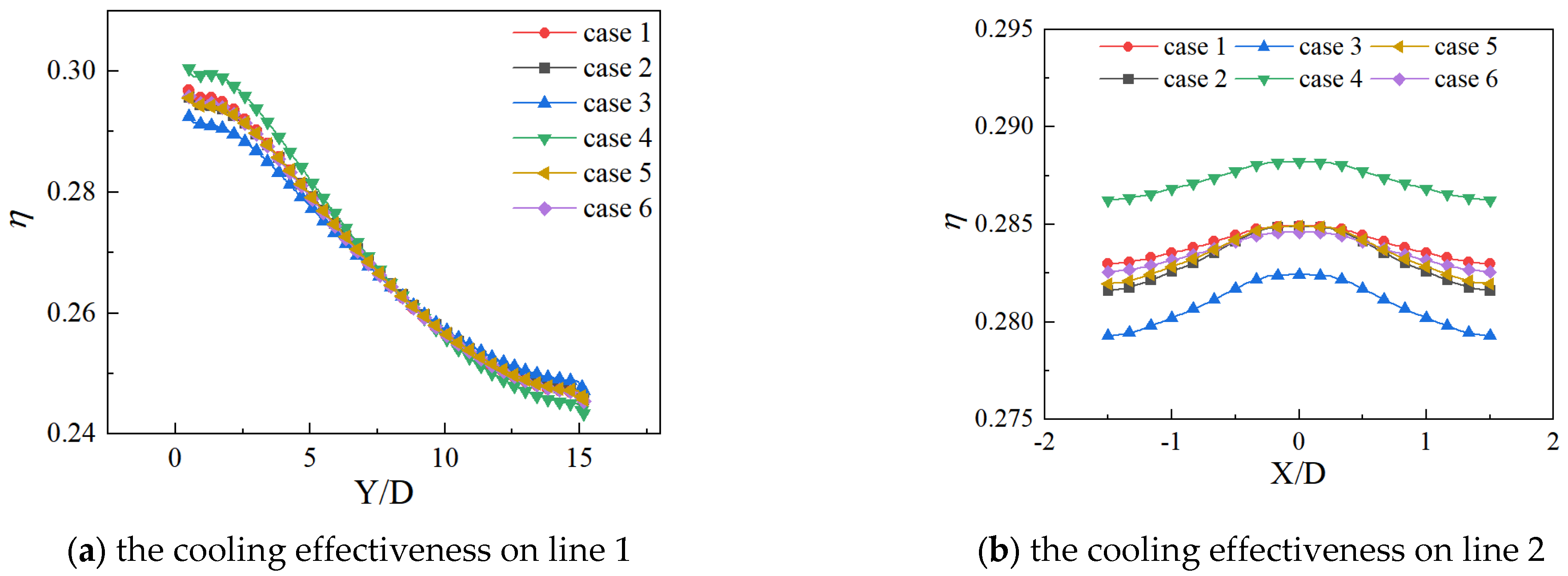
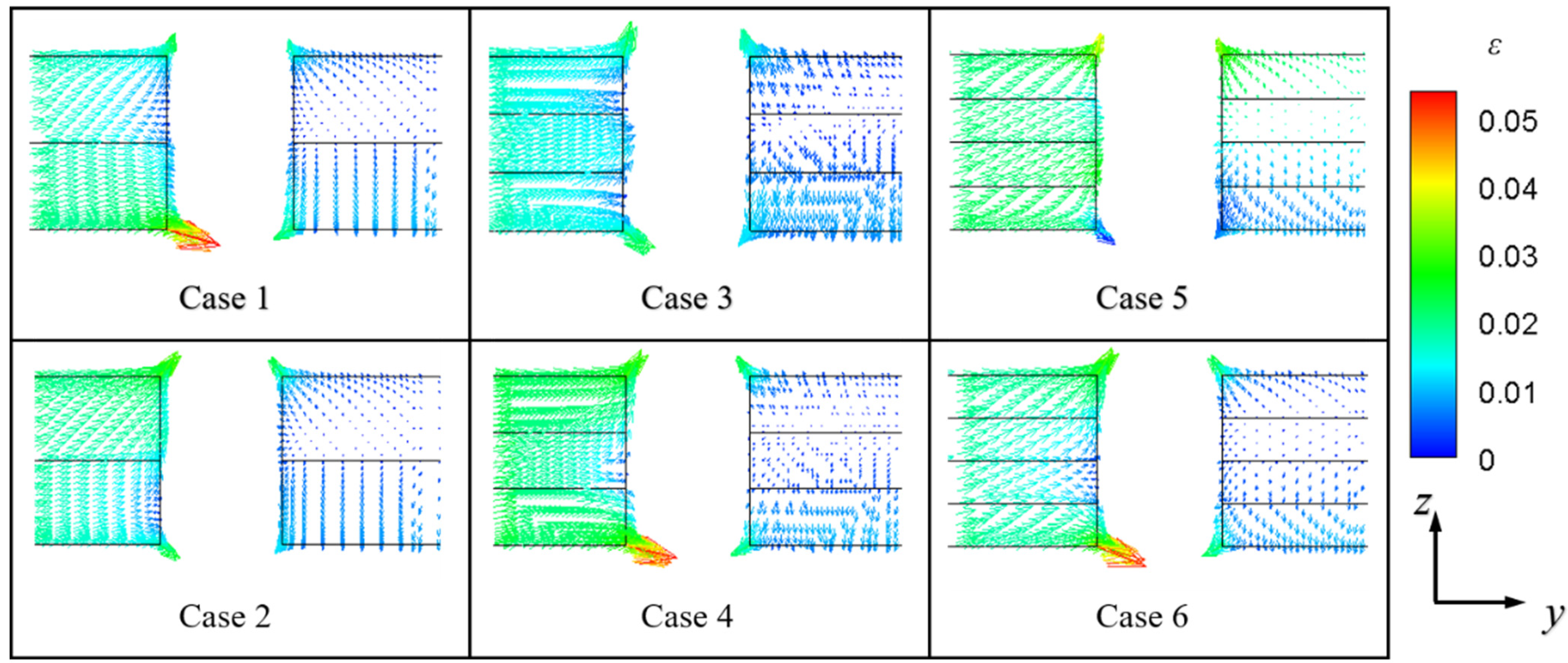
• The stacking sequence of the laminated SiC_f/SiC composites had a certain impact on the performance of film cooling around the film hole. [0-90]₁ and [0-90-90-0]₁ showed similar distributions near the film hole. The maximum difference in overall cooling efficiency was 1.7% between [0-90-0]₁ and [0-90]₁ and [0-90-90-0]₁. Additionally, the overall cooling efficiency of [0-90-0]₁ was sensitive to the flow direction. The distribution of the temperature was different in different stacking sequences near the film-cooling hole.
• The stacking layers of the laminated SiC_f/SiC composites were ignorable for the film cooling performance. The performance of the film cooling in the laminated SiCf/SiC composites was consistent across all stacking layers [0-90]₁, [0-90]₂, and [0-90]₃. Additionally, the overall cooling efficiency was insensitive to the flow direction. The distribution of temperature was different in [0-90]₁, [0-90]₂, and [0-90]₃ near the film-cooling hole.