A Multi-Objective Dynamic Mission-Scheduling Algorithm Considering Perturbations for Earth Observation Satellites
Abstract
1. Introduction
- A mathematical model for the multi-objective dynamic scheduling problem is formulated to maximize the observation profit and minimize the perturbation.
- A multi-objective dynamic mission-scheduling algorithm (MODMSA) is developed for the DMP-PP. To improve the diversity and quality of non-dominated solutions, a two-stage individual representation, a minimum perturbation random initialization, multi-point crossover, and greedy mutation are designed based on the characteristic of the DMP-PP. A profit-oriented local search algorithm is proposed to improved the profits of the solutions, and an adaptive perturbation control strategy is developed to enhance the exploitation in the solution space.
- The MODMSA is evaluated by extensive simulation experiments. The results demonstrate that the MODMSA outperforms other comparison algorithms especially in the diversity of non-dominated solutions.
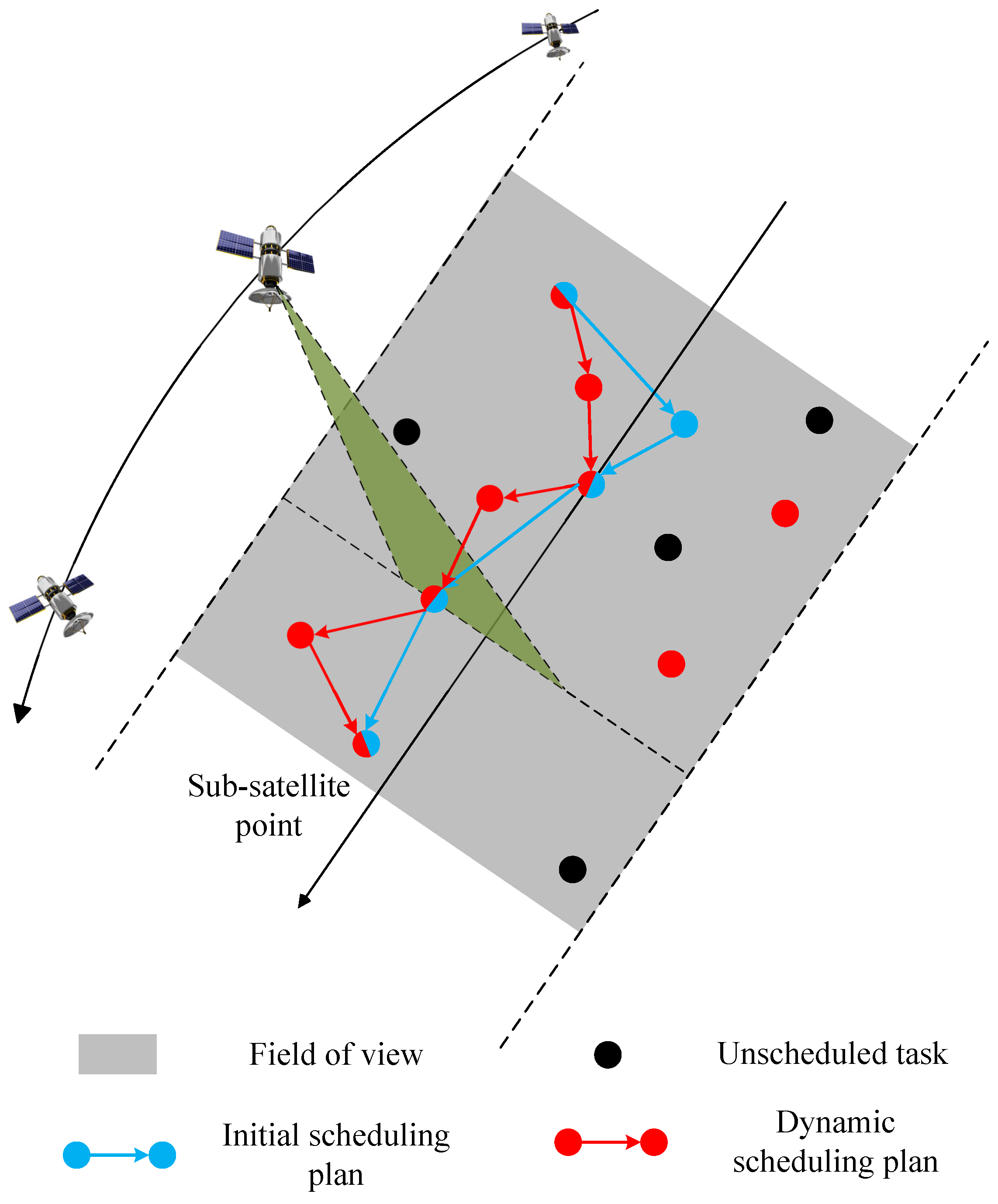
2. Problem Description
2.1. Variables
- : the location information of the mission including the latitude, longitude, and altitude.
- : the profit level, as defined by the Earth observation system, serves to reflect the importance of the mission. The profit level of the dynamic mission is usually higher than that of the static mission.
- : the required observation duration, which determines the size of the observed data.
- : the arrival time of the mission. The arrival time of the dynamic mission is randomly distributed over the scheduling horizon, while the arrival time of the static mission is considered the start time of the scheduling horizon.
- : the effective observation time window (ETW). and are the earliest effective observation time and the latest effective observation time of the mission. The observation for each mission must be completed within the ETW. Compared to the static missions, the ETW length of the dynamic missions is usually shorter because the dynamic missions have an urgent observation deadline.
- and : the start time and end time of VTW .
- and : the identifiers of the EOS and orbit for VTW
- , , and : the look angles for the roll, pitch, and yaw in VTW
- 1. Variance of the observation time within the same VTW.
- 2. Variance of the observation time among different VTWs.
- 3. Rejection.
- : a binary decision variable. is equal to 1 if and only if the mission is observed in VTW .
- : the observation start time of mission .
- : a binary decision variable for the observation order. represents that mission is observed immediately after task on orbit .
2.2. Assumptions
- Only the spot targets are considered in this paper, and the polygon targets can be viewed as multiple independent spot targets. Each spot target only needs to be observed with one pass.
- The dynamic missions are assumed to arrive in batch style, which indicates that dynamic scheduling is only triggered when a certain number of dynamic tasks are submitted, rather than being triggered by one or a few tasks.
- All Earth observation satellites have enough memory and power on each orbit.
- Relay satellites and ground stations are assumed to be sufficient resource to download all observation data. Therefore, the download scheduling for the observation data is not considered.
2.3. Mathematical Model
3. Multi-Objective Dynamic Mission Scheduling Algorithm (MODMSA)
3.1. Framework
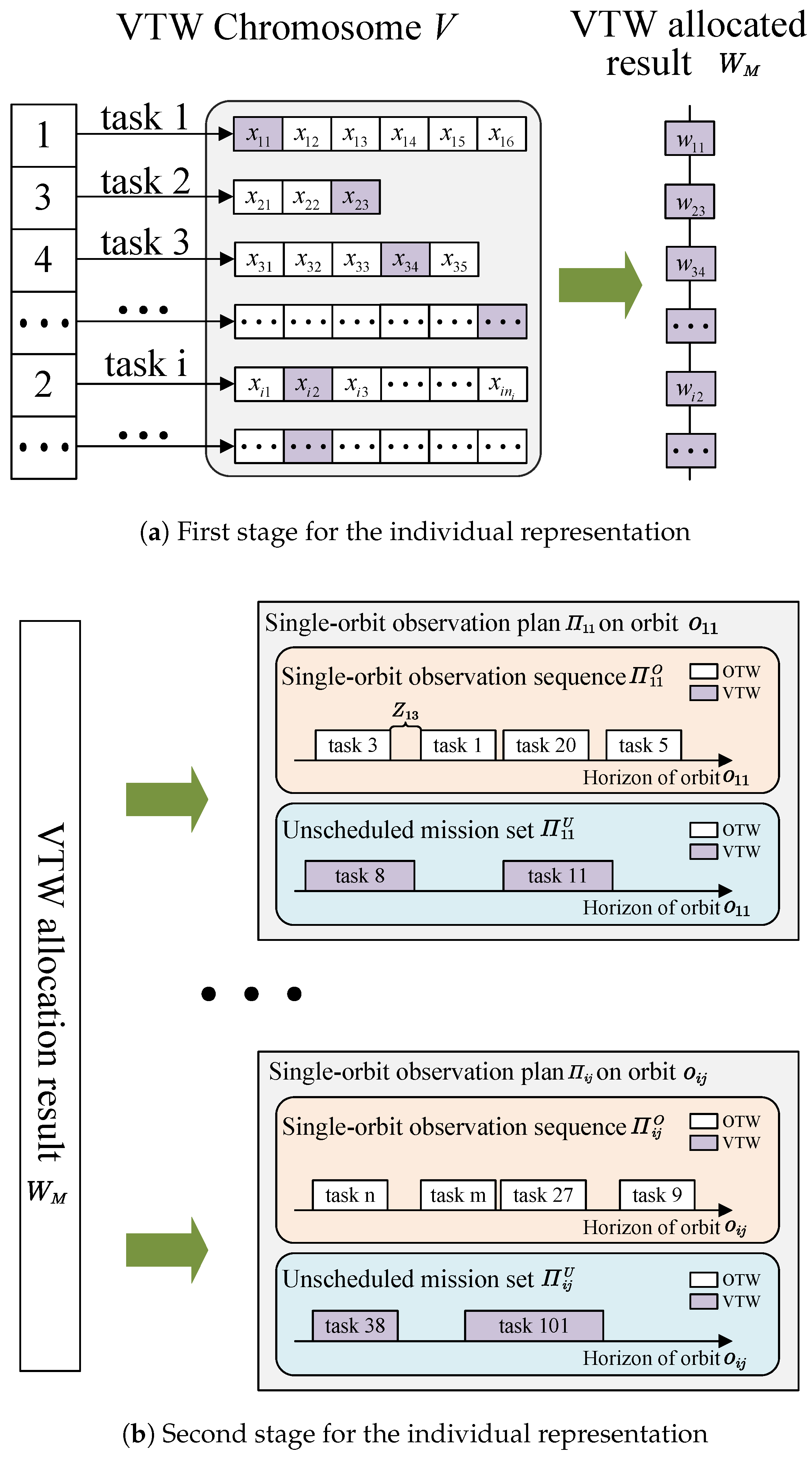
3.2. Two-Stage Individual Representation
3.3. Minimum Perturbation Random Initialization
3.4. Crossover and Mutation
3.5. Profit-Oriented Local Search Algorithm
| Algorithm 1 Profit-oriented local search algorithm. |
| Input: Single-orbit observation plan set , maximum iteration K |
| Output: Improved single-orbit observation plan set |
|
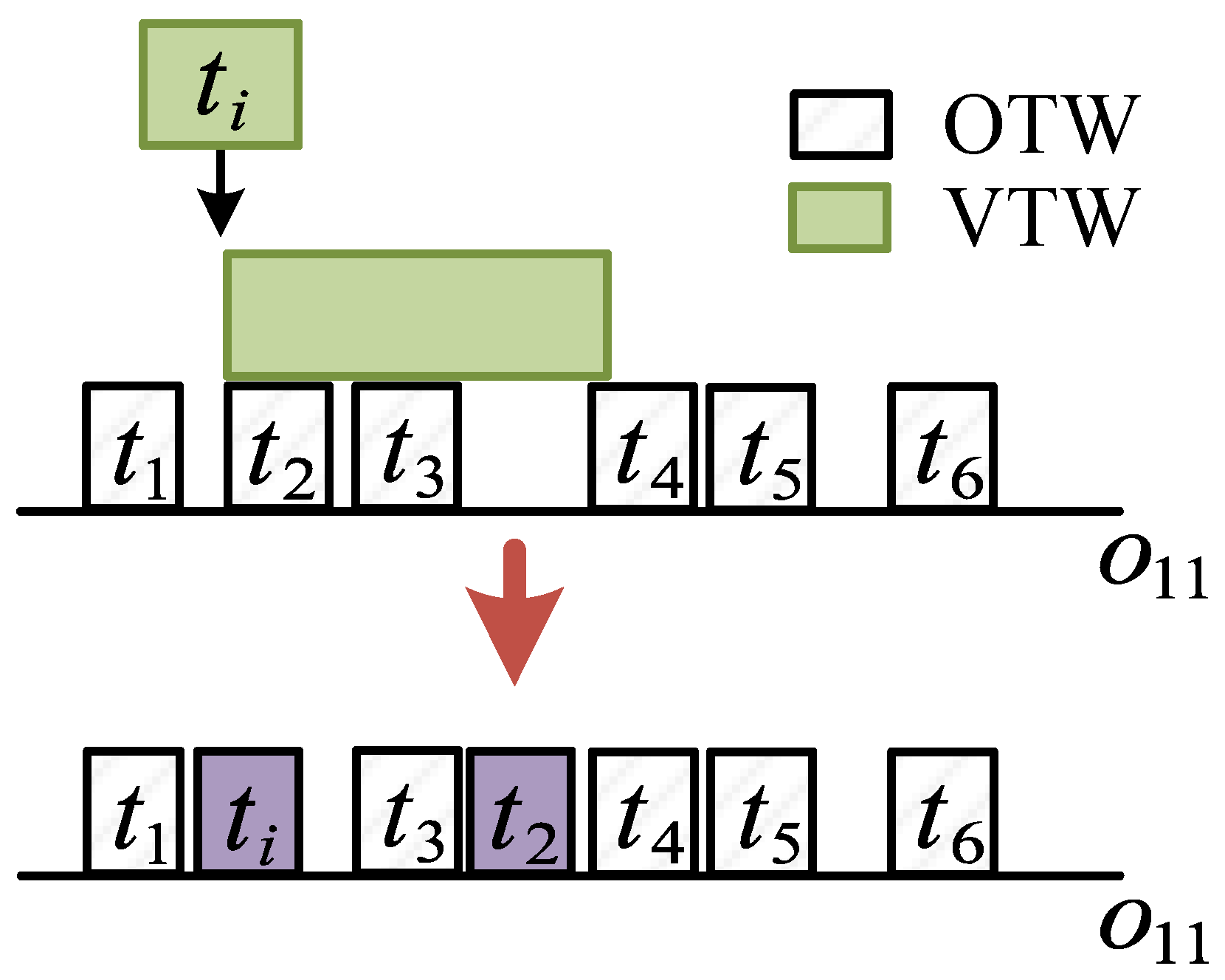
3.5.1. Destroy Operation
3.5.2. Repair Operation
3.6. Adaptive Perturbation Control Strategy
4. Results
4.1. Experimental Setting
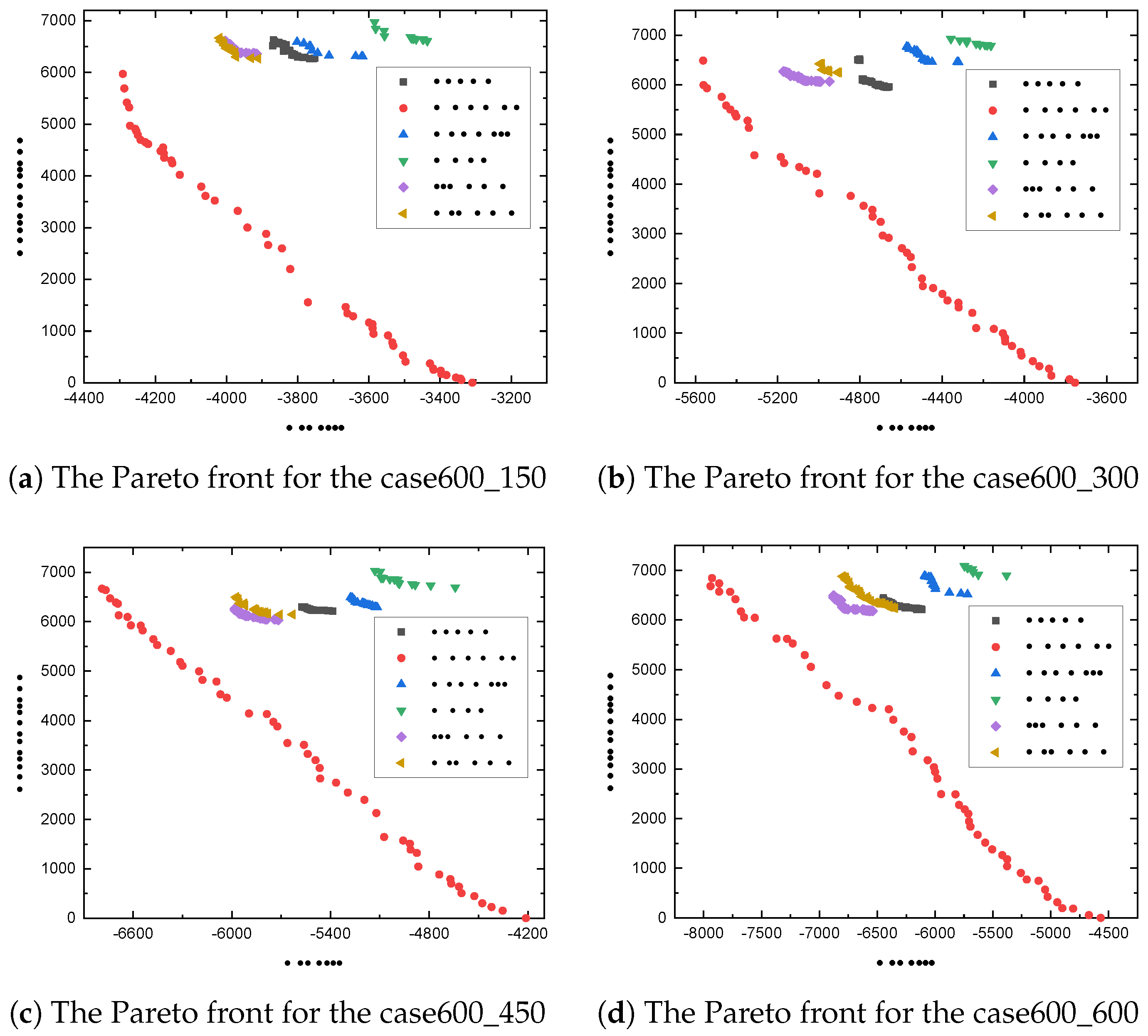
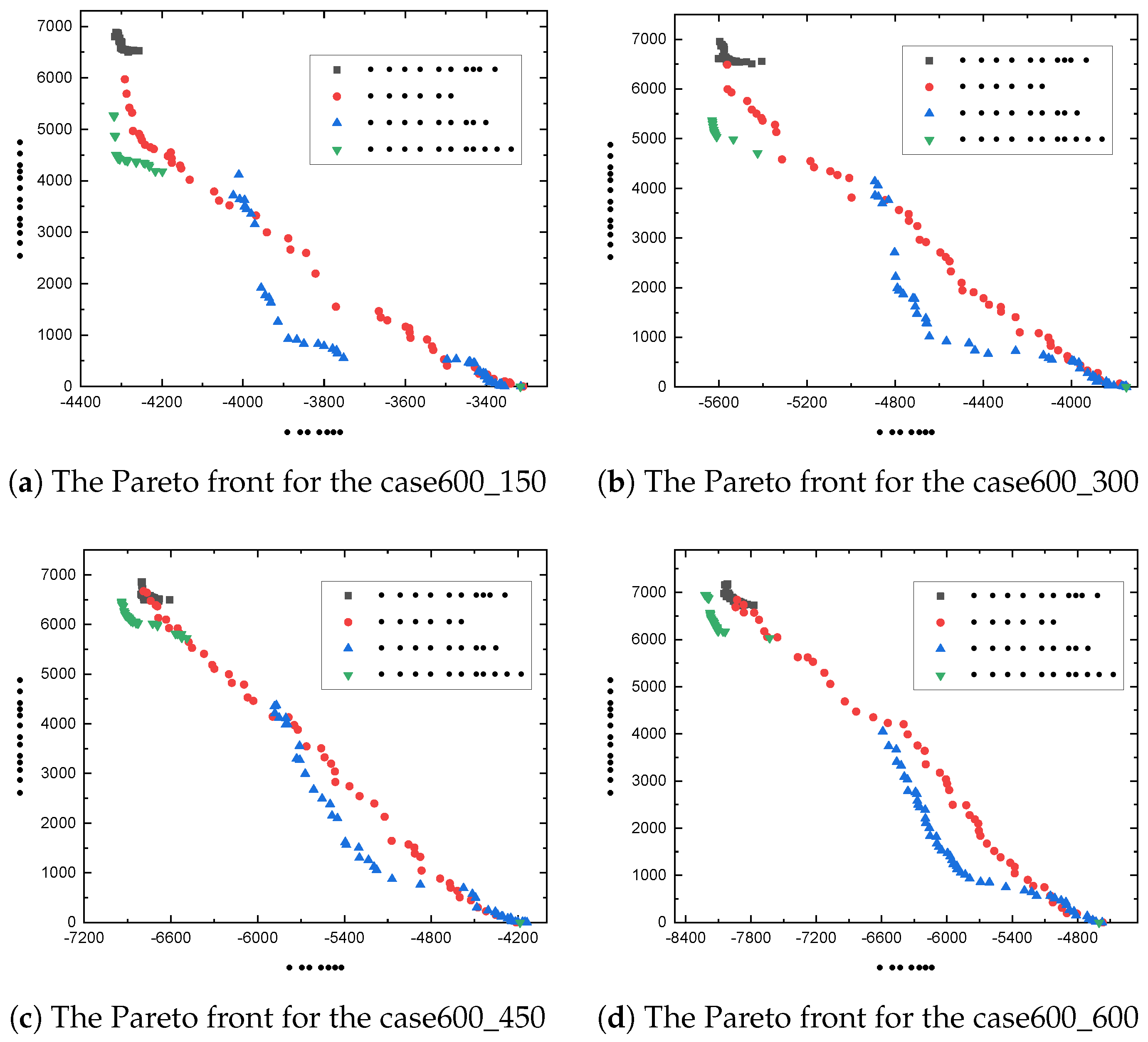
4.2. Experimental Results and Analysis
- MODMSA-INI, which applies the random initialization proposed in [44] and reserves the other procedures of the MODMSA.
- MODMSA-PPCS, which is a variant of the MODMSA, but without the adaptive perturbation control strategy.
- MODMSA-LS, which is a variant of the MODMSA, but without the profit-oriented local search algorithm.
5. Discussion
5.1. Efficiency of MODMSA in Solving Dynamic Mission Scheduling Problems
5.2. Effectiveness of Improvement Procedures
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, G.; Luo, Q.; Du, X.; Chen, Y.; Suganthan, P.N.; Wang, X. Ensemble of Meta-Heuristic and Exact Algorithm Based on the Divide and Conquer Framework for Multi-Satellite Observation Scheduling. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4396–4408. [Google Scholar] [CrossRef]
- Wu, J.; Song, B.; Zhang, G.; Ou, J.; Chen, Y.; Yao, F.; He, L.; Xing, L. A Data-Driven Improved Genetic Algorithm for Agile Earth Observation Satellite Scheduling with Time-Dependent Transition Time. Comput. Ind. Eng. 2022, 174, 108823. [Google Scholar] [CrossRef]
- Wang, X.; Han, C.; Zhang, R.; Gu, Y. Scheduling Multiple Agile Earth Observation Satellites for Oversubscribed Targets Using Complex Networks Theory. IEEE Access 2019, 7, 110605–110615. [Google Scholar] [CrossRef]
- Chu, X.; Chen, Y.; Xing, L. A Branch and Bound Algorithm for Agile Earth Observation Satellite Scheduling. Discret. Dyn. Nat. Soc. 2017, 2017, 7345941. [Google Scholar] [CrossRef]
- Chu, X.; Chen, Y.; Tan, Y. An Anytime Branch and Bound Algorithm for Agile Earth Observation Satellite Onboard Scheduling. Adv. Space Res. 2017, 60, 2077–2090. [Google Scholar] [CrossRef]
- Chen, X.; Reinelt, G.; Dai, G.; Spitz, A. A Mixed Integer Linear Programming Model for Multi-Satellite Scheduling. Eur. J. Oper. Res. 2019, 275, 694–707. [Google Scholar] [CrossRef]
- Valicka, C.G.; Garcia, D.; Staid, A.; Watson, J.; Hackebeil, G.; Rathinam, S.; Ntaimo, L. Mixed-Integer Programming Models for Optimal Constellation Scheduling given Cloud Cover Uncertainty. Eur. J. Oper. Res. 2019, 275, 431–445. [Google Scholar] [CrossRef]
- Lemaître, M.; Verfaillie, G.; Jouhaud, F.; Lachiver, J.-M.; Bataille, N. Selecting and Scheduling Observations of Agile Satellites. Aerosp. Sci. Technol. 2002, 6, 367–381. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, S.; Hao, Y.; Wang, Y. Energy-Dependent Mission Planning for Agile Earth Observation Satellite. J. Aerosp. Eng. 2019, 32, 04018118. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, L.; Cheng, J.; Zhou, J.; Wang, Y. Task Scheduling and Attitude Planning for Agile Earth Observation Satellite with Intensive Tasks. Aerosp. Sci. Technol. 2019, 90, 23–33. [Google Scholar] [CrossRef]
- Hao, H.; Jiang, W.; Li, Y. Improved Algorithms to Plan Missions for Agile Earth Observation Satellites. J. Syst. Eng. Electron. 2014, 25, 811–821. [Google Scholar] [CrossRef]
- Wu, G.; Wang, H.; Pedrycz, W.; Li, H.; Wang, L. Satellite Observation Scheduling with a Novel Adaptive Simulated Annealing Algorithm and a Dynamic Task Clustering Strategy. Comput. Ind. Eng. 2017, 113, 576–588. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, S.; Hu, H. A Simulated Annealing Algorithm with Tabu List for the Multi-Satellite Downlink Schedule Problem Considering Waiting Time. Aerospace 2022, 9, 235. [Google Scholar] [CrossRef]
- Han, C.; Gu, Y.; Wu, G.; Wang, X. Simulated Annealing-Based Heuristic for Multiple Agile Satellites Scheduling Under Cloud Coverage Uncertainty. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 2863–2874. [Google Scholar] [CrossRef]
- Wang, H.; Xu, M.; Wang, R.; Li, Y. Scheduling Earth Observing Satellites with Hybrid Ant Colony Optimization Algorithm. In Proceedings of the 2009 International Conference on Artificial Intelligence and Computational Intelligence, Shanghai, China, 7–8 November 2009; pp. 245–249. [Google Scholar]
- Du, B.; Li, S.; She, Y.; Li, W.; Liao, H.; Wang, H. Area Targets Observation Mission Planning of Agile Satellite Considering the Drift Angle Constraint. J. Astron. Telesc. Instrum. Syst. 2018, 4, 047002. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, E.; Wu, F.; Chang, Z.; Xing, L. Multi-Satellite Scheduling Problem with Marginal Decreasing Imaging Duration: An Improved Adaptive Ant Colony Algorithm. Comput. Ind. Eng. 2023, 176, 108890. [Google Scholar] [CrossRef]
- Cui, K.; Xiang, J.; Zhang, Y. Mission Planning Optimization of Video Satellite for Ground Multi-Object Staring Imaging. Adv. Space Res. 2018, 61, 1476–1489. [Google Scholar] [CrossRef]
- Liu, X.; Laporte, G.; Chen, Y.; He, R. An Adaptive Large Neighborhood Search Metaheuristic for Agile Satellite Scheduling with Time-Dependent Transition Time. Comput. Oper. Res. 2017, 86, 41–53. [Google Scholar] [CrossRef]
- Peng, G.; Vansteenwegen, P.; Liu, X.; Xing, L.; Kong, X. An Iterated Local Search Algorithm for Agile Earth Observation Satellite Scheduling Problem. In Proceedings of the 2018 SpaceOps Conference, Marseille, France, 28 May–1 June 2018. [Google Scholar]
- Peng, S.; Chen, H.; Du, C.; Li, J.; Jing, N. Onboard Observation Task Planning for an Autonomous Earth Observation Satellite Using Long Short-Term Memory. IEEE Access 2018, 6, 65118–65129. [Google Scholar] [CrossRef]
- Du, Y.; Wang, T.; Xin, B.; Wang, L.; Chen, Y.; Xing, L. A Data-Driven Parallel Scheduling Approach for Multiple Agile Earth Observation Satellites. IEEE Trans. Evol. Comput. 2020, 24, 679–693. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.; Meng, Q.Q.; Li, X.; Shao, L.; Zhao, S. An onboard periodic rescheduling algorithm for satellite observation scheduling problem with common dynamic tasks. Adv. Space Res. 2024, 73, 5242–5253. [Google Scholar] [CrossRef]
- Huang, Y.; Mu, Z.; Wu, S.; Cui, B.; Duan, Y. Revising the Observation Satellite Scheduling Problem Based on Deep Reinforcement Learning. Remote Sens. 2021, 13, 2377. [Google Scholar] [CrossRef]
- Wei, L.; Chen, Y.; Chen, M.; Chen, Y. Deep Reinforcement Learning and Parameter Transfer Based Approach for the Multi-Objective Agile Earth Observation Satellite Scheduling Problem. Appl. Soft Comput. 2021, 110, 107607. [Google Scholar] [CrossRef]
- He, Y.; Xing, L.; Chen, Y.; Pedrycz, W.; Wang, L.; Wu, G. A Generic Markov Decision Process Model and Reinforcement Learning Method for Scheduling Agile Earth Observation Satellites. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1463–1474. [Google Scholar] [CrossRef]
- Li, D.; Wang, M.; Dong, Z.; Shen, X.; Shi, L. Earth Observation Brain (EOB): An Intelligent Earth Observation System. Geo-Spat. Inf. Sci. 2017, 20, 134–140. [Google Scholar] [CrossRef]
- Lv, M.; Peng, X.; Xie, W.; Guan, N. Task Allocation for Real-Time Earth Observation Service with LEO Satellites. In Proceedings of the 2022 IEEE 43RD Real-Time Systems Symposium (RTSS 2022), Houston, TX, USA, 5–8 December 2022; pp. 14–26. [Google Scholar]
- Oddo, P.C.; Bolten, J.D. The Value of Near Real-Time Earth Observations for Improved Flood Disaster Response. Front. Environ. Sci. 2019, 7, 127. [Google Scholar] [CrossRef]
- Li, G.; Xing, L.; Chen, Y. A Hybrid Online Scheduling Mechanism with Revision and Progressive Techniques for Autonomous Earth Observation Satellite. Acta Astronaut. 2017, 140, 308–321. [Google Scholar] [CrossRef]
- Niu, X.; Tang, H.; Wu, L.; Deng, R.; Zhai, X. Imaging-Duration Embedded Dynamic Scheduling of Earth Observation Satellites for Emergent Events. Math. Probl. Eng. 2015, 2015, 731734. [Google Scholar] [CrossRef]
- Sun, H.; Xia, W.; Wang, Z.; Hu, X. Agile Earth Observation Satellite Scheduling Algorithm for Emergency Tasks Based on Multiple Strategies. J. Syst. Sci. Syst. Eng. 2021, 30, 626–646. [Google Scholar] [CrossRef]
- Wu, G.; Ma, M.; Zhu, J.; Qiu, D. Multi-Satellite Observation Integrated Scheduling Method Oriented to Emergency Tasks and Common Tasks. J. Syst. Eng. Electron. 2012, 23, 723–733. [Google Scholar] [CrossRef]
- Li, D.; Wang, H.; Zhen, Y.; Gu, Y.; Shi, S. An Online Distributed Satellite Cooperative Observation Scheduling Algorithm Based on Multiagent Deep Reinforcement Learning. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1901–1905. [Google Scholar] [CrossRef]
- Chen, H.; Luo, Z.; Peng, S.; Wu, J.; Li, J. HiPGen: An Approach for Fast Generation of Multi-Satellite Observation Plans via a Hierarchical Multi-Channel Transformer Network. Adv. Space Res. 2022, 69, 3103–3116. [Google Scholar] [CrossRef]
- Cui, J.; Zhang, X. Application of a Multi-Satellite Dynamic mission-scheduling Model Based on Mission Priority in Emergency Response. Sensors 2019, 19, 1430. [Google Scholar] [CrossRef]
- Wu, Q.; Pan, J.; Wang, M. Dynamic Task Planning Method for Multi-Source Remote Sensing Satellite Cooperative Observation in Complex Scenarios. Remote Sens. 2024, 16, 657. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, X.; Qiu, D.; Yang, L.T. Dynamic Scheduling for Emergency Tasks on Distributed Imaging Satellites with Task Merging. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 2275–2285. [Google Scholar] [CrossRef]
- Yang, X.; Hu, M.; Huang, G.; Li, A. A Hybrid Local Replanning Strategy for Multi-Satellite Imaging Mission Planning in Uncertain Environments. IEEE Access 2023, 11, 120780–120804. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm. Available online: https://www.semanticscholar.org/paper/SPEA2%3A-Improving-the-strength-pareto-evolutionary-Zitzler-Laumanns/b13724cb54ae4171916f3f969d304b9e9752a57f (accessed on 27 July 2024). [CrossRef]
- He, L.; Liu, X.; Laporte, G.; Chen, Y.; Chen, Y. An Improved Adaptive Large Neighborhood Search Algorithm for Multiple Agile Satellites Scheduling. Comput. Oper. Res. 2018, 100, 12–25. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Wei, L.; Xing, L.; Wan, Q.; Song, Y.; Chen, Y. A Multi-Objective Memetic Approach for Time-Dependent Agile Earth Observation Satellite Scheduling Problem. Comput. Ind. Eng. 2021, 159, 107530. [Google Scholar] [CrossRef]



| Satellite Parameters | Value |
|---|---|
| Semimajor axis (km) | 6678 |
| Inclination (°) | 96.576 |
| Right ascension of the ascending node (°) | 0, 18, 36 |
| 54, 72, 90 | |
| 108, 126 | |
| 144, 162 | |
| Eccentricity (°) | 0.000627 |
| Argument of perigee (°) | 0 |
| Mean anomaly (°) | 20, 38, 56 |
| 74, 92, 110 | |
| 128, 146 | |
| 164, 2 | |
| 5, 10, 16, 22 | |
| (°/s) | 1.5, 2, 2.5, 3 |
| Parameters related to the MODMSA | Value |
| Pop size | 100 |
| 200 | |
| , , | 2, 2, 1.5 |
| , | 1.5, 1.5 |
| 0.8 | |
| , , , | 0, 0.25 |
| 0.50, 0.75 | |
| , | 0.6, 0.4 |
| , | 0.2, 0.2 |
| Cases | MODMSA | SPEA2 | NSGA-II | MOEA/D | I-MOMA | D-MOMA |
|---|---|---|---|---|---|---|
| Case400_100 | 91.16 | 89.31 | 88.66 | 83.72 | 90.22 | 90.34 |
| Case400_200 | 90.84 | 87.38 | 85.86 | 79.05 | 88.86 | 88.67 |
| Case400_300 | 89.94 | 84.81 | 82.33 | 75.63 | 87.37 | 86.50 |
| Case400_400 | 89.83 | 81.03 | 80.60 | 72.97 | 85.53 | 84.05 |
| Case600_150 | 89.40 | 80.63 | 79.21 | 74.67 | 83.42 | 83.75 |
| Case600_300 | 88.29 | 76.33 | 72.57 | 69.16 | 82.10 | 79.29 |
| Case600_450 | 87.04 | 71.45 | 67.67 | 65.76 | 76.68 | 76.59 |
| Case600_600 | 85.38 | 69.32 | 65.49 | 61.78 | 73.97 | 73.12 |
| Case800_200 | 87.53 | 72.59 | 71.16 | 67.11 | 77.89 | 76.45 |
| Case800_400 | 84.85 | 65.19 | 64.44 | 61.23 | 71.12 | 71.33 |
| Case800_600 | 82.12 | 61.04 | 60.28 | 57.41 | 67.28 | 65.69 |
| Case800_800 | 79.65 | 56.70 | 55.56 | 52.90 | 61.31 | 61.17 |
| Cases | MODMSA | SPEA2 | NSGA-II | MOEA/D | I-MOMA | D-MOMA |
|---|---|---|---|---|---|---|
| Case400_100 | 0 | 3863 | 3820 | 4443 | 3871 | 3836 |
| Case400_200 | 0 | 3930 | 3947 | 4587 | 3983 | 3984 |
| Case400_300 | 0 | 3901 | 3968 | 4511 | 3868 | 3953 |
| Case400_400 | 0 | 3984 | 4001 | 4615 | 3901 | 4029 |
| Case600_150 | 0 | 6265 | 6304 | 6611 | 6359 | 6267 |
| Case600_300 | 0 | 5945 | 6456 | 6787 | 6064 | 6248 |
| Case600_450 | 0 | 6214 | 6291 | 6697 | 6031 | 6145 |
| Case600_600 | 0 | 6210 | 6514 | 6902 | 6180 | 6240 |
| Case800_200 | 0 | 8039 | 8076 | 8360 | 7906 | 7848 |
| Case800_400 | 0 | 7939 | 7979 | 8379 | 7867 | 7917 |
| Case800_600 | 0 | 8051 | 8043 | 8384 | 7960 | 8007 |
| Case800_800 | 0 | 8188 | 8292 | 8686 | 8225 | 8268 |
| Cases | MODMSA | SPEA2 | NSGA-II | MOEA/D | I-MOMA | D-MOMA |
|---|---|---|---|---|---|---|
| Case400_100 | 0.7605 | 0.1634 | 0.1597 | 0.0304 | 0.1722 | 0.1794 |
| Case400_200 | 0.7163 | 0.1722 | 0.1529 | 0.0299 | 0.1735 | 0.1709 |
| Case400_300 | 0.6751 | 0.1573 | 0.1292 | 0.0322 | 0.1798 | 0.1570 |
| Case400_400 | 0.6271 | 0.1317 | 0.1255 | 0.0261 | 0.1708 | 0.1387 |
| Case600_150 | 0.6528 | 0.0540 | 0.0445 | 0.0120 | 0.0595 | 0.0695 |
| Case600_300 | 0.5690 | 0.0796 | 0.0297 | 0.0066 | 0.0955 | 0.0667 |
| Case600_450 | 0.5381 | 0.0590 | 0.0422 | 0.0145 | 0.0922 | 0.0811 |
| Case600_600 | 0.4932 | 0.0686 | 0.0371 | 0.0120 | 0.0872 | 0.0759 |
| Case800_200 | 0.5382 | 0.0261 | 0.0188 | 0.0042 | 0.0472 | 0.0452 |
| Case800_400 | 0.4725 | 0.0311 | 0.0262 | 0.0087 | 0.0500 | 0.0448 |
| Case800_600 | 0.4381 | 0.0265 | 0.0285 | 0.0090 | 0.0436 | 0.0382 |
| Case800_800 | 0.4331 | 0.0312 | 0.0241 | 0.0076 | 0.0390 | 0.0356 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Li, Y.; Liu, Y.; Zhang, K.; Li, X.; Li, Y.; Zhao, S. A Multi-Objective Dynamic Mission-Scheduling Algorithm Considering Perturbations for Earth Observation Satellites. Aerospace 2024, 11, 643. https://doi.org/10.3390/aerospace11080643
Li H, Li Y, Liu Y, Zhang K, Li X, Li Y, Zhao S. A Multi-Objective Dynamic Mission-Scheduling Algorithm Considering Perturbations for Earth Observation Satellites. Aerospace. 2024; 11(8):643. https://doi.org/10.3390/aerospace11080643
Chicago/Turabian StyleLi, Hai, Yongjun Li, Yuanhao Liu, Kai Zhang, Xin Li, Yu Li, and Shanghong Zhao. 2024. "A Multi-Objective Dynamic Mission-Scheduling Algorithm Considering Perturbations for Earth Observation Satellites" Aerospace 11, no. 8: 643. https://doi.org/10.3390/aerospace11080643
APA StyleLi, H., Li, Y., Liu, Y., Zhang, K., Li, X., Li, Y., & Zhao, S. (2024). A Multi-Objective Dynamic Mission-Scheduling Algorithm Considering Perturbations for Earth Observation Satellites. Aerospace, 11(8), 643. https://doi.org/10.3390/aerospace11080643






