High-Precision Composite Control of Driving Current for Non-Contact Annular Electromagnetic Stabilized Spacecraft Subject to Multiple Disturbances

Abstract

Based on the design concept of dynamic and static isolation, disturbance-free payload (DFP) satellites can isolate the effects of interference on sensitive payloads, and can realize the high-precision control of the payload better than a traditional spacecraft. Among these, non-contact annular electromagnetic stabilized spacecraft (NCAESS) can effectively alleviate control output problems such as the six-degree-of-freedom coupling and nonlinear effects found in traditional non-contact spacecraft. As a key actuator, the driving current control of the non-contact annular electromagnetic actuator (NCAEA) will have a direct impact on the attitude performance of NCAESS. However, there are multiple interference effects present in the actual driving current control. Therefore, this paper proposes a composite control scheme to improve the driving accuracy by suppressing these multiple disturbances. Firstly, the variable-switching-frequency pulse-width modulation is used to adjust the switching frequency adaptively to reduce switch ripple. Secondly, feedforward compensation is employed to mitigate the back electromotive force. Thirdly, the robust Smith predictor is utilized to compensate for the digital control delay. Finally, an internal model proportional–integral controller with fuzzy rule is applied to adjust the parameters adaptively. The numerical simulation results demonstrate that the proposed approach can be adopted to enhance the robustness and dynamic response of the driving current effectively, which leads to precise control of the non-contact annular electromagnetic stabilized spacecraft.

1. Introduction

With the advancement of space technology, the next generation of space telescopes, high-resolution agile remote sensing, and gravitational wave detection missions impose higher demands on the attitude control performance of spacecraft [1,2,3]. In order to further improve the attitude control performance of spacecraft, based on the design concept of dynamic and static isolation, our research team has proposed the new concept of non-contact annular electromagnetic stabilized spacecraft (NCAESS), which effectively mitigates the problems of dynamic coupling and nonlinear effects that occur in traditional designs of non-contact spacecraft [4]. In previous studies, we have mainly focused on the influence of the control torque on the attitude of NCAESS. The precision of the torque is linearly related to the driving current of the non-contact annular electromagnetic actuator (NCAEA), the main actuator in NCAESS. In order to ensure the precision of the control torque and improve the control performance of NCAESS, the driving current control of NCAESS is investigated in this paper.

Through analysis, there are multiple disturbances in NCAESS, such as the current ripple that exists when switching power amplifiers are used [5], the back electromotive force generated by the relative motion of the two modules during the NCAESS control process [6], the time delay that exists when digital control is used [7], the time-varying effect of the power amplifiers, and the influence of noise [8]. In order to output precise driving current, it is necessary to use a suitable scheme to suppress the multiple disturbances and improve the robustness of the driving current control.

To address the current ripple problem in switching power amplifiers, traditional methods often involve increasing the switching frequency or using low-pass filters to reduce the magnitude of the current ripple [9]. However, increasing the switching frequency also increases the switching losses of the power amplifier, and to achieve better ripple suppression, low-pass filters require larger values of components such as inductors, which may reduce the dynamic response performance of the power amplifier [10]. J. Chen has introduced an improved active ripple eliminator to suppress the output current ripple of multi-phase buck converters. Experimental results demonstrate its effectiveness in attenuating ripple while preserving the fine-adjustment characteristics of the output voltage [11]. M. Dasohari proposes a driver based on a soft-switching parallel boost converter, showing that the parallel boost converter can be adopted to reduce the current ripple and can be applied in both high- and low-power scenarios [12]. Also, in terms of suppressing ripple by changing the switching frequency, Ref. [13] proposes a variable-switching-frequency pulse-width modulation technique to improve the switching loss, current ripple, and electromagnetic interference performance of power amplifiers.

To solve the problem of back electromotive force disturbance, F. Chen proposes an adaptive controller based on an RBF neural network to control a magnetic-levitation stable platform with back electromotive force disturbance, thereby improving the anti-interference ability of the platform [14]. J. Jeong analyzes the rotational motion error caused by the back electromotive force in magnetic-levitation systems and demonstrates that using a model-based feedforward compensation method can effectively suppress the rotational motion error induced by the back electromotive force [15].

To solve the problem of time delay caused by digital control, compensators are commonly constructed to reduce the effect of the delay. Delay-compensating technology can be classified into model-based technology, such as the robust Smith predictor; model predictive controllers; model-free technology; and so on [16]. J. Liu proposes an improved capacitor circuit by using multi-loop feedback current to mitigate the impact of delay on the network [17]. However, this multi-loop method requires the measurement of multiple state variables, which increases the complexity of the controller and reduces the reliability. Ref. [18] introduces a delay compensation method based on second-order generalized integrators to extend the stable region of a two-loop grid-current feedback control system. A. Katkout used a long-term prediction method to compensate the computational delays in multilevel inverter control loops [19]. S. Karan used a robust Smith predictor to eliminate the delay terms in the unstable control systems [20]. Through an analysis of the above literature, it is found that although model-free technology does not depend on the accuracy of the model, it struggles to fully compensate for the effects of time delays. Model-based technology is sensitive to the accuracy of system modeling. To better compensate for the effects of delay, the robust Smith predictor can be adopted to provide more advantages.

The actual control system is often affected by the combined influence of various forms of disturbances, which will reduce the stability and control effectiveness of the system. C. Jin proposes a composite layered disturbance-rejecting strategy, and combines an extended state observer, as well as the H_∞ controller, to improve the disturbance rejection capability of a magnetic-levitation rotor system with internal uncertainties and external disturbances [21]. S. Chen proposes a composite-structure adaptive compensation technique to improve the pointing precision of a gyroscope with high-frequency tilting flutter and sensor noise effects [22]. Ref. [23] discusses a composite control strategy for a small-inductance brushless DC motor affected by disturbances in the commutation and conduction regions. This strategy combines a BUCK converter, overlapping commutation control, an optimized duty cycle, asymmetric compensation functions, back electromotive force feedforward compensation, and an improved disturbance torque controller to achieve precise acceleration torque control. J. Zou proposes a composite control strategy that combines fuzzy PID control with a recursive least-squares technique to improve the convergence speed of the current [24]. Y. Liu proposes a composite control strategy that incorporates the robust Smith predictor, state observer compensation, and internal model nonlinear controllers to improve the tracking accuracy and positioning performance of a permanent-magnet synchronous-motor servo system affected by delays and external disturbances [25]. Through an analysis of the above literature, it can be concluded that composite control strategies exhibit a better control performance than single algorithms in the face of multiple disturbances.

Inspired by the above idea, a composite control scheme is proposed in this paper to suppress multiple disturbances and thus ensure the control performance of NCAESS. The main contributions of this paper are summarized as follows:

(1)

The proposed scheme suppresses the current ripple effectively without increasing the inductance value of the filter or adopting high switching frequencies. This preserves the dynamic response ability and reduces switching losses.

(2)

The closed-loop control adopts the internal model principle and fuzzy rules to adjust the parameters adaptively, enhancing the robustness and dynamic response capability of the driving current effectively.

(3)

The composite control algorithm can also suppress the disturbance effects caused by back electromotive force, time delay, time variance, and noise disturbance effectively, achieving precise control of the NCAESS.

The rest of this paper is organized as follows: In Section 2, the NCAESS configuration, dynamic model, and driving current scheme adopted in this article are described. The composite controller design of the NCAESS is discussed in Section 3. In Section 4, the effectiveness of the proposed composite control scheme is validated through simulation. Finally, Section 5 presents the conclusions of this paper.

2. Problem Statement

2.1. NCAESS Configuration

NCAESS has been proposed in our previous research to address the issues of dynamic coupling and nonlinear effects. The architectural design of an NCAESS is shown in Figure 1.

An NCAESS consists of two main modules: the payload module (PM) and the support module (SM). The PM is loaded with static load and its attitude is measured with a star sensor. The SM is similar to a traditional satellite platform with structures such as solar panels, and its attitude is controlled through actuators such as a flywheel and an attitude thruster. These two modules are connected by the NCAEA. The outer coil of the NCAEA is used not only to control the rotation of the PM along the x-axis and y-axis but also to control the relative displacement between the PM and SM along the z-axis. A three-dimensional model of the outer coil is shown in Figure 2. The inner coil of the NCAEA is designed as a double-loop structure. The upper-loop coil is adopted to control the relative translation of the two modules along the x-axis and y-axis, while the lower-loop coil is adopted to control the rotation of the PM along the z-axis. A three-dimensional model of the inner coil is shown in Figure 3.

For the outer coil, as shown in Figure 2, the minimum norm allocation is adopted to generate the control input, which can be written as follows:

$$\left[\begin{array}{c}{T}_x\\ T_y\\ F_{zt}\end{array}\right]=\left[\begin{array}{cccc}{r}_h& -r_h& 0& 0\\ 0& 0& r_h& -r_h\\ 1& 1& 1& 1\end{array}\right]\left[\begin{array}{c}{F}_{y+}\\ F_{y-}\\ F_{x-}\\ F_{x+}\end{array}\right]$$

(1)

where r_h is the annular radius of the outer coil; T_x and T_y are the attitude control torque of the PM, deflecting around the x- and y-axes, respectively; and F_x+, F_x−, F_y+, F_y− represent the Lorentz force generated by a₁b₁c₁d₁, a₂b₂c₂d₂, m₁n₁p₁q₁, and m₂n₂p₂q₂, respectively, as shown in Equation (2):

$$\left\{\begin{array}{c}{F}_{x+}=F_{a_1{b}_1}+F_{c_1{d}_1}=N_h{B}_h{i}_{a_1{b}_1{c}_1{d}_1}({\displaystyle {\int }_{-\frac{\alpha }{2}}^{\frac{\alpha }{2}}{r}_{h}d\alpha }+{\displaystyle {\int }_{-\frac{\alpha }{2}}^{\frac{\alpha }{2}}{r}_{h}d\alpha })=2N_h{B}_h\alpha r_h{i}_{a_1{b}_1{c}_1{d}_1}\\ F_{x-}=F_{a_2{b}_2}+F_{c_2{d}_2}=N_h{B}_h{i}_{a_2{b}_2{c}_2{d}_2}({\displaystyle {\int }_{-\frac{\alpha }{2}}^{\frac{\alpha }{2}}{r}_{h}d\alpha }+{\displaystyle {\int }_{-\frac{\alpha }{2}}^{\frac{\alpha }{2}}{r}_{h}d\alpha })=2N_h{B}_h\alpha r_h{i}_{a_2{b}_2{c}_2{d}_2}\\ F_{y+}=F_{m_1{n}_1}+F_{p_1{q}_1}=N_h{B}_h{i}_{m_1{n}_1{p}_1{q}_1}({\displaystyle {\int }_{-\frac{\alpha }{2}}^{\frac{\alpha }{2}}{r}_{h}d\alpha }+{\displaystyle {\int }_{-\frac{\alpha }{2}}^{\frac{\alpha }{2}}{r}_{h}d\alpha })=2N_h{B}_h\alpha r_h{i}_{m_1{n}_1{p}_1{q}_1}\\ F_{y-}=F_{m_2{n}_2}+F_{p_2{q}_2}=N_h{B}_h{i}_{m_2{n}_2{p}_2{q}_2}({\displaystyle {\int }_{-\frac{\alpha }{2}}^{\frac{\alpha }{2}}{r}_{h}d\alpha }+{\displaystyle {\int }_{-\frac{\alpha }{2}}^{\frac{\alpha }{2}}{r}_{h}d\alpha })=2N_h{B}_h\alpha r_h{i}_{m_2{n}_2{p}_2{q}_2}\end{array}\right.$$

(2)

where B_h is the outer magnetic intensity; N_h is the outer-coil turns; α is the angle of the entire circumference occupied by the coil; and $i_{a_1{b}_1{c}_1{d}_1}$, $i_{a_2{b}_2{c}_2{d}_2}$, $i_{m_1{n}_1{p}_1{q}_1}$, $i_{m_2{n}_2{p}_2{q}_2}$ represent the corresponding current coil.

For the inner coil, as shown in Figure 3, the attitude control torque of the PM along the z-axis and the control force between the two modules along the x-axis and y-axis can be written as follows:

$$T_z=4r_p{N}_p{B}_p{l}_2{i}_{zr}$$

(3)

$$F_{xt}=2N_p{B}_p{l}_1{i}_{xt}$$

(4)

$$F_{yt}=2N_p{B}_p{l}_1{i}_{yt}$$

(5)

where B_p is the inner magnetic intensity; N_p is the inner-coil turns; r_p is the force arm; and l₁, l₂ represent the upper and lower working lengths, respectively.

2.2. Dynamic Model

According to Equations (1)–(5), the magnetic field of the NCAESS in this article can be reasonably designed to ensure its good uniformity; therefore, it can be seen that the precision of the control input in the NCAESS is linear to the driving current. In order to ensure the control performance of the NCAESS, this paper conducts research on its driving current control. The proposed switching power amplifier of the NCAESS is shown in Figure 4, which is composed of a BUCK circuit and an H-bridge circuit in series. The BUCK circuit is responsible for adjusting the voltage, while the H-bridge is responsible for changing the direction of the coil current.

For the driving topology adopted in this paper, there are two power circuit states in a switching cycle T_p: the charging interval and the freewheeling interval. The charging interval is shown in Figure 5.

According to Kirchhoff’s current law, the power amplifier model in the charging interval can be written as follows:

$$\left\{\begin{array}{c}{U}_j=L_1{\displaystyle \frac{d{i}_{Lj}(t)}{dt}}+L_{Xj}{\displaystyle \frac{d{i}_{Xj}(t)}{dt}}+R_{Xj}{i}_{Xj}(t)+E_{bj}(t)\hfill \\ i_{Lj}(t)=i_{Xj}(t)+i_{Cj}(t)\hfill \\ {\displaystyle \frac{1}{C_1}}{\displaystyle {\int }_0^t{i}_{Cj}dt=L_{Xj}\frac{d{i}_{Xj}(t)}{dt}+R_{Xj}{i}_{Xj}(t)+E_{bj}(t)}\hfill \end{array}\right.$$

(6)

where U is the power supply voltage; L₁ is the value of the filter inductor; C₁ is the value of the capacitor; R_Xj, L_Xj (j = a₁b₁c₁d₁, a₂b₂c₂d₂, m₁n₁p₁q₁, m₂n₂p₂q₂, zr, xt, yt) represent the equivalent resistance and the inductance value of each coil, respectively; i_Lj(t) represents the current of the filter inductor L₁ in the power amplifier connected to each coil; i_Xj(t) is the current flowing through each coil; i_Cj(t) represents the current flowing through the filter capacitor C₁ of each power amplifier; and E_bj(t) represents the magnitude of the back electromotive force through each coil. Therefore, the state-space equations of the power amplifier during the charging interval can be written as follows:

$$L_1{C}_1{L}_{Xj}{\displaystyle \frac{d^3{i}_{Xj}(t)}{d{t}^3}}+L_1{C}_1{R}_{Xj}{\displaystyle \frac{d^2{i}_{Xj}(t)}{d{t}^2}}+(L_1+L_{Xj}){\displaystyle \frac{d{i}_{Xj}(t)}{dt}}+R_{Xj}{i}_{Xj}(t)=U-E_{bj}(t)-L_1{C}_1{\displaystyle \frac{d^2{E}_{bj}(t)}{d{t}^2}}$$

(7)

While the power amplifier is in the freewheeling state, as shown in Figure 6, according to Kirchhoff’s current law, the power amplifier model can be written as Equation (8):

$$\left\{\begin{array}{c}0=L_1{\displaystyle \frac{d{i}_{Lj}(t)}{dt}}+L_{Xj}{\displaystyle \frac{d{i}_{Xj}(t)}{dt}}+R_{Xj}{i}_{Xj}(t)+E_{bj}(t)+V_{Dj}\hfill \\ i_{Lj}(t)=i_{Xj}(t)+i_{Cj}(t)\hfill \\ {\displaystyle \frac{1}{C_1}}{\displaystyle {\int }_0^t{i}_{Cj}dt=L_{Xj}\frac{d{i}_{Xj}(t)}{dt}+R_{Xj}{i}_{Xj}(t)+E_{bj}(t)}\hfill \end{array}\right.$$

(8)

where V_Dj is the voltage drop through the diode in each power amplifier.

Therefore, the state-space equations of the power amplifier during the freewheeling interval can be written as follows:

$$\begin{array}{l}{L}_1{C}_1{L}_{Xj}{\displaystyle \frac{d^3{i}_{Xj}(t)}{d{t}^3}}+L_1{C}_1{R}_{Xj}{\displaystyle \frac{d^2{i}_{Xj}(t)}{d{t}^2}}+(L_1+L_{Xj}){\displaystyle \frac{d{i}_{Xj}(t)}{dt}}+R_{Xj}{i}_{Xj}(t)\\ =-V_{Dj}-E_{bj}(t)-L_1{C}_1{\displaystyle \frac{d^2{E}_{bj}(t)}{d{t}^2}}\end{array}$$

(9)

According to the state-space averaging method, the average state-space equation of the power amplifier can be obtained using Equation (7) × D_Zj(t) + Equation (9) × (1 − D_Zj(t)); thus, we obtain the following:

$$\begin{array}{l}{L}_1{C}_1{L}_{Xj}{\displaystyle \frac{d^3{i}_{Xj}(t)}{d{t}^3}}+L_1{C}_1{R}_{Xj}{\displaystyle \frac{d^2{i}_{Xj}(t)}{d{t}^2}}+(L_1+L_{Xj}){\displaystyle \frac{d{i}_{Xj}(t)}{dt}}+R_{Xj}{i}_{Xj}(t)\\ =D_{Zj}(t)U+[D_{Zj}(t)-1]V_{Dj}-E_{bj}(t)-L_1{C}_1{\displaystyle \frac{d^2{E}_{bj}(t)}{d{t}^2}}\end{array}$$

(10)

where D_Zj(t) represents the duty cycle for the current control of each coil. Considering a time delay τ in the digital signal control of each coil’s driving current in the NCAESS, the relationship between the control quantity Dj(t) for each channel and the duty cycle D_Zj(t) can be written as follows:

$$D_{Zj}(t)={\displaystyle \frac{1}{V_{tri}}}{D}_j(t-{\tau }_j)$$

(11)

where V_tri represents the amplitude of the triangular carrier wave.

In this paper, the amplitude of the triangular carrier wave is chosen to be 1. In practical scenarios, [D_zj(t) − 1]V_Dj $\ll$ D_zj(t)U − E_bj(t) − L₁C₁d²E_bj(t)/dt², the average state-space equation of the power amplifier can be obtained as follows:

$$\begin{array}{l}{L}_1{C}_1{L}_{Xj}{\displaystyle \frac{d^3{i}_{Xj}(t)}{d{t}^3}}+L_1{C}_1{R}_{Xj}{\displaystyle \frac{d^2{i}_{Xj}(t)}{d{t}^2}}+(L_1+L_{Xj}){\displaystyle \frac{d{i}_{Xj}(t)}{dt}}+R_{Xj}{i}_{Xj}(t)\\ =D_j(t-{\tau }_j)U-E_{bj}(t)-L_1{C}_1{\displaystyle \frac{d^2{E}_{bj}(t)}{d{t}^2}}\end{array}$$

(12)

2.3. Driving Current Scheme

Based on the power amplifier model described above, in order to achieve a precise driving current performance, this paper adopts a composite control scheme to design the NCAESS control system, as shown in Figure 7. The entire control system is divided into four parts: the expected current solution of the outer and inner coils, the composite control algorithm, the switching power amplifier, and the NCAESS. The control system first uses the current calculation module to calculate the expected current of each coil based on the position control torque and translation control force calculated by the PM attitude controller and the relative position controller. Second, the switching power amplifier is controlled by a composite control scheme consisting of variable-switching-frequency pulse-width modulation (VSFPWM), feedforward compensation, robust Smith prediction (RSP), and an internal model proportional–integral (PI) controller with fuzzy rule to achieve high-precision driving current control. Finally, the Lorentz force generated by the driving current and the magnetic field controls the movement of the NCAESS, and the PM attitude $\theta$_pok(k = x,y,z) and the relative position r_spk act as feedback to the PM attitude controller and the relative position controller.

Most of the previous studies only considered the influence of partial disturbances, but there is a comprehensive influence of multiple disturbances in the actual driving current control. Based on the consideration of multiple disturbances, this paper investigates the feasibility of the combined application of VSFPWM, feedforward compensation, RSP, fuzzy control, and PI control. In this process, PI control uses the internal model principle to improve the PI algorithm, further simplifies the difficulty of PI algorithm parameter setting, and effectively inhibits multiple disturbances through the combination of these algorithms. Although many disturbance factors are considered in the composite control scheme designed in this paper, the algorithms involved in pulse-width modulation (PWM), feedforward compensation, Smith prediction, fuzzy control, and PI control are all commonly used in engineering and have the advantages of being simple and reliable. In this paper, some improvements are made to these algorithms, which retain the advantageous stability and reliability of the original algorithms while improving the overall control performance without increasing the complexity too much.

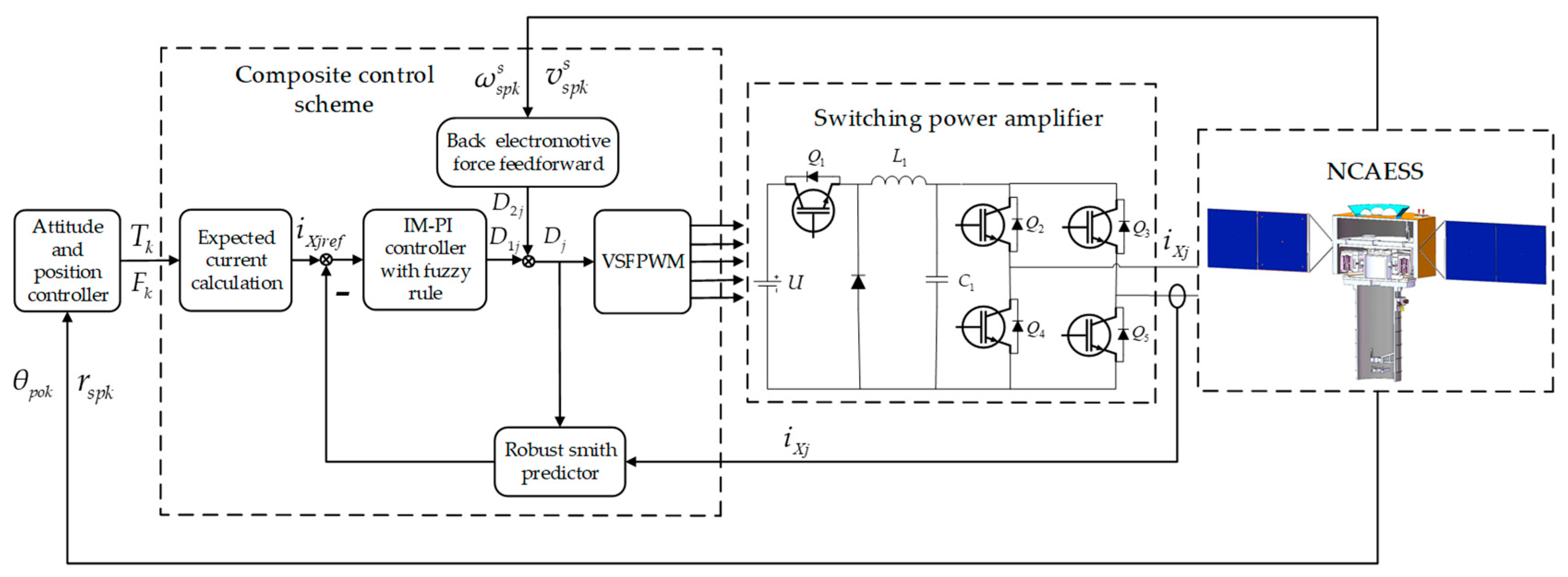
3. Composite Controller Design

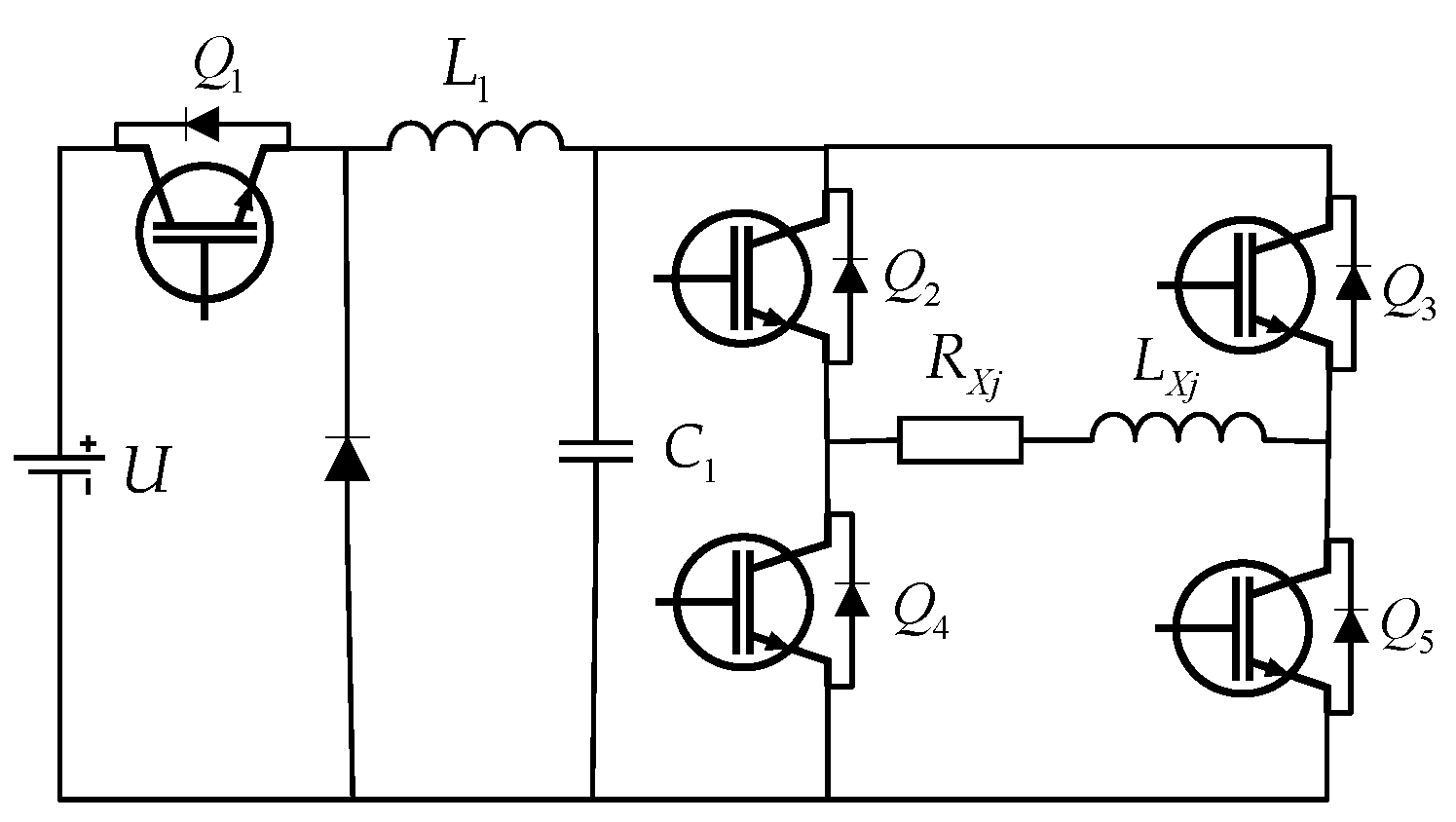
3.1. VSFPWM Based on Current Ripple Prediction

Compared with linear power amplifiers, switching power amplifiers are widely used in driving circuits due to their advantageous high efficiency. However, switching power amplifiers suffer from the current ripple problem, which can reduce the output precision of the driving current. According to Kirchhoff’s current law, the current ripple on the coil is positively correlated with the current ripple on the filter inductor of the power amplifier.

Considering the topology of the power amplifier shown in Figure 4, assuming that the switching frequency is much higher than the fundamental frequency, and that the capacitor C₁ in the BUCK voltage regulator can make the driving current ignore the influence of voltage ripple, the fundamental component of the voltage between the two poles of a power amplifier is equal to the duty cycle multiplied by the power supply voltage U(t). The current ripple on the filter inductor of the power amplifier can be represented as follows:

$${\displaystyle \frac{\Delta I_{Lj}}{D_{Zj}(t-{\tau }_j)T_{sj}}}={\displaystyle \frac{U-U_{oj}-[D_{Zj}(t-{\tau }_j)U-U_{oj}]}{L_1}}$$

(13)

$$\Delta I_{Lj}={\displaystyle \frac{[U-D_j(t-{\tau }_j)U]D_j(t-{\tau }_j)T_{sj}}{L_1}}={\displaystyle \frac{U}{L_1{f}_{sj}}}[D_j(t-{\tau }_j)-{D_j}^2(t-{\tau }_j)]$$

(14)

where U_oj represents the voltage across the terminals of each coil in the NCAESS; D_j(t) is the modulation wave amplitude output by the driving current controller of each coil, having a range of 0 ≤ D_j(t) ≤ 1; T_sj stands for the triangular carrier switching period of each driving current controller; and f_sj is the triangular carrier switching frequency.

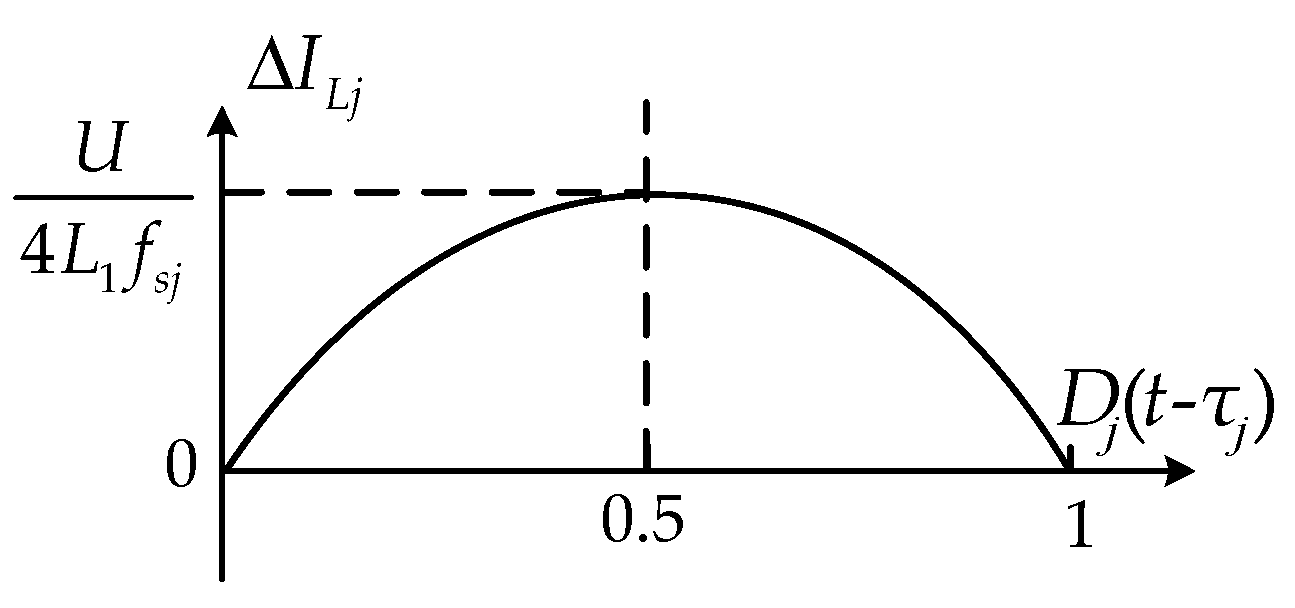
According to Equation (14), it can be seen that the amount of current ripple on the filter inductor is related to the modulation wave amplitude (i.e., the duty cycle), the triangular carrier frequency, and the filter inductor value. The current ripple decreases as the triangular carrier frequency and inductance value increase, while the current ripple and modulation wave amplitude have a nonlinear relationship, as shown in Figure 8. When the modulation wave amplitude is 0.5, that is, when the duty cycle is 50%, the ripple is the largest. When the modulation wave amplitude is larger or smaller than 0.5, the ripple also decreases.

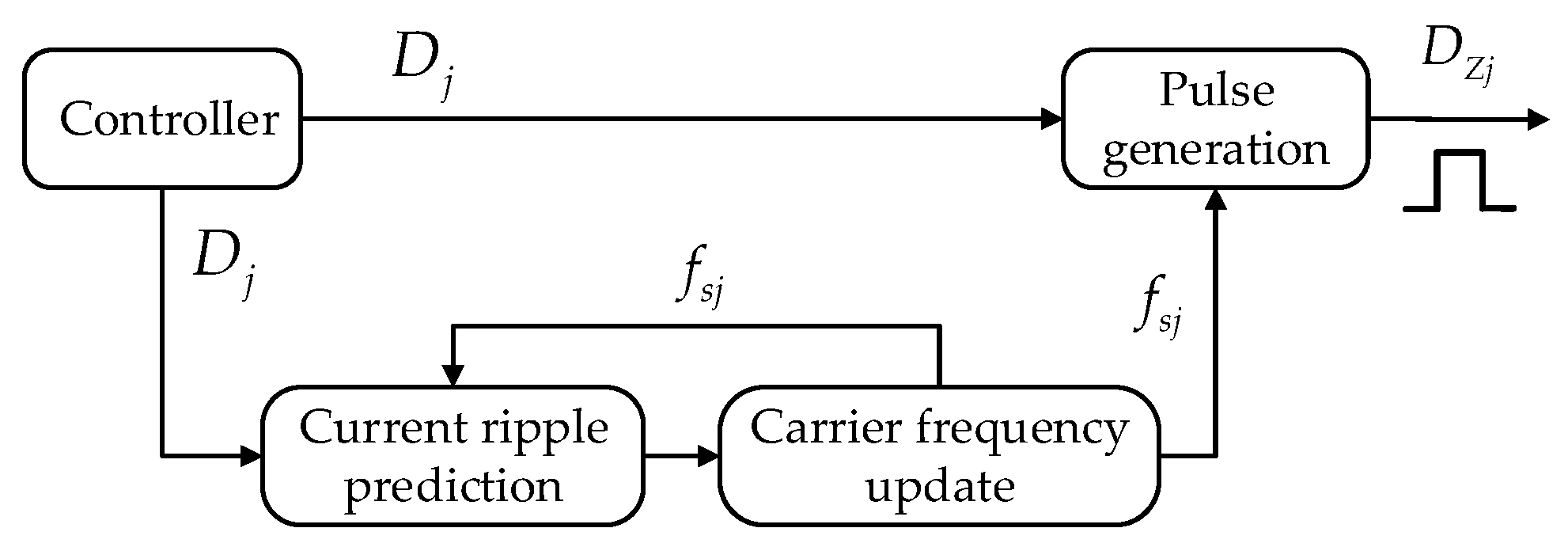
From the above analysis, it can be seen that when the current ripple changes with the change in duty cycle, the current ripple can be reduced by increasing the inductance value or triangular carrier frequency, which is also the traditional method. However, increasing the inductance value is not conducive to the dynamic response capability of the system, and increasing the triangular carrier frequency will aggravate the switching loss. Therefore, this paper predicts the current ripple according to the modulation amplitude and adjusts the triangular carrier frequency adaptively by using the VSFPWM algorithm to control the power amplifier switching element, as shown in Figure 9. According to the NCAESS precision requirements for current ripple, the VSFPWM algorithm updates the triangular carrier switching frequency online, and compares the updated triangular carrier with the modulated wave to generate the pulse that drives the power switching element.

The current ripple value after updating the switching frequency and the calculation of the switching frequency update can be written as follows:

$$\Delta I_{Lj\_update}={\displaystyle \frac{\Delta I_{Lj\_predicted}{f}_{sj\_last}}{f_{sj}}}$$

(15)

$$f_{sj}={\displaystyle \frac{f_{sj\_last}\Delta I_{Lj\_predicted}}{\Delta I_{Lj\_require}}}$$

(16)

where f_{sj_last} is the frequency of the triangular carrier before the frequency update; and ΔI_{Lj_predicted} represents the predicted current ripple value on the filter inductor based on the previous switching frequency in each switching power amplifier. At the same time, the updated triangular carrier frequency is set to no less than 10 kHz in order to ensure normal current control at a low duty ratio. The predicted current ripple value is given as follows:

$$\Delta I_{Lj\_predicted}={\displaystyle \frac{U}{L_1{f}_{sj\_last}}}[D_j(t-{\tau }_j)-{D_j}^2(t-{\tau }_j)]$$

(17)

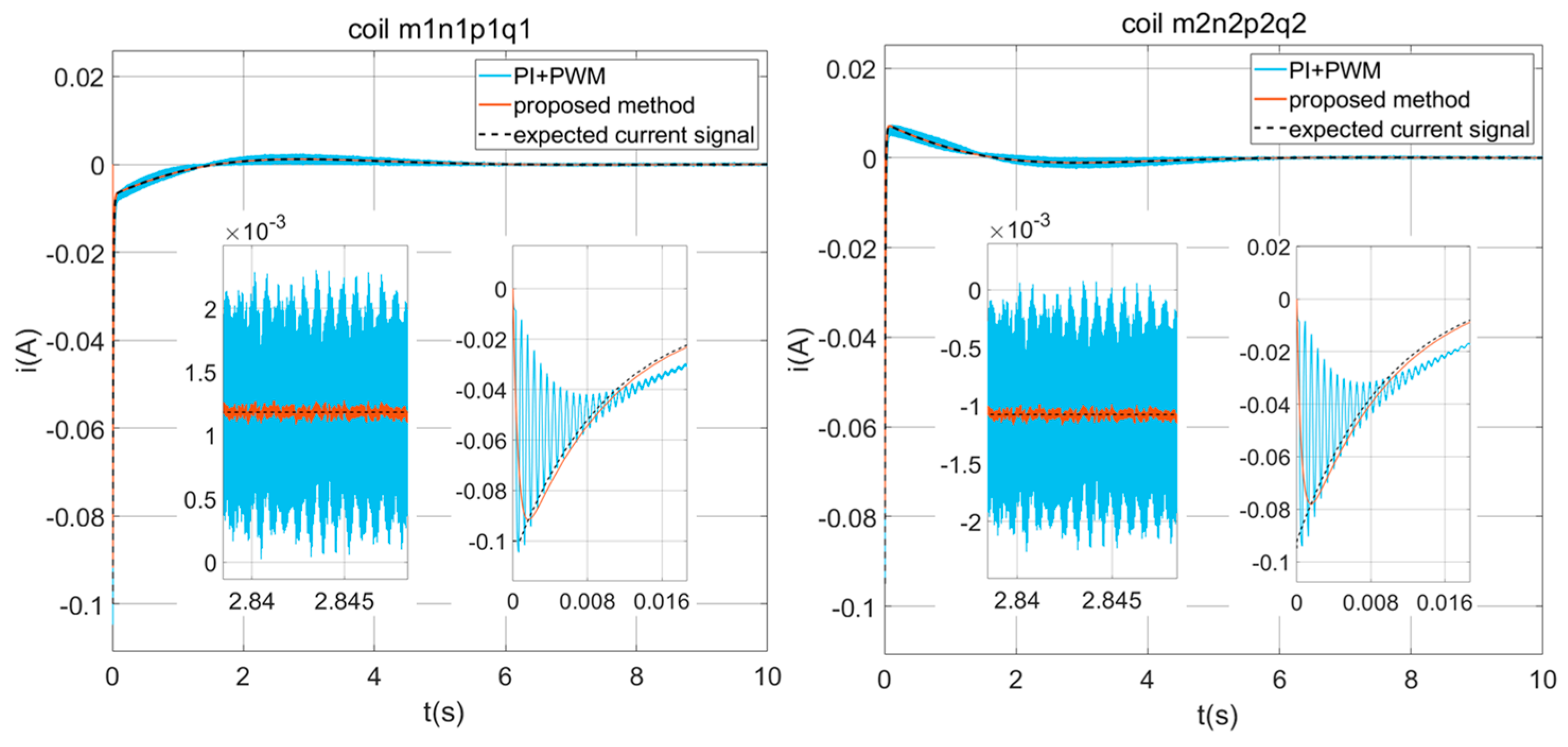
The VSFPWM algorithm predicts the current ripple size on the filter inductor and adjusts the switching frequency adaptively to reduce the current ripple based on the modulation amplitude value. This does not require an increase in the inductance value in the filter or the maintenance of a high switching frequency. Therefore, the dynamic response of the power amplifier can be improved and the switching losses can be reduced while suppressing the current ripple.

3.2. Feedforward Compensation for Back Electromotive Force

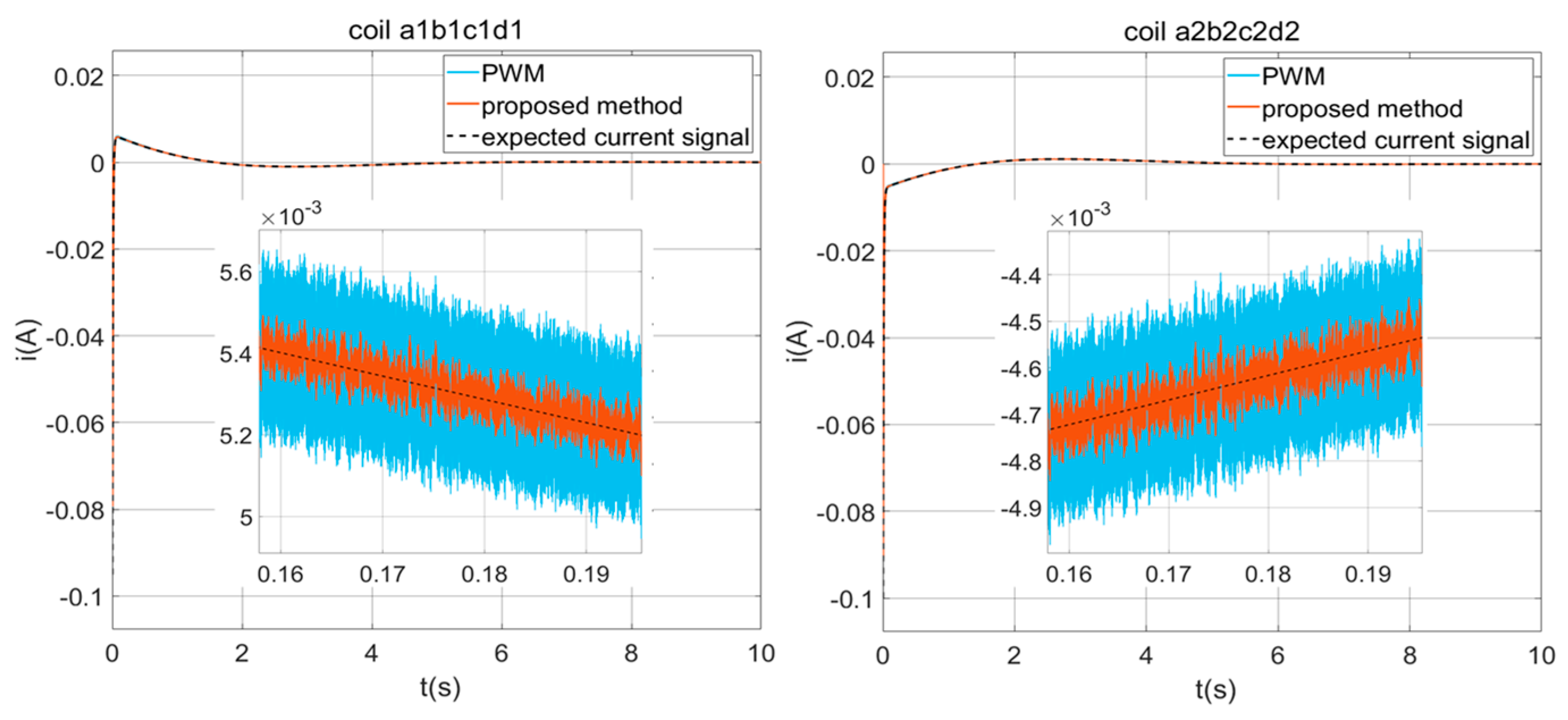
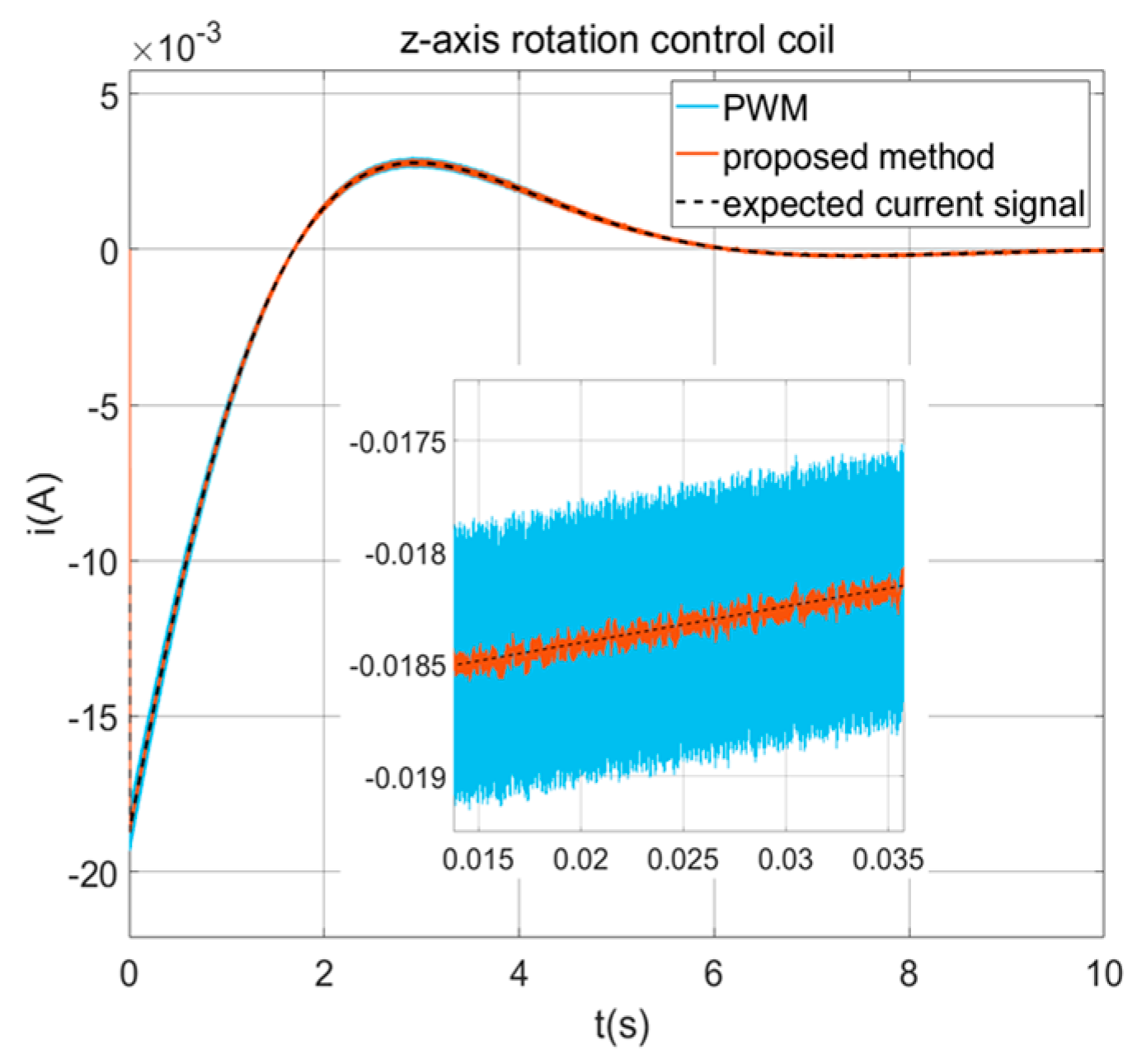
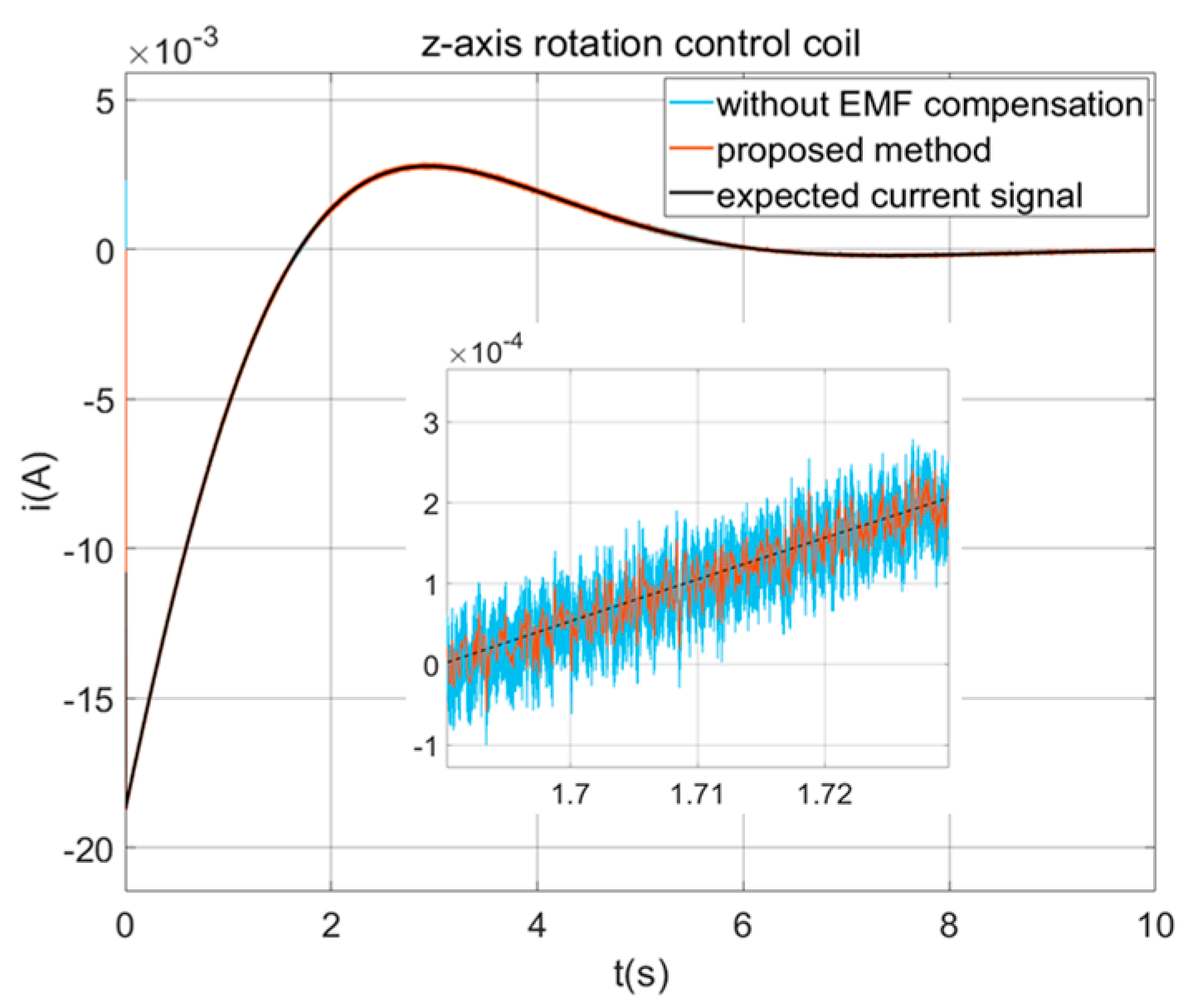
In the attitude maneuver of the NCAESS, the PM moves first and the SM follows. Due to the non-contact connection between these two modules, there is a gap between them; at this time, the relative motion of attitude or position will occur between the two modules of the NCAESS. When entering the steady-state mode, the PM exhibits high attitude accuracy and stability, but the vibration and other disturbances on the SM will cause the position and attitude of the SM to change slightly, resulting in relative motion between the two modules. According to Faraday’s law of electromagnetic induction, the relative motion between the two modules would cause back electromotive force. The generation of back electromotive force will interfere with the driving current and affect the relative motion of the NCAESS.

In order to suppress this impact, this section adopts feedforward compensation to suppress the back electromotive force.

As shown in Figure 2, the outer coil generates a back electromotive force on the NCAESS when the two modules are rotated relative to each other around the x- and y-axes. The magnitude of the back electromotive force can be written as follows:

$$E_{b1}=N_h{B}_h{\omega }_{spi}^s{r}_h{\displaystyle {\int }_{-\frac{\alpha }{2}}^{\frac{\alpha }{2}}}{r}_{h}d\alpha +N_h{B}_h{\omega }_{spi}^s{r}_h{\displaystyle {\int }_{\frac{\alpha }{2}}^{-\frac{\alpha }{2}}}{r}_{h}d\alpha =2N_h{B}_h{\omega }_{spi}^s{r_h}^2\alpha$$

(18)

where ω^s_spi(i = x, y) represents the angular velocity of the relative rotation along the x-axis and y-axis between the two modules.

The disturbances of the back electromotive force generated by the relative rotation around the z-axis and relative translation along the x-axis and y-axis of the two modules can be represented as follows:

$$E_{b2}=4N_p{B}_p{\omega }_{spz}^s{\displaystyle {\int }_{-\frac{l_2}{2}}^{\frac{l_2}{2}}{r}_{p}d{l}_2}=4N_p{B}_p{\omega }_{spz}^s{r}_p{l}_2$$

(19)

$$E_{b3}=2N_p{B}_p{v}_{spi}^s{l}_1$$

(20)

where ω^s_spz and v^s_spi(i = x, y) represent the angular velocity of the relative rotation along the z-axis and the relative velocity of the translation along the x-axis and y-axis between the two modules, respectively.

According to the average state-space equation of the power amplifier, as shown in Equation (12), and the NCAESS back electromotive force model constructed in Equations (18)–(20), the feedforward compensation controller of the back electromotive force can be obtained as follows:

$$D_2(t)={\displaystyle \frac{E_{bjx}(t)}{U}}$$

(21)

where E_bjx (x = 1, 2, 3) represents the magnitude of the back electromotive force on each coil, and E_bj1 (j1 = a₁b₁c₁d₁, a₂b₂c₂d₂, m₁n₁p₁q₁, m₂n₂p₂q₂) = E_b1, E_bj2 (j2 = zr) = E_b2, E_bj3 (j3 = xt, yt) = E_b3.

Based on the constructed feedback compensation controller for back electromotive force, its impact can be effectively suppressed, thereby improving the precision of the driving current when the two modules move relative to each other.

3.3. Robust Smith Prediction for Eliminating Time Delay

Compared to analog control, digital control offers greater robustness and the ability to compute more complex algorithms. However, inherent time delays are introduced in the signal acquisition, algorithm computation, and PWM generation stages. The transfer function of a closed-loop control system for current control with delays can be written as follows:

$${\displaystyle \frac{i_{Xj}(s)}{i_{Xjref}(s)}}={\displaystyle \frac{G_{cj}(s)G_{pj}(s)e^{-{\tau }_{j}s}}{1+G_{cj}(s)G_{pj}(s)e^{-{\tau }_{j}s}}}$$

(22)

where i_Xjref(s) represents the reference current of each coil; i_Xj(s) denotes the NCAESS driving current; τ_j is the delay value in the driving current control system for each coil; G_pj(s) stands for the actual model of each power amplifier with delay; and G_cj(s) represents the closed-loop controller model for the driving current of each coil.

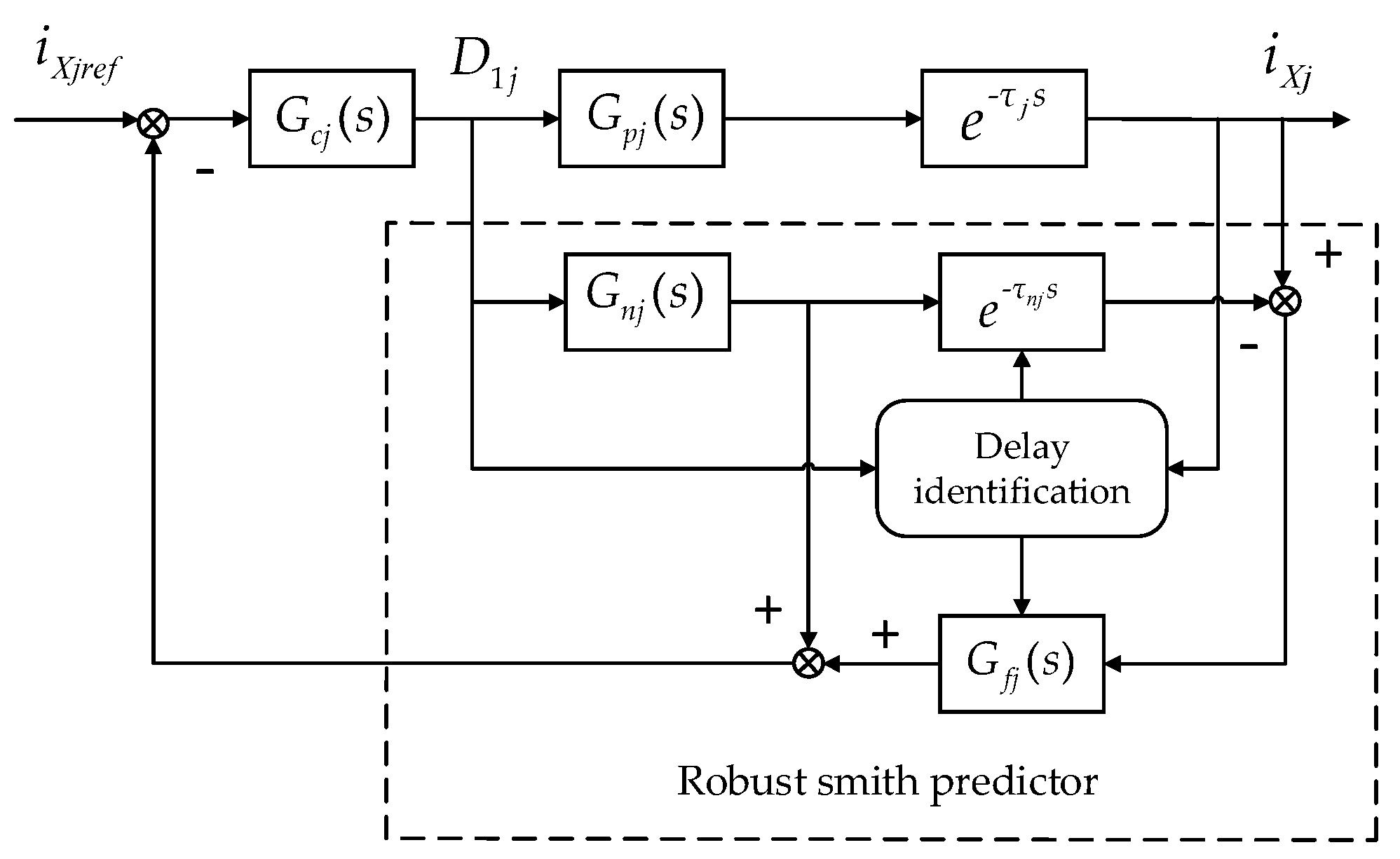
Due to the high-precision control requirement of the NCAESS, the presence of the time delay term $e^{-{\tau }_{j}s}$ in the characteristic equation of the closed-loop control system can affect the stability of the system. However, due to the modeling and parameter identification errors caused by the time-varying performance of the power amplifiers, as well as the uncertainty of time delay, it is difficult to achieve ideal compensation effects with the classical Smith predictor. This section thus adopts the robust Smith predictor to identify the time delay online and compensate for the impact in the closed-loop control system. The structure of the robust Smith predictor is shown in Figure 10.

As shown in Figure 10, D_1j represents the output of the closed-loop controller for the driving current of each coil, τ_nj is the estimated time delay for each driving current control loop, G_nj(s) represents the ideal model of each power amplifier after removing the time delay, and G_fj(s) stands for the filter designed in the RSP used in each control loop. Assuming that the back electromotive force is eliminated through the feedforward compensation, and since L₁C₁L_Xjd³i_Xj(t)/dt³ + L₁C₁R_Xjd²i_Xj(t)/dt² $\ll$ (L₁ + C₁)di_Xj(t)/dt + R_Xji_Xj(t) for the fundamental current, the average state-space equation of the power amplifier can be simplified as shown in Equation (23) after neglecting the effects of the higher-order terms:

$$(L_1+L_{Xj}){\displaystyle \frac{d{i}_{Xj}(t)}{dt}}+R_{Xj}{i}_{Xj}(t)=D_{1j}(t)U$$

(23)

The ideal model of the power amplifier is written below:

$$G_{nj}(s)={\displaystyle \frac{i_{Xj}(s)}{D_{1j}(s)}}={\displaystyle \frac{U}{(L_1+L_{Xj})s+R_{Xj}}}$$

(24)

Based on the correlation between the control input signal and the driving current, this paper employs a cross-correlation function to compute the delay time. The cross-correlation function between the control input and the driving current is as follows:

$$R_{D_{1j}{i}_{Xj}}(\tau )=E[D_{1j}(t)\times i_{Xj}(t-{\tau }_j)]=lim{\displaystyle \frac{1}{T}}{\displaystyle {\int }_0^T}[D_{1j}(t)\times i_{Xj}(t-{\tau }_j)]dt$$

(25)

where i_Xj(t − τ) is the driving current in each coil under the influence of the time delay; and T is the observation time.

N data are sampled at equal time intervals t_s for the closed-loop control quantity and driving current, respectively. For the sampled data, D_1jT = [ D_1j (J), D_1j (J + 1),…, D_1j (J + N − 1)], i_T = [i(J + n_j), i(J + n_j + 1),…, i(J + n_j + N − 1)], J = 1,…, m, where m is a positive integer and n_j = τ_j/t_s. Assuming the time delay interval is [τ_jmin, τ_jmax] and making Nt_s ≥ τ_jmax, the cross-correlation function between the control input and the output signal in the discrete-time form can thus be obtained as follows:

$${\widehat{R}}_{D_{1j}{i}_{Xj}}(n_j)={\displaystyle \frac{1}{N}}{\displaystyle \sum _{k=0}^{N-1}[D_{1j}(J+k)\times i_{Xj}(J+k+n_j)]}$$

(26)

This paper adopts the fast Fourier transform (FFT) to calculate the cross-correlation function in Equation (26) in order to reduce the computational complexity. If ${\widehat{n}}_j$ is taken as the maximum value of the cross-correlation function, then the estimated time delay of each control loop using digital control is τ_nj = ${\widehat{n}}_j$t_s.

The closed-loop transfer function of the NCAESS when using robust Smith prediction can be written as follows:

$${\displaystyle \frac{i_{Xj}(s)}{i_{Xjref}(s)}}={\displaystyle \frac{G_{cj}(s)G_{pj}(s)e^{-{\tau }_{j}s}}{1+G_{cj}(s)G_{nj}(s)+G_{cj}(s)G_{fj}(s)[G_{pj}(s)e^{-{\tau }_{j}s}-G_{nj}(s)e^{-{\tau }_{nj}s}]}}$$

(27)

The design of the filter is as follows:

$$G_{fj}(s)={\displaystyle \frac{G_{pj}(s)-G_{nj}(s)}{G_{pj}(s)e^{-{\tau }_{j}s}-G_{nj}(s)e^{-{\tau }_{nj}s}}}$$

(28)

When the online identification delay of each control loop τ_nj ≈ τ_j, the filter G_fj(s) can be simplified into Equation (29):

$$G_{fj}(s)={\displaystyle \frac{1}{e^{-{\tau }_{nj}s}}}\approx {\displaystyle \frac{1}{{\tau }_{nj}s+1}}$$

(29)

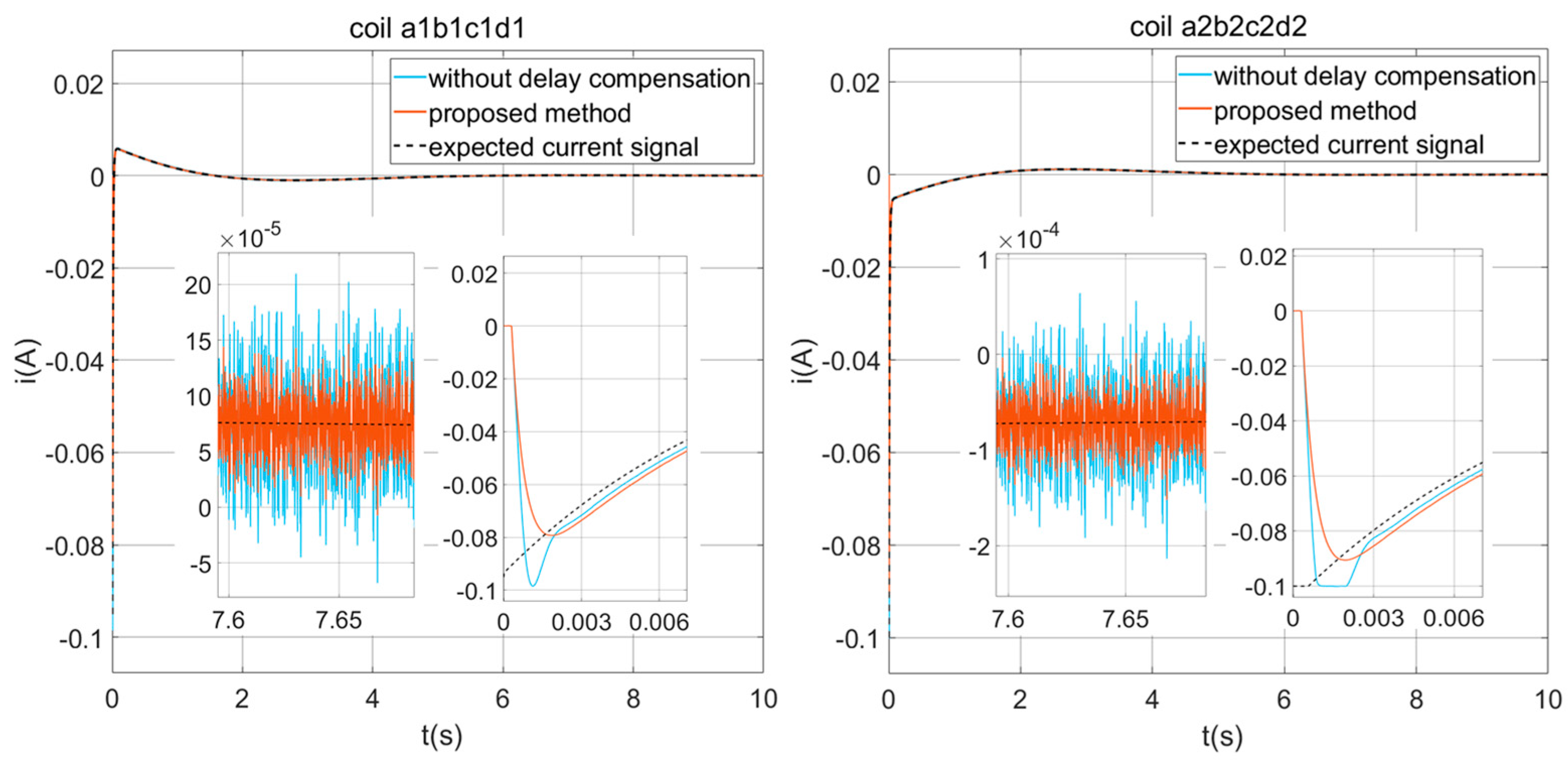
At this point, the characteristic equation of the NCAESS driving current control system for each coil is 1 + G_cj(s)G_pj(s) = 0. From this, it can be concluded that when the power amplifier exhibits time-varying performance and disturbances leading to model uncertainty, the robust Smith predictor can still eliminate the impact of the digital control delay.

3.4. Internal Model PI Controller with Fuzzy Rule

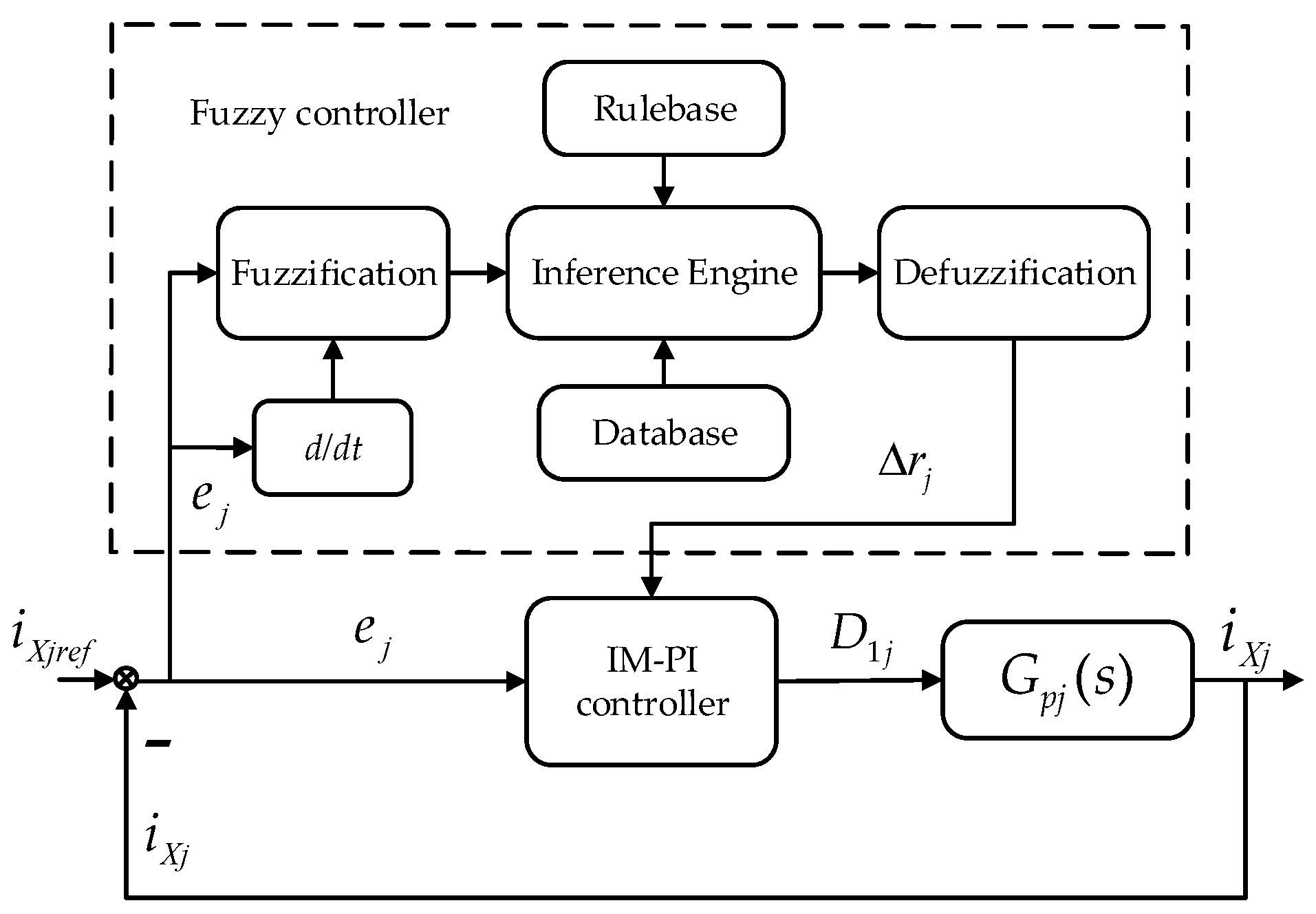
In order to address the impact of power amplifier variation and noise interference on driving current control, it is necessary to tune the controller parameters adaptively. The two parameters of the traditional PI controller would affect the control effect, and it is also difficult to achieve the ideal control results through manual adjustment of these parameters. Moreover, they cannot adaptively adjust with changes in system performance, disturbances, and other influences, which would weaken the robustness of the driving current. This article first uses the internal model principle to tune the parameters of the PI controller, and then combines it with fuzzy rule in order to enable it to adjust the parameters of the internal model PI controller adaptively. A structural diagram of the internal model PI controller with fuzzy rule is shown in Figure 11.

The controller constructed based on the internal model principle is shown in Figure 12, which consists of feedback from the ideal model of the power amplifier and a low-pass filter controller of the same order as the controller. The internal model controller is constructed as shown in Equation (30).

$$G_{IMCj}(s)={\displaystyle \frac{1}{G_{nj}(s)\left(r_{j}s+1\right)}}={\displaystyle \frac{(L_1+L_{Xj})s+R_{Xj}}{U\left(r_{j}s+1\right)}}$$

(30)

where r_j represents the filter parameter. The equivalent feedback for internal model control is constructed as follows:

$$G_c(s)={\displaystyle \frac{G_{IMCj}(s)}{1-G_{IMCj}(s)G_{nj}(s)}}={\displaystyle \frac{(L_1+L_{Xj})s+R_{Xj}}{r_{j}Us}}$$

(31)

We can thus transform the structure of the traditional PI controller through the following expression:

$$G_{PIj}(s)=k_{pj}+{\displaystyle \frac{k_{ij}}{s}}={\displaystyle \frac{k_{pj}(k_{cj}s+1)}{k_{cj}s}}$$

(32)

where k_pj and k_ij are the parameters of the PI controller; and k_pj/k_cj is the equivalent parameter of k_ij.

Comparing Equation (31) with Equation (32), the internal model PI controller is constructed as follows:

$$G_{IM-PIj}(s)={\displaystyle \frac{L_1+L_{Xj}}{r_{j}U}}+{\displaystyle \frac{R_{Xj}}{r_{j}Us}}$$

(33)

As shown in Equation (34), it can be observed that the PI controller is only related to the parameter r_j of the filter when the ideal model of the NCAESS is known. Based on the design experience of the filter parameters, the PI controller can be tuned effectively. This reduces the difficulty and improves the precision of the parameter tuning.

By adjusting the filter parameter r_j, it is found that as the value of r_j decreases, the system response speed can be increased and the robustness can be enhanced. However, too small a value of r_j may lead to the system overshooting. On the other hand, increasing the value of r_j would reduce the response speed and robustness, but would not cause overshooting. In order to balance the overshooting and response speed of the NCAESS driving current control system and to improve the robustness, this paper adopts a fuzzy rule to adjust the filter parameter r adaptively based on the current system situation.

The internal model PI controller with fuzzy rule takes the error e_j between the reference current and the feedback current as well as the changing rate of the error e_cj as input variables, and the change in the parameter r_j of the internal model PI controller Δr_j as the output variable. The Gaussian-type function shown in Equation (33) is used as the membership function of the fuzzy controller. The fuzzy subsets corresponding to the input and output variable domains of the fuzzy controller are {NB, NM, NS, Z, PS, PM, PB}.

$$f(x)=e^{-{\displaystyle \frac{{(x-a_i)}^2}{b_i^2}}}$$

(34)

where a_i is the center value of the function; and b_i is the width of the function.

After obtaining the output of a fuzzy rule, it is necessary to perform defuzzification to obtain precise control values. This paper adopts the centroid method for defuzzification [26], which is represented as follows:

$$M_j={\displaystyle \frac{{\displaystyle \sum (\mu (x_j)x_j)}}{{\displaystyle \sum \mu (x_j)}}}{|}_{x=e_j,e_{cj}}$$

(35)

where M_j represents the centroid position of the fuzzy set; x_j denotes the changing rate of e_j and e_cj; and μ(x_j) represents the membership degree of the variable x_j.

Combining the above contents, the internal model PI controller with fuzzy rule can be represented as follows:

$$G_{FIM-PIj}(s)={\displaystyle \frac{L_1+L_{Xj}}{(r_j+\Delta r_j)U}}+{\displaystyle \frac{R_{Xj}}{(r+\Delta r)Us}}$$

(36)

Obviously, the internal model PI controller with fuzzy rule can be adopted to change the controller parameter r_j adaptively according to the current error situation of the driving current control system, thereby improving the driving current performance.

4. Numerical Simulation

4.1. Initial Conditions

In order to verify the effectiveness of the composite control algorithm designed in this paper, this section sets up a simulation model according to the control system shown in Figure 7 and performs three-axis steady-state control of an NCAESS. The PM attitude, the SM attitude, and the relative position of the two modules are controlled by the proportional differentiation (PD) algorithm, which is commonly used in engineering. The initial parameters used are shown in

Table 1. Parameters of the NCAESS.

Parameter	Value
Semi-major axis	6628.135 km
Eccentricity	0.00099
Inclination	96.5°
Right ascension of ascending node	0°
Argument of perigee	379.9935°
Mean anomaly	0.0065°
Earth gravity model	TJGRACE02S
Magnetic field model	IGRF 13 × 13
Atmospheric drag model	Exponential model
Solar radiation pressure model	Photon radiation
Inertia matrix of the PM	$\left[\begin{array}{ccc}29.875& 0.34& 1.14\\ 0.34& 30.257& 0.55\\ 1.14& 0.55& 30.074\end{array}\right]$ (kg·m2)
Inertia matrix of the SM	$\left[\begin{array}{ccc}304.77& -13.44& 8.74\\ -13.44& 298.21& 2.14\\ 8.74& 2.14& 301.14\end{array}\right]$ (kg·m2)

and

Table 2. Parameters of the NCAEA.

Parameter	Value
Annular radius of the outer coil	0.6 m
Occupied angle	60°
Working length	0.15 m
Arm of force	0.5 m
Power supply voltage	10 V
Filter inductance	0.1 mH
Filter capacitor	100 μF
Outer-coil current-limiting resistor	90 Ω
Inner-coil current-limiting resistor	95 Ω
Equivalent resistance of the outer coil	10 Ω
Equivalent inductance of the outer coil	5 mH
Equivalent resistance of the inner coil	5 Ω
Equivalent inductance of the inner coil	2 mH
Maximum current	100 mA
Air-clearance angle constraint range	±0.9°
Air-clearance translational constraint range	±1.5 mm
Outer magnetic intensity	0.65 T
Inner magnetic intensity	0.65 T
Outer-coil turns	200
Inner-coil turns	150

. Table 1 shows the parameters relating to the NCAESS’s initial orbit, the external environment, and its own moment of inertia. Table 2 shows the parameters relating to the NCAEA’s size, the switching power amplifier, and the magnetic field.

The parameters and fuzzy rules of the driving current composite control scheme designed in this article are shown in

Table 3. Parameters of the proposed controllers.

Parameter	Value
PM attitude controller parameter kp1	50
PM attitude controller parameter kd1	70
SM position controller kp2	70
SM position controller kd2	100
SM attitude controller parameter kp2	300
SM attitude controller parameter kd2	500
Initial PWM switching frequency	10 kHz
Expected peak ripple of inductance current	120 mA
Initial estimated time delay τnj	200 μs
The fuzzy domain of ej/ecj	[−3, 3]
The fuzzy domain of Δrj	[−0.0009, 0.0009]

and

Table 4. Fuzzy rules for Δr.

Value of e	Value of ec
	NB	NM	NS	Z	PS	PM	PB
NB	NB	NB	NB	NB	NB	NB	NB
NM	NB	NB	NM	NS	PS	PM	PB
NS	NB	NB	NB	NM	NS	PS	PM
Z	NB	NB	NM	NS	NM	NB	NB
PS	PM	PS	NS	NM	NB	NB	NB
PM	PB	PM	PS	NS	NM	NB	NB
PB	NB	NB	NB	NB	NB	NB	NB

. Table 3 shows the parameters relating to the PM attitude controller, the SM attitude control, and the relative position controller of the two modules, as well as the parameters of the composite control scheme in the driving current control of each coil. Table 4 shows the fuzzy rules adopted by the internal model proportional–integral controller with fuzzy rule.

After the NCAESS separates from the rocket, the PM and SM are connected through a mechanical locking device. When this mechanical device is unlocked via the detonation of explosive bolts, there is an initial state error between the PM and SM, as shown in

Table 5. Initial state of the NCAESS.

Parameter	Value
Angle error of the PM	[2, −2, 1] (deg)
Angle velocity error of the PM	[0.9, −0.5, 0.5] (deg/s)
Angle error of the SM	[0.4, −0.3, 0.1] (deg)
Angle velocity error of the SM	[0.1, −0.2, 0.2] (deg/s)
Position error of the SM	[0.9, −0.7, 0.5] (mm)
Velocity error of the SM	[0.1, −0.3, 0.3] (mm/s)

.

4.2. Results and Analysis

To verify the effectiveness of the proposed composite control scheme for the driving current, this paper conducts comparative simulations between the PWM and PI algorithms commonly used in driving control and the composite control scheme designed in this paper under the same condition of multiple disturbances [27]. Moreover, to verify the improvement of each algorithm in the composite control scheme on the driving current, comparative simulations are conducted before and after the combination of each algorithm.

Case 1: Simulation of the composite control scheme’s effectiveness.

Figure 13, Figure 14 and Figure 15 show the comparative simulation results for the NCAESS while employing the traditional method and the proposed composite control method during three-axis attitude stabilization control.

As shown in Figure 13, Figure 14 and Figure 15, it can be seen that compared with the combination method of PWM and PI, which is commonly used in driving control, the composite control scheme improves the driving current in the outer-coil a₁b₁c₁d₁, a₂b₂c₂d₂, m₁n₁p₁q₁, and m₂n₂p₂q₂ up to approximately 10 times under the multiple disturbances. Similarly, the driving current in the inner coil responsible for z-axis rotation control is enhanced up to approximately 10 times, too. Furthermore, both types of coils exhibit better dynamic responses with the composite control scheme, alleviating output current fluctuations. The response speed of the driving current for the outer coil is increased to approximately 1.5 ms, while for the inner coil, it is improved to approximately 2 ms. Obviously, the composite control scheme proposed in this paper demonstrates stronger robustness and a better response speed compared to the traditional method, which better meets the precise driving requirements of NCAESS.

Case 2: Simulation of VSFPWM based on current ripple prediction.

In response to the problem of current ripple during the modulation of the switching power amplifiers, the composite control scheme designed in this paper includes a VSFPWM based on current ripple prediction. Considering the similar driving current waveforms in the annular outer-coil a₁b₁c₁d₁, a₂b₂c₂d₂ and the annular outer-coil m₁n₁p₁q₁, m₂n₂p₂q₂, this paper performs a simulation analysis of the driving currents for the annular outer-coil a₁b₁c₁d₁, a₂b₂c₂d₂ and, subsequently, the z-axis rotation control coil. The comparative simulations using the traditional PWM and the VSFPWM are shown in Figure 16 and Figure 17. It can be seen that compared with the traditional PWM, the composite control algorithm using VSFPWM can maintain the current ripple within the range of 100 μA in the outer coil and inner coil by adjusting the switching frequency adaptively. However, the current ripple size in traditional PWM varies with the modulation wave amplitude, and its peak value exceeds the range of 100 μA. Therefore, the composite control scheme, by using VSFPWM, can suppress the switching current ripple effectively.

Case 3: Simulation of feedforward compensation for back electromotive force.

In response to the disturbance of the back electromotive force in the NCAESS, the composite control algorithm designed in this paper uses a feedforward technique to compensate for the back electromotive force. In order to evaluate the effectiveness of this back electromotive force feedforward compensation algorithm, this paper conducts a comparative simulation analysis between using the feedforward compensation and not considering such compensation in the composite control scheme. Figure 18 and Figure 19 show the simulated comparison of the driving current for the outer coil and the inner coil.

As shown in Figure 18 and Figure 19, it is clearly evident that the composite control scheme with back electromotive force feedforward compensation can improve the precision of the driving current in both the outer and inner coils by about one time when outputting low-amplitude current, and reduce the steady-state error by about 30 μA. Therefore, the composite control algorithm using back electromotive force feedforward compensation can suppress the back electromotive force disturbances and improve the precision of the driving current effectively when the two modules move relative to each other.

Case 4: Simulation analysis of robust Smith prediction.

The robust Smith predictor is used to compensate the time delay in the proposed composite control algorithm in this paper. To verify the effectiveness of the robust Smith predictor, this paper conducts a comparative simulation analysis between using the robust Smith predictor for time delay compensation and not considering such time delay compensation. Figure 20 and Figure 21 show the simulated comparison of the driving current of the outer coil and the inner coil, respectively. Figure 20 and Figure 21 indicate that the composite control algorithm using the robust Smith predictor approximately doubles the current accuracy compared to the scenario without time delay compensation. It solves the stability problem caused by the time delay and reduces the overshooting, enhancing the dynamic response of the driving current control system. Therefore, employing the composite control scheme with RSP can compensate for the time delay, enhancing the stability and dynamic response of the driving current control system.

In summary, by adopting the composite control scheme designed in this article, the driving current control system of the NCAESS has stronger robustness and an enhanced dynamic response ability compared to the traditional control scheme under multiple disturbances. And the VSFPWM, back electromotive force feedforward compensation, and robust Smith predictor in the composite control scheme are effective in improving the control effect the driving current.

5. Conclusions

This paper presents a composite strategy for the driving current control of NCAESS, which addresses various disturbances that affect the precision of the switch power amplifiers. These disturbances include the switch ripple, back electromotive force, digital time delay, time-varying performance, and noise disturbances. The proposed method combines the VSFPWM, back electromotive force feedforward compensation, the robust Smith predictor, and an internal model PI algorithm with fuzzy rule to mitigate the above-mentioned disturbances effectively. Through numerical simulations comparing the composite control scheme with the traditional method, it is demonstrated that the proposed method can be adopted to improve the driving precision. Specifically, the VSFPWM maintains the peak value of the current ripple within a range of 100 μA. The back electromotive force feedforward compensation roughly doubles the precision in situations of low-current output. The robust Smith predictor enhances the system stability, reduces the driving noise by a factor of two, and alleviates the overshooting problem caused by time delay. Overall, the proposed composite control scheme in this paper strengthens the robustness and dynamic response, and can thus be adopted to guarantee the high-precision control of NCAESS.