Rotorcraft Airfoil Performance in Martian Environment
Abstract
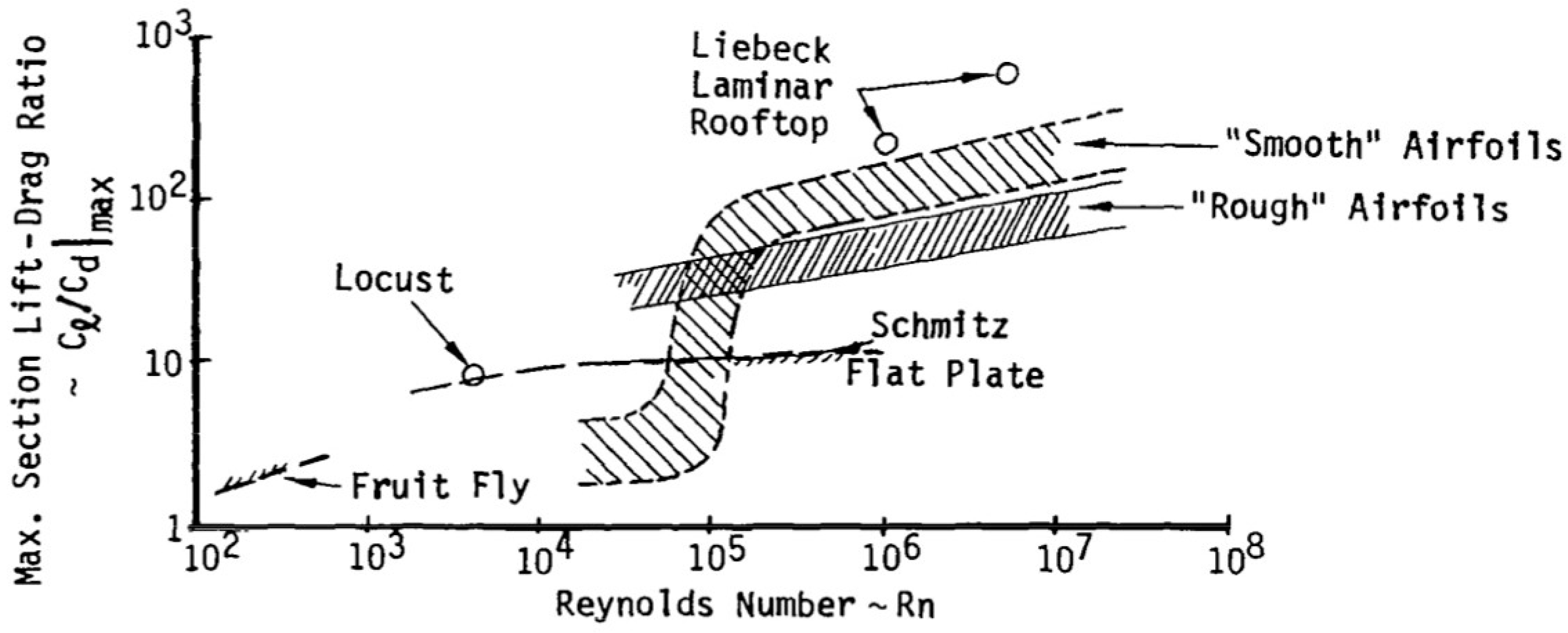
1. Introduction
2. Methods
2.1. The Martian Atmosphere
2.2. Computational Approach
2.2.1. Turbulence and Transition Modelling
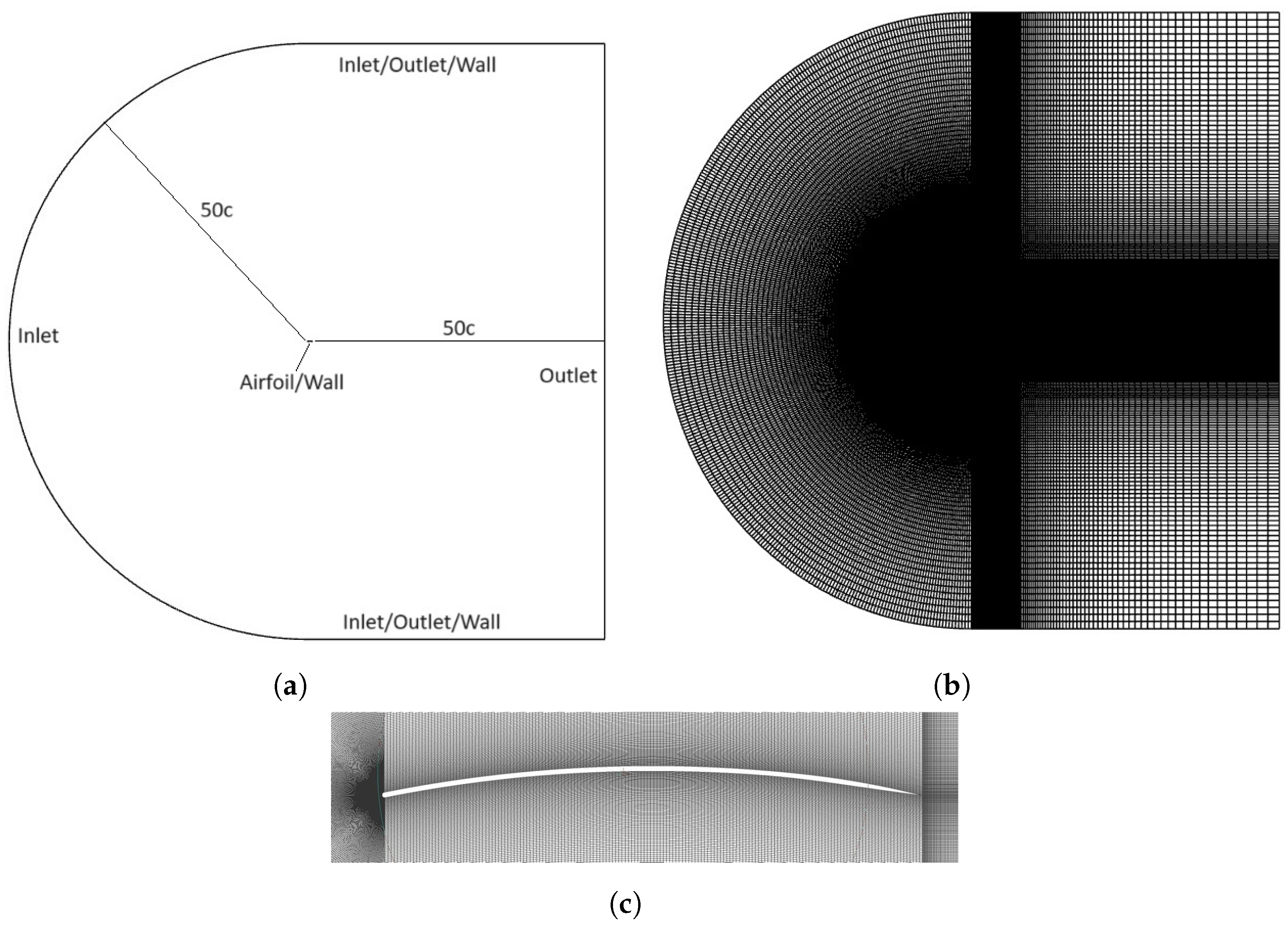
2.2.2. Computational Mesh
2.2.3. Boundary Conditions
2.2.4. Grid Independence Study
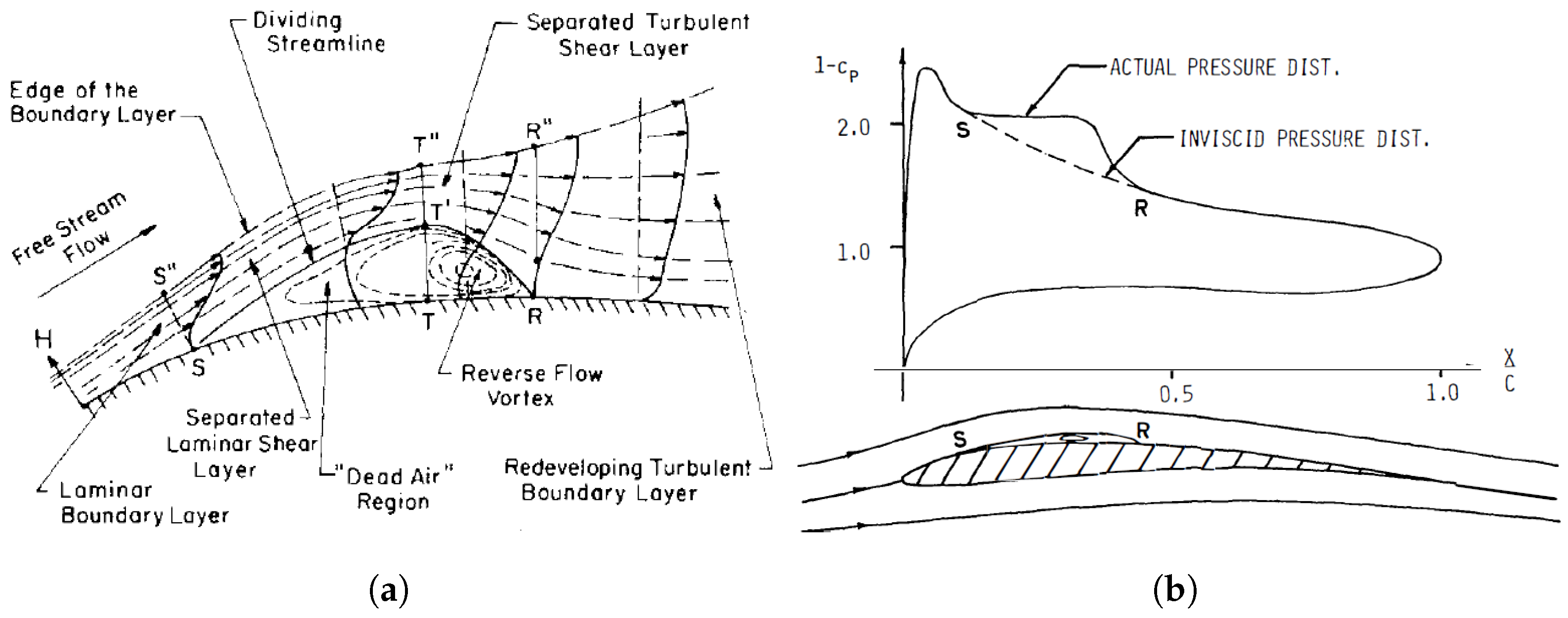
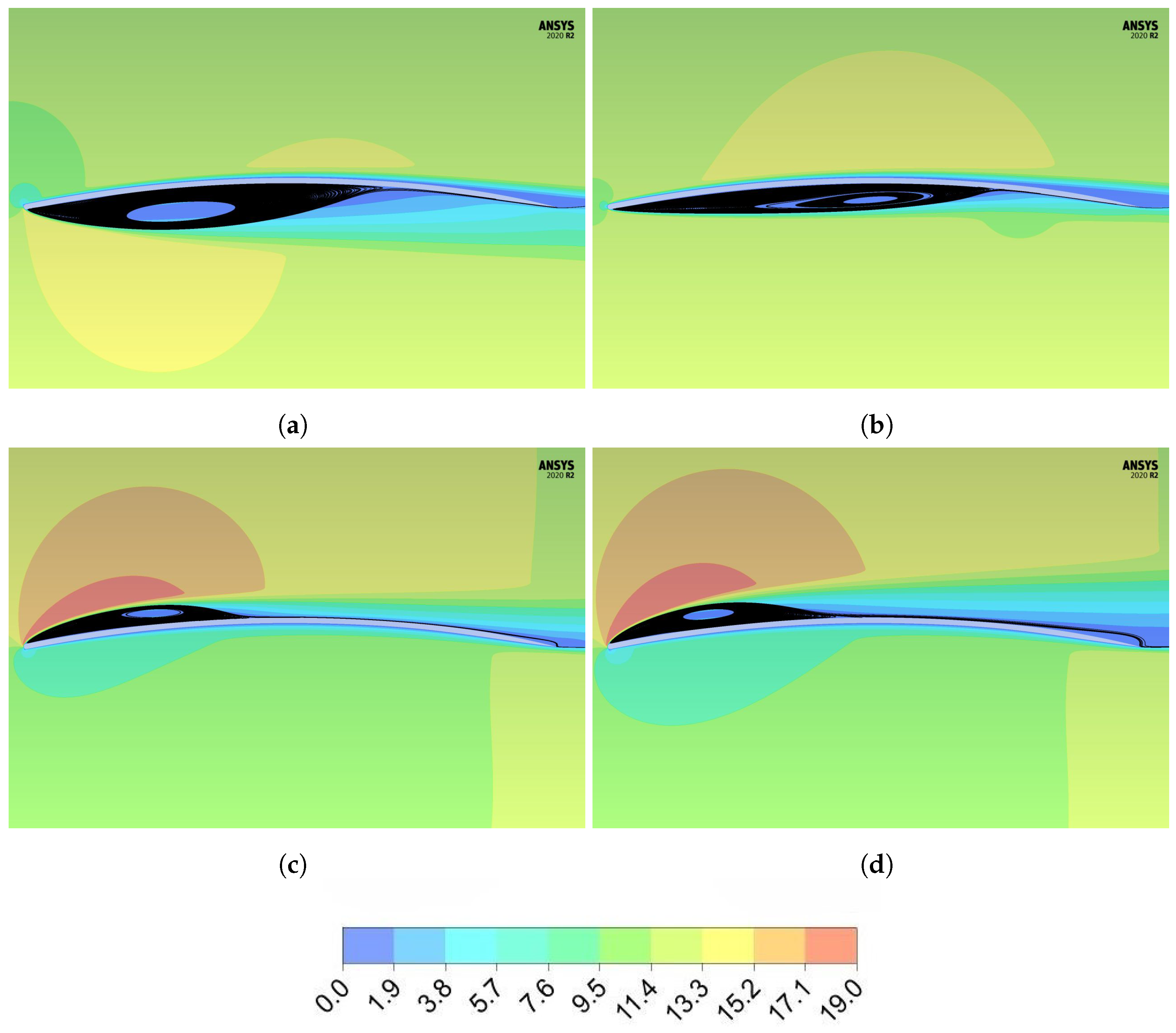
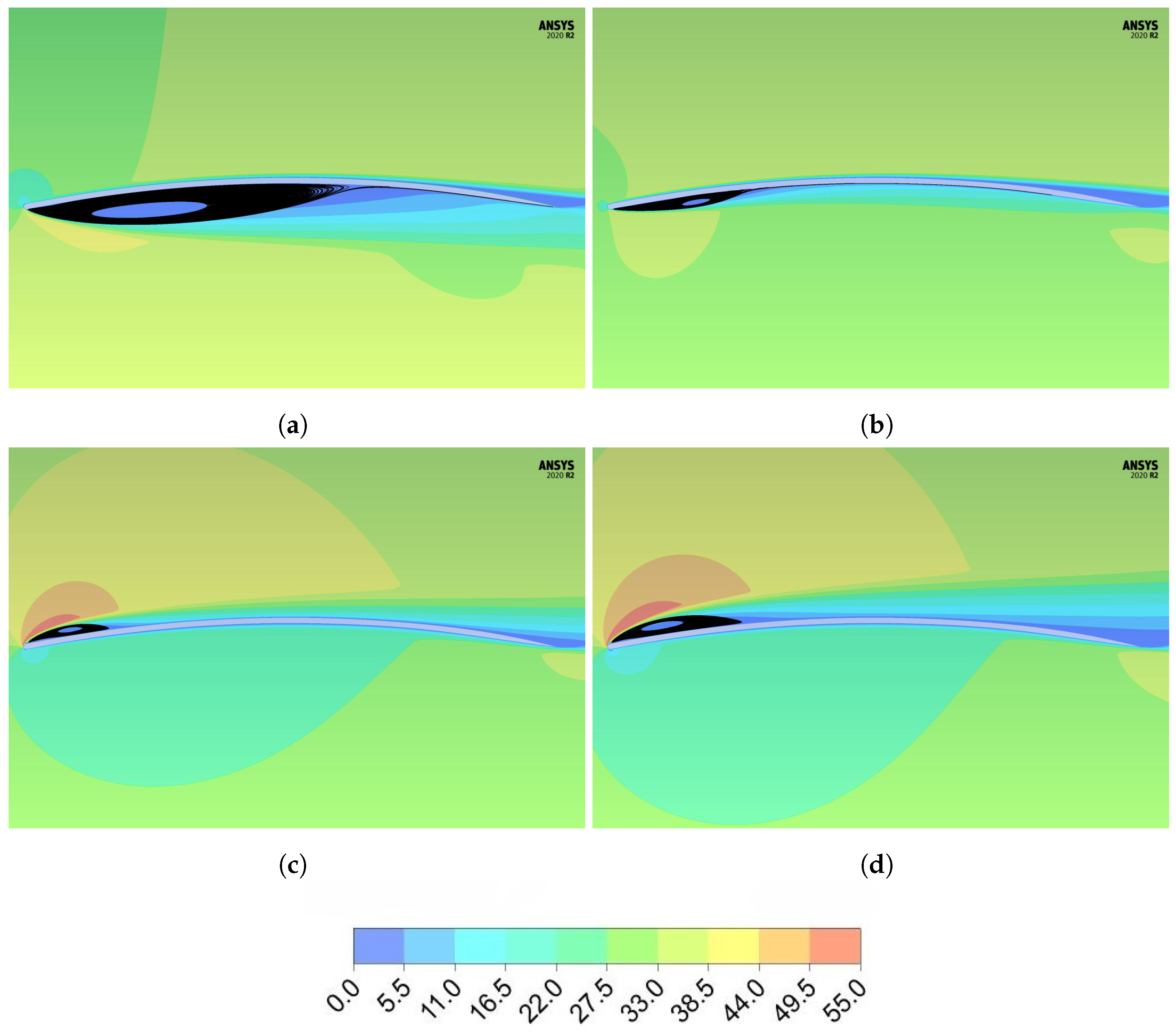
3. Laminar Separation Bubbles
3.1. General Features and Effects
- The bubble region, formed by the recirculating flow and bounded by the streamline ST′R, where the integrated mass flow is zero;
- The shear layer, which is the area between the bubble and the outer edge of the boundary layer, identified with S″T″R″.
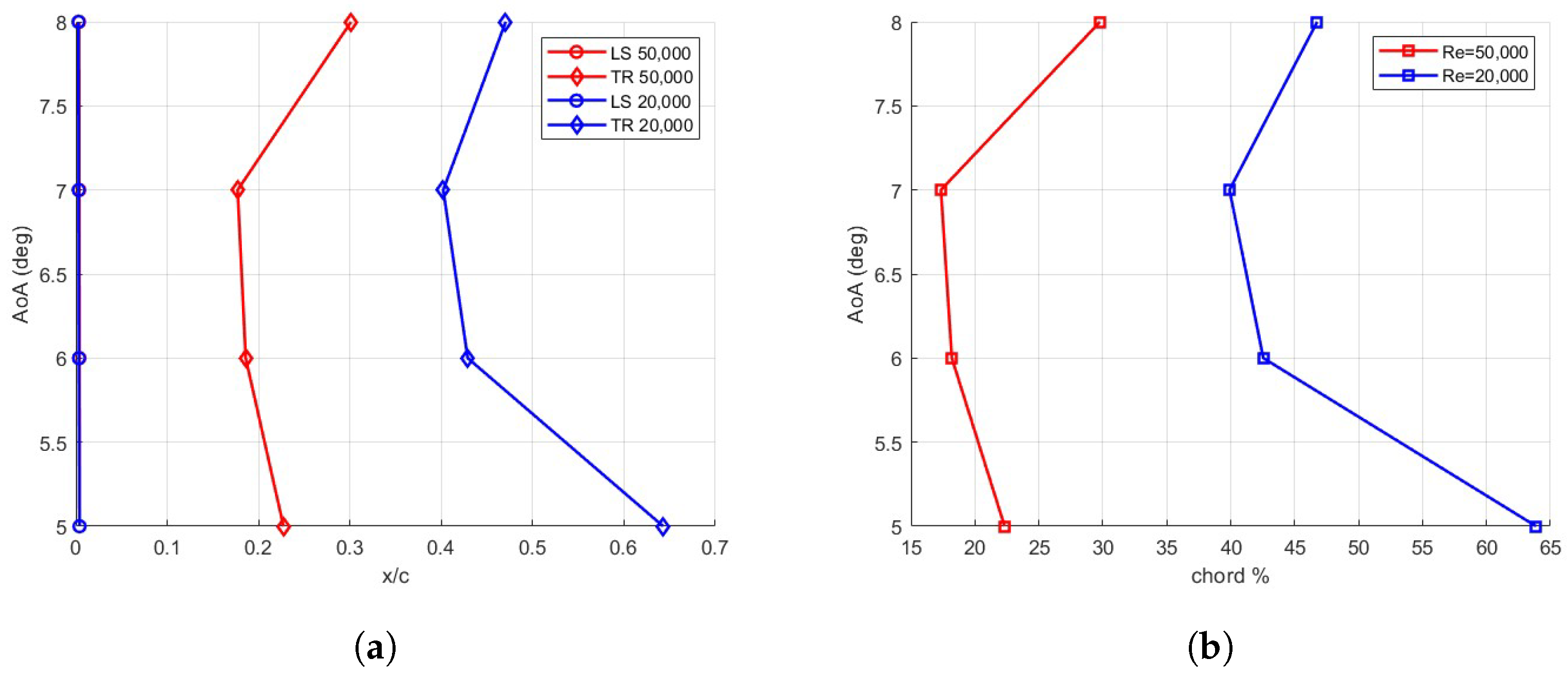
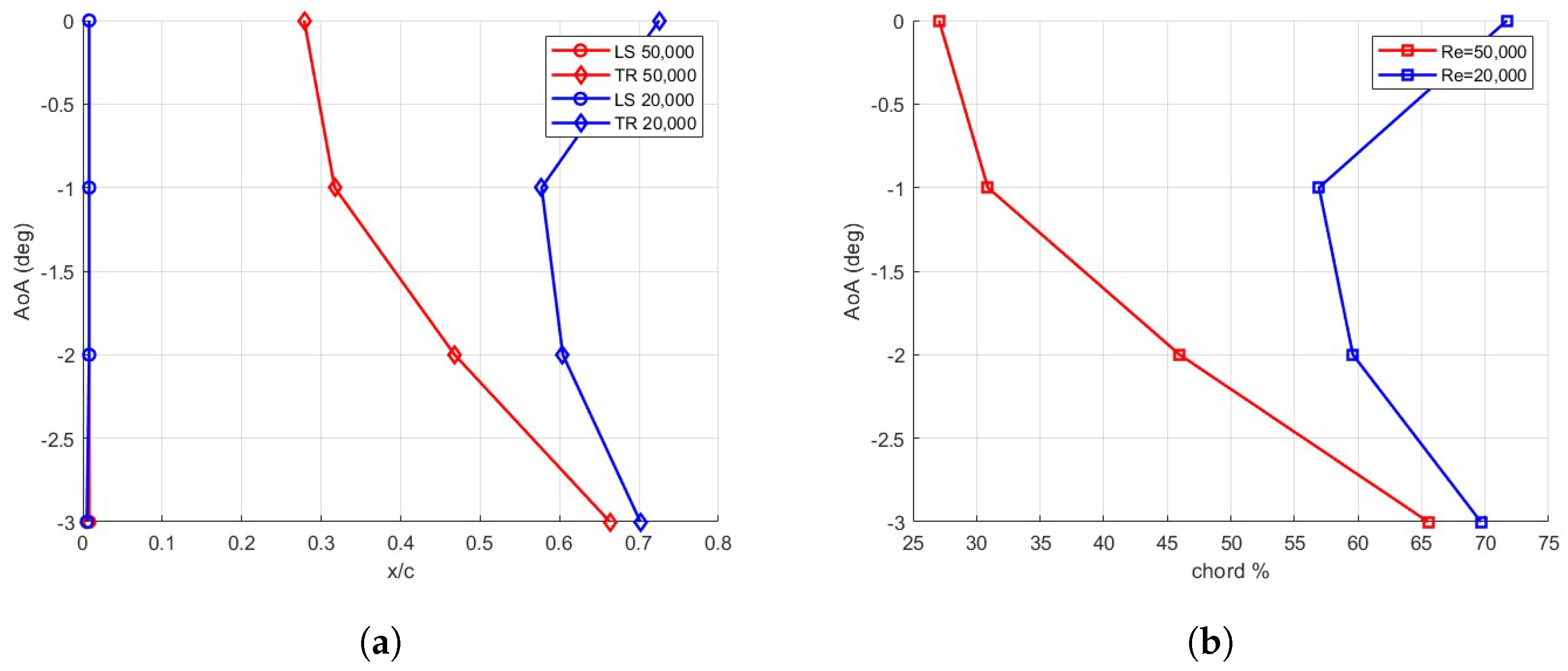
3.2. Angle of Attack
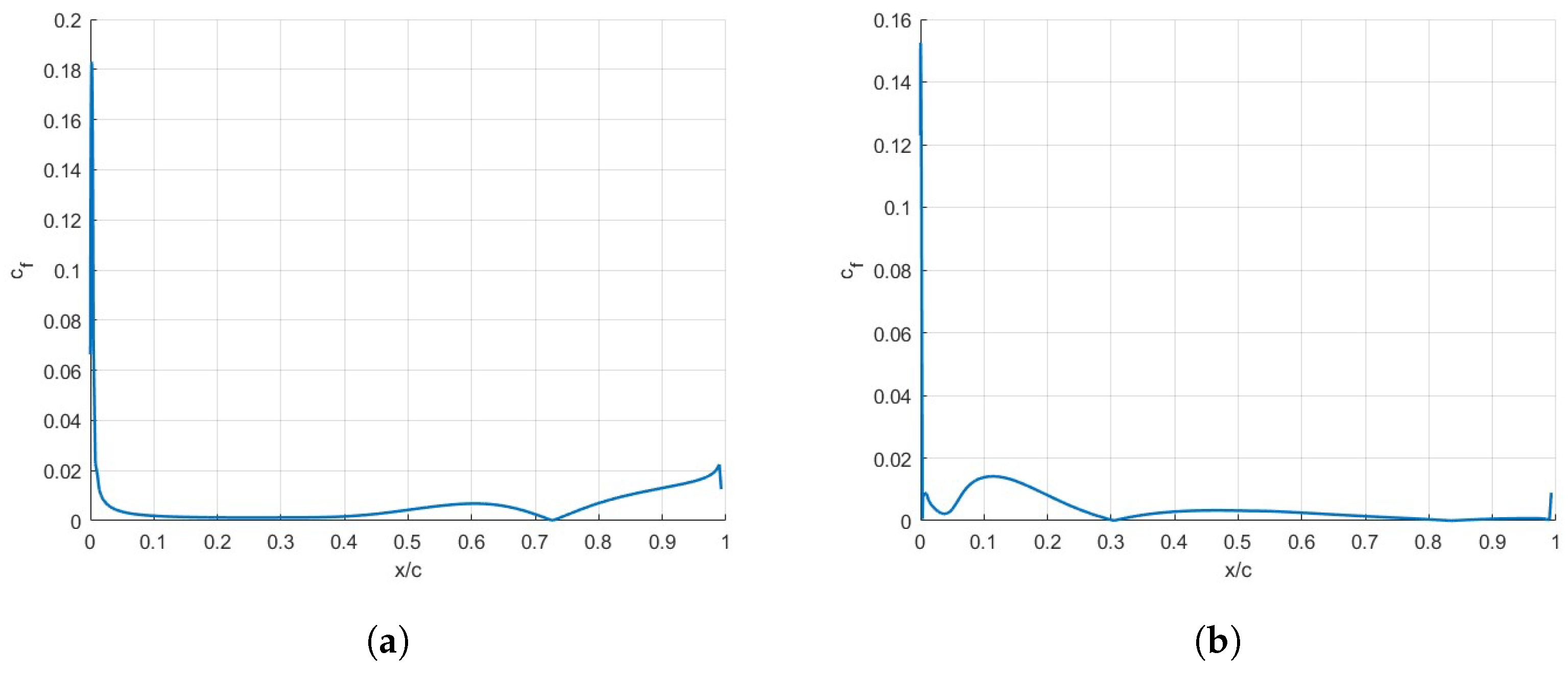
3.3. Effect of the Reynolds Number
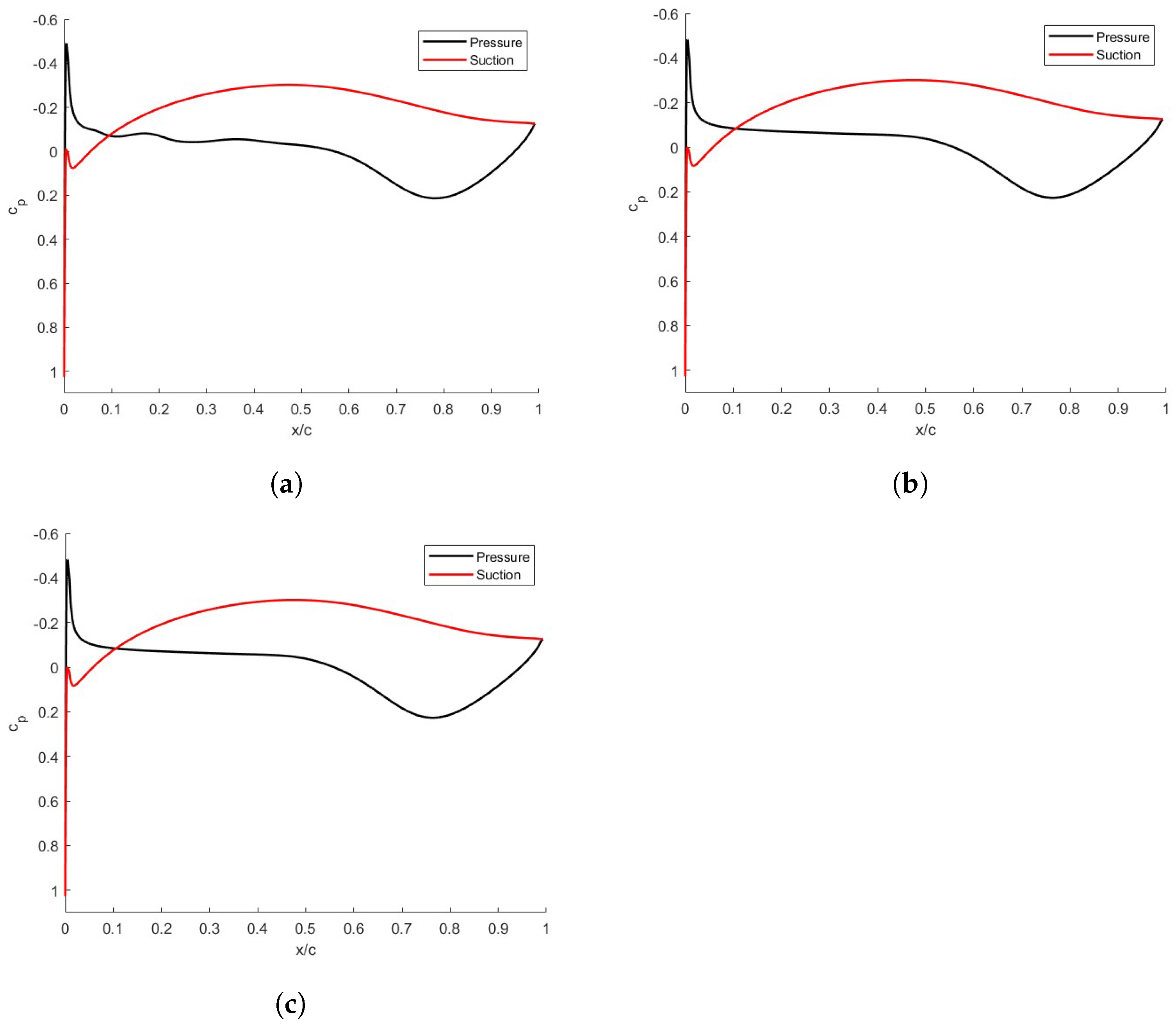
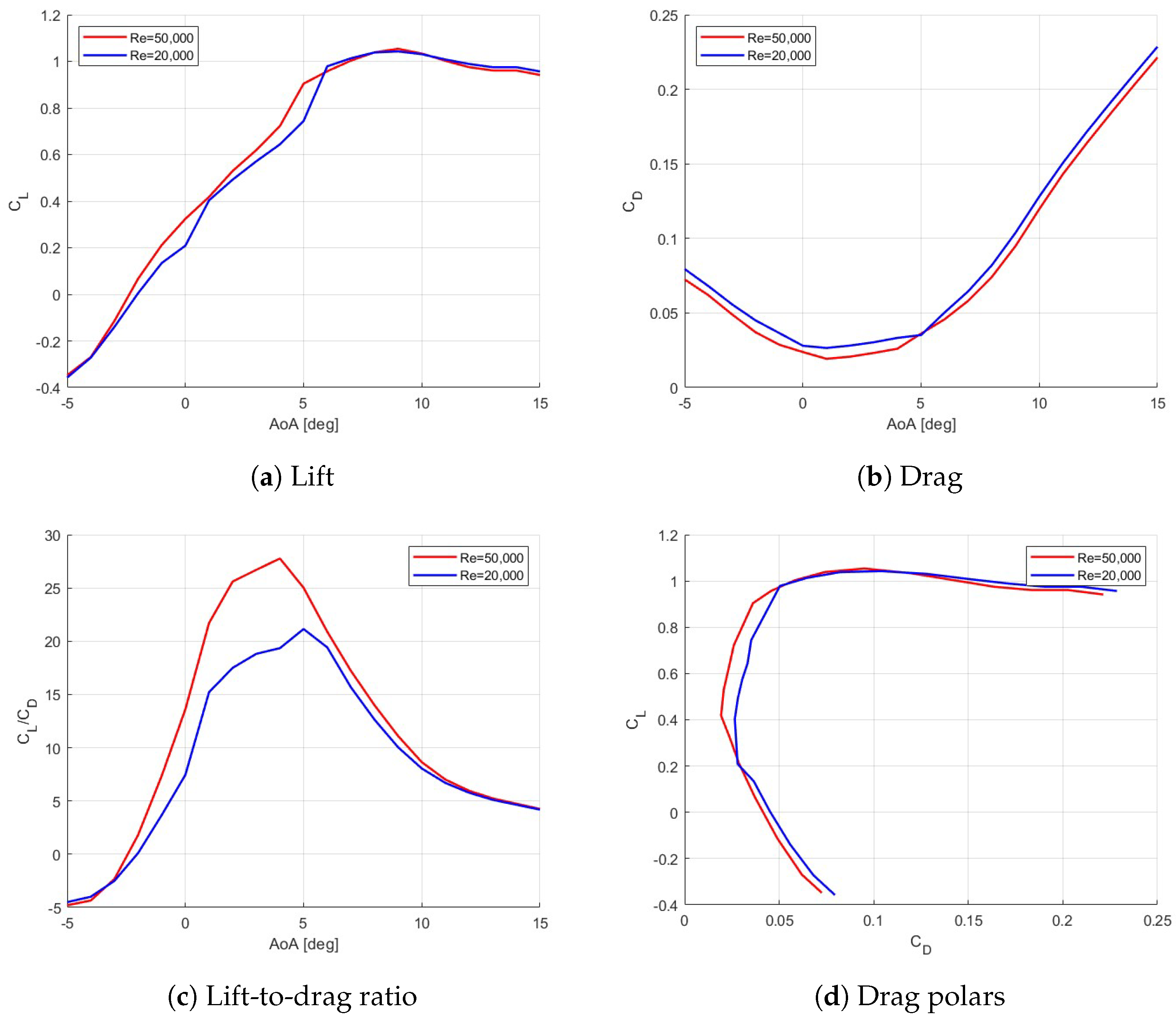
4. Results
5. Conclusions
- The low chord-based Reynolds number regime in the Martin atmosphere causes the formation of Laminar Separation Bubbles on the airfoil, which affect its performance;
- The increase in the Reynolds number from 20,000 to 50,000 has a small impact on performance;
- The model used provides a good representation of the formation of bubbles on the airfoil, but, in some cases, can capture a bubble incorrectly;
- Future works should aim to construct a more reliable model and focus on the other challenges posed by the Martian environment.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Koning, W.J.F.; Johnson, W.; Grip, H.F. Improved Mars helicopter aerodynamic rotor model for comprehensive analyses. AIAA J. 2019, 57, 3969–3979. [Google Scholar] [CrossRef]
- Winslow, J.; Otsuka, H.; Govindarajan, B.; Chopra, I. Basic understanding of airfoil characteristics at low Reynolds numbers (104–105). J. Aircr. 2018, 55, 1050–1061. [Google Scholar] [CrossRef]
- Schmitz, F.W.; Aerodynamics of the Model Airplane. Part 1—Airfoil Measurements. 1967. Available online: https://ntrs.nasa.gov/citations/19700029685) (accessed on 24 July 2024).
- Mueller, T.J.; DeLaurier, J.D. Aerodynamics of small vehicles. Annu. Rev. Fluid Mech. 2003, 35, 89–111. [Google Scholar] [CrossRef]
- McMasters, J.H.; Henderson, M.L. Low-speed single-element airfoil synthesis. In The Science and Technology of Low Speed and Motorless Flight, Part 1; NASA Langley Research Center: Hampton, VA, USA, 1979. [Google Scholar]
- Swift, K.M. An Experimental Analysis of the Laminar Separation Bubble at Low Reynolds Numbers. Master’s Thesis, University of Tennessee, Knoxville, TN, USA, 2009. [Google Scholar]
- Tani, I. Boundary-layer transition. Annu. Rev. Fluid Mech. 1969, 1, 169–196. [Google Scholar] [CrossRef]
- Gaster, M. The Structure and Behaviour of Separation Bubbles. 1967. Available online: https://reports.aerade.cranfield.ac.uk/bitstream/handle/1826.2/2862/arc-rm-3595.pdf?sequence=1&isAllowed=y (accessed on 24 July 2024).
- Von Doenhoff, A.E. A Preliminary Investigation of Boundary-Layer Transition along a Flat Plate with Adverse Pressure Gradient; Technical Report; NASA: Washington, DC, USA, 1938. [Google Scholar]
- Jacobs, E.N. The Aerodynamic Characteristics of Eight Very Thick Airfoils from Tests in the Variable Density Wind Tunnel; NACA: Boston, MA, USA, 1932. Available online: https://ntrs.nasa.gov/citations/19930091465 (accessed on 24 July 2024).
- Hansen, K.L.; Kelso, R.M.; Dally, B.B. Performance variations of leading-edge tubercles for distinct airfoil profiles. AIAA J. 2011, 49, 185–194. [Google Scholar] [CrossRef]
- Koning, W.J.; Romander, E.A.; Cummings, H.V.; Perez Perez, B.N.; Buning, P.G. On improved understanding of airfoil performance evaluation methods at low Reynolds numbers. J. Aircr. 2023, 60, 774–788. [Google Scholar] [CrossRef]
- Radespiel, R.; Windte, J.; Scholz, U. Numerical and experimental flow analysis of moving airfoils with laminar separation bubbles. AIAA J. 2007, 45, 1346–1356. [Google Scholar] [CrossRef][Green Version]
- Collie, S.; Gerritsen, M.; Jackson, P. Performance of two-equation turbulence models for flat plate flows with leading edge bubbles. J. Fluids Eng. 2008, 130, 021201. [Google Scholar] [CrossRef]
- Rezende, A.L.T.; Nieckele, A.O. Evaluation of turbulence models to predict the edge separation bubble over a thin aerofoil. In Proceedings of the 20th International Congress of Mechanical Engineering—COBEM, Gramado, Brazil, 15–20 November 2009. [Google Scholar]
- Menter, F.R.; Esch, T.; Kubacki, S. Transition Modelling Based on Local Variables. In Proceedings of the 5th International Symposium on Engineering Turbulence Modelling and Measurements, Mallorca, Spain, 16–18 September 2002; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Langtry, R.B.; Menter, F.R.; Likki, S.R.; Suzen, Y.B.; Huang, P.G.; Völker, S. A correlation-based transition model using local variables—Part II: Test cases and industrial applications. J. Turbomach. 2006, 128, 423–434. [Google Scholar] [CrossRef]
- Menter, F.R. Turbulence Modeling for Engineering Flows; Ansys, Inc.: Canonsburg, PA, USA, 2011. [Google Scholar]
- Aftab, S.M.A.; Mohd Rafie, A.S.; Razak, N.A.; Ahmad, K.A. Turbulence model selection for low Reynolds number flows. PLoS ONE 2016, 11, e0153755. [Google Scholar]
- Carreño Ruiz, M.; D’Ambrosio, D. Validation of the γ-Re θ Transition Model for Airfoils Operating in the very Low Reynolds Number Regime. Flow Turbul. Combust. 2022, 109, 279–308. [Google Scholar] [CrossRef]
- Koning, W.J.F. Airfoil Selection for Mars Rotor Applications; NASA Ames Research Center Moffett Field: Mountain View, CA, USA, 2019. Available online: https://rotorcraft.arc.nasa.gov/Publications/files/Koning%20CR-2019-220236_FINAL.pdf (accessed on 24 July 2024).
- Choudhry, A.; Arjomandi, M.; Kelso, R. A study of long separation bubble on thick airfoils and its consequent effects. Int. J. Heat Fluid Flow 2015, 52, 84–96. [Google Scholar] [CrossRef]
- Koning, W.J.F.; Johnson, W.; Allan, B.G. Generation of Mars Helicopter Rotor Model for Comprehensive Analyses. In Proceedings of the AHS Aeromechanics Design for Transformative Vertical Flight, San Francisco, CA, USA, 16–18 January 2018. [Google Scholar]
- Menter, F.R.; Langtry, R.B.; Likki, S.R.; Suzen, Y.B.; Huang, P.G.; Völker, S. A correlation-based transition model using local variables—Part I: Model formulation. J. Turbomach. 2006, 128, 413–422. [Google Scholar] [CrossRef]
- Pauley, L.L.; Moin, P.; Reynolds, W.C. The structure of two-dimensional separation. J. Fluid Mech. 1990, 220, 397–411. [Google Scholar] [CrossRef]
- ANSYS, Inc. ANSYS FLUENT 12.0/12.1 Documentation; ANSYS, Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Sanders, D.D. CFD Modeling of Separation and Transitional Flow in Low Pressure Turbine Blades at Low Reynolds Numbers. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2009. [Google Scholar]
- Wang, S.; Zhou, Y.; Alam, M.M.; Yang, H. Turbulent intensity and Reynolds number effects on an airfoil at low Reynolds numbers. Phys. Fluids 2014, 26, 115107. [Google Scholar] [CrossRef]
- Horton, H.P. Laminar Separation Bubbles in Two and Three Dimensional Incompressible Flow. Ph.D. Thesis, Queen Mary University of London, London, UK, 1968. [Google Scholar]
- Russell, J.M. Length and bursting of separation bubbles: A physical interpretation. In The Science and Technology of Low Speed and Motorless Flight, Part 1; NASA Langley Research Center: Hampton, VA, USA, 1979. [Google Scholar]
- Saxena, A. The Laminar Separation Bubble; Personal Report; University of Maryland: College Park, MD, USA, 2009. [Google Scholar]
- O’meara, M.M.; Mueller, T.J. Laminar separation bubble characteristics on an airfoil at low Reynolds numbers. AIAA J. 1987, 25, 1033–1041. [Google Scholar] [CrossRef]
- Bak, C.; Madsen, H.A.; Fuglsang, P.; Rasmussen, F. Observations and hypothesis of double stall. Wind Energy Int. J. Prog. Appl. Wind Power Convers. Technol. 1999, 2, 195–210. [Google Scholar] [CrossRef]
- Koning, W.J.; Perez, B.N.P.; Cummings, H.V.; Romander, E.A.; Johnson, W. ELISA: A Tool for Optimization of Rotor Hover Performance at Low Reynolds Number in the Mars Atmosphere. In Proceedings of the 2024 Transformative Vertical Flight, Santa Clara, CA, USA, 6–8 February 2024. [Google Scholar]
- Augustin, K.; Rist, U.; Wagner, S. Control of laminar separation bubbles by small-amplitude 2D and 3D boundary-layer disturbances. In Proceedings of the Specialists’ Meeting AVT, Prague, Czech Republic, 4–7 October 2004; Volume 111. [Google Scholar]
| Earth | Mars | |
|---|---|---|
| Density [] | 1.225 | 0.017 |
| Temperature [] | 288.20 | 223.20 |
| Dynamic Viscosity [Pa·s] | 1.750·10−5 | 1.130·10−5 |
| Static Pressure, [] | 101.30 | 0.72 |
| Speed of sound [] | 340.35 | 233.13 |
| Mesh Elements | Boundary Distance | CD 0° | CD 5° |
|---|---|---|---|
| 100 k | 50c | 0.0270395 | 0.0373019 |
| 200 k | 50c | 0.0275159 | 0.0364775 |
| 300 k | 50c | 0.0278523 | 0.0354827 |
| 400 k | 50c | 0.0280134 | 0.0352006 |
| 500 k | 50c | 0.0279638 | 0.0351146 |
| 400 k | 50c | 0.0280134 | 0.0352006 |
| 700 k | 100c | 0.027888 | 0.0350659 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giacomini, E.; Westerberg, L.-G. Rotorcraft Airfoil Performance in Martian Environment. Aerospace 2024, 11, 628. https://doi.org/10.3390/aerospace11080628
Giacomini E, Westerberg L-G. Rotorcraft Airfoil Performance in Martian Environment. Aerospace. 2024; 11(8):628. https://doi.org/10.3390/aerospace11080628
Chicago/Turabian StyleGiacomini, Enrico, and Lars-Göran Westerberg. 2024. "Rotorcraft Airfoil Performance in Martian Environment" Aerospace 11, no. 8: 628. https://doi.org/10.3390/aerospace11080628
APA StyleGiacomini, E., & Westerberg, L.-G. (2024). Rotorcraft Airfoil Performance in Martian Environment. Aerospace, 11(8), 628. https://doi.org/10.3390/aerospace11080628






