Abstract
Electromagnetic tethers of hundreds or thousands of meters have been proposed for maneuvring spacecraft in Low Earth Orbit, and in particular, for post-mission disposals. The debate on tether survivability to debris impact is still influencing further advances in the implementation of such technology because of the large area they expose to the debris environment; thin tape geometries have been proposed instead of round ones to increase the survivability to hypervelocity impacts. In this context, this paper introduces a new Ballistic Limit Equation (BLE) for thin tape tethers, derived from experimental results, numerical simulations, and literature data. The resulting equation is non-monotonic with respect to impact angle, presenting a minimum depending on the debris velocity and size; for high obliquities, the debris fragmentation triggered by shock waves propagating into the material reduces the damage. This feature allows to set a minimum particle diameter for risk assessment, excluding a significant part of the debris flux. The proposed BLE confirms the performance of thin tape tethers, with respect to round wires, due to their better ballistic response as well as their reduced cross-section at high-obliquity impacts.
1. Introduction
Tether systems for space have been proposed since the 1970s [1]; they consist of long cables or wires connecting orbital bodies (e.g., satellites, rocket stages, probes) that can be used, among others, for orbital maneuvring, momentum exchange, and attitude control. The first electromagnetic tether was tested on board the Space Shuttle in 1992 [2], as a joint collaboration between NASA and the Italian Space Agency. To date, different concepts have been proposed involving tethered spacecraft [3], with applications spanning from on-orbit servicing operations [4,5] to orbit transfer [6,7,8]; in particular, with regards to electromagnetic tethers, deorbiting devices have been investigated [9,10] or are under development [11,12]. A partial list of the most recent tether missions include TEPCE, that was partially successful in deploying a 1 km long tether with a 3U CubeSat splitting in two halves [13], the STARS mission by JAXA, testing different tether technologies [14], and the MiTEE demonstration mission [15]. In addition, the E.T.Pack project, funded by the European Commission, aims to develop and launch a technology demonstrator of a tether-based post-mission disposal kit before 2027 [16]. Other recent works focus on the development of safe and reliable technologies for the deployment and stabilization of space tethers [17,18,19,20].
One of the potential drawbacks for the widespread employment of tethers is the open debate on their survivability in the near-Earth space environment [21], and, in particular, their response to hypervelocity impacts (HVIs); tether lengths (up to kilometers) and their potential operational lifetime (up to years) make such devices particularly susceptible to debris impact. Previous investigations on tether damage were mostly focused on round wire geometries, providing a first estimation of their ballistic limit, assuming that the damage volume depends on the debris kinetic energy [22,23,24]. To improve tether survivability to HVIs, thin tape geometries have been proposed instead of the classic round wire ones [25,26]; in addition, for tapes, charged particles collection from the magnetosphere is enhanced by the larger active area. The investigation of tape tether response to HVIs and, in particular, of the effect of impact orientation on the tapes has already been partially addressed [27,28], suggesting better survivability of this configuration. This theme will be further elaborated in this work.
Ballistic Limit Equations (BLEs) are employed in the space sector to assess the survivability of structures or components to collisions with space debris; they define the threshold particle size that would cause perforation or failure as a function of other impact parameters (e.g., impact velocity, impact angle, projectile and target materials and geometry) [29]. In general, they are represented as demarcation lines between no-perforation and perforation regions; as a function of the expected debris environment, they help to assess the failure risk of a component, therefore driving and constraining the design of a space mission. In this paper, a new empirical Ballistic BLE for thin tape tethers is introduced and its development is described; it provides the minimum particle diameter dcrit to produce tether failure (cut-off) at a given projectile speed and impact angle. The work is performed for two investigated materials, polyether ether ketone (PEEK) and aluminum Al-1100-H19. The remainder of this paper is organized as follows: The method used for tape damage modeling and BLE development is summarized in Section 2; a description of the experimental results and numerical simulations is then given in Section 3. Section 4, Section 5 and Section 6 introduce the damage models, respectively, for low impact angles (4 and 5) and high obliquity (6). Finally, BLE derivation and uncertainty calculation are discussed in Section 7.
2. BLE Development and Verification Method
2.1. Impact and Tape Tether Geometry
The tape tether geometry investigated in this work can be seen in Figure 1, left: in the case of an impact with a debris with velocity vp, a damage ellipse is defined by two axes, A and B. An “edge impact”, visible on the right, occurs when the projection of the projectile is not contained in the tape surface, causing a damage on its edge. The tether length (i.e., in the z-direction) is not considered a relevant parameter for this study, as it can be considered infinite (tens to thousands of meters) with respect to the debris size (a few millimeters) in the space application; in the experiments reported in Section 3, such length was about two orders of magnitude larger than the projectile size.
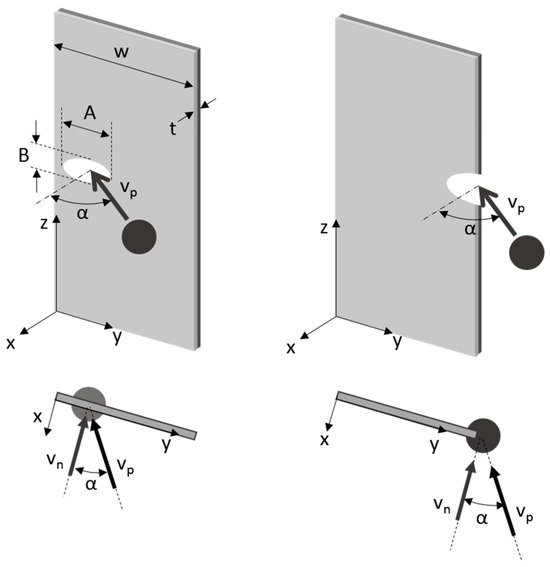
Figure 1.
Tape tether geometry and reference frame for impacts (left); edge impact (right). A and B are the damage ellipse major and minor axes, vn is the projection of the debris velocity vp on the normal to the tape.
2.2. Damage Model
Before introducing the BLE development approach, it is necessary to introduce the damage model employed in this work. It has been observed that, for quasi-normal impacts, the response of a thin tape to HVIs is equivalent to that of a thin plate—a spherical projectile creates a circular perforation hole (elliptical for non-normal impacts), with a diameter comparable to the projectile, with a well-defined and continuous circumference and minor or negligible material accumulation on the hole border. For the aforementioned reasons, in addition to dedicated experimental tests and numerical simulations data [27,28], literature data and models for thin plate perforation have been included in this work. This approach allows investigating the proposed model at tape thicknesses not directly investigated in the referenced works [28].
As reported by Abbas et al. [30], thin metallic plate impacts have been modeled by many authors, considering the projectile and the target density and the geometric dimensions as well as the impact velocity and direction. In particular, Hill [31] proposed a model for the perforation hole diameter reported in Equation (1) and compared it with relevant historical impact data [32,33,34,35]:
where subscripts h, p, and t, respectively, indicate the perforation hole, the impacting projectile, and the impacted target. The main difference between Hill’s model and this study case is the different thickness of the target, that in his case can be sixty times the one investigated in this work (up to 3.175 mm for Hill, 0.05 mm for the experiments reported in Section 3); furthermore, the model reported in Equation (1) does not consider the influence of the impact angle. However, the dp/t ratios that can be found in Hill’s work (from 2 to 12) are in a more comparable range with the tape experimental data (30 and 46).
Similarly, Sorenson [36] and Piekutowski [37] propose a model for the hole diameter based on the hypothesis that when the target thickness t is small with respect to the debris, the hole diameter should be close to the debris one. In general, Piekutowski and Sorensen consider the minimum hole size to be equal to the debris diameter. Their model can be written as follows:
Reflecting these considerations, we propose two models for the damage, based on the previous equations but including a relation with the impact angle, as reported in Equation (3); then, we compare their application limits and reliability in terms of maximal errors. The first one, the Adapted Hill Model (AHM) is similar to Equation (1) and considers the damage as a function of the dp/t ratio, the impact velocity, and the impact angle. The main difference is related to the absence of a totally linear dependence to the particle diameter, following the approach already presented by Francesconi for a first analysis of the experimental dataset [28]. The other one, the Adapted Piekutowski–Sorenson Model (APSM), is based on the same considerations and, in addition, assumes that the minimum size of the perforation hole should be equal to the projectile projection on the tape, . The experimental results employed to develop this model are between 0° and 80°, while the literature data are limited to a maximum impact angle of 56.4°.
The dependence of Equation (3) on the material is not considered in this work as different coefficients ki are independently calculated for the two investigated materials. In addition, the employed experimental and numerical results have been determined at a constant tape thickness t0. To include the dependence on the thickness, the equations have been modified with the addition of the parameter, the influence of which is assessed by employing literature data on thin plates. The definition of the main parameters of Equation (4) is discussed in Section 4 and Section 5.
Last, particular attention is paid to high-obliquity impact angles, in which the assumption of a flat plate cannot be satisfied, and debris fragmentation can influence the impact process; in this case, an additional dedicated model is developed (see Section 6).
2.3. Empirical Procedure for BLE Development
The procedure employed in this work to obtain the BLE is based on an empirical approach proposed by Francesconi [28]; this method has the advantage of making it possible to estimate the failure prediction uncertainty. It consists of four steps, and is applied, respectively, to the Al-1100 and the PEEK tapes in order to calculate the BLE coefficients and their uncertainty for both the tether materials, as follows:
- Test data acquisition: hypothesizing an elliptical damage, high-resolution imaging from experimental samples allows to determine the perforation ellipse major and minor axes A and B (see Figure 1). In this work the experimental dataset is enriched by results from dedicated numerical simulations; the dependence form tape thickness is assessed using literature data.
- Empirical derivation of the damage equation: correlations between the damage major axis A and the impact parameters (particle size and velocity, impact angle, tape dimensions) are evaluated and verified. The damage equation is in the form:
- Empirical determination of the critical damage: Acrit is determined based on available data or theoretical modeling as the maximal damage the tether could endure as a percentage of the tape width before failure in the y-direction (i.e., tether cut-off).
- BLE derivation: by inserting the critical value Acrit in the damage equation and inverting it, the BLE can be obtained.
Usually, BLEs are presented as simple “demarcation lines” between fail and no-fail conditions, with no statistical significance [38]; by contrast, the key advantage of this method is that the BLE is given with uncertainty bands, thanks to the fact that both the damage equation fd and the critical damage value Acrit are obtained mostly from experiments, and, hence, they can be related to suitable confidence intervals. All the available data, even well away from the ballistic limit, can, therefore, be used to statistically follow the critical parameter evolution. In this way, it is possible to provide an estimation of the test conditions at the ballistic limit, even inside the bounds defined by the two closest non-critical and critical experiments.
In this work, the value of A is obtained from experimental as well as numerical results. In parallel, a comparison with historical impact data from Hill [31] and Piekutovski [39] was employed to evaluate the effect of thickness and to validate the damage equations.
3. Experimental and Simulation Data
The experimental impact tests presented in this section were conducted at the CISAS G. Colombo Hypervelocity Impact Facility, using a two-stage light gas gun (LGG) capable of accelerating projectiles in the range 0.6–3 mm of diameter at speeds up to 6 km/s [40,41,42]. For the experimental campaign, a dedicated test setup was designed (see Figure 2); up to three tape samples were mounted in order to maximize the test success rate even at high-obliquity impacts. The possibility to orient the tapes as well as the LGG scattering allowed to define their orientation with respect to the projectile flight path with an accuracy up to ±1°.

Figure 2.
Tethers support structure mounted in the LGG impact chamber: On the left, the tape configuration is at α = 0°, on the right, tethers are oriented at α~90° (high obliquity).
It must be underlined that the impact damage near 90° is highly dependent on the impact angle, and its evaluation is influenced by the angular uncertainty; therefore, for high-obliquity impacts, the ballistic limit equations determination required the utilization of numerical simulations results.
3.1. Test Results
During the experimental campaign, 24 hypervelocity impact tests were performed, varying the projectile speed and impact orientation, on Al-1100-H9 and PEEK tapes with a thickness of 0.05 mm and width of 25 mm [28]. Aluminum spherical projectiles were employed in the campaign; among the tests, 22 were performed with 1.5 mm projectiles and 2 with 2.3 mm ones. The results are summarized in Table A1 in Appendix A, with the ID identifying impact angles less than 80° (numbers) and at 90° (letters); edge impacts are indicated in grey. The result of two shots can also be observed in Figure 3 and Figure 4, showing, respectively, a normal impact on Al-1100 and a 90° impact on PEEK.

Figure 3.
Test no. 8856 (Al-1100-H19, α = 0°): setup (left); detail of the tape damage (right).

Figure 4.
Test no. 8871 (PEEK LITE, α = 90°): setup with highlighted the damage area (left); detail of the tape damage with a marker arrow for analysis (right).
From a preliminary inspection, it is possible to report that the tape damage, indicated by the value A, in conditions of normal impact is very close to the projectile diameter, but it increases with the impact angle. Furthermore, the two tape materials show a similar behavior; it is expected that the damage equations will be analogous in their form and coefficients.
3.2. Numerical Simulations
Numerical simulations were conducted using ANSYS AUTODYN 3D on a multicore with CPU Intel I7 920@2.67 GHz processor and 6 GB RAM. The standard testbed consisted of a spherical Al-1100 projectile impacting on a tape 25.4 mm wide and 0.05 mm thick; the tape was discretized in mesh of about 0.13 mm. For tests with α = 90°, the projectile diameter was raised up to 15 mm and the tape thickness and width, respectively, to 0.50 mm and 35 mm, and, hence, the mesh was increased up to 0.5 and 1 mm after some validation versus simulation runs with better discretization. Further information can be found in [28]. The simulation parameters as well as the damage extension are reported in Appendix B in Table A2 (α = 0–80°) and Table A3 (α~90°). Since the tether structure and the behavior of the materials employed for its construction are known fairly well, quite reliable results were expected. A total of 112 runs were performed (α from 0° to 80° and α~90°) on both materials; about 30 simulations were not successful, with no possibility of a result forecast, while 20 other simulations were interrupted close to the end, and a prediction of an approximate final result was formulated. For the sake of completeness, these results are included in the report tables and highlighted, although they are not reliable enough to be used in the BLE development.
4. Damage Equation Derivation and Verification (α = 0–80°)—Adapted Hill Model
The damage equation for the range 0–80°, reported in Equation (4) (AHM), describes the tether damage as a function of the main geometrical parameters. Data from the experiments and simulations, as well as additional experiment data from the literature, were employed to derive the values of the damage equation coefficients for Al-1100 and PEEK. Results presenting vn < 1 km/s were weighted with the employment of a fragmentation correction coefficient σ, as proposed by Francesconi [28]. For the sake of completeness, the justification for employing such correction is reported here. The dependence of the model on the angle causes the derived equation to have a vertical asymptote for α = 90° (i.e., the damage parameter A tends to infinity), clearly not representing the physics of highly oblique impacts. As represented in Figure 5, with increasing impact angle, the normal velocity vn decreases with respect to the velocity of shock waves propagating inside the debris (top); under a threshold value vn,thr, the shock wave can fragment the debris before it fully interacts with the tether (bottom), letting pieces bounce on the tape surface and reducing the damage with respect to the prediction. Due to this phenomenon, the proposed models reported in Equation (4) cannot fully represent the fragmentation process.
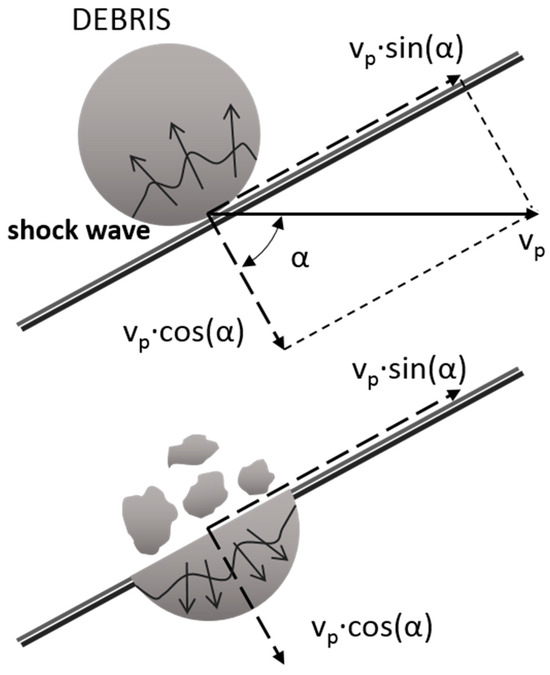
Figure 5.
Debris fragmentation upon highly oblique impact.
Francesconi et al. [28] propose use of an empirical fragmentation correction coefficient σ to apply to the debris diameter dp, that can be defined as follows:
The values of the two coefficients are reported in Table 1. In particular, k6 represents the characteristic velocity of the investigated material and is proposed as an indirect value for the threshold velocity vn,thr.

Table 1.
Fragmentation parameters for Al-1100 and PEEK (Adapted from [28]).
Starting from these considerations, a non-linear fitting was performed using test, simulation, and literature data, as well as the fragmentation coefficient σ. Literature data allowed investigating target thicknesses different from the test and simulation ones (t0 = 0.05 mm), leading to generalization of the proposed model AHM. This generalization can be written as:
The calculation of the coefficient n was performed using available historical data on aluminum thin plate impacts by Hill [31] and Piekutowski [39], considering dp/t ratios comparable to the studied one. A threshold was defined at dp/t = 5, allowing to obtain the parameter n = 0.8759; therefore, Equation (8) is rewritten in a simpler version in Equation (9), with the five coefficients reported in Table 2:

Table 2.
Equation parameters for Al-1100 and PEEK (AHM—final model).
It must be underlined that this generalization is valid for the Al-1100 model. PEEK parameters were derived using the same value of n, and the obtained model, still valid for the investigated tether geometrical parameters, will require further investigation to evaluate the influence of the tape thickness.
In Figure 6 the proposed damage model is compared with the available data from the tape experiments and simulations and from historical data. It must be underlined that the fit standard deviation for this case is less than 10%.
Figure 6.
Comparison between AHM model and results available from tape experiments and simulations (circular marks) and from thin plate historical data (data from Hill [31], Piekutowski [39]).
4.1. Damage Equation Outside the Test Range (dp/cos(α) > w)
The aforementioned damage model was developed comparing the tape to a thin plate, a condition that can be considered satisfied for small debris (Figure 7, left); however, there are configurations in which such a hypothesis cannot be confirmed, i.e., when the debris diameter projection on the tape is larger than the tether width (Figure 7, right). Therefore, the model needs to be adapted to this new configuration; a proposed solution is reported in Equation (10), substituting the debris projection dp/cos(α) with the tether width.
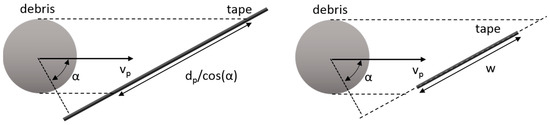
Figure 7.
Geometrical projection of the debris diameter on the tape surface: in the test range case, the tape width is larger than the projection (left); on the (right), the debris projection is larger than w.
4.2. Limitations of Adapted Hill Model
Despite the good results from the AHM, some issues were highlighted on its range of applicability. The model is based on experimental and simulation data with a ratio dp/t in the range 10–46 and it is improved with available literature data from thin plates (dp/t in the range 5–35). For this reason, it is expected that for higher dp/t ratios (dp/t > 50), the model could have lower precision. In particular, Figure 8 shows that for larger debris sizes, the AHM tends to underestimate the damage when it becomes smaller than the debris diameter. For this reason, this model is suggested only for tapes with a small w/t ratio (i.e., w/t < 100), for which large values of dp/t could be reached only for debris with a diameter comparable to the tape, that would already cause damage wide enough to sever it.
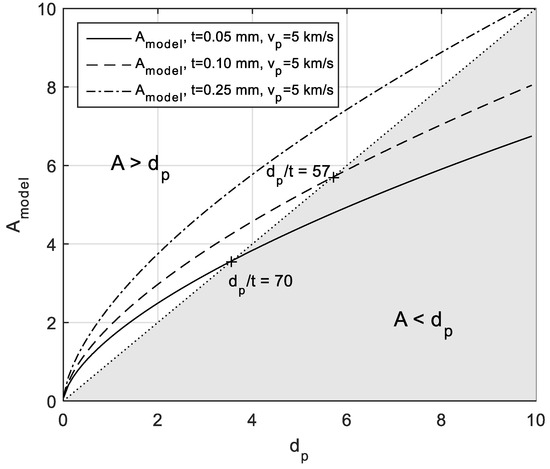
Figure 8.
Comparison of debris size and damage prediction with AHM (normal impacts); large dp/t ratios may cause damage underestimation for large debris size.
Based on these considerations, the following Adapted Piekutowski–Sorenson Model (APSM) model is proposed; thanks to its different formulation, it overcomes such limitations, allowing investigating the higher dp/t ratios.
5. Damage Equation Derivation and Verification (α = 0–80°)—Adapted Piekutowski–Sorenson Model
The APSM, reported in Equation (4), describes the tether damage as a function of the test parameters, considering that for the highest dp/t ratios, the damage tends to become equal to the debris diameter projection on the tape. The equation coefficients are again calculated with the introduced iterations process, starting from experimental data and considering the influence of fragmentation, and then adding simulations and corrected experimental results as well as the thin plate data from historical impact tests. For the sake of brevity, the whole process is not reported and only the final parameters are summarized in Equation (11) and Table 3:

Table 3.
Equation parameters for Al-1100 and PEEK (APSM—final model).
Again, it must be underlined that this generalization is valid for the Al-1100 model. The PEEK parameters were derived using the same literature dataset, and the obtained model, still valid for tether data, would require further investigation to evaluate the influence of the tape thickness. In all the aforementioned cases, it must be remembered that for low normal velocities, the damage size needs to be calculated using the correction parameter σ.
In Figure 9, the proposed damage model is compared with the available data from tape experiments and simulations and from historical data. It must be underlined that the fit standard deviation for this case is less than 10.5%.
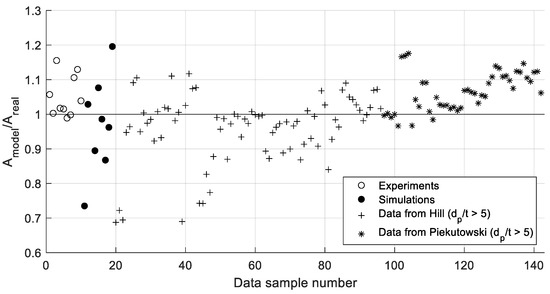
Figure 9.
Comparison between APSM model and results available from tape experiments and simulations (circular marks) and from thin plate historical data (data from Hill [31], Piekutowski [39]).
5.1. Comparison with Adapted Hill Model
A brief comparison between the two elaborated models is reported here. Figure 10 shows that both the AHM and the APSM present similar behavior for small size debris at different thicknesses and velocities; it is determined that for values of dp/t in the range from 5 to 35, the difference is less than 15% for thicknesses up to 0.5 mm. For larger particles, the two model predictions diverge: the APSM shows a linear trend and predicts a damage larger than the debris diameter, while the AHM damage prediction decreases below the particle size for large debris.
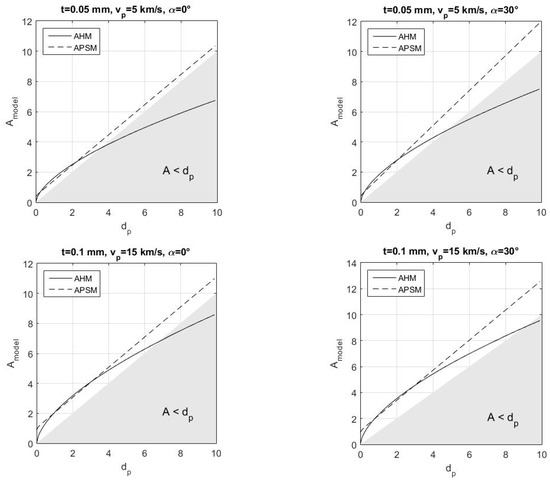
Figure 10.
Comparison of damage prediction as a function of debris size for AHM and APSM, at different thickness, velocity, and impact angle.
5.2. Simplification for Large dp/t Ratios
Figure 10 clearly shows that at different values of thickness, velocity, and impact angle, the APSM presents a linear trend for large dp/t ratios. The deviation between a linear model (i.e., depending only on the parameter ) and APSM can be seen in Figure 11 and decreases under 10% for dp/t > 100. Based on this consideration, it is possible to rewrite Equation (11) in an extremely simplified form:
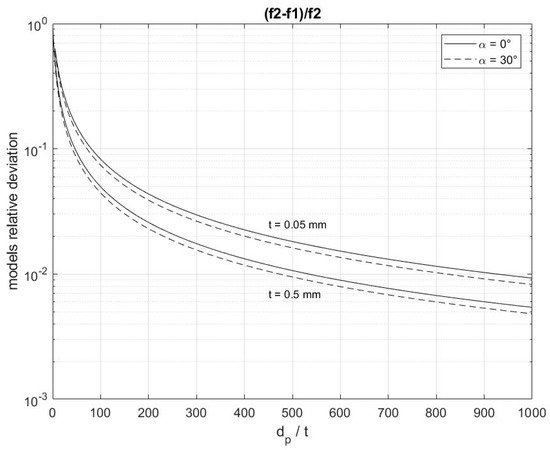
Figure 11.
Difference between APSM and linear model at different thicknesses and impact angles; for dp/t > 100, the relative deviation is under 10% for the investigated tape.
More precisely, the maximal deviations for Al-1100 and PEEK, calculated for a thickness of 0.05 mm and a dp/t ratio of 100, are, respectively, 8.27% and 4.00%.
6. Damage Equation Derivation (α~90°)
For high-obliquity impacts (α~90°), numerical simulations were used to study the tape behavior. It must be considered that in this case the impact physics can be more complex than in the previous one, so a novel damage equation applicable for impact angle α = 90° is derived. The resulting formula is reported in Equation (13) and suggests that the damage at 90° is nearly independent of the impact velocity.
The values of the fit parameters and their standard deviations are given in Table 4; it should be noted that the two tapes (Al-1100 and PEEK) show different behavior (i.e., different parameter values), but for both the cases, the dependence from the tape thickness is similar (c3 is about −1/4 for both the cases). With the values below, the fit correlation index is R2 = 0.91 for Al-1100 and R2 = 0.97 for PEEK; the fit standard deviation is σFIT = 29% for Al-1100 and σFIT = 33% for PEEK.

Table 4.
Equation parameters for Al-1100 and PEEK (α = 90°).
7. Ballistic Limit Equation for Tapes
Following the procedure introduced in Section 2, a ballistic limit equation can be obtained from the damage equations derived in Section 4, Section 5 and Section 6. It is worth underlining that the resulting BLE is a piecewise formula, since the different damage equations are applicable to different ranges of normal velocity vn:
- (1)
- For vn > vn,thr = k6, the BLE is derived from Equation (10) (AHM) or (12) (linearized APSM);
- (2)
- For vn = 0 (α~90°), the BLE is derived from Equation (13);
- (3)
- For 0 < vn < vn,thr = k6, the BLE is constructed linearly joining the value derived from Equation (13) to the one derived from Equation (10) or (12) for vn = k6.
Before elaborating the damage equations in the desired form, a critical value Acrit for the damage major axis shall be assumed; by definition, the tether is cut-off if A ≥ Acrit. In general, Acrit can be different for the two materials and can be represented in the form:
Equation (14) defines the critical damage as the minimum amount of material that has to be removed by the impact from the tether to cause the failure; the coefficients kw are both smaller than 1, and have been calculated as the residual cross-section capable to withstand the tether loads, estimated as about 10 N of tensile load and (only for Al-1100) 2 A of electric current [28]. The values of the two coefficients are reported in Table 5 and were calculated considering the material properties at the maximum operative temperature expected for the tape tether. The lower value for Al-1100 is justified by the need to sustain both the mechanical and thermal load due to the current flow.

Table 5.
Critical damage coefficients for the two investigated materials.
7.1. BLE Derivation for vn > vn,thr = k6—AHM
To obtain the BLE, the critical damage parameterization is inserted in Equation (10) and the resulting formula is inverted, as reported in Equation (15):
It should be noted that Equation (15) identifies a minimum debris velocity vp* below which no critical damage is possible. The value of vp* depends on the tape material and geometry, as well as the impact angle. Unfortunately, such values may not be acceptable, as the AHM model applicability is limited to a ratio dp/t < 100, and the investigated values for tape failure rise to dp/t >> 100. However, this model is still acceptable for predicting small damages or for tethers with small width (w/t ≤ 100); as mentioned in Section 4, for such geometries, the damage model can be assumed to be valid. For example, Figure 12 shows for both Al-1100 and PEEK, the trend of vp* as a function of the angle for a tether of width w = 10 mm and thickness t = 0.1 mm. It can be observed that debris with velocity smaller than vp* do not critically damage the tape tether. The dotted line indicates debris velocity in the condition vn = vn,thr.
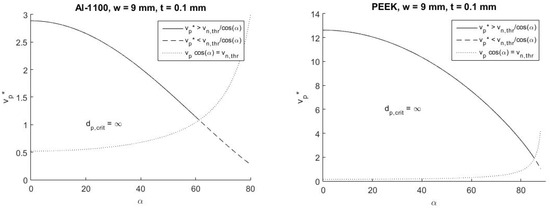
Figure 12.
vp* trend for a 9 millimeter-wide tether at different impact angles for Al1100 (left) and PEEK (right).
The uncertainty of this BLE is estimated by propagating the uncertainties of the individual parameters ki, using the classic method introduced by Kline and McClintok [43]; σFIT is the standard deviation of the model, as reported in Table 2.
Solving Equation (17), the uncertainty can, therefore, be rewritten as follows:
Equation (18) shows that the uncertainty depends mainly on the velocity, the thickness, and the impact angle. In Table 6, its value is reported both for Al-1100 and PEEK for three different impact speeds (two applicable to debris, one to meteoroids), for three different tape thicknesses.

Table 6.
Uncertainty for dp,crit estimation for different thicknesses and velocities.
7.2. BLE Derivation for vn > vn,thr = k6—Linearized APSM
The linearized APSM, reported in Equation (12), is rewritten in the form:
It is clear that such a formulation is totally independent from the tape thickness and the impact velocity, and unlike the AHM, it can be employed for tapes with w/t > 100.
Following the same procedure of Section 7.1, the uncertainty is calculated both for Al-1100 and PEEK and can be written as shown in Equation (20), in this case introducing also the linearization uncertainty ; the resulting values are reported in Table 7.

Table 7.
Uncertainty values for the APSM.
7.3. BLE Derivation for vn = 0 (α = 90°)
The BLE for normal impacts, derived from Equation (13), can be written in the form:
The critical damage, therefore, depends only on the tape material and the geometrical dimensions. For the tether investigated in [28] (thickness of 0.05 mm, width of 25 mm), the value of the particle critical diameter is 6.53 mm for Al-1100 and 4.43 mm for PEEK. Again, the uncertainty formulation and values are reported in Equation (22) and in Table 8.

Table 8.
Uncertainty values for the 90° model.
7.4. BLE Derivation for 0< vn < vn,thr = k6
The BLE in this range is simply obtained by joining the previous models (AHM or APSM calculated in vn,thr = k6 with the α~90° model) with a linear function of vn:
The uncertainty can be obtained by joining with a linear function of vn the uncertainty value calculated with the AHM or the APSM (for vn = k5) to that calculated for α~90°.
8. Results
The new piecewise BLE, described by the previous equations, is represented in Figure 13 (for w/t < 100) and Figure 14 (w/t > 100, study case in [27]), as a function of the impact angle α and for different impact velocities; in all the plots, the BLE is also compared to the classic assumption (for round wires, dash-dot line) that the critical damage can be caused by a particle with size around one-third of the tether equivalent diameter, w∙cos(α). In all the cases, the classic BLE is much more conservative, and this analysis demonstrates that tapes are much less vulnerable with respect to round wires.
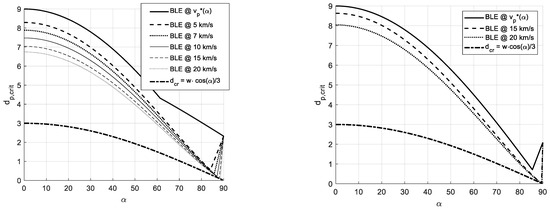
Figure 13.
Piecewise BLE for Al-1100 (left) and PEEK (right), as a function of the impact angle, for a tape having thickness 0.1 mm and width 9 mm (w/t < 100).
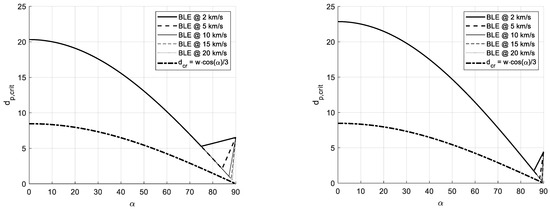
Figure 14.
Piecewise BLE for Al-1100 (left) and PEEK (right), as a function of the impact angle for the investigated tape, where t = 0.1 mm and w = 25.4 mm (w/t > 100).
It also appears that both materials show similar behavior, considering that the critical damage coefficient kw is greater for PEEK; the plots also show the influence of the different fragmentation thresholds, causing the Al-1100 BLE to vary its trend at lower impact angles.
Last, it is important to note the main effect of the BLE formulation for w/t < 100 (AHM, Figure 13) and for w/t > 100 (linearized APSM, Figure 14). In the first case, it is possible to appreciate the BLE dependence on the impact velocity, and a minimum value vp* can be determined below which no critical damage is caused; for higher velocities, a minimum value of dp,crit*, as a function of the impact velocity, can be determined, corresponding to the threshold to debris fragmentation. In the linearized APSM, it is instead possible to note that the BLEs are all overlapping before the fragmentation threshold, as the tape is so thin that the debris velocity does not influence the damage size; again, a minimum value of dp,crit can be determined at the fragmentation threshold.
The possibility to determine these minimum values is an extremely important feature for the BLE, since it sets a minimum particle diameter for risk assessment, allowing to exclude a large part of the flux from risk computation. For example, in the case shown in Figure 14 (left), the investigated tape shows that dp,crit* = 5 mm for an impact velocity of 20 km/s; almost all micrometeoroids are below this size, leading to the conclusion that, for this tether, micrometeoroids do not represent a serious threat. A formulation of dp,crit* is reported in Equation (24), in the condition that .
9. Conclusions
This paper presented the derivation of a new experimental ballistic limit equation for tapes, which represents a significant advancement in the state of the art with respect to previous equations developed for round wires, that are mainly based on geometrical considerations and limited experimental data and which neglect the damage dependence on the impact velocity and angle. By contrast, in this study, special care has been paid to the highly directional impact behavior of tapes.
The BLE derivation combined experimental results (HVI tests performed on tapes with fixed thickness and width) and numerical simulations with data from the state of the art, making it possible to estimate the uncertainty in the failure prediction. Two different damage models were proposed, the Adapted Hill Model (AHM) and the Adapted Piekutowski–Sorenson Model (APSM), investigating their validity; the first one showed a damage underestimation for the higher dp/t ratios, so a linearized form of the latter was used for dp/t > 100.
The resulting equation is non-monotonic with respect to the impact angle, presenting a minimum, depending on the debris velocity and size; for higher obliquities, the debris fragmentation triggered by shock waves propagating into the material reduces the damage on the tether.
Two different formulations were proposed for the BLE, depending on the width-to-thickness ratio and derived from the AHM and the linearized-APSM. For w/t < 100, it was observed that there is a minimum value of debris velocity below which no critical damage is possible, and, furthermore, that there is a minimum velocity-dependent value dp,crit * of the debris diameter below which no critical damage is possible. For higher w/t ratios, the influence of the debris velocity and the tape thickness were considered negligible due to the larger debris size involved in tape failure; the tape is so thin that the debris velocity does not influence the damage size. Again, it was possible to determine a minimum value of dp,crit*, velocity-dependent, at the fragmentation threshold. This feature of BLE is extremely important, since it sets a minimum particle diameter for risk assessment.
Last, it is worth underlining that this study confirms that thin tapes are significantly more resistant than round wires of equivalent cross-section, thanks to the intrinsic ballistic response of tapes.
Further investigation should focus on high-obliquity impacts in order to model the fragmentation phase and improve the proposed damage model.
Author Contributions
Conceptualization, L.O. and A.F.; investigation, L.O.; data analysis, C.G.; resources, C.G.; writing, L.O.; project administration, A.F.; funding acquisition, A.F. All authors have read and agreed to the published version of the manuscript.
Funding
The experimental activities presented in this work were carried out in the framework of Project 262972 (BETs) funded by the European Commission under the FP7 Space Program.
Data Availability Statement
The data employed in developing the proposed models are available upon reasonable request to the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| A | = | damage ellipse major axis, mm |
| B | = | damage ellipse minor axis, mm |
| BLE | = | Ballistic Limit Equation |
| c | = | sound velocity in the material, km/s |
| ci | = | BLE constant (high-obliquity impacts) |
| d | = | diameter, mm |
| fd | = | damage function |
| Ki | = | numerical constant in Sorensen and Piekutowski model |
| ki | = | BLE constant |
| R2 | = | fit correlation index |
| t | = | tether thickness, mm |
| t0 | = | tether thickness in experiments, 0.05 mm |
| v | = | velocity |
| w | = | tether width, mm |
| U | = | uncertainty |
| vn | = | normal impact velocity, km/s |
| vp | = | impact velocity, km/s |
| α | = | impact angle, ° |
| ρ | = | material density, kg/m3 |
| σ | = | fragmentation correction coefficient |
| σFIT | = | standard deviation of the fit equation |
| Subscripts: | ||
| crit | = | critical (i.e., causing tether cut-off) |
| h | = | hole |
| n | = | normal (to the tether surface) |
| p | = | projectile |
| t | = | target |
| thr | = | threshold |
| Acronyms: | ||
| AHM | = | Adapted Hill Model |
| APSM | = | Adapted Piekutowski–Sorenson Model |
| BLE | = | Ballistic Limit Equation |
| HVI | = | Hypervelocity Impact |
| LGG | = | Light Gas Gun |
| PEEK | = | polyether ether ketone |
Appendix A. Test Results
Results of the experimental campaign [28], with ID identifying impact angles less than 80° (numbers) and at 90° (letters); edge impacts are indicated in grey. Uncertainties for the impact angle, the projectile speed, and the damage are also included. The last column on the left reports the value of the normal impact velocity vn: tests 3, 8, 9, 14, and 21 show values less than 1 km/s.

Table A1.
Hypervelocity impact experiments data; in grey, edge impacts.
Table A1.
Hypervelocity impact experiments data; in grey, edge impacts.
| Material | TEST ID | ID | α *, ° | dp, mm | t0, mm | vp **, km/s | A ***, mm | vn = vp·cos(α) |
|---|---|---|---|---|---|---|---|---|
| Al-1100 | 8855 | 1 | 0 | 1.5 | 0.05 | 4.16 | 1.80 | 4.1600 |
| Al-1100 | 8856 | 2 | 0 | 2.3 | 0.05 | 4.20 | 2.70 | 4.2000 |
| Al-1100 | 8864 | 3 | 80 | 1.5 | 0.05 | 4.61 | 6.90 | 0.8005 |
| Al-1100 | 8932 | 4 | 30 | 1.5 | 0.05 | 4.00 | 2.10 | 3.4641 |
| Al-1100 | 8955 | 5 | 0 | 1.5 | 0.05 | 4.72 | 1.90 | 4.7200 |
| Al-1100 | 8956 | 6 | 30 | 1.5 | 0.05 | 4.81 | 2.20 | 4.1656 |
| Al-1100 | 8957 | 7 | 60 | 1.5 | 0.05 | 4.92 | 3.50 | 2.4600 |
| Al-1100 | 8857 | 8 | 80 | 1.5 | 0.05 | 4.15 | 6.60 | 0.7206 |
| Al-1100 | 8863 | 9 | 80 | 1.5 | 0.05 | 3.40 | 5.10 | 0.5904 |
| Al-1100 | 8933 | 10 | 60 | 1.5 | 0.05 | 3.71 | 3.30 | 1.8550 |
| Al-1100 | 8866 | A | 90 | 1.5 | 0.05 | 4.55 | 2.50 | / |
| PEEK | 8873 | 11 | 0 | 1.5 | 0.05 | 4.20 | 1.70 | 4.2000 |
| PEEK | 8874 | 12 | 0 | 2.3 | 0.05 | 4.08 | 2.40 | 4.0800 |
| PEEK | 8934 | 13 | 30 | 1.5 | 0.05 | 3.75 | 1.80 | 3.2476 |
| PEEK | 8939 | 14 | 80 | 1.5 | 0.05 | 3.89 | 7.00 | 0.6755 |
| PEEK | 8941 | 15 | 30 | 1.5 | 0.05 | 1.89 | 1.70 | 1.6368 |
| PEEK | 8942 | 16 | 30 | 1.5 | 0.05 | 1.98 | 1.70 | 1.7147 |
| PEEK | 8952 | 17 | 30 | 1.5 | 0.05 | 4.75 | 1.80 | 4.1136 |
| PEEK | 8953 | 18 | 60 | 1.5 | 0.05 | 4.44 | 2.90 | 2.2200 |
| PEEK | 8954 | 19 | 0 | 1.5 | 0.05 | 4.64 | 1.70 | 4.6400 |
| PEEK | 8935 | 20 | 60 | 1.5 | 0.05 | 3.63 | 3.10 | 1.8150 |
| PEEK | 8940 | 21 | 80 | 1.5 | 0.05 | 4.54 | 8.40 | 0.7884 |
| PEEK | 8869 | A | 90 | 1.5 | 0.05 | 3.52 | 3.00 | / |
| PEEK | 8871 | B | 90 | 1.5 | 0.05 | 4.48 | 2.30 | / |
* uncertainty < 1° ** uncertainty < 1% *** uncertainty < 0.2 mm.
Appendix B. Simulation Parameters and Results
Results of the simulation campaign [28] for impact angles below 80° (Table A2) and above 80° (Table A3); in grey, simulations that were interrupted close to the end, and for which a prediction of an approximate result was formulated.

Table A2.
Numerical simulations at α = 0–80°; interrupted simulations are highlighted.
Table A2.
Numerical simulations at α = 0–80°; interrupted simulations are highlighted.
| Material | ID | α, ° | dp, mm | t, mm | vp, km/s | A, mm | vn = vp·cosα |
|---|---|---|---|---|---|---|---|
| PEEK | 22 | 0 | 0.5 | 0.05 | 5 | 1.27 | 5 |
| PEEK | 23 | 0 | 0.5 | 0.05 | 12 | 1.27 | 12 |
| PEEK | 24 | 0 | 0.5 | 0.05 | 20 | 0.89 | 20 |
| PEEK | 25 | 0 | 1.50 | 0.05 | 5 | 1.82 | 5 |
| PEEK | 26 | 0 | 1.50 | 0.05 | 12 | 2.54 | 12 |
| PEEK | 27 | 0 | 1.50 | 0.05 | 20 | 2.16 | 20 |
| PEEK | 28 | 0 | 2.30 | 0.05 | 12 | 3.05 | 12 |
| PEEK | 29 | 0 | 2.30 | 0.05 | 20 | 3.56 | 20 |
| PEEK | 30 | 80 | 0.5 | 0.05 | 5 | 3.56 | 0.87 |
| PEEK | 31 | 80 | 0.5 | 0.05 | 12 | 3.68 | 2.08 |
| PEEK | 32 | 80 | 0.5 | 0.05 | 20 | 3.68 | 3.47 |
| PEEK | 33 | 80 | 1.50 | 0.05 | 5 | 6.68 | 0.87 |
| PEEK | 34 | 80 | 1.50 | 0.05 | 12 | 4.95 | 2.08 |
| PEEK | 35 | 80 | 1.50 | 0.05 | 20 | 4.06 | 3.47 |
| PEEK | 36 | 80 | 2.30 | 0.05 | 5 | 3.81 | 0.87 |
| PEEK | 37 | 80 | 2.30 | 0.05 | 12 | 5.46 | 2.08 |
| Al-1100 | 38 | 0 | 0.5 | 0.05 | 5 | 1.27 | 5 |
| Al-1100 | 39 | 0 | 0.5 | 0.05 | 12 | 1.14 | 12 |
| Al-1100 | 40 | 0 | 0.5 | 0.05 | 20 | 1.02 | 20 |
| Al-1100 | 41 | 0 | 1.50 | 0.05 | 5 | 2.17 | 5 |
| Al-1100 | 42 | 0 | 1.50 | 0.05 | 12 | 2.03 | 12 |
| Al-1100 | 43 | 0 | 1.50 | 0.05 | 20 | 2.42 | 20 |
| Al-1100 | 44 | 0 | 2.30 | 0.05 | 20 | 3.68 | 20 |
| Al-1100 | 45 | 80 | 0.5 | 0.05 | 12 | 3.94 | 2.08 |
| Al-1100 | 46 | 80 | 0.5 | 0.05 | 20 | 4.46 | 3.47 |
| Al-1100 | 47 | 80 | 1.50 | 0.05 | 5 | 5.08 | 0.87 |
| Al-1100 | 48 | 80 | 1.50 | 0.05 | 12 | 8.00 | 2.08 |
| Al-1100 | 49 | 80 | 1.50 | 0.05 | 20 | 6.98 | 3.47 |
| Al-1100 | 50 | 80 | 2.30 | 0.05 | 5 | 7.11 | 0.87 |
| Al-1100 | 51 | 80 | 2.30 | 0.05 | 12 | 3.94 | 2.08 |

Table A3.
Numerical simulations at α~90°; interrupted simulations are highlighted.
Table A3.
Numerical simulations at α~90°; interrupted simulations are highlighted.
| Material | α, ° | dp, mm | t, mm | w, mm | vp, km/s | A, mm |
|---|---|---|---|---|---|---|
| PEEK | 88 | 0.5 | 0.05 | 25.4 | 5 | 11.05 |
| PEEK | 88 | 0.5 | 0.05 | 25.4 | 12 | 13.72 |
| PEEK | 88 | 0.5 | 0.05 | 25.4 | 20 | 14.72 |
| PEEK | 88 | 1.5 | 0.05 | 25.4 | 5 | 23.51 |
| PEEK | 88 | 1.5 | 0.05 | 25.4 | 12 | 23.51 |
| PEEK | 88 | 1.5 | 0.05 | 25.4 | 20 | 23.51 |
| PEEK | 88 | 2.3 | 0.05 | 25.4 | 5 | 21.99 |
| PEEK | 90 | 0.5 | 0.05 | 25.4 | 5 | 2.03 |
| PEEK | 90 | 0.5 | 0.05 | 25.4 | 12 | 1.27 |
| PEEK | 90 | 0.5 | 0.05 | 25.4 | 20 | 1.52 |
| PEEK | 90 | 1.5 | 0.05 | 25.4 | 5 | 4.70 |
| PEEK | 90 | 1.5 | 0.05 | 25.4 | 12 | 3.81 |
| PEEK | 90 | 1.5 | 0.05 | 25.4 | 20 | 3.94 |
| PEEK | 90 | 2.3 | 0.05 | 25.4 | 5 | 5.33 |
| PEEK | 90 | 2.3 | 0.05 | 25.4 | 12 | 4.19 |
| PEEK | 90 | 2.3 | 0.05 | 25.4 | 20 | 3.17 |
| PEEK | 90 | 9 | 0.05 | 25.4 | 20 | 25.40 |
| PEEK | 90 | 9 | 0.05 | 25.4 | 5 | 25.40 |
| PEEK | 90 | 5 | 0.05 | 25.4 | 20 | 25.40 |
| PEEK | 90 | 5 | 0.05 | 25.4 | 5 | 25.40 |
| PEEK | 90 | 3 | 0.05 | 25.4 | 20 | 16.26 |
| PEEK | 90 | 3 | 0.05 | 25.4 | 5 | 11.18 |
| PEEK | 90 | 5 | 0.20 | 25.4 | 20 | 19.30 |
| PEEK | 90 | 5 | 0.20 | 25.4 | 5 | 21.34 |
| PEEK | 90 | 5 | 0.50 | 25.4 | 20 | 14.22 |
| PEEK | 90 | 5 | 0.50 | 25.4 | 5 | 14.22 |
| PEEK | 90 | 4 | 0.05 | 25.4 | 20 | 22.86 |
| PEEK | 90 | 4 | 0.05 | 25.4 | 5 | 25.40 |
| PEEK | 90 | 5 | 0.05 | 35.0 | 20 | 30.00 |
| PEEK | 90 | 5 | 0.05 | 35.0 | 5 | 33.00 |
| PEEK | 90 | 4 | 0.05 | 35.0 | 20 | 21.00 |
| PEEK | 90 | 4 | 0.05 | 35.0 | 5 | 25.29 |
| PEEK | 90 | 4 | 0.05 | 25.4 | 20 | 24.38 |
| PEEK | 90 | 4 | 0.05 | 25.4 | 5 | 23.00 |
| Al-1100 | 88 | 0.5 | 0.05 | 25.4 | 5 | 0.00 |
| Al-1100 | 88 | 0.5 | 0.05 | 25.4 | 12 | 0.00 |
| Al-1100 | 88 | 0.5 | 0.05 | 25.4 | 20 | 1.91 |
| Al-1100 | 88 | 1.5 | 0.05 | 25.4 | 5 | 23.38 |
| Al-1100 | 88 | 1.5 | 0.05 | 25.4 | 20 | 23.51 |
| Al-1100 | 88 | 2.3 | 0.05 | 25.4 | 5 | 21.60 |
| Al-1100 | 90 | 0.5 | 0.05 | 25.4 | 5 | 1.78 |
| Al-1100 | 90 | 0.5 | 0.05 | 25.4 | 12 | 1.40 |
| Al-1100 | 90 | 0.5 | 0.05 | 25.4 | 20 | 2.41 |
| Al-1100 | 90 | 1.5 | 0.05 | 25.4 | 5 | 3.56 |
| Al-1100 | 90 | 1.5 | 0.05 | 25.4 | 12 | 3.56 |
| Al-1100 | 90 | 1.5 | 0.05 | 25.4 | 20 | 3.56 |
| Al-1100 | 90 | 2.3 | 0.05 | 25.4 | 20 | 1.14 |
| Al-1100 | 90 | 15 | 0.05 | 25.4 | 20 | 25.40 |
| Al-1100 | 90 | 15 | 0.05 | 25.4 | 5 | 25.40 |
| Al-1100 | 90 | 10 | 0.05 | 25.4 | 20 | 25.40 |
| Al-1100 | 90 | 10 | 0.05 | 25.4 | 5 | 25.40 |
| Al-1100 | 90 | 9 | 0.05 | 25.4 | 20 | 15.24 |
| Al-1100 | 90 | 9 | 0.05 | 25.4 | 20 | 15.24 |
| Al-1100 | 90 | 9 | 0.05 | 25.4 | 5 | 25.40 |
| Al-1100 | 90 | 6 | 0.05 | 25.4 | 20 | 24.38 |
| Al-1100 | 90 | 6 | 0.05 | 25.4 | 5 | 25.40 |
| Al-1100 | 90 | 3 | 0.05 | 25.4 | 20 | 16.26 |
| Al-1100 | 90 | 3 | 0.05 | 25.4 | 5 | 12.19 |
| Al-1100 | 90 | 9 | 0.20 | 25.4 | 20 | 25.40 |
| Al-1100 | 90 | 9 | 0.20 | 25.4 | 5 | 17.27 |
| Al-1100 | 90 | 9 | 0.50 | 25.4 | 20 | 15.24 |
| Al-1100 | 90 | 9 | 0.50 | 25.4 | 5 | 15.24 |
| Al-1100 | 90 | 6 | 0.05 | 35.0 | 20 | 24.00 |
| Al-1100 | 90 | 6 | 0.05 | 35.0 | 5 | 24.50 |
References
- Cosmo, M.L.; Lorenzini, E.C. Tethers in Space Handbook; No. NASA/CR-97-206807; NASA: Washington, DC, USA, 1997.
- Dobrowolny, M.; Stone, N.H. A technical overview of TSS-1: The first tethered-satellite system mission. Il Nuovo Cimento C 1994, 17, 1–12. [Google Scholar] [CrossRef]
- Huang, P.; Zhang, F.; Chen, L.; Meng, Z.; Zhang, Y.; Liu, Z.; Hu, Y. A review of space tether in new applications. Nonlinear Dyn. 2018, 94, 1–19. [Google Scholar] [CrossRef]
- Benvenuto, R.; Salvi, S.; Lavagna, M. Dynamics analysis and GNC design of flexible systems for space debris active removal. Acta Astronaut. 2015, 110, 247–265. [Google Scholar] [CrossRef]
- Foust, R.C.; Nakka, Y.K.; Saxena, A.; Chung, S.J.; Hadaegh, F.Y. Automated Rendezvous and Docking Using Tethered Formation Flight. In Proceedings of the 9th International Workshop on Satellite Constellations and Formation Flying, Boulder, CO, USA, 19–21 June 2017. [Google Scholar]
- Mantellato, R.; Olivieri, L.; Lorenzini, E.C. Study of dynamical stability of tethered systems during space tug maneuvers. Acta Astronaut. 2017, 138, 559–569. [Google Scholar] [CrossRef]
- Aslanov, V.S.; Ledkov, A.S. Dynamics of Reusable Tether System with Sliding Bead Capsule for Deorbiting Small Payloads. J. Spacecr. Rocket. 2018, 55, 1519–1527. [Google Scholar] [CrossRef]
- Johnson, L.; Estes, R.; Lorenzini, E.; Martinez-Sanchez, M.; Sanmartin, J.; Vas, I. Electrodynamic tethers for spacecraft propulsion. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998; p. 983. [Google Scholar] [CrossRef]
- Sanmartín Losada, J.R.; Charro, M.; Lorenzini, E.C.; Colombatti, G.; Roussel, J.F.; Serrath, P.; Williams, J.D.; Xie, K.; García de Quirós, K.; Carrasco, J.A.; et al. BETs: Propellant less de orbiting of space debris by bare electrodynamic tethers. In Let’s Embrace Space; Publications Office of the European Union: Luxembourg, 2012; pp. 506–513. ISBN 978-92-79-22207-8. [Google Scholar]
- Colombo, C.; Rossi, A.; Dalla Vedova, F.; Francesconi, A.; Bombardelli, C.; Trisolini, M.; Gonzalo, J.L.; Di Lizia, P.; Giacomuzzo, C.; Khan, S.B.; et al. Effects of Passive De-Orbiting Through Drag and Solar Sails and Electrodynamic Tethers on the Space Debris Environment. In Proceedings of the 69th International Astronautical Congress, Bremen, Germany, 1–5 October 2018. [Google Scholar]
- Valmorbida, A.; Olivieri, L.; Brunello, A.; Sarego, G.; Sánchez-Arriaga, G.; Lorenzini, E.C. Validation of enabling technologies for deorbiting devices based on electrodynamic tethers. Acta Astronaut. 2022, 198, 707–719. [Google Scholar] [CrossRef]
- Castellani, L.T.; González, S.G.; Ortega, A.; Madrid, S.; Lorenzini, E.; Olivieri, L.; Sarego, G.; Brunello, A.; Valmorbida, A.; Tajmar, M.; et al. Deorbit kit demonstration mission. J. Space Saf. Eng. 2022, 9, 165–173. [Google Scholar] [CrossRef]
- Coffey, S.; Crippa, C.; Dutchover, G.; Brunner, M.D.; Sibert, Z.; Kindl, S.; Galysh, I.; Lon Enloe, C.; Carrol, J. TEPCE: A Tethered Electrodynamic Propulsion CubeSat Experiment; Naval Research Laboratory Report NRL/8230/FR--2022/1; U. S. Naval Research Laboratory: Washington, DC, USA, 2022. [Google Scholar]
- Nohmi, M.; Yamagiwa, Y.; Aoki, Y.; Yokota, S. STARS series satellite. Next Gener. CubeSats SmallSats 2023, 2023, 657–691. [Google Scholar] [CrossRef]
- Li, G.; Spence, L.; Miller, M.; Padya, M.; Stankey, N.; Hancock, A.; Lu, R.; Park, C.; Rajesh, A.; Beloiu, A.; et al. Lessons Learned from the Development and Flight of the First Miniature Tethered Electrodynamics Experiment (MiTEE-1). In Small Satellite Conference; 2021; Available online: https://digitalcommons.usu.edu/smallsat/2021/all2021/249/ (accessed on 24 July 2024).
- Sanchez-Arriaga, G.; del Pino, A.; Sharifi, G.; Tarabini Castellani, L.; García-Gonzaléz, S.; Ortega, A.; Cruces, D.; Velasco, A.; Orte, S.; Ruiz, A.; et al. The ET PACK-F Project: Towards a flight-ready deorbit device based on electrodynamic tether technology. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar] [CrossRef]
- Li, X.; Sun, G.; Xue, C. Fractional-order deployment control of space tethered satellite via adaptive super-twisting sliding mode. Aerosp. Sci. Technol. 2022, 121, 107390. [Google Scholar] [CrossRef]
- Zhu, Z.H.; Kang, J.; Bindra, U. Validation of CubeSat tether deployment system by ground and parabolic flight testing. Acta Astronaut. 2021, 185, 299–307. [Google Scholar] [CrossRef]
- Li, X.; Sun, G.; Kuang, Z.; Han, S. Nonlinear Predictive Optimization for Deploying Space Tethered Satellite via Discrete-Time Fractional-Order Sliding Mode. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4517–4526. [Google Scholar] [CrossRef]
- Kang, J.; Zhu, Z.H. Passivity-Based Model Predictive Control for Tethered Despin of Massive Space Objects by Small Space Tug. IEEE Trans. Aerosp. Electron. Syst. 2022, 59, 1239–1248. [Google Scholar] [CrossRef]
- Sarego, G.; Valmorbida, A.; Olivieri, L.; Brunello, A.; Colombatti, G.; Marco, S.; Lorenzini, E.C. Collision Avoidance Maneuvers for space tether systems. In Proceedings of the 3rd IAA Conference on Space Situational Awareness (ICSSA), Madrid, Spain, 4–6 April 2022. [Google Scholar]
- Anz-Meador, P.D. Tether-debris interactions in low Earth orbit. AIP Conf. Proc. 2001, 552, 525–531. [Google Scholar] [CrossRef]
- Pardini, C.; Hanada, T.; Krisko, P.H.; Anselmo, L.; Hirayama, H. Are de-orbiting missions possible using electrodynamic tethers? Task review from the space debris perspective. Acta Astronaut. 2007, 60, 916–929. [Google Scholar] [CrossRef]
- Pardini, C.; Hanada, T.; Krisko, P.H. Benefits and risks of using electrodynamic tethers to de-orbit spacecraft. Acta Astronaut. 2009, 64, 571–588. [Google Scholar] [CrossRef]
- Khan, S.B.; Sanmartin, J.R. Survival Probability of Round and Tape Tethers Against Debris Impact. J. Spacecr. Rocket. 2013, 50, 603–608. [Google Scholar] [CrossRef]
- Khan, S.B.; Sanmartin, J.R. Analysis of tape tether survival in LEO against orbital debris. Adv. Space Res. 2014, 53, 1370–1376. [Google Scholar] [CrossRef]
- Francesconi, A.; Giacomuzzo, C.; Branz, F.; Lorenzini, E.C. Survivability to hypervelocity impacts of electrodynamic tape tethers for deorbiting spacecraft in LEO. In Proceedings of the 6th European Conference on Space Debris, Darmstadt, Germany, 22–25 April 2013. [Google Scholar]
- Francesconi, A. A new Ballistic Limit Equation for thin tape tethers In Proceedings of the 66th International Astronautical Congress, Jerusalem, Israel, 12–16 October 2015.
- Schonberg, W.P. Concise history of ballistic limit equations for multi-wall spacecraft shielding. REACH 2016, 1, 46–54. [Google Scholar] [CrossRef]
- Abbas, H.; Alsayed, S.H.; Almusallam, T.H.; Al-Salloum, Y.A. Characterization of hole-diameter in thin metallic plates perforated by spherical projectiles using genetic algorithms. Arch. Appl. Mech. 2011, 81, 907–924. [Google Scholar] [CrossRef]
- Hill, S.A. Determination of an empirical model for the prediction of penetration hole diameter in thin plates from hypervelocity impact. Int. J. Impact Eng. 2004, 30, 303–321. [Google Scholar] [CrossRef]
- Turpin, W.C.; Carson, J.M. Hole Growth in Thin Plates Perforated by Hypervelocity Pellets. AFML-TR-70–83. 1970. Available online: https://apps.dtic.mil/sti/tr/pdf/AD0712071.pdf (accessed on 24 July 2024).
- Herrmann, W.; Jones, A.H. Survey of Hypervelocity Impact Information; ASRL Report No. 99-1; Massachusetts Institute of Technology: Cambridge, MA, USA, 1961. [Google Scholar]
- Tipton, J. HULL hydrocode analysis results presented at NASA/MSFC WP01 Meteoroid/Orbital Debris Working Group. In NASA Purchase Order; USACOE: Huntsville, AL, USA, 1991; (1991–1993). [Google Scholar]
- Schonberg, W.P.; Bean, A.J.; Darzi, K. Hypervelocity Impact Physics; NASA CR-4343; NASA: Washington, DC, USA, 1991.
- Sorenson, N.R. Systematic investigation of crater formations in metals. In Proceedings of the 7th Hypervelocity Impact Symposium, Tampa, FL, USA, 17–19 November 1964; Volume 6, pp. 281–325. [Google Scholar]
- Piekutowski, A.J. Formation and Description of Debris Clouds Produced by Hypervelocity Impact; NASA CR-4707; NASA: Washington, DC, USA, 1996.
- Schonberg, W.P.; Evans, H.J.; Williamsen, J.E.; Boyer, R.L.; Nakayama, G.S. Uncertainty considerations for Ballistic Limit Equations. In Proceedings of the 4th European Conference on Space Debris, ESOC, ESA SP-587, Darmstadt, Germany, 18–20 April 2005. [Google Scholar]
- Piekutowski, A.J.; Poormon, K.L. Holes Formed in Thin Aluminum Sheets by Spheres with Impact Velocities Ranging from 2 to 10 Km/S. Procedia Eng. 2015, 103, 482–489. [Google Scholar] [CrossRef][Green Version]
- Angrilli, F.; Pavarin, D.; De Cecco, M.; Francesconi, A. Impact facility based upon high frequency two-stage light-gas gun. Acta Astronaut. 2003, 53, 185–189. [Google Scholar] [CrossRef]
- Pavarin, D.; Francesconi, A. Improvement of the CISAS high-shot-frequency light-gas gun. Int. J. Impact Eng. 2004, 29, 549–562. [Google Scholar] [CrossRef]
- Francesconi, A.; Pavarin, D.; Bettella, A.; Angrilli, F. A special design condition to increase the performance of two-stage light-gas guns. Int. J. Impact Eng. 2008, 35, 1510–1515. [Google Scholar] [CrossRef]
- Kline, S.J.; McClintock, F.A. Describing Uncertainties in Single-Sample Experiments. Mech. Eng. 1953, 75, 3–8. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).