Theoretical Investigation of Laser Ablation Propulsion Using Micro-Scale Fluid in Atmosphere

Abstract

Laser ablation propulsion based on liquid propellants is a type of propulsion technology with a high specific impulse and good controllability that can be applied to space thrusters, gas metal arc welding, and extreme ultraviolet light. However, its basic mechanisms, such as flow evolution and thrust formation, have not yet been described in detail. In this study, the laser ablation of micro-scale fluid in the atmosphere was investigated. Flow evolution with different laser energy and fluid mass was observed using a schlieren system. According to the characteristic of flow evolution, a theoretical model of laser ablation propulsion in the atmosphere was established. For the first time, a theoretical hypothesis was proposed that the laser energy is divided into two parts, which act on fluid and air respectively. The model indicates that the impulses generated by fluids and air follow power laws with the laser energy, while the exponentials are 0.5 and 1, respectively. In the atmosphere, due to the shielding effect of a laser-maintained detonation wave on laser, the energy absorbed by the fluid is basically unchanged, while only the energy absorbed by the air changes. Significantly, the theoretical model is consistent with the impulse experiment and current studies.

1. Introduction

When a high-power laser irradiates a substance, a part of the substance will vaporize and even ionize, generating a high specific impulse. This is the concept of laser ablation propulsion proposed by Kantrowitz [1]. Due to the advantages of high energy density and excellent flexibility for supply and storage, liquid propellant has become an ideal choice for laser ablation propulsion technology [2,3], and can be applied in water surface [4], ground [5], air [6] and space [7]. The propulsion effect of laser ablation on droplets can also be applied to gas metal arc welding [8], extreme ultraviolet light [9,10], etc. However, the basic theoretical mechanisms, such as flow evolution and thrust formation, still need to be systematically and meticulously studied.

The laser ablation of a liquid is a typical unsteady process with an extremely uneven distribution in time and space. Generally, the evolution process of laser ablation propulsion is qualitatively described by high-speed photography. The influencing factors include laser energy, liquid viscosity, absorption coefficient, surface curvature, etc. [9,10,11,12,13]. The typical temporal resolution of current studies ranges from 0.1 to 1 μs, and the typical spatial resolution ranges from 2 to 16 μm [9,10,12]. Laser ablation propulsion based on liquid propellants usually occurs as a result of vapor expansion after absorbing laser energy [9,10], or this is combined with the influence of a shock wave [14]. Propulsion performance is generally characterized by impulse or velocity, which is usually expressed as a power function of laser energy. One view is that the velocity of the vapor is constant. When the laser energy rises, the mass of the vapor increases, which leads to the rise of the impulse [9,10,15]. Another view is based on energy conversion, which maintains that the energy of the laser is absorbed by the liquid and converted into the kinetic energy of the vapor. The mass of the vapor is obtained using the Beer–Lambert law or is assumed to be constant. Increasing the laser energy mainly enhances the velocity of the vapor, which leads to the rise of the impulse [13,16]. In general, the understanding of the thrust formation process in laser ablation propulsion is not developed, and the quantitative analysis of flow field and impulse is insufficient. In addition, when the experiment is carried out in the atmosphere, the influence of air is not considered.

In this study, the laser ablation of a micro-scale fluid in the atmosphere was investigated, where the micro-scale refers to the range from 0.1 mm to 1 mm, considering propulsion performance and experimental feasibility. A schlieren system with a temporal resolution of 10 ns and spatial resolution of 1.7 μm was built to observe plume evolution and shock wave propagation. It was proposed that the evolution of the plume and the propagation of the shock wave could be independent of each other according to the schlieren results. Based on this assumption, the impulses generated by the fluid and air were analyzed. The relationships between the impulse and the liquid mass, as well as the laser energy, were studied using a torsion pendulum, which verified the rationality of the theoretical analysis. This article provides a new theoretical perspective for laser ablation propulsion in the atmosphere. Compared with the previous studies, the theoretical model has a certain applicability, which could provide a theoretical reference for the performance improvement of laser ablation propulsion with micro-scale liquid and micro-droplet motion control in the atmosphere.

2. Materials and Methods

2.1. Preparation of Mirco-Scale Fluid Target

The micro-scale fluid was created by placing the fluid in a micro-pit. An aluminum sheet of 25 × 25 × 1.5 mm was chosen as the substance, with the micro-pit array processed on the surface. The diameter of the micro-pit is 0.3 mm, and the depth of the micro-pit is also 0.3 mm. The fluids used in the experiment were ADN aqueous solutions doped with infrared dye, whose absorption coefficients ranged from 14.8 to 43.0 mm⁻¹ when changing the concentrations of the infrared dye. The fluid was injected in the cylindrical micro-pit array using the Inkjet nozzle supply system. The mass of the fluid supplied by the nozzle is calibrated by an electronic balance with an accuracy of 10 μg (ME55, METTLER TOLEDO, Greifensee, Switzerland). Actually, the mass of the fluid was regarded as 1/10 of the total increased mass after injecting the fluid onto a filter paper 10 times. The total mass measured by the balance changed by only 10 μgin multiple tests, which indicated an uncertainty of 1 μg of the fluid mass. The photos of the micro-pit array chip are shown in Figure 1.

2.2. Method of Schlieren System

As an intuitive and non-invasive optical flow diagnosis technology, schlieren technology has significant advantages in high-speed and micro-scale flow field observation. Figure 2 shows the schematic diagram of the experimental setup. The neodymium/yttrium–aluminum–garnet (Nd:YAG) laser (Dawa-200, Beamtech, Beijing, China) provided a pulse at the wavelength of 1064 nm with a duration of about 5.6 ns full width at half maximum (FWHM). The laser was divided into two beams through a spectroscope with the ratio of 95/5. The minor part entered an energy meter (J-50MB-YAG-1561, Coherent, Saxonburg, PA, USA), which was used to monitor the energy of the laser, with the energy range from 50 μJ to 100 mJ and the noise equivalent energy of 50 μJ. The main part was focused by a convex lens (L4) with f = 50 mm and irradiated to the surface of the target. The position of the convex lens L4 was adjusted to make sure the diameter of the ablation spot was 0.3 mm. The micro-pit array chip was fixed on an electrical stage (MTS50/M-Z8, Thorlabs, Newton, NJ, USA), and the position of the chip was adjusted by the stage with the observation of an industrial camera, so that the laser ablation spot coincided with the surface of the micro-pit.

In the schlieren system, a continuous laser beam with a wavelength of 520 nm and maximum power of 480 mW was supplied. The beam was collimated and expanded by adjusting the positions of the convex lenses L1 and L2. The parallel light passes through the flow field and the convex lens L3. The knife edge was placed at the focus of L3 and blocks part of the optical path. By adjusting the position of the four-frame camera (SF4), the image formed by the flow field through L3 was located on the image plane of SF4, which was the schlieren image of the flow field. There was a filter (the central wavelength is 520 nm, and the bandwidth is 10 nm, OD5) between the flow field and L3, which was used to filter out the light emitted by the plasma. The exposure time of the camera was set to 8 ns, and the time interval of the four channels was set from 10 to 100 ns. The pixel resolution calibrated by a test target (R1L3S6P, Thorlabs) was 1.69 μm per pixel. The Nd:YAG laser and SF4 were triggered by a digital delay generator (DG645, Stanford Research Systems, Sunnyvale, CA, USA). By controlling the timing of DG645 and framing camera, the ablation plume and shock wave at different times can be obtained.

2.3. Measurement of Impulse

The impulse was measured by a torsion pendulum system. The schematic diagram of the experimental setup is shown in Figure 3. The experimental setup was placed in a hood made of acrylic to isolate the disturbance of indoor air. The pulsed laser used to ablate the fluid was the same as that described in Section 2.2. The laser was divided into two beams through a splitter with the ratio of 1.15/1. The minor part entered the energy detector to monitor the energy of the laser. The main part was focused by a convex lens with f = 75 mm, and irradiated to the surface of the target. The position of the convex lens was adjusted so that the diameter of the ablation spot was 0.3 mm. The liquid target used in the impulse experiment was also the same as the schlieren experiment. The micro-pit array chip was fixed on the torsion pendulum, and the torsion pendulum was fixed on stage-1, which can move vertically. The position of the torsion pendulum was adjusted using stage-1, combined with an observation of industrial camera, so that the laser was irradiated in the micro-pit. When the pulsed laser ablated the fluid in the micro-pit, the expansion plume and shock wave exerted an impulse on the torsion pendulum, resulting in a damped simple harmonic motion around the pivot. The vibration curve of the torsion pendulum can be measured by the laser displacement sensor with an accuracy of 1 μm and an output frequency of 10 kHz (PNBC001, Wenglor, Tettnang, Germany), and the corresponding impulse can be obtained by analyzing the vibration curve. After recording the curve, the damping rod was moved to the balance position of the torsion pendulum using stage-2, and the amplitude was rapidly attenuated to about 1 μm due to a collision. The next micro-pit was moved to the laser spot position using stage-1, and the damping rod was withdrawn to start the next experiment.

The impulse generated by laser ablation can be obtained using the following formula [17,18]:

$$I={\displaystyle \frac{AJ{\omega }_{\mathrm{n}}}{L_{\mathrm{T}}{L}_{\mathrm{M}}}}{e}^{{\displaystyle \frac{\xi }{\sqrt{1-{\xi }^2}}}\left({\displaystyle \frac{\pi }{2}}-\arctan {\displaystyle \frac{\xi }{\sqrt{1-{\xi }^2}}}\right)}=k_{\mathrm{impulse}}A$$

(1)

where A is the maximum amplitude of the simple harmonic motion, J is the moment of inertia of the torsion pendulum relative to the pivot, ω_n is the inherent resonant frequency, L_T is the distance between the laser ablation position and the rotation axis, L_M is the distance between the measurement position and the rotation axis, ξ is the damping ratio. Using the vibration curve to obtain A, other variables can be calibrated in advance, and then the impulse generated by laser ablation can be calculated.

In this study, L_T is 0.138 m and L_M is 0.136 m, measured by a millimeter scale, and ω_n is 4.396 rad/s. J is 5.23 × 10⁻⁴ kg·m², ξ is less than 0.001, the exponential expression is approximately 1. Then, the k_impulse is 0.123 kg/s. Considering that the accuracy of the laser displacement sensor is 1 μm, the accuracy of the impulse measurement system is 0.123 μN·s. The noise amplitude caused by environmental disturbance is 1~3 μm.

3. Results and Discussion

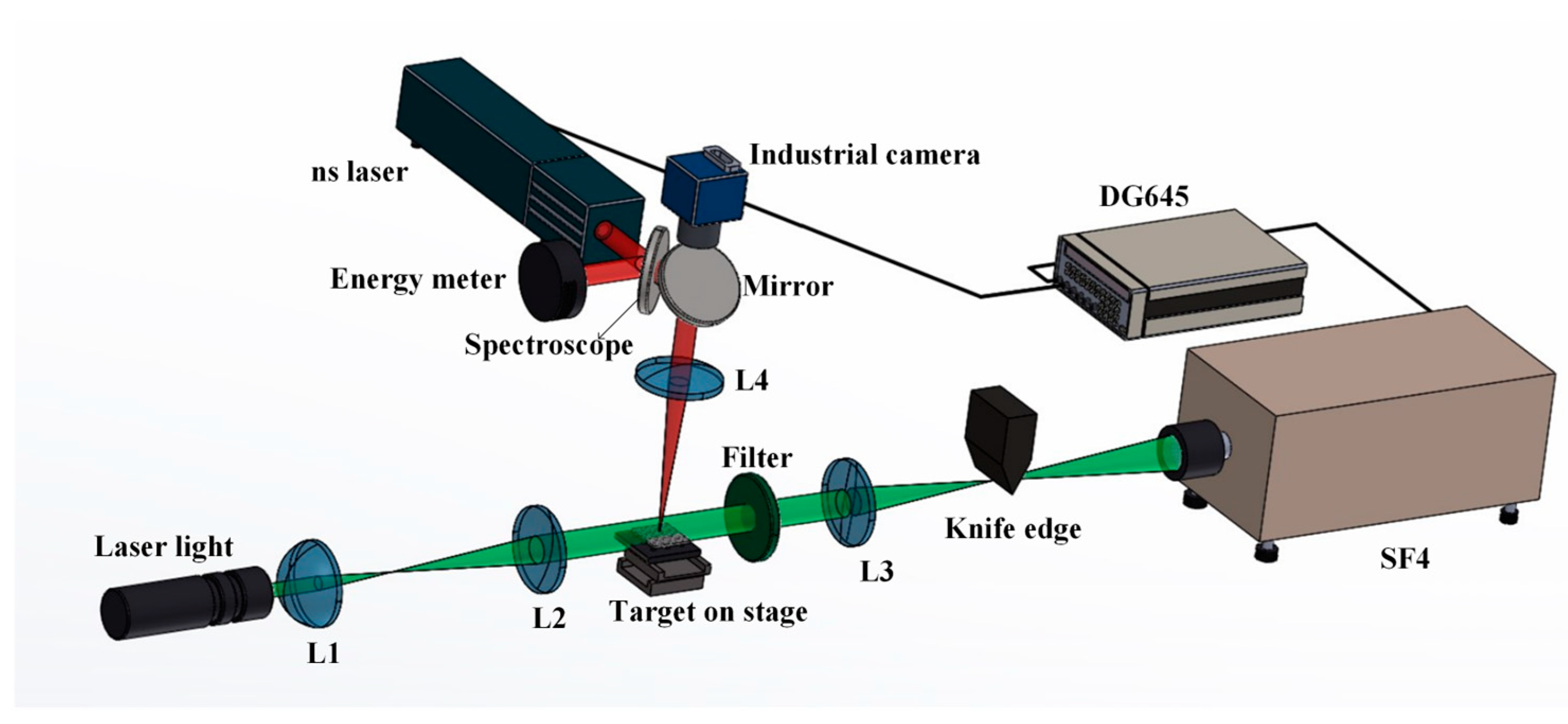
3.1. Flow Evolution and Shock Wave Propagation

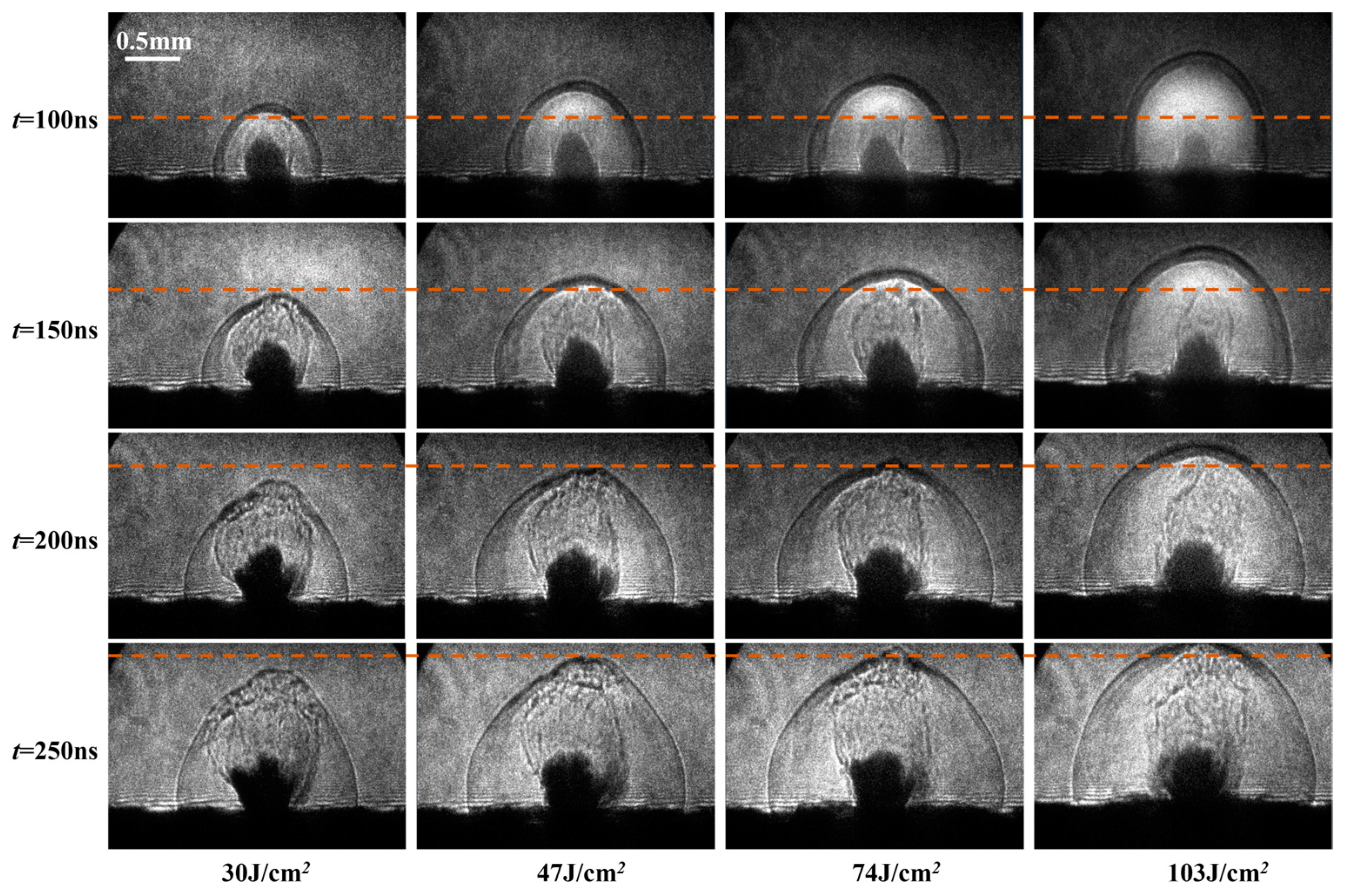
In general, the energy of the laser is the most significant factor affecting the performance of laser ablation propulsion. Therefore, the flow fields of different laser energies should be observed and discussed. Figure 4 shows the schlieren images generated by the ablation of ADN solution with different laser energy densities. The absorption coefficient of the fluid is 43.0 mm⁻¹, and the mass is 9 μg. The moment when the plasma appears is defined as 0 ns, and the four rows are the results of 100–250 ns in turn, with a frame interval of 50 ns. As shown in Figure 4, the flow field generated by laser ablation can be classified into two parts: a strong shock wave propagating in the air and a plume containing vapor and liquid jet. When the laser fluence ranged from 30 to 103 J/cm², it was observed that the propagation distance of the shock wave increased at the same time, which means its energy also increased. However, the evolution of plume and displacement of the vapor front were basically unchanged (when Φ = 30 J/cm², because the plume needs to overcome the resistance of the ambient gas, its front position was relatively backward). Therefore, it is assumed that during laser ablation, only fixed energy E_w acts on the fluid, while E_L − E_w acts on the ambient gas and generates a laser-maintained detonation wave (LSDW). E_L refers to the total energy of the laser, E_w does not change with E_L.

The distribution of laser intensity versus time is assumed to be a Gaussian distribution. When the laser irradiates the target, the laser intensity is weak at first, and the surface of the fluid absorbs laser energy and evaporates, forming vapor with a high temperature and high pressure. With the increase in laser intensity and the deposition of laser energy over time, the surface of the fluid is ionized to form plasma, which expands and produces a shock wave. The shock wave heats and ionizes the ambient gas; then, the plasma behind the shock wave forms a shielding effect on the laser, and the subsequent laser energy is absorbed and developed into a LSDW [19]. The LSDW propagates along the direction against the laser optical path until the laser ends. Due to the shielding effect of the plasma on the laser energy, the fluid can only absorb the early energy of the pulse laser, and the subsequent energy is mainly used for the evolution of LSDW. Therefore, the energy applied to the fluid under a different laser energy is basically unchanged.

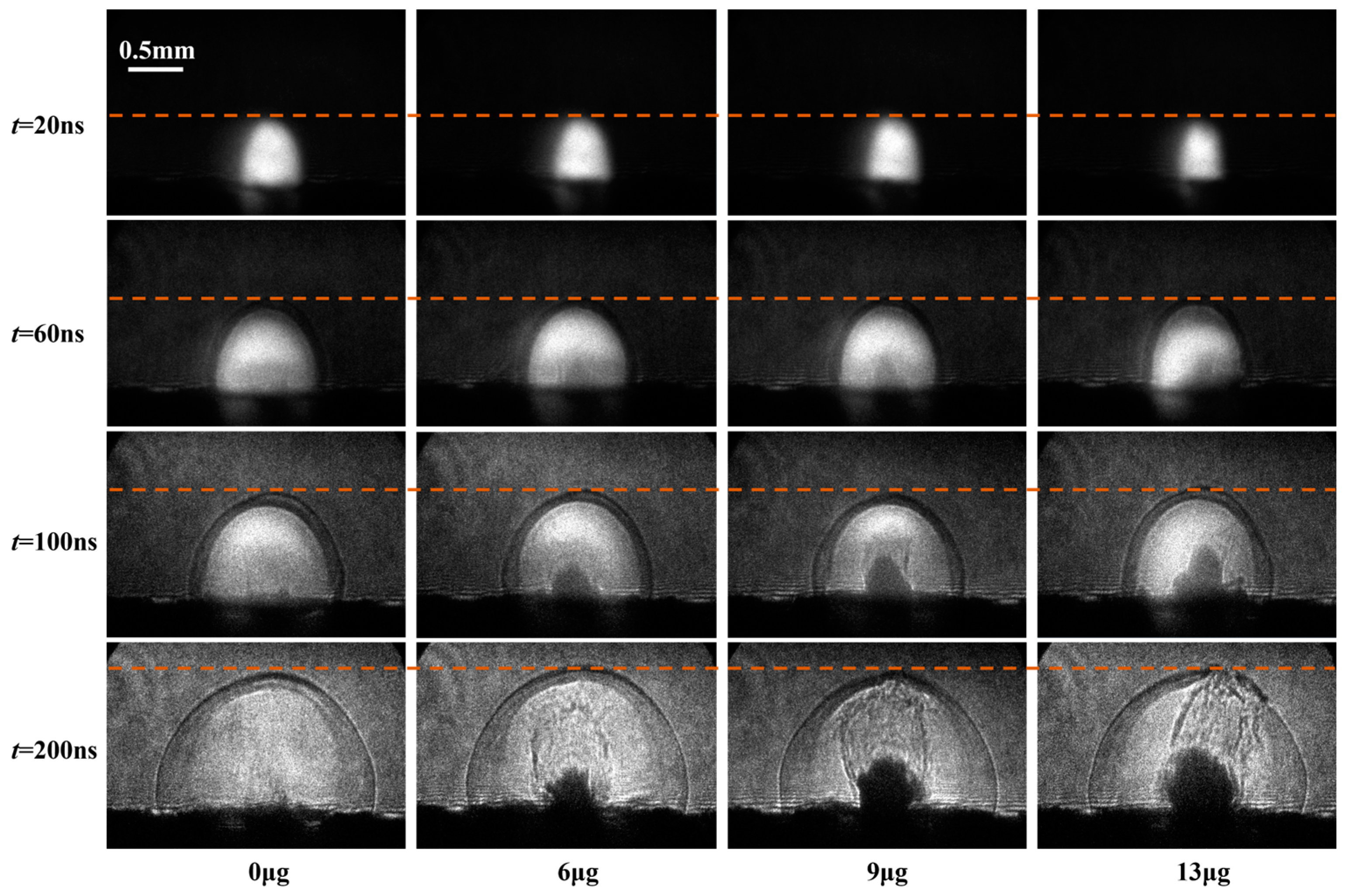
Figure 5 shows the schlieren images of different fluid masses when the laser fluence is 74 J/cm², and the ADN solution massed of 0, 6, 9, and 13 μg are shown from left to right. It was found that for different fluid mass, the evolution process of the shock wave front with time is basically unchanged. It is inferred that in the evolution process of LSDW, when the laser parameters are unchanged, whether the target is metal substrate or liquid of different mass, LSDW is generated during a fixed time. In addition, the evolution of LSDW is also not affected by the state of the plume after the wave. When the laser pulse ends, the evolution process of the shock wave in the air is still independent of the state of the plume behind.

From Figure 5, it can also be seen that in the early stage of flow evolution, the distance between the shock wave and the explosion center is much larger than that of the plume front. With the propagation of the shock wave in the air, its velocity decreases rapidly, while the velocity of the plume decreases slightly. Therefore, the front of the plume gradually catches up with the shock wave, and then the propagation of the vertical shock wave is affected by the plume. Under the above conditions, the conclusion is that the shock wave propagation that is unaffected by the plume is no longer valid, while the propagation of the horizontal shock wave front also remains unaffected.

3.2. Modeling and Theoretical Analysis

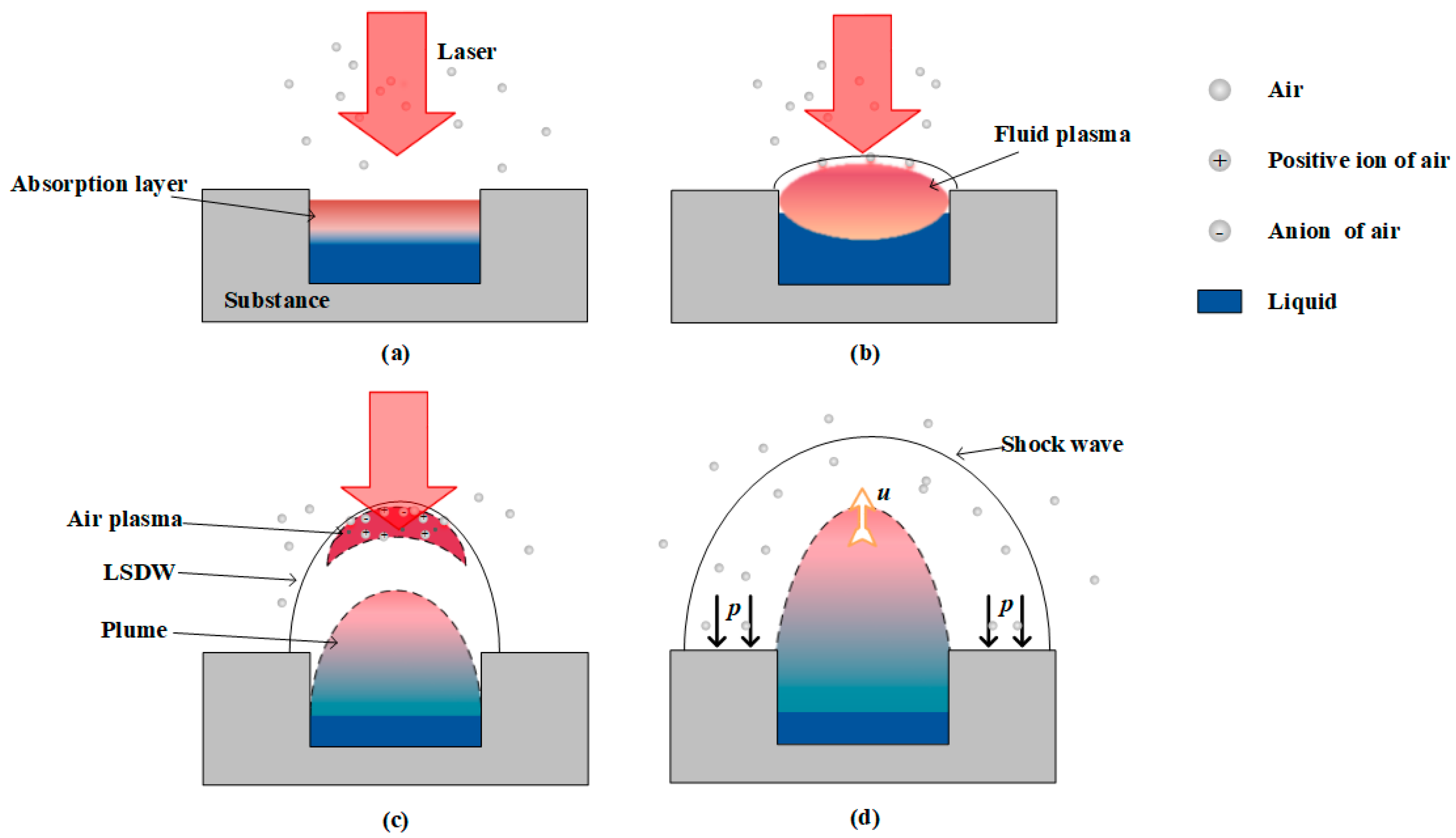
Based on the above results, the model for the process of laser ablation propulsion based on a micro-scale fluid in the atmosphere was established: at the initial moment of the pulsed laser, the surface of the liquid absorbs laser energy following the Beer–Lambert law, as shown in Figure 6a; with the deposition of laser energy, the temperature of the surface fluid increases, along with the evaporation and ionization of the fluid. The high temperature and pressure plasma expands and generates shock wave, and the ambient gas behind the shock wave is heated, as shown in Figure 6b. Due to the shielding effect of the plasma, the subsequent laser energy is absorbed by the post-wave plasma to generate LSDW. The plasma generated by LSDW is far from the explosion center due to its faster velocity, while the plume is much closer, as shown in Figure 6c; after the laser pulse, due to the relatively long distance between the shock wave and the plume, the expansion process of the vapor and the propagation process of the shock wave are independent of each other, as shown in Figure 6d. Only when the front of the plume catches up with the shock wave will the two interact. In short, the evolutions of the plume and the shock wave are independent of each other, and the impulses generated by the two are also independent of each other.

The impulse generated by the vapor is analyzed from the perspective of energy conversion. When the laser irradiates the liquid, the energy of the laser is converted into the thermal energy of the vapor. In the process of vapor expansion, the thermal energy of the vapor is converted into kinetic energy. Since the fluid contains fuel, this process is also accompanied by the release of chemical energy. With the decrease in the temperature and pressure of the plume, the interaction between the plume and the substrate is gradually weakened until negligible, and this is regarded as the end of the laser ablation propulsion process.

When describing the absorption effect of the material on the laser, the Beer–Lambert law is usually used, which is as follows [19]:

$$I(x)=\sigma I_0{e}^{-\alpha x}$$

(2)

where I(x) is the laser intensity at the depth x from the surface, I₀ is the incident laser intensity, σ is the reflectivity of the dielectric surface, and α is the absorption coefficient of the fluid.

Assuming that the fluid begins to be ionized at time t_i, the laser pulse with a total energy of E_L is divided into two parts. The part of the fixed energy E_w acts on the fluid, and the part of the E_L − E_w acts on the ambient gas to generate LSDW. The subscript w represents the working medium, the diameter of the laser spot is D, and the breakdown threshold of the fluid is Φ_th (Φ_th is the incident laser fluence, without considering σ). Equation (2) shows that when the depth x conforms to Equation (3), the fluid at depth x is just ionized [20], as denoted by x_w.

$$\{\begin{array}{l}\sigma {\mathrm{\Phi }}_{\mathrm{th}}=\sigma {\mathrm{\Phi }}_{\mathrm{w}}{e}^{-\alpha x_{\mathrm{w}}}\\ {\displaystyle \frac{\pi }{4}}{D}^2{\mathrm{\Phi }}_{\mathrm{w}}=E_{\mathrm{w}}\end{array}\Rightarrow x_{\mathrm{w}}={\displaystyle \frac{1}{\alpha }}\ln \left({\displaystyle \frac{{\mathrm{\Phi }}_{\mathrm{w}}}{{\mathrm{\Phi }}_{\mathrm{th}}}}\right),0<x_{\mathrm{w}}\le H$$

(3)

In order to make full use of laser energy, we assume that the fluid is a cylinder with diameter D and depth H, and the ionization mass of the fluid is

$$m_{\mathrm{w}}={\displaystyle \frac{\pi }{4}}{D}^2{x}_{\mathrm{w}}{\rho }_{\mathrm{w}}$$

(4)

where ρ_w is the density of working fluid.

Assume that the relative molecular mass and heat capacity ratio of the vapor are constant. The energy absorbed by the fluid with mass of m_w includes laser energy and chemical energy. Part of the energy is used for fluid evaporation, and part of it for the heating of the vapor. The remaining energy can be expressed as

$$W=E_{\mathrm{w}}+m_{\mathrm{w}}\left({E^{\prime }}_{\mathrm{C}}-{\displaystyle \frac{R}{\left(\kappa -1\right){\mu }_{\mathrm{M}}}}\Delta T-Q_v\right)$$

(5)

where E_C′ is the chemical energy released by the unit mass of the fluid, κ is the heat capacity ratio of the vapor, μ_M is the relative molecular mass of the vapor, R is the molar gas constant, ΔT is the increment of vapor temperature, and Q_v is the latent heat of the evaporation of the fluid. Cao Jinle’s studies provided some parameters of ADN solutions for reference, where the combustion heat is 6264.1 J/g, the specific heat capacity of ADN solution is 2.487 J/(g·K), the boiling point is 124 °C, Q_v is 181 J/g [21]. As can be seen from Figure 3 and Figure 4, the mass of vapor was much less than that of fluid, so the second term of Equation (5) was much less than E_w, W ≈ E_w.

Because the process of laser ablation propulsion is very fast, the heat exchange between fluid and environment could be ignored. Assuming that the substance is rigid and ignoring the energy propagated by the fluid to the substrate, then W is equal to the sum of the kinetic energy of vapor and liquid jets. Suppose η₁W is assigned to the kinetic energy of the vapor (1 − η₁), W is assigned to the kinetic energy of liquid jet. Assuming that the velocity distribution in the vapor and liquid jet is uniform, the impulse generated by the vapor and liquid jet can be expressed as

$$I_{\mathrm{w}}=\sqrt{2{\eta }_{1}W{m}_{\mathrm{w}}}+\sqrt{2\left(1-{\eta }_1\right)W\left(m-m_{\mathrm{w}}\right)}\approx \sqrt{2\left(1-{\eta }_1\right)Wm}$$

(6)

where m is the total mass of the fluid. The approximate equals sign is valid only when η₁(m_w + m) << m. For the target without chemical energy, assuming that ΔT = 0, η₁ = 1, and m_wQ_v = Φ_thS (S represents the area of the laser spot), Equation (6) can be written as

$$I_{\mathrm{w}}=\sqrt{2m_{\mathrm{w}}\left({\mathrm{\Phi }}_{\mathrm{w}}-{\mathrm{\Phi }}_{\mathrm{th}}\right)S}$$

(7)

Then, the laser impulse coupling coefficient C_m is

$$C_{\mathrm{m}}=\sqrt{{\displaystyle \frac{2{\rho }_{\mathrm{w}}{x}_{\mathrm{w}}\left({\mathrm{\Phi }}_{\mathrm{w}}-{\mathrm{\Phi }}_{\mathrm{th}}\right)}{{\mathrm{\Phi }}_{\mathrm{w}}^2}}}$$

(8)

Equation (8) is consistent with the vapor regime theory presented by Sinko and Phipps [22].

In the atmospheric environment of this study, LSDW will greatly hinder the absorption of laser energy by the fluid and vapor, which causes m_w and E_w to remain basically unchanged when increasing the laser fluence, and the corresponding impulse is also basically unchanged. If the LSDW is not strong enough to absorb all the laser energy, then m_w and E_w increase with the increase in laser energy, and the corresponding impulse also increases. While increasing the total mass of the fluid, the corresponding impulse would also increase.

Since the evolution process of the shock wave is independent of the plume, the impulse generated by the air can be analyzed according to the Taylor–Sedov model. As mentioned above, while only ambient gas is considered, the total energy of the flow field behind the shock wave is E_L − E_w. Assuming that the substrate is a rigid frictionless interface, the flow field can be regarded as a spherical explosion flow with a total energy of 2(E_L − E_w). The position of the shock wave can be expressed as [23,24]

$$\begin{array}{l}{r}_{\mathrm{H}}={\xi }_0{\left({\displaystyle \frac{2E_{\mathrm{L}}-2E_{\mathrm{w}}}{{\rho }_{\mathrm{g}}}}\right)}^{0.2}{t}^{0.4}\\ {\xi }_0={\left[{\displaystyle \frac{75\left(\kappa -1\right){\left(\kappa +1\right)}^2}{16\pi \left(3\kappa -1\right)}}\right]}^{0.2}\end{array}$$

(9)

The center of the laser spot on the substrate plane is set as the explosion center, r_H is the distance between the shock wave front and the explosion center, ρ_g is the density of air, κ is the heat capacity ratio of air. The state parameters of the flow field can be calculated using the point explosion model. In the range from the explosion center to r_H, the pressure remains basically $\overline{p}$ in a wide range and rapidly increases to p_H when it is close to r_H. The simplified treatment assumes that the pressure behind the shock wave is uniformly $\overline{p}$. When κ = 9/7 and, for a spherical shock wave, $\overline{p}$ ≈ 0.39 p_H [25], the magnitude of p_H can be obtained from the shock wave velocity according to the strong shock wave relationship, so the thrust at time t can be approximately expressed as:

$$F\left(t\right)\approx 0.39\pi r_{\mathrm{H}}^2{p}_{\mathrm{H}}\approx {\displaystyle \frac{0.217\pi }{\kappa +1}}{\rho }_{\mathrm{g}}^{0.2}{\xi }_0^4{\left(E_{\mathrm{L}}-E_{\mathrm{w}}\right)}^{0.8}{t}^{-0.4}$$

(10)

When the p_H drops below 1 MPa, the shock wave no longer has self-similar characteristics because the internal energy of the air involved in the shock wave cannot be ignored. This moment is expressed as t_E, and the p_H at this point is expressed as p_th. The impulse provided during the evolution of the shock wave can be calculated by integration:

$$\{\begin{array}{l}{I}_{\mathrm{g}}={\displaystyle \frac{0.362\pi }{\kappa +1}}{\xi }_0^4{\rho }_{\mathrm{g}}^{0.2}{\left(E_{\mathrm{L}}-E_{\mathrm{w}}\right)}^{0.8}{t}_{\mathrm{E}}^{0.6}\\ t_{\mathrm{E}}={\left({\displaystyle \frac{\left(\kappa +1\right)p_{\mathrm{th}}}{0.422{\xi }_0^2{\rho }_{\mathrm{g}}^{0.6}{\left(E_{\mathrm{L}}-E_{\mathrm{w}}\right)}^{0.4}}}\right)}^{-{\displaystyle \frac{5}{6}}}\end{array}$$

(11)

The expression of t_E is substituted into the first formula; thus, I ∝ (E_L − E_w).

The impulse generated by the vapor and the ambient gas can be regarded as perpendicular to the plane, and the total impulse can be directly obtained by the sum of the two. Ignoring the chemical energy and latent heat of vapor, the total impulse is as follows:

$$I=I_{\mathrm{w}}+I_{\mathrm{g}}\approx \sqrt{2\left(1-{\eta }_1\right)E_{\mathrm{W}}m}+{\displaystyle \frac{0.167\left(E_{\mathrm{L}}-E_{\mathrm{w}}\right)}{\sqrt{p_{\mathrm{th}}/{\rho }_{\mathrm{g}}}}}$$

(12)

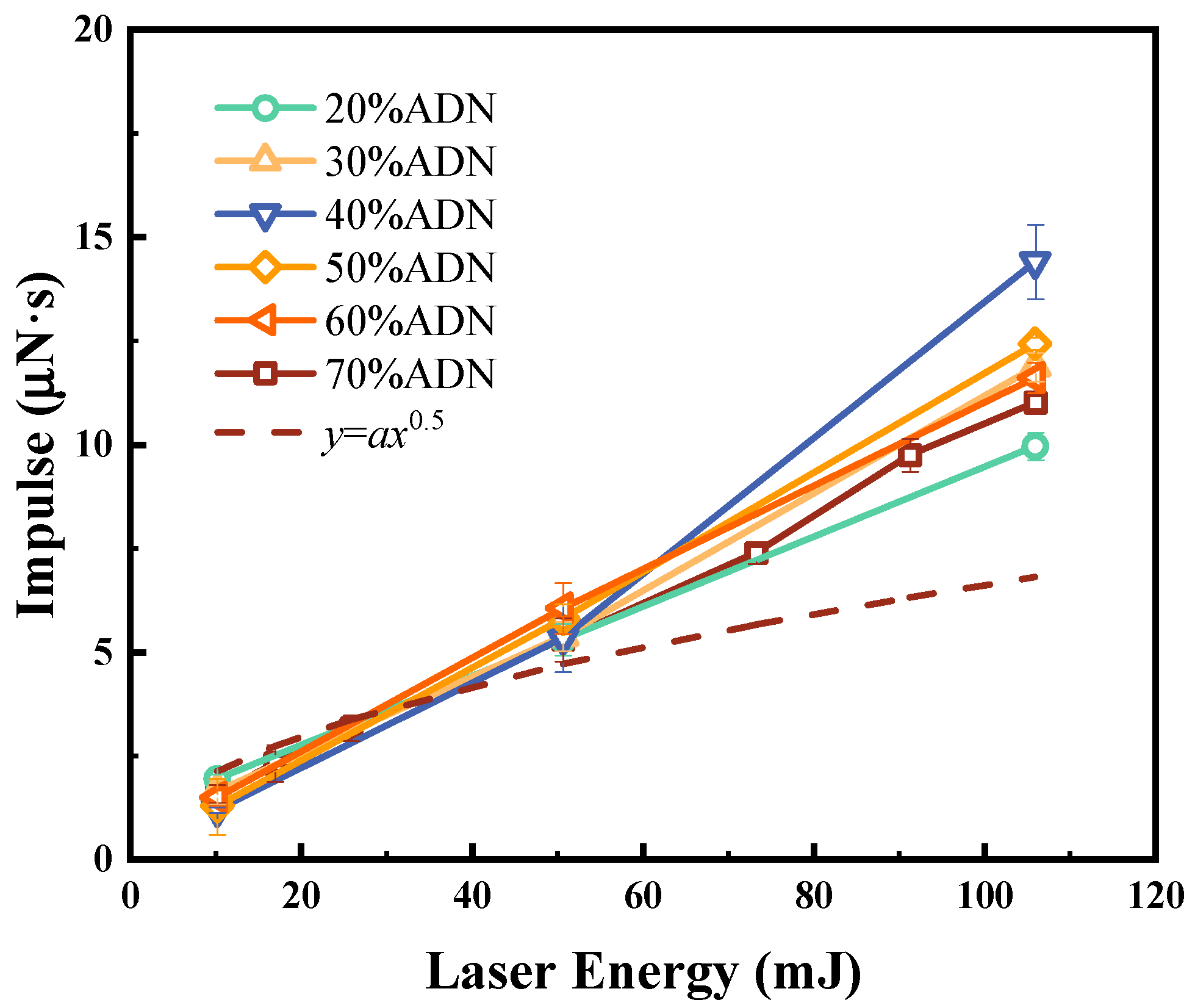
Equation (12) is valid only if the laser energy is sufficient to break down the liquid. When the fluid mass and the laser energy change, E_w is basically unchanged, and m_w is only related to the parameters of the fluid. From the schlieren results, when the total mass m of the fluid increases, m_w increases accordingly. Therefore, the parameter E_L′ = E_L/m is proposed. When E_L′ is small, the impulse generated by the expansion of the vapor is dominant. When E_L′ is large, the impulse generated by shock wave propagation is dominant, and the impulse increases linearly with the increase in laser energy.

3.3. Verification of the Model from Current Research on Impulses

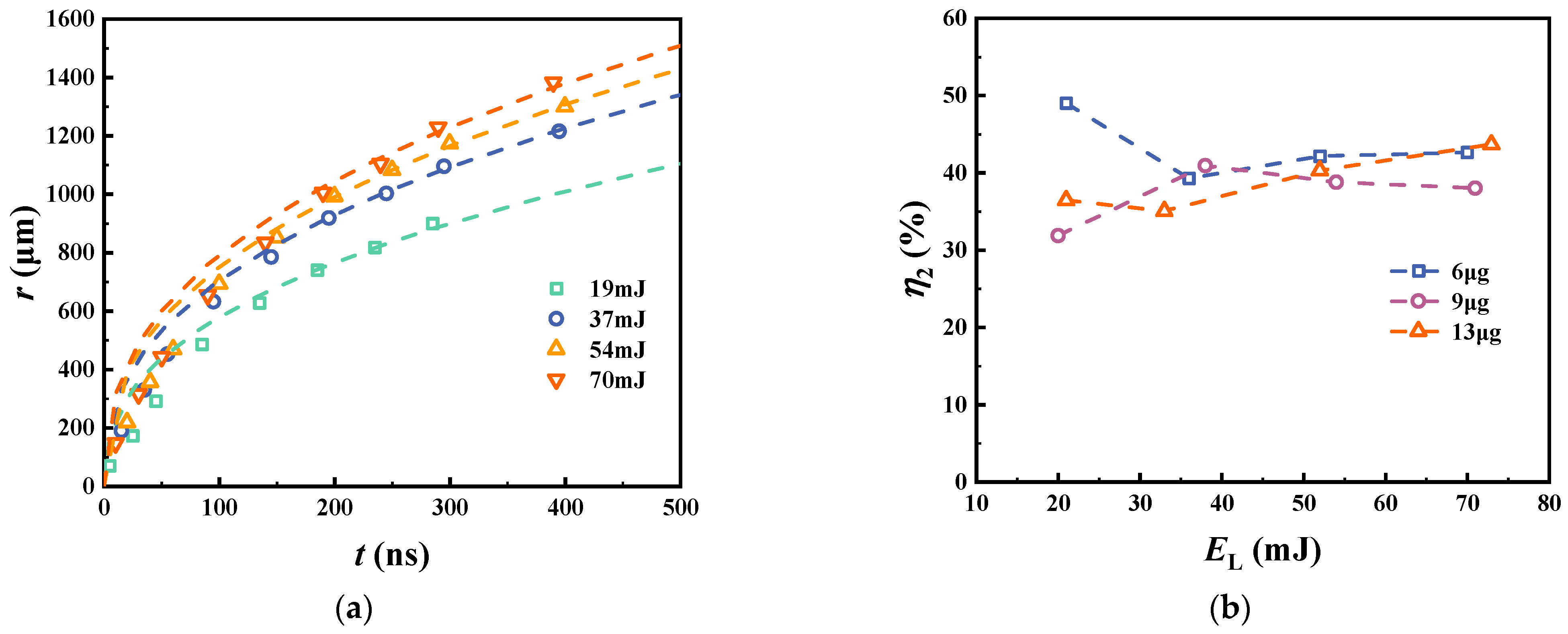
According to the schlieren images, the radial propagations of the shock waves are shown in Figure 7a. The absorption coefficient of the fluid is 43.0 mm⁻¹, and the mass is 9 μg. The energy shown in Figure 7a refers to the total energy of the laser pulse, which corresponds to the fluence shown in Figure 4. The dashed line is the fitting curve with the formula of r = at^0.4. Based on Equation (9), the energy of the shock wave could be calculated from the fitting coefficient a, expressed as E_S. The results show that E_S is much less than E_L, which means there is a missing factor η₂ for converting plasma energy into shock wave energy in Equation (9). Assuming that E_w is 3 mJ (explained in Figure 8), then η₂ = E_S/(E_L − E_w). Figure 7b shows the curves of η₂ with respect to E_L at different fluid mass, which indicate that η₂ seems to be a constant. When the energy of the laser is above 20 mJ, the average value of η₂ is 40.0%, and the standard deviation of η₂ is 2.7%. In fact, the η₂ of 40% is the total result of the conversion of laser energy into plasma energy and plasma energy into shock wave energy, probably caused by the scattering of laser, shock wave in the substance, deviation of the initial process from the Taylor–Sedov model, etc. In Equations (9)–(12), E_L − E_w should be replaced with η₂(E_L − E_w).

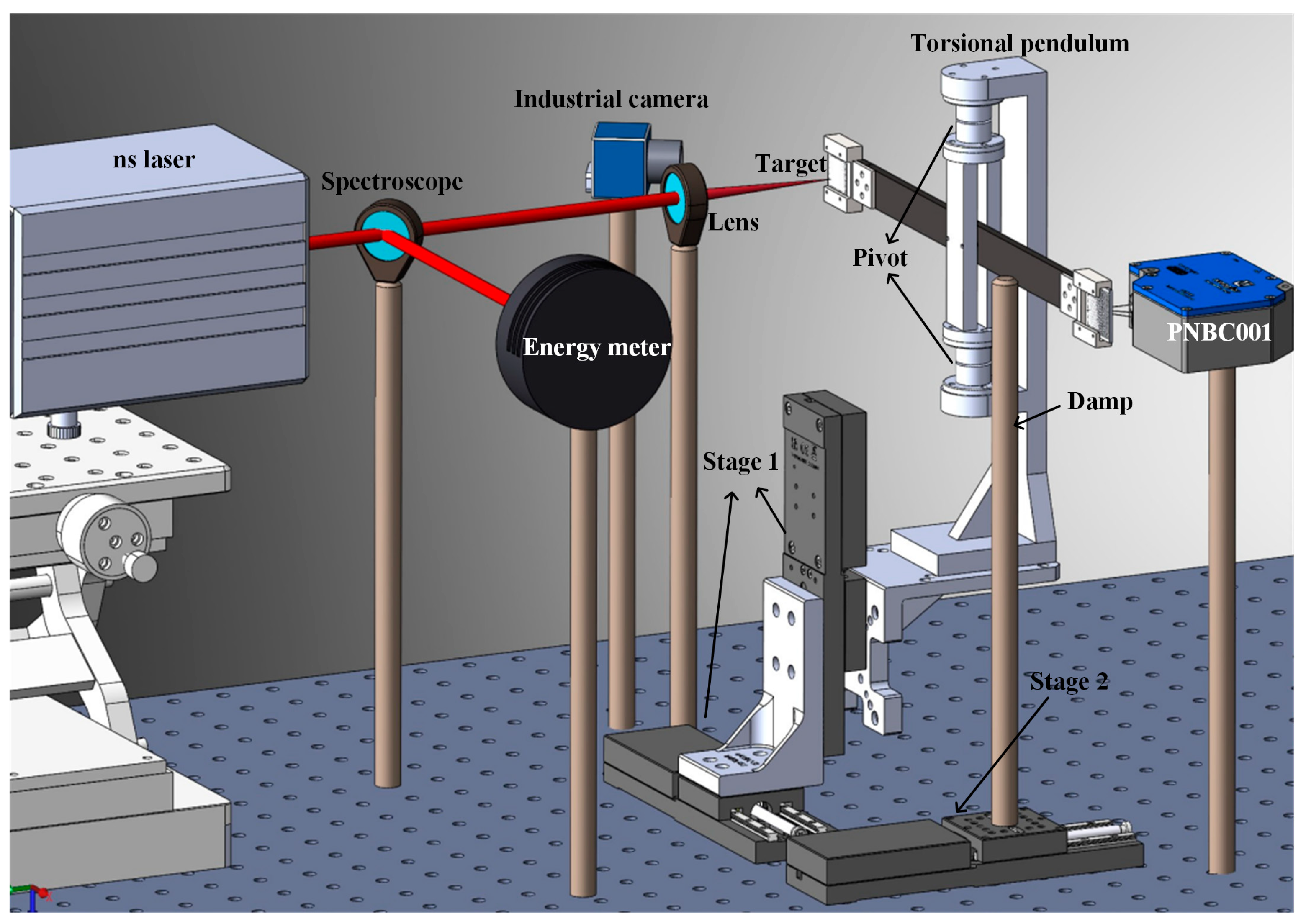
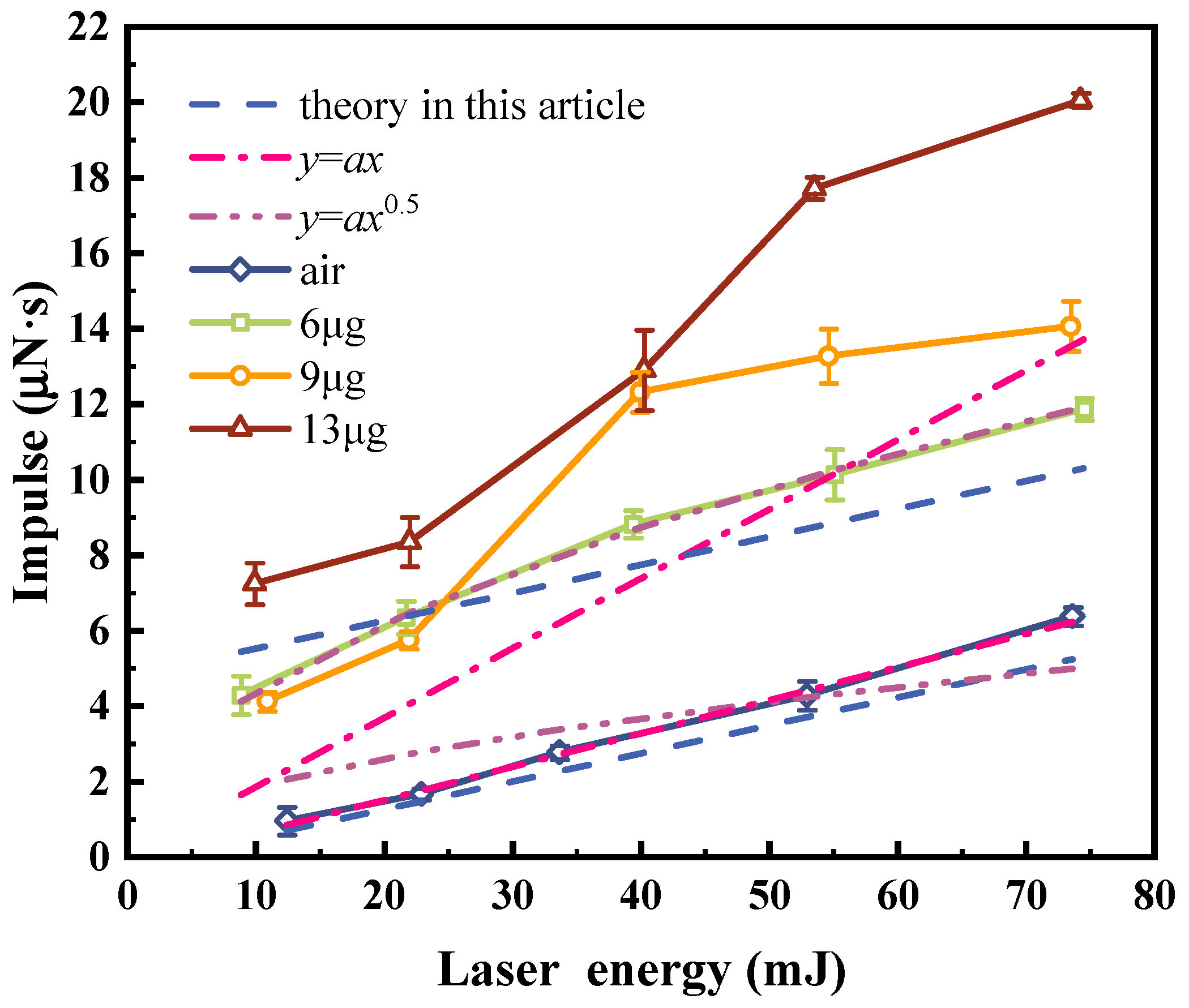
A torsion pendulum system was built to compare the impulse under different liquid masses and different laser energies. The impulse experiment used the same parameters as the schlieren experiment described in Section 3.1. The results are shown in Figure 8, in which the curves of impulse increased with laser energy is given when 0 μg (air), 6 μg, 9 μg, and 13 μg of fluid were supplied into the micro-pit, respectively. In the case of the air, the laser energy varied from 12.4 to 73.7 mJ, and the corresponding impulse varied from 0.95 to 6.37 μN·s, which shows a basic linear increase. It was observed that there was a positive intercept on the x-axis of the curve. After linear fitting, the intercept was about 3.0 mJ, indicating that when the laser directly irradiates the substrate, there is still a part of the energy that does not participate in the evolution of LSDW, and this can be explained as the early ionization of the substrate. Then, the E_w above was set to be 3 mJ. The calculated results are shown as dashed lines, which are in good agreement with the experimental results. Figure 8 also carries out linear fitting and square root fitting for the experimental results, which are plotted by dot dash lines and double dot dash lines. The linear fitting agrees well with the experimental results when the fluid mass is 0, but differs greatly from the experimental results when the fluid mass is 6 μg. The square root fitting agrees well with the experimental results when the fluid mass is 6 μg, but differs greatly from the experimental results when the fluid mass is 0. The linear increase in the impulse in laser ablation for metal targets was reported in previous studies [14,26].

For the case of the involved fluid, the range of laser energies was 8.9 to 74.5 mJ. The impulse ranged from 4.3 to 11.9 μN·s when the mass of the fluid was 6 μg. The impulse increased linearly with the laser energy, and the slope was basically the same as that when the laser directly irradiated the substrate. There was an extra fixed value on the impulse, which was the impulse generated by the vapor. When the masses of the fluids were 9 μg and 13 μg, the impulse increased with the laser energy, but there was a significant increase after the laser energy reached 40 mJ, along with significant damage to the micro-pit. This is probably because some of the substrate was damaged and ejected, providing an additional impulse. On the whole, the curves of the impulse versus laser energy under different conditions were approximately linear, and the slopes were basically the same. When the mass of the fluid increased, the curve of the impulse with the laser energy was basically shifted upward by a fixed value, which was consistent with the theoretical analysis.

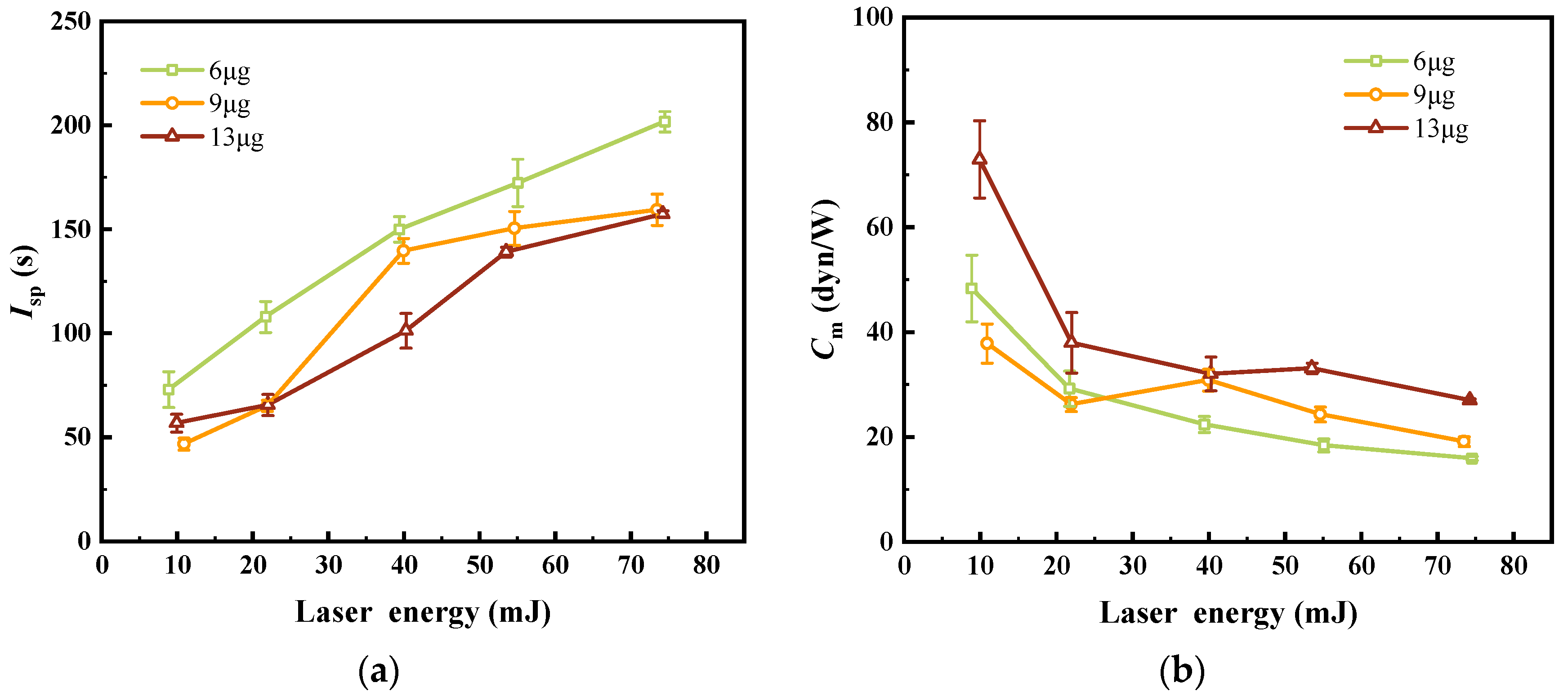
Figure 9 shows the specific impulse I_sp and the impulse coupling coefficient C_m of laser ablation propulsion versus laser energy, which are significant parameters for evaluating performance in laser ablation propulsion [27]. The I_sp and C_m are calculated from the impulse in Figure 8 according to Equation (13), where the m is the mass of the fluid, g is the acceleration of gravity and is approximate to 9.8 m/s². The highest I_sp is 202 s at 74.5 mJ, 6 μg. The highest C_m is 72.9 dyn/W at 9.9 mJ, 13 μg. When the laser energy is increased, the I_sp increases and the C_m decreases. When the fluid mass increases, the I_sp decreases and the C_m increases.

$$\{\begin{array}{l}{I}_{\mathrm{sp}}={\displaystyle \frac{I}{mg}}\\ C_{\mathrm{m}}={\displaystyle \frac{I}{E_{\mathrm{L}}}}\end{array}$$

(13)

Table 1. The slope, intercept, and correlation coefficient of the linear fitting, using I = k_LE_L + b as the formula.

α (mm−1)	m (μg)	kL (s/km)	b (μN·s)	r2adj
-	0	0.089	−0.262	0.996
43.0	6	0.114	3.730	0.973
	9 *	0.071	3.849	0.977
	13 *	0.108	6.071	0.999
26.7	6	0.081	4.220	0.952
	9	0.089	4.724	0.971
	13	0.075	6.317	0.854
14.8	6	0.080	3.506	0.995
	9	0.093	4.047	0.935
	13	0.108	4.316	0.965

* The conditions of abnormal impulse rise.

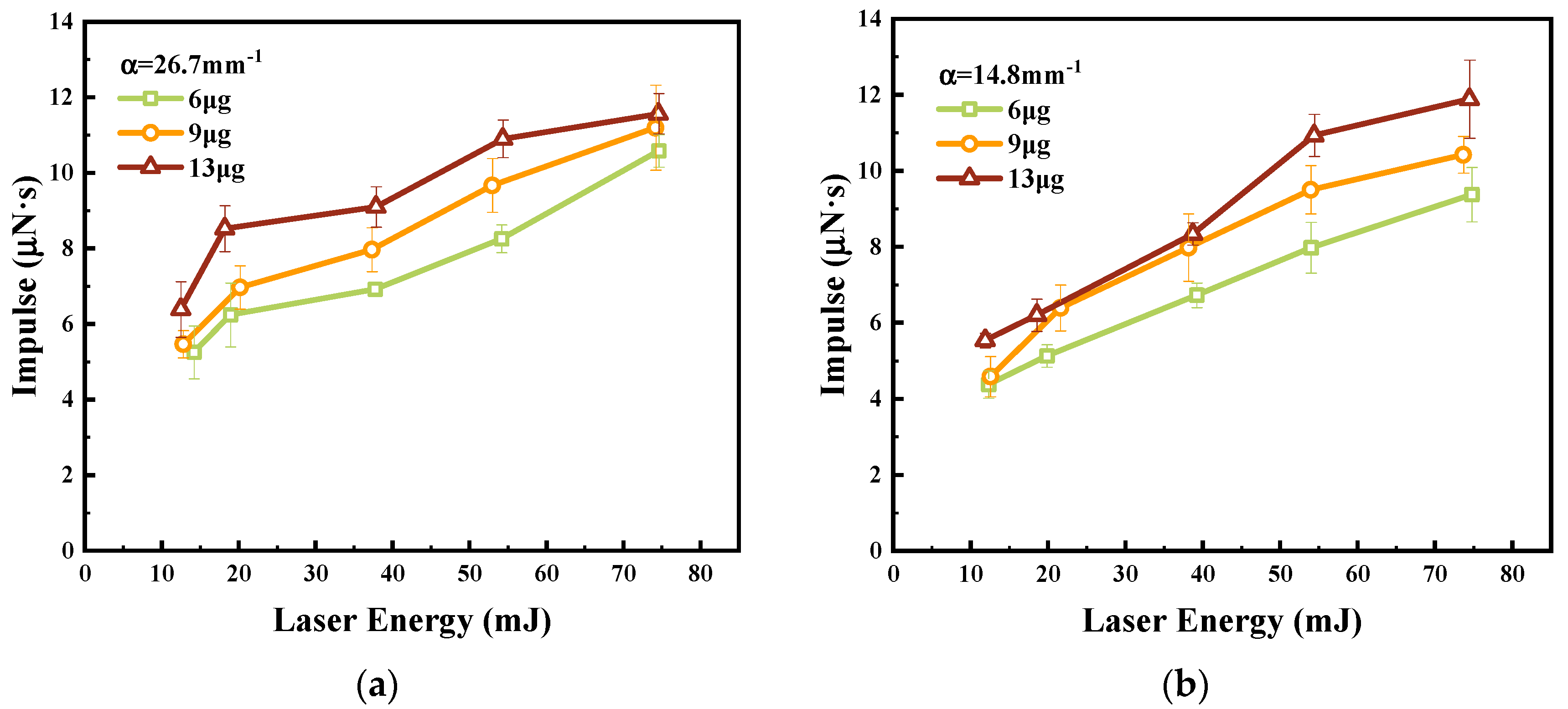
is the linear fitting of the impulse versus laser energy, which contains the slope, intercept, and correlation coefficient. The fitting formula used was I = k_LE_L + b, where I is the impulse, and E_L is the energy of laser. The changed experimental conditions include the absorption coefficient and the mass of fluid. The impulses when α = 26.7 mm⁻¹ or 14.8 mm⁻¹ are shown in Figure A1. In the case of an abnormal large impulse, the abnormal value was uniformly subtracted by a constant I₀, which led to the maximum r² after fitting. As can be seen from Table 1, when the laser directly ablated the substrate, the fitting slope was 0.089. When the fluids with different absorption coefficients and masses were supplied into the micro-pit, the fitting slopes ranged from 0.071 to 0.114, basically around 0.089. Furthermore, the fitting slopes were closer to 0.089 with a lower absorption coefficient and mass. Figure A2 shows the impulses versus laser energy when the fluid mass was 1.4 μg, which also reveals good linearities with similar slopes. The results were in line with expectations, because when the liquid mass was reduced to 0, the laser directly ablated the substrate. For the intercepts of the fitting lines, the intercept increased with the increase in liquid mass. For example, when the liquid mass increased from 6 μg to 13 μg with a liquid absorption coefficient of 43 mm⁻¹, the intercept increased from 3.730 μN·s to 6.071 μN·s, an increase of 63%. Table 1 also shows that the absorption coefficient of the liquid had an effect on the impulse generated by the plume (manifested as the intercept), which requires further study.

Table 2. Comparison of the studies of laser ablation propulsion based on liquid fuel.

Researcher	Environment	Fitting Formula
Sinko [13]	CO2 laser, atmosphere	$I_{\mathrm{sp}}=k\sqrt{I_{\mathrm{E}}}$
Nakano [28]	YAG laser, vacuum	$I_{\mathrm{sp}}\propto E^{0.4552}{D}^{-1.9104}$
Kurilovich [10]	YAG laser, vacuum	$U=35{\left(E_{\mathrm{OD}}-0.05\right)}^{0.59}$
Klein [9]	YAG laser, atmosphere	$U\sim {\displaystyle \frac{u}{\rho R_0^3\Delta H}}\left(E-E_{\mathrm{th}}\right)$
This study	YAG laser, atmosphere	$I=\sqrt{2\left(1-{\eta }_1\right)E_{\mathrm{W}}m}+{\displaystyle \frac{0.167\left(E_{\mathrm{L}}-E_{\mathrm{w}}\right)}{\sqrt{p_{\mathrm{th}}/{\rho }_{\mathrm{g}}}}}$

lists the experimental fitting formulas of the impulse (or specific impulse, velocity) versus laser energy (or intensity) in current investigations. All the studies use liquid as the propellant. Sinko used water, alcohol, and a hexane liquid film on POM as the target, and the thin films were ablated using a TEA CO₂ laser [13]. The experimental results show that the specific impulse is proportional to the square root of laser intensity, which may be due to the low laser intensity and the small absorption coefficients of alcohol and hexane. Under the above conditions, LSDW may not be produced. Both Nakano and Kurilovich placed their experimental setup in a vacuum chamber [10,28], where there was no air and no shock wave, and the impulse generated by the vapor is dominant. In the fitting formulas of Nakano and Kurilovich, the exponentials of laser energy are 0.4552 and 0.59, respectively, close to 0.5. Klein used a Nd:YAG laser to ablate dyed water droplets with the diameter of about 0.9 mm in the atmosphere, and the droplet velocity was proportional to the laser energy in the fitting formula. Klein claimed that the droplet was not broken down but there was a shock wave. Klein explained the experimental results as the mass of vapor m~E − E_th, and the velocity of vapor u ≈ 400 m/s [9]. The theoretical analysis of this article gives another explanation, that is, the impulse generated by the air is proportional to the laser energy, which makes U ∝ (E − E_th). Interestingly, E_th = 3 mJ in Klein’s study, which is the same value as the intercept obtained in this study when the laser directly ablates the substrate. Sinko’s theory predicts that the impulse will be proportional to the square of the laser energy, which corresponds to the square root fitting in Figure 8. Klein’s theory predicts that the impulse will be proportional to the laser energy, which corresponds to the linear fitting in Figure 8. Although the two theories agree better with the experimental results in some conditions, they differ from the experimental results in other cases, which may be due to the particularity of the experimental conditions in this article.

When the mass of the fluid is much larger than 10 μg, the effect of the vapor and air on the fluid cannot be ignored, and the impulse generated by the fluid cannot be considered a constant. Moreover, the substance and the laser intensity may affect the generation of the initial plasma, as shown in Figure 6b, which would influence the evolution of LSDW and the shock wave, as well as the impulse generated by the air. Therefore, the modeling and theoretical analysis in this article is limited to the case of micro-scale fluid and strong LSDW in the atmosphere.

In future research, experiments in vacuum are well worth carrying out to analyze the impulse generated by the fluid, but the explosive evaporation of the fluid should be determined in advance. Another problem is that a quantitative analysis of vapor and liquid jets is absent from this study, and thus requires further research. Factors for converting plasma energy into shock wave energy, such as η₂ and E_w, which act on the fluid, were fully obtained using an experimental fitting, the theoretical explanations and influencing factors of which should be investigated.

4. Conclusions

In this study, laser ablation propulsion based on a micro-scale fluid in the atmosphere was investigated. Based on schlieren images, it was found that the laser energy has little effect on the plume, and the fluid mass has little effect on the shock wave. A corresponding model was established according to the characteristics of the schlieren results, which describe the laser ablation process in terms of time. At the early stage of the laser pulse, the energy was absorbed by the fluid, causing its evaporation and ionization. With the deposition of the laser energy, the laser-maintained detonation wave immediately arose. Due to the shielding effect of the LSDW on the laser, the remaining energy was absorbed by LSDW. In flow evolution, the expansion of vapor and the propagation of shock wave were independent of each other.

The model in this study indicates that the impulses generated by the fluid and air are independent. The impulse generated by the fluid is proportional to the square of the absorbed energy, and the impulse generated by the air is proportional to the absorbed energy. This conclusion is verified by a torsion pendulum system. As the laser energy increases, the impulse increases approximately linearly. For different mass and absorption coefficients of the fluid (include m = 0), the fitting slopes are approximately constant. This work has certain applicability in the atmosphere compared with the current studies, and the analysis of the impulse generated by the fluid is still reasonable in a vacuum. The model in this study can be used to improve the performance of laser ablation propulsion based on a micro-scale fluid.